卡尔曼滤波与维纳滤波在运动模糊图像恢复中的应用
电子监控的常见模糊图像处理应用分析

电子监控的常见模糊图像处理应用分析发表时间:2018-04-16T14:36:18.267Z 来源:《防护工程》2017年第35期作者:高若云1 张月娟2 [导读] 随着信息网络技术的不断发展,在各行各业都开始广泛运用电子监控。
监控系统的效果受到了电子监控图像质量好与坏的影响。
江苏泰州 225300 摘要:监控录像是依据法律法规,借助电视摄录像、音频传输设备、视频传输设备等来观察、获取相关的图像信息以及声音信息,掌握监视相关人员活动的一项技术。
近几年来,监控录像技术得到了普及,在银行、超市、工厂等公共场所都会安装摄像头和监控录像系统。
监控录像在保障和监督公共安全的同时,也会存储大量犯罪分子作案的信息和痕迹,为警方侦查破案提供有用线索和证据。
随着高新技术的快速发展,图像监控系统的监控功能越来越齐全。
在“科技强警”战略中,图像监控系统是非常重要的组成部分,由于其具有全方位、全天候的功能,这就能够促使公安机关的快速反应能力得以提高,并且还会防止一些违法犯罪,维护了社会的安定。
在侦查犯罪、防控犯罪中,图像监控系统发挥着举足轻重的作用。
关键词:电子监控;常见模糊图像;处理;应用分析1模糊图像处理概述模糊图像处理是图像处理领域非常重要的一个内容,通过模糊图像处理可以让图像中模糊现象、噪声等消失,从而让图像的质量得到强化,最终让模糊图像恢复原本的样子。
一般我们主要通过以下途径来进行图像处理:首先确定图像模糊的类型,然后对其退化的原因以及原理等等进行分析,换言之,利用数学建模来描述图像的整个退化过程,以此来确定其数学模型,在此基础上,结合该模型来反方向进行推导,以此来确定恢复该图像的主要因素。
由此可以看出,还原模糊图像的核心是要确定准确的退化模型,也即:掌握图像退化先验知识精确度的实际程度。
我们可以对模糊图像恢复过程进行划分,具体包括以下几个步骤:分析图像出现模糊退化现象的原因,以退化过程为依据进行数学建模以及展开逆向推导思考,从而确保图像能够被精确恢复。
频域复原算法

频域复原算法
频域复原算法是一种用于信号处理和图像处理的技术,它通过对信号或图像进行频域分析和处理,以恢复原始信号或图像。
常见的频域复原算法包括:
- 维纳滤波:维纳滤波是一种经典的频域复原算法,它通过在频域中估计信号的功率谱密度,并根据估计值对信号进行滤波,以恢复原始信号。
维纳滤波在图像处理中常用于去噪和恢复图像的细节。
- 最小二乘法:最小二乘法是一种基于模型的频域复原算法,它通过最小化误差函数来估计信号的参数,以恢复原始信号。
最小二乘法在图像处理中常用于图像去模糊和恢复图像的细节。
- 卡尔曼滤波:卡尔曼滤波是一种递归的频域复原算法,它通过对信号的状态进行估计和更新,以恢复原始信号。
卡尔曼滤波在图像处理中常用于图像去模糊和恢复图像的细节。
这些频域复原算法都有各自的优缺点和适用范围,需要根据具体的应用场景和需求选择合适的算法。
维纳滤波图像恢复的理论分析与实现

式中, 为 M N× M维 的矩阵 ,_ 以写作 由 N n r 个
N× N子矩 阵组 成 的形式 :
Ⅳ一 。函数I Y 和h ,) l 厂 ( ) , ( Y 分别是周期为 和 Ⅳ
收 稿 日期 :20 -31 0 60 — 8
基 金 项 目 :国 家 自然 科 学 基 金 资助 项 目 (0 30 0 6 15 2 )
一
零 延拓 ,以避免 卷积 周期 的交叠 。
数字 像一般有两种常用表示法 : 矩阵法和链 码法 本文研究的数字图像是以矩阵或数组的方式 存储的。如果 以列 向量 Ig n分 别 表示 厂 , ,
g ,)和 n ,),如式 ( ) 所示 。 ( Y ( Y 3 I 00 厂 ,) (
F g 1 I g e e e a e Mo e i. ma e D g n r t d l
小 的恢 复方法 。
g ) J( L 一 ) ( 一OY 卢 , ): J h ,
~
- , d( / 卢) 】 1 l B+凡 X y ( ,)
பைடு நூலகம்M l
Hl H :
I M 一10 厂 ( ,) I M 一1 1 厂 ( ,)
g M 一1 0 ( ,) g M 一1 1 ( ,) g M 一1N 一1 ( , )
I 一1N 一1 厂 ( , )
n 0 0 (,) n 0, ) ( 1
…n 0, 一1 ( N )
到的退化图像 , ( Y n ,)为噪声模型。 根据图 1 所示 图像退化框 图,退化模型可以表
g =
1 图像 的退化模型与图像 的矩 阵表示 I= / ‘
在实际应用中,通常都假定传输系统是线性系 统 ,原始图像. ,) 厂 Y 通过系统 h ,)。 ( Y 是 ( ( Y h ,) 综合所有退化因素得到的系统函数,称为成像系统
维纳、卡尔曼滤波简介及MATLAB实现

现代数字信号处理课程作业维纳、卡尔曼、RLS、LMS算法matlab实现维纳滤波从噪声中提取信号波形的各种估计方法中,维纳(Wiener)滤波是一种最基本的方法,适用于需要从噪声中分离出的有用信号是整个信号(波形),而不只是它的几个参量。
设维纳滤波器的输入为含噪声的随机信号。
期望输出与实际输出之间的差值为误差,对该误差求均方,即为均方误差。
因此均方误差越小,噪声滤除效果就越好。
为使均方误差最小,关键在于求冲激响应。
如果能够满足维纳-霍夫方程,就可使维纳滤波器达到最佳。
维纳滤波器的优点是适应面较广,无论平稳随机过程是连续的还是离散的,是标量的还是向量的,都可应用。
维纳滤波器的缺点是,要求得到半无限时间区间内的全部观察数据的条件很难满足,同时它也不能用于噪声为非平稳的随机过程的情况,对于向量情况应用也不方便。
因此,维纳滤波在实际问题中应用不多。
下面是根据维纳滤波器给出的图像处理matlab实例,在下面实例中维纳滤波和均值滤波相比较,并且做了维纳复原、边缘提取、图像增强的实验:%****************维纳滤波和均值滤波的比较*********************I=imread('lena.bmp');J=imnoise(I,'gaussian',0,0.01);Mywiener2 = wiener2(J,[3 3]);Mean_temp = ones(3,3)/9;Mymean = imfilter(J,Mean_temp);figure(1);subplot(121),imshow(Mywiener2),title('维纳滤波器输出');subplot(122),imshow(uint8(Mymean),[]),title('均值滤波器的输出');%***********************维纳复原程序********************figure(2);subplot(231),imshow(I),title('原始图像');LEN = 20;THETA =10;PSF = fspecial('motion',LEN,THETA);Blurred = imfilter(I,PSF,'circular');subplot(232),imshow(Blurred),title('生成的运动的模糊的图像');noise = 0.1*randn(size(I));subplot(233),imshow(im2uint8(noise)),title('随机噪声');BlurredNoisy=imadd(Blurred,im2uint8(noise));subplot(234),imshow(BlurredNoisy),title('添加了噪声的模糊图像');Move=deconvwnr(Blurred,PSF);subplot(235),imshow(Move),title('还原运动模糊的图像');nsr = sum(noise(:).^2)/sum(im2double(I(:)).^2);wnr2 = deconvwnr(BlurredNoisy,PSF,nsr);subplot(236),imshow(wnr2),title('还原添加了噪声的图像');%****************维纳滤波应用于边缘提取*********************N = wiener2(I,[3,3]);%选用不同的维纳窗在此修改M = I - N;My_Wedge = im2bw (M,5/256);%化二值图像BW1 = edge(I,'prewitt');BW2 = edge(I,'canny');BW3 = edge(I,'zerocross');BW4 = edge(I,'roberts');figure(3)subplot(2,4,[3 4 7 8]),imshow(My_Wedge),title('应用维纳滤波进行边沿提取'); subplot(241),imshow(BW1),title('prewitt');subplot(242),imshow(BW2),title('canny');subplot(245),imshow(BW3),title('zerocross');subplot(246),imshow(BW4),title('roberts');%*************************维纳滤波应用于图像增强***************************for i = [1 2 3 4 5] K = wiener2(I,[5,5]);end K = K + I; figure(4);subplot(121),imshow(I),title('原始图像'); subplot(122),imshow(K),title('增强后的图像');维纳滤波器输出均值滤波器的输出原始图像生成的运动的模糊的图像随机噪声添加了噪声的模糊图像还原运动模糊的图像还原添加了噪声的图像卡尔曼滤波卡尔曼滤波的一个典型实例是从一组有限的,对物体位置的,包含噪声的观察序列预测出物体的坐标位置及速度。
维纳维纳滤波实现模糊图像恢复

维纳滤波实现模糊图像恢复摘要维纳滤波器是最小均方差准则下的最佳线性滤波器,它在图像处理中有着重要的应用。
本文主要通过介绍维纳滤波的结构原理,以及应用此方法通过MA TLAB 函数来完成图像的复原。
关键词:维纳函数、图像复原一、引言在人们的日常生活中,常常会接触很多的图像画面,而在景物成像的过程中有可能出现模糊,失真,混入噪声等现象,最终导致图像的质量下降,我们现在把它还原成本来的面目,这就叫做图像还原。
引起图像的模糊的原因有很多,举例来说有运动引起的,高斯噪声引起的,斑点噪声引起的,椒盐噪声引起的等等,而图像的复原也有很多,常见的例如逆滤波复原法,维纳滤波复原法,约束最小二乘滤波复原法等等。
它们算法的基本原理是,在一定的准则下,采用数学最优化的方法从退化的图像去推测图像的估计问题。
因此在不同的准则下及不同的数学最优方法下便形成了各种各样的算法。
而我接下来要介绍的算法是一种很典型的算法,维纳滤波复原法。
它假定输入信号为有用信号与噪声信号的合成,并且它们都是广义平稳过程和它们的二阶统计特性都已知。
维纳根据最小均方准则,求得了最佳线性滤波器的的参数,这种滤波器被称为维纳滤波。
二、维纳滤波器的结构维纳滤波自身为一个FIR 或IIR 滤波器,对于一个线性系统,如果其冲击响应为()n h ,则当输入某个随机信号)(n x 时,Y(n)=∑-n)()(m n x m h 式(1)这里的输入)()()(n v n s n x += 式(2)式中s(n)代表信号,v(n)代表噪声。
我们希望这种线性系统的输出是尽可能地逼近s(n)的某种估计,并用s^(n)表示,即)(ˆ)(y n sn = 式(3) 因而该系统实际上也就是s(n)的一种估计器。
这种估计器的主要功能是利用当前的观测值x(n)以及一系列过去的观测值x(n-1),x(n-2),……来完成对当前信号值的某种估计。
维纳滤波属于一种最佳线性滤波或线性最优估计,是一最小均方误差作为计算准则的一种滤波。
运动模糊图像经典复原方法分析

运动模糊图像经典复原方法分析摘要:图像复原是数字图像处理的一个研究热点,而运动模糊图像复原又是图像复原中的重要课题之一。
该文主要是针对匀速直线运动造成的模糊图像,描述了逆滤波、维纳滤波和lucy-richardson 算法复原图像的基本原理和过程,并且用matlab对添加噪声和无添加噪声的模糊图像利用三种经典复原方法进行仿真实验,实验结果表明,在无噪声和有噪声两种情况下,逆滤波法、维纳滤波法和l-r算法有其各自的优缺点。
在图像复原过程中,要根据图像的具体信息选择合适的方法,使得复原效果达到最好。
关键词:图像复原;运动模糊图像;逆滤波;维纳滤波;lucy-richardson算法中图分类号:tp18 文献标识码:a 文章编号:1009-3044(2013)13-3120-051 概述图像在获取的过程中不可避免地要受到各种外界因素的影响,造成图像模糊,严重影响了图像的应用。
图像复原就是研究怎样从退化的模糊图像复原出原来清晰的图像[1]。
造成图像退化模糊的原因有很多,其中,图像运动模糊是最常见的一种模糊形式,主要是由于在曝光过程中,照相机或目标物体发生了位置上的相对运动造成的。
这种模糊在实际生活中经常的会遇到[2],比如,相机抖动。
运动模糊图像的复原一直以来都是数字图像处理课程中一个比较困难的课题,对其进行研究具有重要的实用价值和意义,已经有许多经典的复原方法。
主要有逆滤波法[3],维纳滤波法[4],lucy-richardson算法[5-6]、约束最小二乘方法、最大熵方法等。
现在也已经有许多现代数字图像复原技术,比如,基于小波变换的图像复原[7]、基于神经网络的图像复原技术等等。
该文主要是介绍了经典复原方法中的逆滤波法、维纳滤波法和lucy-richardson 算法的基本复原过程和原理,针对添加噪声和无添加噪声的运动模糊图像,通过matlab进行仿真实验,通过分析实验结果,总结出三种方法的各自特点,为日后使用这三种方法复原图像时提供理论基础和选择依据,并为学习其他现代复原技术奠定基础。
第2章 维纳滤波和卡尔曼滤波

维纳 滤波器
相关函数
H(z)或h(n)
平稳
解析形式
卡尔曼 滤波器
前一个估 计值和最 近的观察
状态方程 量测方程
状态变量 估计值
平稳或 递推算法 非平稳
60 年代
2018年10月9日星期二
15:38:36
4
153
2.2 维纳滤波器的离散形式—时域解
§2.2 维纳滤波器的离散形式—时域解 2.2.1 维纳滤波器时域求解的方法 考虑到系统的因果性,即h(n)=0,n<0 (2.2.2) 设期望信号为d(n),计算误差和均方误差为 e(n)=d(n) -y(n)=s(n) -y(n) (2.2.3) (2.2.4)
15:38:36
24
153
2.2 维纳滤波器的离散形式—时域解
v2(n)是一个零均值的白噪声,它的自相关函数矩阵呈对角形,
且
2 rv2v2 (, 0) 2
因此,输出信号的自相关Ryy为
2018年10月9日星期二
15:38:36
25
153
2.2 维纳滤波器的离散形式—时域解
(3) 计算输出信号与期望信号的互相关函数矩阵。 由于两个信 号都是实信号,故 ryd(m)=E[y(n)d(n-m)]=E[y(n)x1(n-m)] =E[(x(n)+v2(n))x1(n-m)]=E[x(n)x1(n-m)] m=0, 1 根据图2.2.2系统H2(z)的输入与输出的关系, 有 x1(n)-b1x(n-1)=x(n) 这样 x1(n)=x(n)+b1x(n-1)
2018年10月9日星期二 15:38:的离散形式—时域解
% 滤波 y = filter(Wopt, 1, x); % 误差 En = d - y'; % 结果 figure, plot(n, d, 'r:', n, y, 'b-'); legend('维纳滤波信号真值','维纳滤波估计值'); title('期望信号 与滤波结果对比'); xlabel('观测点数');ylabel('信号幅度');figure, plot(n , En); title('维纳滤波误差曲线'); xlabel('观测点数');ylabel('误差幅度'); toc
图像复原研究报告

图像复原研究报告1 引言1.1 研究背景及意义随着科技的飞速发展,数字图像在各个领域得到了广泛应用,如医学成像、卫星遥感、安全监控等。
然而,在图像的获取、传输和存储过程中,往往受到各种噪声和模糊的影响,导致图像质量下降。
图像复原技术旨在从退化的图像中恢复出原始图像,对于提高图像质量、挖掘图像潜在信息具有重要意义。
近年来,图像复原技术在计算机视觉、模式识别等领域取得了显著成果,但仍面临许多挑战,如噪声类型多样、图像退化过程复杂等。
因此,研究图像复原技术不仅有助于解决实际问题,还具有很强的理论价值。
1.2 图像复原技术发展概况图像复原技术起源于20世纪50年代,经历了从线性到非线性、从全局到局部的演变过程。
早期的研究主要集中在逆滤波、维纳滤波等经典算法。
随着计算机硬件和算法的发展,图像复原技术逐渐向多尺度和多通道方向发展。
近年来,深度学习技术在图像复原领域取得了重大突破,如基于卷积神经网络的图像去噪、超分辨率等算法。
这些方法在许多国际权威评测中取得了优异的性能,为图像复原技术的研究和应用带来了新的机遇。
1.3 研究内容与组织结构本文主要研究以下内容:1.分析图像退化与复原的基本理论,包括图像退化模型和图像复原方法分类;2.对常见图像复原算法进行详细分析,如逆滤波、维纳滤波和非局部均值滤波等;3.探讨深度学习在图像复原中的应用,包括基于卷积神经网络的图像复原和基于生成对抗网络的图像复原;4.评估图像复原算法的性能,通过实验对比分析不同算法的优缺点;5.总结本文研究成果,并对未来研究方向进行展望。
本文的组织结构如下:1.引言:介绍研究背景、意义和发展概况;2.图像退化与复原基本理论:分析图像退化模型和图像复原方法分类;3.常见图像复原算法分析:详细分析逆滤波、维纳滤波和非局部均值滤波等算法;4.深度学习在图像复原中的应用:探讨基于卷积神经网络和生成对抗网络的图像复原方法;5.图像复原算法性能评估:评估不同算法的性能,并进行实验对比分析;6.结论与展望:总结本文研究成果,并对未来研究方向进行展望。
微弱信号检测技术的原理及应用(含卡尔曼滤波与维纳滤波)

微弱信号检测技术的原理及应用2018年1月一、微弱信号检测的基本原理、方法及技术在自然现象和规律的科学研究和工程实践中,经常会遇到需要检测诸如地震的波形和波速、材料分析时测定荧光光强、卫星信号的接收、红外探测以及生物电信号测量等。
这些测量量被强背景噪声或检测电路的噪声所淹没,无法用传统的测量方法检测出来。
微弱信号,为了检测被背景噪声淹没的微弱信号,人们进行了长期的研究工作,分析背景噪声产生的原因和规律,研究被测信号的特点、相关性以及噪声的统计特性,以寻找出从背景噪声中检测出目标信号的方法。
微弱信号检测技术的首要任务是提高信噪比,这就需要采用电子学、信息论和物理学的方法,以便从强噪声中检测出有用的微弱信号。
微弱信号检测技术不同于一般的检测技术,主要是考虑如何抑制噪声和提高信嗓比,因此可以说,微弱信号检测是一门专门抑制噪声的技术。
抑制噪声的现代信号处理手段的理论基础是概率论、数理统计和非线性科学。
1、经典检测与估计理论时期这一时期检测理论主要是建立在统计学家工作的基础上的。
美国科学家WienerN .将随机过程和数理统计的观点引入到通信和控制系统中,提出了信息传输和处理过程的统计本质,建立了最佳线性滤波理论,即维纳滤波理论。
NorthD.O.于1943年提出以输出最大信噪比为准则的匹配滤波器理论;1946年卡切尼科夫(BA.K)提出了错误判决概率为最小的理想接收机理论,证明了理想接收机应在其输出端重现出后验概率为最大的信号,即是将最大后验概率准则作为一个最佳准则。
1950年在仙农信息理论的基础上,WoodwardP.M.把信息量的概念用于雷达信号的检测中,提出了理想接收机应能从接收到的信号加噪声的混合波形中提取尽可能多的有用信息。
但要知道后验概率分布。
所以,理想接收机应该是一个计算后验概率分布的装里。
1953年以后,人们直接利用统计推断中的判决和统计理论来研究雷达信号检测和参盘估计。
密德尔顿(Middleton D)等用贝叶斯准则(最小风险准则)来处理最佳接收问题,并使各种最佳准则统一于风险理论。
车辆运动模糊图像分块恢复的新方法

b e osr g g e etad u stf t y l a rs rtn I a esn e on hog hoe claa s , y sr u n n f c n na s c r o l et ao . t m i r osw r fud t uh terta nl i i ii ia o c o i s n a e r i ys
T e r lt n l r p rmee s s a e p s in a d s e d , e e h s n a d o l c i g p r t n wee gv n T e h ea i s o bu a a t r, p c o i o s n p e s v n t e t d r f b o kn at i r ie . h o f t a io e p r n a e ut e f h t te p o o e t o h o n a o e s t n a d t e b o k r so ain C f c iey x e me t rs l v r y t a h rp s d me h d o t e b u d r c mp n ai n h lc ・ tr t a e e t l i l s i f y o e o n v
维纳滤波原理及其在图像处理中的应用

维纳滤波原理及其在图像处理中的应用摘要图像由于受到如模糊、失真、噪声等的影响,会造成图像质量的下降,形成退化的数字图像。
退化的数字图像会造成图像中的目标很难识别或者图像中的特征无法提取,必须对其进行恢复。
所谓图像复原就是指从所退化图像中复原出原始清晰图像的过程。
维纳波是一种常见的图像复原方法,该方法的思想是使复原的图像与原图像的均方误差最小原则恢复原图像。
本文进行了对退化图像进行图像复原的仿真实验,分别对加入了噪声的退化图像、运动模糊图像进行了维纳滤波复原,并给出了仿真实验效果以及结果分析。
实验表明退化图像在有噪声时必须考虑图像的信噪比进行图像恢复,才能取得较好的复原效果。
关键词:维纳滤波;图像复原;运动模糊;退化图像AbstractDue to factors such as blurring distorting and noising, image quality deteriorated and led to degenerated digital images which is getting harder to discern the target image or extract the image features. Wiener Filter is often used to recover the degraded image. The principle of the method expects to minimize the mean square error between the recovered image and original image.This paper carried out a restoration simulation experiments on degraded image, restoration of motion blurred images, and the result shows, SNR noise of the autocorrelation function for image restoration must be taken into consideration when restoring degraded images in a noise.Key words: Wiener Filter; motion blurred; degraded image; image restoration概述图像在形成、传输和记录的过程中都会受到诸多因素的影响,所获得的图像一般会有所下降,这种现象称为图像“退化”。
维纳滤波和卡尔曼滤波
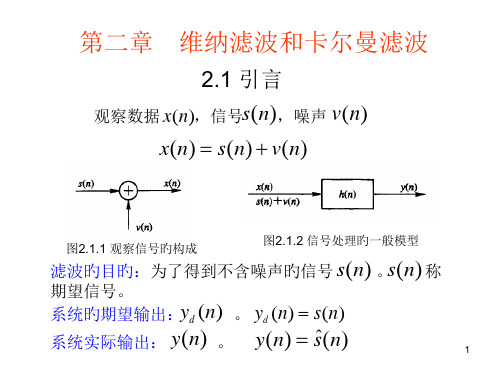
2.2 维纳滤波器旳离散形式--时域解
维纳滤波器设计旳任务就是选择 h(n),使其输出信号 y(n) 与期望信号 d (n)误差旳均方值最小,实质是解维纳-霍夫方程。
2.2.1维纳滤波器时域求解旳措施
假设滤波系统 h(n)是一种线性时不变系统,它旳h(n)和输 入信号都是复函数,设
h(n) a(n) jb(n)
系统实际输出: y(n) 。 y(n) sˆ(n) 1
预测:已知过去旳观察值 x(n 1), x(n 2), , x(n m),估计 目前及后来时刻旳信号值 sˆ(n N ) , N 0 。 滤波:已知目前和过去旳观察值 x(n), x(n 1), , x(n m) ,
估计目前旳信号sˆ(n) 。
卡尔曼滤波是20世纪60年代由卡尔曼提出旳。
2
维纳滤波和卡尔曼滤波比较:
共同点:都处理最佳线性滤波和预测问题,都以均方误差最 小为最优准则,平稳条件下它们得到旳稳态成果一致。 不同点: (1)维纳滤波根据 x(n), x(n 1), , x(n m) 估计信号旳目前值,
它旳解以系统旳系统函数H (z)或单位脉冲响应h(n)形式给出。
M 1
i0
h(i)x(n
i)
17
E
e(n)
2
E
d
(n)
2
M 1
k 0
h
(k
)E
x
(n
k)d
(n)
M 1
M 1 M 1
h(i)E x(n i)d (n) h(k)h(i)E[x*(n k)x(n i)]
i0
k0 i0
M 1
M 1(k
19
2.3离散维纳滤波旳Z域解
时域求解Wiener滤波器很困难,用Z域求解。又因为实际旳系统是因果旳,
数学建模运动模糊图像的复原

2015 高教社杯全国大学生数学建模竞赛
承
诺
书
我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模 竞赛参赛规则》 (以下简称为“竞赛章程和参赛规则” ,可从全国大学生数学建模 竞赛网站下载) 。 我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮 件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问 题。 我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的 成果或其他公开的资料(包括网上查到的资料) ,必须按照规定的参考文献的表 述方式在正文引用处和参考文献中明确列出。 我们郑重承诺, 严格遵守竞赛章程和参赛规则,以保证竞赛的公正、 公平性。 如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。 我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行 公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表 等) 。
三、主要变量符号说明
符号 M N v L 意义 运动图像的长度 运动图像的宽度 运动物体相对于摄像机的水平运动速度 运动模糊图像的模糊尺度 运动模糊图像的模糊角度 未降质图像的能量 摄像机的曝光时间 像素坐标 聚集在图像上的的点而构成的原始图像 聚集在图像上的的点而构成的模糊图像 聚集在图像上的的点而构成的还原图像 加在图像上的加信噪音 未傅里叶变换的点扩展函数 点扩展函数 退化图像的傅里叶变换
图5-1 运动模糊原理图
如图5-1-1所示,当运动物体以速度 v 相对于摄像机一段距离 D 在平面上运 动时,周围的景物 A 点相对于运动物体后移到 A' 。通过光学系统成像于 a ' 点,在 摄像机靶面上像移动速度为: V V ' f max (5-1) D D -摄像机离运动物体的距离 f max -光学系 其中, V -运动物体的速度 统最大焦距 在摄像机每场积分时间内像移量为: l V 't (mm) (5-2) t 为摄像机的积分时间。 像移量的存在导致图像模糊,为得到清晰图像必须对像移量进行控制。然而 在实际工程中,摄像机的积分时间不能无限制的缩小,因为积分时间缩小后,为 了保证图像的质量,必须加大地面的照度,这就限制了摄像机的工作条件。 目前解决运动模糊的主要手段是通过了解图像的退化过程, 建立运动图像的 复原模型,通过数学模型来解决图像的复原问题。现在常用的模糊图像复原方法 有很多种,包括逆滤波、维纳滤波、盲解卷积算法、Lucy-Richardson算法等, 不同的算法效果和使用范围个不相同,但是都有一个共同点,那就是需要预先确 定点扩散函数PSF,在不知道点扩散函数的情况下,进一步的复原工作无法进行。 而对于一般的模糊图像(包括本题给出的运动模糊图像)都没有直接给出点扩散 函数,因此,必须通过已有的模糊图像建立数学模型来估计点扩展函数。 5.2 模型的建立 5.2.1.通过建立数学模型确定退化模型的点扩展函数
维纳滤波在退化图像恢复中的应用研究

摘 要 :图像 由 于 受 到如 模 糊 、 真 、 声等 的影 响 , 造 成 图像 质 量 的 下 降 , 成 退 化 的数 字 图像 。退化 的数 字 图像 会 失 噪 会 形 造 成 图像 中 的 目标 很 难 识 别 或 者 图像 中 的特 征 无 法提 取 , 须 对其 进 行 恢 复 。 纳 波 是 一 种 常 见 的 图像 复 原 方 法 . 必 维 该
App i a i n t y o e e i r t d i a e r so ato lc to sud fd t r o a e m g e t r i n ba e o e e le i s d n wi n r f t rng i
XIபைடு நூலகம்AO ng Fe
c n i e a in w e e tr g d g a e g e o s . o sd r t h n r so n e r d d i o i ma si a n ie n Ke r s win r l rn y wo d : e e ti g;i g e t r t n o n p e d F n t n;moin b u r d;d tro ae ma e i f e ma e r so ai ;P i tS r a u c i o o t — l re o e e r td i g i
进 行 图像 恢 复 . 能取 得 较 好 的 复 原 效 果 才 关 键 词 :维纳 滤 波 ;图像 恢 复 ;P F;运 动 模 糊 ;退 化 图像 S
中图 分 类 号 : P 9 .1 T 31 4
文献标识码 : A
文章 编 号 :1 7 — 2 6 2 1 ) 8 0 7 — 3 6 4 6 3 (0 0 — 13 0 1
第 1 9卷 第 8期
卡尔曼滤波与维纳滤波在信号处理中的应用研究

卡尔曼滤波与维纳滤波在信号处理中的应用研究
卡尔曼滤波是一种线性的、递归的滤波算法,它能够对信号的状态进行估计和预测。
卡尔曼滤波是基于贝叶斯估计理论的一种优化方法,它不仅可以有效地消除噪声和偏差,还可以根据已有的历史数据对信号进行预测。
卡尔曼滤波广泛应用于航空航天、控制理论、信号处理等领域,是一种非常有效的信号处理算法。
维纳滤波是一种信号处理中最常用的滤波算法之一,它能够根据现有数据对信号进行优化处理,消除噪声和干扰,实现信号的恢复和重建。
维纳滤波利用了信号和噪声的统计特性,根据信号的功率谱和噪声的功率谱来进行滤波处理。
维纳滤波不仅可以用于图像处理、语音处理等多种信号处理领域,还可以应用于雷达信号处理、无线通信等工程实践中。
在实际应用中,卡尔曼滤波和维纳滤波通常结合使用,以获得更为准确和可靠的信号处理效果。
如在雷达信号处理中,利用卡尔曼滤波进行预测和估计,再经过维纳滤波进行优化处理,可以有效地消除噪声和干扰,获得高质量的信号信息。
在图像处理中,卡尔曼滤波和维纳滤波也可以结合使用,以实现图像的优化重建和增强。
总的来说,卡尔曼滤波和维纳滤波在信号处理中的应用非常广泛,可以有效地消除噪声和干扰,提高信号和数据的质量和可靠性,对于工程实践和科学研究都具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·20· (总 610)
卡尔曼滤波与维纳滤波在运动模糊图像恢复中的应用
2008 年
3 卡尔曼运动模糊过程分析
κ g (x , y ) = h (x - Α, y - Β) f (Α, Β) dΑdΒ+ n (x , y )
(4)
给定了g (x , y ) , 并不能精确求解出f (x , y )。在此 只能找出一个估算值 f (x , y ) , 使得均方误差式
e2= E [ f (x , y ) - f (x , y ) ]2
术[J ]. 武汉大学学报, 2004, 29 (9) : 7962799.
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
(5)
最小, 其中 f (x , y ) 叫做给定 g (x , y ) 时 f (x , y ) 的
最小二乘方估计。 最小二乘方滤波器的传递函数表示
形式如式 (3) 所示。
3 2007211215 收到, 2008206222 改回 3 3 张 宪, 男, 硕士研究生, 研究方向: 运动图像。
y ) 通过系统 h (x , y )。h
(x , y ) 是综合所有退化因素得到的系统函数, 称为成 像系统的冲击响应或点扩展函数 (PSF )。 图 1 所示的 框图就是一个基本的退化模型, g (x , y ) 就是退化得到
的模糊图像, n (x , y ) 为噪声模型。
根据图 1 所示退化框图, 退化模型可表示为:
恢复处理的方法, 建立在认为图像和噪声是随机过程
的基础上, 而目标是一个未污染图像的估计值, 使得均
方误差最小。 综合考虑本文选用维纳滤波与卡尔曼滤
波进模糊图像恢复, 并在此基础上进行比较与分析。
2 维纳滤波进行模糊图像恢复原理
最小二乘方法滤波也是维纳滤波。 它是使得原始 图像 f (x , y ) 及其恢复图像 f (x , y ) 之间均方误差最小 的恢复方法。
Restora tion of M ob ile Fuzzy Image
张 宪 崔 岩
(国防科技大学继续教育学院 长沙 410073)
【摘 要】通过对运动目标在运动方向上运动的分析, 建立运动模糊图像退化模型, 结合卡尔曼滤波与维纳滤波
在应用方面的特点进行图像恢复。 研究了卡尔曼滤波与维纳滤波在图像恢复方面特点与区别, 说明卡尔曼滤波
to im age resto ra tion of m ob ile ta rget. KEYWO RD S m ovem en t fuzzy, w iner filtering, ka lm an filtering, im age resto ra tion
运动模糊图像是交通车辆视频监视及检测、战场 图像侦察等领域普遍存在的问题。 图像模糊是由于采 集图像时采集设备与目标发生相对运动而产生的。 在 车辆监测中车辆速度较快而成像设备帧频较低时常产 生图像模糊。 多年来人们对图像恢复进行了大量的研 究, 提出了多种基于空间域与频率域恢复的方法, 如维 纳滤波、最小二乘法、最大熵复原法、最大似然估计法 等。 但是这些方法对匀速动动模糊图像效果较好且对 退化函数等先验知识依赖太强, 并且不可避免传统频 率域中出现的振铃效应与鬼影效应。
态变量的估计, 求出现时刻的估计值。把预测值和测量 像:
值进行折衷, 得到误差更小的估计, 而且, 只有这种折
衷是最佳的。 这是卡尔曼滤波的核心。 其目标状态方
程与运动观测方程为:
X (k ) = F (k , k - 1) ·X (k - 1)
+ T (k , k - 1) ·U (k - 1)
(6)
第 21 卷 第 8 期
电脑开发与应用
(总 609) ·19·
文章编号: 100325850 (2008) 0820019202
卡尔曼滤波与维纳滤波在运动模糊图像恢复中的应用
Appl ica tion of Ka lman F ilter ing and W iner F ilter ing to Image
差, 称为预测值的修正量。K (k ) 称为滤波增益, 为点扩
散函数矩阵H (k ) 逆矩阵。 一般对滤波增益K (k ) 通过
以下递推公式求得[4 ]:
K (k ) = P ′(k ) H T (k ) [H (k ) P ′(k ) H T (k )
+ R (k ) ]- 1
(9)
P ′(k ) = F (k ) P (k - 1) F T (k ) + Q k- 1
了一次中值滤波处理, 效果较好。
由图 2, 图 3 可知对运动模糊图像直接采用维纳滤
波有较为明显的条带噪声, 而卡尔曼恢复处理结果却
有较好的效果, 恢复后图像中的车牌号清晰可辨。
5 结 论
维纳滤波与卡尔曼滤波都是解决最佳线性过滤和 预测问题, 并且都是以均方误差最小为准则。因此在平 衡条件下, 它们所得到的稳态结果是一致的。 然而, 它 们解决的方法有很大的区别。
③对X (k ) 的预测值X ′(k ) 加上其修正量, 得到模
糊图像的卡尔曼滤波恢复的估计值X^ (k ) ;
④对模糊图像的
卡
尔曼滤
波
的估计
值
^
X
(k ) 作中
值滤波处理, 进一步改善视觉效果[5]。
[ 1 ] 刘政凯, 衢建雄. 数字图像恢复与重建[M ]. 合肥: 中国 科学技术大学出版社, 1998.
维纳滤波是根据全部过去的和当前的观察数据来 估计信号的当前值, 而卡尔曼滤波是用前一个估计值
ቤተ መጻሕፍቲ ባይዱ
P (k ) = P 1 (k ) + K (k )H (k ) + P 1 (k ) (11) 和最近一个观察数据 (它不需要全部过去的观察数据)
式中Q k- 1 为运动噪声的协方差矩阵, 是一对角矩 阵, 其对角线上的元素即为噪声向量的方差, 实际计算 时一般取降质图像方差。R (k ) 为系统噪声n 的协方差 矩阵, 具体计算时可取单位阵。 对滤波增益K (k ) 的求 解, 通过递推方式进行, 通过滤波增益 K (k ) 对修正量 加权, 以保证残差在可控制范围, 从而实现对非平稳过
g (x , y ) = f (x , y ) 3 h (x , y ) + n (x , y )
(1)
对上式两边进行傅立叶变换, 可以得到:
G (u, v) = H (u, v) F (u, v) + N (u, v)
(2)
频率域恢复最常用的方法是均方误差最小滤波
(维纳滤波) 恢复方法:
F (u , v ) = G (u , v ) H 3 (u , v ) ( H (u , v ) 2+ Κ) (3) 式中, G (u, v ) 是退化图像, H (u , v ) 是点扩散函 数, H 3 (x , y ) 为 H (u , v ) 的复共轭, F (u , v ) 是恢复图 像, Κ为噪声功率谱密度比, 近似一个常数。 维纳滤波 是一种综合考虑退化函数与噪声统计特征两方面进行
来估计信号的当前值, 它是用状态方程和递推方法进 行估计的, 这的解是以估计值 (常常是以状态变量值) 形式给出的。 因此, 运用计算机计算更方便, 而且它可 用于平稳和不平稳的随机过程, 非时变和时变的系统, 从而可得出这样的结论: 在变速运动目标模糊图像的 恢复上, 卡尔曼更适用。
程的运动状态的最佳估计。 具体计算流程:
estab lished, and app lying the ka lm an filtering and w iner filtering to resto re im age. T he cha racteristics and distinction s of ka lm an
filtering and w iner filtering in resp ect to im age resto ra tion i sstudyed in to , and exp lan ined tha t the ka lm an filtering is m o re su itab le
4 实验结果与分析
卡尔曼运动模型是一较好的非平稳运动过程估 计, 以最小均方误差为准则, 来寻求一套递推估计的算 法, 其基本思想是: 采用信号与噪声的状态空间模型, 利用前一时刻的估计值和现时刻的观测值来更新对状
利用交通车辆图像来进行实验, 下面是拍得的一 幅快速行驶汽车图片, 下面分别采用维纳滤波与卡尔 曼 滤波的方法进行恢复, 图 2~ 图 4 分别为未恢复图 像, 维纳滤波恢复后的图像和卡尔曼滤波恢复后的图
(10)
图 2 未恢复图像 图 3 维纳滤波 图 4 卡尔曼滤
图像
波图像
图 3 中, 运用维纳滤波进行恢复时, 取的模糊长度
为60, 实际在图像恢复中模糊长度的选取至关重要, 本
文中是根据先验知识估算汽车在超度行驶过程中的速
度, 经验也表明模糊长度越接近运动目标的真实速度
恢复效果越好。 图 4 是经过卡尔曼滤波处理后又进行
Y (k ) = H (k ) ·X (k ) + N (k )
(7)
其中X (k ) 和 Y (k ) 分别是 k 时刻的状态矢量和观
测矢量 (模糊图像) , F (k , k - 1) 为状态转移矩阵, U (k )
为 K 时刻的动态噪声, T (k , k - 1) 为系统控制矩阵,
