第二章导数与微分
第2章导数与微分总结
1、极限的实质是:动而不达导数的实质是:一个有规律商的极限。
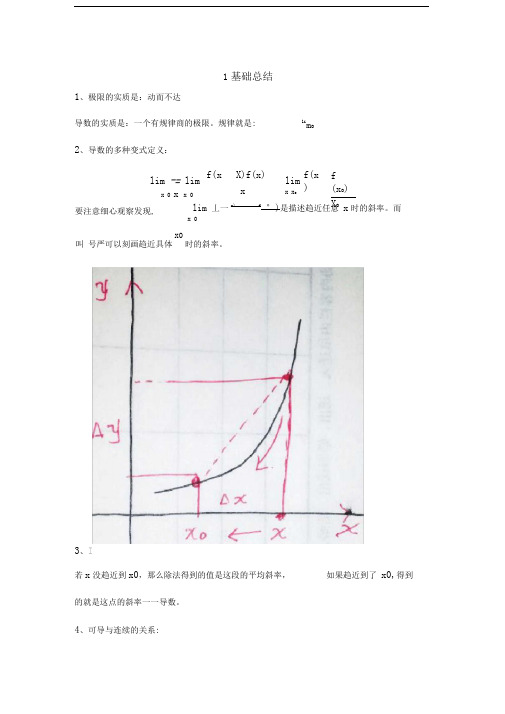
规律就是:2、导数的多种变式定义:lim 丄一x)f°)是描述趋近任意 x 时的斜率。
而x 03、I若x 没趋近到x0,那么除法得到的值是这段的平均斜率, 如果趋近到了 x0,得到的就是这点的斜率一一导数。
4、可导与连续的关系:1基础总结lim -= limx 0 x x 0 f(x X)f(x)xlim x x o f(x )f (x o )X o叫 号严可以刻画趋近具体x0时的斜率。
lim o要注意细心观察发现,导数的实质是定义在某点的左右极限。
既然定义在了某点上,该点自然存在,而 且还得等于左右极限。
因此,可导一定是连续的。
反之,如果连续,不一定可导。
不多说。
同理,如果不连续,肯定某点要么无定义,要么定义点跳跃跑了,肯定 极限有可能存在,但是导数绝不会存在。
同理要注意左右导数的问题。
如果存在左或者右导数,那么在左侧该点一定是存 在的。
如:f(x) x,x 0这个函数,在0点就不存在左导数,只存在右导数。
为什么嫩?看定义:万不要以为导数是一种简单的极限,极限是可以在某点无定义的,而导数却是该 点必须存在! 由此引发了一些容易误判的血案: 例如:A 旦主^謎IC m F 左电鼓 pg 总生戟乞f ( x) f (x)-中的f(x))至u 底是神马。
比如求上图limf(x x) f(x)x 0xlimf(X X)f(0)。
x 0定义里面需要用到f(0)啊!因此,千中 iimf (x)论) x 1x x 0,这个f(x0)千万要等于2/3,而不是1 !定义解决时候一定要注意问。
X X o由此也可以知道,f (x)2x 3, x 1这个函数是不存在导数的,也不存在左导数,3只存在右导数。
5、反函数的导数与原函数的关系:注意,求反函数时候不要换元。
因为换了元虽然对自身来讲函数形式不变, 与原函数融合运算时候就算是换了一个不是自己反函数的一个函数进行运算 果显然是错误的。
高等数学 第二章 导数与微分

(2)算比值: y f (x x) f (x) .
x
x
(3)求极限: f (x) lim y lim f (x x) f (x) .
x x0
x0
x
四、函数可导性与连续性的关系
定理 如果函数 y f (x) 在点 x0 处可导,则函数 y f (x) 在点 x0 处一定连续. 如果函数 f (x) 在点 x0 处连续,则函数 f (x) 在点 x0 处不一定可导.
第二章
导数与微分
导学
我们在解决实际问题时,除了需要确定变量之间的函数关系外,有时 还需要研究函数相对于自变量变化的快慢程度,即函数的变化率,以及当 自变量发生微小变化时函数的近似改变量,这两个问题就是我们本章所要 讨论的主要内容——导数与微分.
第一节
导数的概念
一、导数的定义
设某物体在数轴上做变速直线运动,运动方程为 s s(t) ,现在求该物体在 t0 时刻的瞬时速度 v(t0 ) .
当
u
C (C
为常数)时,有
C v
Cv v2
.
二、反函数的求导法则
定理 2 如果函数 x f ( y) 在区间 I y 内单调、可导且 f ( y) 0 ,那么它的反函数 y f 1(x) 在
区间 Ix {x | x f ( y) ,y I y} 内也可导,且有
[ f 1(x)] 1 或 dy 1 .
当时间 t 由 t0 变到 t0 t 时,物体的路程 s(t) 由 s(t0 ) 变到 s(t0 t) ,
路程的增量 s 为 s s(t0 +t) s(t0 ) ,
物体在
t0
到 t0
t
这段时间内的平均速度为
v
s t
高等数学导数的概念教学ppt课件.ppt

h0
h
h0 h 0.
即 (C ) 0.
9
第二章 导数与微分
第一节 导数的概念
例5 设函数 f ( x) sin x,求(sin x)及(sin x) x . 4
解:(sin x) lim sin( x h) sin x
h0
h
h
lim cos( x
h0
h) sin 2 2h
cos
x.
2 即 (sin x) cos x.
定理2.1.2 凡可导函数都是连续函数.
证 设函数 f ( x)在点 x0可导, 即
lim y x0 x
f ( x0 )
有
lim y
x0
lim
x0
y x
x
f
(
x0
)
lim
x0
x
0
函数 f ( x)在点 x0连续 .
注意: 该定理的逆定理不成立.
15
第二章 导数与微分
第一节 导数的概念
例10 讨论函数 f ( x) x 在x 0处的可导性.
1.左导数:
f( x0 )
lim
x x0
f ( x) f ( x0 ) lim
x x0
x0
f ( x0 x) x
f ( x0 ) ;
2.右导数:
f( x0 )
lim
x x0
f ( x) f ( x0 ) lim
x x0
x0
f ( x0 x) x
f ( x0 ) ;
定理2.1.1
函数 f ( x)在点x0 处可导 左导数 f( x0 ) 和右 导数 f( x0 )都存在且相等.
解: f (0 h) f (0) h ,
《导数与微分》word版

第二章 导数与微分教学要求:正确理解导数概念及其几何意义.知道导数值与导数的联系与区别.熟练掌握求导方法,记住求导的基本公式及求导法那么(四那么运算法那么,反函数、复合函数、隐函数、参数式函数的求导法那么,对数求导法).知道利用定义求导数的方法,会求分段函数分界点处的导数.会计算较简单的导数应用题.会求曲线在某点的切线和法线方程;会求一些物理量的变化率;会计算一些简单的相关变化率问题.理解高阶导数的定义,熟练掌握求二阶导数的方法.会求一些简单的初等函数(如1,,sin ,ln ,ln(1)x e x x x x). 正确理解微分的定义及其与导数的关系.理解微分与函数增量的关系,会用微分近似计算函数改变量和函数值的近似值.理解一阶微分形式不变性.明确可微(可导)与连续之间的关系.教学重点:导数与微分的概念;导数的几何意义和作为变化率的各种实际意义及其应用;函数连续、可导、 可微相互之间的关系;各类函数的求导法那么与求导方法;基本初等函数的导数与微分公式. 教学难点:复合函数求导法那么与高阶导数求导方法的应用.数学中研究导数、微分及其应用的部分称为微分学,研究不定积分、定积分及其应用的部分称为积分学. 微分学与积分学统称为微积分学.微积分学是高等数学最基本、最重要的组成部分,是现代数学许多分支的基础,是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.恩格斯(1820-1895)曾指出:“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”. 微积分的发展历史曲折跌宕,撼人心灵,是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材(本部分内容详见光盘).积分的雏形可追溯到古希腊和我国魏晋时期,但微分概念直至16世纪才应运萌生. 本章及下一章将介绍一元函数微分学及其应用的内容.第一节 导数概念从15世纪初文艺复兴时期起,欧洲的工业、农业、航海事业与商贾贸易得到大规模的发展,形成了一个新的经济时代. 而十六世纪的欧洲,正处在资本主义萌芽时期,生产力得到了很大的发展. 生产实践的发展对自然科学提出了新的课题,迫切要求力学、天文学等基础科学的发展,而这些学科都是深刻依赖于数学的,因而也推动了数学的发展. 在各类学科对数学提出的种种要求中,下列三类问题导致了微分学的产生:(1) 求变速运动的瞬时速度;(2) 求曲线上一点处的切线;(3) 求最大值和最小值.这三类实际问题的现实原型在数学上都可归结为函数相对于自变量变化而变化的快慢程度,即所谓函数的变化率问题. 牛顿从第一个问题出发,莱布尼茨从第二个问题出发,分别给出了导数的概念.内容分布图示★ 引言★ 变速直线运动的瞬时速度★ 平面曲线的切线★ 导数的定义 ★ 关于导数的几点说明★利用定义求导数与求极限 ★例1★例2★ 例3★ 例4★ 例5 ★ 例6 ★ 例7★ 左右导数★ 例8 ★ 例9★ 导数的几何意义 ★ 例10 ★ 例11★ 导数的物理意义★ 可导与连续的关系★ 例12 ★ 例13 ★ 例14★ 内容小结★ 课堂练习★返回内容要点:一、引例: 引例1: 变速直线运动的瞬时速度; 引例2: 平面曲线的切线二、导数的定义:xx f x x f x y x f x x ∆-∆+=∆∆='→∆→∆)()(lim lim )(00000 注:导数概念是函数变化率这一概念的精确描述,它撇开了自变量和因变量所代表的几何或物理等方面的特殊意义,纯粹从数量方面来刻画函数变化率的本质: 函数增量与自变量增量的比值x y ∆∆是函数y 在以0x 和x x ∆+0为端点的区间上的平均变化率,而导数0|x x y ='那么是函数y 在点0x 处的变化率,它反映了函数随自变量变化而变化的快慢程度.根据导数的定义求导,一般包含以下三个步骤:1. 求函数的增量: );()(x f x x f y -∆+=∆2. 求两增量的比值:x x f x x f x y ∆-∆+=∆∆)()(; 3. 求极限 .lim0xy y x ∆∆='→∆ 三、左右导数定理1 函数)(x f y =在点0x 处可导的充要条件是:函数)(x f y =在点0x 处的左、右导数均存在且相等.四、用定义计算导数五、导数的几何意义六、函数的可导性与连续性的关系定理2 如果函数)(x f y =在点0x 处可导,那么它在0x 处连续.注:上述两个例子说明,函数在某点处连续是函数在该点处可导的必要条件,但不是充分条件. 由定理2还知道,若函数在某点处不连续,那么它在该点处一定不可导.在微积分理论尚不完善的时候,人们普遍认为连续函数除个别点外都是可导的. 1872年得多数学家魏尔斯特拉构造出一个处处连续但处处不可导的例子,这与人们基于直观的普遍认识大相径庭,从而震惊了数学界和思想界. 这就促使人们在微积分研究中从依赖于直观转向理性思维,大大促进了微积分逻辑基础的创建工作.例题选讲:导数概念的应用例1 求函数3x y =在1=x 处的导数)1(f '.例2试按导数定义求下列各极限(假设各极限均存在).(1);)2()2(lim ax a f x f a x --→ (2) ,)(lim 0xx f x → 其中.0)0(=f 用定义计算导数例3 求函数C x f =)((C 为常数)的导数.例4设函数,sin )(x x f = 求)(sin 'x 及4|)(sin π='x x . 例5 求函数n x y =(n 为正整数)的导数.例6 求函数)1,0()(≠>=a a a x f x 的导数.例7 求函数)1,0(log ≠>=a a x y a 的导数.左右导数例8 求函数⎩⎨⎧=,,sin )(x x x f 00≥<x x 在0=x 处的导数. 例9 设)(x f 为偶函数,且)0(f '存在. 证明.0)0(='f例10求等边双曲线x y 1=在点⎪⎭⎫ ⎝⎛2,21处的切线的斜率, 并写出在该点处的切线方程和法线方程. 例11 求曲线x y =在点)2,4(处的切线方程.例12 讨论函数||)(x x f =在0=x 处的连续性与可导性.例13 讨论⎪⎩⎪⎨⎧=≠=0,00,1sin )(x x x x x f 在0=x 处的连续性与可导性. 例14设函数⎩⎨⎧<≤+<=,10,10,)(2x x x a x f 问a 取何值时,)(x f 为可导函数. 注:上述两个例子说明,函数在某点处连续是函数在该点处可导的必要条件,但不是充分条件. 由定理2还知道,若函数在某点处不连续,那么它在该点处一定不可导.在微积分理论尚不完善的时候,人们普遍认为连续函数除个别点外都是可导的. 1872年得多数学家魏尔斯特拉构造出一个处处连续但处处不可导的例子(如第十一章第一节的Koch 雪花曲线描述的函数),这与人们基于直观的普遍认识大相径庭,从而震惊了数学界和思想界. 这就促使人们在微积分研究中从依赖于直观转向理性思维,大大促进了微积分逻辑基础的创建工作.课堂练习1. 函数)(x f 在某点0x 处的导数)(0x f '与导函数)(x f '有什么区别与联系?2. 设)(x ϕ在a x =处连续, )()()(22x a x x f ϕ-=, 求)(a f '.3. 求曲线32x x y -=上与x 轴平行的切线方程.莱布尼茨 (Friedrich , Leibniz ,1597~1652)-----博学多才的数学符号大师出生于书香门第的莱布尼兹是德国一们博学多才的学者。
大学高数 第二章 导数与微分
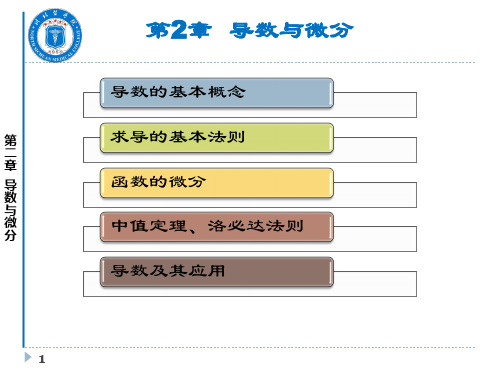
定义 2.1 设函数 f ( x) 在 x0 点及其附近有定义,若 x 在在 x0 点处有增量
第 二 章 导 数 与 微 分
x ( f ( x0 x) 仍有定义) ,函数取得增量 y f ( x0 x) f ( x0 ) ;
f ( x0 x) f ( x0 ) lim 若 存在,则称函数在 x0 点可导 x 0 x
且该极限为函数在 x0 点的导数,记为:
dy df ( x ) |x x0 f '( x) 、 y ' |x x0 、 |x x0 、 dx dx
6
关于导数定义的几点说明
y ①若 lim 不存在,则称函数 y f ( x) 在点 x0 处不可导。 x 0 x
f ( x0 x) f ( x0 ) 存在(即左极限存在) ,则称函数在 x0 点左 x 0 x f ( x0 x) f ( x0 ) (即右极限存在) ,则称函数在 x0 点右 导 可导;同理 lim x 0 x 数
1)求增量: y f ( x x) f ( x) C C 0
y f ( x x ) f ( x ) 0 2)算比值: x x f ( x x) f ( x) lim 0 0 3)求极限: f ( x) lim x 0 x 0 x
11
利用导数的定义求导数的一般步骤
(1)计算函数值增量 y f ( x x) f ( x)
y f ( x x ) f ( x ) (2)写比式: x x
y lim (3)求极限: f '( x) y ' x 0 x
12
例 求 f ( x) C ( C 为常数)的导数.
高中物理课件-高数第二章-导数与微分--课件

例2.已知 f x0 存在,求
lim f x0 ah f x0 bh
h0
h
3、导数的意义
函数 y f x在点x0 处的导数f x0
是因变量 y在点x0处的变化率,它反
映了 在点x0 处因变量随自变量的变
化而变化的快慢程度。
(二)导函数
1、定义:如果函数 y f x 在开区间
四、基本求导法则与导数公式
(一)常数和基本初等函数的导数公式
1. C 0
2. x x1
3. sin x cos x
4. cos x sin x
5. ta n x sec2 x 6. cot x csc2 x
7. sec x sec x tan x 8. csc x csc x cot x
则
k0
lim xx0
f
x f x0 就是曲线C
x x0
在 M0 x0, y0 点处切线的斜率。
二、导数的定义 (一)函数在一点处的导数
1、定义:设函数 y f x在点x0的某个
邻域内有定义,当自变量 x在x0 处取得
增量 x(点 x0
时 , 相应地函数
x 仍在该邻域内)
y 取得增量
chx shx
thx
1 ch2
x
arshx 1 archx 1
1 x2
x2 1
arthx
1
1 x2
例18.求
y cos x2 sin 1 arctan thx x
的导数。
例19.
y sin nxsinn xn为常数,求y
§2-3 高阶导数
(一)二阶导数
1、定义:把 y f x 的导数叫做函数
x xx0 x0
专升本高数数学第二章导数与微分

导数的几何意义
总结词
导数的几何意义是切线的斜率。
详细描述
函数在某一点的导数等于该点处切线的斜率。如果函数在某点可导,那么在该点处一定存在切线,并且切线的斜 率就是函数的导数值。
导数的物理意义
总结词
导数的物理意义是描述物理量变化率的重要工具。
详细描述
在物理学中,许多物理量的变化率都可以用导数来描述。例如,速度是位置函数的导数,加速度是速 度函数的导数等。通过导数的计算,可以深入了解物理量的变化规律和性质。
微分的物理意义是函数值随自变量变化的速率。
02
在物理量中,速度、加速度、角速度等都是微分的应
用,它们都是描述物理量随时间变化的速率。
03
微分可以用来解决物理中的一些问题,如求瞬时速度
、加速度等。
04 导数与微分的应用
CHAPTER
导数在几何中的应用
切线斜率
导数可以用来求曲线上某一点的 切线斜率,从而了解曲线在该点 的变化趋势。
专升本高数数学第二章导数与 微分
目录
CONTENTS
• 导数概念 • 导数的运算 • 微分概念 • 导数与微分的应用
01 导数概念
CHAPTER
导数的定义
总结词
导数是描述函数在某一点附近的变化 率的重要概念。
详细描述
导数定义为函数在某一点处的切线的 斜率,即函数在该点附近的小范围内 变化的速度。导数的计算公式为极限 lim(x->0) [f(x+Δx)-f(x)]/Δx,其中 Δx是自变量的增量。
解的精度。
无穷小分析
03
微分是无穷小分析的基础,可以用来研究函数在无穷小情况下
的性质和变化趋势。
谢谢
第二章 导数与微分
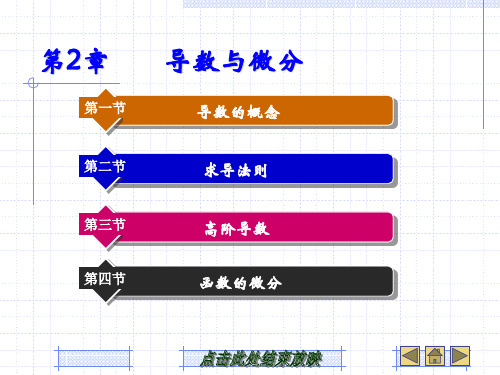
由此可见,当|Δx|很小时,(Δx)^2的作用非常小,可以忽略不计 因此,函数y=x^2在x0有微小改变量Δx时,函数的改变量Δy约为 2x0·Δx, Δy≈2x0·Δx.
从图2-3中不难看出,Δy表示的是以x0为边长的正方形外围 的阴影部分面积,它为图示的Ⅰ、Ⅱ、Ⅲ部分面积之和 2(x0·Δx)+(Δx)2,显然当|Δx|相对于x0很小时,(Δx)^2是微乎其 微的. 当f(x)=x2时,f′(x0)=2x0,因此Δy≈2x0·Δx可以写成 Δy≈f′(x0)·Δx. 由于f′(x0)·Δx是Δx的线性函数,所以通常把 f′(x0)·Δx叫做Δy的线性主部.
一般地,对于给定的可导函数y=f(x),当自变量在x0处有 微小的改变量Δx时,函数值y的改变量Δy可用下式近似计算, 即
已知曲线方程y=f(x),可以求过曲线上点M(x0,y0)处的 切线斜率.在M点的附近取点N(x0+Δx,y0+Δy),其中Δx可正 可负,作割线MN,其斜率为(φ为倾斜角) tanφ=Δy/Δx=[f(x0+Δx)-f(x0)]/Δx.当Δx→0时,割线MN将绕着 点M转动到极限位置MT,如图2-2所示.根据上面切线的定义, 直线MT就是曲线y=f(x)在点M处的切线.自然,割线MN的斜 率tanφ的极限就是切线MT的斜率tanα(α是切线MT的倾斜角).
以上两个问题,虽然它们所代表的具体内容不同,但从 数量上看,它们有共同的本质:都是计算当自变量的增量趋 于零时,函数的增量与自变量的增量之比的极限.在自然科学 、工程技术问题和经济管理中,还有许多非均匀变化的问题 ,也都可归结为这种形式的极限.因此,抽去这些问题的不同 的实际意义,只考虑它们的共同性质,就可得出函数的导数 定义.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章导数与微分数学中研究导数、微分及其应用的部分称为微分学,研究不定积分、定积分及其应用的部分称为积分学.微分学与积分学统称为微积分学.微积分学是高等数学最基本、最重要的组成部分,是现代数学许多分支的基础,是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.恩格斯(1820-1895)曾指出:“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”.微积分的发展历史曲折跌宕,撼人心灵,是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材(本部分内容详见光盘).积分的雏形可追溯到古希腊和我国魏晋时期,但微分概念直至16世纪才应运萌生.本章及下一章将介绍一元函数微分学及其应用的内容.第一节导数概念从15世纪初文艺复兴时期起,欧洲的工业、农业、航海事业与商贾贸易得到大规模的发展,形成了一个新的经济时代.而十六世纪的欧洲,正处在资本主义萌芽时期,生产力得到了很大的发展.生产实践的发展对自然科学提出了新的课题,迫切要求力学、天文学等基础科学的发展,而这些学科都是深刻依赖于数学的,因而也推动了数学的发展.在各类学科对数学提出的种种要求中,下列三类问题导致了微分学的产生:(1)求变速运动的瞬时速度;(2)求曲线上一点处的切线;(3)求最大值和最小值.这三类实际问题的现实原型在数学上都可归结为函数相对于自变量变化而变化的快慢程度,即所谓函数的变化率问题.牛顿从第一个问题出发,莱布尼茨从第二个问题出发,分别给出了导数的概念.内容分布图示★引言★变速直线运动的瞬时速度★平面曲线的切线★导数的定义★几点说明★利用定义求导数与求极限(例1、例2)★例3★例4★例5★例6★例7★左右导数★例8★例9★导数的几何意义★例10★例11★导数的物理意义★可导与连续的关系★例12★例13★例14★例15★内容小结★课堂练习★习题2-1★返回内容要点:一、引例:引例1:变速直线运动的瞬时速度;引例2:平面曲线的切线二、导数的定义:xx f x x f x y x f x x ∆-∆+=∆∆='→∆→∆)()(lim lim )(00000注:导数概念是函数变化率这一概念的精确描述,它撇开了自变量和因变量所代表的几何或物理等方面的特殊意义,纯粹从数量方面来刻画函数变化率的本质:函数增量与自变量增量的比值xy ∆∆是函数y 在以0x 和x x ∆+0为端点的区间上的平均变化率,而导数0|x x y ='则是函数y 在点0x 处的变化率,它反映了函数随自变量变化而变化的快慢程度.根据导数的定义求导,一般包含以下三个步骤:1.求函数的增量:);()(x f x x f y -∆+=∆2.求两增量的比值:x x f x x f x y ∆-∆+=∆∆)()(;3.求极限.lim 0x y y x ∆∆='→∆三、左右导数定理1函数)(x f y =在点0x 处可导的充要条件是:函数)(x f y =在点0x 处的左、右导数均存在且相等.四、用定义计算导数五、导数的几何意义六、函数的可导性与连续性的关系定理2如果函数)(x f y =在点0x 处可导,则它在0x 处连续.注:上述两个例子说明,函数在某点处连续是函数在该点处可导的必要条件,但不是充分条件.由定理2还知道,若函数在某点处不连续,则它在该点处一定不可导.在微积分理论尚不完善的时候,人们普遍认为连续函数除个别点外都是可导的.1872年得多数学家魏尔斯特拉构造出一个处处连续但处处不可导的例子,这与人们基于直观的普遍认识大相径庭,从而震惊了数学界和思想界.这就促使人们在微积分研究中从依赖于直观转向理性思维,大大促进了微积分逻辑基础的创建工作.例题选讲:导数概念的应用例1(讲义例1)求函数3x y =在1=x 处的导数)1(f '.例2(讲义例2)试按导数定义求下列各极限(假设各极限均存在).(1);)2()2(lim a x a f x f a x --→(2),)(lim 0xx f x →其中.0)0(=f 左右导数用定义计算导数例3(讲义例4)求函数C x f =)((C 为常数)的导数.例4(讲义例5)设函数,sin )(x x f =求)(sin 'x 及4|)(sin π='x x .例5(讲义例6)求函数n x y =(n 为正整数)的导数.例6(讲义例7)求函数)1,0()(≠>=a a a x f x 的导数.例7求函数)1,0(log ≠>=a a x y a 的导数.例8(讲义例3)求函数⎩⎨⎧=,,sin )(x x x f 00≥<x x 在0=x 处的导数.例9设)(x f 为偶函数,且)0(f '存在.证明.0)0(='f 例10求等边双曲线x y 1=在点⎪⎭⎫ ⎝⎛2,21处的切线的斜率,并写出在该点处的切线方程和法线方程.例11(讲义例8)求曲线x y =在点)2,4(处的切线方程.例12(讲义例9)讨论函数||)(x x f =在0=x 处的连续性与可导性.例13(讲义例10)讨论⎪⎩⎪⎨⎧=≠=0,00,1sin )(x x x x x f 在0=x 处的连续性与可导性.例14设函数⎩⎨⎧<≤+<=,10,10,)(2x x x a x f 问a 取何值时,)(x f 为可导函数.例15设函数⎩⎨⎧≥++<+=0,10,2)(2x bx x x a e x f x (1)欲使)(x f 在0=x 处连续,b a ,为何值;(2)欲使)(x f 在0=x 处可导,b a ,为何值.注:上述两个例子说明,函数在某点处连续是函数在该点处可导的必要条件,但不是充分条件.由定理2还知道,若函数在某点处不连续,则它在该点处一定不可导.在微积分理论尚不完善的时候,人们普遍认为连续函数除个别点外都是可导的.1872年得多数学家魏尔斯特拉构造出一个处处连续但处处不可导的例子(如第十一章第一节的Koch 雪花曲线描述的函数),这与人们基于直观的普遍认识大相径庭,从而震惊了数学界和思想界.这就促使人们在微积分研究中从依赖于直观转向理性思维,大大促进了微积分逻辑基础的创建工作.课堂练习1.函数)(x f 在某点0x 处的导数)(0x f '与导函数)(x f '有什么区别与联系?2.设)(x ϕ在a x =处连续,)()()(22x a x x f ϕ-=,求)(a f '.3.求曲线32x x y -=上与x 轴平行的切线方程.莱布尼茨(Friedrich ,Leibniz ,1597~1652)-----博学多才的数学符号大师出生于书香门第的莱布尼兹是德国一们博学多才的学者。
他的学识涉及哲学、历史、语言、数学、生物、地质、物理、机械、神学、法学、外交等领域。
并在每个领域中都有杰出的成就。
然而,由于他独立创建了微积分,并精心设计了非常巧妙而简洁的微积分符号,从而使他以伟大数学家的称号闻名于世。
莱布尼兹对微积分的研究始于31岁,那时他在巴黎任外交官,有幸结识数学家、物理学家惠更斯等人。
在名师指导下系统研究了数学著作,1673年他在伦敦结识了巴罗和牛顿等名流。
从此,他以非凡的理解力和创造力进入了数学前沿阵地。
莱布尼兹在从事数学研究的过程中,深受他的哲学思想的支配。
他的著名哲学观点是单子论,认为单子是“自然的真正原子……事物的元素”,是客观的、能动的、不可分割的精神实体。
牛顿从运动学角度出发,以“瞬”(无穷小的“0”)的观点创建了微积分。
他说dx 和x 相比,如同点和地球,或地球半径与宇宙半径相比。
在其积分法论文中,他从求曲线所围面积积分概念,把积分看作是无穷小的和,并引入积分符号⎰,它是把拉丁文“Summa ”的字头S 拉长。
他的这个符号,以及微积分的要领和法则一直保留到当今的教材中。
莱布尼兹也发现了微分和积分是一对互逆的运算,并建立了沟通微分与积分内在联系的微积分基本定理,从而使原本各自独立的微分学和积分学成为统一的微积分学的整体。
莱布尼兹是数字史上最伟大的符号学者之一,堪称符号大师。
他曾说:“要发明,就要挑选恰当的符号,要做到这一点,就要用含义简明的少量符号来表达和比较忠实地描绘事物的内在本质,从而最大限度地减少人的思维劳动,”正象印度——阿拉伯数学促进算术和代数发展一样,莱布尼兹所创造的这些数学符号对微积分的发展起了很大的促进作用。
欧洲大陆的数学得以迅速发展,莱布尼兹的巧妙符号功不可灭。
除积分、微分符号外,他创设的符号还有商“a /b ”,比“a :b ”,相似“∽”,全等“≌”,并“∪”,交“ ”以及函数和行列式等符号。
牛顿和莱布尼茨对微积分都作出了巨大贡献,但两人的方法和途径是不同的。
牛顿是在力学研究的基础上,运用几何方法研究微积分的;莱布尼兹主要是在研究曲线的切线和面积的问题上,运用分析学方法引进微积分要领的。
牛顿在微积分的应用上更多地结合了运动学,造诣精深;但莱布尼兹的表达形式简洁准确,胜过牛顿。
在对微积分具体内容的研究上,牛顿先有导数概念,后有积分概念;莱布尼兹则先有求积概念,后有导数概念。
除此之外,牛顿与莱布尼兹的学风也迥然不同。
作为科学家的牛顿,治学严谨。
他迟迟不发表微积分著作《流数术》的原因,很可能是因为他没有找到合理的逻辑基础,也可能是“害怕别人反对的心理”所致。
但作为哲学家的莱布尼兹比较大胆,富于想象,勇于推广,结果造成创作年代上牛顿先于莱布尼兹10年,而在发表的时间上,莱布尼兹却早于牛顿三年。
虽然牛顿和莱布尼兹研究微积分的方法各异,但殊途同归。
各自独立地完成了创建微积分的盛业,光荣应由他们两人共享。
然而在历史上曾出现过一场围绕发明微积分优先权的激烈争论。
牛顿的支持者,包括数学家泰勒和麦克劳林,认为莱布尼兹剽窃了牛顿的成果。
争论把欧洲科学家分成誓不两立的两派:英国和欧洲大陆。
争论双方停止学术交流,不仅影响了数学的正常发展,也波及自然科学领域,以致发展到英德两国之间的政治摩擦。
自尊心很强的英国民族抱住牛顿的概念和记号不放,拒绝使用更为合理的莱布尼兹的微积分符号和技巧,致使英国在数学发展上大大落后于欧洲大陆。
一场旷日持久的争论变成了科学史上的前车之鉴。
莱布尼兹的科研成果大部分出自青年时代,随着这些成果的广泛传播,荣誉纷纷而来,他也越来越变得保守。
到了晚年,他在科学方面已无所作为。
他开始为宫廷唱赞歌,为上帝唱赞歌,沉醉于研究神学和公爵家族。
莱布尼兹生命中的最后7年,是在别人带给他和牛顿关于微积分发明权的争论中痛苦地度过的。
他和牛顿一样,都在终生未娶。
1761年11月14日,莱布尼兹默默地离开人世,葬在宫廷教堂的墓地。
