第5章截交线与相贯线习题答案
截交线和相贯线习题答案

2.求特殊位置平面与直线的交点,并判别可见性。
3.求特殊位置平面与一般位置平面的交线,并判别可见性.
4.补全侧垂面与一般位置平面交线的两面投影,并判别可见性.
2021/5/23
1
4-5 平面与立体相交 7. 作出半个圆球与平面P的截交线的水平投影和侧面投影。
8. 作出半个圆球被截切后的正面投影和侧面投影。
9. 作出半个圆球被穿槽后的水平投影和侧面投影。
10. 完成物体的侧面投影。
2021/5/23
2
4-5 平面与立体相交 5. 完成圆锥被截切后的水平投影和侧面投影。
2021/5/23
6. 作出物体的侧面投影。
3
4-7 两立体相交 5. 补全圆柱与半圆球相交后的三面投影。
班级
2021/5/23
4
补全主视图上的相贯线
补全主视图上的相贯线
2021/5/23
5
补全主视图上的相贯线
补全俯 左视图上的相贯线
2021/5/23
6
补全主视图上的漏线
2021/5/23
7
2021/5/23
8
部分资料从网络收集整 理而来,供大家参考,
感谢您的关注!
机械制图(含习题集)(第二版)(章 (5)

第4章 组合形体中的截交线和相贯线
图4-1 形体表面的截交线和相贯线
第4章 组合形体中的截交线和相贯线
4.1 截 交 线
平面与平面或平面与曲面之间的交线称为截交线,在棱柱、 棱锥、圆柱、圆锥形体上切口、开槽时,均会在形体上产生截 交线。 4.1.1 棱柱表面的截交线
棱柱被切口时,最明显的情况是各条棱线的长短变得不一 样长。要绘制这种形体的图形,可以先按照完整的棱柱形体绘 制图形,然后度量各棱线的长度变化,连点成线,绘制出截平 面的投影,擦除棱线被截断的部分即可。
第4章 组合形体中的截交线和相贯线 绘制此形体图形时,还是要先绘制出完整的六棱台投影
图形,然后在上面加开槽的情况。正面投影中,开槽的情况 比较简单,由一条水平线和两条斜线组成。水平投影中槽底 的绘制方法与前面介绍的三棱锥的开槽绘制方法相同,这里 不再重复。槽侧面的水平投影要注意槽侧面与槽底的交线、 与棱台上表面的交线以及与棱台侧面棱线的交点(正面投影中 与虚线的交点),绘制出的棱台水平投影中心部分被分割成五 部分,分别表示槽底、槽侧面和棱台上表面的保留部分。
第4章 组合形体中的截交线和相贯线 4.1.2 棱锥、棱台表面的截交线
用一个与棱锥底平面平行的平面截切棱锥,去除锥顶部分, 得到的形体称为棱台。棱台的投影特点为:一个视图为两个形 状类似、大小不等的多边形,这个多边形就是棱锥的特征图形。 另两个视图为由若干个梯形组成的图形。在各视图中,所有侧 棱线的方向都指向锥顶,尽管这个锥顶已经被切除。
第4章 组合形体中的截交线和相贯线 图4-4所示为三棱锥上开槽时图形绘制的情况。对于这样
的立体,绘制时可以先绘制出三棱锥没有开槽时的三面投影, 然后绘制开槽的情况。由于这个槽是由一个水平面和两个侧平 面组成的,因此在正面投影中非常容易绘制,是由一条水平线 和两条垂直线组成的缺口。
第5章截交线和相贯线习题集答案解析
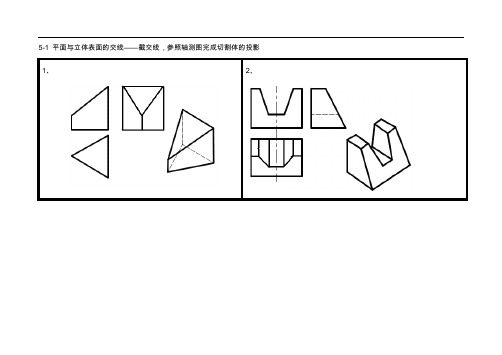
5-1 平面与立体表面的交线——截交线,参照轴测图完成切割体的投影1、2、
3、
4、
5-2 平面与立体表面的交线——截交线,参照轴测图完成切割体的投影
2、
3、 4、
5-4 两回转体表面的交线——相贯线,用表面取点法,画相贯线
1、
2、3、4、
5-5 两回转体表面的交线——相贯线,补画第三视图,用表面取点法,画相贯线
1、2、
3、
§2-2(3)平面与立体表面的交线——截交线 1、 完成同轴的圆锥和圆柱的截交线
5-6 两回转体表面的交线——相贯线,选择正确的左视图。
1、
2、
3、
4、
5-7 两回转体表面的交线——相贯线,补画第三视图,画相贯线
1、
2、
3、
4、
5-8 两回转体表面的交线——相贯线
1、作四棱柱与圆锥相贯后的W 、V 面的投影
2、作圆柱与圆锥相贯后的H 、V 面的投影
5-9 两回转体表面的交线——相贯线.分析立体表面交线,补全或补画相关投影
1、作圆柱与圆锥相贯后的H、V面的投影
2、作圆柱孔与圆锥相贯后的H、V面的投影
5-10 两回转体表面的交线——相贯线.分析立体表面交线,补全正面和侧面投影
1、作圆柱孔与圆相贯后的W、V面的投影
2、作棱柱与圆相贯后的H、V面的投影。
第五章 相贯线

第五章相贯线两立体表面相交,交线称为相贯线。
准确地画出相贯线的投影能更完整地表达立体。
实际中两立体相交可分为三种情况:平面立体与平面立体相交;平面立体与曲面立体相交;两曲立体相交,如图5-0-1所示。
相贯线有如下性质:1.相贯线一般是封闭的空间折线或曲线。
其形状随两相交立体表面的性质和相对位置的变化而不同。
2.相贯线是两立体表面的共有线,是两立体表面公共点的集合。
求相贯线,也就是求两相交立体表面的公共点。
第三节两曲面立体相交两曲面立体相交,相贯线为封闭的空间曲线,特殊情况为平面曲线。
下面介绍常用的两种方法。
一、表面取点法两回转体相交,如果其中有一个是轴线垂直于投影面的圆柱,则相贯线在该投影面上的投影,就积聚在圆柱面的有积聚性的投影上。
于是可以在这个相贯线有积聚性的投影上取一些点,按已知曲面立体表面上的点的一个投影,求其它投影的方法,即表面取点法,作出相贯线的投影。
例1:如图5-3-1所示,求作两正交圆柱的相贯线。
解:相贯线系两圆柱表面公共点的集合,应在铅垂轴线的小圆柱面上,其水平投影重合在水平投影中的小圆周上;同理相贯线的侧面投影也应重合在侧面投影的大圆周上。
故只有它的正面投影需要画出,可以用已知曲面上点的一个投影求另外投影的方法。
作图步骤如下:(1)先求特殊点,即求相贯线上的最前、最后、最左、最右、最上、最下等点。
在水平投影的小圆周上直接确定出相贯线上最左、最右点的投影1、3和最前、最后点的投影2、4;对应在侧面投影中为1″、3″和2″、4″,也是最高、最低点的侧面投影;按投影关系可得出它们的正面投影1′、3′和2′、4′。
因为两曲面立体前后对称相贯,故最前、最后两点的正面投影重合。
(2)求作若干一般位置点。
依连线光滑准确的需要,作出相贯线上若干个中间点的投影。
如在水平投影上取5、6点,其侧面投影为5″、6″,再求出其正面投影5′和6′。
(3)依次光滑连接1′、5′、2′(4′)、6′、3′各点,即得相贯线的正面投影。
第五章_截交线和相贯线

直 观 图
投
影 图
19
退 出
上一页
下一页
返 回
[例5-5] 如图5-6所示,求作被正平面P截切的圆锥的截交线。 当截平面垂直于圆锥轴线时,截交线是一个圆;当截平面过锥 顶时,截交线是过顶点的两条直线;当截平面与圆锥轴线斜交时 (θ>a),截交线是一个椭圆;当截平面与圆锥轴线斜交,且平行 一条素线时(θ=a),截交线是一条抛物线;当截平面与圆锥轴线 平行(θ=0°)或θ<a时,截交线为双曲线。
(2)求一般位置点。在圆球的正面投影上任取a′、(b′), 再通过a′、(b′)作水平圆,求其余两面投影a、b和a″、b″。 (3)判断可见性并光滑连接各点。由于被切去的是圆球的左、 上部分,所以截交线的水平投影和侧面投影都可见。依次连接各点 的同面投影,即得截交线的投影。
24
退 出
上一页
下一页
返 回
22
退 出
上一页
下一页
返 回
[例5-6] 如图5-7所示,求作圆球的截交线。
(a)已知条件
(b)作图结果
图5-7
退 出
求作圆球的截交线
下一页 返 回
23
上一页
作图: (1)求特殊位置点。点M、N、Ⅲ、Ⅳ、Ⅴ、Ⅵ分别是圆球三个 方向轮廊素线圆上的点。其中点M、N是最低、最高点,同时也是最 左、最右点。根据点M、N、Ⅲ、Ⅳ、Ⅴ、Ⅵ的正面的投影m′、n′、 3′、6′、5′、6′可求出相应的水平投影m、n、3、6、5、6及侧 面投影m″、n″、3″、6″、5″、6″。 椭圆长轴端点Ⅰ、Ⅱ。其正面投影1′、(2′)积聚成一点, 位于直线m′n′的中点。可通过1′2′作水平圆,求其余两面投影1、 2和1″、2″。
26
截交线练习题题解
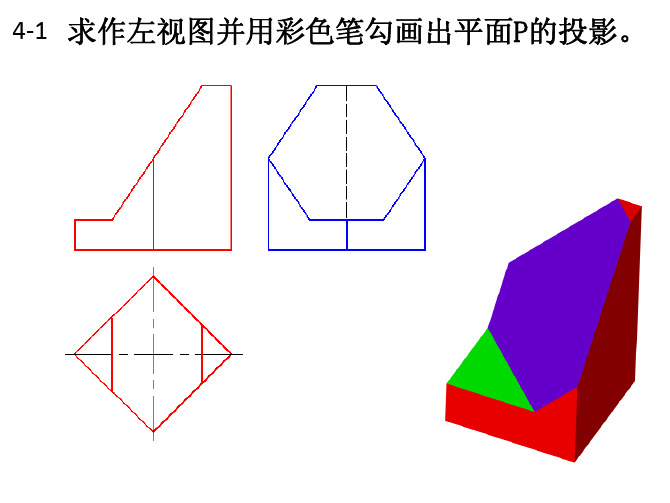
4‐2 求作俯视图并用彩色笔勾画出平面Q的投影。
4-3-1
补画俯视图
4-4
求三棱锥被截切后的俯视图和左视图。
4´ 3´ 6´ 1´ 2´≡5 ´ 5″≡6″
4″ 3″ 2″ 1″
6 4 3 1
5
2
*4‐7
补全俯视图和左视图上所缺的线。
4‐8
4‐29 求作左视图。
4‐30 求圆球被截切后的俯视图和左视图。
4‐31
求圆球被截切后的俯视图和左视图。
5‐39 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷
正确的左视图是 ⑶
5‐40 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷
正确的左视图是 ⑷
4‐19 求作俯视图。
第三节 立体与立体相交
二、平面立体与曲面立体相交
【例】空心圆柱开矩形孔
分析:本例为圆柱与四棱柱 外-内相贯、内内相贯。 交线在水平投影和侧面投 影有重影性,已确定。需要 求其正面投影 过程: (1)先求内棱柱表面与外圆 柱面的交线 (2)再求内棱柱表面与内圆 柱面的交线 注意:由于切割,相交处的 内、外转向轮廓线都不存在 (3)可见性判别,不可见轮廓 线画虚线
54
4-23 补全主视图上所缺的接交线,并作左试图。
4‐24 补全俯视图并求左视图。
4-20 补全左视图
4-21 补全左视图
4‐25 补全左视图并求俯视图。
4‐26 求作俯视图。
4‐27 求作俯视图。
1′ 4′(5′) 6′(7′) 2′(3′)
5 1 3 2 4 7 6
4‐28
相贯线习题集答案

相贯线习题集答案相干线是几何学中一个重要的概念,它涉及到直线和圆的交点问题。
在几何学中,相干线习题集是帮助学生理解和应用相干线概念的重要工具。
本文将为读者提供一些相干线习题集的答案,帮助他们更好地理解和应用这一概念。
1. 问题:已知一个圆的半径为r,圆心坐标为(a,b),一条直线的方程为y = mx + c。
求证:当直线过圆心时,它与圆的交点在直线上对称。
解答:首先,我们可以将直线方程代入圆的方程,得到一个关于x的二次方程。
因为直线过圆心,所以圆心的坐标(a,b)必定满足这个二次方程。
因此,这个二次方程的解必定是x = a的形式。
接下来,我们可以将直线方程和圆的方程联立,解这个方程组,得到交点的坐标。
由于直线过圆心,所以交点的横坐标必定是a,纵坐标可以通过直线方程求出。
因此,交点的坐标为(a,ma + c)。
根据对称性,我们可以得出结论:交点在直线上对称。
因为直线过圆心,所以直线与圆的交点在直线上对称。
2. 问题:已知一个圆的半径为r,圆心坐标为(a,b),一条直线的方程为y = mx + c。
求证:当直线与圆相切时,它与圆的切点在直线上对称。
解答:首先,我们可以将直线方程代入圆的方程,得到一个关于x的二次方程。
因为直线与圆相切,所以这个二次方程必定有一个重根,即两个根相等。
因此,这个二次方程的判别式必定为0。
接下来,我们可以将直线方程和圆的方程联立,解这个方程组,得到交点的坐标。
由于直线与圆相切,所以交点的坐标必定是两个相等的数对。
因此,交点的坐标为(x,mx + c)和(x,mx + c)。
根据对称性,我们可以得出结论:切点在直线上对称。
因为直线与圆相切,所以直线与圆的切点在直线上对称。
通过以上两个习题的解答,我们可以看到相干线的概念在几何学中的重要性。
相干线不仅涉及到直线和圆的交点问题,还可以应用于其他几何图形的求解。
通过理解和应用相干线的概念,我们可以更好地解决几何学中的问题。
总结起来,相干线习题集的答案可以帮助学生更好地理解和应用相干线的概念。
截交线与相贯线习题

第五节截交线与相贯线截交线和相贯线是立体表面常见的两种表面交线,立体被平面截切,表面就会产生截交线,两立体相交,表面就产生相贯线,二者有共同点,也有不同点。
一、截交线的特性及画法【考纲要求】1、掌握特殊位置平面截断棱柱和棱锥的截交线画法;2、掌握特殊位置平面截断圆柱、圆锥、圆球的截交线画法;3、掌握简单的同轴回转体的截交线画法;【要点精讲】(一)截交线的定义:由平面截断基本体所形成的表面交线称为截交线。
(二)截交线的特性:1、任何基本体的截交线都是一个封闭的平面图形(平面体是平面多边形,曲面体是平面曲线或由平面曲线与直线共同组成的图形);2、截交线是截平面与基本体表面的共有线,截交线上的每一点都是截平面与基本体表面的共有点(共有点的集合)。
(三)求截交线的方法:①积聚性求点法;②辅助(素)线法;③辅助平面法。
(四)求截交线的步骤:1、确定被截断的基本体的几何形状;2、判断截平面的截断基本体的位置(回转体判别截平面与轴线的相对位置3、想象截交线的空间形状;4、分析截平面与投影面的相对位置,弄清截交线的投影特性;5、判别截交线的可见性,确定求截交线的方法;6、将求得的各点连接,画出其三面投影。
(五)平面体的特殊截交线及画法:1、特性:平面体的截交线都是由直线所组成的封闭的平面多边形。
多边形的各个顶点是棱线与截平面的交点,多边形的每一条边是棱面与截平面的交线。
2、画法:求平面体截交线的方法主要是用积聚性求点法和辅助线法。
画平面体的截交线就是求出截平面与平面体上各被截棱线的交点(即平面多边形的各个顶点),然后依次连接即得截交线。
根据截交线是截平面与基本体表面的共有线,截交线上的点也是截平面与基本体表面的共有点,我们所要求掌握的是特殊位置平面截切平面立体的截交线,我们可以利用积聚性求点法或辅助平面法,求出截平面与平面立体的各棱线的交点,然后依次连接,也就求出了截交线。
例如图5-1所示,先根据截交线具有积聚性投影的正面投影和具有收缩性的水平投影确定出截平面与六棱柱棱线的六个交点(截交线平面多边形的六个顶点),再利用积聚性求点法求出其侧面投影。
机械制图及计算机绘图第三版习题册参考答案

模块一制图的基本知识与基本技能1-1 抄画平面图形(略)1-2 字体练习(略)1-3 字体练习(略)1-4 在右侧按照1∶1比例绘制左侧图形(略)1-5 标注平面图形的尺寸(略)121-6 标注尺寸(数值从图中度量,取整数)31-7 指出图中尺寸标注的错误,并在下面中正确地标注尺寸41-8 标注平面图形的尺寸(尺寸从图中量取,取整数)1-9 正多边形和椭圆练习(略)1-10 按照1∶1的比例抄绘平面图形,并标注尺寸(略)1-11 按照1∶2的比例抄绘平面图形,并标注尺寸(略)561-12 按照样图上所注尺寸完成下面图形的线段连接(比例1∶1)71-13 按照样图上所注尺寸完成下面图形的线段连接(比例1∶1)1-14 选择合适的比例,绘制拉楔平面图,并标注斜度、锥度和尺寸(略)891-15 斜度和锥度练习1-16 按照样图上所注尺寸,选择合适的比,在下方绘制图形,并标注尺寸(略)10111-17 按照样图上所注尺寸,在下方绘制图形(比例1∶1)121-18 按照样图上所注尺寸,在下方绘制图形(比例1:1)1-19 按照样图上所注尺寸,在下方绘制图形(比例1:1)模块二绘制物体的三视图2-1 绘制三视图(略)14152-2 参照立体图,根据两视图补画第三视图162-3 参照立体图,补画三视图中漏画的图线172-4 根据两视图补画第三视图182-5 根据两视图补画第三视图192-6 根据两视图补画第三视图202-7 根据两视图补画第三视图212-8 根据两视图补画第三视图222-9 点的投影232-10 参照立体图补画第三视图,并求其表面上点的未知投影242-11 直线的投影252-12 在三视图上找出标注字母的棱线的未知投影并描粗,填空说明直线的种类262-13 平面的投影272-14 在三视图上标出平面的投影,并填空2-15 绘制基本几何体的三视图,并标注尺寸(略)28292-16 基本几何体的三视图及尺寸标注302-17 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)312-18 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)32 2-19 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)332-20 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)342-21 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)352-22 根据两视图补画第三视图,并标注尺寸(尺寸从图中量取,取整数)模块三轴测图3-1 看懂两视图,绘制正等轴测图(略)36373-2 看懂两视图,绘制正等轴测图(尺寸从图中量取,取整数)3-3 看懂两视图,绘制正等轴测图(略)38393-4 看懂两视图,补画第三视图,并绘制正等轴测图(尺寸从图中量取,取整数)403-5 看懂两视图,补画第三视图,并绘制正等轴测图(尺寸从图中量取,取整数)3-6 看懂两视图,绘制斜二等轴测图(略)41423-7 看懂两视图,绘制斜等轴测图(尺寸从图中量取,取整数)3-8 看懂两视图,绘制斜等轴测图(尺寸从图中量取,取整数)模块四截交线与相贯线4-1 求作立体表面上点的投影(略)44454-2 求作立体表面上点的投影464-3 求作平面立体上的截交线474-4 求作平面立体上的截交线4-5 求作曲面立体上的截交线(略)48494-6 根据两视图补画第三视图504-7 根据两视图补画第三视图。
《机械制图》孙敬华_习题解答 4-截交线

3-3 完成截切后立体的第三面投影。 (4)
首页
答案
题目
下一题 上一题 立体图
截交线
立体三视图 点线面投影 基本体 截交线 相贯线 轴测图 组合体 机件表达法 标准件常用件 零件图 装配图 零部件测绘 按ESC返回
立体三视图点线面投影基本体组合体机件表达法标准件常用件零件图装配图零部件测绘按esc返回基本体321322323324325326331332333334335336立体三视图点线面投影基本体组合体机件表达法标准件常用件零件图装配图零部件测绘按esc返回首页答案下一题题目32完成截切后立体的第三面投影
3-3 完成截切后立体的第三面投影。 (2)
首页
答案
题目
下一题 上一题 立体图
截交线
立体三视图 点线面投影 基本体 截交线 相贯线 轴测图 组合体 机件表达法 标准件常用件 零件图 装配图 零部件测绘 按ESC返回
3-3 完成截切后立体的第三面投影。 (2)
首页
答案
题目
下一题 上一题 立体图
截交线
立体三视图 点线面投影 基本体 截交线 相贯线 轴测图 组合体 机件表达法 标准件常用件 零件图 装配图 零部件测绘 按ESC返回
3-3 完成截切后立体的第三面投影。 (5)
首页
答案
题目
下一题 上一题 立体图
截交线
立体三视图 点线面投影 基本体 截交线 相贯线 轴测图 组合体 机件表达法 标准件常用件 零件图 装配图 零部件测绘 按ESC返回
3-2 完成截切后立体的第三面投影。 (1)
第五章截交线和相贯线

截交线 形 状
圆
椭圆
抛物线
PV
双曲线
PV
两条素线
投 影 图 及 立 体 图
PV
PV PV
[例一]: 圆锥被正垂面截切,求 截交线,并完成三视图。
截交线 截交线 的空间 的投影 如何找椭圆另 形状? 特性? 一根轴的端点?
★找特殊点 ★补充中间点 ★光滑连接各点 ★分析轮廓线的 投影
擦除多余作图线后的结果
截交线和相贯线
§ 概 述
平面与立体相交叫作截交,立体表面产生的交线叫做截交 线。两立体相交叫作相贯,其表面产生的交线叫做相贯线。
本章主要讨论截交线和相贯线的投影特性及画法。
1.截交的形式
截交线
平面与平面体相交
平面与曲面体相交
2.相贯的形式
相贯线
平面体与平面体 相贯线
平面体与曲面体
曲面体与曲面体
多形体相交
[例二]:求圆锥被截切后的截交线,并完成三视图。 QV
PV
擦除多余作图线后的结果
[例三]:求圆锥被截切后的截交线,并完成三视图。 QV PV
擦除多余作图线后的结果
5. 球体的截切
平面与圆球相交,截交线的形状都是圆,但根据 截平面与投影面的相对位置不同,其截交线的投影可 能为圆、椭圆或积聚成一条直线。
[例一]:求半球体截切后的俯视图和左视图。
两个侧平面截圆球的截交 水平面截圆球的截交线 线的投影,在左视图上为 的投影,在俯视图上为 部分圆弧,在俯视图上积 部分圆弧,在侧视图上 聚为直线。 积聚为直线。
擦除多余作图线后的结果
平面立体和曲面立体的相贯线
相贯线的主要性质
★ 表面性 相贯线位于两立体的表面上(外表面或内表面)。 ★ 封闭性 相贯线一般是封闭的空间折线(通常由直线和曲线 组成)或空间曲线。 ★ 共有性 相贯线是两立体表面的共有线。 ★ 空间性 相贯线一般是空间曲线,有时也为平面曲线或直线
《机械制图》第一章,制图的基本知识习题及参考答案

第1章 制图的基本知识和基本技能
• 第2页:1-3: 1, 2, 3, 4, 5 • 第3页:1-4 :1; 2:1),2),3)
返回总目录
退出
第2页
1-3 尺寸标注
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第2页
1-3 尺寸标注
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第2页
1-3 尺寸标注
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第2页
1-3 尺寸标注
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第2页
1-3 尺寸标注
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第3页 1-4 几何作图
1.作斜度和锥度。
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第3页 1-4 几何作图
2.将下面图形按尺寸数值画在右边。
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第3页 1-4 几何作图
返回总目录
转到:第1章
制图的基本知识和基本技能
退出
第3页 1-4 几何作图
返回总目录
转到:第1章
制图的基本知识和基本技能
退意单击退出
转到:第1章 制图的基本知识和基本技能
机械制图习题集
(第3版)
参考答案
目
• • • • • • • • • •
录
第1章 制图的基本知识和基本技能 第2章 投影基础 第3章 基本立体及立体的形成 第4章 截交线与相贯线 第5章 物体的三视图 第6章 轴测图 第7章 机件的各种表达方法 第8章 标准件和常用件的画法 第9章 零件图 第10章 装配图
截交线 相贯线
返回本章界面
当轴线平行的两圆柱体相交时,相贯线为两条直线。 当两圆锥共顶相交时,相贯线为直线,
返回本章界面
相贯体实例
返回本章界面
5-1 基本体的投影
5-2 基本体的截交线
5-3 相贯线
退出
5-2
基本体的截交线
一、圆柱体的截交线
平面与圆柱表面相交,有三种情况
返回本章界面
5-2
基本体的截交线
1、圆柱体的截交线投影
平面与圆柱表面相交,有三种情况
返回本章界面
求圆柱被一正垂面截切后的截交线。
基本体的截交线
二、圆锥体的截交线
有五种情况
3-3 相贯线
2、近似画法
R=D/2 o 1 2
D
返回本章界面
为了简化作图,两圆 柱正交的相贯线一般 采用近似画法。以相 交两圆柱中较大圆柱 的半径画弧所得。画 图步骤:以1′为圆心, 以R=D/2为半径画弧, 交于小圆柱的中心线 于O点,再以O点为 圆心,以R为半径, 过1′、2′画弧。
圆柱穿孔的相贯线的画法
返回本章界面
孔与孔相交的相贯线画法
返回本章界面
3-3 相贯线
3、特殊画法
两回转体相交,交线一般为空间曲线,在特殊 情况下,交线为平面曲线或直线,
当两回转体 轴线相交且 公切于一个 球时,相贯 线为椭圆
返回本章界面
线
当回转体与球体相交且球心在回转体轴线上时, 相贯线为垂直于轴线的圆
返回本章界面
相贯线
一、相贯线的概念
两曲面立体 相交,其交 线是两曲面 立体的共有 线,该线也 叫相贯线, 相贯线上的 点是两曲面 立体的共有 点。
单击图片演示动画
返回本章界面
截交线练习题题解
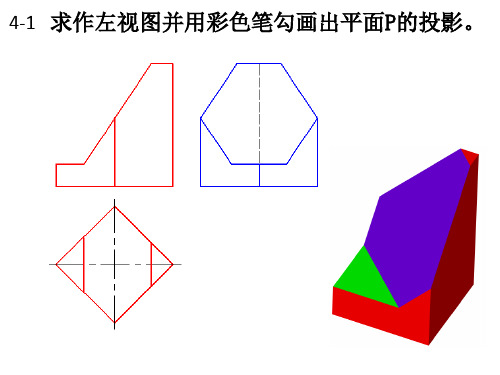
4-28
求作左视图。
4-29 求作左视图。
4-30 求圆球被截切后的俯视图和左视图。
4-31
求圆球被截切后的俯视图和左视图。
5-39 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷
正确的左视图是 ⑶
5-40 已知主视图和俯视图,选择正确的左视图。
⑴
⑵
⑶
⑷正确的左视图是 ⑷来自4-19 求作俯视图。
第三节 立体与立体相交
二、平面立体与曲面立体相交
【例】空心圆柱开矩形孔
分析:本例为圆柱与四棱柱 外-内相贯、内内相贯。 交线在水平投影和侧面投 影有重影性,已确定。需要 求其正面投影 过程: (1)先求内棱柱表面与外圆 柱面的交线 (2)再求内棱柱表面与内圆 柱面的交线 注意:由于切割,相交处的 内、外转向轮廓线都不存在 (3)可见性判别,不可见轮廓 线画虚线
求作左视图。
4-10 求作俯视图并标出平面P的其余两投影。
*4-11
求作左视图。
*4-13
补全主视图和俯视图上所缺的线。
*4-14
补全主视图和俯视图上所缺的线。
*4-15
补全主视图和左视图上所缺的线并标 出P、Q面的投影。
4-16
求作俯视图。
4-17 求作俯视图。
4-18
求作俯视图。
4-1 求作左视图并用彩色笔勾画出平面P的投影。
4-2 求作俯视图并用彩色笔勾画出平面Q的投影。
4-3-1 补画俯视图
4-4
求三棱锥被截切后的俯视图和左视图。
4´ 3´ 5″≡6″ 1´ 2´≡5 ´
4″
3″
2″ 1″
6´
5 6 4 3 1 2
画法几何及工程制图第五章习题详解

a
e d
c
m
还有其他求解办法?
换面法
M f F
L
6
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-圆柱
a
c (d)
b
d
a (b) c
D A
B
C
a
c (d) d
b
d a (b)
c
A
C
a c
b
AA — 最左素线, BB — 最右素线 CC — 最前素线, DD — 最后素线
m
m ) (
m
辅助圆法
m M m
13
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
Z
V
W
X
Y
14
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
b
a
d
c
15
§5.1 立体的投影-根据已知立体作投影图-曲面立体的投影-环
m (n') (n )
s
p 完了吗? S
31
§5.2 平面与立体相交-作图方法-平面与球相交
32
§5.2 平面与立体相交-作图方法-平面与球相交
2'
2"
7' 8' 3'4' 5'6'
1 '
8" 4"
6"
7" 3" 5"
1"
6
4 8
1
2
7 5 3
33
§5.2 平面与立体相交-作图方法-平面与环面相交
p
34
§5.2 平面与立体相交-作图方法-平面与环相交
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-1 平面与立体表面的交线——截交线,参照轴测图完成切割体的投影 1、
2、
3、
4、
5-2 平面与立体表面的交线——截交线,参照轴测图完成切割体的投影
2、
3、
4、
5-4 两回转体表面的交线——相贯线,用表面取点法,画相贯线
1、
2、3、4、
5-5 两回转体表面的交线——相贯线,补画第三视图,用表面取点法,画相贯线
1、2、
3、§2-2(3)平面与立体表面的交线——截交线
1、完成同轴的圆锥和圆柱的截交线
5-6 两回转体表面的交线——相贯线,选择正确的左视图。
1、2、3、4、
5-7 两回转体表面的交线——相贯线,补画第三视图,画相贯线 1、
2、
3、
4、
5-8 两回转体表面的交线——相贯线
1、作四棱柱与圆锥相贯后的W、V面的投影
2、作圆柱与圆锥相贯后的H、V面的投影
5-9 两回转体表面的交线——相贯线.分析立体表面交线,补全或补画相关投影
1、作圆柱与圆锥相贯后的H、V面的投影
2、作圆柱孔与圆锥相贯后的H、V面的投影
5-10 两回转体表面的交线——相贯线.分析立体表面交线,补全正面和侧面投影
1、作圆柱孔与圆相贯后的W、V面的投影
2、作棱柱与圆相贯后的H、V面的投影。
