线性系统理论 西工大解剖
西北工业大学-《827信号与系统》-基础提高-第25-26讲

专业课基础提高课程第25讲第九章系统的状态变量分析法(一)第九章系统的状态变量分析法9-0、引言1、经典的线性系统理论已经发展成熟:(1) 基本模型:微(差)分方程和系统函数(传递函数、转移函数);(2) 分析过程:着重运用频率响应特性的概念;(3) 有效性:系统即可观测又可控制;(4) 局限性:未能完全揭示系统的内部特性,不能有效处理多输入多输出系统。
2、航天技术发展,诞生了现代控制理论,完成了从经典到现代的转变;3、现代系统与控制理论特点:(1)利用描述系统内部特性的状态变量取代描述系统外部特性的系统函数;(2)便捷的运用到多输入多输出系统;(3)可以分析系统的“可观测性”和“可控制性”;(4)可以描述非线性系统和时变系统;(5)便于计算机求解(一阶微分方程、差分方程)。
4、分析方法:状态变量法以系统内部的状态变量x(t)为分析对象;建立f(t)与x(t)以及f(t)、x(t)与y(t)的关系。
9-1 连续系统状态空间方程建立一、引例二、几个常用术语:1、状态:在已知系统激励条件下求解系统所必需具备的最少信息。
状态变量在某一时刻的取值,如:uc(0+)、iL(0+)等。
2、状态变量:随时间变化的一组独立完备变量。
即能够表示系统状态的变量(个数=系统阶数),状态变量之间不能线性求解;与激励一起可以线性表示系统的所有响应;给定电路,通常选独立电容电压和独立电感电流,给定模拟图,选积分器(单位延时器)的输出;3、状态方程:描述系统状态变量、激励与状态变量一阶导数关系的微分(一阶差分)方程组。
4、输出方程:描述系统状态变量、激励与输出响应关系的代数方程组。
5、状态向量:由状态变量做分量所构成的向量。
(n维)6、状态空间:状态变量所有取值的集合。
即状态向量所在的空间。
7、状态轨迹:在状态空间中状态向量端点随时间变化所形成的轨迹。
三、状态空间方程的标准形式:状态方程矩阵形式:输出方程矩阵形式:()1()c du t i t dt C= ()()Ru t Ri t =()()()()L c s u t Ri t u t u t =--+ []()()00()()()11R s c L i t u t R u t u t u t R ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦对有m 个输入,q 个输出的n 阶系统:状态空间方程的标准形式四、状态空间方程的建立1、已知系统的电路图(纯正网络)(直接列写法)1) 选状态变量:独立、完备(个数=系统阶数)一般可选独立电容电压和独立电感电流;2) 初始方程列写:写出独立电容所在节点KCL方程;最好只含一个电容;写出独立电感所在回路KVL方程;最好只含一个电感;3) 消去非状态变量、整理化简方程为标准型方程:4) 列写输出方程,并整理为标准型方程:2、已知系统模型列写(间接列写法)1) 已知系统微分方程列写状态空间方程。
西工大、西交大自动控制原理 第三章 线性系统的时域分析法_04

幅及相位中表现出来了。
可在两个层面上应用主导极点法: 1 略去非主导极点,直接用二阶系统代替。 2 略去非主导极点引起的暂态分量,但不忽略非主
导极点本身(在主导暂态分量系数中计及非主导 极点的影响)。
2 高阶系统动态性能指标的近似估算公式
(1)高阶系统的单位阶跃响应
1 三阶系统的单位阶跃响应
(5)闭环主导极点
闭环主导极点:假若距离虚轴较远的闭环极点的实部
与距离虚轴最近的闭环极点的实部的比值大于或
等于5,且距离虚轴最近的闭环极点的附近也不存
在闭环零点。那么,这个距离虚轴最近的闭环极
点对系统的时间响c(应t )
环主导极点。
起着主导作用,称之为闭
闭环主导极点常以一对具有负实部的共轭复数极点的 形式出现。
三阶系统(有零点时)的单位阶跃响应为:
c(t ) 1 a1ent cosd t a2ent sin t a3e p3t
与无零点的三阶系统相比,可知:
a1 a1
a2 a2
a3 a3
下面进一步讨论三阶系统的闭环极点 ( p3 ) 和闭环零点 (z) 对系统时间响应的影响:
Amplitude
5
c() O
0.5 0.3
p3 n
0.3
n 1
t
1 三阶系统的单位阶跃响应
(2)闭环极点 ( p3) 的影响小结 A:系统输出的时间响应 c(t) 中的暂态分量是由系统的
闭环极点造成的。
B:一个稳定的n 阶系统,必有n 个具有负实部的闭环 极点,系统时间响应c(t) 中就相应n有 项暂态分量。
c(t ) 1 a1ent cosd t a2ent sind t
西工大-线性系统理论第七章

Robust控制器设计及灵敏度分析基础
基于利用状态反馈和输出反馈的控制器设计,能有效
地解决系统地极点配置问题,从而使系统的稳定性和响应 品质得到保证。但是,控制器的设计是在假定受控对象模 型参数已经确切知道的前提下进行的,实际运行中的系统, 由于对象建模误差以及制造公差、环境变化、元件老化等 原因,使对象参数可能处在较大范围的变化之中,通
A
0 1 0 0
0 0
0 1
0 0 1 0 0 0 11 0
, b
0 1
4 , d , c 1 0 0 0 0 0 0 6
式中
A BK BK 1 2 ,C C 0 A 1 1 C 0 闭环系统结构图见图7.1。令闭环系统特征多项式
(7.17)
det I A 与期望的特征多项式 f *() 相等,即 1 f *() det I A 1 K 、矩阵诸元。至此设计便告完成。 可确定 K1 、 2
y(t) yref (t) 。故无静差特性可表示为 即 lim t y(t ) y 0 lim e ( t ) lim ( t ) ref t t
(7.2)
式中
e(t) y(t) yref (t)
(7.3)
称 e(t) 为系统跟踪误差。当受控对象参数发生变化时(这里所 指的参数变化不是无限小的变化),若所设计的控制器任能是
由图7.1所示闭
环结构图可导出鲁 棒控制系统的一般 结构,见图7.2。一
个鲁棒控制系统,实质上是一个包含补偿器的输出反馈系 统,其中饲服补偿器用于实现扰动抑制及渐进调节,根据 外作用模型来构造;镇定补偿器用于使闭环系统镇定,它包 含状态反馈 K1 及 K2,当状态需重构时,还包含状态观测器, 而状态观测器根据受控对象模型来构造。鲁棒控制器则是饲 服补偿器和镇定补偿器的组合。下面来研究鲁棒控制器的一
线性系统理论全PPT课件

为线性系统;
3
• 线性系统满足叠加性; • 线性系统可以用数学变换(付里叶变换, 拉普拉斯变换)和线性代数; • 线性系统的分类
定常系统:参数不随时间变化
时变系统;参数是时间t 的函数
4
2、线性系统理论的主要任务
主要研究线性系统状态的运动规律和改变
这种运动规律的可能性和方法,建立和揭示
系统结构、参数、行为和性能间的确定的和 定量的关系。 分析问题:研究系统运动规律 综合问题:研究改变运动规律的可能性和方法
5
• 建立数学模型 • 数学模型的基本要素是变量、参量、常数 和它们之间的关系 • 变量:状态变量、输入变量、输出变量、
扰动变量
• 参量:系统的参数或表征系统性能的参数
• 常数:不随时间改变的参数
6
• 时间域模型:微分方程组或差分方程组 可用于常系数系统 和变系数系统 • 频率域模型:用传递函数、频率响应
2.1 状态和状态空间
系统动态过程的数学描述
u1
yq
u2
up
x1, x2 ,, xn
y2
yq
1/4,1/50
(1)系统的外部描述 外部描述常被称作为输出—输入描述 例如.对SISO线性定常系统:时间域的外部描述:
u1
yq
u2
up
x1, x2 ,, xn
y2
yq
y ( n) an1 y ( n1) a1 y (1) a0 y bn1u ( n1) b1u (1) b0u
(3) 状态向量:以系统的 n 个独立状态变量
x1 t , L, xn t 作为分量的向量,即 x t x1 t , L, xn t .
西工大线性系统理论第四章

线性系统理论
1 0 0 0 0 0 0 2 1 0 0 0 0 0 1 0 0 0 A 0 0 0 3 0 0 0 0 0 0 3 1 0 0 0 0 0 1 1 0 0 B 0 0 1 0 0 1 1 0 0
动态方程,必含有不能控或/和不能观测的状态变量。
线性系统理论
(a)
(b)
(c)
图4.2 引例2 的三种实现
线性系统理论
下面来研究多变量系统的能控类和能观测类的典型实
现方法,进而讨论最小实现的特性和寻求最小实现的方法。
线性系统理论
4.2 传递函数矩阵的能控规范性和能观测规范型
实现
就单输入—多输出、多输入—单输出、多输入—多输 出系统的情况分别进行研究。
d G( s)
线性系统理论
同理,取 gi ( s ) 的最小公分母且记为 D(s) ,可得 G( s)的 一般形式为 1 n1 n1 G( s) s s s q ,1s q ,0 1,n1 1,1 1,0 q ,n1 D( s ) (4.13) 考虑到多输入—单输出情况,输入矩阵有p列,输出矩阵 1 只有一行,据p个子系统传递函数的公共部分 写出 D( s) 能观测规范型 ( A, c) 是方便的,且写不出能控规范型实现。
线性系统理论
系统输出为诸子系统输出之和,即
y ( s) g1 ( s)u1 ( s) [ g1 ( s) G ( s)u ( s)
g p ( s)u p ( s) g p ( s)][u1 ( s) u p ( s)]T
(4.11)
其中 G(s) 为一行,其展开式为 G( s) d1 g1 ( s) d p g p ( s) (4.12)
线性系统的结构分解

% C = CT = ( C1 0 C3
0)
从上面三个矩阵可以看出来,整个状态空间可 以分为能控能观,能控不能观,不能控能观, 不能控不能观四个部分,分别用 xco , xco , xco , xco 表示,于是有:
⋅ % % x co A11 ⋅ % % x co = A21 ⋅ 0 % x co ⋅ 0 x co %
其秩,rankN = 2 < n
所以该系统是状态不全能观的。
为构造非奇异变换阵R0-1,取 R1′ = C = [0 1 2] ′ R2 = CA = [1 − 2 3] ′ R3 = [0 0 1] 0 1 − 2 2 1 1 得 −1 1 − 2 3 , R = 1 0 2 R0 = 0 1 0 0 0 0 1 其中R3,是在保证R0-1非奇异的条件下任意选取的。 于是系统状态空间表达式变换为
% A11 % % = T −1 AT = A21 A 0 0
0 % A 0 0
22
% A13 % A23 % A
33
% A43
0 % A24 0 % A44
B1 % = T −1 B = B2 B 0 0
xco y = CRO1 = (C1 , 0) xco
经过上述三步,便可以导出系统同时按 能控性和能观性进行分解的表达式:
⋅ % % x co A11 ⋅ % % x co = A21 ⋅ 0 % x co ⋅ 0 x co %
0 xco x A44 co
xco xco y = C 2 RO 2 = (C3 , 0) xco xco
西北工业大学航天学院【硕士课程简介】

02 航天学院序号:课程编号:02M001课程名称:线性系统理论任课教师:周军刘莹莹英文译名:Linear System Theory先修要求:《线性代数》和《矩阵论》中任一门、《复变函数》内容简介:《线性系统理论》是控制类、系统工程类、电类、计算机类、机电类等许多学科专业硕士研究生的一门公共基础理论课,是控制、信息、系统方面系列理论课程的先行课。
《线性系统理论》是最优估计、最优控制、系统辨识、自适应控制等现代控制理论的基础,系统讲述线性系统的运动规律,揭示系统中固有的结构特性,建立系统的结构、参数与性能之间的定性和定量关系,以及为改善系统性能,满足工程指标要求而采取的各类控制器设计方法。
具体的内容包括:线性系统的状态空间描述、状态空间描述与传递函数描述的关系、线性系统的运动分析、能控性、能观性、稳定性理论、线性反馈系统的状态空间综合方法、线性鲁棒性控制基本理论、线性系统的基本代数理论,以及多变量频域设计方法等。
主要参考书:(1)《线性系统理论》阙志宏主编,西安西北工业大学出版社,1995;(2)《现代控制理论引论》周凤歧等,北京国防工业大学出版社,1988;(3)《线性理论》郑大中编著,北京清华大学出版社;(4)《线性系统理论与设计》[美]陈启宗,科学出版社,1988。
序号:课程编号:02M900课程名称:专业英语任课教师:周军英文译名:Professional English先修要求:专业方面的课程内容简介:本课程作为一种基本的专业英语技能,在阅读和学习与本专业的相关的国外文献资料时,发挥着重要的作用。
因此,主要学习和掌握专业外语的基本语法、句法和结构,通过这门课的学习,期望学生能掌握专业英语的特点;扩大专业英语词汇量,尤其关于本专业有关导弹、航天器、无人机等专业知识方面的英语词汇量;提高专业英语(或科技英语)文章的阅读速度;并进行相应专业英语文献的翻译,在此基础上掌握专业英语的写法,为今后从事工程技术和科学研究工作打下稳固的基础。
西北工业大学_信号与线性系统实验报告_实验八、实验九

西北工业大学信号与线性系统实验报告学号姓名:主持人:参与人:主持人: 参与人: 实验八 一阶网络特性测量1.实验内容在电路系统中,一阶系统是构成复杂系统的基本单元。
学习一阶系统的特点有助于对一般系统特性的了解。
一阶系统的传输函数一般可以写成:γ+⋅=s H s H 1)(0 因果系统是稳定的要求:0>γ,不失一般性可设τγ10==H 。
该系统的频响特性为: 11)(+Ω=Ωτj H从其频响函数中可以看出系统响应呈低通方式,其3dB 带宽点τ1。
系统的波特图如下图:θ一阶低通系统的单位冲击响应与单位阶跃响应如下图:2.实验过程1、一阶网络波特图的测量:(1)首先用低频信号源产生一正弦信号,输出信号幅度为2Vpp。
加入到“一阶网络”模块的X输入端。
(2)用示波器测量一阶网络的输出信号Y(t)。
(3)然后从低频开始不断增加信号源的输出频率(1KHz一个步进),并保持其输出幅度不变,测量相应频点一阶网络的输出信号,并记录下输出信号的幅度、输入信号与输出信号的相位差。
以频率与输出幅度(可换算成相对0点的相对电平值,其单位为dB)为变量画出一曲线,同时以频率与输入输出信号相位差为变量画出一曲线。
这两条曲线即为一阶网络的波特图。
2、一阶网络单位阶跃响应测量:(1)按1.3节使JH5004信号产生模块处于模式2,在该模式下,脉冲信号输出端产生一周期为45ms的方波信号。
(2)将脉冲信号加入到“一阶网络”模块的X1输入端。
用示波器测量一阶网络的单位阶跃响应。
3、用二次开发模块的元件,改变一阶网络的元件参数,重复上述实验。
3.实验数据(1)一阶网络波特图的测量主持人:参与人:①频率为1KHZ时的输出信号以及输入输出信号的对比图②频率为2KHZ时的输出信号以及输入输出信号的对比图主持人:参与人:③频率为3KHZ时的输出信号以及输入输出信号的对比图④频率为4KHZ时的输出信号以及输入输出信号的对比图主持人:参与人:⑤频率为5KHZ时的输出信号以及输入输出信号的对比图主持人:参与人:(2)一阶网络单位阶跃响应测量(未改变一阶网络的原件参数)(3)一阶网络波特图的测量(并联一个4.3K)①用示波器测量一阶网络1khz输出及输入输出对比图主持人:参与人:②用示波器测量一阶网络2khz输出及输入输出对比图③用示波器测量一阶网络3khz输出及输入输出对比图主持人:参与人:④用示波器测量一阶网络4khz输出及输入输出对比图主持人:参与人:⑤用示波器测量一阶网络5khz输出及输入输出对比图(4)一阶网络单位阶跃响应测量(并联一个4.3KΩ的电阻)主持人:参与人:4.实验结果分析及思考1、一阶网络波特图实测曲线与理论曲线的对比分析。
西北工业大学_信号与线性系统实验报告_实验一、实验二

西北工业大学信号与线性系统实验报告学号姓名:实验一常用信号的分类与观察1.实验内容(1)观察常用信号的波形特点及其产生方法;(2)学会使用示波器对常用波形参数的测量;(3)掌握JH5004信号产生模块的操作;2.实验过程在下面实验中,按1.3节设置信号产生器的工作模式为11。
(1)指数信号观察:通过信号选择键1,按1.3节设置A组输出为指数信号(此时信号输出指示灯为000000)。
用示波器测量“信号A组”的输出信号。
观察指数信号的波形,并测量分析其对应的a、K参数。
(2)正弦信号观察:通过信号选择键1,按1.3节设置A组输出为正弦信号(此时A组信号输出指示灯为000101)。
用示波器测量“信号A组”的输出信号。
在示波器上观察正弦信号的波形,并测量分析其对应的振幅K、角频率 w。
(3)指数衰减正弦信号观察(正频率信号):通过信号选择键1、按1.3节设置A组输出为指数衰减余弦信号(此时信号输出指示灯为000001),用示波器测量“信号A组”的输出信号。
通过信号选择键2、按1.3节设置B组输出为指数衰减正弦信号(此时信号输出指示灯为000010),用示波器测量“信号B组”的输出信号。
*分别用示波器的X、Y通道测量上述信号,并以X-Y方式进行观察,记录此时信号的波形,并注意此时李沙育图形的旋转方向。
(该实验可选做)分析对信号参数的测量结果。
(4)*指数衰减正弦信号观察(负频率信号):(该实验可选做)通过信号选择键1、按1.3节设置A组输出为指数衰减余弦信号(此时信号输出指示灯为000011),用示波器测量“信号A组”的输出信号。
通过信号选择键2、按1.3节设置B组输出为指数衰减正弦信号(此时信号输出指示灯为000100),用示波器测量“信号B组”的输出信号。
分别用示波器的X、Y通道测量上述信号,并以X-Y方式进行观察,记录此时信号的波形,并注意此时李沙育图形的旋转方向。
将测量结果与实验3所测结果进行比较。
西工大、西交大自动控制原理 第五节 线性系统的稳定性分析9-10

1.系统稳定性概念
线性控制系统的稳定性定义
设线性控制系统在初始扰动的影响 下,其过渡过程随着时间的推移逐渐衰 减并趋向于零,则称该系统渐进稳定(简 称稳定)。反之,若在初始扰动的影响下, 系统过渡过程随着时间的推移而发散, 则称系统为不稳定。
1.系统稳定性概念
线性控制系统的稳定性是系统自身的固有特性。 稳定与否和输入信号及初始偏差的大小无关。
若通过系统自身的调节作用, 使偏差最后 逐渐减小,系统又逐渐恢复到平衡状态, 那么, 这种系统便是稳定的。
1. 系统稳定性概念
c(t)
c(t)
扰动
O (a)
扰动
O t
t (b)
不稳定
稳定
1. 系统稳定性概念
大范围稳定: 不论扰动引起的初始偏差有多大,
当扰动取消后,系统都能够恢复到原有 的平衡状态。
试用Hurwitz判据判断系统的稳定性。
解:(1) 特征方程式的各项系数均大于0。 (2) 各阶Hurwitz行列式为:
D1 a1 1 0
D2
a1 a0
a3 1 a2 2
5 7 0
3
3、稳定判据(代数判据)
(1) Hurwitz稳定判据
a1 a3 a5 1 5 0 D3 a0 a2 a4 2 3 10 45 0
2线性系统稳定的充分必要条件
设线性系统在初始条件为零时,输入一个 理想单位脉冲信号 (t),这时系统的输出称为 脉冲过渡函数(或称脉冲响应)g (t)
若系统闭环传递函数为:
m
Φs
Cs Rs
M s N s
Kg
n1
s sj
s zi
i 1
s2 2ζ k ωk s ωk2
01 线性空间(西北工业大学版)

x y ( 1 x1 2 x 2 n x n ) (1 x1 2 x 2 n x n ) ( 1 1 ) x1 ( 2 2 ) x 2 ( n n ) x n
7
正对应
x ( 1 , 2 , n ) x y ( 1 1 , 2 2 , n n ) y (1 , 2 , n )
1 x x1 x
[结合律] [恒等律]
由此可证, R 是实数域 R 上的线性空间。
2.定理:线性空间具有如下性质 (1) 零元素是唯一的,任一元素的负元素也是唯一的。 (2) 如下恒等式成立: 0 x O , (1) x ( x ) 。 [证明](1)采用反证法: ①零元素是唯一的。 设存在两个零元素 O1 和 O 2 ,则由于 O1
(4) 1 x 是 x 的负元素
1 x 1 1 x x
(5) k ( x y ) ( xy ) k x k y k (k x ) (k y ) (6) (k l ) x x k l x k x l (k x ) (l x ) (7) k (l x ) ( x l ) k x kl (kl ) x (8)
x ( y z ) ( x y) z ;
x y y x;
存在零元素 O ,使 x O x ;
1
(4) 负元律
对于任一元素 x V , 存在一元素 y V , 使 x y O,
且称 y 为 x 的负元素,记为 ( x ) 。则有 x ( x ) O 。 (II)在 V 中定义一个“数乘”运算,即当 x V , k K 时,有唯一 的 kx V (封闭性) ,且数乘运算满足下列性质: (5)数因子分配律 (6)分配律 (7)结合律 (8)恒等律
西工大-线性系统理论第八章

线性系统理论
传递函数矩阵与状态空间法相结合,来分析系统的内部结
构特性,为线性多变量系统的分析提供了一种新的有效手
段为现代频域法的综合奠定了基础。这些研究成果是70年 代以来线性控制理论的新近展,在工业过程的应用中曾获 得卓著的成效。本章介绍多项式矩阵及有理分式矩阵等必 要的数学基础知识,研究多变量系统的矩阵分式描述的性
i
(8.10)
j
线性系统理论
detT , detT detT 1, 式中 为常数, (s)为多项式。 r1 r2 r3 故均为单模矩阵;下列 A (s) 、A (s) 也为单模矩阵:
1 2
A (s) 1 s 3 s 4
s 1 s 2 ,
P(s) Q(s) 不唯一。求 A(s) 的Smith标准型的基本步骤如
下:
(1)将 A(s) 中不恒为零的元素中次数最低者,通过行、
线性系统理论
列交换化为元素;
(2)除元素以外,将第一行及第一列诸元通过初等变 q (s) a (s) 换化为零;(用综合除法计算 ij p (s) 1 j ,于是 a (s) 1 j a (s) 11 11
(8.11)
并称 B(s) 、A(s)等价。由于单模变换时非奇异线性变换,故
多项式矩阵的行列式和秩不变。
线性系统理论
Smith标准型 任意秩为 r 的多项式矩阵 A(s) 经过行、
列运算均等价于下列司密斯(Smith)标准型 S (s)
Fra bibliotek(8.4)
s 1
s 3
线性系统理论
det A (s) 2(s 1) 不恒等于零,尽管 det A (1) 0 ,仍 1 1 称 A (s)为非奇异的。det A (s) 0 ,故 A2(s) 是奇异的。 1 2 以多项式为元素的向量 ai (s)(i 1,, r) ,当选择不全为
西工大、西交大自动控制原理 第四章 线性系统的根轨迹法_03_广义根轨迹

三 节
[例3]
将 s j 代入上式,并整理得:
广 义 根
[(6 2K * ) 5 2 ] j[(8 K * ) 3 ] 0
有:
(6 2K * ) 5 2 0
轨 迹
(8
K * )
3
0
联立解之得:
K
* L
3
0
K
* L
34 3
8 34 3
因根号小于 零,所以此 解不合理, 应舍去。
Q(s)
当参量
T
GK ( 由0
s) ~
G(s)H(s) (Ts 1)
变化时,系统的开环极点
p
1 T
也要变化,对应的系统根轨迹就是参量根轨迹。
参量根轨迹
第 三 节 因原系统的闭环特征(s) 1 G(s)H(s) Ts 1 Q(s) 0
所以等效系统的等效开环传递函数为: Ts
实轴上的根轨迹: ~ 3, 2 ~
渐近线: n m 3 1 2
n
m
a
i 1
pi z j
j 1
nm
31
j 1 2
j (2)
3 2
第 零度根轨迹
三 节
[例3]
广
a
2k
nm
2k
2
k
义 根 轨
k 0 时,a 0 ; k 1时,a 180
这说明两条渐近线均在实轴上,一条在实轴正方向,
取
0,K
* L
3(K L
广 在负反馈控制系统中,除开环根轨迹增益(或开环增益)以 义 外,系统其它参量变化时的根轨迹,称为参量根轨迹。 根 轨 迹 参量根轨迹的绘制
如果从具有相同闭环特征方程式(或具有相同闭环极点)的
西北工业大学航天学院【硕士研究生课程目录】
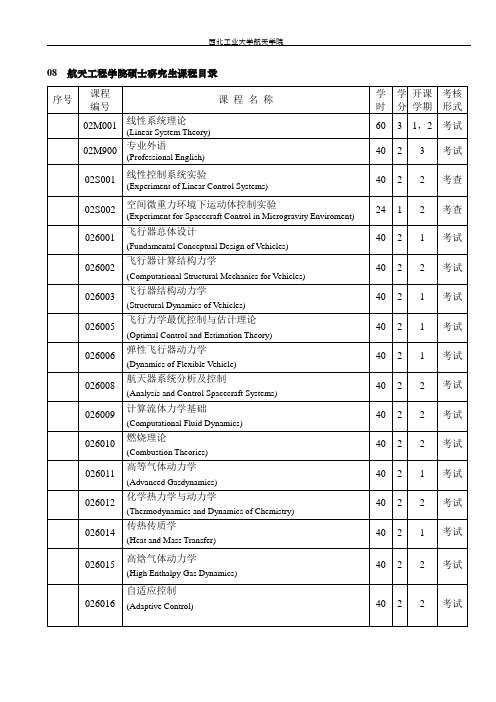
08 航天工程学院硕士研究生课程目录序号课程编号课程名称学时学分开课学期考核形式02M001 线性系统理论(Linear System Theory)60 3 1,2 考试02M900 专业外语(Professional English)40 2 3 考试02S001 线性控制系统实验(Experiment of Linear Control Systems)40 2 2 考查02S002 空间微重力环境下运动体控制实验(Experiment for Spacecraft Control in Microgravity Enviroment)24 1 2 考查026001飞行器总体设计(Fundamental Conceptual Design of Vehicles)40 2 1 考试026002飞行器计算结构力学(Computational Structural Mechanics for Vehicles)40 2 2 考试026003飞行器结构动力学(Structural Dynamics of Vehicles)40 2 1 考试026005飞行力学最优控制与估计理论(Optimal Control and Estimation Theory)40 2 1 考试026006弹性飞行器动力学(Dynamics of Flexible Vehicle)40 2 1 考试026008航天器系统分析及控制(Analysis and Control Spacecraft Systems)40 2 2 考试026009计算流体力学基础(Computational Fluid Dynamics)40 2 2 考试026010燃烧理论(Combustion Theories)40 2 2 考试026011高等气体动力学(Advanced Gasdynamics)40 2 1 考试026012化学热力学与动力学(Thermodynamics and Dynamics of Chemistry)40 2 2 考试026014传热传质学(Heat and Mass Transfer)40 2 1 考试026015高焓气体动力学(High Enthalpy Gas Dynamics)40 2 2 考试026016自适应控制(Adaptive Control) 40 2 2 考试026017 卫星导航原理与应用(Elements and Application of Satellite Positioning & NavigationSystem)40 2 2 考试026018 系统辨识(System Identification)40 2 1 考试026019 最优控制(Optimal Control)40 2 2 考试026020 爆炸气体动力学(Gasdynamics of Explosion)40 2 2 考试026021 轨道力学(Trajectory Dynamics)40 2 1 考试026023 复合材料结构力学(Mechanics of Composite Structures)40 2 1 考试026024 飞行器智能材料与结构(Smart Materials and Structures for Flight Vehicles)40 2 1 考试026025 最优估计(Optimal Estimation)40 2 2 考试026026 现代控制理论基础(Modern Control Theories)40 2 1 考试026027 现代鲁棒控制(Modern Robust Control Theory)40 2 2 考试026028 景象匹配与目标识别技术(Image Matching and Target Recognition Technologies)40 2 1 考试序号课程编号课程名称学时学分开课学期考核形式025001飞行器飞行力学(Flight Dynamics Of Flight Vehicles)40 2 2 考试025002电推进原理与系统结构(Principle and System of Electric Propulsion)40 2 2 考试025004导弹作战效能分析(Effectiveness Analysis Missiles)40 2 1 考试025005飞行器现代结构设计(Modern Aircraft Structure Design)40 2 1 考试025006燃烧诊断学(Combustion Diagnostics)40 2 1 考试025007可靠性设计(Reliability Design)40 2 2 考试025008航天器推进系统(Spacecraft Propulsion Systems)40 2 2 考试025009 航天器制导与控制(Guidance and Control of Space Vehicles) 40 2 2 考试025011 可靠性工程(Reliability Engineering)40 2 2 考试025012 仪器分析(Instrumental Methods of Analysis)40 2 1 考试025013 燃烧与爆轰(Combustion and Detonation)40 2 2 考试025014 运载火箭测试发控工程学(The Rocket Test, Launching and Control Engineering)40 2 2 考试025015 结构动态测试技术(Dynamic Modal Testing Technology of Structure)40 2 2 考试025017 火箭发动机先进设计技术(Modern Design Methods of Rocket Motors)40 2 2 考试025018 组合导航技术(Integrated Navigation System)40 2 2 考试025019 火箭发动机原理(Principle of Rocket Engines)40 2 2 考试025020 导弹空气动力学(Missile Aerodynamics)40 2 1 考试025022 空天光电探测技术(Sky Photoelectric Survey Technology)40 2 1 考试025023 空间机器人学(Space Robotics)40 2 1 考试025024 导弹先进制导与控制系统(Guidance and Control of Missile)40 2 2 考试025025 导弹计算机智能控制系统(Compute Intelligent Control System for Missile)40 2 1 考试025026 飞行器仿真理论与仿真环境(Advanced Simulation Theory and Device for Guide Weapon)40 2 1 考试025027 控制系统的故障检测与诊断技术(The Failure Detection and Diagnosis Technology of ControlSystem)40 2 1 考试。
西工大、西交大自动控制原理 第五章 线性系统的频域分析法_01_频率特性

对数幅频特性的纵坐标在对数相频特性中,相位仍以
度 () 来表示。
第五章 线性系统的频域分析法
频率特性
频率特性的几何表示方法
2 对数频率特性曲线( Bode曲线)
对数分度
12
dec(decade) 4 7 10 20
40 70 100
lg 2 1
十倍频程(dec)
lg 20 10
100
101
102
Frequency (rad/sec) 第五章 线性系统的频域分析法
频率特性
频率特性的几何表示方法 3 对数幅相曲线( Nichols曲线) 对数幅相曲线是将对数幅频特性与对数相频特性这两
条曲线,以 为参变量,画在同一个坐标系里。 其纵坐标为 L( ) 20 lg G( j ) ,以分贝表示;
时域分析法
分析域 方法 计算量 性能指标 适用范围
t 解析 大 有 大
根轨迹法
S 图解
小 无 线性定常系统
第五章 线性系统的频域分析法
考察一个系统的好坏,通常用Байду номын сангаас跃输入下系统的阶跃 响应来分析系统的动态性能和稳态性能。
有时也用正弦波输入时系统的响应来分析,但这种响 应并不是单看某一个频率正弦波输入时的瞬态响应, 而是考察频率由低到高无数个正弦波输入下所对应的 每个输出的稳态响应。
5 掌握稳定宽度的概念,并会做图确定系统的 稳定裕度(幅裕度和相裕度);
6 了解最小相位系统的概念; 7 了解尼柯尔斯图线的应用;
第五章 线性系统的频域分析法
本章要求
8 理解闭环频域指标 9 掌握开环Bode图的三个频段(低、中、
高频段)的概念。并熟练掌握开环频域指标; 10 掌握系统时域性能指标与开、闭环频域性能
西工大—现代控制理论课件ppt课件

y2
up
yq
被控过程
5
典型控制系统由被控对象、传感器、执行器和控制器组成。
被控过程具有若干输入端和输出端。
数学描述方法: 输入-输出描述(外部描述):高阶微分方程、传递函数矩阵。
一种完整的描述。
状态空间描述(内部描述):基于系统内部结构,是对系统的
6
1.2 状态空间描述常用的基本概念
1) 输入:外部对系统的作用(激励); 控制:人为施加的激励;
xn a0 x1 a1x2 an1xn u
得到动态方程
x Ax bu
y x1
y cx
16
式
x1
0 1 0
0 0
中
x2
0
0
1 b , c 1 0
0
xn
1
0
0
0
1
0
xn
a0 a1 a2
an1
0
例1-5
系统的状态变量图
i 2,3,, n
其展开式为 x1 y h0u
x2 x1 h1u y h0u h1u x3 x2 h2u y h0u h1u h2u
xn xn1 hn1u y (n1) h0u (n1) h1u (n2) hn1u #
式中, h0 , h1 ,, hn1 是n个待定常数。是n个。
3、动态方程对于系统的描述是充分的和完整的,即系统中 的任何一个变量均可用状态方程和输出方程来描述。 例1-1 试确定图8-5中(a)、(b)所示电路的独立状态变量。图中u、i分别是是
输入电压和输入电流,y为输出电压,xi为电容器电压或电感器电流。
x3
解 并非所有电路中的电容器电压和电感器电流都是独立变量。对图8-5(a),
线性系统理论1a

• 系统的研究方法 ——经验法 ——理论法:依据数学理论
➢建模(对真实系统的抽象) ➢建立数学描述 ➢分析 ➢设计 • 本课程的研究范围 ——对象:线性动态系统,数学模型已知 ——工具:数学
• §2-3 传递函数矩阵
对SISO系统,系统的传递函数h(s) 与脉冲 响应矩阵函数g(t)之间满足关系式
h (s) L [g (t)]g (t) L 1 [h (s)]
同样,对于p输入q输出的多变量系统,
H (s ) L [G (t)]G (t) L 1 [H (s )]
因为有
t
y(t) G(t )u()d
1
uc(t) c i(t)dt
d(it) Ldtuc(t)R(ti)ur(t)
duc(t) dt
1 i(t) C
di(t) dt
1 Luc
Ri(t) L
1 Lur
(t)
i(t) R ur(t)
L C uc(t)
在已知ur(t)的情况下,只要知道 uc(t)和i(t)的变化特性, 则其他变量的变化均可知道。
x&= f(x,u,t) y=g(x,u,t) ,t t0
• 可根据系统的状态描述对系统进行分类。 1)线性系统与非线性系统
在选定的一组状态变量下,称一个系统为非线性 系统,若其状态空间描述中,f 与(或)g 的某些分 量是x1,…,xn和u1,…,um的非线性函数。反之,若f 与g 的各分量均是x 与u 的线性函数,则称为线性 系统。线性系统的状态描述可表示为:
k
于是系统的输出为:
y G (ttk)u(tk) t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性系统理论
系统描述中常用的几个基本概念
无论是外部描述还是内部描述,下列概念是常用的, 现给出定义以有助于理解系统性质及系统分类。
松弛性
系统在时刻 t0 称为松弛的,当且仅当输出 y[t0, )由输 入 u[t0,)唯一确定。从能量的观点看,在时刻 t0不存在存 储能量,则称系统在时刻 t0是松弛的。式中 u[t0,)表示定 义在时间区间[t0,) 的输入。
线性系统理论
例如一个RLC网络,若所有电容两端的电压和流过电 感的电流在 t0 时刻均为零(即初始条件为零),则网络称 为在 t0 时刻是松弛的。若网络不是松弛的,其输出响应 不仅由 u[t0,)所决定,还与初始条件有关。
在松弛性假定下,系统得输入-输出描述有
y Hu
(1.1)
式中 H是某一算子或函数,例如传递函数就是一种算子。
线性系统理论
线性
一个松弛的系统称为线性的,当且仅当对于任何输入
u1 和 u2 ,以及任何实数 ,均有
H (u1 u2 ) Hu1 Hu2
H ( u1) Hu1
(1.2) (1.3)
否则称为非线性的。式(1.2)称为可加性,式(1.3)称 为齐次性。松弛系统具有这两种特性,称该系统满足叠加 原理。
第一章 线性系统的状态空间描述
为了分析研究系统,建立描述系统的数学方程是首要 的。经典控制理论中的时间域理论对单输入-单输出线性 定常系统用高阶微分方程或传递函数来描述输入-输出变 量间的因果关系,分析的主要方面限于运动的稳定性,不 便用来综合系统。 20世纪60年代以后,现代线性系统理 论又有了新发展,出现了线性系统几何理论、线性系统代 数理论和多变量频域方法等研究多变量系统的新理论和新 方法。
系统的状态空间描述 化输入-输出描述为状态空间描述 由状态空间描述导出传递函数矩阵 线性系统的坐标变换 组合系统的状态空间方程与传递函 数矩阵
线性系统理论
1.1 系统的状态空间描述
系统数学描述的两种基本类型 这里所谓的系统是泛 指一些互相作用的部分构成的整体,它可能是一个反馈控 制系统,也可能是某一控翻装置或受控对象。所研究系统 均假定具有若干输入端和输出端。外部环境对系统的作用
线性系统理论
与经典线性控制理论相比,现代线性系统主要特点是:研 究对象一般是多变量线性系统,而经典线性理论则以单输 入单输出系统为对象;除输入和输出变量外,还描述系统 内部状态的变量;在分析和综合方面以时域方法为主而经 典理论主要采用频域方法;使用更多数据工具。
相关书籍
线性系统理论
线性系统理论
线性系统理论
随着计算机技术的发展,以线性系统为对象的计算方法 和计算辅助设计问题也受到普遍的重视。运用状态空间法 研究系统是现代控制理论的重要标志,状态空间方程是现 代控制理论的最基本的数学模型。本章主要介绍状态空间 描述的基本概念以及建立状态空间方 §1.3 §1.4 §1.5
线性系统理论
系统的两种基本描述的结构示意图见图1.1。以后的研究 可看出,外部描述通常是一种不完全的描述,具有完全不 同的内部结构特性的两个系统可能具有相同的外部特性, 而内部描述是一种完全的描述,能完全表示系统的一切动 态特性。仅当系统具有一定属性的条件下,两种描述才具 有等价关系。
线性系统理论
线性系统理论
一为系统的内部描述,即状态空间描述,这种描述将 系统视为由动力学部件和输出部件组成,将系统的动态过 程细化为两个过程,即输入引起内部状态的变化,
(x1, , xn) 和 (u1, ,up) 间的因果关系常用一阶微分方程组或 差分方程组表示,称为状态方程;还有内部状态和输入一 起引起输出的变化,(y1, , yq ) 和 (x1, , xn ) 、(u1, ,up ) 间的因果 关系是一组代数方程,称为输出方程。外部描述仅描述系 统的终端特性,内部描述则是既描述系统内部特性又描述 终端持性的。
线性系统理论
美国学者R.E.卡尔曼首先把状态空间法应用于多变量线性 系统的研究,提出了能控性和能观测性两个基本概念。 20世纪60年代以后,现代线性系统理论又有了新发展,出 现了线性系统几何理论、线性系统代数理论和多变量频域 方法等研究多变量系统的新理论和新方法。随着计算机技 术的发展,以线性系统为对象的计算方法和计算辅助设计 问题也受到普遍的重视。
线性系统理论
式(1.2 )和式(1.3) 可合并表示为
线性系统理论
讲授: 作者: 出版:西北工业大学出版社
线性系统理论
简介: 线性系统理论(linear systems theory)以状态空
间法为主要工具研究多变量线性系统的理论。20世纪50年 代以后,随着航天等技术发展和控制理论应用范围的扩大, 经典线性控制理论的局限性日趋明显,它既不能满足实际 需要,也不能解决理论本身提出的一些问题,这就推动了 线性系统的研究,于是在1960年以后从经典阶段发展到现 阶段。
称为系统输入,以向量 u [u1 up]T 表示,施于输入端;系 统对外部环境的作用称系统输出,以向量y [y1 yq]T表示,
可在输出端量测,它们均为系统的外部变量。
线性系统理论
描述系统内部所处的行为状态的变量以向量 x [x1 xn]T表
示,它们为内部变量。系统数学描述通常可分为下列两种 基本类型:一为系统的外部描述,即输入-输出描述,这 种描述将系统看成是一个“黑箱”,只能接触系统的输入 端和输出端,不去表示系统内部的结构及变量,只从输入 -输出的因果关系中获悉系统特性。若系统是一个单输入单输出线性定常系统,其外部描述的数学方程就是一个 n 阶微分方程及对应的传递函数。
线性系统理论
因果性
若系统在时刻的输出仅取决于t时刻及在t之前的输入, 而与之后的输入无关,则称系统具有因果性。本书所研究 的实际物理系统都具有因果性,并称为因果系统。若系统 在t时刻的输入尚与t之后的输入有关,则称该系统不具有 因果性,不具因果性的系统能够在预测之后的输入并施加 于系统而影响其输出。
