功动能定理以及保守力
合集下载
大学物理-动能定理
(4) 势能是状态的函数 Ep Ep (x, y, z) 25
4. 势能曲线
Ep (h)
E
Eh
Ep
o
H H h
重力势能
Ep
E
o
Ek
Ep
3-4 动能定理
Ep (x)
AE
B
Ek
Ep
o
x
弹性势能
Ek 0
x
引力势能
26
势能曲线的作用：
3-4 动能定理
（1）根据势能曲线的形状可以讨论物体的运动。
（2）利用势能曲线，可以判断物体在各个位置 所受保守力的大小和方向。
力提供园周运动的向心力而不做功，摩擦力做负
功使滑块动能减少。
W
1 mv2 2
1 2
mv0
2
(1)
34
3-4 动能定理
v2 N m
(2)
R
N m dv
(3)
dt
将式(2)代入式(3)，整理变形为
v2 dv dv d v dv R dt dt d R d
分离变量并积分，得
做功，它们所做元功之和为
dA fij dri f ji drj
因
fij f ji
mi
drji
dri
rij
rij drij
所以
fij
dA fij (dri drj ) fij drij
f ji m j drj
讨论：内力做功的特点
14
成对力的功
对它所作的功为零．
非保守力：力所作的功与路径有关． （例如摩擦力）
23
3. 势能
3-4 动能定理
4. 势能曲线
Ep (h)
E
Eh
Ep
o
H H h
重力势能
Ep
E
o
Ek
Ep
3-4 动能定理
Ep (x)
AE
B
Ek
Ep
o
x
弹性势能
Ek 0
x
引力势能
26
势能曲线的作用：
3-4 动能定理
（1）根据势能曲线的形状可以讨论物体的运动。
（2）利用势能曲线，可以判断物体在各个位置 所受保守力的大小和方向。
力提供园周运动的向心力而不做功，摩擦力做负
功使滑块动能减少。
W
1 mv2 2
1 2
mv0
2
(1)
34
3-4 动能定理
v2 N m
(2)
R
N m dv
(3)
dt
将式(2)代入式(3)，整理变形为
v2 dv dv d v dv R dt dt d R d
分离变量并积分，得
做功，它们所做元功之和为
dA fij dri f ji drj
因
fij f ji
mi
drji
dri
rij
rij drij
所以
fij
dA fij (dri drj ) fij drij
f ji m j drj
讨论：内力做功的特点
14
成对力的功
对它所作的功为零．
非保守力：力所作的功与路径有关． （例如摩擦力）
23
3. 势能
3-4 动能定理
哈里德大学物理第三章
注意
Fi内 0 I i内 0
i i
W
i
i内
0
二、变力的功
微元分析法：
ds dr
P
P
a
F
r
F r
o
b
取微元过程
以直代曲
以不变代变
再求和
§3-1 功 功率
ds
P
dr
P
r
a
F
r
F
o
b
元功： dW F dr F dr cosθ Fcosθds
F
M
m
r
r
o
以上这些力的共同特点？
保守力
1）做功与路径无关，只与起、末点位置有关；
2）做功等于与相互作用物体的相对位置有关的 某函数在始末位置的值之差。
势能
§3-2 保守力与非保守力 势能
二、保守力与非保守力
势能
1. 保守力与非保守力
• 做功与路径无关，只与起点、终点位置有关
b m L1 a
§3-2 保守力与非保守力 势能
保守力在 x 轴的分力，等于其相关势 能对坐标 x 的导数的负值:
F
dW F dr
x
Fx dx dEp x
m
θ
Fx
Fx
dEp x dx
§3-2 保守力与非保守力 势能
练习3：
一质量为 m 的人造地球卫星沿一圆形轨道运动，
§3-4 功能原理
1. 动能定理与功能原理的区别与联系：
功能原理是从动能定理推出的，完全包含在 动能定理之中； 由于保守力的功已反映在势能的改变中，运 用功能原理时，只需要计算非保守力的功， 而动能定理，则需要计算所有力做的功 。 2. 功与能的联系与区别： 功与能的单位与量纲相同； 功是过程量，能量是状态量； 功是能量传递和转化的一种方式和量度。
3 动能定理 功能原理 机械能守恒定理
A Ek2 Ek1
注意 功和动能都与 参考系有关；动能定理仅适用于惯性系 .
动能 能量守恒定律
质点系统动能定理
每一个质点都满足动能定理，则有
A1 12 m 1v12 12m1v120
Ai
1 2
mi vi2
1 2
mi vi20
以上各式左右分别相加
对称性与守恒定律
F1
m2
都有这一特点
A
B
C
保守力作的功，是位置的单值函数；
D
那么，我们就可以引入仅是位置的单
B
值函数的能量，叫作保守力的势能，
也叫作位能。
动能 能量守恒定律
对称性与守恒定律
五 势能
势能 与物体间相互作用及相对位置有关的能量 .
重力功
重力势能
A (mgzB mgzA )
引力功
A
(G
械能的改变。
动能 能量守恒定律
九 机械能守恒定律 功能原理
对称性与守恒定律
A外 A非 保 内 E
当 A外 A非 保内 0 时，有 E1 E2
机械能守恒定律： 只有保守内力作功的情况下，质 点系的机械能保持不变 .
注意： 1、机械能守恒是有条件的。从初态到末态的每一个微元 过程中，外力和非保守内力所做的元功的代数和均为零， 则机械能守恒。
9/4
4dy 9.125J
1
动能 能量守恒定律
对称性与守恒定律
例：质量为 m 的物体放在水平桌面上，物体和桌面的摩 擦系数为 ，物体在外力作用下沿半径为R圆由a运动 到b，移动了半个圆周，求在这一过程中摩擦力的功。
这是力的大小不变，物 体沿曲线运动的例子
注意 功和动能都与 参考系有关；动能定理仅适用于惯性系 .
动能 能量守恒定律
质点系统动能定理
每一个质点都满足动能定理，则有
A1 12 m 1v12 12m1v120
Ai
1 2
mi vi2
1 2
mi vi20
以上各式左右分别相加
对称性与守恒定律
F1
m2
都有这一特点
A
B
C
保守力作的功，是位置的单值函数；
D
那么，我们就可以引入仅是位置的单
B
值函数的能量，叫作保守力的势能，
也叫作位能。
动能 能量守恒定律
对称性与守恒定律
五 势能
势能 与物体间相互作用及相对位置有关的能量 .
重力功
重力势能
A (mgzB mgzA )
引力功
A
(G
械能的改变。
动能 能量守恒定律
九 机械能守恒定律 功能原理
对称性与守恒定律
A外 A非 保 内 E
当 A外 A非 保内 0 时，有 E1 E2
机械能守恒定律： 只有保守内力作功的情况下，质 点系的机械能保持不变 .
注意： 1、机械能守恒是有条件的。从初态到末态的每一个微元 过程中，外力和非保守内力所做的元功的代数和均为零， 则机械能守恒。
9/4
4dy 9.125J
1
动能 能量守恒定律
对称性与守恒定律
例：质量为 m 的物体放在水平桌面上，物体和桌面的摩 擦系数为 ，物体在外力作用下沿半径为R圆由a运动 到b，移动了半个圆周，求在这一过程中摩擦力的功。
这是力的大小不变，物 体沿曲线运动的例子
2-2 动能定理 能量守恒定律
物理学 简明教程
2-2 动能定理 能量守恒定律
F 对空间的积累 W，动能定理
一 功 动能定理
1
恒力作用下的功
W F cos r
F
r
F
r
第二章 动量守恒定律和能量守恒定律
1
物理学 简明教程
2-2 动能定理 能量守恒定律
2 变力的功
dW F cos dr
m' m r2
er
m移动dr时，F作元功为
rA
A
er
r m
r dr
dr
dr
m'
rB
B
dW
F
dr
G
m' m r2
er
dr
第二章 动量守恒定律和能量守恒定律
7
物理学 简明教程
2-2 动能定理 能量守恒定律
m从A到B的过程中 F作功：
W
势能 势能曲线
能量守恒定律
引力势能 重力势能
Ep
G
m'm r
Ep mgy
弹性势能
Ep
1 2
k x2
第二章 动量守恒定律和能量守恒定律
12
物理学 简明教程
2-2 动能定理 能量守恒定律
保守力的功 W (Ep2 Ep1) EP
讨论
——保守力作正功，势能减少．
势能是状态的函数 Ep Ep (x, y, z)
2 保守力与非保守力
保守力所作的功与路径无关，仅决定 于始、末位置．
引力的功
W
(G
m'm) (G rB
2-2 动能定理 能量守恒定律
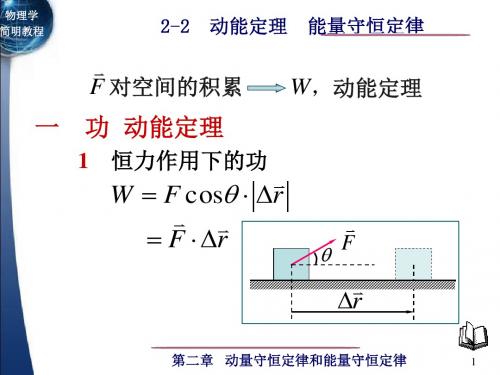
F 对空间的积累 W，动能定理
一 功 动能定理
1
恒力作用下的功
W F cos r
F
r
F
r
第二章 动量守恒定律和能量守恒定律
1
物理学 简明教程
2-2 动能定理 能量守恒定律
2 变力的功
dW F cos dr
m' m r2
er
m移动dr时，F作元功为
rA
A
er
r m
r dr
dr
dr
m'
rB
B
dW
F
dr
G
m' m r2
er
dr
第二章 动量守恒定律和能量守恒定律
7
物理学 简明教程
2-2 动能定理 能量守恒定律
m从A到B的过程中 F作功：
W
势能 势能曲线
能量守恒定律
引力势能 重力势能
Ep
G
m'm r
Ep mgy
弹性势能
Ep
1 2
k x2
第二章 动量守恒定律和能量守恒定律
12
物理学 简明教程
2-2 动能定理 能量守恒定律
保守力的功 W (Ep2 Ep1) EP
讨论
——保守力作正功，势能减少．
势能是状态的函数 Ep Ep (x, y, z)
2 保守力与非保守力
保守力所作的功与路径无关，仅决定 于始、末位置．
引力的功
W
(G
m'm) (G rB
3-4-6 动能定理,保守力与非保守力,功能原理 机械能守恒定律
o
W Fcos d s
os 1
ds
s2
s
3
(3) 功是一个过程量，与路径有关。
(4) 合力的功，等于各分力的功的代数和。
F F i F j F k x y z d r d x i d y j d z k B B W F d r （ F d x F d y F d z ） x y z
21
3-6 功能原理 机械能守恒定律
一 质点系的动能定理
对第 i个质点，有
W W E E k i k i 0
ex i in i
m1
ex F i
外力功 内力功
m2
in m i F i
对质点系，有
i ex i i in i i k i k i 0 k k 0 i ex in
W W E E E E
8
1 2 1 2 W m v m v E E 2 1 k 2 k 1 2 2
合外力对质点所作的功，等于质点动能 的增量 ——质点的动能定理
注意
功是过程量，动能是状态量；
功和动能依赖于惯性系的选取， 但对不同惯性系动能定理形式相同。
9
例 2 一质量为1.0 kg 的小球系
在长为1.0 m 细绳下端，绳的上
势能具有相对性，势能大小与势能零点 的选取有关。 势能是属于系统的。 势能差与势能零点的选取无关。
20
3-5 保守力与非保守力
势能
四 势能曲线
E z p mg
1 2 Ep kx 2
m 'm E G p r
Ep
Ep
Ep
O
x
O
z
W Fcos d s
os 1
ds
s2
s
3
(3) 功是一个过程量，与路径有关。
(4) 合力的功，等于各分力的功的代数和。
F F i F j F k x y z d r d x i d y j d z k B B W F d r （ F d x F d y F d z ） x y z
21
3-6 功能原理 机械能守恒定律
一 质点系的动能定理
对第 i个质点，有
W W E E k i k i 0
ex i in i
m1
ex F i
外力功 内力功
m2
in m i F i
对质点系，有
i ex i i in i i k i k i 0 k k 0 i ex in
W W E E E E
8
1 2 1 2 W m v m v E E 2 1 k 2 k 1 2 2
合外力对质点所作的功，等于质点动能 的增量 ——质点的动能定理
注意
功是过程量，动能是状态量；
功和动能依赖于惯性系的选取， 但对不同惯性系动能定理形式相同。
9
例 2 一质量为1.0 kg 的小球系
在长为1.0 m 细绳下端，绳的上
势能具有相对性，势能大小与势能零点 的选取有关。 势能是属于系统的。 势能差与势能零点的选取无关。
20
3-5 保守力与非保守力
势能
四 势能曲线
E z p mg
1 2 Ep kx 2
m 'm E G p r
Ep
Ep
Ep
O
x
O
z
2-2-动能定理-保守力与非保守力-能量守恒定律(2024版)
第二章 动量守恒定律和能量守恒定律
2 – 2 动能定理 能量守恒定律
物理学简明教程
习题2-3 如图的系统，物体 A，B 置于光滑的桌 面上，物体 A 和 C, B 和 D 之间摩擦因数均不为 零，首先用外力沿水平方向相向推压 A 和 B， 使 弹簧压缩，后拆除外力， 则 A 和 B 弹开过程中， 对 A、B、C、D 及弹簧组成的系统
解： W1 F1d cos300 176 .66 J W2 F2d cos 400 130 .22 J
W W1 W2 306 .88 J
根据动能定理有：
W 1 mv2 0 2
F2
F1
300
400
代入得： v 1.65m s1
第二章 动量守恒定律和能量守恒定律
2 – 2 动能定理 能量守恒定律
机械能 E Ek Ep W ex Wnicn E2 E1
质点系的功能原理: 质点系机械能的增量等于 外力和非保守内力作功之和 .
第二章 动量守恒定律和能量守恒定律
2 – 2 动能定理 能量守恒定律
物理学简明教程
2 机械能守恒定律
功能原理 W ex Wnicn (Ek2 Ep2 ) (Ek1 Ep1)
(C)只有(2)是正确的 (D)只有(3)是正确的
分析（：1）错.(保守力作正功时,系统相应的势能减少).
（3）错.(作用力和反作用力虽然大小相等、方 向相反,但两者所作功的代数和不一定为零；而等于 力与两者相对位移的乘积.)
第二章 动量守恒定律和能量守恒定律
2 – 2 动能定理 能量守恒定律
物理学简明教程
dx vxdt 1.5t 2dt
W
Fdx
2 9t3dt 0
36.0
动能定理【高中物理】
解： W＝ F dr dr F dt dt 12tvdt
v v0 adt
0
t
0
t
0
F dt m
12t dt 3t 2 0 2
t
W
3
0
12 t 3t 2 dt
3
0
36 t 3 dt 9t 4 729 J
作业：P104 3-13
s’
b
F
④ 合力的功为各分力的功的代数和。 3、功率 力在单位时间内所作的功
dW ( Fi ) d r ( Fi d r ) dWi
W 平均功率： P t
W dW 瞬时功率： P lim t 0 t dt dr dW F d r P F F v dt
当弹簧在水平方向不受外力作用时，它将不 发生形变，此时物体位于点0(即位于x=0处)， 这个位置叫做平衡位置 现以平衡位置0为坐标原点，向右为x轴正向。
F kxi
W
k
m
x2
x1
kxdx
1 1 2 2 ( kx2 kx1 ) 2 2
o k F m o x1 m k o F x2
单位：W或Js-1 量纲：ML2T－3
【瓦特（Wate）】
功的其它单位：1eV=1.6×10-19J
例1、一陨石从距地面高为h处由静止开始落向地 面，忽略空气阻力，求陨石下落过程中，万有引 力的功是多少？ a 解：取地心为原点，引力与矢径方 h F b 向相反 R R W F dr r Rh
保守力：某些力对质点做功的大小只与质点的始末 位置有关，而与路径无关。这种力称为保守力。
v v0 adt
0
t
0
t
0
F dt m
12t dt 3t 2 0 2
t
W
3
0
12 t 3t 2 dt
3
0
36 t 3 dt 9t 4 729 J
作业：P104 3-13
s’
b
F
④ 合力的功为各分力的功的代数和。 3、功率 力在单位时间内所作的功
dW ( Fi ) d r ( Fi d r ) dWi
W 平均功率： P t
W dW 瞬时功率： P lim t 0 t dt dr dW F d r P F F v dt
当弹簧在水平方向不受外力作用时，它将不 发生形变，此时物体位于点0(即位于x=0处)， 这个位置叫做平衡位置 现以平衡位置0为坐标原点，向右为x轴正向。
F kxi
W
k
m
x2
x1
kxdx
1 1 2 2 ( kx2 kx1 ) 2 2
o k F m o x1 m k o F x2
单位：W或Js-1 量纲：ML2T－3
【瓦特（Wate）】
功的其它单位：1eV=1.6×10-19J
例1、一陨石从距地面高为h处由静止开始落向地 面，忽略空气阻力，求陨石下落过程中，万有引 力的功是多少？ a 解：取地心为原点，引力与矢径方 h F b 向相反 R R W F dr r Rh
保守力：某些力对质点做功的大小只与质点的始末 位置有关，而与路径无关。这种力称为保守力。
§2-3 功 动能 动能定理
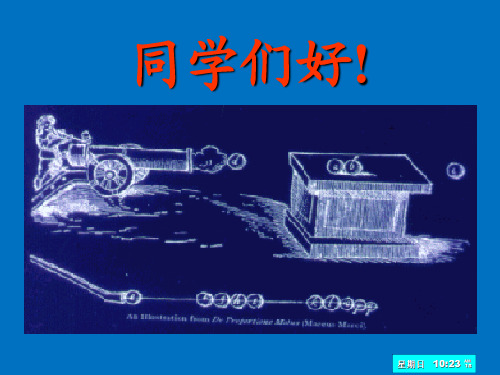
r1
A始末
末 始
f2
d r21
表明：任何一对作用 力和反作用力所作的总功
B1
B2 f2
f1
d
r1
r1
m1
r2
d r2
m2
A2
具有与参考系选择无关的 不变性质。
O
A1
一对力所作的总功的只取决于两质点的相对运动；
一对力做功的代数和与参考系的选择无关；
什么条件下一对内力做功为零?
v
C
m M f
Fi
直角坐标系：
F
Fxi
Fy
j
Fz
k
dr dxi dyj dzk
元功：
dA
F
dr
Fxdx
Fy
dy
Fzdz
总功：
A
b
dA
b
F
cosds
b
F
dr
a
a
a
b
Fxdx Fydy Fzdz
2.合力的功
a
F cos
Aab
b
F
dr
a
b
Fi
dri
r o rA dr rB
a
b
Fi
f12
f21
m2
作为系统考虑时，得到：
b1 a1
F1
dr1
b2 a2
F2
dr2
b1 a1
f12
dr1
b1 a1
f21 dr2
(1 2
m1v12b
1 2
m2v22b )
(1 2
m1v12a
1 2
m2v22a
)
A外 A内 Ekb Eka Ek
第五讲功质点的动能定理ppt课件
F ma 6t
A
6tdx
2 0
6t
3 2
t
2dt
4-2、保守力及其功
一、常见力的功 1.万有引力的功
设质量为m的质点在质量为M的固定质点的万有引力场中运动
,取M为坐标原点
dr
b
分析：
M对m的引力为
F
G
Mm r2
r
变力 微元法
rb
θ
dr
m
元功： dA F d r F d r cos θ
0
3 36t 3dt
0
9t4
3 0
729J
P F v 12t 3t2 288W
三、动能定理 1. 质点的动能定理
F
m dv dt
m
dr
b
P F
a
b
b
b
A
F dr
a
a F dr
a F ds,
b m d v ds a dt
vb va
mvdv
1 2
mvb2
1 2
mva2
4-1 功 动能定理
一、功:
功的定义：力对质点所作的功等于力在质点位移方向
的分量与位移大小的乘积。
即为力与质点位移的点积。
1、恒力直线运动的功：
A F cos | r | F Δr
F
F
θ
Δr
2、变力曲线运动的功
微元法：将 ab 分成许多段微小的位移，每一微小
的位移 dr 中的力看成恒力（大小、方向
元功：dA F d r
k
F
(kxi) (dxi)
x
kxdx
0 xa x xb
A
第 03章 2 次课 -- 动能定理 保守力和非保守力 功能原理
上海师范大学
3 /17
§3. 4 三、质点的动能定理
动能定理
外力F作用在质点上, 对质点做功, 质点的速率发生变化, 因此能量发生变化.
外力所做的功W与质点的能量有什么定量 关系吗?
dv 由 W F dr F cos dr Ft dr Ft ds 和 Ft m
A
dW F dr
W F r
A
W
B
B F dr F cosdr
r
是在力的作用下产生的位移.
W Fi dr Fi dr Wi
合力的功 = 各分力的功的代数和
i
W W1 W2 W3 Wi
5. .直角坐标系中的功
F Fx i Fy j Fz k； dr dxi dyj dzk
W Fx dx Fy dy Fz dz
6. 功的单位
Wx Wy Wz
1 /17
1J 1N m
上海师范大学
§3. 4 二、功率
12 /17
§3.5 四、势能曲线
保守力与非保守力 势 能
势能是空间位置的函数, 将这种函数用图形表示就称为势能曲线.
Ep mgz
1 E p kx 2 2
m'm Ep G r
Ep
Ep
O
Ep
x
O
重力势能曲线
z
x
O
弹性势能曲线
引力势能曲线
z 0, Ep 0
x 0, Ep 0
v v0 e
t 0
x
dt
W b (0 e
动能定理
m1
ex Fi
in m i m2 Fi
系统内质点受力
非保守内力
W外 W保内 W非保内 Ek Ek 0
W保内 （Ep Ep 0 ) W外 W非保内 （Ep Ek ) ( Ep 0 Ek 0 )
第二章 动量守恒定律和能量守恒定律
2-2 动能定理 保守力与非保守力 能量守恒定律
用动能定理求功 2-28题
W
x
0
3 Fdx (3 2 x)dx
0
3 0
W (3 x x 2 )
18 J
1 2 W m 0 18 J 2 6m/s
第二章 动量守恒定律和能量守恒定律
2-2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
r
W F d r F1 d r F2 d r W1 W2
第二章 动量守恒定律和能量守恒定律
功的单位：1 J=1 N· m
量纲：dim W ML2 T 2
2-2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
第二章 动量守恒定律和能量守恒定律
2-2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
2-38题 第一过程动量守恒
m ( M m)V
1 2 第二过程机械能守恒 E P ( M m)V 2 2 2 m EP 选择答案：B 2( M m)
2-39题
m11 m22 选择答案：D 1 1 E p m11 m2 2 2 2
如：万有引力、重力、弹性力。
物体沿任意闭合路径运动一周时, 保守力对它所 做的功为零 。
2-2 动能定理 保守力 能量守恒定律
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
例 以下四种说法中，哪一种是正确的？ （1）作用力与反作用力的功一定是等值异号.
（2）内力不能改变系统的总机械能.
（3）摩擦力只能作负功. （4）同一个力作功在不同的参考系中，也不 一定相同.
第二章 动量守恒定律和能量守恒定律
动能定理 合外力对质点所作的功,等于质 点动能的增量 .
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
注意 动能是状态函数
2 1 p Ek mv 2 2 2m
功是过程量
W Ek2 E k1
功和动能单位都为焦耳，符号为J
第二章 动量守恒定律和能量守恒定律
重力功
W (mgyB mgyA ) 1 2 1 2 弹力功 W ( kxB kx A ) 2 2
A
D
C
ACB
F dr
ADB
F dr
B
非保守力: 力所作的功与路径有关 .（例如摩擦力）
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
r 方向单位矢量
r
结论：万有引力作功与路径无关.
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
2 ） 重力作功
P mg ˆ j ˆ dyˆ dr dxi j
W
B A
y
yA
A
D
dr
C
B
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
例 以下四种说法中，哪一种是正确的？ （1）作用力与反作用力的功一定是等值异号.
（2）内力不能改变系统的总机械能.
（3）摩擦力只能作负功. （4）同一个力作功在不同的参考系中，也不 一定相同.
第二章 动量守恒定律和能量守恒定律
动能定理 合外力对质点所作的功,等于质 点动能的增量 .
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
注意 动能是状态函数
2 1 p Ek mv 2 2 2m
功是过程量
W Ek2 E k1
功和动能单位都为焦耳，符号为J
第二章 动量守恒定律和能量守恒定律
重力功
W (mgyB mgyA ) 1 2 1 2 弹力功 W ( kxB kx A ) 2 2
A
D
C
ACB
F dr
ADB
F dr
B
非保守力: 力所作的功与路径有关 .（例如摩擦力）
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
r 方向单位矢量
r
结论：万有引力作功与路径无关.
第二章 动量守恒定律和能量守恒定律
2– 2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
2 ） 重力作功
P mg ˆ j ˆ dyˆ dr dxi j
W
B A
y
yA
A
D
dr
C
B
3-4 动能定理
ODC；（2）沿OBC。
B 2
C 2
Fy 0
（1）OD段：y=0,dy=0, DC段：x=2, dx=0，Fy=0
WODC
F dr
OD
2 F dr (4 2 0)dx 0 8J
DC 0
O
D
（2）OB段：Fy=0, BC段：y=2
WOBC
dW F d s FT d s P d s P d s mgld cos mglsin d
0
d
W mgl sin d
0
mgl(cos cos 0 )
FT v ds P
l
3－5 保守力与非保守力 势能
一、万有引力、重力、弹性力作功的特点
1、万有引力作功的特点
m' 对m 的万有引力为
m' m F G 2 er r
m 移动dr 时，F作元功为
A
rA e
m'
r
r
rB
m
dr
dr r dr
B
m' m dW F dr G 2 er dr r
z 0, Ep 0
x 0, Ep 0
r , Ep 0
3－6 功能原理 机械能守恒定律
一、质点系的动能定理
设一系统有n个质点，作用于各个质点的力所作的功分别为： W1, W2, …, Wn,使各个质点由初动能Ek10, Ek20, …, Ekn0,变成 末动能，Ek1, Ek2, …, Ekn
W1 E k 1 E k 10 W2 E k 2 E k 20 Wn E n1 E n10
2-2 动能定理 保守力与非保守力 能量守恒定律
0 90 W 0 正功 90 180 W 0 负功
F cos
90 W 0 不作功
➢功的图示法
o rA
曲线下的面积表示变力所作的功。
r
ds rB
➢合力的功等于各分力功的代数和。
W
F d r F1 d r
F2
d
r
W1
W2
➢功的单位：1 J=1 N·m 量纲：dim W ML2T2
解题步骤：
①确定研究对象． ②受力分析，求合外力的功． ③找准初、末状态的动能，运用动能定理列方程求解．
第二章 动量守恒定律和能量守恒定律
2-2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
例1 如图所示，一质量m =225kg的保险箱静止 放置在光滑地面上，甲、乙两人用推力F1=24.0N和 拉力F2=20.0N同时作用于此物体，使它沿直线移动 了d =8.50m。设保险箱与地面间的摩擦可忽略不计。 试计算
第二章 动量守恒定律和能量守恒定律
2-2 动能定理 保守力与非保守力 能量守恒定律
物理学简明教程
2. 功率：功随时间的变化率
平均功率 P W t
瞬时功率
P dW
F
d
r
F
v
Fv
cos
dt
dt
P F v Fvcos
功率的单位 （瓦特）1W 1J s1 1kW 103 W
第二章 动量守恒定律和能量守恒定律
W1 F1d cos1 176.66 J
W2 F2d cos2 130.22 J 则两人做的总功为
W W1 W2 306.88 J
（2）两人对保险箱做功后，它的速率变为多大？ 考虑到保险箱初始速率v0为零，由动能定理
5 动能定理 保守力 功能原理 能量守恒
v1 v 2 m4
3
Wi外 Wi内
i i
问题1: 内力的冲量能改变质 点系的动量? 内力的功能改 变质点系的动能? 问题2: 合外力的冲量=外力 冲量的矢量和? 外力做功的 代数和=合外力的功?
W外 W内 Ek 2 Ek1
作用于质点系的所有外力与 内力做功的代数和等于质点 系动能的增量.
直角坐标系中 F Fx i Fy j Fz k dr dxi dyj dzk
W F cos r F r
单位: 焦耳(J) 物体在力的作用下发生了位移, 力的功等于力在位移方向的分 量与位移的标积.
dW F dr Fx dx Fy dy Fz dz
2. 内力的功也能改变系统的 动能.
P.12/67
第2章 质点动力学
2.3.4 势能 势能差 1. 几种常见力的功M1
结论: 重力对质点的功只与质 点的初末位置有关, 与质点的 运动路径无关.
r
dW G dr
2) 弹性力的功
M 2 mg
z2
O
fx
y
x dW mgk (dxi dyj d zk )
2. 说明: 1) 动量守恒定律只适用于惯性系. 2) 系统动量守恒的条件: (1) 系统不受外力; 或 (2) 合外力=0. 3) 若系统所受外力的矢量和 Fi 0, 而合外力在某方向的 投影为零时, 动量守恒在该方向 上成立. 4) 若内力>>外力, 例如在碰撞, 打 击, 爆炸等相互作用时间极短的 过程中, 外力可略去, 动量守恒对 整个系统适用. 5) 动量守恒定律是自然界最普遍, 最基本的定律之一.
2-2动能定理 保守力和非保守力 能量守恒定律
m'm W G 2 dr rA r
rB
m
dr
m'
r dr
1 1 W Gmm( ) rB rA
rB
B
2-2 动量定理 保守力与非保守力 能量守恒定律
(b) 重力作功
在位移元 功为
y y1
A
D
dr
dr
h
A C
中，重力P做的
y2
P
B
dW P d r
B
ex in nc
机械能 E Ek Ep
W W E E0
ex in nc
——系统的功能定理
系统机械能增量等于外力和非保守内力 作功之和 。
2-2 动量定理 保守力与非保守力 能量守恒定律
说明
W W E E0
ex in nc
1）系统能量改变与功的关系； 2）适用惯性系； 3）改变系统机械能方法 外力作功
2-2 动量定理 保守力与非保守力 能量守恒定律
守恒定律的意义
不究过程细节，而能对系统状态下结论。
讨论 下列各物理量中，与参考系有关的物 理量是哪些？（不考虑相对论效应） (1) 质量 (2)动量 (3) 冲量 (4) 动能 (5)势能 ( 6) 功 答 动量、动能、功。
2-2 动量定理 保守力与非保守力 能量守恒定律
得 v 2 gl(cos cos 0 )
FT v ds
l
1.53 m s
1
P
2-2 动量定理 保守力与非保守力 能量守恒定律
二
保守力与非保守力 势能
A
rA
m'
1 几种力做功的特点 (a) 万有引力作功
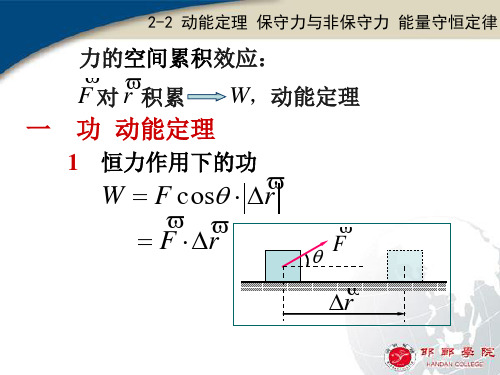
rB
m
dr
m'
r dr
1 1 W Gmm( ) rB rA
rB
B
2-2 动量定理 保守力与非保守力 能量守恒定律
(b) 重力作功
在位移元 功为
y y1
A
D
dr
dr
h
A C
中，重力P做的
y2
P
B
dW P d r
B
ex in nc
机械能 E Ek Ep
W W E E0
ex in nc
——系统的功能定理
系统机械能增量等于外力和非保守内力 作功之和 。
2-2 动量定理 保守力与非保守力 能量守恒定律
说明
W W E E0
ex in nc
1）系统能量改变与功的关系； 2）适用惯性系； 3）改变系统机械能方法 外力作功
2-2 动量定理 保守力与非保守力 能量守恒定律
守恒定律的意义
不究过程细节，而能对系统状态下结论。
讨论 下列各物理量中，与参考系有关的物 理量是哪些？（不考虑相对论效应） (1) 质量 (2)动量 (3) 冲量 (4) 动能 (5)势能 ( 6) 功 答 动量、动能、功。
2-2 动量定理 保守力与非保守力 能量守恒定律
得 v 2 gl(cos cos 0 )
FT v ds
l
1.53 m s
1
P
2-2 动量定理 保守力与非保守力 能量守恒定律
二
保守力与非保守力 势能
A
rA
m'
1 几种力做功的特点 (a) 万有引力作功
动能定理与功的关系
动能定理与功的关系动能定理是物理学中的一个重要定理，用于描述物体的运动状态和能量转化。
它与功是息息相关的，两者之间存在着紧密的关系。
本文将探讨动能定理与功的关系，以及它们在物理学中的应用。
一、动能定理的基本概念动能定理是描述物体运动状态的一个基本原理。
它表明，物体的动能变化等于所受到的净工作。
动能可以简单地定义为物体由于运动而具有的能量。
动能定理可以用数学表达为：ΔK = W其中，ΔK代表物体动能的变化量，W代表物体所受到的净工作。
这个公式说明了物体的动能变化与所受到的净工作之间的关系。
二、功的概念功是物理学中描述力对物体产生效果的量。
在力学中，功可以定义为力在物体上施加的作用力与物体位移的乘积。
功可以使物体加速或减速，改变物体的动能状态。
功可以用数学表达为：W = F·d·cosθ其中，W代表功，F代表力的大小，d代表物体的位移，θ代表力施加的角度。
三、动能定理与功的关系从定义和公式上看，可以发现动能定理与功之间存在着密切的联系。
动能定理可以理解为物体的动能变化等于所受到的净工作，而功则是描述力对物体产生效果的量。
物体的动能变化与所受到的净工作之间的关系就是动能定理与功的关系。
根据功的定义和公式，可以得出动能定理的推导过程：ΔK = WΔK = F·d·cosθΔK = m·a·d·cosθ (根据牛顿第二定律 F = m·a，其中m为物体的质量，a为物体的加速度)ΔK = m·(v^2 - u^2)/2 (根据速度v和初速度u的关系 v^2 = u^2 + 2ad)由上述推导可以看出，动能定理中的动能变化ΔK与功W之间存在着直接的数学关系。
这表明了动能定理与功的紧密联系。
四、动能定理与功的应用动能定理与功在物理学中有着广泛的应用。
它们可以用于解释和分析各种物理现象，如机械能守恒、碰撞等。
在机械能守恒的情况下，物体的总机械能保持不变。
5第五讲 功、动能、动能定理、保守力的功、势能
r v
R
0
0
dt = −cπRv
o
ωt
o′
2R x 8
小球质量为m，沿半径为R的球面由 的球面由A点运 例：小球质量为 ，沿半径为 的球面由 点运 动到B点 点时， 动到 点 ， 在 A点时 ， v0=0， 在 B点时小球对容 点时 ， 点时小球对容 器的正压力为N， 器的正压力为 ， 由做功定义求摩擦力在该过 程中对小球做的功。 程中对小球做的功。 o A θ 解：切向方程 r
功和能、 §2-6 功和能、动能定理
Work and Energy. Theorem of Kinetic Energy
◎牛顿第二定律→力的瞬时效应。 牛顿第二定律→力的瞬时效应。 力的空间累积效应→做功→能量变化。 ◎力的空间累积效应→做功→能量变化。 ----能量守恒定律 能量守恒定律。 ◆----能量守恒定律。 力的时间累积效应→冲量→动量变化。 ◎力的时间累积效应→冲量→动量变化。 ----动量守恒定律 动量守恒定律。 ◆ ----动量守恒定律。 守恒定律的重要意义： 守恒定律的重要意义： 自然界的一切过程都遵守守恒定律。 ●自然界的一切过程都遵守守恒定律。 凡违背守恒定律的过程都不能实现。 ●凡违背守恒定律的过程都不能实现。 守恒定律是解决实际问题的有力工具。 ●守恒定律是解决实际问题的有力工具。
初
末
重力的功与路径无关，仅与物体始末位置有关. 重力的功与路径无关，仅与物体始末位置有关.
17
2) 弹力的功 设弹簧无形变时 其末端为坐标原 点O。 。 r r
a
l0
b
o
x
： F = − kxi k：弹性系数 dA = Fx dx = − kxdx xb 1 2 1 2 Aab = − kxdx = kx a − kx b xa 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F
d r
F
d r
ACB
ADB
A
C
F
dr
F
d r
F
d r
l
ACB
BDA
D
B
l
F
dr
0
掌握
A C
D
物体沿闭合路径运动一周时,
B
保守力对它所作的功等于零 .
非保守力: 力所作的功与路径有关 .（例如摩擦力）
三、势能 (potential energy) 熟练掌握
重力功
重力势能
W (mgy2 mgy1)
b
a
Fdr
cos
b a
F
dr
一、功（work）
力的空间累积效应：
W
B
F
dr
B
F cos ds
A
A
B
单位：焦耳（J）
A
讨论
(1)功是标量， 但有正、负；
0o 90o , dW 0
90o 180 o , dW 0
90o
F
dr
dW
0
F cos
(2) 作功的图示；
B
S A Fds cos
若以{木块、子弹}为一系统，则这 对作用力和反作用力是内力，所以说内 力做功不一定为0。
（5）作功与参照系有关。
例如：传送带将箱子从
低处运到高处，地面上
f静
的人看摩擦力作功了，
而站在传送带上的人看
摩擦力没有作功。
(6）功率 （power） ：
定义：功随时间的变化率。
单位： 焦耳/秒（瓦特）
(7)功的计算方法
W rB G m'm dr
m'
rA
r2
Am
r dr
r dr
rB
B
掌握
万有引力作功只取决于质点的起始 和终了位置，与所经过的路径无关。
2、弹性力作功
F kxi dW kxdx
F F'
o x Px
W
x2 Fdx
x1
x2 x1
kxdx
(
1 2
k x22
1 2
k x12
)
掌握
在弹性限度内，弹性力所作的功只由弹簧 起始和终了位置决定，而与形变过程无关。
（3）动能定理提供了一种计算功的简便方法；
三、解题思路与举例 W E k E k0 E k
1）确定研究对象； 2）受力分析，分析作功的力，不作功的
力不考虑； 3）分析始末运动状态，确定Ek、Ek0；
4）应用定理列方程求解。
例1.用铁锤将一只铁钉击入木板内,设木板对
铁钉的阻力与铁钉进入木板之深度成正比,如
3、重力作功
ya
b x
掌握
重力作功只与质点的起始和终止位 置有关，而与所经过的路径无关。
二、保守力与非保守力
（conservation force ＆ nonconservative force）
分析三种力 作功的特点
保守力：作功只与物体的始末位置有关；
而与路径无关的力。
反之称为非保守力。
掌握
反映保守力作功特点的数学表达式：
用力为f，木块对子弹 的反作用力为f`，木
f'
f
块的位移为s，子弹的
位移为（s+l）。
s
l
f 对木块作功： fs 0
f ` 对子弹作功： f ' (s l) 0
总功为： fs f ' (s l) f ' l
子弹减少的能量转变成木块的动能和热能， 摩擦生热：为一对作用力和反作用力作功之和。
一、万有引力和弹性力作功的特点
1、万有引力作功
m' 对m 的万有引力为
F
G
m'm r2
er
m移动dr时，F作元功为
Am
rA
r dr
r dr
m' rB
B
dW
F
dr
G
m'm r2
er
dr
m从A到B的过程中F作功：
W
F
dr
B
A
G
m'm r2
er
dr
er dr er drcos dr rA
3-4 功 动能定理
恒力的功：
W Fr cos
W
F
r
F
F
r
变力的功??
解决方法：
1.无限分割路径； 2.以直线段代替曲线段；
ds
dr
b
3.以恒力的功代替变力的功；
W
F
cos
r
F
r
4.将各段作功代数求和；
F1
F2
2
1
令 r 0 取极限，
a r
W
n
lim r 0 i 1
Fi r
cos i
W
s
曲线下面的面积等于变 力所做功的代数值.
o
A
ds
B
(3）几个力同时作用在物体上时，所作的功：
F F1 F2 F3
合力对质点所作的功，等于每个 分力所作的功的代数和。
(4) 一对作用力和反作用力大小相等方向相反，
但这对力作功的总和不一定为0。
掌握
例如：子弹穿过木块
过程子弹对木块的作
3. 势能计算 W (Ep Ep0 ) Ep
令 Ep0 0
Ep (x, y, z)
Ep0
0
F
dr
P
质点在某点的势能等于质点从该点沿任何路 径移到势能零点过程中保守力做的功。
讨论
势能是状态的函数 Ep Ep (x, y, z)
势能具有相对性，势能大小与势能零 点的选取有关． 势能是属于系统的． 势能差与势能零点选取无关．
a
Fb
Ft
W
b a
Ftdr
ab
m dv dr dt
v
v0
mvdv
W
1 mv 2 2
1 2
mv
2 0
W
1 mv 2 2
1 mv 2 2
W E k E k 0 E k
掌握
合外力对质点所作的功，等于质点
动能的增量。
——质点动能定理
注意
（1）W为合外力的功。 （2）动能定理适用于惯性系。
果在击第一次时,能将钉击入木板内 1 cm, 再
击第二次时（锤仍然以第一次同样的速度击
钉）,能击入多深？ 第一次
第二 次
解：W
1 2
m
v
2
0
x0
0
kxdx
x
x0
k
x
d
x
,
x0
1cm
1 2
k
x
2 0
1 2
k
x2
1 2
k
x
2 0
,
x
2 x0
x x x 0 ( 2 1) x0 0.41cm P96作业
引力功
W
(G
m' m ) rB
(G
mr'Am)
弹力功
W
( 1 2
k x22
1 2
kx12 )
Ep mgy
引力势能
Ep
G
m' m r
弹性势能
Ep
1 2
k x2
1. 定义位置函数 Ep Ep (x, y, z) 为势能。
2. 保守力的功与势能的关系
W (Ep Ep0 ) EP
即：保守力对物体作的功等于物体势能增量的负值。
掌握
➢受力分析确定要计算作功的力；
➢建立坐标系；
➢确定元功 dW
F
dr
➢求解
W ab dW
例1、物体由静止出发作直线运动，质量为m，
受力 bt ，b 为常量，求在 T 秒内，此
力所作的功。
解：元功 根据牛顿定律和加速度的定义求
二、质点的动能定理
Fn
W
b a
F
dr
b
a
Fdr cos
F cos Ft
3-25
思考题：质量为m = 0.5kg 的质点,在 xoy 坐标平面内运动，其运动方程为 x = 5t2 , y=0.5 (SI),从 t =2 s 到 t = 4 s 这段
时间内，外力对质点作的功为
(A) 1.5 J (C) 4.5J
(B) 300J (D) -1.5J
[B]
§3-5 保守力与非保守力 势能