4锐角三角函数PPT课件

合集下载

沪科版数学九年级上册23.1第4课时一般锐角的三角函数值课件(共16张PPT)

>
>
>
正弦值随锐角增大而增大;余弦值随锐角增大而减小;正切值随锐角增大而增大．
归纳小结
同学们再见！
授课老师：
时间：2024年9月1日
第23章解直角三角形
23.1 锐角的三角函数
第4课时一般锐角的三角函数值
学习目标
学习重难点
重点
难点
1.会用计算器求锐角的三角函数值．2.会用计算器根据一个锐角三角函数的值求对应的锐角．
会用计算器求锐角的三角函数值．
正确使用计算器求锐角的三角函数值．
回顾复习
根据前面学习的特殊角的三角函数值，完成下面的表格．
解：
按键顺序
显示
0.642 787 609
sin
4
0
=
∴ sin 40°= 0.642 8．
如果锐角不是整数度数时应该如何计算呢？
例题示范
例1 用计算器求cos 34°35′的值(精确到0.000 1)．解：
∴ cos 34°35′ = 0.823 3．
例2 求tan 66°15′17″的值 (精确到0.000 1)．解：
思考如何用计算器求锐角的三角函数值呢？
计算器上只要有sin,cos,tan键，就可以用来求锐角的三角函数值．
不同计算器的按键方法各有不同，现在介绍一种计算器，先按ON/C键，再按MODE键，使显示器屏幕出现“DEG”，然后再按有关三角函数的键．
用计算器求sin 40°的值(精确到0.000 1)．
问题引入
任意一个锐角，如何求它的三角函数值呢？比如求sin 36°的值．
步骤1：如图，用刻度尺和量角器，作出Rt△ABC，使∠C=90°，∠A=36°．步骤2：用刻度尺量得∠A的对边BC和斜边AB的长度．步骤3：算出比值，即得出sin 36°的值．

《锐角三角函数》ppt初中数学4

（设13）0°1－所2对s的in直30角°边co长s3为0°a，那么斜边长为2a
2
1
2 例(2)5如如图图,已，知在圆△锥A的BC高中A，O∠等A于=3圆0锥度的，底面半径OB的倍,求α.
你设想30知°道所小对明的怎直样角算边出长的为吗a，？那么斜边长为2a
2
2
tan a 3 (解2)：如过图点,已C知作圆CD锥⊥的A高BA于O点等D于圆锥的底面半径OB的
12 1 3 22
1 3 2
（2）3tan30°－tan45°+2sin60°
3 3 1 2 3
3
2
3 1 3
2 3 1
(3) cos 60 1
1 sin 60 （1）1－2 sin30°cos30° tan 30
求∠A、∠B的度数．
设两条直角边长为a，则斜边长＝
1 （1）cos260°＋sin260°
米．然后他很快就算出旗杆的高度了。
你想知道小明怎样算出的吗？
?
30°
米
10米
例3、(1)如图，在Rt△ABC中， ∠C=90°，AB= 6 ,BC= 3。求∠A的度数。
(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 3 倍,求α.
A
B
6
3
A
C
(1)
O B
(2)
例4 已
1 例5 如图，在△ABC中，∠A=30度，
2
3
sin a 2 仔解（例细：12）：观过1操察点－场,C2说里作s说i有nC3你D一0⊥发°个A现c旗Bo这s于杆3张0点，°表D老有师哪让些小规明律去?测量旗杆高度，小明站在离旗杆底部102米远处，目测旗杆的顶部，视2线与水平线的夹角为30度

《锐角三角函数》PPT教学课件(第1课时)

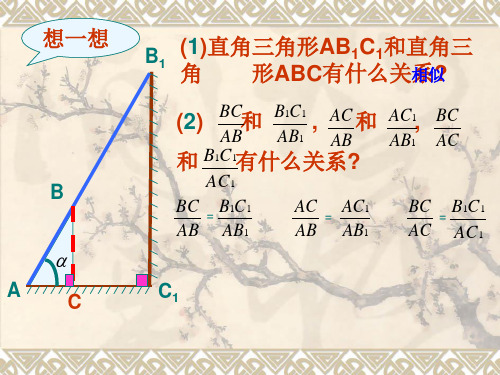
BC AC
= 12 =
AC
34，所以AC=9.故填9.
随堂训练
AB 6.如图，在Rt△ABC中，∠C＝90°，BC
17 15
,则tan
15 A＝_8__．
由正切定义可知tan A＝BACC , 因为 AB 17 , 可设BC＝15a，AB＝17a，从而可
BC 15
用勾股定理表示出第三边AC＝8a，再用正切的定义求解得 tan A＝ BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义：如图，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻
边的比便随之确定，这个比叫做 ∠A的正切，记作tan A，即tan A＝ A的对边
A的邻边
2.tanA的值越大，梯子（坡）越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫

锐角三角函数4市公开课金奖市赛课一等奖课件

拟定角范围
3. 当∠A为锐角，且tanA值
不小于 3
3
时，∠A（
B
）
(A)小于30° (B)不小于 30°
(C) 小于60° (D)不小于 640. °当∠A为锐角，且tanA值
小于时3 ，∠A（ C）
(A)小于30° 30°
(C) 小于60° 60°
(B)不小于 (D)不小于
第11页
☆ 应用练习
tan70°21′=2.8006,
第4页
2已知锐角三角函数值,求角度：
已知三角函数值求角度，要用到sin，Cos，tan第二功效键“sin－１ Cos－１，tan－１”键比如：已知sinα
＝0.2974,求锐角α．按健顺序为：
• 按键顺序
2ndF
sin 0 · 2
9
7
4
=
显示结果 17.30150783
(A)0°＜∠A≤ 30 ° (B) 30°＜∠A≤45°
(C)45°＜∠A≤ 60 ° (D) 60°＜∠A≤ 90 °
第12页
例3、一段公路弯道呈弧形，测得弯道 A⌒B两端距离为200米，AB⌒半径为1000 米，求弯道长（准确到0.1米)
A
R
O
B
第13页
解
按下列顺序依次按键：
显示结果为0.897 859 012.
因此
sin63゜52′41″≈0.8979
第3页
练习:
驶向胜利彼岸
1.使用计算器求下列三角函数值.（准确到0.0001） sin24゜,cos51゜42′20″,tan70゜21′.
答案:sin24°=0.4067, cos51°42′20″=0.6197,

《锐角三角函数》课件

锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02

沪科版数学九年级上册 23.1 锐角三角函数课件(共13张PPT)

(6) tan30°·tan60°＋ cos230°
本节课学习了什么内容？
三角函数 sina cos a tan a
30°
1 2
3 2 3 3
45°
2 2
2 2
1
60°
3 2
1 2
3
拓展探究
求已知锐角的三角函数值：
21..求求csoint7603゜゜4552′′的41值″的.（值精. 确（到精0确.0到0001.）0001）在先角用度如单下位方状法态将为角“度度单” 位的状情态况设下定:屏为幕“显度示”出
显示
按再下按列下列顺顺序序依依次次按按键键
由锐角三角函数值求锐角:
已知tan x=0.7410,求锐角 x.（精确到1′）在角度单位状态为“度” 的情况下（屏幕显示出），按下列顺序依次按键：
显示结果为36.538 445 77.
再按键：
24.2锐角三角函数值
自学检测：
根据三角函数的定义，sin30°是一个常数.用刻度
尺量出你所用的含30°的三角尺中，30°所对的
直角边与斜边的长，与同桌交流，看看这个常数
是什么.
B
sin30°=
对边＝1 Βιβλιοθήκη 边 2理由：30在直角三角形中，如果A一个锐角等于30°，C
那么它所对的直角边等于斜边的一半.
若 tan 1 则α＝______3_0_°____；
3
若 cos 1 ,则α＝______4_5_°____．
2
2.根据下列条件，求出相应的锐角A：
(1) sin A 2 ; (2) cos A 3 0;
2
2
(3) tan(A 20) 1.
基础练习：

锐角三角函数4.ppt

一般地，对于每一个确定的锐角α，在角的
一边上任取一点Ｂ，作ＢＣ⊥ＡＣ于点Ｃ，则比
值 BC , AC , BC都是一个确定的值，与点B在角的边
AB AB AC
上的位置无关，因此，比值 BC , AC , BC都是锐角α
的三角函数。
AB AB AC B
A
C
这几个比值都是锐角∠A的函数，记
作sin A、cos A、tan A、cot A，
AB 5
AB 5
cosA = AC = 4 , AB 5
cosB = BC = 3 , AB 5
tanA = BC = 3 . AC 4
tanB = AC = 4 . BC 3
当∠A+∠B=90°时,
sinA=cosB, cosA=sinB, tanA·tanB=1
B
在直角三角形中，∠A+∠B=90
相等,则这两个锐角相等.
课外探索：
1、在平面坐标系第一象限内是否存在点P，使得OP=4, sin∠POB＝0.5．求点P的坐标,并求出OP所在直线的解析式.
思考：OP所在直线的解析式的比例系数K与∠POB有
什么关系呢?
y
6 5
4
3
2
1
B
0 12 34 5x
课外探索：
2、如图，一根3m长的竹竿AB斜靠在墙上，当端点A离地面的高度AC长为1m时，竹竿AB的倾斜角α的正切 tanα的值是多少？当端点A位于D，离地面的高度CD为2m时，倾斜角β 的正切tanβ的值是多少？
锐角的正切值最大？
A
α
B
5.如图,在Rt△ABC中,锐角A的对边和邻边同时扩
大100倍,sinA的值（ C ）

锐角的三角函数PPT

余弦函数的符号为cos，表示为cos(θ)，其中θ为锐角。
02
余弦函数的图像是一条周期为2π的余弦曲线，表示在直角三角形中，邻边的长度与斜边的长度的比值在[-1,1]之间周期性变化。
04
正切函数的定义
01
正切函数：tan(θ) = sin(θ) / cos(θ)
02
正切函数的定义域：(0, π/2)
余弦函数的值域：[-1, 1]
余弦函数的图像：一个周期为2π的周期函数，图像关于y轴对称
余弦函数的奇偶性：偶函数，f(x) = f(-x)
余弦函数的单调性：在[0, π/2]上是增函数，在[π/2, π]上是减函数
余弦函数的导数：f'(x) = -sin(x)
正切函数的性质
01
02
03
04
05
值域：正弦函数的值域是[-1, 1]
奇偶性：正弦函数是奇函数，即f(x) = -f(-x)
周期性：正弦函数的周期是 2π，即f(x + 2π) = f(x)
最值：正弦函数的最大值是1，最小值是-1
图像：正弦函数的图像是一条正弦曲线，关于原点对称
余弦函数的性质
定义：余弦函数是直角三角形中的一个角与对边和斜边的比值
03
正切函数的值域：(0, ∞)
04
正切函数的图像：在平面直角坐标系中，正切函数的图像是一条以原点为中心的对称曲线，在y轴右侧的部分为单调递增，在y轴左侧的部分为单调递减。
Part Two
锐角三角函数的性质
正弦函数的性质
定义：正弦函数是直角三角形中的一个角（锐角）的正弦值与对边长度的比值
06
正切函数是锐角三角函数中的一种，表示在一个直角三角形中，对边（opposite）的长度与邻边（adjacent）的长度之比。

锐角三角函数说课稿市公开课一等奖省优质课获奖课件.pptx

注意：sinA不表示“sin”乘以“A”. 正弦常见写法有以下两种形式：
(1)sinA，sin42°，sinβ（省去角符号）;
(2)sin∠DEF，sin∠1（不能省去角符号）.
第4页
例题精讲【例1】如图28-1-4，在Rt△ABC中，BC=8， AC=10. 求sinA和sinB值.
第5页
解析依据正弦定义知sinA= ，sinB= . 因为AB未知，所以应先依据勾股定理求出AB.
（1）求证：DC=BC；（2）若AB=5，AC=4，求 tan∠DCE值．
第36页
第37页
第38页
第17页
锐角三角函数概念:锐角A正弦、余弦、正切都叫做∠A锐角三角函数.三角函数实质是一个比值，这些比值只与锐角大小相关，与直角三角形大小无关. 当一个锐角值给定，它三个三角函数值就对应地确定了，另外，并非只有在直角三角形中才有锐角三角函数值，而是只要有角就有三角函数值.
第18页
2. 各锐角三角函数之间关系：（1）互余关系：sinA=cos（90°-A）， cosA= sin（90°-A）. （2）平方关系：sin2A+cos2A=1. （3）弦切关系：tanA=
方法规律
第32页
第33页
7. （6分）在Rt△ABC中，∠C＝90°，∠A，∠B ，∠C对边分别为a，b，c.已知2a＝3b，求∠B三角函数值.
第34页
第35页
8. （6分）如图KT28-1-2所表示，△ABC内接于⊙O，AB是⊙O直径，点D在⊙O上，过点C切线交AD 延长线于点E，且AE⊥CE，连接CD．
解析作出图形如图28-1-10，可得AB=500 m，∠A=20°，在Rt△ABC中，利用三角函数即可求得BC长度.

锐角三角函数复习.ppt

又BC－CD＝BD
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形，除一个直角的已知元素外，还需要几个元素？为什么这些元素中至少要有一条边？试给出可以求解直角三角形的两个条件．
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形，我们用什么方法进行处理，就能把它转化为可以解的直角三角形？
问题4 你认为需要具备哪些知识、掌握哪些方法，就能较顺利地解决有关实际问题？请总结实际问题的一般步骤和注意点．
锐角三角函数z x xk
特殊角的三角函数
解直角三角形
简单实际问题
c
a
b
A
B
C
知识
特殊角的三角函数
2
1
30°
1
1
45°
2
1
60°
30°＋ 60°= 90°
返回
解直角三角形
∠A＋ ∠ B＝90°
a2+b2=c2
三角函数关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返回
简单实际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返回
问题1 已知：如同，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AD＝3，CD＝，怎样求sinA和cos∠BCD的值？怎样求∠B的正切值？
已知：如图，在△ABC中，∠C＝90°，点D在BC上，BD＝4，AD＝BC，cos∠ADC= ，求：（1）DC的长；（2）sinB的值．

《锐角三角函数》PPT教学课件(第2课时)

1
∠ 的对边＝
＝ .

2
斜边
A
可得 AB=2BC=70m，即需要准备70m长的水管.
C
知识讲解
1.正弦
如图，任意画一个Rt△ABC，使∠C＝90°，∠A＝45°，计
算∠A的对边与斜边的比
A
BC
AB
，你能得出什么结论？
即在直角三角形中，当一个锐角等于45°
时，不管这个直角三角形的大小如何，这
数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦
、余弦和正切,记号中习惯省去“∠”；
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角
三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角
切比3，分子根号别忘添.
30°，45°，60°角的正切值可以看成是 3， 9 ， 27.
当A、B为锐角时，
若A≠B，则
sinA≠sinB，
cosA≠cosB，
tanA≠tanB.
知识讲解
注意
1.从函数角度理解∠A的锐角三角函数：把∠A看成自
变量，其取值范围是0°<∠A<90°，sinA，cosA，
在Rt△ABC中,如果锐角A确定,
那么∠ A 的对边与斜边的比、邻
边与斜边的比都是一个定值.
B
斜
边
A
∠A的邻边
∠A的对边
┌
C
知识讲解
归纳：
在有一个锐角相等的所有直角三角形中，这个锐角的邻边与斜
边的比值是一个常数，与直角三角形的大小无关.

锐角三角函数优秀教学课件市公开课一等奖省优质课获奖课件.pptx

用计算器求出以下各角三角函数值，说明你发觉，
并尝试验证.
(1)sin 62°25'30″； (2)sin 80°；
(3)sin 12°25'； (4)cos 27°34'30″;
(5)cos 10°；
(6)cos 77°35'.
【结论】
(1)锐角α正弦值伴随α增大而增大;
(2)sin α=cos(90°-α)，其中α为锐角.
第6页
检测反馈
1.用计算器求sin 62°20'值正确是 ( ) A A.0.8857 B.0.8856 C.0.8852 D.0.8851
解析:按计算器使用说明依次按键得sin 62°20'≈3249，则∠A约为
A.17° B.18° C.19°
(B) D.20°
解析:按计算器使说明依次按键得∠A≈18°.故选B.
3.用计算器求三角函数值(准确到0.001).
(1)sin 23°≈ 0.391 ;
(2)tan 54°53'40″≈ 1.423 .
解析:用计算器求得sin 23°≈0.391，tan 54°53'40″≈1.423.
第7页
4.已知sin α=0.2，cos β=0.8，则α+β≈ 48°24' .(准确到1')
第2页
用计算器求任意锐角三角函数值
求出以下各角三角函数值.
(1)sin 18°； (2)cos 21°28'30″； (3)tan 30°36'.
解:(1)sin 18°≈0.309016994. (2)cos 21°28'30″≈0.930577395. (3)tan 30°36'≈0.591398351.

《锐角三角函数》PPT优秀课件

斜边c
B ∠A的对边a
sin A= ∠A的对边
斜边
A ∠A的邻边b C
∠A的邻边
cos A=
斜边
tan A= ∠A的对边 ∠A的邻边
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
已知直角三角形两边求锐角三角函数的值
如图，在 Rt△ABC 中，∠C=90°，AB=10，BC=6，求sinA，cosA，
即tan A＝ a . b
B
斜边c
∠A的对边a
A
┌ ∠A的邻边b C
再见
在Rt△ABC中，∠C＝90°锐角正弦的定义
斜边 A
B
∠A的对边
┌
C
如图，在Rt△ABC中，∠C＝90° 我们把锐角A的邻边与对边的比叫做∠A的正切，记作tanA，即
B
斜边 ∠A的对边
┌ A ∠A的邻边 C
例1 如图,在 Rt△ABC 中，∠C =90°,AB=10,BC=6,求
sin A, cos A,tan A的值.
tanA的值. 解：由勾股定理,得
B 10
6
A
C
因此 sin A BC = 6 = 3， AB 10 5
cos A AC 8 4 , tan A BC = 6 = 3 .
AB 10 5
AC 8 4
利用勾股定理求三角函数值方法
已知直角三角形中的两条边求锐角三角函数值的一般思路是：当所涉及的边是已知时，直接利用定义求锐角三角函数值；当所涉及的边是未知时，可考虑运用勾股定理的知识求得边的长度，然后根据定义求锐角三角函数值．
课堂练习
1. 如图，旗杆高AB=8m，某一时刻，旗杆影子长BC=16m，则
1

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

tan B的值．
解：在Rt△ABC中,
B
∵∠A=30° ∴∠B=60°,且a=
1
c
2
.
∴b
c2 a2
c2 （ c )2
3c
A
C
22
,
∴
tan
A
tan 30
a
1
c
3c
3
b2 2 3
tan B tan 60 b 3 c 1 c 3 a2 2
课堂练习
12 1．在Rt△ABC中，∠C=90°，AC=5，AB=13，则sin A=13，
5
5
cos A= 13 ，tan A=12．
2．如图，在△ABC中，∠C=90°，BC︰AC=1︰2，
5
25
则sin A= 5 ，cos A=5 ，tan B= __2__．
课堂练习
3．如图，在Rt△ABC中，∠C=90°，b=20，c=20 2
则∠B的度数为 _4_5_°_． 4．在△ABC中，∠C为直角．
(1)已知AC=3，AB= 14 ，求sin A、tanA的值；
4 （2）已知sin B=5
，求sin A，tanB的值．
课堂练习
．
4．解：（1）在Rt△ABC中，根据勾股定理得
．
BC 14 2 32 5
∴sin A BC
5
70
tan A BC 5
AB 14 14
AC 3
（2）∵sinB= AC 4
AB 5
cos A AC 4 AB 5
tan A BC 3 AC 4
例题解析
如图（2），在Rt△ABC中，由勾股定理得
AC AB2 BC2 132 52 12 ，
．
因此，sin A
BC
5
AB 13
， cos
A
AC AB
12 13
，
tan A BC 5 AC 12
.
例题解析
例2.如图，在Rt△ABC中，∠A=30°， ∠c=90°求tan A、
探究新知
类比正弦的情况，在Rt△ABC中，∠C=90° ，当锐角A取一定度数时，不管直角三角形的大小如何，∠A的邻边与斜边的比、∠A的对边与邻边的比都是确定的．
我们把∠A的邻边与斜边的比叫做∠A的余弦，
记作cos A，即
B
co s
A
A 的邻边斜边
b； c
斜边 c
∠A的对边 a
A ∠A的邻边
C b
，
AB 5
设AC=4k，则AB=5k，根据勾股定理得BC=3k．
∴sin A 3 tan B AC 4
5
BC 3
课堂小结
此知识卡片概括锐角三角函数的基本概念
课堂小结
1．正弦的概念，余弦的概念，正切的概念．如图，在Rt△ABC中，∠C=90°．
sin
A
A 的对边斜边
a c
co
s
A
A 的邻边斜边
【知识点解析】锐角三角函数,此微课系统讲解锐角三角函数的相关知识,同时配有适当练习.
例题解析
例1.如图，在Rt△ABC中，∠C=90°，求sin A和cosA和 tanA的值．
解：如图（1），在Rt△ABC中，由勾股定理得
AB AC2 BC2 42 32 5
．
因此
sin A BC 3
第二十八章锐角三角函数
28.1锐角三角函数
第2课时
学习目标
1.理解锐角的余弦、正切的概念． 2.能依据锐角三角函数的定义，求给定锐角的三角函数值．
复习巩固
1.正弦的定义及表示方法：
如图：Rt △ABC中，∠C=90 °
A
sinA=_____,cosA=______
B
C
2.一个锐角的正弦值是一定的吗？
且sin A， cos A，tan A均大于0，无单位；（4）sin A，cos A，tan A的大小只与∠A的大小有关，而与
直角三角形的边长无关；（5）两锐角相等，则其三角函数值相等，两锐角的三角函数值
相等，则这两个锐角相等．
再见
2020年10月5日
20
谢谢您的指导
THANK YOU FOR YOUR GUIDANCE.
复习巩固
如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对
边与斜边的比叫做∠A的正弦，记作sinA 即
B
sin
A
A的对边斜边
a c
A
C
探究新知
【数学探究】余弦的定义,此交互动画主要探究余弦函数的定义,定量的演示余弦函数的基本定义.
探究新知
【数学探究】正切的定义,此交互动画主要探究正切函数的定义,定量的演示正切函数的基本定义.
感谢阅读！为了方便学习和使用，本文档的内容可以在下载后随意修改，调整和打印。欢迎下载！
2020年对边与邻边的比叫做∠A的正切，记作tan A，即
tan
A
A A
的对边的邻边
a． b
斜边
c
A ∠A的邻边
B
∠A的对边 a C b
探究新知
对于锐角A的每一个确定的值，sinA、cosA、tanA都有唯一确定的值与其对应，所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数．
探究新知
b c
tan
A
A A
的对边的邻边
a b
课堂小结
2．概念中应该注意的几个问题：（1）sin A，cos A，tan A是在直角三角形中定义的，∠A是锐角
（注意数形结合，构造直角三角形）；（2）sin A，cos A，tan A是一个完整的符号，如sin A表示
∠A的正弦，习惯省去“∠”号；（3）sin A，cos A，tan A是一个比值，注意比的顺序，