6 第六章 Matlab实现遗传算法
遗传算法的原理及MATLAB程序实现.

1 遗传算法的原理1.1 遗传算法的基本思想遗传算法(genetic algorithms,GA)是一种基于自然选择和基因遗传学原理,借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。
遗传算法是从一组随机产生的初始解(种群)开始,这个种群由经过基因编码的一定数量的个体组成,每个个体实际上是染色体带有特征的实体。
染色体作为遗传物质的主要载体,其内部表现(即基因型)是某种基因组合,它决定了个体的外部表现。
因此,从一开始就需要实现从表现型到基因型的映射,即编码工作。
初始种群产生后,按照优胜劣汰的原理,逐代演化产生出越来越好的近似解。
在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样,后代种群比前代更加适应环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
计算开始时,将实际问题的变量进行编码形成染色体,随机产生一定数目的个体,即种群,并计算每个个体的适应度值,然后通过终止条件判断该初始解是否是最优解,若是则停止计算输出结果,若不是则通过遗传算子操作产生新的一代种群,回到计算群体中每个个体的适应度值的部分,然后转到终止条件判断。
这一过程循环执行,直到满足优化准则,最终产生问题的最优解。
图1-1给出了遗传算法的基本过程。
1.2 遗传算法的特点1.2.1 遗传算法的优点遗传算法具有十分强的鲁棒性,比起传统优化方法,遗传算法有如下优点:1. 遗传算法以控制变量的编码作为运算对象。
传统的优化算法往往直接利用控制变量的实际值的本身来进行优化运算,但遗传算法不是直接以控制变量的值,而是以控制变量的特定形式的编码为运算对象。
这种对控制变量的编码处理方式,可以模仿自然界中生物的遗传和进化等机理,也使得我们可以方便地处理各种变量和应用遗传操作算子。
2. 遗传算法具有内在的本质并行性。
用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法(Genetic Algorithms,GA)是一种模拟自然界生物进化过程的优化搜索算法,它通过模拟自然选择和遗传学机制,如选择、交叉、变异等,来寻找问题的最优解。
由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点,遗传算法在多个领域得到了广泛的应用,包括函数优化、机器学习、神经网络训练、组合优化等。
本文旨在介绍如何使用MATLAB实现遗传算法程序。
MATLAB作为一种强大的数学计算和编程工具,具有直观易用的图形界面和丰富的函数库,非常适合用于遗传算法的实现。
我们将从基本的遗传算法原理出发,逐步介绍如何在MATLAB中编写遗传算法程序,包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。
通过本文的学习,读者将能够掌握遗传算法的基本原理和MATLAB编程技巧,学会如何使用MATLAB实现遗传算法程序,并能够在实际问题中应用遗传算法求解最优解。
二、遗传算法基础遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传学机制的优化搜索算法。
它借鉴了生物进化中的遗传、交叉、变异等机制,通过模拟这些自然过程来寻找问题的最优解。
遗传算法的核心思想是将问题的解表示为“染色体”,即一组编码,然后通过模拟自然选择、交叉和变异等过程,逐步迭代搜索出最优解。
在遗传算法中,通常将问题的解表示为一个二进制字符串,每个字符串代表一个个体(Individual)。
每个个体都有一定的适应度(Fitness),适应度越高的个体在下一代中生存下来的概率越大。
通过选择(Selection)、交叉(Crossover)和变异(Mutation)等操作,生成新一代的个体,并重复这一过程,直到找到满足条件的最优解或达到预定的迭代次数。
选择操作是根据个体的适应度,选择出适应度较高的个体作为父母,参与下一代的生成。
常见的选择算法有轮盘赌选择(Roulette Wheel Selection)、锦标赛选择(Tournament Selection)等。
Matlab遗传算法及实例

Matlab遗传算法及实例Matlab遗传算法工具箱函数及实例讲解转:最近硏究了一下遗传算法,因为要用遗传算法来求解多元非线性模型。
还好用遗传算法的工具箱予以实现了,期间也遇到了许多问题。
借此与大家分享一下。
首先,我们要熟悉遗传算法的基本原理与运算流程。
基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step 1 :对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step 2 :建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step 3 :在Step 2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step 4 :执行比例选择算子进行选择操作。
Step 5 :按交叉概率对交叉算子执行交叉操作。
Step 6 :按变异概率执行离散变异操作。
Step 7 :计算Step 6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step 8 :判断是否满足遗传运算的终止进化代数,不满足则返回Step 4,满足则输出运算结果其次,运用遗传算法工具箱。
运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库。
目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学幵发的遗传算法工具箱GATBXGAOT以及Math Works公司推出的GADS实际上,GAD鉞是大家所看到的Matlab中自带的工具箱。
遗传算法及其MATLAB程序

遗传算法及其MATLAB实现主要内容遗传算法简介遗传算法的MATLAB实现应用举例一、遗传算法简介遗传算法(Genetic Algorithm,GA)最先是由美国Mic-hgan大学的John Holland于1975年提出的。
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。
它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定等5个要素组成了遗传算法的核心内容。
遗传算法的基本步骤:遗传算法是一种基于生物自然选择与遗传机理的随机搜索算法,与传统搜索算法不同,遗传算法从一组随机产生的称为“种群(Population)”的初始解开始搜索过程。
种群中的每个个体是问题的一个解,称为“染色体(chromos ome)”。
染色体是一串符号,比如一个二进制字符串。
这些染色体在后续迭代中不断进化,称为遗传。
在每一代中用“适值(fitness)”来测量染色体的好坏,生成的下一代染色体称为后代(offspring)。
后代是由前一代染色体通过交叉(crossover)或者变异(mutation)运算形成的。
在新一代形成过程中,根据适度的大小选择部分后代,淘汰部分后代。
从而保持种群大小是常数。
适值高的染色体被选中的概率较高,这样经过若干代之后,算法收敛于最好的染色体,它很可能就是问题的最优解或次优解。
主要步骤如下所示:(1)编码:GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。
(2)初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了—个群体。
GA以这N个串结构数据作为初始点开始迭代。
用Matlab实现遗传算法

用GA找到函数最小值x = ga(fitnessfcn,nvars)局部无约束最小值,x是目标函数的适应度函数,nvars是适应度函数的尺寸(设计变量的数量)。
目标函数和适应度函数接受了1×N大小的x矢量,在x返回一个标量的计算值。
x = ga(fitnessfcn,nvars,A,b)在线性不等式约束下,适应度函数的局部最小值。
如果这个问题有m个线性不等式和n个变量,则A是m×n矩阵,b是m×1矩阵。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq)存在线性等式约束下,适应度函数的局部最小值。
如果没有不等式存在,设置A=[] 和 b=[]。
如果问题存在r个线性等式约束和n个变量,那么Aeq 是r ×n矩阵的大小,beq是r大小的矢量。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)定义了一系列设计变量x的最小和最大边界。
以至于在范围内找到一个解。
如果没有边界存在,LB 和 UB设置为空矩阵。
如果x(i)无下界,设置LB(i) = -Inf;如果x(i)无上界,设置UB(i) = Inf。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)服从在非线性约束条件下的最小值,非线性函数接收x,返回C和Ceq向量,分别代表非线性的不等式和等式。
GA最小化适应度函数,在C(x)≤0和Ceq(x)=0的条件下。
如果无边界存在,设置 LB=[] 和 UB=[]。
注意:当人口类型选项设置为“位串”或者“自定义”,非线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)用在结构选项中的值代替默认的优化参数来进行最小化,它也可以用gaoptimset函数来创建,具体参考gaoptimset的用法。
matlab中的遗传算法拟合

matlab中的遗传算法拟合在MATLAB中,遗传算法是一种常用的优化算法,可以用于拟合数据。
遗传算法是一种模拟自然进化过程的优化算法,通过模拟基因的交叉、变异和选择等操作,逐步优化解的质量。
下面我将从多个角度介绍在MATLAB中使用遗传算法进行拟合的步骤和注意事项:1. 准备数据,首先,你需要准备一组实验数据,包括自变量和因变量。
确保数据的准确性和完整性,以获得准确的拟合结果。
2. 定义适应度函数,适应度函数用于评估每个个体的适应程度,即拟合程度。
在拟合问题中,适应度函数通常是计算预测值与实际值之间的误差或损失函数。
你需要根据具体问题定义适应度函数。
3. 初始化种群,在遗传算法中,种群是由多个个体组成的集合。
每个个体代表一个可能的解。
你需要初始化一个种群,设置种群大小和每个个体的基因编码。
4. 选择操作,选择操作用于选择适应度较高的个体作为父代,用于产生下一代个体。
常用的选择方法包括轮盘赌选择、锦标赛选择等。
你可以根据具体问题选择适合的选择操作。
5. 交叉操作,交叉操作模拟基因的交换,通过将两个个体的基因进行交叉,产生新的个体。
交叉操作有多种方式,如单点交叉、多点交叉等。
选择合适的交叉操作方式可以增加种群的多样性。
6. 变异操作,变异操作模拟基因的突变,通过改变个体的某些基因值来引入新的解。
变异操作有多种方式,如位变异、均匀变异等。
变异操作可以增加种群的多样性,避免陷入局部最优解。
7. 更新种群,通过选择、交叉和变异操作,生成新的个体,更新种群。
8. 迭代优化,重复进行选择、交叉和变异操作,直到达到停止条件。
停止条件可以是达到最大迭代次数、达到预定的适应度阈值或者经过一定的迭代次数后适应度不再改变等。
9. 解码和评估,在每次迭代后,对新生成的个体进行解码,转换为实际的参数值。
然后,使用适应度函数评估个体的适应程度。
10. 结果分析,最后,根据迭代过程中适应度的变化情况,选择适应度最高的个体作为最终的拟合结果。
遗传算法 matlab

遗传算法 Matlab什么是遗传算法?遗传算法是一种模拟生物进化过程的优化算法。
它模拟了自然界中的遗传、突变和选择等过程,利用这些操作来搜索和优化问题的解空间。
遗传算法具有以下几个关键步骤:1.初始化种群:通过生成一组随机解来初始化初始种群。
每个解被编码为一个染色体,染色体通常由二进制字符串表示。
2.评价适应度:使用适应度函数评估每个个体的适应度。
适应度函数通常通过衡量个体在解空间中的性能来定义。
3.选择操作:选择操作基于个体的适应度进行,通过概率选择操作来确定哪些个体应该参与繁殖下一代。
适应度较高的个体有更大的概率被选中。
4.交叉操作:选择的个体进行交叉操作,生成下一代的染色体。
交叉操作通过交换个体染色体中的信息来生成新的个体。
5.变异操作:为了保持种群的多样性,变异操作在染色体中进行随机的变异。
这个过程通过随机改变染色体中的部分基因来进行。
6.替换操作:根据新生成的染色体替换当前种群中某些个体,以此来形成新的种群。
7.重复上述步骤:重复执行上述步骤直到满足终止条件(例如达到最大迭代次数或找到满意的解)。
如何在 Matlab 中实现遗传算法?在 Matlab 中,可以使用遗传算法和优化工具箱来实现遗传算法。
以下是实现遗传算法的一般步骤:1.定义适应度函数:根据具体问题定义适应度函数,该函数衡量每个个体在解空间中的性能。
适应度函数的设计将影响到最终结果。
2.初始化种群:使用内置函数或自定义函数来生成初始种群。
每个个体都应该表示为染色体形式的解。
3.设置遗传算法参数:根据具体问题设置遗传算法的参数,如种群大小、迭代次数、选择操作和交叉操作的概率等。
4.编写遗传算法主循环:在主循环中,使用选择操作、交叉操作和变异操作来生成新的染色体,并计算每个个体的适应度。
5.选择操作:使用选择函数根据适应度值选择染色体。
具体的选择函数可以根据问题的特点进行调整。
6.交叉操作:使用交叉函数对染色体进行交叉操作,生成下一代的染色体。
遗传算法在matlab中的实现

遗传算法是一种模拟自然选择与遗传机制的优化算法,它模拟了生物进化的过程,通过优化个体的基因型来达到解决问题的目的。
在工程和科学领域,遗传算法被广泛应用于求解优化问题、寻找最优解、参数优化等领域。
而MATLAB作为一款强大的科学计算软件,拥有丰富的工具箱和编程接口,为实现遗传算法提供了便利。
下面将通过以下步骤介绍如何在MATLAB中实现遗传算法:1. 引入遗传算法工具箱需要在MATLAB环境中引入遗传算法工具箱。
在MATLAB命令窗口输入"ver",可以查看当前已安装的工具箱。
如果遗传算法工具箱未安装,可以使用MATLAB提供的工具箱管理界面进行安装。
2. 定义优化问题在实现遗传算法前,需要清楚地定义优化问题:包括问题的目标函数、约束条件等。
在MATLAB中,可以通过定义一个函数来表示目标函数,并且可以采用匿名函数的形式来灵活定义。
对于约束条件,也需要进行明确定义,以便在遗传算法中进行约束处理。
3. 设置遗传算法参数在实现遗传算法时,需要对遗传算法的参数进行设置,包括种群大小、交叉概率、变异概率、迭代次数等。
这些参数的设置将会直接影响遗传算法的收敛速度和优化效果。
在MATLAB中,可以通过设置遗传算法工具箱中的相关函数来完成参数的设置。
4. 编写遗传算法主程序编写遗传算法的主程序,主要包括对适应度函数的计算、选择、交叉、变异等操作。
在MATLAB中,可以利用遗传算法工具箱提供的相关函数来实现这些操作,简化了遗传算法的实现过程。
5. 运行遗传算法将编写好的遗传算法主程序在MATLAB环境中运行,并观察优化结果。
在运行过程中,可以对结果进行实时监测和分析,以便对遗传算法的参数进行调整和优化。
通过以上步骤,可以在MATLAB中实现遗传算法,并应用于实际的优化问题与工程应用中。
遗传算法的实现将大大提高问题的求解效率与精度,为工程领域带来更多的便利与可能性。
总结:遗传算法在MATLAB中的实现涉及到了引入遗传算法工具箱、定义优化问题、设置算法参数、编写主程序和运行算法等步骤。
利用MATLAB实现遗传算法和MATLAB神经网络工具箱的使用

实验一利用MATLAB完成遗传算法一、实验目的1、熟悉MATLAB言语编程环境2、掌握MATLAB言语命令3、学会利用MATLAB编程完成遗传算法二、实验原理MATLAB是美国Math Works公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算言语和交互式环境,MATLAB可以进行矩阵运算、绘制函数和数据、完成算法、创立用户界面、连接其他编程言语的程序等,主要应用于工程计算、操纵设计等领域。
通过学习遗传算法原理,使用MATLAB编写程序,完成其求解策略。
三、实验内容通过MATLAB编程,利用遗传算法求解:xx=求[-2,2]f-)(f.x,max∈exp05xsin(),.0)(x)200(三、实验要求1、程序设计2、调试3、实验结果4、撰写实验汇报实验二 MATLAB神经网络工具箱的使用一、实验目的1、掌握MATLAB言语命令2、提高MATLAB程序设计能力3、学会使用MATLAB神经网络工具箱二、实验原理MATLAB言语是Math Works公司推出的一套高性能计算机编程言语,集数学计算、图形显示、言语设计于一体,其强大的扩展功能为用户提供了广阔的应用空间。
它附带有30多个工具箱,神经网络工具箱就是其中之一。
利用该工具箱可以方便的构建神经网络的结构模型、设计、训练等,完成神经网络算法。
三、实验内容通过MATLAB编程,利用神经网络工具箱预测公路运量:公路运量主要包含公路客运量和公路货运量两个方面。
据研究,某地区的公路运量主要与该地区的人数、机动车数量和公路面积有关,上表给出了该地区20年的公路运量相关数据。
依据有关部门数据,该地区202X和202X年的人数分别为73.39和75.55万人,机动车数量分别为3.9635和4.0975万辆,公路面积分别为0.9880和1.0268万平方千米。
请利用BP网络预测该地区202X和202X 年的公路客运量和公路货运量。
遗传算法及其MATLAB实现

P k
0.111180
Qk
0.111180
U2
U3 U4 U5 U6 U7 U8 U9 U10
17.370890
9.590546 29.106122 15.686001 11.900541 17.958717 19.763190 26.401669 10.252480
101111011111110
2、初始群体的产生
• 遗传算法是对群体进行的进 化操作,需要给其准备一些 起始搜索点的初始群体数据
• 初始群体太小时会产生病态 基因,且造成有效等位基因 先天缺乏 • 初始群体太大会导致结果难 以收敛且浪费资源,稳健性 下降 • 建议值0~100
假设初始种群中有10个个体,其染色体可随机生成如下:
5、新种群的交配(交叉运算)
• 交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交互两个个体之间的部分染色体 • 先对群体进行随机配对,其次随机设置交叉点位置,最后再相互交换配对染色体之间的部分基因 • 交叉概率一般取0.4~0.99
①交配染色体数量的确定 交配染色体的数量等于染色体总量乘以交配概率。这里假设 交配概率 P c 为0.25,染色体总量为10条,所以 参加交配的染色 体数量为[2.5]条。符号[ ]表示取整,这里取整数2,即交配的染 色体数目为2条。 假定其分别对应U1~U10这10个个体,则其中低于交配概率0.25的U5和U7参加交配。这 样操作的原因是:交配概率越低,低于交配概率以下的随机数的数量就越少,所以参加交配 的染色体数量与交配概率可能会成正比。 ③在交配池发生交配 染色体U5和U7被选中作为交配的父辈,交配点的选择以随机数产生。交配的种类有单 点交配和多点交配,这里取单点交配。计算机随机生成一个介于0~32的整数。假设所产生 的整数为1,那么两个染色体自1位置开始分割,在染色体1位置右端部分进行交换而生成新 的子辈染色体,即 U5=[1 0011 0110 1001 0110 1000 0000 1011 1001] U7=[0 0111 0101 1100 1100 0000 0101 0100 1000] U5*=[1 0111 0101 1100 1100 0000 0101 0100 1000] U7*=[0 0011 0110 1001 0110 1000 0000 1011 1001]
(完整版)遗传算法matlab实现源程序
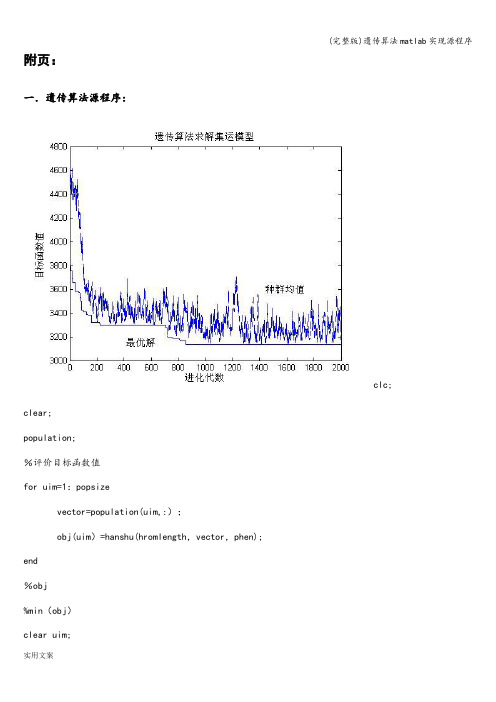
附页:一.遗传算法源程序:clc; clear;population;%评价目标函数值for uim=1:popsizevector=population(uim,:);obj(uim)=hanshu(hromlength,vector,phen);end%obj%min(obj)clear uim;objmin=min(obj);for sequ=1:popsizeif obj(sequ)==objminopti=population(sequ,:);endendclear sequ;fmax=22000;%==for gen=1:maxgen%选择操作%将求最小值的函数转化为适应度函数for indivi=1:popsizeobj1(indivi)=1/obj(indivi);endclear indivi;%适应度函数累加总合total=0;for indivi=1:popsizetotal=total+obj1(indivi);endclear indivi;%每条染色体被选中的几率for indivi=1:popsizefitness1(indivi)=obj1(indivi)/total;endclear indivi;%各条染色体被选中的范围for indivi=1:popsizefitness(indivi)=0;for j=1:indivifitness(indivi)=fitness(indivi)+fitness1(j);endendclear j;fitness;%选择适应度高的个体for ranseti=1:popsizeran=rand;while (ran>1||ran<0)ran=rand;endran;if ran〈=fitness(1)newpopulation(ranseti,:)=population(1,:);elsefor fet=2:popsizeif (ran〉fitness(fet—1))&&(ran<=fitness(fet))newpopulation(ranseti,:)=population(fet,:);endendendendclear ran;newpopulation;%交叉for int=1:2:popsize-1popmoth=newpopulation(int,:);popfath=newpopulation(int+1,:);popcross(int,:)=popmoth;popcross(int+1,:)=popfath;randnum=rand;if(randnum〈 P>cpoint1=round(rand*hromlength);cpoint2=round(rand*hromlength);while (cpoint2==cpoint1)cpoint2=round(rand*hromlength);endif cpoint1>cpoint2tem=cpoint1;cpoint1=cpoint2;cpoint2=tem;endcpoint1;cpoint2;for term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int,ss)==popfath(term)tem1=popcross(int,ss);popcross(int,ss)=popcross(int,term);popcross(int,term)=tem1;endendclear tem1;endfor term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int+1,ss)==popmoth(term)tem1=popcross(int+1,ss);popcross(int+1,ss)=popcross(int+1,term);popcross(int+1,term)=tem1;endendclear tem1;endendclear term;endclear randnum;popcross;%变异操作newpop=popcross;for int=1:popsizerandnum=rand;if randnumcpoint12=round(rand*hromlength);cpoint22=round(rand*hromlength);if (cpoint12==0)cpoint12=1;endif (cpoint22==0)cpoint22=1;endwhile (cpoint22==cpoint12)cpoint22=round(rand*hromlength);if cpoint22==0;cpoint22=1;endendtemp=newpop(int,cpoint12);newpop(int,cpoint12)=newpop(int,cpoint22);newpop(int,cpoint22)=temp;。
遗传算法的Matlab实现讲解

y_mean(i)=mean(fitvalue+Cmin); %第i代平均适应度
pop=newpop; end fplot('2*x+10*sin(5*x)+7*cos(4*x)',[0 10]) hold on plot(x,y,'r*') hold off
temp1=decodechrom(pop,1,chromlength); %将pop每行转化成十进制数
x=temp1*(Xmax-Xmin)/(2^chromlength-1); %将十进制域 中的数转化为变 量域 的数 objvalue=2*x+10*sin(5*x)+7*cos(4*x); %计算目标函数值
Matlab编程实现GA
计算目标函数值
计算目标函数值 % calobjvalue.m函数的功能是实现目标函数的计算,其公式采用本文示 例仿真,可根据不同优化问题予以修改。 %遗传算法子程序
%Name: calobjvalue.m
%实现目标函数的计算 function [objvalue]=calobjvalue(pop,chromlength,Xmax,Xmin)
bestindividual=pop(1,:);
bestfit=fitvalue(1); for i=2:px
if fitvalue(i)>bestfit
bestindividual=pop(i,:); bestfit=fitvalue(i);
MATLAB实验遗传算法和优化设计

实验六 遗传算法与优化设计一、实验目的1. 了解遗传算法的基本原理和基本操作(选择、交叉、变异);2. 学习使用Matlab 中的遗传算法工具箱(gatool)来解决优化设计问题;二、实验原理及遗传算法工具箱介绍1. 一个优化设计例子图1所示是用于传输微波信号的微带线(电极)的横截面结构示意图,上下两根黑条分别代表上电极和下电极,一般下电极接地,上电极接输入信号,电极之间是介质(如空气,陶瓷等)。
微带电极的结构参数如图所示,W 、t 分别是上电极的宽度和厚度,D 是上下电极间距。
当微波信号在微带线中传输时,由于趋肤效应,微带线中的电流集中在电极的表面,会产生较大的欧姆损耗。
根据微带传输线理论,高频工作状态下(假定信号频率1GHz ),电极的欧姆损耗可以写成(简单起见,不考虑电极厚度造成电极宽度的增加):图1 微带线横截面结构以及场分布示意图{}28.6821ln 5020.942ln 20.942S W R W D D D t D W D D W W t D W W D e D D παπππ=+++-+++⎛⎫⎡⎤⎛⎫ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎡⎤⎛⎫⎝⎭ ⎪⎢⎥⎝⎭⎣⎦ (1) 其中πρμ0=S R 为金属的表面电阻率,ρ为电阻率。
可见电极的结构参数影响着电极损耗,通过合理设计这些参数可以使电极的欧姆损耗做到最小,这就是所谓的最优化问题或者称为规划设计问题。
此处设计变量有3个:W 、D 、t ,它们组成决策向量[W, D ,t ] T ,待优化函数(,,)W D t α称为目标函数。
上述优化设计问题可以抽象为数学描述:()()min ..0,1,2,...,jf X s tg X j p ⎧⎪⎨⎪≤=⎩ (2)其中()Tn x x x X ,...,,21=是决策向量,x 1,…,x n 为n 个设计变量。
这是一个单目标的数学规划问题:在一组针对决策变量的约束条件()0,1,...,j g X j p ≤=下,使目标函数最小化(有时也可能是最大化,此时在目标函数()X f 前添个负号即可)。
Matlab实现遗传算法的示例详解

Matlab实现遗传算法的⽰例详解⽬录1算法讲解1.1何为遗传算法1.2遗传算法流程描述1.3关于为什么要⽤⼆进制码表⽰个体信息1.4⽬标函数值与适应值区别1.5关于如何将⼆进制码转化为变量数值1.6关于代码改进2MATLAB⾃带ga函数2.1问题描述2.2⾃带函数使⽤3⾃编遗传算法各部分代码及使⽤3.1代码使⽤3.2Genetic1--主函数3.3PI(PopulationInitialize)--产⽣初始种群3.4Fitness--计算⽬标函数值3.5FitnessF--计算适应值3.6Translate--将⼆进制码转换3.7Probability--染⾊体⼊选概率3.8Select--个体选择3.9Crossing--交叉互换3.10Mutation--基因突变3.11Elitist--最优个体记录与最劣个体淘汰3.12完整代码这篇⽂章⽤了⼤量篇幅讲解了如何从零开始⾃⼰写⼀个遗传算法函数,主要是为了应对学⽣作业等情况,或者让⼤家对遗传算法有更充分的理解,如果要⽤于学术研究,最好还是使⽤⾃带遗传算法,之后可能会推出更多⾃带遗传算法⼯具箱的使⽤。
1 算法讲解1.1 何为遗传算法遗传、突变、⾃然选择、杂交,遗传算法是⼀种借鉴了进化⽣物学各类现象的进化算法。
看到⼀个很形象的⽐喻来描述各类进化算法的区别:爬⼭算法:⼀只袋⿏朝着⽐现在⾼的地⽅跳去。
它找到了不远处的最⾼的⼭峰。
但是这座⼭不⼀定是最⾼峰。
这就是爬⼭算法,它不能保证局部最优值就是全局最优值。
模拟退⽕:袋⿏喝醉了。
它随机地跳了很长时间。
这期间,它可能⾛向⾼处,也可能踏⼊平地。
但是,它渐渐清醒了并朝最⾼峰跳去。
这就是模拟退⽕算法。
遗传算法:有很多袋⿏,它们降落到喜玛拉雅⼭脉的任意地⽅。
这些袋⿏并不知道它们的任务是寻找珠穆朗玛峰。
但每过⼏年,就在⼀些海拔⾼度较低的地⽅射杀⼀些袋⿏。
于是,不断有袋⿏死于海拔较低的地⽅,⽽越是在海拔⾼的袋⿏越是能活得更久,也越有机会⽣⼉育⼥。
第6章 基于GA优化的BP网络算法分析与MATLAB实现

第六章
MATLAB优化算法案例分析与应用
图6- 14 某工作面温度、湿度与通风量之间 的关系图
第六章
MATLAB优化算法案例分析与应用
适 应 度 曲 线 终 止 代 数 = 10 4.5
平均适应度
4
适应度
3.5
3
1
2
3
4
5
6
7
8
9 10 11
进化代数
图6- 15 遗传算法适应度曲线
第六章
MATLAB优化算法案例分析与应用
%
标记中心
[A, id] = max([s.Area]);
bw(labelmatrix(cc)~=id)=0;
bw = imdilate(bw,blk); % 膨胀
im_sep = immultiply(im_org,bw);
% figure,imshow(im_sep);title('seperate brain,gray matter and white matter')
%% 大脑灰白质提取 % lev2 = 50/255; % 阈值
% L = zeros(size(im_sep)); %0=背景
% L(im_sep<lev2 & im_sep>0) = 2; %2=灰质
第六章 MRI大 脑 图 像
MATLAB优化算法案例分析与应用
图6- 3 大脑灰白质原始图像
第六章
-0.1 -0.12
0
GA BP预 测 误 差 回归预测误差
5
10 15 20 25 30 35 40 45
误 差 error
图6- 18 GA_BP预测和回归预测工作面误差 比较
数学建模专题之MATLAB遗传算法优秀课件

Grefenstette, Fitzpattrick
Schaffer
对含噪声的函数进行测试 多种群遗传算法解决多目标优化问题
1 遗传算法概述
年份 1986 1986 1987 1987
1987
1987 1987
1987
1987 1987
续表1.1
贡献者
内容
Goldberg
最优种群大小估计
Grefenstette
A ( A1, A2 , , AN )
其中 Aj ( j 1, 2, , N ) S ,N称为种群规模。
2 标准遗传算法
2.3 遗传算法的若干概念
适应度(Fitness) 在研究自然界中生物的遗传和进化 现象时,生物学家使用适应度这个术语来度量某个物种对 于生存环境的适应程度。对生存环境适应程度较高的物种 将获得更多的繁殖机会,而对生存环境适应程度较低的物 种,其繁殖机会就会相对较少,甚至逐渐灭绝。在遗传算 法中,一般通过适应度函数(Fitness function)来衡量某 一个体的适应度高低。
2 标准遗传算法
2.3 遗传算法的若干概念
个体(Individual) 称S 0,1l为个体空间,个体空间的元
素 a a0a1 al1 S 称为个体,它是染色体带有特征的实
体。分量 a j 0,1 称为基因,正整数 l称为个体的基因长
度。
种群(Population) 称个体空间S中N个个体组成的一个子 集(个体允许重复)称为一个种群,记为:
数学建模专题之 MATLAB遗传算法
Contents
1
遗传算法概述
2
标准遗传算法
3
遗传算法简单举例:函数极值
4
遗传算法求解TSP问题
如何在Matlab中进行遗传算法和优化问题求解

如何在Matlab中进行遗传算法和优化问题求解遗传算法是一种模拟生物进化过程的智能优化算法,常用于解决复杂的优化问题。
在Matlab中,我们可以利用遗传算法工具箱(GA Toolbox)来实现遗传算法求解优化问题。
本文将介绍如何在Matlab中使用遗传算法解决优化问题,并探讨一些优化技巧和应用案例。
第一章:背景介绍遗传算法是通过模拟生物进化过程,利用自然选择、交叉和变异等操作来搜索问题的最优解。
它的应用涵盖了许多领域,如工程设计、组合优化、机器学习等。
在Matlab中,我们可以借助GA Toolbox提供的函数和工具来灵活地实现遗传算法的求解过程。
第二章:遗传算法基本原理遗传算法的基本原理包括个体表示、适应度评估、选择、交叉和变异等操作。
在Matlab中,我们可以使用二进制、实数、整数等不同的编码方案来表示个体。
适应度评估是根据问题的优化目标,对每个个体进行评估和排序。
选择操作通过一定的策略选择优秀个体,并进行复制和保留。
交叉操作模拟生物的基因交叉过程,通过交换基因片段来产生新个体。
变异操作通过改变个体的某些基因值来增加多样性和搜索空间。
第三章:遗传算法的实现步骤在Matlab中,我们可以按照以下步骤实现遗传算法的求解过程:初始化种群、适应度评估、选择操作、交叉和变异操作、更新种群。
在这个过程中,我们可以根据具体问题设计合适的参数设置,如种群大小、进化代数、交叉和变异的概率等。
第四章:遗传算法的优化技巧在使用遗传算法求解优化问题时,有一些技巧可以提高算法的效率和收敛性。
例如,选择合适的编码方案和适应度函数,设计高效的选择策略,引入精英保留机制等。
此外,选取合适的参数设置和优化策略也是非常重要的。
第五章:遗传算法在工程设计中的应用遗传算法在工程设计中有广泛的应用,如优化控制器参数、电路布局优化、结构设计优化等。
本章将以一个典型的结构优化问题为例,介绍如何利用遗传算法在Matlab中进行工程设计的优化。
遗传算法及其MATLAB实现

41组,顾英辉,魏猛,王艺潞
一、遗传算法的概述
1、产生与发展 2、生物学基础 3、算法的特点及定义
二、遗传算法的原理
1、 简单遗传算法 2、简单遗传算法原理 3、遗传算法参数选择
三、遗传算法的流程
1、算法流程图 2、遗传算法举例
四,遗传算法的MATLAB程序设计
• 1、程序设计流程及参数选取 • 1.1、遗传算法的程序设计伪代码 • 1.2、适应度函数调整 • 2、遗传算法工具箱核心函数的用法 • 3、Genetic Algorithm and Direct Search Toolbox适应 度函数设计
1.2 生物学基础
• 以自然选择学说为核心的现代生物进化理论,其基本观点 是:种群是生物进化的基本单位,生物进化的实质是种群 基因频率的改变。基因突变和基因重组、自然选择及隔离 是物种形成过程的三个基本环节,通过他们的综合运用, 种群产生分化,最终导致新物种的形成。 • 新物种形成的途径和方式有两种:渐变式和爆发式。 • 渐变式主要通过变异的逐渐积累而成亚种,再由亚种形成 一个或多个新种,新种又分为两种类型,即继承式新种形 成和分化式新种形成;爆发式不通过亚种这一阶段而迅速 形成新的物种,其分为三种类型,即杂交产生新种,染色 体结构变化形成新种和多倍体化的新种形式。
U L
2
k
1
②解码:解码的目的是为了将不直观的二进制数据串还原成十进制。设某
k k 1 k 2 3 2 1
k i 1 i 1 i k
一个体的二进制编码为 b b b ...b b b , 则对应的解码公式为 x L (b 2 ) U L 2 1 例:设有参数x 【2,4】,现用5位二进制数对x编码,若x=10101,它对应的 十进制为 b 2 1* 2 0 * 2 1* 2 0 * 2 1* 2 21
简单的遗传算法MATLAB实现

遗传算法是对达尔文生物进化理论的简单模拟,其遵循“适者生存”、“优胜略汰”的原理。
遗传算法模拟一个人工种群的进化过程,并且通过选择、杂交以及变异等机制,种群经过若干代以后,总是达到最优(或近最优)的状态。
自从遗传算法被提出以来,其得到了广泛的应用,特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域,遗传算法更是发挥了重大的作用,大大提高了问题求解的效率。
遗传算法也是当前“软计算”领域的重要研究课题。
本文首先结合MATLAB对遗传算法实现过程进行详细的分析,然后通过1个实际的函数优化案例对其应用进行探讨。
1. 遗传算法实现过程现实生活中很多问题都可以转换为函数优化问题,所以本文将以函数优化问题作为背景,对GA的实现过程进行探讨。
大部分函数优化问题都可以写成求最大值或者最小值的形式,为了不是一般性,我们可以将所有求最优值的情况都转换成求最大值的形式,例如,求函数f(x)的最大值,若是求函数f(x)的最小值,可以将其转换成g(x)=-f(x),然后求g(x)的最大值,这里x可以是一个变量,也可是是一个由k个变量组成的向量,x=(x1, x2, …, x k)。
每个x i,i=1,2,…,k, 其定义域为D i,D i=[a i, b i]。
一般规定f(x)在其定义域内只取正值,若不满足,可以将其转换成以下形式,其中C是一个正常数。
1.1 编码与解码要实现遗传算法首先需要弄清楚如何对求解问题进行编码和解码。
对于函数优化问题,一般来说,有两种编码方式,一是实数编码,一是二进制编码,两者各有优缺点,二进制编码具有稳定性高、种群多样性大等优点,但是需要的存储空间大,需要解码过程并且难以理解;而实数编码直接用实数表示基因,容易理解并且不要解码过程,但是容易过早收敛,从而陷入局部最优。
本文以最常用的二进制编码为例,说明遗传编码的过程。
从遗传算法求解的过程来看,需要处理好两个空间的问题,一个是编码空间,另一个是解空间,如下图所示从解空间到编码空间的映射过程成为编码过程;从编码空间到解空间的映射过程成为解码过程。
6 第六章 Matlab实现遗传算法

min f ( x) ? Aineq x Bineq Aeq x Beq a x b e x sin( x2 ) ln x c
三.Matlab函数调用实现GA
Matlab的GA函数
x = ga(fitnessfcn,nvars) x = ga(fitnessfcn,nvars,A,b) x = ga(fitnessfcn,nvars,A,b,Aeq,beq) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options) x = ga(problem) [x, fval] = ga(...) [x, fval, exitflag] = ga(...)
一.遗传算法的基础知识
交叉(Crossover)
交叉是按较大的概率从群体中选择两个个 体,交换两个个体的某个或某些位。如单点 交叉,多点交叉等。
例如: 交叉前: 个体1:00000|01110000000010000 00000| 00000|00000111111000101 个体2:11100|00000111111000101 11100|01110000000010000 11100| 交叉后 :
三.Matlab函数调用实现GA
GA函数调用步骤
第一步:编写适应度函数; 第二步:对GA参数进行设置; options = gaoptimset(‘参数名’, 参数值, …, ‘参数名’, 参数值) 例:options = gaoptimset('PopulationSize', 100) 第三步:调用GA函数; [x fval] = ga(@fitnessfun, nvars) [x fval exitflag output population scores] = ga(@fitnessfcn, nvars) [x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[],options);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.遗传算法的基础知识
适应度函数(Fitness Function)
定义:度量个体适应度的函数。 在某种程度上来说,适应度函数就相当 于实际问题的目标函数,只是它只求最小 值,因此,当实际问题是求最大值时,需要 做相应转换。
一.遗传算法的基础知识
选择(Slection)
选择(或称为复制)是在种群中选择 适应度高(函数更加优化)的个体产生新的 种群的过程。遗传算法中的选择操作就是用 来确定如何从父代群体中按某种方法选取哪 些个体遗传到下一代群体中的一种遗传运 算,用来确定重组或交叉个体。如轮盘赌选 择,随机竞争选择等
2 x1 2 x2
1 1 0 9 4 9 4 不 等 式 必 须 是“ 0” 等 式 不 等 式 都 必 须 返 回 , 若 无 则 为 “ []”
2 x1
2 x2
二.Matlab工具箱实现GA
第3部分:运算参数
参数的设置主要影响到运算过程的速度和运算结果的 精准性,两者在很多时候是相互矛盾的。 运算参数有很多,均有缺省值,一般都不需要修改。各 个参数选项的详细信息在参考书中有详细介绍,另外在工具 箱操作界面的右侧也有相应的英文介绍。
二.Matlab工具箱实现GA
Export to Workspace
将当前问题和参数设置 保存到Matlab工作空间 保存当前问题和参数时 将当前结果的相关信息也 也保存,下次运行保存的 问题时,初始种群为此次 结果的最后种群,而不是重 新产生新种群
将当前的结果 保存到Matlab 工作空间
将当前的参 数设置保存到 Matlab工作空间
三.Matlab函数调用实现GA
Matlab的GA函数
[x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[], options);
fitnessfcn — Fitness function nvars — Number of variables for the problem Aineq — Matrix for inequality constraints Bineq — Vector for inequality constraints Aeq — Matrix for equality constraints Beq — Vector for equality constraints LB — Lower bound on x UB — Upper bound on x nonlcon — Nonlinear constraint Function options — Options structure
一.遗传算法的基础知识
交叉(Crossover)
交叉是按较大的概率从群体中选择两个个 体,交换两个个体的某个或某些位。如单点 交叉,多点交叉等。
例如: 交叉前: 个体1:00000|01110000000010000 00000| 00000|00000111111000101 个体2:11100|00000111111000101 11100|01110000000010000 11100| 交叉后 :
一.遗传算法的基础知识
遗传算法的流程
一.遗传算法的基础知识
随机产生种群
M i n f ( x ) x1 x 2 0 xi 1 1 x 1 x3 x3
一.遗传算法的基础知识
编码与解码 个体(染色体)
基因型 1000101110110101000111
解码
编码
表现型:0.637197
第2部分:约束条件
Linear inequalities(线性不等式):A*x <= b 。其中A是矩阵,b是列向 量,书写格式如A中填写[1,2,3;12,3,43;1,23,4],b中填写[5;4;7]; Linear equalities (线性等式): Aeq*x = beq 。其中Aeq是矩阵,beq是 列向量,格式同上; Bounds (边界):变量的最小和最大值。矩阵形式表示,负无穷大为-Inf,正 无穷大为Inf。 Nonlinear constraint function(非线性限制函数) :类似于“Fitness Function”中的输入,首先生成对应的.M文件,此处输入函数的句柄,调用其中 的(非线性限制)函数。 格式为: function [c,ceq]=game(x) c(1) = (x(1)^2)/9 + (x(2)^2)/4 - 1; ceq = [ ];
min f ( x) ? Aineq x Bineq Aeq x Beq a x b e x sin( x2 ) ln x c
三.Matlab函数调用实现GA
Matlab的GA函数
x = ga(fitnessfcn,nvars) x = ga(fitnessfcn,nvars,A,b) x = ga(fitnessfcn,nvars,A,b,Aeq,beq) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon) x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options) x = ga(problem) [x, fval] = ga(...) [x, fval, exitflag] = ga(...)
三.Matlab函数调用实现
调用GA函数求解(见ga_eg2.m)
四.Matlab编程实现GA
一.遗传算法的基础知识
变异(Mutation) 以较小的概率对个体编码串上的某个或某些位值进 行改变,如二进制编码中0”变为“1”,“1”变为 “0”,进而生成新个体。 它决定了遗传算法的局部搜索能力,同时保持种群 的多样性。交叉运算和变异运算的相互配合,共同 完成对搜索空间的全局搜索和局部搜索。
Run solver Use random states from previous run:重复 运算上一次运算过程—运算结果一致。 Start、Pause、Stop:开始、暂停、停止。 Status and results:状态和结果。提示是 否正常计算,以及正常运算的最优结果。 Final point:最优结果时的参数值。
三.Matlab函数调用实现GA
求下列优化问题
2 f ( x1 , x2 ) 0.5* x12 x2 x1 x2 2 x1 6 x2
min f ( x) ? 1 1 2 x1 1 2 2 x2 2 1 3 x 0, x 0 1 2
Matlab实现遗传算法
学 院:设计艺术学院
课程名称:计算机辅助工业设计 授课班级:2013级工业设计研究生
MATLAB 技术
Contents
1
遗传算法的基础知识
2
Matlab工具箱实现GA
3
Matlab函数调用实现GA
4
Matlab编程实现GA
一.遗传算法的基础知识
遗传算法( Genetic Algorithm :GA)是一种寻 求函数(问题)最优解的数学方法。 基本原理是:模拟自然界生物繁衍过程中基因重 组与进化的自然过程,把待解决问题的参数编成 二进制码或十进制码(也可编成其他进制码), 即基因,若干基因组成一个染色体(个体),许 多染色体进行类似于自然选择、配对交叉和变异 的运算,经过多次重复迭代(即世代遗传)直至 得到最后的优化结果。
二.Matlab工具箱实现GA
第4部分:运行显示
Plot对话框:运算过程的图形显示界面,可 同时选择多项,在运算过程中将显示对应的 运算过程。比如:best fitness将显示每一 代中最佳适应度的函数值;Scores将显示 每一代所有个体的取值等。
二.Matlab工具箱实现GA
第4部分:运行命令和结果
二.Matlab工具箱实现GA
打开工具箱: 键入命令:gatool 点击命令:
二.Matlab工具箱实现GA1Fra bibliotek2 3
4
二.Matlab工具箱实现GA
第1部分:定义函数句柄
在Fitness Function中输入一个计算适应 度函数的.M文件函数的句柄(handle),以 调用文件中函数。格式:@test(与相应的M 文件名一致) 在 Number of variance中输入变量个 数
三.Matlab函数调用实现
调用GA函数求解(见ga_eg2.m)
function ga_eg2 A = [1 1;-1 2; 2 1]; b = [2; 2; 3]; lb = zeros(2,1); [x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb); mesh_lincontest6; hold on; plot3(x(1),x(2),fval,'r*'); function mesh_lincontest6 m=10;n=1000; x=-n:m:n; y=-n:m:n; z= 0.5*(ones(length(x),1)*x).^2 + (ones(length(y),1)*y).^2 ... -(ones(length(x),1)*x).*(ones(length(y),1)*y) -2*(ones(... length(x),1)*x) - 6*(ones(length(y),1)*y); mesh(x,y,z)
specify any linear equality, linear inequality, or nonlinear constraints
三.Matlab函数调用实现GA
调用GA函数求例1的最大值 (见ga_eg1.m)
