变位齿轮的简易计算
变位齿轮计算公式

变位齿轮计算公式变位齿轮是一种特殊的齿轮传动装置,由于其特殊的设计结构,在很多工程领域中被广泛应用。
变位齿轮的计算涉及到很多参数和公式,下面将介绍1200字以上的变位齿轮计算公式。
1.变位齿轮的模数计算公式:变位齿轮的模数实际上是齿轮的基本参数之一,是计算齿轮尺寸和性能的重要依据。
模数的计算公式如下:m=(π*d)/(z+2)其中,m为模数,d为齿轮的总直径,z为齿数。
2.变位齿轮的齿宽计算公式:变位齿轮的齿宽决定了齿轮的受力和传动能力,齿宽的计算公式如下:bw = K * m其中,bw为齿宽,K为齿宽系数,m为模数。
3.变位齿轮的中心距计算公式:变位齿轮的中心距是指两个齿轮中心线之间的距离,中心距的计算公式如下:a=(m*(z1+z2))/2其中,a为中心距,m为模数,z1和z2分别为两个齿轮的齿数。
4.变位齿轮的齿数比计算公式:齿数比是指两个齿轮齿数的比值,齿数比的计算公式如下:i=z2/z1其中,i为齿数比,z1为主动齿轮的齿数,z2为从动齿轮的齿数。
5.变位齿轮的齿侧间隙计算公式:齿侧间隙表示两个齿轮侧面的距离,可以通过以下计算公式进行计算:cg = 0.25 * m * (z1 + z2) + c其中,cg表示齿侧间隙,m表示模数,z1和z2表示两个齿轮的齿数,c表示一个修正系数。
6.变位齿轮的分度圆直径计算公式:分度圆直径是指齿轮两齿间的直径,可以通过以下计算公式进行计算:d=m*z其中,d表示分度圆直径,m表示模数,z表示齿轮的齿数。
7.变位齿轮的螺旋角计算公式:螺旋角表示齿轮齿槽相对于圆柱面的旋转角度,可以通过以下计算公式进行计算:φ = tan^(-1)((cosα1/sinα1)+((z1+z2)/(2m*tanα1)))其中,φ表示螺旋角,α1表示变位齿轮的压力角,z1和z2分别表示两个齿轮的齿数,m表示模数。
8.变位齿轮的齿形因数计算公式:齿形因数是表示齿轮齿形的一个参数,可以通过以下计算公式进行计算:X = (2*m*(cosα1+cosα2))/(π*tan(α1+α2))其中,X表示齿形因数,m表示模数,α1和α2分别表示两个齿轮的压力角。
变位齿轮节圆直径计算公式

变位齿轮节圆直径计算公式变位齿轮是一种常见的机械传动装置,广泛应用于各个领域。
在设计变位齿轮时,需要计算节圆直径,以确保齿轮的正确运行。
本文将介绍如何根据变位齿轮的参数来计算节圆直径,并探讨其在机械传动中的重要性。
我们需要了解什么是变位齿轮。
变位齿轮是一种直齿圆柱齿轮,其齿形与普通直齿圆柱齿轮不同。
它的齿形曲线是由一个齿形参数来描述的,该参数通常用来衡量齿轮齿形的变化程度。
在变位齿轮中,齿形参数的变化会导致齿轮齿面的变形,从而实现变速或变位传动。
为了计算变位齿轮的节圆直径,我们需要知道以下参数:齿数、模数、压力角、齿宽等。
其中,齿数是指齿轮上的齿的数量,模数是指齿轮齿形的基本尺寸,压力角是指齿轮齿面与齿轮轴线之间的夹角,齿宽是指齿轮齿面的宽度。
根据变位齿轮的参数,我们可以使用以下公式来计算节圆直径:节圆直径 = 模数× 齿数 / cos(压力角)在这个公式中,模数和齿数是已知的参数,可以从设计要求或齿轮标准中获取。
压力角是变位齿轮设计中的一个重要参数,它的取值范围通常在20度到30度之间。
通过选择适当的压力角,可以平衡齿面接触性能和传动效率。
计算节圆直径的公式中还包含一个cos(压力角)的项,它是为了修正齿面的变形而引入的。
由于变位齿轮的齿面不规则,其受力情况也不同于普通直齿圆柱齿轮,因此需要对其进行修正,以确保齿轮的正常运行。
通过计算得到的节圆直径,可以确定变位齿轮的基本尺寸,并进一步进行设计和加工。
齿轮的基本尺寸包括齿高、齿根高、齿顶高等,这些尺寸对于齿轮的传动性能和寿命有着重要的影响。
在机械传动中,变位齿轮具有广泛的应用。
它可以实现多种传动比,提供灵活的传动方式,适用于各种不同的工况。
例如,在汽车变速器中,变位齿轮可以根据车速和发动机转速的变化,实现不同的传动比,以满足不同速度下的动力需求。
变位齿轮还广泛应用于工程机械、航空航天等领域。
在这些领域中,变位齿轮能够提供高扭矩、高传动效率的传动方式,满足复杂工况下的要求。
机械设计(6.14.1)--变位齿轮传动的强度计算

变位齿轮传动的受力分析和强度计算原理与标准齿轮的相同,其计算公式也与标准齿轮相同
齿轮啮合节点位置发生变化,Z H 有变化
2/
2cos tan H Z a a =2/2cos tan H t t Z a a =/a a =/t t a a =高高高高高高 高x Σ=x 1+x 2=0:
Z H 高高高高高高高高高高高高高
或/a a >/t t a a >/a a </t t
a a <高x Σ>0高高高高高高高高Z H 高高高εα高高高Z ε高高高
高Z H 高高高εα高高高Z ε高高高或齿面接触强度提高。
当xΣ<0(负传动)时,或齿面接触强度降低。
角变位传动即x Σ=x 1+x 2≠0 :
二、齿根弯曲强度齿根弯曲强度:
变位使齿形变化,齿根厚度和齿根圆角半径变化,引起计算系数Y Fa 和Y sa 的变化,影响齿根弯曲强度。
正变位齿轮的齿厚增大,Y Fa 减小,
齿根圆角半径减小,Y sa 增大。
正变位齿轮的齿根弯曲强度可有提高。
负变位使齿根弯曲强度降低。
变位使端面重合度系数εa 变化,Y ε也发生变化。
变位齿轮参数及计算
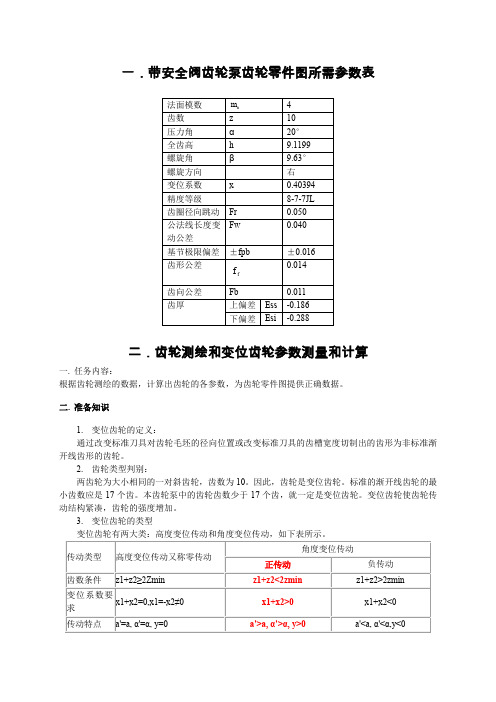
x 0.40394
3.计算其他参数的公式 端面模数 mt mn / cos 啮合角 cos '
a cos a'
总变位系数: xt
z1 z2 (invt' invt ) 2 tan t
12t2tantttzzxinvinv???????分度圆直径d齿顶圆直径mz?2aaddh??齿根圆直径2ffddh??基圆直径cosbtdd??齿顶高ananntthmhxym????齿根高nfnannhmhcx???标准中心距1212add??中心距变动系数ttaaym??齿顶高变动系数tttyxy????固定弦齿厚2cos2tan2cnnnnnsmx?????五计算软件界面
* a
② 然后按全齿高计算模数:
m
③从而从标准模数系列中选择 m 4 ,进行下面的试算,然后校核。
2.验算压力角和计算变位系数 依据公法线长度公式可选择压力角,然后计算变位系数。 ① 通过基圆齿距 Pb Wk1 Wk m cos 公式计算模数 m。 ② 将公法线值和压力角值 20°和 15°分别代入上式验算模数 m, 其中压力角为 20°时算得结果接 近模数 4,故取 n 20 。 ③ 求变位系数
ห้องสมุดไป่ตู้
主要缺点
由于我们的齿轮副的两个齿轮的齿数之和小于 17 齿的两倍,所以这对齿轮是采用角度变位中的 正变位加工而成的。 三. 齿轮参数测量结果: 齿数 z : 10 齿顶圆直径 Da : 49.94 齿根圆直径 D f
31.81
端面公法线长度 Wk 18.876mm 端面公法线长度 Wk 1 30.055mm 斜齿螺旋角 9.63° 啮合中心距离 a 42mm 其他已知参数: 压力角 n 20°or15° 齿顶高系数 径向间隙系数
变位圆柱齿轮跨测齿数的简便计算

变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工周万峰摘要:本文给出一个简便的跨齿数计算的经验公式,并验证了该公式确定的跨齿数是合理的。
关键词:变位齿轮,跨齿数,公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样,五花八门:有教科书上公式,有各种手册上公式,有参考书上的公式,还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式序号用于直齿用于斜齿1234[]+0.5 []+0.5注:早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出,表1中的几个公式大都比较复杂:平方、开放、三角函数等等项目很多,计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此,笔者通过分析研究,并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角时,经验公式为:——齿数,斜齿时代入(,可查手册)。
——变位系数,斜齿时。
——与变位系数正负有关的系数。
当变位系数为正(时p=1.4,当变位系数为负(时p=1.9。
通过大量的算例验证后得知,当变位系数为负时,由经验公式确定的跨齿数与表1中的公式(4)确定的跨齿数是完全一样的(见表2)。
当变位系数为正时,经验公式与表1中的(2)、(3)、(4)确定的跨齿数绝大多数是相同的,只在极少数情况下两者的跨齿数不同。
但在不同的情况下,经验公式的情况比理论公式的情况还好些(见表3)。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表()齿数z 变位系数x跨齿式计算值确定的跨齿数齿数z变位系数x跨齿数计算值确定的跨齿数经验公式理论公式经验公式理论公式经验公式理论公式经验公式理论公式14 0.40 2.61 2.63 3 3 56 -0.4 5.96 5.97 6 6 19 0.60 3.45 3.47 3 3 67 -0.52 6.95 6.96 7 7 24 0.70 4.14 4.18 4 4 80 -0.63 8.19 8.19 8 8 28 0.72 4.61 4.67 5 5 96 -0.7 9.83 9.85 10 10 52 1.0 7.67 7.80 8 8 124 -0.8 12.75 12.79 13 13 100 1.50 13.71 13.96 14 14 150 -1.20 14.89 14.90 15 15注:表2中的“理论公式”为表1中的公式(4)。
变位齿轮参数计算公式

变位齿轮参数计算公式引言变位齿轮是一种常用的齿轮传动装置,可以实现不等速传动。
在实际设计和计算中,需要了解和确定变位齿轮的参数,以便满足传动需求。
本文将介绍一些常用的变位齿轮参数计算公式,帮助读者了解和计算变位齿轮的相关参数。
1. 转速比计算公式对于一个变位齿轮传动系统,转速比是一个重要的参数,表示两轴之间的转速比例关系。
通常以N1、N2分别表示第一齿轮的转速和第二齿轮的转速。
变位齿轮的转速比计算公式如下:转速比 = (N2 - N1) / N12. 锥齿轮的齿数计算公式对于一对变位齿轮中的锥齿轮,其齿数计算公式如下:Z = (Z1 * m1) / m2其中,Z为锥齿轮的齿数,Z1为直齿轮的齿数,m1为直齿轮的模数,m2为锥齿轮的模数。
3. 螺旋角计算公式螺旋角是变位齿轮的一个重要参数,表示齿轮齿线沿轴向的倾斜角度。
对于一对变位齿轮中的螺旋齿轮,其螺旋角的计算公式如下:β = atan(tan(α) - (m2 * (Z2 - Z1)) / (2 * π * a))其中,β为螺旋角,α为压力角,m2为齿数为Z2的螺旋齿轮的模数,Z1为另一齿轮的齿数,a为啮合齿轮的轴向分度圆半径。
4. 齿面距计算公式齿面距是变位齿轮的另一个重要参数,表示两个啮合齿轮齿面上同一点之间的距离。
对于一对变位齿轮中的两个螺旋齿轮,其齿面距的计算公式如下:h = m2 * b / cos(α)其中,h为齿面距,m2为螺旋齿轮的模数,b为螺旋齿轮的齿宽,α为压力角。
5. 压力角计算公式压力角是变位齿轮设计中的一个重要参数,表示齿形曲线的锋角与轴线的夹角。
通常使用以下计算公式得到压力角的值:cos(α) = (Z1 + Z2) / (2 * m2 * a)其中,α为压力角,Z1和Z2分别为两个啮合齿轮的齿数,m2为螺旋齿轮的模数,a为啮合齿轮的轴向分度圆半径。
结论本文介绍了几个重要的变位齿轮参数计算公式,包括转速比、锥齿轮的齿数、螺旋角、齿面距和压力角的计算公式。
(完整版)变位齿轮的计算方法

Wk=Wk*m+0.684xm
式中:Wk*——某齿数齿轮跨测k齿时,模数m=1的公法线长度。
表 2 变位齿轮的yz、xz、Δyz和啮合角α′(α=2ห้องสมุดไป่ตู้°)
α′
(分)
19°
20°
21°
yz
xz
Δyz
yz
xz
Δyz
yz
xz
Δyz
0
1
2
3
4
5
6
7
8
9
-0.00616
606
596
0.00107
118
129
139
150
161
172
183
194
205
0.00001
001
001
001
001
001
001
001
002
002
0.00768
779
790
802
813
825
836
847
859
870
0.00789
801
814
825
837
850
862
874
886
898
0.00022
023
023
024
236
246
257
268
279
290
301
312
0.00216
227
238
249
260
271
282
293
304
315
0.00002
002
002
003
003
(完整版)变位齿轮的计算方法

(完整版)变位齿轮的计算⽅法变位齿轮的计算⽅法1 变位齿轮的功⽤及变位系数变位齿轮具有以下功⽤:(1)避免根切;(2)提⾼齿⾯的接触强度和弯曲强度;(3)提⾼齿⾯的抗胶合和耐磨损能⼒;(4)修复旧齿轮;(5)配凑中⼼距。
对于齿数z=8~20的直齿圆柱齿轮,当顶圆直径d a=mz+2m+2xm时,不产⽣根切的最⼩变位系数x min,以及齿顶厚S a=0.4m和S a=0时的变位系数x sa=0.4m和x sa=0如表1所列。
2 变位齿轮的简易计算将变位齿轮⽆侧隙啮合⽅程式作如下变换:总变位系数中⼼距变动系数齿顶⾼变动系数表 1 齿数z=8~20圆柱齿轮的变位系数或Δy=xΣ-y式中:α——压⼒⾓,α=20°;α′——啮合⾓;z2、z1——⼤、⼩齿轮的齿数。
将上述三式分别除以,则得:由上述公式可以看出,当齿形⾓α⼀定时,x z、y z和Δy z均只为啮合⾓α′的函数。
在设计计算时,只要已知x z、y z、Δy z和α′四个参数中的任⼀参数,即可由变位齿轮的x z、y z、Δy z和啮合⾓α′的数值表(表2)中,查出其他三个参数,再进⾏下列计算。
⼀般齿轮⼿册上均列有此数值表。
式中正号⽤于外啮合,负号⽤于内啮合。
3 计算实例例1:已知⼀对外啮合变位直齿轮,齿数z1=18,z2=32,压⼒⾓α=20°,啮合⾓α′=22°18′,试确定总变位系数xΣ、中⼼距变动系数y及齿顶⾼变动系数Δy。
解:根据α′=22°18′查表2,得:x z=0.01653,y z=0.01565,Δy z=0.00088由此得:例2:已知⼀直齿内啮合变位齿轮副,齿数z1=19,z2=64,α=20°,啮合⾓α′=21°18′。
求xΣ、y及Δy。
解:根据α′=21°18′查表2,得:x z=0.00886,y z=0.00859,Δy z=0.00027。
由此得:其他⼏何尺⼨计算按常规计算进⾏。
变位齿轮几何参数计算

(invα '−invα )
invα '及invα 可根据 a' 、 a 由
表查得
χ ∑ = x1 + x2
χn∑
=
z1 + z2 2 tanα n
(invα 't −invαt )
invα '及invα 可根据 α 't 、α t 查得
χ n ∑ = xn1 + xn2
Δy 或 Δyn
Δy = χ ∑ − y
Δyn = χ n ∑ − yn
按线 图计
算
齿高变动系数 中心距变动系数
Δy 或 Δyn y 或 yn
根据 z∑ 及 χ ∑ 查得 y = χ ∑ − Δy
中心距
α'
α ' = a + ym
注:1.表内公式中的x、xn(xt)本身应带正负号代入;Δy、Δyt永为正号。 2.计算高度变位圆柱齿轮几何尺寸时,公式中的y或yt,Δy或Δyt均为零。
y = z1 + z2 ( cosα −1) 2 cosα '
α ' = a + ym
invat
'=
2(xn1 + xn2 ) z1 + z2
tanα n
+
invα t
yn
=
z1 + z2 2 cos β
( cosαt cosα 't
− 1)
α ' = a + ynmn
Δy 或 Δyn
Δy = χ ∑ − y
名称
代号
已知条件及要求项目
直齿轮
斜齿(人字齿)轮
已 知 z1、z2、m、a' 求 χ ∑ 及 已知 z1、z2、mn (mt )、β、a` 求 χ n ∑
变位齿轮的计算

变位齿轮齿轮的齿数少,切齿时齿根会被挖出凹痕,使齿根部变细,这种现象被称为根切。
作为防止根切的方法,诞生了变位的想法。
变位还可以调节中心距离。
左图 / 产生了根切的齿轮右图 / 未产生根切的齿轮那么,实际上会是个什么样子呢 ? 让我们来试算一下。
m = 3, z1 = 10, z2 = 60, α = 20°为了使 z1 = 10 的齿轮不产生根切,将齿轮做 x1 = +0.5 的正变位。
进行如下所示的计算。
(1) 首先,计算啮合压力角α’。
(2) 接下来,让我们来求中心距离变动系数 y。
(3) 然后求出中心距离 a。
(4) 最后,计算出齿顶圆直径 da。
变位齿轮有正变位和负变位。
虽然齿高相同,但齿厚不同。
齿厚变厚的为正变位齿轮,齿厚变薄的为负变位齿轮。
负变位 / 齿厚变簿1. 分度圆2. 标准齿轮3. 变位量4. 变位齿轮5. 齿高相同正变位 / 齿厚变厚1. 分度圆2. 变位齿轮3. 变位量4. 标准齿轮5. 齿高相同无法改变两个齿轮的中心距离时,对小齿轮施加正变位 ( 避免根切 ),大齿轮施加负变位,以使中心距离相同。
这种情况下,变位量的绝对值相等。
标准齿轮是在各个齿轮的分度圆相切状态下啮合。
而经过变位的齿轮的啮合,如图所示,是在啮合节圆上相切啮合。
啮合节圆上的压力角被称为啮合角。
啮合角与分度圆上的压力角 ( 分度圆压力角 ) 不同。
啮合角是设计变位齿轮时的重要要素。
1. 分度圆2. 啮合节圆特点可以防止在加工时因为齿数少而产生的根切现象。
通过变位可以得到所希望的中心距离。
在齿数比很大的一对齿轮的情况下 :对容易产生磨耗的小齿轮施加正变位,使齿厚变厚。
相反,对大齿轮施加负变位,使齿厚变薄,以使得两个齿轮的寿命均等。
正负变位齿轮参数计算公式

正负变位齿轮参数计算公式
正负变位齿轮通常用于两轴间传递转矩和转速,并且可以实现方
向的变换。
其参数计算公式如下:
1.齿轮齿数:Z1 = Z2
2.分度圆直径:d = m * Z1
3.齿数差:ΔZ = ±(Z2 - Z1)
4.螺旋角:γ = arctan((tan(α)+Δx/p)/cosβ)
其中,m表示模数,α表示齿顶压力角,β表示螺旋角,Δx表
示压力角修正量,p表示传递模数(一般为πm)。
需要注意的是,正负变位齿轮的齿数必须相等,且由于螺旋角的
存在,齿轮的齿顶和齿根曲线都是螺旋线形状,因此制造难度较大。
拓展:正负变位齿轮的用途比较广泛,通常应用于机床传动系统、纺织机械、工程机械等领域。
在一些高精度传动系统中,正负变位齿
轮也经常被用来进行精密调整和微调。
此外,正负变位齿轮还具有耐
磨损、传动效率高等优点,因此越来越受到各行各业的重视和应用。
变位齿轮分度圆计算公式

变位齿轮分度圆计算公式变位齿轮分度圆计算公式是机械设计中非常重要的一部分,它可以帮助我们计算出变位齿轮的分度圆大小,从而保证齿轮的正常运转。
在本文中,我们将详细介绍变位齿轮分度圆计算公式的相关知识。
一、什么是变位齿轮?变位齿轮是一种特殊的齿轮,它的齿形不是标准的圆弧形,而是由两个或多个圆弧形组成的。
变位齿轮的齿形可以根据需要进行设计,以适应不同的传动要求。
变位齿轮通常用于高精度传动系统中,例如机床、航空航天设备等。
二、什么是分度圆?分度圆是齿轮设计中非常重要的一个概念,它是齿轮齿数计算的基础。
分度圆的直径等于齿轮的模数乘以齿数,它是齿轮齿形的基准圆。
在齿轮传动中,两个齿轮的分度圆直径应该相等,才能保证传动的正常运转。
变位齿轮的分度圆大小可以通过以下公式进行计算:d = (z + 2) m / cosα其中,d为分度圆直径,z为齿数,m为模数,α为变位角。
变位角是指变位齿轮齿形的变化角度,它是变位齿轮设计中非常重要的一个参数。
变位角的大小取决于齿轮的齿数、齿形和传动比等因素。
在变位齿轮设计中,变位角的大小应该根据实际情况进行选择,以保证齿轮的正常运转。
四、变位齿轮分度圆计算公式的应用变位齿轮分度圆计算公式是机械设计中非常重要的一部分,它可以帮助我们计算出变位齿轮的分度圆大小,从而保证齿轮的正常运转。
在实际应用中,我们需要根据具体的传动要求和齿轮参数,选择合适的变位角和模数,然后使用分度圆计算公式计算出分度圆直径,最终确定齿轮的设计参数。
变位齿轮分度圆计算公式是机械设计中非常重要的一部分,它可以帮助我们计算出变位齿轮的分度圆大小,从而保证齿轮的正常运转。
在实际应用中,我们需要根据具体的传动要求和齿轮参数,选择合适的变位角和模数,然后使用分度圆计算公式计算出分度圆直径,最终确定齿轮的设计参数。
齿轮变位系数计算公式
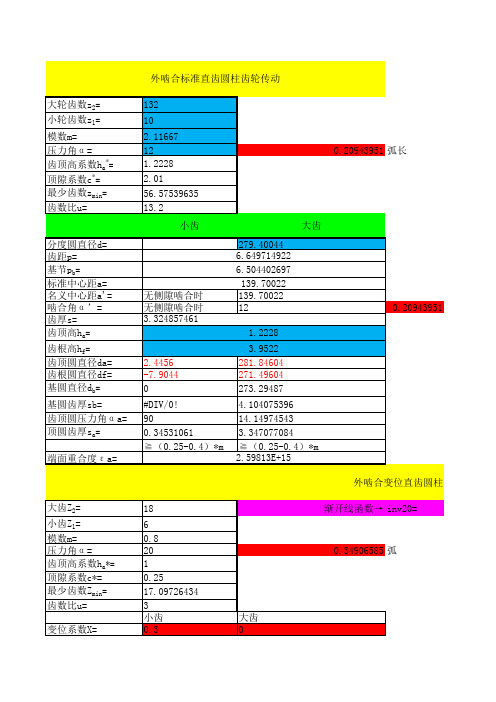
5.440588203
57.29578049 0.94200004 0.808736084
径向变位系数 x2=
0.4096875
分锥角δ2= 36.02737246
0.6288
弧
总
注:是弧度
变位系数X=
18
6 0.8 20 1 0.25 17.09726434 3 小齿 0.3
大齿 0
渐开线函数→ inv20= 0.34906585 弧
分度圆直径d=
4.8
标准中心距a=
9.6
总变位系数x∑=
0.35
啮合角α’=
18.36
名义中心距a'=
9.504884418
中心距的变动系数y= -0.118894478 齿顶高变动系数Δy= 0.468894478
10
0
0
啮合角α’= 名义中心距a'=
插齿刀的参数
切齿啮合角α0'= 切齿标准中心距ao= 切齿名义中心距ao'=
齿根圆直径df=
齿顶圆直径da= 基圆直径db= 齿距p= 基圆齿距pb= 齿厚s= 基圆齿厚sb= 齿顶圆压力角αa= 顶圆齿厚sa= 端面重合度εa=
19.32
齿数zo= 变位系数xo= 顶圆直径dao= 16.53 35 34.45290091 6.405801828 7.5000000 8.495894626 9.396926208
1.503046968 0.856953032 2.36 14.12101251 11.25 2.58546857 2.58546857 19.82692826 14.65599112 17.67949806
齿顶高hae2= 齿根高hfe2= 全齿高he2= 齿顶圆直径dae2= 分度圆直径de2= 齿根角Øf2= 齿顶角Øa2= 顶锥角δa2= 根锥角δf2= Ak2=
齿轮变位系数计算公式
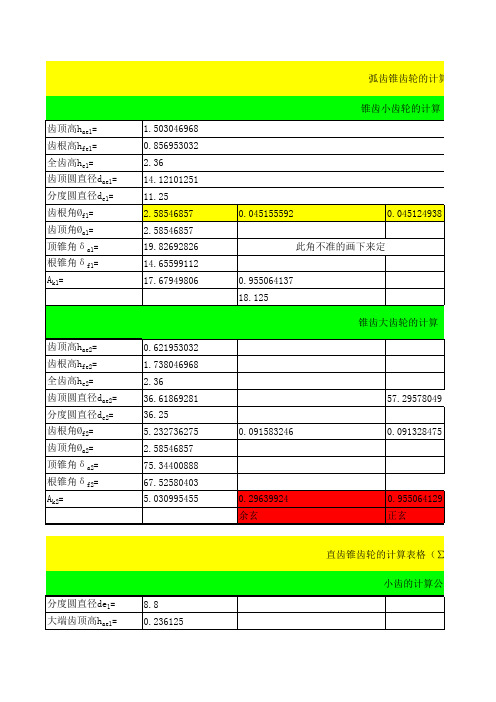
端面基圆齿距pbt=
基圆螺旋角βb=
21.46902352
法向齿厚sn=
2.35619449
端面齿厚st=
2.599772973
端面基圆齿厚sbt= 2.474242055
法向基圆齿厚sbn= 2.3025682
端面齿顶圆压力角α
at=
27.87834641
端面重合度εa=
14.89560191 根据传动要求和齿数和由图2-1a 选得 0.040564012 13.65404495
1.743355127
1.622393438
27.87834641 0.295868875
直齿外齿轮 斜齿外齿轮
公法线长度 跨测齿数 公法线长度 跨测齿厚
公法线长度的计算
Wk= k= Wkn= k=
标准齿轮 9.70116265 5.055555556
直齿外齿轮
公法线长度 跨测齿数
Wk= k=
9.700915
1.570796327 1.616117505 #NUM! 1.299732823
0 0.337197611
0 60 0.582 62.5 28.58 -25 -26.75205269
8.995894626 8 9.396926208 3.141592654 2.952131434 1.570796327 1.336013929 #NUM! 1.217405061
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
1.503046968 0.856953032 2.36 14.12101251 11.25 2.58546857 2.58546857 19.82692826 14.65599112 17.67949806
齿轮变位系数计算公式
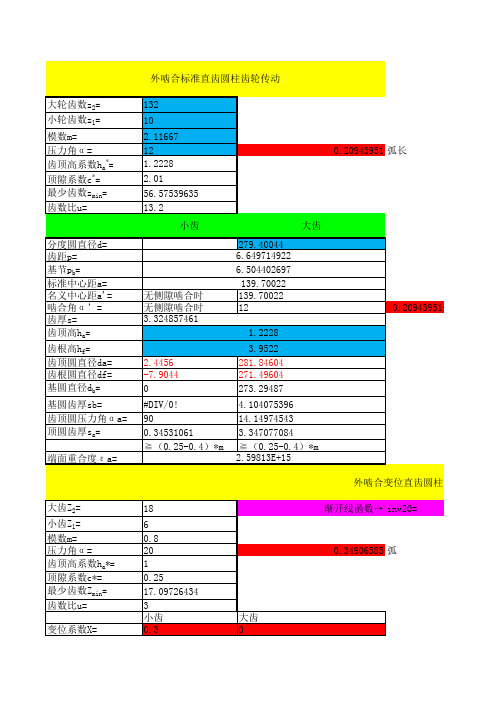
1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮 斜齿外齿轮
跨测齿数 公法线长度 跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度 跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
14.212488
齿根圆直径df=
11.14560191
基圆直径db=
12.5630209
法向齿距pn=
端面齿距pt=
5.199545947
法向基圆齿距pbn=
端面基圆齿距pbt=
基圆螺旋角βb=
21.46902352
法向齿厚sn=
2.35619449
端面齿厚st=
2.599772973
端面基圆齿厚sbt= 2.474242055
0.003117051
0.019 要查出,我没查,用时一定要
0.01
查
弧长
αa1
αa2
1.570796327 0.246959646
位直齿圆柱齿轮传动 0.014904
给定x∑求a' 0.320442451
αa1 0.743891086
αa2 0.479274389
inv20= invαa1= invαa2=
变位系数X=
18
6 0.8 20 1 0.25 17.09726434 3 小齿 0.3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
052 000 599 612 013 290 350 060
56 042
042 000 610 624 014 302 363 061
57 032
032 000 621 636 015 314 376 062
58 021
021 000 632 647 015 325 389 064
59 011
010 000 644 659 015 337 402 065
43 178
177 001 465 473 008 148 196 048
44 168
167 001 476 485 009 160 209 049
45 158
157 001 487 496 009 172 222 050
46 147
146 001 499 508 009 184 235 051
47 137
51 095
095 000 553 565 011 243 299 056
52 084
084 000 565 577 012 254 311 057
53 074
074 000 576 589 013 266 324 058
54 063
063 000 588 600 013 278 337 059
55 053
变位齿轮的简易计算
变位齿轮的应用越来越普遍,但有的仍利用无侧隙啮合方程式进行计算,相当麻烦,且容易出差错。 今推荐用表格法进行计算,简捷、方便、不易出差错。
1 变位齿轮的功用及变位系数
变位齿轮具有以下功用: (1)避免根切; (2)提高齿面的接触强度和弯曲强度; (3)提高齿面的抗胶合和耐磨损能力; (4)修复旧齿轮; (5)配凑中心距。 对于齿数 z=8~20 的直齿圆柱齿轮,当顶圆直径 da=mz+2m+2xm 时,不产生根切的最小变位系数 xmin, 以及齿顶厚 Sa=0.4m 和 Sa=0 时的变位系数 xsa=0.4m 和 xsa=0 如表 1 所列。
1
606
592 014 011 011 000 666 683 017
2
596
582 014 021 021 000 677 694 017
3
586
573 013 032 032 000 689 706 017
4
576
563 013 042 043 000 700 718 018
5
566
554 012 053 053 000 711 730 019
式中正号用于外啮合,负号用于内啮合。 3 计算实例
例 1: 已知一对外啮合变位直齿轮,齿数 z1=18,z2=32,压力角 α=20°,啮合角 α′=22°18′,试 确定总变位系数 xΣ、中心距变动系数 y 及齿顶高变动系数 Δy。 解: 根据 α′=22°18′查表 2,得: xz=0.01653,yz=0.01565,Δyz=0.00088 由此得:
457 009 160 161 001 825 850 025
16 456
448 008 171 172 001 836 862 026
17 445
438 007 182 183 001 847 874 027
18 435
428 007 192 194 002 859 886 027
19 425
418 007 203 205 002 870 898 028
2 变位齿轮的简易计算
将变位齿轮无侧隙啮合方程式作如下变换: 总变位系数
中心距变动系数
齿顶高变动系数
表 1 齿数 z=8~20 圆柱齿轮的变位系数 z xmin xsa=0.4m xsa=0 8 0.53 0.18 0.56 9 0.47 0.22 0.63 10 0.42 0.27 0.70 11 0.36 0.31 0.76 12 0.30 0.35 0.82 13 0.24 0.39 0.88 14 0.18 0.43 0.93 15 0.12 0.46 0.98 16 0.06 0.50 1.03 17 0 0.53 1.08 18 -0.05 0.56 1.13 19 -0.11 0.59 1.18 20 -0.17 0.62 1.23
20 -0.00415 -0.00408 0.00007 0.00214 0.00216 0.00002 0.00882 0.00910 0.00029
21 405
398 007 225 227 002 893 923 030
22 395
389 006 236 238 002 905 935 030
15 529
613 084 275 457 182 063 385 321
16 541
627 086 288 471 183 077 401 324
17 553
640 087 301 486 185 090 418 328
18 565
653 088 313 501 188 104 434 330
19 578
31 303
299 004 334 338 004 0.01009 046 037
32 292
289 004 344 349 005 020 058 038
33 282
279 003 355 360 005 032 070 039
34 272 35 261 36 251 37 241 38 230 39 220
667 089 326 516 190 118 450 332
20 0.01590 0.01680 0.00090 0.02339 0.02530 0.00191 0.03131 0.03467 0.00326
21 602
694 092 352 546 194 145 483 328
22 614
707 093 365 560 195 158 499 331
269 003 366 371 005 043 083 040 259 002 377 383 006 055 095 040 249 002 388 394 006 067 108 041 238 002 399 405 006 087 121 042 228 002 410 417 007 090 133 043 218 002 421 428 007 102 146 044
361
428 067 097 252 155 876 160 285
2
373
441 068 110 267 157 889 176 278
3
385
454 069 122 281 159 902 192 290
4
397
467 070 135 296 161 916 208 292
5
409
480 071 148 310 162 929 224 295
60 -0.00000 -0.00000 0.00000 0.00655 0.00671 0.00016 0.01349 0.01415 0.00066
0 0.01349 0.01415 0.00066 0.02085 0.02238 0.00153 0.02862 0.03145 0.00283
1
11 506
496 010 117 118 001 779 801 023
12 496
486 010 128 129 001 790 814 023
13 486
477 009 139 139 001 802 825 024
14 476
467 009 149 150 001 813 837 024
15 466
40 -0.00210 -0.00208 0.00002 0.00432 0.00439 0.00007 0.01113 0.01158 0.00045
41 199
198 001 443 451 008 125 171 046
42 189
187 001 454 462 008 137 184 047
339 005 290 293 003 962 996 034
28 333
329 004 301 304 003 974 0.01009 035
29 323
319 004 312 315 003 985 021 036
30 0.00313 -0.00309 0.00004 0.00323 0.00326 003 0.00997 0.01033 0.00036
23 626
721 095 378 575 197 172 516 334
24 638
735 097 390 590 200 185 532 337
25 651
748 098 403 605 202 199 549 340
26 663
762 099 416 620 204 213 565 342
27 675
136 001 510 519 009 195 247 052
48 126
126 000 521 531 010 207 260 053
49 116
115 000 532 542 010 219 273 054
50 -0.00105 -0.00105 0.00000 0.00543 0.00554 0.00011 0.01231 0.01286 0.00055
例 2: 已知一直齿内啮合变位齿轮副,齿数 z1=19,z2=64,α=20°,啮合角 α′=21°18′。求 xΣ、
解: 根据 α′=21°18′查表 2,得: xz=0.00886,yz=0.00859,Δyz=0.00027。 由此得:
其他几何尺寸计算按常规计算进行。 此外,变位齿轮的公法线长度的变动量 ΔW=2sinαxm,当 α=20°时,公法线长度变动量 ΔW= 0.684xm,式中 x 为变位系数,应计及正、负号。 因此,变位齿轮的公法线长度为:
