动 态 规 划 算 法
第3章动态规划法

算法设计与分析 2
问题的分解
将待求解问题分解为若干子问题,通过子问题的解得 到原问题的解,这是问题求解的有效途径。但是如何 实施分解? 分治策略的基本思想是将规模为n的问题分解为k个规 模较小的子问题,各子问题相互独立但与原问题求解 策略相同。并不是所有问题都可以这样处理。 问题分解的另一个途径是将求解过程分解为若干阶段 (级),依次求解每个阶段即得到原问题的解。通过 分解得到的各子阶段不要求相互独立,但希望它们具 有相同类型,而且前一阶段的输出可以作为下一阶段 的输入。这种策略特别适合求解具有某种最优性质的 问题。 贪心法属于这类求解策略:对问题P(n),其求解过程 中各贪心选择步骤构成决策序列D=<D1,D2,..Dk>。Di 的最优性仅依赖于D1,D2,..Di-1。贪心法不保证决策 序列D最后求出解的最优性。
算法设计与分析 8
MultiStage_Graph算法复杂度
G用邻接矩阵表示,对于S2到S5的主循环执行 n次。为求满足wjr+cr=min{wji+ci|<j,i>是G的边} 的r,最多要求n-1次比较。因此时间复杂性为 O(n2)。除输入G,输出P外,要求附加存储空 间c、D。 如果G采用邻接表表示,求满足最小性的节点r 仅对属于G的边<j,r>访问一次,此算法的时间 复杂性应该为O(n+e)(e为G的边数)。 一般地,为避免递归过程中的重复计算,每个 子问题首次处理时将结果保存以备查。在上面 的过程中,每一次求得的cj都必须记录下来。
算法设计与分析 5
一个多段图例子
阶段4: C(7,t)=w(7,t)=8 ,C(8,t)=w(8,t)=4 记 D(u,v)是G中起点为 u,终点为v的最短路径,C(u,v) 阶段 3: C(4,t)=min{w(4,7)+C(7,t), w(4,8)+C(8,t)}=12 是该路径上各边权的和。设 D(s,t)= <s,vi1,vi2…vik-1,t>,vir C(5,t)=min{w(5,7)+C(7,t), w(5,8)+C(8,t)}=10 属于Vr (r=1,2..k-1),则D(vi1 ,t)= <vi1,vi2,…vik-1,t>是从 C(6,t)=min{w(6,7)+C(7,t), w(6,8)+C(8,t)}=8 vi1出发到 t的最短路径,D(vi2,t)= <vi2,…vik-1,t>是从vi2出 阶段 2: C(1,t)=min{w(1,4)+C(4,t), w(1,5)+C(5,t)}=19 发到 t的最短路径等等。设 u属于 Vi,有: C(2,t)=min{w(2,4)+C(4,t), w(2,5)+C(5,t), w(2,6)+C(6,t)}=17 C(u,t)=min{w(u,v)+C(v,t)} (4.1) C(3,t)=min{w(3,5)+C(5,t), w(3,6)+C(6,t)}=13 v∈Vi+1 阶段1: C(s,t)=min{w(s,1)+C(1,t), w(s,2)+C(2,t), w(s,3)+C(3,t)}=16 算法设计与分析 沿求解中带下划线的项回溯,得最短路径解: D(s,t)= <s,3,5,8,t>6
物体的动态平衡问题解题技巧

物体的动态平衡问题解题技巧动态平衡问题解题技巧一、总论1、动态平衡问题的产生——当三个平衡力中一个力已知恒定,另外两个力的大小或方向不断变化,但物体仍然平衡时,就会产生动态平衡问题。
典型关键词包括缓慢转动、缓慢移动等。
2、动态平衡问题的解法——解析法和图解法。
解析法:画好受力分析图后,进行正交分解或斜交分解,列出平衡方程,将待求力写成三角函数形式,然后通过角度变化分析判断力的变化规律。
图解法:画好受力分析图后,将三个力按顺序首尾相接形成力的闭合三角形,然后根据不同类型的不同作图方法,作出相应的动态三角形,从动态三角形边长变化规律看出力的变化规律。
3、动态平衡问题的分类——包括动态三角形、相似三角形、圆与三角形(2类)、等腰三角形等。
二、例析1、第一类型:一个力大小方向均确定,一个力方向确定大小不确定,另一个力大小方向均不确定——动态三角形。
例1】如图,一小球放置在木板与竖直墙面之间。
设墙面对球的压力大小为FN1,球对木板的压力大小为FN2.以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置。
不计摩擦,在此过程中,FN1和FN2的变化规律是?解法一:解析法——画受力分析图,正交分解列方程,解出FN1和FN2随夹角变化的函数,然后通过函数讨论。
解析】小球受力如图,由平衡条件,有FN2sinθ-mg=0,FN1cosθ=FN2sinθ,联立可解得FN2=mg/θ,FN1=sinθ/tanθ。
木板在顺时针放平过程中,θ角一直在增大,可知FN1和FN2都一直在减小,因此选B。
解法二:图解法——画受力分析图,构建初始力的三角形,然后“抓住不变,讨论变化”,不变的是小球重力和FN1的方向,然后按FN2方向变化规律转动FN2,即可看出结果。
解析】小球受力如图,由平衡条件可知,将三个力按顺序首尾相接,可形成如右图所示闭合三角形,其中重力mg保持不变,FN1的方向始终水平向右,而FN2的方向逐渐变得竖直。
动态规划法解旅行商问题

#include <iostream>#include <queue>#include <stack>using namespace std;#define L 1 //³ö·¢³ÇÊÐ#define N 6 //Ä¿µÄ³ÇÊиöÊýstruct node{int a;int b;int layer;node(int m,int n,int l){a=m;b=n;layer=l;}};class Trend{private:stack<node> path;int c[N][N];int sign[N],sign2[N];public:Trend(int b[N][N]){for(int i=0;i<N;i++)for(int j=0;j<N;j++){sign[i]=0;c[i][j]=b[i][j];}sign[L-1]=1;}int optpath(int j,int n,int sign[N]) {int min=0;if(n==1){path.push(node(j,L-1,1));return c[j][L-1];}elseif(n<=0)return 1000;for(int k=0,i=0;i<N;i++){int y=0;if(!sign[i]){sign[i]=1;y=1;int sign3[N];copy(sign3,sign);int m=optpath(i,n-1,sign3);if(!k&&c[j][i]){path.push(node(j,i,n));min=c[j][i]+m;k=1;}elseif(k&&c[j][i]&&min>=c[j][i]+m){min=c[j][i]+m;path.push(node(j,i,n));}if(y)sign[i]=0;}}return min;}void prin(){cout<<"×î¶Ì·¾¶³¤¶ÈΪ£º"<<optpath(L-1,N,sign)<<endl<<endl;cout<<"×î¶ÌµÄ·¾¶Îª :"<<endl<<endl;int l=N,begin=L;cout<<L;while(!path.empty()){node k=path.top();if(k.a+1==begin&&yer==l){begin=k.b+1;cout<<"-->"<<k.b+1;l=l-1;}path.pop();}cout<<endl;}void copy(int a[N],int b[N]){for(int i=0;i<N;i++)a[i]=b[i];}};void main(){cout<<"ÂÃÐÐÉÌÎÊÌ⡪¡ª¶¯Ì¬¹æ»®·¨£º"<<endl<<endl;intA[N][N]={{1000,20,30,10,11,28},{15,1000,16,4,2,9},{3,5,1000,2,4,8} ,{19,6,18,1000,3,12},{15,4,7,16,1000,14},{20,35,16,17,30,1000}};cout<<"³ÇÊеĸöÊýΪ£º"<<N<<endl<<endl;cout<<"³ö·¢³ÇÊÐΪ£º"<<L<<endl<<endl;cout<<"³ÇÊÐÖ®¼äµÄ¾àÀëÓÃÁÚ½Ó¾ØÕó±íʾΪ£º"<<endl<<endl;for(int i=0;i<N;i++){for(int j=0;j<N;j++)cout<<A[i][j]<<"\t";cout<<endl<<endl;}Trend path1(A);path1.prin();while(1);}。
“动”中求“静”,“动”“静”互化——中考动态几何问题解题思路初探

解法探究2024年3月下半月㊀㊀㊀动 中求 静 , 动 静 互化中考动态几何问题解题思路初探◉江苏省苏州市高新区实验初级中学㊀袁㊀媛㊀㊀摘要:在初中平面几何的学习中,要运用运动变化的思路研究图形,让静止的几何图形 动 起来,化抽象为具体,让变化的图形形象直观地揭示出恒定不变的几何规律,把相关的知识点串联起来,这样有助于提高分析问题和解决问题的能力.本文中结合中考试题,对常见的动态几何类题型的解题思路与方法进行了初步探索.关键词: 动 静 转化;动 点 类问题;动 线 类问题;动 图 类问题㊀㊀马克思主义哲学告诉我们,运动是绝对的,静止是相对的.在几何的学习过程中,我们发现 静 只是 动 的瞬间,是运动的一种特殊形式, 动 与 静 是可以相互转化的.如果能让静止的几何图形 动 起来,就可以帮助学生加深对图形概念的准确理解,探索图形的性质.教师可以用动态图形创设富有启发性的教学情境,引发学生对问题的讨论与思考;还可以通过动态图形让学生体验数学实验成功的乐趣.更重要的是,动态的几何图形能够把与几何㊁代数相关的知识联系起来,其中蕴含着动静结合㊁数形结合的思想方法,能够在运动变化中发展学生的空间想象能力,不断提高学生综合分析㊁解决问题的能力.在初中几何教学中,与动态图形有关的问题主要有以下几类.1动点 类问题动点问题是中考数学中最常见的题型,涉及面非常广泛.解决动点类问题的思路是化动为静,以相对静止的瞬间去寻求量与量之间的关系.图1例1㊀(2022年江苏省苏州市中考第16题)如图1,在矩形A B C D中,A B B C =23.动点M 从点A 出发,沿边A D 向点D 匀速运动,动点N从点B 出发,沿边B C 向点C 匀速运动,连接MN .动点M ,N 同时出发,点M 运动的速度为v 1,点N 运动的速度为v 2,且v 1<v 2.当点N 到达点C 时,M ,N 两点同时停止运动.在运动过程中,将四边形M A B N 沿MN 翻折,得到四边形M A ᶄB ᶄN .若在某一时刻,点B 的对应点B ᶄ恰好与C D 的中点重合,则v 1v 2的值为.图2解析:如图2所示,在矩形A B C D中,设A B =2a ,B C =3a ,运动时间为t ,则C D =A B =2a ,A D =B C =3a ,B N =v 2t ,AM =v 1t .在运动过程中,将四边形M A B N 沿MN 翻折,得到四边形M A ᶄB ᶄN ,所以B ᶄN =B N =v 2t ,A ᶄM =AM =v 1t .若在某一时刻,点B 的对应点B ᶄ恰好在C D 的中点重合,则D B ᶄ=B ᶄC =a .在R t әB ᶄC N 中,øC =90ʎ,B ᶄC =a ,B ᶄN =v 2t ,C N =3a -v 2t ,则v 2t =53a =B N .因为øA ᶄB ᶄN =øB =90ʎ,所以øA ᶄB ᶄD +øC B ᶄN =90ʎ.又øC N B ᶄ+øC B ᶄN =90ʎ,所以øA ᶄB ᶄD =øC N B ᶄ,故әE D B ᶄʐәB ᶄC N .因此,D E D B ᶄ=B ᶄC C N =B ᶄCB C -B N=a 3a -53a=34,可得D E =34D B ᶄ=34a ,则B ᶄE =D B ᶄ2+D E 2=54a ,于是A ᶄE =A ᶄB ᶄ-B ᶄE =34a ,即D E =34a =A ᶄE .在әA ᶄE M 和әD E B ᶄ中,øA ᶄ=øD =90ʎ,A ᶄE =D E ,øA ᶄE M =øD E B ᶄ,ìîíïïï所以әA ᶄE M ɸәD E B ᶄ(A S A ),则A ᶄM =B ᶄD =a ,即A M =v 1t =a .所以v 1v 2=v 1t v 2t =A M B N =a 53a =35.思路与方法:本题考查矩形背景下的动点问题,通过动态图形,将矩形的性质㊁对称性质㊁中点性质㊁三角形相似㊁全等的判定与性质㊁勾股定理及翻折的272024年3月下半月㊀解法探究㊀㊀㊀㊀运动形式等知识点联系起来.熟练掌握相关性质及三角形全等的判定定理,利用翻折及中点性质,根据三角形全等的性质求出相应线段的长是解题的重要方法.2动线 类问题动线类问题的特点很明显,动线在运动过程中可能会出现多种情况,尽管情况不同,但解题的思路是一致的,那就是 以静制动 ,通过特殊的静止状态去寻找量之间的关系.图3例2㊀(2022年江苏省盐城市中考第14题)如图3,在矩形A B C D 中,A B =2B C =2,将线段A B 绕点A 按逆时针方向旋转,使得点B 落在边C D 上的点B ᶄ处,线段A B 扫过的面积为.解析:由A B =2B C =2,得B C =1,所以A D =B C =1.因为将线段A B 绕点A 按逆时针方向旋转,所以A B ᶄ=A B =2.因为c o s øD A B ᶄ=A D A B ᶄ=12,所以øD A B ᶄ=60ʎ,则øB A B ᶄ=30ʎ.故线段A B 扫过的面积为30ˑπˑ22360=π3.思路与方法:首先由动线A B 旋转的性质可得A B ᶄ=A B =2,再由锐角三角函数可求出øD A B ᶄ=60ʎ,进而求出øB A B ᶄ,最后根据扇形面积公式即可获解.本题考查了旋转的性质㊁矩形的性质㊁扇形的面积公式㊁锐角三角函数等相关知识点.会观察和分析动态图形,灵活运用相关性质是解题的关键.3动图 类问题动图类问题常常结合图形的平移㊁旋转㊁翻折等变换,提出相关问题.解题的思路主要是从寻找图形运动的特殊情况中打开,进而灵活运用相关几何知识(如平行四边形的性质㊁切线的性质㊁圆的有关知识㊁锐角三角函数㊁直角三角形等)解决问题.例3㊀(2022年江苏省苏州市中考全真模拟试题第18题)在әA B C 中,A B =B C =6,øA B C =90ʎ,点D 在A C 上,且A D =22,E 是射线A B 上一动点,连接E D 并将E D 绕着点E 旋转60ʎ得线段E F ,当点F 恰好落在直线A C 上时,可求得A E 的长等于.解析:第一种情况.当E D 顺时针旋转60ʎ得到E F 时,如图4,过点E 作E M ʅA C 于点M.因为图4A B =B C =6,øA B C =90ʎ,所以әA B C 是等腰直角三角形,于是øA =45ʎ.根据旋转的性质,可得øD E F =60ʎ,E F =E D ,所以әD E F 是等边三角形,故øD E M =30ʎ.设DM =x ,则D E =2x ,AM =22+x .因为øA =45ʎ,E M ʅA C ,所以әA E M 是等腰直角三角形,故M E =AM =22+x .在R tәD E M 中,根据勾股定理,可得x 2+(22+x )2=(2x )2,解得x =2+6,或x =2-6(舍).所以M E =AM =22+x =32+6.在әA M E 中,根据勾股定理,可得A E =2A M =6+23.图5第二种情况:当E D 逆时针旋转60ʎ得到E F 时,如图5,作E M ʅA C 交A C 于点M .根据第一种情况,同理可设DM =x ,则有D E =2x ,AM =22-x .在әD E M 中,由勾股定理可得M E =3x ,所以3x =22-x ,解得x =6-2.故M E =A M =32-6.在әAM E 中,根据勾股定理,可得A E =2AM =6-23.综合上述两种情况,A E 的长为6ʃ23.思路与方法:首先要考虑到图形顺㊁逆两种旋转情况,根据旋转的性质可知әD E F 是等边三角形,过点E 作E M ʅA C ,又可证得әA E M 是等腰直角三角形,再设DM =x ,利用勾股定理便可求出x 的值,最后利用勾股定理即可求出A E 的长度.本题考查了图形旋转的性质㊁等边三角形的判定与性质㊁勾股定理等知识点.能够根据题意,按照E D 顺时针旋转与逆时针旋转两种情况,分别画出动态图形进行分类解析是解题的关键.综上所述,解决动态几何问题的基本思路是:把握运动规律,寻求运动中的特殊位置,在 动 中求 静 ,在 静 中探求 动 的普遍规律.在具体解题过程中,要用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,找出其中的等量关系和变量关系,并要特别关注一些不变量和不变关系或特殊关系.在解答动态几何类题型时,经常要用到数形结合思想㊁分类思想㊁转化思想和方程思想等重要的思想方法.Z37。
动态规划法的基本思想

一、动态规划的基本思想在比较基本的算法设计思想里,动态规划是比较难于理解,难于抽象的一种,但是却又十分重要。
动态规划的实质是分治思想和解决冗余,因此它与分治法和贪心法类似,它们都是将问题的实例分解为更小的、相似的子问题,但是动态规划又有自己的特点。
贪心法的当前选择可能要依赖于已经作出的选择,但不依赖于还未做出的选择和子问题,因此它的特征是由顶向下,一步一步地做出贪心选择,但不足的是,如果当前选择可能要依赖子问题的解时,则难以通过局部的贪心策略达到全局最优解。
相比而言,动态规划则可以处理不具有贪心实质的问题。
在用分治法解决问题时,由于子问题的数目往往是问题规模的指数函数,因此对时间的消耗太大。
动态规划的思想在于,如果各个子问题不是独立的,不同的子问题的个数只是多项式量级,如果我们能够保存已经解决的子问题的答案,而在需要的时候再找出已求得的答案,这样就可以避免大量的重复计算。
由此而来的基本思路是,用一个表记录所有已解决的子问题的答案,不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。
比较感性的说,其实动态规划的思想是对贪心算法和分治法的一种折衷,它所解决的问题往往不具有可爱的贪心实质,但是各个子问题又不是完全零散的,这时候我们用一定的空间来换取时间,就可以提高解题的效率。
二、动态规划的基本步骤动态规划算法通常用于求解具有某种最优性质的问题。
在这类问题中,可能会有许多可行解。
每一个解都对应于一个值,我们希望找到具有最优值(最大值或最小值)的那个解。
设计一个动态规划算法,通常可以按以下几个步骤进行:(1)找出最优解的性质,并刻画其结构特征。
(2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
一种基于动态规划的模糊集自动划分方法[发明专利]
![一种基于动态规划的模糊集自动划分方法[发明专利]](https://img.taocdn.com/s3/m/d1e88d46a517866fb84ae45c3b3567ec102ddca8.png)
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 202010638635.X(22)申请日 2020.07.06(71)申请人 河南工业大学地址 450001 河南省郑州市高新技术开发区莲花街100号(72)发明人 母亚双 孙丽君 郭红月 王利东 刘晓东 (74)专利代理机构 昆明明润知识产权代理事务所(普通合伙) 53215代理人 王鹏飞(51)Int.Cl.G06N 5/00(2006.01)G06N 5/04(2006.01)(54)发明名称一种基于动态规划的模糊集自动划分方法(57)摘要本发明涉及一种基于动态规划的模糊集自动划分方法,属于模糊理论系统、知识发现技术领域。
本发明根据动态规划理论,针对传统样本数据模糊化方法需要预先指定模糊集划分个数的问题,设计一个优化目标函数,首先对每个属性的属性值数据从大到小进行排序,然后根据提出的动态规划算法对排好序的数据进行样本区间的自动划分,最后计算每个区间所涵盖属性值数据的均值,并将所有的均值作为参数对该属性上的模糊集进行构建。
本发明对样本数据的模糊化问题进行研究,实现了每个属性上模糊集自动构建的同时又使得所构建的模糊集具备较好的表征效果。
权利要求书2页 说明书8页 附图1页CN 111814979 A 2020.10.23C N 111814979A1.一种基于动态规划的模糊集自动划分方法,其特征在于:首先对每个属性的属性值数据从大到小进行排序,然后根据提出的动态规划算法对排序好的属性值数据进行样本区间的自动划分,最后计算每个区间所涵盖属性值数据的均值,并将所有的均值作为参数对该属性上的模糊集进行构建。
2.根据权利要求1所述的基于动态规划的模糊集自动划分方法,其特征在于具体步骤为:Step1、对数据集的每个属性A k上的属性值v(x i,A k)从大到小进行排序;S t e p2、利用动态规划算法对排序好的属性值数据进行样本区间的自动划分Step3、分别计算划分区间所涵盖属性值数据的平均值Step4、将属性A k上每个划分的平均值作为参数,构建该属性上的模糊集3.根据权利要求2所述的基于动态规划的模糊集自动划分方法,其特征在于:所述步骤Step2的具体步骤为:Step2.1、假设数据集X的属性A k上属性值按从大到小的原则进行排序,排序后的结果为:p1,p2,...,p n;Step2.2、设f(0)=0,B0=Φ,r0=0,f(0)=0表示目标函数的初值为0,B0=Φ表示初始划分,且其不包含任何属性值数据,r0=0表示初始状态,且其从0开始计数;Step2.3、迭代计算f(t),B t,r t,t=1,2,...,n,计算过程根据下面的公式:式中,f(t)表示区间[r t-1,t-1]中目标函数最小的目标函数值,r t表示区间[r t-1,t-1]中使目标函数最小的那个整数,B t表示所产生的一个划分,p i+1,t的定义如下:式中,α是一个参数,0<α≤1;该步骤中的||diff(B t)||的定义如下:表示以[r t-1,t-1]中的整数为下标的属性值数据的进行差分并求和;Step2.4、从B n开始,利用回溯法得到属性A k上所有属性值数据的最优划分Step2.5、输出属性A k上n k个划分:4.根据权利要求2所述的基于动态规划的模糊集自动划分方法,其特征在于:所述步骤Step3的具体步骤为:若用B′s表示n k个划分中的任意一个,即s=1,2,...,n k,将B′s中覆盖的所有属性值数据的平均值记为ms s,则ms s的计算公式如下:式中,p表示B′s中覆盖的所有属性值数据,|B′s|表示B′s中覆盖的属性值数据的个数。
中考数学题中的“动态”题型的解法

.
.
.
B = N 2 (一) F B = 一 2 £=
二
此时 ,=1 s ②当 2 < ≤£ 时, 阴影部分如图 4 1. () S S 方 战 △ f -4 £ ・ 一) = 正 形^ s 肼 ; 一 一 (一) ( f ^ 4
化时 ,位于 l 的右下方 由 l 和正方形所围成的图形的面积为
() 2分三种 情况 讨论 : ①当 O 时 , r 2 阴影部分如 图 4 2。 ()
l 。
5 阴影部分) (
D_
:
/
. ・
/
/ r ,0 ’
0
囤4 ) (1
;
由于 M( ,) o4 ,
~
线 上 的 运动 ,依 次 画 出 变化 的 图形 。如 本 题 点 P在 线 段 D C
和线段 C B上运动时 , 图形 形状 分别是三角形 ( 如图 3 1阴 ()
影部分) 和梯形 ( 如图 3 2 阴影部分) () 。
I \ l
f l
l l
、
r
,
、 L 、
‘
图4 ) (2
M= = -r AF 2
() t 1当 取何值时 , 3 s . = () 2 在平面直角坐标 系中, 画出 s t 与 的函数图像。 分析 : 由于直线 y x t = + 与直线 A 是平行 的, c 所以当 t 取 不同的值时 , 说明直线 f Y 与 轴有 不同的交点 , 但与 直线 A c 的平行关 系( 含重合) 不变 , 从而 断定 R AD N是等腰 三角 t M
・
(一) ( 一) 1 4 t ・4 f:
_
‘
.
城市新区动态过程规划探索——以成都市空港新城镇村体系规划为例

城乡规划与环境建设城市新区动态过程规划探索—以成都市空港新城镇村体系规划为例姚南(成都市规划设计研究院,四川成都610000)【摘要】成都空港新城是在城市“东进”战略下,依托成都第二机场天府国际机场规划布局的城市新 区。
随着天府国际机场建设如火如荼地推进以及空港新城总体规划的基本形成,一批项目开发即将展开。
为避免新区的无序与破碎化开发,应加强对新区形成的动态过程的研究、引导与控制。
文章从城镇化视角切 入,研究空港新城的生长机理,通过动态过程分区施策,以及人口动态转移、镇村动态改造、产业动态转化和公共设施动态融入四大举措,引导镇村逐步有序向城市地区转变。
【关键词】城市新区;动态过程规划;镇村体系【中图分类号】TU982.29城市新区从谋划到全面建成 要经历 ,乃至较为漫长的 ,然而传统规划模式只注重对规划期的终极状态进行规划 ,新区建设动态的与,使新区建设的图不清晰,易受项目 ,统而使开发的效率和效不到 &成都市规划建设空港新城,是城市“南拓”建设 新区 立的 重大发展举措,是城市 “东进”,依托成都第二机场 国际机场规划的城市新区。
国际机场已于2016 动建设,预计2020 全建成,但空港新城的规划建设却相 ,2017 基 成空港新城总体规划的编制。
有序 空港新城所在的12个乡镇为城市新区,是 空港新城镇村体系规划 索的内容,研究 总规蓝图的动态 来找到可的路径。
1动态过程规划的相关研究以英美为代表的西方国家于20世纪60年代前后开始探 索动态规划,我国 自2000 以来也进 理 i ,但业内尚未形成对动态规划、过程规划形成统一的定义。
英国学者 N athaniel Lichfield"1959 ~ 1960)提出的社会规划 理论是英国动态 规划思想的起源。
该理从社会成 收 的,建立起 城市规划政、规划制定、规划 规划项目 果以及该结果可能引起的 社会 相 的有 不.响进 的方法论体系。
中考数学经典总复习专题动线、动形问题完美全文

学 (2)点P 、 Q在运动的过程中,△PCQ面积S有最 大值吗?若有,请求出最大值;若没有,请说明理 由。
动点与函数相结合
抛 与物y轴线交y于= 点 x122C+,m抛x+n物与线x轴的交对于称A轴、交Bx两轴点于,
合 点D,已知A(﹣1,0),C(0,2). 作 (1)求抛物线的表达式;
学 存在,请说明理由;
y
解析:
C
AO
DB
x
动点与函数相结合
抛 与物y轴线交y于= 点 x122C+,m抛x+n物与线x轴的交对于称A轴、交Bx两轴点于,
合 点D,已知A(﹣1,0),C(0,2).
作 互
( 3)点E 是 线 段 BC上的一个动点,过点E 作x轴的垂线与抛物线相交于点F,当点E 运动到什么位置时,四边形CDBF的面积
8
1 2
3
x2+ 2
;
x+2;
∴抛物线的对称轴是x= ∴OD= .3
32.
∵C(0,2 2),
∴OC=2.
5
在Rt△OCD中,由勾股定理,得CD= .2
∵△CDP是以CD为腰的等腰三角形,
∴CP1=CP2=CP3=CD. 作CH⊥x轴于H,
∴HP1=HD=2,
∴∴DP1P(1=4.,32 4),P2(
中考数学---动线、动形问题
• 数学因运动而充满活力,数学因变化而精彩纷呈。动态题是中考 中必考的内容。
• 本节课重点来探究动态几何中的动线、动形问题。
• 一、关于动线、动形问题的解题方法:
• 1.“以静制动”,把动态问题转化成静态问题;
• 2.图形的运动主要有翻折、平移、旋转,在运动过程中,分清哪 些量不变,哪些量发生了变化,以不变的量作为解题基础,以变 化中的规律和特点作为解题的关键。
算法设计与分析报告习题

《算法设计与分析》习题第一章算法引论1、算法的定义?答:算法是指在解决问题时,按照某种机械步骤一定可以得到问题结果的处理过程。
通俗讲,算法:就是解决问题的方法或过程。
2、算法的特征?答:1)算法有零个或多个输入;2)算法有一个或多个输出; 3)确定性;4)有穷性3、算法的描述方法有几种?答:自然语言、图形、伪代码、计算机程序设计语言4、衡量算法的优劣从哪几个方面?答:(1) 算法实现所耗费的时间(时间复杂度);(2) 算法实现所所耗费的存储空间(空间复杂度);(3) 算法应易于理解,易于编码,易于调试等等。
5、时间复杂度、空间复杂度定义?答:指的是算法在运行过程中所需要的资源(时间、空间)多少。
6、时间复杂度计算:{i=1;while(i<=n)i=i*2; }答:语句①执行次数1次,语句②③执行次数f(n), 2^f(n)<=n,则f(n) <=log2n;算法执行时间: T(n)= 2log2n +1时间复杂度:记为O(log2n) ;7.递归算法的特点?答:①每个递归函数都必须有非递归定义的初值;否则,递归函数无法计算;(递归终止条件)②递归中用较小自变量函数值来表达较大自变量函数值;(递归方程式)8、算法设计中常用的算法设计策略?答:①蛮力法;②倒推法;③循环与递归;④分治法;⑤动态规划法;⑥贪心法;⑦回溯法;⑧分治限界法9、设计算法:递归法:汉诺塔问题?兔子序列(上楼梯问题)?整数划分问题?蛮力法:百鸡百钱问题?倒推法:穿越沙漠问题?答:算法如下: (1) 递归法● 汉诺塔问题void hanoi(int n, int a, int b, int c) {if (n > 0) {hanoi(n-1, a, c, b); move(a,b);hanoi(n-1, c, b, a); } }● 兔子序列(fibonaci 数列 )递归实现:Int F(int n) {if(n<=2) return 1; elsereturn F(n-1)+ F(n-2); }● 上楼梯问题 Int F(int n) {if(n=1) return 1 if(n=2) return 2; elsereturn F(n-1)+ F(n-2); }● 整数划分问题问题描述:将正整数n 表示成一系列正整数之和,n=n1+n1+n3+…将最大加数不大于m 的划分个数,记作q(n,m)。
数据结构-贪心算法和动态规划

重复n-1次。
18/65
贪心法的 思考 可以看到,在从Ai到Ai+1的扩展过程中,上
贪心法和动态规划
1/65
主要内 容 动态规划和贪心的认识
工具:马尔科夫过程
贪心法
Prim算法 Kruskal算法 Dijkstra算法
动态规划
最长递增子序列LIS 矩阵连乘的最少乘法 字符串的交替连接 走棋盘/格子取数问题及其应用 带陷阱的走棋盘问题 两次走棋盘问题 Catalan数简介
15/65
贪心 法 根据实际问题,选取一种度量标准。然后按照这种
标准对n个输入排序,并按序一次输入一个量。 如果输入和当前已构成在这种量度意义下的部分最
优解加在一起不能产生一个可行解,则不把此输入 加到这部分解中。否则,将当前输入合并到部分解 中从而得到包含当前输入的新的部分解。 这一处理过程一直持续到n个输入都被考虑完毕, 则记入最优解集合中的输入子集构成这种量度意义 下的问题的最优解。 这种能够得到某种量度意义下的最优解的分级处理 方法称为贪心方法。
是否合法。
如: 2.5.5.25511135,才能判断出是非法的。
当然,它可以通过“25511135”大于“255.255”等其他限界 条件“事先”判断。
10/65
DFS与DP深刻 认识 DFS的过程,是计算完成了str[0…i]的切分,然后
递归调用,继续计算str[i+1,i+2…n-1]的过程; 而DP中,假定得到了str[0…i-1]的所有可能切分方
典型的动态规划举例矩阵连乘问题

二、 LITTLE SHOP OF FLOWERS
PROBLEM
You want to arrange the window of your flower shop in a most pleasant way. You have F bunches of flowers, each being of a different kind, and at least as many vases ordered in a row. The vases are glued onto the shelf and are numbered consecutively 1 through V, where V is the number of vases, from left to right so that the vase 1 is the leftmost, and the vase V is the rightmost vase. The bunches are moveable and are uniquely identified by integers between 1 and F. These id-numbers have a significance: They determine the required order of appearance of the flower bunches in the row of vases so that the bunch i must be in a vase to the left of the vase containing bunch j whenever i < j. Suppose, for example, you have a bunch of azaleas (id-number=1), a bunch of begonias (id-number=2) and a bunch of carnations (id-number=3). Now, all the bunches must be put into the vases keeping their id-numbers in order. The bunch of azaleas must be in a vase to the left of begonias, and the bunch of begonias must be in a vase to the left of carnations. If there are more vases than bunches of flowers then the excess will be left empty. A vase can hold only one bunch of flowers. Each vase has a distinct characteristic (just like flowers do). Hence, putting a bunch of flowers in a vase results in a certain aesthetic value, expressed by an integer. The aesthetic values are presented in a table as shown below. Leaving a vase empty has an aesthetic value of 0.
立体几何中的动态问题

立体几何中的动态问题[解题策略]立体几何中的“动态”问题就变化起因而言大致可分为两类:一是平移;二是旋转.就所求变量而言可分为三类:一是相关线、面、体的测度;二是角度;三是距离.立体几何动态问题的解决需要较高的空间想象能力与化归处理能力,在各省市的高考选择题与填空题中也时有出现.在解“动态”立体几何题时,如果我们能努力探寻运动过程中“静”的一面,动中求静,往往能以静制动、克难致胜.1.去掉枝蔓见本质——大道至简在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.例1 如图1,直线l⊥平面α,垂足为O.正方体ABCD-A1B1C1D1的棱长为2.点A 是直线l上的动点,点B1在平面α内,则点O到线段CD1中点P的距离的最大值为________.图1答案2+2解析从图形分化出4个点O,A,B1,P,其中△AOB1为直角三角形,固定AOB1,点P的轨迹是在与AB1垂直的平面上且以AB1的中点Q为圆心的圆,从而OP≤OQ+QP=12AB1+2=2+2,当且仅当OQ⊥AB1,且点O,Q,P共线时取到等号,此时直线AB1与平面α成45°角.2.极端位置巧分析——穷妙极巧在解决立体几何中的“动态”问题时,对于移动问题,由图形变化的连续性,穷尽极端特殊之要害,往往能直取答案.例2 在正四面体A -BCD 中,E 为棱BC 的中点,F 为直线BD 上的动点,则平面AEF 与平面ACD 所成二面角的正弦值的取值范围是________. 答案 ⎝ ⎛⎦⎥⎤23,1解析 本例可用极端位置法来加以分析.先寻找垂直:记O 为△ACD 的中心,G 为OC 的中点,则BO ⊥面ACD ,EG ⊥面ACD .如图2,过点A ,E ,G 的平面交直线BD 于点F .此时,平面AEF 与平面ACD 所面二面角的正弦值为1.由图形变化的连续性知,当点F 在直线BD 的无穷远处时,看成EF 和BD 平行,此时平面AEF 与平面ACD 所成二面角最小(如图3),其正弦值为23.图2 图3综上可知,平面AEF 与平面ACD 所成二面角的正弦值的取值范围为⎝ ⎛⎦⎥⎤23,1.3.用法向量定平面——定海神针在解决立体几何中的“动态”问题时,有关角度计算问题,用法向量定平面,可将线面角或面面角转化为线线角.例3 在长方体ABCD -A 1B 1C 1D 1中,已知二面角A 1-BD -A 的大小为π6,若空间有一条直线l 与直线CC 1所成的角为π4,则直线l 与平面A 1BD 所成角的取值范围是________. 答案 ⎣⎢⎡⎦⎥⎤π12,5π12解析 如图4,过点A 作AE ⊥BD 于点E ,连接A 1E ,则∠A 1EA =π6.过点A 作AH ⊥A 1E 于点H ,则AH →为平面A 1BD 的法向量,且∠A 1AH =π6.因为l 与直线CC 1所成角的大小为π4,即l 与直线AA 1所成角的大小为π4,那么l 与直线AH 所成角的取值范围为⎣⎢⎡⎦⎥⎤π4-π6,π4+π6.又因为l 与直线AH 所成的角和l 与平面A 1BD 所成的角互余,所以直线l 与平面A 1BD 所成角的取值范围是⎣⎢⎡⎦⎥⎤π12,5π12.图44.锁定垂面破翻折——独挡一面在解决立体几何中的“动态”问题时,对于翻折或投影问题,若能抓住相关线或面的垂面,化空间为平面,则容易找到问题的核心.例4 如图5,在等腰Rt △ABC 中,AB ⊥AC ,BC =2,M 为BC 的中点,N 为AC 的中点,D 为线段BM 上一个动点(异于两端点),△ABD 沿AD 翻折至B 1D ⊥DC ,点A 在平面B 1CD 上的投影为点O ,当点D 在线段BM 上运动时,以下说法错误的是( )图5A .线段NO 为定长B .CO ∈(1,2)C .∠AMO +∠B 1DA >180°D .点O 的轨迹是圆弧 答案 C解析 如图6,记B 2为B 1在平面ADC 上的射影,由B 1D ⊥DC 可得B 2D ⊥DC .记B 2D 交AB 于点K ,则DC ⊥平面B 1B 2K .在△B 1DC 中,作EM ∥B 1D 交B 1C 于点E ,连接AE ,则平面AEM ∥平面B 1B 2K ,平面AEM ⊥平面B 1DC ,从而点A 在平面B 1DC 上的射影O 在直线EM 上.取AM 的中点H ,则NH =12MC =12,OH =12AM =12,ON =22均为定长.易知点O 的轨迹是以点H 为圆心、12为半径的圆弧,因为CO 2=MO 2+MC 2,且MO ∈(0,1),所以CO ∈(1,2).又∠AMO +∠AME =180°,∠AME =∠B 1DK ,由最小角定理知∠B 1DB 2<180°-∠B 1DA , 得∠B 1DK >∠B 1DA ,于是∠AMO +∠B 1DA <180°.故选C.图65.觅得定值明轨迹——动中有静在解决立体几何中的“动态”问题时,探寻变化过程中的不变关系,是解决动态问题的常用手段.例5 如图7,已知线段AB 垂直于定圆所在的平面,B ,C 是⊙O 上的两个点,H 是点B 在AC 上的射影,当点C 运动时,点H 运动的轨迹是( )图7A .圆B .椭圆C .抛物线D .不是平面图形 答案 A解析 如图8,设⊙O 的半径为r ,取BC 的中点M ,则图8OM⊥BC,MH=MC.因为AB⊥平面BCD,所以BC是AC在平面BCD上的射影,从而OM⊥平面ABC,得OM⊥MH,于是OH2=MO2+MH2=MO2+MC2=r2,即OH=r,亦即动点H在以O为球心、r为半径的球面上.又因为BH⊥AD,B为定点,所以动点H又在过点B且垂直于直线AD的定平面上,故点H运动的轨迹是圆.6.构建函数求最值——以数解形在解决立体几何中的“动态”问题时,对于一些很难把握运动模型(规律)的求值问题,可以通过构建某个变量的函数,以数解形.例6 (2016·浙江)如图9,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC 外一点P和线段AC上一点D,满足PD=DA,PB=BA,则四面体P-BCD的体积的最大值是________.图9答案1 2解析设M,N分别为AC,AP的中点,因为BA=BP=BC,PD=DA,所以点B在平面PAC上的射影为△PAC的外心O,且点O在直线ND上.又因为AB=BC=2,∠ABC=120°,所以AC=23,图10BO =AB 2-OA 2≤AB 2-AM 2=1, 当且仅当点O 与点M 重合时取到等号.设AD =x ,∠PDC =θ,因为AC =23,所以DC =23-x , 则S △PDC =12x ·(23-x )sin θ≤12x ·(23-x )≤12⎝⎛⎭⎪⎫2322=32, 当且仅当点M 与点D 重合时取到等号. 因此,四面体P -BCD 的体积为V P -BCD =13S △PCD ·OB ≤13×32×1=12,此时点O ,M ,D 重合,即点D 为AC 的中点,且平面PBD 与平面ABC 垂直相交于BD .总之,解立体几何动态问题的过程实质是数学建模的过程,是创新的过程.方程、函数和图形变换是基础,因此夯实基础是解决此类问题的关键.化整为零的思想、转化思想、数形结合思想、函数思想、分类讨论思想等是解决立体几何动态问题的最佳策略.真正破解动态立体几何问题,需要整体把握动态变化过程,更需要深厚的空间想象之内功.如果说招式是术,那么内功就是修行,即不断积累知识与技巧、经验与经历.。
五种社会形态划分法和三种社会形态划分法的含义及其相互关系

提要:对五种社会形态划分法和三种社会形态划分法的含义及其相互关系的看法,在我国理论界尚存在一些分歧。
拟从两种划分社会形态方法各自的内涵、两种划分社会形态方法的区别、两种划分社会形态方法本质上的一致性、不能用一种划分方法取代另一种划分方法等方面,谈个人的看法,与理论界同仁商榷。
关键词:社会形态五种社会形态划分法三种社会形态划分法经济的社会形态五种社会形态划分法和三种社会形态划分法的含义及其相互关系□赵家祥社会形态划分理论是历史唯物主义的重要内容,在各种历史唯物主义教科书中都对此有所论述。
但在我国理论界,人们对马克思主义的社会形态理论,依然存在着一些不同的看法,本文仅就五种社会形态划分法和三种社会形态划分法的含义及其相互关系谈些自己的看法,与理论界的同仁共同商讨研究。
一、两种划分社会形态方法各自的内涵五种社会形态划分法,是根据生产关系的不同性质,把人类历史发展过程划分为原始社会、奴隶社会、封建社会、资本主义社会、共产主义社会(社会主义社会是它的第一阶段)五种依次更替的社会形态的方法。
社会形态概念,在马克思、恩格斯、列宁的著作中,多数情况下是指“生产关系总和”或“生产关系体系”、“社会经济结构”;但有时也包括生产力,指生产力和生产关系的统一,即社会生产方式;有时还包括上层建筑,指一定的经济基础及与此相适应的上层建筑的统一;而在讲社会形态的发展时,又把生产力、生产关系、上层建筑看作一个有内在联系的统一整体,实际上是把社会形态看作全部要素的总和。
这样,在马克思、恩格斯、列宁的著作中,社会形态概念共有四种含义。
应该如何对待这种情况呢?有两种相反的态度:一种是实用主义的态度,即对经典作家的论述断章取义,各取所需,为我所用,认为只有自己采用的某一种看法符合经典作家的本意,排斥经典作家的其他看法。
另一种是科学的态度,认为在科学史上,任何概念都是发展变化的,都有一个由内涵不够确切到更加确切、外延不够确定到更加确定的过程,即有一个由多义到一义的过程。
高中物理动态平衡问题图解法新人教版必修1

动态平衡“动态平衡”是指物体所受的力一部分是变力,是动态力,力的大小和方向均要发生变化,但变化过程中的每一时刻均可视为平衡状态,所以叫动态平衡,这是力平衡问题中的一类难题.解决这类问题的一般思路是:化“动”为“静”,“静”中求“动”,常采用图解法求解。
1.三角形图解法Ⅰ.恒力F+某一方向不变的力例 如图所示,在固定的、倾角为α斜面上,有一块可以转动的夹板(β不定),夹板和斜面夹着一个质量为m 的光滑均质球体,试求:β取何值时,夹板对球的弹力最小?【解析】对球体进行受力分析,然后对平行四边形中的矢量G 和N 1进行平移,使它们构成一个三角形,如图所示.由G 的大小和方向均不变,而N 1的方向不可变,当β增大导致N 2的方向改变时,N 2的变化和N 1的方向变化如图中的右图所示.显然,随着β增大,N 1单调减小,而N 2的大小先减小后增大,当N 2垂直N 1时,N 2取极小值,且N 2min = Gsin α.【答案】当β=90°时,甲板对球的弹力最小.Ⅱ.恒力F+某一不变的相似关系(通常叫做相似三角形法)例 如图所示,竖直杆OB 顶端有光滑轻质滑轮,轻质杆OA 自重不计,可绕O 点自由转动,OA =OB 。
当绳缓慢放下,使∠AOB 由00逐渐增大到1800的过程中(不包括00和1800)下列说法正确的是( )A .绳上的拉力先逐渐增大后逐渐减小B .杆上的压力先逐渐减小后逐渐增大C .绳上的拉力越来越大,但不超过2GD .杆上的压力大小始终等于G2.辅助圆图解法Ⅰ.恒力F+某一大小不变的力例 如图所示,在做“验证力的平行四边形定则”的实验时,用M 、N 两个测力计通过细线拉橡皮条的结点,使其到达O 点,此时α+β=90°.然后保持M 的读数不变,而使α角减小,为保持结点位置不变,可采用的办法是( A )A 减小N 的读数同时减小β角B 减小N 的读数同时增大β角C 增大N 的读数同时增大β角D 增大N 的读数同时减小β角Ⅱ.恒力F+某一大小不变的角例 如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC 呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA 绳中的拉力F 1和CB 绳中的拉力F 2的大小发生变化,即( BCD )A .F 1先变小后变大B .F 1先变大后变小C .F 2逐渐减小D .F 2最后减小到零 解析:。
动态规划基本方法
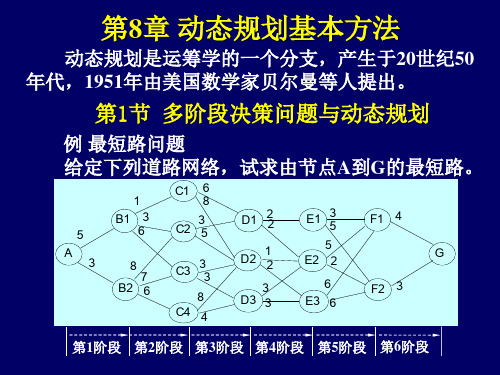
(3)确定决策变量uk及允许决策集Dk(sk); (4)给出状态转移方程 sk+1=Tk(sk,uk); (5)给出满足要求的过程指标函数Vk,n及相应的最 优值函数;
(6)写出递推方程和边界条件,建立基本方程; (7)按照基本方程递推求解。
0≤x1≤s1
=23.7s1
(x1*=0)
f1(1000)=23.7╳1000=23700
s1=1000 s2=900
s3=810
x1*=0
x2*=0
x3*=810
s1-x1*=1000 s2-x2*=900 s3-x3*=0
s4=567 x4*=567 s4-x4*=0
s5=397 x5*=397 s5-x5*=0
2.2 动态规划的基本方程 动态规划的最优性原理(贝尔曼原理):作为整 个过程的最优策略具有这样的性质,即无论过去的状 态和决策如何,对前面的决策所形成的状态而言,余 下的诸决策必须构成最优策略。简言之,最优策略的 子策略也必是最优的。 根据此原理,要求全过程最优策略,可从子过程 策略的最优化入手。对于过程指标函数是阶段指标函 数和的形式,考虑k-子过程最优值函数fk(sk):
第4节 动态规划和静态规划的关系
静态规划所研究的问题是与时间无关的,而动态
规划所研究的问题是和时间有关的。对于某些静态规 划问题,也可人为地引入时间因素,把它看做一个按 阶段进行的动态规划问题,用动态规划的方法求解。
例 用动态规划法求解
max F=4x12-x22+2x32+12 3x1+2x2+x3≤9 xi≥0 i=1,2,3
0≤x4≤s4
0≤x4≤s4
2020年中考数学必考考点 专题34 动态问题(含解析)

专题34 动态问题专题知识回顾一、动态问题概述1.就运动类型而言,有函数中的动点问题、图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。
2.就运动对象而言,几何图形中的动点问题,有点动、线动、面动三大类。
3.就图形变化而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等。
4.动态问题一般分两类,一类是代数综合方面,在坐标系中有动点,动直线,一般是利用多种函数交叉求解。
另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
所以说,动态问题是中考数学当中的重中之重,只完全掌握才能拿高分。
另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考察。
所以说,动态问题是中考数学当中的重中之重,只完全掌握才能拿高分。
二、动点与函数图象问题常见的四种类型:1.三角形中的动点问题:动点沿三角形的边运动,根据问题中的常量与变量之间的关系,判断函数图2.四边形中的动点问题:动点沿四边形的边运动,根据问题中的常量与变量之间的关系,判断函数图象。
3.圆中的动点问题:动点沿圆周运动,根据问题中的常量与变量之间的关系,判断函数图象。
4.直线、双曲线、抛物线中的动点问题:动点沿直线、双曲线、抛物线运动,根据问题中的常量与变量之间的关系,判断函数图象。
三、图形运动与函数图象问题常见的三种类型:1.线段与多边形的运动图形问题:把一条线段沿一定方向运动经过三角形或四边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
2.多边形与多边形的运动图形问题:把一个三角形或四边形沿一定方向运动经过另一个多边形,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
3.多边形与圆的运动图形问题:把一个圆沿一定方向运动经过一个三角形或四边形,或把一个三角形或四边形沿一定方向运动经过一个圆,根据问题中的常量与变量之间的关系,进行分段,判断函数图象。
动态平衡问题的几种解法

动态平衡问题的几种解法在有关物体平衡的问题中,有一类涉及动态平衡。
这类问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,故这是力平衡问题中的一类难题。
解决这类问题的一般思路是:把“动”化为“静”,“静”中求“动”。
下面就介绍几种动态平衡问题的解题方法。
方法一:图解法(三角形法则)原理:当物体受三力作用而处于平衡状态时,其合力为零,三个力的矢量依次恰好首尾相连,构成闭合三角形,当物体所受三个力中二个发生变化而又维持平衡关系时,这个闭合三角形总是存在,只不过形状发生改变而已,比较这些不同形状的矢量三角形,各力的大小及变化就一目了然了。
例题1:如图1所示,一个重力G的匀质球放在光滑斜面上,斜面倾角为,在斜面上有一光滑的不计厚度的木板挡住球,使之处于静止状态。
今使板与斜面的夹角缓慢增大,问:在此过程中,挡板和斜面对球的压力大小如何变化?解析:取球为研究对象,球受重力G、斜面支持力F1、挡板支持力F2。
因为球始终处于平衡状态,故三个力的合力始终为零,三个力构成封闭的三角形。
挡板逆时针转动时,F2的方向也逆时针转动,F1的方向不变,作出如图2所示的动态矢量三角形。
由图可知,F2先减小后增大,F1随增大而始终减小。
点评:三角形法则适用于物体所受的三个力中,有一力的大小、方向均不变(通常为重力,也可以是其它力),另一个力的大小变化,第三个力则大小、方向均发生变化的问题,对变化过程进行定性的分析。
方法二:解析法原理:物体处于动态平衡状态时,对研究对象的任一状态进行受力分析,根据具体情况引入参量,建立平衡方程,求出应变参量与自变参量的一般函数关系,然后根据自变量的变化确定应变量的变化。
例题2:如图3所示,小船用绳索拉向岸边,设船在水中运动时所受水的阻力不变,那么小船在匀速靠岸过程中,下面说法哪些是正确的()A. 绳子的拉力F不断增大B. 绳子的拉力F不变C. 船所受的浮力不断减小D. 船所受的浮力不断增大解析:小船共受四个力作用:重力G、浮力F浮、水的阻力f、绳子拉力F。
用图解法解动态平衡问题——方法指导

F1 F2
mg
物体在三个力的作 用下处于平衡状态,这 三个力首尾相连组成一 个闭合的矢量三角形.
可计算出未知力的大小与方向.
F1
F2 O A
mg B F1´
几何三角形AOB与力三 角形F1´、F2、mg构成相 似三角形.
规律总结 解决动态平衡问题的常用方法
1.图解法
2.解析法
利用三力平衡图示构成闭合 三角形的规律,可以对动态平衡 问题画出不同时刻的三力矢量三 角形,进而判断三力中哪些力不 变,哪些力在变,得出三个力的 大小与方向的变化规律.
(1)根据已知量的变化情况,画出平行四边形边、角 图解法 的变化
(2)确定未知量大小、方向的变化
3.怎样用“相似三角形法”解平衡问题?
物体受到三个共点力的作用而处于平衡状态,画出的
其中任意两个力的合力与第三个力等值、反向的平行四边
形中,可能有力三角形与题设图中的几何三角形相似,进
而得到力三角形与几何三角形对应边成比例,根据比值便
1.什么样的平衡是动态平衡 ?
物体所受的一部分力的大小和方向是动态变化的,但变化过程 中的每一个定态均可视为平衡状态. 有些题目中常出现“缓慢”一词,则物体处于动态平衡状态.
2.解决动态平衡问题的一般思路方法? 化“动” 为“静”,“静”中求“动”.
方法
步骤
解析法(1)列平衡方程求出源自知量与已知量的关系表达式 (2)根据已知量的变化情况来确定未知量的变化情况
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
每天一道算法题(四) (动态规划算法)01背包问题Java 实现动态规划动态规划在wiki上的定义:dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions - ideally, using a memory-based data structure. The next time the same subproblem occurs, instead of recomputing its solution, one simply looks up the previously computed solution。
昨天接触到了动态规划的概念,研究了昨天一晚上以及今天一上午,总算对这个问题有些收获。
动态规划背后的基本思想非常简单。
大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。
从空集合开始,每增加一个元素就求它的最优解,直到所有元素加进来,就得到了总的最优解。
01背包问题01背包问题即的01即每件物品最多放1件,否则不放入。
让我真正了解动态规划概念的是mu399的博客问题:有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?重新定义问题:有承重分别为1-10的背包10个编号分别为a,b,c,d,e的物品各一个3. 从e物品开始依次放入1-10个背包,分别得到最大的价值总和4. 把d物品放入依次放入存在e物品的1-10个背包,如果价值更高,替换掉e()5. c,b,a同理。
1. 01背包的状态转换方程 f[i,j] = Max{f[i-1,j-Wi]+Pi( j = Wi ), f[i-1,j] }f[i,j]:在前i件物品中选择若干件放在承重为 j 的背包中,可以取得的最大价值。
Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第 i件物品应该放入背包中吗?2. 以a8(行为a,列为的8的单元格)举例f[i,j] = a8 = 15f[i-1,j] = b8 = 9f[i-1,j-Wi] 表示我有一个承重为6的背包(等于当前背包承重减去物品a的重量),当只有物品b,c,d,e四件可选时,这个背包能装入的最大价值f[i-1,j-Wi] +Pi =b(8 - 2) + 6 = b6 + 6 = 15 背包的java代码实现public class getPgAnswer{public void testPackage() {Package[] pg = {new Package("e",4,6),new Package("d",5,4),new Package("c",6,5),new Package("b",2,3),new Package("a",2,6)-- 第一个参数表示从pg[0]开始依次放入的物品, -- 第二个参数代表背包的承重,放弃第0列数组int[][] state = new int[pg.length][11];int newValue = 0;* 01背包的状态转换方程* f[i,j] = Max{* f[i-1,j-Wi]+Pi( j = Wi ),* f[i-1,j] }for (int i = 0; i pg.length; i++) {-- 背包的承重量for (int j = 1; j state[i].length; j++) {if (i == 0) {if (pg[i].getWeight() = j) {state[i][j] = pg[i].getValue();state[i][j] = state[i - 1][j];if (j pg[i].getWeight()) {continue;newValue = state[i - 1][j - pg[i].getWeight()]+ pg[i].getValue();-* if (newValue = state[i - 1][j]) {state[i][j] = newValue;state[i][j] = state[i - 1][j];state[i][j] = Math.max(newValue, state[i - 1][j]);for (int i = 0; i state.length; i++) {System.out.println(Arrays.toString(state[state.length - 1 - i]));class Package {private String name;private int weight;private int value;public Package(String name,int weight,int value){ = name;this.weight = weight;this.value = value;public String getName() {return name;public int getWeight() {return weight;public int getValue() {return value;背包的Python实现问题:有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?思路:dynamic programming即把整个问题分解成一系列子问题,所有子问题只计算一次并存起来,下一次相同问题出现,直接从数据结构中取出结果,而不是再次计算 K(i, j) = max(K(i - 1, j), K(i - 1, j - Wi) + Pi)其中 j = Wif[i,j]:在前i件物品中选择若干件放在承重为 j 的背包中,可以取得的最大价值。
Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第 i件物品应该放入背包中吗def package(n, c, weight, values):构建背包问题二维表:param n: 物品数量:param c: 背包重量容积:param weight: 物品重量列表:param values: 物品价值列表:return:# 初始化二维列表res = [[-1 for j in range(c + 1)] for i in range(n + 1)]res[0] = [0 for i in range(1, c + 1)]# 完善背包for i in range(1, n + 1):for j in range(1, c + 1):res[1][j] = values[1] if j = weights[1] else 0res[i][j] = res[i - 1][j]if weights[i] j and res[i - 1][j - weights[i]] + values[i] res[i][j]:res[i][j] = res[i - 1][j - weights[i]] + values[i]# @Note:如果没有上面的res[0] = [0 for i in range(1, c + 1)] 需要增加下面的判定# elif weights[i] == j and values[i] res[i][j]:# res[i][j] = values[i]return resif __name__ == '__main__':# 物品数量# 背包重量容积# 物品重量列表 weights[0] 无效和blog有区别博客是倒着放入商品weights = [-1, 2, 2, 6, 5, 4]# 物品价值列表 values[0] 无效values = [-1, 6, 3, 5, 4, 6]res = package(n, c, weights, values)如果枚举的和总量大于等于选择物品,则需要判断是否选择当前物品*-d[i][j] = min{ d[i+1][j], d[i][j-1] } + 1; (每次状态转移,区间长度增加1)描述阶段的变量称为阶段变量k。
阶段的划分,一般是根据时间和空间的自然特征来进行的,但要便于问题转化为多阶段决策。
最后一个元素相同:求X[1…m-1]和Y[1…n-1]两个子序列的最长公共子序列。
void Trace(int i, int capacity)从表中可以看出一些规律,除了第一行以外,每个格子都是前一行的一个或两个格子推导而来。
比如3金矿8工人的结果,就来自2金矿5工人和2金矿8工人,MAX(500,500+200)=700.if (arr.length == 0) {min_sum[i][j] = min_sum[i - 1][j - 1] + triangle[i][j];本介绍用python解决TSP问题的第二个方法——动态规划法if (ratings[i] ratings[i - 1]) {。
