投资学第10章APT与风险收益多因素模型stu
投资学第十章PPT课件
• rf= 3% 和RP= 7 . 5%
精选课件
7
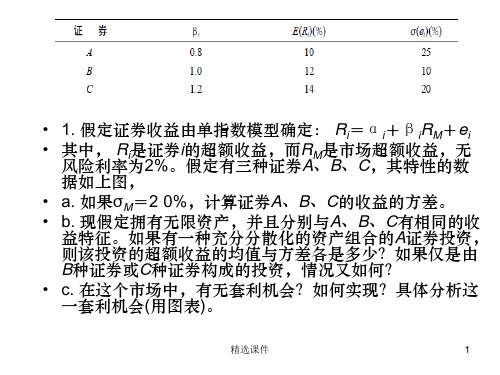
• 4. 假定F1与F2为两个独立的经济因素。无 风险利率为6%,并且,所有的股票都有独 立的企业特有(风险)因素,其标准差为4 5%。 下面是优化的资产组合,在这个经济体系 中,试进行期望收益-贝塔的相关性分析。
• c. The CAPM assumes that one specific factor explains security returns but APT does not.
• State whether each of the consultant’s arguments is correct or incorrect. Indicate, for each incorrect argument, why the argument is incorrect.
• a. 确定期望收益(以美元计)。其收益的标准差 为多少?
• b. 如果分析家验证了50种股票而不是20种,那 么答案又如何?100种呢?
精选课件
15
• a等量地卖空10种负α的股票并将收入等量投资 于10种正的股票,将消除市场的风险暴露并构 建一个零投资的资产组合。预期的美元收益为: 1 000 000 ×0.02+(-1 000 000)(-0.02)= 40 000美元。该资产组合的β为零,因为是等权重 的,其中一半的权数为负,所有的β都等于1。 因此,整体风险中系统性的成分为0。但是, 分析家的利润的方差却不为零,因为这一资产 组合没有充分分散化。总体方差就等于非系统 风险σ2= σ2 (ep) = σ2(ei)/n= 302/20 = 45且σ = 6.7 1%
投资学第10章APT与风险收益多因素模型

则组合风险:
2 P
2 P
2 F
2 (eP )
又:
2(eP )
n 1
i1 n
2
2 (ei)
1 n
2 (ei)
其中,
2 (ei)
2(ei) ,又 n
E (ei)
0
于是有: rP E ( rP ) P F , 且: P P F
28
10.2.3 贝塔与期望收益
▪ 套利准则一:如果两个充分分散化的投资 组合具有相同的β值,则它们在市场中必 有相同的预期收益。
1. 交易者按10%的利率借入一笔6个月资金(假 设1000万元)
2. 签订一份协议(远期利率协议),该协议规定 该交易者可以按11%的价格6个月后从市场借 入资金1051万元(等于1000e0.10×0.5)。
21
3. 按12%的利率贷出一笔1年期的款项金 额为1000万元。
4. 1年后收回1年期贷款,得本息1127万元 (等于1000e0.12×1),并用1110万元 (等于1051e0.11×0.5)偿还1年期的债务 后,交易者净赚17万元(1127万元1110万元)。
▪
4.0%
无风险利率
▪
+1.2*6%
+GDP风险的风险溢价
▪
+(-.3)*(-7%) +利率风险的风险溢价
▪ 总计:13.3%
总收益
▪
用(10-5)式计算的结果:
▪
E(r)=4%+1.2*6%+(-0.3)*(-7%)=13.3%
10.2 套利定价理论
利用证券定价之间的不一致进行资金转移,从中赚取无风险 利润的行为称为套利,套利的特点是: 1)无投资需要,投资者可建立大的头寸来获取高利润; 2)在有效市场内,有利的套利机会会很快消失。
投资学第10章APT与风险收益多因素模型.

而是基于无套利原则和因素模型。 不要求“同质期望”假设,并不要求人人一致 行动。只需要少数投资者的套利活动就能消除 套利机会。 不要求投资者是风险规避的
11
10.2.2 充分分散的投资组合
Well- diversified portfolio 考虑n个证券的等权重资产组 合, 其中每个证券的收益为 :ri E (ri ) i F ei 组合P的收益:rP E (rP ) P F eP 其中, P wi i ,
没用到CAPM严格的假设,得到了与 CAPM差不多的结论
18
Figure 10.4 The Security Market Line
19
10.3 单项资产与套利定价理论
绝大多数单个证券满足该期望收益-贝塔关系 套利定价理论与CAPM:
作用相同 不需要太严格的假设 不需要市场组合 APT的推导以无套利为核心,CAPM则以均值-
14
图10.1 Returns as a Function of the Systematic Factor
15
图10.2 Returns as a Function of the Systematic Factor: An Arbitrage Opportunity
16
图 10.3 An Arbitrage Opportunity
5
10.1.2 多因素证券市场线
CAPM: E (r ) rf [ E (rM ) rf ]
令RPM E (rM ) rf E (r ) rf RPM 双因素SML:E (r ) rf GDP RP GDP IR RP IR 概念:因素组合
套利定价理论与风险收益的多因素模型

属于自融资组合;
套利组合对任何因素的敏感度均为零,即套利
组合没有因素风险;
套利组合的预期收益率应大于零。
8
套利组合(2)
条件一:w1 w2 wn 0 条件二: Pj 0, j 1,2, k , k n w111 w2 21 wn n1 0 w112 w2 22 wn n 2 0 w11k w2 2 k wn nk 0 条件三:w1r1 w2 r2 wn rn 0
多因素套利定价理论(1)
前面都是假定只有一个系统因素影响证券收益。
现分析多个因素产生系统风险影响证券的收益的 情况.以双因素模型为例: ri=E(ri)+β
i1F1+β i2F2
+ei
因素F1和F2代表对宏观因素预期值的偏离。因此
他们的预期值为0
ei代表企业特有的风险,也是对预期值的偏离,
在多因素的证券市场线关系中,因素投资组合将
30
多因素套利定价理论(3)
复制组合的构筑:对于任意一个暴露在F1和F2这两
个宏观因素的系统风险下的投资组合P,分别以其
β 值β
P1,β P2为权重选取因素组合1和因素组合2, P1–β P2的无风险证券(若<0,
再加上权重为1-β 新组合记为Q
E(rQ)=β
ri E ri i1 F1 i 2 F2 ei 其中: F1为第一个共同因素的非 预期变动,E F1 0 ei 为资产本身的非系统变 动;Covei , e j 0; F1 , F2 , ei的相关系数均为零; F2为第一个共同因素的非 预期变动,E F2 0
APT与风险收益多因素模型在基金估值中的应用

一、资本资产定价模型和指数模型
1 实际收益与期望收益 资本资产定价模型揭示各种期望收益之间
的关系,但是在现实中,能够观察到的是 实际的或已实现的持有期收益。而且,期 望收益与 关系也是根据期望收益 E(ri )与E(rm)
E(r) rf (E(rM ) rf ) 因此,资本资产定价模型需要附加的假设 条件下才能起作用并可以检验。
定价模型预测的可能期望收益的部分。如果股票公平
定价则其必定为零。
2019/10/15
4
套利
套利指一个能产生无风险 盈利的交易策略
资本市场均衡:不存在套利机会(无套利 均衡)
套利定价理论:在无套利均衡下资产价格 的决定
一价定律:两种资产未来所有现金流均相等, 那么二者的市场价格应该相等。
5
二、 多因素模型概述 (Multi-Factor model)
指数模型:用一个市场指数替代所有的宏 观经济风险
改进思路:将注意力直接放在风险的根本 来源上比间接地运用市场替代更有效
6
1 证券收益的因素模型
单因素模型:ri E(ri ) i F ei
F表公共因素对其期望的偏离,即未预期到的变化。 根据市场有效性原则,其期望=0
9
2.1 套利、风险套利与均衡
无风险套利使用零投资组合(zeroinvestment portfolio)
无风险套利行为实际上是一价法则(the law of one price)在金融市场中的应用
无风险套利组合的重要性质:任何投资者, 不管其风险态度如何,都愿意更多地拥有 该项组合头寸
16
图 An Arbitrage Opportunity
第10章-套利定价理论与风险收益多因素模型(投资学,上海财经大学)

(二)充分分散的投资组合
rP = E (rP) + PF + eP
F = 宏观因素未预期的变动
对一个充分分散的投资组合: 随着组合中资产数量的增加,ep接近于 0。 因此有: rP = E (rP) + PF
10
(三)β与期望收益
图 10.1的A是一个充分分散的投资组合,期望收益为 10%,β=1。 图 10.1的B是一个β=1的简单股票,它的非系统风险 不能分散掉,呈现为分布在直线两侧的点。
23
计算结果,两人的bF1都为1,bF2都为0,即 他们的组合都是对因素1有单位灵敏度而对 因素2灵敏度为零的纯因素组合,于是他们 的收益率应相同。 但现在计算的结果是投资者甲的收益率为 13.425%,投资者乙的收益率为15.725%。 于是会有很多人套利,如卖出投资者甲的组 合,买进投资者乙的组合。最终纯因素组合 为一均衡的收益率。
28
(七)CAPM与APT两者的联系
一般性结论: 第一,APT模型可以说是CAPM模型的一个 发展,两个模型都是确定资产均衡价格的模 型,都给出了有效的证券定价的方法。
29
第二,APT模型是一个多因素模型,但没有指 明哪些因素及影响程度,而CAPM是一个单因 素模型,指明市场证券组合因素及系数。从 某种程度上说, CAPM是APT只考虑市场组合 这唯一一个因素时的特例。 第三CAPM有很多严格苛刻的假定,不同于 CAPM,APT假定更松宽,更具有弹性,因为 那些与一个难以观测的市场资产组合有关的问 题上对它来说并不是很重要。
27
学术界针对FF三因素模型的指责:
虽然模型建立在单因素CAPM模型之上,与 CAPM模型相比,三因素模型缺乏一种类似 CAPM的解释机理,更多的是一种实证发现, 甚至是“数据加工”的结果。 三因素模型并不是解释股票收益率的屡试不 爽的法宝,对于股票市场上的所谓“趋势效 应”等市场现象缺乏解释效力。
APT与风险收益多因素模型

.2009年9月
5
10.1.1 证券收益的因素模型
扩展:双因素模型
ri E(ri ) iGDPGDP iIRIR ei 其中的又称为因素敏感度、因子载荷、因子
多因素模型的好处: (1)寻找均衡价格 (2)风险管理
.2009年9月
E ( r i) r f iM [ E ( r M ) r f] i[ e E ( r e ) r f]
.2009年9月
31
本章小结
▪ 多因素模型有更好的解释能力 ▪ 无套利原则 ▪ 充分分散化的投资组合 ▪ 多因素套利定价理论 ▪ 多因素资本资产定价模型
.2009年9月
32
E (rC )rfC [E (rA)rf]
.2009年9月
11.2.4 单因素证券市场线
证明:市场组合M也是充分分散化的组,合 若有任一充分分散化投的资组合P,
且P M
1,则有:E(rP) rf E(rM ) rf
P M
E(rP ) rf P[E(rM ) rf ]
没用到CAPM严格的假设,得到了与
投资学 第10章
APT与风险收益多因素模型
.2009年9月
引言
▪ 资本资产定价模型刻画了均衡状态下资产的期望 收益和相对市场风险测度(ß值)之间的关系。 不同资产的ß值决定它们不同的期望收益。
▪ 资本资产定价模型要求大量的假设,其中包括马 柯维茨在最初建立均值—方差模型时所作的一系 列假设,如每个投资者都是根据期望收益率和标 准差,并使用无差异曲线来选择他的最佳组合。
▪ APT与CAPM的比较
➢ APT对资产的评价不是基于马克维茨模型,而是基于 无套利原则和因素模型。
套利定价理论和风险收益多因素模型PPT课件

INVESTMENTS | BODIE, KANE, MARCUS
11-45
强势有效检验:内幕消息
• Jaffe, Seyhun, Givoly和Palmon的研究表 明内幕人员能够通过交易本公司的股票来 获利。
• 美国证券交易委员会(SEC)要求所有的 内部人员登记他们的交易活动。
有效市场假设
INVESTMENTS | BODIE, KANE, MARCUS
11-24
有效市场假设(EMH)
• 莫里斯·肯德尔(1953) 发现股价不存在 任何可预测范式。
• 价格在任何一天都可能上升或下降。 • 我们如何解释股价的随机变化?
INVESTMENTS | BODIE, KANE, MARCUS
• Keim和Stambaugh – 债券收益之间的差幅可以预测收益。
INVESTMENTS | BODIE, KANE, MARCUS
11-41
半强式检验:市场异象
• 市盈率效应 • 小公司效应(1月效应) • 被忽略的公司效应和流动性效应 • 净市率效应 • 盈余报告后的价格漂移
INVESTMENTS | BODIE, KANE, MARCUS
11-25
有效市场假说(EMH)
• 股价可以反映所有已知信息的观点称之为 有效市场假说EMH。
• 由于市场参与者急需新的交易信息,关于 未来良好表现的预测导致目前表现良好。
– 结果: 价格变化到与股票风险相称的收益率。
INVESTMENTS | BODIE, KANE, MARCUS
11-26
有效市场假设(EMH)
INVESTMENTS | BODIE, KANE, MARCUS
投资学PPT 第10章--APT与风险收益多因素模型

2 (ei )
, 又E (ei ) 0
10.2.3 贝塔与期望收益
套利准则一:如果两个充分分散化的投资 组合具有相同的β值,则它们在市场中必 有相同的预期收益。 套利准则二:如果两个充分分散化的投资 组合β值不同,则其风险溢价应正比例于 β
问题:如果以上准则不满足呢?
解:公式 10.9 显示: E(rp ) = rf + P1 [E(r1 ) rf ] + P2 [E(r2 ) – rf ] We need to find the risk premium (RP) for each of the two factors: RP1 = [E(r1 ) rf ] and RP2 = [E(r2 ) rf ] In order to do so, we solve the following system of two equations with two unknowns: 31 = 6 + (1.5 RP1 ) + (2.0 RP2 ) 27 = 6 + (2.2 RP1 ) + [(–0.2) RP2 ] The solution to this set of equations is: RP1 = 10% and RP2 = 5% Thus, the expected return-beta relationship is: E(rP ) = 6% + (P1 10%) + (P2 5%)
n
eP wi ei
2 2 2 则组合风险: P P F 2 ( eP )
1 2 1 2 2 又: (eP ) (ei ) (ei ) n i 1 n n 于是有:rP E (rP ) P F , 且: P P F
与风险收益多因素模型PPT课件

10.1.1 证券收益的因素模型
扩展:双因素模型
ri E(ri ) iGDPGDP iIR IR ei 其中的 又称为因素敏感度、因子载荷、因子
多因素模型的好处: (1)寻找均衡价格 (2)风险管理
6
10.1.2 多因素证券市场线
CAPM: E(r) rf [E(rM ) rf ]
令RPM E(rM ) rf
E(r) rf RPM 双因素SML:E(r) rf GDPRPGDP IRRPIR
概念:因素组合
7
10.2 套利定价理论 (Arbitrage Pricing Theory)
▪ 最早由美国学者斯蒂芬·罗斯于1976年提 出,这一理论的结论与CAPM模型一样,也 表明证券的风险与收益之间存在着线性关 系.
16
SUCCESS
THANK YOU
2020/9/30
图10.1 Returns as a Function of the Systematic Factor
充分分散投资组合A;单个证券S。 且ßA = ßS =1; E(rA) = E(rS) =10%
18
10.2.3 贝塔与期望收益
▪ 套利准则一:如果两个充分分散化的投资组 合具有相同的β值,则它们在市场中必有相 同的预期收益。
▪ 套利准则二:如果两个充分分散化的投资组 合β值不同,则其风险溢价应正比例于β。
11
▪ 套利举例: ▪ 假设现在6个月即期年利率为10%(连续复
利,下同),1年期的即期利率是12%。如 果有人把今后6个月到1年期的远期利率定 为11%,则有套利机会。
▪ 套利过程是:
1.交易者按10%的利率借入一笔6个月资金(假设 1000万元)
2.签订一份协议(远期利率协议),该协议规定 该交易者可以按11%的价格6个月后从市场借入 资金1051万元(等于1000e0.10×0.5)。
投资学第二次作业答案讲解

由公式:
图:通过回归获得证券特征线
可得:
第八章 指数模型
第8章,习题:第9~14题
用以下数据解9~14题,假设指数模型回归使用的是超额收益。 RA = 3% + 0.7RM + eA RB = -2% + 1.2RM + eB σM = 20%;R-squareA = 0.20;R-square B = 0.12 10.将每只股票的方差分解为系统性和公司特定的两个部分。
10
20
190 200
第7章 最优风险资产组合
第7章,习题:第12题;第7章,CFA考题:第1~4题
4.下面哪一种投资组合不属于马克维茨描述的有效边界(见表 7-9) 表 7-9 投资组合 a. b. c. d. W X Z Y 期望收益(%) 15 12 5 9
预期收益率(%)
标准差(%) 36 15 7 21
股票A的系统风险: 股票A的公司特定风险:980 – 196 = 784 股票B的系统风险: 股票B的公司特定风险:4800 – 576 = 4224
图:系统性风险和公司特定风险
第八章 指数模型
第8章,习题:第9~14题
用以下数据解9~14题,假设指数模型回归使用的是超额收益。 RA = 3% + 0.7RM + eA RB = -2% + 1.2RM + eB σM = 20%;R-squareA = 0.20;R-square B = 0.12 11.两只股票之间的协方差和相关系数是多少?
假设可以以无风险利率借入资金,则无风险收益率是多少(由A和B构造)?
图:组合的预期收益率函数
30 25 20 15
由组合方差公式:
股票证券-证券投资09资本资产定价模型和APT模型 精品

一、模型的假设
资本资产定价模型是在如下理论假设的基础上 导出的:
1,投资者通过预期收益和方差来描述和评价资 产或资产组合,并按照马柯维茨均值方差模型确定 其单一期间的有效投资组合;对所有投资者投资起 始期间都相同。
2,投资者为理性的个体,服从不满足和风险厌 恶假定。
第十章 资本资产定价(CAPM)
与套利定价(APT)
资本资产定价模型是现代金融学的基石之一, 它是在马柯维茨资产组合理论的基础上,通过夏普 (W.Sharpe)的《资本资产价格:一个市场均衡理 论》(Capital Asset Prices: A Theory of
Market Equilibrium)、林特纳(J.Lintner)的 《在股票组合和资本预算中的风险资产估值和风险 投资选择》(The Valuation of Risk Assets and the Selection of Risky investments in Stock Portfolios and Capital Budgets),以及莫辛 (J.Mossin)的《资本资产市场均衡》
由于σ2A=β2Aσ2m+σ2eA
(1)
因此先求σ2m: σ2m=(σ2B-σ2eB)/β2B=(0.0625-0.04)/
0.752=0.04
代入(1):
的期望回报率和风险之间的关系:当风险增加时,对
应的期望回报率也增加。非均衡状态下的证券组合都 落在这条直线之上或之下。由资本市场线的方程我们
可以看到,均衡证券市场的特征可以由两个关键的指
标来刻画:其一是CML直线方程的截距,一般也可 将其称为时间价值;其二是CML直线方程的斜率, 一般也称为风险的价值,它告诉我们,当有效证券 组合回报率的标准差增加一个单位时,期望回报率 应该增加的数量。
apt模型-PPT课件

生成,因素为市场组合。在这种情况下, 和市场组合的 1
期望收益率 E 相等。因此 rM E r r r i r f i E M (9-18) f E b r r i r f i 1 f 要使得式(9-18)中CAPM和APT都成立,则 i b。 i
止下来,此时资产期望收益率之间会达到一种均衡。
如果所有资产的期望收益率只受一个因素影响,即资产的
期望收益率可用单因素模型表示,那么均衡时资产的期望 收益率和敏感性之间应满足如下的线性关系:
(9-8) Er b i 0 1i 其中 和 为常数, 是资产 对因素的敏感性。 1 bi i 0
第三节 套利对定价的影响
价格与期望收益率之间的关系: EP 1 P 0 Er P 0
其中, P 是资产当前的价格, E 是资产的预期价格。 P1 0
购买资产,会提高其当前价格,导致期望收益率下降; 出售资产,会使其当前价格下降,期望收益率上升。
这种套利行为,直至3个资产之间的套利机会完全丧失后停
(9-15) K K rf
以此类推,可以得到:
那么套利定价方程可以表述为:
( 9-16 ) E r r r b r b r b i f 1 f i 12 f i 2 K f i K
第四节 APT和CAPM的关系
APT(套利定价模型)和CAPM(资本资产定价模型)比
较:
不同点:假设条件和推导过程完全不同
相同点:都是均衡模型,模型结果类似,CAPM模型可以
看
成是APT模型的一个特例,APT模型是CAPM模型的一般形
式。
《证券投资学》第10章 现代证券投资理论

或某些因素的影响时,两种证券收益之间就存在相关性。
(四)行为金融理论 行为金融理论把投资过程看成是一个心理过程,包括对市场的认知过程、 情绪过程和意志过程,在这个心理过程中由于存在系统性的认知偏差、 情绪偏差而导致投资者决策偏差和资产定价的偏差,如投资者的过度自 信、后悔厌恶、羊群效应等认知和行为偏差。 20世纪90年代中后期,行为金融理论更加注重投资者心理对组合投资决 策和资产定价的影响,1994年雪夫林和斯蒂曼提出了行为资产定价理论, 2000年又提出了行为组合理论。
投资行为模型
1.BSV模型(Barberis,Shleffer,and Vishny,1998)。 BSV模型认为,人们进行投资决策时存在两种错误范式: 其一是选择性偏差(representative bias),即投资者过分重 视近期数据的变化模式,而对产生这些数据的总体特征重 视不够,这种偏差导致股价对收益变化的反映不足(underreaction)。另一种是保守性偏差(conservation),投资者不 能及时根据变化了的情况修正自己的预测模型,导致股价 过度反应(over -reaction)。BSV模型是从这两种偏差出发, 解释投资者决策模型如何导致证券的市场价格变化偏离效 率市场假说的。
第一节 有效市场假说与证券投资理论概述
一、有效市场假说的形成与发展
有效市场假说是由美国芝加哥大学尤金· 法玛提出的,它是现代金 融市场的理论基石。 从理论来源上看,先有收益的统计方法、随机游走过程、奥斯本的 七大假设,然后才有法玛的有效市场假说(1965年《股票市场价格 的行为》)。
二、有效市场假说及其检验
套利定价理论的基本机制 套利定价理论的基本机制是:在给定资产收益率计算公 式的条件下,根据套利原理推导出资产的价格和均衡关系式。 APT作为描述资本资产价格形成机制的一种新方法,其基 础是价格规律:在均衡市场上,两种性质相同的商品不能以 不同的价格出售。套利定价理论是一种均衡模型,用来研究 证券价格是如何决定的。它假设证券的收益是由一系列产业 方面和市场方面的因素确定的。当两种证券的收益受到某种
投资学 第10章 套利定价理论与风险收益的多因素

一:证券收益的因素模型:单因素:的离差公共因素偏离其期望值:F e F )(r E r ii i i ++=β,暗示了一个不正确的假设:股票对所有风险的因素的敏感程度相同。
而多因素模型可以反映其敏感程度。
二:多因素证券市场线:三:无风险套利定价理论(APT ,arbitrage pricing theory ):假设:因素模型能描述证券收益;市场有足够多的证券来分散非系统风险;完善证券市场不允许任何套利机会存在。
四:套利、风险套利与均衡。
五:充分分散的投资组合:将投资分散到数量足够大的证券里,以使各种证券的权重足够小,并最终使得非系统的方差小到可以忽略不计。
六:p p p p e F )(r E r ++=β;)(e p 22F p 2p σσβσ+=∑=)(e w )(e i 2i 2i p 2σσ如果w 相同:)(e n 1)(e w )(e i 2i 2i 2i p 2σσσ==∑所以在一个充分分散的组合里:F )(r E r p p p β+=七:β值与期望收益:期望收益不同、β不同都存在套利机会。
八:接七:两个充分分散的投资组合,β都等于1,期望收益不同,套利。
风险溢价必须与β成比例,不成比例,投资将脱离证券市场线,造成套利机会。
买入期望收益高的,卖出期望收益低的。
β不同时,可以通过组合风险和无风险资产,使得β相同,构造套利策略。
九:单一资产与套利定价理论:如果所有充分分散的组合都满足,那么绝大部分单个股票也将满足。
(未给出证明,不用证明)十:套利定价理论与资本资产定价模型:套利定价凸显了无法分散的风险与可分散风险的区别,前者需要premium 而后者不要。
十一:套利定价理论需要一个假设:理性均衡会消除套利机会。
十二:资本资产定价模型是没有规律的,不同的股票或组合有不同的规律,而套利定价理论表明所有证券都有这种关系(有极少数例外)。
十三:多因素套利定价理论:因素投资组合推导,其中一个β等于1,其他全部等于0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.1.1 证券收益的因素模型
ri = Return on security
βi= Factor sensitivity or factor loading or factor beta
F = Surprise in macro-economic factor
(F could be positive or negative but has expected value of zero)
n i 1
1
n
2
2(ei
)
1
n
2(ei
)
其中, 2(ei )
2(ei n
)
,又E(ei
)
0
于是有:rP E(rP ) P F ,且: P P F
13
图10.1 Returns as a Function of the Systematic Factor
14
▪ APT的基本原理:由无套利原则,在因素 模型下,具有相同因素敏感性的资产(组 合)应提供相同的期望收益率。
11
3. 按12%的利率贷出一笔1年期的款项金 额为1000万元。
4. 1年后收回1年期贷款,得本息1127万元 (等于1000e0.12×1),并用1110万元 (等于1051e0.11×0.5)偿还1年期的债务 后,交易者净赚17万元(1127万元1110万元)。
12
10.2.2 充分分散的投资组合
构建套利组合(Arbitrage portfolio)
1. 零投资:套利组合中对一种证券的购买所需要 的资金可以由卖出别的证券来提供,即自融资 (Self-financing)组合。
2. 无风险:在因子模型条件下,因子波动导致风 险,因此,无风险就是套利组合对任何因子的 敏感度为0。
3. 正收益:套利组合的期望收益大于零。
The expected return on a security is the sum of:
(期望收益等于)
1.The risk-free rate(无风险利 率)
2.The sensitivity to GDP times the risk premium for bearing GDP risk (国民经济风险溢价倍数)
一阶回归和二阶回归(first pass regression and second pass regression.) Example:
Northeast Airlines : GDP 1.2, IR -0.3,RPGDP 6%, RPIR -7%, rf 4% E(r ) 4% 1.2 * 6% (0.3) * (7%) 13.3%
▪ APT与CAPM的比较
➢ APT对资产的评价不是基于马克维茨模型, 而是基于无套利原则和因素模型。
➢ 不要求“同质期望”假设,并不要求人人一致 行动。只需要少数投资者的套利活动就能消除 套利机会。
➢ 不要求投资者是风险规避的
15
10.2.3 贝塔与期望收益 (β & expected return)
ri E(ri ) iGDPGDP iIRIR ei 其中的又称为因素敏感度(factor sensitivity)、 因子载荷(factor loading)、因子(factor beta)
多因素模型的好处: (1)寻找均衡价格(equilibrium price)(2)风险管理(risk management)
➢ 有效率的证券市场不允许持续性的套利机会 – well-functioning security markets do not allow for the persistence of arbitrage opportunities.
9
10.2.1 套利、风险套利与均衡
▪ 无风险套利使用零投资组合(zeroinvestment portfolio)
▪ 绝大多数单个证券满足该期望收益-贝塔关系 ▪ 套利定价理论与CAPM:
➢ 作用相同 ➢ 不需要太严格的假设 -不要求“同质期望”假设,
并不要求人人一致行动。只需要少数投资者的套 利活动就能消除套利机会。 ➢ APT的推导以无套利和因素模型为核心,不要求投 资者是风险规避的,CAPM则以均值-方差模型 为核心
▪ 无风险套利行为实际上是一价法则(the law of one price)在金融市场中的应用
▪ 无风险套利组合的重要性质:任何投资者, 不管其风险态度如何,都愿意更多地拥有 该项组合头寸 - Regardless of wealth or risk aversion, investors will want an infinite position in the risk-free arbitrage portfolio.
Well - diversified portfolio
考虑n个证券的等权重资产组合,
其中每个证券的收益为:ri E(ri ) iF ei
组合P的收益:rP E(rP ) P F eP
其中,P
n i 1
1
n
i ,
eP
n i 1
1
n
ei
则组合风险:
2 P
P2
2 F
2(eP )
又: 2(eP )
10
▪ 套利举例(exemplification ) ▪ 假设现在6个月即期年利率为10%(连续复
利,下同),1年期的即期利率是12%。如 果有人把今后6个月到1年期的远期利率定 为11%,则有套利机会。 ▪ 套利过程是:
1. 交易者按10%的利率借入一笔6个月资金(假 设1000万元)
2. 签订一份协议(远期利率协议),该协议规定 该交易者可以按11%的价格6个月后从市场借 入资金1051万元(等于1000e0.10×0.5)。
20
Figure 10.4 The Security Market Line
21
▪ APT假设证券回报可以用预期到的回报和未预期 到的回报两个部分来解释,构成了一个特殊的因 子模型
ri E(ri ) i F ei E(Ft | t1) 0
预期的回报
未预期到的变化
F是证券i的某个因子的变化,基于有效市场 理论,它是不可预测的。
投资学 第10章
APT与风险收益多因素模型
Arbitrage Pricing Theory and Multifactor Models of Risk and Return
▪ 套利(Arbitrage)
➢ 利用证券定价之间的不一致来赚取无风险利润 的行为
▪ 资本市场均衡(balance):不存在套利机会 ▪ 套利定价理论(Arbitrage Pricing
rp
j i j
(E(ri ) E(rj )) E(rj ) rf
0
E(ri ) rf E(rj ) rf
i
j
假设资产j为市场投资组合M ,则M 1
E(ri ) rf
i
E(rj ) rf
j
E(rM ) rf
E(ri ) rf i E(rM ) rf
10.3 单项资产与套利定价理论 (single asset & APT)
8
10.2 套利定价理论
(Arbitrage Pricing Theory)
▪ Ross (1976)
▪ 三个基本假设
➢ 证券收益能用单因素模型表示 –security returns can be described by a factor model
➢ 有足够多的证券来分散系统风险 – there are sufficient securities to diversify away idiosyncratic risk
30
10.5 APT的局限和因素的确定
▪ APT对系统风险进行了细分,使得投资者能 够测量资产对各种系统因素的敏感系数,因 而可以使得投资组合的选择更准确。例如, 基金可以选择最佳的因素敏感系数的组合。
ei = Firm specific events (zero expected value)
单因素模型(single factormodel):ri E(ri ) i F ei
单因素模型暗含一个不正确的假设: 股票收益对每种风险因素的敏感程度相同。
4
10.1.1 证券收益的因素模型
扩展:双因素模型(double factor model)
Theory):用无套利原则来简化风险-收益 关系
2
10.1 多因素模型概述 (Multi-Factor model)
▪ 指数模型:用一个市场指数替代所有的宏 观经济风险
▪ 改进思路:将注意力直接放在风险的根本 来源上比间接地运用市场替代更有效(it is more useful to focus directly on the ultimate sources of risk)
29
10.4 多因素套利定价理论
▪ 因素资产组合(factor portfolio),亦为跟踪投资 组合(tracking portfolio)
▪ 双因素模型: ri E(ri ) i1F1 i2F2 ei
▪ 多因素模型的应用: ri rf i i1R1 i2R 2 ei ri rf i i1R1 i2R 2 ... inR n ei
要依靠“旧”的F来获利是不可能的!
E(Ft | t1) 0
▪ 若市场有效,则t-1时刻的信息集预测t时刻的价 格无效,这等价于t-1时刻信息无法预测t时刻的 因子,即对于因子的变化没有任何倾向——公平 赌局(Fair game)
▪ 从有效市场的理论来看,价格(回报)的不可预 测,本质上是信息的不可预测,也就是因子的变 化不可预测,这些信息既有宏观的、也有微观的 。
5
10.1.2 多因素证券市场线
