自由度计算例题
自由度计算例题63435
C
E
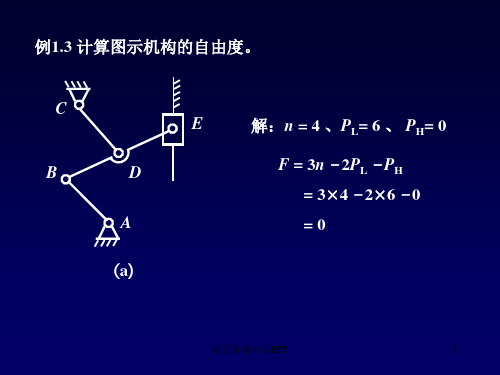
解:n = 4 、PL= 6 、 PH= 0
B
D
F = 3n–2PL–PH = 3×4–2×6–0
A
=0
(a)
语言资格考试PPT
1
A
D
E
解:n = 5 、PL= 7 、 PH= 0
G
F = 3n–2PL–PH
B
C
F
(b)
= 3×5–2×7–0
=1
语言资格考试PPT
(若存在复合铰链、局部自由度或虚约束请指明)
复合铰链:J 局部自由度:D 虚约束:M(N )
F =3n -2PL-PH = 3×9 -2×12 - 2 =1
语言资格考试PPT
8
2020
5
B A
(3)
局部自由度:B、C
D
虚约束:E(F )
C
F = 3n–2PL–PH
= 3×3–2×3–2
E
=1
F
语言资格考试PPT
6
J
I H
F
E
B
A
(4)
复合铰链:D
K
局部自由度:H
虚约束:F(G )
G D
F = 3n–2PL–PH = 3×8–2×11–1 =1
C
语言资格考试PPT
7
提高题:求机构自由度。
E
=1
A
F
语言资格考试PPT
4
例1.6 计算Байду номын сангаас列机构的自由度(若存在复合铰链、局部自由度或 虚约束请指明)
局部自由度:C
虚约束:D(E )
F = 3n - 2PL - PH = 3×3 - 2×3 - 2 = 1
自由度计算习题及答案

自由度计算习题及答案自由度计算习题及答案自由度是统计学中一个重要的概念,用于描述样本数据中可以自由变动的部分。
在统计学中,我们常常需要计算自由度来进行假设检验、方差分析等统计推断。
本文将给出一些自由度计算的习题及答案,帮助读者更好地理解和应用这一概念。
习题一:假设有一组样本数据,包含10个观测值。
我们希望进行一个t检验,假设总体均值为0。
请计算该t检验的自由度。
解答一:t检验的自由度由样本容量和样本数据的分布决定。
对于独立样本t检验,自由度等于两组样本的自由度之和再减去2。
在这个例子中,我们只有一组样本数据,因此自由度为10-1=9。
习题二:某公司想要比较两种不同的广告策略对销售额的影响。
他们随机选择了两组顾客,每组分别观看了不同的广告。
请计算用于比较两组销售额的独立样本t检验的自由度。
解答二:在独立样本t检验中,自由度等于两组样本的自由度之和再减去2。
假设第一组观测了n1个顾客,第二组观测了n2个顾客,那么自由度为n1+n2-2。
习题三:某研究人员想要比较三种不同的治疗方法对患者疼痛程度的影响。
他们随机将患者分为三组,每组接受不同的治疗。
请计算用于比较三组疼痛程度的方差分析的自由度。
解答三:方差分析的自由度由分子自由度和分母自由度组成。
对于一元方差分析,分子自由度为组数减1,即3-1=2。
分母自由度为总样本容量减去组数,即n-3。
在这个例子中,假设每组的样本容量为n,则分母自由度为3n-3。
习题四:某研究人员想要比较两种不同的教学方法对学生成绩的影响。
他们随机将学生分为两组,一组接受传统教学,另一组接受创新教学。
请计算用于比较两组学生成绩的配对样本t检验的自由度。
解答四:配对样本t检验的自由度等于配对观测值的数量减去1。
在这个例子中,假设有n对配对观测值,则自由度为n-1。
通过以上习题及答案的解析,我们可以看到自由度的计算对于统计推断是至关重要的。
正确计算自由度可以确保我们所做的统计分析具有可靠性和准确性。
自由度计算例题

自由度计算例题在机械设计、力学分析以及其他相关领域中,自由度的计算是一个重要的概念和基础技能。
理解和掌握自由度的计算方法,对于解决各种实际问题具有关键意义。
接下来,我们通过几个具体的例题来深入探讨自由度的计算。
例 1:考虑一个平面机构,由三个杆件通过铰链连接而成,形成一个三角形。
其中杆件 1 和杆件 2 的长度分别为 L1 和 L2,杆件 3 的长度为 L3。
在这个平面机构中,每个杆件都可以绕其铰链在平面内自由转动。
我们来计算这个机构的自由度。
首先,确定活动构件的数量 n。
这里有三个杆件,所以 n = 3。
然后,计算低副的数量 P L 。
由于每个铰链都是一个低副,一共有三个铰链,所以 P L = 3。
接下来,根据平面机构自由度的计算公式 F = 3n 2P L ,将 n = 3和 P L = 3 代入公式,得到:F = 3×3 2×3= 9 6= 3这意味着这个平面机构在平面内有 3 个自由度,即可以在平面内沿x 轴、y 轴方向移动以及绕平面内的某个点转动。
例 2:假设有一个空间机构,由四个杆件通过球铰连接而成,形成一个四面体。
杆件 1、2、3 和 4 的长度分别为 L1、L2、L3 和 L4。
对于这个空间机构,每个杆件都可以在空间中自由转动和移动。
活动构件的数量 n 为 4。
低副的数量 P L ,由于每个球铰都是一个低副,一共有四个球铰,所以 P L = 4。
根据空间机构自由度的计算公式 F = 6n 5P L ,将 n = 4 和 P L =4 代入公式,可得:F = 6×4 5×4= 24 20= 4这表明该空间机构在空间中有 4 个自由度,即可以在 x、y、z 三个方向上移动以及绕这三个轴转动。
例 3:再看一个较为复杂的平面机构,由多个杆件和滑块组成。
其中有 5 个杆件通过铰链连接,同时还有 2 个滑块在水平导轨上移动。
活动构件的数量 n = 7(5 个杆件和 2 个滑块)。
计算自由度和体系构造分析例题
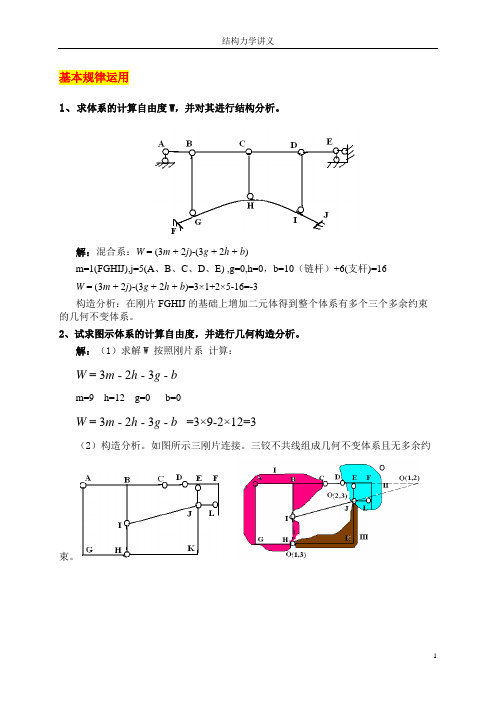
基本规律运用1、求体系的计算自由度W,并对其进行结构分析。
解:混合系:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3构造分析:在刚片FGHIJ的基础上增加二元体得到整个体系有多个三个多余约束的几何不变体系。
2、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)求解W 按照刚片系计算:W = 3m - 2h - 3g - bm=9 h=12 g=0 b=0W = 3m - 2h - 3g - b =3×9-2×12=3(2)构造分析。
如图所示三刚片连接。
三铰不共线组成几何不变体系且无多余约束。
3、试求图示体系的计算自由度,并进行几何构造分析。
解:(1)计算W:W = (3m + 2j)-(3g + 2h + b)m=1(FGHIJ),j=5(A、B、C、D、E) ,g=0,h=0,b=10(链杆)+6(支杆)=16W = (3m + 2j)-(3g + 2h + b)=3×1+2×5-16=-3(2)结构构造分析如图示体系内部(先撤除支座及地基)由三个刚片Ⅰ、Ⅱ、Ⅲ 用三个瞬铰两两相连,且三个瞬铰在一直线上,为几何瞬变体系。
4、如图所示为三角形ABC及其他链杆所组成体系,试考察BC边上G铰不同位置与体系整体几何特性的关系,给出简要分析过程。
(a) (b)(c) (d)解:(1)观察图(a)所示体系,△BEG直接与大地固定铰支,可以将B点看做铰结点,则BE,BG为链杆,因此,与大地直接相连的约束多余三根支杆,所以将大地必须看做是一个刚片。
BG和CD与GC相连,BE和A支座与△AEF相连,通过“找对家”的思路可以找到如图所示三刚片。
G铰位于BC中间时,三虚铰共线,组成瞬变体系。
自由度计算习题及答案

自由度计算习题及答案自由度是机械系统运动分析中的一个重要概念,它表示系统在空间中独立运动的方向数。
在进行自由度计算时,我们通常遵循以下步骤:确定系统的所有约束,然后根据约束的数量来计算系统的自由度。
# 自由度计算习题习题1:考虑一个由三个铰链连接的平面框架结构,每个铰链允许两个方向的平移运动。
计算该结构的自由度。
习题2:一个三维空间中的刚体,被两个球铰链和两个滑块约束。
球铰链允许刚体在任意方向上旋转,滑块允许沿其轴线的平移。
求该刚体的自由度。
习题3:一个平面上的四边形,其四个顶点分别固定在四个不同的点上,但其中两个顶点之间存在一个铰链连接。
计算该四边形的自由度。
# 自由度计算答案习题1答案:平面框架结构的自由度计算公式为:3n - 2j - h,其中n是铰链的数量,j是刚体的数量,h是约束的数量。
在这个例子中,n=3,j=1(整个框架被视为一个刚体),h=0(没有额外的约束)。
代入公式得:3*3 - 2*1 - 0 = 7。
因此,该结构的自由度为7。
习题2答案:对于三维空间中的刚体,自由度计算公式为:6 - 约束数。
在这个例子中,有两个球铰链,每个提供3个旋转自由度,总共6个;两个滑块,每个提供1个平移自由度,总共2个。
因此,约束数为6+2=8。
代入公式得:6 - 8 = -2。
由于自由度不能为负数,这意味着该刚体在空间中被完全约束,自由度为0。
习题3答案:对于平面上的四边形,其自由度计算公式为:3n - 2j - h,其中n是顶点数,j是刚体的数量,h是约束的数量。
在这个例子中,n=4,j=1(四边形被视为一个刚体),h=1(铰链是一个约束)。
代入公式得:3*4 - 2*1 - 1 = 9。
因此,该四边形的自由度为9。
通过这些习题和答案,我们可以看到自由度的计算涉及到对系统约束的详细分析,并使用相应的公式来确定系统的独立运动能力。
在实际应用中,这种分析对于设计机械系统和理解其运动特性至关重要。
机械设计自由度计算121题

1 1
2 2
3 3
4
活动构件数3 低副数4 高副数0 自由度数 3X3-2X4-0=1
虚约束
56 7
4 2 2
3 31
11 4
活动构件数5 低副数7 高副数1 自由度数 3X5-2X7-1=0
5
活动构件数8 低副数11 高副数1 自由度数3X8-2X11-1X1=1
1 11 22
虚约束
8
活动构件数9个
4
9 11
10 低副数12个
虚约束
复合铰
局部自由度 1 1
12
8
11
97
14
10
2 2
1 6
4
9 10 13
5
56
33
4
7
8
虚约束
活动构件数10个 低副数14个 高副数1个 自由度数3X10-2X14-1=1
2 2
1
1
5 5
44 1 3
3
2
活动构件数5个 低副数5个 高副数2个 自由度数3X5-2X5-2=3
复合铰
复合铰
虚约束
3 4
3
1
12 12
2
2 11 1
活动构件数3个 低副数4个 高副数1个 自由度数3X3-2X4-1=0
活动构件数2个 低副数2个 高副数1个 自由度数3X2-2X2-1=1
4
45 35
21
2
3
6
1
7
活动构件数5个 低副数7个 高副数0个 自由度数3X5-2X7-0=1
虚约束
7 8
5
5
4
复合铰
虚约束
2 2
4 4
化工设计自由度计算例题

选择题
在化工设计中,自由度通常指的是?
A. 系统的温度
B. 系统的压力
C. 系统中独立可变的参数数量(正确答案)
D. 系统的流量
对于一个由两个组分、两个相态组成的化工系统,其自由度最多为?
A. 1
B. 2
C. 3
D. 4(正确答案)
在进行化工设计时,若系统的自由度为零,意味着?
A. 系统处于不稳定状态
B. 系统无法进一步调整
C. 系统已达平衡状态(正确答案)
D. 系统必须改变
对于一个只有单一组分、单一相态的化工系统,在给定温度和压力的情况下,其自由度是?
A. 0(正确答案)
B. 1
C. 2
D. 3
在化工设计中,若需要计算一个由三个组分、三个相态组成的系统的自由度,至少需要知道多少个独立的热力学性质?
A. 3
B. 6
C. 9(正确答案)
D. 12
当一个化工系统的自由度大于零时,我们可以说该系统是?
A. 完全确定的
B. 不完全确定的(正确答案)
C. 无法分析的
D. 无效的
在进行相平衡计算时,如果一个系统由水、乙醇和它们的蒸气组成,且处于三相共存状态,那么该系统的自由度至少为?
A. 0
B. 1
C. 2(正确答案)
D. 3
对于一个由四个组分、但只有一个相态的化工系统,在已知其中三个组分的摩尔分数的情况下,系统的自由度是?
A. 0
B. 1(正确答案)
C. 3
D. 4
在化工设计中,若一个系统的自由度减少到零,通常是因为?
A. 增加了新的组分
B. 增加了新的相态
C. 引入了足够的约束条件(正确答案)
D. 改变了系统的温度。
结构力学自由度的计算例题及解析

1. 对于一个简单的平面桁架结构,若共有6个节点和10根构件,那么其自由度为多少?- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中,每个支座具有多少个约束?- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时,若结构有8个节点和12根构件,自由度公式为:自由度 = 3n - 2j,其中n是节点数,j是构件数。
该结构的自由度是多少?- A. 4- B. 6- C. 8- D. 104. 一个平面结构中,假设有4个节点,6根构件,所有构件都在一个平面上,计算其自由度时需考虑:- A. 3自由度每节点,减去2自由度每构件- B. 2自由度每节点,减去1自由度每构件- C. 2自由度每节点,减去2自由度每构件- D. 3自由度每节点,减去1自由度每构件5. 对于一个三维空间的桁架结构,若有10个节点和20根构件,其自由度计算应使用的公式是:- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中,如果节点数为5,构件数为8,计算其自由度时,正确的自由度为: - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构,其自由度为:- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点,8根构件,计算自由度时,如果框架是完全支撑的,结果是:- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构,其中有5个节点和12根构件,计算自由度时所用的公式为: - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7,构件数为10,且结构为刚性框架,计算其自由度时,结果为:- A. 5- B. 7- C. 9- D. 11。
机械原理自由度计算题典型例题

选择题:一个平面机构由4个构件组成,其中有5个低副,则该机构的自由度数为:A. 0B. 1(正确答案)C. 2D. 3一个空间机构有6个活动构件,8个低副和1个高副,该机构的自由度数为:A. 1B. 2(正确答案)C. 3D. 4平面连杆机构中,若各构件均在同一平面内运动,且有一个构件被固定,该机构属于:A. 自由度为1的机构B. 自由度为2的机构(正确答案)C. 自由度为3的机构D. 无法确定自由度一个机械系统由5个活动构件组成,包含7个转动副和2个移动副,该系统的自由度数为:A. 1(正确答案)B. 2C. 3D. 4在计算平面机构自由度时,若机构中存在复合铰链,每增加一个复合铰链,将:A. 增加一个约束,自由度减少1(正确答案)B. 减少一个约束,自由度增加1C. 自由度不变D. 无法确定对自由度的影响一个机构由3个构件通过4个转动副连接而成,其中一个构件被固定,该机构的自由度数为:A. 0(正确答案)B. 1C. 2D. 3空间机构中,若包含n个活动构件,p个低副,q个高副,则该机构的自由度F计算公式为:A. F = 3n - 2p - q(正确答案)B. F = 2n - 3p - qC. F = n - p - qD. F = p + q - n平面四杆机构中,若固定其中一个构件,则该机构的自由度数为:A. 0B. 1(正确答案)C. 2D. 3在计算机构自由度时,局部自由度对机构自由度的影响是:A. 使自由度增加B. 使自由度减少C. 不影响机构自由度(正确答案)D. 无法确定对自由度的影响。
单自由度计算例题
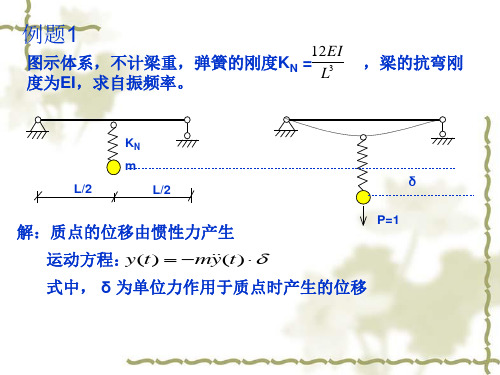
EI
m
KN=3EI/L3
KN
L
L
EI
KN
P=1 L
KN
2
1
KN
1/L
P sin t
m
yt
P=1
L
1
KN
2
3L/4
L
P=1
KN
1/L
L
P=1
KN
KN
5/4
2
=39L3/24EI
yt myt P sint
4、 EI=常数
EA m
A
L
P=1
EA
求自由振动频率,EA=6EI/L2
L
L m
A EA
P=1
=
6EI L3
,不计
梁的自重,θ= 89 EI 。求B点的最大动力位移反应
4mL3
m A
P sinθt
B
C
D
KN
L/3
L/3
L/3
1)求B点的柔度δ
P=1
P=1
2L/9
MP图
11
267 1458
L3 EI
24 L3 1P 1458 EI
P=1
X 基本体系
X=1
M1 图
❖ 求柔度δ
P=1
18L/89
M图
4L3
267 EI
P=1
2L/9
M图
2)求动力荷载为1时在质点出产生的位移
P=1
2L/9
2L/9
MP图
P=1 75L /801
171L /801
M图
* 7L3
534 EI
X=1
M图
P=1
2L /9
自由度的计算例题及解析

自由度的计算例题及解析在统计学的世界里,自由度这个概念就像是那位在聚会中总能找到话题的朋友,既重要又让人有些摸不着头脑。
大家知道,计算自由度其实是为了解决各种统计问题,就像是给我们的数据加了一把钥匙,让我们能更好地了解背后的故事。
说到自由度,首先得了解它的含义,简单来说,就是在某些条件下,我们可以自由选择的变量数量。
就好比你在做菜的时候,有些配料可以随意放,而有些则是固定的,这个选择的自由度就体现在这里。
举个简单的例子吧,想象一下你在参加一场篮球比赛。
比赛中有五个人在场上,但如果我们说,某一个球员的得分是依赖于其他四个人的得分,那你就得考虑自由度了。
假设总得分是固定的,只有四个球员的得分是自由选择的,那么这个场上实际上就只有四个自由度。
明白了吗?就像你有四种方式来打出精彩的三分球,而不管你怎么投,最后的结果得分都是一样的。
再比如说,我们做一个简单的问卷调查,假设问卷里有五个问题。
参与者可以自由选择回答这五个问题,但如果你知道某一个问题的答案了,其他问题的选择就可能受到影响。
假设调查结果的总和是一个固定的数值,那么自由度就会减少。
想象一下,就像在一场足球赛中,某一方得分后,另一方的反击策略可能受到限制。
这样自由度就被“封锁”了,哈哈。
自由度的计算也会让人觉得头疼。
比如,做一个t检验,计算自由度时总得记住“样本数量减去1”这个规则。
哎,真是的,这就像记得别人的生日一样,得多花点心思。
以两组数据为例,如果我们有10个样本,计算自由度就得是10减去1,这样就得到了9。
其实也挺简单,只是要记住这个小规则而已。
说到这里,你可能会想,自由度到底有什么用呢?哦,亲爱的,这可是大有用处!在统计学中,自由度帮助我们确定数据的分布特征。
想象一下,如果我们想要知道一个新产品的受欢迎程度,自由度可以帮助我们分析样本数据,从而预测市场反应。
就像是一位预言家,帮你指引方向,避免在市场的迷雾中迷失自我。
自从我开始深入了解自由度后,发现它真的是一门艺术!从不同的角度来看,每一个数据背后都有故事,每一个自由度的变化也反映了数据的灵活性。
机械设计基础自由度计算例题及解析

机械设计基础自由度计算例题及解析在机械设计中,自由度的计算是一个重要的基础概念。
它对于理解机构的运动特性、确定机构的合理性以及进行机构创新设计都具有关键意义。
下面,我们通过一些具体的例题来深入理解机械设计基础中自由度的计算方法。
一、例题一假设有一个平面机构,由三个活动构件组成,分别是构件 1、构件2 和构件 3。
它们之间通过四个低副连接,其中两个转动副,两个移动副。
解析首先,我们需要明确平面机构自由度的计算公式:F = 3n 2PL PH 。
其中,F 表示自由度,n 表示活动构件的数目,PL 表示低副的数目,PH 表示高副的数目。
在这个例子中,n = 3,PL = 4,PH = 0 (因为题目中没有提到高副)。
将这些值代入公式,可得:F = 3×3 2×4 = 1 。
这意味着该机构具有一个自由度,即只有一个独立的运动输入才能确定机构的运动。
二、例题二考虑一个空间机构,包含四个活动构件,通过五个转动副和三个移动副相连接。
解析对于空间机构,自由度的计算公式为:F = 6n 5PL 6PH 。
这里,n = 4,PL = 8 (五个转动副和三个移动副),PH = 0 。
代入公式计算:F = 6×4 5×8 =-4 。
自由度为负数,说明该机构的运动是不合理的,可能存在结构上的错误或者约束过度的情况。
三、例题三有一个平面机构,由两个构件组成,通过一个转动副和一个移动副连接,同时还有一个局部自由度,即一个构件在某处的独立转动不影响整个机构的运动。
解析在计算自由度时,需要先处理局部自由度。
对于局部自由度,我们在计算时将其排除。
所以,在这个例子中,实际参与计算的活动构件数 n = 1 ,低副数目 PL = 2 。
代入公式:F = 3×1 2×2 =-1 。
这显然是不合理的,因为我们在计算时没有正确处理局部自由度。
正确的处理方法是:将局部自由度从低副中减去。
自由度计算例题
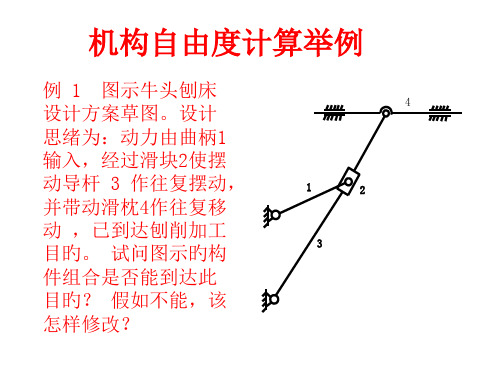
D4 E
B3
1
2
5 F
6
7 G
A C
H
I
8 K 9
局部自由度
D4 E
B3
1
5
7
2F
6 G
A C
H
I
复合铰链
虚约束
8 K 9
n 8 ; PL 11 ; PH 1 F 3n 2PL PH 38 2 111 1
例 3 计算图所示机构旳自由度 (若存在局部自由度、 复合铰链、虚约束请标出)。
合铰链、虚约束请标出)。
I
H
8
ห้องสมุดไป่ตู้
7
G
J
10
6
B
9
C
1
K 11 L
2
A
D E3
4
F
5
虚约束
复合铰链
局部自由度
I
H
8
7
J
G
6
B
10
9
C
1
11
K
L
2
A
E 3D
4
F
5
n 8 ; PL 11; PH 1 F 3n 2PL PH 38 2111 1
例 5 计算下图机构旳自由度 (若存在局部自由度、复 合铰链、虚约束请标出)。
即表达假如按此方案设计机构,机构是不能运动旳。必 须修改,以到达设计目旳。
改善措施: 1、增长一种低副和一种活动构件; 2、用一种高副替代低副。
改善方案
改善方案
改善方案
改善方案
例 2 如图所示,已知: DE=FG=HI,且相互平行;DF=EG, 且相互平行;DH=EI,且相互平行。计算此机构旳自由度 (若存在局部自由度、复合铰链、虚约束请标出)。
自由度计算例题

自由度计算例题在机械原理、结构力学等工程学科中,自由度的计算是一个非常重要的概念。
它有助于我们理解和分析物体或系统的运动可能性,从而为设计和优化提供关键的依据。
下面,我们通过几个具体的例题来深入探讨自由度的计算。
例题一:平面机构自由度计算考虑一个平面四杆机构,由四个杆件通过转动副连接而成。
其中,杆件 1 与机架通过转动副连接,杆件 2 与杆件 1 和杆件 3 分别通过转动副连接,杆件 3 与杆件 2 和杆件 4 分别通过转动副连接,杆件 4 与机架通过转动副连接。
首先,我们需要确定活动构件的数量。
在这里,杆件 1、2、3、4 为活动构件,共 4 个。
然后,计算低副的数量。
转动副的数量为 5 个。
接下来,计算高副的数量。
由于此机构中没有高副,所以高副数量为 0。
根据平面机构自由度的计算公式:F = 3n 2PL PH (其中,F 表示自由度,n 表示活动构件数,PL 表示低副数,PH 表示高副数),将数值代入公式可得:F = 3×4 2×5 0 = 12 10 0 = 2这意味着该平面四杆机构具有 2 个自由度,即它有两种独立的运动方式。
例题二:空间机构自由度计算假设有一个空间六面体机构,由六个杆件通过球铰连接而成。
同样,先确定活动构件的数量,这里是 6 个。
接着,计算低副的数量。
由于是球铰连接,每个连接点都相当于 3个低副,所以低副总数为 3×6 = 18 个。
高副数量为 0。
再根据空间机构自由度的计算公式:F = 6n 5PL 6PH ,代入数值计算:F = 6×6 5×18 0 = 36 90 0 =-54出现负数的自由度是不符合实际情况的,这说明该机构的约束过多,无法实现自由运动,可能是设计上存在问题。
例题三:含有复合铰链的机构自由度计算考虑一个平面机构,其中有三个杆件依次通过转动副连接,在杆件2 和杆件3 的连接点处,还有一个杆件通过转动副与它们相连,形成了一个复合铰链。
自由度计算

题4图 压榨机机构
机构的自由度与确定运动条件
计算机构自由度典型例题分析
典型例题一:计算图示某包装机送纸机构的自由度, 并判断该机构是否有确定运动。
解法2: 复合铰链:D包含2个转动副 (杆4和7)
局部自由度:F’=2 虚约束:杆8及转动副F、I引 入1个虚约束。
计算自由度前直接去除虚约 束和局部自由度: n=6 p5=7 p4=3 F=3n-2p5-p4=1
计算机构自由度典型例题分析
机构的自由度与确定运动条件
典型例题二:计 算 图 示 机 构 的 自 由 度, 如 有 复 合 铰 链、 局 部 自 由 度 和 虚 约 束,需 明 确 指 出。 画 箭 头 的 构 件 为 原 动 件。
局部自由度 复合铰链
复合铰链
1图
(b )
平面机构自由度计算例题及答案

平面机构自由度计算例题及答案在机械原理中,平面机构自由度的计算是一个重要的知识点。
通过计算机构的自由度,可以判断机构的运动可能性和确定性,为机构的设计和分析提供重要依据。
下面我们通过几个例题来详细讲解平面机构自由度的计算方法。
例题 1:如图所示的平面机构,由 4 个杆件组成,其中杆件 1 为机架,杆件2 和杆件 3 通过转动副连接,杆件 3 和杆件 4 通过移动副连接。
试计算该机构的自由度。
分析:首先,我们需要确定机构中的运动副类型和数量。
在这个机构中,有 2 个转动副(分别在杆件 2 和杆件 3 的连接处,以及杆件 1 和杆件 2 的连接处)和 1 个移动副(在杆件 3 和杆件 4 的连接处)。
接下来,我们根据自由度的计算公式 F = 3n 2PL PH 进行计算。
其中,n 为活动构件的数目,PL 为低副的数目,PH 为高副的数目。
在这个机构中,活动构件的数目 n = 3(杆件 2、3、4),低副的数目 PL = 3(2 个转动副和 1 个移动副),高副的数目 PH = 0。
将这些值代入公式,得到:F = 3×3 2×3 0 = 9 6 = 3所以,该机构的自由度为 3。
例题 2:考虑一个平面机构,由 5 个杆件组成,杆件 1 固定不动,杆件 2 与杆件 1 通过转动副连接,杆件 2 与杆件 3 通过移动副连接,杆件 3 与杆件 4 通过转动副连接,杆件 4 与杆件 5 通过移动副连接。
计算该机构的自由度。
分析:首先明确运动副类型及数量。
此机构有 3 个转动副(分别在杆件 1 和杆件 2、杆件 3 和杆件 4 、杆件 4 和杆件 5 的连接处),2 个移动副(分别在杆件 2 和杆件 3、杆件 4 和杆件 5 的连接处)。
然后计算活动构件数目 n = 4(杆件 2、3、4、5),低副数目 PL = 5(3 个转动副和 2 个移动副),高副数目 PH = 0。
将数值代入自由度计算公式:F = 3×4 2×5 0 = 12 10 = 2所以该机构的自由度为 2。
机械原理机构自由度计算

解:活动构件数n=
4
低副数PL=
5
F=3n - 2PL - PH =3×4 - 2×5 =2
高副数PH=
0
1ቤተ መጻሕፍቲ ባይዱ
2
3
4
θ1
重庆大学专用 作者: 潘存云教授
§2-6 自由度计算中的特殊问题
作者:潘存云教授
1
2
3
4
5
6
7
8
A
B
C
D
E
F
例题④计算图示圆盘锯机构的自由度。
解:活动构件数n=
7
低副数PL=
6
F=3n - 2PL - PH
高副数PH=0
=3×7 -2×6 -0
=9
计算结果肯定不对!构件数不会错,肯定是低副数目搞错了!
重庆大学专用 作者: 潘存云教授
⑦已知:AB=CD=EF,计算图示平行四边形 机构的自由度。
1
2
3
4
A
B
C
D
E
F
作者:潘存云教授
重新计算:n=3, PL=4, PH=0
F=3n - 2PL - PH =3×3 -2×4 =1
特别注意:此例存在虚约束的几何条件是:
1
2
3
4
A
B
C
D
E
F
4
F
⑦已知:AB=CD=EF,计算图示平行四边形 机构的自由度。
AB=CD=EF
平行虚约束
应 用
作者:潘存云教授
出现虚约束的场合: 1.两构件联接前后,联接点的轨迹重合,
2.两构件构成多个移动副,且导路平行。
平面机构自由度计算例题及答案

平面机构自由度计算例题及答案在机械原理的学习中,平面机构自由度的计算是一个非常重要的知识点。
它能够帮助我们判断机构是否具有确定的运动,以及机构的运动是否受到合理的约束。
下面,我们通过几个具体的例题来深入理解平面机构自由度的计算方法。
例题 1如下图所示的平面机构,其中构件 1 为机架,构件 2 与构件 1 以转动副连接,构件 3 与构件 2 以移动副连接,构件 4 与构件 3 以转动副连接,构件 5 与构件 4 以转动副连接。
试计算该机构的自由度。
!平面机构示例 1(解题思路首先,我们需要确定活动构件的数量。
在这个机构中,活动构件有构件 2、3、4、5,共 4 个。
然后,计算低副的数量。
转动副有 4 个(构件 2 与构件 1 之间、构件 4 与构件 3 之间、构件 5 与构件 4 之间),移动副有 1 个(构件 3与构件 2 之间),所以低副总数为 5 个。
接下来,计算高副的数量。
在这个机构中没有高副。
最后,根据自由度的计算公式:F = 3n 2PL PH (其中 F 为自由度,n 为活动构件数,PL 为低副数,PH 为高副数),代入数值计算。
n = 4,PL = 5,PH = 0F = 3×4 2×5 0= 12 10 0= 2答案该平面机构的自由度为 2。
例题 2如下图所示的平面机构,构件 1 为机架,构件 2 与构件 1 以转动副连接,构件 3 与构件 2 以转动副连接,构件 4 与构件 3 以转动副连接,同时构件 4 与构件 1 以移动副连接。
计算该机构的自由度。
!平面机构示例 2(解题思路活动构件有构件 2、3、4,共 3 个。
低副方面,转动副有 3 个(构件 2 与构件 1 之间、构件 3 与构件 2之间、构件 4 与构件 3 之间),移动副有 1 个(构件 4 与构件 1 之间),低副总数为 4 个。
高副数量为 0。
n = 3,PL = 4,PH = 0F = 3×3 2×4 0= 9 8 0= 1答案该平面机构的自由度为 1。
自由度计算例题

自由度计算例题在统计学中,自由度(degrees of freedom)是指用于衡量一个估计值或统计量的可自由变动的样本数量。
它是衡量样本数据中信息的度量。
自由度的计算方式因统计问题的不同而异。
下面我们来看一个自由度计算的例题:假设有一个实验,需要将一批样本分成两组,分别为甲组和乙组。
我们需要研究两组样本在某个特定因素上的差异。
首先,我们需要确定一些基本信息。
设甲组的样本数量为n1,乙组的样本数量为n2。
那么,甲组的自由度为n1-1,乙组的自由度为n2-1。
接下来,我们需要考虑合并两组样本的情况。
当我们将两组样本进行合并时,合并后的总样本数量为n1 + n2。
对于这种情况,总的自由度为(n1 + n2)-1。
此外,在某些情况下,我们还需要考虑到样本之间的相关性。
假设两组样本是相关的,那么在计算自由度时需要考虑到相关样本的数量。
具体计算方式根据实际情况而定。
以下是一个示例:假设甲组的样本数量为10,乙组的样本数量为8。
我们需要计算出甲组和乙组的自由度以及合并后总的自由度。
甲组的自由度 = 10 - 1 = 9乙组的自由度 = 8 - 1 = 7合并后总的自由度 = (10 + 8) - 1 = 17通过以上计算,我们得出了甲组、乙组以及合并后所得到的总的自由度。
自由度是统计学中一个重要的概念,它可以帮助我们更准确地评估样本数据的差异和变动情况。
在实际的统计分析中,我们需要根据具体情况灵活地计算自由度,以获得更可靠的结果。
总结起来,自由度是用于衡量样本数据中信息的度量,其计算方式根据不同统计问题的需求而异。
在计算自由度时,我们需要考虑到样本的数量、样本之间的相关性等因素,以获得准确的计算结果。
通过对自由度的合理计算,我们可以更准确地评估样本数据的变异程度,进而进行统计推断、假设检验等相关分析。
