十字相乘法PPT课件
合集下载
十字相乘法公开课获奖课件百校联赛一等奖课件

把下列各式分解因式
(1) x2-7x-8 =(x+1)(x-8) (2) m2-3m-10 =(m+2)(m-5) (3) y2+4y+4 =(y+2)2 (4) a2-2a-8 =(a+2)(a-4) (5) b2-2b-3=(b+1)(b-3)
把下列各式分解因式
(1) x2-5x+4 =(x-1)(x-4) (2) m2-5m-6 =(m+1)(m-6) (3) y2-8y+16 =(y-4)2 (4) a2+4a-21 =(a-3)(a+7) (5) b2+15b-16 =(b-1)(b+16)
=(m+n-2)(m+n-3)
想一想:
把下列各式分解因式
(3) y2-2y(x-1)-15(x-1)2
=[y+3(x-1)][y-5 (x-1)]
=(y+3x-3)(y-5 x+5)
想一想: (4) a2-12a(b+c)+36(b+c)2 =[a-6(b+c)][a-6 (b+c)]
=(a-6b-6c)2
把下列各式分解因式
(1) x2-4x-5 =(x+1)(x-5) (2) m2+5m-6 =(m+6)(m-1) (3) y2+8y-9 =(y+9)(y-1) (4) a2-12a+36 =(a-6)2 (5) b2-7b-18 =(b+2)(b-9)
想一想:
把下列各式分解因式
(1) x2-4xy-5y2 =(x-y)(x-5y) (2) m2+5mn-6n2 =(m+n)(m-6n) (3) y2-8xy+12x2 =(y-2x)(y-6x) (4) a2-12ab+36b2 =(a-6b)2 (5) b2-7bx2-18x4 =(b+2x2)(b-9x2)
十字相乘法[初中七年级数学]课件
![十字相乘法[初中七年级数学]课件](https://img.taocdn.com/s3/m/fcd07150fad6195f312ba677.png)
pq
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
步骤:
x
7
x 1
7
或
1
①竖分二次项与常数项 ②交叉相乘,和相加 ③检验确定,横写因式
x 7x 6x 顺口溜:竖分常数交叉验,
横写因式不能乱。
(顺口溜:竖分常数交叉验,横写因式不能乱。)
试一试:
x2 8x 15 (x 5)(x 3) 小结:
用十字相乘法把形如
x
5
x
3
x2 px q
二次三项式分解因式使
q ab, p a b
(3x) (5x) 8x
练一练: 将下列各式分解因式 z x xk
x2 5x 6
x2 x 6
x2 7x 12
x2 3x 10
小结:用十字相乘法把形如 x2 px q 二次三项
式分解因式 q ab, p a b
下列各式是因式分解吗?
x2 14x 45 (x 5)(x 9)
x2 7x 60 (x 12)(x 5)
x2 29x 138 (x 23)(x 6)
x2 14x 72 (x 4)(x 18)
x2 px q x2 (a b)x ab =(x + a )(x + b)
当q>0时,a、b( 同号 )当q<0时, a、b( 异号 )
试将 x2 6x 16分解因式 x2 6x 16
x2 6x 16
x 8x 2
提示:当二次项系数为-1时 ,先提出负号再 因式分解 。
六、独立练习:把下列
y2 3x 18
各式分解因式
解:原式=
x2 2x 15
十字相乘法(八年级数学精品课件)
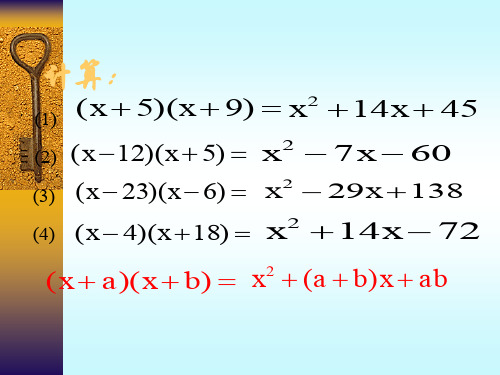
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。
例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
x
7
x 1
x7x 6x
因式分解:
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
十字相乘法(1)PPT课件

十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解能写成 二次三项式。
例1、把 x2-6x+8 分解因式
2020/10/13
1
例2、把 y4-7y2-18 分解因式 例3、把 x2-9xy+14y2 分解因式
练一练: 把下列各式分解因式
1、x2-11x-12 2 、x2+4x-12
3、x2-x-12
4、x2+5x-6
5、x2-5x-14
6、y2-11y+24
2020/10/13
2
用十字相乘法分解下列因式
1、p2+10p+16 2、x4-13x2+36
3、a8+7a4-98
4、x2+3xy-4y2
5、x2y2+16xy+48 6、(2+a)2+5(2+a)-36 7、x4-2x3-48x2
2020/10/13
3
例4、把 6x2-23x+10 分解因式
十字相乘法的要领是:“头尾 分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14、10(y+1)2-29(y+1)+10
2020/10/13
4
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
汇报人:XXXX 日期:20XX年XX月XX日
6
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把(x+1)(x+2)(x+3)(x+4)-3 分解因式
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解能写成 二次三项式。
例1、把 x2-6x+8 分解因式
2020/10/13
1
例2、把 y4-7y2-18 分解因式 例3、把 x2-9xy+14y2 分解因式
练一练: 把下列各式分解因式
1、x2-11x-12 2 、x2+4x-12
3、x2-x-12
4、x2+5x-6
5、x2-5x-14
6、y2-11y+24
2020/10/13
2
用十字相乘法分解下列因式
1、p2+10p+16 2、x4-13x2+36
3、a8+7a4-98
4、x2+3xy-4y2
5、x2y2+16xy+48 6、(2+a)2+5(2+a)-36 7、x4-2x3-48x2
2020/10/13
3
例4、把 6x2-23x+10 分解因式
十字相乘法的要领是:“头尾 分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14、10(y+1)2-29(y+1)+10
2020/10/13
4
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
汇报人:XXXX 日期:20XX年XX月XX日
6
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把(x+1)(x+2)(x+3)(x+4)-3 分解因式
因式分解——十字相乘法 —初中数学课件PPT

如果一个多项式适当分组,使分组 后各组之间有公因式或可应用公式,那 么这个多项式就可以用分组的方法分解 因式。
练一 练
mx+my-nx-ny ① ② ③④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny) =m(x+y)-n(x+y) =(x+y)(m-n)
x2+px+q= x2+(a+b)x+ab= (x+a)(x+b)
x
a
x
ax +
b
bx = (a+b)x
步骤: ①竖分二次项与常数项; ②交叉相乘,和相加; ③检验确定,横写因式.
顺口溜: 竖分常数交叉验, 横写因式不能乱.
将下列各式因式分解: 1.x2+8x+12= (x+2)(x+6) 2.x2-11x-12= (x-12)(x+1) 3.x2-7x+12= (x-3)(x-4) 4.x2-4x-12= (x-6)(x+2) 5.x2+13x+12= (x+1)(x+12) 6.x2-x-12= (x-4)(x+3)
(4)(x-1)(x+2)(x-3)(x+4)+24 解:(x-1)(x+2)(x-3)(x+4)+24
= 9a4-(4a2-4a+1)
= (x2+x-2)(x2+x-12)+24
= 9a4-(2a-1) 2 = (3a2+2a-1)(3a2-2a+1)
= (x2+x) 2-14(x2+x)+48 = (x2+x-2+px+q进行因式分解, 应重点掌握以下三个问题:
练一 练
mx+my-nx-ny ① ② ③④
①②,③④两组,得(mx+my)-(nx+ny)
解1:原式= (mx+my)-(nx+ny) =m(x+y)-n(x+y) =(x+y)(m-n)
x2+px+q= x2+(a+b)x+ab= (x+a)(x+b)
x
a
x
ax +
b
bx = (a+b)x
步骤: ①竖分二次项与常数项; ②交叉相乘,和相加; ③检验确定,横写因式.
顺口溜: 竖分常数交叉验, 横写因式不能乱.
将下列各式因式分解: 1.x2+8x+12= (x+2)(x+6) 2.x2-11x-12= (x-12)(x+1) 3.x2-7x+12= (x-3)(x-4) 4.x2-4x-12= (x-6)(x+2) 5.x2+13x+12= (x+1)(x+12) 6.x2-x-12= (x-4)(x+3)
(4)(x-1)(x+2)(x-3)(x+4)+24 解:(x-1)(x+2)(x-3)(x+4)+24
= 9a4-(4a2-4a+1)
= (x2+x-2)(x2+x-12)+24
= 9a4-(2a-1) 2 = (3a2+2a-1)(3a2-2a+1)
= (x2+x) 2-14(x2+x)+48 = (x2+x-2+px+q进行因式分解, 应重点掌握以下三个问题:
十字相乘法(经典教学课件)

试一试:
因式分解:2x2-3x-2
x
解原式=(x-2)(2x+1)
-2
+1
2x
因式分解:
6 x 7 xy 5 y
2
2
2 x y 3x 5 y
2x
-y
5y
3x
a1a2 x a1c2 a2c1 x c1c2
2
a1 x
c1
a2 x
所以原式可以分解为:a1 x c1
一个二次三项式
两个一次二项式相乘的积
因式分解
例1把下列各式分解因式
⑴ x2 - 7x-12
⑵ y2- 8y+15
利用十字交叉线来分解系数,把二次 三项式分解因式的方法叫做十字相乘法。
练习1:把下列各式分解因式。 (1)x2–3x-4
(2)y2 +2y-8
(3) m2-3m-28
(4)x2y2-7xy-18
作业:
1.(1)X2-7x+12
(3)x2+8x+12 (5)x2+6xy-16y2 2. (1) 2x2-7x+3 (2) x2-4x-12 (4) x2-11x-12 (6) x2-11xy+24y2 (2) 5x2+6xy-8y2
3.(1)(m+n)2-5(m+n)+6 (2) a2-12a(b+c)+36(b+c)2
c2
a2 x c2
1.十字相乘法分解因式的公式:
x (a b)x ab ( x a)(x b)
2
a1a2 x a1c2 a2c1 x c1c2 a1 x c1 a2 x c2
十字相乘法-PPT-课件资料

综合运用 7.分解因式:
综合运用
综合运用
综合运用
(1)请你再选择两个类似的部分试一试, 看看是否符合这一规律; (2)换一个月的月历试一下,是否有同样 的规律? (3)请你利用整式的运算对以上的规律 加以证明.
拓广探索
拓广探索 12.某种产品的原料提价,因而厂家决定对产品进行提价,现有 三种方案: (1)第一次提价p%,第二次提价q%; (2)第一次提价q%,第二次提价p%;
1
p
1
q
q + p = p+q
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式 ,这种方法叫做十字相乘法.
例题 用十字相乘法分解因式:
1 1 3+ 2+
得换一种拆分方式 现在数是对的, 3 2 符号不对,怎么办呢? 46
4 ≠ -8 6 ≠ -8
归纳
用十字相乘法分解因式的步骤:
1
-2
1
-6
补充题
提示:二次项是负的,可以先提取出来. 答案:-(y+6)(y-2)
补充题 答案:(5x-4y)(x+2y)
补充题 答案:(3x-y)(5x+4y)
整体思想 答案:(a+b-1)(a+b-3)
整体思想 答案:(xy-9)(xy+2)
整体思想
整体思想 答案:(2x-1)(5x+8)
整体思想
(2)(x+9)(x-2)
练习 用十字相乘法分解因式:
(1)(x+7)(x-1)
(2)(x-2)(x-4)
练习 用十字相乘法分解因式:
(1)(x+2)(x-1) (2)(x-5)(x+3)
十字相乘法PPT课件

用十字ቤተ መጻሕፍቲ ባይዱ乘法解一元二次方程
学习目标 : 理解并学会熟练运用十字相乘法进行因
式分解,解一元二次方程 .
学习重点 : 准确应用十字相乘法进行因式分解并进
行适当变式练习。
一、温故知新、自主学习
1.类比:
多位数乘以多位 数
125
x +7
× 13
× x -1
3 75
-x -7
③求二次函数y=kx2+x-k+1(k≠0,k 为常数)图象与x轴的交点坐标.
五、自我评价:
1,本节课我主要是学习了: 2,仍感觉有困惑 : 3,我认为我这一节课的表现: (A很棒 B一般 C没发挥出来D还需力). 4,下节课我打算:
=(x+a)(x+b)
其中 p=a+b ,q=ab
二、探究新知、合作交流
1.自主探究:(十字相乘法解一元二次方程) (1)X2+4X+3=0 (2)X2-7X+12=0
(3) X2-7X-30=0
(4)
X2+2X+
3 4
=0
2.合作交流:(十字相乘法法解一元二次方程) (1)3X2-5X+2=0 (2)12y2-5y-2=0
1 2 5
x2 +7x
16 2 5
X2 +6x -7
(x+7 )(x-1)= X2 +6x -7
过程的对称:
2.计算:
(x+1)(x+2)= (x+3)(x-5)=
3.因式分解: X2-7X+12=
学习目标 : 理解并学会熟练运用十字相乘法进行因
式分解,解一元二次方程 .
学习重点 : 准确应用十字相乘法进行因式分解并进
行适当变式练习。
一、温故知新、自主学习
1.类比:
多位数乘以多位 数
125
x +7
× 13
× x -1
3 75
-x -7
③求二次函数y=kx2+x-k+1(k≠0,k 为常数)图象与x轴的交点坐标.
五、自我评价:
1,本节课我主要是学习了: 2,仍感觉有困惑 : 3,我认为我这一节课的表现: (A很棒 B一般 C没发挥出来D还需力). 4,下节课我打算:
=(x+a)(x+b)
其中 p=a+b ,q=ab
二、探究新知、合作交流
1.自主探究:(十字相乘法解一元二次方程) (1)X2+4X+3=0 (2)X2-7X+12=0
(3) X2-7X-30=0
(4)
X2+2X+
3 4
=0
2.合作交流:(十字相乘法法解一元二次方程) (1)3X2-5X+2=0 (2)12y2-5y-2=0
1 2 5
x2 +7x
16 2 5
X2 +6x -7
(x+7 )(x-1)= X2 +6x -7
过程的对称:
2.计算:
(x+1)(x+2)= (x+3)(x-5)=
3.因式分解: X2-7X+12=
十字相乘ppt课件免费

中等难度实例解析
总结词
中等难度实例涉及稍微复杂的因式分 解和乘法运算。
详细描述
例如,将3x^3 - 9x^2 + 6x分解为(x - 2)(3x^2 - 3x + 2),这个过程需要 更深入的理解因式分解的概念,并掌 握更复杂的乘法运算。
高难度实例解析
总结词
高难度实例涉及复杂的因式分解和乘法运算,需要较高的数学技巧。
教师可设计多样化的练习题目,让学生充分练习 和掌握十字相乘法的技巧,提高解题能力。
教师还应关注学生的反馈和表现,及时给予指导 和帮助,促进学生的学习进步。
THANKS FOR WATCHING
感谢您的观看
总结词
求解一元一次方程
详细描述
最后,我们将交叉相乘的结果相加或相减,得到一元一次方程的解。如果一元一次方程有两个解,则原多项式方 程也有两个解。
04 实例解析
简单实例解析
总结词
简单实例主要涉及基本的因式分解和 乘法运算。
详细描述
例如,将2x^2 - 4x + 2分解为(2x 2)(x - 1),这个过程需要理解因式分解 的概念,并掌握基本的乘法运算。
= b,则这两个数就是方程的两个根。
通过这种方法,我们可以将原方程转化为两个一元一 次方程,从而求解出方程的根。
这种方法的关键在于找到合适的 m 和 n,使得它们满 足上述条件。
Hale Waihona Puke 原理的数学表达如果 ax^2 + bx + c = 0 是我们要解的 一元二次方程,那么我们可以通过以下 步骤找到它的根
对学生的建议
学生应熟练掌握十字相乘法的步骤和技巧,通过多练习来提高自己的解题能力。
在学习过程中,学生应积极思考和探索,尝试不同的方法和思路,以培养自己的数 学思维和创新能力。
12.2因式分解的方法(第4课时 十字相乘法)(课件)-七年级数学上册(沪教版2024)

解法:
am+an+bm+bn
=(am+an)+(bm+bn)
=a(m+n)+b(m+n)
=(m+n)(a+b).
观察上述因式分解的过程,解答下列问题:
(1)分解因式:mb-2mc+b2-2bc;
解:原式=(mb-2mc)+(b2-2bc)
=m(b-2c)+b(b-2c)
=(b-2c)(m+b);
(2)△ABC三边a,b,c满足a2-4bc+4ac-ab=0,判
−2
4 2 − 11 − 12.
1
1
−2
6
4 2 − 11 + 12
= + 1 − 12 .
1
1
1
−12
新知探究
如何将 2 + 7 + 12 2 因式分解?
类比二次三项式 2 + 7 + 12的因式分解,同样考虑十字相乘法.
将 2 + 7�� + 12 2 看作关于的二次三项式,它的二次项系数是1,
.
一次项的系数
课本例题
例7
1 2 + 7 + 12;
解 1 2 + 7 + 12
= +3 +4 .
2 2 − 8 + 12;
1
1
3
4
3 2 + 4 − 12;
3 2 + 4 − 12
= −2 +6 .
2 2 − 8 + 12
= −6 −2 .
1
1
−6
如果关于x的二次三项式 2 + + 的常数项q能分解成两个因
数与的积,且一次项系数p又恰好等于a + b,那么 2 + + 就可
十字相乘法非常非常好用详解PPT课件

5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
a p q,b pq
(3x) (5x) 8x
x2-5x+6 X2+5x-6 x2-5x-6 X2+5x+6
注意:
当常数项是正数时,分解的 两个数必同号,即都为正或都为 负,交叉相乘之和得一次项系数。 当常数项是负数时,分解的两个 数必为异号,交叉相乘之和仍得 一次项系数。因此因式分解时, 不但要注意首尾分解,而且需十 分注意一次项的系数,才能保证 因式分解的正确性。
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把 (x+1)(x+2)(x+3)(x+4)-3分解 因式
拓展创新
把下列各式分解因式 1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11 3、x n+1+3xn+2xn-1 4、(x+1)(x+3)(x+5)(x+7)+16
十字相乘法非常非常好用详 解
十字相乘法
“十字相乘法”是乘法公式: (x+p)(x+q)=x2+(p+q)x+pq的 反向运算,它适用于分解二次 三项式。
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
a p q,b pq
(3x) (5x) 8x
x2-5x+6 X2+5x-6 x2-5x-6 X2+5x+6
注意:
当常数项是正数时,分解的 两个数必同号,即都为正或都为 负,交叉相乘之和得一次项系数。 当常数项是负数时,分解的两个 数必为异号,交叉相乘之和仍得 一次项系数。因此因式分解时, 不但要注意首尾分解,而且需十 分注意一次项的系数,才能保证 因式分解的正确性。
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
例7、把 (x+1)(x+2)(x+3)(x+4)-3分解 因式
拓展创新
把下列各式分解因式 1、x2-4xy+4y2-6x+12y+8
2、(x2+2x)(x2+2x-11)+11 3、x n+1+3xn+2xn-1 4、(x+1)(x+3)(x+5)(x+7)+16
十字相乘法非常非常好用详 解
十字相乘法
“十字相乘法”是乘法公式: (x+p)(x+q)=x2+(p+q)x+pq的 反向运算,它适用于分解二次 三项式。
《分解因式-十字相乘法》ppt课件63264

哪组分解来进行分解因式。
a
11
作业
1. 若x2+mx-12能分解成两个整系数的一次因式 乘积,则符合条件的整数m个数是多少?
2. ⑴ x2+5x+6; ⑵ x2-5x+6;
(3) x2+5x-6; (4) x2-5x-6
(5) (x-y)2 +(x-y) -6
a
12
bYE~
a
13
(4)-12= 1× (-12)或(-1)×12或2×(- 6)或(-2)× 6或 3×(-4) 或(-3)× 4
(5)24= 1× 24或(-1)×(-24)或2× 12或(-2)× (-12) 或 3×8或(-3)× (-8)或4× 6或(-4)× (-6)
(6)-24= 1×(- 24)或(-1)×24或2× (-12)或(-2)× 12或3×(8)或(-3)× 8或4×(-6)或(-4)× 6
十字相乘法
a
1
口答计算结果
*小提示: 整式乘法中,有(x+a)(x+b)=x2+(a+b)x+ab
(1)(x+3)(x+4) (2)(x+3)(x-4)
(3) (x-3)(x+4) (4) (x-3)(x-4)
提问:
你有什么快速计算类似以上多项式的方法吗?
a
2
观察与发现
两个一次二项式相乘的积 整式乘法 一个二次三项式
4
试一试
把x2+3x+2分解因式
分析∵ (+1) ×(+2)=+2
(+1)+(+2)=+3
x
1
∴x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
顺口溜:竖分常数交叉验,
x 7x 6x
横写因式不能乱。
试一试: (顺口溜:竖分常数交叉验,横写因式不能乱。) 2 小结:
x x
x 8x 15 ( x 5)(x 3)
5 3
用十字相乘法把形如
x px q
2
二次三项式分解因式使
q ab, p a b
整式乘法中,有
1、口答计算结果
(1)(x+3)(x+4)
(x+a)(x+b)=x2+(a+b)x+ab
(2)(x+3)(x-4)
(3) (x-3)(x+4)
(4) (x-3)(x-4)
2、提问:你有什么快速计算类似 以上多项式的方法吗?
观察与思考
( x 2)(x 3) x 3x 2 x 3 2 (1)
2
x 2 5x 6
x +2 x +3 +3x+2x
反之
x 2 5 x 6 ( a 4 )( a 1 ) a a 4a 4 (1) (2)
a 2 3a 4
a -4 a +1 -4a+a
反之
a 3a 4 (a 4)(a 1)
(2)x2+[(-1)+(-2)]x+(-1) ×(-2)
= [x+(
2 (3)x +
-1)][x+( -2 )]
[(-2) + 1]x + (-2) ×1
观 察 与 思 考
= [x + ( -2)]( x + 1 )
公式推导 归纳总结 2 x + ( a + b )x + a b = x2 + ax + bx + ab = x(x + a) + b(x + a) = (x + a) (x + b) ∴ x2 + ( a + b )x + a b = (x + a) (x + b) 运用公式必须同时具备的三个条件:
一次项系数1 =(-1) +2 ≠1+(-2)
分析: (2)二次项系数为1,常数项-15=1×(-15)=(-1) ×15 =3×(-5)=(-3) ×5,
(2)解: x2-2x-15 =(x+3)(x-5) 2.常数项是负数时,它分解成两个异号因数, 其中绝对值较大的因数和一次项系数符号相 同。
一次项系数-2=3+(-5) ≠(-3) +5
-
-
t 2 10t 56 =(t
- 4)(t __ __ + 14)
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同 当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数 符号)与p符号相同
例1:分解因式 (1)x2+3x+2 (1)解: x2+3x+2 =(x+1)(x+2)
(2)x2 -7x+6
分析: (1)二次项系数为1,常数项2=1×2 = (-1)×(-2), 一次项系数3 = 1+2 ≠ (-1)+(-2) 分析:(2)二次项系数为1,常数项6=1×6 =(-1)×(-6) =2×3 =(-2) ×(-3), 一次项系数-7 =(-1)+(-6) ≠2+3 ≠(-2) +(-3)
(3x) (5x) 8x
练一练: 将下列各式分解因式
x 5x 6
2
x x6
2
x 7 x 12
2
小结: 用十字相乘法把形如
2
x 3 x 10
2
x px q 二次三项式分解因式 q ab, p a b
当q>0时,q分解的因数a、b( 同号 ) 当q<0时, q分解的因数a、b( 异号 )
2
x 7 x 60 ( x 12)(x 5)
2
x 29x 138 ( x 23)(x 6)
2
x 14x 72 ( x 4)(x 18)
2
2 x +
(a+b)x + a b型式子的因式分解
学习目标:
( a + b) x + a b =(x + a) ( x + b ) 2 2、运用公式会对x + (a+b)x + a b型的二次三项式进行因式 分解。
2
类似的
2 ( a 2 )( a 3 ) a 3a 2a (2) (3) (3)
a 2 5a 6
a -2 a -3 -3a-2a
反之
a 5a 6 (a 2)(a 3)
2
下列各式是因式分解吗?
x 14x 45 ( x 5)(x 9)
当q<0时, q分解的因数a、b( 异号 )
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填
2
、 符号
__ + __ +
1) 1)
__ + 3)(x = ( x x 4x 3
x 2 x 3 =(x __ 3)(x
2
-
y 2 9 y 20 =(y __ 4)(y __ 5)
观察:p与a、b符号关系
x 14x 45 ( x 5)(x 9)
2
x 29x 138 ( x 23)(x 6)
2
小结: 当q>0时,q分解的因数a、b( 同号 ) 且(a、b符号)与p符号相同
x 2 7 x 60 ( x 12)(x 5)
x 2 14x 72 ( x 4)(x 18)
2 1.掌握公式x +
1、计算
温故而知新
(1)(x +1) ( x + 2 ) = x2 + ( 1 + 2 )x + 1×2 (2)(x -1) ( x + 2 ) = x2 +[(-1) + 2]x + (-1)×2
(3)(x + a) ( x + b )= x2 +
( a + b )x + a b
2、下列各式能因式分解吗? (1) x2 + ( 1 + 2 )x + 1×2 = (x +1) ( x + 2 ) (2) x2 +[(-1)+2]x+(-1)×2 = (x -1) ( x + 2 ) (3) x2 + ( a + b )x + a b = (x + a) ( x + b )
(1)x2+(1+4)x+1×4 = (x + 1 )(x + 4)
将下列各式因式分解
(1)x2+6x+8
2 (3)x -5x+4 2 (5)x -2x-8
(2)y2+7y+12
2 (4)x +2x-8 2 (6)y -7y-18
+
(7)a2b2-a b-2
小结: 1.运用公式x2 + ( a + b )x + a b = (x + a) (x + b) 必须同时具备的三个条件: (1)二次项系数式是1的二次三项式 (2)常数项是两个数之积 (3)一次项系数是常数项的两个因数之和 2.常数项因数分解的一般规律: (1) 常数项是正数时,它分解成两个同号因 数,它们和一次项系数符号相同。
(1)二次项系数式是1的二次三项式 (2)常数项是两个数之积
(3)一次项系数是常数项的两个因数之和
十字相乘法(借助十字交叉线分解因式的方法)
例一:
步骤:
x
x
x 6 x 7 ( x 7)(x 1) ①竖分二次项与常数项
2
7
7
或
②交叉相乘,和相加 ③检验确定,横写因式
1
(2) 常数项是负数时,它分解成两个异号因数, 其中绝对值较大的因数和一次项系数符号相同。
例3 分解因式 3x -10x+3 2 x 解:3x -10x+3 =(x-3)(3x-1) 3x
2
2
-3
-1 -9x-x=-10x +3
例4 分解因式 5x -17x-12 解:5x -17x-12
2
5x
=(5x+3)(x-4)
-4 x -20x+3x=-17x
1.分解因式 :
我最棒,我能行!
最棒最棒我最棒
(1) x2+5x-6
(2) x2-5x-6
(3) x2+5x+6
(4) x2-5x+6
(5) -6x2+7x+5
因式分解时常数项因数分解的一般规律: 1.常数项是正数时,它分解成两个同号因 数,它们和一次项系数符号相同。
(1)解: x2 -7x+6 =(x-1)(x-6)
例2. 分解因式 (1)x2+x-2
分析:(1)二次项系数为1,常数项-2=(-1) ×2 =1× (-2),
(2)x2-2x-15
(1)解: x2+x-2 =(x-1)(x+2)
