利用双线性变换求其离散传递函数
双馈变流器不平衡控制的正负序分离方法比较研究

双馈变流器不平衡控制的正负序分离方法比较研究【摘要】风电场并网导则要求风电机组在对称和不对称跌落下均具有低电压穿越能力,目前常用的几种不对称控制算法需要准确分离正负序分量。
本文讨论了导数法、T/4延时法、移相90°全通滤波器法和陷波器法四种正负序分离方法的原理及优缺点,并对此四种方法在输入带高斯噪声、低次谐波、频率偏移时的分离效果进行了仿真比较研究。
【关键词】风电机组;低电压穿越;正负序分量引言随着风电技术和风电市场的发展,风电装机容量和并网容量占电网的比例越来越大,并网风电场对于电网安全稳定运行的影响日益突出。
国家标准《风电场接入电力系统技术规定》[1]要求风机在对称和不对称电压跌落时具有一定的低电压穿越能力。
双馈发电机DFIG由于其变流器容量小、成本低、可实现有功无功独立灵活控制[2,3],已成为风电市场的主流机型。
当前针对不对称电压跌落下双馈风电机组的控制的研究比较多,主要的控制策略有双dq-PI控制[4-6]、主辅控制[7,8]、PR控制[9]等[10]。
其中,以双dq-PI 控制为代表的一系列基于正负序分离的控制算法研究的较为深入,这类控制算法要求各不对称量如电网电压、网侧变流器GSC电流和转子电流等的正负序分量参与计算。
目前关于正负序分离算法的研究很多,正负序分离算法主要包括导数法[11,12]、T/4延时法[13,14]、移相90°的全通滤波器法[5,15]和基于陷波器滤波[16]分离方法等。
本文介绍和讨论了导数法、T/4延时法、移相90°的全通滤波器法和陷波器法四种正负序分离法的原理和优缺点,从正负序分离的延时、准确性、抗噪性,输入带谐波及频率偏移对分离效果的影响等几个方面对其进行仿真比较研究。
1.正负序分离方法不对称电压跌落时,电网电压出现负序分量和零序分量,进而导致DFIG定转子电流和网侧电流中产生负序分量。
考虑到双馈风电机组通常采用三相三线制,零序电流不能流通,故不考虑零序分量,则各三相电磁量可表示为:(1)式中,F表示电网电压Vg、转子电流Ir、网侧电流IGSC。
计算机控制系统复习题答案

计算机控制系统课程复习题答案一、知识点:计算机控制系统的基本概念;具体为了解计算机控制系统与生产自动化的关系;掌握计算机控制系统的组成和计算机控制系统的主要特性;理解计算机控制系统的分类和发展趋势;回答题:1.画出典型计算机控制系统的基本框图;答:典型计算机控制系统的基本框图如下:2.简述计算机控制系统的一般控制过程;答:1 数据采集及处理,即对被控对象的被控参数进行实时检测,并输给计算机进行处理;2 实时控制,即按已设计的控制规律计算出控制量,实时向执行器发出控制信号;3.简述计算机控制系统的组成;答:计算机控制系统由计算机系统和被控对象组成,计算机系统又由硬件和软件组成;4.简述计算机控制系统的特点;答:计算机控制系统与连续控制系统相比,具有以下特点:⑴计算机控制系统是模拟和数字的混合系统;⑵计算机控制系统修改控制规律,只需修改程序,一般不对硬件电路进行改动,因此具有很大的灵活性和适应性;⑶能够实现模拟电路不能实现的复杂控制规律;⑷计算机控制系统并不是连续控制的,而是离散控制的;⑸一个数字控制器经常可以采用分时控制的方式,同时控制多个回路;⑹采用计算机控制,便于实现控制与管理一体化;5.简述计算机控制系统的类型;答:1操作指导控制系统;2直接数字控制系统;3监督计算机控制系统4分级计算机控制系统二、知识点:计算机控制系统的硬件基础;具体为了解计算机控制系统的过程通道与接口;掌握采样和保持电路的原理和典型芯片的应用,掌握输入/输出接口电路:并行接口、串行接口、A/D和D/A的使用方法,能根据控制系统的要求选择控制用计算机系统;回答题:1.给出多通道复用一个A/D转换器的原理示意图;2.给出多通道复用一个D/A转换器的原理示意图;3.例举三种以上典型的三端输出电压固定式集成稳压器;答:W78系列,如W7805、7812、7824等;W79系列,如W7805、7812、7824等4.使用光电隔离器件时,如何做到器件两侧的电气被彻底隔离答:光电隔离器件两侧的供电电源必须完全隔离;5.说明隔离电源的基本作用;答:为了实施隔离技术,隔离电源可以为被隔离的各个部分提供独立的或相互隔离的电源供电,以切断各个部分间的电路联系;6.什么是采样或采样过程7.答:采样或采样过程,就是抽取连续信号在离散时间瞬时值的序列过程,有时也称为离散化过程;8. 简述典型的计算机控制系统中所包含的信号形式;答:1 连续信号;2 模拟信号;3 离散信号;4 采样信号;5 数字信号;9. 根据采样过程的特点,可以将采样分为哪几种类型10.答:根据采样过程的特点,可以将采样分为以下几种类型;1 周期采样 ;指相邻两次采样的时间间隔相等,也称为普通采样;2 同步采样;如果一个系统中有多个采样开关,它们的采样周期相同且同时进行采样;3 非同步采样;如果一个系统中有多个采样开关,它们的采样周期相同但不同时开闭;4 多速采样;如果一个系统中有多个采样开关,每个采样开关都是周期采样的,但它们的采样周期不相同;5 随机采样;若相邻两次采样的时间间隔不相等;11. 什么是信号重构答:把离散信号变为连续信号的过程,称为信号重构,它是采样的逆过程;12. 写出零阶保持器的传递函数; 答:零阶保持器的传递函数为01e ()TsH s s--=; 13. 引入零阶保持器对系统开环传递函数的极点有何影响答:零阶保持器的引入并不影响开环系统脉冲传递函数的极点;14. 简述采样定理的基本内容;答:采样定理: 如果连续信号)(t f 具有有限频谱,其最高频率为max ω,则对)(t f 进行周期采样且采样角频率s max 2ωω≥时,连续信号)(t f 可以由采样信号)(*t f 唯一确定,亦即可以从)(*t f 无失真地恢复)(t f ;15. 简述连续信号的定义;答:连续信号是在整个时间范围均有定义的信号,它的幅值可以是连续的,也可以是断续的;16. 简述离散信号的定义;答:模拟信号是在整个时间范围均有定义的信号,它的幅值在某一时间范围内是连续的;模拟信号是连续信号的一个子集,在大多数场合与很多文献中,将二者等同起来,均指模拟信号;17. 简述采样信号的定义;答:采样信号是离散信号的子集,在时间上是离散的、而幅值上是连续的;在很多场合中,我们提及离散信号就是指采样信号;18. 简述数字信号的定义;答:数字信号是幅值整量化的离散信号,它在时间上和幅值上均是离散的;三、知识点:数字控制器的模拟化设计方法;具体为介绍数字控制器的模拟化设计方法,掌握模拟控制器与数字控制器的转换方法,掌握数字PID 控制器的设计方法及存在的问题、改进的办法;回答题:1. 简述比例调节作用;答:比例调节器对偏差是即时反应的,偏差一旦出现,调节器立即产生控制作用,使输出量朝着减小偏差的方向变化,控制作用的强弱取决于比例系数K P;比例调节器虽然简单快速,但对于系统响应为有限值的控制对象存在静差;加大比例系数K P可以减小静差,但是K P过大时,会使系统的动态质量变坏,引起输出量振荡,甚至导致闭环系统不稳定;2.简述积分调节的作用答:为了消除在比例调节中的残余静差,可在比例调节的基础上加入积分调节;积分调节具有累积成分,只要偏差e不为零,它将通过累积作用影响控制量u,从而减小偏差,直到偏差为零;积分时间常数T I大,则积分作用弱,反之强;增大T I将减慢消除静差的过程,但可减小超调,提高稳定性;引入积分调节的代价是降低系统的快速性;3.简述微分调节的作用答:为加快控制过程,有必要在偏差出现或变化的瞬间,按偏差变化的趋向进行控制,使偏差消灭在萌芽状态,这就是微分调节的原理;微分作用的加入将有助于减小超调,克服振荡,使系统趋于稳定;4.为什么会出现比例和微分饱和现象答:当给定值发生很大跃变时,在PID增量控制算法中的比例部分和微分部分计算出的控制增量可能比较大由于积分项的系数一般小得多,所以积分部分的增量相对比较小;如果该计算值超过了执行元件所允许的最大限度,那么,控制作用必然不如应有的计算值理想,其中计算值的多余信息没有执行就遗失了,从而影响控制效果;5.如何消除比例和微分饱和现象答:抑制比例和微分饱和的办法之一是用“积分补偿法”;其中心思想是将那些因饱和而未能执行的增量信息积累起来,一旦有可能再补充执行;6.增量型PID控制算式具有哪些优点答:1计算机只输出控制增量,即执行机构位置的变化部分,因而误动作影响小;2在i时刻的输出ui,只需用到此时刻的偏差,以及前一时刻、前两时刻的偏差e i-1、e i-2和前一次的输出值u i-1,这大大节约了内存和计算时间;3在进行手动—自动切换时,控制量冲击小,能够较平滑地过渡;7.如何利用试凑法调整PID算法的参数答:1先整定比例部分:将比例系数KP由小调大,并观察相应的系统响应趋势,直到得到反应快、超调小的响应曲线;2如果在比例调节的基础上系统的静差不能满足设计要求,则需加入积分环节;3如果即使有比例积分控制器消除了偏差,但动态过程仍不令人满意,则可以加入微分环节,构成PID 控制器;在整定时,可先置微分时间系数TD为零,在第二步整定的基础上,增大微分时间系数TD,同时相应地改变比例系数KP和积分时间系数TI,逐步试凑,以获得满意的调节效果和控制参数;8.何为积分饱和现象答:在标准PID位置算法中,控制系统在启动、停止或者大幅度提降给定值等情况下,系统输出会出现较大的偏差,这种较大偏差,不可能在短时间内消除,经过积分项累积后,可能会使控制量uk很大,甚至超过执行机构的极限u max;另外,当负误差的绝对值较大时,也会出现u<u min的另一种极端情况;显然,当控制量超过执行机构极限时,控制作用必然不如应有的计算值理想,从而影响控制效果;这类现象在给定值突变时容易发生,而且在起动时特别明显,故也称“起动效应”;9.如何消除积分饱和现象答:减小积分饱和的关键在于不能使积分项累积过大;因此当偏差大于某个规定的门限值时,删除积分作用,PID控制器相当于一个PD调节器,既可以加快系统的响应又可以消除积分饱和现象,不致使系统产生过大的超调和振荡;只有当误差e在门限ε之内时,加入积分控制,相当于PID控制器,则可消除静差,提高控制精度;10.等效离散化设计方法存在哪些缺陷答:等效离散化设计方法存在以下缺陷:1 必须以采样周期足够小为前提;在许多实际系统中难以满足这一要求;2 没有反映采样点之间的性能;特别是当采样周期过大,除有可能造成控制系统不稳定外,还使系统长时间处于“开环”、失控状态;因此,系统的调节品质变坏;3 等效离散化设计所构造的计算机控制系统,其性能指标只能接近于原连续系统只有当采样周期T=0时,计算机控制系统才能完全等同于连续系统,而不可能超过它;因此,这种方法也被称为近似设计;计算题:1. 用后向差分法求下列模拟控制器的等效数字控制器,设采样周期T=1s;解:2. 用双线性变换法求下列模拟控制器的等效数字控制器,设采样周期T=;解:3.某连续控制系统的校正装置的传递函数为试分别用前向差分法和后向差分法求该装置的递推输出序列设输入为et,输出为ut ;解:前向差分后向差分4. 已知某连续控制器的传递函数为试用双线性变换法求出相应的数字控制器的脉冲传递函数Dz,其中T=1s;解:应用双线性变换211zsT z-=+5. 已知某连续控制器的传递函数为写出等效的递推型数字PID控制器的差分形式;解:应用后向差分法11z sT--=6. 已知某连续控制器的传递函数为现用数字PID算法实现它,试写出其相应的增量型PID算法输出表达式;设采样周期T=1s;解:应用后向差分法等效离散化11z sT--=四、知识点:计算机控制系统的直接设计方法;具体为掌握数字控制器的直接设计方法,包括最少拍无差有波纹、无波纹系统设计方法,大林方法;了解根轨迹设计法及频域设计法;回答题:1.给出常规的直接设计法或离散化设计法的具体设计步骤;答:直接设计法或称离散化设计法的具体设计步骤如下:1根据已知的被控对象,针对控制系统的性能指标要求及其它约束条件,确定理想的闭环脉冲传递函Φz;数()2确定数字控制器的脉冲传递函数Dz;根据Dz编制控制算法程序;2.什么是最少拍设计3.答:最少拍设计,是指系统在典型输入信号如阶跃信号,速度信号,加速度信号等作用下,经过最少拍有限拍,使系统输出的稳态误差为零;4.最少拍设计有什么不足之处答:最少拍控制器设计时,对于不同的输入,要求使用不同的闭环脉冲传递函数;所以这样设计出的控制器对各种典型输入信号的适应能力较差;若运行时的输入信号与设计时的输入信号形式不一致,将得不到期望的最佳性能;5.最少拍无纹波控制器实现的必要条件是什么6.答:最少拍无纹波控制能够实现的必要条件是被控对象中含有与输入信号相对应的积分环节数;7.大林算法的设计目标是什么答:大林算法的设计目标都是使闭环传递函数Φs相当于一个纯滞后环节和一个惯性环节的串联,其中纯滞后环节的滞后时间τ与被控对象的纯滞后时间完全相同;8.所谓振铃现象是什么答:所谓振铃Ringing现象,是指数字控制器的输出以二分之一采样频率大幅度衰减的振荡;9.振铃幅度如何定义答:振铃幅度RA用来衡量振铃强烈的程度;常用单位阶跃作用下数字控制器第0次输出量与第1次输出量的差值来衡量振铃现象强烈的程度;10.如何消除振铃现象答:有两种方法可用来消除振铃现象;第一种方法是先找出Dz中引起振铃现象的因子z=-1附近的极点,然后令其中的z=1,根据终值定理,这样处理不影响输出量的稳态值;第二种方法是从保证闭环系统的特性出发,选择合适的采样周期T及系统闭环时间常数T c,使得数字控制器的输出避免产生强烈的振铃现象;计算题:1. 已知广义被控对象:1e 1()(1)Ts G s s s s --=+, 给定T =1s ;针对单位斜坡输入设计最小拍有纹波控制系统;解:由已知条件,被控对象含有一个积分环节,有能力产生单位斜坡响应;求广义对象脉冲传递函数为可以看出,Gz 的零点为单位圆内、极点为1单位圆上、单位圆内,故u =0,v =0单位圆上除外,m =1;根据稳定性要求,Gz 中z =1的极点应包含在Φe z 的零点中,由于系统针对等速输入进行设计,故p =2;为满足准确性条件另有Φe z=1-z -12F 1z ,显然准确性条件中已满足了稳定性要求,于是可设解得 1,210-==c c ;闭环脉冲传递函数为则 1111e () 5.435(10.5)(10.368)()()()(1)(10.718)Φz z z D z Φz G z z z ------==-+ 2. 设不稳定对象112.2()1 1.2z G z z--=+,试对单位阶跃输入设计最少拍有纹波控制器; 解:由112.2()1 1.2z G z z--=+知,0, 1, m=1, 1u v p === 3. 给定对象1111210.265(1 2.78)(10.2)()(1)(10.286)z z z G z z z -----++=--,试对单位阶跃输入设计最少拍有纹波数字控制器;解:由题知,1, 0, m=1, 1u v p ===4. 已知广义被控对象:1e 1()1Ts G s s s --=+, 给定T =1s;针对单位阶跃输入设计最小拍无纹波控制系统;解:广义对象脉冲传递函数为可以看出,Gz 的零点为单位圆内、极点为1单位圆上、单位圆内,故w =0,v =0单位圆上除外, m =1;针对阶跃输入进行设计,故p =1;于是可设解得 01c =;闭环脉冲传递函数为则 11e ()10.368()()()0.632(1)Φz z D z Φz G z z ---==- 5. 设对象的传递函数 10()(1)=+G s s s ,采样周期T =1s,试对单位阶跃输入设计最少拍无纹波数字控制器;解:对所给对象求z 变换,可得 6. 已知广义被控对象为21e 1()e 1Ts s G s s s ---=+;其中,T =1s;期望的闭环脉冲传递函数中的时间常数取为T c =,应用史密斯预估器方法确定数字控制器;解:不含纯滞后的广义对象脉冲传递函数为广义对象脉冲传递函数为不考虑纯滞后,闭环系统理想脉冲传递函数为01()0.51Φs s =+,进而1011e 10.865()0.5110.135Ts z Φz s s z ---⎡⎤-==⎢⎥+-⎣⎦Z 求得100100()10.368() 1.369[1()]()1Φz z D z Φz G z z ---==-- 于是得史密斯预估器如下7. 某电阻炉,其传递函数可近似为带纯滞后的一阶惯性环节 用飞行曲线法测得电阻炉的有关参数为d d 1.16,τ30s,680s K T ===;若采用零阶保持器,取采样周期T =6s,要求闭环系统的时间常数为350T s τ=;用大林算法求取对电阻炉实现温度控制的数字控制器的算式;解:根据大林算法。
连续传递函数离散化的方法及原理

目录第一章模拟化设计根底1第一节步骤1第二节在MATLAB中离散化 3 第三节延时e-Ts环节的处理 5 第四节控制函数分类 6 第二章离散化算法10摘要10比拟11第一节冲击响应不变法(imp,无保持器直接z变换法) 11 第二节阶跃响应不变法(zoh,零阶保持器z变换法)11第三节斜坡响应不变法(foh,一阶保持器z变换法) 11 第四节后向差分近似法12 第五节前向差分近似法14 第六节双线性近似法(tustin) 15 第七节预畸双线性法(prevarp) 17 第八节零极点匹配法(matched)18第三章时域化算法19第一节直接算法1—双中间变量向后递推19 第二节直接算法2—双中间变量向前递推20第三节直接算法3—单中间变量向后递推21 第四节直接算法4—单中间变量向前递推(简约快速算法) 21 第五节串联算法22 第六节并联算法23 第四章数字PID控制算法24 第一节微分方程和差分方程25 第二节不完全微分25 第三节参数选择26 第四节c51框架27第五章保持器33第一节零阶保持器33第二节一阶保持器30附录两种一阶离散化方法的结果的比拟31第一章 模拟化设计根底数字控制系统的设计有两条道路,一是模拟化设计,一是直接数字设计。
如果已经有成熟的模拟控制器,可以节省很多时间和局部试验费用,只要将模拟控制器离散化即可投入应用。
如果模拟控制器还不存在,可以利用已有的模拟系统的设计经历,先设计出模拟控制器,再进展离散化。
将模拟控制器离散化,如果用手工进展,计算量比拟大。
借助数学软件MATLAB 控制工具箱,可以轻松地完成所需要的全部计算步骤。
如果需要的话,还可以使用MATLAB 的SIMULINK 工具箱,进展模拟仿真。
第一节 步骤步骤1 模拟控制器的处理在数字控制系统中,总是有传输特性为零阶保持器的数模转换器〔DAC 〕,因此,如果模拟控制器尚未设计,那么应以下列图的方式设计模拟控制器,即在对象前面加上一个零阶保持器,形成一个新对象Ts 1e G s s ()--,然后针对这个新对象求模拟控制器D(s)。
利用双线性变换求其离散传递函数

1 设计背景 (1)1.1 设计目的 (1)1.2 设计内容和要求 (1)1.3 设计工作任务及工作量的要求 (1)2 双线性变换及其原理 (2)2.1 双线性变换的定义 (2)2.2 双线性变换的原理 (2)2.2.1 公式的推导 (2)2.2.2 公式的验证 (2)2.2.2 设计步骤 (4)2.3 双线性变换的主要特性 (6)3 计算机实现程序框图 (7)4 理论计算 (8)5 程序验证 (10)6 结果分析 (11)参考文献 (13)附表程序清单 (14)1 设计背景1.1 设计目的本课程设计以自动控制理论、现代控制理论、MATLAB 及应用等知识为基础,利用双线性变换求连续系统对应的离散化的系统,目的是使学生在现有的控制理论的基础上,学会用MATLAB 语言编写控制系统的离散化的程序,通过上机实习加深对课堂所学知识的理解,掌握一种能方便地对系统进行离散化的设计工具。
1.2 设计内容和要求1 在理论上对连续系统采用双线性变换求离散化推导出算法和计算公式。
2 画出计算机实现算法的框图。
3 编写程序并调试和运行。
4 以下面的系统为例,进行计算。
已知系统闭环传递函数)2)(1(4)(++=s s s s G ,利用双线性变换求其离散传递函数。
5 分析运算结果(离散化步长对系统性能的影响)。
6 程序应具有一定的通用性,对不同参数能有兼容性。
1.3 设计工作任务及工作量的要求1 本次课程设计要求每周学生至少见指导教师4次,其中集中辅导答疑部不于3次。
2 设计说明书的格式按设计说明书格式要求,采用word 软件排版,计算机打印。
(具体包括:封皮、目录、正文、参考文献等)3 程序清单用A4纸打印后,作为附录订装在说明书后面。
4 框图和其他图表放在正文中。
2 双线性变换及其原理2.1 双线性变换的定义双线性变换法又称突斯汀(Tustin )法,是一种基于梯形积分规则的数字积分变换方法。
2.2 双线性变换的原理 2.2.1 公式的推导双线性替换公式(或称“突斯汀(Tustin )”公式),它可以从梯形积分公式中直接推导出来。
计算机控制系统作业参考答案
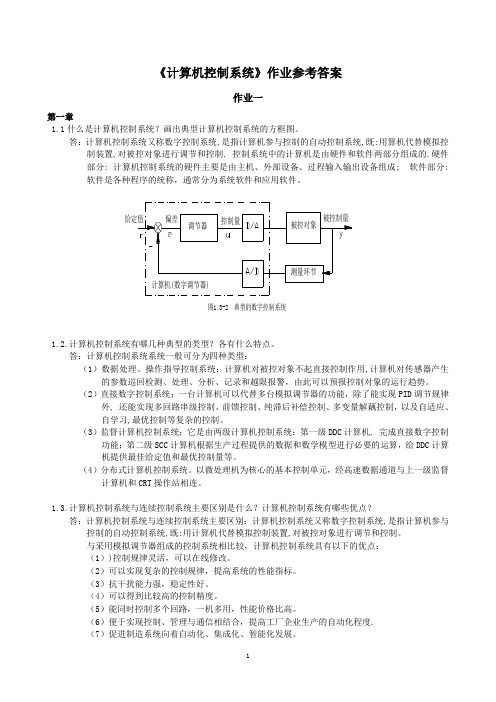
《计算机控制系统》作业参考答案作业一第一章1.1什么是计算机控制系统?画出典型计算机控制系统的方框图。
答:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用算机代替模拟控制装置,对被控对象进行调节和控制. 控制系统中的计算机是由硬件和软件两部分组成的.硬件部分: 计算机控制系统的硬件主要是由主机、外部设备、过程输入输出设备组成; 软件部分: 软件是各种程序的统称,通常分为系统软件和应用软件。
图1.3-2 典型的数字控制系统1.2.计算机控制系统有哪几种典型的类型?各有什么特点。
答:计算机控制系统系统一般可分为四种类型:(1)数据处理、操作指导控制系统;计算机对被控对象不起直接控制作用,计算机对传感器产生的参数巡回检测、处理、分析、记录和越限报警,由此可以预报控制对象的运行趋势。
(2)直接数字控制系统;一台计算机可以代替多台模拟调节器的功能,除了能实现PID调节规律外, 还能实现多回路串级控制、前馈控制、纯滞后补偿控制、多变量解藕控制,以及自适应、自学习,最优控制等复杂的控制。
(3)监督计算机控制系统;它是由两级计算机控制系统:第一级DDC计算机, 完成直接数字控制功能;第二级SCC计算机根据生产过程提供的数据和数学模型进行必要的运算,给DDC计算机提供最佳给定值和最优控制量等。
(4)分布式计算机控制系统。
以微处理机为核心的基本控制单元,经高速数据通道与上一级监督计算机和CRT操作站相连。
1.3.计算机控制系统与连续控制系统主要区别是什么?计算机控制系统有哪些优点?答:计算机控制系统与连续控制系统主要区别:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用计算机代替模拟控制装置,对被控对象进行调节和控制。
与采用模拟调节器组成的控制系统相比较,计算机控制系统具有以下的优点:(1))控制规律灵活,可以在线修改。
(2)可以实现复杂的控制规律,提高系统的性能指标。
第四章线性离散系统的数学描述与Z传递函数分析法

Z传递函数
G ( s ) ( s ) Ts 1 G HG ( z ) Z [( 1 e ) ] ( 1 z ) Z [ ] s s
HG(z)
u (kT )
1 e s
Ts
G (s)
Y (z) Y (s)
图4.2-3 带有零阶保持器的Z传递函数
a 例4.2-3 如上图所示,已知 G(s) ,求 HG(z) . s a a 1 1 1 1 【解】 HG ( z ) ( 1 z ) Z [ ] ( 1 z ) Z [ ] s ( s a ) ss a 1 1 1 ( 1 z )( ) 1 aT 1 1 z 1 e z 1 aT aT z e z1 1 e aT 1 aT 1 e z z e
5 带有零阶保持器的开环Z传递函数 零阶保持器可分解成两个单位阶跃函数之差,
h ( t ) u ( t ) u ( t T ) 0
Ts Ts 1 e 1 e H ( s ) 0 s s s
传递函数
G ( s ) HG ( s ) H ( s ) G ( s ) ( 1 e) 0 s
m 1
或留数法作Z反变换,可求出差分方程的解y(kT)。
例4.1-1 某二阶离散系统的差分方程为
y ( k ) 5 y ( k 1 ) 6 y ( k 2 ) y ( k ) ,输入为单位阶跃序列
0, k 0 r(k) , ,k 0 1
初始条件为0,求y(k).
或
y ( kT ) b r ( kT iT ) a y ( kT iT ) i i
i 0 i 1
m
数字信号处理期末试卷(含答案)

________ 次复乘法,运算效率为__
_。
6、FFT利用 来减少运算量。
7、数字信号处理的三种基本运算是: 。
8、FIR滤波器的单位取样响应
是圆周偶对称的,N=6,
,其幅度特性有什么特性? ,相位有何特 性? 。 9、数字滤波网络系统函数为
。
4、 已知
,
的反变换
。 3、
,变换区间
,则
。 4、
,
,
是
和
的8点循环卷积,则
。
5、用来计算N=16点DFT直接计算需要_
2FFT算法,需要
次复乘法
6、基2DIF-FFT 算法的特点是
7、有限脉冲响应系统的基本网络结构有
8、线性相位FIR滤波器的零点分布特点是
9、IIR系统的系统函数为
次复加法,采用基
转换为
时应使s平面的左半平面映射到z平面的
。
A.单位圆内 B.单位圆外 C.单位圆上 D.单位圆与实轴的交
点
6、 分析问答题(每题5分,共2题)
3、 某线性时不变因果稳定系统单位取样响应为
(长度为N),则该系统的频率特性、复频域特性、离散频率特性分 别怎样表示,三者之间是什么关系? 4、 用
对连续信号进行谱分析时,主要关心哪两个问题以及怎样解决二者的 矛盾?
十一、(7分)信号 包含一个原始信号 和两个回波信号: 求一个能从 恢复 的可实现的滤波器.
附录:
矩形窗(rectangular window) 汉宁窗(Hann window) 汉明窗(Hamming window) 布莱克曼窗(Blackman window)
表1 一些常用的窗函数
表2 一些常用窗函数的特性
PID控制器采用双线性变换法离散存在的问题分析

Science &Technology Vision科技视界0引言PID 控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依据经验和现场调试来确定,这时应用PID 控制技术最为方便。
即当我们不完全了解一个系统和被控对象﹐或不能通过有效的测量手段来获得系统参数时,最适合用PID 控制技术。
随着数字化的发展,对PID 控制器的各种离散方法的层出不穷,各种离散方法都有本身的优点和局限性,本文就其采用双线性变换法离散存在的问题进行分析,从而得出PID 控制器不能采用双线性变换法离散的原因所在。
1PID 控制器及双线性变换法具有比例、积分和微分控制规律的控制称为PID 控制器。
调节PID 的参数,可实现在系统稳定的前提下,兼顾系统的带载能力和抗扰能力,同时,在PID 控制器中引入积分项,系统增加了一个零极点,使之成为一阶或一阶以上的系统,这样系统阶跃响应的稳态误差就为零。
PID 控制器的传递函数为:G C (s )=K p 1+1T is +T d s ()(1)式中,K p 为比例系数;T i 为积分时间常数;T d 为微分时间常数。
双线性变换法也叫做梯形积分法,或称作突斯汀(Tustin)变换法。
用u (k )=u (k -1)+T 2[r (k )+r (k -1)]近似kT(k-1)∫r (t )d t ,也就是用梯形面积之和近似代替数值积分。
其离散公式为:D (z )=D (s )|s =2T z -1z +1(2)映射关系为:|z |2=1+T 2σ()2+ωT 2()21-T 2σ()2+ωT 2()2(3)其特点是:如果D (s )稳定,则相应的D (z )也稳定。
所得D (z )的频率响应在低频段与D (s )频率响应相近,而在高频段相对于D (s )的频率响应有严重畸变[1]。
利用双线性变换求其离散传递函数

1 设计背景 01.1 设计目的 ............................................................................................................................ 0 1.2 设计内容和要求 ................................................................................................................ 0 1.3 设计工作任务及工作量的要求 ........................................................................................ 1 2 双线性变换及其原理 . (1)2.1 双线性变换的定义 ............................................................................................................ 1 2.2 双线性变换的原理 (1)2.2.1 公式的推导 ............................................................................................................. 1 2.2.2 公式的验证 ............................................................................................................. 1 2.2.2 设计步骤 ................................................................................................................. 2 2.3 双线性变换的主要特性 .................................................................................................... 4 3 计算机实现程序框图 ................................................................................................................... 4 4 理论计算....................................................................................................................................... 5 5 程序验证....................................................................................................................................... 6 6 结果分析....................................................................................................................................... 7 参考文献........................................................................................................................................... 7 附表 程序清单 . (8)1 设计背景1.1 设计目的本课程设计以自动控制理论、现代控制理论、MATLAB 及应用等知识为基础,利用双线性变换求连续系统对应的离散化的系统,目的是使学生在现有的控制理论的基础上,学会用MATLAB 语言编写控制系统的离散化的程序,通过上机实习加深对课堂所学知识的理解,掌握一种能方便地对系统进行离散化的设计工具。
双线性变换法

—计算机控制系统—
显然,s平面的虚轴以左映射为z平面单位圆之内的一个小圆,如图 3-6所示。所以,稳定的D(s)对应的D(z)也必定稳定。
图3-6 后向差分法s平面稳定域 在z平面内的映象
—计算机控制系统—
图3-7 梯形规则数值积分
—计算机控制系统—
对式(3-15)两端求z变换,经整理,可得
D(z) C(z) 1 R(z) 2 z 1 T z 1
T
—计算机控制系统—
(3-8) (3-9) (3-10)
—计算机控制系统—
代入式(3-9)得
C(k) C(k 1) Tr(k)
对上式进行z变换,经整理为
D(z) C(z) Tz R(z) z 1
(3-11)
比较式(3-11)与式(3-8),得s和z的置换公式为
s z 1 Tz
(3-12)
推广而言,后向差分的离散化公式为
D(z)
D(s)
|s
z
1
Tz
因为
s z 1
Tz
则
z 1 1 1 Ts
2 2 1 Ts
当 s j 时,可得
z1 1 22
—计算机控制系统—
(3-13)
四、双线性变换法(Tustin变换法)
1、离散化公式
图3-7中曲线r(t)以下的积分面积
所以,采用前向差分法离散化,D(s)稳定,D(z)不一定稳定。
—计算机控制系统—
前向差分法的特点总结如下:
1、直接代换,具有串联性,变换 方便;
2、整个s左半平面映射到z平面z=1 以左的区域,故D(s)与D(z)不具有 相同的稳定性;
3 、 因 为 D(s)|s=0=D(z)|z=1 , 故 稳 态 增益维持不变;
控制系统各种传递函数离散化后的递推公式推导及结果

控制系统各种传递函数离散化后的递推公式推导及结果一、凹口网络传递函数:上式中参数::凹口网络中心频率,;:二阶微分环节阻尼系数;:二阶振荡环节阻尼系数;采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 二、PI调节器采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:*************************************************************** ********************** 三、滞后-超前调节器采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:*************************************************************** ********************** 四、PID 调节器(形式1)参数::一阶微分环节时间常数(第二转折频率);:一阶微分环节时间常数;:一阶惯性环节时间常数;K:PID调节器放大系数。
采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 五、PID 调节器(形式2)采用双线性变换公式对上式离散化:代入H(S)表达式得到:迭代公式:;;*************************************************************** ********************** 六、I型系统期望特性假设一系统的原始开环传递函数为:它的波特图如下图:现对其增加串联迟后校正(近似PI控制器)环节:它的波特图如下:校正后的系统开环传递函数为:1.I型系统期望特性I型系统特点:系统的正向通道(即主通道)包含1个纯积分环节。
《数字信号处理》实验报告

《数字信号处理》实验报告年级:2011级班级:信通4班姓名:朱明贵学号:111100443老师:李娟福州大学2013 年11 月实验一快速傅里叶变换(FFT)及其应用一、实验目的1.在理论学习的基础上,通过本实验,加深对FFT的理解,熟悉MATLAB中的有关函数。
2.熟悉应用FFT对典型信号进行频谱分析的方法。
3.了解应用FFT进行信号频谱分析过程中可能出现的问题,以便在实际中正确应用FFT。
4.熟悉应用FFT实现两个序列的线性卷积和相关的方法。
二、实验类型演示型三、实验仪器装有MATLAB语言的计算机四、实验原理在各种信号序列中,有限长序列信号处理占有很重要地位,对有限长序列,我们可以使用离散Fouier变换(DFT)。
这一变换不但可以很好的反映序列的频谱特性,而且易于用快速算法在计算机上实现,当序列x(n)的长度为N时,它的DFT定义为:反变换为:有限长序列的DFT是其Z变换在单位圆上的等距采样,或者说是序列Fourier变换的等距采样,因此可以用于序列的谱分析。
FFT并不是与DFT不同的另一种变换,而是为了减少DFT运算次数的一种快速算法。
它是对变换式进行一次次分解,使其成为若干小点数的组合,从而减少运算量。
常用的FFT 是以2为基数的,其长度。
它的效率高,程序简单,使用非常方便,当要变换的序列长度不等于2的整数次方时,为了使用以2为基数的FFT,可以用末位补零的方法,使其长度延长至2的整数次方。
(一)在运用DFT进行频谱分析的过程中可能的产生三种误差1.混叠序列的频谱是被采样信号频谱的周期延拓,当采样速率不满足Nyquist定理时,就会发生频谱混叠,使得采样后的信号序列频谱不能真实的反映原信号的频谱。
避免混叠现象的唯一方法是保证采样速率足够高,使频谱混叠现象不致出现,即在确定采样频率之前,必须对频谱的性质有所了解,在一般情况下,为了保证高于折叠频率的分量不会出现,在采样前,先用低通模拟滤波器对信号进行滤波。
控制系统仿真实验报告(20200717013819)

控制系统仿真实验报告班级:测控 1402 班姓名:王玮学号: 14050402072018 年 01 月实验一经典的连续系统仿真建模方法一实验目的 :1了解和掌握利用仿真技术对控制系统进行分析的原理和步骤。
2掌握机理分析建模方法。
3深入理解阶常微分方程组数值积分解法的原理和程序结构,学习用Matlab 编写数值积分法仿真程序。
4掌握和理解四阶 Runge-Kutta法,加深理解仿真步长与算法稳定性的关系。
二实验内容 :1.编写四阶 Runge_Kutta 公式的计算程序,对非线性模型(3)式进行仿真。
(1)将阀位u增大 10%和减小 10%,观察响应曲线的形状;(2)研究仿真步长对稳定性的影响,仿真步长取多大时RK4 算法变得不稳定?(3)利用 MATLAB 中的 ode45() 函数进行求解,比较与(1)中的仿真结果有何区别。
2.编写四阶 Runge_Kutta 公式的计算程序,对线性状态方程(18)式进行仿真(1)将阀位增大 10%和减小 10%,观察响应曲线的形状;(2)研究仿真步长对稳定性的影响,仿真步长取多大时RK4 算法变得不稳定?(4)阀位增大 10%和减小 10%,利用 MATLAB中的 ode45() 函数进行求解阶跃响应,比较与( 1)中的仿真结果有何区别。
三程序代码 :龙格库塔 :%RK4文件clccloseH=[1.2,1.4]';u=0.55; h=1;TT=[];XX=[];for i=1:h:200k1=f(H,u);k2=f(H+h*k1/2,u);k3=f(H+h*k2/2,u);k4=f(H+h*k3,u);H=H+h*(k1+2*k2+2*k3+k4)/6;TT=[TT i];XX=[XX H];end;hold onplot(TT,XX(1,:),'--',TT,XX(2,:));xlabel('time')ylabel('H')gtext('H1')gtext('H2')hold on水箱模型 :function dH=f(H,u)k=0.2;u=0.5;Qd=0.15;A=2;a1=0.20412;a2=0.21129;dH=zeros(2,1);dH(1)=1/A*(k*u+Qd-a1*sqrt(H(1)));dH(2)=1/A*(a1*sqrt(H(1))-a2*sqrt(H(2)));2 编写四阶Runge_Kutta公式的计算程序,对线性状态方程(18)式进行仿真:1阀值 u 对仿真结果的影响U=0.45;h=1;U=0.5;h=1;U=0.55;h=1;2 步长 h 对仿真结果的影响:U=0.5;h=5;U=0.5;h=20;U=0.5;h=39U=0.5;h=50由以上结果知 , 仿真步长越大 , 仿真结果越不稳定。
计算机控制实验报告-离散化方法研究解析

东南大学自动化学院实验报告课程名称:计算机控制技术第 2 次实验实验名称:实验三离散化方法研究院(系):自动化学院专业:自动化姓名:学号:实验室:416 实验组别:同组人员:实验时间:2014年4月10日评定成绩:审阅教师:一、实验目的1.学习并掌握数字控制器的设计方法(按模拟系统设计方法与按离散设计方法);2.熟悉将模拟控制器D(S)离散为数字控制器的原理与方法(按模拟系统设计方法);3.通过数模混合实验,对D(S)的多种离散化方法作比较研究,并对D(S)离散化前后闭环系统的性能进行比较,以加深对计算机控制系统的理解。
二、实验设备1.THBDC-1型控制理论·计算机控制技术实验平台2.PCI-1711数据采集卡一块3.PC机1台(安装软件“VC++”及“THJK_Server”)三、实验原理由于计算机的发展,计算机及其相应的信号变换装置(A/D和D/A)取代了常规的模拟控制。
在对原有的连续控制系统进行改造时,最方便的办法是将原来的模拟控制器离散化。
在介绍设计方法之前,首先应该分析计算机控制系统的特点。
图3-1为计算机控制系统的原理框图。
图3-1 计算机控制系统原理框图由图3-1可见,从虚线I向左看,数字计算机的作用是一个数字控制器,其输入量和输出量都是离散的数字量,所以,这一系统具有离散系统的特性,分析的工具是z变换。
由虚线II向右看,被控对象的输入和输出都是模拟量,所以该系统是连续变化的模拟系统,可以用拉氏变换进行分析。
通过上面的分析可知,计算机控制系统实际上是一个混合系统,既可以在一定条件下近似地把它看成模拟系统,用连续变化的模拟系统的分析工具进行动态分析和设计,再将设计结果转变成数字计算机的控制算法。
也可以把计算机控制系统经过适当变换,变成纯粹的离散系统,用z变化等工具进行分析设计,直接设计出控制算法。
按模拟系统设计方法进行设计的基本思想是,当采样系统的采样频率足够高时,采样系统的特性接近于连续变化的模拟系统,此时忽略采样开关和保持器,将整个系统看成是连续变化的模拟系统,用s域的方法设计校正装置D(s),再用s域到z域的离散化方法求得离散传递函数D(z)。
电子论文-温度传感器动态校准的研究

本文于2000年6月收到。
赵海宇:研究生;于惠忠:副教授。
温度传感器动态校准的研究赵海宇 于惠忠(清华大学工程物理系,北京100084)【摘要】本文综述了传感器动态校准的现状,包括它的概念、特点、数据处理方法等。
特别是针对温度传感器动态校准的方法进行了研究,给出了校准装置的选择和评定结果的一些方法。
关键词:温度传感器 动态校准 数据处理The R esearch of Dynamic C alibration of Therm al SensorsZhao Haiyu ,Y u Huizhong(Department of Engineering Physics Tsinghua University ,Beijing ,100084)Abstract :The research of thermal sens ors ,including its conception ,features and methods of data pro 2cessing ,is viewed in this paper.A type of sens ors ,a thermal sens or ,is discussed in details.The selection of dynamic testers and s ome methods of evaluating the results are given.K eyw ords :Thermal sens or ,dynamic calibration ,data processing.1 引 言随着科学技术的不断发展,非电量的测试与控制技术已经越来越广泛地应用,尤其是在航天、航海、冶金、能源、生物医学、交通运输、自动检测与计量和称重等技术领域。
而且随着社会的发展,这种技术也逐步渗透到人们的日常生活中。
可以毫不夸张地说,测试技术与自动控制技术水平的高低是衡量科学技术现代化程度的重要标志之一[1]。
【精品】计算机控制技术作业33

计算机控制技术作业1连续控制系统分析(第1---3章)一、填空题1.闭环负反馈控制的基本方法是。
2.自动控制系统通常是由被控对象和两大部分构成的。
而后者是由指令生成、综合比较、等六个部件构成的。
3.连续系统传递函数定义为在零初始条件下,输出量与输入量的。
传递函数只取决于,与输入信号特性无关。
4.系统传递函数的分布状况决定了系统的动态响应特性。
5.积分环节的输出量c(t)与输入量r(t)的成正比。
微分环节的输出量c(t)与输入量r(t)的成正比。
6.在一个闭环控制系统中,不同输入与输出量的传递函数相同,而是不同的。
7.连续系统稳定的充分必要条件是它的特征根应全部位于S平面的。
8.稳态误差定义为系统误差响应的,即e ss= 。
9.一个线性系统,若其输入信号为一定幅值及频率的正弦信号,则它的稳态输出是的正弦信号。
10.对数幅频特性L( )定义为L( )= 。
11.截止频率 c定义为L( c)= 时的频率。
12.通常,系统的相稳定裕度γM的大小反映了系统的,而截止频率 c 反映了系统的。
二、单项选择题1.图2.1所示的有源RC网络是一种环节。
A 积分;B 微分;C 惯性。
122.若以电机轴的转速为输入量,电机轴的转角为输出量,则它的传递函数为 环节 。
A 积分;B 微分;C 惯性。
3.图2.2是二阶系统的单位阶跃响应曲线,从该曲线的形状可知它的阻尼比ζ 。
A 1 >ζ> 0;B ζ> 1;C ζ= 0 。
4.图2.3是一阶惯性环节的单位阶跃响应曲线,从一阶惯性环节特性可知,曲线中H 等于 。
A 0.6;B 0.632;C 0.707。
5.某系统的零极点分布如图2.4所示,从中可知该系统是 的。
A 稳定;B 临界稳定;C 不稳定。
图2.1s/图2.236.某系统的传递函数为G(s) = 0.5(s-0.5) / (0.5s+1) ,可知该系统是 。
A 稳定的;B 临界稳定的;C 不稳定的。
东北大学离线作业计算机控制系统(B)答案

东北大学继续教育学院计算机控制系统试卷(作业考核线上) B 卷学习中心:广东博罗奥鹏学习中心[10]院校学号:C47520212090001 姓名古昆明(共 3 页)一、选择题(每题4分)1.二阶系统的超调量与___D__?A.固有频率无关,阻尼比无关B. 固有频率有关,阻尼比有关C. 固有频率有关,阻尼比无关D. 固有频率无关,阻尼比有关2.连续控制系统的不稳定性条件是S平面的__B____部分。
A.单位圆内B. 单位圆外C. 左半D.右半3.计算机控制系统是以___A__为核心部件的自动控制系统。
A.计算机B. 控制器C. 转换器D.保持器4.下列哪个不是计算机控制系统控制过程的步骤?DA.数据采集B. 数据转换C. 计算机控制量D.输出控制信号5.下列哪个不属于计算机控制系统的过程输入通道。
BA.温度B. 压力C. 流量D.继电器6. 单位阶跃输入下输出响应,经过__A__周期就稳定在设定值上。
A. TB.2T C 3T D.4T7.低通滤波器可以让高于_C____Hz虑掉。
A50 B. 60 C. 70 D.808.计算机控制系统稳定性条件是Z平面的__A____部分。
A单位圆内 B. 单位圆外C. 左半 D.右半9.连续控制系统的稳定性条件是S平面的__C____部分。
A单位圆内 B. 单位圆外C. 左半 D.右半10.下列属于共模干扰?BA电容的静电耦合 B. 长线传输的互感C.磁场耦合 D.变压器漏电二、判断题(每题2分)1. 输入输出通道时计算机控制系统的核心。
(错)2. 连续控制系统的传递函数分母式系统的特征多项式,代表系统的固有特性?(对)课程名称:计算机控制系统 1。
第二章 离散传递函数与Z

T T
Y(Z)
V(Z)
F(S)
Y ( z ) Z [ N (s)G2 (s)] V ( z )Z[G1 (s)G2 (s)] NG2 ( z ) V ( z )G1G2 ( z )
V ( z ) Z [V ( s )] Z [ N ( s )G2 ( s ) F ( s )] V ( z )[G1 (s )G2 (s ) F (s )] NG2 F ( z ) V ( z )G1G2 F ( z ) V ( z ) NG2 F ( z ) 1 G1G2 F ( z )
z 1 s 0 1 a1T 1 amT
(1 z 1eb1T )...(1 z 1ebmT ) K z lim H ( s) lim s 0 z 1 (1 z 1e a1T )...(1 z 1e amT )
4.冲激响应不变法
所谓冲激响应不变法是从连续系统的冲激 响应中进行采样而得到离散的冲激响应序 列,对该序列进行Z变换即可求得所对应 的离散传递函数H(z)。 步骤:
若y (k ) y (n)
sT
由台劳级数可得:
e
sT / 2
Ts 1 2
e
sT / 2
Ts 1 , 2
Ts 1 sT 2 ze Ts 1 2
解得:
2 1 z 1 2 z 1 s 1 T 1 z T z 1 H ( z ) H (s) 2 1 z 1 s 1 T 1 z
x(t0 ) e A(t ) Bu ( )d
t0
t
e 为转移矩阵
若采用零阶外推法: 即 kT t (k 1)T ,u(t ) u(kT ) 常数 假设初始时间 则 t0 kT ,t (k 1)T x(kT T ) e x(kT ) e Bu ( )d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计报告学生姓名:学号:学院:班级:题目: 专业方向课程设计仿真组-利用双线性变换求其离散传递函数指导教师:孟杰姜文娟职称: 副教授讲师2017年 1月 13日目录1.题目背景与意义 (1)2.设计题目介绍 (1)2.1 设计内容和要求 (1)2.2设计工作任务及工作量的要求 (1)3 双线性变换法 (1)3.1 双线性变换的定义 (1)3.2 双线性变换法的优缺点 (2)3.2.1 双线性变换法的优点 (2)3.2.2 双线性变换法的缺点 (2)3.2 双线性变换的原理 (2)3.3双线性变换的主要特性 (2)4 设计步骤 (3)5 理论计算 (5)6 结果分析 (6)参考文献 (10)附录1 程序清单 (11)附录2 计算机实现程序框图 (17)1.题目背景与意义本课程设计以自动控制理论、现代控制理论、MATLAB 及应用等知识为基础,利用双线性变换求连续系统对应的离散化的系统,目的是使学生在现有的控制理论的基础上,学会用MATLAB 语言编写控制系统的离散化的程序,通过上机实习加深对课堂所学知识的理解,掌握一种能方便地对系统进行离散化的设计工具。
2.设计题目介绍2.1 设计内容和要求1 在理论上对连续系统采用双线性变换求离散化推导出算法和计算公式2 画出计算机实现算法的框图3 编写程序并调试和运行4 以下面的系统为例,进行计算 已知系统闭环传递函数)2)(1(4)(++=s s s s G ,利用双线性变换求其离散传递函数。
5 分析运算结果(离散化步长对系统性能的影响)6 程序应具有一定的通用性,对不同参数能有兼容性。
2.2设计工作任务及工作量的要求1 本次课程设计要求每周学生至少见指导教师2次,其中集中辅导答疑部不于3次。
2 设计说明书的格式按设计说明书格式要求,采用word 软件排版,计算机打印。
(具体包括:封皮、目录、正文、参考文献等)3 程序清单用A4纸打印后,作为附录订装在说明书后面。
4 框图和其他图表放在正文中。
3 双线性变换法3.1 双线性变换的定义双线性变换法又称突斯汀(Tustin )法,是一种基于梯形积分规则的数字积分变换方法。
3.2 双线性变换法的优缺点3.2.1 双线性变换法的优点双线性变换的主要优点:靠频率的严重非线性关系得到S 平面与Z 平面的单值一一对应关系,整个j Ω轴单值对应于单位圆一周,其中ω和Ω为非线性关系。
在零频率附近,Ω~ω接近于线性关系,Ω进一步增加时,ω增长变得缓慢,(ω终止于折叠频率处),所以双线性变换不会出现由于高频部分超过折叠频率而混淆到低频部分去的现象。
3.2.2 双线性变换法的缺点双线性变换法的缺点:Ω与ω的非线性关系,导致数字滤波器的幅频响应相对于模拟滤波器的幅频响应有畸变,(使数字滤波器与模拟滤波器在响应与频率的对应关系上发生畸变)。
例如,一个模拟微分器,它的幅度与频率是线性关系,但通过双线性变换后,就不可能得到数字微分器。
3.2 双线性变换的原理双线性变换公式可以从梯形积分公式中直接推导出来。
按这种替换公式进行替换,可以保证)(z G 的稳定性,而且,具有一定的仿真精度。
已知梯形积分公式为:)(211++++=k k k k x x Tx x 即: xz Tx z )1(2)1+=-( 则有: 1121-+=-z z T s即: 112+-=z z T s (3.1)(3.1)式称为双线性变换公式,也可写成为:2121sTsT z -+=(3.2)3.3双线性变换的主要特性1、若)(s D 稳定,则)(z D 一定稳定;2、变换前后,稳态增益不变;3、双线性变换后的阶次不变,且分子、分母具有相同的阶次。
4 设计步骤双线性替换不仅可以精度极高的仿真模型,而且能利用计算机程序来实现这种替换。
下面来介绍一种程序替换法。
折线形系统的传递函数为nn n n nn n n b s b s b s b a s a s a s a s E s U s G ++++++++==----111011100......)()()( (4.1) 在双线性替换下得到的Z 传递函数为:;nn n n nn n n e z e z e z e d z d z d z d z E z U z G ++++++++==----111011100......)()()( (4.2) 现需要由i i b a ,(i=0,1,......,n )确定i i e d ,(i=0,1,......,n ),若直接将双线性替换公式代入)(0s G ,可得:nn n n n n nn n n n n b z z T b z z T b z z T b a z z T a z z T a z z T a z G ++-+++-++-++-+++-++-=------)11)(2(...)11()2()11()2()11)(2(...)11()2()11()2()(11110111100 (4.3) 将其分子、分母同时乘以nz )(1+,可得:)()()1(...)1()1(2)1(2)1(...)1()1(2)1(2)(111011100z B z A z b z z T b z T b z a z z T a z T a z G n n n n n n n n n n nn =++++-+-++++-+-=----)()()()( (4.4) 将)(z A ,)(z B 写成向量形式,()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--++⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=---n n nn n n nz z z z T TTT a a a a z A )1(...)1()1()1()2(0)2(...)2(0)2(...)(1110011由于nz )(1+,,......,nz )(1-均为n 阶多项式,可得到:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--+-++---1........................)1(...)1(1...)1(111101011110001001z z z x x x x x x x x x x x x z z z z z z n n nn n n in i i n n ii i n n n)()()( 矩阵ij x 为(n+1)×(n+1)阶;其中第一行诸元素为nz )(1+的展开式的各系数,第一列诸元素为1,阶次n 确定后,这些元素均为已知,并可以证明,其余n ×n个元素可由下式求得:1,11,,1,------=j i j i j i j i x x x x i,j=1,2,......,n从而可得:()[][]Tn nj i n n nz z z x T Tdiag a a a a z A 1...)2( (2)1...)(1,011--⎥⎦⎤⎢⎣⎡=这样就得到了)(0z G 分子分母的各系数的表达式:()()A H a a a a d d d n n n **=-01110......(4.5)其中:⎥⎦⎤⎢⎣⎡=n T T diag H )2( (2)1[]j i x A ,=5 理论计算)2)(1(4)(++=s s s s Gss s s G 234)(23++=(5.1)将112+-=z z T s 代入(5.1)式得上下同时乘以31)(+z将A(z),B(z)写成向量形式:由于,,2)1)(1(-+z z ,均为3阶多项式,可得到:这样就得到了G(z)的分子、分母的各系数的表达式:()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1331111111111331)2()2(210004323210T TTd d d d⎥⎦⎤⎢⎣⎡-+-+----++=32323232812424124241248124T T T T T T T T T T T T 采样周期取T=1时,()[]0832243210-=e e e e6 结果分析分析离散化步长对系统性能的影响:由于对于连续系统离散化的问题,采样周期和步长一样。
所以在这里仅分析T 对系统性能的影响。
以为例,分别,通过MATLAB 程序求其性能指标p t ,r t ,s t 和超调量pos 。
表7.1 不同的T 对系统性能的影响性能指标 s t r t posp t 连续系统 37.5515 1.7458 70.0161 2.9975 T=0.2 32.8000 2 69.9109 3.2000 T=0.5 39 2.5000 66.2127 3.5000 T=1 48 3 62.5573 4 T=5 255 10 29.7149 10 T=10 700 20 14.7137 40 T=1002001.55572600(a) 连续系统(b) T=0.2(c) T=0.5(e) T=5(g) T=100图7.1 连续系统及T 取不同值时单位阶跃响应曲线由以上结果可知,当T 的取值越大时,系统的性能指标,s t ,r t 都随之增大,超调量随之减小,超过某一值时,系统不在稳定;T 的取值越小,与原系统的性能指标越接近。
参考文献[1] 孙增晰.计算机辅助设计.北京:清华大学出版社,1995[2] 郑大钟.线性系统理论.北京:清华大学出版社,2004[3] 姚全珠.软件技术基础.北京:电子工业出版社,2006[4] 王小丹.基于MATLAB 的系统分析与设计.西安:西安电子科技大学出版社,2007附录1 程序清单1 利用双线性变换求其离散传递函数的计算机实现num=input('请输入分子多项式num=');den=input('请输入分母多项式den=');T=input('请输入步长T=');sys=tf(num,den)n=length(den)-1 %计算传递系统阶数for i=1:(n+1)/2d=num(i);num(i)=num(n-i+2);num(n-i+2)=d;e=den(i);den(i)=den(n-i+2);den(n-i+2)=e;end%颠倒原系统分子分母向量顺序disp(num)disp(den)a(1)=1;b=[1,1];c=[1,1];for j=2:n+1;a(j)=a(j-1)*(2/T);end%构造内部向量以1为首项2/T为倍数的等比序列H=diag(a) %显示对角矩阵%求出z+1的n次方的序列的系数矩阵for i=1:n-1;b=conv(b,c);endfor i=1:n+1;A(i,1)=1;endfor j=1:n+1;A(1,j)=b(j);endfor i=2:n+1;for j=2:n+1;A(i,j)=A(i-1,j)-A(i,j-1)-A(i-1,j-1);endenddisp(A) %显示矩阵Adnum=num*H*A %得到离散后的分子系数矩阵dden=den*H*A %得到离散后的分母系数矩阵sys=tf(dnum,dden,T)运行程序,显示如下:> tustin请输入分子多项式num=[0 0 0 4]请输入分母多项式den=[1 3 2 0]请输入步长T=[1]sys =4-----------------s^3 + 3 s^2 + 2 sContinuous-time transfer function.n =34 0 0 00 2 3 1H =1 0 0 00 2 0 00 0 4 00 0 0 81 3 3 11 1 -1 -11 -1 -1 11 -3 3 -1 dnum =4 12 12 4 dden =24 -32 8 0 sys =4 z^3 + 12 z^2 + 12 z + 4-------------------------24 z^3 - 32 z^2 + 8 zSample time: 1 seconds Discrete-time transfer function.2 分析离散化步长对系统性能的影响的计算机实现num=input('请输入分子多项式num=');den=input('请输入分母多项式den=');G0=tf(num,den);[bnum,bden]=cloop(num,den,-1); %计算闭环系统的分子分母多项式sys=tf(bnum,bden);figure(1) %在图1上画图step(sys,150) %画时间为150s的单位阶跃响应曲线[y,t]=step(sys,150); %求出150s内系统的y值和t值[mp,f]=max(y); %求y的最大值及其所在位置tp=t(f) %求峰值时间l=length(t); %计算t的长度ys=y(l);pos=100*(mp-ys)/ys %求超调量posfor i=1:lif y(i)>=1tr=t(i)breakendend%求上升时间trfor j=l:-1:1if y(j)<=0.98*ys,y(j)>=1.02*ysts=t(j)breakendend%求调节时间tsn=length(den)-1;for i=1:(n+1)/2d=num(i);num(i)=num(n-i+2);num(n-i+2)=d;e=den(i);den(i)=den(n-i+2);den(n-i+2)=e;endTs=[0.2,0.5,1,5,10,100]; %T分别取0.2,0.5,1,5,10 ,100for w=1:length(Ts) %T在取不同值是分别执行下面的求值过程T=Ts(w)a(1)=1;b=[1,1];c=[1,1];for j=2:n+1;a(j)=a(j-1)*(2/T);end%构造内部向量以1为首项2/T为倍数的等比序列H=diag(a) %显示对角矩阵for i=1:n-1;b=conv(b,c);endfor j=1:n+1;A(j,1)=1;endfor i=1:n+1;A(1,i)=b(i);endfor j=2:n+1;for i=2:n+1;A(j,i)=A(j-1,i)-A(j,i-1)-A(j-1,i-1);endenddisp(A) %显示矩阵Adnum=num*H*A %得到离散后的分子系数矩阵dden=den*H*A %得到离散后的分母系数矩阵sys=tf(dnum,dden,T)[dbnum,dbden]=cloop(dnum,dden,-1);figure(2)dstep(dbnum,dbden,150);[y,t]=dstep(dbnum,dbden);[mp,f]=max(y); %求y的最大值及其所在位置tp=f*T %求峰值时间l=length(y); %计算t的长度ys=y(l);pos=100*(mp-ys)/ys %求超调量posfor i=1:lif y(i)>=1tr=i*T %求上升时间break;endendfor i=l:-1:1if y(i)<=0.98*ys,y(i)>=1.02*ys;ts=i*T %求调节时间breakendendend附录2 计算机实现程序框图。
