英汉双语材料力学8PPT课件
英汉双语材料力学12

4
§12–1 SUMMARY OF STATICALLY INDETERMINATE
STRUCTURES Structures that the whole constraint reactions and the internal forces in such structures can not be determined only by the static equilibrium equations are all called statically indeterminate structures or systems. In the statically indeterminate structure the constraints in excess of the number needed to support the structure in a statically determinate manner are called static
11P 16
P
A
X 1l 3 5Pl3 0 3EI 48EI
5 X 1 P 16
(f)
3Pl 16
C
5P 16 5Pl 32
B
⑤Determine other constraint reactions. The reactions at the end A may be found out by the static equilibrium equations. Their magnitudes and directions are shown in Fig.(f).
P
A
X 1l 3 5Pl3 0 3EI 48EI
⑤求其它约束反力
5 X 1 P 16
(完整版)材料力学中英对照词汇

(完整版)材料力学中英对照词汇材料力学中英对照词汇A安全因数safety factorB半桥接法half bridge闭口薄壁杆thin-walled tubes比例极限proportional limit边界条件boundary conditions变截面梁beam of variable cross section 变形deformation 变形协调方程compatibility equation 标距gage length泊松比Poisson’s ratio补偿块compensating blockC材料力学mechanics of materials冲击荷载impact load初应力,预应力initial stress纯剪切pure shear纯弯曲pure bending脆性材料brittle materialsD大柔度杆long columns单位荷载unit load单位力偶unit couple单位荷载法unit-load method单向应力,单向受力uniaxial stress等强度梁beam of constant strength低周疲劳low-cycle fatigue电桥平衡bridge balancing电阻应变计resistance strain gage电阻应变仪resistance strain indicator 叠加法superposition method叠加原理superposition principle 动荷载dynamic load断面收缩率percentage reduction in area多余约束redundant restraintE二向应力状态state of biaxial stressF分布力distributed force复杂应力状态state of triaxial stress复合材料composite materialG杆,杆件bar刚度stiffness刚架,构架frame刚结点rigid joint高周疲劳high-cycle fatigue各向同性材料isotropical material功的互等定理reciprocal-work theorem工作应变计active strain gage工作应力working stress构件structural member惯性半径radius of gyration of an area惯性积product of inertia惯性矩,截面二次轴距moment of inertia广义胡克定律generalized Hook’s lawH横向变形lateral deformation胡克定律Hook’s law滑移线slip-linesJ基本系统primary system畸变能理论distortion energy theory畸变能密度distortional strain energy density极惯性矩,截面二次极矩polar moment of inertia极限应力ultimate stress极限荷载limit load挤压应力bearing stress剪力shear force剪力方程equation of shear force剪力图shear force diagram剪流shear flow剪切胡克定律Hook’s law for shear剪切shear交变应力,循环应力cyclic stress截面法method of sections截面几何性质geometrical properties of an area截面核心core of section静不定次,超静定次数degree of a statically indeterminate problem静不定问题,超静定问题statically indeterminate problem静定问题statically determinate problem 静荷载static load静矩,一次矩static moment颈缩neckingK开口薄壁杆bar of thin-walled open cross section抗拉强度ultimate stress in tension抗扭截面系数section modulus in torsion 抗扭强度ultimate stress in torsion抗弯截面系数section modulus in bendingL拉压刚度axial rigidity拉压杆,轴向承载杆axially loaded bar理想弹塑性假设elastic-perfectly plastic assumption力法force method力学性能mechanical properties连续梁continuous beam连续条件continuity condition梁beams临界应力critical stress临界荷载critical loadM迈因纳定律Miner’s law名义屈服强度offset yielding stress莫尔强度理论Mohr theory of failure敏感栅sensitive gridN挠度deflection挠曲轴deflection curve挠曲轴方程equation of deflection curve 挠曲轴近似微分方程approximately differential equation of the deflectioncurve内力internal forces扭力矩twisting moment扭矩torsional moment扭矩图torque diagram扭转torsion扭转极限应力ultimate stress in torsion 扭转角angel of twist扭转屈服强度yielding stress in torsion 扭转刚度torsional rigidityO欧拉公式Euler’s formulaP疲劳极限,条件疲劳极限endurance limit疲劳破坏fatigue rupture疲劳寿命fatigue life偏心拉伸eccentric tension偏心压缩eccentric compression平均应力average stress平面弯曲plane bending平面应力状态state of plane stress平行移轴定理parallel axis theorem平面假设plane cross-section assumptionQ强度strength强度理论theory of strength强度条件strength condition切变模量shear modulus切应变shear strain切应力shear stress切应力互等定理theorem of conjugate shearing stress 屈服yield屈服强度yield strength全桥接线法full bridgeR热应力thermal stressS三向应力状态state of triaxial stress三轴直角应变花three-element rectangular rosette三轴等角应变花three-element delta rosette失稳buckling伸长率elongation圣维南原理Saint-Venant’s principle实验应力分析experimental stress analysis塑性变形,残余变形plastic deformationductile materials塑性材料,延性材料塑性铰plastic hingeT弹簧常量spring constant弹性变形elastic deformation弹性模量modulus of elasticity体积力body force体积改变能密度density of energy ofvolume change体应变volume strainW弯矩bending moment弯矩方程equation of bending moment弯矩图bending moment diagram弯曲bending弯曲刚度flexural rigidity弯曲正应力normal stress in bending 弯曲切应力shear stress in bending弯曲中心shear center位移法displacement method位移互等定理reciprocal-displacement theorem稳定条件stability condition稳定性stability稳定安全因数safety factor for stability X细长比,柔度slenderness ratio线性弹性体linear elastic body约束扭转constraint torsion相当长度,有效长度equivalent length 相当应力equivalent stress小柔度杆short columns形心轴centroidal axis形状系数shape factor许用应力allowable stress许用应力法allowable stress method 许用荷载allowable load许用荷载法allowable load methodY应变花strain rosette应变计strain gage应变能strain energy应变能密度strain energy density应力stress应力速率stress ratio应力比stress ratio应力幅stress amplitude应力状态state of stress应力集中stress concentration应力集中因数stress concentration factor 应力-寿命曲线,S-N曲线stress-cycle curve应力-应变图stress-strain diagram应力圆,莫尔圆Mohr’s circle for stresses Z正应变normal strain正应力normal stress中面middle plane中柔度杆intermediate columns中性层neutral surface中性轴neutral axis轴shaft轴力axial force轴力图axial force diagram轴向变形axial deformation轴向拉伸axial tension轴向压缩axial compression主平面principal planes主应力principal stress主应力迹线principal stress trajectory主轴principal axis主惯性矩principal moment of inertia主形心惯性矩principal centroidalmoments of inertia主形心轴principal centroidal axis转角angel of rotation转轴公式transformation equation自由扭转free torsion组合变形combined deformation组合截面composite area最大切应力理论maximum shear stress theory最大拉应变理论maximum tensile strain theory最大拉应力理论maximum tensile stress theory最大应力maximum stress最小应力minimum stress。
材料力学(英汉对照)06_Bending_Deformation
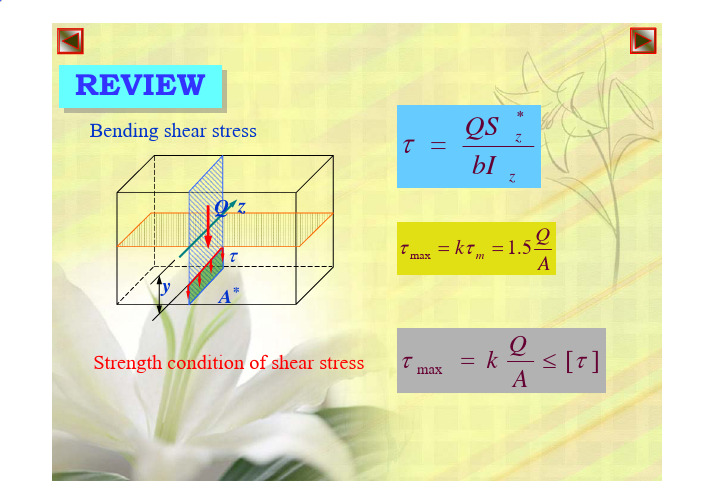
REVIEW REVIEWBending shear stressQS τ = bI* z zQ zτy A*τ max = kτ m = 1.5Q AStrength condition of shear stressτ maxQ = k ≤ [τ ] APart one: Basic DeformationsChapter 6. Bending DeformationContaining Sections: Containing Sections:6.1 Introduction 6.1 Introduction 6.2 Equation of Elastic Curve 6.2 Equation of Elastic Curve 6.3 Direct Integration Method 6.3 Direct Integration Method 6.4 Method of Superposition 6.4 Method of Superposition 6.5* Moment-Area Method 6.5* Moment-Area Method 6.6 Stiffness Condition of Beams and Ways to Improve the Stiffness of 6.6 Stiffness Condition of Beams and Ways to Improve the Stiffness of Beams Beams 6.7 Statically Indeterminate Beams 6.7 Statically Indeterminate BeamsChapter 6. Bending Deformation6.1 IntroductionTensional deformation Torsional deformationNL ∆l = EAM nL ϕ= GI pϕxBending deformationdx vDeflection Deflection 截面形心的竖向位移 挠度 vv 挠度θElastic CurveSlope Slope 转角 θ 转角 θ截面绕中性轴的转角Chapter 6. Bending Deformation6.2 Equation of Elastic CurveWhen deduce the bending normal stress formula, we get : Consider the small deformation : From mathematical relation :1 M (x) = ρ (x) EI z1 ρ (x)Curvature 曲率 Flexural rigidity 抗弯刚度EI zdv θ ≈ tan θ = = v' ( x) dx1ρ=v" ≈ v" 2 3 2 (1 + v ′ )Deduce further, we can get the approximate differential equation of elastic curve (挠曲线近似微分方程):M (x) v ′′ ( x ) = θ ′ = E IZ公式的适用条件: 1) 材料服从虎克定律; 2) 小变形,忽略剪力对挠度的影响。
材料力学(英汉对照)01_Introduction

Sorted by characters: Sorted by characters: Static force(静载荷)):载荷由零缓慢增加,到达某值后保持不变 Static force(静载荷 :载荷由零缓慢增加,到达某值后保持不变 Dynamic force(动载荷)):引起构件加速度的突加载荷或冲击载荷 Dynamic force(动载荷 :引起构件加速度的突加载荷或冲击载荷 Alternating force(交变载荷)):随时间作周期变化的载荷 Alternating force(交变载荷 :随时间作周期变化的载荷
1.1 Task of Mechanics of Materials 1.1 Task of Mechanics of Materials 1.2* Relation between Mechanics of Materials and Practices 1.2* Relation between Mechanics of Materials and Practices 1.3 Basic Hypothesis of Deformable Body 1.3 Basic Hypothesis of Deformable Body 1.4 Internal Force and Stress 1.4 Internal Force and Stress 1.5 Displacement, Deformation and Strain 1.5 Displacement, Deformation and Strain 1.6 Basic Deformation modes of Bar Member 1.6 Basic Deformation modes of Bar Member
chapterintroductionnewworesnewworesmechanicsmaterials材料力学strength强度stiffness刚度stability稳定性deformablebody变形体externalforce外力internalforce内力surfaceforce表面力bodyforce体力concentratedforce集中力supportreaction支反力resultantforcemoment合力合力矩equationequilibrium平衡方程freebodydiagram分离体图methodsection截面法mechanicsmaterials材料力学strength强度stiffness刚度stability稳定性deformablebody变形体externalforce外力internalforce内力surfaceforce表面力bodyforce体力concentratedforce集中力supportreaction支反力resultantforcemoment合力合力矩equationequilibrium平衡方程freebodydiagram分离体图methodsection截面法normalstressshearstressnormalstrainshearstrainvolumeelementelasticdeformationplasticdeformationhookesmoduluselasticityshearmoduluselasticitydisplacementcrosssectionareaisotropyuniformitycontinuitybasichypothesis正应力切应力剪应力线应变切应变剪应变单元体弹性变形塑性变形law虎克定律弹性模量切变模量位移横截面面积各向同性均匀连续基本假设normalstressshearstressnormalstrainshearstrainvolumeelementelasticdeformationplasticdeformationhookesmoduluselasticityshearmoduluselasticitydisplacementcrosssectionareaisotropyuniformitycontinuitybasichypothesis正应力切应力
材料力学简介(英文)课件

陈继乐
1
1. The research object of Mechanics of Materials 2. The task of Mechanics of Materials and its relation
5
3.The properties and the fundmental assumptions of the solid deformable bodies
1.Continuity:The material of a solid deformable body is continuously distributed over its volume so that there are not any cracks, defects or holes etc . 2.Homogeneity:The material of the solid deformable body is homogeneously distributed over its volume. 3.Isotropy:The mechanical properties are the same in all directions at a point.
• Strength , Rigidity, Stability Strength: Capacity to resist failure of a component or an element. Rigidity: Capacity to resist deformations of a component or an element. Stability: Capacity to remain the original state in equilibrium of a
英汉双语材料力学9

z
x
Pz
z
j
Pz
Py
Py P
y P
y
Solution:1.Resolve the external force along the centroid principal axis of inertia of the cross section
Py Psinj
Pz Pcosj
2.Study the bending in two planes : ①Internal forces
Lmax
D1
M zmax Wz
M ymax Wy
D2
f
f
2 y
f
2 z
( Py L3 )2 ( Pz L3 )2
3EI z
3EI y
As
pIyla=nIazr
the beam bending.
produce
tg f y I y tgj
fz Iz
23
[例1]结构如图,P过形心且与z轴成j角,求此梁的最大应力与挠
deflection of it is respectively []=12MPa and L/200 ,E=9GPa,Try to
determine the dimension of the section and check the rigidity of the beam.
Solution:①Analysis of external force—
②Analysis of internal forces:Determine the internal-force equation and its diagram corresponding to each external force component and the critical section.
材料力学简介英文 ppt课件

3.The properties and the fundmental assumptions of the solid deformable bodies
1.Continuity:The material of a solid deformable body is continuously distributed over its volume so that there are not any cracks, defects or holes etc . 2.Homogeneity:The material of the solid deformable body is homogeneously distributed over its volume. 3.Isotropy:The mechanical properties are the same in all directions at a point.
1.Axial tension
2.Shear
3.Torsion
4.Bending
Thank You!
component or an element.
The tasks of mechanics of materials
Under the request that the strength, rigidity, stability are satisfied, offer the necessary theoretical foundation and calculation method for determining reasonable shapes and dimensions, choosing proper materials for the components at the most economic price.
材料力学(双语)压杆稳定

y(0) = y′(0) = 0; y( L) = y′( L) = 0
M0 A = 0, B = − , kL = 2nπ P
∴ kL = 2nπ
and
kL = nπ
In order to determine the minimum critical pressure“k”must be the minimum value except zero, that is:
π 2 EI min Pcr = ( μL ) 2
General form of Euler’s formula of the critical pressure
μ—Leng1 Euler’s formula of the slender compressive column under various constraint conditions
6
10.2 Euler Formula of Critical Load
1. Critical pressure for the column with two hinged ends
Suppose the pressure has reached the critical value and the column has been in tiny bending state as shown in the figure. Start to determine the critical force with the deflective curve.
P cr =
π 2 EI
l
2
P P cr ≈ cr ≈ cr ≈ 2 P 2 (0.5l) (0.7l) (2l)2
π 2 EI
π 2 EI
英汉双语材料力学13

一、动载荷:
§13-1 基本概念
载荷不随时间变化(或变化极其平稳缓慢)且使构件各部件
加速度保持为零(或可忽略不计),此类载荷为静载荷。
载荷随时间急剧变化且使构件的速度有显著变化(系统产生
惯性力),此类载荷为动载荷。
二、动响应:
构件在动载荷作用下产生的各种响应(如应力、应变、位
移等),称为动响应。
实验表明:在静载荷下服从虎克定律的材料,只要应力不
1、Dynamic stress of the body in the straight-line motion
Example 1 The effective area of the steel wire rope in a crane is A, [? ] is
known . Weight per unit volume of the body is ? and the body moves up at the acceleration a. Try to check the strength of the rope(neglect the weight of the
areaof the rotating arm(neglecting the weight of the rotating arm).
GG
Solution:①The free body diagram is
shown inertia force is
O
GG ? man ? ? 2Rm ? ? 2LG / g
?
d
?
Nd A
?
1 (G? A
qL)(1?
a g
)
?
1 2.9?10
?
4
(50?103
英汉双语材料力学2

bolt
Characteristic:It can
P P
pass general loads and can be dismounted.
§2-1 连接件的剪切与挤压强度计算
一、连接件的受力特点和变形特点:
沿铆钉的剪切面剪断,如
沿n– n面剪断 。 ②挤压破坏 铆钉与钢板在相互接触面 上因挤压而使溃压连接松动,
Q n
P
发生破坏。
③拉伸破坏
钢板在受铆钉孔削弱的截面处,应力增大,易在连接处拉断。
2、Practical calculation of shear
Method of the practical calculation:According to possibility of breakage of the member some assumptions by which basic characteristic subjected to force actions can be reflected and calculations can be simplified are used. Then calculate its nominal stress, determine the corresponding permissible stress in accordance with the result of direct test. At last do the strength calculation. Applying range:volume of the member is not large and real stress is quite
英汉双语材料力学11

L EA
L
GI P
M (x)M0(x)dx L EI
f A
M
L
(x)M0 (x)dx EI
二、普遍形式的莫尔定理
莫尔定理(单位力法)
A
N ( x)N0( x) dx M n ( x)M n0( x) dx
L EA
L
GI P
M (x)M0(x)dx L EI
3、What we must pay attention to as we apply Mohr’s theorem: ① M(x):The internal force of the structure acted by original loads.
Example 3 Determine the displacement and the angle of rotation of point C by
the energy method .
q A
x
C
a
a
BA
P0 =1
B
C
a
a
Solution:①Plot the diagram of the structure acted by the unit load
a
U 2
1
( P x)2 dx P2a3
0 2EI 2
12 EI
W
U
fC
Pa 3 6EI
思考:分布荷载时,可否用此法求C点位移? q
§11–2 MOHR’S THEOREM(METHOD OF UNIT FORCE)
q(x) A
1、Provement of the theorem:
Fig a
fA P0=1
Mechanics of Materials
英汉双语材料力学15 ppt课件

5. Explore the new rule from tests and check the theory of stress analysis and the
2020/11/29
5
calculation method.
§15–1 概 述
一、实验应力分析方法的作用: 1.设计时,测定模型的应力或变形,依此来确定构件的合理尺 寸和结构形式。 2.工作中,测定构件的真实应力或变形,找出最大应力的位置 和数值,以评价工程结构的安全可靠性,并为提高设备的 工作能力提供依据。
3.对破坏或失效构件进行分析,提出改进措施,防止再次破坏。
4.测定外载的大小、方向以及各种动响应。
5.从试验中探索新的规律,并对应力分析理论和计算方法进行
202校0/11核/29 。
6
二、Brief introduction of methods in the stress analysis of experiments
tensile
Fig.14 Sketch of the tensile test
2020/11/29
of Galileo
Fig.15 Sketch of the bending test of Galileo
11
伽利略 (1564—1642)
2020/11/29
12
Mushenbluic (1692—1761)
Fig.37 Tensile-test machine of Mushenbluic
2020/11/29
Fig.38 Method to clamp two ends of a tensile specimen
13
穆申布洛依克 (1692—1761)
英汉双语材料力学15

穆申布洛依克 (1692—1761)
Hydraulic verstile testing machine controlled by the computer
2. Other methods:
Since the early 20th century,the developments of electricity,optics acousics and materials science have provided conditions for the productionof other measurement methods of the stress analysis in experiments.Then the resistancestrain method,ordinary photoelasticity method,hologram photoelasticity method,sound launching method and so on are made fast developments and wide applications.
3.对破坏或失效构件进行分析,提出改进措施,防止再次破坏。 4.测定外载的大小、方向以及各种动响应。 5.从试验中探索新的规律,并对应力分析理论和计算方法进行
校核。
二、Brief introduction of methods in the stress analysis of experiments
2.其它方法:
20世纪初至今,电学、光学、声学和材料科学的发展, 为试验应力分析其它测量方法的产生创造了条件。于是,电 阻应变法、普通光弹法、全息光弹法、散斑法、声发射法等 方法都有了快速发展和广泛应用。
§15–2 Principle and application of the strainometer of the resistance
材料力学(英文版)Chap1
1-9
M. Vable
Mechanics of Materials: Chapter 1
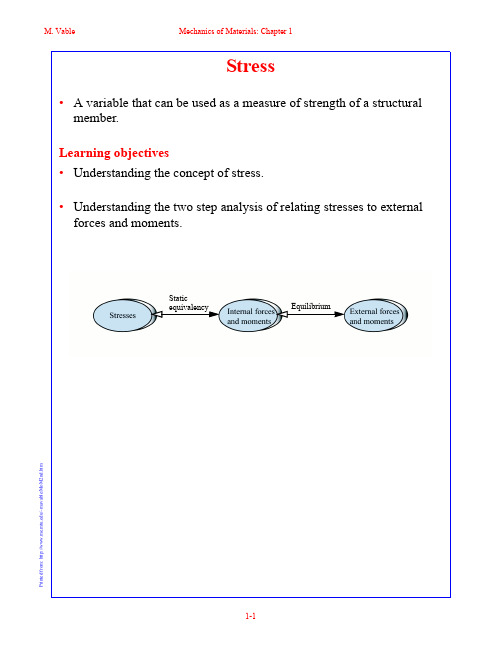
C1.5 An adhesively bonded joint in wood is fabricated as shown in Fig. C1.5. The joint is to support a force P = 25 kips, what should be the length L of the bonded region if the adhesive strength in shear is 300 psi.
C1.4. (b)Determine the maximum shear stress in pin H.
G
H
F
300
300
A
B
C
D
E
3m
3m
3m
3m
4 kN 2 kN 3 kN Fig. C1.4
HC HG HB HA
Pin H
Printed from: /~mavable/MoM2nd.htm
• The normal stress acting in the direction of the axis of a slender member (rods, cables, bars, columns, etc.) is called the axial stress.
• The compressive normal stress that is produced when one surface presses against other is called the bearing stress.
M. Vable
Mechanics of Materials: Chapter 1
材料力学(英汉对照)08_Strength_Theories
(σ
1
−
σ
3 )2 ]
σ3
σ2 σ1 Strength
σr
σr
theory
σ r ≤ [σ ]
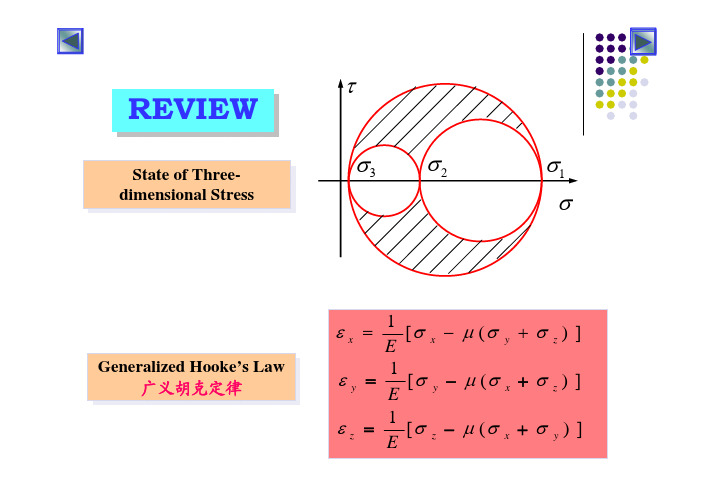
Chapter 8. Strength Theories
8.4 Application of Strength Theories
Select of strength theories 强度理论的选用
(1)Effect of material properties
≤ [τ ] = τ 0
n
σ0
=
⎧σ
⎨ ⎩
σ
s b
Determined by one tension experiment
τ0
=
⎧τ
⎨ ⎩
τ
s b
Determined by one torsion experiment
Strength condition of tension + torsion
τ
σ2
ε1 = εb
σ 1 − µ (σ 2 + σ 3 ) = σ b
● 强度条件:
∵
σ1
ε
−
1
=
1 E
µ (σ 2
[σ
+
1
σ
− µ (σ 2
3)
≤
σb
n
+ σ 3 ), = [σ ]
ε
b
=
σb
E
● 第二强度理论由Mariotte在十七世纪后期提出,可以很好地解释脆性 材料受压时沿纵向截面开裂的现象。
Chapter 8. Strength Theories
Chapter 8. Strength Theories
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 强度理论
§8–1 强度理论的概念 §8–2 四个强度理论及其相当应力 §8–3 莫尔强度理论及其相当应力 §8-4 强度理论的应用
4
§8–1 CONCEPTS OF STRENGTH THEORIES
1、Opening words:
1)、Investigation of the tensile, compressive and torsional tests of cast iron and low-carbon steel
§8–2 四个强度理论及其相当应力 一、最大拉应力(第一强度)理论:
认为构件的断裂是由最大拉应力引起的。当最大拉应力达到 单向拉伸的强度极限时,构件就断了。
1、破坏判据: 1b ;(10)
2、强度准则:1 ;(1 0)
3、实用范围:实用于破坏形式为脆断的构件。
10
2、Theory of the maximum tensile strain(the second strength):
1、铸铁与低碳钢的拉、压、扭试验现象是怎样产生的?
P 铸铁拉伸
铸铁压缩
M
P
低碳钢
铸铁
P
2、组合变形杆将怎样破坏?
P
M
6
2、Theories of strength:Some assumptions about the cause of the strength failure of materials . 3、Types of failure of materials:⑴ yield; ⑵ rupture 1)、Galileo planted the seed of the first strength theory; 2)、Mariotto’s statement about the rupture of material due to
P Tension of
cast iron
M
Compression of cast iron
P
Lowcarbon steel
Cast iron
P
2)、How will the member rupture in Combined deformations?
P
M
5
§8–1 强度理论的概念 一、引子:
7
二、强度理论:是关于“构件发生强度失效(failure by lost strength)起因”的假说。
三、材料的破坏形式:⑴ 屈服; ⑵ 断裂 。 1、伽利略播下了第一强度理论的种子; 2、马里奥特关于变形过大引起破坏的论述,是第二强度理论的 萌芽; 3、杜奎特(C.Duguet)提出了最大剪应力理论;
This theory considers the main cause of rupture to be the maximum tensile stress. The member will rupture as the maximum tensile stress reaches the strength limit in axial tension.
excessive deformation is the flush of the second strength theory; 3)、C.Duguet proposed the theory of the maximum shearing stress;
4)、Maxwell brought forward the theory of the maximum distortional energy theory early, which was known after his letters were published.
1)、Criterion of rupture: 1b ;(10)
2)、strength condition:
1 ;(1 0)
3)、Application range:May be applied to the members with the failure form of brittle rupture.
tension
1b ;(10)
1E 1123 E b
1)、Criterion of failure:ition: 1 2 3
3)、Application range:May be applied to the members with the failure form of brittle rupture .
4、麦克斯威尔最早提出了最大畸变能理论(maximum distortion energy theory);这是后来人们在他的书信出版后才知道的。
8
§8–2 FOUR STRENGTH THEORIES AND
THEIR EQUIVALENT STRESSES
1、Theory of the maximum tensile stress(the first strength):
11
二、最大伸长线应变(第二强度)理论:
认为构件的断裂是由最大伸长线应变引起的。当最大伸长线
应变达到单向拉伸试验下的极限应变时,构件就断了。
1b ;(10)
Mechanics of Materials
1
2
CHAPTER 8 STHENGTH THEORIES
§8–1 Concepts of strength theories §8–2 Four strength theories and their equivalent stresses §8–3 Mohr’s strength theory and its equivalent stress §8-4 Applications of strength theories
This theory considers the main cause of rupture to be the maximum tensile strain. The member will rupture as the maximum tensile strain reaches the limit strain in axial
