假设检验的原理与过程(u检验为例).
合集下载
假设检验
2
故有
X 0.700 U ~ N 0 , 1 . 0.006
因而，U 的观察值 u 就较集中在零的周围， 若 H 0不真（即 H 1为真， ），则 0.700%
U 的观察值 u 大到一定程度，就认为样本
对于给定的 0 1 ，查正态分布 表的分位数 u ，使
2
（1）提出原假设 H 0 及备择建设 H 1 ；
（2）构造检验统计量，在 H 0 为真的条 件下，确定该统计量的分布； （3）确定 H 0的拒绝域；在给定显著性水 平的 0 1 条件下，查统计量所服从的分 布表，求出临界值，从而确定拒绝域 W ； （4）推断：由样本观察值算出统计量的 观察值，若落在拒绝域W 中，则拒绝 H 0 ，否 则接受 H 0 。
为此检验的检验函数。
1, x W ( x) 0, x W
定义4.2 (势函数) 对于给定假设的一个检验函数 ( x) ，则称
g ( ) E ( ( x)) P { X W }
为此检验的势函数。 g ( ) ( ) 当 0 时 当
1
断准则是类似的：当μ ≤ μ0时拒绝原假设H0 (接收H1 )，
否则接收H0 。该检验的势函数也是μ的函数，具体如 下：对μ ϵ (-≦，≦) ，
对双侧检验问题，也可类似进行讨论。仍选用μ作
为检验统计量，考虑到(4.6)的备择假设H1分散在二侧，
故其拒绝域亦应在二侧，即拒绝域应有如下形式
对给定的显著性水平α(0<α<1)，由 可定
2
事件 { U u } 是小概率事件。为使否定原假
2
设具有较强的说服力，一般 应取得较小， 并将 { U u } 称为拒绝域，记为 W , u 称为临
故有
X 0.700 U ~ N 0 , 1 . 0.006
因而，U 的观察值 u 就较集中在零的周围， 若 H 0不真（即 H 1为真， ），则 0.700%
U 的观察值 u 大到一定程度，就认为样本
对于给定的 0 1 ，查正态分布 表的分位数 u ，使
2
（1）提出原假设 H 0 及备择建设 H 1 ；
（2）构造检验统计量，在 H 0 为真的条 件下，确定该统计量的分布； （3）确定 H 0的拒绝域；在给定显著性水 平的 0 1 条件下，查统计量所服从的分 布表，求出临界值，从而确定拒绝域 W ； （4）推断：由样本观察值算出统计量的 观察值，若落在拒绝域W 中，则拒绝 H 0 ，否 则接受 H 0 。
为此检验的检验函数。
1, x W ( x) 0, x W
定义4.2 (势函数) 对于给定假设的一个检验函数 ( x) ，则称
g ( ) E ( ( x)) P { X W }
为此检验的势函数。 g ( ) ( ) 当 0 时 当
1
断准则是类似的：当μ ≤ μ0时拒绝原假设H0 (接收H1 )，
否则接收H0 。该检验的势函数也是μ的函数，具体如 下：对μ ϵ (-≦，≦) ，
对双侧检验问题，也可类似进行讨论。仍选用μ作
为检验统计量，考虑到(4.6)的备择假设H1分散在二侧，
故其拒绝域亦应在二侧，即拒绝域应有如下形式
对给定的显著性水平α(0<α<1)，由 可定
2
事件 { U u } 是小概率事件。为使否定原假
2
设具有较强的说服力，一般 应取得较小， 并将 { U u } 称为拒绝域，记为 W , u 称为临
假设检验
22
表
u值（取正）、 值与统计结论 值 取正）、P值与统计结论 ）、
u值 值 ＜1.96 ＜1.645 ≥1.96 ≥1.645 ≥2.58 ≥2.33 P值 值 ＞0.05 ≤0.05 ≤0.01 统计结论 不拒绝H0，差别无统计学 不拒绝 ， 意义 拒绝H0，接受 ， 拒绝 ，接受H1，差别有 统计学意义 拒绝H0，接受H1，差别有 拒绝 ，接受 ， 高度） （高度）统计学意义
5
x = 74.2, µ0 = 72
本例： 的可能原因有二： 本例：造成 X − µ ≠ 0 的可能原因有二：
① 抽样误差造成的； 抽样误差造成的； ② 本质差异造成的
如何做出判断， 如何做出判断 ， 统计上是通过假设检验来 回答这个问题 假设检验的目的— 假设检验的目的 判断差别是由哪种原因造成
9
假设H0成立的条件下， 假设H 成立的条件下， 出现| |≥k或 应为小概率事件， 出现| x -μ0|≥k或t≥tα,v 应为小概率事件， )≤α(0.05）， ），若计算出的 即P(t≥tα,v)≤α(0.05），若计算出的 它发生的概率P (0.05） t≥tα,v，它发生的概率P应≤α(0.05）,根 据小概率原理， 据小概率原理，小概率事件在一次试验中不 易发生。 易发生。但实际上不易发生的事件已经发生 故认为是假设错了,即认为H 了，故认为是假设错了,即认为H0的假设不成 拒绝H 立,拒绝H0 总结： p≤α,拒绝 拒绝H 总结：t≥tα,v,，p≤α,拒绝H0
x − µ0 k k P {x − µ 0 ≥ k } ≤ α → P ≥ ≤ α → P t ≥ ≤ α成立 s s s n n n
假设α=0.05，
k 应有 P t ≥ (为临界值 tα ,v ) ≤ 0.05 成立 s n
07《卫生统计学》第七章_假设检验基础(6版) (1)
2 2 d
sd t
n 1
n
2 7950 8832500
10 1
10
528.336IU / g
d d d 795.0 4.785 sd s d n 528.336 10
确定概率P：按ν =9查t 界值表，得P<0.01 判断结果:在α=0.05的水准上，拒绝H0，接受H1，可以认为 维生素E缺乏组大鼠肝脏维生素A含量低于正常饲料组。
二、 假设检验的基本步骤
• 确定检验水准： 检验水准（size of a test），亦称为 显著性水准（significance level），符号 为α，即拒绝或不拒绝H0所要冒出错的风 险大小。一般取α=0.05或α= 0.01。
二、 假设检验的基本步骤
• 确定单侧检验(one sided test)还是双侧检验(two sided test)： 如果根据现有的专业知识无法预先判断该病 病人的脉搏是高于还是低于一般健康成年男，两 种可能性都存在，研究者对这两种可能性同等关 心，那么，就是要推断两总体均数有无差别，应 当采用双侧检验；如果根据专业知识，已知病人 的脉搏不会低于一般人，或是研究者只关心病人 的脉搏是否高于一般，而不关心是否低于一般， 则应当采用单侧检验(one sided test)。
二、 假设检验的基本步骤
本例的资料符合t 检验的应用条件，已知 μ=72次/min ， x =75.572次/min ，s=5.0次/min ， n=25，代入公式计算t 值，结果：
x x 75.5 72.0 t 3.50 sx s n 5.0 25
3. 确定P值
第二节 t 检验
1. 一组样本资料的 t 检验
sd t
n 1
n
2 7950 8832500
10 1
10
528.336IU / g
d d d 795.0 4.785 sd s d n 528.336 10
确定概率P：按ν =9查t 界值表，得P<0.01 判断结果:在α=0.05的水准上，拒绝H0，接受H1，可以认为 维生素E缺乏组大鼠肝脏维生素A含量低于正常饲料组。
二、 假设检验的基本步骤
• 确定检验水准： 检验水准（size of a test），亦称为 显著性水准（significance level），符号 为α，即拒绝或不拒绝H0所要冒出错的风 险大小。一般取α=0.05或α= 0.01。
二、 假设检验的基本步骤
• 确定单侧检验(one sided test)还是双侧检验(two sided test)： 如果根据现有的专业知识无法预先判断该病 病人的脉搏是高于还是低于一般健康成年男，两 种可能性都存在，研究者对这两种可能性同等关 心，那么，就是要推断两总体均数有无差别，应 当采用双侧检验；如果根据专业知识，已知病人 的脉搏不会低于一般人，或是研究者只关心病人 的脉搏是否高于一般，而不关心是否低于一般， 则应当采用单侧检验(one sided test)。
二、 假设检验的基本步骤
本例的资料符合t 检验的应用条件，已知 μ=72次/min ， x =75.572次/min ，s=5.0次/min ， n=25，代入公式计算t 值，结果：
x x 75.5 72.0 t 3.50 sx s n 5.0 25
3. 确定P值
第二节 t 检验
1. 一组样本资料的 t 检验
假设检验
t分布与正态分布的比较
正态分布
T分布(n’=6)
T分布(n’=2)
T分布与正态分布的比较
t值表
1)表中左侧第一列的数值是自由度n '，它的值为n ' = n − 1。 随着n ' 值的不同，t分布曲线的形式也是呈现不同的态势。 每一横行的数据，属于一条t分布曲线。最下面一行n ' = ∞， t分布曲线与标准正态曲线重合，因此t分布表中这一 行的数据与标准正态分布表中的值是相同的。 2)表中顶端一行是显著性水平α的值。它的值等于分布图 α 中位于两尾部面积之和，单侧尾部面积为 。如下图 ２ α ３ 表中间的数值是代表t分布在图中单侧尾部面积为 时， ) ２ 所对应的t临界值如下图所示。 t α＝
(? 无效假设H 0：µ１ ≤ µ２的否定域为u ≥ u α。 )
(三 )总体方差σ１和σ２未知，但σ１２＝σ２２且为小样本时，两个总体均值之差的假设检验
此时的检验统计− (µ1 − µ 2 )
)
1 2 1 SC + n 1 n2 其服从自由度为n 1 + n 2 − 2的t分布。
中心极限定理：给出一 个具有任何函数形式的 总体，其平均值为 µ，方差 σ２有限。 若从这一总体抽出容量 为 n的样本，则当样本容量 很大时，由这些样本算 出的 x 的抽样分布近似服从平 均值为 µ，方差为 σ２ / n正态分布。在实际问题 中，常需 要在总体方差未知的条 件下对总体均数进行检 验。此时，通常用 s２近似代替 σ２， 对大样本来说误差不大 ，由中心极限定理可知 x的分布近似正态分布。 此时的检 验统计量为 U= x − µ0 s/ n ~ N (0,1)
p(H 0 )0.05，接受H 0 ∴ 认为可以用49.1秒作为该运动员400米跑成绩的代表值。
假设检验
假设检验基本步骤
• 1- 建立假设 例：单个总体均值进行检验， 有三类假设： H0：u=u0， H1：u>u0 H0：u=u0， H1：u<u0 H0：u=u0， H1：u≠u0
假设检验基本步骤
• 2- 选择检验统计量， 确定拒绝域形式
检验 总体均值 正态总体方差 检验统计量 样本均值 样本方差
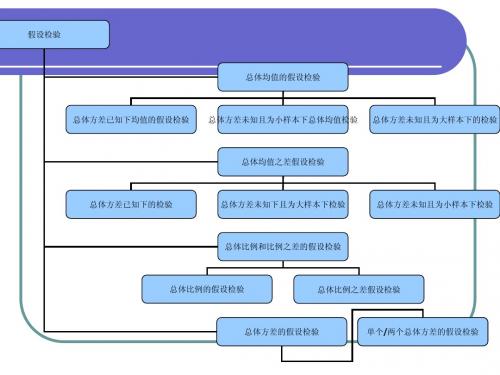
假设检验比较方法汇总
比率P Remark ** 当n较大， np〉5且np（1-p）〉5时， 二项分布可用 正态分布近似， 但Mintab应用时一般不勾选“使用基于 正态分布的检验和区间” **要想从比率数据中获得显著性的结论， 样本量要想当 大才有可能。 单总体 BS>单比率检验
双总体
BS>双比率检验
假设检验基本步骤
• 5- 根据样本观测值，计算检验统计量，判断
• 判断检验结论的三种方法 当给定第一类风险α 相同时， 三种方法得到的结论是一致的。 --P值着眼于考虑这个事件出现是小概率事件，其发生概率是那么小，以至于 我们认为它在一次试验发生是非同寻常的， 以此来拒绝原假设。
--置信区间着重于考虑原假设的参数值偏离1- α 置信区间有多远，以此来拒 绝原假设。
拒真概率α， 纳伪概率： β， 通常取α=0.05
**在样本量一定的情况下， α减小，β会增大 α增大，β会减小 想要同时减小α， β， 只有增大样本量n才行
假设检验基本步骤
• 4- 给出临界值，确定拒绝域
假设检验基本步骤
• 5- 根据样本观测值，计算检验统计量，判断
• 判断检验结论的三种方法 1- P值比较法 P值：当原假设成立时，出现目前状况或对备择假设更有利状况的概率 P值 < α 拒绝H0 （ α 通常取0.05） P值：对于此样本拒绝原假设将犯的第一类错误
第八章 假设检验
或 n 若所得的置信区间不包含u0，则拒绝H0， 否则不能拒绝。
x z2
x z2 /
s n
上例，我们用求置信区间的方法，来判断 原假设是否合理。 大样本下满足中心极限定理，样本均值的 抽样分布服从正态分布，从而有置信区间：
x z2 s 24 ＝986 1.96 n 40
假设检验的步骤
1.确定原假设和备选假设 2.选择检验统计量 3.指定检验的显著性水平 4.建立拒绝原假设的规则 5.收集样本数据，计算检验统计量的值 6.将检验统计量的值域拒绝规则的临界值比较， 以决定是否拒绝原假设。或者，由检验统计量 的值计算p值，利用p值确定是否拒绝原假设。
x 2.92 3 z 2.67 / n 0.18 / 6
x z ~ N (0,1) / n
根据显著性水平α=0.01，对应的拒绝域面积为 0.01，临界值为-2.33 Z<-2.33，所以拒绝H0，即可认为没听咖啡的容量 不足3磅。 统计证据支持对HILLTOP咖啡重量不足采取投诉措 施。
（978.56,993.44）该区间不包含u0=1000， 因此我们拒绝原假设H0.检验表明，该包 装机未能正常工作。
总体均值的检验：小样本情形
小样本下，已知总体为正态分布，我们考 虑以下两种情况： 1.总体方差已知 2.总体方差未知 在总体方差已知的情况下，即使样本容量 较小，但样本平均数的抽样分布总是以平 均值 为均值，以 x 为标准差的正态分 布。因此其检验过程和检验统计量同大样 本情形。
拒绝域为α/2 拒绝域为α/2
z / 2
拒绝域
0
z / 2
x z2
x z2 /
s n
上例，我们用求置信区间的方法，来判断 原假设是否合理。 大样本下满足中心极限定理，样本均值的 抽样分布服从正态分布，从而有置信区间：
x z2 s 24 ＝986 1.96 n 40
假设检验的步骤
1.确定原假设和备选假设 2.选择检验统计量 3.指定检验的显著性水平 4.建立拒绝原假设的规则 5.收集样本数据，计算检验统计量的值 6.将检验统计量的值域拒绝规则的临界值比较， 以决定是否拒绝原假设。或者，由检验统计量 的值计算p值，利用p值确定是否拒绝原假设。
x 2.92 3 z 2.67 / n 0.18 / 6
x z ~ N (0,1) / n
根据显著性水平α=0.01，对应的拒绝域面积为 0.01，临界值为-2.33 Z<-2.33，所以拒绝H0，即可认为没听咖啡的容量 不足3磅。 统计证据支持对HILLTOP咖啡重量不足采取投诉措 施。
（978.56,993.44）该区间不包含u0=1000， 因此我们拒绝原假设H0.检验表明，该包 装机未能正常工作。
总体均值的检验：小样本情形
小样本下，已知总体为正态分布，我们考 虑以下两种情况： 1.总体方差已知 2.总体方差未知 在总体方差已知的情况下，即使样本容量 较小，但样本平均数的抽样分布总是以平 均值 为均值，以 x 为标准差的正态分 布。因此其检验过程和检验统计量同大样 本情形。
拒绝域为α/2 拒绝域为α/2
z / 2
拒绝域
0
z / 2
卫生统计学课件_第六章_假设检验
16
公式：t
自由度：对子数 - 1
适用条件：两组配对计量资料。 例题：p. 34, 例8
三、两个小样本均数比较的 t 检验
▲目的：由两个样本均数的差别推断两样本
所代表的总体均数间有无差别。 ▲计算公式及意义： t 统计量： 自由度：n1 + n2 –2
18
▲ 适用条件：
（1）已知/可计算两个样本均数及它们的标准差 ；
38
(2）当不能拒绝
II 类错误的概率 β 值的两个规律：
1. 当样本量一定时, α 愈小, 则 β 愈大，反之…; 2.当 α 一定时, 样本量增加, β 减少.
39
4. 正确理解P值的意义， P值很小时“拒绝H0 ”，P值的
大小不要误解为总体参数间差异的大小； 拒绝H0 只是说 差异不为零。 统计学中的差异显著或不显著，和日常生活中所说的差 异大小概念不同. （不仅区别于均数差异的大小，还区别 于均数变异的大小)
统计推断
用样本信息推论总体特征的过程。
包括：
参数估计: 运用统计学原理，用从样本计算出来的统计
指标量，对总体统计指标量进行估计。
假设检验：又称显著性检验，是指由样本间存在的差
别对样本所代表的总体间是否存在着差别做出判断。
第一节
▲显著性检验;
假设检验
▲科研数据处理的重要工具;
▲某事发生了：
是由于碰巧？还是由于必然的原 因？统计学家运用显著性检验来 处理这类问题。
45
41
是非判断： （ ）1．标准误是一种特殊的标准差，其 表示抽样误差的大小。 （ ）2．N一定时，测量值的离散程度越 小，用样本均数估计总体均数的抽样误差 就越小。 （ ）3．假设检验的目的是要判断两个样 本均数的差别有多大。
公式：t
自由度：对子数 - 1
适用条件：两组配对计量资料。 例题：p. 34, 例8
三、两个小样本均数比较的 t 检验
▲目的：由两个样本均数的差别推断两样本
所代表的总体均数间有无差别。 ▲计算公式及意义： t 统计量： 自由度：n1 + n2 –2
18
▲ 适用条件：
（1）已知/可计算两个样本均数及它们的标准差 ；
38
(2）当不能拒绝
II 类错误的概率 β 值的两个规律：
1. 当样本量一定时, α 愈小, 则 β 愈大，反之…; 2.当 α 一定时, 样本量增加, β 减少.
39
4. 正确理解P值的意义， P值很小时“拒绝H0 ”，P值的
大小不要误解为总体参数间差异的大小； 拒绝H0 只是说 差异不为零。 统计学中的差异显著或不显著，和日常生活中所说的差 异大小概念不同. （不仅区别于均数差异的大小，还区别 于均数变异的大小)
统计推断
用样本信息推论总体特征的过程。
包括：
参数估计: 运用统计学原理，用从样本计算出来的统计
指标量，对总体统计指标量进行估计。
假设检验：又称显著性检验，是指由样本间存在的差
别对样本所代表的总体间是否存在着差别做出判断。
第一节
▲显著性检验;
假设检验
▲科研数据处理的重要工具;
▲某事发生了：
是由于碰巧？还是由于必然的原 因？统计学家运用显著性检验来 处理这类问题。
45
41
是非判断： （ ）1．标准误是一种特殊的标准差，其 表示抽样误差的大小。 （ ）2．N一定时，测量值的离散程度越 小，用样本均数估计总体均数的抽样误差 就越小。 （ ）3．假设检验的目的是要判断两个样 本均数的差别有多大。
假设检验的原理与应用
假设检验的原理与应用假设检验是一种通过收集样本数据来验证关于总体的某个特定假设的统计推断方法。
它常被应用于科学研究、市场调研和质量控制等领域，具有重要的理论和实际价值。
本文将介绍假设检验的原理，并结合一些典型案例展示其应用。
一、假设检验的原理假设检验的原理基于两个相互竞争的统计假设——原假设和备择假设。
原假设（H0）是我们要考察的假设，通常表示目前的观点或常规认知；备择假设（H1或Ha）则是我们希望通过数据来支持的新假设。
假设检验的目标是根据样本数据提供的证据，对两个假设进行比较，从而得出是否拒绝原假设的结论。
假设检验的基本步骤包括：确定原假设和备择假设、确定统计检验方法和显著性水平、收集样本数据、计算检验统计量，并与临界值进行比较、得出结论。
其中，显著性水平是用来衡量拒绝原假设的程度，通常设定为0.05或0.01。
如果计算得到的检验统计量超过了临界值，就可以拒绝原假设，并支持备择假设。
二、假设检验的应用案例1. 药物疗效检验假设某种新药物针对某种疾病的疗效优于现有药物，我们可以设置原假设H0：新药物和现有药物的疗效没有差异，备择假设H1：新药物的疗效优于现有药物。
通过将患者随机分为两组，一组使用新药物，一组使用现有药物，然后收集数据并进行统计分析，我们可以计算出一个检验统计量，比如t值。
如果t值超过了设定的临界值，我们就可以拒绝原假设，对新药物的疗效表示支持。
2. 市场调研假设市场调研机构欲了解某款产品是否拥有更高的市场占有率，我们可以设置原假设H0：该产品和现有市场占有率没有显著差异，备择假设H1：该产品的市场占有率高于现有水平。
通过对一定样本规模的消费者进行调查，获得相应数据，再通过统计分析得出一个检验统计量，比如z值。
如果z值超过了显著性水平对应的临界值，我们就可以拒绝原假设，认为该产品的市场占有率具有一定提升。
三、假设检验的限制与改进虽然假设检验在许多领域应用广泛，但也存在一些限制。
首先，假设检验只能提供二元结果，即接受或拒绝原假设，不能给出两个假设具体差异的程度。
假设检验的原理和方法
统计推断(statistical inference)
第四章
do
something
第四章 统计推断
统计推断
由一个样本或一糸列样本所得的结果来推断总体的特征
假设检验
参数估计
统计推断的过程
分析误差产生的原因
任务
确定差异的性质
排除误差干扰
对总体特征做出正确判断
第四章
第一节
第二节
第三节
第四节
第五节
330
实例
?
三、假设检验的步骤
治疗前 0 ＝126 2 ＝240
N ( 126，240 ）
治疗后 n ＝6 x ＝136 未知 那么 ＝0 ? 即克矽平对治疗矽肺是否有效？
例：设矽肺病患者的血红蛋白含量具平均数0＝126(mg/L)， 2 ＝240 (mg/L)2的正态分布。现用克矽平对6位矽肺病患者进行治疗，治疗后化验测得其平均血红蛋白含量x =136(mg/L)。
1 、提出假设
对立
无效假设/零假设/检验假设
备择假设/对应假设
0 ＝
0
误差效应
处理效应
H0
HA
例：克矽平治疗矽肺病是否能提高血红蛋白含量？
检验治疗后的总体平均数是否还是治疗前的126(mg/L)？
本例中零假设是指治疗后的血红蛋白平均数仍和治疗前一样，二者来自同一总体，接受零假设则表示克矽平没有疗效。
可能错误
例：上例中 P＝0.1142>0.05所以接受H0，从而得出结论：使用克矽平治疗前后血红蛋白含量未发现有显著差异，其差值10应归于误差所致。
P( u >1.96) =0.05
P( u >2.58) =0.01
第四章
do
something
第四章 统计推断
统计推断
由一个样本或一糸列样本所得的结果来推断总体的特征
假设检验
参数估计
统计推断的过程
分析误差产生的原因
任务
确定差异的性质
排除误差干扰
对总体特征做出正确判断
第四章
第一节
第二节
第三节
第四节
第五节
330
实例
?
三、假设检验的步骤
治疗前 0 ＝126 2 ＝240
N ( 126，240 ）
治疗后 n ＝6 x ＝136 未知 那么 ＝0 ? 即克矽平对治疗矽肺是否有效？
例：设矽肺病患者的血红蛋白含量具平均数0＝126(mg/L)， 2 ＝240 (mg/L)2的正态分布。现用克矽平对6位矽肺病患者进行治疗，治疗后化验测得其平均血红蛋白含量x =136(mg/L)。
1 、提出假设
对立
无效假设/零假设/检验假设
备择假设/对应假设
0 ＝
0
误差效应
处理效应
H0
HA
例：克矽平治疗矽肺病是否能提高血红蛋白含量？
检验治疗后的总体平均数是否还是治疗前的126(mg/L)？
本例中零假设是指治疗后的血红蛋白平均数仍和治疗前一样，二者来自同一总体，接受零假设则表示克矽平没有疗效。
可能错误
例：上例中 P＝0.1142>0.05所以接受H0，从而得出结论：使用克矽平治疗前后血红蛋白含量未发现有显著差异，其差值10应归于误差所致。
P( u >1.96) =0.05
P( u >2.58) =0.01
假设检验
1、建立检验假设及确定检验水准 H0： =0 山区成年男子平均脉搏 数与一般人群相等 H1 ： >0 山区成年男子平均脉搏 数高于一般人群 单侧 =0.05
23
2 选定检验方法及计算检验统计量
不同分析目的、不同设计类型和不同资料类 型，选用不同检验方法。 样本均数与总体均数比较用单样本t检验 配对设计的两样本均数的比较用配对t 检验 完全随机设计的两样本均数比较时，选用成 组设计的两样本均数比较的t 检验
32
用到假设检验比较的例子：
例1：单样本均数与已知总体均数差异的比较 例2：两个样本均数所代表的总体均数之间差异 的比较 能否列举出其它比较的实例？
不同机器性能是否一致？ 不同人群的患病率是否相似？ 不同年龄的红细胞数测量值是否不同？ 不同厂家产品质量对比？
33
例3 某医生测得18例慢性支气管炎患者及16例 健康人的尿17酮类固醇排出量(mg/dl)分别为 X1 和X2, 试问两组的尿17酮类固醇排出量有无 不同。 成组设计 X 1: 3.14 5.83 7.35 4.62 4.05 5.08 4.98 4.22 4.35 2.35 2.89 2.16 5.55 5.94 4.40 5.35 3.80 4.12 X 2: 4.12 7.89 3.24 6.36 3.48 6.74 4.67 7.38 4.95 4.08 5.34 4.27 6.54 4.62 5.92 5.18
未 知 且 n未知，且体 较小，按t分布 ) % 可 信 区 间 为 ： 较 小 的 总 n均 数 的 1 0 0 ( 1 ( X t / 2( ) S X , X t / 2( ) S X ) 或 X t / 2( ) S X
应用统计学(第五章 统计推断)
差与已知总体的方差存在显著差异
检验统计量： χ2 (n 1) s2 σ02
例题5 已知某农田受到重金属污染，抽样测定其镉含量
(μg/g)分别为：3.6、4.2、4.7、4.5、4.2、4.0、3.8、
3.7，试检验污染农田镉含量的方差与正常农田镉含量的方 差0.065是否相同。
解：假设 H0：σ 2 σ02 , H A：σ 2 σ02
P(μ-1.960 σ x ≤ x < μ+1.960 σ x)=0.95
否定区
接受区
否定区
左尾
0.025
μ-1.960σ x
0.95
0.025
0 μ+1.960σ x
右尾
临界值： ± uσ x= ± 1.960σ x
双尾检验 = 0.01
P(μ-2.576 σ x ≤ x < μ+2.576 σ x)=0.99
解： 假设： H0： μ ≤ μ0， HA ： μ > μ0 确定显著水平：α＝0.05 检验统计量：u x μ0 379.2 377.2 1.818 σ n 3.3 9 u0.05=1.645，计算得：u=1.818>u0.05，P<0.05
推断：否定H0，接受HA。
即：栽培条件的改善，显著提高了豌豆籽粒重量。
4)推断
接受/否定H0(HA，实际意义)
例题1 正常人血钙值服从的正态分布，平均值为2.29 mM，标准差为 0.61mM。现有8名甲状旁腺减退患者经治疗后，测得其血钙值平均为 2.01mM，试检验其血钙值是否正常。
1)提出假设 2)确定显著水平 3)计算概率 4)推断
1)提出假设
H0
零假设 /无效假设
对 /检验假设
检验统计量： χ2 (n 1) s2 σ02
例题5 已知某农田受到重金属污染，抽样测定其镉含量
(μg/g)分别为：3.6、4.2、4.7、4.5、4.2、4.0、3.8、
3.7，试检验污染农田镉含量的方差与正常农田镉含量的方 差0.065是否相同。
解：假设 H0：σ 2 σ02 , H A：σ 2 σ02
P(μ-1.960 σ x ≤ x < μ+1.960 σ x)=0.95
否定区
接受区
否定区
左尾
0.025
μ-1.960σ x
0.95
0.025
0 μ+1.960σ x
右尾
临界值： ± uσ x= ± 1.960σ x
双尾检验 = 0.01
P(μ-2.576 σ x ≤ x < μ+2.576 σ x)=0.99
解： 假设： H0： μ ≤ μ0， HA ： μ > μ0 确定显著水平：α＝0.05 检验统计量：u x μ0 379.2 377.2 1.818 σ n 3.3 9 u0.05=1.645，计算得：u=1.818>u0.05，P<0.05
推断：否定H0，接受HA。
即：栽培条件的改善，显著提高了豌豆籽粒重量。
4)推断
接受/否定H0(HA，实际意义)
例题1 正常人血钙值服从的正态分布，平均值为2.29 mM，标准差为 0.61mM。现有8名甲状旁腺减退患者经治疗后，测得其血钙值平均为 2.01mM，试检验其血钙值是否正常。
1)提出假设 2)确定显著水平 3)计算概率 4)推断
1)提出假设
H0
零假设 /无效假设
对 /检验假设
假设检验基础
2 1 2 2
第一类错误和第二类错误
假设检验的结果
实际情况
拒绝 H0
H0 成立 H0 不成立
接受 H0
I 型错误() 把握度(1-) II 型错误()
第一类错误和第二类错误
第一类错误（Type I Error）
拒绝了实际上是成立的H0； “弃真”
第二类错误（Type II Error）
t x 0 ; sx
U x 0
x
或U
x 0 sx
d 0 d t sd sd / n
t x1 x2
2 2 s1 ( n1 1) s2 ( n2 1) 1 1 ( ) n1 n2 2 n1 n2
;U
x1 x 2
2 2 s1 s2 n1 n2
= 3.768)
0.001,23
(3) (4)
P <0.001
按＝0.05水准，拒绝H0，接受H1 。 差别有统计学意义，可以认为病毒性肝炎 患者的转铁蛋白含量较低。
成组设计的两样本均数比较的Z检验
U检验：两样本含量n1、n2大于50或100。方差齐性
Z
x1 x 2 s s n1 n2
(2)计算检验统计量
d 10.67 t 3.305 sd / n 11.18 / 12
可以认为该药对高血压教育干预对该地区儿童的血红蛋白 有影响，且血红蛋白(%)有所增加。
(3)确定 P 值。 查t 界值表得，P < 0.05。 (4)作结论：按= 0.05水准，拒绝H0 ，接受H1，
例7-3 两种方法测定血清Mg2+ （mmol/l）的结果
肝炎组
2＝？
均 数: 273.18 标准差: 9.77
第一类错误和第二类错误
假设检验的结果
实际情况
拒绝 H0
H0 成立 H0 不成立
接受 H0
I 型错误() 把握度(1-) II 型错误()
第一类错误和第二类错误
第一类错误（Type I Error）
拒绝了实际上是成立的H0； “弃真”
第二类错误（Type II Error）
t x 0 ; sx
U x 0
x
或U
x 0 sx
d 0 d t sd sd / n
t x1 x2
2 2 s1 ( n1 1) s2 ( n2 1) 1 1 ( ) n1 n2 2 n1 n2
;U
x1 x 2
2 2 s1 s2 n1 n2
= 3.768)
0.001,23
(3) (4)
P <0.001
按＝0.05水准，拒绝H0，接受H1 。 差别有统计学意义，可以认为病毒性肝炎 患者的转铁蛋白含量较低。
成组设计的两样本均数比较的Z检验
U检验：两样本含量n1、n2大于50或100。方差齐性
Z
x1 x 2 s s n1 n2
(2)计算检验统计量
d 10.67 t 3.305 sd / n 11.18 / 12
可以认为该药对高血压教育干预对该地区儿童的血红蛋白 有影响，且血红蛋白(%)有所增加。
(3)确定 P 值。 查t 界值表得，P < 0.05。 (4)作结论：按= 0.05水准，拒绝H0 ，接受H1，
例7-3 两种方法测定血清Mg2+ （mmol/l）的结果
肝炎组
2＝？
均 数: 273.18 标准差: 9.77
东华大学《概率论与数理统计》课件 第七章 假设检验
1. 2为已知, 关于的检验(U 检验 )
在上节中讨论过正态总体 N ( , 2 ) 当 2为已知时, 关于 = 0的检验问题 :
假设检验 H0 : = 0 , H1 : 0 ;
我们引入统计量U
=
− 0 0
，则U服从N(0,1)
n
对于给定的检验水平 (0 1)
由标准正态分布分位数定义知，
~
N (0,1),
由标准正态分布分位点的定义得 k = u1− / 2 ,
当 x − 0 / n
u1− / 2时, 拒绝H0 ,
x − 0 / n
u1− / 2时,
接受H0.
假设检验过程如下:
在实例中若取定 = 0.05, 则 k = u1− / 2 = u0.975 = 1.96, 又已知 n = 9, = 0.015, 由样本算得 x = 0.511, 即有 x − 0 = 2.2 1.96,
临界点为 − u1− / 2及u1− / 2.
3. 两类错误及记号
假设检验是根据样本的信息并依据小概率原
理，作出接受还是拒绝H0的判断。由于样本具有 随机性，因而假设检验所作出的结论有可能是错
误的. 这种错误有两类:
(1) 当原假设H0为真, 观察值却落入拒绝域, 而 作出了拒绝H0的判断, 称做第一类错误, 又叫弃
设 1,2, ,n 为来自总体 的样本,
因为 2 未知, 不能利用 − 0 来确定拒绝域. / n
因为 Sn*2 是 2 的无偏估计, 故用 Sn* 来取代 ,
即采用 T = − 0 来作为检验统计量.
Sn* / n
当H0为真时,
− 0 ~ t(n −1),
Sn* / n
由t分布分位数的定义知
u检验
u检验、t检验、F检验、X2检验常用显著性检验1.t检验适用于计量资料、正态分布、方差具有齐性的两组间小样本比较。
包括配对资料间、样本与均数间、两样本均数间比较三种，三者的计算公式不能混淆。
2.t'检验应用条件与t检验大致相同，但t′检验用于两组间方差不齐时，t′检验的计算公式实际上是方差不齐时t检验的校正公式。
3.U检验应用条件与t检验基本一致，只是当大样本时用U检验，而小样本时则用t检验，t检验可以代替U检验。
4.方差分析用于正态分布、方差齐性的多组间计量比较。
常见的有单因素分组的多样本均数比较及双因素分组的多个样本均数的比较，方差分析首先是比较各组间总的差异，如总差异有显著性，再进行组间的两两比较，组间比较用q检验或LST检验等。
5.X2检验是计数资料主要的显著性检验方法。
用于两个或多个百分比(率)的比较。
常见以下几种情况：四格表资料、配对资料、多于2行*2列资料及组内分组X2检验。
6.零反应检验用于计数资料。
是当实验组或对照组中出现概率为0或100％时，X2检验的一种特殊形式。
属于直接概率计算法。
7.符号检验、秩和检验和Ridit检验三者均属非参数统计方法，共同特点是简便、快捷、实用。
可用于各种非正态分布的资料、未知分布资料及半定量资料的分析。
其主要缺点是容易丢失数据中包含的信息。
所以凡是正态分布或可通过数据转换成正态分布者尽量不用这些方法。
8.Hotelling检验用于计量资料、正态分布、两组间多项指标的综合差异显著性检验。
计量经济学检验方法讨论计量经济学中的检验方法多种多样，而且在不同的假设前提之下，使用的检验统计量不同，在这里我论述几种比较常见的方法。
在讨论不同的检验之前，我们必须知道为什么要检验，到底检验什么？如果这个问题都不知道，那么我觉得我们很荒谬或者说是很模式化。
检验的含义是要确实因果关系，计量经济学的核心是要说因果关系是怎么样的。
那么如果两个东西之间没有什么因果联系，那么我们寻找的原因就不对。
概率论与数理统计：第七章 假设检验
得拒绝域为 W = {u u }
其中, u = x μ0 σ/ n
U
=
X
σ
μ0
/n
ua/2
，则称 X 与m0的
差异是显著的，则拒绝H0
如果
U
ห้องสมุดไป่ตู้
=
X μ0 σ/ n
< ua/ 2
，则称 X 与m0的
差异是不显著的，则接受H0
x与μ 0有无显著差异的判断,
是在显著性水平α之下做出的。
厦大经院-国贸-2012秋季学期
关于显著性水平
是一个概率值，弃真概率；在后面“假设 检验的两类错误”再具体介绍；
H0称为原假设, H1称为备择假设
厦大经院-国贸-2012秋季学期
原假设
试图推翻的假设，又称“零假设”
表示为 H0
指定为 = ， ，
如，H0：m = 3190
厦大经院-国贸-2012秋季学期
备择假设
通常是试图支持的假设
指定为: , > ， <
表示为 H1，如 H1 ： m < 3910 H1 ： m ≠ 3910 H1 ： m > 3910
2. 原假设H0不真, 观察值却落入接受域， 从而作出接受H0的判断，
这类错误“以假为真”，记为 错误 ,
犯第Ⅱ类错误的概率：
= P { 接受H0 | H0不正确 }
厦大经院-国贸-2012秋季学期
错误和 错误的关系
小， 就大
大， 就小
不能 同时减少 两类错误
当样本容量 n 一定，若减少第I类错误的概率， 第Ⅱ类错误的概率往往增大； 要使两类错误的概率都减小，只能增加样本容量。
在一次试验中, 小概率事件不会发生 。
假设检验法的原理和步骤
假设检验法的原理和步骤一、常用核心概念什么是假设检验：假设就是对从总体参数(均值、比例等)的具体数值所作的陈述，比如，我认为配方一比配方二的效果要好。
而假设检验就是先对总体的参数提出某种假设，然后利用样本的信息判断假设是否成立的过程，比如上面的假设信息我该接受还是拒绝。
什么是显著性水平：显著性水平是一个概率值，原假设为真时，拒绝原假设的概率，表示为α，常取值为0.05、0.01、0.10。
一个公司招聘，本来准备招聘100个人，公司希望只有5%的人是混水摸鱼招聘进来，所以可能会有5个人混进来，所谓显著性水平α，就是你允许有多少比例混水摸鱼的能通过测试。
原假设与备择假设：待检验的假设又叫原假设(零假设)，一般表示为H0，原假设一般表示两者没有显著性差异。
与原假设进行对比的叫备择假设，表示为H1。
一般在比较的时候，主要有等于、大于、小于。
检验统计量：即计算检验的统计量。
根据给定的显著性水平，查表得出相应的临界值。
再将检验统计量的值与该显著性水平的临界值进行比较，得出是否拒绝原假设的结论。
P值：是一个概率值，如果原假设为真，p值是抽样分布中大于或小于样本统计量的概率。
左检验时，p值为曲线上方小于等于检验统计量部分的面积。
右检验时，p值为曲线上方大于等于检验统计量部分的面积。
假设检验的两种错误：类型 I 错误(弃真)，如原假设为真，但否定它，则会犯类型 I 错误。
犯类型 I 错误的概率为α（即您为假设检验设置的显著性水平）。
α为 0.05 表明，当您否定原假设时，您愿意接受 5% 的犯错概率。
为了降低此风险，必须使用较低的α值。
但是，使用的α值越小，在差值确实存在时检测到实际差值的可能性也越小。
类型 II 错误(采伪)，如原假设为假，但无法否定它，则会犯类型 II 错误。
犯类型 II 错误的概率为β，β依赖检验功效。
可以通过确保检验具有足够大的功效来降低犯类型 II 错误所带来的风险。
方法是确保样本数量足够大，以便在差值确实存在时检测到实际差值。
第6章 假设检验
二、 假设检验的步骤 提出原假设和备择假设 /备择假设 确定适当的检验统计量 规定显著性水平: 根据显著性水平α及检验
统计量的查找临界值，并确定拒绝域。注 意是单侧检验还是双侧检验
计算检验统计量的值: 从总体中抽取某一样 本，据样本资料计算检验统计量的值 作出统计决策: 若检验统计量的值落在拒绝 域内就拒绝H0，否则接受H0
置信水平
拒绝域
a/2
1 - 接受域
H0值
a/2
临界值
临界值
样本统计量
双侧检验 （显著性水平与拒绝域 ）
抽样分布
拒绝域 a/2 1 - 接受域 H 0值 样本统计量 置信水平 拒绝域 a/2
临界值
临界值
例如 ，一个灯光厂需要生产平均使用寿命 µ = 1000小时的灯泡。为了观察生产工艺过程是否正常， 从一批产品中抽取150个进行检验，得到平均使用 寿命980小时，能否断定这个厂生产的灯泡平均使 用寿命为1000小时？为什么？ 不希望在1000小时任何一边超越太多，假设： H0: µ = 1000 （平均使用寿命为1000） H1: µ ≠ 1000 （平均使用寿命不是1000） 我们在这里提出的原假设是µ =1000，所以只要 µ >1000或µ <1000二者中有一个成立就可以否定原假 设（平均使用寿命为1000）。
标准误计算公式
σ已知： σ未知： S
X
n
X
S n
实例：如某年某市120名12岁健康男孩，已求 得 均数为143.07cm，标准差为5.70cm，按公 式计算，则标准误为：
SX
5 . 70 120
0 . 52
标准误的应用
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【例4-1】测定了某品种37头犊牛100g血液中总蛋白的
含量，其平均数为4.263g；该品种成年母牛100g血液中
总蛋白含量为7.570g，标准差为1.001。问该品种犊牛
血液中总蛋白含量是否显著低于成年母牛？（请作单侧
检验
或
） 单尾（侧）检验
（1）提出假设
左尾（侧）检验
犊牛血液中总蛋白含量显著高于成年母牛 犊牛血液中总蛋白含量显著低于成年母牛
1
u2
e2
2
u= 0
样本统计量
做出统计推断或决策
（确定显著性水平与拒绝域 ）
一
拒绝域
双
侧 检
a/2
验
1 -a 接受域
置信水平 拒绝域 a/2
临界值
样本统计量 临界值
显著性水平==小概率标准（事先给定）==界定拒绝（接受）域
概率
推断或决策 区域
（确定显著性水平与拒绝域 ）
置信水平
二
拒绝域
单
侧 检
a
1 -a
验
接受域
临界值
H0值
样本统计量
概率
推断或决策 区域
概率
推断或决策 区域
假设检验过程总结
（）构造、计算检验统计量 服从一种分布，如u、t、F分布等
也代表着一种差异 统计量出现的概率
原假设为真时，观察样本所引起的（大于）
（3）假设正确的概率保证 差异的概率；
这一类试验的数据假设检验其备择假设只有一种情况， 即只有一个否定区间（一尾）
一尾检验比两尾检验更容易否定无效假设，因此应用一 尾检验必须有非常充分的理由
在常用的假设检验中，我们一般采用两尾检验，而对一 尾检验谨慎使用。
双尾（侧）检验
（1）提出假设
H0：μ=7.570g HA：μ≠7.570g
犊牛和成年母牛间血液中总蛋白含量无显著差异 犊牛和成年母牛间血液中总蛋白含量存在显著差异
（2）计算 值
上一张 下一张 首 页 退 出
计算公式：u x x
总体标准误：
（3）查表、推断 P＜0.01 差异极显著
否定无效假设H0 ，接受备择假设HA 说明犊牛和成年母牛间血液中总蛋白含量 存在极显著差异。
（2）计算 值
上一张 下一张 首 页 退 出
计算公式：u x x
总体标准误：
（3）查表、推断 P＜0.01 差异极显著
否定无效假设H0 ，接受备择假设HA 说明犊牛血液中总蛋白含量极显著 低于成年母牛
【例4-1】测定了某品种37头犊牛100g血液中总蛋白的
含量，其平均数为7.570g；该品种成年母牛100g血液中
... 因此我们拒 绝假设 = 50, 因为小概率
... 如果这是总 体的真实均值
正态分布
20
0 = 50
H0
构造统计量
样本均值 标准正态分布
U变换：为了能使正态分布应用起来更方便一些，可以将x作一变换，令：
u x u变换
随机变量u服从标准正态分布，记为：u～N（0，1）
f (u)
含义是差异由抽样误差所致的概率
做出统计推断
概率大小（小概率拒绝==不该发生的小概 率事件发生了）
显著性水平 小概率标准 拒绝（接受）域
【例4-1】测定了某品种37头犊牛100g血液中总蛋白的 含量，其平均数为4.263g；该品种成年母牛100g血液中 总蛋白含量为7.570g，标准差为1.001。问该品种犊牛 和成年母牛血液中总蛋白含量是否存在显著差异？
假设检验的原理与过程（u检验为例）
（提出假设→抽取样本→作出决策）
已知总体
某地区人口的平均年龄是50岁
☺☺ ☺
☺☺ ☺☺ ☺☺
提出假设
我认为人口的平均 年龄是50岁
抽取随机样本
☺X均=值20☺
作出决策
拒绝假设!
别无选择.
提出假设并构造统计量
抽样分布—正态分布
这个值不像我 们应该得到的 样本均值 ...
总体标准误：
（3）查表、推断 P＜0.01 差异极显著
否定无效假设H0 ，接受备择假设HA 说明犊牛血液中总蛋白含量极显著 高于成年母牛
双侧检验
t检验
双（一）尾检验补充说明
两尾检验是应用最广泛的一种检验方法，但有的时 候，我们的目的非常明确，即所抽样本只可能是大于总 体平均值，或只可能是小于总体平均值： 例如：某种新型针剂只可能好于常规针剂；某些有毒物 质只能对被试动物产生毒害作用，等等
总蛋白含量为4.263g，标准差为1.001。问该品种犊牛
血液中总蛋白含量是否显著高于成年母牛？（请作单侧
检验
或
） 单尾（侧）检验
（1）提出假设
右尾（侧）检验
犊牛血液中总蛋白含量显著低于成年母牛 犊牛血液中总蛋白含量显著高于成年母牛
（2）计算 值
上一张 下一张 首 页 退 出
计算公式：u x x