随机过程模型PPT课件
合集下载
随机过程简介PPT课件

4
第4页/共12页
X1(t) 在固定时刻读得各样本的瞬时波面高度
t X2(t)
t
Xk(t)
tj
第5页/共12页
t
5ห้องสมุดไป่ตู้
给出随机过程的定义:设T是一无限实数集(例如海洋中 无数的波浪), 把依赖于参数tT的一族(无限多个)随机变量 称为随机过程, 记为{X(t), tT}, 这里对每一个tT, X(t)是
•
自然界的事物都是变化着的,在经典物理学的研究中,我们多把事物的运动变化形式看作是可确知的,
例如自由落体运动的速度V(t)=gt;静水压力随水深的变化规律
• P(h)=γh.这些变化都是可以用确定的函数描述的,从而被称之为确定过程。
1
第1页/共12页
•
然而还有另外一种过程,在空间与时间上是高度不规则和不重复的物理现象,其变
10
第10页/共12页
随机过程的不同描述方式在本质上是一致的. 在理论分 析时往往以随机变量族的描述方式作为出发点, 而在实际测量 和数据处理中往往采用样本函数族的描述方式。 这两种描述 方式在理论和实际两方面互补。
11
第11页/共12页
感谢您的观看!
12
第12页/共12页
程. 且它们的状态空间是(-, +).(连续型随机过程)
9
第9页/共12页
例3设某城市的120急救电话台迟早会接到用户的呼叫, 以X(t) 表示时间间隔(0,t]内接到的呼叫次数, 它是一个随机变量, 且 对于不同的t0, X(t)是不同的随机变量. 于是, {X(t),t0}是
一随机过程. 且它的状态空间是{0,1,2,...}. (离散型随机过程)
程的一个样本函数:
随机过程及其统计描述ppt课件.ppt

任意时刻下,观测目的是X取什么值;全程的情况下, 观测目的是X(t)的函数形式.
7
12.1 随机过程的概念
随机相位正弦波
随机过程举例
考虑: X (t) a cos(t ), t (,)
式中 a,是正常数,是 (0, 2 ) 上服从均匀分布的随机变量。
当 在(0, 2 ) 内随机的取一个值 i ,可得样本函数:
2
0 cos(t1 ) cos(t2 ) f ( )d
a2
2
2
0 cos(t1 ) cos(t2 )d
a2
4
2
0 {cos[(t1 t2 ) 2 ] cos(t1 t2 )}d
a2 2
cos (t1
t2 )
方差函数
2 X
(t)
RX
(t , t )
2 X
(t)
a2 2
18
12.2 随机过程的统计描述
随机过程举例
抛掷一枚硬币的试验,样本空间是S={H,T}, 现借此定义随机过程:
cos t,
X (t) t,
当出现H, 当出现T,
t (, )
可将此随机过程改写为
X (t) Y cost (1Y )t ,
其中
Y
1, 0,
出现H 出现T
,
t (, )
X对Y和t的依赖,决定了X是一个随机过程. 确定了 Y之后,即可确定任意时刻和全程的观测结果.
集平均(统计平均)
X (t)是随机过程的所有样本函数在时刻 t 的函数值的平均值,通常称
这种平均为集平均或统计平均。
12
12.2 随机过程的统计描述
(二) 随机过程的数字特征
均方值函数
Ψ
随机过程的基本概念ppt课件

求X(t)的均值、均方值和方差。
.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数: rX()KXX 2 ()RX()X 2mX 2
相关时间:
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意:X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征(连续)
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } (1)如果 KX(t1,t2)0,则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度: fX(x,t)fX(x)
二维概率密度: fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0
.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数: rX()KXX 2 ()RX()X 2mX 2
相关时间:
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意:X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征(连续)
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } (1)如果 KX(t1,t2)0,则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度: fX(x,t)fX(x)
二维概率密度: fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0
随机过程课件.ppt

随机过程的统计描述 二 有限维分布族
两种描述
分布函数 特征数
设随机过程X (t),t T,对每一固定的t T ,随机变量X (t)的分布函数与t有关, 记为FX (x,t) PX (t) x,x R,称它为随机过程X (t),t T的一维分布函数 FX (x,t),t T称为一维分布函数族
为了描述随机过程在不同时刻状态之间的统计联系, 一般地,对任意n(n 2,3,L )个不同的时刻,t1,t2,L tn T
研究生课程
随机过程
汪荣鑫编 主讲教师:田ቤተ መጻሕፍቲ ባይዱ俊
2013年9月
第一章 随机过程基本概念
第1节 随机过程及其概率分布
1)随机过程概念 随机过程被认为是概率论的“动力学”部分,即
它的研究对象是随时间演变的随机现象,它是从 多维随机变量向一族(无限多个)随机变量的推广。
自然界中事物的变化过程可以大致分成为两类: 确定性过程:事物变化的过程可用时间的确定函数表示;
4
x1 (t )
3
2
1
t1' t1 t2 t2' t3 t3' t4' t4
t
4
例5:考虑抛掷一颗骰子的试验:
(1) 设X n是第n次(n 1)抛掷的点数,对于n 1, 2,L 的不同值,
X n是随机变量,服从相同的分布,P( X n
i)
1 6
,i
1, 2,3, 4,5, 6
因而X n , n 1构成一随机过程,称为伯努利过程或伯努利随机序列,
它的状态空间为1,2,3,4,5,6。
(2) 设Yn是前n次抛掷中出现的最大点数,Yn , n 1也是
一随机过程,它的状态空间仍是1, 2,3, 4,5, 6。
随机过程课件

。每个可能取的值称为一个状态。
对随机过程 {X (t) , t T} 进行一次试验 (即在 T 上进行一次全程观测) , 其结果是 t 的函数, 记为
x(t) , t T , 称它为随机过程的一个 样 本 函 数 或 样本曲线 .
所有不同的试验结果构成一族样本函数.
随机过程 总体
样本函数 个体
(4)连续参数、连续状态的随机过程。如例3,T=[0,∞], 状态空间为[-∞,∞]。
离散参数的随机过程亦称为随机序列。
四、随机过程的分布函数族
给定随机过程 {X (t),t T}.
对固定的 t T, 随机变量 X (t) 的分布函数一 般与 t 有关, 记为 FX (x,t) P{X (t) x}, x R.
1 0.5
-4
-2
-0.5
2
4
-1
当t固定时,X(t)是随机变量,故{X(t), t>0}是一族随机变量。
另一方面,对随机变量 做一φ次试验得一个试验值 ,
就是一条样本曲线。X (t) a cos(0t )
二、随机过程的概念
1 定义 参数集:设T是实数轴 (, )上的一个子集,且包含无限多
个数。随机过程是一族随机变量,可用 {X (t),t T} 来表示。T称为 随机过程的参数集。
在次概数率是论一中个曾随指机出变,量在,单记位X时(t间)为内[0一,t]电内话的站呼接叫到次的数呼唤 次数可用一离散型随机变量 X()表示,且有
P{X() k} k e , k 0, 1,2, ,( 0)
k! 在[0,t]时间内接到的呼唤次数,这一随机变量可记为X(t)。
P{X(t) k} (t)k et , k 0, 1,2, ,( 0)
《数学随机过程》PPT课件
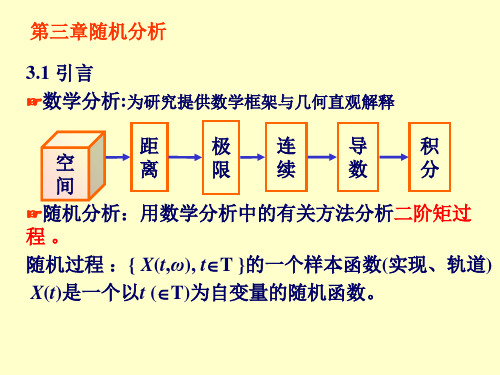
所以X与Y不相关。 故 (X,Y )=0 X与Y不相关
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
《概率论与数理统计》课件-随机过程

《概率论与数理统计》经典课件 -随机过程
目录
• 随机过程基础 • 随机过程的基本类型 • 随机过程的分析与变换 • 随机过程的应用 • 随机过程的计算机模拟 • 随机过程的未来发展与挑战
01
随机过程基础
随机过程的定义与分类
定义
随机过程是由随机变量构成的数 学结构,每个随机变量对应一个 时间点或位置。
分类
根据不同的特性,随机过程可以 分为离散随机过程和连续随机过 程,平稳随机过程和非平稳随机 过程等。
随机过程的统计特性
均值函数
方差函数
自相关函数
谱密度函数
描述随机过程的平均行 为。
描述随机过程的波动程 度。
描述随机过程在不同时 间点的相关性。
描述随机过程的频率特 性。
随机过程的概率模型
01
02
蒙特卡洛方法在金融、物理、工程等领域有广泛应用,如期权定价、核反应堆模拟 等。
离散事件模拟方法
离散事件模拟方法是一种基于 事件驱动的模拟方法,通过模 拟离散事件的发生和影响来逼 近真实系统。
离散事件模拟方法适用于描述 离散状态变化的过程,如交通 流模拟、排队系统模拟等。
离散事件模拟方法的关键在于 事件的时间点和顺序的确定, 以及事件影响的计算。
连续时间模拟方法
连续时间模拟方法是一种基于时间连 续变化的模拟方法,通过模拟时间连 续变化的过程来逼近真实系统。
连续时间模拟方法的关键在于时间步 长的选择和状态变化的计算,需要保 证模拟结果的准确性和稳定性。
连续时间模拟方法适用于描述连续状 态变化的过程,如人口增长模拟、生 态系统模拟等。
06
随机过程的未来发展与挑战
控制系统
利用随机过程理论,分析和设计 控制系统,提高系统的稳定性和
目录
• 随机过程基础 • 随机过程的基本类型 • 随机过程的分析与变换 • 随机过程的应用 • 随机过程的计算机模拟 • 随机过程的未来发展与挑战
01
随机过程基础
随机过程的定义与分类
定义
随机过程是由随机变量构成的数 学结构,每个随机变量对应一个 时间点或位置。
分类
根据不同的特性,随机过程可以 分为离散随机过程和连续随机过 程,平稳随机过程和非平稳随机 过程等。
随机过程的统计特性
均值函数
方差函数
自相关函数
谱密度函数
描述随机过程的平均行 为。
描述随机过程的波动程 度。
描述随机过程在不同时 间点的相关性。
描述随机过程的频率特 性。
随机过程的概率模型
01
02
蒙特卡洛方法在金融、物理、工程等领域有广泛应用,如期权定价、核反应堆模拟 等。
离散事件模拟方法
离散事件模拟方法是一种基于 事件驱动的模拟方法,通过模 拟离散事件的发生和影响来逼 近真实系统。
离散事件模拟方法适用于描述 离散状态变化的过程,如交通 流模拟、排队系统模拟等。
离散事件模拟方法的关键在于 事件的时间点和顺序的确定, 以及事件影响的计算。
连续时间模拟方法
连续时间模拟方法是一种基于时间连 续变化的模拟方法,通过模拟时间连 续变化的过程来逼近真实系统。
连续时间模拟方法的关键在于时间步 长的选择和状态变化的计算,需要保 证模拟结果的准确性和稳定性。
连续时间模拟方法适用于描述连续状 态变化的过程,如人口增长模拟、生 态系统模拟等。
06
随机过程的未来发展与挑战
控制系统
利用随机过程理论,分析和设计 控制系统,提高系统的稳定性和
《随机过程》课件 (2)
随机过程在实际应用中的重要 性
随机过程在许多领域中起到重要的作用,例如金融学、通信工程、物理学、 天气预报等。通过建立和分析随机过程模型,我们可以更好地理解和预测复 杂系统中的随机变化。
2 连续时间
随机过程在连续的时间范围内进行观测和分析。这包括连续的时间流逝和可能具有连续 状态值的过程。
随机过程的性质和特征
随机性
随机过程的结果是不确定的,无法预测每个时间点的具体数值。
时序关联
随机过程的值在时间上相互关联,前一时刻的值对后一时刻的值具有一定的影响。
统计稳定
随机过程具有一定的平稳性质,即其统计性质在时间上保持不变。
《随机过程》PPT课件 (2)用随机过程的例子解释概率论基本概念。随机过程的定义
随机过程是指一种随着时间的推移而产生变化的数学模型。它可以描述在不 同时间发生的随机事件,并提供了一种分析和预测的方法。
随机过程的分类
1 离散时间
随机过程在离散时间点上进行观测和分析。这包括离散的时间步长和离散的状态值。
《随机过程》课件

泊松过程
定义
泊松过程是一种计数随机过程,其事件的发生是 相互独立的,且具有恒定的平均发生率。
例子
放射性衰变、电话呼叫次数、交通事故等。
应用领域
物理学、工程学、保险学等。
03
随机过程的变换与函数
随机过程的线性变换
线性变换的定义
线性变换是指对随机过程中的每个时间点,将该点的随机变量或随机向量乘以一个常数 或矩阵,并加上另一个常数或矩阵。
应用
微分在随机过程的理论和应用中非常重要,例如在金融 领域中,可以通过计算股票价格的导数来预测股票价格 的变动趋势。
积分的定义
随机过程的积分是指对随机过程中的每个时间点,将该 点的随机变量进行积分。
积分的性质
积分运算可以改变随机过程的统计特性,例如期望、方 差和协方差等。
应用
积分在随机过程的理论和应用中也有重要应用,例如在 信号处理中,可以通过对信号进行积分来提取信号的特 征或进行信号的合成。
连续随机过程
01
定义
连续随机过程是在时间或空间上 连续取值的随机现象的数学模型 。
02
03
例子
应用领域
电子信号、温度波动、随机漫步 等。
物理、工程、金融等。
马尔可夫过程
定义
马尔可夫过程是一种特殊的随机过程,其未来状态只依赖于当前 状态,与过去状态无关。
例子
赌徒输赢的过程、天气变化等。
应用领域
统计学、计算机科学、人工智能等。
将随机信号视为随时间变化的随机变量序列,具有时间和概率的统 计特性。
随机模型
根据实际需求建立信号的随机模型,如高斯过程、马尔可夫过程等 。
信号的滤波与预测
滤波器设计
根据随机模型设计滤波 器,用于提取有用信号 或抑制噪声。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
The Gambler’s Ruin Problem
•
$0 $1 $2 $3 $4
1 0 0 0 0
1p 0 p 0 0
P= 0 1p 0 p 0
0
0 1p 0 p
5
5
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
6
6
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
7
7
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
• A continuous –time stochastic process is simply the stochastic process in which the state of the system can be viewed at any time, not just at discrete instants in time.
The study of how a random variable evolves over time includes stochastic processes.
An explanation of stochastic processes – in particular, a type of stochastic process known as a Markov chain is included.
• Let Xt be the value of the system characteristic at time t. In most situations, Xt is not known with certainty before time t and may be viewed as a random variable.
• A discrete-time stochastic process is simply a description of the relation between the random variables X0, X1, X2 …..
14
14
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
11
11
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
The Gambler’s Ruin Problem
• At time 0, I have $2. At times 1, 2, …, I play a game in which I bet $1, with probabilities p, I win the game, and with probability 1 – p, I lose the game. My goal is to increase my capital to $4, and as soon as I do, the game is over. The game is also over if my capital is reduced to 0.
8
8
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
9
9
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.10 Nhomakorabea10
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
整体 概述
2
一 请在这里输入您的主要叙述内容
二
请在这里输入您的主要 叙述内容
三 请在这里输入您的主要叙述内容
2
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
Description
Sometimes we are interested in how a random variable changes over time.
– Let Xt represent my capital position after the time t game (if any) is played
– X0, X1, X2, …. May be viewed as a discrete-time stochastic process
12
12
0 0 0 0 1
PP P
01 2 3
1-P 1-P 1-P
13
13
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
5.1 What is a Stochastic Process?
• Suppose we observe some characteristic of a system at discrete points in time.
We begin by defining the concept of a stochastic process.
3
3
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
4
4
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
Chapter 17 Markov Chains
to accompany Operations Research: Applications & Algorithms,
4th edition, by Wayne L. Winston
1
1
Copyright © 2004 Brooks/Cole, a division of Thomson Learning, Inc.
