正态总体参数的区间估计
正态总体均值的区间估计

的下α/2分位数。
实例二
总结词
在未知总体标准差的情况下,可以使用样本标准差来估 计总体均值的区间。
详细描述
当总体标准差未知时,我们可以使用样本标准差来代替总 体标准差进行区间估计。具体来说,对于一个样本容量为n 的随机样本,其样本均值和样本标准差分别为和s。根据中 心极限定理,当样本容量n足够大时,样本均值近似服从正 态分布,其均值和标准差分别为μ和s/√n。因此,可以使 用μ±Zα/2s/√n来估计总体均值的置信区间。
实例三:小样本下的总体均值区间估计
总结词
在小样本情况下,可以使用t分布的性质来估计总体均 值的区间。
详细描述
当样本容量n较小时,样本均值的标准误差较大,使用 正态分布进行区间估计可能不准确。此时可以使用t分布 进行区间估计。具体来说,对于一个自由度为n-1的t分 布,其上侧分位数记为tα/2(n-1),那么可以使用 μ±tα/2(n-1)s/√n来估计总体均值的置信区间。与正态 分布相比,t分布的尾部更厚,因此在小样本情况下更为 稳健。
THANKS
感谢观看
理论依据
许多统计方法和模型都以正态分布为基础。
实际应用
在自然科学、社会科学和工程领域中,许多 现象都可以用正态分布来描述和分析。
03
总体均值的区间估计方法
样本均值和样本标准差
样本均值
表示样本数据的平均水平,计算公式 为 $bar{x} = frac{1}{n} sum_{i=1}^{n} x_i$,其中 $n$ 是样 本数量,$x_i$ 是每个样本值。
区间估计的应用
区间估计在统计学、经济学、社会学等领域有着广泛的应用。例如,在市场调查中,通过 抽样调查得到样本数据,然后利用区间估计方法估计总体市场占有率或平均价格等指标。
7.8 两个正态总体参数的区间估计

2 1
2 2
)
1
nm
因此,均值差1−2的置信水平1−α的置信区间为
(( X Y ) z 2
2 1
n
2 2
m
,(X
Y
)
z
2
2 1
2 2
)
nm
两个正态总体参数的区间估计
2.均值差1−2的置信区间 (方差12 =22 = 2,但 2 未知情形)
易知 ( X Y ) (1 2 ) ( X Y ) (1 2 ) ~ N (0,1)
枢轴量 T X Y (1 2 ) ~ t(n m 2)
S 1 n 1 m
根据 t分布的性质,取分位数tα/2 (n+m−2) 有
P{|
X Y (1 2 )
S 1 n 1 m
|
t
2(n
m
2)}
1
因此,均值差1−2的置信水平1−α置信区间为
2
(2n)=
2 0.05
(18)=28.869,12
2 (2n)
2 0.95
(18)
9.39
计算得:2nX 1062 1/λ 的置信水平为0.90的置信区间为 ( 1062 , 1062) (36.787,113.099)
28.869 9.39
两个正态总体参数的区间估计
2
,
2 2
m
)
由正态分布的性质可得
X
Y
~
N (1
2
,
2 1
正态总体参数的区间估计实验结论

正态总体参数的区间估计实验结论正态总体参数的区间估计是统计学中一种常用的方法,可以帮助我们估计未知正态总体参数的取值范围。
通过构建置信区间,我们可以在一定的置信水平下对总体参数的取值范围进行估计。
以下是一个关于正态总体参数的区间估计实验结论。
在本实验中,我们以某个地区的成年人男性身高为研究对象,采集了一组样本数据。
通过对样本数据的分析和计算,得出了平均身高和标准差的估计值,并以此构建了置信区间。
首先,我们计算出了样本数据的均值为175cm,并且样本的标准差为5cm。
接下来,我们选择了一个置信水平为95%的置信区间进行计算。
根据正态分布的性质,我们可以使用标准正态分布表来确定置信区间的边界。
通过查表,我们找到了置信水平为95%对应的临界值,记为z。
在本实验中,z的取值为1.96。
然后,我们可以根据样本的均值、标准差和样本容量来计算置信区间的上限和下限。
置信区间的上限计算公式为:上限 = 均值 + z * (标准差/ √样本容量);置信区间的下限计算公式为:下限 = 均值 - z * (标准差/ √样本容量)。
根据实验数据的计算,最终得出了置信区间为(172.04cm,177.96cm)。
这意味着在95%的置信水平下,我们可以合理地推断该地区成年男性的平均身高位于该区间内。
这个实验结论具有以下几个指导意义。
首先,通过正态总体参数的区间估计,我们可以更准确地估计未知总体参数的取值范围,有助于我们了解总体的特征。
其次,通过选择合适的置信水平,我们可以控制估计结果的可靠性和精确度。
在本实验中,我们选择了95%的置信水平,意味着我们有95%的把握让估计结果覆盖真实总体参数。
最后,置信区间的上下限提供了关于总体参数范围的重要信息,可以用来支持决策和制定策略。
总之,正态总体参数的区间估计是一种重要的统计方法,可以为我们提供对未知总体参数取值范围的估计。
通过该方法,我们可以在一定的置信水平下对总体参数进行准确的估计,从而为实际问题的分析和决策提供科学依据。
正态总体均值及方差的区间估计

第十九讲 正态总体均值及方差的区间估计1. 单个正态总体方差的区间估计设总体),(~2σμN X , ),,(21n X X X 为来自X 的一个样本,已给定置信度(水平)为α-1,求2σ的置信区间。
①当μ已知时,由于),(~2σμN X i ,因此,)1,0(~N X i σμ-(,2,1=i n , )。
由2χ分布的定义知:∑=-ni i n X 1222)(~)(χσμ,据)(2n χ分布上α分位点的定义,有:αχσμχαα-=<-<∑=-1)}()()({21222122n X n P ni i从而αχμσχμαα-=⎪⎪⎭⎪⎪⎬⎫-<<⎪⎪⎩⎪⎪⎨⎧--=-∑∑1)()()()(2112221222n X n X P ni i ni i 故2σ的置信度为α-1的置信区间为:⎪⎪⎪⎪⎭⎫ ⎝⎛---==∑∑)()(,)()(211221222n X n X ni i n i i ααχμχμ ②当μ未知时,据抽样分布有:)1(~)1(222--n S n χσ类似以上过程,得到第七章 参数估计第5节 正态总体均值及方差的区间估计单个正态总体均值的区间估计 ①当2σ已知时,μ的置信水平为α-1的置信区间为:⎪⎪⎭⎫ ⎝⎛±2ασz n X (5.1) ②当2σ未知时,μ的置信水平为α-1的置信区间为⎪⎪⎭⎫ ⎝⎛-±)1(2n t n SX α.(5.4)注意:当分布不对称时,如2χ分布和F 分布,习惯上仍然取其对称的分位点,来确定置信区间,但所得区间不是最短的。
αχσχαα-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--<<---1)1()1()1()1(21222222n S n n S n P 2σ的置信度为α-1的置信区间为:⎪⎪⎭⎫⎝⎛-----)1()1(,)1()1(2122222n S n n S n ααχχ σ的置信度为α-1的置信区间为:⎪⎪⎪⎭⎫ ⎝⎛-----)1()1(,)1()1(2122222n S n n S n ααχχ 例2 有一大批袋装糖果, 现从中随机地取出16袋, 称得重量(以克计)如下:506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496 设袋装糖果的重量近似地服从正态分布, 求总体标准差σ的置信水平为0.95的置信区间.解:总体均值μ未知,σ的置信度为α-1的置信区间为:⎪⎪⎪⎭⎫ ⎝⎛-----)1()1(,)1()1(2122222n S n n S n ααχχ 此时,,975.021,025.02,05.0=-==ααα16=n ,查表得,488.27)15(025.0=χ,262.6)15(975.0=χ由给出的数据算得.4667.382=s 因此,σ的一个置信度为0.95的置信区间为(4.58,9.60).2. 两个正态总体均值差的区间估计设总体),(~),,(~222211σμσμN Y N X ,且X 与Y 相互独立,),,(21m X X X 来自X 的一个样本,),,,(21n Y Y Y 为来自Y 的一个样本,且设2221,,,S S Y X 分别为总体X 与Y 的样本均值与样本方差,对给定置信水平α-1,求21μμ-的一个置信区间。
第五节正态总体参数的区间估计汇总

解: Q S 2 是 2 的无偏估计,且统计量:
(n 1)S 2
2
~ 2(n 1)
是不依赖于任何未知参数的。
概率统计
故对于给定的置信水平,
按照 2分布的上 分
位点的定义有:
P
{|
(n
1)
2
s2
|
2
2(n
1)}
1
从中解得:
P{
求: 的 95% 的置信区间.
X
解: 由已知: Q 1 95% 5%,
n
~ N (0,1)
查正态分布表得: z z0.05 z0.025
((z0.025 ) 1 0.025 0.975)
2
2
u(1 0.025) 1.96
得:
0.029
n
z
2
1.96 0.014 16
概率统计
例4. 求 例3 中的 (1), (2)两种情况下, 2 的置信度为
0.9 的置信区间.
(1) 用金球测定观察值为: 6. 683, 6. 681, 6. 676,
取统计量:
解: 在(1)中
6. 678, 6. 679, 6. 672
(n 1) s2 (6从而 的 95%的置信区间为:
(2.705 0.014, 2.705 0.014) (2.691, 2.719)
即用 X 2.705 来估计 值的可靠程度达到 95%
的区间范围是 (2.691, 2.719)
(2). 方差 2 未知的情形
Q 2 未知,但考虑到样本方差是 2的无偏估计,
2
1
2(n
1)
(n 1)S 2
7.5正态总体均值与方差的区间估计

1)
1,
即
P
X
S n t / 2 (n 1)
X
S n
t
/
2
(n
1)
1
,
于是得 的置信度为 1 的置信区间
X
S n
t
/
2
(n
1)
.
例1 有一大批糖果, 现从中随机地取16袋, 称得
重量(克)如下:
506 508 499 503 504 510 497 512
514 505 493 496 506 502 509 496
2
2
/
2
(n
1)
1,
即
(n 1)S 2
P
2
/
2
(
n
1)
2
(n 1)S 2
2 1
/
2
(n
1)
1 ,
于是得方差 2 的置信度为1 的置信区间
(n
2 /
1)S 2(n
2
1)
,
(n
2 1
/2
1)S 2 (n 1)
.
进一步可得:
标准差 的一个置信度为1 的置信区间
n 1S ,
只要n1和n2都很大(实用上 50即可), 则有
1 2的一个置信度为1 的近似置信区间
X
Y
z / 2
S12 n1
S22 n2
.
(3)
2 1
22
2,
但 2 为未知,
1 2的一个置信度为1 的置信区间
X Y t / 2(n1 n2 2)Sw
1 n1
1 n2
.
其中
Sw2
2. 两个总体方差比 12 的置信区间 22
总体参数的区间估计公式

总体参数的区间估计公式在进行区间估计时,我们首先需要收集到一个样本,并根据样本对总体参数进行估计。
然后根据样本的统计量,结合分布的性质和抽样方法,建立置信区间。
设总体参数为θ,我们希望得到它的置信水平为1-α的置信区间。
置信水平表示我们对总体参数的估计的可信程度,一般常用的置信水平有90%、95%和99%等。
参数估计的方法有很多,具体的方法选择取决于总体参数的性质、样本的大小以及其他假设条件。
常见的参数估计方法有:1.总体均值的区间估计:假设总体呈正态分布,样本大小为n,则总体均值的区间估计公式为:[样本均值-Z值(α/2)*总体标准差/√(n),样本均值+Z值(α/2)*总体标准差/√(n)]其中Z值(α/2)为标准正态分布的分位数,可以从标准正态分布表中查得。
2.总体比例的区间估计:假设总体为二项分布,样本大小为n,成功的次数为x,则总体比例的区间估计公式为:[样本比例-Z值(α/2)*√(样本比例*(1-样本比例)/n),样本比例+Z值(α/2)*√(样本比例*(1-样本比例)/n)]其中Z值(α/2)为标准正态分布的分位数,可以从标准正态分布表中查得。
3.总体方差的区间估计:假设总体呈正态分布,样本大小为n,则总体方差的区间估计公式为:[(n-1)*样本方差/卡方分布(α/2),(n-1)*样本方差/卡方分布(1-α/2])]其中卡方分布是用于描述自由度为n-1的卡方随机变量的概率分布,可以从卡方分布表中查得。
以上是常见的总体参数区间估计公式,这些公式是根据统计学理论推导而来的,适用于不同情况下的参数估计。
在实际应用中,我们根据具体问题和假设条件选择适当的参数估计方法,计算置信水平的区间估计,从而对总体参数进行估计和推断。
正态总体参数的区间估计实验结论

正态总体参数的区间估计实验结论在统计学中,正态分布是一种非常重要的分布,许多自然现象和实验数据都可以用正态分布来描述。
而在实际应用中,我们常常需要估计正态总体的参数,比如均值和标准差。
在这篇文章中,我将介绍如何利用区间估计的方法来估计正态总体的参数,并给出一个实验结论。
让我们来回顾一下区间估计的基本原理。
区间估计是通过样本数据来估计总体参数的一种方法,其核心思想是利用样本数据给出一个参数的估计区间,该区间包含真实参数的概率较高。
在正态总体参数的区间估计中,我们通常使用样本均值和样本标准差来进行估计。
接下来,我将介绍一个实际的例子来说明正态总体参数的区间估计方法。
假设我们有一批产品的重量数据,我们想要估计这批产品的平均重量。
我们随机抽取了一部分产品进行称重,得到了样本均值和样本标准差。
根据中心极限定理,我们知道样本均值的分布是正态分布的,可以利用这一性质来构建参数的置信区间。
假设我们得到的样本均值为100,样本标准差为5,样本量为30。
我们可以利用正态分布的性质来构建样本均值的置信区间,假设置信水平为95%,那么我们可以计算出置信区间为(98, 102)。
这意味着在95%的置信水平下,真实的总体平均重量落在98到102之间。
通过这个简单的例子,我们可以看到区间估计的重要性和实际应用。
在实际问题中,我们往往无法得知总体参数的真实值,只能通过样本数据来进行估计。
区间估计可以帮助我们对参数的估计进行更准确的评估,同时也可以给出参数估计的不确定性范围。
总的来说,正态总体参数的区间估计是统计学中一种常用的方法,通过构建置信区间来估计总体参数的真实值。
在实际应用中,我们可以根据样本数据来进行参数的估计,同时也可以评估参数估计的置信水平。
通过区间估计的方法,我们可以更准确地了解总体参数的情况,为决策提供更可靠的依据。
希望本文能帮助读者更好地理解正态总体参数的区间估计方法,并在实际问题中应用到实践中。
正态分布总体的区间估计与假设检验汇总表
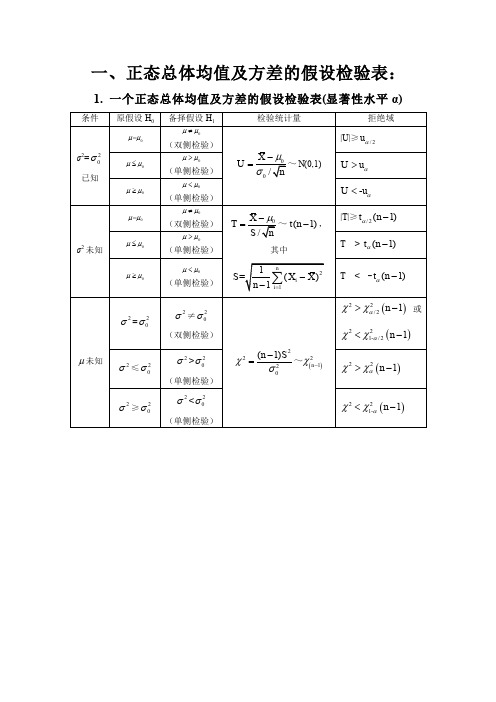
(单侧检验)
2
(n
1)S 2
2 0
~2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
(单侧检验)
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
,
2 2
已知
1 =2 1 2 1 2
1 2
1 2
(单侧检验)
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1,2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
(双侧检验)
2 1
>
2 2
(单侧检验)
F
S12 S22
~
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ~ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
~2n1
(n 2 /
1)S 2
正态总体参数的区间估计

总体均值μ的区间估计是一种基于抽样 调查的方法,通过样本均值和标准差 来估计总体均值的范围,常用t分布或z 分布计算置信区间。
详细描述
在进行总体均值μ的区间估计时,首先 需要收集样本数据,计算样本均值和 标准差。然后,根据样本数据的大小 和置信水平,选择适当的分布(如t分 布或z分布)来计算置信区间。最后, 根据置信区间的大小和分布特性,可 以得出总体均值μ的可能取值范围。
正态分布的性质
集中性
正态分布的曲线关于均值μ对称。
均匀变动性
随着x的增大,f(x)逐渐减小,但速 度逐渐减慢。
随机变动性
在μ两侧对称的位置上,离μ越远, f(x)越小。
正态分布在生活中的应用
金融
正态分布在金融领域的应用十分 广泛,如股票价格、收益率等金 融变量的分布通常被假定为正态 分布。
生物医学
THANKS
感谢观看
实例二:总体方差的区间估计
总结词
在正态分布下,总体方差的区间估计可以通过样本方 差和样本大小来计算。
详细描述
当总体服从正态分布时,根据中心极限定理,样本方差 近似服从卡方分布。因此,总体方差σ²的置信区间可以 通过以下公式计算:$[s^2 cdot frac{n - 1}{n} cdot F^{-1}(1 - frac{alpha}{2}), s^2 cdot frac{n - 1}{n} cdot F^{-1}(1 - frac{alpha}{2})]$,其中$s^2$是样本 方差,$n$是样本容量,$F^{-1}$是自由度为1的卡方 分布的逆函数,$alpha$是显著性水平。
详细描述
当总体服从正态分布时,根据中心极限定理,样本均值 近似服从正态分布。因此,总体均值μ的置信区间可以通 过以下公式计算:$[bar{x} - frac{s}{sqrt{n}} cdot Phi^{-1}(1 - frac{alpha}{2}), bar{x} + frac{s}{sqrt{n}} cdot Phi^{-1}(1 - frac{alpha}{2})]$,其中$bar{x}$是样 本均值,$s$是样本标准差,$n$是样本容量,$Phi^{1}$是标准正态分布的逆函数,$alpha$是显著性水平。
7.9 单正态总体参数的区间估计(1)

概率论与数理统计
07
参数估计
问题
如何让与θ的误差体现在估计中?ˆθ•湖中鱼数的真值[ ]对给定的置信水平(置信度)1-α
办法称为未知参数θ的置信度为1-α的置信区间.12
ˆˆ(,)θθ置信下限(X 1, X 2, …, X n )和置信上限(X 1, X 2, …, X n )1ˆθ2
ˆθ12
ˆˆ()1P θθθα<<≥−使含义若1-α=0.95,抽样100次中约有95个包含θ.12
ˆˆ(,)θθ
单个正态总体均值的区间估计σ2已知μ的置信度为1-α的置信区间为2~(,)
X N n
σμ/2()1/X P u n
αμασ−<=−/2/2()1P X u X u n n αασσμα−<<+=−/2/2(,);X u X u n n αασσ−+/2()
X u n ασ±2~(0,1)n X N σμ−
➢置信区间长度注➢相同置信水平下,置信区间选取不唯一.
l = 2σn u α/2 /2/2(,)
X u X u n n αασσ−+单个正态总体均值的区间估计
例滚珠直径X ~N (μ, 0.0006),从某天生产的滚珠中随机抽取6个,测得直径为(单位:mm) 1.46 1.51 1.49 1.48 1.52 1.51
求μ 的置信度为95%的置信区间.解/2/2(,)
X u X u n n αασσ−+单个正态总体均值的区间估计
1.495x =,0.05α=,
0.05/20.025 1.96u u ==0.0006(1.495 1.96)6±⨯(1.4754,1.5146)=。
正态分布总体均值和方差的区间估计

(n
1)
1
因此,当总体 N (, 2 ) 中的参数
为未知的情况下,方差 2的置信区间为
(n 1)s2
2 1
(n
1)
2
,
(n 1)s2
2
2
(n
1)
注 临界值 2 (n 1), 2 (n 1)不是唯一的。
2
1 2
可以选取
2 (n 1), 2 (n 1)
2
1
3
3
例5:某自动车床生产的零件,其长度X服从 正态分布,现抽取16个零件,测得长度(单 位:mm)如下:
s
2 2
是分别来自于两总体
且容量各为m和n的独立样本的方差。
考虑统计量 由于
s12 / s22
12
/
2 2
(m 1)s12
2 1
~
2 (m 1)
(n 1)s22 ~ 2 (n 1)
2 2
所以
(m 1)s12
2 1
/(m
1)
(n
1)
s
2 2
/(n
1)
2 2
s12
12
/ s22
/
2 2
~
F(m 1, n 1)
1 x (14.6 15.1 14.9 14.8 15.2 15.1) 14.95
6
2 0.06, 0.06
x1.96
14.95 1.96
0.06 14.75
n
6
x 1.96
14.95 1.96
0.06 15.15
n
6
故所求置信区间为 14.75,15.15
n 注 对于不是服从正态分布的总体,只要
正态总体参数的区间估计实验结论

正态总体参数的区间估计实验结论引言:在统计学中,参数估计是一项重要的工作,通过样本数据来对总体参数进行估计。
而对于正态总体参数的估计,我们通常使用区间估计的方法来得出结果。
本文将介绍正态总体参数的区间估计实验的结论,并对其意义进行探讨。
实验方法:为了进行正态总体参数的区间估计实验,我们首先需要收集一定数量的样本数据。
然后,根据这些数据的特征,我们可以计算出样本均值和样本标准差。
接下来,我们可以使用统计学中的方法,如t 分布或z分布,来计算出参数的置信区间。
实验结果:经过实验计算,我们得出了正态总体参数的区间估计结果。
以均值为例,我们可以得到一个置信区间,表示在给定置信水平下,总体均值可能位于该区间内。
例如,我们得出了一个95%的置信区间为(μ1, μ2)。
解释和讨论:正态总体参数的区间估计结果是基于样本数据得出的,因此其准确性和可靠性需要进行评估。
在本实验中,我们选择了95%的置信水平,这意味着在重复进行实验的情况下,我们可以有95%的信心认为总体参数位于所得的置信区间内。
区间估计的结果对于统计推断和决策具有重要意义。
在实际应用中,我们可以根据置信区间的上下限来进行决策或评估。
如果待估计的参数值落在置信区间内,我们可以认为该参数是可接受的。
反之,如果参数值超出置信区间,我们可能需要进一步调查或采取相应的行动。
除了均值,我们还可以对正态总体的其他参数进行区间估计,如标准差或方差。
这些参数的区间估计结果也可以为我们提供有关总体特征的重要信息。
总结:正态总体参数的区间估计是统计学中常用的方法之一,可以帮助我们对总体特征进行推断和决策。
本文介绍了正态总体参数区间估计实验的结论,并讨论了其意义和应用。
通过区间估计,我们可以对总体参数进行准确且可靠的估计,为实际问题的解决提供重要依据。
参考文献:[1] 赵建华, 刘曙光. 结果的区间估计[J]. 数学的实践与认识, 2006(06):44-47.[2] 李凯锋. 正态总体参数的区间估计[J]. 统计与决策, 2009, (17):96-97.[3] 陈杰, 窦令媛. 正态总体参数的区间估计及应用[J]. 现代商贸工业,2019(03):93-94.。
第7章 参数估计7.5 正态总体均值与方差的区间估计

续例) 续例 求补充1中总体标准差 例2 (续例 求补充 中总体标准差σ 的置信度为 0.95的置信区间 的置信区间. 的置信区间 解
α
2
975,
n − 1 = 15,
附表2-2 附表
查 χ 2 ( n − 1) 分布表可知 :
= 1 − α,
即
S12 σ12 S12 1 1 P 2 < 2< 2 S2 F1−α / 2 (n1 − 1, n2 − 1) S2 Fα / 2 (n1 − 1, n2 − 1) σ 2
2 S12 S1 1 1 2 . , 2 S F (n − 1, n − 1) S F (n1 − 1, n2 − 1) 2 1−α / 2 2 α/2 1 2
注意: 在密度函数不对称时,如χ 2 分布和 F分布, 注意: 在密度函数不对称时, 习惯上仍取对称的分位点来确定置信区间(如图). 习惯上仍取对称的分位点来确定置信区间(如图).
二、两个总体 N ( µ1 ,σ ), N ( µ 2 ,σ )的情况
2 1 2 2
设给定置信度为1 − α , 并设 X 1 , X 2 ,L, X n 为
σ 于是得 的一个置信度为1 − α 的置信区间 σ
2 1 2 2
= 1 − α,
例5
2
生产的钢管内径, 研究由机器 A 和机器 B 生产的钢管内径
随机抽取机器 A 生产的管子 18 只, 测得样本方差
为s1 = 0.34(mm 2 ); 抽取机器 生产的管子 13 只, 抽取机器B生产的管子
2 测得样本方差 s 2 = 0.29(mm 2 ). 设两样本相互独
其中
正态分布参数区间估计

正态分布N (μ,σ)参数区间估计允许μ为任意的实数,σ为任意的正实数。
基于Wolfram Mathematica ,给出了正态分布N (μ,σ)抽样定理,从而得到参数μ,σ2,σ的区间估计。
在σ已知和未知情形下,通过均值分布、中位值分布、卡方分布三种方法估计总体均值μ,区间长度均值分布最短,卡方分布次之,中位值分布最长,但当样本量n 较大时,区间长度趋于接近。
在μ已知和未知情形下,通过卡方分布可以估计总体方差的置信区间,通过卡分布、卡方分布可以估计总体标准差的置信区间。
最后给出不同情形下不同方法的MMA 程序及运行结果。
◼抽样分布定理引理1:X Ν(μ,σ)⇔X -μσΝ 0,1 .转换分布TransformedDistributionX -μσ,X 正态分布NormalDistribution [μ,σ]NormalDistribution [0,1]转换分布TransformedDistribution [μ+X σ,X 正态分布NormalDistribution [],假设Assumptions →σ>0]NormalDistribution [μ,σ]引理2:X χ(ν)⇔X 2 χ2(ν).转换分布TransformedDistribution X 2,X 卡分布ChiDistribution [ν]ChiSquareDistribution [ν]转换分布TransformedDistribution X ,X 卡方分布ChiSquareDistribution [ν]ChiDistribution [ν]引理3:X Ν 0,1 ,Y χ2(n )⇒Xt (n ).=转换分布TransformedDistributionX,{X 正态分布NormalDistribution [],Y 卡方分布ChiSquareDistribution [n ]} ;概率密度函数PDF [ ,x ]==⋯PDF [学生t 分布StudentTDistribution [n ],x ]//幂展开PowerExpand //完全简化FullSimplify [#,n >0&&x ≠0]&True定理1:X i Ν(μ,σ)⇒X -Νμ,σn⇔X --μσnΝ 0,1 .CharacteristicFunction NormalDistribution [μ,σ],t nn;特征函数CharacteristicFunction 正态分布NormalDistribution μ,σn,t ;%⩵%%//完全简化FullSimplify [#,n >0&&n ∈整数域Integers ]&True定理2:X i Ν(μ,σ)⇒ i =1nX i -μσ2=∑i =1n (X i -μ)2σ2χ2(n )⇔σχ(n ).转换分布TransformedDistributionX [i ]-μσ,X [i ] 正态分布NormalDistribution [μ,σ]NormalDistribution [0,1]n =7;=转换分布TransformedDistribution i =1nY [i ]2,数组Array [Y,n ] 联合分布ProductDistribution [{正态分布NormalDistribution [],n }]ChiSquareDistribution [7]定理3:X i Ν(μ,σ)⇒(n -1)S 2σ2χ2 n -1⇔σχ n -1 .令Y i =X i -μσ,则(n -1)S 2σ2=i =1n2=i =1n-= i =1nY i -Y 2= i =1nY i 2-2Y Y i +Y 2= i =1nY i 2-2Y i =1nY i +n Y 2= i =1nY i 2-n Y 2χ2n -1 ⇒σχ n -1 .2 正态分布\\正态分布统计分析\\正态分布参数区间估计.nbn =n0=35;=转换分布TransformedDistribution i =1nY [i ]2-1ni =1nY [i ]2,数组Array [Y,n ] 联合分布ProductDistribution [{正态分布NormalDistribution [],n }] ;Block {n =n0},显示Show 直方图Histogram 伪随机变数RandomVariate ,2×106 ,500,"概率密度函数PDF" ,绘图Plot [⋯PDF [卡方分布ChiSquareDistribution [n -1],x ],{x,5,65},绘图样式PlotStyle →粗Thick ]定理4:X i Ν(μ,σ)⇒X --μSnt n -1 .根据定理1,得X iΝ(μ,σ)⇒X --μσnΝ 0,1 ,根据定理3,得(n -1)S 2σ2χ2 n -1 ,根据引理3,X --μσn=X --μSnt n -1 .定理5:F Xn +12=正则化的不完全贝塔函数BetaRegularized12补余误差函数Erfc-x +μ2σ ,1+n2,1+n 2,n =2k +1.次序分布OrderDistribution {正态分布NormalDistribution [μ,σ],n },n +12;累积分布函数CDF [%,x ]//完全简化FullSimplifyBetaRegularized 12Erfc ,1+n 2,1+n 2推论:μ=x +2σ反互补误差函数InverseErfc 2正规化不完全贝塔函数的逆InverseBetaRegularized q,1+n 2,1+n 2.In[2]:=解方程Solve 正则化的不完全贝塔函数BetaRegularized12补余误差函数Erfc-x +μ2σ ,1+n 2,1+n 2⩵q,μOut[2]=μ→x +2σInverseErfc 2InverseBetaRegularized q,1+n 2,1+n 2定理6:-2 i =1n对数Log12补余误差函数Erfc-X i +μ2σχ2 2n .正态分布\\正态分布统计分析\\正态分布参数区间估计.nb3In[5]:=转换分布TransformedDistribution -2对数Log12补余误差函数Erfc-X +μ2σ,X 正态分布NormalDistribution [μ,σ] ;概率密度函数PDF [%,x ]⩵⋯PDF [卡方分布ChiSquareDistribution [2],x ]//完全简化FullSimplify [#,x >0]&Out[6]=True**参数区间估计**In[7]:=需要Needs ["HypothesisTesting`"]μ0=20;σ0=3;X =伪随机变数RandomVariate [正态分布NormalDistribution [μ0,σ0],10001];n =长度Length [X ];S =标准偏差StandardDeviation [X ];α=0.01;"参数的极大似然估计:"清除Clear [μ,σ]{μ1,σ1}={μ,σ}/.求分布参数FindDistributionParameters [X,正态分布NormalDistribution [μ,σ]]"一、总体均值μ的区间估计""(一)均值分布U =X --μσnN(0,1)——σ已知"σ=σ0;Sw =σn ;m =平均值Mean [X ];"1.计算法"Q =分位数Quantile 正态分布NormalDistribution [0,1],1-α 2 ;{m -Sw Q,m +Sw Q }"2.MeanCI"MeanCI X,KnownVariance →σ2,置信级别ConfidenceLevel →1-α"3.NormalCI"NormalCI [m,Sw ,置信级别ConfidenceLevel →1-α]"区间长度:"L =2Sw Q"相对区间长度:"r =L /m "(二)均值分布T =X -μSnt (n -1)——σ未知""1.计算法"Sw =S n ;m =平均值Mean [X ];Q =分位数Quantile 学生t 分布StudentTDistribution [n -1],1-α 2 ;{m -Sw Q,m +Sw Q }4 正态分布\\正态分布统计分析\\正态分布参数区间估计.nb"2.MeanCI"MeanCI [X,KnownVariance →无None,置信级别ConfidenceLevel →1-α]"3.StudentTCI"StudentTCI [m ,Sw ,n -2,置信级别ConfidenceLevel →1-α]"区间长度:"L =2Sw Q"相对区间长度:"r =L /m"(三)均值近似分布U =X --μσn~N[0,1]——σ未知""1.计算法"σ=σ1;Sw =σn ;m =平均值Mean [X ];Q =分位数Quantile 正态分布NormalDistribution [0,1],1-α 2 ;{m -Sw Q,m +Sw Q }"2.MeanCI"MeanCI X,KnownVariance →σ12,置信级别ConfidenceLevel →1-α"3.NormalCI"NormalCI [m,Sw ,置信级别ConfidenceLevel →1-α]"区间长度:"L =2Sw Q"相对区间长度:"r =L /m"(四)中位值分布F Xn +12=正则化的不完全贝⋯BetaRegularized [12补余误差函数Erfc [-x +μ2σ],1+n 2,1+n2],n =2k +1——σ已知""1.等尾区间:"σ=σ0;x =中位数Median [X ];μL =x +2σ反互补误差函数InverseErfc 2正规化不完全贝塔函数的逆InverseBetaRegularized 1-α 2,1+n 2,1+n 2;μU =x +2σ反互补误差函数InverseErfc 2正规化不完全贝塔函数的逆InverseBetaRegularized α 2,1+n 2,1+n 2;{μL,μU }"等尾区间长度:"L =μU -μL"相对区间长度:"r =2L μU +μL "(五)中位值分布F Xn +12=正则化的不完全贝⋯BetaRegularized [12补余误差函数Erfc [-x +μ2σ ],1+n 2,1+n2],n =2k +1——σ未知""1.等尾区间:"σ=σ1;x =中位数Median [X ];正态分布\\正态分布统计分析\\正态分布参数区间估计.nb5中位数μL =x +2σ反互补误差函数InverseErfc 2正规化不完全贝塔函数的逆InverseBetaRegularized 1-α 2,1+n 2,1+n 2;μU =x +2σ反互补误差函数InverseErfc 2正规化不完全贝塔函数的逆InverseBetaRegularized α 2,1+n 2,1+n 2;{μL,μU }"等尾区间长度:"L =μU -μL"相对区间长度:"r =2L μU +μL"(六)卡方分布-2 i =1n对数Log [12补余误差函数Erfc [-X i +μ2σ]] χ2(2n )——σ已知"清除Clear [μ]σ=σ0;x =-2 i =1n对数Log12补余误差函数Erfc-X i +μ2σ;F =卡方分布ChiSquareDistribution [2n ];μL =μ/.求根FindRoot 累积分布函数CDF [F,x ]==α2,{μ,μ1} ;μU =μ/.求根FindRoot 累积分布函数CDF [F,x ]⩵1-α2,{μ,μ1} ;{μL,μU }"等尾区间长度:"L =μU -μL"相对区间长度:"r =2L μU +μL"(七)卡方分布-2 i =1n对数Log [12补余误差函数Erfc [-X i +μ2σ ]]~χ2(2n )——σ未知"清除Clear [μ]σ=σ0;x =-2 i =1n对数Log12补余误差函数Erfc-X i +μ2σ;F =卡方分布ChiSquareDistribution [2n ];μL =μ/.求根FindRoot 累积分布函数CDF [F,x ]==α2,{μ,μ1} ;μU =μ/.求根FindRoot 累积分布函数CDF [F,x ]⩵1-α2,{μ,μ1} ;{μL,μU }"等尾区间长度:"L =μU -μL"相对区间长度:"6 正态分布\\正态分布统计分析\\正态分布参数区间估计.nbr =2L μU +μL"二、总体方差σ2的区间估计""(一)卡方分布χ2=∑i =1n (X i -μ)2σ2χ2(n )——μ已知"μ=μ0;T =n 平均值Mean (X -μ)2 ;F =卡方分布ChiSquareDistribution [n ];"1.等尾区间:"QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;VL =T QL;VU =T QU;{VL,VU }"等尾区间长度:"L =VU -VL"相对区间长度:"r =2L VL +VU "(二)卡方分布χ2=(n -1)S 2σ2χ2(n -1)——μ未知"T = n -1 S 2;F =卡方分布ChiSquareDistribution [n -1];"1.等尾区间:"QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;VL =T QL;VU =T QU;{VL,VU }"等尾区间长度:"L =VU -VL"相对区间长度:"r =2L VL +VU "(三)卡方分布χ2=∑i =1n (X i -μ )2σ2~χ2(n )——μ未知"μ=μ1;T =n 平均值Mean (X -μ)2 ;F =卡方分布ChiSquareDistribution [n ];"1.等尾区间:"QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;VL =T QL;VU =T QU;{VL,VU }"等尾区间长度:"L =VU -VL"相对区间长度:"r =2L VL +VU"三、总体标准差σ的区间估计""(一)卡分布χ(n )——μ已知"μ=μ0;T =n Mean (X -μ)2 ;F =卡分布ChiDistribution [n ];"1.等尾区间:"正态分布\\正态分布统计分析\\正态分布参数区间估计.nb7QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;σL =T QL;σU =T QU;{σL,σU }"等尾区间长度:"L =σU -σL"相对区间长度:"r =2L σL +σU "(二)卡分布χ(n -1)——μ未知"T =n -1S;F =卡分布ChiDistribution [n -1];"1.等尾区间:"QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;σL =T QL;σU =T QU;{σL,σU }"等尾区间长度:"L =σU -σL"相对区间长度:"r =2L σL +σU "(三)卡分布χχ(n )——μ未知"μ=μ1;T =n Mean (X -μ)2 ;F =卡分布ChiDistribution [n ];"1.等尾区间:"QL =分位数Quantile F,1-α 2 ;QU =分位数Quantile F,α 2 ;σL =T QL;σU =T QU;{σL,σU }"等尾区间长度:"L =σU -σL"相对区间长度:"r =2L σL +σU "(四)卡方分布-2 i =1n对数Log [12补余误差函数Erfc [-X i +μ2σ]] χ2(2n )——μ已知"清除Clear [σ]μ=μ0;x =-2 i =1n对数Log12补余误差函数Erfc-X i +μ2σ;F =卡方分布ChiSquareDistribution [2n ];σL =σ/.求根FindRoot 累积分布函数CDF [F,x ]⩵1-α2,{σ,σ1} ;σU =σ/.求根FindRoot 累积分布函数CDF [F,x ]⩵α2,{σ,σ1} ;{σL,σU }8 正态分布\\正态分布统计分析\\正态分布参数区间估计.nb"等尾区间长度:"L =σU -σL"相对区间长度:"r =2L σL +σU"(五)卡方分布-2 i =1n对数Log [12补余误差函数Erfc [-X i +μ2σ]] χ2(2n )——μ未知"清除Clear [σ]μ=μ1;x =-2 i =1n对数Log12补余误差函数Erfc-X i +μ2σ;F =卡方分布ChiSquareDistribution [2n ];σL =σ/.求根FindRoot 累积分布函数CDF [F,x ]⩵1-α2,{σ,σ1} ;σU =σ/.求根FindRoot 累积分布函数CDF [F,x ]⩵α2,{σ,σ1} ;{σL,σU }"等尾区间长度:"L =σU -σL"相对区间长度:"r =2L σL +σUOut[11]=参数的极大似然估计:Out[13]={19.9803,3.00134}Out[14]=一、总体均值μ的区间估计Out[15]=(一)均值分布U =X --μσnN(0,1)——σ已知Out[17]=1.计算法Out[19]={19.9031,20.0576}Out[20]=2.MeanCIOut[21]={19.9031,20.0576}Out[22]=3.NormalCIOut[23]={19.9031,20.0576}Out[24]=区间长度:Out[25]=0.154542Out[26]=相对区间长度:Out[27]=0.00773471Out[28]=(二)均值分布T =X -μSn t (n -1)——σ未知正态分布\\正态分布统计分析\\正态分布参数区间估计.nb9Out[29]= 1.计算法Out[32]={19.903,20.0577} Out[33]= 2.MeanCIOut[34]={19.903,20.0577} Out[35]= 3.StudentTCIOut[36]={19.903,20.0577} Out[37]=区间长度:Out[38]=0.154648Out[39]=相对区间长度:Out[40]=0.00774003Out[41]=(三)均值近似分布U=X--μσ n~N[0,1]——σ未知Out[42]= 1.计算法Out[45]={19.903,20.0576} Out[46]= 2.MeanCIOut[47]={19.903,20.0576} Out[48]= 3.NormalCIOut[49]={19.903,20.0576} Out[50]=区间长度:Out[51]=0.154611Out[52]=相对区间长度:Out[53]=0.00773817Out[54]=(四)中位值分布F X n+12=BetaRegularized[12Erfc,1+n2,1+n2],n=2k+1——σ已知Out[55]= 1.等尾区间:Out[59]={19.8529,20.0466} Out[60]=等尾区间长度:Out[61]=0.193686Out[62]=相对区间长度:Out[63]=0.00970872Out[64]=(五)中位值分布F X n+12=BetaRegularized[12Erfc,1+n2,1+n2],n=2k+1——σ未知Out[65]= 1.等尾区间:Out[69]={19.8529,20.0466}Out[70]=等尾区间长度:10正态分布\\正态分布统计分析\\正态分布参数区间估计.nbOut[71]=0.193773Out[72]=相对区间长度:Out[73]=0.00971306Out[74]=(六)卡方分布-2 i =1n Log [12Erfcχ2(2n )——σ已知Out[78]={19.9015,20.0722}Out[79]=等尾区间长度:Out[80]=0.170753Out[81]=相对区间长度:Out[82]=0.00854324Out[83]=(七)卡方分布-2 i =1n Log [12Erfcχ2(2n )——σ未知Out[87]={19.9015,20.0722}Out[88]=等尾区间长度:Out[89]=0.170753Out[90]=相对区间长度:Out[91]=0.00854324Out[92]=二、总体方差σ2的区间估计Out[93]=(一)卡方分布χ2=∑i =1n (X i -μ)2σ2 χ2(n )——μ已知Out[95]= 1.等尾区间:Out[98]={8.68869,9.34535}Out[99]=等尾区间长度:Out[100]=0.656658Out[101]=相对区间长度:Out[102]=0.0728243Out[103]=(二)卡方分布χ2=(n -1)S 2σ2 χ2(n -1)——μ未知Out[105]= 1.等尾区间:Out[108]={8.68917,9.3459}Out[109]=等尾区间长度:Out[110]=0.656728Out[111]=相对区间长度:Out[112]=0.0728279Out[113]=(三)卡方分布χ2=∑i =1n (X i -μ )2σ2~χ2(n )——μ未知正态分布\\正态分布统计分析\\正态分布参数区间估计.nb 11Out[115]= 1.等尾区间:Out[118]={8.68832,9.34495}Out[119]=等尾区间长度:Out[120]=0.65663Out[121]=相对区间长度:Out[122]=0.0728243Out[123]=三、总体标准差σ的区间估计Out[124]=(一)卡分布χ(n )——μ已知Out[126]= 1.等尾区间:Out[129]={2.94766,3.05702}Out[130]=等尾区间长度:Out[131]=0.109358Out[132]=相对区间长度:Out[133]=0.0364242Out[134]=(二)卡分布χ(n -1)——μ未知Out[136]= 1.等尾区间:Out[139]={2.94774,3.05711}Out[140]=等尾区间长度:Out[141]=0.109366Out[142]=相对区间长度:Out[143]=0.0364261Out[144]=(三)卡分布χχ(n )——μ未知Out[146]= 1.等尾区间:Out[149]={2.9476,3.05695}Out[150]=等尾区间长度:Out[151]=0.109355Out[152]=相对区间长度:Out[153]=0.0364242Out[154]=(四)卡方分布-2 i =1n Log [12Erfcχ2(2n )——μ已知Out[158]={2.89486,3.15965}Out[159]=等尾区间长度:12 正态分布\\正态分布统计分析\\正态分布参数区间估计.nbOut[160]=0.264793Out[161]=相对区间长度:Out[162]=0.0874698Out[163]=(五)卡方分布-2 i =1n Log [12Erfcχ2(2n )——μ未知Out[167]={2.86679,3.12718}Out[168]=等尾区间长度:Out[169]=0.260386Out[170]=相对区间长度:Out[171]=0.0868828正态分布\\正态分布统计分析\\正态分布参数区间估计.nb 13。
正态总体均值方差的区间估计
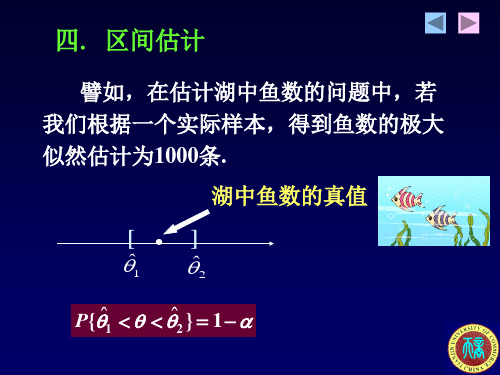
2
)
(2) σ12=σ22=σ2, σ2未知,μ1- μ2的1-α置信区间 ① 对于μ1- μ2,构造枢轴变量: ( X Y ) ( 1 2 ) T ~ t (n1 n2 2) S 1 / n1 1 / n2 ② 构造T的 一个1-α区间:
P(| T | t (n1 n2 2)) 1
X
③ μ的1-α置信区间:
( X t / 2 ( n 1 ) S n , X t / 2 ( n 1 ) S n )
1-α
例1 设正态总体的方差为1, 根据取自该总体的容 量为100的样本计算得到样本均值为5, 求总体均 值的置信度为0.95的置信区间.
解 已知σ2=1, α=0.05, μ的1-α置信区间:
③ 变形得到μ1- μ2的1-α置信区间:
2
( ( X Y ) t ( n1 n2 2) S
2
1 1 , n1 n2 1 1 ) n1 n2
( X Y ) t ( n1 n2 2) S
2
例 4 某工厂利用两条自动化流水线罐装番茄酱, 分别从两条流水线上抽取随机样本: X 1 , X 2 , , X 12
未知
① 构造枢轴变量: (n 1)S 2 2 Q ~ ( n 1) 2 ② 构造Q的 一个1-α区间:
P{1 Q 2 } 1
f(x)
α/2 λ1 α/2 X 2 λ (n 1)2 (n 1)
2 1
③ 解不等式得到σ2的1-α置信区间:
若 1 2 的置信区间的上限小于零, 则可认为1 2 ;
(2)构造F的 一个1-α区间: P(λ1<F< λ2)=1-α
正态总体参数的区间估计

第19讲 正态总体参数的区间估计教学目的:理解区间估计的概念,掌握各种条件下对一个正态总体的均值和方差进行区间估计的方法。
教学重点:置信区间的确定。
教学难点:对置信区间的理解。
教学时数: 2学时。
教学过程:第六章 参数估计§6.3正态总体参数的区间估计1. 区间估计的概念我们已经讨论了参数的点估计,但是对于一个估计量,人们在测量或计算时,常不以得到近似值为满足,还需估计误差,即要求知道近似值的精确程度。
因此,对于未知参数θ,除了求出它的点估计ˆθ外,我们还希望估计出一个范围,并希望知道这个范围包含参数θ真值的可信程度。
设ˆθ为未知参数θ的估计量,其误差小于某个正数ε的概率为1(01)αα-<<,即ˆ{||}1P θθεα-<=-或αεθθεθ-=+<<-1)ˆˆ(P这表明,随机区间)ˆ,ˆ(εθεθ+-包含参数θ真值的概率(可信程度)为1α-,则这个区间)ˆ,ˆ(εθεθ+-就称为置信区间,1α-称为置信水平。
定义 设总体X 的分布中含有一个未知参数θ。
若对于给定的概率1(01)αα-<<,存在两个统计量1112(,,,)n X X X θθ= 与2212(,,,)n X X X θθ= ,使得12{}1P θθθα<<=-则随机区间12(,)θθ称为参数θ的置信水平为1α-的置信区间,1θ称为置信下限,2θ称为置信上限,1α-称为置信水平。
注(1)置信区间的含义:若反复抽样多次(各次的样本容量相等,均为n ),每一组样本值确定一个区间12(,)θθ,每个这样的区间要么包含θ的真值,要么不包含θ的真值。
按伯努利大数定理,在这么多的区间中,包含θ真值的约占100(1)%α-,不包含θ真值的约仅占100%α。
例如:若0.01α=,反复抽样1000次,则得到的1000个区间中,不包含θ真值的约为10个。
(2)置信区间的长度表示估计结果的精确性,而置信水平表示估计结果的可靠性。
第五节 正态总体均值与方差的区间估计 7-5

\ 2 的置信度为 1 - a 的置信区间为 2 2 ( n - 1)S ( n - 1)S ( 2 ) , 2 a / 2 ( n - 1) 1 - a / 2 ( n - 1)
而 的置信度为 1 - a 的置信区间为 (
n - 1S
2 / 2 ( n - 1) a
,
n - 1S
2 1 - a / 2 ( n - 1)
2 2 1 2 的置信区间包含1, 在实际中我们认为 1 , 由于 2
2 两者没有显著差别。 2
17
全章要求
1. 了解点估计的概念, 掌握矩估计法、极大 似然估计法; 2. 了解估计量的评选标准:
无偏性、有效性、一致性。
2 1 n1 + 2 n 2 2
~ N(0,1),
即 可 得 到 1 - 2的 一 个 置 信 度 为 a的 置 信 区 间 12 ( X - Y z a / 2 1 n1 + 2 n 2 ). 2
2. 当 和 均 未 知 时求 1 - 2的 置 信 区 间 ,
2 1 2 2
1
第七章 参 数 估 计
§5.正态总体均值与方差的区间估计
一. 单个正态总体的均值与方差的区间估计: 二. 两个正态总体的区间估计:
2
一. 单个正态总体的均值与方差的区间估计:
设总体 ~ N(, ), X1 , X2 , , Xn是一个样本 X .
2
1 .当 2 已知时,求 的置信区间。 X - 选取 Z = n
本题中的置信下限大于零,实际中可认为μ1比μ2大。
13
三. 两个总体方差比的置信区间:
仅讨论总体均值 1 , 2 未知的 情况,由于
2 ( n1 - 1) S1
第4节正态总体参数的区间估计

3
, 给定 ,0 1 , 定义 设是总体的一个未知参数
确定两个统计量
ˆ , ˆ 分别称为置信下限和置信上限. 区间. 1 2
ˆ , ˆ ]为 的 置信水平为 1 的 置信 则称区间 [ 1 2
1.75 1.96 1.96 0.49, n 50
所以 的置信区间为
(4.10 0.49, 4.10 0.49 ) (3.61, 4.59 ) .
10
例3 在上例中 , 为使 的置信水平是 0.95 的置信区间
的长度 L 1.5, 求样本容量 .
, u0.025 1.96, 1.75, 解 0.05
u / 2
x
X | | u / 2 X u / 2 X u / 2 / n n n
于是所求 的置信区间为 ( X u 有时简记为 ( X u / 2
2
n
, X u 2 ), n n
7
).
2 某厂生产滚珠,直径 X 服从正态分布 N ( , ). 例1 为了估计 , 抽检 6 个滚珠, 测得直径为 ( mm) : 14.70, 15.21,14.90,14.91,15.32,15.32,
对给定的置信水平 1 ,
按标准正态分布的 水平双侧分位数的定义,
查正态分布表得 u 2 ,
6
1.
已知时 的置信区间
2
/2
( x)
X U ~ N (0,1) , / n
1
O
/2
X P{ | | u 2 } 1 , n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 寻找一个待估参数θ和估计量T的样本函数 S(T, θ),且其分布为已知.
6
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
4. 对于给定的置信水平1-α,根据S(T, θ)的分布,
确定常数a, b,使得
P(a ≤S(T, θ)≤b)= 1
5. 对“a≤S(T, θ)≤b”作等价变形,得到如下形式: P{ˆ1 ˆ2 } 1
取 U X置信水~平N是(0多, 1少) ?
n
寻找一个待估参数和 估计量的函数 ,要求 其分布为已知.
有了分布,就可以求出 U取值于任意区间的概率.
2
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
对于给定的置信水平(大概率),根据U的分布, 确定一个区间, 使得U取值于该区间的概率为 置信水平.
n
u / 2
X
n u / 2
置信区间为:
( X n u / 2 , X n u / 2 )
12
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
例2 已知幼儿身高服从正态分布,现从5~6岁的幼 儿中随机地抽查了9人,其高度分别为:
115, 120, 131, 115, 109, 115, 115, 105, 110cm; 假设标准差 0 7,置信度为95%;试求总体均值 的置信区间。
所以μ的置信度为0.99置信区间是 11.90, 12.40
16
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
例4 用仪器测量温度,重复测量7次, 测得温度 分别为: 115,120,131,115,109,115,115 C; 设温度
目录
上一页 下一页 返回
结束
教材上讨论了以下几种情形:
单个正态总体均值 和方差 2的区间估计.
两个正态总体均值差
和方差比 的区间估计.
1 2
2 1
/
2 2
下面我们举几个例子
10
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
一、单个正态总体参数的区间估计
1、正态总体均值μ的区间估计
(1)、正态总体X~N(μ,σ2),方差σ2已知:
目录
上一页 下一页 返回
结束
(2) 、正态总体X~N(μ,σ2),方差σ2未知: 不能用“(1)”中的方法,但
Q T X n ~ t(n 1),
S 可查自由度为 n 1的t分布表得t / 2 ,
P(| T | t / 2 ) 1 ,
X
| S
n | t / 2 ,
14
概率论与数理统计(湘潭大学)
第七章 参数估计
§7.3 正态总体参数的区间估计
1
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
二、置信区间的求法
例1 设X1,…Xn是取自 N (, 2 )的样本, 2已知, 求参数μ的置信度为1-α的置信区间.
解:选μ的点估计为 X
寻找未知参数的
明确问题,是求什么参数的置信一区个间良? 好估计.
结束
P{X
n u 2
X
n u 2}
1
于是所求 的 置信区间为
[ X n u 2, X n u 2 ]
也可简记为
X
n u 2
5
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
从例1解题的过程,我们归纳出求置信区间的 一般步骤如下: 1. 明确问题, 是求什么参数的置信区间?
置信水平 1-α是多少? 2. 寻找参数θ的一个良好的点估计
Q U X ~ N (0,1) / n
给定α,可查表得uα/2,使P(|U|<uα/2)=1-α
P(| X
n | u / 2 ) 1 ,
| X
n | u / 2 ,
11
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
X
|
n | u / 2 ,
u / 2
X
n u / 2 ,
目录
上一页 下一页 返回
结束
X
| S
n | t / 2 ,
即
X
t / 2 S
n t / 2 ,
同乘以 S 得: n
S n
t / 2
X
S n t / 2
置信区间为: ( x
S n t / 2 , x
S n t / 2 )
15
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
例3 设有一批配料粉,每袋净重X(单位:克)服从正 态分布.从中任取8袋,测得净重分别为:13.1,11.9, 12.4,12.3,11.9,12.1,12.4,12.1. 试求μ的置信度为0.99 的置信区间.
则 [ˆ1,ˆ2 ]就是θ的100(1-α)%的置信区间.
7
概率论与数理Biblioteka 计(湘潭大学)目录上一页 下一页 返回
结束
可见,确定区间估计很关键的是 要寻找一个待估参数θ
和 估计量T 的样本函数S(T, θ ),
且 S(T, θ)的分布为已知,不依赖于任何未知参数 (这样我们才能确定一个大概率区间).
解 n 8, 经计算得 x 12.15, s2 0.04
查表可得 t / 2 (n 1) t0.005 (7) 3.4995
从而
x
s n
t
/
2
(n
1)
12.15
0.04 0.4995 11.90 8
s
0.04
x n t / 2 (n 1) 12.15
0.4995 12.40 8
对给定的置信水平 1 ,
查正态分布表得 u 2,
使
P{|
X
n
|
u
2} 1
为什么 这样取?
3
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
对给定的置信水平 1 ,
查正态分布表得 u 2,
使
P{|
X
n
|
u
2}
1
从中解得
P{X
n u 2
X
n
u
2}
1
4
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
而这与总体分布有关, 所以至关重要是
总体分布的形式是否已知,是怎样的类型。
8
概率论与数理统计(湘潭大学)
目录
上一页 下一页 返回
结束
这里,我们主要讨论总体分布为正态的情 形. 若样本容量很大,即使总体分布未知,应 用中心极限定理,可得总体的近似分布,于是 也可以近似求得参数的区间估计.
9
概率论与数理统计(湘潭大学)
解 已知 0 7, n 9, 0.05. 可得 x (115 120 110) / 9 115.
查正态分布表得临界值u / 2 1.96,得置信区间
(115 1.96 7 / 9 , 115 1.96 7 / 9) (110.43 , 119.57).
13
概率论与数理统计(湘潭大学)
