求均匀带电球体的场强分布
电场的高斯定理
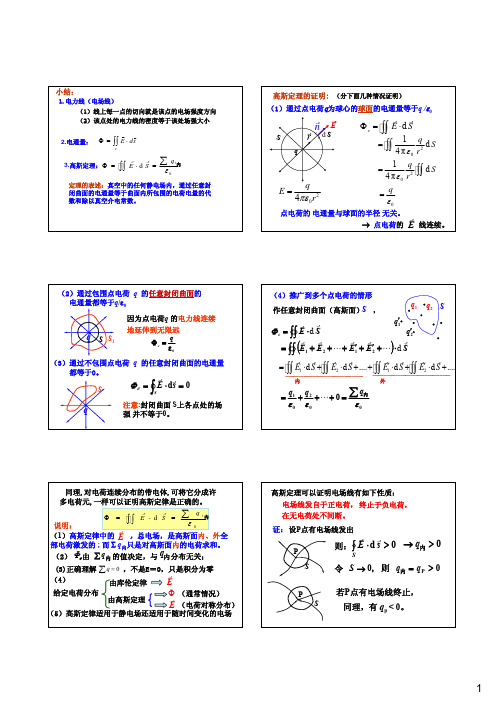
= = =
−σ1 +σ 2ε o
σ1 −σ2
σ
2ε 1+
σo
2
2ε o
σ EA = EC = 0
板外电场为 0 。
E2
=
σ2 2ε o
r 2i
r i
带电平板电容
r 器间的场强 i
EB
=
σ εo
均匀带电体,体密度为ρ,
空腔内任一点的场?
O1
rv1 rv2 O2
E= ρ r 3ε 0
v E1
=
ρ 3ε 0
(3)正确理解 (4)
∑q = 0
,不是E=0,只是积分为零
r
由库伦定律
E
给定电荷分布 由高斯定理
Φr E
(通常情况) (电荷对称分布)
(5)高斯定律适用于静电场还适用于随时间变化的电场
高斯定理可以证明电场线有如下性质: 电场线发自于正电荷, 终止于负电荷, 在无电荷处不间断。
证: 设P点有电场线发出
解:
r l
选择高斯面——同轴柱面
上下底r面 Err⊥dSr 侧面 E // dS,且同一
r
柱面上E 大小相等。
E
r
r dSr E
∫ ∫ ∫ Φ =
rr E ⋅dS
S
=
rr E ⋅dS +
测
rr E ⋅dS
上下底
= E ⋅ 2πrl Φ = lλ
εo
E= λ 2 πε o r
方向:垂直带电线
无限长均匀带电直线 E = λ
因为 qin = 0 ,有
E=0
S
球层内的空腔中没有电场。
0 (r < R1)
大学物理简明教程(吕金钟)第四章习题答案
第四章电磁学基础静电学部分4.2解:平衡状态下受力分析+q受到的力为:处于平衡状态:(1)同理,4q 受到的力为:(2)通过(1)和(2)联立,可得:,4.3解:根据点电荷的电场公式:点电荷到场点的距离为:两个正电荷在P点产生的电场强度关于中垂线对称:所以:当与点电荷电场分布相似,在很远处,两个正电荷q组成的电荷系的电场分布,与带电量为2q的点电荷的电场分布一样。
4.4解:取一线元,在圆心处产生场强:分解,垂直x方向的分量抵消,沿x方向的分量叠加:方向:沿x正方向4.5解:(1(2)两电荷异号,电场强度为零的点在外侧。
4.7解:线密度为λ,分析半圆部分:点电荷电场公式:++在本题中:电场分布关于x 轴对称:,进行积分处理,上限为,下限为:方向沿x轴向右,正方向分析两个半无限长:,,,两个半无限长,关于x轴对称,在y方向的分量为0,在x方向的分量:在本题中,r为场点O到半无限长线的垂直距离。
电场强度的方向沿x轴负方向,向左。
那么大O点的电场强度为:4.8解:E的方向与半球面的轴平行,那么通过以R为半径圆周边线的任意曲面的电通量相等。
所以通过S1和S2的电通量等效于通过以R为半径圆面的电通量,即:4.9解:均匀带电球面的场强分布:球面R 1、R2的场强分布为:根据叠加原理,整个空间分为三部分:根据高斯定理,取高斯面求场强:图4-94 习题4.8用图S1S2RO场强分布:方向:沿径向向外4.10解:(1)、这是个球对称的问题当时,高斯面对包围电荷为Q当,高斯面内包围电荷为q方向沿径向(2)、证明:设电荷体密度为这是一个电荷非足够对称分布的带电体,不能直接用高斯定理求解。
但可以把这一带电体看成半径为R、电荷体密度为ρ的均匀带电球体和半径为R`、电荷体密度为-ρ的均匀带电体球相叠加,相当于在原空腔同时补上电荷体密度为ρ和-ρ的球体。
由电场叠加原理,空腔内任一点P的电场强度为:在电荷体密度为ρ球体内部某点电场为:在电荷体密度为-ρ球体内部某点电场为:所以4.11解:利用高斯定理,把空间分成三部分场强分布:方向:沿径向向外4.12 解:取闭合圆柱面为高斯面,高斯定理场强分布:方向沿径矢方向4.14 解:无限大带电平面的电场分布为:,场强叠加(1)电荷面密度均为σ在一区:在二区:在三区:(2)电荷面密度分别为σ和-σ在一区:在二区:在三区:方向为垂直于平面方向4.16解:把总的电场力做功看做是正电荷+q电场力做功和负电荷-q电场力做功的叠加,得用公式(4—14):(1)把单位正电荷从O点沿OCD移到D点,电场力做功。
大学物理:2第二讲 电场强度计算续、高斯定理

2
R
r
x
p dE// x
E
qx
4 0 r 3
iˆ
dE dE
cos x / r
1
讨论:1. x 0 : Eo 0
E
qx
40 (R2
x2 )3/2
iˆ
o
y
r
圆环中心电场为零
2.
x R :
Ep
q
40 x2
iˆ
R
o
z
E
x px
p
R
x
●无论带电体形状如何,在离其足够远处均可视为
点电荷。 2
例4:半径为R的簿圆盘均匀带电,面电荷密度为。
求中心轴线上一点 p处的电场强度。
解:将圆盘分割成许多带 电细圆环,其电量
dq ds 2 rdr
细圆环电场
dr
l
r
Ep
o xpx
dE
dqx
40 (r2
x2 )3/2
2 rxdr rxdr 40 (r2 x2 )3/2 20 (r2 x2 )3/2
3
dE
rxdr 20 (r2 x2
二、电通量
●通过某一曲面的电力线数,叫做 通过该曲面的电通量。记为“e”.
电通量的计算
s
de E dS
e
E dS
S
通过闭合曲面的电通量
e S E dS
规定:曲面正法线由曲面指向外
E de dSn
ds E
ds
E
q
s
11
例:点电荷q位于球面内球心处,求通过该球面的
电通量。
解:球面上的电场强度
各点产生的电场。
解:由对称性可知,该球壳产生的
大学物理第7章 电场题库答案(含计算题答案)

9题图第七章 电场 填空题 (简单)1、两无限大平行平面的电荷面密度分别为σ+和σ+,则两无限大带电平面外的电场强度大小为σε ,方向为 垂直于两带电平面并背离它们 。
2、在静电场中,电场强度E 沿任意闭合路径的线积分为 0 ,这叫做静电场的 环路定理 。
3、静电场的环路定理的数学表达式为 0lE dl =⎰ ,该式可表述为 在静电场中,电场强度的环流恒等于零 。
4、只要有运动电荷,其周围就有 磁场 产生;5、一平行板电容器,若增大两极板的带电量,则其电容值会 不变 ;若在两极板间充入均 匀电介质,会使其两极板间的电势差 减少 。
(填“增大”,“减小”或“不变”)6、在静电场中,若将电量为q=2×108库仑的点电荷从电势V A =10伏的A 点移到电势V B = -2伏特的B 点,电场力对电荷所作的功A ab = 92.410⨯ 焦耳。
(一般)7、当导体处于静电平衡时,导体内部任一点的场强 为零 。
8、电荷在磁场中 不一定 (填一定或不一定)受磁场力的作用。
9、如图所示,在电场强度为E 的均匀磁场中,有一半径为R 的半球面,E 与半球面轴线的夹角为α。
则通过该半球面的电通量为 2cos B R πα-⋅ 。
10、真空中两带等量同号电荷的无限大平行平面的电荷面密度分别为σ+和σ+,则两无限大带电平面之间的电场强度大小为 0 ,两无限大带电平面外的电场强度大小为σε 。
11、在静电场中,电场力所做的功与 路径 无关,只与 起点 和 终点位置 有关。
12、由高斯定理可以证明,处于静电平衡态的导体其内部各处无 净电荷 ,电荷只能分布于 导体 外表面 。
因此,如果把任一物体放入空心导体的空腔内,该物体就不受任何外 电场的影响,这就是 静电屏蔽 的原理。
(一般)13、静电场的高斯定理表明静电场是 有源 场, (一般)14、带均匀正电荷的无限长直导线,电荷线密度为λ。
它在空间任意一点(距离直导线的垂直距离为x 处)的电场强度大小为02xλπε ,方向为 垂直于带电直导线并背离它 。
求真空中均匀带电球体的场强分布

求真空中均匀带电球体的场强分布
本文旨在探讨真空中均匀带电球体的场强分布情况。
首先,我们需要明确均匀带电球体的定义,即球体内部任意一点的电荷密度均匀分布。
其电场可以通过库仑定律计算得到,即$E =
frac{1}{4pi epsilon_0}frac{Q}{r^2}$,其中$Q$为球体总电荷量,$r$为球心到该点的距离,$epsilon_0$为真空介电常数。
针对均匀带电球体的电场分布,我们可以采用高斯定理求解。
选择球体为高斯面,由于球体内部的电荷密度均匀,所以高斯面内的电场也必须是均匀的。
根据高斯定理,我们可以得到高斯面内的电荷量为$Q_{in} = frac{4}{3}pi r^3rho$,其中$rho$为球体单位体积内的电荷密度。
由于高斯面内的电场与球心的距离$r$有关,我们可以对高斯面内的电场进行积分,得到$Etimes 4pi r^2 =
frac{Q_{in}}{epsilon_0}$,即$E = frac{1}{4pi
epsilon_0}frac{Q}{r^2}$,与库仑定律得到的结果一致。
根据上述推导,我们可以得出结论,真空中均匀带电球体的场强分布是均匀的,与球心距离的平方成反比。
这一结论对于电荷分布均匀的球体有重要的应用价值,在电学中有着广泛的应用。
- 1 -。
均匀带电球体内外的电场强度公式

一、电场的概念电场是指电荷周围空间内的物理场,它描述了电荷对空间内其它电荷的作用力。
在物理学中,电场是一种很重要的概念,它可以帮助我们理解电荷之间相互作用的规律,也是电磁学的重要内容之一。
二、均匀带电球体的电场强度定义均匀带电球体是指球体内每一点的电荷密度都是相同的,而且球体外部没有电荷分布。
对于这样的球体,可以利用高斯定律求出球体内外的电场强度。
三、均匀带电球体内部的电场强度1. 对于均匀带电球体内部的一点P,其到球心的距离记为r,球体的半径记为R。
2. 根据高斯定律,球体内部的电场强度公式为E = k * Q * r / R^3,其中,k为电场常数,Q为球体的总电荷量。
3. 由上式可以看出,均匀带电球体内部的电场强度与点P到球心的距离成正比,与球体的总电荷量成正比,与球体的半径的立方成反比。
这说明球体内部的电场强度分布是均匀的,且与点P到球心的距离成线性关系。
四、均匀带电球体外部的电场强度1. 对于均匀带电球体外部的一点Q,其到球心的距离记为r。
2. 根据高斯定律,球体外部的电场强度公式为E = k * Q / r^2,其中,k为电场常数,Q为球体的总电荷量。
3. 由上式可以看出,均匀带电球体外部的电场强度与点Q到球心的距离成反比,与球体的总电荷量成正比。
随着点Q到球心的距离增大,电场强度逐渐减小。
五、结论通过本文对均匀带电球体内外的电场强度公式的推导和分析,我们可以得出以下结论:1. 均匀带电球体内部的电场强度与点到球心的距离成正比,与球体的总电荷量成正比,与球体的半径的立方成反比。
2. 均匀带电球体外部的电场强度与点到球心的距离成反比,与球体的总电荷量成正比。
均匀带电球体内外的电场强度公式为E = k * Q * r / R^3 (r < R) 和 E = k * Q / r^2 (r > R)。
这些公式在电磁学理论研究和工程实践中具有重要的应用价值。
在物理学中,电场是一种很重要的概念,它可以帮助我们理解电荷之间相互作用的规律,也是电磁学的重要内容之一。
求均匀带电球体的场强分布

1.求均匀带电球体的场强分布。
电势分布。
已知球体半径为R ,带电量为q 。
解:(运动学3册)例1—1 质点作平面曲线运动,已知m t y tm x 21,3-==,求:(1)质点运动的轨道方程;(2)s t 3=地的位矢;(3)第2s 内的位移和平均速度;(4)s t 2=时的速度和加速度;(5)时刻t 的切向加速度和法向加速度:(6)s t 2=时质点所在处轨道的曲率半径。
解:(1)由运动方程消去t ,得轨道方程为:912x y -=(2)s t 3=时的位矢j i j y i x r 89)3()3()33(-=+=,大小为m r 126481|)3(|≈+=,方向由)3(r 与x 轴的夹角'︒-==3841)3()3(arctanx y a 表示。
(3)第2s 内的位移为j i j y y i x x r 33)]1()2([)]1()2([-=-+-=∆,大小m r 2399||=+=∆,方向与与x 轴成︒-=∆∆=45arctanxya ,平均速度v 的大小不能用v 表示,但它的y x ,分量可表示为tyv t x v y x ∆∆=∆∆=,。
(4)由,,23当时tj i j dtdyi dt dx v -=+=,43)2(j i v -=大小'︒-=-=⋅=+=-853)34arctan(,5169)2(1a s m v 方向为。
j dtdva 2-==即a 为恒矢量,.,21轴负方向沿y s m a a y -⋅-== (5)由质点在t 时刻的速度22249t v v v y x +=+=,得切向加速度2494t t dt dv a +==τ,法向加速度222496ta a a n +=-=τ。
注意:||dt dv dt dv ≠,因为dt dv 表示速度大小随时间的变化率,而||dtdv表示速度对时间变化率的模,切向加速度τa 是质点的(总)加速度a 的一部分,即切向分量,其物理意义是描述速度大小的变化;法向加速度n a 则描述速度方向的变化。
半径为r的均匀带电球体的场强分布

半径为r的均匀带电球体的场强分布半径为r的均匀带电球体的场强分布,这是一个相当有趣的话题。
我们得明白一个概念:什么是场强?场强就像是一个物体周围的能量波动程度,越大就越强烈。
一个半径为r的均匀带电球体的场强分布会是怎样的呢?我们要明确一点:这个球体是带电的,所以它会产生磁场。
而磁场又会影响到周围的电荷,使得它们也产生电场。
这样一来,整个空间就会被充满了电磁波和能量。
这些能量并不是均匀分布的,而是呈现出一种特殊的分布方式。
让我们来分析一下这种分布方式。
我们可以将这个球体看作是一个巨大的磁铁,它的磁场是由许多小的磁极组成的。
这些磁极之间的相互作用会产生一种能量波动,从而形成磁场。
同样地,这个球体内的电荷也会受到磁场的影响,产生一种能量波动,从而形成电场。
这种能量波动并不是随意分布的。
相反,它们会遵循一定的规律。
具体来说,这些能量波动会在球体的表面上形成一种类似于涟漪的现象。
这是因为球体内的电荷会受到磁场的影响,从而沿着球体的表面运动。
当它们运动到球体的边缘时,就会反弹回来,并在球体的表面上形成一种类似于涟漪的现象。
这种现象看起来非常有趣。
如果你把手指放在球体的表面上,你就会发现手指会感受到一种微弱的电流流动。
这就是因为球体内的电荷在运动过程中产生了电流。
这种电流是非常微弱的,几乎无法被人感知到。
除了在表面上形成涟漪之外,这个球体内的能量波动还会在空间中形成一种环形的结构。
这种结构类似于一个大型的电流环,可以在整个空间中传递能量。
这种结构的强度是非常有限的,只能传递非常微弱的能量波动。
半径为r的均匀带电球体的场强分布是一种非常有趣的现象。
虽然它看起来非常复杂,但实际上它只涉及到一些简单的物理原理。
如果你对电磁学感兴趣的话,不妨试着研究一下这个问题吧!。
大学物理复习资料1

2 3
1 2 3 4
Q
A
B
C
.P
E
1 2 Q S 同理可得: 0 2 3
Q Q Q 1 2 3 4 2S 2S 2S 按电场叠加原理可求得: Q Q Q EB EA EC 2 o S 2 o S 2 o S (2)第二板接地 则 4与大地构成一导体 4 0
qQ U2 U3 4 π 0 R3 4 π 0 R3 4 π 0 R3 q q qQ 4 π 0 R3
R2
R3
U1 U 2
q 4 π 0 R1
q 4 π 0 R2
(2)外壳接地, 电荷分布
U1
q 4 π 0 R1
q 4 π 0 R2
复习课
题型: 选择10题共30分, 填空10题共30分, 计算5题共40分 比例:静电场(第11、12章): 31分; 第13章: 19分; 第14章: 19分; 第15章: 11分; 第16章: 17分; 第17章: 3分。。
11章 真空中的静电场
1、利用场强叠加原理求场强:
E
q q 1 1 i r E ri E dE 3 3 40 r 40 ri 40
R
o
练习题:例11-16、17;习题11-6、7、8、14
例11-16
均匀带电圆环半径为R,带电总量为q
求 圆环轴线上一点的电势 解 建立如图坐标系,选取电荷元 dq
dq dl
dq dV 4 0 r
dq r
R
dl
4 0 R x
2 2
O
P
x
Vp
2 R
半径为r的均匀带电球体的场强分布

半径为r的均匀带电球体的场强分布1. 前言嘿,大家好!今天咱们聊聊一个有趣的话题——均匀带电球体的场强分布。
别急,听起来可能有点复杂,但我保证,用通俗的语言说清楚它,你会发现其实这也不是啥难事。
想象一下,如果我们把一个球体看成一个超级巨大的电池,里面充满了电。
电场强度就是它给周围环境带来的“电力效果”。
那么,这个效果到底是怎么分布的呢?接着往下看吧!2. 球体的电场强度2.1 球体内部的情况首先,我们从球体内部开始说起。
假设这个球的半径是 r,均匀带电,那么在球体内部(也就是距离球心小于 r 的地方),电场强度可就不是你想象中的那么简单了。
根据高斯定律,电场强度 E 在球心附近是渐渐增大的,像是在蓄势待发的气球,越靠近外面,感觉越强烈。
不过,等你到了球体的中心,电场强度 E 实际上是零。
这就像是在一场盛大的派对上,你越靠近,音乐声越响,越靠近边缘,气氛却静悄悄的。
那么,为啥在球心电场强度为零呢?这其实是因为球体内的每一部分都在“拉扯”着你,正负电荷互相抵消,形成了一种神奇的平衡。
就像两个孩子在拔河比赛中,两个方向的力量完全相等,结果没谁能赢一样。
2.2 球体外部的情况再来看看球体外部的电场强度。
嘿嘿,这可有意思了!一旦你离开球体,电场强度就会开始变得越来越强。
此时,电场强度 E 和球体的总电荷量 Q 以及距离 r 的关系就变得简单多了,直接用公式E = kQ/r² 来描述,k 是个常数。
这个公式告诉我们,电场强度随着距离的增加而迅速减小,像是风筝越飞越高,线就拉得越长。
想象一下,当你站在球体的边缘,越往外走,你会觉得电场的吸引力在逐渐减弱,像是热情的朋友开始慢慢退场。
而且,这种分布是非常均匀的,就像在广场上,虽然大家都分散了,但离得越远,人越少。
3. 电场的实际应用3.1 生活中的电场说到这里,很多小伙伴可能会想,“这跟我有什么关系呢?”其实,这可大有文章!电场的概念在我们的生活中随处可见,比如手机信号、静电等都是电场的一种表现形式。
均匀带电球体内外各处场强计算例题

均匀带电球体内外各处场强计算例题《均匀带电球体内外各处场强计算例题》一、引言在电学中,均匀带电球体内外各处场强计算是一个基础而重要的问题。
理解和掌握这一问题对于建立电学基础知识体系和解决实际问题都具有重要意义。
本文将从简单到复杂,由浅入深地探讨这一问题,帮助读者全面、深入地理解场强计算的例题。
二、理论基础在进行场强计算之前,我们首先需要了解几个基本概念和公式。
根据库仑定律,两个点电荷之间的电场力与它们之间的距离成反比,与电荷量的乘积成正比。
通过这一定律,我们可以得出球体内外各处的电场强度公式。
1. 球体内部场强计算公式当我们需要计算球体内的电场强度时,可以利用以下公式进行计算:\[ E = \frac{kQ}{r^2} \]其中,E代表电场强度,k代表库仑常数,Q代表球体内的电荷量,r代表观察点到球心的距离。
通过这个公式,我们可以相对简单地计算出球体内各处的电场强度。
2. 球体外部场强计算公式当我们需要计算球体外的电场强度时,可以利用以下公式进行计算:\[ E = \frac{kQ}{r^2} \]当 r 大于球体半径 R 时,球体可以看成点电荷,其中 Q 为球体带电量。
以上两个公式为我们提供了计算场强的基本工具,我们将会根据这些公式来解决均匀带电球体内外各处场强计算例题。
三、均匀带电球体内部场强计算现在,我们来看一个均匀带电球体内部场强计算的例题。
假设有一个半径为 R 的均匀带电球体,带电量为 Q,我们需要计算球体内一点 P 处的电场强度。
解题步骤如下:1. 我们先找到球体的球心O,并设定观察点 P 到球心 O 的距离为 r。
2. 利用球体内部场强计算公式,代入 Q 和 r 的数值,求出点 P 处的电场强度 E。
3. 根据所求点 P 的位置,确定 r 的数值,继而求出 E 的数值。
通过以上步骤,我们可以得出点 P 处的电场强度 E 的具体数值,并且可以明确该点的场强方向。
四、均匀带电球体外部场强计算接下来,我们来看一个均匀带电球体外部场强计算的例题。
均匀带电球体的电场强度分布

均匀带电球体的电场强度分布
1. 均匀带电球体的电场
1) 电场强度分布
电场强度分布是均匀带电球体的一个重要特征,由于球体本身的形状,电场强度分布也是在球面的表面的,就像一个由圆圈组成的带电球体
一样,它的电场强度分布是十分均匀的。
这就意味着,从中心向外沿
球面增加角度,电场强度也是随着角度的变化而变化,在空间中各点
的电场强度(或电压)是一致的。
所以,在球表面和球内部,同一距
离所对应的相同角度处电场强度也是相同的,这种电场强度分布显然
也就是均匀带电球体的特征。
2)均匀体积密度
此外,均匀带电球体的另一个重要特征是体积密度分布的均匀性,也
就是说,在球体内各点之间的电荷密度都是同等的,也就是说,在带
电球体中,中心和各个面积上,电荷密度是一致的,也就是电荷本身
分布在球体内部是均匀的,这又是一个体现均匀带电球体特性的重要
特征。
3)增加距离分布
最后,当均匀带电球体不断增加距离的时候,其电场强度的分布也会
发生变化,从而体现出新的特性,我们知道,随着距离的增加,电场
强度逐渐减弱,远离球体,电场强度逐渐降低,由此,增加距离得到
的均匀带电球体的新特性就是外部电场强度的衰减,内部电场强度保持不变。
这就是均匀带电球体的距离变化引起的一些特性。
第7章 静电场 复习题(2)

第七章 电场7-1回答下列问题:(1)在电场中某一点的场强定义为0q =F E ,若该点没有检验电荷,那么该点的场强如何?不变 如果电荷在电场中某点受到的电场力很大,该点的场强是否一定很大?不一定提示:电场强度是电场的基本性质,由电荷的分布决定,而与试验电荷无关。
因而若该点没有试验电荷,场强并不发生变化;若该点的电场力很大,场强不一定很大。
(2)根据点电荷的场强公式:304q rπε=r E ,从形式上看,当所考察的场点和点电荷的距离0→r 时,则按上述公式E →∞,但这是没有意义的。
对这个问题如何解释。
提示:点电荷的场强公式304q rπε=r E 是由库仑定律0304qq F rπε=r 推导而来,而库仑定律是经验公式,当0→r 时,点电荷的模型不成立,库仑定律不成立,此时点电荷的场强公式也不成立。
7-2—个带正电荷的质点。
在电场力作用下从A 点出发经C 点运动到B 点,其运动轨迹如图7-2所示。
巳知质点运动的速率是递减的,下面关于C 点场强方向的四个图示中正确的是( )。
①质点沿曲线运动时,加速度的 方向总是指向曲线凹的一边; ②依题意,质点的切向加速度a τ与线速度υ反向;③电场强度E 的方向即为质点在该点加速度a 的方向,将a 分解为切向加速度a τ与法向加速度n a 提示:D7-3 如7-3题图所示,闭合曲面S 内有—点电荷q ,P 为S 面上一点,在S 面外A 点有—点电荷`q ,若将`q 移至B 点,则( )(A)穿过S 面的电通量改变、P 点的电场强度不变; (B)穿过S 面的电通量不变,P 点的电场强度改变; (C)穿过S 面的电通量和P 点的电场强度都不变; (D)穿过S 面的电通量和P 点的电场强度都改变。
提示:B7-4 在真空中有A 、B 两块板,板面积为S ,分别带有电量q +、q -,相距为d ,若忽略边缘效应,则两板间的相互作用力为多少?解:A 板上的电荷q +在B 板q 产生的场中,0022q E Sσεε==。
几种典型带电体的场强和电势公式

d
l
l
d
i
4 0
1 d
l
1 d
i
。
U
p d
4 0
ln
l
d d
。
(2)在直线的中垂线上,与直线的距离为 d 的 Q 点处:
电场强度矢量为:
EQ
d
4 0
d
l
j
l 2 d 2
4 0 d
2l
j
l 2 4d 2
。
2
电势:
l l 2 d 2
UQ
d
4 0
ln
2 l
2 l 2 d 2
几种电荷分布所产生的场强和电势
1、均匀分布的球面电荷(球面半径为 R,带电量为 q)
电场强度矢量:
E(r)
1
qr ,
(球面外,即r R)
Hale Waihona Puke 4 0 r 3E(r) 0 。 (球面内,即r R)
电势分布为:
U r 1 q , (球外)
4 0 r
U r 1 q 。 (球内)
4 0 R
2、均匀分布的球体电荷(球体的半径为 R,带电量为 q)
PSin r3
0
其大小为 E P 4 0r 2
3Cos 2 1 ,
方向为 arctg E Er
tg
1
E Er
tg
1
1 2
tg
。其中
为
E
与
r
0
之间的夹角。
电势:U r
1 4 o
P Cos r2
1 4 0
P
r
r3
。
电场强度矢量的另一种表达式为:
E
均匀带电球体表面电场强度的计算论文

方法计算。
3
由于在大多数普通电磁学教材中,都只计算了球体内外的场强,而在球面上的 场强都没有给出,所以,在这里我们通过场强的叠加原理,来计算球面上的电场强 度叫 如图3.1所示,均匀带电球匾上的电荷量为q,电荷面密度为",
Keywords:
with spherical; electric field intensity; superposition principle; surface charge density; Gauss theorem; mutation
摘要I
AbstractII
引言1
1.电场强度与电场的叠加原理的概念1
图3.1均匀带电球面几何模型
我们把球面分成无限多个带电圆环球,位于&到0^0之间的球带面积为
ds=2旅'sin&d&,所带电量为dq=P2腻'sin&d&,其中。为球面的面电荷密度 亠。根据带电圆环在其轴线上的Q(l-cos&)sin&/8
4V%)(1-cos&)%
令u=cose
则Er(r)=^ir
2务\R2+r -2rRu^
在球面上时,即R=i
£•([)ctf?2「(r-7?u) du
2*o_1(R2+r2-2i7?u)%
;fR(l-u) du
26 L(用+疋-2用u)%
_ oR~「7?(l-u) du
26-12V2/? (l_u)%
cR-pi (1-u) du
q
带电球体电场与电势的分布

带电球体电场与电势的分布王峰在高三物理复习教学中,遇到带电体的内、外部场强、 一般以带电金属导体为例,指出其内部场强处处为零, 体上的电势处处相等; 但对带电金属导体的内、 缘介质球的内、外部电场、电势的大小分布很少有详细说明; 会遇到此类问题,高三学生已初步学习了简单的微积分, 来推导出上述问题的答案,并给出相应的“ Er ”和“考。
其所带电荷全部分布在金属球体 的表面,所以此模型与带电球壳模型的电场、电势分布的情况是一致的。
电场分布:1.1.1内部(r <R ):如图(1)所示,在均匀带电金属球(壳)内的任意点 P 处,均有通 过直径相似对称的两个带电球冠面 $和S 2,当两条线夹角 很小时,$和S 2可以近似看 作两个带电圆面,且 0和S 2两个面的尺寸相对它们距离 P 点距离很小,这样 S 1和S 2两个 带电面就可以近似处理为点电荷,它们在 P 点各自产生电场强度 E 1P 与E 2P ,计算如下所 示:设球体带电总量为 Q ,且均匀分别在导体球外表面上(南通市启秀中学物理学科 江苏 南通 226006)电势的分布特点问题时,我们 在电势上金属体是一个等势体,带电外部场强、电势的大小的分布特点及带电绝 而在电场一章的复习中,常常 笔者在此处利用微积分的数学方法,r ”的关系曲线图,供大家参本文中对电场、电势的分布推导过程均是指在真空环境 对电势的推导均取无穷远处为电势零参考点的,即 U 带电的导体球:因为带电导体球处于稳定状态时,中,即相对介电常数0 1 ;•/ E 1P KE 2P K图(1)Q? (r 1 sin )24 R 2r12Qsi n 2K 4R 2Q? (r 2 sin )24 R 2Qsin 21、2且E 1P 与E 2P 等大反向二E p 0,即均匀带电导体球(或球壳)内部的电场强度处处为零。
1.1.2外部(r >R ):如图(2)所示,要计算带电金属球(壳)的外部 P 点的电场强度,可以把带电导体球的表面分割成许多的单元面ds ,将每个单元面上电荷在 P 点产生的电场dE 进行叠加,求出 P 点的合场强E P 。
均匀带电球体内外各处场强计算例题

【均匀带电球体内外各处场强计算例题】1. 概述均匀带电球体内外各处场强计算是电场理论中的经典问题之一,掌握这个问题的解决方法对于深入理解电场的性质和规律具有重要意义。
在本文中,我将根据提供的内容,详细探讨均匀带电球体内外各处场强的计算方法,帮助您全面理解这一问题,并对电场理论有更深入的认识。
2. 均匀带电球体内部场强计算假设半径为R的均匀带电球体带有总电荷量Q,我们要计算球心到球体内某点的电场强度。
根据库仑定律,我们知道电场强度E与电荷量Q和距离r的平方成反比,可表示为E=kQ/r^2,其中k为电场常数。
对于均匀带电球体内部的场强计算,我们可以将球体划分为无数个微小电荷元,然后利用积分的方法对每个微小电荷元的电场强度进行求和,得到总的电场强度。
具体的推导过程略。
3. 均匀带电球体外部场强计算球体外部的场强计算相对而言要简单一些。
根据库仑定律,我们同样可以利用积分的方法将球体划分为无数个微小电荷元,然后对每个微小电荷元的电场强度进行求和,得到球体外某点的电场强度。
在球体外部,可以将球体近似看作点电荷,因此外部的场强计算可以直接使用库仑定律进行求解。
4. 总结与回顾通过上述的详细讨论,我们对均匀带电球体内外各处场强的计算有了更全面的认识。
在计算内部场强时,我们需要将球体划分为无数微小的电荷元,并利用积分方法对每个电荷元的电场强度进行求和;而在计算外部场强时,可以将球体近似看作点电荷,直接使用库仑定律计算。
这些方法和步骤的掌握将对深入理解电场理论起到至关重要的作用。
5. 个人观点和理解对于均匀带电球体内外场强的计算,我个人认为需要在掌握基本原理的基础上进行大量的练习,才能真正掌握解决问题的方法。
通过不断的实践,我们可以更加灵活地运用积分和库仑定律,对各种不同情况进行场强的计算,从而提高自己的理论水平和解决问题的能力。
总结:本文围绕均匀带电球体内外各处场强的计算例题进行了详细的讨论和解释。
通过对内外场强计算方法的探讨,相信读者对这一问题有了更深入和全面的理解。
电磁场与电磁波习题集

r π r r E(z, t) = ex Exm cos(ωt − kz + φx ) + ey Eym cos(ωt − kz + φy − ) 2
磁场为平行平面场,且具有轴对称性,应用安培环路定理, 解 磁场为平行平面场,且具有轴对称性,应用安培环路定理, r r 得 ∫C H ⋅ dl = 2πρHφ = I r r I H = eφ 0< ρ <∞ 磁场强度 2πρ r µI eφ 2πρ 0 < ρ < a r 磁感应强度 B = r e µ0 I a < ρ < ∞ φ 2πρ r r µ − µ0 I r B r eφ ⋅ ρ <a µ0 2πρ 磁化强度 M = − H = µ0 0 a< ρ <∞
则得
E1x = 2 y, E1y = 5x
湖南人文科技学院通信与控制工程系 刘宗良主讲
电磁场与电磁波
习题
10
D1x = ε1E1x = 10ε 0 y, D1y = ε1E1y = 25ε 0 x
r r r 又由 en ⋅ (D − D2 ) = 0 ,有 1
r r r r r r r ez ⋅[ex D1x + ey D1y + ez D1z − (ex D2 x + ey D2 y + ez D2 z ]z=0 = 0
在磁场中运动产生的, 在磁场中运动产生的,故得
r ∂B r r r r εin = ∫ (v × B) ⋅ dl − ∫ ⋅ dS C S ∂t r ∂B r r r r r = ∫ [exv × ez B0 cos(ωt)] ⋅ eydl − ∫ [ez B0 cos(ωt)] ⋅ ez dS C S ∂t = vtωbB0 sin(ωt ) − vbB0 cos(ωt)
均匀带电球面产生电场的场强分布

均匀带电球面产生电场的场强分布"了解电场强度分布:用均匀带电球面说明"电场在物理学中扮演着重要的角色,其中最重要的一种就是均匀带电球面产生的电场。
均匀带电球面是指一个带有球面电荷分布的球形物体,在这种情况下,每点上的电荷分布及电场场强分布都是不变的。
在均匀带电球面产生电场的场强分布概述如下:1. 均匀带电球的外部电场强度当在球外观察电场时,它的外部场强与距离球心的距离成反比,其具体表达式为:$$E=\frac{Q}{4πε_or^2}$$其中,Q表示球上的电荷量,ϵ0表示真空介电常数,r表示球心和观察点的距离。
2. 均匀带电球的内部电场强度球面的内部电场强度是只有电荷之前电场强度,而当到达球心时,场强正比于电荷方向上平均分布。
3. 均匀带电球的电场线强度把球面上任意两点之间的间距作为距离,电场线强度与距离成反比,并且与球面上的电荷分布密切相关。
因此,可以把电场线强度表达式正确地写成:$$E_{line}=\frac{Q_{on line}}{2πε_or}$$其中,Qon line表示球面上线段上的电荷量,即两个点之间的电荷量,ϵ0表示真空介电常数,r表示两个点之间的距离。
总之,根据均匀带电球面产生电场,场强分布符合反比定律,且与球面上的电荷分布密切相关。
综上所述,均匀带电球面产生电场的场强分布概括如下:(1)球外的电场强度在四周被等式$$E=\frac{Q}{4πε_or^2}$$表达,且与距离r的反比;(2)球内的电场强度仅为电荷之前,并正比于电荷方向上平均分布;(3)球面上的电场线强度以两点距离的反比表达,其公式为$$E_{line}=\frac{Q_{on line}}{2πε_or}$$。
均匀带电球体内外各处场强计算过程

均匀带电球体内外各处场强计算过程让我们来了解一下什么是均匀带电球体。
均匀带电球体是指球体上的电荷均匀分布。
电场强度的计算是通过库仑定律来实现的,该定律描述了两个电荷之间的相互作用力。
在这里,我们需要计算球体内外各处的电场强度。
对于球体内部的电场强度计算,我们可以采用高斯定律。
高斯定律表明,如果一个闭合曲面内没有电荷,则曲面上的电场强度积分等于零。
根据球对称性,我们可以选择一个球面作为高斯面,球心与球面上的电荷中心对齐。
在球面上,电场强度的大小是均匀的,并且指向球心。
因此,高斯面上的电场强度积分可以简化为电场强度乘以球面积。
根据高斯定律,这个积分应该等于球体内的总电荷除以电介质常数。
而对于球体外部的电场强度计算,则需要使用库仑定律。
根据库仑定律,两个电荷之间的相互作用力与两个电荷之间的距离的平方成反比。
在这种情况下,球体的电荷可以近似看作位于球心的点电荷。
假设球体上的电荷为Q,半径为R,我们可以使用库仑定律计算球体外部某一点的电场强度。
根据库仑定律的公式,电场强度与球体上电荷的大小和球体与观察点之间的距离有关。
对于球体内部的电场强度计算,首先我们需要确定球体内部的电荷分布情况。
在均匀带电球体中,电荷分布是均匀的,即每个微元上的电荷都相等。
我们可以通过球体内部的电荷总量除以球体内部的体积来得到每个微元上的电荷。
然后,我们选择一个球面作为高斯面,并计算球面上的电场强度积分。
由于球体内部的电荷均匀分布,球面上的电场强度大小是均匀的,并且指向球心。
因此,电场强度积分可以简化为电场强度乘以球面积。
我们将电场强度积分等于球体内部的总电荷除以电介质常数,解出电场强度的大小。
通过高斯定律和库仑定律,我们可以计算均匀带电球体内外各处的电场强度。
在球体内部,我们使用高斯定律,并确保电荷均匀分布。
在球体外部,我们使用库仑定律,并将球体近似为点电荷。
这样,我们就可以准确地计算出均匀带电球体内外各处的电场强度。
这个过程需要注意电荷的均匀分布、选择适当的高斯面和正确应用高斯定律和库仑定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
