静电场之均匀带电球面球体和球壳的电场
大物习题册答案及详解(山东理工大学大二上学期2020版)

4.如图所示,一点电荷q位于正立方体的A角上,则通过侧面abcd的电通量Φe=q/24ε0
考点: 高斯定理公式 (课本118页 6-18) 解法:1.建立一正方体高斯面(补7个如图正方体),使A点位于正中心
考点:电势是一个与引进电荷无关,完全由电场自身的性质和相对位置决定的物理量。电场中某点电势的大小与零 电势点的选取有关。
2.在边长为a的正方体中心处放置一电量为Q的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为
(B)
(A)Q/4πε0a
(B)Q/2πε0a
(C)Q/πε0a
(D)Q/2√2πε0a
q/(1/r-1/r0)/4πε0
考点:电势的计算
解法:U=∫
r0 r
E·dr
=∫
r0 qdr r 4πε0r
2
=q/(1/r-1/r0)/4πε0
(课本122页
6-29b)
பைடு நூலகம்
3.一质量为m、电量为q的小球,在电_场__力__作__用下,从电势为U的a点移动到电势为零的b点,若已知小球在b点的 速率为Vb,则小球在a点的速率Va=√Vb2-2qU/m
②均匀带电球面内的电势UP2=Q/4πε0R(课本123页例6-8结论得), ③UP=UP1+UP2.
6.在带电量为-Q的点电荷A的静电场中,将另一带电量为q的点电荷B从a点移到b点,a、b两点距离点电荷A的距 离分别为r1和r2,如图所示,则移动过程中电场力做的功为(C) (A)-Q(1/r1-1/r2)/4πε0 (B)qQ(1/r1-1/r2)/4πε0 (C)-qQ(1/r1-1/r2)/4πε0 (D)-qQ/4πε0(r2-r1) 考点:电场力的功 解法:Aeab=q(UA-UB)=q(-Q/4πε0r1— -Q/4πε0r2)=-qQ(1/r1-1/r2)/4πε0 (课本123页 6-31)
高斯定理(高斯定理是什么?高斯定理怎么用?)
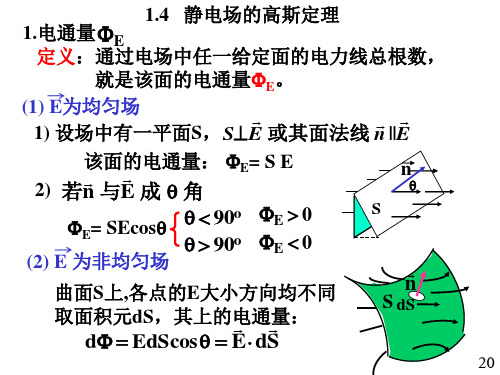
选取闭合的柱形高斯面
E dS S'
S
0 底面积
2S'E S'
E
S'
0
S' E
S'
E 20
E
EE
E
E 2 0
E
x
O
( 0)
讨论
无的 限电 大场 带叠 电加 平问 面题
0
0
高斯定理举例:
均匀带电球面(球体、球壳等)的 电场分布 均匀带电直线(圆柱面、圆柱体等)
的电场分布 均匀带电无限大平面的电场分布
例:均匀带电球壳的电场强度
一半径为R , 均匀带电 Q 的薄
球壳 . 求球壳内外任意点的电场强
度. 解(1)0 r R
r S +
r +
+
O
+ 1+ + +
+R +
S
s (柱面)
h 0
2 rhE h 0
E
2 0 r
z
+
+
r h
+
+o
x+
E y en
E
O
r
讨论
o
E O
无限长均匀带电柱面的电场分布
对称性分析: 视为 无限长均匀带电直 线的集合;
r
P
dE '
选同轴圆柱型高斯 面;
由高斯定理计算
dE
dE dE'
0 rR
高斯 Carl Friedrich
Gauss 德国 1777~1855 数学家、天文学家
静电场的高斯定理

例7-10 求电荷呈“无限长”圆柱形轴对称均匀分布时 所激发的电场强度。
解:电场分布也应有柱对称性,方向沿径向。 作与带电圆柱同轴的圆柱形高斯面,
高为h,半径为r
•当r>R 时,
sE dS 侧面 E dS E 2 r h 为什么?
r h
E 2 r h h 0
P点的场强
E 2 0 r
1
0
d V
V
关于高斯定理的几点讨论
以上是通过用闭合曲面的电通量概念来说明高斯 定理,仅是为了便于理解而用的一种形象解释, 不是高斯定理的证明
高斯定理是在库仑定律基础上得到的,但是前者 适用范围比后者更广泛。后者只适用于真空中的 静电场,而前者适用于静电场和随时间变化的场, 高斯定理是电磁理论的基本方程之一。
③ 场源电荷为无限长均匀带电直线、均匀带电直圆柱面、直 圆柱体或同轴导体圆筒等,则电场的分布具有柱对称性。
(2) 选取高斯面
用高斯定理求场强时,选取恰当的高斯面是解题的关键。
选取高斯面的原则:
① 选取的高斯面必须通过所考查的场点。 ② 应使高斯面上各点的场强大小相等, 方向与该处面元 的
法线平行(这样则可将E提到积分号外,只对面积积分); 或者使高斯的部分面上各点场强大小相等,方向与 的法线 平行,另一部分面上各点场强为零或场强的方向与面元的 法线垂直(即通过这部分的E通量为零)。
高斯定理解题步骤: 总结
(1)分析电场的对称性
根据题意画出示意图,分析电场的分布情况 (最好画出电场 线),看是否具有某种特殊的对称性,这可从产生电场的场 源电荷的分布看出。
常见的情况有以下几种:
① 场源电荷为均匀带电球面、均匀带电球体、同心的均匀带 电导体球壳等,则电场的分布具有球对称性;
均匀带电球体内外的电场强度公式

一、电场的概念电场是指电荷周围空间内的物理场,它描述了电荷对空间内其它电荷的作用力。
在物理学中,电场是一种很重要的概念,它可以帮助我们理解电荷之间相互作用的规律,也是电磁学的重要内容之一。
二、均匀带电球体的电场强度定义均匀带电球体是指球体内每一点的电荷密度都是相同的,而且球体外部没有电荷分布。
对于这样的球体,可以利用高斯定律求出球体内外的电场强度。
三、均匀带电球体内部的电场强度1. 对于均匀带电球体内部的一点P,其到球心的距离记为r,球体的半径记为R。
2. 根据高斯定律,球体内部的电场强度公式为E = k * Q * r / R^3,其中,k为电场常数,Q为球体的总电荷量。
3. 由上式可以看出,均匀带电球体内部的电场强度与点P到球心的距离成正比,与球体的总电荷量成正比,与球体的半径的立方成反比。
这说明球体内部的电场强度分布是均匀的,且与点P到球心的距离成线性关系。
四、均匀带电球体外部的电场强度1. 对于均匀带电球体外部的一点Q,其到球心的距离记为r。
2. 根据高斯定律,球体外部的电场强度公式为E = k * Q / r^2,其中,k为电场常数,Q为球体的总电荷量。
3. 由上式可以看出,均匀带电球体外部的电场强度与点Q到球心的距离成反比,与球体的总电荷量成正比。
随着点Q到球心的距离增大,电场强度逐渐减小。
五、结论通过本文对均匀带电球体内外的电场强度公式的推导和分析,我们可以得出以下结论:1. 均匀带电球体内部的电场强度与点到球心的距离成正比,与球体的总电荷量成正比,与球体的半径的立方成反比。
2. 均匀带电球体外部的电场强度与点到球心的距离成反比,与球体的总电荷量成正比。
均匀带电球体内外的电场强度公式为E = k * Q * r / R^3 (r < R) 和 E = k * Q / r^2 (r > R)。
这些公式在电磁学理论研究和工程实践中具有重要的应用价值。
在物理学中,电场是一种很重要的概念,它可以帮助我们理解电荷之间相互作用的规律,也是电磁学的重要内容之一。
静电场复习

解:(1)
4o r 2 1 q 2 we o E 2 4 2 32 o r
2
E
q
+ -
+ R3 -
dV 4 r U V V E d
电场力的功与电势能:E
E
W
q0
E d
V
E q0
W
q 0 ( V ) qUab V
qq E 点电荷q的电场中某处另一点电荷的电势能: 4 r E qV
关于电势与电场强度关系的讨论
在电场中任一点,场强等于该点处电势梯度的负值, 即电场强度的大小与电势变化率的最大值对应。
(2)
W2 we dV
q
2 2
R3
8o r
dr
W2
q
2
8o R3
8.1105 ( J )
例6、内半径为R1,外半径为R2的圆柱形电容器( R2 <2 R1 ),中间充以两种不同介质,相对介电常数分别 为r1和r2 = r1/2,分界面半径为r。两介质的介电强 度都是EM 。问:当电压升高时,哪层介质先被击穿 ?最大电压为多少? r2 解:
x
a 0dx dx a o o
0
U 外2
a Edx 0dx dx x x a o o
0 a 0
x U内 dx x o o
0
( a x a)
+
-
-a
a o
9.0静电场之基本内容

空间某点的所产生的场强等于各个 ri是电荷Qi到场点P的矢径。 点电荷在该点产生场强的矢量和 当电荷连续分布时,可将带电体分成许 dE = dq 3 r 4πε 0 r 多点电荷,每个点电荷产生的场强为 全部电荷产生 E = 1 dq r 4πε 0 ∫ r 3 的合场强为 点电荷dq可根据线密度λ, 面密度σ或体密度ρ决定 dq = λdl,dq = σdS和dq = ρdV。
4.典型源电荷的电场 (1)点电荷 E = 1 Q r 4πε 0 r 3 的电场为 其中r是点电荷 Q到场点的矢径。 Q>0 Q<0 r r P E EP
点电荷产生的场强与其电量Q成正比, 与场点到点电荷的距离的平方成反比, 方向在场点到点电荷的连线上。 正点电荷产生场强的方向沿径向向外, 负点电荷产生场强的方向沿径向向内。 (2)无限长均匀带 E = λ r 2 ε 2 π r 电直线的场强为 0
n
θ
E
∫
S
E ⋅ dS 对于封闭的曲面,通常取外
法线方向为曲面的正方向。
7.高斯定理:在静电场中,通过任一闭合曲面(称为高 斯面)的电通量等于该曲面包围的电量的代数和除以ε0
ΦE =
∫
S
E ⋅ dS =
1
ε0
高斯定理说明电场是有源场,正电荷 q ∑ i
i
是电场的源头,负电荷是电场的汇尾。
注意:任何一点的场强E是所有电荷在 该处产生的,而 ∑ qi 是高斯面内的电 i 荷,不包括高斯面外的电荷,因为高 斯面外的电荷产生的电通量为零。
湖南大学物电院周群益第九章第九章静电场静电场基本内容基本内容范例范例92电偶极子的电场电偶极子的电场范例范例93均匀带电线段的电场均匀带电线段的电场范例范例91点电荷的电场点电荷的电场范例范例94平行直线电荷的电场平行直线电荷的电场范例范例95均匀带电圆环圆盘和圆圈在轴线上的电场均匀带电圆环圆盘和圆圈在轴线上的电场范例范例98直线电荷与共面带电线段之间的作用力直线电荷与共面带电线段之间的作用力范例范例97均匀带电圆柱面圆柱体和圆柱壳的电场均匀带电圆柱面圆柱体和圆柱壳的电场范例范例99直线电荷与共面圆弧电荷之间的作用力直线电荷与共面圆弧电荷之间的作用力范例范例910点电荷在有孔带电平面轴线上的运动规律点电荷在有孔带电平面轴线上的运动规律范例范例96均匀带电球面球体以及球壳的电场均匀带电球面球体以及球壳的电场基本内容基本内容1
静电场补充习题

第5章 静电场一、选择题1. 关于真空中两个点电荷间的库仑力 [ ] (A) 是一对作用力和反作用力(B) 与点电荷的电量成正比, 电量大的电荷受力大, 电量小的电荷受力小 (C) 当第三个电荷移近它们时, 力的大小方向一定会发生变化 (D) 只有在两点电荷相对静止时, 才能用库仑定律计算2. 将某电荷Q 分成q 和(Q -q )两部分, 并使两部分离开一定距离, 则它们之间的库仑力为最大的条件是 [ ] (A) 2Q q =(B) 4Q q = (C) 8Q q = (D) 16Q q =3. 正方形的两对角处, 各置点电荷Q , 其余两角处各置点电荷q ,若某一Q 所受合力为零, 则Q 与q 的关系为 [ ] (A) Q =-2.8q (B) Q =2.8q (C) Q =-2q (D) Q =2q4. 两点电荷间的距离为d 时, 其相互作用力为F . 当它们间的距离增大到2d 时, 其相互作用力变为[ ] (A) F 2 (B) F 4 (C)2F (D) 4F5. 关于静电场, 下列说法中正确的是[ ] (A) 电场和检验电荷同时存在, 同时消失(B) 由q F E /=知, 电场强度与检验电荷电量成反比(C) 电场的存在与否与检验电荷无关(D) 电场是检验电荷与源电荷共同产生的6. 电场强度定义式qFE =的适用范围是[ ] (A) 点电荷产生的场 (B) 静电场 (C) 匀强电场 (D) 任何电场7. 由场强的定义式qFE =可知[ ] (A) E 与F 成正比, F 越大E 越大 (B) E 与q 成反比, q 越大E 越小(C) E 的方向与F 的方向一致 (D) E的大小可由q F /确定8. 关于电场强度, 以下说法中正确的是[ ] (A) 电场中某点场强的方向, 就是将点电荷放在该点所受电场力的方向 (B) 在以点电荷为中心的球面上, 由该点电荷所产生的场强处处相同(C) 场强方向可由q F E /=定出, 其中q 可正, 可负(D) 以上说法全不正确T5-1-3图9. 关于电场线, 下列叙述中错误的是[ ] (A) 电场线出发于正电荷, 终止于负电荷 (B) 除电荷所在处外, 电场线不能相交(C) 某点附近的电场线密度代表了该点场强的大小(D) 每条电场线都代表了正的点电荷在电场中的运动轨迹10. 关于电场线, 以下说法中正确的是[ ] (A) 电场线一定是电荷在电场力作用下运动的轨迹 (B) 电场线上各点的电势相等 (C) 电场线上各点的电场强度相等(D) 电场线上各点的切线方向一定是处于各点的点电荷在电场力作用下运动的加速度方向11. 在静电场中, 电场线为平行直线的区域内[ ] (A) 电场相同, 电势不同 (B) 电场不同, 电势相同 (C) 电场不同, 电势不同 (D) 电场相同, 电势相同12. 一个带电体要能够被看成点电荷, 必须是[ ] (A) 其线度很小 (B) 其线度与它到场点的距离相比足够小 (C) 其带电量很小 (D) 其线度及带电量都很小13. 电场强度计算式30π4rrq E ε=的适用条件是 [ ] (A) 点电荷产生的电场, 且不能r → 0 (B) 轴线为l 的电偶极子, 且r >>l (C) 半径为R 的带电圆盘, 且r ≈ R (D) 半径为R 的带电球体, 且r < R14. 关于电偶极子有下列说法, 其中正确的是 [ ] (A) 电偶极子在电场中所受合力一定为零(B) 电介质被电场极化后, 其分子都可以看作电偶极子 (C) 电偶极子两电荷连线的垂直平分面上场强处处为零 (D) 电偶极子两电荷连线的垂直平分面上电势处处不为零15. 一均匀带电球面, 面内电场强度处处为零, 则球面上的带电量为dS σ的电荷元在球面内产生的场强[ ] (A) 处处为零 (B) 不一定为零 (C) 一定不为零 (D) 是一常数16. 一均匀带电的球形橡皮气球, 在被吹大的过程中, 场强不断变小的点是 [ ] (A) 始终在气球内部的点 (B) 始终在气球外部的点 (C) 从气球外变到气球内表面上的点 (D) 找不到这样的点17. 在边长为a 的正方体中心处放置一电量为Q 的点电荷, 强度的大小为:[ ] (A) a Q 0π2ε (B) a Q0π3ε(C) a Q 0πε (D) aQ0π4εT5-1-15图a Q18. 半径为R 的均匀带电球面, 若其面电荷密度为σ, 则在球面外距离球面R 处的电场强度大小为 [ ] (A)0εσ (B) 02εσ (C) 04εσ (D) 08εσ19. 两个点电荷相距一定距离, 若在这两个点电荷连线的中点处场强为零, 则这两个点电荷的带电情况为[ ] (A) 电量相等, 符号相同 (B) 电量相等, 符号不同 (C) 电量不等, 符号相同 (D) 电量不等, 符号不同20. 边长为a 的正方体中心放置一点电荷Q , 则一个侧面中心处的电场强度大小为 [ ] (A) 20π4a Q ε (B)20π8a Q ε (C)20πa Q ε (D) 20π2aQε21. 一个带电量为q 的点电荷位于一边长为a 的立方体的一个顶角上体一个q 不在其上的侧面的电通量为:[ ] (A) 06εq (B) 012εq(C) 024εq (D) 048εq22. 有N 根电场线同时穿过三个大小不等的面S 1、S 2和S 3.如果S 1的通量关系是[ ] (A) 321ΦΦΦ>> (B) 321ΦΦΦ== (C) 321ΦΦΦ<< (D) 321ΦΦΦ<>23. 一个点电荷, 放在球形高斯面的中心, 下列哪种情况通过该高斯面的电通量有变化? [ ] (A) 将另一点电荷放在高斯面外 (B) 将另一点电荷放在高斯面内 (C) 将中心处的点电荷在高斯面内移动(D) 缩小高斯面的半径24. 在无限大均匀带电平面M 的附近, 有一面积为S 的平面N .要使通过N 的电通量最大, 应使[ ] (A) N 面与M 面平行 (B) N 面与M 面垂直(C) N 面的法线与M 面的法线成45°夹角 (D) N 面的法线与M 面的法线成30°夹角25. 高斯定理0d ε∑⎰⎰=⋅i sq S E, 说明静电场的性质是[ ] (A) 电场线是闭合曲线 (B) 库仑力是保守力 (C) 静电场是有源场 (D) 静电场是保守场T5-1-23图26. 根据高斯定理⎰⎰∑=⋅siqS E 0d ε,下列说法中正确的是[ ] (A) 通过闭合曲面的电通量仅由面内电荷的代数和决定 (B) 通过闭合曲面的电通量为正时面内必无负电荷 (C) 闭合曲面上各点的场强仅由面内的电荷决定(D) 闭合曲面上各点的场强为零时, 面内一定没有电荷27. 电场中一高斯面S , 内有电荷q 1、q 2,S 面外有电荷q 3、q 4.关于高斯定理d ε∑⎰⎰=⋅isqS E , 正确的说法是[ ] (A) 积分号内E只是q 1、q 2共同激发的(B) 积分号内E是q 1、q 2、q 3、q 4共同激发的(C) 积分号内E只是q 3、q 4共同激发的(D) 以上说法都不对28. 高斯定理成立的条件是[ ] (A) 均匀带电球面或均匀带电球体所产生的电场 (B) 无限大均匀带电平面产生的电场(C) 高斯面的选取必须具有某些简单的对称性 (D) 任何静电场29. 在任何静电场中, 任一闭合曲面上各点的电场强度是由 [ ] (A) 曲面内的电荷提供 (B) 曲面外的电荷提供(C) 曲面内的电荷和曲面外的电荷共同提供(D) 电场强度的通量由曲面内的电荷和曲面外的电荷共同提供30. 关于高斯面上的场强E,下面说法哪一个对?[ ] (A) 如果高斯面上E处处为零, 则该面内必无电荷(B) 如果高斯面内无电荷, 则高斯面上E处处为零(C) 如果高斯面内有电荷, 则高斯面上E处处不为零(D) 以上说法都不正确31.以下说法中正确的是[ ] (A) 高斯面上的场强处处为零时, 通过该高斯面的电通量一定为零 (B) 高斯面上的场强处处为零时, 通过该高斯面的电通量不一定为零(C) 高斯面内电荷代数和为零时, 高斯面上各点的场强一定为零(D) 高斯面内电荷代数和不为零时, 高斯面上各点的场强一定不为零32. 闭合面S 内有一点电荷Q , P 为S 面上一点, 若在S 面外附近再放入一个点电荷q , 则[ ] (A) 通过S 面的电通量改变, P 点的场强不变 (B) 通过S 面的电通量不变, P 点的场强改变 (C) 通过S 面的电通量和P 点的场强都不变 (D) 通过S 面的电通量和P 点的场强都改变T5-1-32图33. 两个同号的点电荷相距l , 要使它们的电势能增加一倍, 应该怎样移动点电荷? [ ] (A) 外力作功使点电荷间距离减小为l /2 (B) 外力作功使点电荷间距离减小为l /4 (C) 电场力作功使点电荷间距离增大为2 l (D) 电场力作功使点电荷间距离增大为4 l34. 将点电荷Q 从无限远处移到相距为2l 的点电荷+和-q 的中点处, 则电势能的增加量为[ ] (A) 0 (B)l q 0π4ε (C) l Qq 0π4ε (D) lQq0π2ε35. 当产生电场的全部电荷分布在有限区域时, 取无限远处的电势为零. 照这样的规定, 下述情况中电势能为正的是[ ] (A) +q 在负点电荷的场中 (B) +q 在正点电荷的场中 (C) -q 在正点电荷的场中 (D) -q 在电偶极子连线中点36. 下面关于某点电势正负的陈述中, 正确的是 [ ] (A) 电势的正负决定于试探电荷的正负(B) 电势的正负决定于移动试探电荷时外力对试探电荷作功的正负(C) 空间某点电势的正负是不确定的, 可正可负, 决定于电势零点的选取 (D) 电势的正负决定于带电体的正负37. 在下列情况中, 零电势可以选在无限远处的是[ ] (A) 孤立带电球体的电势 (B) 无限大带电平板的电势(C) 无限长带电直导线的电势 (D) 无限长均匀带电圆柱体的电势38. 由定义式⎰∞⋅=RR l E Ud 可知[ ] (A) 对于有限带电体, 电势零点只能选在无穷远处(B) 若选无限远处为电势零点, 则电场中各点的电势均为正值 (C) 已知空间R 点的E , 就可用此式算出R 点的电势(D) 已知R →∞积分路径上的场强分布, 便可由此计算出R 点的电势39. 若将彼此远离的27滴具有相同半径并带有相同电荷的水滴聚集成一个大水滴,此时大水滴的电势是小水滴电势的[ ] (A) 54倍 (B) 27倍 (C) 81倍 (D) 9倍40. 静电场中某点电势的数值等于[ ] (A) 试验电荷q 0置于该点时具有的电势能 (B) 单位试验电荷置于该点时具有的电势能 (C) 单位正电荷置于该点时具有的电势能(D) 把单位正电荷从该点移到电势零点外力所做的功41. 边长为a 的正方体中心处放置一电量为Q 的点电荷,则在一个侧面中心处的电势为: [ ] (A) a Q 0π4ε (B) a Q0π2ε(C)aQ 0πε (D)aQ0π8ε42. 两个点电荷相距一定距离, 若这两个点电荷连线的中垂线上电势为零, 则这两个点电荷的带电情况为[ ] (A) 电量相等, 符号相同 (B) 电量相等, 符号不同 (C) 电量不同, 符号相同 (D) 电量不等, 符号不同43. 如图所示, 一带负电的油滴在两个带电的水平放置的大平行金属板之间保持稳定; 若油滴获得了附加的负电, 要维持油滴稳定应采取怎样的措施? [ ] (A) 使金属板互相靠近些(B) 改变板上的电荷的正负极 (C) 使油滴离正电板远一些 (D) 减小两板之间的电势差44. 在电场中有a 、b 两点, 在下述情况中b 点电势较高的是 [ ] (A) 正电荷由a 移到b 时, 外力克服电场力作正功 (B) 正电荷由a 移到b 时, 电场力作正功(C) 负电荷由a 移到b 时, 外力克服电场力作正功 (D) 负电荷由a 移到b 时, 电场力作负功45. 等边三角形的三个顶点上分别放置着均为正的点电荷q 、2 q 、和3 q , 三角形的边长为a , 若将正电荷Q 从无穷远处移至三角形的中心点处, 所需做的功为[ ] (A) a Qq 0π44.3ε (B) aQq 0π7.1ε (C) a Qq 0π6.2ε (D) aQq 0π4.3ε46. 一电偶极子放在均匀电场中, 当电偶极矩的方向与场强方向不一致时, 其所受合力F 和力偶矩M分别为[ ] (A) 0,0==M F (B) 0,0≠=M F(C) 0,0=≠M F (D) 0,0≠≠M F47. 相距为r 1的两个电子, 在重力可忽略的情况下由静止开始运动到相距为r 2. 两电子系统在从相距为r 1到相距为r 2期间, 两电子系统的下列哪个量是不变的? [ ] (A) 动能总和 (B) 电势能总和 (C) 动量总和 (D) 电相互作用力48. 已知一负电荷从T5-1-48图所示的电场中M 点移到N 点.有人根据这个图得出下列几点结论,其中哪一点是正确的? [ ] (A) 电场强度E M < E N ; (B) 电势U M < U N ; (C) 电势能W M < W N ; (D) 电场力的功A > 0. 49. 关于电场强度和电势的关系, 下列说法中正确的是[ ] (A) 电势不变的空间, 电场强度一定为零 (B) 电势不变的空间, 电场强度不为零T5-1-43图T5-1-45图a q q q 3T5-1-46图pE q-q +T5-1-48图MN(C) 电势为零处, 电场强度一定为零 (D) 电场强度为零处, 电势一定为零50. 已知空间某区域为匀强电场, 则该区域内 [ ] (A) 电势差相等的各等势面间距不等 (B) 电势差相等的各等势面间距相等(C) 电势差相等的各等势面间距不一定相等 (D) 不同点间一定无电势差51. 一点电荷在电场中某点所受的电场力为零, 则该点 [ ] (A) 场强一定为零, 电势一定为零 (B) 场强不一定为零, 电势一定为零 (C) 场强一定为零, 电势不一定为零 (D) 场强不一定为零, 电势不一定为零52. 根据场强和电势梯度的关系式lUE l d d -=可知, 下列叙述中正确的是 [ ] (A) 场强为0处, 电势一定为0 (B) 电势为0处, 场强一定为0(C) 场强处处为0的区域, 电势一定处处相等 (D) 电势处处相等的区域, 场强不一定处处为053. 带电-q 的粒子在带电+q 的点电荷的静电力作用下在水平面内绕点电荷作半径为R 的匀速圆周运动. 如果带电粒子质量及点电荷的电量均增大一倍, 并使粒子的运动速率也增大一倍, 则粒子的运动半径将变为[ ] (A) R /4 (B) R /2 (C) 2R (D) 4R54. 如T5-1-54图所示, 在一条直线上的连续三点A 、B 、C 的电势关系为U A >U B >U C . 若将一负电荷放在中间点B 处, 则此电荷将 [ ] (A) 向A 点加速运动 (B) 向A 点匀速运动 (C) 向C 点加速运动 (D) 向C 点匀速运动55. 两个带不等量的同性电荷的小球由静止释放, 仅在静电斥力作用下运动.下列陈述中错误的是[ ] (A) 两带电体间由于距离增加而斥力渐减(B) 两带电小球的总动量不变 (C) 两带电体间的电场不变(D) 两带电体的动能和势能之和为定值56. 关于电荷仅在电场力作用下运动的下列几种说法中, 错误的是 [ ] (A) 正电荷总是从高电势处向低电势处运动(B) 正电荷总是从电势能高的地方向电势能低的地方运动 (C) 正电荷总是从电场强的地方向电场弱的地方运动 (D) 正电荷加速的地方总是与等势面垂直57. 边长为a 的正方体中心放置一电荷Q , 则通过任一个侧面S 的电通量⎰⎰⋅sS E d 为[ ] (A)04εQ (B) 06εQ (C) 08εQ (D) 6QT5-1-54图58. 欲使一个半径为R 的均匀带电球体表面上的场强和球内各点的场强大小相等, 则必须使其电荷体密度 ρ 与半径r 的关系为 [ ] (A)r ∝ρ (B) r 1∝ρ (C) ρ 与r 无关 (D) 21r∝ρ59. 一个带电球体(非导体), 体电荷密度ρ与距球心距离r 成正比, 即r ∝ρ, 则球体表面处场强1E 与球体内部场强2E 的关系为[ ] (A) 21E E > (B) 21E E <(C) 21E E = (D) 不能确定60. 当一对电偶极子对称放置在圆球面内的一条直径上时 [ ] (A) 球面上场强处处相等 (B) 球面上场强处处为零 (C) 球面上总的电通量为零 (D) 球面内没有包围电荷61. 真空中一“无限大”均匀带负电荷的平面如图所示,其电场的场强分布图线应是(设场强方向向右为正、向左为负)[ ]62. 如T5-1-62图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,轴线方向单位长度上的带电量分别为1λ 和2λ, 则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小[ ] (A) r 021π2ελλ+ (B) 202101π2π2R R ελελ+(C) 101π4R ελ (D) 063. 图示为一具有球对称性分布的静电场的E ~ r 关系曲线,请指出该静电场E 是由下列哪种带电体产生的.[ ] (A) 半径为R 的均匀带电球面(B) 半径为R 的均匀带电球体 (C) 半径为R 、电荷体密度为Ar =ρ (A 为常数)的非均匀带电球体(D) 半径为R 、电荷体密度为r A /=ρ (A 为常数)的非均匀带电球体T5-1-59图x x 02εσx x xT5-1-62图T5-1-63图二、填空题1. 把总电量为Q 的同种电荷分成两部分,一部均匀分布在地球上,另一部分均匀分布在月球上,使它们之间的库仑力与万有引力抵消.已知地球的质量为kg 1098.524⨯=M ,月球的质量为kg 1034.722⨯=m ,则电荷Q 的最小值为 .2. 真空中有两个点电荷,电量分别为μC 0.16μC,0.821-==q q ,相距20cm .在离这两个电荷都是20cm 的地方,其场强的大小为 V ⋅m -1.3. 半径为R 的均匀带电球面, 若其面电荷密度为σ, 则在球面外距离球面R 处的电场强度大小为 .4. 两个同心均匀带电球面,半径分别为a R 和b R (b a R R <) , 所带电量分别为a Q 和b Q ,设某点与球心相距r , 当b a R r R <<时, 该点的电场强度的大小为 .5. 一个带电量为q 的点电荷位于一边长为a 的立方体的一个顶角上,则通过该立方体一个q 不在其上的侧面的电通量为 .6. 有两个点电荷电量都是+q ,相距为2a .今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面,在球面上取两块相等的小面积S 1和S 2, 其位置如T5-2-6图所示.设通过S 1 和 S 2的电场强度通量分别为1Φ和2Φ,通过整个球面的电场强度通量为S Φ,则1Φ、2Φ与S Φ的关系为 .7. 如T5-2-7所示,一半径为R 的均匀带正电圆环,其电荷线密度为λ.在其轴线上有A 、B 两点,它们与环心的距离分别为R R 83、.现有一质量为m 、带电量为q 的粒子从A 点运动到B 点,在此过程中电场力所作的功为 .8. 一长为L 、半径为R 的圆柱体,置于电场强度为E 的均匀电场中,圆柱体轴线与场强方向平行.则:(A) 穿过圆柱体左端面的电通量为 ;(B) 穿过圆柱体右端面的电通量为 ; (C) 穿过圆柱体侧面的电通量为 ; (D) 穿过圆柱体整个表面的电通量为 .T5-2-5图qaT5-2-7图 T5-2-8图X O1S 2S a 2a q qT5-2-6图9. 真空中一半径为R 的均匀带电球面,总电量为Q (Q > 0).今在球面上挖去非常小块的面积ΔS (连同电荷),且假设不影响原来的电荷分布,则挖去S ∆后球心处电场强度的大小E = ,其方向为 .10. A 、B 为真空中两个平行的“无限大”均匀带电平面,已知两平面间的电场强度大小为E 0 , 两平面外侧电场强度大小都为 E 0 / 3 ,方向如图.则A 、B 两平面上的电荷面密度分别为A σ= ,B σ= .11. 在空间有一非均匀电场,其电场线分布如T5-2-11图所示.在电场中作一半径为R 的闭合球面S ,已知通过球面上某一面元S ∆的电场强度通量为,e Φ∆则通过该球面其余部分的电场强度通量为 .12. 如T5-2-12图,若电荷q 和-q 被包围在高斯面S 内,则通过该高斯面的电通量=⋅⎰⎰S E Sd ,式中E 为处 的场强.13. 有一个球形的橡皮膜气球,电荷q 均匀地分布在球面上,在此气球被吹大的过程中, 被气球表面掠过的点(该点与球中心距离为r ),其电场强度的大小将由 变 为 .14. 在场强为E(方向垂直向上)的均匀电场中,有一个质量为m 、带有正电荷q 的小球,该小球被长度为L 的细线悬挂着.当小球作微小摆动时,其摆动周期T =_____________________ .三、计算题15. 设电荷体密度沿X 轴方向按余弦规律x cos 0ρρ=分布在整个空间,式中ρ为电荷体密度,0ρ为其幅值,试求空间的场强分布.16. T5-3-16图示一厚度为d 的“无限大”均匀带电平板,电荷体密度为ρ.试求板内外的场强分布,并画出场强在X 轴的投影值随坐标x 变化的图线,即E x -x 图线(设原点在带电平板的中央平面上,OX 轴垂直于平板).T5-2-11图ST5-2-9图T5-2-10图T5-2-12图T5-3-16图T5-2-14图11 25. 氢原子的电荷分布可采用下述模型:一个电量为+e 的点电荷被以它为核心的球对称分布的负电荷所包围,负电荷的体密度分布为0/2e)(a r C r --=ρ,式中a 0是玻尔半径,m 1053.0100-⨯=a ,而C 是待定常量. 求距核为a 0处的电场强度.。
均匀带电球体表面电场强度的计算 论文

图2.2球壳与高斯面几何模型
= ( ) (2.2.6)
E S=
E= = (2.2.7)
E= n(2.2.8)
当r>R 时,E= n(2.2.9)
作电场随r变化的曲线如图所示,此曲线为一连续曲线。即带电薄层内的场强从一壁到另一壁是连续变化的,在任何地方都没有突变。
角取值从0到
那么就有
E = (4.3)
令u=cos
则 (4.4)
在球面上时,即R=r
=
===ຫໍສະໝຸດ === = = (4.5)
由E = 可得:
在球面外,即r>R时
由图可知
= (4.6)
在球面内,即R<r时可知:
(4.7)
综上所述可知:
(4.8)
4.2均匀带电半球面轴线上的场强
有一个均匀带电的半球面,它的半径为R,电荷的面密度为 ,求球心处的电场强度。我在这里求轴线任意一点p上的电场强度?
方向沿x轴方向。这与电磁学书上给出的结论一致,可以保证它的正确性。
4.3不均匀带电球体表面空间场强的分布
在静电学中,我们经常可以见到均匀带电球面空间场强的计算这类问题,它是将现实中的问题理想化的模型,但是在现实生活中,我们遇见的问题比较复杂,就像我们要讨论的问题:不均匀带电球面空间场强的分布问题,例如我们会遇到带电球面电荷密度为极角θ的余弦的函数的情况,因此,研究非均匀带电球面场强分布对研究电荷分布有非常重要的意义。
1.电场强度与电场的叠加原理的概念
1.1电场强度
静止点电荷Q激发的静电场,把在电场中所要研究的点叫场点 。在场点中放置一个静止的试探电荷q,有库仑定律可知,它所受到的电场力为 ,其中 不但与场点有关,而且与试探电荷q有关,但 只和场点有关,我们将之称为该点的电场强度。以E为电场强度,其大小为 。
第6、7部分:电学习题

第6部分 真空中的静电场一、选择题1. 根据高斯定理⎰⎰∑=⋅siqS E 0d ε,下列说法中正确的是[ ](A) 通过闭合曲面的电通量仅由面内电荷的代数和决定(B) 通过闭合曲面的电通量为正时面内必无负电荷 (C) 闭合曲面上各点的场强仅由面内的电荷决定(D) 闭合曲面上各点的场强为零时, 面内一定没有电荷2. 高斯定理成立的条件是[ ](A) 均匀带电球面或均匀带电球体所产生的电场 (B) 无限大均匀带电平面产生的电场 (C) 高斯面的选取必须具有某些简单的对称性 (D) 任何静电场3.将点电荷Q 从无限远处移到相距为2l 的点电荷+和-q 的中点处, 则电势能的增加量为[ ] (A) 0 (B)l q 0π4ε (C) l Qq 0π4ε (D) lQq0π2ε4. 在下列情况中, 零电势可以选在无限远处的是[ ](A) 孤立带电球体的电势 (B) 无限大带电平板的电势 (C) 无限长带电直导线的电势 (D) 无限长均匀带电圆柱体的电势5.在空间有一非均匀电场,其电场线分布如图所示。
在电场中作一半径为R 的 闭合球面S ,已知通过球面上某一面元S ∆的电场强度通量为e ∆Φ,则通过该 球面其余部分的电场强度通量为[ ](A)-e ∆Φ (B)24e R S π∆Φ∆ (C) 24e R SSπ-∆∆Φ∆ (D) 0 6.有一半径为b 的圆环状带电导线,其轴线上有两点P 1和P 2,到环心距离如图所示,设无穷远处电势为零,P 1、P 2点的电势分别为U 1和U 2,则21U U 为[ ] (A)31; (B)52; (C) 21; (D) 257.在边长为a 正方体中心处放置一电量为Q 的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为[ ] (A)a 4Q 0πε (B) R 2Q 0πε (C) R Q 0πε (D) R22Q0πε8. 如图所示,一电偶极子放在均匀电场中, 当电偶极矩的方向与场强方向不一致时,其所受合力F和力偶矩M分别为[ ](A) 0,0==M F (B) 0,0≠=M F(C) 0,0=≠M F (D) 0,0≠≠M F9. 已知一负电荷从图5-1-48所示的电场中M 点移到N 点.有人根据这个图得出下列几点结论,其中哪一点是正确的[ ](A) 电场强度E M < E N ; (B) 电势U M < U N ;(C) 电势能W M< W N;(D) 电场力的功A > 0. 10. 边长为a 的正方体中心放置一电荷Q , 则通过任一个侧面S的电通量⎰⎰⋅sS E d 为[ ](A)04εQ (B) 06εQ (C) 08εQ(D) 6Q11.一个容量为10μF 的电容器,充电到500V ,则它所储存的能量为[ ] (A) 1.25J (B)2.50J (C)5.00J (D) 0.25J二、填空题1. 一个带电荷量为q 的点电荷位于一边长为a 的立方体的一个顶角上, 则通过该立方体一个q 不在其上的侧面的E 通量为 .2.如图所示,一半径为R 的均匀带正电圆环,其电荷线密度为λ.在其轴线上有A 、B 两点,它们与环心的距离分别为R R 83、.现有一质量为m 、带电荷量为q 的粒子从A 点运动到B 点,在此过程中电场力所做的功为 .3.真空中一半径为R 的均匀带电球面,总电荷量为Q (Q > 0).今在球面上挖去非常小块的面积S ∆(连同电荷),且假设不影响原来的电荷分布,则挖去S ∆后球心处电场强度的大小E = ,其方向为 . 4.在静电场中,一质子(带电荷e =1.6×10-19C )沿四分之一的圆弧轨道从A 点移到B 点,如图所示,电场力作功8.0×10-15J ,则当质子沿四分之三的圆弧轨道从B 点回到A 点时,电场力作功A =S____________________。
大学物理Ⅱ 高斯定理
P
l
e
E dS S
E dS
侧 E dS 上底 E dS 下底 E dS
侧 EdS E 侧 dS E 2r l
根据高斯定理得 E 2r l 1 l 0
E 2 0 r
用高斯定理求场强小结:
1 . 对称性分析
电荷分布对称性→场强分布对称性
点电荷 球对称性 均匀带电球面
均匀带电球壳
球体
轴对称性 柱对称
无限带电直线
无限带电圆柱 无限圆柱面 无限同轴圆柱面
无限大平面 面对称性 无限大平板
若干无限大平面
2. 高斯面的选择
①高斯面必须通过所求的场强的点。
②高斯面上各点场强大小处处相等,方向处处与该 面元线平行;或者使一部分高斯面的法线与场强方 向垂直;或者使一部分场强为零。
+ q+ +
+
0
R
r
高斯定理的应用
例2 均匀带电球体的电场。球半径为R,带电为q。
解:电场分布也应有球对称性,方向沿径向。
作同心且半径为r的高斯面
1)r R时 ,
E ds E ds
E 4r2
s
s
r
q
0
4 r3
3
0
q
4 R3
4 r3330E qr4 0R3
R
高斯面
高斯定理的应用
Φe前 Φe后 Φe下
s
E
dS
0
y
P
N
en
o
zM
en
E
en
Q
Rx
Φe左
s左
E
dS
ES左
cosπ
ES左
Φe右 s右E dS ES右 cos ES左
(完整版)大学物理静电场试题库

真空中的静电场 一、选择题1、下列关于高斯定理的说法正确的是(A ) A 如果高斯面上E 处处为零,则面内未必无电荷。
B 如果高斯面上E 处处不为零,则面内必有静电荷。
C 如果高斯面内无电荷,则高斯面上E 处处为零。
D 如果高斯面内有净电荷,则高斯面上E 处处不为零。
2、以下说法哪一种是正确的(B )A 电场中某点电场强度的方向,就是试验电荷在该点所受的电场力方向B 电场中某点电场强度的方向可由0q FE 确定,其中0q 为试验电荷的电荷量,0q可正可负,F 为试验电荷所受的电场力C 在以点电荷为中心的球面上,由该点电荷所产生的电场强度处处相同D 以上说法都不正确3、如图所示,有两个电2、 下列说法正确的是(D )A 电场强度为零处,电势一定为零。
电势为零处,电场强度一定为零。
B 电势较高处电场强度一定较大,电场强度较小处电势一定较低。
C 带正电的物体电势一定为正,带负电的物体电势一定为负。
D 静电场中任一导体上电势一定处处相等。
3、点电荷q 位于金属球壳中心,球壳内外半径分别为21,R R ,所带静电荷为零B A ,为球壳内外两点,试判断下列说法的正误(C )A 移去球壳,B 点电场强度变大 B 移去球壳,A 点电场强度变大C 移去球壳,A 点电势升高D 移去球壳,B 点电势升高4、下列说法正确的是(D )A 场强相等的区域,电势也处处相等B 场强为零处,电势也一定为零C 电势为零处,场强也一定为零D 场强大处,电势不一定高5、如图所示,一个点电荷q 位于立方体一顶点A 上,则通过abcd 面上的电通量为(C ) A 06q ε B 012q ε C 024q ε D 036qε6、如图所示,在电场强度E 的均匀电场中,有一半径为R 的半球面,场强E 的方向与半球面的对称抽平行,穿过此半球面的电通量为(C ) A E R 22π B E R 22π C E R 2π DE R 221π7、如图所示两块无限大的铅直平行平面A 和B ,均匀带电,其电荷密度均为)(20-•〉m C σσ,在如图所示的c b a 、、三处的电场强度分别为(D ) A 0,,00,εσ B 0,2,00,εσ C 000,,2εσεσεσ D 00,0,εσεσ8、如图所示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的.(B )A 半径为R 的均匀带电球面.B 半径为R 的均匀带电球体.C 半径为R 的、电荷体密度为Ar =ρ(A 为常数)的非均匀带电球体D 半径为R 的、电荷体密度为r A /=ρ(A 为常数)的非均匀带电球体 9、设无穷远处电势为零,则半径为R 的均匀带电球体产生的电场的电势分布规律为(图中的0U 和b 皆为常量):(C)10、如图所示,在半径为R 的“无限长”均匀带电圆筒的静电场中,各点的电场强度E 的大小与距轴线的距离r 关系曲线为(A )da bc qA11、下列说法正确的是( D )(A )闭合曲面上各点电场强度都为零时,曲面内一定没有电荷(B )闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零 (C )闭合曲面的电通量为零时,曲面上各点的电场强度必定为零。
大学物理知识总结习题答案(第四章)静电场

第四章 静电场本章提要1.电荷的基本性质两种电荷,量子性,电荷首恒,相对论不变性。
2.库仑定律两个静止的点电荷之间的作用力12122204kq q q q r r==F r r πε 其中922910(N m /C )k =⨯⋅122-1-2018.8510(C N m )4k -==⨯⋅επ3.电场强度q =F E 0q 为静止电荷。
由10102204kq q q q r r==F r r πε 得112204kq q r r ==E r r πε4.场强的计算(1)场强叠加原理电场中某一点的电场强度等于各个点电荷单独存在时在该点产生的电场强度的矢量和。
i =∑E E(2)高斯定理电通量:在电场强度为E 的某点附近取一个面元,规定S ∆=∆S n ,θ为E 与n 之间的夹角,通过S ∆的电场强度通量定义为e cos E S ∆ψ=∆=⋅∆v S θ取积分可得电场中有限大的曲面的电通量ψd e sS =⋅⎰⎰E Ò高斯定理:在真空中,通过任一封闭曲面的电通量等于该封闭曲面的所有电荷电量的代数和除以0ε,与封闭曲面外的电荷无关。
即i 01d sq=∑⎰⎰E S g Ò内ε5.典型静电场(1)均匀带电球面0=E (球面)204q r πε=E r (球面外)(2)均匀带电球体304q R πε=E r (球体) 204q r πε=E r (球体外)(3)均匀带电无限长直线场强方向垂直于带电直线,大小为02E r λπε=(4)均匀带电无限大平面场强方向垂直于带电平面,大小为2E σε=6.电偶极矩电偶极子在电场中受到的力矩=⨯M P E思考题4-1 020 4qq r ==πεr 与FE E 两式有什么区别与联系。
答:公式q FE =是关于电场强度的定义式,适合求任何情况下的电场。
而公式0204q rπε=E r是由库仑定理代入定义式推导而来,只适于求点电荷的电场强度。
4-2一均匀带电球形橡皮气球,在气球被吹大的过程中,下列各场点的场强将如何变化?(1) 气球部 (2) 气球外部 (3) 气球表面答:取球面高斯面,由00d ni i q ε=⋅=∑⎰⎰ÒE S 可知(1)部无电荷,而面积不为零,所以E = 0。
静电场

静电场一个基本定律和一个叠加原理:库伦定律和电场强度叠加原理两个重要定理:高斯定理和静电场环路定理两个基本计算:电场强度和电势计算两个计算思路:定义式计算和特定情况下的简捷计算(高斯定理)一.知识点1. 库伦定律2. 静电场叠加原理3. 电偶极矩定义4. 电通量定义及其计算5. 高斯定理6. 静电场环路定理7. 电场力是保守力电势能概念掌握电场力做功和电势能的关系电势差8. 电势的定义及其含义二.基本计算1.电场强度计算1)根据静电场叠加原理,可以计算任意形状的带电体在空间激发的电场(1)点电荷点电荷系(2)连续带电体:1维、2维和3维体系熟悉简单带电体系在空间电场的分布电偶极子:均匀带点细棒:荷电圆环:荷电圆盘:2) 通过高斯定理,可以求解电荷分布对称体系的电场强度分布,如:均匀带电的无限长细棒:均匀带电球面:均匀带电球体:均匀带电的无限大平面薄板:均匀带电的无限长圆柱体:2. 电通量的计算,功、电势能的计算3. 电势的计算1)根据定义,可直接计算,计算中注意:积分上限为势能零点点电荷电势:点电荷系电势:均匀带正电圆环轴线上电势:2)如已知电场强度,可以通过电场强度对选择路径的积分得到均匀带电球体电场中的电势:均匀带电的无限长圆柱体:均匀带电的球面重点掌握利用高斯定理求解对称带电体系的电场强度分布,并进一步会计算电势。
注:以上知识点涉及到的例题和习题是复习重点。
三. 练习题1. 点电荷在真空中的分布如图所示,图中S 为闭合曲面,则通过闭合曲面的电通量⎰⋅sS d E = ,式中E是哪些点电荷在闭合曲面上任一点产生的场强的矢量和?答:是 。
题1图 题2图2. 如图所示,在场强为E 的均匀电场中,A,B 两点距离为d ,AB 连线方向与E方向一致,从A 点经任意路径到B 点的场强线积分l d E AB⋅⎰= 。
3. 有4个点电荷,电量都是Q ,分别放在边长为a 的正方形的四个顶点上,在中心放一点电荷q 0 ,当q 0= 时,各点电荷都处于平衡。
《静电场中的导体与电介质》选择题解答与分析

13静电场中的导体与电介质 13.1静电平衡1. 当一个带电导体达到静电平衡时: (A) 表面上电荷密度较大处电势较高. (B) 表面曲率较大处电势较高. (C) 导体内部的电势比导体表面的电势高. (D) 导体内任一点与其表面上任一点的电势差等于零. 答案:(D) 参考解答:静电平衡时的导体电荷、场强和电势分布的特点: (1) 电荷仅分布在导体的表面,体内静电荷为零.(2) 导体表面附近的场强方向与导体表面垂直,大小与导体表面面电荷密度成正比;(3) 导体为等势体,表面为等势面.答案(D)正确,而(A)(B)(C)均需考虑电势是一个相对量,在场电荷的电量以及分布确定的同时,还必须选定一个电势零点,在这样的情况下,场中各点电势才能确定。
给出参考解答,进入下一题:2. 设一带电导体表面上某点附近电荷面密度为σ,则紧靠该表面外侧的场强为0/εσ=E . 若将另一带电体移近,(1) 该处场强改变,公式0/εσ=E 仍能用。
(2) 该处场强改变,公式0/εσ=E 不能用。
上述两种表述中正确的是(A) (1) . (B) (2).答案:(A) 参考解答:处于静电平衡的导体,其表面上各处的面电荷密度与相应表面外侧紧邻处的电场强度的大小成正比,即0εσ=E . 将另一带电体移近带电导体,紧表面外侧的场强会发生改变,电荷面密度为σ也会改变,但公式0εσ=E 仍能用。
给出参考解答,进入下一题:3. 无限大均匀带电平面(面电荷密度为σ)两侧场强为)2/(0εσ=E ,而在静电平衡状态下,导体表面(该处表面面电荷密度为σ)附近场强为0/εσ=E ,为什么前者比后者小一半?参考解答:关键是题目中两个式中的σ不是一回事。
下面为了讨论方便,我们把导体表面的面电荷密度改为σ′,其附近的场强则写为./0εσ'=E对于无限大均匀带电平面(面电荷密度为σ),两侧场强为)2/(0εσ=E .这里的 σ 是指带电平面单位面积上所带的电荷。
《大学物理》静电场练习题及答案

《大学物理》静电场练习题及答案一、简答题1、为什么在无电荷的空间里电场线不能相交?答案:由实验和理论知道,静电场中任一给定点上,场强是唯一确定的,即其大小和方向都是确定的.用电场线形象描述静电场的空间分布时,电场线上任一点的切线方向表示该点的场强方向.如果在无电荷的空间里某一点上有几条电场线相交的话,则过此交点对应于每一条电场线都可作出一条切线,这意味着交点处的场强有好几个方向,这与静电场中任一给定点场强具有唯一确定方向相矛盾,故无电荷的空间里电场线不能相交.2、简述静电场中高斯定理的文字内容和数学表达式。
答案:在真空中的静电场内,通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。
0ε∑⎰=⋅内S SqS d E3、写出静电场的环路定理,并分别说明其物理意义。
答案:静电场中,电场强度的环流总是等于零(或0l=⋅⎰l d E),静电场是保守场。
4、感生电场与静电场有哪些区别和联系?5、在电场中某一点的电场强度定义为0q F E=.若该点没有试验电荷,那么该点的电场强度又如何? 为什么?答案: 电场中某一点的电场强度是由该电场自身性质所决定,与这一点有无试验电荷没有任何关系。
6、在点电荷的电场强度公式中,如果0→r ,则电场强度E 将趋于无限大。
对此,你有什么看法? 答案: 这表明,点电荷只是我们抽象出来的一个物理模型,当带电体较小而作用距离较大时使用点电荷模型较为方便、精确。
但当作用距离r 很小时,点电荷模型的误差会变大,这时我们不能再用点电荷的电场强度公式而要采用更精确的模型。
二、选择题1、如图所示,两个同心均匀带电球面,内球面半径为1R 、带有电荷1Q ,外球面半径为2R 、带有电荷2Q ,则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A 、20214r Q Q επ+B 、()()2202210144R r Q R r Q -π+-πεε C 、()2120214R R Q Q -+επ D 、2024r Q επ2、A 和B 为两个均匀带电球体,A 带电荷q +,B 带电荷q -,作一与A 同心的球面S 为高斯面,如图所示。
电磁学复习---填空题(有解答)

mv sin θ 2π mv cos θ R= ,h = . eB eB
2007.7 Zhang Wei-Jia
电磁学复习题---填空题 电磁学复习题 填空题
6. 一磁场的磁感应强度为 B = a i + b j + ck ,则通过 一半径为R 开口向z 一半径为R,开口向z轴正方向的半球壳的磁通量 。(以球壳从内向外为正 以球壳从内向外为正) 为 。(以球壳从内向外为正)
I
S1
S2
b
h
a
b
a+b a + 2b ln / ln a a+b
2007.7 Zhang Wei-Jia
电磁学复习题---填空题 电磁学复习题 填空题
8. 无限长密绕直螺线管通以电流I, 内部充满均匀、 无限长密绕直螺线管通以电流I 内部充满均匀、 各向同性的磁介质,磁导率为µ, 各向同性的磁介质 , 磁导率为 , 管上单位长度绕有 n匝导线,则管内部的磁感应强度为 匝导线, 匝导线 ,内部的磁 能密度为 。
0
表时间,则两板间的位移电流的大小 大小为 表时间,则两板间的位移电流的大小为 其方向与场强方向 。
,
π r 2ε 0
RC
2007.7
E0e
−
t RC
,相反 相反
Zhang Wei-Jia
电磁学复习题---填空题 电磁学复习题 填空题
11.如图所示,CDEF为矩形,边长分别为L和2L。在DC 如图所示,CDEF为矩形 边长分别为L 2L。 为矩形, 如图所示 延长线上CA=L处的A点有点电荷q CA=L处的 CF的中点 的中点B 延长线上CA=L处的A点有点电荷q,在CF的中点B点有 点电荷-q(q>0),若使单位正电荷从C点沿CDEF CDEF路径运 点电荷-q(q>0),若使单位正电荷从C点沿CDEF路径运 动到F 动到F点,则电场力所作的功等于 。
静电场知识点

元电荷点电荷1.元电荷:是自然界中带电量最小的电荷,任何带电体的电量都是元电荷的整数倍,元电荷是质子或电子所带的电量,即e=1.60×10-19C2.点电荷:带一定电荷量,忽略带电体的大小和形状的一种理想化模型电荷守恒定律:(1)起电方式:摩擦起电、接触起电、感应起电(2)带电实质:物体带电的实质是得失电子(3)内容:电荷既不能创生,也不能消灭,只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分,在转移的过程中,电荷的总量保持不变。
这个结论叫做电荷守恒定律。
注意:当完全相同的带电金属球相接触时,同种电荷电量平均分配,异种电荷先中和后平分。
比荷1.比荷:带电体的电荷量与其质量的比值,叫做比荷(q/m)2.电子的比荷:元电荷e的数值最早是由美国物理学家密立根测得的,e=1.60×10-19C。
电子的电荷量e与电子的质量me之比,叫做电子的比荷。
它也是一个重要的物理量。
电子的质量me=9.1×10-31kg,所以电子的比荷为e/m=1.76×1011C/kg。
库仑定律1.内容:在真空中两个静止的点电荷间的作用力跟它们的电量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在它们的连线上。
2.表达式:F=k,式中k表示静电力常量,k=9.0×109N•m2/C2。
3.适用条件:真空中的静止点电荷。
(1)当带电体间的距离远大于它们本身的尺寸时,可把带电体看做点电荷。
但不能根据公式错误地推论:当r→0时,F→∞。
其实在这样的条件下,两个带电体已经不能再看做点电荷了。
(2)对于两个均匀带电绝缘球体,可将其视为电荷集中于球心的点电荷,r为两球心之间的距离。
(3)对两个带电金属球,要考虑金属球表面电荷的重新分布。
电场(1)定义:存在于电荷周围,能传递电荷间相互作用的一种特殊物质。
(2)基本性质:对放入其中的电荷有电场力的作用。
电场强度1.意义:是描述电场的强弱和方向(即力的性质)的物理量。
静电场之均匀带电球面球体和球壳的电场

当Q > 0时,场强的方向沿着径向向外;
当Q < 0时,场强的方向沿着径向向内。
在球的外表面, 场强大小为
对于球面内的点P2,同样作高斯面,高斯 面内Q = 0,根据高斯定理得E = 0 (r < R)
kQ E0 R2
可见:在均匀带电球面内,场强为零;在 可见:球面内外 均匀带电球面外,各点的场强与电荷全部 的场强发生跃变。
{范例9.6} 均匀带电球面、球体和球壳的电场
(2)一均匀带电球壳,内部是空腔,球壳内外半径分别为R0和 R,带电量为Q,求空间各点的电场强度和电势,对于不同的 球壳厚度,电场强度和电势随距离变化的规律是什么?
根据高斯定理可先求
反过来,利用均匀带电球体的电
电场强度,再求电势。 势先求球壳的电势,再求电场。
EA
dU A dr
0.
(r ≤ R0)
{范例9.6} 均匀带电球面、球体和球壳的电场
U R3
(r > R)
U(3R2 r2 )(r < R)C
rC
30r
6 0
B点在正电荷球体之内,负电荷球体 之外,正负电荷球产生的电势为
UB
(3R2 r2 ) 60
,
UB
R03 3 0 r
B rB O R0 A rA R
kQ (R3 R03
)
(r
R03 r2
).
{范例9.6} 均匀带电球面、球体和球壳的电场
U R3
(r > R)
U
(3R2 r2 )
(r < R)
C
rC
30r
6 0
C点在正负电荷球体之外, 正负电荷球产生的电势为
B rB O R0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
kQ
球面内部的场强为零,球面外 部场强随距离的增加而减小。
在球面的内外表面, 电场强度不连续。
均匀带电球面内外的电势是连续 的,球面内电势是一个常量,球 面外电势随距离的增加而减小。
球体内场强与距离成正比,球体 外的电场强度与球面外电场强度 的变化规律是相同的;在球的内 外表面,电场强度是连续的。
R
U
E ds Edr Edr
r r R
高斯面内的电量为q = ρVr = QVr/VR = Qr3/R3, k Q
根据高斯定理得方程ΦE = E4πr2 = q/ε0,
Qr kQ r
2R
3
(R r )
2 2
kQ R
2 2 球体内 E U (3 R r ) 3 (r < R) 3 3 2R 4 π 0 R R 场强为 球心处的场强为零,球内场强与半径成正比。 均匀带电球体不 在r = R处,E k Q E 场强在球面上的 是等势体,球心 0 2 R 场强有 变化是连续的。 处的电势最高。
B rB
O R0 A
rA
R
在球壳的空腔中同时填充两个半径为R0,电荷体密度为 ρ和-ρ的球体,空间各点的电势就是半径分别为R和R0, 电荷体密度分别为ρ和-ρ的均匀带电体球产生的。 A点在两个球体之内,正 负电荷球产生的电势为
U
A
(3 R r )
2 2
6 0
2
,
U
2
A
(3 R 0 r )
{范例9.6} 均匀带电球面、球体和球壳的电场
(1)一均匀带电球面,半径为R,带电量为Q,求电荷产生的电场强 度和电势。如果电荷均匀分布在同样大小的球体内,求球体的电 场强度和电势。(2)一均匀带电球壳,内部是空腔,球壳内外半径 分别为R0和R,带电量为Q,求空间各点的电场强度和电势,对于 不同的球壳厚度,电场强度和电势随距离变化的规律是什么? [解析](1)如图所示,不论球面还是球体,由 于电荷分布具有球对称性,所激发的电场 也是球对称的,用高斯定理求解比较简单。 r 设Q > 0,不论场点在球内还是 在球外,由于对称的缘故,电场 线都沿着球心到场点的连线。 对于球外的点P1,以O为球心,过 P1点作一个半径r的高斯球面S1。
6 0
2
R0 3 0r
(3 R
2 2
3
R
B点的 电势为
U
B
B
r
2
)
2 R0 r
3
)
kQ 2( R R0 )
3 3
(3 R
r
2
2 R0 r
3
(R0 ≤ r ≤ R) 这正好是空 腔中的电势。
3
当r = R0时,B 点的电势为
U
B
3kQ 2( R R0 )
3 3
E4πr2
S1 P1 E r
高斯面所包围的电量为Q, 根据高斯定理ΦE = Q/ε0,
可得场 强大小
E Q 4 π 0r
2
kQ r
2
(r > R) 在球的外表面, 场强大小为
E0 kQ R
2
当Q > 0时,场强的方向沿着径向向外; 当Q < 0时,场强的方向沿着径向向内。
对于球面内的点P2,同样作高斯面,高斯 面内Q = 0,根据高斯定理得E = 0 (r < R) 可见:在均匀带电球面内,场强为零;在 均匀带电球面外,各点的场强与电荷全部 集中在球心处的点电荷所激发的场强相同。
E ds Edr
r r r
kQ r
2
dr
kQ r
kQ r
当r = R时,球壳 外表面的电势为
球面所有电荷到 (r > R) U0 球心的距离都是 R R,球面的电势 可见:均匀带电球面外各点的电势与电荷全 就是所有电荷在 部集中在球心处的点电荷所产生的电势相同。 球心产生的电势。
均匀带电球体中心的电势最高, 球体内的电势随距离的增加而加 速减小,球体外电势与球面外电 势的变化规律是相同的。
{范例9.6} 均匀带电球面、球体和球壳的电场
(2)一均匀带电球壳,内部是空腔,球壳内外半径分别为R0和 R,带电量为Q,求空间各点的电场强度和电势,对于不同的 球壳厚度,电场强度和电势随距离变化的规律是什么? 根据高斯定理可先求 电场强度,再求电势。 均匀带电球体的电量与 电荷体密度的关系为 球体外部的电势用 U 电荷密度表示为
U C
B rB
O R0 A
rA
R
3
3 0r,U C R Nhomakorabea 3 0r
3
R
C点的 U C U C U C 电势为 C点的场强大小为
EC
( R R0 )
3 3
3 0 r
kQ r
(R ≤ r)
dU C dr
kQ r
2
可见:C点的电势和场强等效于全部电荷集中在球心产生的。
{范例9.6} 均匀带电球面、球体和球壳的电场
U
A
3kQ ( R R0 ) 2(R
2
R R0 R0 )
2
3
EA = 0 (r ≤ R0)
2
C
rC
U
kQ 2( R R0 )
3
B
(3 R (r
2
r
3
2 R0 r
3
)
B rB
O R0 A
rA
EB
kQ ( R R0 )
2 2
6 0
3kQ ( R R0 )
2
A点的 U U U 电势为 空腔内的电势为常量。
A A A
( R R0 )
2
2 0
3kQ ( R
3
2
R0 )
3
2( R R0 )
A
2(R
R R0 R0 )
2
A点的场强大小为
EA
dU dr
0.
(r ≤ R0)
3 3
R0 r
2
)
(R0 ≤ r ≤ R) (R ≤ r) [讨论]
R
UC
kQ r
EC
kQ r
2
①当R0 = 0时,空腔缩为一点,球壳就变成球体。
3kQ A点(球心) UA (r = 0) 当r = 0时,UB = UA,EB = EA = 0。 的电势为 2R kQ B点的 U k Q (3 R 2 r 2 ) B点的场强 E B 3 r (0 ≤ r ≤ R) B 3 R 2R 大小为 电势为
{范例9.6} 均匀带电球面、球体和球壳的电场
U
R
3
3 0r
(r > R)
U
(3 R r )
2 2
6 0
(r < R)
C
rC
B点在正电荷球体之内,负电荷球体 之外,正负电荷球产生的电势为
U
B
B rB
O R0 A
rA
(3 R r )
2 2
6 0
U
B
,
U
U
B
2 2
6 0
(r < R)
其中ε0 = 1/4πk,称为真空介电常数。
{范例9.6} 均匀带电球面、球体和球壳的电场
U
R
3
3 0r
(r > R)
U
(3 R r )
2 2
6 0
(r < R)
C
rC
如图所示,A、B、C三点代表三个区域。 3Q 均匀带电球壳的 Q 3 3 V 4 π (R R 0 ) 电荷体密度为
②当R0→R时,球 壳就变成球面。
A点的 电势为
U
A
kQ R
B点的电势UB→UA。
不妨取球壳内半径与外半径之比为0.5。 在球壳的内 空腔内的场强为零,球壳内的 外表面,电 场强随距离增加而增强,球壳 场强度是连 外的场强随距离的增加而减小。 续的。
空腔内的电势是常数,球壳中的电 势随距离的增加而加速减小,球壳 外电势随距离的增加而减速减小。
( R R0 )
2
B点的场强大小为
EB
dU dr
B
kQ ( R R0 )
3
(r
R0 r
2
3
).
{范例9.6} 均匀带电球面、球体和球壳的电场
U
R
3
3 0r
(r > R)
U
(3 R r )
2 2
6 0
(r < R)
C
rC
C点在正负电荷球体之外, 正负电荷球产生的电势为
反过来,利用均匀带电球体的电 势先求球壳的电势,再求电场。
Q V
4 3 πR
3
4 3
k r
πR
3
kQ r
R
3
3 0r
(r > R)
球体内部的电势用电荷密度表示为
U kQ 2R
3
(3 R r )
2 2
