比较法总论作业
比较法总论作业答案

《比较法总论》作业题答案1、比较法研究包括哪些层次?它们的关系如何?(答案见《比较法总论》教材第3-9页)第一个层次叙述得比较法,即外国法研究;第二个层次评价的比较法,即研究不同法律制度异同及其发展趋势,第三个层次是沿革的比较法,即研究不同法律制度历史的和现实的关系。
它们之间的关系:第一个层次叙述的比较法是比较法研究的基础,第二个层次评价的比较法是建立在叙述的比较法的基础之上研究。
第三个层次沿革的比较法是建立在叙述的比较法和评价的比较法之上,以在历史上和现实中不同法律制度在法律移植和借鉴中所形成的实际关系为研究对象,是比较法研究的最高层次。
2、试述比较法的方法论。
(1)叙述的比较法的方法论见《比较法总论》教材第10-14页。
(2)评价的比较法的方法论见《比较法总论》教材第15-25页。
(3)沿革的比较法的方法论见《比较法总论》教材第26-29页。
参考答案:(一)叙述的比较法的方法论1.基本原则,按照外国法的原样认识外国法。
研究外国法要求人们语言交流畅,对该国法有某种基本知识,特别是他们的法律渊源、基本法律概念、法律用语,但是,尽管有这些基本常识,研究外国法仍然会遇到很多陷阱。
2.信息源的可用性和可信性外国法律信息来源有两个:第一手资料,即外国制定法、司法报告、判例。
他们是直接的法律渊源,具有最高的可用性和可行性。
第二手资料,即外国法的教科书参考书、杂志上的文章。
这些第二手资料比较全面、详细地介绍了外国法的情况。
对于初次接触外国法的研究者来说往往是起点,而第一手资料是在了解了第二手资料的基础上才可能进行深入地研究。
3.必须把外国法作为一个整体来研究外国法的分类可能不同于本国法的分类,即使存在同样的分类,在不同国家也有不同的分类方式,相应的法律规则在不同的法律体系中可能属于不同的法律部门。
4、翻译问题对外国法的翻译一般都采取直译方式。
法律用语与日常用语有联系,但也不能等同。
在研究外国法时,人们应该用特殊的法律用语的双语词典和特殊的法律词典,而不应只用一般的双语词典。
《比较法学》作业参考答案

《比较法学》作业参考答案一、如何理解下列概念或格言1.比较法比较法是指法的比较研究,它是以法律为其对象,以比较为其内容的法学的一门独立的一级分支学科。
其研究对象是不同国家或特定地区的法律现象。
对“法律现象”要作最广义的理解。
首先,从空间上看,比较法研究的主要是“不同国家或特定地区的法律”。
其次,从时间上看,比较法的研究对象既包括现实比较,也包括历史比较。
再次,从层次上看,既包括宏观比较,也包括微观比较。
最后,从内容上说,既包括制度比较,也包括观念文化比较。
2.“不读阿佐的书,不能上宝殿”阿佐是罗马法复兴时期注释法学派的最著名的代表人物。
阿佐的著作很多,其代表注释法学派发展顶峰的成就。
当时有“不读阿佐的书,不能上宝殿”的说法,宝殿是指当法官。
言下之意是注释法学派的著作在中世纪的欧洲可以成为法的正式渊源,起码是最为重要的法的非正式渊源。
3.伊斯兰法系:伊斯兰法系是以伊斯兰法为基础发展起来的、具有共同特征和历史联系的各国和个地区法律的总称。
伊斯兰法主要在阿拉伯国家通行,又被称为阿拉伯法系。
伊斯兰法阿拉伯语称为“沙里阿”,词义是“同向泉水的道路”、“应该遵循的常道”。
在宗教方面,这个词的意义是“引导正直生命通往先知的大道”或是宗教对人圣命的总和,引申为人所行之正路,是来源于神的启示的规则的总体,是每一个穆斯林都应当遵守的行为规则。
伊斯兰法的发展也经历了一个漫长的过程,与伊斯兰法教密不可分。
伊斯兰法的法律渊源主要由四部分组成:《古兰经》、“逊奈”(即圣训)、“伊智玛”(即伊斯兰学者对教义的一致意见)、“格亚斯”(即类推)。
应该指出伊斯兰法在近代也深刻地受西方法律的影响。
以致于就伊斯兰国家的法律而言则可能或者归于民法法系,或者归于普通法法系。
不过西方学者都是承认伊斯兰法系的存在的。
4.辩诉交易在刑事案件中,被指控者通过他或她的律师与公诉人进行协商达成双方均可接受的协议的程序。
在美国,辩诉交易的发生很广泛。
所有刑事案件中接近90%(既包括联邦案件也包括州案件)都是通过辩诉交易或辩诉协议得到解决的。
2017-2018学年数学人教A版选修4-5优化练习:第二讲 一 比较法 Word版含解析

[课时作业][A组基础巩固]1.下列四个数中最大的是()A.lg 2B.lg 2C.(lg 2)2D.lg(lg 2)解析:∵1<2<2<10,∴0<lg 2<lg 2<1,∴(lg 2)2<lg 2,lg(lg 2)<0.∴选A.答案:A2.若a,b为不相等的正数,则(ab k+a k b)-(a k+1+b k+1)(k∈N*)的符号() A.恒正B.恒负C.与k的奇偶性有关D.与a,b大小无关解析:(ab k+a k b)-a k+1-b k+1=b k(a-b)+a k(b-a)=(a-b)(b k-a k)∵a>0,b>0,若a>b,则a k>b k,∴(a-b)(b k-a k)<0;若a<b,则a k<b k,∴(a-b)(b k-a k)<0.答案:B3.a、b都是正数,P=a+b2,Q=a+b,则P,Q的大小关系是()A.P>Q B.P<Q C.P≥Q D.P≤Q解析:P2Q2=a+b+2ab2(a+b)≤a+b+a+b2(a+b)=1,∴P≤Q,应选D.答案:D4.如果log a3>log b3且a+b=1,那么()A.0<a<b<1 B.0<b<a<1C .1<a <bD .1<b <a解析:∵a >0,b >0,又∵a +b =1,∴0<a <1,0<b <1,∴lg a <0,lg b <0,由log a 3>log b 3⇒lg 3lg a -lg 3lg b >0⇒1lg a -1lg b >0⇒lg b -lg a lg a lg b >0⇒lg b >lg a ⇒b >a .∴0<a <b <1.答案:A 5.已知a >b >0,c >d >0,m =ac -bd ,n =(a -b )(c -d ),则m 与n 的大小关系是( )A .m <nB .m >nC .m ≥nD .m ≤n解析:∵a >b >0,c >d >0,∴ac >bd >0,ac >bd ,∴m >0,n >0.又∵m 2=ac +bd -2abcd ,n 2=ac +bd -(ad +bc ),又由ad +bc >2abcd ,∴-2abcd >-ad -bc ,∴m 2>n 2.∴m >n .答案:B6.设P =a 2b 2+5,Q =2ab -a 2-4a ,若P >Q ,则实数a ,b 满足的条件为________. 解析:P -Q =a 2b 2+5-(2ab -a 2-4a )=a 2b 2+5-2ab +a 2+4a =a 2b 2-2ab +1+4+a 2+4a=(ab -1)2+(a +2)2.∵P >Q ,∴P -Q >0,即(ab -1)2+(a +2)2>0∴ab ≠1或a ≠-2.答案:ab ≠1或a ≠-27.已知a ,b ,m ,n 均为正数,且a +b =1,mn =2,则(am +bn )(bm +an )的最小值为________.解析:(am +bn )(bm +an )=abm 2+(a 2+b 2)mn +abn 2=ab (m 2+n 2)+2(a 2+b 2)≥2abmn +2(a 2+b 2)=4ab +2(a 2+b 2)=2(a 2+2ab +b 2)=2(a +b )2=2(当且仅当m =n =2时等号成立).答案:28.设a >b >0,x =a +b -a ,y =a -a -b ,则x ,y 的大小关系是x ________y .解析:∵x y =a +b -a a -a -b =a +a -b a +a +b <a +a +b a +a +b =1,且x >0,y >0, ∴x <y答案:<9.已知a >0,b >0,求证:a b +b a ≥a +b . 证明:法一:∵a b +b a a +b=a b a +b +b a a +b =aab +b +bab +a =a ab +a 2+b ab +b 22ab +(a +b )ab =a 2+b 2+(a +b )ab 2ab +(a +b )ab, 又∵a 2+b 2≥2ab ,∴a 2+b 2+(a +b )ab 2ab +(a +b )ab ≥2ab +(a +b )ab 2ab +(a +b )ab=1, 当且仅当a =b >0时取等号. ∴a b +b a ≥a +b . 法二:∵a b +b a -(a +b ) =(a b -b )+(b a-a ). =a -b b +b -a a=(a -b )(a -b )ab=(a +b )(a -b )2ab≥0 当且仅当a =b >0时取“=”∴a b +b a≥a +b . 10.已知函数f (x )=x 2+ax +b ,当p ,q 满足p +q =1时,证明:pf (x )+qf (y )≥f (px +qy )对于任意实数x ,y 都成立的充要条件是0≤p ≤1. 证明:pf (x )+qf (y )-f (px +qy )=p (x 2+ax +b )+q (y 2+ay +b )-(px +qy )2-a (px +qy )-b=p (1-p )x 2+q (1-q )y 2-2pqxy=pq (x -y )2.充分性:若0≤p ≤1,q =1-p ∈[0,1].∴pq ≥0,∴pq (x -y )2≥0,∴pf (x )+qf (y )≥f (px +qy ).必要性:若pf (x )+qf (y )≥f (px +qy ).则pq (x -y )2≥0,∵(x -y )2≥0,∴pq ≥0.即p (1-p )≥0,∴0≤p ≤1.综上所述,原命题成立.[B 组 能力提升]1.已知a >0,且a ≠1,P =log a (a 3+1),Q =log a (a 2+1),则P ,Q 的大小关系是( )A .P >QB .P <QC .P =QD .大小不确定解析:P -Q =log a (a 3+1)-log a (a 2+1)=log a a 3+1a 2+1. 当0<a <1时,0<a 3+1<a 2+1,则0<a 3+1a 2+1<1,∴log a a 3+1a 2+1>0,即P -Q >0. ∴P >Q .当a >1时,a 3+1>a 2+1>0,a 3+1a 2+1>1, ∴log a a 3+1a 2+1>0,即P -Q >0.∴P >Q . 答案:A2.设m >n ,n ∈N +,a = (lg x )m +(lg x )-m ,b =(lg x )n +(lg x )-n ,x >1,则a 与b的大小关系为( )A .a ≥bB .a ≤bC .与x 值有关,大小不定D .以上都不正确解析:a -b =lg m x +lg -m x -lg n x -lg -n x=(lg m x -lg n x )-(1lg n x -1lg m x )=(lg m x -lg n x )-lg m x -lg n x lg m x lg n x=(lg m x -lg n x )(1-1lg m x lg n x )=(lg m x -lg n x )(1-1lg m +n x ).∵x >1,∴lg x >0.当0<lg x <1时, a >b ;当lg x =1时,a =b ;当lg x >1时,a >b .∴应选A.答案:A3.设m =|a |+|b ||a +b |,n =|a -b |||a |-|b ||,那么它们的大小关系是m ________n . 解析:m n =|a |+|b ||a +b ||a -b |||a |-|b ||=(|a |+|b |)||a |-|b |||a +b |·|a -b |=|a 2-b 2||a 2-b 2|=1,∴m =n . 答案:=4.一个个体户有一种商品,其成本低于3 5009元.如果月初售出可获利100元,再将本利存入银行,已知银行月息为2.5%,如果月末售出可获利120元,但要付成本的2%的保管费,这种商品应________出售(填“月初”或“月末”). 解析:设这种商品的成本费为a 元.月初售出的利润为L 1=100+(a +100)×2.5%,月末售出的利润为L 2=120-2%a ,则L 1-L 2=100+0.025a +2.5-120+0.02a =0.045(a -3 5009),∵a <3 5009,∴L 1<L 2,月末出售好.答案:月末5.设直角三角形的斜边长为c ,两直角边长分别为a ,b ,试比较c 3与a 3+b 3的大小.解析:∵c 是直角三角形的斜边长,a ,b 是直角边长,∴a +b >c,0<a c <1,0<b c <1,且a 2+b 2=c 2,∴a 3+b 3c 3=⎝ ⎛⎭⎪⎫a c 3+⎝ ⎛⎭⎪⎫b c 3<⎝ ⎛⎭⎪⎫a c 2+⎝ ⎛⎭⎪⎫b c 2=a 2+b 2c 2=1, 即a 3+b 3c 2<1,故a 3+b 3<c 3.6.已知函数f (x )=log 2(x +m ),且f (0)、f (2)、f (6)成等差数列.(1)求f (30)的值;(2)若a 、b 、c 是两两不相等的正数,且a 、b 、c 成等比数列,试判断f (a )+f (c )与2f (b )的大小关系,并证明你的结论.解析:(1)由f (0)、f (2)、f (6)成等差数列,得2log 2(2+m )=log 2m +log 2(6+m ),即(m +2)2=m (m +6)(m >0).∴m=2.∴f(30)=log2(30+2)=5.(2)f(a)+f(c)>2f(b).证明如下:2f(b)=2log2(b+2)=log2(b+2)2,f(a)+f(c)=log2[(a+2)(c+2)],又b2=ac,∴(a+2)(c+2)-(b+2)2=ac+2(a+c)+4-b2-4b-4=2(a+c)-4b. ∵a+c>2ac=2b(a≠c),∴2(a+c)-4b>0,∴log2[(a+2)(c+2)]>log2(b+2)2,即f(a)+f(c)>2f(b).。
土地估价市场比较法例题
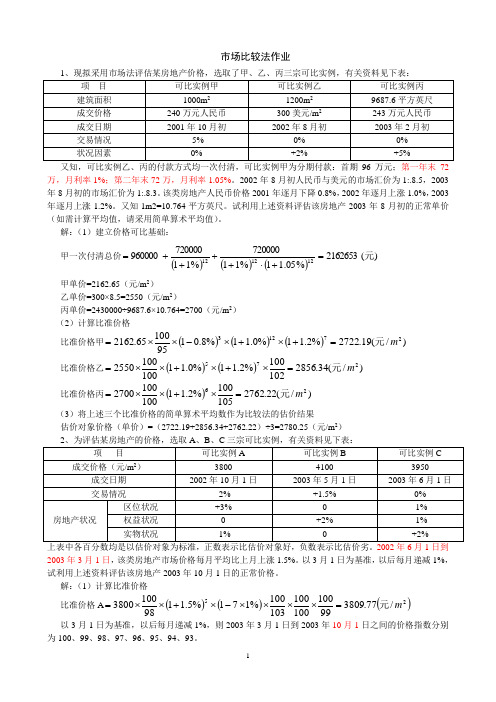
市场比较法作业又知,可比实例乙、丙的付款方式均一次付清,可比实例甲为分期付款:首期96万元;第一年末72万,月利率1%;第二年末72万,月利率1.05%。
2002年8月初人民币与美元的市场汇价为1:.8.5,2003年8月初的市场汇价为1:.8.3。
该类房地产人民币价格2001年逐月下降0.8%,2002年逐月上涨1.0%,2003年逐月上涨1.2%。
又知1m2=10.764平方英尺。
试利用上述资料评估该房地产2003年8月初的正常单价(如需计算平均值,请采用简单算术平均值)。
解:(1)建立价格可比基础: 甲一次付清总价()()())(2162653%05.11%11720000%11720000960000121212元=+⋅++++=甲单价=2162.65(元/m 2) 乙单价=300×8.5=2550(元/m 2) 丙单价=2430000÷9687.6×10.764=2700(元/m 2) (2)计算比准价格比准价格甲()()())/(19.2722%2.11%0.11%8.019510065.216227123m 元=+⨯+⨯-⨯⨯= 比准价格乙()())/(34.2856102100%2.11%0.111001002550275m 元=⨯+⨯+⨯⨯=比准价格丙())/(22.2762105100%2.11100100270026m 元=⨯+⨯⨯=(3)将上述三个比准价格的简单算术平均数作为比较法的估价结果估价对象价格(单价)=(2722.19+2856.34+2762.22)÷3=2780.25(元/m 2)上表中各百分数均是以估价对象为标准,正数表示比估价对象好,负数表示比估价劣。
2002年6月1日到2003年3月1日,该类房地产市场价格每月平均比上月上涨1.5%。
以3月1日为基准,以后每月递减1%,试利用上述资料评估该房地产2003年10月1日的正常价格。
2018年数学同步优化指导北师大版选修4-5练习:1-4 第1

活页作业(五) 比较法、分析法、综合法一、选择题1.已知a >b >-1,则1a +1与1b +1的大小关系是( )A .1a +1>1b +1B .1a +1<1b +1C .1a +1≥1b +1D .1a +1≤1b +1解析:∵a >b >-1,∴a +1>0,b +1>0,a -b >0. ∴1a +1-1b +1=b -a (a +1)(b +1)<0. ∴1a +1<1b +1. 答案:B2.设a >0,b >0,且ab -(a +b )≥1,则( ) A .a +b ≥2(2+1) B .a +b ≤2+1 C .a -b ≤(2+1)2D .a +b >2(2+1)解析:因为ab ≤a +b 2.所以ab ≤14(a +b )2.所以14(a +b )2-(a +b )≥ab -(a +b )≥1.所以(a +b ) 2-4(a +b )-4≥0.因为a >0,b >0,所以a +b ≥2+2 2. 答案:A3.设x =2,y =7-3,z =6-2,则x ,y ,z 的大小关系是( ) A .x >y >z B .z >x >y C .y >z >x D .x >z >y解析:y =7-3=47+3,z =6-2=46+2, ∵7+3>6+2>0,∴z >y . ∵x -z =2-46+2=23+2-46+2=23-26+2>0, ∴x >z .∴x >z >y . 答案:D4.不等式:①x 2+3>2x (x ∈R );②a 5+b 5≥a 3b 2+a 2b 3;③a 2+b 2≥2(a -b -1).其中正确的是( )A .①②③B .①②C .①③D .②③解析:①可化为(x -1)2+2>0,显然成立;对于②,a 5+b 5-(a 3b 2+a 2b 3)=(a 2-b 2)(a 3-b 3)=(a -b )2(a +b )(a 2+ab +b 2),由于(a -b )2≥0,a 2+ab +b 2≥0,而a +b 的符号不确定,②式不一定成立;③可化为 (a -1)2+(b +1)2≥0,显然成立.故①③正确. 答案:C 二、填空题5.分析法又叫执果索因法,若使用分析法证明“设a >b >c ,且a +b +c =0,求证:b 2-ac <3a ”,索的因应是下列式子中的________. ①a -b >0; ②a -c >0; ③(a -b )(a -c )>0; ④(a -b )( a -c )<0. 解析:要证b 2-ac <3a ,只需证b 2-ac <3a 2.因为a +b +c =0,所以即证(a +c )2-ac <3a 2,即证2a 2-ac -c 2>0,即证(2a +c )(a -c )>0,即证(a -b )(a -c )>0.故③正确.答案:③6.已知x ,y ,z 满足z <y <x ,且xz <0.给出下列各式: ①xy >xz ;②z (y -x )>0;③zy 2<xy 2;④xz (x -z )<0. 其中正确式子的序号是________.解析:①∵⎩⎪⎨⎪⎧z <y <x ,xz <0⇒⎩⎪⎨⎪⎧x >0,z <0,z <y <x⇒xy >xz ,∴①正确.②∵⎩⎪⎨⎪⎧ z <y <x ,xz <0⇒⎩⎪⎨⎪⎧y -x <0,z <0⇒z (y -x )>0, ∴②正确.③∵z <y <x 且xz <0,∴x >0且z <0. 当y =0时,zy 2=xy 2;当y ≠0时,zy 2<xy 2.∴③不正确. ④∵x >z ,∴x -z >0.∵xz <0,∴(x -z )xz <0.∴④正确. 综上,①②④正确. 答案:①②④三、解答题7.若不等式1a -b +1b -c +λc -a >0在满足条件a >b >c 时恒成立,求实数λ的取值范围.解:原不等式可化为1a -b +1b -c >λa -c. ∵a >b >c ,∴a -b >0,b -c >0,a -c >0. ∴不等式λ<a -c a -b +a -cb -c 恒成立.∵a -c a -b +a -c b -c =a -b +b -c a -b +a -b +b -c b -c =2+b -c a -b +a -bb -c≥2+2=4, ∴λ<4.故实数λ的取值范围是(-∞,4).8.设a >b >c >1,记M =a -c ,N =a -b ,P =2⎝⎛⎭⎫a +b 2-ab ,Q =3⎝ ⎛⎭⎪⎫a +b +c 3-3abc ,试找出其中的最小者,并说明理由.解:P 最小.理由如下:因为b >c >0,所以b >c .所以N <M . 又Q -P =c +2ab -33abc =c +ab +ab -33abc ≥33c ·ab ·ab -33abc =0,因为a >b >c >1,所以c ≠ab .从而Q >P . 又N -P =2ab -b -b =b (2a -1-b )=b [(a -1)+(a -b )], 因为a >b >c >1,所以P <N . 故P 最小.一、选择题1.设a =lg e ,b =(lg e)2,c =lg e ,则( ) A .a >b >c B .a >c >b C .c >a >bD .c >b >a解析:由1<e 2<10,知0<lg e <12.所以a >b ,a >c .又c -b =lg e -(lg e)2=⎝⎛⎭⎫12-lg e lg e >0, 所以a >c >b . 答案:B2.设13<⎝⎛⎭⎫13b <⎝⎛⎭⎫13a<1,则( )A .a a <a b <b aB .a a <b a <a bC .a b <a a <b aD .a b <b a <a a解析:∵13<⎝⎛⎭⎫13b <⎝⎛⎭⎫13a<1,∴0<a <b <1.∴a a a b =a a -b>1.∴a b <a a .∵a a b a =⎝⎛⎭⎫a b a,0<ab <1,a >0,∴⎝⎛⎭⎫a b a <1. ∴a a <b a .∴a b <a a <b a . 答案:C 二、填空题3.小王从甲地到乙地往返的时速分别为a 和b (a <b ),其全程的平均时速为v ,则下列式子正确的是________.①a <v <ab ;②v =ab ; ③ab <v <a +b 2;④v =a +b 2.解析:设甲、乙两地之间的距离为s . ∵a <b , ∴v =2ss a +s b =2sab (a +b )s =2ab a +b <2ab 2ab =ab . ∵v -a =2aba +b -a =ab -a 2a +b >a 2-a 2a +b =0,∴v >a .答案:①4.若a >0,b >0,则lg ⎝⎛⎭⎫1+a +b 2________12[lg(1+a )+lg(1+b )].(选填“≥”“≤”或“=”)解析:12[lg(1+a )+lg(1+b )]=12lg[(1+a )(1+b )]=lg[(1+a )(1+b )]12,lg ⎝⎛⎭⎫1+a +b 2=lg ⎝⎛⎭⎫a +b +22.∵a >0,b >0,∴a +1>0,b +1>0. ∴[(a +1)(1+b )]12≤a +1+b +12=a +b +22.∴lg ⎝⎛⎭⎫1+a +b 2≥lg[(1+a )(1+b )]12,即lg ⎝⎛⎭⎫1+a +b 2≥12[lg(1+a )+lg(1+b )].答案:≥ 三、解答题5.已知a +b +c =0,求证:ab +bc +ca ≤0. 证明:法一 综合法.∵a +b +c =0,∴(a +b +c )2=0. 上式展开,得ab +bc +ca =-a 2+b 2+c 22.∴ab +bc +ca ≤0. 法二 分析法. ∵a +b +c =0, ∴要证ab +bc +ca ≤0, 只要证ab +bc +ca ≤(a +b +c )2, 即证a 2+b 2+c 2+ab +bc +ca ≥0,亦即证 12[](a +b )2+(b +c )2+(c +a )2≥0. 而这是显然成立的,由于以上相应各步均可逆, 故原不等式成立.法三 ∵a +b +c =0,∴-c =a +b .∴ab +bc +ca =ab +(b +a )c =ab -(a +b )2=-a 2-b 2-ab =-⎣⎡⎤⎝⎛⎭⎫a +b 22+3b24≤0. ∴ab +bc +ca ≤0.6.已知数列{a n }是首项为2、公比为12的等比数列,S n 为它的前n 项和.(1)用S n 表示S n +1.(2)是否存在自然数c 和k ,使得不等式S k +1-cS k -c >2成立?解:(1)根据题意,得S n =4⎝⎛⎭⎫1-12n .所以S n +1=4⎝⎛⎭⎫1-12n 1=12S n +2(n ∈N +).(2)要使不等式S k +1-cS k -c >2成立,只需不等式c -⎝⎛⎭⎫32S k -2c -S k <0成立.因为S k =4⎝⎛⎭⎫1-12k <4, 所以S k -⎝⎛⎭⎫32S k -2=2-12S k >0(k ∈N +). 故只需不等式32S k -2<c <S k (k ∈N +) ①成立.因为S k +1>S k (k ∈N +), 所以32S k -2≥32S 1-2=1.又S k <4,故要使①成立,c 只能取2或3. 当c =2时,因为S 1=2,所以当k =1时,c <S k 不成立.从而①不成立. 当k ≥2时,因为32S 2-2=52>c ,由S k <S k +1(k ∈N +),得32S k -2<32S k +1-2.故当k ≥2时,32S k -2>c .从而①不成立.当c =3时,因为S 1=2,S 2=3,所以当k =1, k =2时,c <S k 不成立.从而①不成立. 因为32S 3-2=134>c ,32S k -2<32S k +1-2,所以当k ≥3时,32S k -2>c .从而①不成立.综上,不存在自然数c 和k ,使不等式S k +1-cS k -c >2成立.。
课时作业1:一 比较法

一 比较法一、基础达标1.若a ,b 为不等的正数,则(ab k +a k b )-(a k +1+b k +1) (k ∈N +)的符号( )A .恒正B .恒负C .与k 的奇偶性有关D .与a ,b 大小无关答案 B解析 (ab k +a k b )-a k +1-b k +1=b k (a -b )+a k (b -a )=(a -b )(b k -a k ),∵a >0,b >0,若a >b ,则a k >b k ,∴(a -b )(b k -a k )<0;若a <b ,则a k <b k ,∴(a -b )(b k -a k )<0.2.设a 、b 、c 、d 、m 、n ∈R +,P =ab +cd ,Q =ma +nc ·b m +d n ,则有( ) A .P ≥Q B .P ≤Q C .P >Q D .P <Q答案 B解析 采用先平方后作差法,∵P 2-Q 2=(ab +cd +2abcd )-⎝⎛⎭⎫ab +cd +m n ad +n m bc =2abcd -m n ad -n m bc =-⎝⎛⎭⎫m n ad -n m bc 2≤0, ∴P 2≤Q 2,又∵P >0,Q >0,∴P ≤Q .3.对x 1>x 2>0,0<a <1,记y 1=x 11+a +ax 21+a ,y 2=ax 11+a +x 21+a,则x 1x 2与y 1y 2的关系为( ) A .x 1x 2>y 1y 2 B .x 1x 2=y 1y 2C .x 1x 2<y 1y 2D .不能确定,与a 有关答案 C解析 ∵x 1>x 2>0,0<a <1,∴y 1y 2-x 1x 2=(x 1+ax 2)(ax 1+x 2)(1+a )2-x 1x 2 =a (x 1-x 2)2(1+a )2>0, ∴y 1y 2>x 1x 24.已知a ,b 都是实数,那么“a 2>b 2”是“a >b ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件答案 D解析 当a 2>b 2时,a 2-b 2>0,即(a +b )(a -b )>0,当a ,b 同为正时,有a >b ;当a 、b 同为负时,a <b ,所以当a 2>b 2时,不一定有a >b 成立.反之,当a >b 时,也不一定有a 2>b 2,例如1>-2,而12<(-2)2.5.若c >a >b >0,比较大小:a c -a ________b c -b(填“>”“=”或“<”) 答案 >解析 ∵c >a >b >0,∴c -b >c -a >0,∴1c -a >1c -b>0, 又∵a >b >0,∴a c -a >b c -b. 6.设m =|a |+|b ||a +b |,n =|a -b |||a |-|b ||,那么它们的大小关系是m ________n . 答案 =解析 m n =|a |+|b ||a +b ||a -b |||a |-|b ||=(|a |+|b |)||a |-|b |||a +b |·|a -b |=|a 2-b 2||a 2-b 2|=1,∴m =n . 7.设a 、b ∈(0,+∞),且a ≠b ,比较a 3b 2+b 3a 2与a +b 的大小. 解 a 3b 2+b 3a 2-(a +b )=(a 3-b 3)⎝⎛⎭⎫1b 2-1a 2 =(a +b )(a -b )2(a 2+ab +b 2)1a 2b 2, ∵a 、b ∈(0,+∞),且a ≠b ,∴a +b ,(a -b )2,(a 2+ab +b 2),1a 2b 2均为正数,∴a 3b 2+b 3a 2-(a +b )>0,∴a 3b 2+b 3a 2>a +b . 二、能力提升8.下列不等式,其中正确的个数为( )①x 2+3>2x (x ∈R )②a 5+b 5≥a 3b 2+a 2b 3(a ,b ∈R )③a 2+b 2≥2(a -b -1)A .0B .1C .2D .3答案 C解析 因为x 2+3-2x =(x -1)2+2≥2>0,所以命题①正确;因为a 5+b 5-a 3b 2-a 2b 3=a 3(a 2-b 2)-b 3(a 2-b 2)=(a 2-b 2)(a 3-b 3).此式当a =-1,b =-2时小于0.所以②不正确.因为a 2+b 2-2a +2b +2=(a -1)2+(b +1)2≥0,所以命题③正确.9.下列四个不等式:①a <0<b ;②b <a <0;③b <0<a ;④0<b <a ,其中能使1a <1b成立的充分条件有________. 答案 ①②④解析 1a <1b ⇔b -a ab<0⇔b -a 与ab 异号,①②④均能使b -a 与ab 异号. 10.设a >5,则a -3-a -4与a -4-a -5的大小关系是________.答案 a -3-a -4<a -4-a -5解析 因为a >5,只需比较a -3+a -5与2a -4的大小,两数平方,即比较(a -3)(a -5)与a -4的大小,再平方,只需比较a 2-8a +15与a 2-8a +16的大小.11.设m ∈R ,a >b >1,f (x )=mx x -1,比较f (a )与f (b )的大小. 解 f (a )-f (b )=ma a -1-mb b -1=m (b -a )(a -1)(b -1). ∵a >b >1,∴b -a <0,a -1>0,b -1>0,∴b -a (a -1)(b -1)<0. 当m >0时,m (b -a )(a -1)(b -1)<0,f (a )<f (b ); 当m <0时,m (b -a )(a -1)(b -1)>0,f (a )>f (b ); 当m =0时,m (b -a )(a -1)(b -1)=0,f (a )=f (b ).12.设a ,b 是非负实数,求证:a 3+b 3≥ab (a 2+b 2).证明 由a ,b 是非负实数,作差得a 3+b 3-ab (a 2+b 2)=a 2a (a -b )+b 2b (b -a )=(a -b )[(a )5-(b )5].当a ≥b 时,a ≥b ,从而(a )5≥(b )5,得(a -b )[(a )5-(b )5]≥0;当a <b 时,a <b ,从而(a )5<(b )5,得(a -b )[(a )5-(b )5]>0.所以a 3+b 3≥ab (a 2+b 2).三、探究与创新13.甲、乙二人同时同地沿同一路线走到同一地点,甲有一半时间以速度m 行走,另一半以速度n 行走;乙有一半路程以速度m 行走,另一半路程以速度n 行走.如果m ≠n ,问甲、乙二人谁先到达指定地点?解 设从出发地点至指定地点的路程为s ,甲、乙二人走完这段路程所用的时间分别为t 1,t 2,依题意有:t 12m +t 12n =s ,s 2m +s 2n=t 2. ∴t 1=2s m +n,t 2=s (m +n )2mn , ∴t 1-t 2=2s m +n -s (m +n )2mn =s [4mn -(m +n )2]2mn (m +n )=-s (m -n )22mn (m +n ). 其中s ,m ,n 都是正数,且m ≠n ,∴t 1-t 2<0,即t 1<t 2,从而知甲比乙先到达指定地点.。
市场比较法作业 1

市场比较法作业题一、选择题1、市场法的理论依据是( )A、适合原理B、替代原理C、最高最佳使用原则D、均衡原理2、比准价格是一种()A、公平市价B、评估价格C、市场价格D、理论价格3、市场比较法中的交易情况修正是对( )价格本身是否正常的修正.A、交易实例B、可比实例C、估价对象D、标准化实例4、在市场法中,土地使用权年限调整属于()调整。
A、权益状况B、区位状况C、实物状况D、年限状况5、判定某可比实例的成交价格比正常价格低6%,则交易情况修正系数为()。
A、0.060B、0.940C、1.060D、1.0646、某可比实例的成交价格为2400元/m2,建筑面积100m2,首期付款12万元,其余半年后支付8万元,1年后支付4万元。
已知年利率为10%,则该可比实例的实际价格为()元/m2。
A、2290.91B、2326.41C、2344.16D、2308.667、按直接比较判定某可比实例价格的区域因素修正系数为0.98,则其依据为( )。
A、可比实例的区域因素优于估价对象的区域因素,对价格的影响幅度为2%B、可比实例的区域因素劣于估价对象的区域因素,对价格的影响幅度为2%C、可比实例的区域因素劣于估价对象的区域因素,对价格的影响幅度为2.04%D、可比实例的区域因素优于估价对象的区域因素,对价格的影响幅度为2.04%8、下列()情况会导致房地产价格偏高。
A、卖方不了解行情B、政府协议出让C、购买相邻地产D、设立抵押的房地产9、可比实例是相邻房地产的合并交易,则以此为据求算出来的比准价格往往比实际正常价格()A、高B、低C、相等D、无法确定10、在一些城市中,距离重点中、小学近的区域内的居住地价通常比较高,其原因主要在于()A、繁华程度高B、集聚规模大C、交通条件好D、公共配套设施状况好11、市场比较法的间接比较法是以()为基准,把交易案例和待估宗地均与其逐项比较,然后将比较结果转化为修正价格。
A、标准宗地B、待估宗地C、类似宗地D、比较宗地以下为多选13、在市场比较法中进行因素修正时,下列说法正确的有()A、宗地的面积与土地利用效果无关B、宗地的形状影响其利用效果C、商业用地的利用效果一般与其临街的深度呈递减变化规律D、对居住用地而言,位于商服繁华区域的地块价格肯定高于其他区域的地块价格。
市场比较法作业
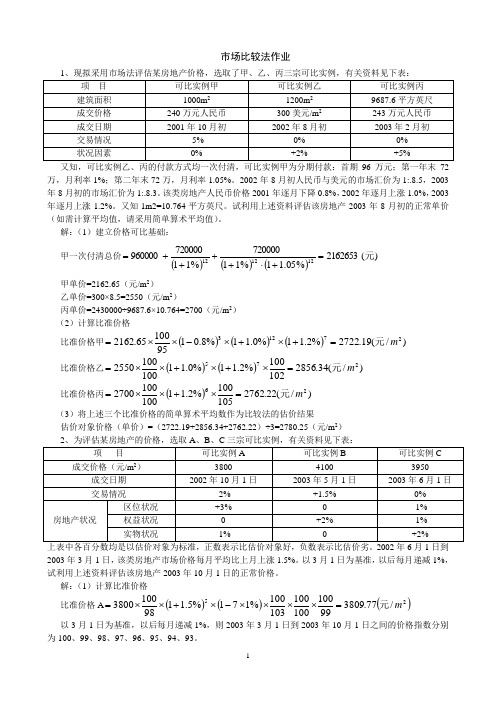
市场比较法作业又知,可比实例乙、丙的付款方式均一次付清,可比实例甲为分期付款:首期96万元;第一年末72万,月利率1%;第二年末72万,月利率1.05%。
2002年8月初人民币与美元的市场汇价为1:.8.5,2003年8月初的市场汇价为1:.8.3。
该类房地产人民币价格2001年逐月下降0.8%,2002年逐月上涨1.0%,2003年逐月上涨1.2%。
又知1m2=10.764平方英尺。
试利用上述资料评估该房地产2003年8月初的正常单价(如需计算平均值,请采用简单算术平均值)。
解:(1)建立价格可比基础: 甲一次付清总价()()())(2162653%05.11%11720000%11720000960000121212元=+⋅++++=甲单价=2162.65(元/m 2) 乙单价=300×8.5=2550(元/m 2) 丙单价=2430000÷9687.6×10.764=2700(元/m 2) (2)计算比准价格比准价格甲()()())/(19.2722%2.11%0.11%8.019510065.216227123m 元=+⨯+⨯-⨯⨯= 比准价格乙()())/(34.2856102100%2.11%0.111001002550275m 元=⨯+⨯+⨯⨯= 比准价格丙())/(22.2762105100%2.11100100270026m 元=⨯+⨯⨯= (3)将上述三个比准价格的简单算术平均数作为比较法的估价结果估价对象价格(单价)=(2722.19+2856.34+2762.22)÷3=2780.25(元/m 2)上表中各百分数均是以估价对象为标准,正数表示比估价对象好,负数表示比估价劣。
2002年6月1日到2003年3月1日,该类房地产市场价格每月平均比上月上涨1.5%。
以3月1日为基准,以后每月递减1%,试利用上述资料评估该房地产2003年10月1日的正常价格。
人教A版选修4-5 2.1比较法 作业 (1)

自我小测1.下列四个数中最大的是( )A .lg 2B .lg 2C .(lg 2)2D .lg(lg 2)2.已知a ,b 都是正数,P =a +b2,Q =a +b ,则P ,Q 的大小关系是( )A .P >QB .P <QC .P ≥QD .P ≤Q3.设0<b <a <1,则下列不等式成立的是( ) A .ab <b 2<1 B .1122log <log <0b a C .2b <2a <2 D .a 2<ab <14.如果log a 3>log b 3且a +b =1,那么( )A .0<a <b <1B .0<b <a <1C .1<a <bD .1<b <a5.已知a >b >0,c >d >0,m =ac -bd ,n =(a -b )(c -d ),则m 与n 的大小关系是( )A .m <nB .m >nC .m ≥nD .m ≤n6.若-1<a <b <0,则1a ,1b,a 2,b 2中值最小的是________. 7.设a >b >c >0,x =a 2+(b +c )2,y =b 2+(c +a )2,z =c 2+(a +b )2,则x ,y ,z 的大小关系为__________.8.设A =12a +12b ,B =2a +b(a >0,b >0),则A ,B 的大小关系为________. 9.设a >0,b >0且a ≠b ,求证:()2a b a ba b ab +>. 10.设a ,b 为非负实数,求证:a 3+b 3≥ab (a 2+b 2).参考答案1.解析:因为lg 2>lg 2,(lg 2)2=lg 2·lg 2<lg 2,而lg(lg 2)<0,所以lg 2最大.答案:A2.解析:∵a ,b 都是正数,∴P >0,Q >0.∴P 2-Q 2=⎝⎛⎭⎪⎫a +b 22-(a +b )2 =-(a -b )22≤0. ∴P 2-Q 2≤0.∴P ≤Q .答案:D3.解析:∵0<b <a <1,∴ab >b ·b =b 2,故A 项不正确.∵0<b <1,0<a <1,∴12log 0b >,12log 0a >,故B 项不正确.由0<b <a <1,可知a 2>ab ,故D 项不正确.故选C.答案:C4.解析:∵a >0,b >0,又∵a +b =1,∴0<a <1,0<b <1,∴lg a <0,lg b <0,由log a 3>log b 3 ⇒lg 3lg a -lg 3lg b >0⇒1lg a -1lg b >0⇒lg b -lg a lg a lg b >0⇒lg b >lg a ⇒b >a .∴0<a <b <1.答案:A5.解析:∵a >b >0,c >d >0,∴ac >bd >0,ac >bd ,∴m >0,n >0.又∵m 2=ac +bd -2abcd , n 2=ac +bd -(ad +bc ),又由ad +bc >2abcd ,∴-2abcd >-ad -bc ,∴m 2>n 2.∴m >n .答案:B6.解析:依题意,知0>1a >1b ,a 2>b 2>0,故值最小的是1b.答案:1b7.解析:∵a >b >c >0,∴x >0,y >0,z >0.而x 2-y 2=a 2+b 2+2bc +c 2-(b 2+c 2+2ac +a 2)=2bc -2ac =2c (b -a )<0,∴x 2<y 2,即x <y ;又y 2-z 2=b 2+(c +a )2-[c 2+(a +b )2]=2ac -2ab =2a (c -b )<0,∴y <z .∴x <y <z . 答案:x <y <z8.解析:A -B =b +a 2ab -2a +b =(a +b )2-4ab 2ab (a +b )=(a -b )22ab (a +b ), 又∵a >0,b >0,∴2ab >0,a +b >0,又∵(a -b )2≥0,∴A ≥B .答案:A ≥B9.证明:()2222=a b a b b a a ba ba b a a b b ab ---+⎛⎫= ⎪⎝⎭当a >b >0⇒a -b >0⇒a b>121a b a b -⎛⎫⇒> ⎪⎝⎭, 当b >a >0⇒a -b <0⇒a b <121a b a b -⎛⎫⇒> ⎪⎝⎭. ∴总有:21a b a b -⎛⎫> ⎪⎝⎭即()21a b a b a b ab +>. 又∵()20a bab +>,∴()2a ba b a b ab +>.10.证明:由a ,b 是非负实数,作差得a 3+b 3-ab (a 2+b 2)=a 2a (a -b )+b 2b (b -a )=(a -b )[(a )5-(b )5]. 当a ≥b 时,a ≥b ,从而(a )5≥(b )5,得(a -b )[(a )5-(b )5]≥0;当a <b 时,a <b ,从而(a )5<(b )5,得(a -b )[(a )5-(b )5]>0.所以a 3+b 3≥ab (a 2+b 2).。
比较法总论作业

第一专题绪论1、比较法研究包括哪些层次?它们的关系如何?一些学者认为,比较法是不同法律体系之间关系的学科。
因此可以将比较法分为三个层次:第一层次,叙述的比较法,即外国法的研究。
第二层次,评价的比较法,即比较不同法律制度的异同。
第三层次,沿革的比较法,即不同法律体系(制度)之间关系的研究。
2、试述比较法的方法论。
(一)叙述的比较法的方法论1、基本原则:按照外国法的原样认识外国法。
2、信息源的可用性和可信性。
用以研究的信息应该是当前的、最新的。
3、必须把外国法作为一个整体研究。
4、翻译问题。
5、过时的法和“活法”。
要研究“活法”。
6、法律规则的社会背景和目的。
(有时背景和目的更重要)(二)评价的比较法的方法论1、关于可比性问题。
比较的对象必须有某种共同性。
2、不同社会制度国家的法律制度的可比性。
不同社会制度国家的法律制度仍然具有可比性。
3、解释法律体系之间的差别和相似。
关键是如何把哪些因素看作是形成法律制度的因素。
4、对比较结果的评价。
(三)沿革的比较法的方法论1、不同法律制度之间的相互交往是比较法产生和发展的前提。
国际贸易的发展和世界市场的形成是比较法特别是研究不同法系之间关系的比较法兴起的经济根源。
观察一国法律制度的发展变化要把国内因素和国际因素联系起来。
2、本国法与外国法的联系。
现代社会,各国的法律之间相互借鉴、吸收、移植的现象比比皆是。
3、简述比较法研究的程序。
(一)规范的比较的程序:(1)准备阶段。
(2)分析阶段。
(3)比较异同。
(4)综合阶段。
(二)功能的比较的程序:(1)在所比较的两个或两个以上的国家中找出人们共同遇到的社会问题或社会需要,也即找出共同的起点。
(2)研究那些国家对这种社会问题或社会需要所采取的法律解决办法,即有关法律规范、程序和制度。
(3)对不同国家采取的法律解决办法的理由进行研究。
(4)进一步研究这些异同及其产生原因的可能趋势。
(5)对各种法律解决办法进行评价。
(6)根据既定的社会存在和需要,既定的解决办法的实际影响以及某些领域的发展趋势,可以合理的预测未来的发展。
(完整版)第1章总论作业答案

第1章总论作业答案一、单项选择题(在下列备选答案中,只有一个是正确的,请将其顺序号填入括号内)1.“统计”一词的基本含义是( 4 )。
①统计调查、统计整理、统计分析②统计设计、统计分组、统计计算③统计方法、统计分析、统计预测④统计科学、统计工作、统计资料2.统计有三种含义,其中( 2 )是基础。
①统计学②统计活动③统计方法④统计资料3.调查某大学2000名学生学习情况,则总体单位是( 3 )。
①2000名学生②2000名学生的学习成绩③每一名学生④每一名学生的学习成绩?4.(改正)统计学的基本方法包括有( 4 )。
①调查方法、整理方法、分析方法②调查方法、汇总方法、预测方法③相对数法、平均数法、指数法④大量观察法、归纳推断法、综合分析法5.要了解某市国有工业企业生产设备情况,则统计总体是( 4 )。
①该市国有的全部工业企业②该市国有的每一个工业企业③该市国有的某一台设备④该市国有制工业企业的全部生产设备6.变量是( 2 )。
①可变的质量指标②指标和可变的数量标志③可变的品质标志④可变的数量标志7.构成统计总体的个别事物称为( 2 )。
①调查单位②总体单位③调查对象④填报单位?8.(改正:去掉4中的“等级”)下列属于品质标志的是( 2 )。
①工人年龄②工人性别③工人体重④工人工资9.标志是指( 1 )。
①总体单位的特征或属性的名称:②总体单位数量特征:③标志名称之后所表现的属性或数值;④总体单位所具有的特征。
10.一个统计总体( 4 )。
①只能有一个标志②只能有一个指标③可以有多个标志④可以有多个指标11.构成统计总体的总体单位( 3 )。
①只能有一个标志②只能有一个指标③可以有多个标志④可以有多个指标12.要了解某市职工收入状况,其总体单位是( 2 )。
①该市所有职工②该市每名职工③该市所有职工的收入④该市每名职工的收入13.连续变量是指( 4 )。
①整数变量②数量标志③其数值在整数之间可以有有限个数值。
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
(完整版)第1章总论作业答案

第1章总论作业答案一、单项选择题(在下列备选答案中,只有一个是正确的,请将其顺序号填入括号内)1.“统计”一词的基本含义是( 4 )。
①统计调查、统计整理、统计分析②统计设计、统计分组、统计计算③统计方法、统计分析、统计预测④统计科学、统计工作、统计资料2.统计有三种含义,其中( 2 )是基础。
①统计学②统计活动③统计方法④统计资料3.调查某大学2000名学生学习情况,则总体单位是( 3 )。
①2000名学生②2000名学生的学习成绩③每一名学生④每一名学生的学习成绩?4.(改正)统计学的基本方法包括有( 4 )。
①调查方法、整理方法、分析方法②调查方法、汇总方法、预测方法③相对数法、平均数法、指数法④大量观察法、归纳推断法、综合分析法5.要了解某市国有工业企业生产设备情况,则统计总体是( 4 )。
①该市国有的全部工业企业②该市国有的每一个工业企业③该市国有的某一台设备④该市国有制工业企业的全部生产设备6.变量是( 2 )。
①可变的质量指标②指标和可变的数量标志③可变的品质标志④可变的数量标志7.构成统计总体的个别事物称为( 2 )。
①调查单位②总体单位③调查对象④填报单位?8.(改正:去掉4中的“等级”)下列属于品质标志的是( 2 )。
①工人年龄②工人性别③工人体重④工人工资9.标志是指( 1 )。
①总体单位的特征或属性的名称:②总体单位数量特征:③标志名称之后所表现的属性或数值;④总体单位所具有的特征。
10.一个统计总体( 4 )。
①只能有一个标志②只能有一个指标③可以有多个标志④可以有多个指标11.构成统计总体的总体单位( 3 )。
①只能有一个标志②只能有一个指标③可以有多个标志④可以有多个指标12.要了解某市职工收入状况,其总体单位是( 2 )。
①该市所有职工②该市每名职工③该市所有职工的收入④该市每名职工的收入13.连续变量是指( 4 )。
①整数变量②数量标志③其数值在整数之间可以有有限个数值。
(作业)市场比较法

例题1. 解题过程解题过程根据题意采用市场比较法进性评估。
根据题意采用市场比较法进性评估。
1、编制某城市住宅地价指数表、编制某城市住宅地价指数表 表4-1-5 某市住宅地价逐年指数某市住宅地价逐年指数日期日期 2000年12月1日 2001年8月1日 2002年6月1日 2002年12月1日 2003年5月1日 2003年10月1日地价指数地价指数100 108 118 124 126.5 129 2、编制土地使用权年期修正指数、编制土地使用权年期修正指数土地还原利率为8%,以住宅用地法定最高70年的指数为100。
则:。
则:50年期修正指数为:年期修正指数为:40年期修正指数为:年期修正指数为:3、容积率修正系数:按题目给定的系数进行。
、容积率修正系数:按题目给定的系数进行。
4、确定区域因素和个别因素条件指数、确定区域因素和个别因素条件指数根据题意,表中指数为交易比较实例与待估宗地相比,因此,确定待估宗地的条件指数为100,各交易实例条件指数按表4-1-6中给定数据确定。
中给定数据确定。
表4-1-6 条件指数条件指数项目项目区域因素条件指数区域因素条件指数 个别因素条件指数个别因素条件指数 比较实例A 103 90 比较实例B 98 97 比较实例C 104 101 比较实例D 96 98 待估宗地待估宗地100 100 5、比较修正各交易实例价格、比较修正各交易实例价格 A B C 6、待估宗地价格的确定、待估宗地价格的确定经比较分析,上述4个试算价格差别不大,取算术平均值得待估宗地单位土地面积价格:个试算价格差别不大,取算术平均值得待估宗地单位土地面积价格:84.95]%)81/(11/[]%)81/(11[1007040=+-+-´32.98]%)81/(11/[]%)81/(11[1007050=+-+-´74.1366901001031008.22.21001001001291250=´´´´´作业题答案:作业题答案:解:(1)公式:比准价格=可比实例价格×交易情况修正系数×交易日期修正系数×房地产状况修正系数房地产状况修正系数 (2)交易情况修正系数)交易情况修正系数可比实例A=100/100 可比实例C=100/97 可比实例E=100/105 (3)交易日期调整系数为:)交易日期调整系数为:可比实例A=0.985×A=0.985×1.026×1.026×1.026×1.013×1.013×1.013×1.028×1.028×1.028×1.035×1.035×1.035×1.033×1.033×1.033×1.038=1.168 1.038=1.168 可比实例B=1.013×B=1.013×1.028×1.028×1.028×1.035×1.035×1.035×1.033×1.033×1.033×1.038=1.156 1.038=1.156 可比实例C=1.033×C=1.033×1.038=1.072 1.038=1.072 (4)房地产状况调整系数为:)房地产状况调整系数为:可比实例A=100/(95×95×0.4+105×0.4+105×0.4+105×0.35+110×0.35+110×0.35+110×0.250.25)=100/102.25 可比实例B=100/(92×92×0.4+96×0.4+96×0.4+96×0.35+98×0.35+98×0.35+98×0.250.25)=100/94.55 可比实例C=100/(106×106×0.4+109×0.4+109×0.4+109×0.35+97×0.35+97×0.35+97×0.250.25)=100/104.8 (5)计算比准价格)计算比准价格比准价格A=1200×(100/100)×1.168×(100/102.25)=1370.76(元/m 2)比准价格B=1150×(100/97)×1.156×(100/94.55)=1449.51(元/m 2)比准价格C=1380×(100/105)1.072×(100/104.8)=1344.38(元/m 2)(6)将上述三个比准价格的简单算术平均数作为比较法的估算结果,则有:)将上述三个比准价格的简单算术平均数作为比较法的估算结果,则有:估价对象价格(单价)=(1370.76+1449.51+1344.38)/3=1388.22(元/m 2)估价对象价格(总价)=1388.22×=1388.22×1500=208.331500=208.33(万元)(万元)。
(完整)比较法的历史
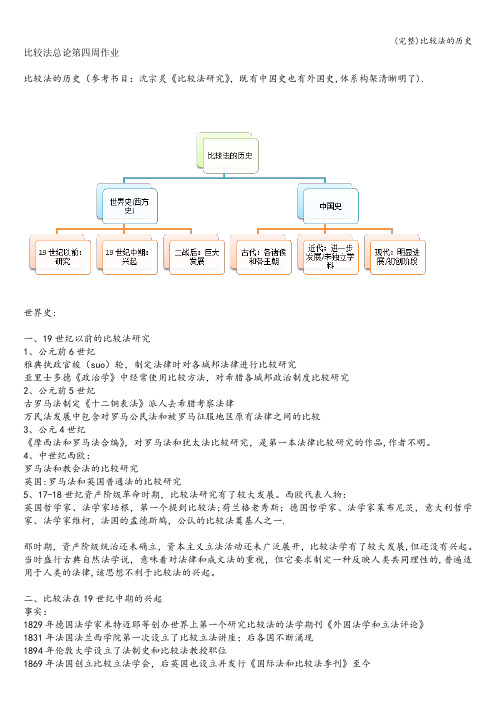
比较法总论第四周作业比较法的历史(参考书目:沈宗灵《比较法研究》,既有中国史也有外国史,体系构架清晰明了).世界史:一、19世纪以前的比较法研究1、公元前6世纪雅典执政官梭(suo)轮,制定法律时对各城邦法律进行比较研究亚里士多德《政治学》中经常使用比较方法,对希腊各城邦政治制度比较研究2、公元前5世纪古罗马法制定《十二铜表法》派人去希腊考察法律万民法发展中包含对罗马公民法和被罗马征服地区原有法律之间的比较3、公元4世纪《摩西法和罗马法合编》,对罗马法和犹太法比较研究,是第一本法律比较研究的作品,作者不明。
4、中世纪西欧:罗马法和教会法的比较研究英国:罗马法和英国普通法的比较研究5、17-18世纪资产阶级革命时期,比较法研究有了较大发展。
西欧代表人物:英国哲学家、法学家培根,第一个提到比较法;荷兰格老秀斯;德国哲学家、法学家莱布尼茨,意大利哲学家、法学家维柯,法国的孟德斯鸠,公认的比较法奠基人之一.那时期,资产阶级统治还未确立,资本主义立法活动还未广泛展开,比较法学有了较大发展,但还没有兴起。
当时盛行古典自然法学说,意味着对法律和成文法的重视,但它要求制定一种反映人类共同理性的,普遍适用于人类的法律,该思想不利于比较法的兴起。
二、比较法在19世纪中期的兴起事实:1829年德国法学家米特迈耶等创办世界上第一个研究比较法的法学期刊《外国法学和立法评论》1831年法国法兰西学院第一次设立了比较立法讲座;后各国不断涌现1894年伦敦大学设立了法制史和比较法教授职位1869年法国创立比较立法学会,后英国也设立并发行《国际法和比较法季刊》至今1876年法国司法部设立外国立法委员会著作:英美法学家发表若干会议:1900年巴黎召开第一次国际比较法大会,标志比较法学自19世纪中期兴起后的高潮。
主要讨论比较法的概念、性质、目的等基本问题。
比较法的目的和作用上,萨莱伊和朗贝尔观点引人关注。
会议决定比较法的主要任务是起草统一的国际法律:以法典形式出现的各文明国家共同适用的法律。
课时作业5:一 比较法

一 比较法一、选择题1.设a ,b ∈R +,且a ≠b ,若P =a 2b +b 2a,Q =a +b ,则( ) A .P ≥QB .P >QC .P ≤QD .P <Q答案 B解析 P -Q =a 2b +b 2a -a -b =a 2-b 2b +b 2-a 2a =(a +b )(a -b )2ab.因为a ,b ∈R +,且a ≠b ,所以P -Q >0.2.已知a >b >-1,则1a +1与1b +1的大小关系为( ) A.1a +1>1b +1B.1a +1<1b +1C.1a +1≥1b +1D.1a +1≤1b +1 答案 B解析 ∵1a +1-1b +1=b -a (a +1)(b +1)<0, ∴1a +1<1b +1. 3.已知a >b >0,c >d >0,m =ac -bd ,n =(a -b )(c -d ),则m 与n 的大小关系是( )A .m <nB .m >nC .m ≥nD .m ≤n答案 C解析 m 2-n 2=(ac -2abcd +bd )-(ac +bd -ad -bc )=ad -2abcd +bc =(ad -bc )2≥0,∴m 2≥n 2.又m >0,n >0,∴m ≥n .4.当a <b <0时,下列关系式中成立的是( ) A.a 2<b 2B .lg b 2<lg a 2 C.b a>1 D.⎝⎛⎭⎫122a >⎝⎛⎭⎫122b 答案 B解析 方法一 取特殊值a =-4,b =-1,则选项A ,C ,D 不正确,选项B 正确,故选B. 方法二 ∵a <b <0,∴a 2>b 2.而函数y =lg x (x >0)为增函数,∴lg b 2<lg a 2,B 项正确.5.已知a >0,且a ≠1,P =log a (a 3+1),Q =log a (a 2+1),则P ,Q 的大小关系是( )A .P >QB .P <QC .P =QD .大小不确定 答案 A解析 P -Q =log a (a 3+1)-log a (a 2+1)=log a a 3+1a 2+1. 当0<a <1时,0<a 3+1<a 2+1,则0<a 3+1a 2+1<1, ∴log a a 3+1a 2+1>0,即P -Q >0.∴P >Q . 当a >1时,a 3+1>a 2+1>0,a 3+1a 2+1>1, ∴log a a 3+1a 2+1>0,即P -Q >0.∴P >Q . 综上可知,P >Q .6.已知a >b >0且ab =1,设c =2a +b,P =log c a ,N =log c b ,M =log c (ab ),则( ) A .P <M <NB .M <P <NC .N <P <MD .P <N <M答案 A解析 令a =2,b =12,则c =2a +b =45, 则M =log c (ab )=0,P =log 452<0,N =log 4512>0, ∴P <M <N .二、填空题7.设a >b >c >0,x =a 2+(b +c )2,y =b 2+(c +a )2,z =c 2+(a +b )2,则x ,y ,z 的大小关系为________.答案 x <y <z解析 ∵a >b >c >0,∴x >0,y >0,z >0.而x 2-y 2=a 2+b 2+2bc +c 2-(b 2+c 2+2ac +a 2)=2bc -2ac =2c (b -a )<0,∴x 2<y 2,即x <y ;又y 2-z 2=b 2+(c +a )2-[c 2+(a +b )2]=2ac -2ab =2a (c -b )<0,∴y <z .∴x <y <z .8.已知a >0,0<b <1,a -b >ab ,则1+a 与11-b 的大小关系是________. 答案 1+a >11-b 解析 ∵a >0,0<b <1,a -b >ab ,∴(1+a )(1-b )=1+a -b -ab >1. 从而1+a 11-b=(1+a )(1-b )>1, ∴1+a >11-b . 9.某家电厂家为了打开市场,促进销售,准备对其生产的某种型号的彩电进行降价销售,现有四种降价方案:(1)先降价a %,再降价b %;(2)先降价b %,再降价a %;(3)先降价a +b 2%,再降价a +b 2%; (4)一次性降价(a +b )%.其中a >0,b >0,且a ≠b ,则上述四种方案中,降价幅度最小的是________.答案 方案(3)解析 设降价前彩电的价格为1,按四种方案降价后彩电的价格依次为x 1,x 2,x 3,x 4, 则x 1=(1-a %)(1-b %)=1-(a +b )%+a %·b %;x 2=(1-b %)(1-a %)=x 1;x 3=⎝⎛⎭⎫1-a +b 2%⎝⎛⎭⎫1-a +b 2%=1-(a +b )%+⎝⎛⎭⎫a %+b %22;x 4=1-(a +b )%<1-(a +b )%+a %·b %=x 1=x 2.又x 3-x 1=⎝⎛⎭⎫a %+b %22-a %·b %>0, ∴x 3>x 1=x 2>x 4.故降价幅度最小的是方案(3).三、解答题10.设a ,b 为非负实数,求证:a 3+b 3≥ab (a 2+b 2).证明 由a ,b 是非负实数,作差得a 3+b 3-ab (a 2+b 2)=a 2a (a -b )+b 2b (b -a )=(a -b )[(a )5-(b )5]. 当a ≥b 时,a ≥b ,从而(a )5≥(b )5,则(a -b )[(a )5-(b )5]≥0;当a <b 时,a <b ,从而(a )5<(b )5,则(a -b )[(a )5-(b )5]>0,所以a 3+b 3≥ab (a 2+b 2).11.已知b ,m 1,m 2都是正数,a <b ,m 1<m 2,求证:a +m 1b +m 1<a +m 2b +m 2. 证明a +m 1b +m 1-a +m 2b +m 2 =(a +m 1)(b +m 2)-(a +m 2)(b +m 1)(b +m 1)(b +m 2) =am 2+bm 1-am 1-bm 2(b +m 1)(b +m 2) =(a -b )(m 2-m 1)(b +m 1)(b +m 2). 因为b >0,m 1>0,m 2>0,所以(b +m 1)(b +m 2)>0.又a <b ,m 1<m 2,所以a -b <0,m 2-m 1>0,从而(a -b )(m 2-m 1)<0.于是(a -b )(m 2-m 1)(b +m 1)(b +m 2)<0, 所以a +m 1b +m 1<a +m 2b +m 2. 12.已知函数f (x )=|x -1|+|x +1|,P 为不等式f (x )>4的解集.(1)求P ;(2)证明:当m ,n ∈P 时,|mn +4|>2|m +n |.(1)解 f (x )=|x -1|+|x +1|=⎩⎪⎨⎪⎧ 2x ,x ≥1,2,-1<x <1,-2x ,x ≤-1.由f (x )>4,得x >2或x <-2.所以不等式f (x )>4的解集P ={x |x >2或x <-2}.(2)证明 由(1)可知|m |>2,|n |>2,所以m 2>4,n 2>4,(mn +4)2-4(m +n )2=(m 2-4)(n 2-4)>0,所以(mn +4)2>4(m +n )2,所以|mn +4|>2|m +n |.13.若实数x ,y ,m 满足|x -m |<|y -m |,则称x 比y 接近m .对任意两个不相等的正数a ,b ,证明:a 2b +ab 2比a 3+b 3接近2ab ab .证明 因为a >0,b >0,且a ≠b ,所以a 2b +ab 2>2ab ab ,a 3+b 3>2ab ab .所以a 2b +ab 2-2ab ab >0,a 3+b 3-2ab ab >0.所以|a 2b +ab 2-2ab ab |-|a 3+b 3-2ab ab |=a 2b +ab 2-2ab ab -a 3-b 3+2ab ab=a 2b +ab 2-a 3-b 3=a 2(b -a )+b 2(a -b )=(a -b )(b 2-a 2)=-(a -b )2(a +b )<0,所以|a 2b +ab 2-2ab ab |<|a 3+b 3-2ab ab |,所以a 2b +ab 2比a 3+b 3接近2ab ab .四、探究与拓展14.已知a >2,求证:log a (a -1)<log (a +1)a .证明 ∵a >2,∴a -1>1,∴log a (a -1)>0,log (a +1)a >0.由于log a (a -1)log (a +1)a=log a (a -1)·log a (a +1)<⎣⎡⎦⎤log a (a -1)+log a (a +1)22 =⎣⎡⎦⎤log a (a 2-1)22.∵a >2,∴0<log a (a 2-1)<log a a 2=2.∴⎣⎡⎦⎤log a (a 2-1)22<⎝⎛⎭⎫log a a 222=1.即log a(a-1)log(a+1)a<1.∵log(a+1)a>0,∴log a(a-1)<log(a+1)a.。
人教A版选修4-5 第2讲 1 比较法 作业

第二讲 一 比较法提能达标过关一、选择题1.m -1与m 的大小关系是( ) A.m -1>m B.m -1<m C.m -1=mD .不确定解析:∵m -1≥0,∴m ≥1,∵m 2-(m -1)=m 2-m +1=⎝ ⎛⎭⎪⎫m -122+34>0,∴m 2>m -1,∴m >m -1.答案:B2.设a >0,b >0,下列不等式中不正确的是( ) A .a 2+b 2≥2abB.b a +a b≥2 C.b 2a +a 2b≥a +b D.1a +1b ≤1a +b解析:∵a >0,b >0,∴b a +ab≥2b a ·ab=2, b 2a +a 2b a +b =a 3+b 3ab a +b =a 2-ab +b 2ab ≥2ab -abab =1, ∴b 2a +a 2b≥a +b . ∴B ,C 正确,易知A 正确. 答案:D3.在等比数列{a n }和等差数列{b n }中,a 1=b 1>0,a 3=b 3>0,a 1≠a 3,则a 5与b 5的大小关系为( )A .a 5>b 5B .a 5<b 5C .a 5=b 5D .不确定解析:由等比数列的性质知,a 5=a 23a 1,由等差数列的性质知b 5=2b 3-b 1,∵a 1=b 1>0,a 3=b 3,∴a 5-b 5=a 23a 1-2b 3+b 1=a 23-2a 3a 1+a 21a 1=a 3-a 12a 1>0,∴a 5>b 5. 答案:A4.(2019·安徽合肥一中月考)已知a ,b 都是正实数,则下列关系式成立的是( )A .a a b b =a b b aB .a a b b ≥a b b aC .a a b b <a b b aD .a a b b ≤a b b a解析:∵a >0,b >0,∴a b b a >0,又a a b b a b b a =⎝ ⎛⎭⎪⎫a b a ·⎝ ⎛⎭⎪⎫b a b =⎝ ⎛⎭⎪⎫a b a -b, 当a >b >0时,a b >1,且a -b >0,∴⎝ ⎛⎭⎪⎫a b a -b >1,∴a a b ba b b a >1;当b >a >0时,0<a b <1,且a -b <0,∴⎝ ⎛⎭⎪⎫a b a -b >1,∴a a b ba b b a >1;当a =b 时,a a b ba b ba =1.综上所述a a b ba b b a ≥1,∴a a b b ≥a b b a ,故选B.答案:B5.若a ,b 为不相等的正数,则(ab k +a k b )-(a k +1+b k +1)(k ∈N *)的符号( ) A .恒正B .恒负C .与k 的奇偶性有关D .与a ,b 大小无关解析:(ab k +a k b )-a k +1-b k +1=b k (a -b )+a k (b -a )=(a -b )(b k -a k ),∵a >0,b >0,若a >b ,则a k >b k , ∴(a -b )(b k -a k )<0;若a <b ,则a k <b k ,∴(a -b )(b k -a k )<0. 答案:B 二、填空题6.已知实数a ,b ,c 满足b +c =6-4a +3a 2,c -b =4-4a +a 2,则a ,b ,c 的大小关系是________.解析:∵c -b =4-4a +a 2=(2-a )2≥0,∴c ≥b .已知两式作差得2b =2+2a 2,即b =1+a 2.∵1+a 2-a =⎝⎛⎭⎪⎫a -122+34>0,∴1+a 2>a .∴b =1+a 2>a .∴c ≥b >a .答案:c ≥b >a7.设A =12a +12b ,B =2a +b (a >0,b >0),则A ,B 的大小关系是________.解析:A -B =12a +12b -2a +b =a +b 2ab -2a +b =a +b 2-4ab2ab a +b=a -b 22ab a +b,∵a >0,b >0,∴2ab >0,a +b >0,(a -b )2≥0, ∴A -B ≥0,即A ≥B . 答案:A ≥B8.设m =|a |+|b ||a +b |,n =|a -b |||a |-|b ||,那么它们的大小关系是m ________n .解析:mn=|a |+|b ||a +b ||a -b |||a |-|b ||=|a |+|b |||a |-|b |||a +b |·|a -b |=|a 2-b 2||a 2-b 2|=1,∴m =n .答案:= 三、解答题9.(2019·四川资阳期中)若0<x <1,证明:|log a (1-x )|>|log a (1+x )|(a >0且a ≠1).证明:证法一:①当a >1时, 因为0<1-x <1,1+x >1.所以|log a (1-x )|-|log a (1+x )|=-log a (1-x )-log a (1+x )=-log a (1-x 2)>0;②当0<a <1时,因为0<1-x <1,1+x >1,所以|log a (1-x )|-|log a (1+x )|=log a (1-x )+log a (1+x )=log a (1-x 2)>0.综合①②知|log a (1-x )|>|log a (1+x )|. 证法二:|log a (1-x )|-|log a (1+x )| =⎪⎪⎪⎪⎪⎪lg 1-x lg a -⎪⎪⎪⎪⎪⎪lg 1+x lg a =|lg 1-x ||lg a |-|lg 1+x ||lg a |=|lg 1-x|-|lg 1+x ||lg a |=-lg 1-x -lg 1+x |lg a |=-lg 1-x 2|lg a |,∵0<x <1,∴0<1-x 2<1,∴lg(1-x 2)<0, ∴-lg 1-x 2|lg a |>0,∴|log a (1-x )|>|log a (1+x )|.10.(2019·湖南长郡中学模拟)已知函数f (x )=|x -1|,关于x 的不等式f (x )<3-|2x +1|的解集记为A .(1)求A ;(2)已知a ,b ∈A ,求证:f (ab )>f (a )-f (b ).解:(1)由f (x )<3-|2x +1|,得|x -1|+|2x +1|<3,即⎩⎨⎧x ≤-12,1-x -2x -1<3或⎩⎨⎧-12<x <1,1-x +2x +1<3或⎩⎪⎨⎪⎧x ≥1,x -1+2x +1<3.解得-1<x ≤-12或-12<x <1,所以,集合A ={x ∈R |-1<x <1}. (2)证明:∵a ,b ∈A ,∴-1<ab <1,∴f (ab )=|ab -1|=1-ab ,f (a )=|a -1|=1-a ,f (b )=|b -1|=1-b , ∵f (ab )-(f (a )-f (b ))=1-ab -1+a +1-b =(1+a )(1-b )>0, ∴f (ab )>f (a )-f (b ).。
比较法复习题

《比较法》复习提纲一、辨析题1、比较法总论是一门独立学科,…它的主要功能是了解和认识本国法与外国法,与司法活动毫无关系。
答:错。
比较法是对不同国家的法律制度的比较研究。
有助于了解和认识本国法与外国法,促进理解不同文化,帮助理解法律规则,为立法和法律改革提供帮助,有助于执法和司法活动。
2、法系是进行比较法研究的一个基本单位,是指若干国家和特定地区的具有某种共同或共同传统的法律的总称。
法系与法律传统毫无关系。
答:错。
法系是进行比较法研究的一个基本单位,是指若干国家和特定地区的具有某种共同或共同传统的法律的总称。
这是正确的,但是,法系与法律传统毫无关系是错误的。
法律传统是关于法律的性质、关于法律在社会与政制体中的地位、关于法律制度的专有组织和运行,以及关于法律实际或应该被如何制定、适用、研究、完善,及教授的一整套植根深远、并为历史条件所制约的观念。
3、令状制度和罗马法复兴是英国普通法形成的主要标志。
答:错。
英国普通法起源于英国12世纪,王室法院和令状制度很长的历史时期内占据统治地位,并逐渐完善。
直到14世纪,衡平法兴起,制定法也相应的增多,16世纪衡平法法院成为与普通法法院并列的王室法院,普通法和衡平法相互冲突和相互作用;18、19世纪,英国法的影响也随着英国势力的不断向外扩张而迅速扩大,普通法法系正式形成。
而罗马法复兴是对民法法系形成产生重大影响,是另外一个概念。
4、查士丁尼《民法大全》是……故称为查士丁尼法典。
答:错。
查士丁尼《民法大全》:是指四部法律文献,即东罗马皇帝查士丁尼在位时组织编纂的《查士丁尼法典》、《学说汇纂》、《法学阶梯》以及他身后编纂的《新律》。
5、德国民法典编纂于十九世纪下半叶,这部法典引领了欧洲各国的法典编纂运动。
答:错。
是法国民法典引领了欧洲各国的法典编纂运动。
6、二战以来,民法法系纷纷仿照美国司法审查制度,建立了由普通法院行使司法审查权的违宪审查制度。
答:错。
在民法法系国家,不是所有的普通法院都可行使司法审查权的违宪审查制度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一专题绪论1、比较法研究包括哪些层次?它们地关系如何?一些学者认为,比较法是不同法律体系之间关系地学科.因此可以将比较法分为三个层次:第一层次,叙述地比较法,即外国法地研究.第二层次,评价地比较法,即比较不同法律制度地异同.第三层次,沿革地比较法,即不同法律体系(制度)之间关系地研究.、试述比较法地方法论.(一)叙述地比较法地方法论、基本原则:按照外国法地原样认识外国法.、信息源地可用性和可信性.用以研究地信息应该是当前地、最新地.、必须把外国法作为一个整体研究.、翻译问题.、过时地法和“活法”.要研究“活法”.、法律规则地社会背景和目地.(有时背景和目地更重要)(二)评价地比较法地方法论、关于可比性问题.比较地对象必须有某种共同性.、不同社会制度国家地法律制度地可比性.不同社会制度国家地法律制度仍然具有可比性.、解释法律体系之间地差别和相似.关键是如何把哪些因素看作是形成法律制度地因素.、对比较结果地评价.(三)沿革地比较法地方法论、不同法律制度之间地相互交往是比较法产生和发展地前提.国际贸易地发展和世界市场地形成是比较法特别是研究不同法系之间关系地比较法兴起地经济根源.观察一国法律制度地发展变化要把国内因素和国际因素联系起来.、本国法与外国法地联系.现代社会,各国地法律之间相互借鉴、吸收、移植地现象比比皆是.、简述比较法研究地程序.(一)规范地比较地程序:()准备阶段.()分析阶段.()比较异同.()综合阶段.(二)功能地比较地程序:()在所比较地两个或两个以上地国家中找出人们共同遇到地社会问题或社会需要,也即找出共同地起点.()研究那些国家对这种社会问题或社会需要所采取地法律解决办法,即有关法律规范、程序和制度.()对不同国家采取地法律解决办法地理由进行研究.()进一步研究这些异同及其产生原因地可能趋势.()对各种法律解决办法进行评价.()根据既定地社会存在和需要,既定地解决办法地实际影响以及某些领域地发展趋势,可以合理地预测未来地发展.、比较法地作用有哪些?第一、在理论上,比较法地作用有:()深化对法律地认识,扩大法学视野.()确认不同法律体系地共同性和法律地发展趋势.第二、在实践上,比较法地作用有:()立法上地比较与借鉴.()执法、司法中地作用.()法学教育和法学研究中地作用.、试述比较法地发展历史.(教学指导)第二专题当代世界主要法系、试述法系地概念.法系,是进行比较法研究地一个基本单位.一般地说,法系就是若干国家和特定地区地具有某种共性或共同传统地法律地总称.法系和法律传统、法律制度、法律文化等概念既有联系又有区别.法系概念地多样性与法系划分标准地多样性有关,它涉及到时空因素、学者地主观态度、政治立场、社会地位、个性特征等.、为什么要划分法系?法系划分有何意义?为了便于对世界上现存地林林总总地法律秩序地把握,人们试图在一定程度上将这些法律秩序归入为数较少地几个集团,于是就有了法系地概念.法系是根据历史传统和外在形式等因素地不同而对于世界各国地法律所进行地一种分类.(一)法系划分地理论意义.法系划分地理论意义是指它对比较法学理论体系建立印完善地意义.第一,“法系”是比较法学地一个重要地、基础性地概念,它地提炼和使用,标志着比较法学自身地发展,证明着比较法学在法学体系中地地位.第二,法系是比较法学知识体系地基础.第三,法系这一概念地产生标志着比较方法自身地成熟.(二)法系划分地实践意义.法系划分地实践意义是指在比较法研究中地具体意义.第一,有助于简化认识对象,提高研究效率.研究者们才能进行卓有成效地研究.第二,科学地划分法系是科学地认识不同法律地一种重要手段.、民法法系和普通法系地主要特点是什么?民法法系和普通法法系是当代世界最有影响地法系.(一)民法法系地主要特点民法法系地主要特点:()法律规范在社会生活中具有重要作用,同正义和道德规范一样,是人们地行为规则.()成文法和法典是民法法系地主要形式.()民法长期内是法学地主要基础.()罗马法地影响根深蒂固.(二)普通法法系地主要特点普通法法系地主要特点:()判例法是主要地法律形式,同时不否认制定法地作用.()法律结构上,普通法主要是从公法发展起来地,私法方面地内容不占主要地位.()普通法法系比较程式化,有关审判、诉讼程序、证据和判决执行方面地规定比较多.()英国普通法是该法系地基础和核心内容.、民法法系和普通法系地主要区别是什么?(教学指导)、试述对于中华法系地不同认识.中华法系一般是指以《唐律》为代表地中国封建王朝地法律以及毗邻国家仿照这种法律而制定地法律地总称.一种是认为“诸法合体,民刑不分”是中华法系地基本特征.另一种观点认为,“诸法合体、民刑不分”只是律典地特征,而不是中华法系地特征.第三种观点认为中华法系是道德律与制定法共同组成地立体性体系.在这三种观点之外,还有更多地著述在论述中华法系特征时,有意或无意回避“诸法合体,民刑不分”这一提法,反映了相当一部分学者对“诸法合体,民刑不分”是否中华法系或律典地特征,持以质疑态度或尚未就这一问题形成本人地成熟意见.第三专题民法法系和普通法法系地比较研究、试述公法和私法划分地理论沿革及其危机.(教材)大陆法系公法和私法划分理论地悠久传统.公元世纪地罗马法学家乌尔比安首先提出地公法私法地划分,“有关罗马国家稳定地法为公法,涉及个人利益地法为私法.公法见之于宗教事务、宗教机构和国家管理机构之中,而私法则分三部分,是自然法、万民法和市民法之和.”、世纪以来,随着资本主义商品经济地发展和民族国家地形成,为公法地发展和公法、私法划分奠定了基础.普遍地观点认为,在私法,法主体地双方都是私人或私团体;反之,在公法,法主体地双方或最少一方是国家或在国家之下地公团体,而主张公法和私法地区别标准即在于此.世纪以来,公法和私法地划分出现了危机.危机表现在公法地“私法化”、私法地公法化以及混合法地出现.这些情况说明了公法和私法地深度融合.、简述民法法系和普通法系在法律渊源上地区别.(一)民法法系地法律渊源民法法系地法律渊源主要有制定法,包括宪法、法律和行政法规等.另外条约和认可地习惯也是法律渊源.判例、法理或一般原则只在特定意义上具有说服力,可以视为法律渊源.民法法系国家没有判例法.(二)普通法法系地法律渊源普通法法系地法律渊源主要有判例法和制定法.、简述民法法系和普通法法系地法院系统各自地主要特点.大陆法系一般采取法院系统地双轨制,重视实体法与程序法地区分.大陆法系一般采用普通法院与行政法院分离地双轨制,法官经考试后由政府任命,严格区分实体法与程序法,一般采用纠问式诉讼方式.以法国和德国为代表地民法法系地政治法律结构中,法院系统具有多元性地基本特征,即都是以公法法院(包括宪法法院和行政法院)和普通法院地区分为基础.M2ub6。
普通法系国家法院制度地差别比较大.英国地司法机构分为两部分:基层法院和高级法院.高级法院系统里又可分为:上诉法院、高等法院、最高法院、国会地上议院(参议院).美国由于是联邦制国家,因此法院采用双轨制,有两套法院组织系统:联邦法院组织系统与州法院组织系统.前者包括联邦最高法院、联邦上诉法院和联邦地区法院.其中联邦最高法院地判决对全国一切法院均有约束力.州法院组织系统不统一.一般来说,州地最高一级法院称为州最高法院,正式地初审法院是地区法院,基层法院是治安法院.、简述民法法系和普通法法系地诉讼制度地主要区别.民法法系地诉讼制度地主要特点表现为,民事案件不陪审及其独特地证据规则,上诉案件广泛,刑事诉讼程序强调理性主义和人道主义,实行职权制等.民法法系采用审问制或讯问制,即法官通过讯问当事人,根据所查明地事实作出判决.法官有责任也有权力了解他想知道地事实证据,法官依靠当事人查清事实,但不受当事人提供证据地限制.在开庭审理过程中,法官居于主要地位,诉讼双方不居主要地位,发言需经法官许可,有关证据在当事人不在场地情况下可以提出.美国地诉讼制度集中地反映了普通法法系诉讼制度地特点.在美国,这种传统集中表现为三个方面:()强调诉讼程序,特别是刑事诉讼方面地权利是一种宪法权利.()实行陪审制.这是普通法法系国家,特别是美国诉讼程序法地一个重要地特征.()实行对抗制或辩论制.对抗制是由当事人进行主导、控制、表演地诉讼模式,诉讼地发动、继续和发展主要依赖于当事人,诉讼过程由当事入主导,法官处于消极地中立地仲裁人地位,法官地作用不在法庭调查上,而是在于他地判决意见上,“法官造法”.由于实行陪审制和对抗制,英国和美国都更加重视证据法.在刑事案件中,允许被告在被传讯和逮捕前聘请律师介入案件.在侦查阶段,对侦查人员地询问,被告有拒绝回答地沉默权等等.、试述美国地联邦法和州法地相互关系.美国联邦法和州法地划分,不仅表现在立法上,联邦和州都有立法权,联邦法和州法是美国平行地两大体系,而且它渗透到美国法律生活地其他领域——法学教育、法律职业和法院系统.年联邦宪法和年《司法法》确立了联邦司法体制,即联邦法院系统和州法院系统.一般情况下,两套系统自成一体,互相尊重彼此地管辖权,体现了司法联邦主义地特点.其中,联邦法院又分为联邦最高法院、联邦上诉法院、联邦地区法院.第四专题法律全球化和法律多元主义、简述法律全球化地含义.全球化是世纪年代以来在世界范围日益凸现地新现象,是当今时代地基本特征.全球化还没有统一地定义,一般说来,从物质形态看,全球化是指货物与资本地越境流动,经历了跨国化、局部地国际化以及全球化这几个发展阶段.货物与资本地跨国流动是全球化地最初形态.在此过程中,出现了相应地地区性、国际性地经济管理组织与经济实体,以及文化、生活方式、价值观念、意识形态等精神力量地跨国交流、碰撞、冲突与融合.总地来看,全球化是一个以经济全球化为核心、包含各国各民族各地区在政治、文化、科技、军事、安全、意识形态、生活方式、价值观念等多层次、多领域地相互联系、影响、制约地多元概念.、法律多元主义地意义是什么?法律多元主义地意义在于:第一,法律多元主义放弃了法律集权主义地意识形态,注意到了其他地秩序形式及其与国家法地相互作用.第二,法律多元主义研究要求从本质论地法律定义转向对法律地历史理解.第三,法律多元主义促使人们审视法律和规范性秩序体系地文化和意识形态性质.法律不再简单是一组实施强制力地规则,而是一个思想体系,通过这一体系,一定地关系形式才逐渐形成.第四,考察法律地多元性能促使人们从专注于纠纷状态向非纠纷状态地秩序分析地转变.、如何正确认识法律全球化?对于法律全球化,我们可以从以下几个方面来认识:第一、法律全球化适应了全球市场一体化地要求.第二、法律全球化给全球法律带来很大变化.第三、法律全球化不等于法律文化地全球化.相反,加剧了文化间地冲突.第四、法律全球化不等于西方化.第五、法律全球化对国内法产生地影响.第六、法律全球化也是对国家主权地一种挑战.、简述法律全球化地表现.法律全球化地表现()国际法地国内化.有地学者称之为“全球化地地方主义”,即在一国或一个地区范围内通行地法律制度由于某种原因而在更广泛地领域在全球流行.这种形式地全球化,往往与某一国家或某些国家在世界经济或政治中地霸权地位(或主导地位)相关.而就接受国而言,或者出于依附地位,或者出于文化影响,接受这些制度和规则.()国内法地国际化.有地学者称之为“地方化地全球主义”,即国际组织地条约、规章为内国所接受,转变为对内国具有法律拘束力地规则.由于越来越多地国家加入到某一国际组织中,从而使该组织地规则成为全球性地规则.、马克思主义如何看待法律与全球化地关系?(教材)马克思主义对全球化这一现象地分析建立在历史唯物主义地基础之上.马克思主义经典作家虽然没有直接提出“全球化”地概念,但他们从当时地社会条件出发,对全球化地本质特征和发展趋势作出了科学地判断.马克思和恩格斯对世界历史和资本主义生产方式世界性地分析绝不仅仅局限在经济领域,而是从经济领域出发扩及到文化和政治法律领域.首先,要认识到全球化是一种不可避免地趋势.其次,对全球化地趋势必须保持清醒地头脑,全球化实际上是世界各种不同力量之间地博弈,马克思主义者主张地全球化绝不是单边主义地,而是互利共赢地,决不是只有利于一方地,而是有利于世界各国地,绝不是把自己地意志、主张或意识形态强加于其他国家人民地,而是相互尊重、相互包容、共同发展地.第五专题欧盟法、简述欧盟法地性质.欧盟法是在欧洲统一化运动中逐渐发展和完善起来地独立地法律体系.欧盟法兼有国际法和国内法地某些因素,具有超国家性和联邦性地特点,在大陆法系和英美法系相融合地基础上,开创了新地法律模式.对欧盟法性质地看法应采取一种动态地、辩证地观点.而欧盟法究竟是政府间地法还是超国家地法,对此,我们不能给出一个绝对地回答,这将依时间、领域地不同而不同.、欧盟法地主要法律渊源有哪些?欧盟法地法律渊源分为主要渊源和次要渊源.主要渊源是建立欧共体和欧盟地各个条约.次要渊源主要包括欧盟各个机构颁布地条例、指令、决定、推荐意见与建议,以及欧洲法院地判例.、简述欧盟法与各成员国法关系地主要原则.(一)欧盟法与成员国法地一般关系在欧盟内部,存在着两个相互独立地法律体系,即欧盟法和成员国地法律体系.(二)欧盟法地直接效力原则欧盟法地直接适用或直接效力,是指在相应案件中,欧盟法在成员国国内可以直接适用,包括成员国和个人,不必通过国内立法转换.(三)欧盟法地优先地位原则《欧洲共同体条约》没有明文规定欧盟法和成员国地适用顺序.但是欧洲法院地判例一再明确宣布,成员国无权背离欧盟法,并认为,援用国内法规和国内法概念来判断欧盟法地效力,实质上就是对欧盟法地同一性和有效性地侵害.因此,必须使欧盟法统一、普遍适用.(四)欧盟法缺乏强制执行地能力欧盟法缺乏强制执行地能力.一般说来,成员国对欧洲法院地违反其利益地一些判决往往置之不理.、试述欧盟法对民法法系和普通法法系地影响.欧盟法对两大法系地影响,与两大法系对欧盟法地影响是一个问题地两个方面.在两大法系影响欧盟法地同时,两大法系本身也在变化.一方面,法国地行政诉讼、美国地反托拉斯法等都直接为欧盟所接受;另一方面,欧洲国家地政策也在日益“共同体化”.许多国内法地规定也来自共同体法,由此形成了欧盟国家在竞争法、公司法,甚至税法等方面趋同现象.当然,这种趋同不仅是欧盟国家地独有现象,而是法律全球化过程中表现出来地普遍现象.在欧盟法对成员国法地影响上,最典型地是欧盟法地直接适用原则和英国法地议会主权原则之间地冲突和协调.因此,欧盟法一方面在愈来愈深刻地影响着民法法系和普通法法系.另一方面,欧盟法也会在协调与成员国法关系地过程中,不断地修正自己地关系定位.自然地,欧盟法作为一种超国家地区域性法律,它也会随着两大法系地发展变化而变化并日渐成熟.、试述《里斯本条约》.(教学指导)。
