理论力学之动力学习题答案 北航
北航理论力学复习课件

L,质点M相对管子的相对速度为 vr 。则图示瞬时,质 点M受到管子底部的滑动摩擦力的大小F=______;质 点M相对于管子的相对加速度 ar =____________。
N
A
M F
v Fe r
mar mg N F Fe Fc
A: 平衡力系; B: 力偶; C: 合力; D: 力螺旋。
7
4. 平面运动刚体上三个点A、B、C构成等边三角形,某瞬时 各点加速度或速度的矢量如图所示,则图中______所示的 运动是不可能的。
A: 图(a);
B: 图(b);
C: 图(a)和(b)。
B aB
aA
C aC
A
图(a)
B vB
vA
C vC
A: 一定增加 B: 一定不增加 C: 一定守恒
D: 多种可能,不能确定
17
1. 若刚体绕其中心惯性主轴以匀角速度作定轴转动,则 下列答案正确的有___________。
A: 该刚体的动量为零
B: 该刚体对转轴的动量矩为零;
C: 该刚体的惯性力系等价于零力系; D: 该刚体是动平衡的。
18
2.质量为m的均质圆盘在质量为m的均质板AB上纯滚动, 板放在水平面上。若在板上作用一水平常力 F (如图所 示),系统由静止开始运动。当系统具有动能时,则 __________。
A: 摩擦力向左
B:摩擦力向右 C: 摩擦力大小为零
14
4. 在惯性系中,若质点所受的合力始终指向某一固 定点,则该点可能作_B__C__D__。
4. 若质点的加速度始终垂直于速度(均不为零),则该 点可能作__A__B__C_。
北航空气动力学课后答案(1至9章)

第一章 1.1解:)(k s m 84.259m k R 22328315∙===-RT p ρ=36m kg 63.5063032.5984105RT P =⨯⨯==ρ 气瓶中氧气的重量为354.938.915.0506.63G =⨯⨯==vg ρ1.2解:建立坐标系根据两圆盘之间的液体速度分布量呈线性分布 则离圆盘中心r.距底面为h 处的速度为0u kn u +=当n=0时 u=0推出0u 0= 当n=h 时 u=wr 推出hwr k =则摩擦应力τ为hwr u dn du u ==τ上圆盘半径为r 处的微元对中心的转矩为θθτdrd hwr u r rdrd h wr u r dA d 3=⋅=⋅=T则⎰⎰==T 2D 0332032D u drd hr uωπθωπ1.4解:在高为10000米处T=288.15-0.0065⨯10000=288.15-65=223.15压强为⎪⎭⎫ ⎝⎛=Ta T Pa P 5.2588MKN43.26Ta T pa p 2588.5=⎪⎭⎫ ⎝⎛=密度为2588.5Ta T a ⎪⎭⎫⎝⎛=ρρmkg4127.0Ta T a 2588.5=⎪⎭⎫⎝⎛=∴ρρ1-7解:2M KG 24.464RTPRT p ==∴=ρρ空气的质量为kg 98.662v m ==ρ第二章2-2解流线的微分方程为yx v dyv dx =将v x 和v y 的表达式代入得ydy x dx yx 2dyx y 2dx 22==, 将上式积分得y 2-x 2=c.将(1.7)点代入得c=7因此过点(1.7)的流线方程为y 2-x 2=482-3解:将y 2+2xy=常数两边微分 2ydy+2xdx+2ydx=0整理得ydx+(x+y )dy=0 (1) 将曲线的微分方程yx V dyV dy =代入上式得 yVx+(x+y )V y =0 由22y 2xy 2x V ++=得 V x 2+V y 2=x 2+2xy+y 2 ((2)由(1)(2)得()y v y x v y x =+±=,2-5解:直角坐标系与柱坐标系的转换关系如图所示 速度之间的转换关系为{θθθθθθcos v sin v v sin v cos v v r y r x +=-=由θθθθθθcos r1y v sin yrsin r 1xv cos x rrsin y rcos x =∂∂=∂∂⎪⎩⎪⎨⎧-=∂∂=∂∂⇒⎭⎬⎫==()()⎪⎭⎫⎝⎛--∂∂+-∂∂=∂∂∂∂+∂∂⋅∂∂=∂∂θθθθθθθθθsin r 1sin V cos V cos sin V cos V r x v v x r r v x v r r x x xθθθθθθθθθθθθθsin cos V sin V sin V cos V r 1cos sin r V cos r V r r r ⎪⎭⎫⎝⎛-∂∂--∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂=θθθθθθθθθθθθθθcos sin V r1sin V r 1sin V r 1cos sin V r 1cos sin r V cos r V 22r r 2r +∂∂++∂∂-∂∂-∂∂=()()θθθθθθθθθcos r1cos V sin V sin cos V sin V r y v v V y r V V V V r r y x y xy +∂∂++∂∂=∂∂⋅∂∂+∂∂⋅∂∂=∂∂θθθθθθθθθθθθθcos r1sin V cos V cos V sin V sin cos r V sin r V r r r ⎪⎭⎫ ⎝⎛-∂∂++∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂=θθθθθθθθθθθθθcos sin V r1cos V r 1cos V r 1cos sin v V r 1cos sin r V sin r V 22r r 2r -∂∂++∂∂+∂∂+∂∂=zV V V r 1r V z V y V x V div zr r z y x ∂∂+⎪⎭⎫ ⎝⎛∂∂++∂∂=∂∂+∂∂+∂∂=∴θυθ2-6解:(1)siny x 3x V 2x -=∂∂ siny x 3y V 2y =∂∂ 0y V x V y x =∂∂+∂∂∴此流动满足质量守恒定律(2)siny x 3x V 2x =∂∂ siny x 3y V 2y =∂∂ 0siny x 6yVx V 2y x ≠=∂∂+∂∂ ∴此流动不满足质量守恒定律(3)V x =2rsin rxy 2=θ V y =-2rsin 2ry 22-=θ33r y 2x V x =∂∂ 332y r 2y y x 4y V +-=∂∂ 0ryx 4y V x V 32y x ≠-=∂∂+∂∂∴此流动不满足质量守恒方程(4)对方程x 2+y 2=常数取微分.得xdydy dx -= 由流线方程yx v dy v dx =(1) 由)(得2r k v v r k v 422y 2x =+= 由(1)(2)得方程3x r ky v ±= 3yr kx v = 25x r kxy 3x V =∂∂∴25y r kxy 3y V ±∂∂ 0y Vx V y x =∂∂+∂∂∴此流动满足质量守恒方程2—7解:0x Vz V 0r yz 23r yz 23z V y V z x 2727y z =∂∂-∂∂=⋅+⋅-=∂∂-∂∂同样 0yV x V x y =∂∂-∂∂ ∴该流场无旋()()()2322222223222z y x z y x z y x d 21zy xzdzydy xdx dz v dy v dx v d ++++⋅=++++=++=Φ c zy x 1222+++-=Φ∴2—8解:(1)a x V x x =∂∂=θ a yV y y =∂∂=θ a z Vz z -=∂∂=θ021v ;021v ;021v z y x =⎪⎪⎭⎫ ⎝⎛∂∂+∂∂==⎪⎭⎫ ⎝⎛∂∂+∂∂==⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=y V x V x V z V z V x V x x z x y z (2)0y V x V 210x V z V 210z V y V 21x y z z x y y z x =⎪⎪⎭⎫⎝⎛∂∂-∂∂==⎪⎭⎫ ⎝⎛∂∂-∂∂==⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=ωωω;; 位该流线无旋,存在速度∴ (3)azdz 2aydy ax dx dz v dy v dx v d z y x -+=++=ϕc az ay 21ax 21222+-+=∴ϕ2—9解:曲线x 2y=-4.()04y x y x f 2=+=, 切向单位向量22422422y2x 2y2x yx 4x x y 2yx 4x x f f fx f f fy +-+=+-+=v t ⋅∇=⋅=∇=ϕϕ切向速度分量 把x=2.y=-1代入得()()x 2x y x 2x j yi x 2+-+--=∂∂+∂∂=∇=ϕϕϕ 2121y x 4x 2xy y x 4x x 2242242+=⎪⎪⎭⎫ ⎝⎛+-+= 23t v v t -=⋅= j 23i 23j 21i 2123t v v t t --=⎪⎭⎫⎝⎛+-==2—14解:v=180hkm =50s m根据伯努利方程22V 21V 21p ρρρ+=+∞∞ pa p =∞驻点处v=0.表示为1531.25pa 501.22521V 21pa p 22=⨯⨯==-∞ρ相对流速为60s m 处得表示为75.63760225.12125.1531V 21V 21pa p 222-=⨯⨯-=-=-∞ρρ第三章3—1解:根据叠加原理.流动的流函数为()xyarctg 2Q y V y x πϕ+=∞, 速度分量是22y 22x y x y2Q x V y x x 2Q V y V +⋅=∂∂-=+⋅+=∂∂=∞πϕπϕ; 驻点A 的位置由V AX =0 V Ay =0求得 0y V 2Qx A A =-=∞;π 过驻点的流线方程为2x y arctg 2y x y arctg 2y y Q V Q V A A A =+=+∞πθπ θθππθππsin 2r x y arctg 2y -⋅=⎪⎭⎫ ⎝⎛-=∞∞V V Q 或即 在半无限体上.垂直方向的速度为θπθθππ-sin v r sin 2y x y 2v 222y ∞==+=Q Q 线面求极值()0-sin v -cos sin v 2d dv 22y=+=∞∞θπθθπθθθ 当0sin =θ 0v v min y y ==2-tg -=θπθmax y y v v =用迭代法求解2-tg -=θπθ得 取最小值时,y 1v 2183.1139760315.1 ==θ 取最大值时,y 2v 7817.2463071538.4 ==θ由θπθθππ-sin v r sin 2y x y 2v 222y ∞==+=Q Qθπθθθππ-cos sin v r cos 2v y x x 2v v 22x +=+=++=∞∞∞Q Q 可计算出当∞∞===v 6891574.0v v 724611.0v x y 1,时,θθ6891514.0v v 724611.0v x y 2=-==∞,时,θθ 合速度∞=+=v v v 2y 2x V3—3解:设点源强度为Q.根据叠加原理.流动的函数为 xa 3-y arctg 2a x y arctg 2a x y arctg 2πθπθπθϕ+++-=两个速度分量为()()()⎥⎥⎦⎤⎢⎢⎣⎡+++++++--=222222a 3-y x xy a x a x y a x a x 2x πθ()()()⎥⎥⎦⎤⎢⎢⎣⎡++++++-=222222y a 3-y x a3-y y a x y y a x y 2v πθ对于驻点.0v v y x ==.解得a 33y 0x ==A A ,3—4解:设点源的强度为Q.点涡的强度为T.根据叠加原理得合成流动的位函数为Q ππθϕ2lnr 2Γ+=πθϕπθϕθ2r 1r 12r 1r r Γ=∂∂==∂∂=V V ; 速度与极半径的夹角为Qarctg arctg r Γ==V V θθ3—5根据叠加原理得合成流动的流函数为⎪⎪⎭⎫ ⎝⎛+--+=∞y a y yaarctg a y y aarctg V ϕ 两个速度分量为()()()()⎥⎦⎤⎢⎣⎡++---+++=∂∂=∞1y v 2222x y a x a x a y a x a x a V ϕ ()()⎥⎦⎤⎢⎣⎡+--++=∂∂-=∞2222y y v y a x yy a x y a V ϕ 由驻点()0a 30,得驻点位置为±==y x v v零流线方程为0ay y aarctg a y y x aarctgy =--++∞∞V V 对上式进行改变.得⎪⎭⎫ ⎝⎛-=-+a y tan ay2a y x 222当0x =时.数值求解得a 03065.1y ±=3—9解:根据叠加原理.得合成流动的流函数为a y y arctg 2a y y arctg 2y v -++-=∞ππϕQ Q速度分量为()()2222x y a x ax 2y a x a x 2y v v +-+++++-=∞ππQ Q()()2222y y a x ax 2y a x a x 2v +-+++++-=ππQ Q由0v v y x ==得驻点位置为⎪⎪⎭⎫ ⎝⎛+±∞0v a a 2,πQ 过驻点的流线方程为ay yarctg 2a y y arctg 2y v =-++--∞ππQ Q 上面的流线方程可改写为ay yarctg a y y arctg y v 2--+=∞Q π 222a y x ay2a y y arctg a y y arctg tan y v 2tan -+=⎪⎪⎭⎫ ⎝⎛--+=⎪⎪⎭⎫ ⎝⎛∴∞Qπ 容易看出y=0满足上面方程当0y ≠时.包含驻点的流线方程可写为⎪⎭⎫ ⎝⎛-=-+∞Q y v 2tan ay2a y x 222π当12v a ===∞πQ 时.包含驻点的流线方程为tany y21y x 22--=-+3—10解:偶极子位于原点.正指向和负x 轴夹角为α.其流函数为 22yx x sin ycos 2+--=ααπϕM 当45=α时22y x xy 222+--=πϕM3—11解:圆柱表面上的速度为a2sin v 2v πθΓ--=∞ 222222a 4a 2sin v 4v ππθΓ+Γ=∞ 222222v a 4av 2sin 4sin 4v v ∞∞∞Γ+Γ+=⎪⎪⎭⎫ ⎝⎛ππθθ 压强分布函数为222p v asin 41sin 41v v 1⎪⎪⎭⎫ ⎝⎛Γ+-=⎪⎪⎭⎫ ⎝⎛-=∞∞θπθC第四章4—1解:查表得标准大气的粘性系数为n kg 1078.1u 5-⨯= 65el 1023876.11078.16.030225.1u ⨯=⨯⨯⨯==-∞LV R ρ 平板上下两面所受的总得摩擦阻力为N S V L R F 789.021e 664.0222=⨯⨯=∞ρ 4—2解:沿边阶层的外边界.伯努利方程成立代表逆压梯度代表顺压梯度,时;当时当0m 0m 00m 00m m v v v 21p 12201002〈〉∴〉∂∂〈〈∂∂〉-=-=∂∂-=∂∂=+--xpx p x v x v x v xx p c m m m ρρρρδδδ4—4解:(a )将2x y 21y 23v v ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=δδδ带入(4—90)中的第二式得δδδδδ28039dy vv 1v v 0x x =⎪⎪⎭⎫ ⎝⎛-=⎰** 由牛顿粘性定律δτδu u 23y v u 0y x w =⎪⎪⎭⎫ ⎝⎛∂∂==下面求动量积分关系式.因为是平板附面层0dx dv =∴δ积分关系式可表示为dxd v 2w **=δρτδ 将上述关系式代入积分关系式.得δρδδv dxu d 14013=边界条件为x=0时.0=δ 积分上式.得平板边界层的厚度沿板长的变化规律()64.428039646.0x x x64.4ll ⨯==∴=**R R δδ(b )()74.164.483x x 83dy v v 1lx =⨯=∴=⎪⎪⎭⎫ ⎝⎛-=*∞*⎰R δδδδ(c )由(a )知()64.4x x l =R δ(d )646.0x x646.0v 21324xx 64.4u23l f l 2wf l w =∴====R C R C R δρτδδδτ)得—由(; (e )单面平板的摩擦阻力为()292.1x x 292.1s v 21b bdx v 21l f l 2f l02f=∴===⎰R C R X C C X F F δδρρ摩阻系数为假设版宽为4—6解:全部为层流时的附面层流厚度由式(4—92)得 ()01918.048.5L e ==LR L δ全部为湍流时的附面层流厚度由式(4—10)得()0817.037.0L 51e ==-L LR δ第五章5-1 一架低速飞机的平直机翼采用NACA2415翼型.问此翼型的f .f x 和c 各是多少?解:此翼型的最大弯度f =2% 最大弯度位置f x =40% 最大厚度c =15%5-2 有一个小α下的平板翼型.作为近似.将其上的涡集中在41弦点上.见图。
北航《理论力学(第二学期)》考题整理

A
(a)
B
A
(b)
B
A:情况(a)时 AB 杆的角加速度大; B:情况(b)时 AB 杆的角加速度大; C:条件不足,不能确定。 二、 填空题(第 8 小题 5 分,其余每空 4 分,共 65 分, 将计算的最简结果填写在 空格上) 1、定轴转动刚体绕 O 轴在铅垂面内运动,若其质量为 2m,对转轴的转动惯量为 J, 质心到转轴的距离 OC=b,根据系统的广义坐标 (如图 3 所示) , 建立其运动微分方 程。答:运动微分方程为: 2、匀 质 三 角 板 用 圆 柱 铰 链 与 铅 垂 的 AB 杆 和 CD 杆 连 接 , 如 图 4 所 示 。 已 知
=
O
。
已知图示瞬时刚体的角速度为 (方向由 O 点指向 A B 点) ,角加速度为 (方向由 O 点指向 B 点) 。求正
4
A
图7
北京航空航天大学交通科学与工程学院《理论力学(第二学期) 》复习资料
方体上顶点 B 速度 vB 和加速度 aB 。 答:
B 点速度的大小 vB = B 点加速度的大小 aB =
4、两个相同的均质杆 AC、BC(各质量均为 m 长为 L)由铰链 C 连接在图示平面内 运动,已知图示瞬时铰链 C 的速度大小为u,杆的角速度的大小为ω,方向如图 3A-D 所示,则该瞬时图 3_______所示情况,系统得动能最大。
AB=2L,CD=AC=L,各刚体的质量分别为 m1 , m2 , m3 ,若图示瞬时 AB 杆
3
北京航空航天大学交通科学与工程学院《理论力学(第二学期) 》复习资料
的角速度为 (方向如图)。该瞬时系统动量的大小 P=
。
B
O
m2
D
北航2021年 第二学期 理论力学复习题

北航2021年第二学期理论力学复习题北航2021年第二学期理论力学复习题理论力学的学习练习和参考解答一、填空题1.把一个质量为m的小球扔到中面上,阻力R??如果坐标轴X垂直向上,小球的运动微分方程为。
2.质点在运动过程中,在下列条件下,各作何种运动?①at?0,an?0(答):;②at?0,an?0(答):;③at?0,an?0(答):;④at?0,an?0(答):。
3.质量为10kg的粒子在水平力F的作用下在光滑的水平面上移动,设置F?3.4T(tin s,f in n),初始时刻(t×10)的粒子位于坐标原点,其初始速度为零。
那么t?在3S时,粒子的位移等于,速度等于。
4.在平面极坐标系中,质点的径向加速度为__________;横向加速度为_______。
5.哈密顿正则方程用泊松括号表示为,。
6.质量m?2kg的重物m,挂在长l?0.5m的细绳下端,重物受到水平冲击后获得了速度v0?5m?s?1,则此时绳子的拉力等于。
7.平面自然坐标系中的切向加速度为,法向加速度为。
8.如果fv,则力所作的功与无关,只与的位置有关。
南半球在地面附近有一股向南的气流;北半球的河岸侵蚀更为严重。
10.已知力的表达式为fx?axy,则该力做功与路径_(填fy??az,fz??ax。
“有关”或“无关”),该力_保守力(填“是”或“不是”)。
11.一个质量群由三个质量分别为M0、2m0和3m0的粒子组成,它们在某一时刻的位矢和速度22度分别为r1?i?j、v1?2i、r2?j?k、v2?i、r3?k、v3?我Jk、然后是粒子群相对于坐标原点的动量于,相对于坐标原点的动量矩等于_。
12.在光滑的水平直管中有一个质量为m的小球,直管以恒定的角速度运动?绕穿过管道一端的垂直轴旋转,如果在某个时间球zoyapvxm1到达点P,与点O保持一定距离,沿管取x轴,y轴垂直向上并垂直于管,z轴水平向前并垂直于管表面,如图所示。
理论力学之静力学习题答案北航
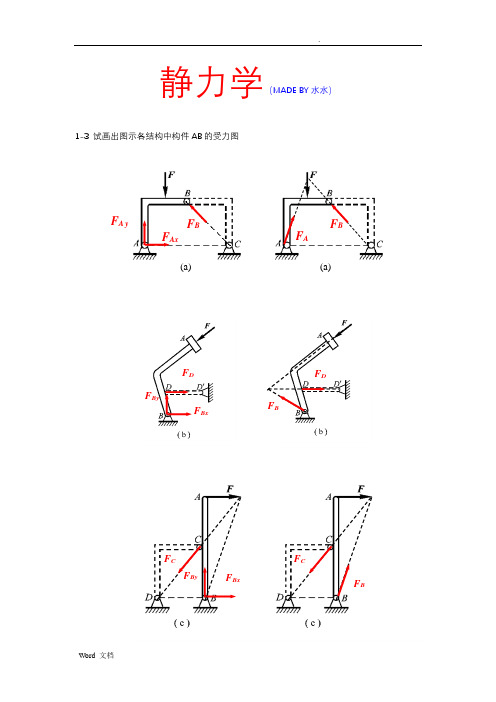
静力学(MADE BY 水水)1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5aF AxF A yF DF ByF A F BxF B F AF Ax F A yT E F CxF C yN’F BF DF A N F AF BF D1-5b1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==F 2F BC F ABB45oy xF CD C60o F 130oF BCx y45030解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F Aθ aM F A 354.0= 其中:31tan =θ。
理论力学之静力学习题答案北航

1-3 试画出图示各结构中构件AB 的受力图1-4 试画出两结构中构件ABCD 的受力图F AxF A yF B(a)(a)F DFBxF ByF AxF A yF ByF AF BxF A1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5b1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
F AxF A y F DxF DyWT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF BxF ByT EN’F BF DF A NF AF BF D解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:对C 点有:解以上二个方程可得:解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:对C 点由几何关系可知:解以上两式可得:2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):F ABF CDF BF C其中:。
对BC 杆有:。
A ,C 两点约束力的方向如图所示。
2-4四连杆机构在图示位置平衡,已知OA=60cm,BC=40cm,作用在BC 上力偶的力偶矩M 2=1N ·m 。
试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力。
理论力学之静力学习题答案北航

理论力学之静力学习题答案北航静力学(MADE BY水水)1-3 AB的受力图试画出图示各结构中构件FF A BB F A A(a)(a)FF DD F By F B F BxFF CC FF By Bx F B的受力图1-4 试画出两结构中构件ABCDFF AAFF A y FF By BAx F Bx F Dba和所示刚体系整体合格构件的受力图1-5 试画出图F1-5a A F B F DN'F F B A N F DFT C yE F y AFF Cx Ax1-5b F DyF Dx W WF T Bx E F Ax FFF B y Cx y A F Dy F By F Bx F C y F Dx1-8在四连杆机构的ABCD的铰链B和C上分别作用有力F和F,机构在图示位置平衡。
试21求二力F和F之间的关系。
21解:杆AB,BC,CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B和C为研究对象,受力如图所示:由共点力系平衡方程,对B点有:对C点有:解以上二个方程可得:y yF BC B C x F BC o45x o30F o60CD F2F F AB12(解法几何法)点上的力构成封闭C和为研究对象,和分别选取销钉BC根据汇交力系平衡条件,作用在B的力多边形,如图所示。
点由几何关系可知:对B F F2BC点由几何关系可知:对C o30o45F AB o60F F CD1解以上两式可得:F BC点处的约束。
试求M上作用有主动力偶在图示结构中,二曲杆重不计,曲杆2-3 ABA和C力。
两点连线的BC点处受到约束力的方向沿B在AB)受力如图所示(为二力杆BC解:,故曲杆点处的约束力必须构成一个力偶才能使曲A的作用,M受到主动力偶AB方向。
曲杆点和B F B(设力偶逆时针为正):保持平衡。
AB受力如图所示,由力偶系作用下刚体的平衡方程有杆ABF BF C。
北京航空航天大学本科理论力学习题课动.ppt

dvr dvr dR dt dR dt
dR dt
vr
cos
mvr
cos
dvr dR
mR 2
cos
vrdvr R2dR
v2 r
2R2
C
22
aa 0, ae 2R, aC 2 vr
x': 0 ae arx' aC cos450 y': 0 0 ary' aC sin 450
ar
a2 rx '
a2 ry '
12
习题1-10:求滑块A的加速度绳索的拉力。
v0
s FvA
FN
mg
ma F FN mg
x : mx F cos mg
x
(
x2
2R4x R2)2
mx Fx
15
y’
方法三:求滑块的速度
动点:滑块A
vr
动系:ox’y’,x’轴平行于绳
速度分析
θ
运动分析
va v x’ e
绝对运动: 直线运动 相对运动: 直线运动 牵连运动: 定轴转动
va ve vr ve x vr ( )R
y : 0 ve vr sin x : x va vr cos
动点:圆盘中心O 动系:AB杆
A
AB
运动分析: 绝对运动: 直线运动
v r 300 n ae
相对运动: 直线运动 AB 牵连运动: 定轴转动
y'
aa
o ve Rar va
aB et
速度分析
vr 0,
va ve vr va ve
AB
ve OA
va 2R
加速度分析 aa aet aen ar aC
北航空气动力学期末考试题及答案

北航空气动力学期末考试题及答案一、选择题(每题2分,共10分)1. 以下哪项不是流体的基本属性?A. 质量B. 温度C. 密度D. 粘性答案:A2. 流体静压与流体的哪个物理量无关?A. 密度B. 重力加速度C. 速度D. 高度答案:C3. 流体流动中,流线与等速线的关系是什么?A. 流线与等速线重合B. 流线与等速线垂直C. 流线与等速线平行D. 流线与等速线相交答案:B4. 根据伯努利方程,流体流速增加时,其压力如何变化?A. 增加B. 减少C. 保持不变D. 先增加后减少答案:B5. 马赫数是如何定义的?A. 速度与声速的比值B. 速度与光速的比值C. 速度与重力加速度的比值D. 速度与流体密度的比值答案:A二、填空题(每题2分,共10分)1. 流体的连续性方程表明,在不可压缩流体中,流速与截面积成________关系。
答案:反比2. 当流体的雷诺数小于2300时,流体流动处于________状态。
答案:层流3. 在流体力学中,马赫锥是用于描述________现象的几何图形。
答案:激波4. 根据牛顿第二定律,作用在流体上的力等于流体质量与________的乘积。
答案:加速度5. 流体的粘性系数μ与流体的________成正比。
答案:温度三、简答题(每题10分,共20分)1. 简述流体的粘性对流动的影响。
答案:流体的粘性对流动的影响主要体现在边界层的形成和流动的阻力上。
粘性较大的流体在流动时会在固体表面附近形成边界层,边界层内流体速度梯度较大,导致能量损失和阻力增加。
同时,粘性还会影响流体的层流和湍流状态,粘性较大的流体更容易维持层流状态,而粘性较小的流体则容易形成湍流。
2. 描述伯努利方程的物理意义及其在航空中的应用。
答案:伯努利方程描述了流体在流动过程中能量守恒的物理现象,即流体的总能量(包括动能、势能和压力能)在流动过程中保持不变。
在航空中,伯努利方程被用于解释和计算飞机机翼的升力。
根据伯努利方程,机翼上方的流速快于下方,导致上方压力低于下方,从而产生升力。
理论力学之静力学习题答案北航

理论力学之静力学习题答案北航(总27页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除静力学(MADE BY 水水)1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF DF BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5aF AxF A yF DF ByF AF BxF BF AF AxF A y F DyT EF CxF C yN’F BF DF A N F AF BF D1-5b1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==F 2F BC F ABB45oy xF CD C60o F 130oF BCxy45030解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
北航 理论力学习题课(习题)

F1
D:力螺旋
F2
2
BUAA
题5:空间汇交力系的平衡方程独立的充分必要条件:
⎧ ∑ Fx = 0 ⎪ ⎨∑ Fy = 0 ⎪ ⎩ ∑ Fz = 0
A:三个轴正交; B:三轴不共面; C:三轴相交不共面; D:三轴的单位向量不相关
题6:空间汇交力系的平衡方程能否用取矩式给出? 题7:给出空间汇交力系的平衡方程的三矩式:
M P
问题:摩擦因数大于1的值为什么不是该题的解?
2009-10-14
18
BUAA
题24:已知 WA, a,b,f。求平衡时, WBmax
a
A
a
WA
b f 为板与圆盘间的静滑动摩擦因数
O
WB
2009-10-14 19
BUAA
题25: 系统在图示位置平衡,已知F, M, a..如何求A, B处的约束力
z
FR
F1
o
F2
y
⎧ ∑ M l1 = 0 ⎪ ⎨ ∑ M l2 = 0 ⎪ ⎩ ∑ M l3 = 0
确定三根轴的位置
3
x
2009-10-14
Fn
BUAA
题8:给出空间平行力系平衡方程的三矩式
z
Fi
o x
y
⎧∑ M x = 0 ⎪ ⎨∑ M y = 0 ⎪ ⎩∑ M L = 0
如何确定L轴?
2009-10-14
3
| F 2 + F 3 |=
M 2
b
a
1
不计自重
2009-10-14 14
BUAA
题19:确定图示结构
BUAA
题20: 正方体的边长为a,作用有力系如图所示,其中三个力的 大小为F,两个力偶矩的大小为M=Fa,方向如图。若使该立方体 平衡,只需在其上施加一个力即可。则在Oxyz坐标系中:
北航2021年 第二学期 理论力学复习题

北航2021年第二学期理论力学复习题北航2021年第二学期理论力学复习题《理论力学》课程学习练习题及参考解答一、填空题1.在介质中上抛一质量为m的小球,已知小球所受阻力r??kv,若选择坐标轴x铅直向上,则小球的运动微分方程为_____________________。
2.质点在运动过程中,在以下条件下,各并作何种运动?①at?0,an?0(请问):;②at?0,an?0(请问):;③at?0,an?0(请问):;④at?0,an?0(请问):。
3.质量为10kg的质点,受水平力f的作用,在光滑水平面上运动,设f?3?4t(t以s 计,f以n计),初瞬间(t?0)质点位于坐标原点,且其初速度为零。
则t?3s时,质点的位移等于_______________,速度等于_______________。
4.在平面极坐标系中,质点的径向加速度为__________;纵向加速度为_______。
5.哈密顿正则方程用泊松括号则表示为,。
6.质量m?2kg的重物m,摆在长l?0.5m的细绳下端,重物受水平冲击后赢得了速度v0?5m?s?1,则此时绳子的拉力等同于。
7.平面自然坐标系中的切向加速度为,法向加速度为。
8.如果fv,则力所作的功与毫无关系,只与的边线有关。
9.在南半球地面附近自南向北的气流有朝的偏向;而北半球的河流岸冲刷较为严重。
10.未知力的表达式为fx?axy,则该力作功与路径_(填上fy??az,fz??ax。
“有关”或“毫无关系”),该力_保守力(填上“就是”或“不是”)。
11.一质量组由质量分别为m0、2m0、3m0的三个质点组成,某时刻它们的位矢和速22度分别为r1?i?j、v1?2i、r2?j?k、v2?i、r3?k、v3?i?j?k。
则该时刻质点组相对于坐标原点的动量等于,相对于座标原点的动量矩等同于_。
12.一光滑水平直管中有一质量为m的小球,直管以恒定角速度?绕通过管子一端的竖直轴转动,若某一时刻,小球zoyapvxm1到达距o点的距离为a的p点,取x轴沿管,y轴竖直向上,并垂直于管,z轴水平向前,并于管面垂直,如图所示,此时小球相对于管子的速度为v,则惯性离心力大小为,方向为,科里奥利力大小为,方向为。
北航空气动力学课后答案(1至9章)-精选.pdf

3 vt vtt
2
31
1
i
j
22
2
33 ij
22
2—14 解: v=180 km
=50 m
h
s
根据伯努利方程 p
1
2
V
2
1
2
V
2
p pa
驻点处 v=0,表示为 p pa
1
2
V
2
1 1.225
50 2
1531.25pa
2
相对流速为 60 m s 处得表
示为 p pa
1
2
V
2
1
2
V
2
1531 .25
1
u kn u 0
当 n=0 时
u=0 推出
u 0
0
当 n=h 时 u=wr 推出 k wr
h
则摩擦应力 为
du
wr
u
u
dn
h
上圆盘半径为 r 处的微元对中心的转矩为
3
wr
wr
d
dA r u rdrd r u
drd
h
h
D
3
则
2
2u
r drd
0
0
h
3
uD 32
1.4 解:在高为 10000 米处 T=288.15-0.0065 10000=288.15-65=223.15
V yA
arctg y A Q
2
x
2
xA 2
Q 即y
2V
y arctg 或 r
x
2 V sin
在半无限体上,垂直方向的速度为 v y
Qy
2
2
北航空气动力考试及答案

北航空气动力考试及答案一、单项选择题(每题2分,共20分)1. 空气动力学的研究对象是什么?A. 流体力学B. 固体力学C. 空气动力学D. 热力学答案:C2. 以下哪个不是空气动力学的基本原理?A. 连续性方程B. 动量方程C. 能量方程D. 牛顿第二定律答案:D3. 以下哪个参数是空气动力学中不需要考虑的?A. 速度B. 压力C. 温度D. 重力加速度答案:D4. 以下哪个参数是空气动力学中需要考虑的?A. 密度B. 温度C. 湿度D. 颜色答案:A5. 以下哪个不是空气动力学中的流动类型?A. 层流B. 湍流C. 涡流D. 固体流答案:D6. 以下哪个是空气动力学中的流动类型?A. 层流B. 湍流C. 涡流D. 以上都是答案:D7. 以下哪个参数是空气动力学中不需要考虑的?A. 速度B. 压力C. 温度D. 颜色答案:D8. 以下哪个参数是空气动力学中需要考虑的?A. 密度B. 温度C. 湿度D. 以上都是答案:D9. 以下哪个不是空气动力学的基本原理?A. 连续性方程B. 动量方程C. 能量方程D. 牛顿第三定律答案:D10. 以下哪个是空气动力学的基本原理?A. 连续性方程B. 动量方程C. 能量方程D. 以上都是答案:D二、多项选择题(每题3分,共15分)1. 空气动力学的研究对象包括以下哪些?A. 流体力学B. 固体力学C. 空气动力学D. 热力学答案:ACD2. 以下哪些是空气动力学的基本原理?A. 连续性方程B. 动量方程C. 能量方程D. 牛顿第二定律答案:ABC3. 以下哪些参数是空气动力学中需要考虑的?A. 速度B. 压力C. 温度D. 湿度答案:ABC4. 以下哪些是空气动力学中的流动类型?A. 层流B. 湍流C. 涡流D. 固体流答案:ABC5. 以下哪些参数是空气动力学中不需要考虑的?A. 速度B. 压力C. 温度D. 颜色答案:D三、填空题(每题2分,共20分)1. 空气动力学是研究______在流体中的运动规律的科学。
北航7系理论力学d-ch6F

e I
vBr 2vr
I 20
ar a N aR r ( r rAB ) r rAB 2 aN r2 r 40 r r v r r 0 20 0 .5 r 0 .5 r 2 aR r r 40 r v 2 r r r 40 2 2 0 .5 r aa (ae aR aK ) 2 aN 2 50 r αr ωr ωr 2 2 4 2 r r r 0 16 2013-11-2 2
2013-11-2
15
BUAA
rOA ae
刚体定点运动与点的复合运动的应用 解:取B点为动点,圆盘I为动系
用复合运动方法分析 aR aK vr ro
I a N
r
aa ae a K a r
2 ae 0 (0 rOA ) ae 2r0
aK 2e v Br
2013-11-2
ω , ω ?
13
BUAA
vr ro
刚体一般运动习题
习题6-7:已知 vr 和 ω 0 ,求该瞬时B 点的绝对加速度。
I
rOA
解:取ABC圆锥为研究对象
r 运动分析:
ABC圆锥作刚体一般运动
a B a A a (a rAB ) rAB a A o (o rOA )
x
BUAA
z A’
思考题:将OAB一次转动后到OA’B’
A( 0, 450 , 900 ) 0 1 0 cos 450 0 sin 450 cos 90 0 sin 45 sin 900 cos 450 0 0
0
sin 900 cos 900 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动力学(MADE BY水水)
1-3 解: 运动方程:tanly,其中kt。
将运动方程对时间求导并将030代入得
34coscos22lklklyv
938cossin2232lklkya
1-6 证明:质点做曲线运动, 所以质点的加速度为:ntaaa,
设质点的速度为v,由图可知: aavvyncos
,所以: yvvaan
将cvy,2nva 代入上式可得 cva3 证毕 1-7
证明:因为n2av,vaavasinn
所以:va3v 证毕
1-10
x y o a
na
v yv
ta y z
o a
na
x 解:设初始时,绳索AB的长度为L,时刻t时的长度 为s,则有关系式:
tvLs0,并且 222xls
将上面两式对时间求导得: 0vs,xxss22
由此解得:xsvx0 (a) (a)式可写成:svxx0,将该式对时间求导得:
2002vvsxxx
(b)
将(a)式代入(b)式可得:3
220220
x
lvxxvxax
(负号说明滑块A的加速度向上)
取套筒A为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有: gFFammN 将该式在yx,轴上投影可得直角坐标形式的运动微分方程:
NFFymFmgxmsincos
其中: 2222sin,coslxllxx0,3220yxlvx
将其代入直角坐标形式的运动微分方程可得: 23
220)(1)(xlxlvgmF
1-11
ov ov F NF
gm
y
A x
O
Av
A
x
O
Bv B
R 解:设B点是绳子AB与圆盘的切点,由于绳子相对圆盘无滑动,所以RvB,由于绳子始终处于拉直状态,因此绳子上A、B两点的速度在 A、B两点连线上的投影相等,即:
cosABvv
(a)
因为
xRx22cos (b) 将上式代入(a)式得到A点速度的大小为:
22RxxRvA (c) 由于xvA
,(c)式可写成:RxRxx22,将该式两边平方可得:
222222)(xRRxx
将上式两边对时间求导可得: xxRxxRxxx2232222)(2 将上式消去x2后,可求得: 22242)(RxxRx
(d)
由上式可知滑块A的加速度方向向左,其大小为 22242)(RxxRaA
取套筒A为研究对象,受力如图所示, 根据质点矢量形式的运动微分方程有: gFFammN 将该式在yx,轴上投影可得直角坐标形式的 运动微分方程:
mgFFymFxmNsincos
其中:
x Av A
O
NF B
R gm
F
y xRxxR22cos,sin
, 0,)(22242yRxxRx
将其代入直角坐标形式的运动微分方程可得
2525)(,)(225222242RxxRmmgFRxxRmFN
1-13 解:动点:套筒A;
动系:OC杆; 定系:机座; 运动分析: 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理
reavvv 有:eacosvv,因为AB杆平动,所以vva,
由此可得:ecosvv,OC杆的角速度为OAve,coslOA,所以 lv2cos
当045时,OC杆上C点速度的大小为: lavlavavC245cos02
1-15 解:动点:销子M
动系1:圆盘 动系2:OA杆 定系:机座; 运动分析:
av ev
rv
e1v e2v r2v
r1v
x 绝对运动:曲线运动 相对运动:直线运动 牵连运动:定轴转动 根据速度合成定理有
r1e1a1vvv, r2e2a2vvv
由于动点M的绝对速度与动系的选取无关,即a1a2vv,由上两式可得:
r1e1vvr2e2vv (a)
将(a)式在向在x轴投影,可得: 0r20e20e130cos30sin30sinvvv
由此解得: smbOMvvv/4.0)93(30cos30sin)(30tan)(30tan020120e1e20r2
32.02e2OMv smvvvvM/529.022r2e2a2
1-17 解:动点:圆盘上的C点;
动系:O1A杆; 定系:机座; 运动分析:绝对运动:圆周运动; 相对运动:直线运动(平行于O1A杆); 牵连运动:定轴转动。 根据速度合成定理有
reavvv (a)
将(a)式在垂直于O1A杆的轴上投影以及在O1C轴上投影得: 0e0a30cos30cosvv
,0r0a30sin30sinvv
av ev rv Rvv
ae,Rvvra,5.02O1e1RRCv
根据加速度合成定理有
Caaaaarnetea (b)
将(b)式在垂直于O1A杆的轴上投影得
Caaaa0ne0te0a30sin30cos30sin
其中:2aRa,21ne2Ra,r12vaC 由上式解得:2te11232Ra
1-19 解:由于ABM弯杆平移,所以有
MAMA,aavv 取:动点:滑块M; 动系:OC摇杆; 定系:机座; 运动分析: 绝对运动:圆周运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理
reavvv 可求得: m/s2222eabvvvvAM,m/s2erbvv,
rad/s3245.12211AO
vA
根据加速度合成定理
aa tea
nea
ra Ca
av ev rv
nea
tea Caaaaaarnetenata 将上式沿Ca方向投影可得: Caaaate0na0ta45sin45cos 由于221nam/s316la,2tem/s1ba,2rm/s82vaC,根据上式可得:
2ta231527316s/m.a
, 2ta1rad/s1610.la
1-20 解:取小环M为动点,OAB杆为动系
运动分析 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 由运动分析可知点的绝对速度、相对速度和牵连速度的方向如图所示, 其中: rrOMv260cos0e
根据速度合成定理:
reavvv 可以得到:
rrvv3260tan2tan0ea
,rvv460cos0er
加速度如图所示,其中: 2022e260cosrrOMa
, 2r82rvaC 根据加速度合成定理: Caaaarea naa ra taa Ca av M O A B rv ev 'x Ca aa
M
O
A
B ra
ea
