概率论与数理统计第三章课件

合集下载

概率论与数理统计课件第三章ppt

Y X
y1
y2
...
yj
… pi·
x1 p11 p12 … p1 … p1·
x... 2 p... 21 x... i p... i1
p· p·1
p... 22 p... i2
p·2
…j
… p2
… j...
… …
p...pi·jj
… … … …
…
p... 2· p... i ·
1
j
例1.设袋中有五个同类产品，其中有两个是次品，每次从袋中任意抽取一个，
设(X,Y)为连续型随机变量，其联合分布函数和联合概率密度分别为F(x,y)和 f(x,y),则
f X
(x)
d dx
FX
(x)
f (x, y)dy
fY
( y)
d dy
FY
(
y)
f
(x,
y)dx
分别称为(X,Y)关于X和Y的边缘概率密度
函数，简称边缘概率密度。
例2. 设(X,Y)的分布密度是
e(xy) , x 0, y 0
3.1
例1.甲乙掷色子,观察点数。
w1i={甲掷i点} w2j={乙掷j点}
X,Y (i, j)
i,j=(1,2,…,6)
二维随机变量的定义
对于随机试验E，Ω是其样本空间。X(w) 和 Y(w)是定义在样本空间Ω上的两个随机变量, 由它们构成的向量(X,Y)称为二维随机变量或二维随机向量。
y
w.
Y X
y1
y2
...
yj
…
x1 p11 p12 x... 2 p... 21 p... 22
x... i p... i1 p... i2

概率论与数理统计第三章PPT

乘法公式应用举例（波里亚罐子模型）
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地抽取一个球，观看颜色后放回罐中，并且再加进c个与所抽出的球具有相同颜色的球. 这种手续进行四次，试求第一、二次取到白球且第三、四次取到红球的概率.
随机取一个球，观看颜色后放回罐中，并且再加进c个与所抽出的球具有相同颜色的球. b个白球, r个红球
解: 设Wi={第i次取出是白球}, i=1,2,3,4 Rj={第j次取出是红球}， j=1,2,3,4 于是W1W2R3R4表示事件“连续取四个球，第一、第二个是白球，第三、四个是红球. ”
用乘法公式容易求出 P(W1W2R3R4) =P(W1)P(W2|W1)P(R3|W1W2)P(R4|W1W2R3)
用它们可计算两个事件同时发生的概率
(3)
注意P(AB)与P(A | B)的区别！
请看下面的例子
例甲、乙两厂共同生产1000个零件，其中300件是乙厂生产的. 而在这300个零件中，有189个是标准件，现从这1000个零件中任取一个，问这个零件是乙厂生产的标准件的概率是多少？
设B={零件是乙厂生产}
P A 4 10 0.4
4 3 12 10 9 90 6 4 24 P AB P A P B | A 10 10 90 P AB P A P B | A
P16例4

P ABC P A P B | A P C | AB
二、乘法法则 P ( AB) 由条件概率的定义： P ( A | B)
P ( B)
若已知P(B), P(A|B)时, 可以反求P(AB). 即若P(B)>0,则P(AB)=P(B)P(A|B) (2) 将A、B的位置对调，有 (2)和(3)式都称为乘法公式, 利若 P(A)>0, 则P(BA)=P(A)P(B|A) 而 P(AB)=P(BA) 故若P(A)>0,则P(AB)=P(A)P(B|A)

概率论与数理统计课件第三章

f
(x,
y)
1
21 2
1
2
exp
1
2(1 2 )
(x
1)2
2 1
2
(x
1)( y 1 2
2 )
(y
2)2
2 2
其中1、2、1、 2、都是常数，且1 0， 2 0，1 1.
则称（X,Y）服从参数为1、2、1、的二2、维正态分布，
记为
(X
,Y)
~
N (1,
2
,
2 1
,
2 2
2F(x, y) f (x, y) xy
(5)若(X,Y)为二维连续型随机向量,联合概率密度为f(x,y),则
F(x,y) P{X x,Y y}
返回
X
18
第
页
例5 设二维随机变量（X,Y）的概率密度为
Ae2(x y) , x 0, y 0
f (x, y)
0, 其他
（1）确定常数A；
分别为(X,Y)关于X和Y的边缘分布函数.
返回
X
25
第
页
例1 设二维随机向量（X,Y）的联合分布函数为
(1 e2x )(1 e3y ), x 0, y 0,
F(x, y)
0, 其他.
求边缘分布 FX (x), FY ( y)
当x
0时，FX
(x)
lim (1
y
e2 x
)(1
e3 y
)
1
e2 x
返回
X
14
第
例3 设随机变量Y~N(0，1),令
0, X 1 1,
| Y | 1
0,
|Y
|

概率论与数理统计(浙大版)第三章PPT参考课件

X,Y的边缘分布律为：

记为
P(Y y j ) P( X ，Y y j ) pij == pgj j 1, 2,L
i 1

记为
P( X xi ) P( X xi，Y ) pij == pig i 1, 2,L
j 1
注意：
X Y y1
(1) 0 pij 1
(2) pij 1
ij
2020/2/15
(2)表格法
X Y y1 y2 y3
x1 p11 p12 p13 x2 p21 p22 p23
(X,Y)的概率分布表：描述(X,Y)的取值规律
P((X ,Y ) G)
pij
( xi , yj )G

1 2
4 x(1
2x)dx

1

1

1
0
23 6
2020/2/15
21
§2 边缘分布
二维随机变量(X,Y)作为整体，有分布函数
其中X和Y都是随机变量，它们的分布函数
记为：
称为边缘分布函数。
FX (x)，FY ( y)，
F(x, y),
FX (x) F(x, )
事实上，
FY ( y) F(, y)
i 1,2, , m, ; j 1,2, , n,
中心问题：(X,Y)取这些可能值的概率分别为多少？
2020/2/15
二维（X，Y）的联合分布律:
(1)公式法
p( xi , yj ) P( X xi ,Y yj ) pij
pij的性质：
(i, j 1,2, )

p2 p2 j

第三章概率论与数理统计教程课件

例2. 设r.v.X服从泊松分布，求其 D(X)
3 - 17
方差的性质定理
(1) D(c)=0;
(2) D(aX)=a2D(X)
(3) D(X+b)=D(X)

(4)D(aX+b)=a2D(X)
(5)两个独立随机变量 X 1 , X 2
D( X 1 X 2 ) D( X 1 ) D( X 2 )
例题
1 设随机变量X~P(2), 则E(X)=( D(X)= ( ), E(X2)=( ) ),
2 若随机变量X~B(n, p), 已知E(X)=2.4， D(X)=1.44, 则n=( ), p=( )
3 若随机变量X~U(a, b), 已知E(X)=2.4， D(X)=3, 则a=( ), b=( )
(如甲进行很多次射击, 其得分的平均分为1.8) 而乙的得分为 E(X2)=00.6+1 0.3+2 0.1=0.5 显然,乙的成绩比甲的差.
3-5
连续随机变量的数学期望
设X是连续型随机变量，其密度函数为f（x），如果
积分 xf ( x)dx 绝对收敛，即

x f ( x)dx
1 f ( x) , x 2 (1 x )
求X的数学期望。
3-7
二维随机变量的数学期望
离散r.v.
E( X ) x i p( x i , y j )
i j
E( X ) xi p X ( xi )
i
E (Y ) y j p( x i , y j )
3 - 21
§3.6 原点矩与中心矩
(1) 若E(Xk), k=1, 2, …存在, 则称它为X k 的k阶原点矩. 记作 k E( X )

概率论与数理统计第四版第三章PPT课件

例2 设二维连续型随机变量( X , Y )具有概率密
度为：
ke(2x3y) x0,y0
f(x,y) 0
其它
1. 求常数 k ;
2. 求 F( x , y ) ;
3. 求 P{ X < Y }
休息结束
解： 1. 求常数 k ;
y

ke(2x3y) x0,y0
f(x,y)
0
其它
x
Q f(u ,v)du dvF ( , )1
3) P{(X,Y)G} f (u,v)dudv G y
(X,Y)
G
x
休息结束
4) 若 f ( x , y ) 在 ( x , y ) 处连续，则有：
2F( x, y) f( x, y)
xy
以上关于二维随机变量的讨论，可以容易地推广到 n ( n > 2 )维随机变量的情况。
休息结束
第三章多维随机变量及其分布
休息结束
§3.1 二维随机变量
到现在为止，我们只讨论了一维随机变量及其分布。但有些随机现象用一个随机变量来描述还不够，而需要用几个随机变量来描述。
休息结束
在射箭时,命中点的位
置是由一对坐标( X, Y )来
确定的。
飞机的重心在空中的位置是
由三个随机变量( X，Y，Z ）来
休息结束
F(x2,y2)F(x1,y2)(F (x2,y1)F (x1,y1))
P{(X,Y)D} 0
y
( x1 , y2 ) ( x2 , y2 )
D
( x1 , y1 )
( x2 , y1 )
x
休息结束
二维离散型随机变量的联合分布列设二维离散型随机变量( X , Y )所有可

概率论与数理统计ppt课件

称这种试验为等可能概型(或古典概型)。
*
例1：一袋中有8个球，其中3个为红球，5个为黄球，设摸到每一球的可能性相等，从袋中不放回摸两球，记A={恰是一红一黄}，求P(A)．解：
（注：当L>m或L<0时，记）
例2：有N件产品，其中D件是次品，从中不放回的取n件，记Ak＝{恰有k件次品}，求P(Ak)．解：
*
第四章随机变量的数字特征 4.1 数学期望 4.2 方差 4.3 协方差及相关系数 4.4 矩、协方差矩阵第五章大数定律和中心极限定理 5.1 大数定律 5.2 中心极限定理第六章数理统计的基本概念 6.1 总体和样本 6.2 常用的分布
*
第七章参数估计 7.1 参数的点估计 7.2 估计量的评选标准 7.3 区间估计第八章假设检验 8.1 假设检验 8.2 正态总体均值的假设检验 8.3 正态总体方差的假设检验 8.4 置信区间与假设检验之间的关系 8.5 样本容量的选取 8.6 分布拟合检验 8.7 秩和检验第九章方差分析及回归分析 9.1 单因素试验的方差分析 9.2 双因素试验的方差分析 9.3 一元线性回归 9.4 多元线性回归
解：设 Ai={ 这人第i次通过考核 }，i=1,2,3 A={ 这人通过考核 }，
亦可：
*
例：从52张牌中任取2张，采用(1)放回抽样，（2）不放回抽样，求恰是“一红一黑”的概率。
利用乘法公式
与不相容
（1）若为放回抽样：
（2）若为不放回抽样：
解：设 Ai={第i次取到红牌}，i=1,2 B={取2张恰是一红一黑}
①
②
①
1 2 N
①
②
1 2 N
……

概率论与数理统计ppt课件(完整版)

*
几何概型的概率的性质
对任一事件A ,有
三.统计定义:
(一) 频率
在相同的条件下, 共进行了n次试验,事件A发生的次数nA, 称为A的频数, nA/n称为事件A发生的频率, 记为fn(A).
频率的特性: 波动性和稳定性.
*
四.概率公理化定义:
定义: 设S是样本空间, E是随机试验. 对于E的每个事件A对应一个实数P(A), 称为事件 A的概率, 其中集合函数P(.)满足下列条件: 对任一事件A,有P(A)≥0; (非负性） P(S)=1;（规范性) 设A1,A2,…是两两互不相容的事件,则有 P(A1 A2 …)=P(A1)+P(A2)+… (可列可加性)
2. 样本空间与随机事件
(一) 样本空间: 定义随机试验E的所有可能结果组成的集合称为 E的样本空间, 记为S. 样本空间的元素称为样本点，用表示.
样本空间的分类:
1.离散样本空间:样本点为有限个或可列个. 例 E1,E2等.
2.无穷样本空间:样本点在区间或区域内取值. 例灯泡的寿命{t|t≥0}.
*
(二) 乘法公式:
P(AB)>0, 则有 P(ABC)=P(A)P(B|A)P(C|AB).
一般, 设A1, A2, …,An是n个事件,(n≥2), P(A1A2 ...An-1)>0, 则有乘法公式:
P(A1A2…An)=P(A1)P(A2|A1)…P(An-1|A1A2…An-2) P(An|A1A2…An-1).
*
B
A
S
2.和事件:
3.积事件：事件A B={x|x A 且 x B}称A与B的积，即事件A与B同时发生. A B 可简记为AB.
类似地, 事件为可列个事件A1, A2, ...的积事件.

西北工业大学《概率论与数理统计》课件-第3章多维随机变量及其分布

第三章多维随机变量及其分布关键词：二维随机变量分布函数分布律概率密度边缘分布函数边缘分布律边缘概率密度条件分布函数条件分布律条件概率密度随机变量的独立性Z=X+Y的概率密度Z=Y/X及Z=XY的概率密度M=max(X,Y)及N=min(X,Y)的概率密度例：研究某一地区学龄儿童的发育情况。

仅研究身高H 的分布或仅研究体重W 的分布是不够的。

需要同时考察每个儿童的身高和体重值，研究身高和体重之间的关系，这就要引入定义在同一样本空间（即某地区全部学龄前儿童）的两个随机变量。

问题的提出实际中，某些随机试验的结果需要同时用两个或两个以上的随机变量描述例：研究某种型号炮弹的弹着点分布。

每枚炮弹的弹着点位置需要由横坐标和纵坐标来确定，而它们是定义在同一样本空间的两个随机变量。

一、二维随机变量的定义设E是一个随机试验，样本空间S={e}；设X=X(e)和Y=Y(e)是定义在S上的随机变量，由它们构成的向量(X,Y)叫做二维随机向量或二维随机变量。

S ey()()(),X e Y ex(X,Y)的性质不仅与X及Y有关，还依赖于X,Y间的相互关系，需将(X,Y)作为整体研究二、二维随机变量的分布函数设(X ,Y )是二维随机变量，对于任意实数x , y ，二元函数称为二维随机变量(X ,Y )的分布函数，或称为随机变量X 和Y 的联合分布函数。

{}(,)()()(,)F x y P X x Y y P X x Y y =≤≤==≤≤ 记成1、定义：若将(X ,Y )看成平面上随机点的坐标，则F (x ,y )在(x ,y )处的函数值即为随机点落在(x ,y )左下方无穷域内的概率2、几何意义：(X ,Y )落在矩形区域[x 1<x ≤x 2, y 1<y ≤y 2]上的概率为x 1x 2yy 1y 20xy(x,y )1212(,)P x x x y y y <≤<≤()()()()22211211,,,,F x y F x y F x y F x y --+=3、性质：1212,(,)(,)y x x F x y F x y <⇒≤任意固定当x 1x 2(x 1,y )(x 2,y )yy 2xy 1(x ,y 1)(x ,y 2)1212,(,)(,)x y y F x y F x y <⇒≤任意固定0(,)1F x y ≤≤ (,)0 (,)0(,)0,(,)1y F y x F x F F -∞=-∞=-∞-∞=+∞+∞=对任意固定，对任意固定，(1) 不减性:F (x , y )关于x , y 单调不减，即(2) 有界性:且(3) 右连续性0(,)(,)lim F x y F x y εε+→+=0(,)(,)lim F x y F x y εε+→+=(),,F x y x y 关于右连续，即：()222112111212(,)(,)(,)(,),0F x y F x y F x y F x y P x X x y Y y --+=<≤<≤≥ 1x 2x 1y 2y 01212,,x x y y <<若则22211211(,)(,)(,)(,)0F x y F x y F x y F x y --+≥(4)三、二维离散型随机变量及其分布律1、定义：,,,,21m x x x X 的可能值为设,,,,21n y y y Y 的可能值为中心问题：(X ,Y )取这些可能值的概率分别为多少？若二维随机变量（X ,Y ）所有可能的取值是有限对或可列无限对，则称（X ,Y ）是二维离散型随机变量。

东华大学《概率论与数理统计》课件第三章二维随机变量

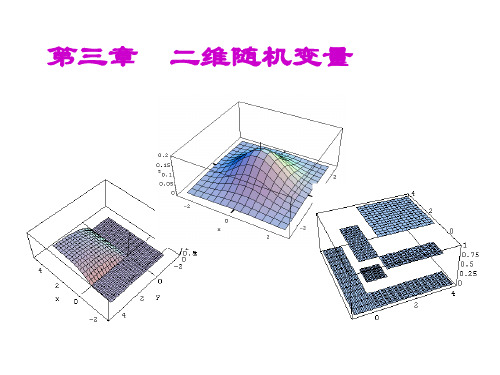
Y
X
y1
y2
yn
x1
p11
p12
p1 n
x2
p21
p22
p2n
n
pi• =
pij
j =1
p1•
p2•
xm
pm1
pm2
pmn
m
p• j =
pij
p•1
p•2
p• n
i =1
其中， pij = P( X = xi ,Y = y j ) ，
pm•
n
m
p• j = pi• = 1
j −1
( x,
y)
=
1 s
,
0,
(x, y) S (x, y) S
3.体积为v的空间区域V上
(
x,
y,
z)
=
1 v
,
0,
(x, y, z) V (x, y, z) V
基本概念：随机向量、联合分布函数。离散型随机变量：联合概率分布、阶梯型分布函
数。连续型随机变量：概率密度函数、连续型分布函
数。
即
FY
(
y)
=
F
(+,
y)
=
lim
x→+
F
(
x,
y)
F ( x) = F ( x,+)
1 = F(+,+)
0 = F(−, y) O
二维随机变量 (X ,Y) 的分布函数： F(x, y) = P(X x,Y y)
y
y
(x,y)
0
x
x
二维分布函数 F(x,y) 的性质： (1)（非降性） F(x, y) 是 x 或 y 的单调非降函数.

概率论与数理统计图文课件最新版-第3章-多维随机变量及其分布

比如:
概率统计
比如：
1 x y 0
F( x, y) 0 x y 0
对这二元函数来验证第4条性质。
现找 4 个点如下：
( x2 , y2 ) (1, 1); ( x1, y2 ) (1, 1)
( x2 , y1 ) (1, 1); ( x1, y1 ) (1, 1)
F(1,1) F(1,1) F(1, 1) F(1, 1)
0
x 0, y 0 其它
求: (1) 分布函数 F( x, y)
(2) ( X ,Y )落在G内的概率
其中 G: x y 1 及 x 轴、y 轴所围区域
解: (1) Q
x
F(x, y)
y
f ( x, y)dxdy
当 x 0, y 0 时
xy
F( x, y)
0 dx 0
2,4,8,10,14,16,20这7个数不能被3整除,但能
被2整除
6,12,18这3个数能被2 整除,又能被3整除
不难验证:
1 1
7473
pi j 0, 0 0 pi j 21 21 21 21 1
概率统计
故得： (X,Y) 的联合分布律为:
XY
0 1
01
7
4
21 21
7
P( x1 X x2 , y1 Y y2 )
F ( x2 , y2 ) F ( x2 , y1 ) F ( x1, y1 ) F ( x1, y2 )
如图:
y
y2 L
y1 L M
M
x
0 x1
x2
概率统计
2. 二维随机变量分布函数 F(x,y) 的性质
性质1 F(x,y) 分别对 x 和 y 单调非减, 即:

概率论与数理统计3.3二维随机变量函数的分布ppt课件

解:
1 x2 y2
f (x, y) e 2 , ( x , y )
2
FZ (z) P(Z z) P( X 2 Y 2 z)
当z<0,显然FZ(z)=0,
当z≥0,
FFFFZZZZ((((zzzz))))xx2xx222yy2yy222zz2zz22222122111eeeexx2xx22222y22y2yy2d22dddxxxxddddyyyy
( x z )2 2
e dx 22 2
2
2 e 令x z t e2 e e edt dx 2 e 2
zzz44222
e2 dx e2 4
z
2
4
(( xx
t
2
zz 22
))22
(x
z 2
)2
z2 4
1
z2
e4
2
X~ N(μ1 , σ12) Y~ N(μ2 , σ22) X与Y相互独立
二维离散型随机变量函数的分布
设(X,Y)为离散型随机变量，
P(X xi ,Y y j ) pij, i, j 1,2,...
Z=g(X,Y)为一维离散型随机变量.若对于不同的(xi,yj),g (xi,yj)的值互不相同,则Z的分布律为
P(Z g(xi , y j )) pij i, j 1,2,...
k
p(i)q(k i) i0
离散型卷积公式
例3:设X,Y相互独立,且X~P(λ1), Y~P(λ2) 证明:Z=X+Y~P(λ1+λ2)
证: P( X k) 1k e1 , k0,1,2,,
k!
P(Y k) k2 e2 , k0,1,2,,
k!
P(Z k) P( X Y k) Pik0( X i,Y k i)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Y X
x1 x2 … xi …
y1 y2 … yj …
p11 p12 … p1j … p21 p22 … p2j … … … ……… pi1 pi2 … pi j … … … ………
概率论与数理统计第三章
联合分布列的基本性质 (1) pij 0, i, j = 1, 2,… (非负性)
(2) pij = 1. (正则性)
xy
F(x,y)= p(u,v)dvdu --
则称 (X, Y) 为二维连续型随机变量。称p(x, y) 为联合密度函数。
概率论与数理统计第三章
联合密度函数的基本性质
(1) p(x, y) 0. (非负性)
(2)
p(x,y)dxdy1
(正则性)
- -
注意： P(X,Y) D p(x,y)dxdy
若X, Y是两个定义在同一个样本空间上的随机变量，则称(X, Y) 是两维随机变量.
➢ 同理可定义 n 维随机变量 (随机向量).
概率论与数理统计第三章
3.1.2 联合分布函数
定义3.1.2 (以下仅讨论两维随机变量)
任对实数 x 和 y, 称 F(x, y) = P( X x, Y y)
设随机变量 X 在 1，2，3 ， 4 四个整数中等可能地取值，另一个随机变量 Y 在 1到X 中等可能地取一整数值。试求（X, Y）的联合分布列.
概率论与数理统计第三章
3.1.4 联合密度函数
设二维随机变量(X, Y) 的分布函数为 F(x, y)，若存在非负可积函数 p(x, y)，使得
F(, y) = F(x, ) =0， F(+, +) = 1. (3) F(x, y) 关于 x 和 y 分别右连续. (右连续性) (4) 当a<b, c<d 时，有 (非负性)
F(b, d) F(b, c) F(a, d) + F(a, c) 0. 注意：上式左边 = P(a<Xb, c<Y d).
第三章多维随机变量及其分布
§3.1 多维随机变量及其联合分布 §3.2 边际分布与随机变量的独立性 §3.3 多维随机变量函数的分布 §3.4 多维随机变量的特征数 §3.5 条件分布与条件期望
概率论与数理统计第三章
§3.1 多维随机变量及其联合分布
3.3.1 多维随机变量 ➢ 定义3.1.1
D
概率论与数理统计第三章
3.1.5 常用多维分布
一、多项分布
若每次试验有r 种结果：A1, A2, ……, Ar
记 P(Ai) = pi ,
i = 1, 2, ……, r
记 Xi 为 n 次独立重复试验中 Ai 出现的次数.
则 (X1, X2, ……, Xr)的联合分布列为： P (X 1 n 1 ,X 2 n 2 ,......,X r n r )= n 1 ! n 2 n !!n r !p 1 n 1 p 2 n 2
解: (X1, X2) 的可能取值数对及相应的概率如下：
P(X1=0, X2=0) = P(|Y|≥1, |Y|≥2) = P(|Y|≥2) = 2 2Φ(2) = 0.0455
P(X1=0, X2=1) = P(|Y|≥1, |Y|<2) = P(1≤|Y|<2) = 2[Φ(2) Φ(1)] = 0.2719
为(X, Y) 的联合分布函数.
注意：
F(x, y)为(X, Y)落在点(x, y)的左下区域的概率.
概率论与数理统计第三章
X2 x2
(x1, x2)
x1
X1
概率论与数理统计第三章
联合分布函数的基本性质
(1) F(x, y) 关于 x 和 y 分别单调增. (单调性) (2) 0 F(x, y) 1，且 (有界性)
P(X1=1, X2=0) = P(|Y|<1, |Y|≥2) = 0 P(X1=1, X2=1) = P(|Y|<1, |Y|<2) = P(|Y|<1) = 0.6826
概率论与数理统计第三章
列表为：
X1 X2 0 1
0
0.0455 0
1
0.2719 0.6826
概率论与数理统计第三章
课堂练习
XY 04 13 22 31 40
其对应的概率分别为：
P(X=0, Y=4)= 0.54=1/16 P(X=1, Y=3)= C410.50.53 =1/4 P(X=2, Y=2)= C420.520.52 =6/16
P(X=3, Y=1)= C430.530.51 =1/4
P(X=4, Y=0)= 0.54 =1/16
n2,
......, Xr
nr)=n1
n2 N
n
N nr
概率论与数理统计第三章
三、二维均匀分布
若二维连续随机变量 (X, Y) 的联合密度为：
p n r r
概率论与数理统计第三章
二、多维超几何分布
口袋中有 N 只球，分成 r 类。
第 i 种球有 Ni 只， N1+N2+……+Nr = N. 从中任取 n 只，
记 Xi 为取出的n 只球中，第i 种球的只数.
则 (X1, X2, ……, Xr)的联合分布列为：
N1N2
P统计第三章
列表为：
XY
0 1 2 3 4
01234
0 0 0 0 1/16 0 0 0 1/4 0 0 0 6/16 0 0 0 1/4 0 0 0 1/16 0 0 0 0
概率论与数理统计第三章
例3.1.2 设随机变量 Y ~ N(0, 1), 求 X1 1 0,, ||Y Y|| 1 1, X2 1 0,, ||Y Y|| 2 2的联合分布列.
概率论与数理统计第三章
3.1.3 联合分布列二维离散随机变量
若(X, Y) 的可能取值为有限对、或可列对，则称(X, Y)为二维离散随机变量.
概率论与数理统计第三章
二维离散分布的联合分布列
称 pij = P(X=xi, Y=yj)， i, j=1, 2, ..., 为(X,Y) 的联合分布列，其表格形式如下:
概率论与数理统计第三章
确定联合分布列的方法
(1) 确定随机变量 (X, Y) 的所有取值数对. (2) 计算取每个数值对的概率. (3) 列出表格.
概率论与数理统计第三章
例3.1.1 将一枚均匀的硬币抛掷4次，X表示正面向上
的次数，Y表示反面朝上次数。求 (X, Y) 的联合分布列.
解：概率非零的(X,Y) 可能取值对为: