活度与活度因子
电化学2

25C时摩尔甘汞电极的电极电势为0.2801V
A.醌·氢醌电极
醌和氢醌的活度几乎相等,由电极反应的能斯特方程
(醌 • 氢醌)=( 醌 • 氢醌)+0.0592lgc(H ) 25C时( 醌 • 氢醌)=0.6993V (醌 • 氢醌)=0.6993V+0.0592lgc(H ) pH lg 1/ c(H ) 所以(醌 • 氢醌)=0.6993V-0.0592pH
铜锌原电池(丹尼耳电池):
Zn 棒
多孔素烧 瓷杯
ZnSO4(aq)
Cu棒 CuSO4(aq)
阳极(负极):Zn(s) Zn2 (1mol / kg) 2e 阴极(正极):Cu2+ (1mol / kg) 2e Cu(s) 电池反应:Zn(s) Cu2+ (1mol / kg) Zn2 (1mol / kg) Cu(s) 书写电极反应1)物质的量平衡及电量平衡
简称标准电势,与物质本性及温度有关。(表7-4)
为什么标准电极电势的值有正有负?
答:因为规定了用还原电极电势,待测电极放 在阴极位置,令它发生还原反应。但是比氢活 泼的金属与氢电极组成电池时,实际的电池反 应是金属氧化,氢离子还原,也就是说电池的 书面表示式是非自发电池,电池反应是非自发 反应,电动势小于零,电极电势为负值。如果 是比氢不活泼的金属,则与氢电极组成自发电 池,电极电势为正值。
IR AH
ES Ex
IR AC
IR AH
AC AH
Ex
AH AC
ES
标准电池 待测电池
工作电源
检流计
电位计
韦斯顿标准电池:高度可逆,电动势稳定
电池反应: (-) Cd(Hg)→Cd2++Hg(l)+2e(+)Hg2SO4(s)+2e-→2Hg(l)+SO42净反应: Hg2SO4(s)+Cd(Hg)(a)+8/3H2O
高等化工热力学PPT

qi为组分i的有效摩尔体积,zi为有效体积分数,
zi qi xi / K j 1 q j x j
i,II ai,II / xi i,IV ai,IVc o / ci
活度因子反映了实际溶液偏离理想溶液的程度(非理想性)。 活度因子等于1为理想溶液,小于1为负偏差非理想溶液,大于1为
正偏差非理想溶液。但正偏差或负偏差的概念是与活度标准态的选 择相关的。
对于同一种物质,采用不同的活度标准状态,其逸度仍然是
2 2 ln 2 [ A21 2( A A D ) x 3 Dx 12 21 2 2 ]x1
(2) Van Laar
Q ( x1 A12 x2 A21) x1x2[1 D12 x1x2 / A12 ]
2 2 ln 1 A [ 1 D ( 3 x 2 x ) / A ] x 12 12 1 1 12 2
E K 1 p p Vm xj RT xi x[i , K ] j 1 x j x[ j , K ] E K 1 E K 1 K 1 Q T p H V m m ln K Q x j x xj 2 j j 1 x j x[ j , K ] RT j 1 x j x[ j , K ] RT j 1 x j x[ j , K ]
定义实际溶液的活度为
ai,I f i / f i* ai,III f i / K Hi ( m)
ai,II f i / K Hi ai ,IV f i / K Hi (c)
电解质的活度和活度因子

解 b+ = 0.00869 mol kg-1 b- = 0.00869 + 0.02500 = 0.03369 mol kg-1 Ksp = 2.022×10-4
将这些数据代入得
2.022 10 4 0.00869 0.03369
1
/
2
0.831
3/23/2024
离子强度
从大量实验事实看出,影响离子平均活度系数的主要 因素是离子的浓度和价数,而且价数的影响更显著。 1921年,Lewis提出了离子强度(ionic strength)的概念 。当浓度用质量摩尔浓度表示时,离子强度Ib等于:
弛豫效应(relaxation effect)
由于每个离子周围都有一个 离子氛,在外电场作用下,正负 离子作逆向迁移,原来的离子氛 要拆散,新离子氛需建立,这里 有一个时间差,称为弛豫时间。
在弛豫时间里,离子氛会变 得不对称,对中心离子的移动产 生阻力,称为弛豫力。这力使离 子迁移速率下降,从而使摩尔电 导率降低。
3/23/2024
德拜-休克尔-昂萨格电导理论
Debye Huckel's Onsager 电导公式 考虑弛豫和电泳两种效应,推算出某一浓度时电解
质的摩尔电导率与无限稀释时的摩尔电导率之间差值的 定量计算公式,称为 Debye Huckel's Onsager 电导公式:
m m - ( 'm ) c/cO
3/23/2024
R
3/23/2024
PETER JOSEPH WILLIAM DEBYE
PETER JOSEPH WILLIAM DEBYE (1884-1966) Dutch-born physical chemist, made extraordinary
§8.4 电解质的平均活度和平均活度因子

电解质的平均活度和平均活度因子
电解质的平均活度和平均活度因子
离子强度
1
电解质的平均活度和平均活度因子
非电解质化学势表示式
B B (T ) RT ln B,m
B (T ) RT ln aB,m
mB m
mB aB,m B,m m 当溶液很稀,可看作是理想溶液,γ B,m→1,则:
def
1 ( )
离子平均质量摩尔浓度(mean molality of ions) 1 def m (m m )
m a m m aB a a a ( )
m
6
m mB
+ + +
Cl Cl (T ) RT ln aCl
HCl H Cl
aHCl aH+ aCl
( H+ Cl ) RT ln(aH+ aCl )
3
定义:
离子平均活度(mean activity of ions)
a def (aH aCl )
4
对任意价型电解质
M + A + M
z+
A
z
B B (T ) RT ln aB
+ + (T ) RT ln a+ (T ) RT ln a
B +
( ) RT ln(a a )
从电解质的mB求m±
1
m mB
1
上次课复习活度与活度因子

第17 次课 2 学时注:本页为每次课教案首页第五章 相平衡相平衡是热力学在化学领域中的重要应用之一。
研究多相体系平衡的规律在化学、化工的科研和生产中有重要的意义,例如:溶解、蒸馏、重结晶、萃取、提纯及金相分析等方面都要用到相平衡的知识§5.1引言本节介绍几个基本概念相:是体系内部物理性质与化学性质完全均匀相同的一部分。
相与相之间在指定条件下有明显的界面,在界面上宏观性质的改变是飞跃式的。
相数:体系中相的总数叫相数,用F 表示。
相数的确定:气体,不论有多少种气体混合,只有一个气相。
液体,按其互溶程度可以组成一相、两相或三相共存。
固体,一般有一种固体便有一个相。
两种固体粉末无论混合得多么均匀,仍是两个相(固体溶液除外,它是单相)。
自由度(degrees of freedom ):确定平衡体系的状态所必须的独立强度变量的数目称为自由度,用字母f 表示。
这些强度变量通常是压力、温度和浓度等。
这些变量的数值,在一定的范围内,可以任意的改变而不会引起相的内容和数量的改变。
如果已指定某个强度变量,除该变量以外的其它强度变量数称为条件自由度,用*f 表示。
例如:指定了压力,1*-=f f ;指定了压力和温度,2**-=f f 。
相图(phase diagram ):表达多相体系的状态如何随温度、压力、组成等强度性质变化而变化的图形,称为相图。
§5.2多相体系平衡的一般条件1.多相体系的热力学平衡状态在一个多相的热力学封闭体系中,相与相之间应该是互相敞开的,即在相之间应该有热的交换,功的传递以及物质的交流。
在无非体积功时,如果体系的各种性质都不随时间而改变,则体系就处于热力学的平衡状态。
热力学的平衡状态中包括四中平衡:热平衡、力平衡、相平衡和化学平衡。
2.热力学平衡条件1)热平衡条件若体系由α,β两相组成,在U 、V 不变的条件下,有微量的热自α相流入β相,引起体系的熵变为βαdS dS dS +=,平衡时0=dS ,有0=+-βαδδT Q T Q ,所以βαT T =,这就是热平衡条件。
活度和活度因子

真实溶液
为了精确地表达溶液中溶剂对于理想稀溶液旳偏差,引入了渗透因子(也称为渗透 系数)旳概念。 合理旳渗透因子g定义为:
溶液中溶剂化学势旳体现式为:
代入
得出用溶液中溶质旳质量摩尔浓度为变量表达旳溶剂旳化学势为: 定义溶剂A旳渗透因子为:
利用上式又可推得质量摩尔浓度作为溶液构成变量表达旳稀溶液中溶剂旳化学势:
气、液两相平衡时,组分B在气、液两相旳化学势相等:。若将气相看作是理想气 体混合物,则气相旳化学势为
从而
上式中消去相同旳项,并取指数得到:定律 所计算得到旳分压之比。
这一关系可由右图看出。图中实曲线为 混合物中组分B旳蒸汽压—构成线,虚 斜线为假设B符合乌拉尔定律时旳蒸汽 压—构成线。
活度及活度因子
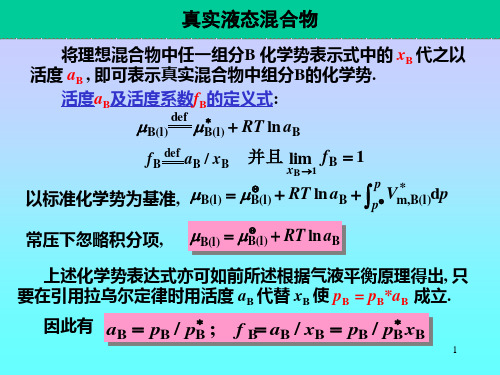
真实液态混合物
按下式定义真实液态混合物中组分B旳活度及活度因子
式中: 因为纯液态B在一定温度T、压力p下旳化学势,当初,必然,于是有;
因为原则态压力定为,故压力p下旳化学势:
在常压下,积分项近似为零,故近似有
真实液态混合物中组分B旳原则态为原则压力下旳纯液体B,为温度T下原则态 时B旳化学势,即原则化学势。活度相当于“有效旳摩尔分数”。活度因子则 相当于真实液态混合物中组分B偏离理想情况旳程度。 组分B旳活度可由测定与液相成平衡旳气相重B旳分压力及同温度下纯液态Bde 蒸汽压得出。
渗透因子旳一种主要规律是当溶质旳质量摩尔浓度时,。在比较小时。 对于溶质B,在温度T、压力p下真实溶液中化学势旳体现式要求为:
式中 称为溶质B旳活度因子。且
式中极限条件,不但所要讨论旳那种溶质B旳趋近于零,还要求溶液中其 他溶质旳b也同步趋近于零。
在p和相差不大时,上上页两式可表达为:
谢谢
活度与活度因子

xB 1, x,B 1, ax,B 1
那个状态的化学势。
这个状态实际上是存在的,那就是纯组分B。
非理想稀溶液
非理想稀溶液中组分B的化学势表示式,由于 浓度的表示式不同,化学势表示式也略有差异。
(1)浓度用摩尔分数 xB 表示
当气-液平衡时
B(l)
B(g)
B
(T )
RT
ln
pB p
稀溶液中溶质服从Henry定律
x1dln1 x2dln 2 x1d ln x1 x2d ln x2 0
因为 所以
dlnxB
dxB xB
,
dx1 dx2
x1dln1 x2dln 2 0
双液系中活度因子之间的关系
x1dln1 x2dln 2 0
这说明了双液系中活度因子之间是有关系的
对上式进行定积分,
1 1 1
pB kx,B xB
非理想稀溶液中
pB k x,B x,B xB kx,Bax,B
x,B 是溶质浓度用摩尔分数表示的活度因子
非理想稀溶液
(1)浓度用摩尔分数 xB 表示
pB kx,B x,B xB k a x,B x,B
代入化学势的表示式
B(l)
B(g)
B
(T )
RT
ln
pB p
时仍服从
Henry定律那个假想状态的化学势。
非理想稀溶液
(2)浓度用质量摩尔浓度 mB 表示
若溶质浓度与Henry定律发生偏差,则校正为
pB km,B m,BmB
令:
B
m,B (T ,
p)
RT
ln
m m,B B
m
am,B
m m,B B
电解质溶液的活度、活度因子

a , a , ,
无法测量
活度 aB
B B RT ln aB
aB
B
bB b
a 平均离子活度
平均离子活度因子
b 平均离子质量摩尔浓度
电解质溶液的活度、活度因子
任意电解质 M A M z A z
整体电解质的化学势为阴、阳离子化学势的代数和:
RT ln a RT ln a
(
) 1/
b 平均离子质量摩尔浓度(mean molality of ions)
b
(
b
b
)1 /
电解质溶液的活度、活度因子
a b
a
b b
γ±——可测, b±——由b可求 (强电解质)
注意
a
a a
a
(
b b
)
① a,a+, a-和 a±四种活度,都代表各自的校正浓度或有效浓度;
谢谢观看
PPT模板下载:/moban/ 节日PPT模板:/jieri/ PPT背景图片:/beijing/ 优秀PPT下载:/xiazai/ Word教程: /word/ 资料下载:/ziliao/ 范文下载:/fanwen/ 教案下载:/jiaoan/ 字体下载:/ziti/
0.013mol
kg 1
注意 离子强度是针对溶液中的所有电解质
电解质溶液的活度、活度因子
电解质 类型 1-1 1-2 2-1 2-2 1-3 3-1 3-2 1-4
电解质 示例 NaCl Na2SO4 CuCl2 CuSO4 Na3PO4 FeCl3
Al2(SO4)3 K4[Fe(CN6)]
b
a
( RT ln a ) ( RT ln a )
(
电解质的活度与平均离子活度因子

56电解质的活度与平均离子活度因子与非电解质溶液一样,活度对电解质溶液同样重要,它不仅是研究电解质溶液理论的依据,而且,在原电池电动势计算中也是不可缺少的。
本专题就来讨论电解质和离子的活度。
1. 电解质的化学势与活度将NaCl 溶于水中,由于它能完全解离,系统中除了水外,只有+Na 离子和−Cl 离子。
按照化学势定义,+Na 离子的化学势应为O2H Cl ,,,NaNan np T n G−++⎟⎟⎠⎞⎜⎜⎝⎛∂∂=μ (56-1)但是,式(56-1)在实验上是不可操作的,因为要在保持−Cl n 不变的条件下,改变+Na 离子物质的量是不可能的。
只有在保持水的量不变的条件下,改变NaCl 物质的量才是实验可操作的,此时−+−+−+⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂=Cl ,,,ClNa ,,,Nad d d O2H Na O2H Cl n nGn nG G n np T n np T()NaCl Cl Na d n −++=μμ (56-2)式中−+==Cl Na NaCl d d d n n n 。
由于在恒温恒压,保持水的量不变的条件下,G 随NaCl n 的变化率即为电解质NaCl 的化学势,故由式(56-2)可得−++=Cl Na NaCl μμμ (56-3)它表明,电解质NaCl 的化学势等于它解离产生的+Na 离子和-Cl 离子化学势之和。
现若是2CuCl 水溶液,同样可以写出d d d Cl,,,ClCu ,,,CuO2H 2Cu 2O2H Cl 2−+−+−+⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂=n nGn n G G n np T n np T()22222CuCl Cl Cu Cu CuClCl Cu d 2d d d n n n n −+++−−++=⎟⎟⎠⎞⎜⎜⎝⎛+=μμμμ (56-4) 式中2/d d 2Cu Cl =+−n n ,因为解离生成1mol +2Cu 离子必伴生2mol −Cl 离子。
化学势与活度

惯例I参考 状态化学势
iL,S i RT lnai
5. 实际液态或固态混合物 ——所有组分以惯例I做参考
pi pi xi i piai
a ——活度
——活度因子
iL,S i RT lnai
理想溶液 i 1, ai xi
iL,S i RT ln xi
6. 实际溶液——溶剂用惯例I,溶质用惯例II
惯例Ⅱ参考 状态
系统温度、压力下,具有 理想稀溶液特性的液态或 固态虚拟纯组分B的化学势
理想稀溶液溶 质的化学势
id,dil.sol B
x,B
RT ln
xB
3. 惯例III——一定浓度理想稀溶液中的溶质
从理想稀溶液看惯例III:
pA pA* xA pB KHb,BbB
id,dil.sol B
pA pA xA A pA aA
a ——活度
——活度因子
L,S A
AV
Ad
(g)
RT
ln
pA
/
pd
Ad (g) RT ln pA aA / p d
Ad (g) RT ln pA / p d RT ln aA
惯例I参考 状态化学势
L,S A
A*
RT
ln aA
6. 实际溶液——溶剂用惯例I,溶质用惯例II
a ——活度
pB KHx,B xB x,B KHx a ,B x,B ——活度因子
L,S B
BV
Bd
(g)
RT
ln
pB
/
pd
Bd (g) RT ln KHx,Bax,B / p d
Bd (g) RT ln KHx,B / p d RT ln ax,B
平均离子活度和平均离子活度因子

b± = {(ν + b )
(ν − b )
}
= (ν + ν −
)
b
此式为离子平均质量摩尔浓度与电解质整体浓度的关系.
2
离子强度
• 25℃时某些电解质水溶液中的离子平均活度系数γ± b/(mol⋅kg−1) 0.001 0.005 0.01 0.05 0.10 0.50 1.00 2.00 HCl 0.965 0.928 0.904 0.830 0.796 0.757 0.809 1.009 NaCl 0.966 0.929 0.904 0.823 0.778 0.682 0.658 0.671 KCl 0.965 0.927 0.901 0.815 0.769 0.650 0.605 0.575 HNO3 0.965 0.927 0.902 0.823 0.785 0.715 0.720 0.783 CaCl2 K2SO4 H2SO4 0.887 0.783 0.724 0.574 0.518 0.448 0.500 0.792 0.89 0.78 0.71 0.52 0.43 0.830 0.639 0.544 0.340 0.265 0.154 0.130 0.124 BaCl2 0.88 0.77 0.72 0.56 0.49 0.39 0.59
• 德拜 − 休克尔离子氛模型 “离子氛”模型动画
• 离子氛模型使溶液中众多正、负 离子间的静电相互作用, 可以简化 为中心离子与离子氛之间的静电 作用.
5
德拜−休克尔极限公式
德拜-休克尔极限公式: 由离子氛模型出发, 加上一些近似 处理, 推导出稀溶液中的单种离子活度因子公式和平均离子 活度因子公式:
1
平均离子活度和平均离子活度因子
活度与活度因子

•实验表明,实际溶液中往往各组分同时产生负偏差,各组分的化学势小于同浓 度时若为理想溶液时各组分的化学势。 • 同时产生负偏差的原因,往往是由于异种分子A、B之
间的作用力大于同种分子之间A与A或B与B之间的作 用,特别是在A和B分子间有化学(键)作用而形成化 合物时,更易产生负偏差。
无热溶液(athermal solution)
因为
HE
0
,所以
H E (
nB
)p
0
即
2
GE (
)
[
T nBT
]p
T
(1 T
G E nB
)p
0
则
( ln B
T
)p
0
所以在无热溶液中,各组分的活度系数均与T无关。
4.13 分配定律
“在定温、定压下,若一个物质溶解在两个同时存 在的互不相溶的液体里,达到平衡后,该物质在两相中 浓度之比等于常数” ,这称为分配定律。用公式表示为:
在正规溶液中,因为 S E 0 ,所以:
S E
( nB
)p
0
又因为
所以
2GE (nBT ) p
0
SE
GE ( T ) p
因为
GE (
nB
)p
BE
RT
ln B
(BE 称为超额化学势)
正规溶液(regular solution)
代入上式,得:
[
(
RT ln T
分配定律的应用: (1)可以计算萃取的效率问题。例如,使某 一定量溶液中溶质降到某一程度,需用一定体积 的萃取剂萃取多少次才能达到。 (2)可以证明,当萃取剂数量有限时,分若 干次萃取的效率要比一次萃取的高。
《活度与活度因子》课件

活度在分离技术中的应用
利用不同溶质的活度差异,可以实现分离和纯化技术,如萃取、层析等。
活度与溶剂的关系
活度与溶剂的特性密切相关,不同溶剂对溶质的溶解度和活度系数有显著影 响。
溶液基本概念与单位
了解溶液的基本概念和表示方法,以及溶液浓度的计量单位(mol/L,%浓度 等)。
活度与浓度的区别与联系
活度可以通过描述溶液中溶质的行为来影响化学反应的速率,不同溶液中活 度的差异会导致反应速率的变化。
活度与表面张力的关系
溶质对溶液的表面张力有影响,并且活度的变化也会对表面张力产生一定的 影响。
活度与溶解度的关系
溶质在溶液中的溶解度与活度密切相关,活度可以通过描述溶质的活跃程度 来解释溶解度的变化。
活度通过考虑溶质与溶剂的相互作用,对浓度进行修正,以更准确地描述物 质在溶液中的活跃程度。计算方法包括理想溶液活度系数和实际溶液活度系 数。
活度的种类
自由活度
描述溶质自由分子的活动程 度。
组分活度
描述化学中的 活动程度。
活度系数和活度因子的区别
《活度与活度因子》PPT 课件
活度是指物质在溶液中的活跃程度,本课件将介绍活度的定义、种类、计算 方法,以及活度与化学反应、生物体内的作用等方面的内容。
什么是活度?
活度是指物质在溶液中的活跃程度,与浓度有些许不同。它考虑了溶质与溶 剂之间的相互作用,并可以描述物质在溶液中的行为。
活度的定义及计算方法
活度与浓度是描述溶液中溶质含量的两个重要参数,二者互相关联,但并不完全一致。
活度与温度的关系
随着温度的变化,溶液中溶质的活度也会发生变化,因为温度会影响溶质与溶剂之间的相互作用。
活度与压强的关系
一些溶质在溶液中的溶解度和活度与压强之间存在关系,如气体在液体中的 溶解度与气体分压的关系。
8.4电解质的平均活度和平均活度因子

( ) mB
_
1
m mB
Na 2SO4 (B)
m 3 4mB mB 3 a 4 m
3
2
mB aB a 4 m
3
1 3
3
二、离子强度
路易斯(Lewis)提出: 离子强度
§8.4 电解质的平均活度和平均活度因子
电解质的平均活度和平均活度因子
离子强度
一、电解质的平均活度和平均活度因子
溶液中某组分的化学势
B B RT ln B
对于强电解质溶液
C v A v v C v _ A
Z
Z
RT ln ,
RT ln
γ (γ γ )
v v
1 v
v v m (m m )
1 v
定义: 离子平均活度因子
从电解质的
mB 求 m
m- -mB
1
1
m mB
m (m m )
[( mB ) ( mB ) ]
对1-1价电解质 对1-2价电解质
1 2 I mB zB 2
lg γ A z z I
试计算下列溶液的离子强度: (1)0.025 mol· -1NaCl; kg (2)0.025 mol· -1CuSO4; kg (3)0.025 mol· -1LaCl3。 kg
解: I
1 2 bB zB 2
(1)I =1/2 [0.025×12 + 0.025×(-1)2] = 0.025 mol· -1 kg (2)I =1/2[0.025×22 + 0.025×(2)2] = 0.1 mol· -1 kg
活度与活度因子

式,便得实际混合物或溶液中组分 i 的化学势为
μi
= μio + RT ln( fi
/
po)
=
μio
+
RT
ln(
f
∗ i
/
po)
+
RT
ln
ai
= μi∗ + RT ln ai
(18-4)
与理想混合物一样,式中 μi∗ = μio + RT ln( fi∗ / po ) 为参考状态的化学势,其参考状态﹡也为
1. 活度与逸度的关系
对于理想液体或固体混合物,专题 17 已经指出,由于其遵守 Raoult 定律
fi
=
f
∗ i
xi
将它代入逸度的定义式,得到了组分化学势的表示式为
(18-1)
μi = μi∗ + RT ln xi
(18-2)
式中 μi∗ = μio + RT ln( fi∗ / po ) ,为系统温度和压力下,组分 i 纯液体或纯固体的化学势。在
那里曾指出,建立这个理想模型的目的是试图将它作为研究的基础,通过修正的方法,以用 来解决实际混合物或溶液的问题。
现在,假定引入一个校正因子 γ i ,使式(18-1)能适用于实际混合物或溶液
fi = γ i fi∗xi = fi∗ai
(18-3)
式中 ai = γ i xi ,称为组分 i 的活度, γ i 称为活度因子。于是,将式(18-3)代入逸度的定义
lim aA = 1 xA →1 xA
溶质:
μB
=
μ
Δ B
+
RT
ln
ab,B
(18-15)
§4.11 活度与活度因子

因为 所以
dxB dlnxB , dx1 dx2 xB x1dln 1 x2dln 2 0
10
x1dln 1 x2dln 2 0
这说明了双液系中活度因子之间是有关系的
对上式进行定积分,
x2 1 1 dln 1 2 ( x2 0) x1 dln 2 当 x1 1 时, 1 1
B (T , p) RT ln ax ,B
* B
3
* B B (T , p) RT ln ax ,B
* B (T , p) 是在T,p时,当 xB 1, x ,B 1, ax 上是存在的,那就是纯组分B。
4
非理想稀溶液 非理想稀溶液中组分B的化学势表示式,由于 浓度的表示式不同,化学势表示式也略有差异。 (1)浓度用摩尔分数 xB 表示 当气-液平衡时 pB B(l) B(g) B (T ) RT ln p
代入化学势的表示式
B(l) B(g)
B
k x ,B (T ) RT ln RT ln ax ,B p
* x ,B (T , p ) RT ln a x ,B
* B (T , p)是在T,p时,当 xB 1, x ,B 1, a x ,B 1那个假想
pB x ,B xB * pB
对于非理想的液态混合物,Lewis提出了活度的概念 将Raoult定律应修正为: 则化学势表示式为:
* B
B (T , p) RT ln( x ,B xB )
2
* B B (T , p) RT ln( x ,B xB )
如定义:
ax ,B x ,B xB
B
活度与活度因子
p p
VB( 溶质)dp
b,B ab,B /( bB / b )
并且
bB 0
m b ,B 1
常压下
a b ,B pB k b ,B b
B b,B RT ln ab,B
及
b ,B
a b ,B bB / b
pB k b ,B b B
4
真实溶液
而活度因子fA = aA/xA不能灵敏反映稀溶液中溶剂的非理想性.
溶剂A 的渗透因子A:
得
因
A(l)
def
A(l) A RT ln x A
a A x AA
稀溶液
A ln a A / ln x A ;
B
ln x A ln( 1 M A bB )
B
M A bB
aB exp{( B(l) B(l) ) / RT } B / B
同样, 对液态溶液中的溶剂, 对液态溶液中的溶质,
aA A / A
aB B / lim {B /( bB / b )}
B bB 0
对气态混合物中任一组分,
~ pB B / lim{B /( yB p)}
真实液态混合物
将理想混合物中任一组分B 化学势表示式中的 xB 代之以 活度 aB , 即可表示真实混合物中组分B的化学势. 活度aB及活度系数fB的定义式:
B(l)
fB
def
B(l) RT ln aB
并且 lim f B 1
xB 1
def
aB / xB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
度用 mB , cB 表示,则对应有am,B , ac,B 和 m,B, c,B ,
显然它们彼此不相等。
溶质B的化学势
非理想溶液中组分B的化学势表示式,由于浓度 的表示式不同,化学势表示式也略有差异。
(1)浓度用摩尔分数 xB 表示 B B RT ln( pB / p ) B (T) RT ln(kx / p ) RT ln ax,B
• 此种溶液即为“非理想溶液”或“实际溶液”。
非理想溶液不具备理想溶液的特性,下面就以蒸气压组成图来讨论实际溶液对理想溶液的偏差:
1、正偏差: •若实际溶液在一定浓度时蒸气压比同浓度时若为理想溶液
时的蒸气压大,即实际溶液的蒸气压大于用拉乌尔定律的 计算值。这种情况称为“正偏差”(如图)。
• 两种组分A、B同时产生正偏差 的原因,往往是由于A、B分子 间的作用力小于A与A及B与B 分子间的作用力所引起的。
•对理想溶液来说,其中任何组分B的化学势为:
B B* (T , p) RT ln xB
•其中
* B
为温度
T
时纯B组分的化学势,其蒸气压为
pB*
。
•对于非理想溶液,上式就不适用。
•对于稀溶液,我们已得到溶剂(A)的化学势表达式:
A A* (T , p) RT ln xA
式中 A* 为温度 T 时纯溶剂A的化学势,其蒸气压为 ;
式中 cB 和 cB 分别为溶质B在两个互不相溶的溶剂 ,
中的浓度,K 称为分配系数(distribution coefficient)。
分配定律
影响K值的因素有温度、压力、溶质及两种溶剂的 性质,在溶液浓度不太大时能很好地与实验结果相符。 这个经验定律可以从热力学得到证明。定温定压下,达 到平衡时,溶质B在, 两相中的化学势相等,即
RT ln am,B
B (T , p) RT ln am,B
am,B
m,B
mB m
B (T, p) 是在T,p时,当 mB m , m,B 1, am,B 1
时仍服从Henry定律那个假想状态的化学势, m 1mol kg。1
(3) 浓度用物质的量浓度cB 表示
B
B
(T
)
RT
ln
或 xAdlnaA + xB dln aB = 0
d ln x,A
xB xA
d
ln x,B
所得的为X值
d ln ax,A
xB xA
d
ln
ax,B
4、可逆电动势测定法:
通常指电解质溶液的a:下册内容。
4.12 渗透因子和超额函数
溶液中溶剂占多数,如果也用活度因子 A 来表
示,偏差不明显,所以Bjerrum建议用渗透系数 来表 示溶剂的非理想程度。
(
ln
T
B
)
p
正规溶液(regular solution)
根据热力学函数间的关系,
GE H E TS E
当H E TSE 或 S E 0 ,则 GE H E,这时溶液 的非理想性完全由混合热效应引起,这种非理想溶液 称为正规溶液。
正规溶液(regular solution)
在正规溶液中,因为 S E 0 ,所以:
G mix re =(n11 n2 2 ) (n11* n2 2* )
= nB RT ln aB nB RT ln xB nB RT ln B
B
B
B
GE nB RT ln B
B
超额函数(excess function)
GE nB RT ln B
B
加和项中包含了溶质和溶剂的活度因子,可以衡 量整个溶液的不理想程度。
渗透系数的定义:
(1) A A* RT ln xA
或
(2)
xA xB
ln A xA
或
(3) (M A mB )1 ln aA
渗透系数(osmotic coefficient)
以(1)式为例: A A* RT ln xA
因为: A A* RT ln A xA
比较两式得
ln A ln xA
H E
(GE )
T 2[
T T
]p
RT 2
B
nB
(
ln
T
B
)
p
超额函数(excess function)
(4)超额熵 S E
S E mix Sre mix Sid
因为
(
G T
)
p
S
S E
(
G E T
)
p
[ T
(
B
nB RT ln B ]p
= R
B
nB ln B
RT
B
nB
活度的求算
1、蒸气压法:
溶剂:pA p*AxA x,A
x,A
pA p*A xA
溶质: C,B
pB kC , B cB
(pA实验可测)
或:
m,B
PB km,B mB
其中Henry常数 kc,B 可用 ( pB / cB )cB 0 外推得到。
2、凝固点下降法(溶剂活度):
稀溶液或理想溶液中溶剂:
4.11 活度与活度因子
•活度的概念 •溶质B的化学势
非理想溶液
• 理想溶液中,溶剂或溶质均遵守拉乌尔定律,没有体积 变化和热效应。
• 但这类理想溶液(或类似理想溶液)毕竟只是极少数, 大多数溶液中由于不同分子之间的作用与同种分子间的 作用有着较大的差别,甚至溶剂和溶质分子之间有化学 作用,因此在溶液中各组分分子所处的环境与其在纯态 时的很不相同,因此在形成溶液时往往伴随着体积变化 和热效应发生。
kcc p
RT ln ac,B
= B (T , p) RT ln ac,B
ac,B
c,B
cB c
B (T , p) 是在T,p时,当 cB c , c,B 1, ac,B 1 时假
想状态的化学势, c 1mol dm3 。
显然 B* (T, p) B(T, p) B (T, p) ,但B 物质的化学势 B 是相同的,并不因为浓度的表示方 法不同而有所不同。
B
nB RT ln B )]T
显然
=RT
B
nB
(
ln
p
B
)T
mixVre 0
超额函数(excess function)
(3)超额焓 H E
H E mix H re mix Hid mix Hre
根据Gibbs-Helmhotz方程
(因为mix Hid 0)
(G )
[
T T
]p
H T2
ln
xA
Δfus
H
* m,
A(
1
R
Tf
1 Tf
)
对非理想溶液,用ax,A代替xA:
ln
ax, A
Δfus
H
* m,
A(
1
R
Tf
1 Tf
)
Δfus
H
* m,
A
R(T
f
)2
ΔTf
(Tf实验可测)
3、由Gibbs-Duhem公式
从溶质(溶剂)的活度求溶剂(溶质)的活度:
二元溶液: xAdA + xBdB = 0
当 GE 0 ,表示体系对理想情况发生正偏差; 当 GE 0 ,则发生负偏差。
超额函数(excess function)
(2)超额体积 V E
V E V mix re V mix id V mix re (因为 V mix id 0)
(
G p
)T
V
V E
(
G E p
)T
[ ( p
无热溶液(athermal solution)
GE H E TS E
如果 TSE H E ,或 H E 0 ,则 GE TS E ,
这种溶液的非理想性完全由熵效应引起的,所以称为 无热溶液。
无热溶液(athermal solution)
因为
HE
0
,所以
H E (
nB
)p
0
即
2(GE )
ln xA
例如,298 K时,xA 0.9328 的KCl水溶液中, a(H2O) 0.9364, (H2O) 1.004,这数值很不显著。
而 0.944,就显著地看出溶剂水的非理想程度。
超额函数(excess function)
用活度因子表示溶质的非理想程度,用渗透系数 可以较显著地表示溶剂的非理想程度,而超额函数用 来较方便地表示整个溶液的非理想程度。
• 可以理解为溶液中A、B分子间 的距离明显大于纯溶剂A或B中 分子间的距离。
•特别是在A组分原为缔合分子(如水),在形成溶液时 发生部分缔合解离的情况下,更易产生正偏差。 •由纯物质混合制备具备正偏差的溶液时,往往发生吸热 现象。溶液中各组分的化学势将大于同浓度时若为理想 溶液时各组分的化学势。
2、负偏差:
分配定律的应用: (1)可以计算萃取的效率问题。例如,使某 一定量溶液中溶质降到某一程度,需用一定体积 的萃取剂萃取多少次才能达到。 (2)可以证明,当萃取剂数量有限时,分若 干次萃取的效率要比一次萃取的高。
例、苯甲酸在水层和氯仿层中分配,苯甲酸在水中有离解 现象,在氯仿层中将缔合成双分子:
水中: C6H5COOH= C6H5COO- + H+
=B* (T, p) RT ln ax,B
* B
(T
,
p)是在T,p时,当
xB
1,
x,B
1, ax,B
