第三章 立体表面交线的投影作图
工程制图PPT【第3章 基本体的投影及表面交线】

e’
e”
b” b’
[例]完成圆锥被切割后的水平投影和侧面投影。
5’6’ 3 ’4’ 1 ’2 ’
6” 4”
2”
5” 3”
1”
2
4
6
5
1
3
圆球的截交线
投影面平行面与球相交
截交线总是圆
[例] 完成圆球被正垂面切割后的水平投影和侧面投影。
b’
b”
g’h’ c’d ’ e’f ’
a’
h” d”
f”
g” c”
结论1
结论2
相贯线向大圆柱 的轴线方向凸起
两圆柱相交
[例]求两圆柱的相贯
线。
1 ’ 5’ 6’ 3 ’ 2 ’4’
1 ”3” 5”6”
4”
2”
01 分析形状 02 作特殊点
03 作一般点
4
1
3
5
6
2
Ⅳ Ⅲ
Ⅰ Ⅴ
Ⅵ Ⅱ
04 判断可见性 05 平滑连接 06 整理轮廓
两圆柱正交产生相贯线的形式 两外表面相交 外表面与内表面相交 两内表面相交
外表面与内表面相交
1’
3’
2 ’4’
1 ”3”
4”
2”
4
1
3
2
两内表面相交
1’
3’
2 ’4’
1 ”3” 2”
4”
4
1
3
2
求圆柱被穿竖孔和横孔后的相贯线
圆柱与圆锥相交 [例]求圆柱与圆锥正交时相贯线的投影。
3’
4’
5’7’
6’8’
1 ’2’
3“4”
7”8“
5”6“
1”
2”
立体表面交线的投影PPT

虚虚相贯
2、相贯线的主要性质 ★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线 (通常由直线和曲线组成)或空间曲线。
★ 共有性
相贯线是两立体表面的共有线(同时也是分界线)。
其作图实质是找出相贯的两立体表面的若干共有点 的投影。
3、相贯线的求法 • 表面取点法
利用投影的积聚性直接找点。
例2:圆锥被水平面截切,求出截交线的另外两个投影。
具体步骤如下:
(1)先求特殊点。
3’ 2’ 1’ 5” 4” 3” 2” 1”
(4’) (5’)
(2)再求一般点。
(3)依次光滑连接各点。
5
4 3
2 1
平面与圆锥相交
例3:求圆锥被截切后的正面投影.
分析: 截交线的正面投影为双曲线.
作图: 1 、求特殊点。
=45°
例2、 补画被挖切后立体的投影 。
分 析: 该立体是在圆柱筒的上
部开出一个方槽后形成的。 构成方槽的平面为垂直
于轴线的水平P和两个平行 于轴线的侧平面Q 。它们与 圆柱体和孔的表面都有交线, 平面P与圆柱的交线为圆弧, 平面Q与圆柱的交线为直线, 平面P和Q彼此相交于直线 段。
平面与圆柱相交
y
在相贯线水平投影 上任取一点 。
1``(2″() 6″) (3)判别可见性, 5`` 3`` 按顺序光滑连接。
4″
外表面和外表面相交
4
1
y
2
5 36
相贯线 1 y
53 辅助素线
两圆柱相交的三种形式 — 相贯线的画法
外表面和内表面相交
外表面和内表面相交
挖孔后
切割后
内表面和内表面相交
第三章 立体的投影及表面交线PPT课件

(3')1'
3"
1"
2' (4') 5'
(4) 3
4"
2" 5"
Ⅲ
ⅣⅠ ⅡⅤ
1 (2) 5
图4-10 圆柱体开出一方槽的投影
32
③判断可见性,连线、加深
(3')1' 2' (4') 5'
(4) 3
3"
1"
4"
2" 5"
Ⅲ
ⅣⅠ ⅡⅤ
1 (2) 5
图4-12 圆柱体开出一方槽的投影
33
④检查、完成。
4״
7 ׳5 ׳6׳
5״ 6״
7״
5 7
6
3 1
2 4
19
我们采用的是 哪种解题方法?
积聚法!
20
例2:补全被截切六棱柱的水平投影和侧面投影
1’ 2’(3’)
4’(5’) 6’(7’)
1”
3”
2”
5”
4”
6”
7”
注意:
6
要逐个截平面分析和绘
制截交线。当平面体只有局
7
部被截切时,先假想为整体
常
平面
见 基本体
的
基
本
几
曲面
何 基本体
体
6
一、平面基本体
1.棱柱
⑴ 棱柱的组成
A
由两个底面和几个侧棱面
组成。侧棱面与侧棱面的交线
(B)
叫侧棱线,侧棱线相互平行。
⑵ 棱柱的三视图 ⑶ 棱先画柱反面映上底面取形点状的视图。
机械制图3_立体表面交线的投影作图

s’
V S
s” W
a’
X
m’
b’
c’d’
M
A d
m
a
d” m” Ba”(b”) C b c
c”
Y
圆锥的三面投影图
Z
s’
V S
s” W
a’
X
m’
b’
c’d’
M
A d
m
a
d” m” Ba”(b”) C b c
c”
Y
s’
s”
2’ m’ a’
已知圆锥面上M点
3’
m”
的水平投影m,求出 其m’和m”。
b’ d”
1'
2'3'
3"
4'5'
5"
6'7'
7"
8'
5
7
3
8
1
6
2
4
1" 8"
解题步骤
1.分析 截平面为正垂面,截交 线的侧面投影为圆,水平投影为
2" 椭圆;
2.求出截交线上的特殊点Ⅰ、 Ⅳ、 Ⅴ、 Ⅷ;
4" 3.求出若干个一般点Ⅱ、Ⅲ、
Ⅵ、Ⅶ;
4.光滑且顺次地连接各点,
6"
作出截交线,并且判别可见性
5.整理轮廓线。
s” W
m’
b’
c’d’
M
A d
m
a
d” m” Ba”(b”) C b c
c”
Y
圆锥的三面投影图
s’
s”
已知圆锥表面的点
M的正面投影m’,求
出M点的其它投影。
中职机械制图教学:第三章

.
【例3-1】画出图示平面切割体的三视图。
.
【例3-2】在四棱柱上切割一个通槽,已知通槽 的正面投影,求作水平和侧面投影。
.
二、平面切割回转曲面体
平面切割曲面体时,截交线的形状取决于曲面体表面 的形状以及截平面与曲面体的相对位置。
平面与回转曲面体相交时,其截交线一般为封闭的平 面曲线,特殊情况下是直线,或直线与平面曲线组成的封 闭的平面图形。
a
(2)圆柱面上取点
a
.
O A
O1 A1 a
利用投影 的积聚性
2.圆锥体表面取点
SO
(1) 轮廓线素线的投影与 曲面的可见性的判断
(2)圆锥面上取点
s●
●
A O1 ●s
★辅助直线法 ★辅助圆法
如何在圆锥面 过锥顶作 上作直线? 一条素线。
k(n)
n● s
k
●(n) k
.
3.圆球体表面取点
(1) 轮廓线的投影与
同一立体被多 个平面截切,要逐 个截平面进行截交 线的分析和作图。
●
解题步骤:
●
★空间及投影分析
截交线的形状
截交线的投影特性
●
★求截交线
●
★分析圆柱体轮廓素线的投影
.
例1:求左视图
解题步骤:
★空间及投影分析 截交线的形状 截交线的投影特性
★求截交线 ★分析圆柱体轮廓素线的投影
.
例2:求左视图
● ● ● ●
★找特殊点 ★补充中间点 ★光滑连接各点 ★分析轮廓线的
投影
.
3、 圆球表面的截交线
平面与圆球相交,截交线的形状都是圆,但 根据截平面与投影面的相对位置不同,其截交线 的投影可能为圆、椭圆或积聚成一条直线。 例:求半球体截切后的俯视图和左视图。
机械制图第三章 基本体及立体表面交线

基本体及立体表面交线
第一节 平面立体的投影
任何立体都是由表面(平面或曲面)所围成。 单一的几何立体称为基本体。 表面全部为平面的立体称为平面立体,如棱柱、棱锥、棱 台等。 表面为曲面或既有曲面又有平面的立体称为曲面立体,常 见的曲面立体是回转体,如圆柱、圆锥、球和圆环等,如 图3-1所示。
常 见 的 基 本 立 体
图3-21 圆锥体表面取点
(2) 辅助纬圆法。
(b)
图3-22 圆锥体表面取点
图3-23
常见圆锥的三面投影示例
三、圆球
球面是由母线圆(或半圆)绕其直径旋转而成。
图3-24 圆球的形成
1. 圆球的投影分析 圆球的三面投影均为与其直径相等的圆。它们分别
是球三个不同方向的轮廓圆的投影。
图3-25 圆球的投影分析
图3-15 圆柱体的三视图
画圆柱体投影时,一般先画出轴线和圆的中心 线及投影为圆的那个投影,然后画出其余投影。
*轮廓素线与圆柱体的对应
(a)
图3-16 圆柱体的轮廓素线分析
(b)
3. 圆柱面上取点
已知圆柱表面上点 M 、N 的正面 投影,求作它们的水平及侧面投影。
图3-17 圆柱体表面取点、取线
(d)
第二节 回转体的投影
表面由平面与曲面围成,或全部由曲面围成的立体称 为曲面立体。
常见曲面是回 转面,它是由一直 线或曲线以一定直 线为轴线回转形成。 由回转曲面组成的 立体,称回转体, 如圆柱体、圆锥体、 球体等。
图3-13 回转体的形成
一、圆柱体
圆柱体是由顶面、底面和圆柱面所组成。 圆柱面上任意一条平行于轴线的直线,称为圆柱面的素线。
棱柱的投影特征: 一面投影为多边形,其边是各棱面的积聚性投影;另两
03 基本立体及其表面交线的投影

X
后 前
a (a1)
c (c1 )
b (b1)
左
右
YH
1、度量关系:长对正、高平齐、宽相等。 2、位置关系:如图。
六棱 柱
空间分析
V YW
W
作图时,先画反映特征的水平投影,再 按投影规律完成其它两个投影。
a’’
六棱柱表面求点?
( b’ ) a’
b’’
b’’
b
作图分析:
b
a
(1) 由于前棱面的水平投影和侧面投影均具有积聚性,故可直接 求出a和a``。 (2) 由于左前棱面只有水平投影有积聚性,故只能利用积聚性 求出b,再根据YH=YW,由b和b`求出b``。
一、利用积聚性求相贯线
柱柱相贯 两圆柱的轴线分别垂直于不同的投影面时,相交的两圆 柱的表面相对于投影面有积聚性。
我们只讨论: 两轴线垂直相交的两圆柱的相贯线.
例24. 试求两轴线垂直相交圆柱相贯线的投影。
分析:两个圆柱体的圆柱面 分别在俯视图和左视图上具 有积聚性,因此,它们的相 贯线投影也分别处于这两个 积聚圆上,找出这两个投影, 其主视图投影就很容易求出 了。
第三章
基本立体及其表面交线的投影
§3.1 平面立体的投影 §3.2 曲面立体的投影
§3.3 平面立体的截交线
§3.4 回转体的截交线
§3.5 回转体的相贯线
常 见 的 基 本 立 体
平 面 平面+平面 立 体
棱柱
棱锥
圆柱 曲 面 立 体
曲面+平面
圆锥
曲面+曲面
圆球
圆环
画立体的投影图时,规定: 可见的轮廓线画粗实线, 不可见的轮廓线画细虚线。
第三章立体表面交线的投影作图

第三章⽴体表⾯交线的投影作图班级姓名学号 .装订线A.三⾓形B.平⾏线C.梯形D.三⾓形或四边形、五边形11. 平⾯与圆锥表⾯相交产⽣的交线可能是()。
A.椭圆 B.抛物线、三⾓形C.双曲线、圆、椭圆D.圆、椭圆、双曲线、抛物线、等腰三⾓形三、判断题:(每题2分,共30分) 1. 截交线上的点均为截平⾯与⽴体表⾯的公有点。
()2. 两⽴体表⾯相交产⽣的交线为截交线。
()3. 平⾯与⽴体表⾯相交产⽣的交线称相贯线。
()4. 两⽴体表⾯相交产⽣的交线为相贯线。
()5. 截交线是封闭的平⾯图形。
()6. 求作两回转体的相贯线,通常采⽤表⾯取点法(积聚性法)和辅助平⾯法。
()7. 截平⾯与圆柱轴线倾斜,截交线为椭圆或椭圆弧加直线。
()8. 截交线是空间折线或曲线。
()9. 当截平⾯(正垂⾯)与圆柱轴线(铅垂线)的夹⾓变化时,所得截交线--椭圆长轴的投影也相应变化,但短轴投影不变。
()10. 平⾯与⽴体表⾯相交产⽣的交线称截交线。
()11. 截平⾯与圆柱轴线平⾏,截交线为矩形。
()12. 平⾯切割圆锥产⽣截交线可能是椭圆、圆、抛物线或双曲线。
()13. 两等径正交相贯的圆柱所产⽣的相贯线某⼀投影为两条相交的直线。
()14. 相贯线⼀般是封闭的空间曲线。
()15. 平⾯切割球产⽣截交线可能是圆或椭圆。
()四、绘图题:(每题2分,共192分) 1. 曲⾯切割体补全三视图2. 补画视图中漏画的相贯线3. 完成平⾯体被切割后的三⾯投影班级姓名学号 .装订线4. 完成曲⾯体被切割后的三⾯投影5. 完成平⾯体被切割后的三⾯投影7. 补画视图中漏画的相贯线8. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影班级姓名学号 .装订线9. 选择正确的左视图(在括号内画" √ ")10. 补画视图中漏画的相贯线11. 补画视图中漏画的相贯线12. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影班级姓名学号 .装订线13. 完成平⾯体被切割后的三⾯投影14. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影15. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影16. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影17. 补画视图中漏画的相贯线班级姓名学号 .装订线18. 补画视图中漏画的相贯线19. 补画视图中漏画的相贯线20. 选择正确的左视图(在括号内画" √ ")21. 完成平⾯体被切割后的三⾯投影班级姓名学号 .装订线22. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影23. 补画视图中漏画的相贯线24. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影25. 完成曲⾯体被切割后的三⾯投影26. 完成平⾯体被切割后的三⾯投影班级姓名学号 .装订线27. 完成曲⾯体被切割后的三⾯投影28. 完成平⾯体被切割后的三⾯投影29. 完成平⾯体被切割后的三⾯投影30. 完成曲⾯体被切割后的三⾯投影32. 完成曲⾯体被切割后的三⾯投影班级姓名学号 .装订线33. 补画视图中漏画的相贯线34. 完成平⾯体被切割后的三⾯投影35. 完成平⾯体被切割后的三⾯投影36. 完成平⾯体被切割后的三⾯投影37. 曲⾯切割体补全三视图班级姓名学号 .装订线38. 完成曲⾯体被切割后的三⾯投影39. 完成平⾯体被切割后的三⾯投影40. 完成曲⾯体被切割后的三⾯投影41. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影42. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影班级姓名学号 .装订线43. 选择与主视图对应的俯视图及轴测图的编号填⼊表格内44. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影45. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影46. 完成平⾯体被切割后的三⾯投影47. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影48. 曲⾯切割体补全三视图班级姓名学号 .装订线49. 完成曲⾯体被切割后的三⾯投影50. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影51. 完成曲⾯体被切割后的三⾯投影52. 曲⾯切割体补全三视图班级姓名学号 .装订线53. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影54. 曲⾯切割体补全三视图55. 补画视图中漏画的相贯线57. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影班级姓名学号 .装订线58. 完成曲⾯体被切割后的三⾯投影59. 选择正确的左视图(在括号内画" √ ")60. 完成曲⾯体被切割后的三⾯投影61. 曲⾯切割体补全三视图62. 完成平⾯体被切割后的三⾯投影班级姓名学号 .装订线63. 完成曲⾯体被切割后的三⾯投影64. 完成曲⾯体被切割后的三⾯投影65. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影66. 完成平⾯体被切割后的三⾯投影67. 完成曲⾯体被切割后的三⾯投影班级姓名学号 .装订线68. 完成曲⾯体被切割后的三⾯投影69. 完成平⾯体被切割后的三⾯投影70. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影71. 补画视图中漏画的相贯线72. 完成曲⾯体被切割后的三⾯投影班级姓名学号 .装订线73. 完成曲⾯体被切割后的三⾯投影74. 完成平⾯体被切割后的三⾯投影75. 完成曲⾯体被切割后的三⾯投影76. 选择与三视图对应的轴测图编号填⼊括号内77. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影78. 补画视图中漏画的相贯线班级姓名学号 .装订线79. 完成平⾯体被切割后的三⾯投影80. 完成曲⾯体被切割后的三⾯投影81. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影82. 完成曲⾯体被切割后的三⾯投影班级姓名学号 .装订线83. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影84. 完成曲⾯体被切割后的三⾯投影85. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯点的另两个投影86. 完成平⾯体被切割后的三⾯投影87. 已知平⾯⽴体的两视图,补画第三视图,并作出⽴体表⾯两点的另两个投影88. 选择正确的左视图(在括号内画" √ ")。
第三章立体表面交线的三视图画法
b. 连线
c. 检查、加深
尤其注意检查回转体轮廓线的投影。
例:圆柱与圆柱相贯,求其相贯线。
●
●
●
●
●
●
●●Βιβλιοθήκη ●求相贯线的投影:
利用积聚性,采 用表面取点法。 ☆ 找特殊点 ☆ 补充中间点 ☆ 光滑连接
空间及投影分析: 小圆柱轴线垂直于H面,水平投影积聚为圆,根
据相贯线的共有性,相贯线的水平投影即为该圆。 大圆柱轴线垂直于W面,侧面投影积聚为圆,相贯 线的侧面投影在该圆上。
截平面 :用以截切物体的平面。 截交线 :截平面与物体表面的交线。
截断面 :因截平面的截切,在物体上形成的平面。
3.1 平面立体截交线的画法
一、平面立体截切的基本形式
截交线的性质:
•平面立体的截交线是一个由直线组成的封闭的平 面多边形,其形状取决于平面立体的形状及截平 面在平面立体上的截切位置。 •截交线是截平面与立体表面的共有线。
1(2)
1(2) 2 1
2
1
例:求左视图
截交线的空间形状是怎样的? 截交线的已知投影呢? 截交线的侧面投影是什么形 状?
● ●
●
● ● ● ●
●
●
●
●
●
★找特殊点 ★补充中间点 ★光滑连接各点
★分析轮廓线的投影
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
第三章基本几何体的投影
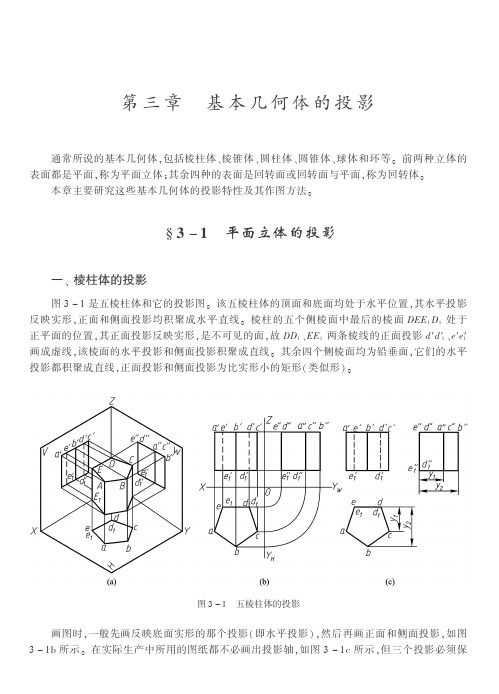
第三章 基本几何体的投影通常所说的基本几何体,包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。
前两种立体的表面都是平面,称为平面立体;其余四种的表面是回转面或回转面与平面,称为回转体。
本章主要研究这些基本几何体的投影特性及其作图方法。
§3-1 平面立体的投影一、棱柱体的投影图3-1是五棱柱体和它的投影图。
该五棱柱体的顶面和底面均处于水平位置,其水平投影反映实形,正面和侧面投影均积聚成水平直线。
棱柱的五个侧棱面中最后的棱面DEE1D1处于正平面的位置,其正面投影反映实形,是不可见的面,故DD1、EE1两条棱线的正面投影d′d′1、e′e′1画成虚线,该棱面的水平投影和侧面投影积聚成直线。
其余四个侧棱面均为铅垂面,它们的水平投影都积聚成直线,正面投影和侧面投影为比实形小的矩形(类似形)。
图3-1 五棱柱体的投影画图时,一般先画反映底面实形的那个投影(即水平投影),然后再画正面和侧面投影,如图3-1b所示。
在实际生产中所用的图纸都不必画出投影轴,如图3-1c所示,但三个投影必须保持左右、上下、前后的对应关系,即V 、H 两面投影左右对正,V 、W 两面投影上下平齐,H 、W 两面投影前后相等。
二、棱锥体的投影图3-2是正三棱锥体和它的投影图。
该三棱锥体的底面处于水平位置,其水平面投影反映实形,正面和侧面投影积聚成水平直线。
三棱锥的右侧棱面SBC 为正垂面,其正面投影s ′b ′c ′积聚成直线,水平面投影sbc 和侧面投影s ″b ″c ″为类似形。
前棱面SAB 和后棱面SAC 均为一般位置平面,因而,它们的三面投影均为类似形(正面投影两个三角形重合)。
图3-2 正三棱锥体的投影画图时,先画出底面三角形ABC 和锥顶S 的投影,然后顺次连接各棱线SA 、SB 、SC 的同面投影,如图3-2b所示。
通过棱柱和棱锥体的投影分析,可归纳如下几点:1)由于平面立体的棱线是直线,所以画平面立体的投影图就是先画出各棱线交点的投影,然后顺次连线,并注意区分可见性。
立体及其表面交线的投影知识.pptx

立体及其表面交线的投影 图3-5 圆球
立体及其表面交线的投影 图3-5 圆球
立体及其表面交线的投影
圆球表面上的点
已知圆球面上点A、B、C的正面投影a′、b′、c′,求 各点的其他投影,如图3-5(b)所示。因a′为可见,且在平 行于正面的最大圆上,故其水平投影a在水平对称中心线 上,侧面投影a″在垂直对称中心线上;b′为不可见,且在 垂直对称中心线上,故点B在平行于侧面的最大圆的后半 部,可由b′先求出b″,最后求出b。以上两点均为特殊位 置点,可直接作图求出其另外两投影。由于点c在球面上 不处于特殊位置,故需作辅助纬圆求解。
立体及其表面交线的投影
圆柱表面上的点
在图3-3(b)中,圆柱面上有两点M和N,已知其正 投影m′和n′,求另外两投影。由于点N在圆柱的转向轮 廓线上,其另外两投影可直接求出;而点M可利用圆 柱面有积聚性的投影,先求出点M的水平投影m,再由 m和m′求出m″。点M在圆柱面的右半部分,故其侧面 投影m″不可见。
立体及其表面交线的投影
2.2 圆锥 1. 圆锥面的形成 圆锥面是由一条直母线绕与它相交的轴线旋转而
成的。圆锥体由圆锥面和底面组成。
2. 圆锥的投影 图3-4表示一直立圆锥,它的正面投影和侧面投影 为同样大小的等腰三角形。正面投影s′a′和s′b′是圆锥面 的最左和最右素线的投影,它们把圆锥面分为前、后 两半;侧面投影s″c″和s″d″是圆锥面最前和最后素线的 投影,它们把圆锥面分为左、右两半。
立体及其表面交线的投影
作图: 先画出完整圆柱体的三视图,再按凹槽和切口的 宽度(左右方向)和深度依次画出正面投影和水平投 影,最后求出侧面投影。由于圆柱最前、最后素线的 上端被切去一段,使侧面投影的轮廓线向中心“退 缩”,呈“凸”字形。圆柱底部被切去的部分是左右 两边,最前、最后素线完整(图3-8(b))。
工程制图 第三章立体的投影及表面交线

圆
两条相交直线
椭圆
抛物线
双曲线
截平面垂直于圆锥 轴线,截交线为垂直 于轴线的圆。
截平面平行于圆锥轴 线,或截平面倾斜于截平 面过锥顶,截交线为两相 交直线。
截平面倾斜于圆 锥轴线,且b=f, 截交线为抛物线。
截平面倾斜于圆 锥轴线,且b>f, 截交线为椭圆。
截平面平行于圆锥 轴线,或截平面倾斜 于圆锥轴线,且b<f 截交线为双曲线。
截交线上的特殊点
极限点 转向点 特征点 结合点
1.
平面与圆柱相交
截平面平行于轴线, 交线为平行于轴线的 两条平行直线
截平面垂直于轴线, 交线为 圆
截平面倾斜于轴线, 交线为 椭圆
截平面垂直于圆柱 轴线,截交线为垂 直于轴线的圆
截平面平行于 圆柱轴线,截 交线平行于轴 线的两条直线
截平面倾斜于 圆柱轴线,截交 线为椭圆
截交线
3.1.1 平面与平面立体相交
由于平面立体是由平面围成的,截交线是封闭的平面多边 形,多边形的边是截平面与平面立体表面的交线。求截交线的 问题可以简化为求平面与平面的交线问题,进而简化为求直线 与平面交点的问题。
例1 三棱锥被一正垂面所截切,求截交线的投影。
s’ 3 s 3
2
1
a ’
b ’
c’
2
1 a(c) y
b
a 1 s 2
c 3
Ⅲ
y
Ⅰ
A
Ⅱ
B
b
分析:截平面与三棱柱的3条棱线都相交,所以截交线是一个三 角形。三角形的顶点为各棱线与平面的交点。可利用直线上点的投 影性质作出投影。
例2
求立体截切后的投影
现代工程制图基础教学课件第3章 立体及其表面交线的投影

轴线的水平投影
投影特点:
1) 轴线的水平投影积聚为一点 (对称中心线的交点)。
2) 圆母线的水平投影成为直线, 延长后通过轴线的有积聚性的水 平投影。
3) 圆心O 旋转成的水平圆的水 平投影,用点画线表示。
4) 正面投影中,上、下两条水 平线是圆母线上最高点C 和最低点 D 旋转形成的纬圆的正面投影。
交线 情况
截平面垂直于 轴线(θ=90°), 交线为圆
截平面倾斜 于轴线,且θ > 90°,交线为椭圆
截平面倾斜 于轴线,且θ =α,交线为抛 物线
截平面倾斜于 轴线,且θ <α,或 平行于轴线 (θ=0°),交线为 双曲线
第3章 立体及其表面交线的投影
截平面通过 锥顶,交线为通 过锥顶的两条相 交直线
第3章 立体及其表面交线的投影
3.1 平面立体的投影及其与平面相交 3.2 曲面立体的投影及其与平面相交 3.3 相贯线
第3章 立体及其表面交线的投影
返回封面
3.1 平面立体的投影及其与平面相交
3.1.1 平面立体的投影 3.1.2 平面与平面立体相交
第3章 立体及其表面交线的投影
返回章目录
基本立体可分为
作截交线的步骤:
1) 求特殊点
转向轮廓线上的点
特殊点是一些能确定截交线形状和范围的点,包括 截交线在对称轴上的顶点
2) 求一般点
极限位置点
为了能光滑地作出截交线的投影,还需在特殊点之间再作一些中间点。
3) 判别可见性并光滑连线
第3章 立体及其表面交线的投影
返回章目录
平面与圆柱面的交线有三种情况:
s
●
s●
s
注意:转向轮廓素线的投影与可见性的判断
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③判断可见性,光滑连线,完成作图。
Ⅴ Ⅵ
5'
5" 6"
6'
5⑹
(c) 求一般点
(d) 光滑连线
图3-32 两圆柱垂直相交时的相贯线
⑶相贯线的简化画法
图3-33 相贯线的简化画法
完成习题册36页1.2
三.两圆柱相对大小的变化对相贯线的影响
图3-34 两圆柱的直径大小不同,相贯线不同
四.两圆柱相贯的三种形式
2' (4') 5' 6' (4") 3" (2") 1" 5" 6"
1' (3')
Ⅳ Ⅲ Ⅰ Ⅱ Ⅴ Ⅵ
(a) 题图 图3-24 圆柱体开出一方槽的投影
3
4 2⑹ 5
( b)
1
③判断可见性,连线、加深
1' (3')
2' (4') 5' 6'
(4") 3"
(2") 1" 5"
6"
3
4 2⑹ 5
1
(c) 图3-24 圆柱体开出一方槽的投影
作图步骤:
③画出切去Ⅲ部分的投影
(e) 图3-25 圆柱体切割后的投影
作图步骤:
④画出切去Ⅳ部分的投影,并检查、完成全图
(f) 图3-25 圆柱体切割后的投影
课堂练习
完成习题册 P33 (1)
小结
运用作特殊点的方法作曲立面体的截交线投影
作业布置: 完成习题册 P33 (2)(3)
课后反思
— 本章完 —
回 目 录
课后反思
本节内容难度大,课堂上主要以其中 较典型的为例讲解,学生能基本掌握简 单组合体相贯线的投影作图。
求特殊点 作中间点 判断可见性
光滑连线
二、利用表面上取点法作图 1.两圆柱相交
1' 2' (4') 4" 3" 1" 2"
⑴形体分析与投影分析;
⑵作图: ①先找特殊点:Ⅰ、Ⅱ、Ⅲ、Ⅳ 的投影;
3'
Ⅳ
1
4 2
(a) 题图
Ⅰ
Ⅱ
Ⅲ
(b) 形体分析,找特殊点
⑶
图3-32 两圆柱垂直相交时的相贯线
②再求一般点Ⅴ 、 Ⅵ的投影;
概 述:
立体包含基本立体和组合体。柱、锥、球、圆环等 几何体是组成机件的基本体,基本体的组合称组合体,本 章着重研究基本体、切割体和相贯体的形体特征,立体的 投影与作图方法。
§3-1 平面切割平面体
§3-2 平面切割圆柱体 §3-3平面与圆锥、球相交
§3-4相贯体的投影作图
• §3-1 平面切割平面体
图3-21 正四棱锥被一正垂面截切
作图:①求正垂面与立体的交线
3'
2' (4') 1' 4"
3" 2"
1"
4 3 1 2
(b) 求正垂面与立体的交线
图3-21 正四棱锥被一正垂面截切
作图:②整理、加深
3'
2' (4') 1' 4"
3" 2"
1"
4 3 1 2
(c) 整理、加深
图3-21 正四棱锥被一正垂面截切
(b)
3、 切割体的尺寸标注
图3-29 切割体的尺寸标注
课堂练习
完成习题册 P35(1)
习题册 P35(1)
作业布置: 完成习题册 P33.34.35
求截交线的投影小结
• 一般步骤:
1.分析被截立体和截平面之间的相对位置,再由它们对投 影面的相对位置,预见截交线的投影特征。 2.确定作图方法 表面取点法;辅助素线法;辅助纬圆法 3.作图
1' 2' (4') 3' 4" 1" (3") 2"
Ⅳ
Ⅲ Ⅱ
Ⅰ
4
1 3
2
(c) 求特殊点的投影 图3-37 求圆柱与圆锥正交的相贯线的投影
②用辅助平面法,求一般点 Ⅴ、Ⅵ、Ⅶ、Ⅷ的投影;
(7") 8" 5' (8') 6' (7') L
5" (6")
Ⅶ Ⅷ Ⅵ Ⅴ
R 8 5 6
(d) 求一般点的投影 图3-37 求圆柱与圆锥正交的相贯线的投影
§3-4 相贯体的投影作图
一、相贯体及相贯线的概念 相贯体—两相交的立体 相贯线—相交立体表面的交线 立体相贯三种情况: 1.平面体与平面体相贯 2.平面体与曲面体相贯 3.曲面体与曲面体相贯
相贯体
相贯线
图3-30 相贯的基本概念
两回转体相贯
相贯线性质: 1.相贯线为相交体的表面所共有; 2.相贯线一般为封闭光滑的空间曲线,特殊情况可能 为不封闭的空间曲线,也可能为平面曲线或直线。
④检查、完成
(d) 图3-24 圆柱体开出一方槽的投影
[例4] 求圆柱切割后的投影。
分析:形体分析与投影分析;
(a) 题图
(b) 形体分析
图3-25 圆柱体切割后的投影
作图步骤:
①作圆柱体的三视图
(c) 图3-25 圆柱体切割后的投影
作图步骤:
②画出切去Ⅰ、Ⅱ部分的投影
(d) 图3-25 圆柱体切割后的投影
§3-1 平面切割平面体
一、切割体及截交线的概念
• • • • 切割体——基本体被平面截切后的部分 截平面——截切立体的平面 截断面——立体被截切后的断面 截交线——截平面与立体表面的交线
• 截交线性质: 1.截交线是截平面与立体表面的共有线。 2.截交线是封闭的线条。 3.截交线的形状取决于: ① 立体表面的几何形状 ② 截平面与立体的相对位置
回转切割体的投影
1.圆柱切割体
表3-1 平面与圆柱相交的三种方式
[例1] 作出斜切圆柱体的截交线。
分析:空间分析与投影分析; 作图步骤: ①作圆柱体的三视图
②找特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ的投影 ③作一般点Ⅴ、Ⅵ、Ⅶ、Ⅷ的投影 ④光滑连线 3' (4') 2' 1' 1" 4" 3" 2" (8')
Ⅷ Ⅳ Ⅵ Ⅰ
R 7 L
③判断可见性,光滑连线,完成作图。
(e) 光滑连线 图3-37 求圆柱与圆锥正交的相贯线的投影
六、回转体相交的特殊情况
1. 两相交回转体同轴——相贯线为垂直于公共回转轴线的圆
图3-38 同轴回转体的相贯线
2.公切于球的两圆柱或圆柱与圆锥相贯——相贯线为椭圆
图3-39 公切于球的两圆柱或圆柱与圆锥的相贯线
图3-26 圆锥体切割后的投影
课堂练习
完成习题册 P34(1)(2)
习题册 P34(1)
习题册 P34(2)
2.圆球切割体
平面与球面的交线总是圆
图3-27 平面与球面交线的基本作图
[例1] 画出立体的投影
解:分析:形体与投影分析; 作图:①完成平面P 的投影 ②完成平面Q的投影
Q
P
(a) 图3-28 球体切割后的投影
• • • •
作图要领: 作图开始之前,对相贯线的形状、投影特征有个初步 的分析和预见; 相交物体有圆柱,可利用积聚性投影,找出相贯线未 知投影; 弄清辅助平面法的作图原理; 认真检查作图结果。
注意: • 根据相交体的形状、相交体的相对位置、相交体与投 影面的相对位置来选择辅助平面。 • 同一题,可根据所求共同点的位置不同而选不同的辅 助平面。 • 辅助平面为特殊位置平面。
七、相交回转体的尺寸注法
图3-40 相交回转体的尺寸注法
完成习题册37页1.2
求相贯线的投影小结
• 一般步骤: 1.分析相贯线形状,对投影特征有个初步的分析和 预见; 2.对组合体运用形体分析法; 3.借助特殊点的相对位置,分析判断交线趋势和大 概形状。 4.作图 注意: • 影响交线的三个主要因素: 相交物体的表面性质、相对位置、相对尺寸大小 • 记熟一些典型表面相贯线的投影特征 • 善于联系整体相交分析和解决部分形体相交问题
• 作图步骤:
求特殊点
作中间点
判断可见性
光滑连线
特殊点: 转向轮廓线上的共有点;极限点;对称轴上的顶点。
课后反思
本节内容难度大,课堂上主要以其中 较典型的为例讲解,学生能基本掌握圆 锥和球体被切割后的投影作图。
• §3-4 相贯体的投影作图
• 班别:17秋数模班 上课时间:2017年12月27日1-2节
作图: ③检查、完成
(d) 检查、完成
图3-21 正四棱锥被一正垂面截切
课堂练习
完成习题册 P30 (2)
小结
运用作特殊点的方法作平面体的截交线投影
作业布置: 完成习题册 P30.31.32
课后反思
本节内容难度较大,课件上例子引 用较多,学生能基本掌握平面体被切割 后的投影作图,课件不够生动,需改进! 加动画
第三章 截交线与相贯线的投影作图 (立体表面交线的投影作图)
本章教学目标要求: 1.要求学生掌握平面切割立体截交线的投影作图 2.要求学生熟练运用作特殊点的方法作曲面体的 截交线投影 3.掌握相贯线的画法和识读,常见的相贯线类型 本章重点难点: 平面切割立体截交线的投影作图,相贯线的画法 和识读
回 目 录
(a)
相贯线为封闭 的空间曲线
பைடு நூலகம்
(b) 相贯线为不封闭 的空间曲线
(c) 相贯线为平面曲线
(d) 相贯线为直线
