盖斯定律
盖斯定律

17
解: 设计Ag + 1/2Cl2 = AgCl(s)反应热力学循环 Ag(s) + 1/2Cl2 = AgCl(s)
rH
Ag+(aq) + Cl (aq) fH (Ag+, aq) = 105.4 kJmol-1 fH (Cl ,,aq) = 167.3 kJmol-1 AgCl(s)的生成热为: fHm=fH(Ag+,aq)+fHm(Cl , aq) + rH = 105.4 + (167.3) + (65.3)
反应CO(g)+1/2O2(g) CO2(g) 的焓变 rHm 为:
rHm = fHm,CO2(g) - fHm,CO(g)
5
H2(g) + 1/2O2(g) H2O (l), 可以两种不同途径进行 rH H2(g) + 1/2O2(g) H2O (l) rH = -285.8 kJmol-1
22
•燃烧热的概念 •由燃烧热计算反应热公式: • rHm = cHm,(反应物) - cHm,(生成 物) (p34)
由燃烧热计算反应热
23
§3-7 过程的自发性, 熵, 热力学 第二、三定律
一、过程的自发性
●自发过程:不凭借外力就能发生的过程称为
自发过程
●自发反应:不凭借外力就能发生的反应称为
H2= B.E.(生)
rHm= 2fH (HF,g) fHm (H2,g) fHm (F2,g)
= 268.6 2 = 537.2 kJmol-1 rHm = H 1 H2 2 537.2 = 436 + 155 H2 2 H2 = 1/2(436 + 155 + 537.2)= 564.1kJmol-1 即,H—F键的键焓为64.1kJmol-1。
《盖斯定律》 知识清单

《盖斯定律》知识清单一、盖斯定律的定义盖斯定律是指在条件不变的情况下,化学反应的热效应只与起始和终了状态有关,而与变化途径无关。
换句话说,不管化学反应是一步完成还是分几步完成,其反应热是相同的。
为了更好地理解这一定义,我们可以想象一个从 A 地到 B 地的旅程。
无论您是选择直接的路线到达 B 地,还是经过了一些迂回的道路最终到达 B 地,两地之间的距离(就好比反应的热效应)是不会改变的。
二、盖斯定律的原理盖斯定律的原理基于能量守恒定律。
在化学反应中,能量的转化和守恒是始终不变的。
当反应物转化为生成物时,所释放或吸收的能量是一定的,不会因为反应的步骤不同而有所改变。
例如,碳燃烧生成二氧化碳,可以一步完成(直接燃烧生成二氧化碳),也可以分两步进行(先燃烧生成一氧化碳,一氧化碳再燃烧生成二氧化碳),但总的能量变化是相同的。
三、盖斯定律的应用1、计算难以直接测量的反应热有些化学反应的反应热很难直接通过实验测量得到,但我们可以通过盖斯定律,利用已知反应的热效应来计算。
比如,要计算反应 C(s) + 1/2O₂(g) = CO(g) 的反应热,我们可能无法直接测量,但如果我们知道反应 C(s) + O₂(g) = CO₂(g) 和反应CO(g) + 1/2O₂(g) = CO₂(g) 的反应热,就可以通过盖斯定律来计算出目标反应的反应热。
2、设计合理的反应途径在化工生产中,为了提高反应的效率、降低成本等,我们可以根据盖斯定律来设计合理的反应途径。
例如,在合成氨的工业生产中,通过对反应步骤和条件的优化,以达到提高产率、节约能源的目的。
3、比较不同反应的热效应通过盖斯定律,我们可以将不同的反应转化为具有相同终态和始态的反应,从而比较它们的热效应大小。
四、盖斯定律的计算方法1、虚拟路径法假设一个反应可以通过多种途径完成,我们可以虚拟出一条与已知反应相关的路径,然后根据盖斯定律进行计算。
例如,已知反应 A + B = C 的反应热为ΔH₁,反应 C = D 的反应热为ΔH₂,要计算反应 A + B = D 的反应热,可以将两个反应相加,得到 A + B = C +(C = D) = D,反应热为ΔH₁+ΔH₂。
盖斯定律的内容

盖斯定律的内容弗里德曼-盖斯定律是物理学家弗里德曼·盖斯的名字,他提出的一个基本物理学原理,即“物质的总势能保持不变,这一原理也被称为物质势能守恒定律”。
弗里德曼-盖斯定律通常被形象地称为“物质楔子(桩)”,因为它表明了在一切变化中,物质总量是恒定的,从而体现了变化过程中物质总量的势能保持不变。
物质势能守恒定律是现代物理学中最基本的定律,不仅是所有物理学规律的基础,也是物理过程及其产生的工程应用的基础。
它可以应用于任何system,以描述物质总量的保持:也就是说,它表明在某一系统中,物质的总量:原子数无论是在运动、发生变化,或在发生化学反应时,其总量都是不变的。
物质势能守恒定律是自然界最基本的定律之一。
在化学反应中,反应和生成物的原子数是一样的。
因此,从物质守恒定律的角度来说,在化学反应中,物质的总量是不变的。
在典型的机械系统中,可以用弗里德曼-盖斯定律来描述机械系统的能量守恒。
比如,处于物理内力的作用下,当物体的运动方向改变时,势能会变化,但所有的物质势能统统会恒定,即,总势能保持不变。
例如,在滑行坡、跳跃和滚动中,某一物体受重力及其他力作用,会出现势能变化,然而该物体的物质总量是不变的。
由于弗里德曼~盖斯定律表明了物质总量的守恒,因此在核反应中也能发挥作用。
由于大量的能量随着电子而释放,一个原子的碎片可以转化为其他更小的原子,但是使用弗里德曼-盖斯定律,由于发生核反应时原子数量没有发生变化,所以可以确定该反应不会增加物质总量,即使原子发出了大量的能量,物质总量也不变。
此外,弗里德曼·盖斯定律还可以用于研究电力系统,它主要是指在一个电路中,电势能保持不变,即,从蓄电池向电路注入的电能,相当于用电位器或其他电气器件发出的电能,即电势能的总量保持不变。
总的来说,弗里德曼-盖斯定律是物理学的基础,对工程领域也有重要的影响,它在我们的日常生活中也扮演着重要的角色。
而且,弗里德曼-盖斯定律也是科学研究中最基本的物理学定律之一,用来表示在物理/化学、电学/机械等过程中物质的总量保持不变,是研究这些过程的基础和保证。
盖斯定律的原理及应用

盖斯定律的原理及应用1. 引言盖斯定律是流体力学中的基本定律之一,描述了管道中流体的流动行为。
它由爱尔兰工程师亨利·盖斯于1799年提出,是流体力学领域中的重要原理。
本文将介绍盖斯定律的基本原理以及其在实际应用中的作用。
2. 盖斯定律的原理盖斯定律表述了液体或气体通过管道时的流量与压力之间的关系。
根据盖斯定律,管道内流体的流量Q与压力差△P之间呈线性关系。
具体可以用以下公式表示:Q = kA△P其中,Q表示流量,A表示管道的横截面积,△P表示压力差,k 为比例常数。
该公式可以简化为Q ∝△P。
盖斯定律的基本原理可以通过流体的动量守恒和能量守恒来推导。
根据动量守恒定律,流体在管道中的动量变化等于施加在其上的力乘以时间。
而根据能量守恒定律,单位时间内流过管道某一截面的功率等于管道前后的压力差。
基于这两个定律,可以推导出盖斯定律的数学表达式。
3. 盖斯定律的应用盖斯定律在很多实际应用中起着重要作用,以下列举几个常见的应用场景:3.1 水管系统的设计在设计水管系统时,盖斯定律可以用于确定不同管段的管径。
通过测量进水口和出水口处的压力差,可以根据盖斯定律计算出流量,然后根据流量要求确定相应的管径。
这有助于确保水流的稳定性和高效性。
3.2 汽车制动系统盖斯定律在汽车制动系统中有广泛应用。
制动系统中的刹车片通过液压系统施加力来减速汽车。
根据盖斯定律,当刹车踏板施加的力增大时,液压系统中的压力增加,从而提高了制动力。
这使得汽车的制动更加可控和安全。
3.3 喷气发动机的燃烧室设计盖斯定律在喷气发动机的燃烧室设计中也起着重要作用。
喷气发动机中的燃油通过喷射和燃烧产生高温高压的气体,从而产生推力。
盖斯定律可以用于确定燃烧室中燃气的流动速度和压力分布,有助于提高燃烧效率和推力。
3.4 水力发电站的设计盖斯定律在水力发电站的设计中也有重要应用。
水力发电利用水流的动能来驱动发电机,产生电能。
通过应用盖斯定律,可以计算出水流的流量和压力,从而设计合适的水轮机和水管系统,以提高发电效率。
盖斯定律的定义式

盖斯定律的定义式盖斯定律是一条物理定律,适用于气体在不同压力和温度下的状态变化。
它描述了气体的压力、体积和温度之间的关系。
该定律是由英国科学家詹姆斯·盖斯于1662年发现的。
盖斯定律的定义式可以用数学表示为:P1V1/T1 = P2V2/T2。
在这个公式中,P1和P2分别代表气体在两个不同压力下的压强,V1和V2分别代表气体在两个不同体积下的体积,T1和T2分别代表气体在两个不同温度下的温度。
盖斯定律的核心思想是,在恒定温度下,气体的压力和体积成反比,即当压力增加时,体积减少。
这可以通过盖斯定律的定义式进行解释。
当气体受到压缩时,其分子之间的碰撞频率增加,从而导致压强的增加。
另一方面,当气体的体积减小时,分子之间的碰撞频率也会增加,从而导致压强的增加。
同样地,在恒定温度下,气体的压力和温度成正比,即当温度增加时,压力也会增加。
这可以通过盖斯定律的定义式进行解释。
当气体受热时,其分子的平均动能增加,分子运动更加活跃,从而导致压强的增加。
盖斯定律的实际应用非常广泛。
例如,在汽车引擎中,气缸内的燃烧气体受到活塞的压缩,根据盖斯定律,气体的压力随着体积的减小而增加,从而产生动力推动活塞。
此外,盖斯定律也被用于计算气体的体积和压力的变化,例如在高空气球、潜水艇和空气压缩机等设备的设计和操作中。
盖斯定律只适用于理想气体,即气体分子之间无相互作用力,体积可以忽略不计。
对于实际气体,分子之间的相互作用力和体积的影响不能忽略。
在这种情况下,需要使用其他更复杂的方程来描述气体的行为,如范德瓦尔斯方程和理查德方程等。
总结起来,盖斯定律是描述气体在不同压力和温度下的状态变化的物理定律。
它通过压力、体积和温度之间的关系来解释气体分子之间的碰撞和运动。
盖斯定律在物理学和工程学领域有着广泛的应用,但只适用于理想气体情况下的简化描述。
对于实际气体,需要考虑其他因素来准确描述其行为。
盖斯定律的定义式

盖斯定律的定义式盖斯定律是一个物理学定律,它描述了在流体通过管道时液体或气体的流动速度与管道横截面积之间的关系。
根据盖斯定律,当流体通过管道时,流体的速度是与管道横截面积成反比的,即流速越大,管道横截面积越小。
这一关系可以用以下数学公式表示:Q = AV其中,Q是流体通过管道的流量,A是管道的横截面积,V是流体的流速。
这个公式显示了流量与流速之间的关系。
盖斯定律的正式定义可以被表述为:在恒温条件下,单位时间内通过平面单位面积垂直到达或离开平面的理想流体流过量是与此平面垂直至单位时间内到达或离开该平面流体的速度的乘积成正比,且与此平面垂直的面积成正比。
也就是说,流体通过面积的流量与流体的速度成正比,并且与面积的大小成正比。
盖斯定律可以通过实验来验证。
首先,我们需要一个流体和一个管道。
我们可以通过改变管道的横截面积来改变流体的流速。
当我们改变管道的横截面积时,我们会发现流体的流速也会相应地改变。
如果我们将流体通过管道流出,并且将流出的流体量和流速进行测量,我们会发现它们之间存在着一定的关系,这正是盖斯定律所描述的关系。
盖斯定律的应用非常广泛。
例如,当我们在自来水龙头上打开水源时,我们会发现水流量和水压之间存在着一定的关系。
根据盖斯定律,当我们把水龙头的出水口变小,水流速度就会增加,从而增加水流量。
这一定律也可以用于设计和优化管道系统,以确保流体能够以所需的速度流动。
盖斯定律还可以应用于气体动力学和流体力学的研究中,用于分析和计算流体在管道、喷嘴、喷泉等装置中的运动。
它在工程设计、流体力学实验和计算流体力学等领域起着重要的作用。
需要注意的是,盖斯定律是在满足一定的条件下成立的。
首先,流体必须是理想流体,即不可压缩且不受黏性和湍流的影响。
其次,流体必须在稳态下进行流动,即流体的流速和流量保持恒定。
最后,流体必须是在恒温条件下流动,即流体的温度保持不变。
总结来说,盖斯定律描述了流体通过管道时流速与管道横截面积之间的关系,它可以通过实验验证,并广泛应用于工程设计和流体力学研究中。
1.2.1盖斯定律

④ 3C (s) +2Fe2O3(s)=4Fe(S)+3CO2(g)
∆H4=+467.9kJ·mol-1
⑤ 3CO(g) +Fe2O3(s)= 2Fe(S) + 3CO2(g)
∆H5=-24.8kJ·mol-1
2C (s) + O2(g) = 2CO (g)
ΔH
目标式=①式- ×⑤式+ ×④式
H2S(g)+
O (g)
2
= S(g)+H2O(g)
ΔH2
ΔH3
2S(g) = S2(g)
ΔH4
则ΔH4的正确表达式为 ( A )
A、ΔH4= (ΔH1+ΔH2−3ΔH3)
C、ΔH4=
(ΔH1+ΔH2−3ΔH3)
D、ΔH4=
B、ΔH4= (3ΔH3−ΔH1−ΔH2)
(ΔH1−ΔH2−3ΔH3)
理由;若不可以,能否设计路径使之可测定?
途径一
∆H1 + ∆H2 = ∆H3
∆H1 = ∆H3 - ∆H2
2CO(g)+O2(g)
ΔH1
ΔH2
2C(s)+2O2(g)
始态
2CO2 (g)
途径二
终态
8
环节2、知识精讲
思考与讨论
用图示的方法设计测定N2(g) + 2O2(g) = 2NO2(g)的∆H3的路径?
求 H2 (g) + O2 (g)= H2O (g) 的反应热 ΔH1。
H2 (g) +
O (g)
2
化学反应的盖斯定律

盖斯定律的数学表达
盖斯定律可以用数学表达式来表示。对于一个化学反应,其焓变(ΔH)可以表示为:ΔH = Σ(ΔHₘ)rxn + Σ(ΔHₘ)vap + Σ(ΔHₘ)solv等式中,ΔHₘ表示物质的标准摩尔生成焓,rxn表示化学反应方程式中各物质的计量系数,vap和solv分别表示气体和 溶液的体积变化。
反应热的比较
利用盖斯定律,可以比较不同化学反应的反应热 大小,从而判断反应的能量变化趋势。
3
反应热的测量
通过实验测量反应过程中温度的变化,结合盖斯 定律,可以更准确地测定化学反应的反应盖斯定律,可以选择出能量 最低的反应路径,即最有利于发 生的反应路径。
比较不同路径
实验结果分析与结论
分析数据
对实验数据进行统计分析,计算不同温度下反应 的焓变值。
验证盖斯定律
比较不同温度下反应的焓变值,验证盖斯定律的 正确性。
结论总结
根据实验结果得出结论,总结盖斯定律在化学反 应中的应用和意义。
盖斯定律在化学反应
04
中的应用
反应热的计算
1 2
计算反应热
盖斯定律可以用于计算化学反应的反应热,通过 已知的反应热和温度变化,可以求得未知反应的 反应热。
在化学合成中,可以利用盖斯定律优 化合成路径,降低能耗和减少环境污 染。
计算焓变和熵变
通过盖斯定律,可以计算化学反应的 焓变和熵变,进而了解反应的能量变 化和自发性的变化。
02
盖斯定律的原理
能量守恒原理
心理学天使盖斯定律

心理学天使盖斯定律天使盖斯定律(Engel's Law)是由德国经济学家埃恩斯·盖斯(Ernst Engel)于19世纪提出的经济学定律,他发现人们的收入增加时,他们花在食物上的比例减少,而非食物上的支出比例增加。
这一定律不仅可以在经济学领域得以应用,也能够在心理学上得到体现。
在心理学中,我们可以将盖斯定律理解为:随着个体收入增加,其在需求和欲望上的分配比例也会发生变化。
换句话说,随着收入的增加,人们会将更多的精力和资源投入到自身心理需求的满足上,而非物质需求。
盖斯定律所反映的心理学规律,对我们理解个体行为和心理需求的变化具有重要意义。
通过深入研究和理解盖斯定律,我们可以更好地把握个体的心理活动和需求变化,从而更好地指导个体的心理健康和幸福感。
本文将结合心理学理论和盖斯定律,探讨盖斯定律在心理学领域的应用和意义。
I. 盖斯定律的心理学解释盖斯定律的经济学内容已经有较为深入的研究和理解,但在心理学领域,对盖斯定律的解释和理解还相对较少。
从心理学的角度来看,盖斯定律可以被视作一个关于个体行为和欲望变化的一般规律。
随着个体收入的增加,个体的需求和欲望也会发生相应的变化。
在心理学中,盖斯定律可以被理解为需求和欲望的变化规律。
随着个体收入的增加,个体在需求和欲望上的分配比例也会发生变化。
简单来说,随着收入的增加,个体对非物质需求的关注度会相应增加,而对物质需求的关注度则会相应减少。
这一规律反映了人们内心深处的需求和欲望变化,而非简单的物质财富的积累。
盖斯定律的心理学解释,也可以从心理需求的层次结构来理解。
心理学家马斯洛(Abraham Maslow)提出的需求层次理论将个体的需求分为生理需求、安全需求、社交需求、自尊需求和自我实现需求五个层次。
盖斯定律所反映的心理学规律,可以被视作在这一需求层次结构下,随着收入的增加,个体更多地投入到非物质需求的满足上的一种心理规律。
需要注意的是,盖斯定律所反映的心理学规律并不意味着个体完全放弃对物质需求的追求。
盖斯定律及其计算

盖斯定律及其计算盖斯定律是描述毛细管流动的一种定律,由法国科学家亨利·盖斯于1799年提出,因此被称为盖斯定律。
它是液体通过毛细管流动时压强变化的定量描述,被广泛应用于理解液体在毛细管中的流动、液体表面张力的测量以及测量一些细小孔隙的直径等领域。
首先,我们来推导一下盖斯定律的数学表达式。
盖斯定律表明,在理想毛细管中,液体通过毛细管的流量与液体在毛细管两侧的压强差成正比。
设液体通过毛细管的流量为Q,液体在毛细管两侧的压强差为ΔP,液体的粘度为η,毛细管的半径为r,则盖斯定律可以表示为:Q=ΔPπr^4/8ηl其中,l为毛细管的长度。
从上述公式可以看出,液体通过毛细管的流量与毛细管的半径的四次方成正比,与压强差成正比,与液体的粘度成反比。
然而,盖斯定律只适用于细长而直径均匀的理想毛细管,在现实中的毛细管流动中有一些修正因素需要考虑。
例如,现实中的毛细管往往存在一定的粗糙度,从而导致流动的摩擦阻力增加,需要考虑修正因子;液体与毛细管表面之间的相互作用也会影响流动情况,需要考虑液-壁作用的修正因子。
这些修正因子可以通过实验测量得到,从而得到更准确的结果。
盖斯定律的一个重要应用就是测量液体的表面张力。
当液体在毛细管中流动时,液体上升的高度可以通过盖斯定律计算,进而得到液体的表面张力。
设液体在毛细管中上升的高度为h,毛细管的直径为d,则表面张力可以通过以下公式计算:T = 4ηh/gd其中,g为重力加速度。
表面张力的测量是盖斯定律在实际应用中的一种重要方式,它可以应用于液体的质量测量、液体粘度的测量以及液体中添加物的测量等领域。
总结起来,盖斯定律是描述液体通过毛细管流动的定律,它可以通过液体在毛细管两侧的压强差来计算液体通过毛细管的流量。
盖斯定律是描述理想毛细管流动的理论,需要考虑一些修正因子才能适用于实际情况。
盖斯定律的一个重要应用就是测量液体的表面张力,通过液体在毛细管中上升的高度可以计算液体的表面张力。
高中化学--盖斯定律

高中化学--盖斯定律盖斯定律(英语:Hess's law),又名反应热加成性定律(the law of additivity of reaction heat):若一反应为二个反应式的代数和时,其反应热为此二反应热的代数和。
也可表达为在条件不变的情况下,化学反应的热效应只与起始和终了状态有关,与变化途径无关。
它是由瑞士化学家Germain Hess发现并用于描述物质的热含量和能量变化与其反应路径无关,因而被称为赫斯定律。
1.含义(1)不管化学反应是一步完成或分几步完成,其反应热是相同的。
(2)化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
2.意义利用盖斯定律,可以间接地计算一些难以测定的反应热。
例如:C(s)+O2(g)===CO(g)上述反应在O2供应充分时,可燃烧生成CO2;O2供应不充分时,虽可生成CO,但同时还部分生成CO2。
因此该反应的ΔH不易测定,但是下述两个反应的ΔH却可以直接测得:(1)C(s)+O2(g)===CO2(g) ΔH1=-393.5 kJ·mol-1(2)CO(g)+O2(g)===CO2(g) ΔH2=-283.0kJ·mol-1根据盖斯定律,就可以计算出欲求反应的ΔH。
分析上述两个反应的关系,即知:ΔH=ΔH1-ΔH2。
则C(s)与O2(g)生成CO(g)的热化学方程式为C(s)+O2(g)===CO(g)ΔH=-110.5 kJ·mol-1。
注意:1、热化学方程式可以进行方向改变,方向改变时,反应热数值不变,符号相反;2、热化学方程式中物质的化学计量数和反应热可以同时改变倍数;3、热化学方程式可以叠加,叠加时,物质和反应热同时叠加。
3.练习1、已知下列热化学方程式:①Fe2O3(s)+3CO(g)===2Fe(s)+3CO2(g) ΔH1=-26.7 kJ·mol-1②3Fe2O3(s)+CO(g)===2Fe3O4(s)+CO2(g) ΔH2=-50.75 kJ·mol-1③Fe3O4(s)+CO(g)===3FeO(s)+CO2(g) ΔH3=-36.5 kJ·mol-1则反应FeO(s)+CO(g)===Fe(s)+CO2(g)的焓变为( )A.+7.28 kJ·mol-1 B.-7.28 kJ·mol-1C.+43.68 kJ·mol-1 D.-43.68 kJ·mol-1[解析] 根据盖斯定律,首先考虑目标反应与三个已知反应的关系,三个反应中,FeO、CO、Fe、CO2是要保留的,而与这四种物质无关的Fe2O3、Fe3O4要通过方程式的叠加处理予以消去:因此将①×3-②-③×2得到:6FeO(s)+6CO(g)=6Fe(s)+6CO2(g) ΔH=+43.65kJ·mol-1化简:FeO(s)+CO(g)=Fe(s)+CO2(g) ΔH=+7.28 kJ·mol-1答案A2.已知:H2O(g)===H2O(l) ΔH=Q1 kJ·mol-1C2H5OH(g)===C2H5OH(l) ΔH=Q2 kJ·mol-1C2H5OH(g)+3O2(g)===2CO2(g)+3H2O(g) ΔH=Q3 kJ·mol-1若使46 g酒精液体完全燃烧,最后恢复到室温,则放出的热量为( ) A.(Q1+Q2+Q3) KJ B.0.5(Q1+Q2+Q3)kJC.(0.5Q1-1.5Q2+0.5Q3) kJ D.(3Q1-Q2+Q3)kJ[解析] 46 g酒精即1 mol C2H5OH(l) 根据题意写出目标反应C2H5OH(l)+3O2(g)===2CO2(g)+3H2O(l) ΔH然后确定题中各反应与目标反应的关系则ΔH=(Q3-Q2+3Q1)kJ·mol-1 答案D3.能源问题是人类社会面临的重大课题,H2、CO、CH3OH都是重要的能源物质,它们的燃烧热依次为-285.8 kJ·mol-1、-282.5 kJ·mol-1、-726.7 kJ·mol-1。
《盖斯定律及应用》课件

对可逆过程的依赖性
总结词
盖斯定律的应用依赖于可逆过程,但实 际反应往往难以达到可逆状态。
VS
详细描述
盖斯定律仅适用于可逆过程,但在实际反 应中,由于各种因素的限制,如反应动力 学、热力学ቤተ መጻሕፍቲ ባይዱ化学平衡等,反应很难完全 达到可逆状态。因此,在应用盖斯定律时 需要考虑这些因素的影响。
对热力学过程的依赖性
详细描述
盖斯定律表明,一个系统的热力学状态变化只取决于起始和 最终状态,而与变化过程中所经历的中间状态无关。这意味 着,通过不同的反应路径,可以达到相同的最终状态,这些 路径的热力学行为是等效的。
盖斯定律的发现与起源
总结词
盖斯定律由苏格兰物理学家和数学家詹姆斯·克拉克·盖斯于19世纪提出。
详细描述
盖斯定律的发展趋势与展望
盖斯定律的理论研究进展
盖斯定律基本原理的完善
随着理论物理学的发展,盖斯定律的基本原理得到进一 步明确和阐述,为相关领域的研究提供更坚实的理论基 础。
盖斯定律与其他理论的融合
盖斯定律与热力学、统计力学等理论相互渗透,形成更 广泛的理论体系,推动相关领域的发展。
盖斯定律在交叉学科中的应用
要点二
详细描述
盖斯定律在多个领域中具有重要意义。在化学反应计算中 ,盖斯定律可以用于计算不同反应路径的能量变化,有助 于理解化学反应的本质和过程。在能源利用方面,盖斯定 律有助于优化能源转换过程,提高能源利用效率。此外, 在环境保护领域,盖斯定律可以帮助我们更好地理解和控 制环境污染物的生成和转化过程。
总结词
盖斯定律的应用受到热力学过程的限制,不 适用于非热力学平衡过程。
详细描述
盖斯定律适用于等温、等压或绝热过程,但 不适用于非热力学平衡过程。在非平衡过程 中,化学反应的热效应不仅与反应途径有关 ,还与反应条件有关。因此,在应用盖斯定 律时需要确保所研究的反应过程符合热力学 的基本原理。
盖斯定律定义

盖斯定律定义什么是盖斯定律?盖斯定律(Gates’ Law)是由微软公司的联合创始人比尔·盖茨(Bill Gates)提出的一个观点。
该定律指出:“计算机软硬件的发展速度每18个月翻一番。
”这一定律也被称为“盖斯定律”。
盖斯定律是对计算机技术发展速度的一种描述和预测。
根据这个定律,计算机的处理能力、存储容量和传输速度等方面的性能将以指数级增长。
换句话说,计算机技术将以非常快的速度不断进步和发展。
盖斯定律的由来盖斯定律最早是由比尔·盖茨在1965年提出的。
当时他观察到计算机技术的发展速度非常快,而且这种发展速度呈现出指数级增长的趋势。
他通过对计算机硬件和软件的发展进行研究和分析,总结出了这个定律。
在过去的几十年里,盖斯定律一直被广泛应用于计算机科学和信息技术领域。
它不仅是对计算机技术发展速度的一种描述,还是对计算机产业发展趋势的一种预测。
盖斯定律的意义盖斯定律的意义在于提醒人们计算机技术的发展速度是非常快的,并且这种速度呈现出指数级增长的趋势。
这意味着计算机领域的创新和进步将会非常迅速,我们将会看到更多更强大的计算机技术和应用的出现。
盖斯定律的发现和应用也对计算机产业的发展起到了重要的推动作用。
它鼓励人们不断探索和创新,推动计算机技术的进步。
同时,它也为计算机产业的发展提供了一种预测和规划的依据,帮助企业和研究机构制定战略和决策。
盖斯定律的影响盖斯定律的影响在计算机科学和信息技术领域是巨大的。
它激发了无数人对计算机技术的研究和开发,推动了计算机产业的蓬勃发展。
盖斯定律的应用也促使人们不断追求计算机技术的创新和突破。
在过去的几十年里,我们已经见证了计算机硬件和软件的巨大进步,从大型机到个人电脑,再到移动设备和云计算,计算机技术的发展给人们的生活带来了巨大的改变。
盖斯定律的影响还延伸到了其他领域。
随着计算机技术的发展,它与其他学科的交叉融合越来越紧密,如人工智能、大数据、物联网等。
盖斯定律

2、已知燃烧热求ΔH
已知:CH4(g) 、H2(g)、CO的燃烧热(△H)分别为- 890.3kJ/mol、-285.8 kJ/mol、-285.0 kJ/mol, 根据已知数据计算反应CH4(g)+CO2(g)===2CO(g)+ 2H2(g) △H=
①CH4(g)+2O2(g)=CO2(g)+2H2O(l)△H=−890.3kJ⋅mol−1 ②H2(g)+1/2O2(g)=H2O(l)△H=−285.8kJ⋅mol−1 ③CO(g)+1/2O2(g)=CO2(g)△H=−285.0kJ⋅mol−1 依据盖斯定律①−②×2−③×2得到: CH4(g)+CO2(g)=2CO(g)+2H2(g)△H=+251.3KJ/mol
724 kJ能量 ×
4、白磷与氧可发生如下反应:P4+5O2=P4O10。已知断 裂下列化学键需要吸收的能量分别为:P-P akJ·mol-1、 P-O bkJ·mol-1、P=O ckJ·mol-1、O=O dkJ·mol-1
则该反应的△H为? (6a+5d-4c-12b)kห้องสมุดไป่ตู้·mol1
5、1.7 g NH3(g)发生催化氧化反应生成气态产物,放出 22.67 kJ的热量写出其热化学反应方程式
−41kJ/mol
A ×
2、下列实验装置(加热装置)或操作合理的是
盐酸
Na2SiO3溶液
A.除去 SO2 气 B.中和热 C.吸收 D.证明碳酸的 体中的 HCl 的测定 氨气 酸性比硅酸强
3.已知断裂1 mol N-N 键吸收193 kJ热量,断裂1 mol N≡N键吸收941 kJ热量,且N4的结构为
则1 mol N4气体转化为N2时要吸收
简述盖斯定律

简述盖斯定律
盖斯定律是经济学中一种基本定律,又称盖斯供求定律(Gresham's Law),它指出:在有固定的汇率的情况下,优质货币会被劣质货币取代,从而形成一种“推搡”现象。
盖斯定律由16世纪英国银行家、经济学家、外交家、法官、会计师盖斯(Thomas Gresham)首先提出。
盖斯定律可以从以下几个角度解释:首先,它表明在有固定的汇率的情况下,优质货币的价值会低于劣质货币,从而使得劣质货币充斥市场,优质货币却被收藏者购买起来;其次,它指出,由于优质货币不会流通在市场中,因此汇率的固定不会改变;最后,它指出,在有固定汇率的情况下,劣质货币会取代优质货币,从而导致优质货币流通的减少。
盖斯定律的理论实践价值对经济和投资起到重要作用,它有助于实现经济稳定,促进货币的流通,防止货币的恶性通货膨胀等。
盖斯定律ppt课件

【思考与讨论】
游览一座山峰你喜欢徒步呢还是坐缆车?
终态 h = 300 m
上升的高度和势能的变化只与始态和终态的海拔差有关
【思考与讨论】
反应热与 途径无关
反应热研究的是化学反应前后能量的变化
始态
终态
反应热研究的是化学反应前后能量的变化,与途径无关
① C(s) + O2(g) = CO2(g)
ΔH1= −393.5kJ/mol
② CO(g) + 1/2O2(g) = CO2(g) ΔH2= −283.0kJ/mol ③ C(s) + 1/2O2(g) = CO(g) ΔH3=?
C(s) + 1/2O2(g) = CO(g) ΔH3=?
+) CO(g) + 1/2O2(g) = CO2(g) ΔH2= −283.0 kJ/mol
若不可以,能否设计路径使之可测定?
很难直接测得这个反应的反应热,可通 过盖斯定律获得它们的反应热数据。
思路1:虚拟路径法
思路2:代数运算法
盖斯定律——虚拟路径法
① C(s) + O2(g) = CO2(g)
ΔH1= −393.5kJ/mol
② CO(g) + 1/2O2(g) = CO2(g) ΔH2= −283.0kJ/mol
2△H3= -571.6 kJ/mol
+) 2CO2(g)+2H2O(l) =CH3COOH(l)+2O2(g) -△H1= 870.3 kJ/mol
--------------------------------------------------------------------------------------------------------------------------------------
盖斯定律-

盖斯定律盖斯定律,亦称为“比尔盖斯定律”、“盖斯法则”,指出了计算机软件的生产与质量之间的不可逆关系。
它的全称是“比尔盖斯定律”(Bill Gates' Law),是由微软的比尔盖茨在20世纪80年代初提出的。
这一定律提出了生产组件化软件的方法,以使软件系统的适应性、可维护性和可扩展性得到提高,从而缩短了开发周期和降低了成本。
盖斯定律的本质意义是:增加人员和时间,可以增加系统的大小、调整和修正软件缺陷,但是无法更正低造的架构、低效的算法和设计,所以在软件设计的初期就要考虑到维护的问题。
接下来本文将对盖斯定律的含义、原理、特点和应用进行详细阐述。
一、盖斯定律的含义盖斯定律的核心思想是:软件开发是一种难以逆转的过程,除非在软件设计的初期就考虑到软件维护的问题,否则在软件开发的后期进行修改将会是非常困难甚至是不可能的。
这是因为软件开发具有渐进式的特点,即如果软件系统在设计中未考虑到后期维护的问题,那么软件的复杂程度将会越来越大,任何一次修改都会对系统产生巨大的影响,而维护成本也会随之上升。
二、盖斯定律的原理盖斯定律的原理主要包括两个方面:一是软件开发的成本非线性增长,二是软件代码的复杂性具有时间性质。
首先,盖斯定律所表达的非线性增长法则是指,随着软件系统的规模增加,软件开发所需的成本也相应地增加,并呈现出非线性增长。
因此,我们要花费较少的成本开发小规模的软件,但是随着软件规模的增加,成本将呈指数式增长,这是一个非常显著的特点。
比如说,单纯在一个程序上修补一个 Bug 可能只需要几分钟的时间,但是如果在一个庞大的系统中发现了一个 Bug,那么修复这个 Bug 可能需要数天乃至数周的时间。
其次,软件代码的复杂性具有时间性质,这意味着软件系统的复杂性与时间的累积逐渐增加。
在软件开发过程中,每个新增的功能都会向系统的复杂性增加一些贡献,而且随着时间的推移,这种累积将会成倍增加。
例如,某个软件系统在初期只有一小部分代码,而随着时间的推移,代码会逐渐增加,代码的复杂性也会随之增加,这使得软件的维护成本逐年增加。
盖斯定律的例题及解析

盖斯定律的例题及解析一、什么是盖斯定律盖斯定律(Gauss’s Law),也称高斯定理,是电磁学中的基本定律之一,用于描述电场的性质。
根据盖斯定律,通过任何闭合曲面的电通量等于该闭合曲面内的电荷总量除以真空电容率。
数学公式表示为:其中,S为闭合曲面,E为电场强度,dS为曲面上的面元,Q为闭合曲面内的电荷总量,ε₀为真空电容率。
二、盖斯定律的应用1. 理解电场盖斯定律可以帮助我们理解电场的分布情况。
通过计算电通量,可以确定电场是从正电荷向外发散还是向内收敛。
当闭合曲面内没有电荷时,电通量为零,表示电场无源。
而当闭合曲面内有电荷时,电通量不为零,表示电场有源。
2. 计算电场强度通过盖斯定律,可以利用已知的电荷分布计算出电场强度。
首先选择一个合适的闭合曲面,使得计算电通量相对简便。
然后根据所选曲面的形状和对称性,确定哪些面元的电通量可以直接求得。
最后,根据高斯定律公式计算出电场强度。
3. 研究电荷分布盖斯定律也可用于研究电荷的分布情况。
通过观察闭合曲面内的电通量,可以推断出曲面内的电荷分布情况。
例如,如果电通量是正的,表示闭合曲面内存在正电荷;如果电通量是负的,表示闭合曲面内存在负电荷。
通过这种方式,我们可以了解电荷在空间中的分布情况。
三、盖斯定律的例题分析1. 球形电荷分布假设有一个半径为R的均匀带电球体,其电荷密度为ρ。
求球心处的电场强度。
解析:1.选择一个球形闭合曲面,以球心为球心,半径为r(r > R)。
2.根据球对称性,球面上的所有面元的电通量都相等。
由于电场和面元的夹角为零度,电通量可直接求得。
3.根据盖斯定律公式,电通量等于在球体内的电荷总量除以真空电容率。
公式表示为:4.解方程得到电场强度E。
2. 无限长均匀带电线假设有一条无限长均匀带电线,线密度为λ。
求距离线上一点P距离为r处的电场强度。
解析:1.选择一个以点P为球心的球形闭合曲面,半径为r。
2.根据线对称性,球面上的所有面元的电通量都相等。
盖斯定律的定义式

盖斯定律的定义式
盖斯定律的定义式是:一个反应,在定压或定容条件下,不论是一步完成还是分几步完成,其反应热是相同的,总反应方程式的焓变等于各部分分布反应按一定系数比加和的焓变。
盖斯定律(Hess's law),又名反应热加成性定律(the law of additivity of reaction heat),即若一化学反应为两个反应式的代数和时,其反应热为这二个反应的反应热的代数和。
该定律也可表达为在条件不变的情况下,化学反应的热效应只与起始和终了状态有关,与变化途径无关。
该定律是化学热力学的基础,由俄国化学家盖斯(G.H.Hess)发现并提出,因而被称为盖斯定律。
高中化学 盖斯定律
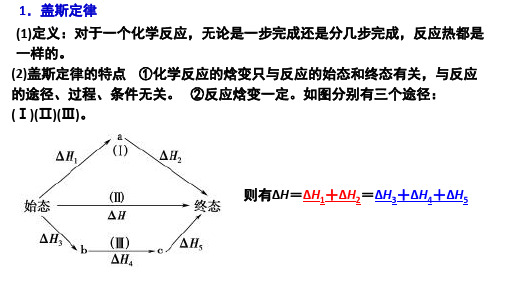
不能很好的控制反应的程度,故不能直接通过实验测得△H1
CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
(1)消元法 写出目标方程式确定“多余物质”(要消去的物质)然后用消元法逐一消去 “多余物质”,导出“四则运算式”
分析: CO(g) △H1 + △H2 = △H3
H1
H2
C(s)
H3 CO2(g)
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
— CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+1/2O2(g) = CO(g) △H1=?
∴△H1 = △H3 - △H2 = -393.5 kJ/mol -(-283.0 kJ/mol)= -110.5 kJ/mol
ΔH2
C
ΔH3=ΔH1+ΔH2 ΔH1=ΔH3- ΔH2
(2)唯一法:对于比较复杂的几步反应,可以换个角度: 找唯 一,调方向,改倍数,不多余
测定 C(s)+1/2O2(g)=CO(g) 的焓变△H1
CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
盖斯定律的应用 (1)科学意义:对于无法或较难通过实验测定的反应的焓变,可应用盖斯定律 计算求得。 (2)方法——“叠加法”若一个化学反应的化学方程式可由另外几个化学反 应的化学方程式相加减而得到,则该化学反应的焓变即为另外几个化学反 应焓变的代数和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 化学反应热的计算第1课时 化学反应热的计算[目标要求] 1.理解盖斯定律的意义。
2.能用盖斯定律和热化学方程式进行有关反应热的简单计算。
一、盖斯定律 1.含义(1)不管化学反应是一步完成或分几步完成,其反应热是相同的。
(2)化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。
例如,ΔH 1、ΔH 2、ΔH 3之间有如下的关系:ΔH 1=ΔH 2+ΔH 3。
2.意义利用盖斯定律,可以间接地计算一些难以测定的反应热。
例如:C(s)+12O 2(g)===CO(g)上述反应在O 2供应充分时,可燃烧生成CO 2;O 2供应不充分时,虽可生成CO ,但同时还部分生成CO 2。
因此该反应的ΔH 不易测定,但是下述两个反应的ΔH 却可以直接测得:(1)C(s)+O 2(g)===CO 2(g)ΔH 1=-393.5 kJ·mol -1(2)CO(g)+12O 2(g)===CO 2(g)ΔH 2=-283.0 kJ·mol -1根据盖斯定律,就可以计算出欲求反应的ΔH 。
分析上述两个反应的关系,即知:ΔH =ΔH 1-ΔH 2。
则C(s)与O 2(g)生成CO(g)的热化学方程式为C(s)+12O 2(g)===CO(g) ΔH =-110.5kJ·mol -1。
思维拓展 热化学方程式的性质(1)热化学方程式可以进行方向改变,方向改变时,反应热数值不变,符号相反。
(2)热化学方程式中物质的化学计量数和反应热可以同时改变倍数。
(3)热化学方程式可以叠加,叠加时,物质和反应热同时叠加。
二、反应热的计算1.根据热化学方程式进行物质和反应热之间的求算例1 由氢气和氧气反应生成4.5 g 水蒸气放出60.45 kJ 的热量,则反应:2H 2(g)+ O 2(g)===2H 2O(g)的ΔH 为( )A .-483.6 kJ·mol -1B .-241.8 kJ·mol -1C .-120.6 kJ·mol -1D .+241.8 kJ·mol -12.利用燃烧热数据,求算燃烧反应中的其它物理量例2甲烷的燃烧热ΔH=-890.3 kJ·mol-11 kg CH4在25℃,101 kPa时充分燃烧生成液态水放出的热量约为()A.-5.56×104 kJ·mol-1B.5.56×104 kJ·mol-1C.5.56×104 kJ D.-5.56×104 kJ3.利用盖斯定律的计算例3已知下列热化学方程式:①Fe2O3(s)+3CO(g)===2Fe(s)+3CO2(g)ΔH1=-26.7 kJ·mol-1②3Fe2O3(s)+CO(g)===2Fe3O4(s)+CO2(g)ΔH2=-50.75 kJ·mol-1③Fe3O4(s)+CO(g)===3FeO(s)+CO2(g)ΔH3=-36.5 kJ·mol-1则反应FeO(s)+CO(g)===Fe(s)+CO2(g)的焓变为()A.+7.28 kJ·mol-1B.-7.28 kJ·mol-1C.+43.68 kJ·mol-1D.-43.68 kJ·mol-1知识点一盖斯定律及应用1.运用盖斯定律解答问题通常有两种方法:其一,虚拟路径法:如C(s)+O2(g)===CO2(g),可设置如下:ΔH1=ΔH2+ΔH3其二:加合(或叠加)法:即运用所给方程式就可通过加减的方法得到新化学方程式。
如:求P4(白磷)===4P(红磷)的热化学方程式。
已知:P4(s,白磷)+5O2(g)===P4O10(s)ΔH1①4P(s,红磷)+5O2(g)===P4O10(s)ΔH2②即可用①-②得出白磷转化为红磷的热化学方程式。
答案P4(白磷)===4P(红磷)ΔH=ΔH1-ΔH22.已知:H2O(g)===H2O(l)ΔH=Q1 kJ·mol-1C2H5OH(g)===C2H5OH(l)ΔH=Q2 kJ·mol-1C2H5OH(g)+3O2(g)===2CO2(g)+3H2O(g)ΔH=Q3 kJ·mol-1若使46 g酒精液体完全燃烧,最后恢复到室温,则放出的热量为()A.(Q1+Q2+Q3) Kj B.0.5(Q1+Q2+Q3) kJC.(0.5Q1-1.5Q2+0.5Q3) kJ D.(3Q1-Q2+Q3) kJ知识点二反应热的计算3.已知葡萄糖的燃烧热是ΔH=-2 840 kJ·mol-1,当它氧化生成1 g液态水时放出的热量是()A.26.0 kJ B.51.9 kJ C.155.8 kJ D.467.3 kJ2H 2(g)+O 2(g)===2H 2O(l)ΔH =-571.6 kJ·mol -1CO(g)+12O 2(g)===CO 2(g)ΔH =-282.8 kJ·mol -1现有CO 、H 2、CO 2组成的混合气体67.2L (标准状况),经完全燃烧后放出的总热量为710.0 kJ ,并生成18 g 液态水,则燃烧前混合气体中CO 的体积分数为( )A .80%B .50%C .60%D .20% 答案 B练基础落实 1.已知:(1)Zn(s)+1/2O 2(g)===ZnO(s)ΔH =-348.3 kJ·mol -1(2)2Ag(s)+1/2O 2(g)===Ag 2O(s)ΔH =-31.0 kJ·mol -1则Zn(s)+Ag 2O(s)===ZnO(s)+2Ag(s)的ΔH 等于( )A .-317.3 kJ·mol -1B .-379.3 kJ·mol -1C .-332.8 kJ·mol -1D .+317.3 kJ·mol -12.已知25℃、101 kPa 条件下: 4Al(s)+3O 2(g)===2Al 2O 3(s)ΔH =-2 834.9 kJ·mol -1 4Al(s)+2O 3(g)===2Al 2O 3(s)ΔH =-3 119.1 kJ·mol -1由此得出的正确结论是( )A .等质量的O 2比O 3能量低,由O 2变为O 3为吸热反应B .等质量的O 2比O 3能量低,由O 2变为O 3为放热反应C .O 3比O 2稳定,由O 2变为O 3为吸热反应D .O 2比O 3稳定,由O 2变为O 3为放热反应3.能源问题是人类社会面临的重大课题,H 2、CO 、CH 3OH 都是重要的能源物质,它们的燃烧热依次为-285.8 kJ·mol -1、-282.5 kJ·mol -1、-726.7 kJ·mol -1。
已知CO 和H 2在一定条件下可以合成甲醇CO(g)+2H 2(g)===CH 3OH(l)。
则CO 与H 2反应合成甲醇的热化学方程式为( )A .CO(g)+2H 2(g)===CH 3OH(l) ΔH =-127.4 kJ·mol -1B .CO(g)+2H 2(g)===CH 3OH(l) ΔH =+127.4 kJ·mol -1C .CO(g)+2H 2(g)===CH 3OH(g) ΔH =-127.4 kJ·mol -1D .CO(g)+2H 2(g)===CH 3OH(g) ΔH =+127.4 kJ·mol -14.已知火箭燃料二甲基肼(CH 3—NH —NH —CH 3)的燃烧热为-6 000 kJ·mol -1,则30 g 二甲基肼完全燃烧放出的热量为( )A .1 500 kJB .3 000 KjC .6 000 kJD .12 000 kJ用关系式求反应热5.在一定条件下,充分燃烧一定量的丁烷放出热量为Q kJ(Q >0),经测定完全吸收生成的CO 2需消耗 5 mol·L -1的KOH 溶液100 mL ,恰好生成正盐,则此条件下反应C 4H 10(g)+132O 2(g)===4CO 2(g)+5H 2O(g)的ΔH 为( )A .+8Q kJ·mol -1B .+16Q kJ·mol -1C .-8Q kJ·mol -1D .-16Q kJ·mol -1练综合拓展6.比较下列各组热化学方程式中ΔH 的大小关系。
(1)S(s)+O 2(g)===SO 2(g) ΔH 1 S(g)+O 2(g)===SO 2(g) ΔH 2 ΔH 1______ΔH 2(2)CH 4(g)+2O 2(g)===CO 2(g)+2H 2O(l) ΔH 1 CH 4(g)+2O 2(g)===CO 2(g)+2H 2O(g) ΔH 2 ΔH 1______ΔH 2(3)煤作为燃料有两种途径: 途径1——直接燃烧C(s)+O 2(g)===CO 2(g) ΔH 1<0 途径2——先制水煤气C(s)+H 2O(g)===CO(g)+H 2(g) ΔH 2>0 再燃烧水煤气:2CO(g)+O 2(g)===2CO 2(g) ΔH 3<0 2H 2(g)+O 2(g)===2H 2O(g) ΔH 4<0ΔH 1、ΔH 2、ΔH 3、ΔH 4的关系式是______________________________________。
7.发射卫星时可用肼(N 2H 4)作燃料,用二氧化氮作氧化剂,这两种物质反应生成氮气和水蒸气。
已知:N 2(g)+2O 2(g)===2NO 2(g) ΔH =+67.7 kJ·mol -1N 2H 4(g)+O 2(g)===N 2(g)+2H 2O(g) ΔH =-534 kJ·mol -1 12H 2(g)+12F 2(g)===HF(g) ΔH =-269 kJ·mol -1 H 2(g)+12O 2(g)===H 2O(g) ΔH =-242 kJ·mol -1(1)肼和二氧化氮反应的热化学方程式为__________________________;此反应用于火箭推进,除释放大量能量和快速产生大量气体外,还有一个很大的优点是______________。
(2)有人认为若用氟气代替二氧化氮作氧化剂,则反应释放的能量更大。
肼和氟反应的热化学方程式为__________________。
第2课时 习题课1.下列与化学反应能量变化相关的叙述正确的是( ) A .生成物总能量一定低于反应物总能量B .放热反应的反应速率总是大于吸热反应的反应速率C .应用盖斯定律,可计算某些难以直接测量的反应焓变D .同温同压下,H 2(g)+Cl 2(g)===2HCl(g)在光照和点燃条件下的ΔH 不同2.在298 K 、100 kPa 时,已知:2H 2O(g)===O 2(g)+2H 2(g) ΔH 1 Cl 2(g)+H 2(g)===2HCl(g) ΔH 2 2Cl 2(g)+2H 2O(g)===4HCl(g)+O 2(g) ΔH 3 则ΔH 3与ΔH 1和ΔH 2间的关系正确的是( ) A .ΔH 3=ΔH 1+2ΔH 2 B .ΔH 3=ΔH 1+ΔH 2 C .ΔH 3=ΔH 1-2ΔH 2 D .ΔH 3=ΔH 1-ΔH 23.下列热化学方程式或离子方程式中,正确的是( )A .甲烷的标准燃烧热为-890.3 kJ·mol -1,则甲烷燃烧的热化学方程式可表示为CH 4(g)+2O 2(g)===CO 2(g)+2H 2O(g) ΔH =-890.3 kJ·mol -1B .500 ℃、300 MPa 下,将0.5 mol N 2和1.5 mol H 2置于密闭容器中充分反应生成NH 3(g),放热19.3 kJ ,其热化学方程式为N 2(g)+3H 2(g)2NH 3(g) ΔH =-38.6kJ·mol -1C .氯化镁溶液与氨水反应:Mg 2++2OH -===Mg(OH)2↓D .氧化铝溶于NaOH 溶液:A12O 3+2OH -===2AlO -2+H 2O4.已知:(1)Fe 2O 3(s) +32C(s)===32CO 2(g)+2Fe(s) ΔH 1=+234.1 kJ·mol -1(2)C(s)+O 2(g)===CO 2(g) ΔH 2=-393.5 kJ·mol -1则2Fe(s)+32O 2(g)===Fe 2O 3(s) 的ΔH 是( )A .-824.4 kJ·mol -1B .-627.6 kJ·mol -1C .-744.7 kJ·mol -1D .-169.4 kJ·mol -15.100 g 碳燃烧所得气体中,CO 占13体积,CO 2占23体积,且C(s)+12O 2(g)===CO(g)ΔH (25℃)=-110.35 kJ·mol -1,CO(g)+12O 2(g)===CO 2(g)ΔH (25℃)=-282.57 kJ·mol -1。
