人教版小学数学六年级下册第三单元《圆柱的体积》
《圆柱的体积》教学设计

《圆柱的体积》教学设计
环节三: 循序渐进 巩固提升
1.比一比:三款蛋糕哪个更大?
2.算一算:
3.说一说: 知道哪些条件就可以求出圆柱的体积?
1.提问:第三款蛋糕的
体积是多少?怎么算?用到了哪个公式? 2.请同学们先说一说
解题方法,再动笔计算。
巡视学生书写情况,堂批。
3.总结方法。
1.回归主题情境,解决圆柱体积相关的实际问题。
2. 对比题组,加深学生对圆柱体积公式的灵活运用。
3.总结方法。
环节四: 总结反思 课后延伸
1. 回顾反思,总结方法和所学知识。
2.课后延伸:说一说这些立体图形有怎样的共同点?课后查找直柱体相关资料,继续探究这些图形的秘密吧! 1.这节课我们学习了什么?有哪些收获?
2. 提问:这些立体图形有怎样的共同点?规律背后藏着什么数学秘密?请同学们通
过查找资料,继续探究图形的秘密!
1.整理和反思,进一步巩固所学知识,归纳数学学习的方法。
2.激发学生思考与探索的欲望。
【板书设计】
圆柱的体积
=底面面积×高 圆柱的体积 =底面面积×高
V = πr 2
h
V = S h 转化
转化
× 宽 × 高
V = πr×r×h V = πr 2
h。
【一课一练】人教版小学数学六年级下册第三单元《圆柱与圆锥)》-第3课时圆柱的体积(二)-附答案

第3课时圆柱的体积(二)1.圆柱的底面直径扩大到原来的2倍,高缩小到原来的12,圆柱的体积()A.扩大到原来的2倍B.缩小到原来的12C.不变D.扩大到原来的4倍2.一个圆柱形水池,底面直径20米,深2米,池内最多容水(每立方米水重1吨)()A.125.6吨B.628吨C.439.6吨D.314吨3.如图:这个杯子()装下3000ml牛奶。
A.能B.不能C.无法判断4.将一根2m长的圆柱形木棒沿横截面切成两段圆柱后(如图),表面积比原来增加了6.4dm2。
这根圆柱形木棒原来的体积是()dm3。
A.128B.64C.12.85.把直径是4厘米的圆柱沿底面平均分成若干个扇形.切开拼成一个近似的长方体,长方体右侧面的面积是40平方厘米,圆柱的体积是。
6.一个圆柱的侧面积是18.84 cm2,高是10 cm,底面积是cm2,体积是cm3。
7.一个圆柱体的高减少2.5分米,体积减少100立方分米,这个圆柱体的底面积是平方分米.8.一个圆柱体的底面半径是3厘米,高是6厘米,侧面积是平方厘米,表面积是平方厘米,体积是立方厘米。
9.求下面圆柱的体积.(图中单位:厘米)◆基础知识达标10.一个圆柱的底面半径是3分米,高是2分米,它的侧面积是平方分米,表面积是平方分米,体积是立方分米。
11.一个圆锥的底面积是9平方分米,高是6分米,它的体积是立方分米,与它等底等高的圆柱体积是立方分米.12.如图,圆柱体的体积是立方分米(单位:分米)13.一台压路机的滚筒长2米,侧面积是5.024平方米,这个滚筒的体积是立方米。
14.一个高5厘米的圆柱体,沿底面直径将圆柱体锯成两块,其表面积增加40平方厘米,原来这个圆柱体的体积是立方厘米。
15.一种圆珠笔笔芯的内直径约0.3厘米,灌装的油墨高7.5厘米.一枝这样的笔芯内能灌装立方厘米的油墨?16.把一个棱长为20厘米的正方体削成一个尽可能大的圆柱,这个圆柱的体积是立方厘米,削去部分的体积是立方厘米。
六年级数学下册《圆柱的体积》

CHENLI
10
例5 一个圆柱形水桶,从里面量得底面直径是 20厘米,高是25厘米,求这个水桶的容积是多 少立方分米?
(1)水桶底面积
3.14×(20 )²
2
=3.14×10²
=314(平方厘米)
(2)水桶容积
314 × 25
=7850(立方厘米) =7.85(立方分米)
答:这个水桶的容积是7.85立方分米
CHENLI
15
已知圆柱的底面半径和高,怎样求体 积?
已知圆柱的底面直径和高体积?
CHENLI
16
练一练: 一个圆柱的体积是
62.8立方分米,高是5分 米,底面积是多少?
CHENLI
17
人教版版六年级数学下册
教师:张忠安
CHENLI
1
d h
CHENLI
2
CHENLI
3
圆 柱的体 积
CHENLI
4
圆柱体切开后可以拼成一个什么形体?
CHENLI
5
CHENLI
6
因为:长方体的体积
V=Sh
所以:圆柱体的体积
V=Sh
CHENLI
7
h
r
r
与拼 半成 径长 和方 高体 的的 关长 系、 ?宽
、 高
CHENLI
8
圆柱体积的计算公式是:
V= r²h
CHENLI
9
例4 一根圆柱形钢材,底面积是50平方厘米,高是 2.1米。他的体积是多少? (想:由于底面积和高的单位不统一,先要进行 单位换算)
2.1米=210厘米
50 × 210 =10500 立方厘米 答:它的体积是 10500 立方厘米
人教版六年级数学下册第三单元_第03课时_圆柱的体积例5例6(教学设计)
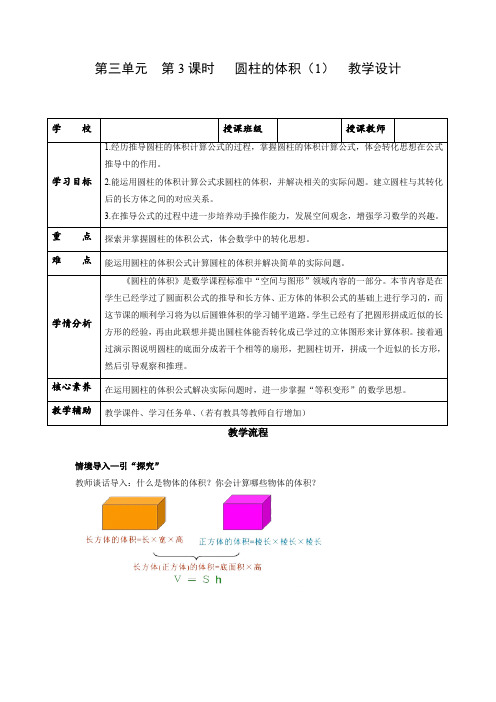
第三单元第3课时圆柱的体积(1)教学设计情境导入—引“探究”教师谈话导入:什么是物体的体积?你会计算哪些物体的体积?长方体和正方体的体积计算公式?长方体的体积和正方体的体积的通用公式是什么呢?用字母怎样表示?V长=长×宽×高V正=棱长×棱长×棱长V=底面积×高字母表示:V=Sh思考:圆柱的体积怎样计算呢?前面的学习中我们遇到过这样的问题吗?知识链接—构“联系”回忆一下圆面积的计算公式是如何推导出来的?(结合课件演示)这是一个圆,我们把它平均分割,再拼合就变成了一个近似的长方形。
长方形的长相当于圆周长的一半,长方形的宽就当于圆的半径,用周长的一半×半径就可以求出圆的面积,所以推导出圆的面积公式。
圆柱的体积该怎么计算呢?今天我们就一起来研究这个问题。
(板书课题:圆柱的体积)学习任务一:圆柱体积公式的推导【设计意图:由复习圆面积公式的推导过程入手,实现知识的迁移,从而调动学生学习的积极性,激发学生探求新知的欲望,在教学中充分运用课件中的动画直观演示的同时,广泛让学生动手、动脑、动口,在操作中感知,在猜想中验证,在观察中理解,在比较中归纳。
让学生在自主探究、合作交流中发现和解决问题,培养学生乐学、积极探究的学习态度,获得成功的体验。
这样进行教学,不仅有利于学生理解公式的推导过程,而且在公式的推导过程中,充分让学生感受和体验“转化”这一解决数学问题重要的思想方法。
】新知探究—习“方法”结合教材的内容,探究圆柱体积公式的推导。
1.提问:什么是圆柱的体积?圆柱的体积怎么求?(说一说、想一想、猜一猜)让学生自由发言。
(1)学生猜想可以把圆柱转化成什么图形?(借助于圆面积公式的推导进行知识迁移学习)出示推导示意图,建立直观,巩固旧知(2)阅读教材内容,利用手中的学具进行探索,小组交流。
2.圆柱体积公式的推导(1)多媒体课件演示圆柱体等分转化为长方体。
(让学生观察)通过课件的演示、观察、思考:(1) 圆柱体通过切拼后,转化为近似的长方体,什么变了?什么没变?(2) 长方体的底面积与原来圆柱体的哪部分有关系?有什么关系?(3) 长方体的高与原来圆柱体的哪部分有关系?有什么关系?(4) 你认为圆柱的体积可以怎样计算?3.交流展示,小组讨论,交流汇报。
《圆柱的体积》(教案)六年级下册数学人教版

《圆柱的体积》(教案)六年级下册数学人教版教学内容:本节课主要教学圆柱的体积计算公式,以及如何应用该公式解决实际问题。
引导学生复习圆柱的基本概念,然后通过实验探究圆柱体积的计算方法,结合生活实例,让学生掌握圆柱体积的计算技能。
教学目标:1. 知识与技能:使学生掌握圆柱的体积计算公式,并能运用公式解决实际问题。
2. 过程与方法:通过实验和观察,培养学生观察能力、空间想象能力和逻辑思维能力。
3. 情感、态度与价值观:激发学生对数学学习的兴趣,培养学生合作交流、自主探究的精神。
教学难点:1. 圆柱体积计算公式的推导过程。
2. 圆柱体积计算在实际问题中的应用。
教具学具准备:1. 教具:圆柱体积计算公式卡片、圆柱模型、多媒体课件。
2. 学具:直尺、圆规、剪刀、彩纸、计算器。
教学过程:一、导入1. 复习圆柱的基本概念,引导学生回顾已学过的圆柱相关知识。
2. 提问:同学们,我们已经学习了圆柱的哪些知识?请大家举例说明。
二、探究圆柱体积计算公式1. 提问:同学们,你们知道圆柱的体积如何计算吗?2. 引导学生通过实验探究圆柱体积的计算方法。
3. 实验一:测量圆柱的底面半径和高,计算圆柱体积。
4. 实验二:观察圆柱体积与底面积、高的关系,推导圆柱体积计算公式。
三、讲解圆柱体积计算公式1. 结合实验结果,讲解圆柱体积计算公式。
2. 强调圆柱体积计算公式中的各个参数含义。
3. 举例说明圆柱体积计算公式的应用。
四、练习与应用1. 出示练习题,让学生独立完成。
2. 讲解练习题,分析解题思路和方法。
3. 结合生活实例,让学生运用圆柱体积计算公式解决实际问题。
五、课堂小结2. 强调圆柱体积计算在实际问题中的重要性。
板书设计:1. 圆柱的基本概念2. 圆柱体积计算公式的推导3. 圆柱体积计算公式的应用作业设计:1. 课后练习题:计算给定圆柱的体积。
2. 家庭作业:结合生活实例,运用圆柱体积计算公式解决实际问题。
课后反思:本节课通过实验和观察,引导学生探究圆柱体积的计算方法,并掌握了圆柱体积计算公式。
人教版数学六年级下册 利用圆柱的体积求不规则物体的体积

高
8cm
从题目中你获
得了哪些条件?
10cm
杯子是圆柱形 牛奶体积
小组讨论
1. 怎样判断杯子能不能装下2袋这样的 牛奶? 2.在小组内说一说如何计算杯子的容积, 计算容积时需要注意什么?
6 下图中的杯子能不能装下2袋这样的牛奶? (数据是从杯子里面测量得到的。)
比较杯子容积和(2袋)
8cm
牛奶体积的大小。
度是18cm
所求问题
这个瓶子的 容积是多少
阅读与理解
这个瓶子不是一个 完整的圆柱,无法 直接计算容积。
能不能转化成 圆柱呢?
分析与解答
不管是正放还是倒置,瓶子 里的容积都是由水的体积和 无水部分的体积组成的。
倒置前后,水 和无水部分的 形状发生了变 化,但体积都 没有变。
7 cm 18 cm
等积
在五年级计算土豆的体积时, 也是用了转化的方法。
1 小明和妈妈出去游玩,带了一个圆柱形保温壶, 从
里面量底面直径是8 cm,高是15 cm。如果两人游玩
期间要喝1L水,带这壶水够喝吗? 比较保温壶的容
3.14×(8÷2)²×15
积和1 L的大小
=3.14×16×15
V圆柱 = π(d÷2)²h
=753.6 (cm³)
1.一个圆柱高4厘米,如果它的高增加1厘米,它的表面积就增 加50.24平方厘米,这个圆柱的底面半径是多少?体积是多少?
50.24平方厘米 底面周长
1厘米
底面半径:50.24÷1÷3.14÷2=8(厘米) 体积:3.14×8²×4=803.84(立方厘米) 答:这个圆柱的底面半径是8厘米,体积是803.84立方厘米。
10 cm
1.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后 倒置放平,无水部分高10 cm,内径是6 cm。小明喝 了多少水?
《圆柱的体积》教案-2023-2024学年六年级下册数学人教版

5.比较圆柱与长方体、正方体体积的关系。
二、核心素养目标
《圆柱的体积》核心素养目标-2023-2024学年六年级下册数学人教版。本节课致力于培养学生的以下核心素养:
1.空间观念:通过圆柱体积的学习,使学生能够形成对立体图形的认识,提高空间想象力;
2.逻辑推理:学会运用转化、归纳等数学思想,理解并掌握圆柱体积公式的推导过程;
其次,圆柱体积公式的推导是本节课的一个重点,也是学生理解的难点。我采用了长方体切割和拼接的方法来引导学生理解圆柱体积的形成,但从学生的反馈来看,这个过程还需要更多的引导和解释。在今后的教学中,我可能会尝试更多种推导方法,或者让学生自己动手操作,以提高他们的理解和记忆。
另外,实践活动环节,学生分组讨论和实验操作的部分非常活跃,他们能够将所学的知识应用到解决实际问题中。但我注意到,有些小组在讨论时可能会偏离主题,或者在进行实验操作时不够精确。这提醒我在今后的教学中,需要更加明确讨论的主题和实验的操作步骤,确保活动的有效性和准确性。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“圆柱体积在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
《圆柱的体积》教案-2023-2024学年六年级下册数学人教版
一、教学内容
《圆柱的体积》教案-2023-2024学年六年级下册数学人教版。本章节内容为人教版六年级下册数学第七章《立体几何》第三节:圆柱的体积。主要内容包括:
新人教版小学六年级数学下册第3单元 圆柱与圆锥《圆柱的体积》课堂素养训练

(1)求一段圆木所占空间的大小,是求它的( C )。
A.表面积
B.容积
C.体积
(2)求一个圆柱形铁桶能装多少水,是求这个铁桶的( B )。
A.表面积
B.容积
C.体积
(3)圆柱的体积不变,若高扩大为原来的2倍,则底面积应该( B )。
A.不变
B.缩小为原来的
1 2
C.扩大为原来的2倍
3. 填一填。 0.65 m3=( 650 )dm3 3 m3 5 dm3=( 3.005 )m3
5 dm3=( 5 )L 7.05 L=( 7 )L( 50 )mL
4. 求下面各圆柱的体积。
3.14×22×4=50.24(cm3)
12.56×2=25.12(cm3)
3.14×(2÷2)2×7=21.98(cm3)
5. 一个圆柱形油桶,从里面量底面直径是6 dm,高是9 dm,桶内装的油
占全桶的
3 4
。桶内装有油多少升?
3.14×(6÷2)2×9×34=190.755(dm3) 190.755 dm3=190.755 L
答:桶内装有油190.755L。
6. 丁丁的爸爸买了一些珊瑚和假山作为家里圆柱形水族箱的装饰物,把 它们放入水族箱后,水面上升了3.5 cm。已知水族箱的底面内半径为 30 cm,则珊瑚和假山的总体积是多少?
人教版小学六年级数学下册•
3 圆柱与圆锥
圆柱的体积
1. 下面的说法正确吗?正确的画“√”,错误的画“✕”。 (1)圆柱的体积等于底面积乘高。 ( √ ) (2)圆柱的体积就是它的容积。 ( ✕ ) (3)一。 (√ )
2. 选择题。(把正确答案的字母代号填在括号里)
3.14×302×3.5=9891(cm3) 答:珊瑚和假山的总体积是9891cm3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
3.14(×5 2)2 × 2
一根圆柱形铁棒,底面周长是 12.56厘米,长是100厘米,它的 体积是多少?
3.14×(12.56÷3.14÷2) ²×100
=3.14×2²×100
=12.56×100
=1256(立方厘米)
圆柱形水桶内所盛水的体积,就 叫做这个圆柱形容器的容积。
下面这个杯子能不能装下这袋奶?(杯 子的数据是从里面测量得到的.)
答:它的体积是3000立方厘米。
求圆柱的体积。(单位:厘米)
2 10 3.14 ×(10÷2)2×2=157(立方厘米)
量得底面直径是 20厘米,高是13
厘米
容积?
(1)水桶的底面积:3.14×( 220)2=314(cm2) (2)水桶的容积: 314×13=4082(cm3)
4分米
求各圆柱的 体积。
圆柱体的体积
高 宽
长
真 棒!
棱长
长方体的体积=长×宽×高 正方体的体积=棱长×棱长×棱长
v长=a b h
v正 =a3
V=s底
h
高
Байду номын сангаас
V=s底
宽
长
h
棱长
等底等高的长方体和正方体面积相等。
圆的面积公式推导过程:
圆的面积公式推导过程:
S=π r 2
r
πr
S=πr ×r =π r 2
把圆柱的底面平均分的份数越多, 切拼成的立体图形越接近长方体。
长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。
长方体体积=底面积×高
圆柱体积=底面积×高
V=Sh
=
判断正误,对的画“√”,错误的画“×”。
(1)圆柱体的底面积越大,它的体积越大。×( ) (2)圆柱体的高越长,它的体积越大。×( ) (3)圆柱体的体积与长方体的体积相等。(×) (4)圆柱体的底面直径和高可以相等。√( )
做一做 一根圆柱形木料,底面积为 75cm2,长 90cm。它的体积是 多少?
V柱=S底h =75×90 =6750(立方厘米)
答:它的体积是6750立方厘米
一根圆柱形木 料,底面积是75 平方厘米,长90 厘米。它的体积 是多少?
圆柱体积=底面积×高
75×90=6750(立方厘米)
答:它的体积是6750立方厘米。
8cm
10cm
498ml
先要计算出杯子的容积.
杯子的底面积: 3.14×(8÷2)2 =3.14×42 =3.14×16 =50.24(c㎡)
杯子的容积: 50.24×10 =502.4(ml)
502.4ml>498ml
答:这个杯子能装下这袋奶.
智慧城堡
加油啊!
圆柱体积=底面积×高
1.5米=150厘米 20×150=3000(立方厘米)
讨论
已知圆的半径和高,怎样求圆柱的体积?
V=s底 =兀 r2 h
h
求下面圆柱的体积。(只列式不计算。)
1、底面积24平方厘 米,高12厘米。
1 2
2、底面半径 2 厘
米, 高55 厘米。
2
24×12
3.14×22× 5
求下面圆柱的体积。(只列式不计算。)
3、底面直径 5 分米, 高 2 分米。
10分米 0.5分米
0.8米
此课件下载可自行编辑修改,供参 感谢您的支持,我们努力做得更好
