材料力学(金忠谋)第六版答案第05章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第06章.doc

弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
家电公司研发部资料材料力学习题答案(五)

+-++(a)(b)(c)(d)M M M MeMeMeFa图图图M 图挠曲线挠曲线挠曲线挠曲线第五章梁弯曲时的位移5-1试画出图示梁挠曲线的大致形状。
根据梁的弯矩图确定梁挠曲线的大致形状,M >0,挠曲线向下凸;M <0,挠曲线向上凸。
5-2图示各梁EI=常数。
试写出各梁的位移边界条件,并画出梁挠曲线的大致形状。
F(c)题 5 - 1 图(a)(b)(d)++-M 图M 图FL/2m/32m/3FL挠曲线挠曲线(a)(b)设梁的最左端断点为坐标原点,x 轴正方向向右。
则各梁边界条件、弯矩图及梁的挠曲线大致形状如下: (a)(0)0ω=(b)(0)()0L ωω== (c)(0)()0L ωω== (d)(0)(2)0a ωω==(e)()(3)0a a ωω==(f)(0)0ω=(a)(b)qL/4F(d)(c)L(f)(e)题 5 - 2 图+--M 图M 图+qL2/64qL2/8FaFa挠曲线挠曲线(c)(d)+-M 图M 图-2mmFL挠曲线挠曲线(e)(f)5-3试画出图示梁挠曲线的大致形状。
2(a)(b)(c)题 5 - 3 图(3)++--qa2qa/423qa/42qa2/2qa2/2(a)(b)+-m(c)5-4如要使图示结构B端的挠度为零,则长度x应为多少?试画出此时AB梁的挠曲线大致形状。
答:Lx32=解:固定端约束反力如图所示。
则AB梁上距离A端l处的横截面上的弯矩为M(l)=Fl-F(L-x)由挠曲线微分方程得:EIω”=-M(l)=F(L-x)-Fl积分得:EIω’=F(L-x)l-2Fl2+C1;再积分得:EIω=2F(L-x)l2-6Fl3+C1l+C2;由边界条件l=0 ,ω’=0得C1=0;由ω=0得C2=0L题 5 - 4 图题 5 - 5 图刚性杆qBB∴EI ω=2F (L -x )l 2-6F l 3;由题意知l =L 时,ω=0得x =32L AB 梁挠曲线大致形状:M (l )=Fl -3F L ;0<l <3L 时,M (l )<0;3L<l <L 时,M (l )>05-5图示刚架在端点C 处受集中力F 作用,试求当B 点的铅垂位移为零时La的比值。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学(金忠谋)第六版答案第02章

习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1)作轴力图; (2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-= CB 段应力 a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变 45105.2101.05.2-⨯-=⨯-==E σε N-图CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε (4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(1)轴力图(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max == 2-3 直径为1cm 的圆杆,在拉力P =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
解:(1) 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- (2) ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
材料力学第六版答案第06章

材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
4解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
材料力学第5章答案

材料力学(柴国钟、梁利华)第5章答案本页仅作为文档封面,使用时可以删除This document is for reference only-rai'21 year.March宓 lOxlO 6 “ ““小a. = 一― y. = ----------- x65 = 26. \MPa ; a 11/: 1 24907500 2=_如1= — _ xl 15 = -46.2MP" 3L5 249075005.2如图所示,圆截面梁的外伸部分系空心圆截面,轴承人和D 可视为狡支座。
试求该轴横截面上的最大正应力。
竺竺 =l ()xl ()x35 = 14. IMA//. • 2249075003kND3kN400 解:剪力图和弯矩图如下:试确定图示梁的危险截面,分别计•算图示三种截面上1、2、3点处的正应力。
12z.x z 120x180' c 45x120'川4 (b) /. = ---------------- — 2x ----------- = 45360000"〃”' 12 12_一x90 = l9.8MP" ; 6 = --” =」("⑴-x60 = l3.2MP“1L 453600002I - 45360000咕一整儿"踪歸9。
"9•林, 30x150 + 120x301. =+30xl50x(115-75)2+ 口;字)-+ 120x30x(165-115)2 = 24907500””/5.1 解:(a )叮一¥^=册®心5.W 612y 2 =10xl06120x180’ ~~12-x60 = 10・3MP“ 6=一 10xl06>,3=" 120x180sx90 = -15.4MPt/ (、30x150x75 + 120x30x165 11C \C) >\ = -------------------------------------------------------- = 11 jmmnux(c)800 200 300M R _32M 〃 _ 32X 1.344X 1()6苗 /rx60‘%=63.4MP"b/xnux w=常32:09x"62.1M&Q (1_Q 4) /rx60-X (1-0.754)故,= 63 AMPa5.3图示简支梁受均布载荷作用。
《材料力学》第五章课后习题参考答案

错误原因及避免方法
错误原因
1. 对材料力学的基本原理理解不深入,导致选择错误的公式或方法进行 计算。
2. 计算过程中出现数值错误或单位不统一等问题,导致结果偏差较大。
错误原因及避免方法
• 对计算结果缺乏分析和讨论,无法判断其 合理性和准确性。
错误原因及避免方法
01
避免方法
02
03
04
1. 加强对材料力学基本原理 的学习和理解,掌握各种公式 和方法的适用范围和条件。
题目一
分析并比较不同材料在拉伸过程中的力学行为差异。
题目二
讨论材料疲劳破坏的机理及影响因素。
要求
掌握材料在拉伸过程中的应力-应变曲线,理解弹性模量 、屈服强度、抗拉强度等概念,能够运用所学知识分析不 同材料的力学行为。
要求
了解材料疲劳破坏的基本概念,掌握疲劳破坏的机理和影 响因素,能够运用所学知识分析实际工程中的疲劳破坏问 题。
知识点综合运用
弹性力学基础
运用弹性力学的基本原理,分析 材料在弹性阶段的力学行为,计
算弹性模量等参数。
塑性力学基础
运用塑性力学的基本原理,分析材 料在塑性阶段的力学行为,理解屈 服强度、抗拉强度等概念。
疲劳破坏理论
运用疲劳破坏的基本理论,分析材 料在交变应力作用下的力学行为, 讨论疲劳破坏的机理和影响因素。
加强实践应用
除了理论学习外,我还计划通过 实践应用来加深对材料力学的理 解。例如,可以尝试利用所学知 识解决实际工程问题,或者参加 相关的实验和课程设计等。
拓展相关学科领域
材料力学是一门基础学科,与其他学 科领域有着密切的联系。因此,我计 划拓展相关学科领域的学习,如结构 力学、弹性力学等,以便更全面地了 解材料的力学性能和工程应用。
新版材料力学(金忠谋)第六版答案第05章-新版.pdf
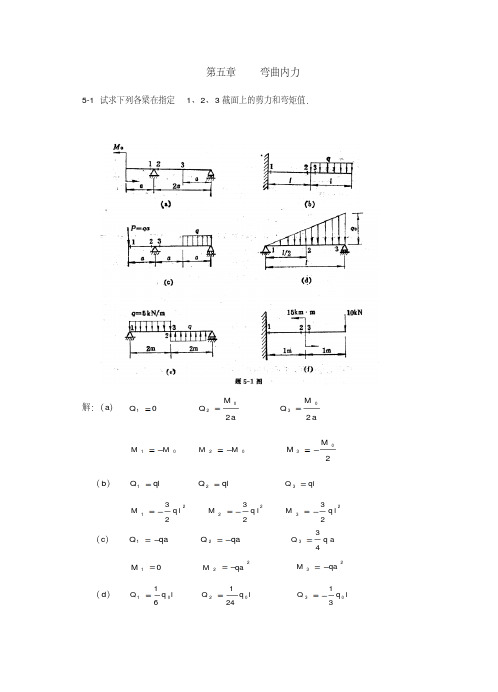
32 qa
4
( i) M 图
3 qa
2
3
1
1
ql
ql
P
8
2
4
0.5a
qa (j)Q 图
1 qa
2
3
5
a
ql
8
8
( k)Q 图
3 P
4
( l) Q 图
12 qa
2
1
2
ql
128
1 Pa
4
2
qa (j)M 图
1 ql 2 8
( k)M 图
( l) M 图
1 Pa
2
5-3 利用 q、 FS 、M 的微分关系作出下列各梁的剪力图和弯矩图,
Rx
2
P 2l a
l
8
a x
M1
M1
(M 图 ) P。试分析小车处于什么位
P
P
L
5-9 作图示梁 ABC 的剪力图和弯矩图。
解:
D
B
C
E
P
P
A
D
B
C
P
(Q 图) 5-10 用叠加法作下列各梁的弯矩图
D
B
C
E
Pa
A
D
B
C
Pa
( M 图)
1 Pa
2
( a)
5
2
Pl
Pl
9
3
1 Pl
3
( d)
12 ql
4
解:
8m 10 KN 10 KN
20 KN ( a)Q 图
20 KN
15 KN
4m 15 KN
( b)Q 图
1 q0l
材料力学练习册5-6详细答案
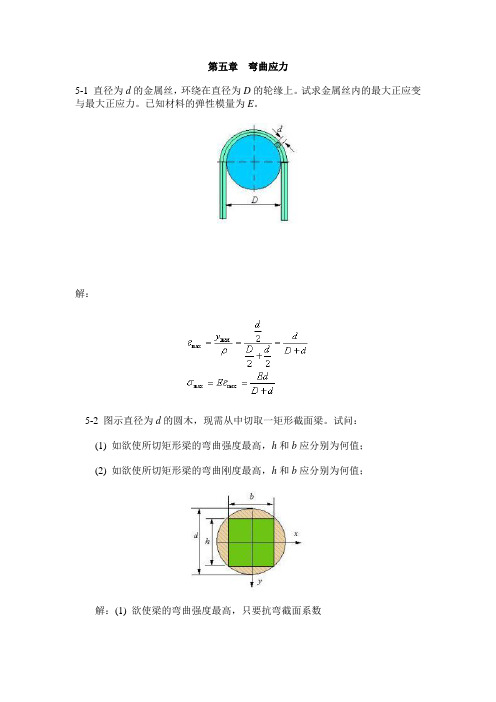
第五章弯曲应力5-1 直径为d的金属丝,环绕在直径为D的轮缘上。
试求金属丝内的最大正应变与最大正应力。
已知材料的弹性模量为E。
解:5-2 图示直径为d的圆木,现需从中切取一矩形截面梁。
试问:(1) 如欲使所切矩形梁的弯曲强度最高,h和b应分别为何值;(2) 如欲使所切矩形梁的弯曲刚度最高,h和b应分别为何值;解:(1) 欲使梁的弯曲强度最高,只要抗弯截面系数取极大值,为此令(2) 欲使梁的弯曲刚度最高,只要惯性矩取极大值,为此令5-3 图示简支梁,由№18工字钢制成,在外载荷作用下,测得横截面A 底边的纵向正应变ε=3.0×10-4,试计算梁内的最大弯曲正应力。
已知钢的弹性模量E =200GPa ,a =1m 。
解:梁的剪力图及弯矩图如图所示,从弯矩图可见:5-4 No.20a 工字钢梁的支承和受力情况如图所示。
若[]MPa 160=σ,试求许可载荷F 。
5-5 图示结构中,AB 梁和CD 梁的矩形截面宽度均为b 。
如已知AB 梁高为1h ,CD 梁高为2h 。
欲使AB 梁CD 梁的最大弯曲正应力相等,则二梁的跨度1l 和2l 之间应满足什么样的关系?若材料的许用应力为[σ],此时许用载荷F 为多大?5-6 某吊钩横轴,受到载荷kN 130F =作用,尺寸如图所示。
已知mm 300=l ,mm 110h =,mm 160b =,mm 75d 0=,材料的[]MPa 100=σ,试校核该轴的强度。
5-7 矩形截面梁AB,以固定铰支座A及拉杆CD支承,C点可视为铰支,有关尺寸如图所示。
设拉杆及横梁的[]MPaσ,试求作用于梁B端的许可载荷F。
=1605-8 图示槽形截面铸铁梁,F=10kN,M e=70kN·m,许用拉应力[σt]=35MPa,许用压应力[σc]=120MPa。
试校核梁的强度。
解:先求形心坐标,将图示截面看成一大矩形减去一小矩形惯性矩弯矩图如图所示,C截面的左、右截面为危险截面。
材力习题册(第六版)参考答案(1-3章)

D
)
2.轴向拉伸细长杆件如图 2 所示,其中 1-1 面靠近集中力作用的左端面,则正确的说法 A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C.1-1 面上应力非均匀分布, 2-2 面上应力均匀分布 D.1-1 面上应力均匀分布, 2-2 面上应力非均匀分布
(图 B 端 D 任意点 A ) B 都是横截面 D 都是 45 斜截面
0 0
14. 轴向拉伸杆,正应力最大的截面和剪应力最大的截面 (
15. 设轴向拉伸杆横截面上的正应力为 σ ,则 45 斜截面上的正应力和剪应力 ( D )。 B 均为 σ D 均为 σ /2 C δ 和ψ D σ s、 δ 和 ψ
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
B 内力与外力无关 D 内力沿杆轴不变 ) 。 σ >300MPa σ <200MPa B ) 。 B. 剪切面面积为 bh,挤压面面积为 bc; D. 剪切面面积为 bh,挤压面面积为 ch。 C ) ,计算挤压面积
19. 一拉伸钢杆,弹性模量 E=200GPa,比例极限为 200MPa,今测得其轴向应变 ε = 0.0015,则横截面上的正应力 ( A C σ =Eε =300MPa 200MPa<σ <300Mpa
= -2(arctan
)=2.5×
rad
2.试求图示结构 m m 和 n n 两截面的内
-2-
【材料力学】第五章 截面的几何性质习题答案

5-1 试用积分法确定图示平面图形的形心位置。
解:(1)建立极坐标极坐标(α,ρ),取微面积dA d d ραρ=⋅。
则cos yρα=,(2)求形心位置222322cos ()cos 43434r r AC d d d d ydA rrr y AA rππραρραρρααπππ⋅⋅⋅⋅=====⎰⎰⎰⎰⎰由对称性可知:43Cr z π=。
图形形心为(43r π,43r π)。
y700图题5-1b 图题5-2b5-2 确定图示平面图形力的形心位置。
解:(1)选取通过矩形I 的形心C 1,矩形II 形心C 2,矩形III 形心C 3 (2)求形心位置 由于截面左右对称,故:400m mCz=。
3131150400150150800200400150500150700222m m =305m m150800200400500150i C ii C ii A y y A ==⎛⎫⎛⎫⨯⨯+⨯⨯++⨯⨯- ⎪ ⎪⎝⎭⎝⎭==⨯+⨯++⨯∑∑图形形心为(305,400)。
5-4(a)题5-4图解:(1)矩形341212z bhaI ==(2)箱形箱形与方形面积,即:22226 5.4 5.4a a bt at t ==→=333322224(0.9)(1.8)(0.9)(1.8)()(2)()(2)5.45.45.45.4121212120.4567z a a a a a a a a b t b t b t b t I a++--++--=-=-=(3)工字形截,即:面23332 1.62 5.2a a at at t =⨯+→=工字形截面方形面积33333341.6(22)(1.6)81.6(22)(1.6)8 5.25.2121212120.8695z a aa a a aa a t a t aI a+⨯-+-=-=-=10.45670.869515.4810.4312z z z I I I ==工方箱::::::5-8图示矩形h=2b=200mm ,(1)试求矩形通过坐标原点O 1的主惯性轴的位置及主惯性矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 弯曲内力5-1 试求下列各梁在指定1、2、3截面上的剪力和弯矩值.解:(a ) 01=Q a M Q 202=aM Q 203= 01M M -= 02M M -= 23M M -= (b ) ql Q =1 ql Q =2 ql Q =32123ql M -= 2223ql M -= 2323ql M -= (c ) qa Q -=1 qa Q -=2 qa Q 433=01=M 22qa M -= 23qa M -=(d ) l q Q 0161=l q Q 02241= l q Q 0331-=01=M 202161l q M =03=M (e ) KN Q 51= KN Q 51-= KN Q 51-= 01=M 02=M 03=M (f ) KN Q 101= KN Q 102= KN Q 103= m KN M ⋅=51 m KN M ⋅=52 m KN M ⋅-=1035-2 试写出下列各梁的剪力方程和弯矩方程,并作剪力图和弯矩图,确定|F max |和|M max |。
解:(a ) l M x Q 03)(=003(x)M x l M M -=lM Q 0max 3=0max2M M =(b ) 0)(1=x Q pa x M =)(1p x Q -=)(2 )()(2a x p pa x M --=p Q =max pa M=max(c ) p x Q -=)(1 px x M -=)(1p x Q 21)(2=)(23)(2a x p px x M ---= p Q =max pa M=max(a )Q 图 (b )Q 图 (c )Q 图02M0M P a(a )M 图 (b )M 图 (c )M 图4/qa (d )Q 图 (e )Q 图 (f )Q 图22ql22ql 22ql 22ql(d )M 图 (e )M 图 (f )M 图3 qa 3 l q 041a 8 ql 4 l q 04(g )Q 图 (h )Q 图 (i )Q 图 2921 21qa 20121l q2(g )M 图 (h )M 图 (i )M 图qa 3 ql 83 ql 1 P 412 4(j )Q 图 (k )Q 图 (l )Q 图221qa 21281ql Pa 18 2(j )M 图 (k )M 图 (l )M 图5-3 利用q 、S F 、M 的微分关系作出下列各梁的剪力图和弯矩图,并求出|Smax F |和|M max |。
解:P 31 P 31Pqa P 31P qa 2 (a )Q 图 (b )Q 图 (c )Q 图Pa32 221qa(a )M 图 (b )M 图 (c )M 图qa qa KN 0.1qa KN 0.1(d )Q 图 (e )Q 图 (f )Q 图23qa(d )M 图 (e )M 图 (f )M 图KN 5.12 ql 1 ql 11KNm 16 KN 5.3 44(g )Q 图 (h )Q 图 (i )Q 图m KN ⋅12321ql32m KN ⋅2(g )M 图 (h )M 图 (i )M 图ql 5ql 8KN 2 (j )Q 图 (k )Q 图 (l )Q 图 23249qa(j )M 图 (k )M 图 (l )M 图l q 01 l q 05 ql 813ql 8(m )Q 图 (n )Q 图 (o )Q 图23213ql2061l q 204l q 219ql 23ql(m )M 图 (n )M 图 (o )M 图5-4 木梁浮在水面上,承受载荷如图示,求作其剪力图和弯矩图。
解:KN 20 KN 15l q 081 8m KN 10KN 10 4m 0.5aKN 20 KN 15l q 08(a )Q 图 (b )Q 图 (c )Q 图m KN ⋅30 201211a q m KN ⋅15 m KN ⋅15201211a qm KN ⋅80 m KN ⋅80(a )M 图 (b )M 图 (c )M 图5-5 求作下列各饺接梁的剪力图和弯矩图。
解:qa 25qa 21a 1qa 1 qa 1 qa(a )Q 图 (b )Q 图 (c )Q 图21qa 221 2123qa(a )M 图 (b )M 图 (c )M 图qa21qa 22qa(d )Q 图 (e )Q 图 (f )Q 图2qa1m KN ⋅8 m KN ⋅6(d )M 图 (e )M 图 (f )M 图5-6 根据q 、S F 、M 的微分关系,检查并改正下列各梁的S F 图和M 图的错误。
解:qa 41qa4aqa qa qa 47(a )Q 图 (b )Q 图S F S FS F S F2324921422qa (a )M 图 (b )M 图qaqa 32 qa 133(c )Q 图 (d )Q 图22qa22181qa261qa 2131qa (c )M 图 (d )M 图5-7 起吊一根自重为q (N /m )的等截面钢筋混凝土梁,求吊装时的起吊位置应为多少才最合理(最不易使杆折断)? 解:令 21M M =2121qx M -= )(x lql l l q M -+⋅⋅-=22422l l l l x 207.0222=+±-=2Mx xL1M 1M (M 图)5-8 小车可在梁上移动,它的每个轮子对梁的作用力均为P 。
试分析小车处于什么位置时梁内的弯矩最大(以x 表示梁上小车的位置)?解:[]la x l P R --=)(2[]ax x l x lPx R x M --=⋅=)(2)(0)(=dx x dM ()042=--a x l lP42al x -= ()822a l l P x R M mzx-=⋅= axP P L5-9 作图示梁ABC 的剪力图和弯矩图。
解:PA DBC AD B CPa(Q 图) (M 图)5-10 用叠加法作下列各梁的弯矩图241ql Pa 2 22ql 267ql 27235ql(a ) (b ) (c )Pl 95Pl 322167qlPl 31281ql 22qa 22qa(d ) (e ) (f )5-11 求作下列图示平面刚架的内力图。
解:(a)PPaPa P(M图) (Q图) (N图) (b)40KN⋅m40KN340KN⋅m40KN20KN3(M图) (Q图) (N图)(c )qa221qa 21qa221qa(M 图) (Q 图) (N 图)(d )2M M(M 图) (Q 图) (N 图)(e )qa 41(M 图) (Q 图) (N 图)(f )21221qaqa(M 图) (Q 图) (N 图)(g )Pl 1Pl 21 Pl 21PPl 2P P (M 图) (Q 图) (N 图)(h )2 Pa 433 3(M 图) (Q 图) (N 图)5-12 简支梁上的分布载荷按抛物线规律变化,其方程为)1(4)(0lxl x q x q -=试作剪力图和弯矩图。
解:l q 031 20121l ql q 031 (Q 图) (M 图)5-13 已知梁的剪力图,试求此梁的载荷及弯矩图(设梁上没有集中力偶作用)。
解:KN 20 KN 60(a ) m KN /2 (b ) m KN /30m KN ⋅54 m KN ⋅67.141 m KN ⋅48 m KN ⋅140m KN ⋅60(M 图) (M 图)5-14 已知梁的弯矩图,试求此梁的载荷及剪力图。
SF SFKN 5.37 KN 25 m KN ⋅40 KN 20 解:KN 20 KN 1667.29 KN 25KN 333.8(Q 图) (Q 图)5-15 图示梁上作用有集度为m =m (x )的分布力偶矩,试建立m 、S F 、M 之间的微分关系。
)(x m解:∑=0MdM M dx x m dx Q M +=+⋅+)( Q Q ∴ )(x m Q dxxdM+= dx dM5-16 悬臂梁上表面受切向分布力t 作用,t 为单位长度上的力N /m ,已知t 、h 、L 。
试分别作此梁的轴力、剪力和弯矩图。
解: htL 21tL(N 图) (Q 图) (M 图)阅读使人充实,会谈使人敏捷,写作使人精确。
5-17 某简支梁上作用有n 个间距相等的集中力,其总载荷为P ,所以每个载荷等于P /n ,梁的跨度为l ,载荷的间距为l /(n +1)。
(1)试导出梁中最大弯矩的一般公式;(2)将(1)的答案与承受均布载荷q 的简支梁的最大弯矩相比较,设P =ql 。
解:若n 为偶数,则m ax M 一侧有2n 个P 。
)122()122()12(22max +⨯---+--+--⨯=n l n l n p n l l n p n l l n p l p M )2321(1n n l n p +++++⨯= 2)12(2)1(+⨯+=n n n n pl )1(8)2(++=n n pl 若n 为奇数,则m ax M 一侧有21-n 个P 。
)1212()12(22max +⨯----+--⨯=n l n l n p n l l n p l p M )21321()1(4)1(4-+++++--=n n n pl n n pl pl 2)1121(21)1(444+-⨯-⨯+++-=n n n n pl n pl pl pl )1(8+=n npl 若p ql =阅读使人充实,会谈使人敏捷,写作使人精确。
pl ql M 81812max ==∞=n pl M 81max →1=n pl M 41max =2=n pl M 61max =3=n pl M 61max =4=n pl M 203max =。
