建筑力学1-第八章 剪切
合集下载
工程力学剪切的定义
工程力学剪切的定义工程力学是研究物体受力和变形规律的学科，是工程学的基础课程之一。
在工程力学中，剪切是一个重要的概念和现象。
剪切是指物体内部发生的相对滑动。
在工程实践中，剪切力的计算和控制对于确保工程结构的稳定性和安全性具有重要意义。
剪切力是指作用在物体上的力沿着物体表面滑动的力。
当物体受到剪切力作用时，物体内部的各层材料会发生相对滑动，导致物体的形状和结构发生变化。
剪切力会导致物体内部的剪切应力产生，剪切应力是物体内部各层材料之间相对滑动产生的应力。
在工程实践中，剪切力的大小和方向对于工程结构的设计和分析具有重要影响。
首先，剪切力的大小与物体的几何形状和受力情况有关。
在设计工程结构时，需要根据受力分析计算剪切力的大小，以确保结构的安全性和稳定性。
其次，剪切力的方向会影响物体的变形和破坏形式。
不同方向的剪切力作用在物体上会导致不同的变形形式，如剪切位移和剪切应变等。
在实际工程中，剪切力常常通过施加剪切载荷来产生。
例如，在桥梁设计中，由于车辆荷载和风荷载的作用，桥梁梁板上会产生剪切力。
设计师需要根据受力分析计算出桥梁上各个截面的剪切力大小和作用方向，以确保桥梁的安全性。
同样，在建筑设计中，地震力会产生剪切力，设计师需要根据地震力的大小和方向来设计建筑结构，以确保建筑物能够承受地震力的作用。
除了对剪切力的计算和分析外，工程师还需要考虑剪切力对工程结构的影响。
剪切力会导致物体内部各层材料的相对滑动，从而引起结构的变形和破坏。
在设计工程结构时，需要考虑剪切力对结构的影响，选择合适的材料和结构形式来抵抗剪切力的作用。
同时，在工程施工过程中，也需要注意剪切力对结构的影响，采取相应的施工措施来减小剪切力的作用。
剪切是工程力学中的重要概念和现象。
剪切力的计算和控制对于确保工程结构的稳定性和安全性具有重要意义。
工程师需要根据受力分析计算剪切力的大小和方向，并考虑剪切力对结构的影响，选择合适的材料和结构形式来抵抗剪切力的作用。
建筑力学D08剪切和扭转
T2 = −m2 − m3 = −(4.78 + 4.78) = −9.56kN ⋅ m
×
③绘制扭矩图
m2
m3
m1
m4
n A
扭矩图
B
C
⊕
D
6.37kN.m
–
4.78kN.m
–
9.56kN.m
T
max
= 9.56 kN ⋅ m, BC段为危险截面。 段为危险截面。 段为危险截面
×
画图示杆的扭矩图。 例5 画图示杆的扭矩图。
×
三、剪切虎克定律： 剪切虎克定律： 单元体ab 的倾角γ 称为切应变 切应变， 单元体 的倾角γ 称为切应变， 切应变是单元体直角的改变量 单元体直角的改变量。 切应变是单元体直角的改变量。实 验表明，在弹性范围内， 验表明，在弹性范围内，切应力与 dy 切应变成正比， 切应变成正比，即 a
γ τ´
×
⒋ 极惯性矩
dρ
I p = ∫ A ρ 2 dA = ∫ ρ 2 ⋅ 2 ρ ⋅ π ⋅ dρ =
D 2 0
ρ
O
D
πD 4
32
=
极惯性矩的单位： 极惯性矩的单位：m4
×
d D
环形截面： 环形截面： I P
π
32
(D4 − d 4 )
同一截面，扭矩 极惯性矩I 为常量， 同一截面，扭矩T ，极惯性矩 P 为常量，因此各点切应 成正比， 力τ 的大小与该点到圆心的距离ρ 成正比，方向垂直于圆的 半径，且与扭矩的转向一致。 半径，且与扭矩的转向一致。
A
a
1
2 B 3
b
b
4
a
C
16T1 T1 = τ1 = WP1 π D 3 16 ×1000 = π × 53 = 40.74 MPa
建筑力学_第八章-090514
达到最大值，在圆心处τ ＝0。
b）在任一圆周上，剪应力与圆周线平行，与半径垂直。
§8-5 等直圆杆在扭转时的应力强度条件
3、力学关系
j j T Ad A G d d xA2 d A G d d xIp
Ip
2d A—极惯性矩
A
T
T
d/2 ρ O
max
D/2
d/2 O
§8-2 连接接头的强度计算
（2）铆钉的剪切与挤压强度计算 运用截面法将铆钉假象地沿剪切面1－1截开
由静力平衡条件得:
Q=P
mQ A1 . 2 5 4 1 230 9.5 9 N /m2m 9.5 9 M P [m ]
4
［τm」=100MPa
§8-2 连接接头的强度计算
铆钉所受的挤压力为 有效挤压面积
知F=50kN，b=150mm，δ =10mm， d=17mm，a=80mm，[σ ]=160MPa， [τ ]=120MPa，[σ bs]=320MPa，铆钉 和板的材料相同，试校核其强度。
解：1.板的拉伸强度
2.板的剪切强度
Fs F 50103 A 4ad 40.080.01
a
b
T
O2
d
a
c
b a’
b’
dj
T
a
dx b
dj
dx
§8-5 等直圆杆在扭转时的应力强度条件
扭转
2、物理关系(剪切虎克定律)
G
GGd djxG
应力分布
d/2 ρ O
maxG RGd d R j xGR
max
说明：
a）剪应力与半径成正比，在外圆周上剪应力
建筑力学8剪切和扭转1239
破坏前无明显征兆。
03
疲劳扭转破坏
杆件在反复扭矩作用下，即使应力低于材料的屈服强度，也可能发生疲
劳破坏。疲劳破坏通常从截面的高应力区开始，逐渐扩展到整个截面，
最终导致杆件的断裂。
2023
PART 03
剪切与扭转组合受力分析
REPORTING
2023
PART 03
剪切与扭转组合受力分析
REPORTING
实验过程控制
严格控制实验过程中的 温度、湿度等环境因素， 避免对实验结果产生影
响。
数据处理与分析
对实验数据进行处理和 分析，得出准确的实验
结果和结论。
实验操作注意事项
试件准备
选择合适的试件尺寸和 形状，保证试件的质量
和精度。
设备调试
在实验前对设备进行调 试和校准，确保设备处
于正常工作状态。
实验过程控制
剪切与扭转的复合效应
探讨了剪切与扭转同时作用下的复合 效应，包括应力分布、变形特点和稳 定性分析等方面。
实验方法与应用案例
介绍了剪切和扭转实验的方法、技术 和应用案例，包括材料性能测试、结 构分析和优化设计等方面。
本次课程重点内容回顾
剪切力学的基本概念
介绍了剪切力的定义、剪切应力和剪 切应变等基本概念，以及剪切变形的 特点和影响因素。
刚度评估
通过计算构件在剪切和扭 转组合作用下的变形量， 评估构件的刚度是否满足 要求。
稳定性评估
综合考虑构件的强度、刚 度和稳定性等因素，对构 件在剪切和扭转组合作用 下的稳定性进行评估。
2023
PART 04
剪切与扭转实验方法及设 备介绍
REPORTING
2023
PART 04
建筑力学_第八章-090514
7
Chapter 1
§8-2 连接接头的强度计算
二、挤压的实用计算
1.挤压的概念
College of Sci. & Eng.
FF
F
F
挤压面
压溃(塑性变形)
挤压计算对联接件与被联接件都需进行
在外力直接压迫的部位及附近局部区域发生较大变形而
8 破坏。
Chapter 1
§8-2 连接接头的强度计算
College of Sci. & Eng.
由静力平衡条件得:Q=PmQ A
1.25 103
42
99.5N
/ mm 2
99.5MP [ m ]
19
4
［τm」=1C0ha0pMter P1 a
§8-2 连接接头的强度计算
College of Sci. & Eng.
铆钉所受的挤压力为 有效挤压面积
Pbs= P Abs= d×t
[τ ]=120MPa，[σ bs]=320MPa，铆钉 和板的材料相同，试校核其强度。
解：1.板的拉伸强度
2.板的剪切强度
Fs F 50103 A 4ad 4 0.08 0.01
15.7106 15.7MPa [ ]
FN F A (b 2d )d
12
Chapter 1
§8-2 连接接头的强度计算
College of Sci. & Eng.
13
Fs F
A lb
bs
Fbs Abs
F cb
Chapter 1
§8-2 连接接头的强度计算
College of Sci. & Eng.
工程力学上课课件：剪切与挤压共31页文档
拉
60、生活的道路一旦选定，就要勇敢地 走到底 ，决不 回头。 ——左
剪的圆孔最小直d和最大厚度t 。
解 1）确定圆孔的最小直径。 冲剪的孔径等于冲头的直径，冲头
冲头
工作时需满足抗压强度条件，即
凸模
FN 4F
A d2
d
4F
4401030
4403m 4 m
故取最小直径为35mm。
t t
F 工件
d
d
2）求钢板得最大厚度。钢板剪切面上的剪力FQ=F， 剪切面的面积为dt。为能冲断圆孔，需满足下列条件
（2）若铆钉按图示排列，所需板宽b为多少？
F
F
解： 可能造成的破坏：
（1）因铆钉被剪断而使铆接被破坏； （2）铆钉和板在钉孔之间相互挤压过大，而使铆接被破坏； （3）因板有钉孔，在截面被削弱处被拉断。
可采用假设的计算方法： 假定每个铆钉所受的力都是一样的。
（1）铆钉剪切计算
F/2n
F/n
Q
F/2n
如图，上钢板孔左侧与铆钉上部左侧，下钢板右侧与铆钉 下部右侧相互挤压。
发生挤压的接触面称为挤压面。挤压面上的压力称为挤
压力，用Fjy表示。相应的应力称为挤压应力，用jy表示。
jy
F jy A jy
必须指出，挤压与压缩不同。挤压力作用在构件的表面， 挤压应力也只分布在挤压面附近区域，且挤压变形情况比较 复杂。当挤压应力较大时，挤压面附近区域将发生显著的塑 性变形而被压溃，此时发生挤压破坏。
三、剪应变 剪切胡克定律
构件在发生剪切变形时，截面沿外力的方向产生相对错 动。在构件受剪部位的某处取一小立方体——单元体，在剪 力的作用下，单元体将变成平行六面体，其左右两截面发生
60、生活的道路一旦选定，就要勇敢地 走到底 ，决不 回头。 ——左
剪的圆孔最小直d和最大厚度t 。
解 1）确定圆孔的最小直径。 冲剪的孔径等于冲头的直径，冲头
冲头
工作时需满足抗压强度条件，即
凸模
FN 4F
A d2
d
4F
4401030
4403m 4 m
故取最小直径为35mm。
t t
F 工件
d
d
2）求钢板得最大厚度。钢板剪切面上的剪力FQ=F， 剪切面的面积为dt。为能冲断圆孔，需满足下列条件
（2）若铆钉按图示排列，所需板宽b为多少？
F
F
解： 可能造成的破坏：
（1）因铆钉被剪断而使铆接被破坏； （2）铆钉和板在钉孔之间相互挤压过大，而使铆接被破坏； （3）因板有钉孔，在截面被削弱处被拉断。
可采用假设的计算方法： 假定每个铆钉所受的力都是一样的。
（1）铆钉剪切计算
F/2n
F/n
Q
F/2n
如图，上钢板孔左侧与铆钉上部左侧，下钢板右侧与铆钉 下部右侧相互挤压。
发生挤压的接触面称为挤压面。挤压面上的压力称为挤
压力，用Fjy表示。相应的应力称为挤压应力，用jy表示。
jy
F jy A jy
必须指出，挤压与压缩不同。挤压力作用在构件的表面， 挤压应力也只分布在挤压面附近区域，且挤压变形情况比较 复杂。当挤压应力较大时，挤压面附近区域将发生显著的塑 性变形而被压溃，此时发生挤压破坏。
三、剪应变 剪切胡克定律
构件在发生剪切变形时，截面沿外力的方向产生相对错 动。在构件受剪部位的某处取一小立方体——单元体，在剪 力的作用下，单元体将变成平行六面体，其左右两截面发生
建筑力学 第一章 剪切和扭转讲义
h 2
2m 2 2 P 57kN d 0.07
m
P
L
h
b
40
d
切应力和挤压应力的强度校核
As bL
Fs Fb P
Abs L h 2
Fs P 57 103 28.6MPa As bL 20 100
Fb P 57 103 bs 95.3MPa bs Abs L h 2 100 6
m
h L
P
A
d
41
b
综上，键满足强度要求。
连接件的强度计算
4.其它连接件的实用计算方法 焊缝剪切计算
h l
45
有效剪切面
L
42
连接件的强度计算
1.23
4.其它连接件的实用计算方法
N
0.89
N
lw / he 10
1.62
b
角焊缝的构造与计算
0.72
45 。
N
45 。
A
30 C
τ
当焊缝轴线与外力作用方向平行时，称为侧面角焊缝， 又称侧缝； 垂直时，称为正面角焊缝，又称端缝； 呈夹角时，称为斜焊缝。
思考：（2）应力集中在工程中的影响？
答：应力集中对塑性材料影响不很大,但对脆性材料,应力集中将大大降低构件的强度。
思考：（3）如何避免应力集中的不良影响？
24
第二节
[例 1]
连接接头的强度计算
两块钢板用三个直径相同的铆钉连接, 已知钢板宽度b = 100 mm, 厚度t = 10 mm,铆钉直径d = 20 mm, 铆钉许用切应力[ ]= 100 M Pa, 许用挤压切应力 [bs]= 300 MPa,钢板许用拉应力 []= 160MPa。 试求许用荷载 F 若有n 个铆钉,则
2m 2 2 P 57kN d 0.07
m
P
L
h
b
40
d
切应力和挤压应力的强度校核
As bL
Fs Fb P
Abs L h 2
Fs P 57 103 28.6MPa As bL 20 100
Fb P 57 103 bs 95.3MPa bs Abs L h 2 100 6
m
h L
P
A
d
41
b
综上，键满足强度要求。
连接件的强度计算
4.其它连接件的实用计算方法 焊缝剪切计算
h l
45
有效剪切面
L
42
连接件的强度计算
1.23
4.其它连接件的实用计算方法
N
0.89
N
lw / he 10
1.62
b
角焊缝的构造与计算
0.72
45 。
N
45 。
A
30 C
τ
当焊缝轴线与外力作用方向平行时，称为侧面角焊缝， 又称侧缝； 垂直时，称为正面角焊缝，又称端缝； 呈夹角时，称为斜焊缝。
思考：（2）应力集中在工程中的影响？
答：应力集中对塑性材料影响不很大,但对脆性材料,应力集中将大大降低构件的强度。
思考：（3）如何避免应力集中的不良影响？
24
第二节
[例 1]
连接接头的强度计算
两块钢板用三个直径相同的铆钉连接, 已知钢板宽度b = 100 mm, 厚度t = 10 mm,铆钉直径d = 20 mm, 铆钉许用切应力[ ]= 100 M Pa, 许用挤压切应力 [bs]= 300 MPa,钢板许用拉应力 []= 160MPa。 试求许用荷载 F 若有n 个铆钉,则
建筑力学第八章：
个约束;
高速铁路新型板式轨道设计理论与力学性能研究《建筑力学》 第八章：超静定结构解法
8.1 超静定结构及超静定次数的确定
课堂练习： 判定下列结构的超静定次数：
3 3
3
3
n 12
2
3
1
n6 高速铁路新型板式轨道设计理论与力学性能研究《建筑力学》 第八章：超静定结构解法
8.1 超静定结构及超静定次数的确定
高速铁路新型板式轨道设计理论与力学性能研究《建筑力学》 第八章：超静定结构解法
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 1. 去掉一个支座链杆相当于解除1个约束。
2. 在杆件内添加一个铰，相当于解除1个约束； 3. 去掉一个固定铰支座,或拆开一个单铰相当于解除
2个约束； 4. 去掉一个固定端支座相当于解除3个约束； 5. 切断一根梁（杆）或切开一个闭合框相当于解除3
A B C A B
高速铁路新型板式轨道设计理论与力学性能研究《建筑力学》 第八章：超静定结构解法
C
8.1 超静定结构及超静定次数的确定
超静定次数的确定： 超静定次数=多余约束的个数 确定方法：如果从原结构中去掉 n个约束后，结构成为静 定结构，则原结构的超静定次数=n
B B
X1
n 1
X 1 ——多余约束力
静定基不唯一
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 2. 在杆件内添加一个铰，相当于解除一个约束；
X3
X1
X2
也称：刚结点（刚性联结）变铰结点相当于解除一个约束；
高速铁路新型板式轨道设计理论与力学性能研究《建筑力学》 第八章：超静定结构解法
8.1 超静定结构及超静定次数的确定
建筑力学课件7剪切与扭转
P 103 M e 2n 60
由此得
PkW M e Nm 9550 nr/min)，则 如果功率P的单位用马力(
1马力 735.5N m / s
(10-1)
P马力 M e N m 7024 nr / min 对于外力偶的转向，主动轮上的外力偶的转向与轴的转向相同，而从
r0
根据上述分析可得，薄壁圆筒扭转时横截面上各点处的切应力 值均 相等，其方向与圆周相切(如图10.9c所示)。于是，由横截面上内力与 应力间的静力关系，得 代替，而积分 r r0 为圆筒横截面面积，将其代入上式，得 dA A 2r0 A T T (10-3) 2r02 2 A0 这里 。由图10.9b所示的几何关系，可得薄壁圆筒表面上的切应 变 和相距为 A0 r02 的两端面间的相对扭转角 之间的关系式： (10-4) l 式中， 为薄壁圆筒的外半径。 r / l
上节阐明了圆轴扭转时，横截面上内力系合成的结果是一 力偶，并建立了其力偶矩(扭矩)与外力偶矩的关系。现在 进一步分析内力系在横截面上的分布情况，以便建立横截 面上的应力与扭矩的关系。下面先研究薄壁圆筒的扭转应 力。
设一薄壁圆筒(如图10.9a所示)，壁厚 远小于其平均半径 ，两端受一对大小相等，转向相反的外力偶作用。加 r0 r0 ≤ 10 力偶前，在圆筒表面刻上一系列的纵向线和圆周线，从而形成一系列 的矩形格子。扭转后，可看到下列变形情况(如图10.9b所示)。
A
由于
dA r T 为常数，且对于薄壁圆筒， 可用其平均半径
r
通过薄壁圆筒的扭转试验可以发现，当外力偶矩在某一范围内时，相 对扭转角 与扭矩 成正比，如图10.10a所示。利用式(10-3)和式(10-4)， 即得 与 间的线性关系T (如图10.10b所示)为 (10-5)
由此得
PkW M e Nm 9550 nr/min)，则 如果功率P的单位用马力(
1马力 735.5N m / s
(10-1)
P马力 M e N m 7024 nr / min 对于外力偶的转向，主动轮上的外力偶的转向与轴的转向相同，而从
r0
根据上述分析可得，薄壁圆筒扭转时横截面上各点处的切应力 值均 相等，其方向与圆周相切(如图10.9c所示)。于是，由横截面上内力与 应力间的静力关系，得 代替，而积分 r r0 为圆筒横截面面积，将其代入上式，得 dA A 2r0 A T T (10-3) 2r02 2 A0 这里 。由图10.9b所示的几何关系，可得薄壁圆筒表面上的切应 变 和相距为 A0 r02 的两端面间的相对扭转角 之间的关系式： (10-4) l 式中， 为薄壁圆筒的外半径。 r / l
上节阐明了圆轴扭转时，横截面上内力系合成的结果是一 力偶，并建立了其力偶矩(扭矩)与外力偶矩的关系。现在 进一步分析内力系在横截面上的分布情况，以便建立横截 面上的应力与扭矩的关系。下面先研究薄壁圆筒的扭转应 力。
设一薄壁圆筒(如图10.9a所示)，壁厚 远小于其平均半径 ，两端受一对大小相等，转向相反的外力偶作用。加 r0 r0 ≤ 10 力偶前，在圆筒表面刻上一系列的纵向线和圆周线，从而形成一系列 的矩形格子。扭转后，可看到下列变形情况(如图10.9b所示)。
A
由于
dA r T 为常数，且对于薄壁圆筒， 可用其平均半径
r
通过薄壁圆筒的扭转试验可以发现，当外力偶矩在某一范围内时，相 对扭转角 与扭矩 成正比，如图10.10a所示。利用式(10-3)和式(10-4)， 即得 与 间的线性关系T (如图10.10b所示)为 (10-5)
建筑力学与结构——剪切与扭转
▪ τ与γ关系，如同σ与ε一样。实验证明：当 剪应力 τ不超ห้องสมุดไป่ตู้材料的比例极限τb时， 剪应力与剪应变成正比，如图7-8所示， 即：
式(7-5)称为剪切虎克定律。式中G称为材料的剪切弹性 模量，它是表示材料抵抗剪切变形能力的物理量，其单 位与应力相同，常采用GPa。各种材料的G值均由实验 测定。钢材的G值约为80GPa。G值越大，表示材料抵抗 剪切变形的能力越强，它是材料的弹性指标之一。对于 各向同性的材料，其弹性模量E、剪变模量G和泊松比μ 三者之间的关系为：
单元7 剪切与扭转
1.剪切和挤压的概念 ； 2.剪应力和压应力的计算和校核 ； 3.剪切虎克定律公式和剪应力互等定理 ； 4.圆轴的扭矩的概念和公式 ； 5.圆轴圆轴扭转强度计算，最大剪应力；
第一讲
教学目标： 1.理解剪切和挤压的概念 . 2.能够运用公式计算剪应力和压应力 . 3.理解识记虎克定律公式，灵活运用 . 4.理解扭矩概念和能够计算扭矩 5.扭矩应力计算和最大剪应力
式中 [σc]——材料的许用挤压应力，由试验测得。许 用挤压应力[σc]比许用压应力[ σ]高，约为1．7～2．0倍， 因为挤压时只在局部范围内引起塑性变形，周围没有发生塑 性变形的材料将会阻止变形的扩展,从而提高了抗挤压的能 力。
【例7-1】 图7—6(a)所示一铆钉连接件，受轴向拉力F 作用。已知：F=100kN,钢板厚δ＝８mm,宽＝100mm,铆钉直 径d＝16mm,许用剪应力［τ］＝140MPa,许用挤压应力
扭矩的单位与力矩相同，常用N·m或kN·m。 2．扭矩正负号规定
为了使由截面的左、右两段轴求得的扭矩具有相同的正负
号，对扭矩的正、负作如下规定：采用右手螺旋法则，以右 手四指表示扭矩的转向，当拇指的指向与截面外法线方向一
式(7-5)称为剪切虎克定律。式中G称为材料的剪切弹性 模量，它是表示材料抵抗剪切变形能力的物理量，其单 位与应力相同，常采用GPa。各种材料的G值均由实验 测定。钢材的G值约为80GPa。G值越大，表示材料抵抗 剪切变形的能力越强，它是材料的弹性指标之一。对于 各向同性的材料，其弹性模量E、剪变模量G和泊松比μ 三者之间的关系为：
单元7 剪切与扭转
1.剪切和挤压的概念 ； 2.剪应力和压应力的计算和校核 ； 3.剪切虎克定律公式和剪应力互等定理 ； 4.圆轴的扭矩的概念和公式 ； 5.圆轴圆轴扭转强度计算，最大剪应力；
第一讲
教学目标： 1.理解剪切和挤压的概念 . 2.能够运用公式计算剪应力和压应力 . 3.理解识记虎克定律公式，灵活运用 . 4.理解扭矩概念和能够计算扭矩 5.扭矩应力计算和最大剪应力
式中 [σc]——材料的许用挤压应力，由试验测得。许 用挤压应力[σc]比许用压应力[ σ]高，约为1．7～2．0倍， 因为挤压时只在局部范围内引起塑性变形，周围没有发生塑 性变形的材料将会阻止变形的扩展,从而提高了抗挤压的能 力。
【例7-1】 图7—6(a)所示一铆钉连接件，受轴向拉力F 作用。已知：F=100kN,钢板厚δ＝８mm,宽＝100mm,铆钉直 径d＝16mm,许用剪应力［τ］＝140MPa,许用挤压应力
扭矩的单位与力矩相同，常用N·m或kN·m。 2．扭矩正负号规定
为了使由截面的左、右两段轴求得的扭矩具有相同的正负
号，对扭矩的正、负作如下规定：采用右手螺旋法则，以右 手四指表示扭矩的转向，当拇指的指向与截面外法线方向一
建筑力学电子教案_剪切
对有几个螺栓的情况，关键在于求得每个螺栓所 受外力，然后按单个螺栓作进一步计算。对销、螺栓 等连结，还要确定受剪面是一面还是两面。
上述方法也适用于被连结部件在扭转和弯曲时其 连结部分计算。
建筑力学电子教案
例3-1 销钉如图(a)所示。已知外力F=18 kN, 被连接的构件A和 B的厚度分别为 t=8 mm, t1=5mm, 销钉直径d=15mm; 销钉材
投影面积（直径平面）。
建筑力学电子教案
挤压强度条件是
c c
c 是材料的容许挤压应力，当连结件与被连结件材 料不同从而 c 不同时，要选较小的 c 。
剪切强度计算关键在于求得受剪面上的剪力和受挤 压面上的挤压力，受剪面平行于外力作用线，受挤压面 垂直于外力作用线。
建筑力学电子教案
m F1
Fn F1
m F1 F1 n F/2
(b)
建筑力学电子教案
F
B A
t1t t1 F
c
F
Fc F
m
n
A F
m n
t
c
Fc Ac
F td
18103 N 8 15mm2ห้องสมุดไป่ตู้
150 MPa
c 200 MPa
建筑力学电子教案
F
B A
t1t t1 F
c
F A
F
Fc F
m
n
m n
t
故 ,c ，c 销钉是安全的。
建筑力学电子教案
剪切
构件连接的实用计算
建筑力学电子教案
§8-1 概 述
构件相互连接时，可采用螺栓（销钉）连接、焊接、铆接 等方式。象螺栓等这些连接件，在传力时主要受剪切，同时在 侧面上还伴随有局部挤压。
上述方法也适用于被连结部件在扭转和弯曲时其 连结部分计算。
建筑力学电子教案
例3-1 销钉如图(a)所示。已知外力F=18 kN, 被连接的构件A和 B的厚度分别为 t=8 mm, t1=5mm, 销钉直径d=15mm; 销钉材
投影面积（直径平面）。
建筑力学电子教案
挤压强度条件是
c c
c 是材料的容许挤压应力，当连结件与被连结件材 料不同从而 c 不同时，要选较小的 c 。
剪切强度计算关键在于求得受剪面上的剪力和受挤 压面上的挤压力，受剪面平行于外力作用线，受挤压面 垂直于外力作用线。
建筑力学电子教案
m F1
Fn F1
m F1 F1 n F/2
(b)
建筑力学电子教案
F
B A
t1t t1 F
c
F
Fc F
m
n
A F
m n
t
c
Fc Ac
F td
18103 N 8 15mm2ห้องสมุดไป่ตู้
150 MPa
c 200 MPa
建筑力学电子教案
F
B A
t1t t1 F
c
F A
F
Fc F
m
n
m n
t
故 ,c ，c 销钉是安全的。
建筑力学电子教案
剪切
构件连接的实用计算
建筑力学电子教案
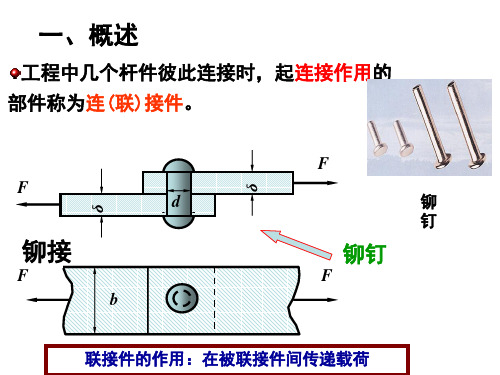
§8-1 概 述
构件相互连接时，可采用螺栓（销钉）连接、焊接、铆接 等方式。象螺栓等这些连接件，在传力时主要受剪切，同时在 侧面上还伴随有局部挤压。
第八章 剪切和扭转 建筑力学
压头 试件 FS F FS
受剪面面积
τu =
Fu 2 As
[τ ] = τ u / n
组合变形及连接部分的计算
图示装置常用来确定胶接处的抗剪强度， 例8-7 图示装置常用来确定胶接处的抗剪强度，如已知破坏时 的荷载为10kN，试求胶接处的极限切应力。 的荷载为 ，试求胶接处的极限切应力。 F F
① ① 10mm
第八章 剪切和扭转
§8-1 剪切的概念及实例 §8-2 连接接头的强度计算 §8-3 扭转的概念及实例 扭矩的计算、 §8-4 扭矩的计算、扭矩图 §8-5 圆轴扭转时的应力和变形 §8-6 圆轴扭转时的强度条件和刚度条件
§8-1
剪切的概念及实例
键 连 接
m
榫齿 连接
铆钉（或螺栓）连接 铆钉（或螺栓）
2）结论： 结论： a)变形后，横截面仍保持平面，其形状、大小与横截面间 变形后，横截面仍保持平面，其形状、 变形后 的距离均不改变，而且，半径仍为直线， 成立。 的距离均不改变，而且，半径仍为直线，平面假设成立。 b)相邻截面绕轴线作相对转动。 相邻截面绕轴线作相对转动。 相邻截面绕轴线作相对转动 c)横截面上各点的剪（切）应力的方向必与圆周线相切。 横截面上各点的剪（ 横截面上各点的剪 应力的方向必与圆周线相切。
σ=
FN，max 140000 = = 111MPa < [σ ] A 12.66 ×10 − 4
斜杆满足拉伸强度的要求
§8-3 扭转的概念及实例
m A' A γ m B ϕ B'
外力偶作用平面和杆件横截面平行
γ：剪切角 (切应变) 应变 γ ϕ：相对扭转角
圆轴扭转变形
Τ
O
O
受剪面面积
τu =
Fu 2 As
[τ ] = τ u / n
组合变形及连接部分的计算
图示装置常用来确定胶接处的抗剪强度， 例8-7 图示装置常用来确定胶接处的抗剪强度，如已知破坏时 的荷载为10kN，试求胶接处的极限切应力。 的荷载为 ，试求胶接处的极限切应力。 F F
① ① 10mm
第八章 剪切和扭转
§8-1 剪切的概念及实例 §8-2 连接接头的强度计算 §8-3 扭转的概念及实例 扭矩的计算、 §8-4 扭矩的计算、扭矩图 §8-5 圆轴扭转时的应力和变形 §8-6 圆轴扭转时的强度条件和刚度条件
§8-1
剪切的概念及实例
键 连 接
m
榫齿 连接
铆钉（或螺栓）连接 铆钉（或螺栓）
2）结论： 结论： a)变形后，横截面仍保持平面，其形状、大小与横截面间 变形后，横截面仍保持平面，其形状、 变形后 的距离均不改变，而且，半径仍为直线， 成立。 的距离均不改变，而且，半径仍为直线，平面假设成立。 b)相邻截面绕轴线作相对转动。 相邻截面绕轴线作相对转动。 相邻截面绕轴线作相对转动 c)横截面上各点的剪（切）应力的方向必与圆周线相切。 横截面上各点的剪（ 横截面上各点的剪 应力的方向必与圆周线相切。
σ=
FN，max 140000 = = 111MPa < [σ ] A 12.66 ×10 − 4
斜杆满足拉伸强度的要求
§8-3 扭转的概念及实例
m A' A γ m B ϕ B'
外力偶作用平面和杆件横截面平行
γ：剪切角 (切应变) 应变 γ ϕ：相对扭转角
圆轴扭转变形
Τ
O
O
建筑力学-第八章-剪切
F bs Aj
A j (b d )t
8.2 剪切的实用计算 剪切变形十分复杂,剪应力在横截面上的实际 分布规律很难确定,工程上常采用下列实用计算。 ■ 名义剪应力 τ = F/A 即名义剪应力是假设F沿截面均匀分布而得出的。 用名义剪应力来进行强度计算的方法称为剪 切的实用计算方法。
d b
P s
P
S > 2d
t P d b
P
P s
P
例1. 拉杆用4个相同的 铆钉固定于格板，铆 钉的材料与拉杆相同。 设P = 80 kN, b = 80mm, t =10mm, d =16mm, s = 3d, [σ]=160MPa, [τ]=100MPa, [σc]=300MPa。试校核 铆钉和拉杆的强度。
双剪切
Q = P1/2 = P/2n,
A = πd2/4
n = 1.78
τ = Q/A = 2P/nπd2 ≤ [τ] 试取 n = 2, 校核铆钉的挤压强度。
σc = P1/ Ac= P/ntd = 156 MPa ≤ [σc ]
2.根据主板的抗拉强度条件来确定板宽b
P P1 P 1 P1 b
P
欢迎光临
建筑力学ぜ【ڛ
剪切和扭转
8. 剪切和扭转 8.1 剪切及其实用计算
剪切的概念 在垂直于杆轴方向的横向力作用下,杆的两相邻 横截面将发生相对错动(滑移),这种变形称为剪切。
钢杆受剪图
a
1
2 2
F F c F
3 4
F a c 1 2 b 3 4 d F
b F
d
受力特点：作用在构件上的力大小相等、方向相 反、作用线与轴线垂直且相距很近的一对外力。 变形特点：以两作用力间横截面为分界面 ,构件 两部分沿该面(剪切面)发生相互错动。
剪切和挤压—剪切和挤压的概念与实例(建筑力学)
剪切与挤压
通常把相对错动的截面称为剪切面。剪切面平行于力的作 用线，位于方向相反的两横向外力作用线之间。剪切面上的 内力FQ与截面相切，称为剪力（图ｄ），可用截面法求得。
像这种只有一个剪切面的称为单剪。
剪切与挤压
图中的销钉有两个剪切面， 称为双剪。
构件在受剪切时，常伴随着挤压 现象。相互接触的两个物体相互传递 压力时，因接触面的面积较小，而传 递的压力却比较大，致使接触表面产 生局部的塑性变形，甚至产生被压陷 的现象，称为挤压。
剪切与挤压
两构件相互接触的局部受压面称为 挤压面；
挤压面上的压力称为挤压力； 由于挤压引起的应力称为挤压应力；
在工程中也有一些非连接件也发生剪 切破坏，如地基的混凝土板受柱子向下 的压力和基础向上的支持力，使混凝土 板产生剪切变形。
剪切与挤压
当钢板受到轴向拉力Ｆ作用后，铆钉就受到了上、下钢板
传来的如图ｂ所示的力的作用，其受力特点是铆钉两侧面所 受力的合力大小相等，方向相反，作用线平行且相距很近。
当外力足够大时，铆钉的上半部将沿力的方向向右移动， 而下半部将沿力的方向向左移动，在截面m-m面处产生相对 错动，而使之发生所谓的剪切变形（图ｃ)。
第八章 剪切与挤压
剪切与挤压
学习目标：
1.弄清连接件的受力特点和变性特点。 2. 会分析连接件的剪切面和挤压面。 3.掌握剪切与挤压的实用计算。
重点：
剪切与挤压的实用以看到两个或两个以上构件用铆钉、螺 栓、销或榫等部件连接起来。我们把这些起连接作用的部件 称为连接件。
建筑力学课件剪切
P
b
P
l
l
除杆件整体必须满足强度、刚度和稳定性的要求外，连接件本身 也应具有足够的强度.
a
注：连接件本身不是杆件
如榫接与焊缝
连(联)接件发生的变形-----剪切变形
F
m m F
作用在连接件两侧面上的一对合力大小相等、 方向相反且相距很近，并使各自作用部分沿着 与合力作用线之间的截面m-m（剪切面）发生相 对错动。这种变形称为剪切变形。
挤压面上存在着由挤压力产生 的挤压正应力，它的分布十分复杂。
实用计算假定挤压应力均匀分布 在挤压面上，以平均挤压应力作 为挤压面上的名义挤压应力。 FC
(a)
d
smax
s max t s sj
C
(b) (b)
(c)
挤压面 计算挤压面积=dt
(c)
AC挤压面面积
挤压面为平面----AC为实际面积 挤压面为半圆柱面---AC为计算面积 AC=d•t
上式计算得到的名义挤压应力与接触中点处的 最大理论挤压应力值相近。
四、切应力互等定理
y
τ'
dy dz z dx
τ
x
由空间力系平衡 方程，∑Mz = 0
τ = τ′
切应力互等定理:对一个单元体，在相互垂直的两个截 面上，沿垂直于两平面交线作用的切应力必成对出现， 且大小相等，方向都指向（或都背离）两平面的交线。
变形特点 ：平行力间的截面发生相对错动，直至剪切破坏
剪切面 ：发生相对错动而被剪断的面。可以是平面或曲面 内力：剪力；方法：截面法；代表符号FQ此处没规定 其正负号）。
以铆钉连接为例计算剪力，沿剪切面切开, 取部分铆钉研 究，受力如图。
双剪：FQ=F/2
b
P
l
l
除杆件整体必须满足强度、刚度和稳定性的要求外，连接件本身 也应具有足够的强度.
a
注：连接件本身不是杆件
如榫接与焊缝
连(联)接件发生的变形-----剪切变形
F
m m F
作用在连接件两侧面上的一对合力大小相等、 方向相反且相距很近，并使各自作用部分沿着 与合力作用线之间的截面m-m（剪切面）发生相 对错动。这种变形称为剪切变形。
挤压面上存在着由挤压力产生 的挤压正应力，它的分布十分复杂。
实用计算假定挤压应力均匀分布 在挤压面上，以平均挤压应力作 为挤压面上的名义挤压应力。 FC
(a)
d
smax
s max t s sj
C
(b) (b)
(c)
挤压面 计算挤压面积=dt
(c)
AC挤压面面积
挤压面为平面----AC为实际面积 挤压面为半圆柱面---AC为计算面积 AC=d•t
上式计算得到的名义挤压应力与接触中点处的 最大理论挤压应力值相近。
四、切应力互等定理
y
τ'
dy dz z dx
τ
x
由空间力系平衡 方程，∑Mz = 0
τ = τ′
切应力互等定理:对一个单元体，在相互垂直的两个截 面上，沿垂直于两平面交线作用的切应力必成对出现， 且大小相等，方向都指向（或都背离）两平面的交线。
变形特点 ：平行力间的截面发生相对错动，直至剪切破坏
剪切面 ：发生相对错动而被剪断的面。可以是平面或曲面 内力：剪力；方法：截面法；代表符号FQ此处没规定 其正负号）。
以铆钉连接为例计算剪力，沿剪切面切开, 取部分铆钉研 究，受力如图。
双剪：FQ=F/2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
γ
剪切角是对剪切变形的一个度量，称为切应变
剪切虎克定律
τ = Gγ
G:切变模量
§8－2 连接接头的强度计算
一、连接件的受力特点和变形特点： 连接件的受力特点和变形特点： 1、连接件 在构件连接处起连接作用的部件，称为连接件 连接件。例如： 连接件 螺栓、铆钉、键等。连接件虽小，起着传递载荷的作用。 螺栓 特点：可传递一般 力， P P 可拆卸。
③剪切面： 剪切面 构件将发生相互的错动面，如 n– n 。 ④剪切面上的内力： 剪切面上的内力 内力 — 剪力Q ，其作用线与 Q 剪切面 剪切面平行。 n P
n
（合力） P n n P （合力） 剪切面 n P
3、连接处破坏三种形式： 、连接处破坏三种形式 ①剪切破坏 沿铆钉的剪切面剪断，如 沿n– n面剪断 。 ②挤压破坏 铆钉与钢板在相互接触面 上因挤压而使溃压连接松动， 发生破坏。 ③拉伸破坏
F σ bs = ≤ [σ ] Aj
A j = (b − d )t
四、应用
1、校核强度： τ ≤ [τ ] ； σ bs ≤ [σ bs ]
Pjy Q 2、设计尺寸： AQ ≥ ； A jy ≥ [τ ] [σ jy ]
3、设计外载： Q ≤ AQ [τ ] ； P jy ≤ A jy [σ
jy
]
Q n
钢板在受铆钉孔削弱的截面处，应力增大，易在连接处拉断。
（合力） P n n P （合力） 剪切面 n P
3、连接处破坏三种形式： 、连接处破坏三种形式 ①剪切破坏 沿铆钉的剪切面剪断，如 沿n– n面剪断 。
Q n
（合力） P n n P （合力） 剪切面 n P
3、连接处破坏三种形式： 、连接处破坏三种形式 ②挤压破坏 铆钉与钢板在相互接触面 上因挤压而使溃压连接松动， 发生破坏。
（合力） P n n P （合力）
1、剪切面--As ： 错动面。 剪力--Fs： 剪切面上的内力。
2、名义剪应力--τ：
Fs τ = As
Q n P 剪切面 n 3、剪切强度条件（准则）：
Fs τ = ≤ [τ ] As
其中 :
[τ ] =
τ
jx
n
工作应力不得超过材料的许用应力。
2、挤压的实用计算 挤压：构件局部面积的承压现象。 挤压力：在接触面上的压力，记Fbs。 1、挤压力―Fbs ：接触面上的合力。
Q n
（合力） P n n P （合力） 剪切面 n P
3、连接处破坏三种形式： 、连接处破坏三种形式 ③拉伸破坏 钢板在受铆钉孔削弱的截 面处，应力增大，易在连 接处拉断。 Q
n
1、剪切的实用计算 实用计算方法： 实用计算方法：根据构件的破坏可能性，采用能反映受力基本 特征，并简化计算的假设，计算其名义应力，然后根据直接试 验的结果，确定其相应的许用应力，以进行强度计算。 适用：构件体积不大，真实应力相当复杂情况，如连接件等。 适用 实用计算假设： 实用计算假设：假设剪应力在整个剪切面上均匀分布，等于剪 切面上的平均应力。
第八章 剪切和扭转
§8－1 §8－2 剪切的概念及实例 连接接头的强度计算
§8－3 扭转的概念及实例 §8－4 §8－5 §8－6 扭矩的计算·扭矩图 扭矩的计算 扭矩图 圆轴扭转时的应力和变形 圆轴扭转时的强度条件和刚度条件
受力特点：作用在构件上的力大小相等、 受力特点：作用在构件上的力大小相等、方向 相反、作用线与轴线垂直且相距很近的一对外力。 相反、作用线与轴线垂直且相距很近的一对外力。 变形特点： 变形特点：以两作用力间横截面为分界面 ,构件 构件 两部分沿该面(剪切面)发生相互错动。 两部分沿该面(剪切面)发生相互错动。
假设：挤压应力在有效挤压面上均匀分布。
2、挤压面积：接触面在垂直Fbs方向上的投影面的面积。
挤压面积 A jy = dt 3、挤压强度条件（准则）： 工作挤压应力不得超过材料的许用挤压应力。
Fbs σ bs = ≤ [σ bs ] Abs
3、连接板的强度计算 由于铆钉孔削弱了连接板的横截面面积。使连接板 的抗拉强度受到影响。 假设连接板截面上的正应力均匀分布，则连接板应 满足的拉伸强度条件为
2、受力特点和变形特点： 受力特点和变形特点： 以铆钉为例： （合力） P n ①受力特点： 受力特点 构件受两组大小相等、方向相 反、作用线相互很近（差一个几 n P （合力） 何平面）的平行力系作用。 ②变形特点： 变形特点 构件沿两组平行力系的交界面 发生相对错动。
（合力） P n n P （合力）