结构化学量子力学基础课外习题解答
《量子力学基础和原子、分子及晶体结构》习题和思考题

《结构化学》课程作业题第一部分:《量子力学基础和原子结构》思考题与习题1. 经典物理学在研究微观物体的运动时遇到过哪些困难?举例说明之。
如何正确对待归量子论?2. 电子兼具有波动性的实验基础是什么?宏观物体有没有波动性?“任何微观粒子的运动都是量子化的,都不能在一定程度上满足经典力学的要求”,这样说确切吗?3. 怎样描述微观质点的运动状态?为什么?波函数具有哪些重要性质?为什么?4. 简述薛定谔方程得来的线索。
求解该方程时应注意什么?5. 通过一维和三维势箱的解,可以得出哪些重要結論和物理概念?6. 写出薛定谔方程的算符表达式。
你是怎样理解这个表达式的? *7. 量子力学中的算符和力學量的关系怎样?8. 求解氢原子和类氢离子基态和激发态波函数的思想方法是怎样的? 9. 通过氢原子薛定谔方程一般解的讨论明确四个量子数的物理意义。
10. 怎样根据波函数的形式讨论“轨道”和电子云图象?为什么不能说p +1和p -1就是分别代表p x 和p y ? 11. 样来研究多电子原子的结构?作过哪些近似?用过哪些模型?试简单说明之。
12. 电子的自旋是怎样提出的?有何实验依据?在研究原子内电子运动时,我们是怎样考虑电子自旋的?*13. 哈特里-福克SCF 模型考虑了一些什么问题?交换能有何意义?14. 怎样表示原子的整体状态?光谱项、光谱支项各代表什么含义?洪特规则、选择定则又是讲的什么内容?15. 原子核外电子排布的规律是什么?现在哪些问题你比过去理解得更加深入了?通过本部分的学习,你对微观体系的运动规律和特点掌握了多少?在思想方法上有何收获?16. 巴尔末起初分析氢原子光谱是用波长)(422-=n n c λ,其中c 为常数,n 为大于2的正整数,试用里德伯常数H R ~求出c 值。
17. 试计算氢原子中电子处于波尔轨道n = 1和n = 4时的动能(单位:J )和速度(单位:m·s -1)。
18. 已知电磁波中电场强度ε服从波动方程222221t c x ∂∂⋅=∂∂εε,试说明如下函数⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=t x t x y νλπεε2c o s 0),(是这个方程的解。
结构化学习题答案

刘义武
L/O/G/O
参考书
• 结构化学习题解析 • 物质结构学习指导 • 结构化学500题解
周公度等著 倪行等著 刘国范等
• 结构化学学习指导
韦吉崇等
常用物理常数
普朗克常数 h 6.626×10−34 J•s 波尔兹曼常数 k 1.381×10−23 J•K-1
真空中光速 c 2.998×108 m•s -1
10
解:
(1) λ = h/p = h/mυ = 6.626×10−34 J ∙ s / 10-10 kg×0.01m ∙ s -1 = 6.626×10−22 m (2) λ = h/p = h/√ 2mT 6.626×10−34 J ∙ s
=
√ 2×1.675×10-27 kg×100 eV ×1.602×10−19 C
= 5.272 ×10−22 m
电子:
∆x = =
=
h h
4 π • ∆p x 4 π • m• ∆υ
6.626×10−34 J ∙ s
4 ×3.142× 9.110×10−31 kg×106 m ∙ s -1 × 10 %
= 5.787 ×10−10 m
子弹、花粉的不确定关系不具有实际意义。 电子的不确定关系具有实际意义。
14
x2 + y2 2 d d d2 2 2 (x + y ) = (2x) = 2 x2+ y2 不是算符 的本征函数。 2 2 d x dx dx (a-x)e-x
2 d d2 (a-x)e-x = 2 (ae-x - xe-x) dx dx2 d (ae-x ∙ (-1) – (e-x + xe-x ∙(-1))) = dx d = (-ae-x – e-x +xe-x) dx
《量子力学基础和原子、分子及晶体结构》习题和思考题

《结构化学》课程作业题 2009.1.15第一部分:《量子力学基础和原子结构》思考题与习题1. 经典物理学在研究微观物体的运动时遇到过哪些困难?举例说明之。
如何正确对待归量子论?2. 电子兼具有波动性的实验基础是什么?宏观物体有没有波动性?“任何微观粒子的运动都是量子化的,都不能在一定程度上满足经典力学的要求”,这样说确切吗?3. 怎样描述微观质点的运动状态?为什么?波函数具有哪些重要性质?为什么?4. 简述薛定谔方程得来的线索。
求解该方程时应注意什么?5. 通过一维和三维势箱的解,可以得出哪些重要結論和物理概念?6. 写出薛定谔方程的算符表达式。
你是怎样理解这个表达式的? *7. 量子力学中的算符和力學量的关系怎样?8. 求解氢原子和类氢离子基态和激发态波函数的思想方法是怎样的? 9. 通过氢原子薛定谔方程一般解的讨论明确四个量子数的物理意义。
10. 怎样根据波函数的形式讨论“轨道”和电子云图象?为什么不能说p +1和p -1就是分别代表p x 和p y ? 11. 样来研究多电子原子的结构?作过哪些近似?用过哪些模型?试简单说明之。
12. 电子的自旋是怎样提出的?有何实验依据?在研究原子内电子运动时,我们是怎样考虑电子自旋的?*13. 哈特里-福克SCF 模型考虑了一些什么问题?交换能有何意义?14. 怎样表示原子的整体状态?光谱项、光谱支项各代表什么含义?洪特规则、选择定则又是讲的什么内容?15. 原子核外电子排布的规律是什么?现在哪些问题你比过去理解得更加深入了?通过本部分的学习,你对微观体系的运动规律和特点掌握了多少?在思想方法上有何收获?16. 巴尔末起初分析氢原子光谱是用波长)(422-=n n c λ,其中c 为常数,n 为大于2的正整数,试用里德伯常数H R ~求出c 值。
17. 试计算氢原子中电子处于波尔轨道n = 1和n = 4时的动能(单位:J )和速度(单位:m·s -1)。
结构化学练习题带答案

结构化学复习题一、选择填空题第一章量子力学基础知识1.实物微粒和光一样,既有性,又有性,这种性质称为性。
2.光的微粒性由实验证实,电子波动性由实验证实。
3.电子具有波动性,其波长与下列哪种电磁波同数量级?(A)X射线(B)紫外线(C)可见光(D)红外线4.电子自旋的假设是被下列何人的实验证明的?(A)Zeeman (B)Gouy (C)Stark (D)Stern-Gerlach5.如果f和g是算符,则 (f+g)(f-g)等于下列的哪一个?(A)f2-g2; (B)f2-g2-fg+gf; (C)f2+g2; (D)(f-g)(f+g)6.在能量的本征态下,下列哪种说法是正确的?(A)只有能量有确定值;(B)所有力学量都有确定值;(C)动量一定有确定值;(D)几个力学量可同时有确定值;7.试将指数函数e±ix表示成三角函数的形式------8.微观粒子的任何一个状态都可以用来描述;表示粒子出现的概率密度。
9.Planck常数h的值为下列的哪一个?(A)1.38×10-30J/s (B)1.38×10-16J/s (C)6.02×10-27J·s (D)6.62×10-34J·s 10.一维势箱中粒子的零点能是答案: 1.略. 2.略. 3.A 4.D 5.B 6.D 7.略 8.略 9.D 10.略第二章原子的结构性质1.用来表示核外某电子的运动状态的下列各组量子数(n, 1, m, m s)中,哪一组是合理的?(A)2,1,-1,-1/2;(B)0,0,0,1/2;(C)3,1,2,1/2;(D)2,1,0,0。
2.若氢原子中的电子处于主量子数n=100的能级上,其能量是下列的哪一个:(A)13.6Ev; (B)13.6/10000eV; (C)-13.6/100eV; (D)-13.6/10000eV;3.氢原子的p x状态,其磁量子数为下列的哪一个?(A)m=+1; (B)m=-1; (C)|m|=1; (D)m=0;4.若将N原子的基电子组态写成1s22s22p x22p y1违背了下列哪一条?(A)Pauli原理;(B)Hund规则;(C)对称性一致的原则;(D)Bohr理论5.B原子的基态为1s22s2p1,其光谱项为下列的哪一个?(A) 2P;(B)1S; (C)2D; (D)3P;6.p2组态的光谱基项是下列的哪一个?(A)3F;(B)1D ;(C)3P;(D)1S;7.p电子的角动量大小为下列的哪一个?(A)h/2π;(B)31/2h/4π;(C)21/2h/2π;(D)2h/2π;8.采用原子单位,写出He原子的SchrÖdinger方程。
结构化学基础习题答案_周公度_第4版.

141
2.701.05106.60108.5060010J h J s s ---⨯==⨯-⨯
图中直线与横坐标的交点所代表的v即金属的临界频率0v ,由图可知, 141
04.3610v s -=⨯。因此,金属钠的脱出功为:
34141
0196.60104.36102.8810W hv J s s J
/u v λ=
式中, u是微粒的传播速度,它不等于微粒的运动速度υ ,但③中用了/u v λ=,显然是错的。
在④中, E hv =无疑是正确的,这里的E是微粒的总能量。若计及E中的势能,则⑤也不正确。
【1.7】子弹(质量0.01kg ,速度1000m ·s -1
,尘埃(质量10-9kg ,速度10m ·s -1
01.量子力学基础知识
【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm,这是Li原子由电子组态(1s2(2p1→ (1s2(2s1跃迁时产生的,试计算该红光的频率、波数以及以k J ·mol -1
为单位的能量。
解:81
141
2.99810m s 4.46910s 670.8m c
νλ--⨯⋅===⨯ 41
、作布郎
运动的花粉(质量10-13kg ,速度1m ·s -1、原子中电子(速度1000 m ·s -1等,其速度的不确定度均为原速度的10%,判断在确定这些质点位置时,不确定度关系是否有实际意义?
解:按测不准关系,诸粒子的坐标的不确定度分别为:
子弹:3434
1
6.26106.63100.01100010%h J s x m m v kg m s ---⨯⋅∆===⨯⋅∆⨯⨯⋅尘埃:342591
②
③ ④ ⑤
结构化学练习之量子力学基础习题附参考答案汇总

量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
《量子力学基础和原子、分子及晶体结构》习题和思考题

《量⼦⼒学基础和原⼦、分⼦及晶体结构》习题和思考题《结构化学》课程作业题第⼀部分:《量⼦⼒学基础和原⼦结构》思考题与习题1. 经典物理学在研究微观物体的运动时遇到过哪些困难?举例说明之。
如何正确对待归量⼦论?2. 电⼦兼具有波动性的实验基础是什么?宏观物体有没有波动性?“任何微观粒⼦的运动都是量⼦化的,都不能在⼀定程度上满⾜经典⼒学的要求”,这样说确切吗?3. 怎样描述微观质点的运动状态?为什么?波函数具有哪些重要性质?为什么?4. 简述薛定谔⽅程得来的线索。
求解该⽅程时应注意什么?5. 通过⼀维和三维势箱的解,可以得出哪些重要結論和物理概念?6. 写出薛定谔⽅程的算符表达式。
你是怎样理解这个表达式的? *7. 量⼦⼒学中的算符和⼒學量的关系怎样?8. 求解氢原⼦和类氢离⼦基态和激发态波函数的思想⽅法是怎样的? 9. 通过氢原⼦薛定谔⽅程⼀般解的讨论明确四个量⼦数的物理意义。
10. 怎样根据波函数的形式讨论“轨道”和电⼦云图象?为什么不能说p +1和p -1就是分别代表p x 和p y ? 11. 样来研究多电⼦原⼦的结构?作过哪些近似?⽤过哪些模型?试简单说明之。
12. 电⼦的⾃旋是怎样提出的?有何实验依据?在研究原⼦内电⼦运动时,我们是怎样考虑电⼦⾃旋的?*13. 哈特⾥-福克SCF 模型考虑了⼀些什么问题?交换能有何意义?14. 怎样表⽰原⼦的整体状态?光谱项、光谱⽀项各代表什么含义?洪特规则、选择定则⼜是讲的什么内容?15. 原⼦核外电⼦排布的规律是什么?现在哪些问题你⽐过去理解得更加深⼊了?通过本部分的学习,你对微观体系的运动规律和特点掌握了多少?在思想⽅法上有何收获?16. 巴尔末起初分析氢原⼦光谱是⽤波长)(422-=n n c λ,其中c 为常数,n 为⼤于2的正整数,试⽤⾥德伯常数H R ~求出c 值。
17. 试计算氢原⼦中电⼦处于波尔轨道n = 1和n = 4时的动能(单位:J )和速度(单位:m·s -1)。
北师大_结构化学课后习题答案

北师大 结构化学 课后习题 第一章 量子理论基础习题答案1 什么是物质波和它的统计解释?参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言,衍射强度(即波的强度)大的地方,粒子出现的数目就多,而衍射强度小的地方,粒子出现的数目就少。
对一个粒子而言,通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子,在相同的条件下重复多次相同的实验,一定会在衍射强度大的地方出现的机会多,在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释,对于单个粒子,ψψ=ψ*2代表粒子的几率密度,在时刻t ,空间q 点附近体积元τd 内粒子的几率应为τd 2ψ;在整个空间找到一个粒子的几率应为 12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件? 参考答案合格波函数的基本条件是单值,连续和平方可积。
由于波函数2ψ代表概率密度的物理意义,所以就要求描述微观粒子运动状态的波函数首先必须是单值的,因为只有当波函数ψ在空间每一点只有一个值时,才能保证概率密度的单值性;至于连续的要求是由于粒子运动状态要符合Schrödinger 方程,该方程是二阶方程,就要求波函数具有连续性的特点;平方可积的是因为在整个空间中发现粒子的概率一定是100%,所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理? 参考答案在经典理论中,一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份(如各种不同的波长和频率)。
而在量子力学中,按波函数的统计解释,态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加,使粒子部分地处于Q 1状态,部分地处于Q 2态,……。
各种态都有自己的权重(即成份)。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么? 参考答案根源就在于微观粒子的波粒二象性。
结构化学课后习题及答案
01.量子力学基础知识【1.1】将锂在火焰上燃烧,放出红光,波长λ=670.8nm ,这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的,试计算该红光的频率、波数以及以k J·mol -1为单位的能量。
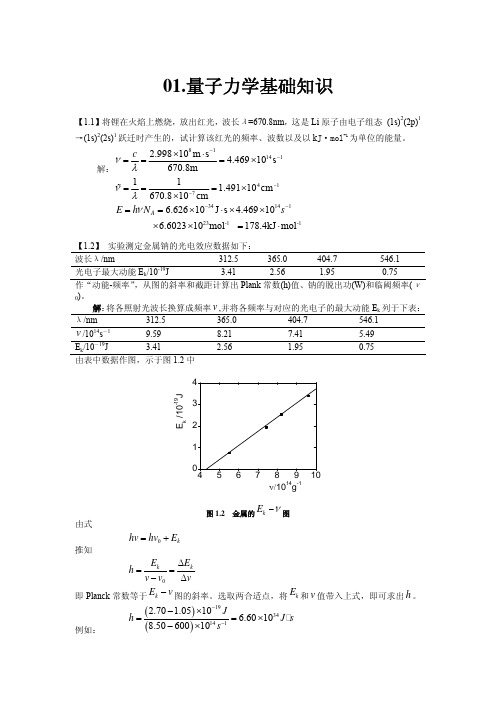
解:811412.99810m s 4.46910s 670.8m cνλ−−×⋅===× 41711 1.49110cm 670.810cm νλ−−===××%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν−−==×⋅××××=⋅【1.2】 实验测定金属钠的光电效应数据如下:波长λ/nm 312.5 365.0 404.7 546.1 光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”,从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。
解:将各照射光波长换算成频率,并将各频率与对应的光电子的最大动能E k 列于下表:v λ/nm 312.5 365.0 404.7 546.1v /1014s -19.59 8.21 7.41 5.49E k /10-19J 3.41 2.56 1.95 0.75 由表中数据作图,示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的kE ν−图由式 0k hv hv E =+推知0k kE E h v v v Δ==−Δ即Planck 常数等于图的斜率。
选取两合适点,将和v 值带入上式,即可求出h 。
例如: k E −v k E ()()19341412.708.50 1.0510 6.601060010J h J s s −−−×==×−×图中直线与横坐标的交点所代表的即金属的临界频率,由图可知,。
结构化学练习之量子力学基础习题附参考 答案

1 / 21量子力学基础习题一、填空题(在题中的空格处填上正确答案)1101、光波粒二象性的关系式为_______________________________________。
1102、德布罗意关系式为____________________;宏观物体的λ值比微观物体的λ值_______________。
1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________。
1104、测不准关系是_____________________,它说明了_____________________。
1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…。
正交性的数学表达式为 ,归一性的表达式为 。
1106、│ψ (x 1, y 1, z 1, x 2, y 2, z 2)│2代表______________________。
1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____。
1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,(1)体系哈密顿算符的本征函数集为_______________________________ ;(2)体系的本征值谱为____________________, 最低能量为____________ ;(3)体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ;(4)势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ;(5)若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________。
1109、质量为m 的粒子被局限在边长为a 的立方箱中运动。
波函数ψ211(x ,y ,z )= _________________________;当粒子处于状态ψ211时,概率密度最大处坐标是_______________________;若体系的能量为2247ma h ,其简并度是_______________。
中国科学技术大学结构化学习题参考答案

间恒为零。 取 xy 平 面
为
解之可得两个特解 7. (a)
(b) 在区间 8. 用 不 确 定 原 virial定理应成立。 9. 要求
整数,且
,得n为
12.
是的本 征函数, 所以动量 平方有确 粒子的 定值 几率为
-12
4. (a) 1.2 Å (b) 1.2×10 Å 5. 6. 势能算符 则圆周上的波函数不为零,其他区
作为用圆周面,则θ=90 °,r=a,Schröinger方程
理估算其电子的动能,对于Coulomb作用体系,
,
,利用单
值条件
10. 电 离能等 于轨
。
该
体
道能
量之负
2
值。
系 只有 一 个边 界 条件11. 2n 。
(即单值条件),无法
确定其通解的两个系 数 ,只 求 特解 就 可以。
了。
,当n=3
。
时有最大值
在
区间为
有限值,则k必
须是纯虚数,
此时本征值为
实数。
以忽略万有引力的贡献。
。完全可
13. 和具有相同的本征函数,本征值相差常数c。本题说明能量零点
的选取不影响体系的状态。
,
,
,
17. 0.32。
14.
15.
。
16. 0.°,135°
20.
21. ①
第 五章 多原子分 子
;(c)
3.
;(d) ;
; (e) 。
1. 。 2. 。
;
。
4. 相同。
; ,
, ,
。
11(略)。
5. 。 6.
7.
。 8. 四面体构型。
结构化学第一章课后作业

第一章 量子理论基础2.如何理解合格波函数的基本条件?答:(1)单值:由于波函数ψψψ*2||=被赋予了概率密度的物理意义,所以就要求描述微观粒子运动状态的波函数必须是单值的,因为当波函数ѱ在空间每一点只有一个值时,波函数模的平方才能具备单值性。
(2)连续:ѱ必须是连续的,而且ѱ对坐标(x,y,z)进行求一阶导数后,所获得的新函数也应该为连续函数。
(3)有界,平方可积(归一化):波函数ѱ模的平方ψψψ*2||=必须是可积的,也就是有限的,因为ѱ模的平方的物理意义是代表粒子在空间某点出现的概率密度,而在整个空间中发现粒子的概率一定是100%,即1*=⎰τψψd 。
@知识点:合格波函数三个条件:即单值,连续,有界平方可积(归一化),三者缺一不可。
例:由下图的四个函数图象进行分析: (a)中单值,连续,并且有界,为合格波函数。
(b)中函数不连续,不是合格波函数。
(c)中函数不单值,不是合格波函数。
(d)中函数既不连续,也无界,不是合格波函数。
,4. 测不准原理的根源是什么?答:根源为实物粒子具有波粒二象性,即由于实物粒子具有波动性,不能同时确定微观粒子的坐标和动量,即微观粒子的坐标确定的越精确,则其动量就越不确定,反之亦然。
@知识点:测不准原理,又叫不确定关系,海森堡于1927年提出,并于1932年获得诺贝尔奖。
定义:有这样一些成双可测量,要同时测定他们的精确值是不可能的,其中一个测的越精确,则另一个测得越不精确。
例:ΔX·ΔP≥h ΔE·Δt≥h5. 铝的逸出功是4.2ev,用200nm的光照射时,(1)产生的光电子动能是多少?(2)与其相联系的de Brolie 波长是多少?(3)如果电子位置不确定量与德布罗意波长相当,其动量不确定量为多少? 答:(1)由k E w h +=ν 得J W chW h E k 191978341022.3106.12.410210310626.6----⨯=⨯⨯-⨯⨯⨯⨯=-=-=λν 其中1ev=1.6×10-19J 1nm=10-9m(2)m mE hphk9193134108656.01022.3101.9210626.62----⨯=⨯⨯⨯⨯⨯===λ(3)ΔX ·ΔP ≥hs m kg x h P /1065.7108656.010626.625934⋅⨯=⨯⨯=∆≥∆--- @知识点:1)光电效应方程:k E w h +=ν=k E h +0νw=0νh 称为束缚功,当νν<0时,电子克服原子核的束缚而发出,该电子叫光电子。
结构化学章节习题(含答案!)

第一章 量子力学基础一、单选题: 13x lπ为一维势箱的状态其能量是:( a ) 22229164:; :; :; :8888h h h hA B C D ml ml ml ml2、Ψ321的节面有( b )个,其中( b )个球面。
A 、3B 、2C 、1D 、03、立方箱中2246ml h E ≤的能量范围内,能级数和状态数为( b ).A.5,20B.6,6C.5,11D.6,174、下列函数是算符d /dx的本征函数的是:( a );本征值为:( h )。
A 、e 2xB 、cosXC 、loge xD 、sinx 3E 、3F 、-1G 、1H 、2 5、下列算符为线性算符的是:( c )A 、sine xB 、d 2/dx 2 D 、cos2x6、已知一维谐振子的势能表达式为V = kx 2/2,则该体系的定态薛定谔方程应当为( c )。
A [-m 22 2∇+21kx 2]Ψ= E ΨB [m 22 2∇- 21kx 2]Ψ= E Ψ C [-m 22 22dx d +21kx 2]Ψ= E Ψ D [-m 22 -21kx 2]Ψ= E Ψ 7、下列函数中,22dxd ,dx d的共同本征函数是( bc )。
A cos kxB e –kxC e –ikxD e –kx28、粒子处于定态意味着:( c )A 、粒子处于概率最大的状态B 、粒子处于势能为0的状态C 、粒子的力学量平均值及概率密度分布都与时间无关系的状态.D 、粒子处于静止状态9、氢原子处于下列各状态 (1)ψ2px (2) ψ3dxz (3) ψ3pz (4) ψ3dz 2 (5)ψ322 ,问哪些状态既是M 2算符的本征函数,又是M z 算符的本征函数?( c )A. (1) (3)B. (2) (4)C. (3) (4) (5)D. (1) (2) (5) 10、+He 离子n=4的状态有( c )(A )4个 (B )8个 (C )16个 (D )20个 11、测不准关系的含义是指( d ) (A) 粒子太小,不能准确测定其坐标; (B)运动不快时,不能准确测定其动量(C) 粒子的坐标的动量都不能准确地测定; (D )不能同时准确地测定粒子的坐标与动量12、若用电子束与中子束分别作衍射实验,得到大小相同的环纹,则说明二者( b ) (A) 动量相同 (B) 动能相同 (C) 质量相同13、 为了写出一个经典力学量对应的量子力学算符,若坐标算符取作坐标本 身,动量算符应是(以一维运动为例) ( a )(A) mv (B) i x ∂∂ (C)222x ∂-∂14、若∫|ψ|2d τ=K ,利用下列哪个常数乘ψ可以使之归一化:( c )(A) K (B) K 2 (C) 1/K15、丁二烯等共轭分子中π电子的离域化可降低体系的能量,这与简单的一维势阱模型是一致的, 因为一维势阱中粒子的能量 ( b )(A) 反比于势阱长度平方 (B) 正比于势阱长度 (C) 正比于量子数16、对于厄米算符, 下面哪种说法是对的 ( b )(A) 厄米算符中必然不包含虚数 (B) 厄米算符的本征值必定是实数(C) 厄米算符的本征函数中必然不包含虚数17、对于算符Ĝ的非本征态Ψ ( c )(A) 不可能测量其本征值g . (B) 不可能测量其平均值<g >.(C) 本征值与平均值均可测量,且二者相等18、将几个非简并的本征函数进行线形组合,结果 ( b )(A) 再不是原算符的本征函数(B) 仍是原算符的本征函数,且本征值不变 (C) 仍是原算符的本征函数,但本征值改变19. 在光电效应实验中,光电子动能与入射光的哪种物理量呈线形关系:( B )A .波长B. 频率C. 振幅20. 在通常情况下,如果两个算符不可对易,意味着相应的两种物理量( A)A .不能同时精确测定B .可以同时精确测定C .只有量纲不同的两种物理量才不能同时精确测定 21. 电子德布罗意波长为(C )A .λ=E /h B. λ=c /ν C. λ=h /p 22. 将几个非简并的本征函数进行线形组合,结果( A ) A .再不是原算符的本征函数B .仍是原算符的本征函数,且本征值不变C .仍是原算符的本征函数,但本征值改变23. 根据能量-时间测不准关系式,粒子在某能级上存在的时间τ越短,该能级的不确定度程度ΔE (B )A .越小 B. 越大 C.与τ无关24. 实物微粒具有波粒二象性, 一个质量为m 速度为v 的粒子的德布罗意波长为:A .h/(mv)B. mv/hC. E/h25. 对于厄米算符, 下面哪种说法是对的 ( B )A .厄米算符中必然不包含虚数B .厄米算符的本征值必定是实数C .厄米算符的本征函数中必然不包含虚数 26. 对于算符Ĝ的非本征态Ψ (A ) A .不可能测得其本征值g. B .不可能测得其平均值<g>.C .本征值与平均值均可测得,且二者相等 27. 下列哪一组算符都是线性算符:( C )A . cos, sinB . x, logC . x d dx d dx,,22二 填空题1、能量为100eV 的自由电子的德布罗依波波长为( 122.5pm )2、函数:①xe ,②2x ,③x sin 中,是算符22dxd 的本征函数的是( 1,3 ),其本征值分别是( 1,—1;)3、Li 原子的哈密顿算符,在( 定核 )近似的基础上是:(()23213212232221223222123332ˆr e r e r e r e r e r e mH +++---∇+∇+∇-= )三 简答题1.计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
结构化学课后答案第1章量子理论基础

第一章 量子理论基础习题答案1 什么是物质波和它的统计解释?参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言,衍射强度(即波的强度)大的地方,粒子出现的数目就多,而衍射强度小的地方,粒子出现的数目就少。
对一个粒子而言,通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子,在相同的条件下重复多次相同的实验,一定会在衍射强度大的地方出现的机会多,在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释,对于单个粒子,ψψ=ψ*2代表粒子的几率密度,在时刻t ,空间q 点附近体积元τd 内粒子的几率应为τd 2ψ;在整个空间找到一个粒子的几率应为12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件?参考答案合格波函数的基本条件是单值,连续和平方可积。
由于波函数2ψ代表概率密度的物理意义,所以就要求描述微观粒子运动状态的波函数首先必须是单值的,因为只有当波函数ψ在空间每一点只有一个值时,才能保证概率密度的单值性;至于连续的要求是由于粒子运动状态要符合Schrödinger 方程,该方程是二阶方程,就要求波函数具有连续性的特点;平方可积的是因为在整个空间中发现粒子的概率一定是100%,所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理?参考答案在经典理论中,一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份(如各种不同的波长和频率)。
而在量子力学中,按波函数的统计解释,态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加,使粒子部分地处于Q 1状态,部分地处于Q 2态,……。
各种态都有自己的权重(即成份)。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么?参考答案根源就在于微观粒子的波粒二象性。
5 铝的逸出功是4.2eV ,用2000Å的光照射时,问(a )产生的光电子动能是多少?(b)与其相联系的德布罗依波波长是多少?(c)如果电子位置不确定量与德布罗依波波长相当,其动量不确定量如何?参考答案(a)根据爱因斯坦光电方程W m h +=221υν,又λνc =,得光电子动能: JW c h m T 1919191910834210219.31072.610939.9106.12.410200*********.621------⨯=⨯-⨯=⨯⨯-⨯⨯⨯⨯=-⋅==λυ (b)由德布罗依关系式,相应的物质波波长为mmT h P h 10253419313410781.810546.710626.610219.3101.9210626.62------⨯=⨯⨯=⨯⨯⨯⨯⨯===λ (c) 由不确定关系式h Px x ≥∆⋅∆,若位置不确定量λ≈∆x ,则动量不确定量125103410546.710781.810626.6----⋅⋅⨯=⨯⨯==≈∆s m Kg P hPx λ6 波函数e -x (0≤x≤∞)是否是合格波函数,它归一化了吗?如未归一化,求归一化常数。
结构化学习题、详解、答案

第一章 量子力学基础题 解1.1. 给出黑体辐射频率分布函数),(T R ν的单位。
解: 黑体辐射的频率分布函数),(T R ν表示黑体辐射的频率分布,ννd ),(T R 表示在温度T 单位时间内由单位黑体表面积上所发射的频率在νννd ~+间的辐射能量。
121s m J s )(---⋅⋅=νR2m J )(-⋅=νRs m w s m sJm J 2-22⋅⋅=⋅⋅=⋅--式中w 是功率.1.2. 分别计算红光λ=600 nm 和X 射线λ=100 pm 的1个光子的能量、动量和质量。
解:λνc=,νh E =,λhp =,2ch m ν=(1) 波长1λ=600 nm 的红光,813419119310m s 6.62610J s 3.31310J 60010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 12793411s m kg 10104.1m10600s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 19361128123.31310J 3.68110kg (310m s )h m c ν---⨯===⨯⨯⋅ (2)X 射线2λ=100 pm8134152212310m s 6.62610J s 1.98810J 10010mE h ν----⨯⋅==⨯⋅⨯=⨯⨯ 124123422s m kg 10626.6m10100s J 10626.6----⋅⋅⨯=⨯⋅⨯==λhp 15322228121.98810J2.20910kg (310m s )h m c ν---⨯===⨯⨯⋅ 1.3. 计算波长λ=400nm 的光照射到金属铯上所产生的光电子的初速度。
已知铯的临阈波长为600nm解:根据W h T -=ν其中,201, 2e Tm W h υν== 2012e m h h υνν=-51 6.03010(m s )υ-====⨯⋅1.4. 氢原子光谱中巴尔麦系中波长最长的一条谱线的波数、波长和频率各是多少?波长最短的一条呢?解:氢原子光谱中巴尔麦系谱线的波数可表达为4, 3, )121(~~22=-=n n R ν 其中5-11.09710cm ,R=⨯ 称为Rydberg 常数。
结构化学 第一章练习题答案

现代结构化学 2010.9第一章 量子力学基础知识练习题1.(北师大95)微观粒子体系的定态波函数所描述的状态是( B ) A. 波函数不随时间变化的状态 B .几率密度不随时间变化的状态 C. 自旋角动量不随时间变化的状态 D. 粒子势能为零的状态2.(北大93)ψ是描述微观体系(运动状态)的波函数。
3.(北师大20000)若11i e αψψψ=+,其中α为实常数,且1ψ已归一化,求ψ的归一化常数。
解:设11()i A e αψψψ=+是归一化的,2*21111()()(2)1i i i i d A e e d A e e ααααψψτψψψψτ*-=++=++=⎰⎰A ==4.(东北师大99)已知一束自由电子的能量值为E,写出其德布罗意波长表达式,并说明可用何种实验来验证(10分)h h P mv λ=== E=1/2mv 2 (mv)2=2mE 电子衍射实验 5.(中山97)(北大98)反映实物粒子波粒二象性的关系式为(,hE hv P λ==)6.(中山97)一维势箱长度为l ,则基态时粒子在(2l)处出现的几率密度最大。
(中山2001)一维势箱中的粒子,已知n xlπψ=,则在(3(21),,.......,222l l n ln n n-)处出现的几率密度最大。
解法1:ψ的极大和极小在ψ2中都为极大值,所以求ψ的极值(包括极大和极小)位置就是几率密度极大的位置。
n xl πψ='cos 0(21)0,1,2,3 (2)(21) 0,1,2,3...2 0 (21)2n n x l l n x m m l m lx m nx l m nππψππ==+==+==≤≤∴+≤解法2:n x l πψ= 几率密度函数222sin n x P l l πψ==求极值:(sin2α=2Sin α•cos α)22'2s i n c o s22sin 022sin 0 = 0,1,2,3,...22= 0 20,212 1,3,5 (21)2n x n x n P l l l l n n x l l n x n x m m l l ml x n x m x l m n l nm n m m mlx m n nππππππππ======≤≤∴≤===∴==-为边界,不是极值点为极大值,为极小值...极大值位置为 7.(北大93)边长为l 的立方势箱中粒子的零点能是(2238h E ml =)8.(北大94)两个原子轨道1ψ和2ψ互相正交的数学表达式为(120d ψψτ*=⎰) 9. 一维谐振子的势能表达式为212V kx =,则该体系的定态薛定谔方程中的哈密顿算符为( D )A. 212kxB. 222122kx m ∇- C. 222122kx m -∇- D. 2222122d kx m dx -+ E. 2222122d kx m dx --10.(北师大04年) 设算符123ˆˆ,,A A A ∧和4ˆA 对任意f 的作用为1234ˆˆˆˆ2,,df A f A f f A f A f f f dx====⨯, 指出哪些算符为线性算符(23ˆˆ,A A ) 11.1,2ψψ是某原子的可能状态,下列哪些组合也是该原子的可能状态? a. 12ψψ- b. 12ψψ⨯ c . 12ψψ÷ d. 12ψψ+ (a, d)12. 写出一个电子在长度为a 的一维势箱中运动的Hamilton 算符.222ˆ2d H m dx=- 13.(北师大02年)(1) 给出用原子单位表示的下列算符表达式(a)电子的动量平方算符为 2222222222ˆˆˆˆ()x y z P P P P x y z ∂∂∂=++=-++∂∂∂(b) 原子核看作不动,He 原子的Hamilton 算符2212121211221ˆ22a a H r r r =-∇-∇--+ (c)角动量在z 方向分量的算符 z zˆM M ()ˆ 1y x zxp yp i x y y xM i φ∂∂=-=-+∂∂∂=-=∂或 (2). H 原子处于态 122s s ψψ=,1s ψ和2s ψ分别为H 原子的1s 和2s 原子轨道,对应的能量分别为1,2s s E E ,给出H 原子的平均能量。
