第十三章量子力学基础2作业答案

合集下载

量子力学基础试题及答案

量子力学基础试题及答案一、单项选择题（每题2分，共10分）1. 量子力学中，物质的波粒二象性是由哪位科学家提出的？A. 爱因斯坦B. 普朗克C. 德布罗意D. 海森堡答案：C2. 量子力学的基本原理之一是不确定性原理，该原理是由哪位科学家提出的？A. 玻尔B. 薛定谔C. 海森堡D. 狄拉克答案：C3. 量子力学中，描述粒子状态的数学对象是：A. 波函数B. 概率密度C. 动量D. 能量答案：A4. 量子力学中，哪个方程是描述粒子的波动性质的基本方程？A. 薛定谔方程B. 麦克斯韦方程C. 牛顿第二定律D. 相对论方程答案：A5. 量子力学中，哪个原理说明了粒子的波函数在测量后会坍缩到一个特定的状态？A. 叠加原理B. 波函数坍缩原理C. 不确定性原理D. 泡利不相容原理答案：B二、填空题（每题3分，共15分）1. 在量子力学中，粒子的动量和位置不能同时被精确测量，这一现象被称为______。

答案：不确定性原理2. 量子力学中的波函数必须满足______条件，以确保物理量的概率解释是合理的。

答案：归一化3. 量子力学中的粒子状态可以用______来描述，它是一个复数函数。

答案：波函数4. 量子力学中的______方程是描述非相对论性粒子的波函数随时间演化的基本方程。

答案：薛定谔5. 量子力学中的______原理表明，不可能同时精确地知道粒子的位置和动量。

答案：不确定性三、简答题（每题5分，共20分）1. 简述量子力学与经典力学的主要区别。

答案：量子力学与经典力学的主要区别在于，量子力学描述的是微观粒子的行为，它引入了波粒二象性、不确定性原理和量子叠加等概念，而经典力学主要描述宏观物体的运动，遵循牛顿力学的确定性规律。

2. 描述量子力学中的波函数坍缩现象。

答案：波函数坍缩是指在量子力学中，当对一个量子系统进行测量时，系统的波函数会从一个叠加态突然转变到一个特定的本征态，这个过程是不可逆的，并且与测量过程有关。

《原子物理与量子力学》第十三章习题解答

2
7.4 任意方向自旋算符的本征值和本征函数（P241）任意方向自旋算符的本征值和本征函数（）已知
（1）本征态）久期方程
本征值方程
HUST
APPLIED PHY有
由归一化条件，由归一化条件，得
HUST
APPLIED PHYSICS
4
ˆ ② S n 取 − h 2 时，有
第十三章
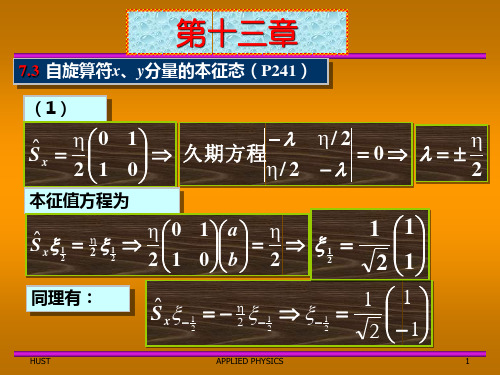
7.3 自旋算符、y分量的本征态（P241）自旋算符x、分量的本征态分量的本征态（）（1）
本征值方程为
同理有：同理有：
HUST
APPLIED PHYSICS
1
（2）S y 的本征值也为 ± h / 2 本征值方程为）ˆ
同理有：同理有：
HUST
APPLIED PHYSICS
HUST
APPLIED PHYSICS
9
（2））
HUST
APPLIED PHYSICS
10
7.6 Bose子系的态函数（P241）子系的态函数（子系的态函数）（1）可能状态为个（粒子数加）。）可能状态为4个粒子数加1）
（2）态函数可表示为如下种形式：种形式：）态函数可表示为如下4种形式
HUST
APPLIED PHYSICS
5
（2）S z 的取值情况应将以上求得的本征态向） ˆ 的取值情况: ˆ 展开有： S z 的本征态 χ 1、 χ − 1 展开有： 2 2
展开， ①ξ +向 χ 12、 χ − 12 展开，有：
HUST
APPLIED PHYSICS
6
ˆ 符合经典规律。方向投影的平均值 S n 在z方向投影的平均值 S z 符合经典规律。

量子力学(二)习题参考答案

2µ (U1 − E ) h2 2µ E h2
ψ 2 '' ( x) + k 2ψ 2 ( x ) = 0, k =
西华师大物理与电子信息学院
4
四川省精品课程——量子力学补充习题参考答案
ψ 3'' ( x) − β 2ψ 3 ( x) = 0, β =
其解分别为：
2µ (U 2 − E ) h2
ψ 1 ( x) = A1eα x + B1e −α x ψ 2 ( x) = C sin(kx + δ ) ψ 3 ( x ) = A2e β x + B2 e− β x
2
2
⑤
而透射系数
⑥
2）、当 E＜U0 时，有ψ 2 '' ( x ) − k3 2ψ 2 ( x ) = 0 ， k3 = 其解为：ψ 2 ( x ) = Ce
− k3 x
+ De k3 x = Ce − k3 x （ψ 2 有限条件）
⑦
以下可以重复前面的求解过程。不过，为了简单我们亦可以在前面得到的结果⑤中做代换 k2 ＝i k3 ，得到
由（18）式，（16）、（17）变成或由（19）式，（16）、（17）变成
（20）或（21）式就是讲义上习题 2．7 的结果。 a) 将 δ = 0 代入ψ 2 ( x) 中有：ψ 2 ( x) = C sin kx 由连续性条件：ψ 2 ( a) = ψ 3 ( a ) → C sin( ka ) = B2 e − β a
ψ m (ϕ ) =
除了 m=0 的态之外， E m 圴是二重简并的。 5、梯形式——— U ( x ) =
0, x < 0 U 0 , x > 0

(完整版)南华物理练习第13章答案

第十三章早期量子论和量子力学基础练习一一. 选择题1. 内壁为黑色的空腔开一小孔，这小孔可视为绝对黑体，是因为它（ B ） (A) 吸收了辐射在它上面的全部可见光； (B) 吸收了辐射在它上面的全部能量； (C) 不辐射能量； (D) 只吸收不辐射能量。

2. 一绝对黑体在温度T 1 = 1450K 时，辐射峰值所对应的波长为λ1，当温度降为725K 时，辐射峰值所对应的波长为λ2，则λ1/λ2为（ D ） (A)2； (B) 2/1； (C) 2 ； (D) 1/2 。

3. 一般认为光子有以下性质（ A ）(1) 不论在真空中或介质中的光速都是c ；(2) 它的静止质量为零；(3) 它的动量为h ν/c 2； (4) 它的动能就是它的总能量；(5) 它有动量和能量，但没有质量。

以上结论正确的是（ A ）(A) （2）（4）； (B) （3）（4）（5）； (C) （2）（4）（5）； (D) （1）（2）（3）。

4. 已知某单色光照射到一金属表面产生了光电效应，若此金属的逸出电势是U 0（使电子从金属逸出需做功eU 0），则此单色光的波长λ必须满足：（A ） (A) 0hc eU λ≤； (B) 0hc eU λ≥； (C) 0eU hc λ≤； (D) 0eU hcλ≥。

二. 填空题1. 用辐射高温计测得炉壁小孔的辐射出射度为22.8W/cm 2，则炉内的温度为 1.416×103K 。

2. 设太阳表面的温度为5800K ，直径为13.9×108m ，如果认为太阳的辐射是常数，表面积保持不变，则太阳在一年内辐射的能量为 1.228×1034 J ，太阳在一年内由于辐射而损失的质量为1.3647×1017 kg 。

3. 汞的红限频率为1.09×1015Hz ，现用λ=2000Å的单色光照射，汞放出光电子的最大初速度0v =57.7310 m/s ⨯ ，截止电压U a = 1.7V 。

量子力学课后习题答案

量子力学习题及解答第一章量子理论基础1．1 由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长m λ与温度T 成反比，即m λ T=b （常量）；并近似计算b 的数值，准确到二位有效数字。

解根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ，（1）以及 c v =λ，（2）λρρd dv v v -=，（3）有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。

本题关注的是λ取何值时，λρ取得极大值，因此，就得要求λρ 对λ的一阶导数为零，由此可求得相应的λ的值，记作m λ。

但要注意的是，还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零，如果小于零，那么前面求得的m λ就是要求的，具体如下：01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThcλλ=--)1(5 如果令x=kThcλ ，则上述方程为 x e x =--)1(5这是一个超越方程。

首先，易知此方程有解：x=0，但经过验证，此解是平庸的；另外的一个解可以通过逐步近似法或者数值计算法获得：x=4.97，经过验证，此解正是所要求的，这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。

据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体（如遥远星体）的发光颜色来判定温度的高低。

1．2 在0K 附近，钠的价电子能量约为3eV ，求其德布罗意波长。

解根据德布罗意波粒二象性的关系，可知E=hv ，λh P =如果所考虑的粒子是非相对论性的电子（2c E e μ<<动），那么ep E μ22= 如果我们考察的是相对性的光子，那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ，远远小于电子的质量与光速平方的乘积，即eV 61051.0⨯，因此利用非相对论性的电子的能量——动量关系式，这样，便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里，利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后，对Ec hc e 22μλ=作一点讨论，从上式可以看出，当粒子的质量越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强；同样的，当粒子的动能越大时，这个粒子的波长就越短，因而这个粒子的波动性较弱，而粒子性较强，由于宏观世界的物体质量普遍很大，因而波动性极弱，显现出来的都是粒子性，这种波粒二象性，从某种子意义来说，只有在微观世界才能显现。

量子力学作业及参考答案

15-1 将星球看做绝对黑体，利用维恩位移定律测量m λ便可求得T ．这是测量星球表面温度的方法之一．设测得：太阳的m 55.0m μλ=，北极星的m 35.0m μλ=，天狼星的m 29.0m μλ=，试求这些星球的表面温度．解：将这些星球看成绝对黑体，则按维恩位移定律：K m 10897.2,3⋅⨯==-b b T m λ对太阳： K 103.51055.010897.236311⨯=⨯⨯==--mbT λ对北极星：K 103.81035.010897.236322⨯=⨯⨯==--mbT λ对天狼星：K 100.11029.010897.246333⨯=⨯⨯==--mbT λ15-3 从铝中移出一个电子需要4.2 eV 的能量，今有波长为2000οA 的光投射到铝表面．试问：(1)由此发射出来的光电子的最大动能是多少?(2)遏止电势差为多大?(3)铝的截止(红限)波长有多大?解：(1)已知逸出功eV 2.4=A 据光电效应公式221m mv hv =A +则光电子最大动能：A hcA h mv E m -=-==λυ2max k 21eV0.2J 1023.3106.12.41020001031063.6191910834=⨯=⨯⨯-⨯⨯⨯⨯=----m2max k 21)2(mvE eUa==∴遏止电势差 V 0.2106.11023.31919=⨯⨯=--a U(3)红限频率0υ,∴000,λυυcA h ==又∴截止波长 1983401060.12.41031063.6--⨯⨯⨯⨯⨯==Ahc λm 0.296m 1096.27μ=⨯=-15-4 在一定条件下，人眼视网膜能够对5个蓝绿光光子(m 105.0-7⨯=λ)产生光的感觉．此时视网膜上接收到光的能量为多少?如果每秒钟都能吸收5个这样的光子，则到达眼睛的功率为多大? 解：5个兰绿光子的能量J1099.1100.51031063.65187834---⨯=⨯⨯⨯⨯⨯===λυhcn nh E功率 W 1099.118-⨯==tE15-5 设太阳照射到地球上光的强度为8 J ·s -1·m -2，如果平均波长为5000οA ，则每秒钟落到地面上1m 2的光子数量是多少?若人眼瞳孔直径为3mm ，每秒钟进入人眼的光子数是多少? 解：一个光子能量 λυhch E ==1秒钟落到2m 1地面上的光子数为21198347ms1001.21031063.6105888----⋅⨯=⨯⨯⨯⨯⨯===hcEn λ每秒进入人眼的光子数为11462192s1042.14/10314.31001.24--⨯=⨯⨯⨯⨯==dnN π15-6若一个光子的能量等于一个电子的静能，试求该光子的频率、波长、动量．解：电子的静止质量S J 1063.6,kg 1011.934310⋅⨯=⨯=--h m 当 20c m h =υ时，则Hz10236.11063.6)103(1011.92034283120⨯=⨯⨯⨯⨯==--hc m υο12A 02.0m 104271.2=⨯==-υλc122831020122sm kg 1073.21031011.9sm kg 1073.2-----⋅⋅⨯=⨯⨯⨯=====⋅⋅⨯==c m cc m c E p cpE hp 或λ15-7 光电效应和康普顿效应都包含了电子和光子的相互作用，试问这两个过程有什么不同? 答：光电效应是指金属中的电子吸收了光子的全部能量而逸出金属表面，是电子处于原子中束缚态时所发生的现象．遵守能量守恒定律．而康普顿效应则是光子与自由电子(或准自由电子)的弹性碰撞，同时遵守能量与动量守恒定律．15-8 在康普顿效应的实验中，若散射光波长是入射光波长的1.2倍，则散射光子的能量ε与反冲电子的动能k E 之比k E /ε等于多少? 解：由 2200mc h c m hv +=+υ)(00202υυυυ-=-=-=h h h cm mcE kυεh =∴5)(00=-=-=υυυυυυεh h E k已知2.10=λλ由2.10=∴=υυλυc2.11=υυ则52.0112.110==-=-υυυ15-10 已知X 光光子的能量为0.60 MeV ，在康普顿散射之后波长变化了20%，求反冲电子的能量．解：已知X 射线的初能量,MeV 6.00=ε又有00,ελλεhchc =∴=经散射后 000020.1020.0λλλλ∆λλ=+=+= 此时能量为 002.112.1ελλε===hc hc反冲电子能量 MeV 10.060.0)2.111(0=⨯-=-=εεE15-11 在康普顿散射中，入射光子的波长为0.030 οA ，反冲电子的速度为0.60c ，求散射光子的波长及散射角．解：反冲电子的能量增量为202022020225.06.01c m cm cm cm mcE =--=-=∆由能量守恒定律，电子增加的能量等于光子损失的能量，故有 20025.0c m hchc=-λλ散射光子波长ο121083134103400A043.0m 103.410030.0103101.925.01063.610030.01063.625.0=⨯=⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯=-=------λλλc m h h由康普顿散射公式2sin0243.022sin22200ϕϕλλλ∆⨯==-=cm h可得 2675.00243.02030.0043.02sin2=⨯-=ϕ散射角为 7162'=οϕ15-12 实验发现基态氢原子可吸收能量为12.75eV 的光子． (1)试问氢原子吸收光子后将被激发到哪个能级?(2)受激发的氢原子向低能级跃迁时，可发出哪几条谱线?请将这些跃迁画在能级图上．解：(1)2eV 6.13eV 85.0eV 75.12eV 6.13n -=-=+-解得 4=n 或者 )111(22n Rhc E -=∆75.12)11.(1362=-=n解出 4=n题15-12图题15-13图(2)可发出谱线赖曼系3条，巴尔末系2条，帕邢系1条，共计6条.15-13 以动能12.5eV 的电子通过碰撞使氢原子激发时，最高能激发到哪一能级?当回到基态时能产生哪些谱线?解：设氢原子全部吸收eV 5.12能量后，最高能激发到第n 个能级，则]11[6.135.12,eV 6.13],111[2221nRhc nRhc E E n -==-=-即得5.3=n ，只能取整数，∴ 最高激发到3=n ，当然也能激发到2=n 的能级．于是ο322ο222ο771221A 6563536,3653121~:23A 121634,432111~:12A1026m 10026.110097.18989,983111~:13===⎥⎦⎤⎢⎣⎡-=→===⎥⎦⎤⎢⎣⎡-=→=⨯=⨯⨯===⎥⎦⎤⎢⎣⎡-=→-R R R n R R R n RR R n λυλυλυ从从从可以发出以上三条谱线．题15-14图15-14 处于基态的氢原子被外来单色光激发后发出巴尔末线系中只有两条谱线，试求这两条谱线的波长及外来光的频率．解：巴尔末系是由2>n 的高能级跃迁到2=n 的能级发出的谱线．只有二条谱线说明激发后最高能级是4=n 的激发态．ο1983424ο101983423222324A4872106.1)85.04.3(1031063.6A6573m 1065731060.1)51.14.3(10331063.6e 4.326.13e 51.136.13e 85.046.13=⨯⨯-⨯⨯⨯=-==⨯=⨯⨯-⨯⨯⨯⨯=-=∴-=∴-==-=-=-=-=-=-=-----E E hc E E hcE E hc E E hch VE V E V E a mn mn βλλλλυ基态氢原子吸收一个光子υh 被激发到4=n 的能态 ∴ λυhcE E h =-=14Hz 1008.310626.6106.1)85.06.13(15341914⨯=⨯⨯⨯-=-=--hE E υ15-15 当基态氢原子被12.09eV 的光子激发后，其电子的轨道半径将增加多少倍? 解： eV 09.12]11[6.1321=-=-nE E n 26.1309.126.13n =-51.16.1309.12.1366.132=-=n , 3=n12r n r n =,92=n,19r r n =轨道半径增加到9倍.15-16德布罗意波的波函数与经典波的波函数的本质区别是什么?答：德布罗意波是概率波，波函数不表示实在的物理量在空间的波动，其振幅无实在的物理意义,2φ仅表示粒子某时刻在空间的概率密度．15-17 为使电子的德布罗意波长为1οA ，需要多大的加速电压? 解： ooA 1A 25.12==uλ 25.12=U∴ 加速电压 150=U 伏15-18 具有能量15eV 的光子，被氢原子中处于第一玻尔轨道的电子所吸收，形成一个光电子．问此光电子远离质子时的速度为多大?它的德布罗意波长是多少?解：使处于基态的电子电离所需能量为eV 6.13，因此，该电子远离质子时的动能为eV 4.16.13152112=-=+==E E mvE k φ它的速度为31191011.9106.14.122--⨯⨯⨯⨯==mE v k -15s m 100.7⋅⨯=其德布罗意波长为：o953134A 10.4m 1004.1100.71011.91063.6=⨯=⨯⨯⨯⨯==---mvh λ15-19 光子与电子的波长都是2.0οA ，它们的动量和总能量各为多少? 解：由德布罗意关系：2mc E =，λhmv p ==波长相同它们的动量相等．1-241034s m kg 103.3100.21063.6⋅⋅⨯=⨯⨯==---λhp光子的能量eV 102.6J 109.9103103.3316824⨯=⨯=⨯⨯⨯====--pc hch λυε电子的总能量 2202)()(c m cp E +=,eV 102.63⨯=cp而 eV 100.51MeV 51.0620⨯==c m∴ cp c m >>2∴ MeV 51.0)()(202202==+=c m c m cp E15-20 已知中子的质量kg 1067.127n -⨯=m ，当中子的动能等于温度300K 的热平衡中子气体的平均动能时，其德布罗意波长为多少? 解：kg 1067.127n -⨯=m ,S J 1063.634⋅⨯=-h ,-123K J 1038.1⋅⨯=-k中子的平均动能 mpKT E k 2232==德布罗意波长 oA 456.13===mkTh phλ15-21 一个质量为m 的粒子，约束在长度为L 的一维线段上．试根据测不准关系估算这个粒子所具有的最小能量的值．解：按测不准关系，h p x x ≥∆∆，x x v m p ∆=∆，则h v x m x ≥∆∆,xm h v x ∆≥∆这粒子最小动能应满足222222min 22)(21)(21mLhxm hxm h m v m E x =∆=∆≥∆=15-22 从某激发能级向基态跃迁而产生的谱线波长为4000οA ，测得谱线宽度为10-4οA ，求该激发能级的平均寿命．解：光子的能量 λυhch E ==由于激发能级有一定的宽度E ∆，造成谱线也有一定宽度λ∆，两者之间的关系为： λλ∆=∆2hcE由测不准关系，h t E ≥∆⋅∆，平均寿命t ∆=τ，则λλτ∆=∆=∆=c Eh t 2s 103.51010103)104000(81048210----⨯=⨯⨯⨯⨯=15-23 一波长为3000οA 的光子，假定其波长的测量精度为百万分之一，求该光子位置的测不准量．解：光子λhp =，λλλλ∆=∆-=∆22hhp由测不准关系，光子位置的不准确量为cm 30A 103103000o962=⨯=====-λλ∆λλ∆λ∆∆p h x。

大学物理第13章量子物理习题解答

习题13-1设太阳就是黑体，试求地球表面受阳光垂直照射时每平方米得面积上每秒钟得到得辐射能。

如果认为太阳得辐射就是常数，再求太阳在一年内由于辐射而损失得质量。

已知太阳得直径为1、4×109 m ，太阳与地球得距离为1、5×1011 m ，太阳表面得温度为6100K 。

【解】设太阳表面单位面积单位时间发出得热辐射总能量为0E ，地球表面单位面积、单位时间得到得辐射能为1E 。

()484720 5.671061007.8510W/m E T σ-==⨯⨯=⨯22014π4πE R E R →=太阳地球太阳()()()29232102110.7107.85 1.7110W/m 1.510R E E R→⨯==⨯=⨯⨯太阳2地球太阳太阳每年损失得质量()()()790172287.851040.710365243600 1.6910kg 3.010E S t m c π⨯⨯⨯⨯⨯⨯⨯∆∆===⨯⨯太阳 13-2 用辐射高温计测得炉壁小孔得辐出度为22、8 W/cm 2，试求炉内温度。

【解】由40E T σ=得()1/41/440822.810 1.416 K 5.6710E T σ-⎛⎫⨯⎛⎫=== ⎪ ⎪⨯⎝⎭⎝⎭13-3黑体得温度16000T = K ，问1350λ= nm 与2700λ= nm 得单色辐出度之比为多少？当黑体温度上升到27000T =K 时，1350λ= nm 得单色辐出度增加了几倍？【解】由普朗克公式()5/1,1hc k TT eλρλλ-∝-34823911 6.6310310 6.861.3810600035010hc k T λ---⨯⨯⨯==⨯⨯⨯⨯ 21123.43 5.88hc hck T k T λλ==()()11 3.48 6.8621,700 1.03,350T e T ρλρλ-==()()12 6.86 5.8811, 2.66,T e T ρλρλ-==13-4在真空中均匀磁场（41.510B -=⨯T ）内放置一金属薄片，其红限波长为2010λ-=nm 。

第十三章量子力学基础2作业答案

(薛定谔方程、一维无限深势阱、隧道效应、能量和角动量量子化、电子自旋、多电子原子)一. 选择题[ C ]1. （基础训练10）氢原子中处于2p 状态的电子，描述其量子态的四个量子数(n ，l ，m l ，m s )可能取的值为(A) (2，2，1，21-)． (B) (2，0，0，21)．(C) (2，1，-1，21-)． (D) (2，0，1，21)．★提示：2p 电子对应的量子数n = 2; l = 1，只有答案（C ）满足。

[C ]2. （基础训练11）在激光器中利用光学谐振腔(A) 可提高激光束的方向性，而不能提高激光束的单色性． (B) 可提高激光束的单色性，而不能提高激光束的方向性． (C) 可同时提高激光束的方向性和单色性.(D) 既不能提高激光束的方向性也不能提高其单色性．[D ]3. （自测提高7）直接证实了电子自旋存在的最早的实验之一是(A) 康普顿实验． (B) 卢瑟福实验．(C) 戴维孙－革末实验． (D) 斯特恩－革拉赫实验．[ C ]4. （自测提高9）粒子在外力场中沿x 轴运动，如果它在力场中的势能分布如图19-6所示，对于能量为 E < U 0从左向右运动的粒子，若用 ρ1、ρ2、ρ3分别表示在x < 0，0 < x <a ，x > a 三个区域发现粒子的概率，则有(A) ρ1 ≠ 0，ρ2 = ρ3 = 0． (B) ρ1 ≠ 0，ρ2 ≠ 0，ρ3 = 0． (C) ρ1 ≠ 0，ρ2 ≠ 0，ρ3 ≠ 0． (D) ρ1 = 0，ρ2 ≠ 0，ρ3 ≠ 0． ★提示：隧道效应。

二. 填空题1. （基础训练17）在主量子数n =2，自旋磁量子数21=s m 的量子态中，能够填充的最大电子数是___4___．★提示：主量子数n =2的L 壳层上最多可容纳228n =个电子（电子组态为2622s p ），如仅考虑自旋磁量子数21=s m 的量子态，则能够填充的电子数为上述值的一半。

南华物理练习第13章答案

以上结论正确的是（ A ）(A) （2）（4）； (B) （3）（4）（5）； (C) （2）（4）（5）； (D) （1）（2）（3）。

4. 已知某单色光照射到一金属表面产生了光电效应，若此金属的逸出电势是U 0（使电子从金属逸出需做功eU 0），则此单色光的波长λ必须满足：（A ） (A) 0hc eU λ≤； (B) 0hceU λ≥； (C) 0eU hc λ≤； (D) 0eU hc λ≥。

二. 填空题1. 用辐射高温计测得炉壁小孔的辐射出射度为22.8W/cm 2，则炉内的温度为 1.416×103K 。

3. 汞的红限频率为1.09×1015Hz ，现用λ=2000Å的单色光照射，汞放出光电子的最大初速度0v =57.7310 m/s ⨯ ，截止电压U a = 1.7V 。

物理学(王铭)量子基础习题解答

解
A
粒子带两个正电荷，质量为4，就是He核。
一、选择题 4. 关于不确定关系有以下几种理解： (1) 粒子的动量不可能确定。 (2) 粒子的坐标不可能确定。 (3) 粒子的动量和坐标不可能同时确定。 (4) 不确定关系不仅适用于电子和光子，也适用于其它粒子。其中正确的是： [ ] (A) (1)、(2) (B) (2)、(4) (C) (3)、(4) (D) (4)、(1)
解
概率密度
单值、连续、有限
三、计算题 1. 如图所示，一电子以初速度v0=6.0×106m/s逆着场强方向飞入电场强度为E = 500Vm-1的均匀电场中，问该电子在电场中要飞行多长距离d，可使得电子的德布罗意波长达到=1Å。(飞行过程中，电子的质量认为不变，即为静止质量me = 9.11×10-31kg ，基本电荷e = 1.60×10-19C )
解
3.29 1021J
由德布罗意波长可得粒子的动量，在求动能。
填充题静质量为me的电子，经电势差U12为的静电场加速后，若不考虑相对论效应，电子的德布罗意波长＝。。
解
用德布罗意波长公式计算。
二、填充题 8. 设描述微观粒子运动的波函数为，则表示；须满足的条件是；其归一化条件是。
二、填充题 4. 根据量子力学理论，氢原子中电子的角动量在外磁场方向上的投影为，当角量子数l＝2时，的可能取值为。
解
★副量子数 l: l=0，1，2，3…(n-1) ★磁量子数 ml： ml =0, ±1, ± 2, … ±l
解
A
波函数的平方就是概率密度。
一、选择题 6．氢原子中处于3d量子态的电子，描述其量子态的四个量子数(n, l, ml , ms)可能取的值为[ ] (A) (3，1，1，－1/2) (B) (1，0，1，－1/2) (C) (2，1，2，1/2) (D) (3，2，0，1/2)

量子力学习题答案9页word

2.1 如图所示右设粒子的能量为，下面就和两种情况来讨论（一）的情形此时，粒子的波函数所满足的定态薛定谔方程为其中其解分别为（1）粒子从左向右运动右边只有透射波无反射波，所以为零由波函数的连续性得得解得由概率流密度公式入射反射系数透射系数（2）粒子从右向左运动左边只有透射波无反射波，所以为零同理可得两个方程解反射系数透射系数（二）的情形令,不变此时，粒子的波函数所满足的定态薛定谔方程为其解分别为由在右边波函数的有界性得为零（1）粒子从左向右运动得得解得入射反射系数透射系数(2) 粒子从右向左运动左边只有透射波无反射波，所以为零同理可得方程由于全部透射过去，所以反射系数透射系数2.2如图所示在有隧穿效应，粒子穿过垒厚为的方势垒的透射系数为总透射系数2.3以势阱底为零势能参考点，如图所示（1）左中 0 a x时只有中间有值在中间区域所满足的定态薛定谔方程为其解是由波函数连续性条件得∴∴ 相应的因为正负号不影响其幅度特性可直接写成由波函数归一化条件得所以波函数（2） ∞∞左中右0 x显然时只有中间有值在中间区域所满足的定态薛定谔方程为其解是由波函数连续性条件得当，为任意整数，则当，为任意整数，则综合得∴当时，，波函数归一化后当时，，波函数归一化后2.4如图所示左中0 a 显然其中其解为由在右边波函数的有界性得为零∴再由连续性条件，即由得则得得除以得再由公式 ,注意到令,其中，不同n对应不同曲线, 图中只画出了在的取值范围之内的部分65n=0只能取限定的离散的几个值，则E 也取限定的离散的几个值，对每个E ，确定归一化条件得2.5则该一维谐振子的波函数的定态薛定谔方程为令则上式可化成令则只有当有解2.6由和已知条件可得第三章3.1能量本征值方程为即分离变量法，令则有令则同理令则式中能级简并度为3.2角动量算符在极坐标系下则由能量本征值方程令其解为由周期性得归一化条件则3.4由能量本征值方程令当令此时满足的方程为时时只考虑时令其解分别为由波函数有界性得由波函数连续性得再由公式,注意到令,其中，不同n 对应不同曲线,图中只画出了在的取值范围之内的部分65只能取限定的离散的几个值，则E也取限定的离散的几个值，对每个E，确定归一化条件得 1 可求得3.5同理方差算符则由测不准关系代入，验证该式是成立的第四章4.1在动量表象中，则代入得令得则归一化后的4.5本征方程的矩阵形式上式存在非零解的条件是即解得当再由得当，同样第六章6.3解：在z S ˆ 表象，nS ˆ的矩阵元为其相应的久期方程为即所以nS ˆ的本征值为2±。

[0131]《量子力学基础》在线作业及参考答案

[0131]《量子力学基础》
[判断题]
自由粒子的能级是简并的。

参考答案：正确
[判断题]塞曼效应与电子的自旋有关。

参考答案：正确
[判断题]力学量的平均值一定是实数。

参考答案：正确
[判断题]量子力学中的算符都是幺正算符。

参考答案：错误
[判断题]量子的概念是由爱因斯坦提出的。

参考答案：错误
[判断题]波函数归一化后就完全确定了。

参考答案：错误
[判断题]自旋角动量算符与轨道角动量算符的引入方式不同，因而不能满足同一个对易关系。

参考答案：错误
[判断题]量子力学仅讨论在经典物理中存在的力学量。

参考答案：错误
[判断题]任意态的几率流密度都与时间无关。

参考答案：错误
[判断题]量子力学的建立始于人们对光的波粒二象性的认识。

参考答案：正确
[判断题]泡利首次提出电子具有自旋的假设。

参考答案：错误
[判断题]无论是属于相同本征值还是不同本征值的本征函数都必定相互正交。

参考答案：错误
[判断题]
量子力学是18 世纪20 年代诞生的科学。

参考答案：错误
[判断题]量子力学中用算符表示微观粒子的力学量。

参考答案：错误
第五批
[填空题]填空题
参考答案：1268740100038.doc。

大学物理_第十三章_课后答案

a sin ϕ = (2k + 1)
λ 2 ， k = 1,2,3 ⋅ ⋅ ⋅
x 1.4 = = 3.5 × 10 −3 = tan ϕ ≈ sin ϕ f 400 由 2a sin ϕ 2 × 0.6 λ= = × 3.5 × 10 −3 2k + 1 2k + 1 故 1 = × 4.2 × 10 −3 2k + 1 mm o λ = 6000 A 当 k = 3 ，得 3
得 (2)因第四级缺级，故此须同时满足
0.20(a + b) = 2 × 6000 × 10 −10 0.30(a + b) = 3 × 6000 × 10 −10 a + b = 6.0 × 10 −6 m (a + b) sin ϕ = kλ a sin ϕ = k ′λ a+b a= k ′ = 1.5 × 10 −6 k ′ 4
答：因为衍射角 ϕ 愈大则 a sin ϕ 值愈大，分成的半波带数愈多，每个半波带透过的光通量就愈小，而明条纹的亮度是由一个半波带的光能量决定的，所以亮度减小． 13-5 若把单缝衍射实验装置全部浸入水中时，衍射图样将发生怎样的变化?如果此时用公
a sin ϕ = ± (2k + 1)
式在水中的波长?
λ 答：不矛盾．单缝衍射暗纹条件为 a sin ϕ = kλ = 2 k 2 ，是用半波带法分析(子波叠加问题)． ϕ 相邻两半波带上对应点向方向发出的光波在屏上会聚点一一相消，而半波带为偶数，故
形成暗纹；而双缝干涉明纹条件为 d sin θ = kλ ，描述的是两路相干波叠加问题，其波程差为波长的整数倍，相干加强为明纹．
o
a+b =
解：

量子力学基础知识习题解答可修改全文

01.量子力学基础知识本章主要知识点一、微观粒子的运动特征 1. 波粒二象性：,hE h p νλ==2. 测不准原理：,,,x y z x p h y p h z p h t E h ∆∆≥∆∆≥∆∆≥∆∆≥3. 能量量子化；二、量子力学基本假设1. 假设1：对于一个量子力学体系，可以用坐标和时间变量的函数(,,,)x y z t ψ来描述，它包括体系的全部信息。

这一函数称为波函数或态函数，简称态。

不含时间的波函数(,,)x y z ψ称为定态波函数。

在本课程中主要讨论定态波函数。

由于空间某点波的强度与波函数绝对值的平方成正比，即在该点附近找到粒子的几率正比于*ψψ，所以通常将用波函数ψ描述的波称为几率波。

在原子、分子等体系中，将ψ称为原子轨道或分子轨道；将*ψψ称为几率密度，它就是通常所说的电子云；*d ψψτ为空间某点附近体积元d τ中电子出现的几率。

对于波函数有不同的解释，现在被普遍接受的是玻恩（M. Born ）统计解释，这一解释的基本思想是：粒子的波动性（即德布罗意波）表现在粒子在空间出现几率的分布的波动，这种波也称作“几率波”。

波函数ψ可以是复函数，ψψψ⋅=*2合格（品优）波函数：单值、连续、平方可积。

2. 假设2：对一个微观体系的每一个可观测的物理量，都对应着一个线性自厄算符。

算符：作用对象是函数，作用后函数变为新的函数。

线性算符：作用到线性组合的函数等于对每个函数作用后的线性组合的算符。

11221122ˆˆˆ()A c c c A c A ψψψψ+=+ 自厄算符：满足**2121ˆˆ()d ()d A A ψψτψψτ=∫∫的算符。

自厄算符的性质：（1）本证值都是实数；（2）不同本证值的本证函数相互正交。

3. 假设3：若某一物理量A 的算符ˆA作用于某一状态函数ψ，等于某一常数a 乘以ψ，即：ˆAa ψψ=，那么对ψ所描述的这个微观体系的状态，物理量A 具有确定的数字a 。

量子力学——第二章作业参考答案

+
∂ψ * Vψ ∂t
=
2⎛
2m
⎜ ⎝
∂ψ ∂t
∇2ψ *
+
∂ψ * ∂t
∇2ψ
⎞ ⎟
，
⎠
将（5）式代入（2）式得
∂ω ∂t
=
∇i⎡⎢ ⎣
2
2m
⎛ ⎜ ⎝
∂ψ ∂t
∇2ψ
*
+
∂ψ * ∂t
∇2ψ
⎞⎤ ⎟⎥ ⎠⎦
，
（5）
引入能流密度 s
=
−
2 ⎛ ∂ψ
2m
⎜ ⎝
∂t
∇2ψ *
+
∂ψ * ∂t
∇2ψ
⎞ ⎟
ψ
+ψ *Vψ
⎞ ⎟，
⎝ 2m
⎠
动量算符 Pˆ = −i ∇ 是厄米算符，有
( ) ( ) ∫ ∫ ∫ ∫ d 3rψ *Pˆ 2ψ = d 3rψ *Pˆ Pˆψ = d 3r Pˆψ * Pˆψ = d 3r 2∇ψ *i∇ψ ，从而
得到能量平均值
∫ < E >=
d 3r
⎛ ⎜ ⎝
2
2m
∇ψ
* i∇ψ
ψ ( x,t) =
1 2π
∫∞ ϕ −∞
(
p
')
exp
⎡ ⎢
⎣
i
⎛ ⎜ ⎝
p'
x
−
p '2 2m
t
⎞⎤ ⎟⎥ ⎠⎦
dp '
∫ = 1
2π
∞
δ
−∞
(
p
−
p
') exp
⎡ ⎢ ⎣

量子力学作业答案精选全文完整版

可编辑修改精选全文完整版量子力学课后习题答案2.1证明在定态中，概率流密度与时间无关。

证：对于定态，可令)]r ()r ()r ()r ([m2i ]e )r (e )r (e )r (e )r ([m2i )(m 2i J e)r ( )t (f )r ()t r (**Et iEt i **Et i Et i **Etiψψψψψψψψψψψψψψψ∇-∇=∇-∇=∇-∇===-----）（）（，可见t J 与无关。

2.2 由下列定态波函数计算几率流密度： ikr ikr e re r -==1)2( 1)1(21ψψ 从所得结果说明1ψ表示向外传播的球面波，2ψ表示向内(即向原点) 传播的球面波。

解：分量只有和r J J 21在球坐标中 ϕθθϕθ∂∂+∂∂+∂∂=∇sin r 1e r 1e r r 0 r m r k r m r k r r ik r r r ik r r m i r e rr e r e r r e r m i mi J ikr ikr ikr ikr30202201*1*111 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )1(==+----=∂∂-∂∂=∇-∇=--ψψψψ r J 1与同向。

表示向外传播的球面波。

rm r k r m r k r r ik r r r ik r r m i r e r r e r e r r e r m i mi J ikr ikr ikr ikr3020220*2*222 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )2(-=-=---+-=∂∂-∂∂=∇-∇=--ψψψψ可见，r J与2反向。

表示向内(即向原点) 传播的球面波。

2.3 一粒子在一维势场⎪⎩⎪⎨⎧>∞≤≤<∞=a x a x x x U ，，，0 00)( 中运动，求粒子的能级和对应的波函数。

解：t x U 与)(无关，是定态问题。

第13章量子力学基础习题解答

140第13章量子力学基础13-1 将星球看成黑体，由维恩位移定律k m 10897.2,3⋅⨯==-b b T m λ 对北极星：k 103.81035.010897.23311⨯=⨯⨯==--bm bT λ对天狼星：k 100.11029.010897.24322⨯=⨯⨯==--bm bT λ13-2 由斯特藩-玻耳兹曼定律4)(T T M σ=及维恩位移定律b T m =λ，可得辐出度与峰值波长关系为 44)(mb T M λσ=所以 422411m m M M λλ=即 63.3)5.0/69.0()/(:42112===m m M Mλλ13-3 太阳表面单位时间单位面积辐射的能量为.4T E σ=以太阳为中心，t 时间通过半径为R 的球面的能量为tE R E 24π='。

根据相对论质能关系式2mc E ∆=',可得太阳一年内由于辐射而损失的质量为2422244cTRt ctE R cE m σππ∆=='=164828109/58001067.5360024365)1096.6(4⨯⨯⨯⨯⨯⨯⨯⨯⨯=-πkg 1037.117⨯=13-4 太阳每秒钟发射到地球表面每平方厘米的辐射能量为0.14J. 每个光子的能量为λεhchv ==则发射的光子的数目为个1783491087.31031062.61055014.014.0⨯=⨯⨯⨯⨯⨯==--εN .13-5 （1）单位时间内传到金属单位面积上的能量为J 1039-⨯.每个光子的能量为λεhchv ==则单位时间内照射到金属单位面积上的光子数为个983479100.6100.31063.6100.4103⨯=⨯⨯⨯⨯⨯⨯=---N141（2）由爱因斯坦光电效应方程A mv hv m +=221光电子的初动能A hv mv m-=221eV 1.10.2106.1100.41031063.6197834=-⨯⨯⨯⨯⨯⨯=---13-6 由爱因斯坦光电产应方程A mv hv m +=221光子的最大初动能A hcA hv mvm-=-=λ221eV 0.22.4106.1102001031063.6199834=-⨯⨯⨯⨯⨯⨯=---a m eu mv =221，所以遏止电势差V 0.2/212==e mv u m aA ch=0λ，红限波长nm 2966.1102.41031062.6198340=⨯⨯⨯⨯⨯==--Ahc λ13-7 (1) 红光光子的能量、动量和质量分别为kg1016.3)103(1084.2s m kg 1047.91070001062.6p J1084.21070001031063.6362819211128103411191083411---------⨯=⨯⨯==⋅⋅⨯=⨯⨯==⨯=⨯⨯⨯⨯==cE m hhv E λ(2) X 射线的能量、动量和质量分别为kg1082.8)103(1094.7s m kg 1065.21025.01063.6p J1094.71025.01031063.63228152221231034221510834222---------⨯=⨯⨯==⋅⋅⨯=⨯⨯==⨯=⨯⨯⨯⨯===cE m h hchv E λλ(3) r 射线的能量、动量和质量分别为kg1078.1)103(106.1s m kg 1034.51024.11063.6p J106.11024.11031063.63228152331221234221512834333---------⨯=⨯⨯==⋅⋅⨯=⨯⨯==⨯=⨯⨯⨯⨯===cE m h hchv E λλ14213-8 由康普顿散射公式 2sin22sin222ϕλϕλ∆c m h ==m 1043.212-⨯=c λ又因为%10=λλ∆,所以︒︒=⨯⨯==A A 43.201.05.00243.02%10λ∆λ 13-9 X 射线的能量为0.6MeV ,相应X 射线的波长为6.00hc =λ经散射后 002.1λλ∆λλ=+= 散射后X 射线能量为02.1λλhc hc=反冲电子量为MeV 1.0)2.111(6.0)2.111(0=-⨯=-=-λλλhc hchc13-10 散射前后能量守恒，所以有2022200)111()(c m cvcm m hchc --=-=-λλ整理得m cm cvhchc122022103.4)111(-⨯=---=λλ517.0100243.02103103.422sin ,2sin22110121221020=⎪⎪⎭⎫⎝⎛⨯⨯⨯-⨯=⎪⎪⎭⎫ ⎝⎛-==-=---c c λλλϕϕλλλλ∆ 8162)517.0arcsin(2'︒==ϕ 13-11 （1）由康普顿公式2sin22ϕλλc =∆02202201201145sin2,45sin2λλλλ∆λλλλ∆︒=︒=c c故401020220111040004.0:-===λλλλ∆λλ∆由能量守恒，反冲电子获得的动能为λλhchcE k -=20202101011,λ∆λλλ∆λλ+-=+-=hchcE hchcE k k143故⎪⎪⎭⎫⎝⎛∆+-⎪⎪⎭⎫ ⎝⎛∆+-=2020210101211111:λλλλλλk k E E =10-8 (2) 入射光波长与c λ相差不大时，康普顿效应显著。

人教版(2019)高二物理必修第三册第十三章能量量子化课后作业(带解析)

新人教版必修第三册课后作业第十三章能量量子化一、选择题1.关于对热辐射的认识,下列说法中正确的是()A.热的物体向外辐射电磁波,冷的物体只吸收电磁波B.温度越高,物体辐射的电磁波越强C.辐射强度按波长的分布情况只与物体的温度有关,与材料的种类及表面状况无关D.常温下我们看到的物体的颜色就是物体辐射电磁波的颜色2.(多选)以下关于辐射强度与波长关系的说法中正确的是()A.物体在某一温度下只能辐射某一固定波长的电磁波B.当铁块呈现黑色时,说明它的温度不太高C.当铁块的温度较高时会呈现赤红色,说明此时辐射的电磁波中该颜色的光强度最强D.早、晚时分太阳呈现红色,而中午时分呈现白色,说明中午时分太阳温度最高3.(多选)以下宏观概念中,哪些是“量子化”的()A.物体的带电荷量B.物体的质量C.物体的动量D.学生的个数4.(多选)下列说法正确的是()A.微观粒子的能量变化是跳跃式的B.能量子与电磁波的频率成正比C.红光的能量子比绿光大D.电磁波波长越长,其能量子越大5.某激光器能发射波长为λ的激光,发射功率为P,c表示光速,h为普朗克常量,则激光器每秒发射的光量子数为()A.λPℎc B.ℎPλcC.cPλℎD.λPhc6.人眼对绿光最为敏感,正常人的眼睛接收到波长为530 nm 的绿光时,只要每秒有6个绿光的光子射入瞳孔,眼睛就能察觉。

普朗克常量为6.63×10-34 J·s,光速为3.0×108 m/s,则人眼能察觉到绿光时所接收到的最小功率是()A.2.3×10-18 WB.3.8×10-19 WC.7.0×10-10 WD.1.2×10-18 W7.(多选)下列关于氢原子光谱和能级的说法正确的是()A.氢原子光谱中的亮线是由于氢原子从高能级向低能级跃迁时释放出光子形成的B.氢原子光谱不是连续的,是一些分立的亮线,说明了氢原子的能级是量子化的C.原子能量越高原子越稳定D.原子从高能态向低能态跃迁会放出光子,光子能量等于两个能级之差二、非选择题8.某小灯泡功率P=1 W,设其发光向四周均匀辐射,平均波长λ=10-6 m,求在与小灯泡相距d=1.0×104 m处,每秒落在垂直于光线方向且面积为1 cm2的球面(以小灯泡为球心)上的光子数是多少?(普朗克常量h=6.63×10-34 J·s)9.某广播电台发射功率为10 kW、在空气中波长为187.5 m的电磁波,则:(1)该电台每秒从天线发射多少个光子?(2)若发射的能量子四面八方视为均匀的,试求在离天线2.5 km处直径为2 m的环状天线每秒接收的光子个数以及接收功率。

结构化学练习之量子力学基础习题附参考答案

量子力学基础习题一、填空题在题中的空格处填上正确答案1101、光波粒二象性的关系式为_______________________________________;1102、德布罗意关系式为____________________；宏观物体的λ值比微观物体的λ值_______________;1103、在电子衍射实验中,│ψ│2对一个电子来说,代表___________________;1104、测不准关系是_____________________,它说明了_____________________;1105、一组正交、归一的波函数ψ1, ψ2, ψ3,…;正交性的数学表达式为 ,归一性的表达式为 ;1106、│ψ x 1, y 1, z 1, x 2, y 2, z 2│2代表______________________;1107、物理量xp y - yp x 的量子力学算符在直角坐标系中的表达式是_____;1108、质量为 m 的一个粒子在长为l 的一维势箱中运动,1体系哈密顿算符的本征函数集为_______________________________ ；2体系的本征值谱为____________________, 最低能量为____________ ；3体系处于基态时, 粒子出现在0 ─ l /2间的概率为_______________ ；4势箱越长, 其电子从基态向激发态跃迁时吸收光谱波长__________ ；5若该粒子在长l 、宽为2l 的长方形势箱中运动, 则其本征函数集为____________,本征值谱为 _______________________________;1109、质量为m 的粒子被局限在边长为a 的立方箱中运动;波函数ψ211x ,y ,z = _________________________；当粒子处于状态ψ211时,概率密度最大处坐标是_______________________；若体系的能量为2247ma h ,其简并度是_______________; 1110、在边长为a 的正方体箱中运动的粒子,其能级E =2243ma h 的简并度是_____,E '=22827ma h 的简并度是______________;1111、双原子分子的振动,可近似看作是质量为μ= 2121m m m m +的一维谐振子,其势能为V =kx 2/2,它的薛定谔方程是_____________________________;1112、1927年戴维逊和革未的电子衍射实验证明了实物粒子也具有波动性;欲使电子射线产生的衍射环纹与Cu 的K α线波长为154 pm 的单色X 射线产生的衍射环纹相同, 电子的能量应为___________________J;1113、对于波函数ψj 、ψj ,其归一性是指 ,正交性是指 ;1114、若算符Fˆ满足或满足 , 则算符F ˆ为厄米算符;1115、一个质量为m 的微观粒子在箱长为a 的一维势箱中运动时,体系的势能为 ,体系的零点能为 ;1116、质量为 m 的一个粒子在长为l 的一维势箱中运动,1体系哈密顿算符的本征函数集为_______________________________ ；2体系的本征值谱为____________________,最低能量为____________ ；1117、质量为m 的粒子被局限在边长为a 的立方箱中运动;波函数ψ211x ,y ,z = _________________________；当粒子处于状态ψ211时,概率密度最大处坐标是_______________________；若体系的能量为2247ma h ,其简并度是_______________; 1118、对于立方箱中的粒子,考虑E < 15h 2/8ml 2的能量范围;在此范围内有个态在此范围内有个能级1119、对氢原子 1s 态：1 2ψ在 r 为_______________处有最高值；2 径向分布函数 224ψr π在 r 为____________处有极大值； 3 电子由 1s 态跃迁至 3d 态所需能量为_____________;1120、对于立方势箱中的粒子,考虑出22815ma h E <的能量范围,在此范围内有个能级在此范围内有个状态二、选择填空题选择正确的答案,填在后面的括号内1201、首先提出能量量子化假定的科学家是：---------------------------A EinsteinB BohrC SchrodingerD Planck1202、任一自由的实物粒子,其波长为λ,今欲求其能量,须用下列哪个公式---------------A λch E = B 222λm h E = C 2) 25.12 (λe E = D A,B,C 都可以1203、下列哪些算符是线性算符-----------------------------------------------------A dxd B ∇2C 用常数乘 D1204、下列函数中A cos kxB e -bxC e -ikxD 2ekx - 1 哪些是dxd 的本征函数；--------------------------------------------------------------- 2 哪些是的22dxd 本征函数；------------------------------------------------------------- 3 哪些是22dx d 和dxd 的共同本征函数;----------------------------------------------- 1205、线性算符Rˆ具有下列性质 RˆU + V = R ˆU +R ˆV R ˆcV = c R ˆV 式中c 为复函数,下列算符中哪些是线性算符 -----------------------------------A AˆU =λU , λ=常数 B BˆU =U C CˆU =U 2 D D ˆU = xU d d E EˆU =1/U1206、电子自旋存在的实验根据是：---------------------------------------------------------------A 斯登--盖拉赫Stern-Gerlach 实验B 光电效应C 红外光谱D 光电子能谱1207、一个在一维势箱中运动的粒子,1 其能量随着量子数n 的增大：------------------------A 越来越小B 越来越大C 不变2 其能级差 E n +1-E n 随着势箱长度的增大：-------------------A 越来越小B 越来越大C 不变1208、立方势箱中的粒子,具有E =22812mah 的状态的量子数; n x n y n z 是--------- A 2 1 1 B 2 3 1 C 2 2 2 D 2 1 31209、处于状态ψ x =sin x a π的一维势箱中的粒子,出现在x =4a 处的概率为----- A P =ψ4a = sin a π·4a = sin 4π = 22 B P =ψ 4a 2= 21 C P = a 2ψ 4a =a1 D P =a2 ψ 4a 2= a 1 E 题目提法不妥,所以以上四个答案都不对1210、在一立方势箱中,2247ml h E ≤的能级数和状态数分别是势箱宽度为l ,粒子质量为m ：-----------------------------------------------------------------A 5,11B 6,17C 6,6D 5,14E 6,141211、关于光电效应,下列叙述正确的是：可多选 ---------------------------A 光电流大小与入射光子能量成正比B 光电流大小与入射光子频率成正比C 光电流大小与入射光强度成正比D 入射光子能量越大,则光电子的动能越大1212、提出实物粒子也有波粒二象性的科学家是：----------------------------A de BröglieB A. EinsteinC W. HeisenbergD E. Schrödinger1213、微粒在间隔为1eV的二能级之间跃迁所产生的光谱线的波数v~应为：--------------------------------A 4032 cm-1B 8065cm-1C 16130cm-1D 2016cm-11eV=×10-19J1214、普朗克常数是自然界的一个基本常数,它的数值是：-------------------A ×10-23尔格B ×10-30尔格·秒C ×10-34焦耳·秒D ×10-16尔格·秒1215、首先提出微观粒子的运动满足测不准原理的科学家是：-----------------A 薛定谔B 狄拉克C 海森堡D 波恩1216、下列哪几点是属于量子力学的基本假设多重选择：------------------- Ａ电子自旋保里原理Ｂ微观粒子运动的可测量的物理量可用线性厄米算符表征Ｃ描写微观粒子运动的波函数必须是正交归一化的Ｄ微观体系的力学量总是测不准的,所以满足测不准原理1217、描述微观粒子体系运动的薛定谔方程是：----------------------------------A 由经典的驻波方程推得B 由光的电磁波方程推得C 由经典的弦振动方程导出D 量子力学的一个基本假设1218、一电子被1000V的电场所加速,打在靶上,若电子的动能可转化为光能,则相应的光波应落在什么区域AX光区B紫外区C可见光区D红外区1219、由戴维逊－革末的衍射实验,观察某金属单晶晶面间距d为104pm上反射,若一级衍射的布拉格角控制为45º,则此实验要用多大的加速电压来加速电子单位：V---A<10 B25C70 D1501220、一维势箱的薛定谔方程求解结果所得的量子数n,下面论述正确的是A 可取任意整数B 与势箱宽度一起决定节点数C 能量与n 2成正比例D 对应于可能的简并态三、判断题对判断给出的命题的对错,正确的题号后画√,错误的题号后画×1301、根据测不准原理,任一微观粒子的动量都不能精确测定,因而只能求其平均值;1302、波函数平方有物理意义, 但波函数本身是没有物理意义的;1303、任何波函数ψ x , y , z , t 都能变量分离成ψ x , y , z 与ψ t 的乘积; 1304、ψ=cos x , p x 有确定值, p 2x 没有确定值,只有平均值;1305、一维势箱中的粒子,势箱长度为l , 基态时粒子出现在x =l /2处的概率密度最小; 1306、波函数本身是连续的,由它推求的体系力学量也是连续的;1307、测不准关系式是判别经典力学是否适用的标准;1308、光照射到金属表面时,金属中有光电子产生,且照射光的强度越大,电子逸出金属表面的动能越大;1309、量子力学中力学量算符都是线性的、厄米的;1310、在电子的衍射实验中采用单个电子穿过晶体粉末,在足够长的时间后,在屏上得到了衍射环纹,这说明单个电子也可以产生波;四、简答题1401、对一个运动速率v<<c 的自由粒子,有人作了如下推导：mv v E v h hp mv 21=====νλ A B C D E 结果得出211=的结论;问错在何处说明理由; 1402、简述一个合格的波函数所应具有的条件1403、被束缚在0<x <a 区间运动的粒子,当处于基态时,出现在≤x ≤ 区间内的概率是多少1404、一维势箱中一粒子的波函数ψn x =2/l 1/2sin n πx /l 是下列哪些算符的本征函数,并求出相应的本征值;A x p ˆ Ｂ 2ˆx p Ｃ x ˆ ＤH ˆ= m h 2)2/(2π22d d x1405、说明下列各函数是Hˆ,M ˆ2, M ˆz 三个算符中哪个的本征函数 ψ2pz , ψ2px 和ψ2p11406、一维势箱中运动的一个粒子,其波函数为a x n a πsin 2,a 为势箱的长度,试问当粒子处于n =1或n =2的状态时,在0 ～a /4区间发现粒子的概率是否一样大,若不一样,n 取几时更大一些,请通过计算说明;1407、θθcos 3cos 53-是否是算符)d d sin cos d d (ˆ222θθθθF +-= 的本征函数,若是,本征值是多少1408、下列休克尔分子轨道中哪个是归一化的若不是归一化的,请给出归一化系数;原子轨道ϕϕϕ321,,是已归一化的a. ()ϕϕ21121+=ψb. ()ϕϕϕ3212241+-=ψ 1409、已知一函数fx =2e 2x ,问它是否是x pˆ的本征函数相应的本征值是多少1410、有一粒子在边长为a 的一维势箱中运动;1计算当n =2时,粒子出现在0≤x ≤a /4区域中的概率；2根据一维势箱的2ψ图,说明0≤x ≤a/4区域中的概率; 五、证明题1501、已知一维运动的薛定谔方程为:m h 228[π-22d d x+V x ψ=E ψ ψ1和ψ2是属于同一本征值的本征函数, 证明:ψ1x d d 2ψ-ψ2x d d 1ψ=常数 1502、试证明实函数Φ2 φ=1/π1/2cos2φ和Φ2’φ=2/π1/2sin2φcos φ都是Φ方程22d d φ+ 4 Φ φ=0 的解; 1503、证明函数x +i y ,x -i y 和z 都是角动量算符zM ˆ的本征函数,相应的本征值是多少1504、已知有2n 个碳原子相互共轭的直链共轭烯烃的π分子轨道能量可近似用一维势阱的能级公式表示为E k = 2222)12(8+n mr h k k =1,2,…,2n 其中,m 是电子质量,r 是相邻碳原子之间的距离,k 是能级序号;试证明它的电子光谱第一吸收带即电子基态到第一激发态的激发跃迁波长λ与n 成线性关系;假定一个粒子在台阶式势阱中运动,势阱宽度为l ,而此台阶位于l /2～l 之间;1505、证明同一个厄米算符的、属于不同本征值的本征函数相互正交;1506、证明厄米算符的本征值是实数;1507、已知Aˆ和B ˆ是厄米算符,证明A ˆ+B ˆ和A ˆ2也是厄米算符; 1508、证明描述在一球面上运动的粒子刚性转子的波函数θψcos 2121⎪⎭⎫ ⎝⎛π3=是三维空间中运动的自由粒子势能V=0的薛定谔方程的解,并求粒子的能量; 已知)]sin 1)(sin sin 1)(1[2222222222φθr θθθθr r r r r m ∂∂+∂∂∂∂+∂∂∂∂-=∇ ; 1509、证明描述在一球面上运动的粒子刚性转子的波函数φθθψi 21e sin cos 21-⎪⎭⎫ ⎝⎛2π15=是在三维空间中运动的自由粒子势能V =0的薛定谔方程的解,并求粒子的能量;已知)]sin 1)(sin sin 1)(1[2222222222φθr θθθθr r r r r m ∂∂+∂∂∂∂+∂∂∂∂-=∇ ; 1510、证明波函数φθθψi 21e sin cos 21-⎪⎭⎫ ⎝⎛2π15=是角动量平方的本征函数,并求粒子的角动量;已知角动量平方算符)sin 1sin cos (ˆ2222222φθθθθθM ∂∂+∂∂+∂∂-= ; 六、计算题1601、波长λ=400 nm 的光照射到金属铯上,计算金属铯所放出的光电子的速率;已知铯的临阈波长为600 nm;1602、光电池阴极钾表面的功函数是 eV;当波长为350 nm 的光照到电池时,发射的电子最大速率是多少1 eV=×10-19J, 电子质量m e =×10-31 kg1603、设体系处在状态ψ=c 1ψ211+ c 2ψ210中, 角动量M 2和M z 有无定值;其值为多少若无,则求其平均值;1604、函数ψ x = 2a 2sin a x π - 3a2sin a x π2 是不是一维势箱中粒子的一种可能状态如果是, 其能量有没有确定值本征值如有, 其值是多少如果没有确定值, 其平均值是多少1605、在长为l 的一维势箱中运动的粒子, 处于量子数为n 的状态, 求：1 在箱的左端1/4区域内找到粒子的概率；2 n 为何值时, 上述概率最大3 当n →∞时, 此概率的极限是多少4 3中说明了什么1606、1 写出一维简谐振子的薛定谔方程；2 处于最低能量状态的简谐振子的波函数是ψ0= π2α1/4 exp-α2x 2/2 此处,α=4π2k μ/h 21/4,试计算振子处在它的最低能级时的能量;3 波函数ψ在x 取什么值时有最大值计算最大值处ψ2的数值;1607、氢分子在一维势箱中运动,势箱长度l =100nm,计算量子数为n 时的de Broglie 波长以及n =1和n =2时氢分子在箱中49nm 到51nm 之间出现的概率,确定这两个状态的节面数、节面位置和概率密度最大处的位置;1608、限制在一个平面中运动的两个质量分别为m 1和m 2的质点 , 用长为R 的、没有质量的棒连接着,构成一个刚性转子;1 建立此转子的Schrödinger 方程, 并求能量的本征值和归一化的本征函数；(2) 求该转子基态的角动量平均值;已知角动量算符 Mˆ=M ˆz =-i π2h φ∂∂; 1609、氢原子中,归一化波函数：和都是归一化的所描述的状态,其能量平均值是aR ；能量出现的概率是b ；角动量平均值是c ；角动量出现的概率是d ；角动量Z 分量的平均值是e ；角动量Z 分量出现的概率是f;1610、已知类氢离子的某一状态波函数为：则a 此状态的能量为； b 此状态的角动量的平方值；c 此状态角动量在Z 方向的分量为；d 此状态的值分别为； e 此状态角度分布的节面数为；2125、多电子原子的一个光谱支项为 3D 2, 在此光谱支项所表征的状态中,原子的总轨道角动量等于a ；原子总自旋角动量等于b ；原子总角动量等于c ；在磁场中 , 此光谱支项分裂出d 个蔡曼 Zeeman 能级 ;2403、一个电子主量子数为 4, 这个电子的 l , m , m s 等量子数可取什么值这个电子共有多少种可能的状态量子力学基础习题参考答案1100、填填空题在题中的空格处填上正确答案1101、E =h ν p =h /λ1102、,mvh p h ==λ 小 1103、电子概率密度1104、∆x ·∆p x ≥π2h微观物体的坐标和动量不能同时测准, 其不确定度的乘积不小于π2h;1105、a ∫ψ*iψi d τ = 0, i ≠jb ∫ψ*iψi d τ = 11106、电子1出现在x 1,y 1,z 1, 同时电子2出现在x 2, y 2, z 2处的概率密度 1107、-i ·π2h x y∂∂ - y x ∂∂1108、1ψ =l2sin l x n π n =1, 2, 3,…2 E = 2228ml h n ; 228mlh 3 1/24 增长 5ψ=l2sin l x n xπl 22sin ly n y 2πE = 2228ml hn x + 222)2(8l m h n y1109、1ψ211x ,y ,z =38a sin a π2 x sin a πy sin a π z2a /4, a /2, a /2 3a /4, a /2, a /236 1110、3, 4 1111、[]ψψμπE x k h =+∇-22128221112、T = ()λh m m p 22122==×10-17 J 1113、），j i d j i ==⨯⎰1*τψψ），j i d j i ≠=⨯⎰0*τψψ 1114、ττd F d F ψψ=ψψ⎰⎰ΛΛ**)(ττd F d F 2*12*1)(ψψ=ψψ⎰⎰ΛΛ1115、零,228ma h1116、1 ψ =l2sin l x n π n =1, 2, 3,…2 E = 2228ml h n ; 228mlh 1117、 1ψ211x ,y ,z =38asin a π2 x sin a πy sin a π z 2 a /4, a /2, a /2 3a /4, a /2, a /23 61118、17,51119、1 O 或核附近 2 a 0 或 pm 3 8×9 eV1120、E = )(222zyxn n n ++ 228ma h共有17个状态, 这些状态分属6个能级;1200、选择填空题选择正确的答案,填在后面的括号内1201、D1202、B1203、D1204、1 B, C 2 A, B, C 3 B, C1205、A, D1206、A1207、1 B 2 A1208、C1209、E1210、B1211、C,D1212、A1213、B1214、C1215、C1216、A ,B1217、D1218、A1219、C1220、C1300、判断题对判断给出的命题的对错,正确的题号后画√,错误的题号后画×1301、×1302、×1303、×1304、×1305、×1306、×1307、×1308、×1309、√1310、×1400、简答题1401、A,B两步都是对的, A中v是自由粒子的运动速率, 它不等于实物波的传播速率u, C中用了λ= v/ν, 这就错了; 因为λ= u/ν;又D 中E =h ν是粒子的总能量, E 中E =21mv 2仅为v <<c 时粒子的动能部分,两个能量是不等的; 所以 C, E 都错;1402、1 单值的; 2 连续的, 一级微商也连续; 3 平方可积的, 即有限的;1403、P = aaa275.025.0⎰sin 2a x π d x = + π1=1404、A.不是 B.是,本征值为 n 2h 2/4l 2C.不是D.是,本征值为 n 2h 2/8ml 21405、p p z 022= 是M zˆ,M ˆ,H ˆ2共同的本征函数 p x 2为p 12和p 12-的线性组合,是M ˆ,Hˆ2共同的本征函数p 12 是M z ˆ,M ˆ,Hˆ2共同的本征函数 1406、P =⎰⎰π=⎪⎪⎭⎫ ⎝⎛π402240d sin 2d sin 2a/a/x a xn a x a x n a =2sin 2141ππ-n nn =1,P =πn 2141-n =2,P =41.n =2时,粒子出现在0—a /4区间概率更大些;1407、θθθsin cos d d-= θθθcos cos d d 22-= θθθθ23cos sin 3cos d d-= θθθθθcos sin 6cos 3cos d d 23322+-=()=-θθFcos 3cos 5ˆ3 ()θθθθθθcos 3cos 15cos 3cos sin 30cos 153232+-++--=()θθθθcos 6cos sin 30cos 30232++--=()θθθθθθcos 6cos sin 30cos 30cos 30cos 3023332+++---=()θθcos 36cos 6032+--=12()θθcos 3cos 532- 是,本征值为1221408、归一化条件：112=∑=ni i cA =∑=212i i c 21)212=,a 是归一化的;B23)42()41(2)(22312=-+=∑=i i c ,b 不是归一化的;归一化因子32即61; 1409、x x x x f p2e 2d di )(ˆ -= x2e i 4 -= )(i 2x f -=)(i x f hπ=fx 是x pˆ的本征函数,本征值为πi h; 1410、x ax n a a d )sin 2(240π⎰ 当n =2时 =⎥⎦⎤⎢⎣⎡ππ-044sin 882a a x a a a =4182=⋅a a 22ψ1500、证明题1501、11ψ212d d xψ = 21ψ222d d x ψ ψ1222d d x ψ - ψ2212d d x ψ = 0xd dψ1x d d 2ψ - ψ2x d d 1ψ = 0 ψ1x d d 2ψ - ψ2xd d 1ψ = 常数1502、将()()φφ2cos /12/12πΦ=代入()φΦ方程()()()()()()02cos 42cos 42cos 42sin 22cos 4/1/1/1/1/12/12/12/12/12/122=+-=+-=⎥⎦⎤⎢⎣⎡+πππφφφφφφφφφd dd d说明()φΦ2是()φΦ方程的解;将()()φφφcos sin /22/12πΦ'=代入()φΦ方程()()()()()()[]()0cos sin 4cos sin 2cos sin 2cos sin 4cos sin 4/2/2/2sin cos /2/22/12/12/1222/12/122=+--=+-=⎥⎦⎤⎢⎣⎡+πππππφφφφφφφφφφφφφφd dd d 说明()φΦ'2也是()φΦ方程的解; 1503、()()()[]()()()()()()[]iy x y iy x x i iy x y x i yhzxy hz MM +-+-=+--=π∂∂∂∂π∂∂∂∂π22ˆˆ 故x +i y 是M z ˆ本征函数,本征值为 π2h()()()[]()()()()()()[]iy x y iy x x i iy x y x i yhzxy hz MM ----=---=π∂∂∂∂π∂∂∂∂π22ˆˆ 故x -i y 是M z ˆ本征函数,本征值为 π2h - ()()()()[]z z y z x i z yhzM ⋅==--=π∂∂∂∂π002ˆ故z 是M zˆ本征函数,本征值为 01504、第一吸收带是由HOMO 到LUMO 跃迁产生; 对本题HOMO k =n ; LUMO k =n +1;()()[]()()()1282281222228212121++==-+=∆++n mr mr n mr hn h n h n n EE hc∆=λ所以 ()()h n mrc hhc n mr Ehc/1282128+===⨯+∆λ 即h mrc h mrcn /8/16+=λ1505、设u 1,u 2,...,u n ,...是算符Aˆ的分别属于本征值λ,,λ,λn 21.的本征函数,则有 ,ˆu u Am m m λ= ,ˆu u An n n λ=()****ˆm m mm m u λuλu A==可得τu u λτu A u n m n n m d d ˆ**⎰⎰=()τu u λτu u A n mm n m d d ˆ**⎰⎰= 根据的厄米性,从上式可得τu u λτu u λn m m n m n d d **⎰⎰= ()0d *=-⎰τu u λλn m m nλλm n ≠ 0d *=∴⎰τu u n m1506、按厄米算符的定义,有()ud τu A ud τA u ⎰⎰=ˆˆ**同时下列本征方程成立:()***ˆˆu λu A λu,u A==代入上式,得: τu u λτu u λd d ***⎰⎰=由此可得 *λλ=故λ必为实数;1507、1. ∫u B A ˆˆ+v d τ=∫u A ˆv d τ+∫u B ˆv d τ =∫Aˆuv d τ+∫B ˆuv d τ =∫A ˆu +B ˆuv d τ =∫A ˆu +B ˆuv d τ =∫B Aˆˆ+v d τ 由此得证2. ∫u A A ˆˆv τd =∫u AˆA ˆv τd =∫Aˆu A ˆv τd =∫Aˆu A ˆv τd =∫A Aˆˆuv τd=∫Aˆ2uv τd 由此得证 1508、三维空间自由粒子的薛定谔方程ψψE H =ˆ 222ˆ∇-=mH 当r 为常数,ψ与r,φ无关;⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=θθθθmr H sin cos 2ˆ2222 θN θθθθmr H cos sin cos 2ˆ2222⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-= ψ =()θθmr N cos cos 222---=ψ2222cos mr θN mr = 22maE =∴ 当ψ与φ无关,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=θθθθsin cos ˆ2222 M 2ˆ2=ψM2=M1509、三维空间自由粒子的薛定谔方程 ψψE H =ˆ 222ˆ∇-=mH 当r 为常数,ψ与r 无关,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=2222222sin 1sin cos 2ˆφθθθθθmr H )e sin cos (ˆˆi φθθN H H-=ψ =⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-2222222sin 1sin cos 2φθθθθθmr N φθθi e sin cos - =222mrN -ψ-φθθi e sin cos -+φφφθθθθθθi i i 2e sin cos e cos sin e sin cos ----- =222mr N φθθi e sin cos ⎪⎪⎭⎫ ⎝⎛++-θθθψ222sin 11sin cos 式中θθθ222sin 1sin cos +-=1=ψH ˆmr N 262 N φθθi e sin cos =mr262 ψ,2226mr E =∴ 1510、φθθN φθθθθθM ψi 2222222e sin cos sin 1sin cos ˆ-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-= =2N -ψ-φθθi e sin cos -+φφφθθθθθθi i i 3e sin cos e cos sin e sin cos ----- =2 N φθθi e sin cos ⎪⎪⎭⎫ ⎝⎛++-θθθψ222sin 11sin cos 式中θθθ222sin 1sin cos +-=1 226ˆ =ψMN φθθi e sin cos -=ψ26 ,26 为一常数,证毕; 6=M 1600、计算题1601、1-241-9--34s kg m 10626.6s kg m 100.1106.626⋅⋅⨯=⋅⋅⨯⨯==-λhp T = m p 22 = 3123410109.92)10626.6(--⨯⨯⨯ J = ×10-17 J 1602、T = h ν- h ν0= λhc -0λhcT = 1/2 mv 2 v = )11(20λλ-m hc = ×105 m ·s -11603、1ψ是Mˆ2属于同一本征值2π2h 2的本征函数的线性组合, 所以,ψ是Mˆ2的本征函数, 其本征值亦为2π2h 22ψ是Mˆz 属于本征值h 和0的本征函数的线性组合, 它不是M ˆz 的本征函数, 其M z 无确定值, 其平均值为<M z >= 22.2121)2/(c c h c +π 1604、1. 该函数是一维箱中粒子的一种可能状态, 因a 2sin a x π及a2sin a x π2是方程的解,其任意线性组合也是体系可能存在的状态;2. 其能量没有确定值, 因该状态函数不是能量算符的本征函数;3. <E > = 22135mah 1605、1 ψn =l2sin l x n πP 1/4=∫4/0l 2n ψd x =41 - πn 21sin 2πn2 n =3, P 1/4,max = 41 + π613 lim ∞→n P 1/4 = lim ∞→n 41 - πn 21sin 2πn =414 3说明随着粒子能量的增加, 粒子在箱内的分布趋于平均化;1606、1 - μ228πh 22dx d + 21kx 2 ψ=E ψ2 E = μα2228πh =π4h μK=21h ν 3 x =0时 , dxd ψ= 0, 有最大值 ψ00 = π2α1/4最大值处 x =0 ψ02=πα21/2= πα1607、E kmh p h2==λ 势箱中⎪⎭⎫⎝⎛==lhn E m kE2228故λ= 2l /n =200/n nm()()[]()()π-π⨯π-=π==⎰⎰n n n dxl x n l dx p 98.0sin 02.1sin 02.0//221251951492sin ψn =1 P 1=n =2 P 2=n =1时无节面,概率密度最大在50nm 处; n =2时节面数=n -1=1,节面在50nm 处,概率密度最大在25nm 和75nm 处;1608、1 Schrödinger 方程为 - I h 228π22d d φφψ）（ = E ψ φ E = I h m 2228π, ψ φ =π21e im φm =0,±1,±2,...2 <Mˆ> = 0 1609、a ； b ；c ；d1e f0 1610、a－；b0；c0；d2,0,0；e0。

第十三章 量子力学基础2作业答案

量子力学基础试题及答案

《原子物理与量子力学》第十三章习题解答

量子力学(二)习题参考答案

(完整版)南华物理练习第13章答案

量子力学课后习题答案

量子力学作业及参考答案

大学物理第13章 量子物理习题解答

第十三章 量子力学基础2作业答案

南华物理练习第13章答案

物理学(王铭)量子基础习题解答

量子力学习题答案9页word

[0131]《量子力学基础》在线作业及参考答案

大学物理_第十三章_课后答案

量子力学基础知识习题解答可修改全文

量子力学——第二章作业参考答案

量子力学作业答案精选全文完整版

第13章量子力学基础习题解答

人教版(2019)高二物理必修第三册 第十三章 能量量子化 课后作业(带解析)

结构化学练习之量子力学基础习题附参考答案

第十三章量子力学基础2作业答案

大学物理第13章量子物理习题解答

第十三章量子力学基础2作业答案

人教版(2019)高二物理必修第三册第十三章能量量子化课后作业(带解析)