培优专题(四) 一次函数与方程、不等式的实际应用问题

合集下载

一次函数与方程、不等式详细教案

一次函数与方程、不等式详细教案第一章：一次函数的概念与性质1.1 一次函数的定义介绍一次函数的定义：形式为y = kx + b（k、b为常数，k≠0）的函数。

强调一次函数的图像为直线。

1.2 一次函数的斜率与截距解释斜率k的意义：直线的倾斜程度。

解释截距b的意义：直线与y轴的交点。

1.3 一次函数的图像特点描述一次函数图像的形状、方向和位置。

第二章：一次函数的图像与解析式2.1 一次函数图像的绘制利用斜率和截距绘制一次函数的图像。

2.2 一次函数解析式的求解介绍求解一次函数解析式的方法：观察图像或给定的点。

2.3 一次函数图像与解析式的关系解释图像与解析式之间的联系。

第三章：一次函数的应用3.1 线性方程的解法介绍解线性方程的方法：代入法、消元法等。

3.2 实际问题中的一元一次方程举例说明一元一次方程在实际问题中的应用。

3.3 一次函数与不等式介绍一次函数与不等式的关系：图像与解集。

第四章：一元一次不等式的解法4.1 不等式的基本性质介绍不等式的加减乘除性质。

4.2 一元一次不等式的解法介绍解一元一次不等式的方法：同解变形、图像法等。

4.3 不等式的应用举例说明一元一次不等式在实际问题中的应用。

第五章：一次函数与方程的综合应用5.1 实际问题中的一次函数与方程组举例说明一次函数与方程组在实际问题中的应用。

5.2 一次函数与方程的综合解法介绍一次函数与方程的综合解法：代入法、图像法等。

5.3 一次函数与方程的拓展应用探讨一次函数与方程在其他领域的应用。

第六章：一次函数的图像与几何性质6.1 一次函数图像的交点介绍如何求出两条一次函数图像的交点。

强调交点在解析几何中的应用。

6.2 一次函数图像与坐标轴的交点解释一次函数与x轴、y轴的交点求解方法。

6.3 一次函数图像的距离和角度介绍如何利用一次函数图像求解两点间的距离和角度。

第七章：一次函数图像的变换7.1 一次函数图像的平移介绍如何对一次函数图像进行上下、左右平移。

一次函数与方程不等式练习题及教案设计

一次函数、方程与不等式练习题及教案设计教案章节：一、一次函数的概念与性质1.1 理解一次函数的定义1.2 掌握一次函数的斜率和截距1.3 理解一次函数的图像特点二、一次函数的图像与解析式2.1 绘制一次函数的图像2.2 解析一次函数图像的斜率和截距2.3 一次函数图像的交点与解方程三、一次函数的应用题3.1 线性方程的应用题3.2 线性方程组的应用题3.3 实际问题转化为一次函数应用题四、一次方程的解法4.1 代入法解一次方程4.2 消元法解一次方程组4.3 图像法解一次方程五、一次不等式与一次方程的关系5.1 理解一次不等式的定义5.2 掌握一次不等式的解法5.3 一次不等式与一次方程的联系与区别教案设计：一、教学目标：1. 让学生理解一次函数的定义和性质。

2. 学会绘制一次函数的图像，并解析图像的斜率和截距。

3. 能够将实际问题转化为一次函数应用题，并求解。

二、教学方法：1. 采用问题驱动的教学方法，引导学生通过解决实际问题来学习一次函数的概念和性质。

2. 利用多媒体工具，展示一次函数的图像，帮助学生直观理解一次函数的特点。

3. 通过小组合作学习，培养学生的团队协作能力和问题解决能力。

三、教学内容：1. 引入一次函数的概念，引导学生通过观察图像来理解一次函数的性质。

2. 教授一次函数的图像与解析式，让学生学会绘制一次函数的图像，并能够解析图像的斜率和截距。

3. 提供一次函数的应用题，让学生通过解决实际问题来巩固一次函数的知识。

四、教学评估：1. 通过课堂练习题，检查学生对一次函数概念和性质的理解。

2. 通过小组讨论，评估学生对一次函数图像与解析式的掌握情况。

3. 通过课后作业，评估学生对一次函数应用题的解决能力。

五、教学资源：1. 多媒体教学课件，展示一次函数的图像和实际应用题。

2. 练习题和作业，供学生巩固知识和进行自我评估。

六、一次方程的解法6.1 理解一次方程的解法6.2 掌握代入法解一次方程6.3 学会消元法解一次方程组七、一次方程组的应用题7.1 理解一次方程组的定义7.2 学会解一次方程组的方法7.3 解决实际问题转化为一次方程组应用题八、一次不等式的解法8.1 理解一次不等式的解法8.2 掌握解法一次不等式的方法8.3 解决实际问题中的一次不等式九、一次不等式与一次方程的综合应用题9.1 理解一次不等式与一次方程的综合应用题9.2 学会解决一次不等式与一次方程的综合应用题9.3 解决实际问题中的综合应用题十、总结与复习10.1 总结一次函数、方程与不等式的关系10.2 复习一次函数、方程与不等式的解法10.3 巩固一次函数、方程与不等式的应用题解法教案设计：六、教学目标：1. 让学生理解一次方程的解法。

专题5.4 一次函数与方程、不等式的关系【十大题型】(学生版)

专题5.4一次函数与方程、不等式的关系【十大题型】【浙教版】【题型1一次函数与一元一次方程的解】 (1)【题型2两个一次函数与一元一次方程】 (2)【题型3利用一次函数的变换求一元一次方程的解】 (3)【题型4一次函数与二元一次方程（组）的解】 (3)【题型5不解方程组判断方程组解的情况】 (4)【题型6一次函数与一元一次不等式的解集】 (5)【题型7两个一次函数与一元一次不等式】 (6)【题型8绝对值函数与不等式】 (7)【题型9一次函数与一元一次不等式组的解集】 (9)【题型10一次函数与不等式组中的阴影区域问题】 (10)【例1】（2022秋•白塔区校级月考）直线y＝3x﹣m﹣4经过点A（m，0），则关于x的方程3x﹣m﹣4＝0的解是．【变式1-1】（2022春•安阳县期末）一次函数y＝kx+b的图象如图所示，则关于x的方程kx+b＝0的解为．【变式1-2】（2022春•雷州市校级期末）一次函数y＝kx+b（k≠0，k，b是常数）的图象如图所示，则关于x的方程kx+b＝4的解是（）A．x＝3B．x＝4C．x＝0D．x＝b【变式1-3】（2022秋•招远市期末）已知关于x的一次函数y＝3x+n的图象如图，则关于x的一次方程3x+n＝0的解是（）A．x＝﹣2B．x＝﹣3C．D．【题型2两个一次函数与一元一次方程】【例2】（2022秋•双流区期末）已知一次函数y＝5x+m的图象与正比例函数y＝kx的图象交于点（﹣2，4）（k，m是常数），则关于x的方程5x＝kx﹣m的解是．【变式2-1】（2022秋•龙岗区期末）如图，函数y＝2x+b与函数y＝kx﹣1的图象交于点P，则关于x的方程kx﹣1＝2x+b的解是．【变式2-2】（2022秋•苏州期末）已知一次函数y＝kx+1与的图象相交于点（2，5），求关于x的方程kx+b＝0的解．【变式2-3】（2022秋•包河区期末）已知直线y＝x+b和y＝ax+2交于点P（3，﹣1），则关于x的方程（a﹣1）x ＝b﹣2的解为．【题型3利用一次函数的变换求一元一次方程的解】【例3】（2022春•江都区校级月考）若一次函数y＝kx+b（k为常数且k≠0）的图象经过点（﹣2，0），则关于x 的方程k（x﹣5）+b＝0的解为．【变式3-1】（2022•姜堰区一模）若一次函数y＝ax+b（a、b为常数，且a≠0）的图象过点（2，0），则关于x 的方程a（x+1）+b＝0的解是．【变式3-2】（2022秋•庐阳区校级期中）若关于x的一次函数y＝kx+b的图象经过点A（﹣1，0），则方程k（x+2）+b＝0的解为．【变式3-3】（2022秋•庐阳区校级期中）将直线y＝kx﹣2向下平移4个单位长度得直线y＝kx+m，已知方程kx+m ＝0的解为x＝3，则k＝，m＝．【题型4一次函数与二元一次方程（组）的解】【例4】（2022春•夏津县期末）如图，根据函数图象回答问题：方程组y=kx+3y=ax+b的解为．【变式4-1】（2022•贵阳）在平面直角坐标系内，一次函数y＝k1x+b1与y＝k2x+b2的图象如图所示，则关于x，y 的方程组y−k1x=b1y−k2x=b2的解是．【变式4-2】（2022秋•西乡县期末）已知二元一次方程组x−y=−5x+2y=−2的解为x=−4y=1，则在同一平面直角坐标系中，直线l1：y＝x+5与直线l2：y=−12x﹣1的交点坐标为（）A．（4，1）B．（1，﹣4）C．（﹣1，﹣4）D．（﹣4，1）【变式4-3】（2022•德城区二模）若以关于x、y的二元一次方程x+2y﹣b＝0的解为坐标的点（x，y）都在直线y=−12x+b﹣1上，则常数b的值为（）A．12B．1C．﹣1D．2【题型5不解方程组判断方程组解的情况】【例5】（2022秋•泰兴市校级期末）已知关于x，y的方程组y=kx+by=(3k−1)x+2（1）当k，b为何值时，方程组有唯一一组解；（2）当k，b为何值时，方程组有无数组解；（3）当k，b为何值时，方程组无解．【变式5-1】（2022秋•苏州期末）若二元一次方程组3x+y=−12x+my=−8有唯一的一组解，那么应满足的条件是（）A．m=23B．m≠23C．m=−23D．m≠−23【变式5-2】（2022春•覃塘区期中）如果关于x，y的方程组x+y=1ax+by=c有唯一的一组解，那么a，b，c的值应满足的条件是（）A．a≠b B．b≠c C．a≠c D．a≠c且c≠1【变式5-3】（2022春•高明区期末）k为何值时，方程组kx−y=−133y=1−6x有唯一一组解；无解；无穷多解？【题型6一次函数与一元一次不等式的解集】【例6】（2022•海淀区校级自主招生）已知一次函数y＝kx+b中x取不同值时，y对应的值列表如下：A．x＞1B．x＞2C．x＜1D．无法确定【变式6-1】（2022春•龙岗区期末）如图，已知一次函数y＝kx+b的图象经过点A（﹣3，2），B（1，0），则关于x的不等式kx+b＜2解集为．【变式6-2】（2022春•湖南期中）已知关于x的不等式ax+1＞0（a≠0）的解集是x＜1，则直线y＝ax+1与x轴的交点是（）A．（0，1）B．（﹣1，0）C．（0，﹣1）D．（1，0）【变式6-3】（2022春•高明区校级期末）如图，直线y＝kx+b与直线y=−12x+52交于点A（m，2），则关于x的不等式kx+b≤−12x+52的解集是（）A．x≤2B．x≥1C．x≤1D．x≥2【题型7两个一次函数与一元一次不等式】【例7】（2022•钟山县校级模拟）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k2x＞k1x+b的解集为（）A．x＞3B．x＜3C．x＞﹣1D．x＜﹣1【变式7-1】（2022•烟台）如图，直线y＝x+2与直线y＝ax+c相交于点P（m，3），则关于x的不等式x+2≤ax+c 的解集为．【变式7-2】（2022春•楚雄州期末）已知关于x的一次函数y＝kx+b（k≠0）的图象过点A（2，4）、B（0，3）．（1）求一次函数y＝kx+b的解析式；（2）若关于x的一次函数y＝mx+n（m＜0）的图象也经过点A，则关于x的不等式mx+n≥kx+b的解集为．【变式7-3】（2022春•潮安区期末）已知直线y＝kx+5交x轴于A，交y轴于B且A坐标为（5，0），直线y＝2x﹣4与x轴于D，与直线AB相交于点C．（1）求点C的坐标；（2）根据图象，写出关于x的不等式2x﹣4＞kx+5的解集；（3）求△ADC的面积．【题型8绝对值函数与不等式】【例8】（2022秋•临海市校级月考）小敏学习了一次函数后，尝试着用相同的方法研究函数y＝a|x﹣b|+c的图象和性质．（1y＝|x﹣2|和y＝|x﹣2|+1的图象；（2）猜想函数y＝﹣|x+1|和y＝﹣|x+1|﹣3的图象关系；（3）尝试归纳函数y＝a|x﹣b|+c的图象和性质；（4）当﹣2≤x≤5时，求y＝﹣2|x﹣3|+4的函数值范围．【变式8-1】（2022秋•玄武区期末）请你用学习“一次函数”时积累的经验和方法研究函数y＝|x|的图象和性质，并解决问题．（1）完成下列步骤，画出函数y＝|x|的图象；①列表、填空；x…﹣3﹣2﹣10123…y…31123…②描点；③连线．（2）观察图象，当x时，y随x的增大而增大；（3）根据图象，不等式|x|＜12x+32的解集为．【变式8-2】（2022春•确山县期末）画出函数y＝|x|﹣2的图象，利用图象回答下列问题：（1）写出函数图象上最低点的坐标，并求出函数y的最小值；（2）利用图象直接写出不等式|x|﹣2＞0的解集；（3）若直线y＝kx+b（k，b为常数，且k≠0）与y＝|x|﹣2的图象有两个交点A（m，1），B（12，−32），直接写出关于x的方程|x|﹣2＝kx+b的解．【变式8-3】（2022春•重庆期末）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数y＝|2x+4|+x+m性质及其应用的部分过程，请按要求完成下列各小题．（1）如表是部分x，y的对应值：x…﹣6﹣5﹣4﹣3﹣2﹣1012…y…0n﹣2﹣3﹣4﹣1258…根据表中的数据可以求得m＝，n＝；（2）请在给出的平面直角坐标系中，描出以如表中各组对应值为坐标的点，再根据描出的点画出该函数的图象；（3）结合你所画的函数图象，写出该函数的一条性质；（4）若一次函数y＝kx+b（k≠0）的图象经过点（﹣4，﹣2）和点（1，5），结合你所画的函数图象，直接写出不等式kx+b＜|2x+4|+x+m的解集．【题型9一次函数与一元一次不等式组的解集】【例9】（2022秋•青田县月考）如图，可以得出不等式组ax+b＜0cx+d＞0的解集是（）A．x＜﹣1B．﹣1＜x＜0C．﹣1＜x＜4D．x＞4【变式9-1】（2022春•南康区期末）如图，直线y＝﹣x+m与直线y=12x+3交点的横坐标为﹣2．则关于x的不x+m＞12x+3+3＞0的解集为．【变式9-2】（2022•富阳区二模）如图，直线y＝kx+b经过点A（﹣1，3），B（−52，0）两点，则不等式组0＜kx+b＜﹣3x的解集为．【变式9-3】（2022•青羊区校级自主招生）如图，直线y1＝ax+2与y2＝bx+4交于点N（1，a+2），将直线y1＝ax+2向下平移后得到y3＝ax﹣5，则能使得y3＜y2＜y1的x的所有整数值分别为（）A．1，2，3B．2，3C．2，3，4D．3，4，5【题型10一次函数与不等式组中的阴影区域问题】【例10】（2022•黄冈中学自主招生）如图，表示阴影区域的不等式组为（）A．2x+y≥53x+4y≥9B．2x+y≤53x+4y≤9C．2x+y≥53x+4y≥93x+4y≥9D．2x+y≤5【变式10-1】（2022秋•包河区期中）图中所示的阴影部分为哪一个不等式的解集（）A．x﹣y≤﹣5B．x+y≥﹣5C．x+y≤5D．x﹣y≤5【变式10-2】（2012春•南岸区期末）如图，用不等式表示阴影区域为（）A．x+y≤0，且x﹣y≥0B．x+y≥0，且x﹣y≥0C．x+y≥0，且x﹣y≤0D．x+y≤0，且x﹣y≤0【变式10-3】（2022春•广水市期末）阅读材料：在平面直角坐标系中，二元一次方程x ﹣y ＝0的一个解x =1y =1可以用一个点（1，1）表示，二元一次方程有无数个解，以方程x ﹣y ＝0的解为坐标的点的全体叫作方程x ﹣y ＝0的图象．一般地，在平面直角坐标系中，任何一个二元一次方程的图象都是一条直线，我们可以把方程x ﹣y ＝0的图象称为直线x ﹣y ＝0．直线x ﹣y ＝0把坐标平面分成直线上方区域，直线上，直线下方区域三部分，如果点M （x 0，y 0）的坐标满足不等式x ﹣y ≤0，那么点M （x 0，y 0）就在直线x ﹣y ＝0的上方区域内．特别地，x ＝k （k 常数）表示横坐标为k 的点的全体组成的一条直线，y ＝m （m 为常数）表示纵坐标为m 的点的全体组成的一条直线．请根据以上材料，探索完成以下问题：（1）已知点A （2，1）、B （83，32）、C （136，54）、D （4，92），其中在直线3x ﹣2y ＝4上的点有（只填字母）；请再写出直线3x ﹣2y ＝4上一个点的坐标；（2）已知点P （x ，y ）的坐标满足不等式组0≤x ≤40≤y ≤3则所有的点P 组成的图形的面积是；（3）已知点P （x ，y ）的坐标满足不等式组0≤x ≤10≤y ≤2x −y ≥0，请在平面直角坐标系中画出所有的点P 组成的图形（涂上阴影），并求出上述图形的面积．。

一次函数与方程、不等式的综合问题

一次函数与方程、不等式的综合问题二、方法剖析与提炼例1.如图，是一次函数123+-=x y 的图象，观察图象思考：当0=y 时，=x ，由此可知方程0123=+-x 的解为．【解答】（1）当0=y 时，=x ；（2）解为．【解析】（1）y=0即寻找在一次函数图象上纵坐标为0的点，它的横坐标为4，则=x 4；（2）0123=+-x 的解即一次函数123+-=x y 中当y =0时x 的值．【解法】解一元一次方程.【解释】一次函数图象与x 轴交点的横坐标即一次方程的解.例2．若直线42-=x y 与直线m x y +-=【解答】解得m 的取值范围是2>m ．【解析】（1）两条直线的交点的横纵坐标即为两直线解析式联立方程组的解；（2）利用交点在第一象限，横坐标、纵坐标都大于0列不等式组求解m 的取值范围．【解法】用方程思想求交点坐标，解不等式组【解释】需要学生理解求两直线的交点坐标的方法就是联立两直线的解析式组成方程组，方程组的解就是交点的横纵坐标.例3.（2020长沙）如图，直线l ：y =﹣x +1与x 轴，y 轴分别交于A ，B 两点，点P ，Q 是直线l 上的两个动点，且点P 在第二象限，点Q 在第四象限，∠POQ=135°．（1）求∆AOB 的周长；（2）设AQ=t>0试用含t 的代数式表示点P 的坐标．Oyx48124812函数与方程的关系直线的交点问题转化为求方程组的解GH【解答】（1）∴△AOB 周长为22+．（2）∴1PB t=在Rt △PBH 中，45PBO ∠=︒， ∴PH=、BH=；∴222(,)22t P t t+-．【解析】（1）求三角形的周长即求边长，在函数图象中一般可利用点的坐标求得线段的长；（2）求点的坐标可转化为求某些特殊线段的长．本题中可尝试过P 点作x 轴、y 轴的垂线,利用直角三角形求解．由题意可得，AQ 、OA 、OB 的长，联想到可利用△P BO ∽△OAQ 求出PB 的长．【解法】利用勾股定理、三角形相似求线段长.【解释】求点的坐标转化为求垂线段的长，利用相似三角形的对应边成比例求线段需要学生仔细观察几何图形和已知条件找到解决问题的方法.例4.（1）如图1，直线y kx b =+经过(21)A ，， (12)B --，两点，求不等式122x kx b >+>-的解集．（2）如图2，直线y 1=kx +b 过点A （0，2），且与直线y 2=mx 交于点P （1，m ），求不等式组mx >kx +b>mx －2的解集．利用线段长与点的坐标之间的关系求解图2yO AB图1【解答】（1）令121,22y x y ==-，则不等式122x kx b >+>-即为12y y y >>；在图中画出121,22y x y ==-的图象，观察得到不等式122x kx b >+>-的解集为12x -<<．（2）在图中画出32y mx =-的图象，∵3y 的图象是由2y 向下平移2个单位得到，∴P 是线段AB 的中点，∴点B 的横坐标为2；观察得到不等式mx >kx +b>mx －2的解集为12x <<．【解析】（1）先把不等式的问题转化成函数值的比较问题，从不等式组122x kx b >+>-得到三个函数121,,22y x y kx b y ==+=-；要比较函数值得大小先要找到函数值相等的情况，即求函数图象的交点，12y y y y 和，和的函数图象的交点分别为A 和B ；要得到12y y y >>观察图象得到是点A 、点B 之间的部分，所以不等式122x kx b >+>-的解集为12x -<<．（2）本题中3y 的图象没有给出，与1y 的交点也是未知，需要我们自己求得．3y 的图象是由2y 向下平移2个单位得到，OA=OC ，可得OP 是△ABC 的中位线，由P 是AB 的中点，求得点B 的横坐标为2；这样第2题的解答也可用类似第一题的办法解决．【解法】利用一次函数的图象求不等式的解.【解释】某些求不等式解的问题一般可把不等式的问题转化成函数值的比较问题，此类问题比较抽象。

培优专题(四) 一次函数与方程、不等式的实际应用问题

数学
人教版八年级下册
课件目录
首
页
末
页
2．某市出租车计费方法如图1所示，x(km)表示行驶里程，y(元)表示车费，请根据图象回答下列问题：
图1 (1)出租车的起步价是多少元？当x＞3时，求y关于x的函数解析式；
数学
人教版八年级下册
课件目录
首
页
末
页
(2)若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程．
数学
人教版八年级下册
课件目录首页末页
8．[2014· 番禺]某化妆品公司每月付给销售人员的工资有两种方案．方案一：没有底薪，只拿销售提成；方案二：底薪加销售提成．已知每件商品的销售提成方案二比方案一少7元．设销售人员月销售x件商品时的月工资为y元．如图4，l1表示方案一中y与x
函数关系的图象，l2表示方案二中y与x函数关系的图象．解答
(2)若某人计划在商场购买价格为5880元的电视机一台，请分析选哪种方案更省钱．解：(1)方案一：y＝0.95x；方案二：y＝0.9x＋300； (2)∵0.95×5880＝5586(元)，0.9×5880＋300＝5592(元)，∴选择方
案一更省钱．
数学
人教版八年级下册
课件目录首页末页
12
22
30
设按计划全部售出后的总利润为y百元，其中批发量为x吨，且加工销售量为15吨．
(1)求y与x之间的函数关系式；
(2)若零售量不超过批发量的4倍，求该生产基地按计划全部售完荸荠后获得的最大利润．
数学
人教版八年级下册
课件目录首页末页
解： (1)依题意可知零售量为 (25－ x)吨，则 y＝ 12x＋ 22(25－ x)＋ 30×15， ∴ y＝－ 10x＋ 1 000； (2)依题意有： x≥ 0， 25－ x≥0，解得：5≤x≤25， 25－ x≤4x， ∵－ 10＜ 0，∴ y 随 x 的增大而减小． ∴当 x＝ 5 时， y 有最大值，且 y 最大值＝ 950. ∴最大利润为 950 百元．

方程不等式与一次函数专题(实际应用)

方程、不等式与一次函数专题练习（实际应用）题型一：方程、不等式的直接应用典型例题1：（2009，株洲）初中毕业了，孔明同学准备利用暑假卖报纸赚取140～200元钱，买一份礼物送给父母．已知：在暑假期间，如果卖出的报纸不超过1000份，则每卖出一份报纸可得0.1元；如果卖出的报纸超过1000份，则超过部分．．．．每份可得0.2元．（1）请说明：孔明同学要达到目的，卖出报纸的份数必须超过1000份．（2）孔明同学要通过卖报纸赚取140～200元，请计算他卖出报纸的份数在哪个范围内．典型例题2：（2007，福州，10分）李晖到“宁泉牌”服装专卖店做社会调查．了解到商店为了激励营业员的工作积极性，实行“月总收入＝基本工资＋计件奖金”的方法，并获得如下信息：假设月销售件数为x 件，月总收入为y 元，销售1件奖励a 元，营业员月基本工资为b 元．（1）求a ，b 的值；（2）若营业员小俐某月总收入不低于1800元，则小俐当月至少要卖服装多少件？配套练习：3、(2009,益阳)开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1支钢笔和3本笔记本；小亮用31元买了同样的钢笔2支和笔记本5本.(1)求每支钢笔和每本笔记本的价格；(2)校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出.4、（2009，济南）自20XX 年爆发全球金融危机以来，部分企业受到了不同程度的影响，为落实“促民生、促经济”政策，济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案，调整后月工资由基本保障工资和计件奖励工资两部分组成（计件奖励工资=销售每件的奖励金额×销售的件数）．下表是甲、乙两位职工今年五月份的工资情况信息：（1）试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元？（2）若职工丙今年六月份的工资不低于2000元，那么丙该月至少应销售多少件产品？5、（2009，青岛）北京奥运会开幕前，某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．（1）该商场两次共购进这种运动服多少套？（2）如果这两批运动服每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？（利润率100%=⨯利润成本）题型二：方案设计典型例题6、（2009，深圳）迎接大运，美化深圳，园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A 、B 两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A 种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B 种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A 种造型的成本是800元，搭配一个B 种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？典型例题7：(2008、湖北咸宁)“５、１２”四川汶川大地震的灾情牵动全国人民的心，某市A 、B 两个蔬菜基地得知四川C 、D 两个灾民安置点分别急需蔬菜240吨和260吨的消息后，决定调运蔬菜支援灾区。

八上一次函数与方程组、不等式知识点+例题+练习 (非常好分类全面)

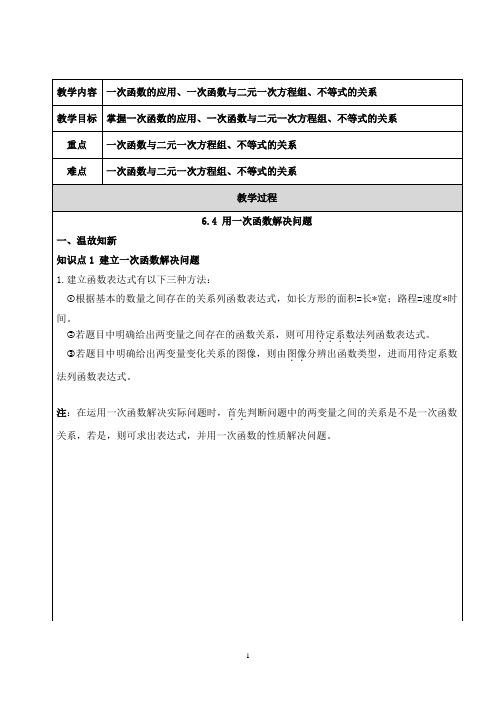
例1 从2014年起，中国的鞋号已“变脸”，新的国家标准要求鞋号用毫米数标注．据了解大多数市民还不了解此新标准，小明对新旧鞋号的标注变化进行了对比研究，发现新标准鞋子毫米数y与旧鞋号x之间存在着一次函数关系，并得到相关数据如下：旧鞋号 x 36 38 40新标准毫米数y230 240 250（1）请你帮助小明根据上述数据归纳出新标准毫米数与旧鞋号标注之间的换算关系式，并用一句简明的数学语言来表示；（2）如果小明的爸爸穿的一双42号凉鞋坏了，准备买一双同样尺寸的新凉鞋，那么应买一双多少毫米数的新凉鞋？例2 某种拖拉机的油箱可储油40L，加满油并开始工作后，•油箱中的余油量y（L）与工作时间x（h）之间为一次函数关系，如图所示．（1）求y与x的函数解析式．（2）一箱油可供拖位机工作几小时？知识点2 图像法解决实际问题注：读图时一定要明确横纵坐标表示的量所代表的意义。

例3 某公司推销一种产品，设x（件）是推销产品的数量，y（元）是推销费，如图表示了公司每月付给推销员推销费的两种方案，看图解答下列问题：（1）求yl 与y2的函数表达式；（2）解释图中表示的两种方案是如何付推销费的；（3）如果你是推销员，应如何选择付费方案．二、典型例题题型1 运用一次函数的关系解决生活中的实际问题例 1 如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：（1）求整齐摆放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数表达式；（2）若桌面上有12个饭碗，整齐叠放成一摞，求出它的高度；（3）若桌面上有若干个饭碗，整齐叠放成一摞，已测得它的高度为37.5cm，你能求出此时有多少个饭碗吗？题型2利用图表信息解决实际问题例2 某厂家生产两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产A种购物袋x个，每天共获利y元．(1)求y与x的函数关系式；(2)如果该厂每天最多投入成本10000元，那么每天最多获利多少元？题型3 建立一次函数模型解决实际问题例3 某下岗职工购进一批苹果到农贸市场零售，已知买出的苹果数量x（kg）与收入y（元）的关系如下表：在平面直角坐标系中描点，观察点的分布情况，探求收入y（元）与买出数量x（kg）之间的函数关系式。

专题4 一次函数与方程、不等式的关系-重难点题型(举一反三)(浙教版)(解析版)

专题5.4 一次函数与方程、不等式的关系-重难点题型【浙教版】【知识点1 一次函数与一元一次方程、不等式的关系】【例1】（2020秋•包河区期中）根据一次函数y＝kx+b的图象，直接写出下列问题的答案：（1）关于x的方程kx+b＝0的解；（2）代数式k+b的值；（3）关于x的方程kx+b＝﹣3的解．【解题思路】（1）利用函数图象写出函数值为0时对应的自变量的值即可；（2）利用函数图象写出x＝1时对应的函数值即可（3）利用函数图象写出函数值为﹣3时对应的自变量的值即可．【解答过程】解：（1）当x＝2时，y＝0，所以方程kx+b＝0的解为x＝2；（2）当x＝1时，y＝﹣1，所以代数式k+b的值为﹣1；（3）当x＝﹣1时，y＝﹣3，所以方程kx+b＝﹣3的解为x＝﹣1．【变式1-1】（2021秋•泰兴市校级期末）已知一次函数y＝kx+1与y=−12x+b的图象相交于点（2，5），求关于x的方程kx+b＝0的解．【解题思路】首先将（2，5）点代入一次函数解析式求出k，b的值，进而解方程得出答案．【解答过程】解：∵一次函数y＝kx+1与y=−12x+b的图象相交于点（2，5），∴5＝2k+1，5=−12×2+b，解得：k＝2，b＝6，则kx+b＝0为：2x+6＝0，解得：x＝﹣3．【变式1-2】一次函数y＝kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b＝4的解为多少？【解题思路】先求出函数的解析式，再把y＝4代入，即可求出x．【解答过程】解：把（0，1）和（2，3）代入y＝kx+b得：{b=12k+b=3，解得：k＝1，b＝1，即y＝x+1，当y＝4时，x+1＝4，解得：x＝3，∴方程kx+b＝4的解为x＝3．【变式1-3】已知一次函数y＝kx﹣6的图象如图（1）求k的值；（2）在图中的坐标系中画出一次函数y＝﹣3x+3的图象（要求：先列表，再描点，最后连线）；（3）根据图象写出关于x的方程kx﹣6＝﹣3x+3的解．【解题思路】（1）将点（4，0）代入y＝kx﹣6，利用待定系数求出k的值；（2）利用描点法画出一次函数y＝﹣3x+3的图象；（3）根据图象写出它们的交点坐标，即可得到关于x的方程kx﹣6＝﹣3x+3的解．【解答过程】解：（1）∵一次函数y＝kx﹣6的图象过点（4，0），∴4k﹣6＝0，∴k=3 2；（2）列表：描点：在平面直角坐标系中描出两点（0，3）、（1，0），连线：过点（0，3）、（1，0）画直线，得出一次函数y＝﹣3x+3的图象；（3）一次函数y＝kx﹣6与y＝﹣3x+3的图象交于点（2，﹣3），则关于x的方程kx﹣6＝﹣3x+3的解为x＝2．【题型2 一次函数的与一元一次不等式（数形结合）】【例2】（2021春•高明区期末）一次函数y1＝ax+b与y2＝cx+d的图象如图所示，下列说法：①对于函数y1＝ax+b来说，y随x的增大而增大；②函数y＝ax+d不经过第二象限；③不等式ax﹣d≥cx﹣b的解集是x≥4；④a﹣c=14（d﹣b），其中正确的是（）A．①②③B．①③④C．②③④D．①②④【解题思路】根据题意和函数图象中的数据，可以判断各个小题中的结论是否成立，从而可以解答本题．【解答过程】解：由图象可得，对于函数y＝ax+b来说，y随x的增大而增大，故①正确；a＞0，d＞0，则函数y＝ax+d经过第一、二、三象限，不经过第四象限，故②不正确；由ax﹣d≥cx﹣b可得ax+b≥cx+d，故不等式ax﹣d≥cx﹣b的解集是x≥4，故③正确；4a+b＝4c+d可以得到a﹣c=14（d﹣b），故④正确；故选：B．【变式2-1】（2021•安徽模拟）已知一次函数y1＝kx+3（k为常数，且k≠0）和y2＝x﹣3．当x＜2时，y1＞y2，则k的取值范围是（）A．﹣2≤k≤1且k≠0B．k≤﹣2C．k≥1D．﹣2＜k＜1且k≠0【解题思路】解不等式kx+3＞x﹣3，根据题意得出k﹣1＜0且−6k−1≥2且k≠0，解此不等式即可．【解答过程】解：∵一次函数y1＝kx+3（k为常数，且k≠0）和y2＝x﹣3，当x＜2时，y1＞y2，∴kx+3＞x﹣3，∴kx﹣x＞﹣6，∴k﹣1＜0且−6k−1≥2且k≠0，当k﹣1＜0时，−6k−1≥2时，k≥﹣2，所以不等式组的解集为﹣2≤k＜1且k≠0；当k＝1时，也成立，故k的取值范围是﹣2≤k≤1且k≠0，故选：A ．【变式2-2】（2021春•盐湖区校级期末）我们知道，若ab ＞0．则有{a ＞0b ＞0或{a ＜b ＜0．如图，直线y ＝kx +b 与y ＝mx +n 分别交x 轴于点A （﹣0.5，0）、B （2，0），则不等式（kx +b ）（mx +n ）＞0的解集是（）A ．x ＞2B ．﹣0.5＜x ＜2C ．0＜x ＜2D ．x ＜﹣0.5或x ＞2【解题思路】由若不等式（kx +b ）（mx +n ）＞0，则{kx +b ＞0mx +n ＞0或{kx +b ＜0mx +n ＜0，然后分类讨论，分别根据函数图象求得解集．【解答过程】解：∵若ab ＞0．则有{a ＞0b ＞0或{a ＜0b ＜0，∴若不等式（kx +b ）（mx +n ）＞0，则{kx +b ＞0mx +n ＞0或{kx+b ＜0mx +n ＜0．当{kx +b ＞0mx +n ＞0，由图得：{x ＜−0.5x ＞2，此时该不等式无解．当{kx +b ＜0mx +n ＜0，由图得：{x ＞−0.5x ＜2，此时不等式组的解集为﹣0.5＜x ＜2．综上：﹣0.5＜x ＜2．故选：B ．【变式2-3】（2021春•中山市期末）一次函数y 1＝ax +b 与y 2＝cx +d 的图象如图所示，下列说法：①对于函数y 1＝ax +b 来说，y 随x 的增大而减小；②函数y ＝ax +d 的图象不经过第一象限；③不等式ax +b ＞cx +d 的解集是x ＞3；④d ﹣b ＝3（a ﹣c ）．其中正确的有（）A ．①③B ．②③④C ．①②④D ．②③【解题思路】仔细观察图象：①根据函数图象直接得到结论；②观察函数图象可以直接得到答案；③以两条直线的交点为分界，哪个函数图象在上面，则哪个函数值大；④根据两直线交点可以得到答案．【解答过程】解：由图象可得：对于函数y 1＝ax +b 来说，y 随x 的增大而减小，故①说法正确；由于a ＜0，d ＜0，所以函数y 2＝ax +d 的图象经过第二，三，四象限，即不经过第一象限，故②说法正确，由图象可得当x ＜3时，一次函数y 1＝ax +b 图象在y 2＝cx +d 的图象上方，∴ax +b ＞cx +d 的解集是x ＜3，故③说法不正确；∵一次函数y 1＝ax +b 与y 2＝cx +d 的图象的交点的横坐标为3，∴3a +b ＝3c +d∴3a ﹣3c ＝d ﹣b ，∴d ﹣b ＝3（a ﹣c ）．故④说法正确，故选：C ．【题型3 一次函数的与一元一次不等式（取值范围）】【例3】（2021春•海淀区期末）在平面直角坐标系xOy 中，直线l ：y 1＝x +1与直线l 2：y 2＝2x ﹣2交于点A ．（1）求点A 的坐标；（2）当y 1＞y 2时，直接写出x 的取值范围；（3）已知直线l 3：y 3＝kx +1，当x ＜3时，对于x 的每一个值，都有y 3＞y 2，直接写出k 的取值范围．【解题思路】（1）由直线l ：y 1＝x +1与直线l 2：y 2＝2x ﹣2交于点A ，故可联立方程组：{y =x +1，y =2x −2．得{x =3y =4，故A （3，4）．（2）根据函数图象，可知：当y 1＞y 2时，x ＜3．（3）当x ＜3时，对于x 的每一个值，都有y 3＞y 2，故当x ＜3，y 3﹣y 2＞0恒成立，得1≤k ≤2．【解答过程】解：（1）由题意得：{y =x +1，y =2x −2．解得：{x =3，y =4．∴A （3，4）．（2）如图，当y 1＞y 2时，x ＜3．（3）当x ＜3，y 3＞y 2恒成立，则x ＜3，y 3﹣y 2＞0恒成立．∵y 3＝kx +1，y 2＝2x ﹣2，∴y 3﹣y 2＝（kx +1）﹣（2x ﹣2）＝（k ﹣2）x +3．∴若x ＜3，y 3﹣y 2＞0恒成立，则[（k ﹣2）x +3]min ＞0．当k ﹣2＝0，即k ＝2，[（k ﹣2）x +3]min ＝3＞0．当k ﹣2＞0，即k ＞2，[（k ﹣2）x +3]min 不存在．当k ﹣2＜0，即k ＜2，[（k ﹣2）x +3]min ＝3（k ﹣2）+3≥0，故k ≥1．综上：1≤k ≤2．【变式3-1】（2021春•茌平区期末）已知：如图一次函数y 1＝﹣x ﹣2与y 2＝x ﹣4的图象相交于点A ．（1）求点A 的坐标；（2）若一次函数y 1＝﹣x ﹣2与y 2＝x ﹣4的图象与x 轴分别相交于点B 、C ，求△ABC 的面积．（3）结合图象，直接写出y 1≥y 2时x 的取值范围．【解题思路】（1）将两个函数的解析式联立得到方程组{y =−x −2y =x −4，解此方程组即可求出点A 的坐标；（2）先根据函数解析式求得B 、C 两点的坐标，可得BC 的长，再利用三角形的面积公式可得结果；（3）根据函数图象以及点A 坐标即可求解．【解答过程】解：（1）解方程组{y =−x −2y =x −4，得{x =1y =−3，所以点A坐标为（1，﹣3）；（2）当y1＝0时，﹣x﹣2＝0，x＝﹣2，则B点坐标为（﹣2，0）；当y2＝0时，x﹣4＝0，x＝4，则C点坐标为（4，0）；∴BC＝4﹣（﹣2）＝6，∴△ABC的面积=12×6×3＝9；【变式3-2】（2021春•海珠区期末）已知一次函数y1＝ax+b的图象交x轴和y轴于点B和D；另一个一次函数y2＝bx+a的图象交x轴和y轴于点C和E，且两个函数的图象交于点A（1，4）（1）当a，b为何值时，y1和y2的图象重合；（2）当0＜a＜4，且在x＜1时，则y1＞y2成立．求b的取值范围；【解题思路】（1）把A（1，4）代入y1＝ax+b求得a+b＝4，得到b＝4﹣a，于是得到结论；（2）根据题意列不等式即可得到结论；【解答过程】解：（1）∵y1＝ax+b的图象过点A（1，4），∴a+b＝4，∴b＝4﹣a，∴y1＝ax+（4﹣a），y2＝（4﹣a）x+a，∵y1和y2的图象重合，∴a＝4﹣a，∴a＝2，b＝2；即当a＝2，b＝2时，y1和y2的图象重合；（2）∵a+b＝4，如图1，∴a＝4﹣b，∴y1＝（4﹣b）x+b，y2＝bx+（4﹣b），∵0＜a＜4，0＜4﹣b＜4且x＜1时，y1＞y2成立，∴由图象得4﹣b＜b，∴2＜b＜4；【变式3-3】（2020春•赣县区期末）如图，在平面直角坐标系xOy中，一次函数y＝kx+b的图象经过点A（﹣2，4），且与正比例函数y=−23x的图象交于点B（a，2）．（1）求a的值及一次函数y＝kx+b的解析式；（2）若一次函数y＝kx+b的图象与x轴交于点C，且正比例函数y=−23x的图象向下平移m（m＞0）个单位长度后经过点C，求m的值；（3）直接写出关于x 的不等式0＜−23x ＜kx +b 的解集．【解题思路】（1）先确定B 的坐标，然后根据待定系数法求解析式；（2）先求得C 的坐标，然后根据题意求得平移后的直线的解析式，把C 的坐标代入平移后的直线的解析式，即可求得M 的值；（3）找出直线y =−23x 落在y ＝kx +b 的下方且在x 轴上方的部分对应的x 的取值范围即可．【解答过程】解：（1）∵正比例函数y =−23x 的图象经过点B （a ，2），∴2=−23a ，解得，a ＝﹣3，∴B （﹣3，2），∵一次函数y ＝kx +b 的图象经过点A （﹣2，4），B （﹣3，2），∴{−2k +b =4−3k +b =2，解得{k =2b =8，∴一次函数y ＝kx +b 的解析式为y ＝2x +8；（2）∵一次函数y ＝2x +8的图象与x 轴交于点C ，∴C （﹣4，0），∵正比例函数y =−23x 的图象向下平移m （m ＞0）个单位长度后经过点C ，∴平移后的函数的解析式为y =−23x ﹣m ，∴0=−23×（﹣4）﹣m ，解得m =83；（3）∵一次函y ＝kx +b 与正比例函数y =−23x 的图象交于点B （﹣3，2），且一次函数y ＝2x +8的图象与x 轴交于点C （﹣4，0），∴关于x 的不等式0＜−23x ＜kx +b 的解集是﹣3＜x ＜0．【题型4 一次函数与一元一次不等式（面积问题）】【例4】（2021春•诸城市期末）如图，直线y＝kx+b分别与x轴、y轴交于点A（﹣2，0），B（0，3）；直线y＝1﹣mx分别与x轴交于点C，与直线AB交于点D，已知关于x的不等式kx+b＞1﹣mx的解集是x＞−4 5．（1）分别求出k，b，m的值；（2）求S△ACD．【解题思路】（1）首先利用待定系数法确定直线的解析式，然后根据关于x的不等式kx+b＞1﹣mx的解集是x＞−45得到点D的横坐标为−45，再将x=−45代入y=32x+3，得：y=95，将x=−45，y=95代入y＝1﹣mx求得m＝1即可；（2）先确定直线与x轴的交点坐标，然后利用三角形的面积公式计算即可．【解答过程】解：（1）∵直线y＝kx+b分别与x轴、y轴交于点A（﹣2，0），B（0，3），{−2k+b=0b=3，解得：k=32，b＝3，∵关于x的不等式kx+b＞1﹣mx的解集是x＞−4 5，∴点D的横坐标为−4 5，将x=−45代入y=32x+3，得：y=95，∴D（−45，95），将x=−45，y=95代入y＝1﹣mx，解得：m＝1；（2）如图，过点D作DH⊥AC于H，则DH=9 5对于y ＝1﹣x ，令y ＝0，得：x ＝1，∴点C 的坐标为（1，0），∴S △ACD =12•AC •DH =12×[1﹣（﹣2）]×95=2710．【变式4-1】（2021春•东辽县期末）已知直线y ＝kx +5交x 轴于A ，交y 轴于B 且A 坐标为（5，0），直线y ＝2x ﹣4与x 轴于D ，与直线AB 相交于点C ．（1）求点C 的坐标；（2）根据图象，写出关于x 的不等式2x ﹣4＞kx +5的解集；（3）求△ADC 的面积．【解题思路】（1）根据点A 的坐标利用待定系数法可求出直线AB 的解析式，联立直线AB 、CD 的解析式成方程组，通过解方程组即可求出点C 的坐标；（2）根据直线AB 、CD 的上下位置关系结合点C 的坐标，即可得出不等式2x ﹣4＞kx +5的解集；（3）利用一次函数图象上点的坐标特征可求出点D 的坐标，再根据三角形的面积公式即可求出△ADC 的面积．【解答过程】解：（1）∵直线y ＝kx +5经过点A （5，0），∴5k +5＝0，解得：k ＝﹣1，∴直线AB 的解析式为y ＝﹣x +5．联立直线AB 、CD 的解析式成方程组，{y =−x +5y =2x −4，解得：{x =3y =2，∴点C 的坐标为（3，2）．（2）观察函数图象可知：当x ＞3时，直线y ＝2x ﹣4在直线y ＝﹣x +5的上方， ∴不等式2x ﹣4＞kx +5的解集为x ＞3．（3）当y ＝2x ﹣4＝0时，x ＝2，∴点D 的坐标为（2，0），∴S △ACD =12（x A ﹣x D ）•y C =12×（5﹣2）×2＝3．【变式4-2】（2020春•宁化县校级月考）如图，直线l1：y＝2x与直线l2：y＝kx+3在同一平面直角坐标系内交于点P（a，2）．（1）求出不等式2x≤kx+3的解集；（2）求出△OAP的面积．【解题思路】（1）利用一次函数图象上点的坐标特征先求出a的值，然后观察函数图象，写出直线y＝kx+3在直线y＝2x上方所对应的自变量的取值范围即可；（2）先求出直线l2的解析式，再求出A点坐标，然后利用三角形面积公式求解．【解答过程】解：（1）把P（a，2）代入y＝2x得2a＝2，解得a＝1，则P（1，2），当x≤1时，2x≤kx+3，所以不等式2x≤kx+3的解集为x≤1；（2）把P（1，2）代入y＝kx+3得k+3＝2，解得k＝﹣1，所以直线l2的解析式为y＝﹣x+3，当y＝0时，﹣x+3＝0，解得x＝3，则A（3，0），所以△OAP的面积=12×2×3＝3．【变式4-3】已知一次函数y1＝﹣2x﹣3与y2=12x+2．（1）在同一平面直角坐标系中，画出这两个函数的图象；（2）根据图象，不等式﹣2x﹣3＞12x+2的解集为x＜﹣2；（3）求两图象和y轴围成的三角形的面积．【解题思路】（1）先求出直线y1＝﹣2x﹣3，y2=12x+2与x轴和y轴的交点，再画出两函数图象即可；（2）直线y1＝﹣2x﹣3的图象落在直线y2=12x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3＞12x+2的解集；（3）根据三角形的面积公式求解即可．【解答过程】解：（1）函数y1＝﹣2x﹣3与x轴和y轴的交点分别是（﹣1.5，0）和（0，﹣3），y2=12x+2与x轴和y轴的交点分别是（﹣4，0）和（0，2），其图象如图：（2）观察图象可知，函数y1＝﹣2x﹣3与y2=12x+2交于点（﹣2，1），当x＜﹣2时，直线y1＝﹣2x﹣3的图象落在直线y2=12x+2的上方，即﹣2x﹣3＞12x+2，所以不等式﹣2x﹣3＞12x+2的解集为x＜﹣2；故答案为x＜﹣2；（3）∵y1＝﹣2x﹣3与y2=12x+2与y轴分别交于点A（0，﹣3），B（0，2），∴AB＝5，∵y1＝﹣2x﹣3与y2=12x+2交于点C（﹣2，1），∴△ABC的边AB上的高为2，∴S△ABC=12×5×2＝5．【题型5 一次函数的与一元一次不等式（求点的坐标）】【例5】如图，直线y＝kx+b与坐标轴相交于点M（3，0），N（0，4），且MN=5.（1）求直线MN的解析式；（2）根据图象，写出不等式kx+b≥0的解集；（3）若点P 在x 轴上，且点P 到直线y ＝kx +b 的距离为125，直接写出符合条件的点P的坐标．【解题思路】（1）把点M 、N 的坐标分别代入一次函数解析式，列出关于系数k 、b 的方程组，通过解方程组求得它们的值；（2）直线y ＝kx +b 在x 轴及其上方的部分对应的x 的取值范围即为所求；（3）作△OMN 的高OA ．根据三角形的面积公式求出OA =OM⋅ON MN =3×45=125，则点P 的坐标是（0，0）；在x 轴上作O 关于M 的对称点为（6，0），易得（6，0）到直线y ＝kx +b 的距离也为125．【解答过程】解：（1）∵直线y ＝kx +b 与坐标轴相交于点M （3，0），N （0，4），所以{3k +b =0b =4，解得：{k =−43b =4， ∴直线MN 的解析式为：y =−43x +4；（2）根据图形可知，当x ≤3时，y ＝kx +b 在x 轴及其上方，即kx +b ≥0，则不等式kx +b ≥0的解集为x ≤3；（3）如图，作△OMN 的高OA ．∵S △OMN =12MN •OA =12OM •ON ，∴OA =OM⋅ON MN =3×45=125，∴点P 的坐标是（0，0）；在x 轴上作O 关于M 的对称点为（6，0），易得（6，0）到直线y ＝kx +b 的距离也为125，所以点P 的坐标是（0，0）或（6，0）．【变式5-1】（2021春•顺德区期末）一次函数y 1＝kx +b 和y 2＝﹣4x +a 的图象如图所示，且A （0，4），C （﹣2，0）．（1）由图可知，不等式kx +b ＞0的解集是 x ＞﹣2 ；（2）若不等式kx +b ＞﹣4x +a 的解集是x ＞1．①求点B 的坐标；②求a 的值．【解题思路】（1）根据函数图象和题意可以直接写出不等式kx +b ＞0的解集；（2）①由题意可以求得k 、b 的值，然后将x ＝1代入y 1＝kx +b 即可求得点B 的坐标； ②根据点B 也在函数y 2＝﹣4x +a 的图象上，从而可以求得a 的值．【解答过程】解：（1）∵A （0，4），C （﹣2，0）在一次函数y 1＝kx +b 上，∴不等式kx +b ＞0的解集是x ＞﹣2，故答案为：x ＞﹣2；（2）①∵A （0，4），C （﹣2，0）在一次函数y 1＝kx +b 上，∴{b =4−2k +b =0，得{k =2b =4，∴一次函数y 1＝2x +4，∵不等式kx +b ＞﹣4x +a 的解集是x ＞1，∴点B 的横坐标是x ＝1，当x ＝1时，y 1＝2×1+4＝6，∴点B 的坐标为（1，6）；②∵点B （1，6），∴6＝﹣4×1+a ，得a ＝10，即a 的值是10．【变式5-2】（2020秋•南京期末）已知直线y ＝kx +b 经过点A （5，0），B （1，4）．（1）求直线AB 的函数关系式；（2）若直线y ＝2x ﹣4与直线AB 相交于点C ，求点C 的坐标；（3）根据图象，直接写出当x 在什么范围内，不等式2x ﹣4＞kx +b ．【解题思路】（1）利用待定系数法即可求得函数的解析式；（2）解两个函数解析式组成方程组即可求解；（3）关于x 的不等2x ﹣4＞kx +b 的解集就是函数y ＝kx +b 的图象在下边的部分自变量的取值范围．【解答过程】解：（1）根据题意得{5k +b =0k +b =4，解得{k =−1b =5，则直线AB 的解析式是y ＝﹣x +5；（2）根据题意得{y =−x +5y =2x −4，解得：{x =3y =2，则C 的坐标是（3，2）；（3）根据图象可得不等式的解集是x ＞3．【变式5-3】在平面直角坐标系中，直线y ＝﹣2x +1与y 轴交于点C ，直线y ＝x +k （k ≠0）与y 轴交于点A ，与直线y ＝﹣2x +1交于点B ，设点B 的横坐标为﹣2．（1）求点B 的坐标及k 的值；（2）求直线y ＝﹣2x +1、直线y ＝x +k 与y 轴所围成的△ABC 的面积；（3）根据图象直接写出不等式﹣2x +1＞x +k 的解集．【解题思路】（1）对于y ＝﹣2x +1，计算自变量为﹣2时的函数值可得到B 点坐标，然后把B 点坐标代入y ＝x +k 可得到k 的值；（2）先确定两直线与y 轴的交点A 、C 的坐标，然后利用三角形面积公式求解；（3）观察函数图象，写出直线y ＝﹣2x +1在直线y ＝x +k 上方所对应的自变量的范围即可．【解答过程】解：（1）当x ＝﹣2时，y ＝﹣2×（﹣2）+1＝5，则B （﹣2，5）．把B （﹣2，5）代入y ＝x +k 得﹣2+k ＝5，解得k ＝7；（2）当x ＝0时，y ＝﹣2x +1＝1，则C （0，1）；当x ＝0时，y ＝x +7＝7，则A （0，7）所以AC ＝7﹣1＝6，所以S △ABC =12×6×2＝6；（3）x ＜﹣2．【例6】（2021•济南二模）中国古代数学专著《九章算术》“方程”一章记载用算筹（方阵）表示二元一次方程组的方法，发展到现代就是用矩阵式(a 1b 1a 2b 2)(x y )=(c 1c 2)来表示二元一次方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2，而该方程组的解就是对应两直线（不平行）a 1x +b 1y ＝c 1与a 2x +b 2y ＝c 2的交点坐标P （x ，y ）．据此，则矩阵式(4−1−31)(x y )=(3−1)所对应两直线交点坐标是（2，5）．【解题思路】根据题意得出方程组，求出方程组的解，再得出答案即可．【解答过程】解：根据题意得：{4x −y =3①−3x +y =−1②，①+②，得x ＝2，把x ＝2代入①，得8﹣y ＝3，解得：y ＝5，所以方程组的解为{x =2y =5，∴两直线交点坐标是（2，5），故答案为：（2，5）．【变式6-1】如图，直线y ＝﹣2x +6与直线y ＝mx +n 相交于点M （p ，4）．（1）求p 的值；（2）直接写出关于x ，y 的二元一次方程组{y =−2x +6y =mx +n 的解；（3）判断直线y ＝3nx +m ﹣2n 是否也过点M ？并说明理由．【解题思路】（1）根据直线y ＝﹣2x +6经过点M ，即可求出p ．（2）由图象可知交点的坐标就是方程组的解．（3）先求出m +n ＝4，用代入法可以解决．【解答过程】解：（1）∵直线y ＝﹣2x +6经过点M （p ，4），∴4＝﹣2p +6，∴p ＝1．（2）由图象可知方程组的解为{x =1y =4，（3）结论：直线y ＝3nx +m ﹣2n 经过点M ，理由如下：∵点M （1，4）在直线y ＝mx +n 上，∴m +n ＝4，∴当x ＝1，时，y ＝3nx +m ﹣2n ＝m +n ＝4，∴直线y ＝3nx +m ﹣2n 经过点M ．【变式6-2】（2021秋•文成县期末）如图，l 1，l 2分别表示两个一次函数的图象，它们相交于点P ，（1）求出两条直线的函数关系式；（2）点P 的坐标可看作是哪个二元一次方程组的解；（3）求出图中△APB 的面积．【解题思路】（1）由图可得两函数与坐标轴的交点坐标，用待定系数法可求出它们的函数解析式；（2）联立两个一次函数的解析式，所得方程组的解即为P 点坐标．（3）△ABP 中，以AB 为底，P 点横坐标的绝对值为高，可求出△ABP 的面积．【解答过程】解：（1）设直线l 1的解析式是y ＝kx +b ，已知l 1经过点（0，3），（1，0），可得：{b =3k +b =0，解得{b =3k =−3，则函数的解析式是y ＝﹣3x +3；同理可得l 2的解析式是：y ＝x ﹣2．（2）点P 的坐标可看作是二元一次方程组{y =−3x +3y =x −2的解．（3）易知：A （0，3），B （0，﹣2），P （54，−34）；∴S △APB =12AB •|x P |=12×5×54=258．【变式6-3】（2020秋•西安期末）学校准备五一组织老师去隆中参加诸葛亮文化节，现有甲、乙两家旅行社表示对老师优惠，设参加文化节的老师有x 人，甲、乙两家旅行社实际收费为y 1、y 2，且它们的函数图象如图所示，根据图象信息，请你回答下列问题：（1）当参加老师的人数为多少时，两家旅行社收费相同？（2）当参加老师的人数为多少人时，选择甲旅行社合算？（3）如果全共有50人参加时，选择哪家旅行社合算？【解题思路】（1）当两函数图象相交时，两家旅行社收费相同，由图象即可得出答案．（2）由图象比较收费y 1、y 2，即可得出答案．（3）当有50人时，比较收费y1、y2，即可得出答案．【解答过程】解：（1）当两函数图象相交时，两家旅行社收费相同，由图象知为30人；（2）由图象知：当有30人以下时，y1＜y2，所以选择甲旅行社合算；（3）由图象知：当有50人参加时，y1＞y2，所以选择乙旅行社合算；。

8.一次函数与方程不等式培优练习.doc

8. 一次函数与方程、不等式培优练习姓名一.选择题01．已知一次函数y＝32x＋m，和y＝12-x＋n的图象交点A(－2，0)，且与y轴分别交于B、C两点，那么△ABC的面积是( ) A．2 B．3 C．4 D．602．已知关于x的不等式ax＋1＞0(a≠0)的解集是x＜1，则直线y＝ax＋1与x轴的交点是( )A．(0，1) B．(－1，0) C．(0，－1) D．(1，0)第3题图第6题图第7题图第2-9题图第2-10题图03．如图，直线y＝kx＋b与x轴交于点A(－4，0)，则y＞0时，x的取值范围是( ) A．x＞－4 B．x＞0 C．x＜－4 D．x＜004．直线kx－3y＝8，2x＋5y＝－4交点的纵坐标为0，则k的值为( )A．4 B．－4 C．2 D．－205．直线y＝kx＋b与坐标轴的两个交点分别为A(2，0)和B(0，－3)．则不等式kx＋b＋3≥0的解集为( ) A．x≥0B．x≤0C．x≥2D．x≤206．如图是在同一坐标系内作出的一次函数y1、y2的图象l1、l2，设y1＝k1x＋b1，y2＝k2x＋b2，则方程组111222y k x by k x b⎧⎨⎩＝＋，＝＋的解是( ) A．22xy=-⎧⎨=⎩B．23xy=-⎧⎨=⎩C．33xy=-⎧⎨=⎩D．34xy=-⎧⎨=⎩07．(浙江金华)一次函数y1＝kx＋b与y2＝x＋a的图象如图，则下列结论：①k＜0；②a＞0；③当x＜3时，y1＜y2中，正确的个数是( )A．0 B．1 C．2 D．308．如果直线y＝kx＋3与y＝3x－2b的交点在x轴上，当k＝2时，b等于( )A．9 B．－3 C．32-D．94-09．若直线122y x=-与直线14y x a=-+相较于x轴上一点，则直线14y x a=-+不经过( ) A．第四象限B．第三象限C．第二象限D．第一象限二.填空题01．若直线y＝ax＋7经过一次函数y＝4－3x和y＝2x－1的交点，则a＝_________．02．一次函数y＝2x＋a与y＝－x＋b的图象都过A(－2，0)，且与y轴分别交于B、C点，则S△ABC=_ _．03．已知直线y＝2x＋b和y＝3bx－4相交于点(5，a)，则a＝___________．04．已知函数y＝－x＋m与y＝mx－4的图象交点在x轴的负半轴上，则m的值为__________．05．直线y＝－2x－1与直线y＝3x＋m相交于第三象限内一点，则m的取值范围是___________．06．若直线122ay x=-+与直线31544y x=-+的交点在第一象限，且a为整数，则a＝_________．07．两条直线y1＝ax＋b，y2＝cx＋5，学生甲解出它们的交点坐标为(3，－2)，学生乙因抄错了c而解出它们的交点坐标为(34，14)，则这两条直线的解析式为____________．08．若直线l1：y＝x－2与直线l2：y＝3－mx在同一坐标系的交点在第一象限，则m的取值范围．09．如图，已知一次函数y ＝2x ＋b 和y ＝ax －3的图象交于点P(－2，－5)，则根据图象可得不等式2x ＋b ＞ax －3的解集是________．10．(武汉)如图，直线y ＝kx ＋b 经过A(2，1)，B(－1，－2)两点，则不等式12x ＞kx ＋b ＞－2的解集为_______．三.解答题01．直线l 1经过点(2，3)和(－1，－3)，直线l 2与l 1交于点(－2，a)，且与y 轴的交点的纵坐标为7．⑴求直线l 2、l 1的解析式；⑵求l 2、l 1与x 轴围成的三角形的面积；⑶x 取何值时l 1的函数值大于l 2的函数值？02．如图，直线l 1的解析式为y ＝－3x ＋3，l 1与x 轴交于点D ，直线l 2经过点A(4，0)，B(3，32)．⑴求直线l 2的解析式；⑵求S △ADC ；⑶在直线l 2上存在异于点C 的另一点P ，使得S △ADP ＝S △ADC ，求P 点坐标．l 203．某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，那么服药后2h 时血液中含药量最高，达每毫升6μg(1μg＝10－3mg)，接着就逐步衰减，10h 后血液中含药量为每毫升3μg，每毫升血液中含药量y(μg)随时间x(h)的变化如图所示，当成人按规定剂量服药后，⑴分别求x≤2和x≥2 时，y 与x 之间的函数关系式；⑵如果每毫升血液中含药量在4μg 或4μg 以上时，治疗疾病才是有效的，那么这个有效时间是多长？04.已知x 、y 、z 都为非负数，满足x ＋y －z ＝1，x ＋2y ＋3z ＝4，记ω＝3x ＋2y ＋z ．求ω的最大值与最小值．05．已知一次函数y＝ax＋b与y＝bx＋a的图象相交于A(m，4)，且这两个函数的图象分别与y轴交于B、C两点(B上C下)，△ABC的面积为1，求这两个一次函数的解析式．06．如图，直线OC、BC的函数关系式为y＝x与y＝－2x＋6．点P(t，0)是线段OB上一动点，过P作直线l与x轴垂直．⑴求点C坐标；⑵设△BOC中位于直线l左侧部分面积为S，求S与t之间的函数关系式；⑶当t为何值时，直线l平分△COB面积．07．某服装厂现有A种布料35m，B种布料26m，现计划用这两种布料生产男、女两款式的时装共40套．已知做一套男时装需要A种布料0.6m、B种布料0.9m，可获利90元；做一套女时装需要A种布料1.lm，B 种布料0.4m，可获利100元，若设生产男时装套数为x套，用这批布料生产这两种时装所获得总利润为y 元．⑴求y与x的函数关系式，并求出x的取值范围；⑵该服装厂生产这批服装中，当生产男时装多少套时，所获得利润最大？最大利润是多少元？08．一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机软⑴用含x，y 的式子表示购进C型手机的部数；⑵求出y与x之间的函数关系式；⑶假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元．①求预估利润P（元）与x（部）的函数关系式；（注：预估利润P＝预售总额一购机款一各种费用）②求预估利润的最大值，并写出此时购进三款手机各多少部．08.已知直线l1经过点(2，5)和(－1，－1)两点，与x轴的交点是点A，将直线y＝－6x＋5的图象向上平移4个单位后得到l2，l2与l1的交点是点C，l2与x轴的交点是点B，求△ABC的面积．yxOCBAl2l109．（江苏无锡）某企业在生产甲、乙两种节能产品时需用A、B两种原料，生产每吨节能产品所需原料的数量如下表所示：销售甲、乙两种产品的利润m（万元）与销售量n（吨）之间的函数关系如图所示．已知该企业生产了甲种产品x吨和乙种产品y吨，共用去A原料200吨．⑴.写出x与y满足的关系式；⑵.为保证生产的这批甲种、乙种产品售后的总利润不少于220万元，那么至少要用B原料多少吨？10.（自贡）抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食全部转移到具有较强抗震能力的A、B两个仓库．已知甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨，从甲、乙两库到A、B两库的路程和运费如下表（表中“元/吨·千米”表示每吨粮食运送1千米所需人民币）路程（千米）运费（元/吨·千米）甲库乙库甲库乙库A库20 15 12 12B库25 20 10 8⑴若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；⑵当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？。

专题训练4：一次函数与方程、不等式的实际应用

小专题(十四) 一次函数与方程、不等式的实际应用一、利用两个函数的比较列不等式求值或多个函数的比较画函数图象比较求值1．“五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．根据以上信息，解答下列问题：(1)设租车时间为x小时，租用甲公司的车所需费用为y1(元)，租用乙公司的车所需费用为y2(元)，分别求出y1，y2关于x的函数解析式；(2)请你帮助小明计算并选择哪个出游方案合算．2、德州)下表中给出A，B，C三种手机通话的收费方式.收费方式月通话费/元包时通话时间/h超时费/(元/min)A 30 25 0.1B 50 50 0.1C 100 不限时(1)123函数解析式；(2)填空：若选择方式A最省钱，则月通话时间x的取值范围为_____________；若选择方式B最省钱，则月通话时间x的取值范围为_______________________；若选择方式C最省钱，则月通话时间x的取值范围为______________________________；(3)小王、小张今年5月份通话费均为80元，但小王比小张通话时间长，求小王该月的通话时间．3、某社区活动中心为鼓励居民加强体育锻炼，准备购买10副某种品牌的羽毛球拍，每副球拍配x （x≥2）个羽毛球，供社区居民免费借用.该社区附近A 、B 两家超市都有这种品牌的羽毛球拍和羽毛球出售，且每副球拍的标价均为30元，每个羽毛球的标价为3元，目前两家超市同时在做促销活动： A 超市：所有商品均打九折（按标价的90％）销售；B 超市：买一副羽毛球拍送2个羽毛球.设在A 超市购买羽毛球拍和羽毛球的费用为y A （元），在B 超市购买羽毛球拍和羽毛球的费用为y B （元）.请解答下列问题：（1）分别写出y A 和y B 与x 之间的关系式；（2）若该活动中心只在一家超市购买，你认为在哪家超市购买更划算？（3）若每副球拍配15个羽毛球，请你帮助该活动中心设计出最省钱的购买方案.4、某商家到梧州市一茶厂购买茶叶,购买茶叶数量为x 千克(x>0)，总费用为y 元，现有两种购买方式。

一次函数的性质与应用问题

2023中考数学重难题型押题培优导练案（北京专用）专题11一次函数的性质与应用问题（北京真题5道+模拟30道）【方法归纳】题型概述，方法小结，有的放矢考点考查年份考查频率一次函数的性质与应用问题（大题）2016.2019.2020.2021.2022 5年4考1.一次函数综合题（1）一次函数与方程、不等式之间的关系：利用待定系数法确定一次函数的解析式，一次函数与x轴和y轴交点、不等式的解集、一次函数的平移、参数的确定等、（2）一次函数与几何图形的面积问题:首先要根据题意画出草图，结合图形分析其中的几何图形，再求出面积．（3）一次函数的优化问题:通常一次函数的最值问题首先由不等式找到x的取值范围，进而利用一次函数的增减性在前面范围内的前提下求出最值．（4）用函数图象解决实际问题:从已知函数图象中获取信息，求出函数值、函数表达式，并解答相应的问题．2.一次函数的应用（1）分段函数问题：分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符合实际．（2）函数的多变量问题：解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数．（3）常见题型：行程问题、表格问题、图象问题、最大利润问题、方案问题常用的解题思路：①建立函数模型的方法；②分段函数思想的应用．【典例剖析】典例精讲，方法提炼，精准提分【例1】（2022·北京·中考真题）在平面直角坐标系xOy中，函数y=kx+b(k≠0)的图象经过点(4,3)，(−2,0)，且与y轴交于点A．(1)求该函数的解析式及点A的坐标；(2)当x>0时，对于x的每一个值，函数y=x+n的值大于函数y=kx+b(k≠0)的值，直接写出n的取值范围．【答案】(1)y =12x +1，(0,1)(2)n ≥1【解析】【分析】（1）利用待定系数法即可求得函数解析式，当x =0时，求出y 即可求解．（2）根据题意x +n >12x +1结合x >0解出不等式即可求解．(1)解：将(4,3)，(−2,0)代入函数解析式得，3=4k +b 0=−2k +b ，解得k =12b =1，∴函数的解析式为：y =12x +1，当x =0时，得y =1，∴点A 的坐标为(0,1)．(2)由题意得，x +n >12x +1，即x >2−2n ，又由x >0，得2−2n ≤0，解得n ≥1，∴n 的取值范围为n ≥1．【点睛】本题考查了待定系数法求函数解析式及解不等式，熟练掌握待定系数法求函数解析式及函数的性质是解题的关系．【例2】（2021·北京·中考真题）在平面直角坐标系xOy 中，一次函数y =kx +b(k ≠0)的图象由函数y =12x 的图象向下平移1个单位长度得到．（1）求这个一次函数的解析式；（2）当x >−2时，对于x 的每一个值，函数y =mx(m ≠0)的值大于一次函数y =kx +b 的值，直接写出m 的取值范围．【答案】（1）y =12x−1；（2）12≤m ≤1【解析】【分析】（1）由图象的平移及题意可直接求得一次函数的解析式；（2）由题意可先假设函数y =mx (m ≠0)与一次函数y =kx +b 的交点横坐标为−2，则由（1）可得：m =1，然后结合函数图象可进行求解．【详解】解：（1）由一次函数y =kx +b (k ≠0)的图象由函数y =12x 的图象向下平移1个单位长度得到可得：一次函数的解析式为y =12x−1；（2）由题意可先假设函数y =mx (m ≠0)与一次函数y =kx +b 的交点横坐标为−2，则由（1）可得：−2m =12×(−2)−1，解得：m =1，函数图象如图所示：∴当x >−2时，对于x 的每一个值，函数y =mx (m ≠0)的值大于一次函数y =kx +b 的值时，根据一次函数的k 表示直线的倾斜程度可得当m =12时，符合题意，当m <12时，则函数y =mx (m ≠0)与一次函数y =kx +b 的交点在第一象限，此时就不符合题意，综上所述：12≤m ≤1．【点睛】本题主要考查一次函数的图象与性质，熟练掌握一次函数的图象与性质是解题的关键．【真题再现】必刷真题，关注素养，把握核心1．（2016·北京·中考真题）如图，在平面直角坐标系xOy中，过点A(−6,0)的直线l1与直线l2:y=2x相交于点B(m,4)．（1）求直线l1的表达式；（2）过动点P(n,0)且垂直于x轴的直线与l1，l2的交点分别为C，D，当点C位于点D上方时，写出n的取值范围．【答案】（1）y=12x+3；（2）n<2【解析】【分析】（1）先求出点B坐标，再利用待定系数法即可解决问题．（2）由图象可知直线l1在直线l2上方即可，由此即可写出n的范围．【详解】解：（1）∵点B在直线l2上，∴4=2m，∴m=2，点B(2,4)设直线l1的表达式为y=kx+b，由题意2k+b=4−6k+b=0，解得k=12b=3，∴直线l1的表达式为y=12x+3．（2）由图象可知n<2．【点睛】本题考查两条直线平行、相交问题，解题的关键是灵活应用待定系数法，学会利用图象根据条件确定自变量取值范围．2．（2019·北京·中考真题）在平面直角坐标系xOy中，直线l：y=kx+1(k≠0)与直线x=k，直线y=−k 分别交于点A，B，直线x=k与直线y=−k交于点C．（1）求直线l与y轴的交点坐标；（2）横、纵坐标都是整数的点叫做整点．记线段AB，BC，CA围成的区域（不含边界）为W．①当k=2时，结合函数图象，求区域W内的整点个数；②若区域W内没有整点，直接写出k的取值范围．【答案】（1）直线l与y轴交点坐标为（0,1）；（2）①整点有（0，-1），（0,0），（1，-1），（1,0），（1,1），（1,2）共6个点，②-1≤k＜0或k=-2.【解析】【分析】（1）令x=0，y=1，直线l与y轴的交点坐标（0，1）；（2）①当k=2时，A（2，5），B−3,−2，C（2，-2），在W区域内有6个整数点；②当x=k+1时，2y=-k+1，则有k2+2k=0，k=-2，当0＞k≥-1时，W内没有整数点；【详解】解：（1）令x=0，y=1，∴直线l与y轴的交点坐标（0，1）；（2）由题意，A（k，k2+1），,−k，C（k，-k），①当k=2时，A（2，5），B−3,−2，C（2，-2），2在W区域内有6个整数点：（0，0），（0，-1），（1，0），（1，-1），（1，1），（1，2）；②直线AB的解析式为y=kx+1，当x=k+1时，y=-k+1，则有k2+2k=0，∴k=-2，当0＞k≥-1时，W内没有整数点，∴当0＞k≥-1或k=-2时W内没有整数点；【点睛】本题考查一次函数图象上点的特征；能够数形结合解题，根据k变化分析W区域内整数点的情况是解题的关键．3.（2020·北京·中考真题）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到，且经过点(1，2)．（1）求这个一次函数的解析式；（2）当x>1时，对于x的每一个值，函数y=mx(m≠0)的值大于一次函数y=kx+b的值，直接写出m的取值范围．【答案】（1）y=x+1；（2）m≥2【解析】【分析】（1）根据一次函数y=kx+b(k≠0)由y=x平移得到可得出k值，然后将点（1，2）代入y=x+b可得b 值即可求出解析式；（2）由题意可得临界值为当x=1时，两条直线都过点（1，2），即可得出当x>1，m>2时，y=mx(m≠0)都大于y=x+1，根据x>1，可得m可取值2，可得出m的取值范围．【详解】（1）∵一次函数y=kx+b(k≠0)由y=x平移得到，∴k=1，将点（1，2）代入y=x+b可得b=1，∴一次函数的解析式为y=x+1；（2）当x>1时，函数y=mx(m≠0)的函数值都大于y=x+1，即图象在y=x+1上方，由下图可知：临界值为当x=1时，两条直线都过点（1，2），∴当x>1，m>2时，y=mx(m≠0)都大于y=x+1，又∵x>1，∴m可取值2，即m=2，∴m的取值范围为m≥2．【点睛】本题考查了求一次函数解析式，函数图像的平移，一次函数的图像，找出临界点是解题关键．【模拟精练】押题必刷，巅峰冲刺，提分培优一、解答题1．（2022·北京房山·二模）已知，在平面直角坐标系xOy中，直线l:y=ax+b(a≠0)经过点A（1，2），与x 轴交于点B（3，0）．(1)求该直线的解析式；(2)过动点P(0，n)且垂直于y轴的直线与直线l交于点C，若PC≥AB，直接写出n的取值范围．【答案】(1)y=−x+3(2)n≤n≥3+【解析】【分析】（1）直接利用待定系数法求解析式；（2）根据P点的坐标，表示出C的坐标，表示出PC的长度，根据PC≥AB 列出不等式即可解出n的取值范围．(1)解：将点A（1，2），B（3，0）带入l:y=ax+b(a≠0)得：{a+b=23a+b=0，解得{a=−1 b=3，∴直线l的表达式为y=−x+3．(2)解：∵A（1，2），B（3，0）∴AB==∵PC⊥y轴，当y=n时−x+3=n 解得x=3−n∴C（3−n，n）∴PC=|3−n|∵PC≥AB即3−n≥n−3≥∴|3−n|≥解得n≤【点睛】本题考查待定系数法求一次函数解析式，两点间的距离公式，根据题意列出不等式是解题的关键．2．（2022·北京朝阳·二模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到，且经过点（2，2）．(1)求这个一次函数的表达式；(2)当x<2时，对于x的每一个值，函数y=mx(m≠0)的值大于一次函数y=kx+b的值，直接写出m的取值范围．【答案】(1)y=2x−2(2)1≤m≤2【解析】【分析】（1）由平移可知平移前后平移后的直线平行，所以k=2，然后将点（2，2）带入y=2x+b可得b=−2．（2）当x=2时，得到点(2,2)是临界点，此时可得由函数图象知道函数值大于代表对应的函数图象在上方，可得到2m≥2，分析图象另外的临界为两条直线平行即可得到答案．(1)解：（1）∵一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到，∴k=2，把（2，2）代入y=2x+b，解得b=−2∴这个一次函数的表达式为y=2x−2．(2)分析两个临界图象如图所示：分析可得到答案为：1≤m≤2．【点睛】本题考查一次函数图象平行时的解析式求法，一次函数与不等式的联系，明确直线平行时，直线的k相等，在解决一次函数与不等式联系的题型时，运用数形结合的思想方法正确找到临界是解题的关键．3．（2022·北京东城·二模）如图，在平面直角坐标系xOy中，双曲线y=k(k≠0)经过点A(2,−1)，直线l：xy=−2x+b经过点B(2,−2)．(1)求k,b的值；(2)过点P(n,0)(n >0)作垂直于x 轴的直线，与双曲线y =k x (k ≠0)交于点C ，与直线l 交于点D ．①当n =2时，判断CD 与CP 的数量关系；②当CD ≤CP 时，结合图象，直接写出n 的取值范围．【答案】(1)k =-2，b =2；(2)①CD =CP ；②1≤n ≤2【解析】【分析】（1）直接利用待定系数法即可确定这两个值；（2）①过点P (n ,0)(n >0)作垂直于x 轴的直线，与双曲线交于点C ，与直线l 交于点D ，由（1）得，双曲线的解析式为y =−2x ，直线的解析式为：y =-2x +2，得出C (n ，−2n )，D （n ，-2n +2），得出DC =|−2n−(−2n +2)|=|2n−2n −2|，CP =|−2n|=2n ，当n =2时，代入求解即可；②考虑当CD =CP 时，解方程确定n 的值，然后作出函数图象，结合图象求解即可．(1)解：∵双曲线经过点A (2,-1)，∴k =2×(-1)=-2，∵直线l 经过点B （2，-2），∴-2=-2×2+b ，解得b =2，即k 、b 的值分别为：-2；2；(2)①过点P (n ,0)(n >0)作垂直于x 轴的直线，与双曲线交于点C ，与直线l 交于点D ，由（1）得，双曲线的解析式为y =−2x ，直线的解析式为：y =-2x +2，)，D（n，-2n+2）∴C(n，−2n∴DC=|−2n−(−2n+2)|=|2n−2n−2|，CP=|−2n|=2n，当n=2时，P(2,0)、C(2,-1)、D(2,-2)，此时点C与点A重合，点D与点B重合，∴CD=-1-（-2）=1，CP=0-(-1)=1，∴CD=CP；②设直线l：y=-2x+2与x轴交于K，如图：在y=-2x+2中，令y=0得x=1，∴K（1，0），由图可知，当P位于K及右侧，（2，0）及左侧时，CD≤CP，∴1≤n≤2．【点睛】题目主要考查一次函数与反比例函数综合问题，包括待定系数法确定函数解析式，坐标系中两点间的距离及数形结合思想等，理解题意，综合运用这些知识点是解题关键．4．（2022·北京北京·二模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象由函数y=−x的图象平移得到，且经过点(1,1)．(1)求这个一次函数的表达式；(2)当x>−1时，对于x的每一个值，函数y=mx−1(m≠0)的值小于一次函数y=kx+b的值，直接写出m 的取值范围．【答案】(1)y=−x+2(2)−4≤m≤−1【解析】【分析】（1）根据一次函数y=kx+b(k≠0)的图象由函数y=−x的图象平移得到，得出k=−1，把(1,1)代入y=−x+b(k≠0)，即可求出b的值，得出一次函数关系式；（2）根据函数图象结合题意先推理得出m＜0，然后将x=−1代入y=-x+2得出函数值y=3，根据题意即可列出mx−1≤3，得出x≥4m ，根据此时x＞−1得出4m≤−1，解得m≥−4，结合图象得出m的取值范围即可．(1)解：∵一次函数y=kx+b(k≠0)的图象由函数y=−x的图象平移得到，∴k=−1．∵一次函数y=−x+b(k≠0)的图象经过点(1,1)，∴1=−1+b，∴b=2，∴这个一次函数的表达式为y=−x+2．(2)根据函数y=-x+2的函数图象可知，要使当x>−1时，对于x的每一个值，函数y=mx−1(m≠0)的值小于一次函数y=kx+b的值，则m一定要小于0，把x=−1代入y=-x+2得：y=3，∴mx−1＜3，∴x＞4，m∵x＞−1，∴4≤−1，m∴4≥−m，即−m≤4，∴m≥−4，故m的取值范围为−4≤m≤−1．【点睛】本题主要考查了求一次函数解析式，一次函数的性质，熟练掌握平移后一次函数关系式中的k值不变，是解题的关键．5．（2022·北京丰台·二模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象由函数y=x的图象向下平移4个单位长度得到．(1)求这个一次函数的解析式；(2)一次函数y=kx+b的图象与x轴的交点为A，函数y=mx(m<0)的图象与一次函数y=kx+b的图象的交点为B，记线段OA，AB，BO围成的区域（不含边界）为W，横、纵坐标都是整数的点叫做整点，若区域W内恰有2个整点，直接写出m的取值范围．【答案】(1)y=x−4(2)−2<m<−1或−1<m<02【解析】【分析】（1）根据平移的规律写出解析式即可；（2）先求出A点的坐标，再根据题意，找出符合题意的整数点，进行求解即可．(1)∵一次函数y=kx+b(k≠0)的图象由函数y=x的图象向下平移4个单位长度得到，∴这个一次函数的解析式y=x−4；(2)当y=0=x−4时，x=4，∴一次函数的解析式y=x−4与x轴的交点为(4,0)，当x=1时，可知在第四象限内，整点有(1,−1),(1,−2)，当x=2时，可知在第四象限内，整点有(2,−1)，当x=3时，可知在第四象限内无整点，把(1,−1),(2,−1),(1,−2)分别代入y=mx(m<0)，得−1=m或−1=2m或−2=m，或m=−2，解得m=−1或m=−12∵区域W内恰有2个整点，∴函数y=mx(m<0)的图象要在(1,−1),(2,−1)之间，或在(1,−1),(1,−2)之间，<m<0．∴−2<m<−1或−12【点睛】本题考查了一次函数图象平移的规律（左加右减，上加下减），一次函数的图象和性质，熟练掌握知识点并正确理解题意是解题的关键．6．（2022·北京密云·二模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象经过点A(0,−3)和点B(5,2)．(1)求这个一次函数的表达式；(2)当x≥2时，对于x的每一个值，函数y=mx+2(m≠0)的值小于一次函数y=kx+b的值，直接写出m 的取值范围．【答案】(1)y=x−3(2)m<−32【解析】【分析】（1）通过待定系数法将点A(0,−3)和点B(5,2)代入解析式求出k，b的值，进而可得一次函数表达式；（2）由题意知y=x−3，将x=2代入y=x−3得y=−1，则(2,−1)，根据题意：mx+2<x−3，如图，分当m=1时和当m≠1时两种情况进行分析，由一次函数的图象与性质可知，当m<−32时，当x≥2时，对于x 的每一个值，mx+2<x−3成立，进而可得m的取值范围．(1)解∵一次函数y=kx+b(k≠0)的图象点A(0,−3)和点B(5,2)，∴{5k+b=2 b=−3，解得：{k=1b=−3，∴一次函数的表达式为：y=x−3．(2)解：由（1）得：y=x−3，将x=2代入y=x−3得y=−1，则(2,−1)，根据题意：mx+2<x−3，如图，当m=1时，y=x−3与y=x+2平行，可知当x≥2时，mx+2<x−3不成立；，当m≠1时，将(2,−1)代入y=mx+2中得2m+2=−1，解得m=−32时，当x≥2时，对于x的每一个值，mx+2<x−3成立；由一次函数的图象与性质可知，当m<−32，综上所述，m<−32∴m的取值范围为m<−3．2【点睛】本题考查了待定系数法求一次函数解析式，一次函数与一元一次不等式，一次函数的图象与性质．运用数形结合的思想是解题的关键．7．（2022·北京西城·二模）在平面直角坐标系xOy中，一次函数y=−x+b的图象与x轴交于点(4,0)，且与反比例函数y=m的图象在第四象限的交点为(n,−1)．x(1)求b，m的值；(2)点P(x p,y p)是一次函数y=−x+b图象上的一个动点，且满足m<y p<4，连接OP，结合函数图象，直接x p写出OP长的取值范围．【答案】(1)b=4，m=-5OP【解析】【分析】（1）把(4,0)代入y=-x+b，即可求出b值，从而得出一次函数解析式，再把(n,-1)代入一次函数解析式求出n值，然后把(n ,-1)代入反比例函数银析式求出值即可；（2）先画出示意图，如图，由mx p <y p <4，得出0<xP <5，点P 在线段BD 上运动，连接OD ，过点O 作OC ⊥BD 于C ，求出OC 、OD 的长，即可由OC ≤OP <OD 求解．(1)解：把(4,0)代入y =-x +b ，得0=-4+b ，解得：b =4，∴一次函数解析式为y =-x +4，把(n ,-1)代入y =-x +4，得-1=-n +4，解得：n =5，把(5,-1)代入y =m x 得，−1=m 5,解得：m =-5；(2)解：如图，∵m x p <y p <4，∴0<xp <5，∴点P 在线段BD 上运动，连接OD ，过点O 作OC ⊥BD 于C ，∵A （4，0），B （0，4），D （5，-1），∴OA =OB =4，ODAB =∵S △OAB =12OA ⋅OB =12AB ⋅OC ，∴4×4=，∴OC∴OC≤OP<OD，OP∴【点睛】本题考查待定系数法求一次函数与反比例函数解析式，一次函数与反比例函数交点问题，垂线段最短，图象法求不等式解集，熟练掌握一次函数与反比例关系函数性质是解题的关键．8．（2022·北京平谷·二模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象由函数y=1x平移2得到，且过点(0,−1)．(1)求这个一次函数y=kx+b(k≠0)的表达式；(2)当x>−2时，对于x的每一个值，函数y=mx+1的值大于一次函数y=kx+b(k≠0)的值，求m的取值【答案】(1)y =12x−1(2)12≤m ≤32【解析】【分析】（1）先根据一次函数图象的平移可得k =12，再将点(0,−1)代入即可得；（2）先根据mx +1>12x−1可得(m−12)x +2>0，从而问题可转化为当x >−2时，函数y =(m−12)x +2的值大于0，再分①m =12和②m >12两种情况，解不等式即可得．(1)解：∵一次函数y =kx +b (k ≠0)的图象由函数y =12x 平移得到，∴k =12，∵一次函数y =12x +b 的图象经过点(0,−1)，∴b =−1，则这个一次函数的表达式为y =12x−1．(2)解：当x >−2时，对于x 的每一个值，函数y =mx +1的值大于一次函数y =12x−1的值，则m ≥12，mx +1>12x−1，即(m−12)x +2>0，则所求问题可转化为当x >−2时，函数y =(m−12)x +2的值大于0，①当m =12时，y =2>0符合题意；②当m >12时，则−2(m−12)+2≥0，解得m ≤32，所以此时m 的取值范围为12<m ≤32，综上，m 的取值范围为12≤m ≤32．本题考查了一次函数图象的平移、待定系数法、一元一次不等式的应用，较难的是题（2），正确将问题进行转化，并分两种情况讨论是解题关键．9．（2022·北京东城·一模）对于平面直角坐标系xOy中的点C及图形G，有如下定义：若图形G上存在A，B两点，使得△ABC为等腰直角三角形，且∠ABC=90°，则称点C为图形G的“友好点”．(1)已知点O(0,0)，M(4,0)，在点C1(0,4)，C2(1,4)，C3(2,−1)中，线段OM的“友好点”是_______；(2)直线y=−x+b分别交x轴、y轴于P，Q两点，若点C(2,1)为线段PQ的“友好点”，求b的取值范围；(3)已知直线y=x+d(d>0)分别交x轴、y轴于E，F两点，若线段EF上的所有点都是半径为2的⊙O的“友好点”，直接写出d的取值范围．【答案】(1)C1、C3(2)1≤b<3或b>3d≤+2(3)【解析】【分析】（1）根据“友好点”的定义逐个判断即可；（2）分两种情况讨论，直线PQ在点C上方或下方．过B作PQ的垂线，垂足为B，交x轴于H，根据题目中的定义知：BQ或BP的长度要大于或等于BC的长度，求解即可；（3）首先分析得到E点的运动范围，作出图形知OE≥2，当EH平分∠FEO时，其中H（2，0），是其最大，即得结论．临界值，根据勾股定理求出最大值为(1)解：如图所示，由题意知三角形OC1M为等腰直角三角形，C1符合题意；过C2作C2A⊥OM于A，则AM=3，C2A=4，三角形AMC2不是等腰三角形，C2不符合题意；过C3作C3B⊥OM于B，则C3B=AB=1，三角形ABC3是等腰直角三角形，符合题意；故答案为：C1、C3．(2)解：分两种情况讨论，当直线PQ在C点上方时，过C作CB⊥PQ于B，延长BC交x轴于H，如图所示，则△BPH为等腰直角三角形，BP=BH>BC，故在线段PQ上必存在A点，使得∠ABC=90°，AB=BC，将x=2，y=1代入y=－x+b得：b=3，即b>3；当直线PQ在C点下方时，过C作CB⊥PQ于B，CB延长线交x轴于H，则当BQ≥BC时，符合题意，当直线PQ过H点时，BQ=BC，如图所示，此时，－1+b=0，即b=1，即1≤b<3，综上所述，b的取值范围为：1≤b<3或b>3．(3)解：根据题意，AB为⊙O的弦，根据定义可知，∵∠ACB=45°BC=2∴∠AOB=90°，当AB取得最小，点C在⊙O上，此时AB=12EF则OC=12则d=当AB取得最大值时，AB为⊙O的直径，当AB的长度变化时，总能在EF上找到点C使得∠ACB=45°，则符合题意的点C在如图中阴影部分中运动，通过分析可知，当直线EF在下图中的位置时，d取得最大值，此时，∠HEO=22.5°，即EH为∠EHF的平分线，过H作HM⊥EF于M，则HM=OH=2，∴FM=2，由勾股定理得：FH=+2，即d=+2即OE=OF=∴【点睛】本题考查了新定义的问题，涉及到一次函数与圆的性质的综合应用，所用到的数学思想方法为数形结合、分类讨论，该题综合性较强．解题关键是读懂题意，借助定义作出符合题意的图形．10．（2022·北京昌平·二模）在平面直角坐标系xOy中，直线y=kx+b(k≠0)与直线y=x平行，且过点(2,1)．(1)求这个一次函数的解析式；(2)直线y=kx+b(k≠0)分别交x，y轴于点A，点B，若点C为x轴上一点，且S△ABC=2，直接写出点C的坐标．【答案】(1)y=x-1(2)(5,0)或(-3,0)【解析】【分析】(1)首先根据直线y=kx+b(k≠0)与直线y=x平行，可求得k=1，再把点(2,1)代入解析式，即可求得b，据此即可求得解析式；(2)首先可求得A、B的坐标，设点C的坐标为(x,0)，可得AC=|1-x|，再根据三角形的面积公式列出方程，解方程即可求得．(1)解：∵直线y=kx+b(k≠0)与直线y=x平行∴k=1∴直线为y=x+b把点(2,1)代入解析式，得2+b=1解得b=-1故这个一次函数的解析式为y=x-1；(2)解：在y=x-1中，令y=0，则x=1，故A(1,0)令x=0，则y=-1，故B(0,-1)，OB=1设点C的坐标为(x,0)，则AC=|1-x|，∵S△ABC=12AC⋅OB=2∴|1−x|=4解得x=5或x=-3故点C的坐标为(5,0)或(-3,0)．【点睛】本题考查了利用待定系数法求一次函数的解析式，求直线与坐标轴的交点坐标，三角形面积公式，解绝对值方程，根据三角形面积公式得到绝对值方程是解决本题的关键．11．（2022·北京顺义·一模）在平面直角坐标系xOy中，一次函数y=kx+b(k≠0)的图象平行于直线y=12x，且经过点A(2,2)．(1)求这个一次函数的表达式；(2)当x<2时，对于x的每一个值，一次函数y=kx+b(k≠0)的值大于一次函数y=mx−1(m≠0)的值，直接写出m的取值范围．【答案】(1)y=12x+1(2)12≤m≤32【解析】【分析】（1）根据一次函数图象平移时k不变可知k=1，再把点A（2，2）代入求出b的值，进而可得出结论．2（2）由函数解析式y=mx−1(m≠0)可知其经过点（0，-1），由题意可得临界值为当x=2，两条直线都过点A（2，2），将点A（2，2）代入到一次函数y=mx−1(m≠0)，可求出m的值，结合函数图象的性质即可得出m的取值范围．(1)x的图象平行，解：∵一次函数y=kx+b(k≠0)的图象与函数y=12∴k=1，2x+b的图象过点A（2，2），∵一次函数y=12×2+b，∴2=12∴b=1，x+1；∴这个一次函数的表达式为y=12(2)对于一次函数y=mx−1(m≠0)，当x=0时，有y=−1，可知其经过点（0，-1）．当x<2时，对于x的每一个值，一次函数y=kx+b(k≠0)的值大于一次函数y=mx−1(m≠0)的值，即一次函数y=kx+b(k≠0)图象在函数y=mx−1(m≠0)的图像上方，由下图可知：临界值为当x=2时，两条直线都过点A（2，2），将点A（2，2）代入到函数y=mx−1中，，可得2=2m−1，解得m=32结合函数图象及性质可知，当x<2，m≤3时，一次函数y=kx+b(k≠0)的值大于一次函数2y=mx−1(m≠0)的值，又∵如下图，当m <0时，，根据一次函数的图象可知，不符合题意．∴m 的取值范围为：12≤m ≤32．【点睛】本题考查的是一次函数的图象与几何变换、待定系数法求函数解析式等知识，熟练掌握一次函数的图象与性质，学会运用数形结合的思想思考问题是解题关键．12．（2022·北京石景山·一模）在平面直角坐标系xOy 中，直线l 1:y =12x +b 与直线l 2:y =2x 交于点A (m,n )．(1)当m =2时，求n ，b 的值；(2)过动点P (t,0)且垂直于x 轴的直线与l 1，l 2的交点分别是C ，D ．当t ≤1时，点C 位于点D 上方，直接写出b 的取值范围．【答案】(1)n =4；b =3；(2)b ＞32【解析】【分析】（1）将点A （2，n ）代入y =2x ，求出n 的值，得到A 点坐标，再将点A 坐标代入直线l 1的表达式求得b 的值；（2）把x =t 分别代入直线l 1与直线l 2的解析式，求出C ，D 两点的纵坐标，根据点C 位于点D 上方，列出关于t 的不等式，即可求解．(1)解：当m =2时，A (2,n )，∵直线l 2:y =2x 过点A (2,n )，∴n =2×2=4，∴A(2,4)，∵直线l1:y=12x+b过点A(2,4)，∴4=12×2+b，解得：b=3，(2)∵过动点P（t，0）且垂直于x轴的直线与l1，l2的交点分别为C，D，∴C（t，12t+b），D（t，2t），∵点C位于点D上方，∴12t+b＞2t，解得b＞32t，∵t≤1，∴b＞32．【点睛】本题考查了待定系数法求一次函数解析式，一次函数图象上点的坐标特征，难度适中．13．（2022·北京市十一学校二模）在平面直角坐标系xOy中，已知点P(1,2)，Q(−2,2)，函数y=mx．(1)当函数y=mx的图象经过点Q时，求m的值并画出直线y=－x－m．(2)若P，Q两点中恰有一个点的坐标（x，y）满足不等式组y>mxy<−x−m（m<0），求m的取值范围．【答案】(1)m=－4，画图见解析(2)－3≤m<0或m≤－4【解析】【分析】（1）根据待定系数法，将Q点坐标代入y=mx即可求值，进而画出直线的图象；（2）不等式组表达含义为P、Q中的一点位于反比例函数图象上方，位于一次函数图象下方，根据m<0的条件，数形结合即可求出m的取值范围．(1)解：∵函数y=mx的图象经过点Q，∴m=－2×2=－4，一次函数的解析式为：y=－x+4，图象如下．(2)解：由题意知，P、Q中的一点位于反比例函数图象上方，位于一次函数图象下方，∵m<0，∴反比例函数经过二、四象限，故P点在反比例函数图象上方，∴存在两种情况，①Q在反比例函数图象上方，在一次函数图象下方，P在一次函数图象上或上方，即：2>m−22<2−m−1−m≤2，解得：－3≤m<0；②Q在反比例函数图象上或下方，P在一次函数图象下方，即：2≤m−2−1−m>2，解得：m≤－4；综上所述，m的取值范围为：－3≤m<0或m≤－4．【点睛】本题考查了待定系数法求反比例函数解析式，解决本题难点是分析出反比例函数、一次函数的图象与P、Q 两点的位置关系，得到关于m的不等式组．14．（2022·北京丰台·一模）在平面直角坐标系xOy中，一次函数y＝kx+b（k≠0）的图象由函数y＝2x的图象平移得到，且经过点（2，1）．(1)求这个一次函数的解析式；(2)当x＞0时，对于x的每一个值，函数y＝mx（m≠0）的值大于一次函数y＝kx+b的值，直接写出m的取值范围．【答案】(1)y=2x−3(2)m≥2【解析】【分析】（1）由一次函数图象平移可知k=2，将(2,1)代入y=2x+b，求b的值，进而可得一次函数解析式；（2）如图，由图象可知，m≥2时，当x＞0时，对于x的每一个值均有mx>kx+b，进而可得答案．(1)解：由题意知，k=2将(2,1)代入y=2x+b得，2×2+b=1解得b=−3∴一次函数解析式为y=2x−3．(2)解：如图，由图象可知，m≥2时，当x＞0时，对于x的每一个值均有mx>kx+b∴m的取值范围为m≥2．【点睛】本题考查了一次函数图象的平移，一次函数解析式，一次函数与不等式等知识．解题的关键在于对知识的熟练掌握与灵活运用．15．（2022·北京·东直门中学模拟预测）如图，在平面直角坐标系xOy中，点A(1,4)，B(3,m)．的图象上，求m的值；x(2)如果点A，B均在一次函数y2=ax+b的图象上，①当m=2时，求该一次函数的表达式；②当x≥3时，如果不等式mx−1>ax+b始终成立，结合函数图象，直接写出m的取值范围．【答案】(1)m=43(2)①y2=−x+5；②m>12【解析】【分析】（1）先将A代入反比例函数解析式求出k的值，再将B点代入反比例函数解析式，求出m；（2）①当m=2时，将A，B点坐标代入一次函数解析式，待定系数法求解即可；②根据函数图象即可求出m取值范围．(1)解：∵点A(1,4)，B(3,m)均在反比例函数y1=kx的图象上，∴1×4=k=3m，解得：m=43；(2)解：①当m=2时，点B(3,2)，把点A(1,4)，B(3,2)代入得：a+b=43a+b=2，解得：a=−1b=5，∴该一次函数的表达式为y2=−x+5；②如图，根据图象得：直线y=ax+b与直线y=mx-1的交点的横坐标小于3，∴当x≥3时，不等式mx−1>ax+b始终成立，．即3m−1>m始终成立，解得：m>12【点睛】本题考查了反比例函数与一次函数，熟练掌握待定系数法求解析式以及一次函数图象是解题的关键．16．（2022·北京一七一中一模）在平面直角坐标系xOy中，直线l与双曲线y=k(k≠0)的两个交点分别为xA(−3,−1)，B(1,m).(1)求k和m的值；(2)求直线l的解析式；(3)点P为直线l上的动点，过点P作平行于x轴的直线，交双曲线y=k(k≠0)于点Q.当点Q位于点P的左侧时，x求点P的纵坐标n的取值范围.【答案】(1)k=3，m=3(2)y=x+2(3)−1<n<0或n>3【解析】【分析】（1）利用待定系数法可求k，然后把B(1,m)代入即可求得m；（2）根据（1）中求得的点A和B的坐标，利用待定系数法即可求得直线l的解析式；（3）结合图象可知，直线l在B点的上方或在A点的上方、x轴的下方时符合题意．(1)。

一次函数与方程不等式练习题及教案设计

一次函数与方程不等式练习题及教案设计教案章节一：一次函数的概念与性质【教学目标】1. 理解一次函数的定义。

2. 掌握一次函数的斜率和截距。

3. 了解一次函数的图像特点。

【教学内容】1. 引入一次函数的概念。

2. 讲解一次函数的斜率和截距。

3. 分析一次函数的图像特点。

【教学活动】1. 教师通过实际例子引导学生理解一次函数的概念。

2. 学生通过例题学习如何求一次函数的斜率和截距。

3. 学生绘制一次函数的图像，观察其特点。

【练习题】1. 求下列一次函数的斜率和截距：y = 2x + 3。

2. 绘制一次函数y = -x + 4 的图像。

教案章节二：一次函数的图像与方程【教学目标】1. 学会如何绘制一次函数的图像。

2. 理解一次函数与方程的关系。

3. 学会如何求解一次方程。

【教学内容】1. 讲解如何绘制一次函数的图像。

2. 引入一次函数与方程的关系。

3. 讲解如何求解一次方程。

【教学活动】1. 教师演示如何绘制一次函数的图像。

2. 学生通过例题学习一次函数与方程的关系。

3. 学生练习求解一次方程。

【练习题】1. 绘制一次函数y = 3x 2 的图像。

2. 求解方程2x + 3 = 7。

教案章节三：一次不等式与一次函数的关系【教学目标】1. 理解一次不等式与一次函数的关系。

2. 学会如何解一次不等式。

3. 学会如何求解一次不等式与一次函数的交点。

【教学内容】1. 讲解一次不等式与一次函数的关系。

2. 讲解如何解一次不等式。

3. 讲解如何求解一次不等式与一次函数的交点。

【教学活动】1. 教师通过实际例子讲解一次不等式与一次函数的关系。

2. 学生通过例题学习如何解一次不等式。

3. 学生练习求解一次不等式与一次函数的交点。

【练习题】1. 求解不等式2x + 3 > 7。

2. 求解一次不等式3x 2 < 4 与一次函数y = 2x + 1 的交点。

教案章节四：一次函数与方程不等式的应用【教学目标】1. 学会如何应用一次函数、方程和不等式解决实际问题。

一次函数与方程、不等式的应用

2．(2020·福建)某公司经营甲、乙两种特产，其中甲特产每吨成本价为10万元，销售价为10.5万元；乙特产每吨成本价为1万元，销售价为1.2万元．由于受有关条件限制，该公司每月这两种特产的销售量之和都是100吨，且甲特产的销售量都不超过20吨．
(1)若该公司某月销售甲、乙两种特产的总成本为235万元，问这个月该公司分别销售甲、乙两种特产各多少吨？
5．(2020·铜仁)某文体商店计划购进一批同种型号的篮球和同种型号的排球，每一个排球的进价是每一个篮球的进价的 90%，用 3 600 元购买排球的个数要比用 3 600 元购买篮球的个数多 10 个．
(1)问每一个篮球、排球的进价各是多少元？ (2)该文体商店计划购进篮球和排球共 100 个，且排球个数不低于篮球个数的 3 倍，篮球的售价定为每一个 100 元，排球的售价定为每一个 90 元．若该批篮球、排球都能卖完，问该文体商店应购进篮球、排球各多少个才能获得最大利润？最大利润是多少？
则 M＝400a＋600(40－a)＋2×40×100＝－200a＋32 000， ∵a≤3(40－a)，∴a≤30. ∵－200＜0，∴M 随 a 的增大而减小． ∴当 a＝30 时，M 取得最小值，最小值为 26 000 元．答：购买甲、乙两种办公桌分别为 30 张、10 张时，费用最少，为 26 000 元．
(2)求该公司一个月销售这两种特产则销售乙种特产(100－x)吨，根据题意，得
10x＋(100－x)×1＝235，解得x＝15. ∴100－x＝85. 答：这个月该公司销售甲、乙两种特产分别为15吨、85吨．
(2)设利润为w元，销售甲种特产a吨，根据题意，得 w＝(10.5－10)a＋(1.2－1)×(100－a)＝0.3a＋20. ∵0≤a≤20， ∴当a＝20时，w取得最大值，w最大＝26. 答：该公司一个月销售这两种特产所能获得的最大总利润是26万元．

八年级数学培优——一次函数与方程、不等式

八年级数学培优——一次函数与方程、不等式考点·方法·破译1．一次函数与一元一次方程的关系：任何一元一次方程都可以转化成kx ＋b ＝0(k 、b 为常数；k ≠0)的形式；可见一元一次方程是一次函数的一个特例．即在y ＝kx ＋b 中；当y ＝0时则为一元一次方程．2．一次函数与二元一次方程(组)的关系：⑴任何二元一次方程ax ＋by ＝c (a 、b 、c 为常数；且a ≠0；b ≠0)都可以化为y ＝a c x b b -+的形式；因而每个二元一次方程都对应一个一次函数； ⑵从“数”的角度看；解方程组相当于求两个函数的函数值相等时自变量的取值；以及这个函数值是什么；从“形”的角度看；解方程组相当于确定两个函数图像交点的坐标．3．一次函数与一元一次不等式的关系：由于任何一元一次不等式都可以转化成ax ＋b ＞0或ax ＋b ＜0(a 、b 为常数；a ≠0)的形式；所以解一元一次不等式可以看成是当一次函数的函数值大于或小于0时；求相应自变量的取值范围．经典·考题·赏析【例1】直线l 1：y ＝k 1x ＋b 与直线l 2：y ＝k 2x 在同一平面直角坐标系中的图象如图所示；则关于x 的不等式k 1x ＋b ＞k 2x 的解为( )A ．x ＞－1B ．x ＜－1C ．x ＜－2D ．无【变式题组】01．直线l 1：y ＝k 1x ＋b 与直线l 2：y ＝k 2x 在同一平面直角坐标系中的图象与例题相同；则关于x 的不等式k 2x ＞k 1x ＋b 的解集为________．第2题图第3题图第3题图02．一次函数y 1＝kx ＋b 与y 2＝x ＋a 的图象如图；则下列结论：①k ＜0；②a ＞0；③当x ＜3时；y 1＜y 2中；正确的个数是( ) A ．0 B ．1 C ．2 D ．303．如图；已知一次函数y ＝2x ＋b 和y ＝ax －3的图象交于点P (－2；－5)；则根据图象可得不等式2x ＋b ＞ax －3的解集是________．04．如图；直线y ＝kx ＋b 经过A (2；1)；B (－1；－2)两点；则不等式错误!x ＞kx ＋b ＞－2的解集为_________．【例2】若直线l1：y＝x－2与直线l2：y＝3－mx在同一平面直角坐标系的交点在第一象限；求m的取值范围．【变式题组】01．如果直线y＝kx＋3与y＝3x－2b的交点在x轴上；当k＝2时；b等于()A．9 B．－3 C．3 2 -D．9 4 -02．若直线122y x=-与直线14y x a=-+相交于x轴上一点；则直线14y x a=-+不经过()A．第四象限B．第三象限C．第二象限D．第一象限03．两条直线y1＝ax＋b；y2＝cx＋5；学生甲解出它们的交点坐标为(3；－2)；学生乙因抄错了c而解出它们的交点坐标为(34；14)；则这两条直线的解析式为____________．04．已知直线y＝3x和y＝2x＋k的交点在第三象限；则k的取值范围是________．【例3】在直角坐标系中；若一点的纵横坐标都是整数；则称该点为整点；设k为整数；当直线y＝x－2与y＝kx＋k的交点为整点时；k的取值可以取()A．4个B．5个C．6个D．7个【变式题组】01．从2；3；4；5这四个数中；任取两个数p和q(p≠q)；构成函数y＝px－2和y＝x＋q；并使这两个函数图象的交点在直线x＝2的右侧；则这样的有序数对(p；q)共有()A．12对B．6对C．5对D．3对02．直线l：y＝px(p是不等于0的整数)与直线y＝x＋10的交点恰好是整点(横坐标和纵坐标都是整数)；那么满足条件的直线l有()A．6条B．7条C．8条D．无数条03．点A、B分别在一次函数y＝x；y＝8x的图像上；其横坐标分别是a、b(a＞0；b＞0)．若直线AB为一次函数y＝kx＋m的图象；则当ba是整数时；求满足条件的整数k的值．【例4】已知x、y、z都为非负数；满足x＋y－z＝1；x＋2y＋3z＝4；记ω＝3x＋2y＋z．求ω的最大值与最小值．【变式题组】01．已知x满足不等式：31752233x xx-+--≥；|x－3|－|x＋2|的最大值为p；最小值为q；则pq的值是()A．6 B．5 C．－5D．－102．已知非负数a、b、c满足条件：3a＋2b＋c＝4；2a＋b＋3c＝5．设S＝5a＋4b＋7c的最大值为m；最小值为n；则n－m＝________．03．若x＋y＋z＝30；3x＋y－z＝50；x、y、z均为非负数；则M＝5x＋4y＋2z的取值范围是()A．100≤M≤110 B．110≤M≤120 C．120≤M≤130 D．130≤M≤140【例5】已知直线l1经过点(2；5)和(－1；－1)两点；与x轴的交点是点A；将直线y ＝－6x＋5的图象向上平移4个单位后得到l2；l2与l1的交点是点C；l2与x轴的交点是点B；求△ABC的面积．【变式题组】01．已知一次函数y＝ax＋b与y＝bx＋a的图象相交于A(m；4)；且这两个函数的图象分别与y轴交于B、C两点(B上C下)；△ABC的面积为1；求这两个一次函数的解析式．02．如图；直线OC、BC的函数关系式为y＝x与y＝－2x＋6．点P(t；0)是线段OB上一动点；过P作直线l与x轴垂直．⑴求点C坐标；⑵设△BOC中位于直线l左侧部分面积为S；求S与t⑶当t为何值时；直线l平分△COB面积．第2题图演练巩固·反馈提高01．已知一次函数y＝32x＋m；和y＝12x＋n的图象交点A(－2；0)；且与y轴分别交于B、C两点；那么△ABC的面积是()A．2 B．3 C．4D．602．已知关于x的不等式ax＋1＞0(a≠0)的解集是x＜1；则直线y＝ax＋1与x轴的交点是()A．(0；1) B．(－1；0) C．(0；－1) D．(1；0)第3题图第6题图03．如图；直线y＝kx＋b与x轴交于点A(－4；0)；则y＞0时；x的取值范围是() A．x＞－4 B．x＞0 C．x＜－4D．x＜004．直线kx－3y＝8；2x＋5y＝－4交点的纵坐标为0；则k的值为() A．4 B．－4 C．2D．－205．直线y＝kx＋b与坐标轴的两个交点分别为A(2；0)和B(0；－3)．则不等式kx＋b ＋3≥0的解集为()A．x≥0 B．x≤0 C．x≥2D．x≤206．如图是在同一坐标系内作出的一次函数y1、y2的图象l1、l2；设y1＝k1x＋b1；y2＝k2x＋b2；则方程组111222y k x by k x b⎧⎨⎩＝＋，＝＋的解是()A．22xy=-⎧⎨=⎩B．23xy=-⎧⎨=⎩C．33xy=-⎧⎨=⎩D．34xy=-⎧⎨=⎩07．若直线y＝ax＋7经过一次函数y＝4－3x和y＝2x－1的交点；则a＝_________．08．已知一次函数y＝2x＋a与y＝－x＋b的图象都经过A(－2；0)；且与y轴分别交于B、C两点；则S△ABC＝_________．09．已知直线y＝2x＋b和y＝3bx－4相交于点(5；a)；则a＝___________．10．已知函数y＝－x＋m与y＝mx－4的图象交点在x轴的负半轴上；则m的值为__________．11．直线y＝－2x－1与直线y＝3x＋m相交于第三象限内一点；则m的取值范围是___________．12．若直线122ay x=-+与直线31544y x=-+的交点在第一象限；且a为整数；则a＝_________．13．直线l1经过点(2；3)和(－1；－3)；直线l2与l1交于点(－2；a)；且与y轴的交点的纵坐标为7．⑴求直线l2、l1的解析式；⑵求l2、l1与x轴围成的三角形的面积；⑶x取何值时l1的函数值大于l2的函数值？14．如图；直线l1的解析式为y＝－3x＋3；l1与x轴交于点D；直线l2经过点A(4；0)；B(3；32-)．⑴求直线l2的解析式；⑵求S△ADC；⑶在直线l2上存在异于点C的另一点P；使得S△ADP＝S△ADC；求P点坐标．l2第14题图15．已知一次函数图象过点(4；1)和点(－2；4)．求函数的关系式并画出图象．⑴当x为何值时；y＜0；y＝0；y＞0？⑵当－1＜x≤4时；求y的取值范围；⑶当－1≤y＜4时；求x的取值范围．16．某医药研究所开发了一种新药；在实验药效时发现；如果成人按规定剂量服用；那么服药后2h时血液中含药量最高；达每毫升6μg(1μg＝10－3mg)；接着就逐步衰减；10h 后血液中含药量为每毫升3μg；每毫升血液中含药量y(μg)随时间x(h)的变化如图所示；当成人按规定剂量服药后；⑴分别求x≤2和x≥2时；y与x之间的函数关系式；⑵如果每毫升血液中含药量在4μg或4μg以上时；治疗疾病才是有效的；那么这个有效时间是多长？第16题图。

一次函数与方程,不等式的应用

知识点睛一、一次函数与一元一次方程的关系直线y b k 0kx =+≠（）与x 轴交点的横坐标，就是一元一次方程b 0(0)kx k +=≠的解。

求直线y b kx =+与x 轴交点时，可令0y =，得到方程b 0kx +=，解方程得x bk=-，直线y b kx =+交x 轴于(,0)bk-，b k -就是直线y b kx =+与x 轴交点的横坐标。

二、一次函数与一元一次不等式的关系任何一元一次不等式都可以转化为a b 0x +>或a b 0x +<(b a 、为常数，0a ≠)的形式，所以解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量相应的取值范围。

三、一次函数与二元一次方程（组）的关系1.一次函数的解析式y b k 0kx =+≠（）本身就是一个二元一次方程，直线y b k 0kx =+≠（）上有无数个点，每个点的横纵坐标都满足二元一次方程y b k 0kx =+≠（），因此二元一次方程的解也就有无数个。

2.二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解可看做是两个一次函数1111b c x b a y +-=与2222b cx b a y +-=的图像的交点，共有三种情况： 1）当2121b b a a ≠时，方程组有唯一解 2）当212121c c b b a a ==时，方程组有无数个解， 3）当212121c c b b a a ≠=时，方程组无解。

例题精讲一、一次函数与一元一次方程综合【例1】已知直线(32)2y m x =++和36y x =-+交于x 轴上同一点，m 的值为（）A ．2-B ．2C ．1-D ．0练习1：已知一次函数y x a =-+与y x b =+的图象相交于点()8m ，，则a b +=______．练习2：已知一次函数y kx b =+的图象经过点()20，，()13，，则不求k b ，的值，可直接得到方程3kx b +=的解是x =______．二、一次函数与一元一次不等式综合【例2】已知一次函数25y x =-+．（1）画出它的图象；（2）求出当32x =时，y 的值；（3）求出当3y =-时，x 的值；（4）观察图象，求出当x 为何值时，0y >，0y =，0y <变式：已知15y x =-，221y x =+．当12y y >时，x 的取值范围是（）A ．5x >B ．12x < C ．6x <- D ．6x >-练习：当自变量x 满足什么条件时，函数41y x =-+的图象在：（1）x 轴上方；（2）y 轴左侧；（3）第一象限．【例3】已知一次函数23y x =-+（1）当x 取何值时，函数y 的值在1-与2之间变化?（2）当x 从2-到3变化时，函数y 的最小值和最大值各是多少?变式：直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示，则关于x 的不等式21k x k x b >+的解集为______．l 2l 13-1O yx练习：若解方程232x x +=-得2x =，则当x _________时直线2y x =+上的点在直线32y x =-上相应点的上方．【例4】如图，直线y kx b =+经过()21A ，，()12B --，两点，则不等式122x kx b >+>-的解集为______．BAO yx练习：已知一次函数经过点（1，-2）和点（-1，3），求这个一次函数的解析式，并求：（1）当2x =时，y 的值；（2）x 为何值时，0y <？（3）当21x -≤≤时，y 的值范围；（4）当21y -<<时，x 的值范围．三、一次函数与二元一次方程（组）综合【例5】已知直线3y x =-与22y x =+的交点为（-5，-8），则方程组30220x y x y --=⎧⎨-+=⎩的解是________．变式：图中两直线L 1，L 2的交点坐标可以看作方程组( )解．A ．121x y x y -=⎧⎨-=-⎩ B. 121x y x y -=-⎧⎨-=⎩C ．321x y x y -=⎧⎨-=⎩ D. 321x y x y -=-⎧⎨-=-⎩练习：已知方程组y ax c y kx b -=⎧⎨-=⎩（a b c k ，，，为常数，0ak ≠）的解为23x y =-⎧⎨=⎩，则直线y ax c=+和直线y kx b =+的交点坐标为________．练习：已知24x y =⎧⎨=⎩，是方程组73228x y x y -=⎧⎨+=⎩的解，那么一次函数y =________和y =________的交点是________．【例6】 b 取什么整数值时，直线32y x b =++与直线2y x b =-+的交点在第二象限？练习：已知直线62+-=-k y x 和143+=+k y x ，若交点在第四象限。

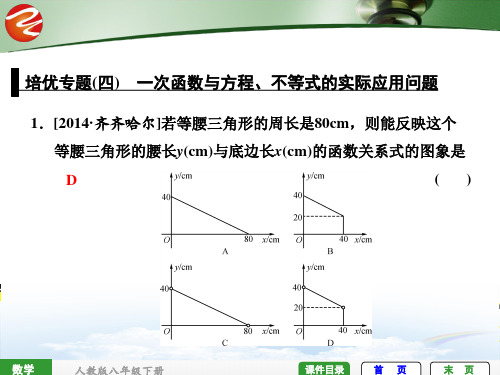
培优专题(四) 一次函数与方程、不等式的实际应用问题

一次函数与方程、不等式详细教案

一次函数与方程不等式练习题及教案设计

专题5.4 一次函数与方程、不等式的关系【十大题型】(学生版)

一次函数与方程、不等式的综合问题

培优专题(四) 一次函数与方程、不等式的实际应用问题

方程不等式与一次函数专题(实际应用)

八上 一次函数与方程组、不等式 知识点+例题+练习 (非常好 分类全面)

专题4 一次函数与方程、不等式的关系-重难点题型(举一反三)(浙教版)(解析版)

8.一次函数与方程不等式培优练习.doc

专题训练4： 一次函数与方程、不等式的实际应用

一次函数的性质与应用问题

一次函数与方程不等式练习题及教案设计

一次函数与方程、不等式的应用

八年级数学培优——一次函数与方程、不等式

一次函数与方程,不等式的应用

八上一次函数与方程组、不等式知识点+例题+练习 (非常好分类全面)

专题训练4：一次函数与方程、不等式的实际应用