初中数学基本运算能力训练(加强版)1
九年级数学竞赛培优专题及答案 20 直线与圆的位置关系1(含答案)
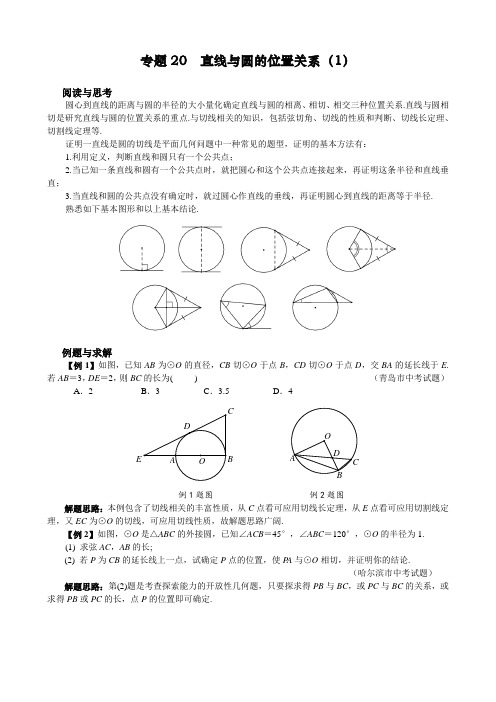
专题20 直线与圆的位置关系(1)阅读与思考圆心到直线的距离与圆的半径的大小量化确定直线与圆的相离、相切、相交三种位置关系.直线与圆相切是研究直线与圆的位置关系的重点.与切线相关的知识,包括弦切角、切线的性质和判断、切线长定理、切割线定理等.证明一直线是圆的切线是平面几何问题中一种常见的题型,证明的基本方法有: 1.利用定义,判断直线和圆只有一个公共点;2.当已知一条直线和圆有一个公共点时,就把圆心和这个公共点连接起来,再证明这条半径和直线垂直;3.当直线和圆的公共点没有确定时,就过圆心作直线的垂线,再证明圆心到直线的距离等于半径. 熟悉如下基本图形和以上基本结论.例题与求解【例1】如图,已知AB 为⊙O 的直径,CB 切⊙O 于点B ,CD 切⊙O 于点D ,交BA 的延长线于E .若AB =3,DE =2,则BC 的长为( ) (青岛市中考试题)A .2B .3C .3.5D .4例1题图 例2题图解题思路:本例包含了切线相关的丰富性质,从C 点看可应用切线长定理,从E 点看可应用切割线定理,又EC 为⊙O 的切线,可应用切线性质,故解题思路广阔.【例2】如图,⊙O 是△ABC 的外接圆,已知∠ACB =45°,∠ABC =120°,⊙O 的半径为1. (1) 求弦AC ,AB 的长;(2) 若P 为CB 的延长线上一点,试确定P 点的位置,使P A 与⊙O 相切,并证明你的结论.(哈尔滨市中考试题)解题思路:第(2)题是考查探索能力的开放性几何题,只要探求得PB 与BC ,或PC 与BC 的关系,或求得PB 或PC 的长,点P 的位置即可确定.E【例3】已知△ABC 是⊙O 的内接三角形,BT 为⊙O 的切线,B 为切点,P 为直线AB 上一点.过点P 作BC 的平行线交BT 于点E ,交直线AC 于点F .(1) 当点P 在线段AB 上时(如图),求证:P A •PB =PE •PF ;(2) 当点P 为线段BA 的延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明;如果不成立,请说明理由. (北京市中考试题)解题思路:本例是“运动型”的开放性问题,要求点在运动变化中,判断原结论是否成立,通过观察、比较、归纳、分析等系列活动,逐步确定应有的结论.【例4】已知:如图1,把矩形纸片ABCD 折叠,使得顶点A 与边DC 上的动点P 重合(P 不与点D ,C 重合),MN 为折痕,点M ,N 分别在边BC ,AD 上.连接AP ,MP ,AM ,AP 与MN 相较于点F ,⊙O 过点M ,C ,P .(1) 请你在图1中作出⊙O (不写作法,保留作图痕迹);(2)AF AN 与APAD是否相等?请说明理由; (3) 随着点P 的运动,若⊙O 与AM 相切于点M 时,⊙O 又与AD 相切于点H .设AB 为4,请你通过计算,画出这时的图形(图2、图3供参考).(宜昌市中考试题)解题思路:对于(3),只依靠AB 的长不能画出图形,需求出关键的量,因为∠C =90°,⊙O 过点M ,C ,P ,故将画出矩形的条件转化为求出CP (或MP )的长.当矩形确定后,依据线段CP 的长,就可确定P 点的位置.TTC MNNN【例5】如图,已知△ABC 内接于⊙O ,AD ,BD 为⊙O 的切线,作DE ∥BC ,交AC 于点E ,连接EO 并延长交BC 于点F .求证:BF =FC . (太原市竞赛试题)解题思路:要证明BF =FC ,只需证FO ⊥BC 即可,连接OA ,OB ,OD ,将问题转化为证明∠DAO =∠EFC .【例6】如图,在等腰△ABC 中,已知AB =AC ,∠C 的平分线与AB 交于点P ,M 是△ABC 的内切⊙I 与边BC 的切点,作MD ∥AC ,交⊙I 于点D ,求证:PD 是⊙I 的切线. (全国初中数学联赛试题)解题思路:设⊙I 切AB 于点S ,连接IM ,IS ,ID ,直接证明∠PDI =90°困难,不妨证明∠PDI =∠PSI ,即证明△PIS ≌△PID .能力训练A 级1. P A ,PB 切⊙O 于A ,B ,∠APB =78°,点C 是⊙O 上异于A ,B 的任意一点,则∠ACB =__________.2.如图,以△ABC 的边AB 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线交AC 于点E .要使DE ⊥AC ,则△ABC 的边必须满足的条件是__________. (武汉市中考试题)第2题图 第3题图3. 如图,P A 切⊙O 于点A ,C 是AB 上任意一点,∠P AB =62°,则∠C 的度数是__________.(荆门市中考试题)P4.直角梯形ABCD 中,AD ∥BC ,∠B =90°,AD +BC <DC .若腰DC 上有一点P ,使AP ⊥BP ,则这样的点( )A .不存在B .只有一个C .只有两个D .有无数个5.如图,已知AB 是⊙O 的直径,CD ,CB 是⊙O 的切线,D ,B 为切点,OC 交⊙O 于点E ,AE 的延长线交BC 于点F ,连接AD ,BD ,给出以下四个结论:①AD ∥OC ;②E 为△CDB 的内心;③FC =FE .其中正确的结论是 ( )A .①②B .②③C .①③D .①②③6.如图,ABCD 为⊙O 的内接四边形,AC 平分∠BAD 并与BD 相交于E 点,CF 切⊙O 于点C 并与AD 的延长线相交于点F .图中的四个三角形①△CAF ,②△ABC ,③△ABD ,④△BEC ,其中一定相似的是( ) (连云港市中考试题)A .①②③B .②③④C .①③④D .①②④第5题图 第6题图 第7题图7.如图,△ABC 内接于⊙O ,AE 切⊙O 于点A ,BC ∥AE . (1) 求证:△ABC 是等腰三角形;(2) 设AB =10cm ,BC =8cm ,点P 是射线AE 上的点,若以A ,P ,C 为顶点的三角形与△ABC 相似,问这样的点有几个? (南昌市中考试题)8.如图,Rt △ABC 中,∠C =90°,以AC 为直径的⊙O 交斜边AB 于点E ,OD ∥AB . 求证:(1) ED 是⊙O 的切线;(2) 2DE 2=BE •OD .ACB9.如图,在△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的边,且a ,b 是关于x 的一元二次方程x 2+4(c +2)=(c+4)x 的两个根. 点D 在AB 上,以BD 为直径的⊙O 切AC 于点E .(1) 求证:△ABC 是直角三角形;(2) 若tan A =34时,求AE 的长. (内蒙古中考试题)10.如图,在Rt △ABC 中,∠ABC =90°,以AB 为直径作⊙O 交AC 边于点D ,E 是边BC 中点,连接DE .(1) 求证:直线DE 是⊙O 的切线;(2) 连接OC 交DE 于点F ,若OF =CF ,求tan ∠ACO 的值. (武汉市中考试题)11.如图,⊙O 的半径r =25,四边形ABCD 内接于⊙O ,AC ⊥BD 于点H ,P 为CA 延长线上一点,且∠PDA =∠ABD .(1) 试判断PD 与⊙O 的位置关系,并说明理由;(2) 若tan ∠ADB =34,P A =43-33AH ,求BD 的长;(3) 在(2)的条件下,求四边形ABCD 的面积. (成都市中考试题)ABC BECB 级1.如图,AB 是⊙O 的直径,CD 是弦,过点C 的切线与AD 的延长线交于点E .若∠DAB =56°, ∠ABC =64°,则∠CED =__________.2.如图,⊙O 与矩形ABCD 的边AD ,AB ,BC 分别相切于点E ,F ,G ,P 是EG 上的一点,则∠EPF =__________. (广州市中考试题)第1题图 第2题图 第3题图3.如图,直线AB ,AC 与⊙O 分别相切于点B ,C 两点,P 为圆上一点,P 到AB ,AC 的距离分别为4cm ,6cm ,那么P 到BC 的距离为__________cm. (全国初中数学联赛试题)4.如图,在Rt △ABC 中,∠A =90°,⊙O 分别与AB ,AC 相切于点E ,F ,圆心O 在BC 上,若AB =a ,AC =b ,则⊙O 的半径等于( )A .abB .a +b 2C .aba +bD .a +b ab5.如图,在⊙O 的内接△ABC 中,∠ABC =30°,AC 的延长线与过点B 的⊙O 的切线相交于点D .若⊙O 的半径OC =1,BD ∥OC ,则CD 的长为( )A .1+33 B .233 C .33D . 2第4题图 第5题图 第6题图6.如图,⊙O 的内接△ABC 的外角∠ACE 的平分线交⊙O 于点D .DF ⊥AC ,垂足为F ,DE ⊥BC ,垂足为E .给出以下四个结论:①CE =CF ;②∠ACB =∠EDF ;③DE 是⊙O 的切线;④AD =BD .其中正确的结论是( ) (苏州市中考试题)A .①②③B .②③④C .①③④D .①②④7.如图,已知AC 切⊙O 于点C ,CP 为⊙O 的直径,AB 切⊙O 于点D ,与CP 的延长线交于点B .若AC =PC .求证:(1) BD =2BP ;(2) PC =3BP . (天津市中考试题)8.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AB =12cm ,AD =8cm ,BC =22cm ,AB 为⊙O 的直径.动点P 从点A 开始沿AD 边向点D 以1cm/s 的速度运动,动点Q 从点C 开始沿CB 边向点B 以2cm/s 的速度运动. P ,Q 分别从点A ,C 同时出发,当其中一个动点到达端点时,另一个动点也随之停止.设运动时间为t (s).(1) 当t 为何值时,四边形PQCD 为平行四边形?(2) 当t 为何值时,PQ 与⊙O 相切? (呼和浩特市中考试题)9.如图,已知在△ABC 中,∠ABC =90°,O 是AB 上一点,以O 为圆心,OB 为半径的半圆与AB 交于点E ,与AC 切于点D ,AD =2,AE =1.求证:S △AOD ,S △BCD 是方程10x 2-51x +54=0的两个根. (河南省中考试题)10.如图,点O 在∠APB 的平分线上,⊙O 与P A 相切于点C . (1) 求证:直线PB 与⊙O 相切;(2) PO 的延长线与⊙O 交于点E ,若⊙O 的半径为3,PC =4,求弦CE 的长.(武汉市中考试题)CCABDE11.如图,直线y =43x +4交x 轴于点B ,交y 轴于点A ,⊙O ′过A ,O 两点.(1) 如图1,若⊙O ′交AB 于点C ,当O ′在OA 上时,求弦AC 的长; (2) 如图2,当⊙O ′与直线l 相切于点A 时,求圆心O ′的坐标;(3) 当O ′A 平分△AOB 的外角时,请画出图形,并求⊙O ′的半径的长.12.如图,AB 是⊙O 的直径,AB =d ,过点A 作⊙O 的切线并在其上取一点C ,使AC =AB ,连接OC 交⊙O 于点D ,BD 的延长线交AC 于点E . 求AE 的长. (四川省竞赛试题)C专题20 直线与圆的位置关系(1)例1、B 提示:连接OD ,则~ODE CBE ∆∆例2、(1)AC =AB = (2)提示:若PA 是⊙O 的切线,则PA ⊥AO ,又BO ⊥AO ,得PA ∥BD ,PB ADBC DC∴=,9030AOD OAC ∠=︒∠=︒,, 120AOC ∠=︒,22AD OD DC ∴==,2PB BC ∴=,即当2PB BC =时,PA 是 ⊙O 的切线例3、 提示(1)证明~PFA PBE ∆∆ (2)当P 为BA 延长线上一点时,第(1)题的结论仍成立例4、(1)略 (2)AF AP AN AD ≠,理由如下:假设AF APAN AD≠,则MN ∥CD 。
初中数学计算能力提升训练测试题.doc

计算能力训练(整式1)6、( 1)计算( 1 )9 210=2(2)计算(x2)3x 5计算能力训练(整式2)计算:(1) ( 3 a2 b3c) ( 2 ab 2 ) 2 ( 3a3b) ;(2)(2a2 3a 5)(3 a 2 ) ;2 3(3)1.25 x3( 8x 2 ) ;(4)(3x) (2x 23x 5) ;(5)2x 3 y (x 2 y) ;(6)利用乘法公式计算:4m 3 2n 4m 32n (7) 5x 2 y 2 y 5x(8)已知a b 5, ab 6 ,试求 a2ab b2的值计算能力训练(整式 3)1、2a 2b 3c 2a 2 b2、3 (x 2 y)33 (x 2 y)34234、当 x5 时, 试求整式 3x 2 2x 2 5x 13x 1 的值5、已知 xy 4 , xy 1 ,试求代数式 ( x 2 1)( y 2 1) 的值6、计算:( 2a 3m 2 n3 a 2m n b 2n 5 2 m ) (a 2m )a8、试确定 52010 7 2011 的个位数字计算能力训练(分式 1) 1.(辨析题)不改变分式的值,使分式( ? )1 x 1 y510的各项系数化为整数,分子、分母应乘以1 x 1 y39A .10B .9C .45D .902.(探究题)下列等式:①( a b) =- a b ; ② x y = x y; ③ a b =- a b ;c c x x c c④m n=-m n中 , 成立的是()mmA .①②B .③④C .①③D .②④23.(探究题)不改变分式23xx的值,使分子、分母最高次项的系数为正数,正确5x 3 2x 3的是(?)A . 3x 2x 2B . 3x 2 x 2C . 3x 2x 2D . 3x 2 x 25x 32x 35x 3 2x 35x 32x 35x 32x 34.(辨析题)分式 4 y 3x ,x 2 1 ,x 2 xy y 2,a 2 2ab 中是最简分式的有()4ax 4 1 x yab 2b 2A .1个B .2个 C.3个 D.4 个5.(技能题)约分:( 1)x 26x 9 ; ( 2)m 23m 2 .x 29m 2m6. (技能题)通分:( 1)x 2 ,y; ( 2)a 1,6.6ab 222a 1 a 29a bc a 17. (妙法求解题)已知1x 2的值x+ =3,求x 4 x 2x1计算能力训练(分式 2)1. 根据分式的基本性质,分式a可变形为()a bA .a B .aa D .aa bC .-ba ba ba 2.下列各式中,正确的是()A . x y = x yx y x y; B .x y =x yx yx y; C . x y = x yx y x y; D . xy = x y xy x y3.下列各式中,正确的是()A . a m aB . a b =0C . ab 1 b 1D .x y1b m ba bac 1 c 1x 2 y 2x y4.( 2005·天津市)若 2,则a 2 2a 3a=a 2 7a 的值等于 _______ .312a 2 ab =_________.5.( 2005·广州市)计算 2b 2a6.公式 x 22 ,2x 33 ,5 的最简公分母为( )( x 1)(1 x)x 1A .( x-1 ) 2B .( x-1 )3 C.( x-1 ) D .( x-1 ) 2( 1-x ) 37.x1 ? ,则?处应填上 _________,其中条件是 __________ .x 1 x 2 1拓展创新题8.(学科综合题)已知 a 2-4a+9b 2+6b+5=0,求 1 -1的值.a b9.(巧解题)已知 x 2+3x+1=0,求 x 2+ 1的值.x 2计算能力训练 ( 分式方程 1)选择1、(2009 年安徽)甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前 天完成任务,则甲志愿者计划完成此项工作的天数是 【A .8 B.7 C .6 D .5】3 2、(2009 年上海市 )3 .用换元法解分式方程 x 13x1 0 时,如果设x 1y ,x x 1x将原方程化为关于 y 的整式方程,那么这个整式方程是()A .y 2y 3 0 . y 23y 1 0B C .3 y 2y 1 0. 3 y 2 y 1 0D3、(2009 襄樊市)分式方程x 3 x 1的解为()x x 1 A .1 B .-1 C .-2D .-34、(2009 柳州) 5.分式方程 12的解是()2x x 3A . x 0B . x 1C . x 2D . x 35 、( 2009 年孝感)关于 x 的方程2 xa1 的解是正数,则 a 的取值范围是x1a >-且 a ≠A . 1 . a >-1 0BC .a <- 1D . a <- 1 且 a ≠- 26、( 2009 泰安)某服装厂准备加工 400 套运动装,在加工完 160 套后,采用了新技术,使得工作效率比原计划提高了 20%,结果共用了 18 天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工 x 套,则根据题意可得方程为( A )160400 18( B )160400 160 18x(1 20%) xx(1 20%) x( C ) 160400 160 18( D )400400 160 18x20% xx(1 20%) x7、(2009 年嘉兴市)解方程8 2的结果是()4 x 2 2 xA . x 2B . x 2C . x 4D .无解8、(2009 年漳州)分式方程 21的解是()x 1 xA .1B .1C .1D .13 39、(09 湖南怀化)分式方程1 2 的解是( )3x 1A . x1 . x 21 D . 1 BC . x x23 310、( 2009 年安徽)甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前 3天完成任务,则甲志愿者计划完成此项工作的天数是【 】A .8 B.7 C .6 D .511、( 2009年广东佛山)方程 1 2 的解是()x 1 xA .0B .1C .2D .312、( 2009 年山西省)解分式方程1x 2 1 ,可知方程()x 2 2 x A .解为 x 2 B .解为 x4 C .解为 x 3 D .无解13、( 2009年广东佛山)方程 1 2 的解是( )x 1 xA .0B .1C .2D .314、( 2009 年山西省)解分式方程1x 2 1 ,可知方程()x 2 2 x A .解为 x 2 B .解为 x4 C .解为 x 3 D .无解计算能力训练 ( 分式方程 2)填空1、( 2009 年邵阳市)请你给 x 选择一个合适的值,使方程 21 成立,你选择的 xx 1 x =________。
2024年中考数学教学工作计划例文(6篇)

2024年中考数学教学工作计划例文本学期,我负责初一1班和2班的数学教学任务。
为确保工作的精确性和全面性,我制定了以下教学工作计划:一、教学理念:本学期,我将以“推动课堂改革,提升教学实效性”为核心,致力于提升每位学生的学习水平。
我将深入领会并贯彻学校的教育理念,坚持以学生为主体,勇于在教学方法上创新,努力成为一位杰出的数学教师。
二、工作目标:通过本学期的教学,期望学生能具备一定的数学素养,能自发地运用数学知识解决实际问题,形成坚实的数学基础。
培养一批数学优秀生,使他们掌握有效的学习方法。
减少不及格人数,营造良好的学习风气,养成良好的数学学习习惯。
并建立和谐的师生关系,促进学生的全面发展。
(一)、深入学习,树立新教学观念:开学初期,我将全面研读数学新课程标准,深入探究,以理解其核心理念为教学指导,确保教学实践与《标准》要求相一致,以实现对所有学生的有效教学,促进他们的全面发展。
(二)、了解学生心理特点,激发学习动力:初中阶段,学生心理发生显著变化,对“独立自主”的需求增强,但可能对中学阶段的挑战准备不足。
因此,教师需激发学生的学习兴趣,让他们了解数学在日常生活中的应用,通过实际体验增强他们对数学学习的直接兴趣。
教师在言行上要尊重学生的自尊心,鼓励他们积极参与课堂讨论。
(三)、以课堂教学为关键:(1)作为教师,我将全面掌握教材,精心备课,充分考虑学生、教学方法等因素。
设计教学内容时,要确保各环节过渡自然,提出的问题应具有层次性和挑战性,以满足不同学生的学习需求。
在学生方面,通过设立学习小组,利用小组合作的方式,促进优生帮助差生,带动中等生,以此提高整体教学质量。
2024年中考数学教学工作计划例文(二)一、教材内容体系分析本册教材共涵盖六章内容,其中关于空间与图形的章节为两章,即第四章《相似图形》与第六章《证明》(一);关于数与代数的章节为三章,分别是第一章《一元一次不等式和一元一次不等式组》、第二章《分解因式》及第三章《分式》;而关于统计与概率的内容则集中在一章,即《数据的搜集与处理》。
新人教版(2024版)版)初中数学七年级上册 第四章整式的加减 4.1.1单项式 教学设计

课堂教学设计
、章节、港珠澳大桥
港珠澳大桥是集主桥、海底隧道和人工岛于一体的世界上最长的
跨海大桥.一辆汽车从香港口岸行驶到东人工岛的平均速度为96
km/h,在海底隧道和主桥上行驶的平均速度分别为72 km/h和92
km/h.请根据这些数据回答下列问题:
(1)汽车在主桥上行驶t h的路程是多少千米?如果汽车通过海底隧
道需要a h,从香港口岸行驶到东人工岛的时间
(2)是通过海底隧道时间的1.25倍,你能用含a的代数式表示香港
口岸到西人工岛的全长吗?
(3)如果汽车通过主桥需要b h,通过海底隧道所需时间比通过主
桥的时间少0.15h,你能用含b的代数式表示主桥与海底隧道长
度的和吗?主桥与海底隧道的长度相差多少千米?
要解决上面的问题,需要进一步学习代数式.在本章中,我们
将学习一类基本的代数式--整式,以及整式的加减运算.你将进一
步学习列代数式表示数量和数量关系,体会数与整式在加减运算
中的一致性,为后续学习方程、不等式、函数等内容打下基础
引起学生的学习兴趣,激
发学生学习数学的热情
例1.用单项式填空,并指出它们的系数和次数.
(1)每包书有12册,n包书有_______册.
(2)底边长为a,高为h的三角形的面积是______.
(3)一个长方体的长和宽都是a,高是h,它的体积是____
(4)一台电视机原价a元,现按原价的9折出售,这台电视机现在售价为_____元.
(5)一个长方形的长为0.9,宽是a,这个长方形的面积是_________.
例2、填空
例3、用字母表示数后,同一个式子可以表示不同的含义.你能赋予0.9a一个含义吗?项式的概念
学抽象能力核心素养。
数学新课程标准试题及答案

数学新课程标准试题及答案【篇一:2014版初中数学新课程标准理论测试题及答案】lass=txt>学校姓名分数一、填空题(每空1分,共35分)1、义务教育阶段数学课程目标分为总目标和学段目标,从2、数学课程目标包括3、在各学段中,安排了四个部分的课程内容:“” “”“”“ ”。
“”内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题,培养学生的问题意识、应用意识和创新意识,积累学生的活动经验,提高学生解决现实问题的能力。
4、在数学课程中,应当注意发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、、和模型思想。
为了适应时代发展对人才培养的需要,数学课程还要特别注重发展学生的和。
5、教学活动是师生积极参与、 6、有效的数学教学活动是教师教与学生学的统一,应体现“”的理念,促进学生的。
7、数学课程标准包括前言、 8、好的教学活动,应是学生 9、数学知识的教学,要注重知识的“,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好的关系,引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同的层次进行理解。
10、评价结果的呈现应采用11、学生的现实主要包括生活现实、、其他学科现实三个方面。
12、数学教学在总体目标中突出了“方向及目标价值取向。
13、对学生的培养目标在具体表述上作了修改,提出了“两能”,即的能力、的能力。
14、教材一方面要符合数学的二、选择题(每题2分,共20分)1、义务教育阶段的数学课程是培养公民素质的基础课程,它不具有()a、基础性b、普及性c、发展性d、连续性2、对于教学中应当注意的几个关系,下列说法中错误的是() a、面向全体学生与关注学生个体差异的关系。
b、“预设”与“生成”的关系。
c、合情推理与演绎推理的关系。
d、使用现代信息技术与教学思想多样化的关系。
3、()是对教材编写的基本要求。
a、直观性b、科学性c、教育性d、合理性4、()是考查学生课程目标达成状况的重要方式,合理地设计和实施它有助于全面考查学生的数学学业成就,及时反馈教学成效,不断提高教学质量。
初中数学计算能力训练及强化练习

For personal use only in study and research;not for commercial use初中数学计算能力训练计算是一种能力,亦是提高成绩的关键数学是一门严谨的学科,魅力又在于“活”,数学处处都与计算密切相关,计算不是枯燥的代名词,充满了观察、推理、判断,培养学生思考问题的灵活性以及周密严谨的思维能力等。
中考数学满分120分,与计算相关的题目约占100分,准确、快速地得出计算结果,能有效提高学生理科成绩,帮助学生直达名校!学生常见的计算问题有哪些?学生在分析计算错误时,不知道如何分析,往往归因于“粗心马虎”,告诉自己“下次注意”就可以,可事实却总是事与愿违。
在计算方面学生容易出现哪些问题呢?1.看到题目,不仔细审题,就慌忙答题,要求解周长,仅求出边长,做到一半发现遗漏隐含条件或有其他简单方法,思路大乱。
2.在大脑停止思考时,容易疏忽大意,抄错数。
3.没有严格依据法则和运算律来运算。
准确记忆法则和运算律是前提,关键是无论何时何地都能正确地运用。
比如两式相减求绝对值,如果前面有负号,容易错;乘法满足分配律,不少学生也误认为除法也满足分配律等。
4.没有按照计算流程来走,认为一步一步写计算很麻烦,计算时跳步太大。
5.越是成功在望,越容易大意,不少同学在倒数计算第二步时放松警惕,结果导致结果错误。
6.缺乏检查意识,不知道怎么检查。
误以为检查就是把题目再做一遍,对异常结果不敏感,不知道积累自己的易错点,不善于结合题目背景进行检查,比如价格不可能是负数等。
初中数学计算能力训练目录<1>()1100251013÷-+÷⨯3<2>3021220093026π-⎛⎫⎛⎫-++-︒ ⎪ ⎪⎝⎭⎝⎭<3>cos 45cos 60sin 45cos30︒-︒︒-︒<4>2cos30sin120tan 45sin 135cos120tan 60︒-︒-︒︒+︒+︒31--<6>04211tan 45cos60sin 452-+-- <7>22cos30sin 45cos 602sin 30tan 60tan 45--+⋅<8>()((200920092010200812332⎛⎫-- ⎪⎝⎭<9>3⎫÷<11>))(21131- <12>()357921n ++++⋅⋅⋅++ <13>2311112222n⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ <14>()()222223557799112123n n ++++⋅⋅⋅+⨯⨯⨯⨯++ <15>()()()()27343532x x x x +-++-<16>()()222222x xy y x xy y -+++<17>当x =()()()()2212241x x x x x -++---的值<18>因式分解: 2105ax ay by bx -+-<19>因式分解:42242mx mx y my -+<20>因式分解:4245x x --<21>因式分解:()222164x x -+ <22>因式分解:32128xy x y --+<23>因式分解:2269a b b -+- <24>22b b a a b-++ <25>21613962x x x x-----+ <26>232396127962x x x x x x x x++-+---+<27>当11a b =+=22112b a b a b a ab b ⎛⎫-÷ ⎪-+-+⎝⎭的值 <28>已知210x x +-=,求()()254x x +-的值<29>已知2310x x +-=,求2352362x x x x x -⎛⎫÷+- ⎪--⎝⎭的值 <30>已知210x x +-=,求221x x+的值 <31>已知234x y z ==,求22222232x y z x xy z -+-+的值<32>已知tan θθ=为锐角,求4cos 3sin 2cos sin θθθθ-+的值 <33>已知a b c k b c c a a b===+++,求k 的值 <34>已知112a b -=,求223a ab b a ab b----的值<35>2<36>先化简2x -<37>已知x y ==,求22x xy y ++的值<38>已知8,3x y xy +=-=,求 <39>配方:2257y x x =++<40>配方:21572y x x =-++ <41>配方:()()3002100y x x =-+<42>配方:1126s t t ⎛⎫=- ⎪⎝⎭<43>配方:()()2000.5300.6m n n =+- <44>45243x x x -++=-<45>(220x x -+=<46>()22x x x +=+7x =1=<49>236x x += <50>221142y y =--+ <51>2152142x x+=-- <52>22416214x x x x x x --=++--- <53>()()21117217231x x x x x x +=++-+-+ <54>2124111x x x x x x -+=+-- <55>()()222161711x x x x +++=++ <56>42222112x x x x x++++=5=<58>2312341m nm n-=⎧⎨+=⎩<59>121117x yx y⎧-=⎪⎪⎨⎪+=⎪⎩<60>168xy xxy x+=⎧⎨-=⎩<61>221235x yx xy y+=⎧⎨++=⎩<62>42x yxy+=-⎧⎨=⎩<63>22104x yx y⎧+=⎨+=⎩<64>864x yy zz x+=⎧⎪+=⎨⎪+=⎩<65>421593106a b ca b ca b c++=⎧⎪-+=⎨⎪++=⎩<66>221345x y y z z x--+===<67>10573244x y zx z⎧==⎪⎨⎪+=⎩<68>:3:2:5:466x yy zx y z=⎧⎪=⎨⎪++=⎩<69>请写出满足x<≤x<70>解不等式()()()2131x x x x--≥-+并把解集在数轴上表示出来<71>21x <+并把解集在数轴上表示出来<72>求不等式2752x x -<-的最大整数解<73>解不等式2560x x -->并把解集在数轴上表示出来<74>解不等式2560x x -+<并把解集在数轴上表示出来<75>解不等式2560x x --+>并把解集在数轴上表示出来<76>解不等式2560x x ---<并把解集在数轴上表示出来<77>解不等式组()3214213212x x x x ⎧--≤⎪⎪⎨+⎪>-⎪⎩并把解集在数轴上表示出来 <78>解不等式组()3172513x x x x --≤⎧⎪⎨--<⎪⎩并把解集表示在数轴上 <79>解不等式组()33121318x x x x -⎧+≥+⎪⎨⎪--<-⎩并写出该不等式的整数解<80>求不等式组205121123x x x ->⎧⎪+-⎨+≥⎪⎩的非正整数解 <81>求不等式组10223x x x +>⎧⎪-⎨≤+⎪⎩的最大整数解For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文For personal use only in study and research; not for commercial use。
《19.2.1正比例函数》作业设计方案-初中数学人教版12八年级下册

《正比例函数》作业设计方案(第一课时)一、作业目标本作业设计旨在通过正比例函数的基础知识学习,使学生能够理解正比例函数的概念、图像及性质,掌握正比例函数的基本运算,为后续学习打下坚实基础。
二、作业内容1. 基础知识练习:(1)理解正比例函数的概念,掌握其定义及表达形式。
(2)能根据已知条件,判断一个函数是否为正比例函数。
(3)理解正比例函数的图像特征,并能根据函数表达式绘制其图像。
2. 运算技能训练:(1)掌握正比例函数的基本运算,包括加减、乘除等。
(2)通过实例练习,掌握正比例函数在实际问题中的应用。
3. 问题解决能力培养:(1)通过典型例题,提高学生运用正比例函数知识解决实际问题的能力。
(2)鼓励学生探索不同解题方法,培养其创新思维能力。
三、作业要求1. 学生需独立完成作业,不得抄袭他人答案。
2. 学生在完成作业过程中,应注重思考与总结,形成自己的解题思路。
3. 作业应字迹工整,答案准确,步骤完整。
4. 在解决问题时,学生应尝试多种方法,拓展思路,提高解题能力。
四、作业评价1. 教师将对每位学生的作业进行批改,评价其正确性、规范性及创新性。
2. 评价标准包括基础知识掌握、运算技能、问题解决能力等方面。
3. 对于优秀作业,将在课堂上进行展示,鼓励其他学生学习借鉴。
五、作业反馈1. 教师将根据学生作业情况,进行针对性的辅导和指导,帮助学生解决学习中遇到的问题。
2. 对于共性问题,教师将在课堂上进行讲解和示范,确保学生能够掌握相关知识。
3. 鼓励学生之间互相交流学习心得和解题方法,形成良好的学习氛围。
4. 定期组织学生进行阶段性测试,检验学生对正比例函数知识的掌握情况,及时调整教学策略。
通过以上作业设计,旨在通过系统性的练习和思考,让学生更加深入地理解和掌握正比例函数的知识,同时提高其运算能力和问题解决能力。
相信在教师与学生共同努力下,学生们将能够取得良好的学习效果,为后续的数学学习打下坚实的基础。
2023最新义务教育数学新课程标准(2022版)学习检测试题及答案

2023最新义务教育数学新课程标准(2022版)学习检测试题及答案一、选择题1.在义务教育阶段, ()主要表现为:运算能力、推理意识或推理能力。
(分值:2分)A. 数学思维 (答案)B. 数学思想C. 数学语言D. 数学眼光2.在义务教育阶段,数学眼光,主要表现在以下四个方面,下列表述不正确的是()(分值:2分)A. 抽象能力(包括数感、量感、符号意识)B. 几何直观C. 空间观念D. 创新意识E. 科学精神 (答案)3.义务教育数学课程目标是以学生发展为本,以核心素养为导向,进一步强调学生获得数学的四项基本(简称“四基”),以下说法不正确的一项是()(分值:2分)A. 基础知识B. 基本技能C. 基本思想D. 基本活动经验E. 基本方法 (答案)4.数学课程目标里,有发展运用数学知识与方法,训练四项能力(简称“四能”)进而形成正确的情感、态度和价值观的描述,下列哪一项是不正确的()(分值:2分)A. 发现问题的能力B. 提出问题的能力C. 分析问题的能力D. 解决问题的能力E. 探究问题的能力 (答案)5.数学核心素养,主要表现以下三个方面(简称“三会”),以下表述不正确的一项是()(分值:2分)A. 会用数学的眼光观察现实世界B. 会用数学的思维思考现实世界C. 会用数学的语言表达现实世界D. 会用数学的方法获取更高分数 (答案)6.义务教育阶段数学课程内容由四个学习领域组成,下列说法错误的一项是()(分值:2分)A. 数与代数B. 图形与几何C. 统计与概率D. 综合与实践E. 计算和应用 (答案)7.对义务教育数学课程理念下列描述不正确的一项()(分值:2分)A. 确立核心素养导向的课程目标设计B. 体现结构化特征的课程内容实施C. 促进学生发展的教学活动心 D. 探索激励学习和改进教学的评价E. 促进信息技术与数学课程融合F. 发展学生的数学思维 (答案)8.数学为人们提供了一种描述与交流现实世界的表达方式,下列对数学语言的作用,说法不正确的是() (分值:2分 )A. 可以简约精确的描述自然现象科学情境和日常生活中的数量关系与空间形式。
