基本形体转动惯量

常见刚体转动惯量

常见刚体转动惯量刚体转动惯量是描述刚体围绕某一轴旋转时所表现出的惯性特性。

研究刚体转动惯量的目的是为了更好地理解刚体的运动规律和性质。

在物理学中，刚体转动惯量通常用I表示，它是刚体质量分布在旋转轴周围的离散点上的质量分布和离转轴距离的平方乘积之和。

刚体转动惯量的大小与刚体的形状、质量分布和旋转轴的位置有关。

对于具有均匀质量分布的刚体，其转动惯量可用简单的公式进行计算。

例如，对于一个球体，其转动惯量可表示为2/5 * m * r^2，其中m为球体的质量，r为球体的半径。

对于其他形状的刚体，如长方体或圆柱体，可以通过相应的公式计算其转动惯量。

刚体转动惯量在物理学中有着广泛的应用。

在工程领域，研究刚体转动惯量可以帮助设计合适的机械系统，确保其运动的稳定性和平衡性。

在运动学和动力学领域，刚体转动惯量是分析刚体旋转运动的重要参数。

在天文学中，研究天体的转动惯量可以帮助科学家理解宇宙中的星系和行星的运动规律。

除了了解刚体转动惯量的物理意义，我们还可以从中体会到自然界的奥秘和美妙。

刚体转动惯量的大小不仅取决于其形状和质量分布，还取决于旋转轴的位置。

这意味着刚体的旋转运动是一种既复杂又精确的过程。

正是由于刚体转动惯量的存在，我们才能观察到日常生活中的许多有趣现象，如陀螺的旋转、滚筒的滚动和车辆的转弯等。

当我们试图推动一个旋转的陀螺或转动的滚筒时，我们会感受到转动惯量的作用。

由于转动惯量的存在，我们需要施加更大的力才能改变刚体的旋转状态。

这也是为什么陀螺和滚筒在旋转时保持稳定的原因。

刚体转动惯量的概念使我们能够更好地理解和解释这些现象。

刚体转动惯量是描述刚体围绕某一轴旋转时所表现出的惯性特性。

它与刚体的形状、质量分布和旋转轴的位置有关，具有重要的物理意义和广泛的应用。

通过研究刚体转动惯量，我们可以更好地理解和解释刚体旋转运动的规律，并体会到自然界的奥秘和美妙。

希望这篇文章能够使读者对刚体转动惯量有更深入的了解，并对物理学产生更大的兴趣。

转动惯量公式是什么怎么计算

转动惯量公式是什么怎么计算
在经典力学中，转动惯量通常以I或J表示，SI单位为kg·m ²。

对于一个质点，I=mr²，其中m是其质量，r是质点和转轴的垂直距离。

转动惯量公式是什么怎么计算
1转动惯量是什么
转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

在经典力学中，转动惯量（又称质量惯性矩，简称惯矩）通常以I或J表示，SI 单位为kg·m²。

对于一个质点，I=mr²，其中m 是其质量，r是质点和转轴的垂直距离。

转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

2质量转动惯量
其量值取决于物体的形状、质量分布及转轴的位置。

刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航
天、电力、机械、仪表等工业领域也是一个重要参量。

电磁系仪表的指示系统，因线圈的转动惯量不同，可分别用于测量微小电流（检流计）或电量（冲击电流计）。

在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上，精确地测定转动惯量，都是十分必要的。

转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。

形状规则的匀质刚体，其转动惯量可直接用公式计算得到。

而对于不规则刚体或非均质刚体的转动惯量，一般通过实验的方法来进行测定，因而实验方法就显得十分重要。

转动惯量应用于刚体各种运动的动力学计算中。

转动惯量标准

转动惯量标准
转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。

转动惯量的SI单位为kg·m²。

对于一个质点，I=mr²，其中，m是其质量，r是质点和转轴的垂直距离。

转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。

在规则物体中，其转动惯量可以按照相应公式直接计算；对于外形复杂和质量分布不均的物体，转动惯量可通过实验方法来测定。

实验室中最常见的转动惯量测试方法为三线摆法。

此外，转动惯量的量纲为L²M，在SI单位制中，它的单位是kg·m²。

转动惯量是刚体转动时惯性的量度，其量值取决于物体的形状、质量分布及转轴的位置。

刚体对一轴的转动惯量，可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。

以上内容仅供参考，建议查阅关于转动惯量的书籍文献，或者咨询物理学专业人士，以获取最准确的信息。

转动惯量计算公式

转动惯量计算公式转动惯量（也称为惯性矩或转动惯性）是物体抵抗转动的能力的度量，是物体转动时的一项重要物理性质。

在机械工程、物理学、航空航天等领域中，转动惯量的计算是解决相关问题的关键。

转动惯量可以通过各种形状的物体的质量分布来计算，例如直线、薄片、圆筒、球体等。

不同形状的物体转动惯量的计算公式也有所不同。

在本文中，我们将介绍几种常见形状的物体的转动惯量计算公式。

1. 直线的转动惯量计算公式当物体是一个直线时，其转动惯量可以用关于质量和长度的公式来计算。

以下是直线转动惯量的计算公式：•绕质心轴的转动惯量：$I = \\frac{1}{3} m l^2$•绕端点轴的转动惯量：$I = \\frac{1}{12} m l^2$其中，I是转动惯量，I是物体的质量，I是直线的长度。

2. 圆筒的转动惯量计算公式圆筒是一种常见的物体形状，例如水桶、轮胎等。

对于圆筒的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{1}{2} m r^2$•绕圆轴的转动惯量：I=II2其中，I是转动惯量，I是圆筒的质量，I是圆筒的半径。

3. 薄片的转动惯量计算公式薄片是一个平面形状的物体，例如纸片、金属片等。

对于薄片的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{1}{4} m a^2$•绕边缘轴的转动惯量：$I = \\frac{1}{3} m a^2$其中，I是转动惯量，I是薄片的质量，I是薄片的边长。

4. 球体的转动惯量计算公式球体是一个球形物体，例如篮球、乒乓球等。

对于球体的转动惯量计算，有以下公式：•绕质心轴的转动惯量：$I = \\frac{2}{5} m r^2$•绕直径轴的转动惯量：$I = \\frac{2}{3} m r^2$其中，I是转动惯量，I是球体的质量，I是球体的半径。

5. 其他形状的转动惯量计算公式除了上述常见形状的物体，其他形状的转动惯量计算公式也可以通过积分或者几何关系得到。

转动惯量计算公式单位

转动惯量计算公式单位转动惯量是描述物体转动惯性的一个重要物理量，它在物理学中有着广泛的应用。

那咱们就来好好聊聊转动惯量计算公式以及它所涉及的单位。

先来说说转动惯量的计算公式吧。

对于一个质点，转动惯量 I 等于质量 m 乘以质点到转轴的距离 r 的平方，即 I = m * r²。

要是一个刚体是由多个质点组成的，那转动惯量就得把每个质点的转动惯量加起来。

举个例子啊，就说一个均匀圆盘吧。

假设圆盘的质量是 M ，半径是 R ，那它的转动惯量 I 就是 1/2 * M * R²。

在计算转动惯量的时候，单位可太重要啦。

质量的单位通常是千克（kg），距离的单位通常是米（m），所以转动惯量的单位就是千克·米²（kg·m²）。

我想起之前给学生们上课的时候，讲到这个知识点，有个学生就迷糊了，怎么都搞不清楚单位的换算。

我就给他举了个特别形象的例子。

我说：“你就想象啊，这质量就好比是一群小人儿，距离呢，就是小人儿排队的长度。

那转动惯量呢，就是这些小人儿按照一定规则排好队形成的一个大场面。

千克就是小人儿的数量，米就是队伍的长度，那千克·米²就像是这个大场面的规模。

” 这学生听了之后，眼睛一下子亮了，好像突然就开窍了。

在实际的物理问题中，准确地运用转动惯量计算公式和单位，能帮助我们更好地理解物体的转动行为。

比如说，在机械设计中，要考虑零件的转动惯量，以确保机器的运行平稳；在天体物理学中，研究天体的自转也离不开转动惯量的计算。

总之，转动惯量计算公式和单位虽然看起来有点复杂，但只要咱们多琢磨，多联系实际，就能轻松掌握，为解决各种物理问题打下坚实的基础。

所以啊，同学们，别害怕转动惯量这个概念，好好理解它，就能在物理学的世界里畅游啦！。

转动惯量的概念_它是描述转动惯性大小的物理量

1、转动惯量的概念：它是描述转动惯性大小的物理量①对某轴转动惯性的大小用转动惯量I描述，其定义为：I=∑mi p i2即转动惯量=各质点的质量与该点到转轴距离平方乘积之和。

显然，I的单位为kg〃m2 ②对定点的转动惯性的大小，由于转轴的方向不断变化，要用一个张量才能描述。

其中Ixx ,Iyy,……叫惯量系数2、转动惯量的计算公式对定轴的转动惯量I,由刚体的质量分布和转轴的位置决定。

已知转轴的位置和刚体的质量分布，求I的计算公式有：①I=∑mi pi2（pi为质点i到轴的距离）；②对质量连续分布的刚体，I=∫p2dm（ρ为质量元dm到轴之距离）3、回转半径设刚体绕轴S的转动惯量为I，若有一质点的质量等于刚体的质量m，它到轴的距离K满足:I=mk2=∫p2dm，则K就称为该刚体绕轴S的回转半径.由定义,有4、计算转动惯量及回转半径的步骤，例一般步骤是：①选取坐标系和质量元dm②由公式I=∫p2dm和m=∫dm求出I以及刚体的总质量m③由I=mk2求出k计算的关键是确定dm和ρ计算中常用到下列已知结果：半径为r的均质球壳绕直径的转动惯量 I=(2/3)mr2半径为r的均质圆盘绕过圆心且垂直圆面的轴的转动惯I=(1/2)mr2[例1]求质量密度为的非均质圆球绕直径的回转半径K。

解：取半径为r→r+dr的球壳做作质量元，它的质量dm和对直径的转动惯量dI分别为：dI=(2/3)r2dm∴球体对直径的转动惯量I和总质量m分别为所以回转半径绕定点转动时转动惯量有一定的空间分布.我们以定点O为原点，在过O的轴ON上取一点Q，使，当刚体转动时，轴ON也随刚体绕O点转动而动，按此规则，所得到的Q点的集合将在空间形成一个包围O点的椭球面，曲面包围的是一个椭球，称为惯量椭球,它形象的描述了刚体绕定点O转动的转动惯量的空间分布.曲面方程为二次曲面：应注意：（1）惯量椭球是形象描述刚体绕定点转动时，转动惯量空间分布而按上述规则所得到的球，它与刚体无共同之处，它不是刚体，即使刚体为椭球,它们也无共同之处（见图3.5.1）（2）惯量椭球是在动坐标系中的立体图形。

10种常见刚体转动惯量公式

10种常见刚体转动惯量公式
10种常见刚体转动惯量公式
10种常见刚体转动惯量公式
刚体转动惯量是指刚体在转动运动时所需要的转动势能。

它可以衡量刚体转动时所需要的力的大小。

常见的刚体转动惯量公式有以下10种：
1.圆柱体转动惯量公式：I=1/2mr^2
2.圆锥体转动惯量公式：I=1/3mr^2
3.球体转动惯量公式：I=2/5mr^2
4.圆筒体转动惯量公式：I=1/2mr^2
5.正方体转动惯量公式：I
6.三棱锥体转动惯量公式：I=1/3mr^2
7.六棱锥体转动惯量公式：I=1/4mr^2
8.五棱锥体转动惯量公式：I=1/5mr^2
9.四棱锥体转动惯量公式：I=1/6mr^2
10.八棱锥体转动惯量公式：I=1/8mr^2
在上述公式中，m表示刚体的质量，r表示刚体的转动半径。

转动惯量知识点总结

转动惯量知识点总结一、转动惯量的概念转动惯量是刚体绕轴线旋转时所具有的惯性特征，它与刚体的质量分布和轴线的位置有关。

在欧拉角速度矢量下，刚体绕固定轴的角动量随时间的变化率正比于力矩，且比例常数即为该轴的转动惯量。

转动惯量通常用大写字母I表示，单位为千克·米平方（kg·m²）。

对于质点系来说，转动惯量的计算公式为：I = Σmiri²其中，mi为质点i的质量，ri为质点i到转轴的距离。

对于连续体来说，转动惯量的计算需要用到积分来表示：I = ∫r²dm其中，r为质点到转轴的距离，dm为质点的微元质量。

转动惯量的概念在刚体转动运动的研究中起着非常重要的作用，它对于研究刚体的稳定性、振动特性、转子动力学等方面都具有重要意义。

二、转动惯量的计算1. 轴对称体的转动惯量轴对称体指的是绕对称轴旋转时，其转动惯量在各个轴上都相等。

常见的轴对称体包括圆柱体、球体等。

对于轴对称体来说，其转动惯量的计算公式为：I = 1/2mr²其中，m为轴对称体的质量，r为轴对称体相对于转轴的距离。

2. 复合体的转动惯量复合体是由多个不同形状的物体组合而成的，对于复合体的转动惯量的计算需要考虑各个部分的转动惯量之和。

对于复合体来说，其转动惯量的计算公式为：I = ΣIi其中，Ii为各个部分的转动惯量。

3. 平行轴定理平行轴定理是指，如果已知一个物体绕通过其质心的轴的转动惯量，那么它绕与该轴平行且距离为d的轴的转动惯量可以通过以下公式进行计算：I = Icm + md²其中，Icm为物体绕通过其质心的轴的转动惯量，m为物体的质量，d为两个轴之间的距离。

通过以上计算方法，可以得到各种形状的物体绕不同轴旋转时的转动惯量。

三、转动运动的相关知识点1. 角速度和角加速度角速度和角加速度是描述刚体转动运动的重要物理量。

角速度表示单位时间内角度的增量，通常用希腊字母ω表示，其计算公式为：ω = Δθ/Δt其中，ω为角速度，Δθ为角度的增量，Δt为时间的增量。

几种常见刚体的转动惯量

转动惯量是物体在转动时所受到的力的量纲，它可以反映物体的质量，影响物体的转动情况。

转动惯量的大小与物体的形状，质量和分布有关。

转动惯量的单位为克·米2。

常见刚体的转动惯量可分为三类：球体、圆柱体和轴对称体。

球体的转动惯量球体的转动惯量可以用公式表示为：I=2/5 MR2，其中M为球体的质量，R为球体的半径。

由于球体的形状和质量分布恒定，因此球体的转动惯量只与质量和半径有关，与其他参数无关。

圆柱体的转动惯量圆柱体的转动惯量可以用公式表示为：I=1/2 MR2，其中M为圆柱体的质量，R为圆柱体的半径。

由于圆柱体的形状和质量分布恒定，因此圆柱体的转动惯量只与质量和半径有关，与其他参数无关。

轴对称体的转动惯量轴对称体的转动惯量可以用公式表示为：I=1/2 MR2，其中M为轴对称体的质量，R为轴对称体的半径。

由于轴对称体的形状和质量分布恒定，因此轴对称体的转动惯量只与质量和半径有关，与其他参数无关。

以上就是常见刚体的转动惯量的介绍，可以看出，转动惯量与物体的形状，质量和分布有关，因此，在计算物体转动惯量时，必须考虑到这些因素。

转动惯量是物体转动运动中重要的参数，它可以反映物体的质量，影响物体的转动情况。

因此，转动惯量的研究和应用是重要的。

例如，转动惯量可以用来计算物体的角动量，进而计算物体的角速度和角加速度，从而更好地控制物体的运动。

此外，转动惯量也可以用来计算物体的转矩，从而更好地控制物体的运动。

总之，转动惯量是物体转动的重要参数，它可以反映物体的质量，影响物体的转动情况，因此，转动惯量的研究和应用是重要的。

转动惯量

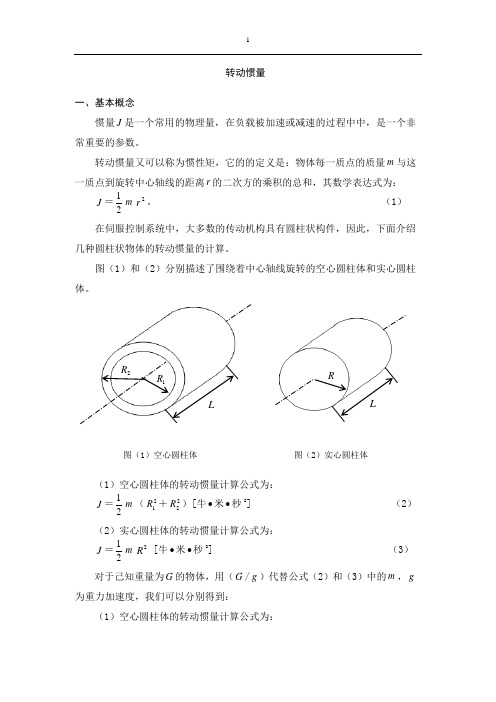
转动惯量一、基本概念惯量J 是一个常用的物理量，在负载被加速或减速的过程中中，是一个非常重要的参数。

转动惯量又可以称为惯性矩，它的的定义是：物体每一质点的质量m 与这一质点到旋转中心轴线的距离r 的二次方的乘积的总和，其数学表达式为：J ＝21m 2r 。

（1）在伺服控制系统中，大多数的传动机构具有圆柱状构件，因此，下面介绍几种圆柱状物体的转动惯量的计算。

图（1）和（2）分别描述了围绕着中心轴线旋转的空心圆柱体和实心圆柱体。

图（1）空心圆柱体图（2）实心圆柱体（1）空心圆柱体的转动惯量计算公式为：J ＝21m （21R ＋22R ）[牛∙米∙秒2] （2）（2）实心圆柱体的转动惯量计算公式为：J ＝21m 2R [牛∙米∙秒2] （3）对于己知重量为G 的物体，用（G /g ）代替公式（2）和（3）中的m ，g 为重力加速度，我们可以分别得到：（1）空心圆柱体的转动惯量计算公式为：J ＝gR R G 2)(2221+[牛∙米∙秒2] （4）（2）实心圆柱体的转动惯量计算公式为：J ＝gGR 22[牛∙米∙秒2] （5）如果重量不知道，但知道旋转物体的体积V 和密度γ，则可用（V γ/g ）代替公/式（2）和（3）中的m ，我们可以得到：（1）空心圆柱体的转动惯量计算公式为：J ＝)(24142R R gL -γπ[牛∙米∙秒2] （6）（2）实心圆柱体的转动惯量计算公式为：J ＝42R gL γπ[牛∙米∙秒2] （7）二、计算举例说明1.换向器的惯性矩K JK J ＝81.910)(32244-⨯-⨯K K KiK l D D γπ[克∙厘米∙秒2]。

换向器的几何尺寸：换向器的外径K D ＝0.6[厘米]；换向器的内径Ki D ＝0.38[厘米]；换向器的轴向长度K l ＝0.5[厘米]。

在几何尺寸和材料已知的情况下，换向器的惯性矩K J 为：K J ＝81.910)(32244-⨯-⨯K K KiK l D D γπ＝＝81.9105.75.0)38.06.0(32244-⨯⨯⨯-⨯π＝4.079×510- [克∙厘米∙秒2]，式中，K γ是换向器材料的平均比重，取K γ≈7.5[克/厘米3]。

常见刚体的转动惯量

附录
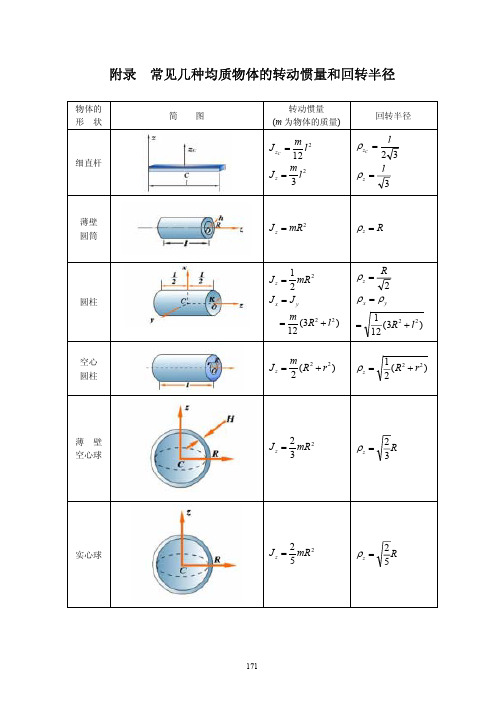
物体的形状
常见几种均质物体的转动惯量和回转半径
简图转动惯量 (m 为物体的质量) 回转半径
J zC =
细直杆
m 2 l 12 m Jz = l2 3
2 3 l ρz = 3
C
ρz =
l
Hale Waihona Puke 薄壁圆筒J z = mR 2
ρz = R
圆柱
1 mR 2 2 Jx = Jy Jz = = m ( 3R 2 + l 2 ) 12
ρz =
3 r 10 3 (4r 2 + l 2 ) 80
ρx = ρy
=
圆环
3 J z = m( R 2 + r 2 ) 4
ρ z = R2 + r2
3 4
Jz =
椭圆形薄板
m 2 (a + b2 ) 4 m J y = a2 4 m J y = b2 4
1 2 a + b2 2 a ρx = 2 b ρy = 2
1-1 FR=645N. 1-2
Mx =
(
)
第二章 2-1 合力大小为 2F，方向沿对角线 DH。 2-2 a/F1+b/F2+c/F3=0, F1/(bF3)=F2/(cF1)=F3/(aF2). 2-3 合力大小为：(a) (q1+q2)l/2; (b) qlcosθ; 过图形形心与 q 平行. 2-4 xC=1.319m, yC=3.333m, zC=1.361m. 2-5 xC=21.43mm, yC=21.43m, zC=-7.143mm. 2-6 xC=19.05mm. 2-7 重心离地面高度为 0.659 m ,离 B 端距离为 1.68 m 第三章 3-1 均为静不定 . 3-2 P>4Q=60kN. 3-3 (a) FA=-63.22kN, FB=-88.74kN, FC=30kN; (b) FB=8.42kN, FC=3.45kN, FD=57.4kN. 3-4 (a) FAx=0, FAy=6kN, MA=32kN⋅m; (b) FAx=0, FAy=-15kN, FB=40kN, FCx=0, FCy=5kN, FD=15kN. 3-5 (a) FAx=0, FAy=-F+M/a+qa/2, FB=2F-2M/a+5qa/2, FC=M/a+qa/2; (b) FAx=0, FAy=7qa/6, MA=2qa2, FC=5qa/6. 3-6 FAx=1200N, FBA=-1500N, FB=-1050N. 3-7 FEx=F, FEy=-F/3. 3-8 FAx=(2Q-P)/4, FAy=(6Q+7P)/4, FCx=(P-6Q)/4, FCy=3(P+2Q)/4, Fk=1.414P. 3-9 FAx=FBy=500N, FAB=700N, FBC=100N. 3-10 FAx=FBy=30kN, FCx=FCy=10kN, FBE=0, FCE=14.142kN. 3-11 FAx=0, FAy=M/(2a), FDx=0, FDy=M/a, FBx=0, FAy=-M/(2a) 3-12 FAx=-F, FAy=-F, FDx=2F, FDy=F, FBx=-F, FBy=0. 3-13 FAx=-120kN, FAy=-160kN, FB=226.3kN, FC=-80kN. 3-14 FAx=267kN, FAy=-87.5kN, FB=550kN, FCx=209kN, FCy=-187.5kN. 3-15 FAD=FBD=31.55kN, FCD=-1.55kN. 3-16 FN=500N, FTA=750N, FTB=433N. 3-17 F1=F2=5kN, F3=-7.07kN, F4=F5=5kN, F1=-10kN. 3-18 FNA=8.33kN, FNB=78.33kN, FNC=43.34kN. 3-19 a=35cm. 3-20 FT=707N, FAx=400kN, FAy=800kN, FAz=500kN, FBy=-500kN, FBz=0. 3-21 M=22.5N⋅m, FAx=75kN, FAy=0, FAz=50kN, Fx=75kN, Fy=0. 3-22 F=70.9N, FAx=-47.6kN, FAz=-68.8kN, FBx=-19kN, FAz=-207kN. 3-23 128.23 N. 3-24 GAmin=1.37kN. 3-25 11.55 kN. 3-26 Fmin=280N. 3-27 d≥110mm. 3-28 6.0N≤F≤46.1N. 3-29 lmin=100mm. 3-30 bmin=fh/3, 与门重无关. 3-31 M=P2(Rsinθ-r), F=P2sinθ, FN=P1-P2cosθ. 3-32 θ=1°9′. 3-33 M=1.867kN⋅m, F≥0.752. 3-34 1， 4， 7， 9， 13， 14， 11. 3-35 F1=-16.9kN, F2=3.1kN, F3=15.0kN 3-36 (a) FAB=-F/2; (b) FAB=-2kN. 3-37 F1=-5.333F(压)，F2=2F (拉)， F3=-1.667F (压). 3-38 FCD=-0.866F (压). 第四章 4-1

刚体的转动惯量公式

刚体的转动惯量公式
刚体的转动惯量是描述刚体在转动过程中抵抗改变转动状态的物理量。

转动惯量的大小与刚体的形状和质量分布有关，可以通过转动惯量公式来计算。

对于一个刚体围绕某个轴转动，其转动惯量可以表示为I，根据刚体的形状和质量分布的不同，转动惯量公式也会有所不同。

以下是一些常见形状的刚体转动惯量公式：
1. 杆状刚体绕其一端的转动惯量：
对于一个质量为m、长度为L的细长杆，其绕一端的转动惯量可以表示为I=1/3 * m * L^2。

2. 球状刚体绕其直径轴的转动惯量：
对于一个质量为m、半径为R的均匀球体，其绕直径轴的转动惯量可以表示为I=2/5 * m * R^2。

3. 圆环状刚体绕其对称轴的转动惯量：
对于一个质量为m、半径为R的圆环，其绕对称轴的转动惯量可以表示为I=m * R^2。

需要注意的是，上述公式仅适用于均匀分布质量的刚体。

对于非均匀分布的刚体，转动惯量公式需要根据具体的质量分布情况进行积分计算。

转动惯量公式在物理学中有着广泛的应用，例如在刚体的转动运动方程中，转动惯量是一个重要的物理量。

通过转动惯量的计算，我们可以了解刚体在转动过程中的惯性特性，进而分析和预测其转动运动的行为。

各种不同形状物体转动惯量的测量数据

各种不同形状物体转动惯量的测量数据以各种不同形状物体转动惯量的测量数据为标题，我们来探究一下物体的转动惯量与其形状的关系。

什么是转动惯量呢？简单来说，转动惯量是描述物体对于绕某个轴旋转时抵抗旋转的物理量。

对于一个刚体，其转动惯量与其形状、质量、轴的位置等因素有关。

我们先来看看一些简单形状的物体的转动惯量。

对于一个质量均匀分布的球体，其转动惯量可以用公式I=2/5mr²来计算。

其中，m 为球体质量，r为球体半径。

实验测量表明，球体的转动惯量与其质量和半径的平方成正比。

接下来看看另一种简单形状的物体——圆盘。

同样地，假设圆盘质量均匀分布，则其转动惯量I=1/2mr²。

与球体相比，圆盘的转动惯量与其质量和半径的平方成正比系数更小，这是因为圆盘的质量分布不如球体那么集中于中心。

我们再来看看更为复杂的形状——长方体。

设长方体的质量为m，长宽高分别为a、b、c，则其转动惯量I=1/12m(a²+b²)。

可以看到，长方体的转动惯量不仅与其质量有关，也与其形状有关。

对于其他形状的物体，如圆锥、圆环等，其转动惯量的计算公式也比较复杂，需要通过物理模型和实验测量来确定。

但可以肯定的是，不同形状的物体的转动惯量与其形状紧密相关。

除了形状因素，物体的质量分布和旋转轴的位置也会影响其转动惯量。

比如一个质量分布不均匀的物体，其转动惯量会因为质量分布的不同而不同。

同样地，对于同一物体，绕不同轴旋转时其转动惯量也会不同。

物体的转动惯量与其形状、质量分布和旋转轴的位置等因素密切相关。

通过实验测量和理论计算，我们可以准确地确定一个物体的转动惯量，从而更好地理解物体的旋转运动。

常见转动惯量公式

常见转动惯量公式转动惯量这个概念在物理学中可是相当重要的哦！咱先来说说啥是转动惯量。

简单来讲，转动惯量就是描述物体转动时惯性大小的一个物理量。

想象一下，有个大圆盘和一个小圆盘，你要是用同样的力气去让它们转动，大圆盘可就没那么容易转起来，这就是因为大圆盘的转动惯量大。

常见的转动惯量公式里，有个很基础的，就是对于一个质点，它的转动惯量 I = mr²，这里的 m 是质点的质量，r 是质点到转轴的距离。

就像我之前在课堂上做过的一个小实验，我拿了一根细长的棍子，在棍子的一端绑了个小重物，然后让同学们试着转动这根棍子。

当重物离转轴比较近的时候，转动起来相对轻松；但把重物挪到离转轴远的地方，再转动就费劲多啦。

这其实就是因为重物到转轴的距离 r 发生了变化，从而导致转动惯量变大了。

再来说说对于一个均匀细棒，绕通过一端且垂直于棒的轴的转动惯量 I = 1/3 mL²，这里的 L 是棒的长度。

这个公式在解决很多实际问题中都特别有用。

比如说，有一次我带着学生们去工厂参观，看到了一个大型的旋转机械部件，形状就类似于一个长长的细棒。

当时我就引导学生们思考，如果要计算这个部件的转动惯量，就可以用这个公式。

还有对于一个圆环，绕通过圆心且垂直于圆环平面的轴的转动惯量I = mR²，这里的 R 是圆环的半径。

记得有一次，我和朋友一起骑自行车，车轮就可以近似看作一个圆环。

我们就讨论起来，要是车轮变大或者变小，对于骑行时的感受会有啥影响，这其实就和车轮的转动惯量有关。

对于一个均匀圆盘，绕通过圆心且垂直于盘面的轴的转动惯量 I = 1/2 mR²。

生活中也有很多这样的例子，像家里的电风扇的扇叶，就可以看作是圆盘。

扇叶大小不同，转动起来的感觉也不一样，这背后就有转动惯量在起作用。

在学习转动惯量公式的时候，可不能死记硬背，得结合实际的例子去理解。

多观察生活中的现象，你就会发现转动惯量无处不在，而且能更好地掌握这些公式的应用。

最全的转动惯量的计算资料

最全的转动惯量的计算资料转动惯量是描述物体的转动特性的物理量，它的计算涉及到物体的形状、质量分布以及围绕哪个轴进行转动等因素。

以下是最全的转动惯量的计算资料。

1.转动惯量的定义转动惯量（或称为角动量的惯性矩）是描述物体转动惯性大小的物理量，通常用字母I表示。

对于质量分布连续的物体，其转动惯量可以通过积分计算得到。

2.刚体的转动惯量刚体的转动惯量取决于物体的形状和围绕的轴。

对于质量分布均匀的刚体，其转动惯量可以通过以下公式计算：I=(1/2)*m*r^2其中，I是转动惯量，m是质量，r是质量到转轴的距离。

3.基本几何体的转动惯量针对常见的几何体，转动惯量的计算公式如下：-线段绕自身一端转动：I=(1/3)*m*L^2其中，I是转动惯量，m是质量，L是线段的长度。

-圆环绕轴转动：I=m*R^2其中，I是转动惯量，m是质量，R是圆环的半径。

-矩形薄片绕轴转动：I=(1/12)*m*(a^2+b^2)其中，I是转动惯量，m是质量，a和b是矩形薄片的长度和宽度。

-矩形薄棒绕轴转动：I=(1/12)*m*(L^2+B^2)其中，I是转动惯量，m是质量，L和B是矩形薄棒的长度和宽度。

-圆盘绕轴转动：I=(1/2)*m*R^2其中，I是转动惯量，m是质量，R是圆盘的半径。

-球体绕直径转动：I=(2/5)*m*R^2其中，I是转动惯量，m是质量，R是球体的半径。

4.复杂体的转动惯量对于复杂形状的物体，转动惯量的计算可能需要使用积分方法。

下面是一些常见的复杂体的转动惯量计算公式：-绕X轴或Y轴对称的物体：I = ∫(r^2 * dm)其中，I是转动惯量，r是质点到转轴的距离，dm是质点的质量微元。

-长方体绕对称轴：I=(1/12)*m*(a^2+b^2)其中，I是转动惯量，m是质量，a和b是长方体的两个相邻边的长度。

-均匀圆环绕直径转动：I=m*R^2其中，I是转动惯量，m是质量，R是圆环的半径。

-均匀圆盘绕对称轴转动：I=(1/2)*m*R^2其中，I是转动惯量，m是质量，R是圆盘的半径。

球体转动惯量

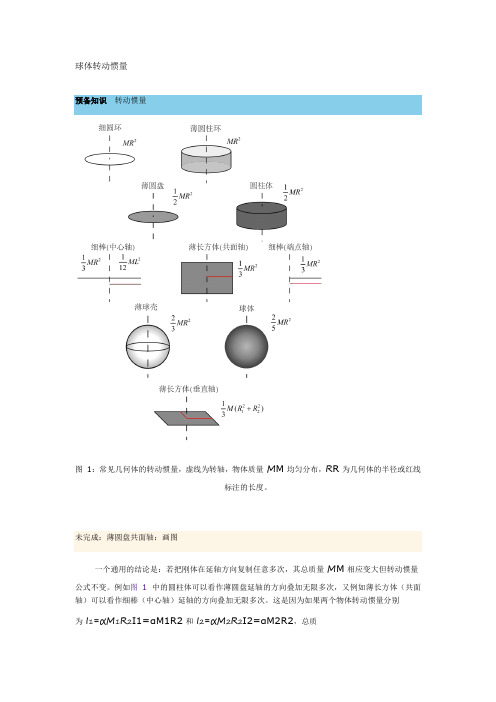
球体转动惯量预备知识转动惯量图1：常见几何体的转动惯量，虚线为转轴，物体质量M M均匀分布，R R为几何体的半径或红线标注的长度。

未完成：薄圆盘共面轴：画图一个通用的结论是：若把刚体在延轴方向复制任意多次，其总质量M M相应变大但转动惯量公式不变。

例如图 1 中的圆柱体可以看作薄圆盘延轴的方向叠加无限多次，又例如薄长方体（共面轴）可以看作细棒（中心轴）延轴的方向叠加无限多次。

这是因为如果两个物体转动惯量分别为I1=αM1R2I1=αM1R2和I2=αM2R2I2=αM2R2，总质量M=M1+M2M=M1+M2，那么总转动惯量为I=I1+I2=αM R2I=I1+I2=αMR2，系数αα不变。

1. 细圆环、薄圆柱环细圆环和薄圆柱环的所有质量与转轴的距离都为R R，可以看成许多质点的叠加，每个质点转惯量为m i R2miR2，所以I=∑i m i R2=MR2(1)(1)I=∑imiR2=MR22. 细棒（端点轴）细棒的线密度为λ=M/Lλ=M/L，如果划分成长度为ΔrΔr的小段，第i i段距离转轴r i ri，有I=limΔr→0∑iλΔr⋅r2i=∫L0λr2dr=13λL3=13ML2(2)(2)I=limΔr→0∑iλΔr⋅ri2 =∫0Lλr2dr=13λL3=13ML23. 细棒（中心轴）细棒（中心轴）可以看做两个等质量的细棒（端点轴），质量都为M1M1，每个具有转动惯量（式 2 ）M1R2/3M1R2/3，乘以22得总转动惯量为（M=2M1M=2M1）I=13MR2=112ML2(3)(3)I=13MR2=112ML2其中L=2R L=2R。

由此可以看出，若一个物体可以拆分成转动惯量相同的若干部分，那么转动惯量公式不变。

4. 薄长方体（共面轴）薄长方体（共面轴）可以看成许多细棒（中心轴）组成，所以转动惯量的系数仍然为I=13MR2=112ML2(4)(4)I=13MR2=112ML25. 薄圆盘、圆柱薄圆盘可以看做许多宽度为ΔrΔr的细圆环组成1，质量面密度为σ=M/(πR2)σ=M/(πR2)，第i i个圆环的半径为r i ri，面积为2πr iΔr2πriΔr，总转动惯量为I=∫R0r2dm=∫R0r2σ⋅2πrdr=2πσ∫R0r3dr(5)(5)I=∫0Rr2dm=∫0Rr2σ⋅2πrdr=2πσ∫0Rr3dr也可以在极坐标极坐标中直接根据定义写出积分I=∫r2σds=∫2π0∫R0σr2⋅rdrdθ=2πσ∫R0r3dr=12σπR2R2=12MR2(6)(6)I=∫r2σds=∫02π∫0Rσr2⋅rdrdθ=2πσ∫0Rr3dr=12σπR2R2=12MR2圆柱可看做由许多相同的薄圆盘组成，转动惯量系数相同。

转动惯量公式

nema标准中的计算是如下（转化公式）：J=A×0.055613×（Pn^0.95）÷（n/1000）^2.4-0.004474×（Pn^1.5）÷（n/1000）^1.8A小于等于1800rpm时取24，A大于1800rpm时取27 Pn为功率（kw） n 为同步转速高压电动机在设计时，要求计算出转子的转动惯量。

下面对计算方法做一分析。

转动惯量是物体在转动时惯性的度量，它不仅与物体质量的大小有关，还与物体质量分体情况有关。

机械工程师手册给出了一些简单形状物体的转动惯量。

1、圆柱体沿轴线转动惯量：Kg•m2 (1)式中：M —圆柱体质量KgR —圆柱体外径半径 m2、空心圆柱体沿轴线转动惯量：Kg•m2 (2)式中： M —空心圆柱体质量KgR —空心圆柱体外半径 mr —空心圆柱体内半径m3、薄板沿对称线转动惯量：Kg•m2 (3)式中：M —薄板质量Kga —薄板垂直于轴线方向的宽度m物体的转动惯量除了用J表示外，在工程上有的用物体的重量G和物体的回转直径D的平方的乘积GD2来表示，也称为物体的飞轮力矩或惯量矩，单位N•m2或Kg f m2。

物体的飞轮力矩GD2和转动惯量J之间的关系，用下式表示：N•m2 (4)式中：g —重力加速度 g=9.81 m/s2将重力单位N化为习惯上的重力单位Kgf ，则（4）变为：Kg f m2 (5)由以上公式，可以对鼠笼型高压电机的转动惯量进行计算。

计算时，将高压电机转子分解为转子铁心（包括导条和端环）、幅铁、转轴三部分，分别算出各部分的Jn，各部分的转动惯量相加即得电机的转动惯量J。

如需要，按（5）式换算成飞轮力矩GD2。

一般产品样本中要求给定的是转动惯量J，兰州引进的电磁设计程序计算出的是飞轮力矩GD2。

计算程序如下：1、转子铁心的转动惯量，按空心圆柱公式（2）进行计算，考虑导条端环度大小的因素，以系数c进行修正。

机械设计转动惯量计算公式

1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)； D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-材料比重(gf /cm 3)。

2. 丝杠折算到马达轴上的转动惯量：2i Js J =(kgf·c m·s 2) J s (kgf·c m·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w 2s 2⎪⎭⎫ ⎝⎛=π (kgf·c m·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)；g-重力加速度，g = 980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf ·cm ·s 2)；J s -丝杠转动惯量(kgf ·cm ·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf ·c m·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2)；R-齿轮z 分度圆半径(cm)； w-工件及工作台重量(kgf)。