椭圆的概念及其性质
椭圆的基本性质

椭圆的基本性质椭圆是一种常见的几何图形,具有一些特定的性质。
在本文中,我们将介绍椭圆的基本概念以及与它相关的一些重要性质。
1. 椭圆的定义与特点椭圆是平面上到两个固定点的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
椭圆的形状可以用离心率来描述,当离心率小于1时,椭圆更加接近于一个圆形;当离心率等于1时,椭圆退化为一个特殊的圆;当离心率大于1时,椭圆的形状变得更加扁平。
2. 椭圆的中心与轴椭圆的中心是指位于椭圆的中心点,它同时也是椭圆的两个轴(主轴和次轴)的交点。
主轴是通过椭圆的中心,并且与椭圆的两个焦点重合的直线段;次轴是与主轴垂直,并通过椭圆的中心的直线段。
主轴的长度称为椭圆的长轴,次轴的长度称为椭圆的短轴。
3. 椭圆的焦点和准线椭圆的焦点是椭圆上到两个固定点的距离之和等于常数的点,它们位于椭圆的主轴上,并且与椭圆的中心对称。
准线是与主轴平行,并且通过椭圆的焦点的直线段。
4. 椭圆的半长轴与半短轴椭圆的半长轴是指从椭圆的中心到椭圆的一条主轴上的一个顶点的距离,长度记为a。
半短轴是指从椭圆的中心到椭圆的一条次轴上的一个顶点的距离,长度记为b。
椭圆的离心率e与半长轴a和半短轴b之间存在着如下关系:e = √(1 - b^2/a^2)。
5. 椭圆的周长与面积椭圆的周长可以使用椭圆的长轴和短轴来计算,公式为:C =4aE(e),其中E(e)为椭圆的第二类完全椭圆积分,是一个与椭圆离心率有关的特殊函数。
椭圆的面积可以使用椭圆的长轴和短轴来计算,公式为:S = πab。
6. 椭圆的离心率与轨道的形状离心率可以帮助我们描述椭圆的形状,离心率越小,椭圆越接近于完美的圆形;离心率越大,椭圆越扁平。
在天文学中,行星的轨道通常是椭圆,其中太阳位于椭圆的一个焦点上。
例如,地球的轨道就是一个离心率接近于0.017的椭圆。
通过以上对椭圆的基本性质的介绍,我们对椭圆有了更深入的了解。
椭圆作为一种重要的几何图形,在数学、物理和工程等领域都有广泛的应用。
椭圆的定义与性质

椭圆的定义与性质椭圆是在平面上的一个几何图形,它的形状类似于一个椭圆形的椭圆。
椭圆由两个焦点和一条连接这两个焦点的线段组成。
椭圆的定义可以通过以下方式来描述:给定两个不重合的点F1和F2,以及一个正常数a,椭圆是平面上到这两个点F1和F2的距离之和等于2a的所有点P的集合。
椭圆有许多有趣的性质。
首先,椭圆是一个闭合图形,它的形状在两个焦点F1和F2之间变化。
其次,椭圆的中点O是焦点F1和F2之间的中点,并且椭圆的长轴是连接这两个焦点的线段。
长轴的长度为2a,其中a为椭圆的半长径。
椭圆的短轴是与长轴垂直且通过中点O的线段,其长度为2b,其中b为椭圆的半短径。
椭圆的长轴和短轴之间的关系可以通过以下公式表示:长轴的长度的平方等于短轴的长度的平方加上焦距的长度的平方。
椭圆的形状也可以由离心率来描述。
离心率是一个衡量椭圆形状的参数,表示焦点之间的距离与半长径之间的比值。
离心率小于1的椭圆形状更加圆形,而离心率等于1的椭圆是一个特殊的圆,离心率大于1的椭圆形状更加扁平。
除了这些基本的定义和性质之外,椭圆还有许多其他的性质。
例如,椭圆上的任意一点到焦点F1和F2的距离之和等于2a,这被称为椭圆的焦点性质。
椭圆还具有对称性,即关于长轴和短轴都有对称性。
椭圆还可以通过旋转的方式来得到新的椭圆,这被称为椭圆的旋转性质。
总结起来,椭圆是平面上的一个几何图形,由两个焦点和一条连接这两个焦点的线段组成。
椭圆具有闭合性、中点、长轴和短轴、离心率等基本性质。
此外,椭圆还有焦点性质、对称性和旋转性质等其他有趣的性质。
通过研究椭圆的定义和性质,我们可以更深入地理解和应用椭圆在数学和物理等领域中的重要性。
椭圆的定义与性质

椭圆的定义与性质椭圆是数学中的一个重要几何概念,它在几何学、物理学、天文学等领域中都有广泛的应用。
本文将从椭圆的定义、性质以及应用等方面进行探讨。
一、椭圆的定义椭圆是平面上一组点的集合,这组点到两个给定点的距离之和等于常数的情况。
这两个给定点称为焦点,而常数称为离心率。
椭圆的定义可以用数学表达式表示为:对于平面上的点P(x, y),到焦点F1和F2的距离之和等于常数2a,即PF1 + PF2 =2a。
其中,a为椭圆的半长轴。
二、椭圆的性质1. 焦点与半长轴的关系:椭圆的两个焦点到椭圆中心的距离之和等于2a,即F1C + F2C = 2a。
这表明椭圆的中心C位于焦点连线的中垂线上。
2. 离心率与形状的关系:离心率e是椭圆的一个重要参数,它决定了椭圆的形状。
当离心率e=0时,椭圆退化为一个圆;当0<e<1时,椭圆的形状趋近于圆;当e=1时,椭圆退化为一个抛物线;当e>1时,椭圆的形状趋近于双曲线。
3. 半短轴与半长轴的关系:椭圆的半长轴为a,半短轴为b,它们之间的关系可以用离心率e来表示,即e = √(1 - b²/a²)。
通过这个公式,我们可以计算出椭圆的半短轴。
4. 焦点与直径的关系:椭圆的焦点到椭圆上任意一点的距离之和等于椭圆的直径。
这个性质在椭圆的应用中非常重要,例如在天文学中,可以用椭圆的性质来描述行星的轨道。
三、椭圆的应用1. 天文学中的椭圆轨道:行星绕太阳运动的轨道可以近似看作椭圆,根据椭圆的性质,可以计算出行星的轨道参数,如离心率、半长轴等。
2. 椭圆的光学性质:椭圆镜是一种常见的光学元件,它可以将入射光线聚焦到一个点上,用于望远镜、显微镜等光学仪器中。
3. 椭圆的工程应用:在建筑、桥梁等工程设计中,椭圆形状的结构可以提供更好的力学性能和美观效果。
总结:椭圆作为一种重要的数学概念,在几何学和应用数学中都有广泛的应用。
通过对椭圆的定义与性质的探讨,我们可以更好地理解椭圆的形状特征以及其在各个领域中的应用。
椭圆的相关知识点

椭圆的相关知识点第一篇:椭圆的基本概念和性质1.椭圆的定义椭圆是平面上到两个定点(焦点)距离之和等于定长(长轴)的点的轨迹,长轴的中点为圆心,短轴为长轴的一半。
2.椭圆的方程椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中 a 和 b 分别为长半轴和短半轴的长度。
椭圆的一般方程为$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$,式中 A、B、C、D、E、F 均为常数。
3.椭圆的对称性椭圆有四个轴线:长轴和短轴,以及两个对称轴线(分别为横向和纵向)。
椭圆具有关于两个轴线的对称性,关于圆心对称。
4.椭圆的几何性质椭圆的周长公式为 $l=4aE(e)$,面积公式为 $S=\piab$。
其中,$e=\sqrt{1-\frac{b^2}{a^2}}$ 为椭圆的离心率,$E(e)$ 为第一类的椭圆积分(椭圆弧长度)。
椭圆的内切圆为其一条边界切线上的圆,其直径长度为短轴的长度,而斜切和垂直切的切线则分别过长轴的端点和中点。
椭圆的离心率决定了其形状的扁瘤程度,离心率越小则椭圆越接近于圆形,越大则越接近于扁平的形状。
5.椭圆的应用椭圆在数学、物理、工程、生物学和地球科学等领域中有广泛的应用。
例如,它们可以用于描述球形天体的轨道、电子轨道、反射镜的形状、ATM 窗口的形状、荷载分布、地球的椭球形等等。
第二篇:椭圆的参数方程、焦点坐标和切线方程1.椭圆的参数方程对于椭圆的标准方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,我们可以将其表示为参数方程:$$\begin{cases}x=a\cos\theta\\y=b\sin\theta\end{cases}$$其中,$\theta$ 为参数,表示$\overrightarrow{OP}$ 与 $x$ 轴正半轴的夹角。
2.椭圆的焦点坐标椭圆有两个焦点,它们分别位于长轴上,与圆心的距离为 $c=\sqrt{a^2-b^2}$ ,其中 $a$ 和 $b$ 分别为长轴和短轴的长度。
有关椭圆的所有知识点

有关椭圆的所有知识点
1. 椭圆的定义:椭圆是一种特殊的抛物线,它是二维平面上的曲线,其中两条轴的长度不相等,椭圆的方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
2. 椭圆的性质:
(1)椭圆的对称轴是两个相交的线段,其中一个线段的长度大于另一个,称为长轴,另一个线段称为短轴;
(2)椭圆的中心点是两个对称轴的交点;
(3)椭圆的长轴和短轴的长度分别为a和b,椭圆的面积为S=πab;
(4)椭圆的边界是一个抛物线,称为椭圆弧,可以用参数方程表示:$$x=a\cos t,
y=b\sin t$$
3. 椭圆的标准方程:
(1)椭圆的标准方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
(2)椭圆的中心在原点时,标准方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
(3)椭圆的中心在(h,k)处时,标准方程为:$$\frac{(x-h)^2}{a^2}+\frac{(y-
k)^2}{b^2}=1$$
4. 椭圆的对称性:
(1)椭圆是一种具有对称性的曲线,其对称轴是两个相交的线段,其中一个线段的长度大于另一个,称为长轴,另一个线段称为短轴;
(2)椭圆的对称性可以用参数方程表示:$$x=a\cos t,y=b\sin t$$
(3)椭圆的对称性可以用参数方程表示:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
5. 椭圆的离心率:椭圆的离心率是椭圆的一个重要参数,它可以表示椭圆的形状,它的定义是:椭圆的离心率等于椭圆的长轴与短轴之比,即:$$e=\frac{a-b}{a}$$。
椭圆的性质及知识点总结

椭圆的性质及知识点总结一、椭圆的定义和基本性质1.1 椭圆的定义椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
设d1和d2分别表示P到F1和F2的距离,则椭圆的定义可以用数学表达式表示为|d1 + d2| = 2a 。
1.2 椭圆的基本性质(1)椭圆对称轴:椭圆有两个对称轴,分别称为长轴和短轴。
长轴的端点是两个焦点F1和F2,短轴与长轴垂直并通过椭圆的中心点。
(2)椭圆的焦点和离心率:椭圆的焦点是定义椭圆的两个定点F1和F2,离心率e是一个表示椭圆形状的参数,e的取值范围是0<e<1。
(3)椭圆的三大定律:椭圆有三个基本定律,分别是:(a)椭圆内到两个焦点的距离之和等于长轴的长度;(b)椭圆内到两个焦点的距离之差等于长轴的长度;(c)椭圆的面积等于πab,其中a和b分别是长轴和短轴的长度。
1.3 椭圆的方程椭圆的标准方程是x^2/a^2 + y^2/b^2 = 1,其中a和b分别是长轴和短轴的长度,椭圆的中心点位于原点(0,0)。
二、椭圆的相关知识点2.1 椭圆的离心率椭圆的离心率e的定义是e=c/a,其中c为焦距,a为长半轴的一半。
离心率越接近于0,椭圆形状越圆;离心率越接近于1,椭圆形状越扁。
2.2 椭圆的参数方程椭圆也可以用参数方程表示,参数方程为:x = a * cosθy = b * sinθ其中θ为参数,a和b分别是长轴和短轴的长度。
2.3 椭圆的焦半径椭圆的焦半径是指从椭圆的焦点到该椭圆上的任意一点P的距离,椭圆上各点的焦半径之和等于椭圆的周长。
2.4 椭圆的切线椭圆上的切线有一个特点:与椭圆相切的切线在切点处与切线的法线垂直。
根据这个特点可以求出椭圆上任意一点处的切线方程。
2.5 椭圆的焦点坐标椭圆的焦点坐标可以通过椭圆的离心率和焦距来求解。
焦点坐标为(±ae, 0),a为长轴的一半,e为椭圆的离心率。
2.6 椭圆的面积椭圆的面积可以通过参数法求解,面积为πab,其中a和b分别是长轴和短轴的长度。
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是数学上的一个重要概念,它在几何学、天文学等领域有着广泛的应用。
本文将介绍椭圆的基本概念与性质,包括定义、方程、焦点、短轴、长轴等内容,以便读者对椭圆有更深入的了解。
1. 定义椭圆可以定义为平面上到两个固定点的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
2. 方程椭圆的标准方程为(x/a)² + (y/b)² = 1,其中a和b分别表示椭圆的长轴和短轴的长度。
当a=b时,椭圆退化为一个圆。
3. 焦点与离心率椭圆的焦点是椭圆上到两个焦点的距离之和等于椭圆的长轴长度。
椭圆的离心率是焦点与椭圆的长轴之比,通常用e表示。
当e=0时,椭圆退化为一个圆;当0<e<1时,椭圆的形状是扁平的;当e=1时,椭圆的形状是长条状。
4. 短轴与长轴椭圆的长轴是通过椭圆中心且垂直于短轴的直线段,长度为2a;短轴是通过椭圆中心且垂直于长轴的直线段,长度为2b。
长轴和短轴的长度决定了椭圆的形状。
5. 面积与周长椭圆的面积可以用公式πab来计算,其中π是圆周率。
椭圆的周长没有一个简单的数学公式,但可以用近似公式2π√((a²+b²)/2)来估算。
6. 焦点与直线关系对于一条过椭圆的焦点的直线,该直线与椭圆的两个交点到焦点的距离之和等于椭圆的长轴长度。
这个性质在椭圆的构造和证明中有着重要的应用。
7. 椭圆的投影当一个椭圆被一个平面所截,就会产生一个椭圆的投影。
椭圆的投影可以是一个椭圆、一个圆、一个椭圆的一部分或一个直线段,具体取决于投影平面与椭圆的相对位置。
8. 椭圆与锥面椭圆是一个椭圆锥的截面。
椭圆锥可以由一个两个焦点之间距离不变的点沿着一条直线轨迹旋转而生成,椭圆就是锥面与一个平面的交线。
总结:椭圆是一个重要的数学概念,具有许多独特的性质和应用。
通过了解椭圆的定义、方程、焦点、离心率,以及与直线、投影、锥面的关系,我们对椭圆的基本概念和性质有了更深入的了解。
椭圆的定义与性质探究

椭圆的定义与性质探究椭圆是数学中一种重要的几何图形,具有独特的定义和性质。
本文将对椭圆进行深入的探究,包括椭圆的定义、性质及其在实际生活中的应用。
一、椭圆的定义椭圆是平面上到两个定点的距离之和等于常数的点的轨迹。
这两个点称为椭圆的焦点,常数称为椭圆的离心率。
椭圆的离心率介于0到1之间,当离心率为0时,椭圆退化成一个点,当离心率为1时,椭圆退化成一条线段。
二、椭圆的性质1. 离心径:椭圆的两个焦点到任意一点的距离之和等于常数,这个常数称为离心径。
椭圆的离心径长度等于长轴的长度。
2. 长轴和短轴:椭圆的两个焦点的连线称为椭圆的长轴,长轴的中点称为椭圆的中心。
长轴的长度为2a,短轴的长度为2b,长轴和短轴的两倍称为椭圆的主轴。
3. 焦半径和引线:椭圆上的任意一点到两个焦点的距离分别称为焦半径,而椭圆上的任意一条直线与焦点的连线相交,且平分焦半径,称为引线。
4. 离心角:椭圆上任意一点的离心角等于该点的切线与长轴之间的夹角。
5. 第一焦点定理:椭圆上任意一点的焦半径之和等于该点到两个焦点的距离。
6. 第二焦点定理:椭圆上的任意一条切线与连结焦点的两条引线之和相等。
三、椭圆的应用椭圆在现实生活中有广泛的应用。
以下是其中的几个例子:1. 天体轨道:行星、卫星等天体的轨道往往呈椭圆形状,椭圆的性质帮助科学家研究天体的运动规律。
2. 抛物线天线:抛物线天线是一种应用了椭圆的特性的天线,其形状使得抛物面成为抛物线,从而实现更强的信号聚集效果。
3. 建筑设计:在建筑设计中,椭圆形状常用于设计建筑物的地面、门廊和窗户,赋予建筑物一种独特的美感。
4. 运动轨迹:体育项目中,例如足球、篮球的运动轨迹在空中表现出的是一个抛物线,而当球员的移动是椭圆的路径时,也能够帮助球员更好地调整位置。
四、总结椭圆是一种具有独特性质的几何图形,其定义、性质及应用都具有广泛的意义和价值。
通过深入了解和探究椭圆,我们可以更好地理解并运用它在各个领域中的特性。
椭圆的定义与性质

椭圆的定义与性质椭圆是我们在数学中经常遇到的一个几何形状,它与圆形有着密切的关系。
本文将从椭圆的定义、特点与性质等角度进行阐述。
一、定义椭圆可以被定义为平面上满足一定条件的点的集合。
具体而言,对于一个给定的点F(焦点)和一条给定的长度2a(长轴),满足到该点F到椭圆上任意一点P到两条焦点的距离之和等于2a的性质(即FP1 + FP2 = 2a)的所有点的集合就是椭圆。
二、性质1. 椭圆的长短轴在定义中提到了长轴,那么自然会有短轴的概念。
椭圆的长轴是连接两个焦点的线段,而短轴则是与长轴垂直,并且通过椭圆中心O的线段。
长轴的长度2a通常被称为椭圆的主轴,短轴的长度2b则被称为椭圆的副轴。
2. 椭圆的离心率椭圆的离心率是一个重要的性质,它可以帮助我们了解椭圆的形状。
离心率e定义为焦点到中心距离与长轴长度的比值,即e = c/a,其中c是焦距。
当离心率小于1时,我们可以得到一个完整的椭圆。
当离心率接近于1时,椭圆的形状趋近于一个圆。
当离心率等于1时,我们则可以得到一个特殊的椭圆,也称之为扁平椭圆或者简称为抛物线。
3. 椭圆的焦点性质椭圆有一个独特的性质:对于椭圆上的任意一点P,其到两个焦点的距离之和等于椭圆的长轴长度,即FP1 + FP2 = 2a。
这一性质也可以用来定义椭圆。
4. 椭圆的几何形状在平面上,椭圆呈现出一种特殊的形状。
与圆相比,椭圆的形状更加扁平。
椭圆的形状还与长轴和短轴的长度之间的比例有关。
5. 椭圆的焦平面性质椭圆与焦平面有着特殊的关系。
如果我们在椭圆上选择任意两个不同的点P和Q,并且做出焦点F1和F2到这两个点的连线,那么这两条连线所组成的平面与椭圆的法线相交于同一点。
这个点就是椭圆的焦点平面上的点。
6. 椭圆的参数方程椭圆的参数方程也是我们在研究椭圆性质时常用的一种表示方法。
一般而言,我们可以使用参数t或θ来表示椭圆上的点的坐标。
通过参数方程,可以更加方便地描述椭圆上的点的位置。
结语:椭圆作为几何学中的一种重要形状,具有独特的定义和性质。
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是一种常见的几何图形,具有许多独特的性质和应用。
本文将介绍椭圆的基本概念和性质,包括定义、标准方程、焦点、直径、离心率、轨道和应用等方面。
1.椭圆的定义椭圆可以定义为平面上到两个固定点(焦点)的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
椭圆也可以视为一个平面上到定点的连线长度之和等于一定长度(主轴)的点的轨迹。
2.椭圆的标准方程以坐标原点为中心的椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b 分别表示椭圆的长短半轴。
可以看出,a表示椭圆离心率对应的焦距长度,b表示椭圆的短半轴长度。
3.焦点和直径椭圆的焦点是椭圆的一个重要属性,它是椭圆离心率定义的核心。
可以通过标准方程中的离心率公式e = c/a(c为焦点到原点的距离),求得焦点的坐标表达式为(c, 0)和(-c, 0)。
椭圆的直径是通过椭圆中心并且同时与椭圆上两个点相交的线段。
对于以坐标原点为中心的椭圆,直径的长度为2a。
4.椭圆的离心率椭圆的离心率是描述椭圆形状的重要指标。
离心率的取值范围为0到1,离心率为0时表示圆形,离心率为1时表示扁平的线段。
椭圆的离心率定义为离心焦距和长半径之比,即e = c/a。
5.椭圆的轨迹椭圆的轨迹是指通过一定规则的运动得到的点所形成的图形。
在天体力学中,行星绕太阳运动的轨迹就是椭圆。
椭圆的轨迹具有许多独特的性质,例如对称性、曲率等。
6.椭圆的应用椭圆在现实生活中有许多重要的应用。
例如,在通信中,为了提高信号传输的质量和距离,卫星轨道通常选择为椭圆轨道。
此外,椭圆也被广泛应用于地理测量、天体力学、光学设计等领域。
总结:椭圆作为几何图形中的重要一员,具有许多独特的概念和性质。
通过本文的介绍,我们了解到椭圆的定义、标准方程、焦点、直径、离心率、轨迹和应用。
对于几何学的学习和实际应用,理解和掌握椭圆的基本概念与性质至关重要。
椭圆的定义及性质

椭圆的一个顶点,则椭圆的方程为
.
解析:设椭圆的方程为
x2 a2
y2 b2
c
a
3 5
=1(a>b>0),则已知 b 4,
a2 b2
c2,
a 5, 解得 b 4,
c 3,
所以椭圆方程为 x2 y2 =1. 25 16
小结:椭圆的标准方程及其简单几何性质
x2
y2
a 2 b2 1(a b 0)
y2 x2 a2 b2 1(a b 0)
图形
对称性 顶点
范围
焦点 焦距
离心率
曲线关于x轴、 y轴、原点对称 长轴顶点(±a,0) 短轴顶点(0,±b)
a x a, b y b
(-c,0)和(c,0)
曲线关于x轴、 y轴、原点对称 长轴顶点(0,±a) 短轴顶点(±b,0)
椭圆关于x轴、y轴、原点对称.
yy B2
AA11
AA2 2
O O
x
在
x2 a2
y2 b2
BB11
1中令y=0, 可得x= a
从而:A1(-a,0),A2(a,0)
同理:B1(0, -b),B2(0, b)
y
B2
A1
A2
O
x
B1
线段A1A2叫椭圆的长轴: 长为2a 线段B1B2叫椭圆的短轴: 长为2b
2.当2a=2c时,轨迹是一条线段, 是以 F1、F2为端点的线段. 3.当2a<2c时,无轨迹,图形不存在. 4.当c=0时,轨迹为圆.
二.椭圆的标准方程
(1)焦点在x轴
x2 a2
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是一种常见的几何图形,具有一些独特的性质和应用。
本文将介绍椭圆的基本概念以及一些相关的性质。
一、椭圆的定义与特点椭圆可以由一个固定点F(焦点)和到该点距离的总和等于常数2a (长轴)的点P的轨迹组成。
根据定义,椭圆上的任意点到焦点F和焦点到点到点P的距离之和等于常数2a。
椭圆还有一个参数b,称为短轴。
这两个参数构成了椭圆的两个辅助直径。
椭圆的中心是离焦点F和点P等距离的点O。
长轴和短轴的长度分别为2a和2b,其中2a>2b。
两个焦点F与F'关于中心O对称。
椭圆有一些特殊的性质:1. 椭圆上的任意点P到焦点的距离之和等于2a。
2. 椭圆的离心率e是一个介于0和1之间的数,定义为焦点到椭圆的中心的距离与长轴的一半的比值。
离心率决定了椭圆形状的“瘦胖程度”。
当e=0时,椭圆退化成一个点;当e=1时,椭圆退化成一个线段。
3. 椭圆的面积等于πab,其中π是圆周率。
二、椭圆的方程与坐标表示椭圆的方程可以通过焦点和离心率进行表示。
一般形式的椭圆方程为:(x^2/a^2) + (y^2/b^2) = 1其中,a和b分别表示长轴和短轴的长度。
椭圆的中心位于原点(0,0)处。
椭圆还可以通过参数方程进行表示:x = a * cosθy = b * sinθ其中,θ为参数,0 ≤ θ ≤ 2π。
三、椭圆的性质1. 焦点定理:椭圆上的任意点P到焦点F1和F2的距离之和等于2a。
2. 切线性质:椭圆上的任意点P处的切线斜率等于y/x的导数值,即m = (dy/dx) = -b^2 / a^2 * (x / y)。
3. 点到椭圆的距离:点(x1, y1)到椭圆(x^2/a^2) + (y^2/b^2) = 1的距离为d = sqrt[(x1^2/a^2) + (y1^2/b^2) - 1]。
4. 对称性:椭圆关于x轴和y轴对称。
5. 垂直角性质:椭圆上的任意点P处,直线PF1和PF2的夹角相等于直线PL1和PL2的夹角。
椭圆的定义与性质

椭圆的定义与性质1.椭圆的定义(1)第一定义:平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两个焦点的距离叫做焦距.(2)第二定义:平面内与一个定点F和一条定直线l的距离的比是常数e(0<e<1)的动点的轨迹是椭圆,定点F叫做椭圆的焦点,定直线l叫做焦点F相应的准线,根据椭圆的对称性,椭圆有两个焦点和两条准线.2.椭圆的标准方程和几何性质标准方程x2a2+y2b2=1(a>b>0)\f(y2,a2)+\f(x2,b2)=1(a>b>0)图形性质范围-a≤x≤a -b≤y≤b-b≤x≤b-a≤y≤a 顶点A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)B1(0,-b),B2(0,b)B1(-b,0),B2(b,0) 焦点F1(-c,0) F2(c,0) F1(0,-c) F2(0,c)准线l1:x=-错误!l2:x=错误!l1:y=-错误!l2:y=错误!轴长轴A1A2的长为2a 短轴B1B2的长为2b焦距F1F2=2c离心率e=错误!,且e∈(0,1)a,b,c的关系c2=a2-b2对称性对称轴:坐标轴对称中心:原点1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)动点P到两定点A(-2,0),B(2,0)的距离之和为4,则点P的轨迹是椭圆.( )(2)椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c(其中a为椭圆的长半轴长,c为椭圆的半焦距).( )(3)椭圆的离心率e越大,椭圆就越圆.( )(4)已知点F 为平面内的一个定点,直线l 为平面内的一条定直线.设d为平面内一动点P到定直线l 的距离,若d =错误!|PF |,则点P 的轨迹为椭圆.( )[解析] (1)错误,|P A |+|PB |=|A B|=4,点P 的轨迹为线段AB ;(2)正确,根据椭圆的第一定义知PF 1+PF2=2a ,F 1F 2=2c ,故△PF 1F2的周长为2a +2c ;(3)错误,椭圆的离心率越大,椭圆越扁.(4)正确,根据椭圆的第二定义.[答案] (1)× (2)√ (3)× (4)√2.(教材习题改编)焦点在x 轴上的椭圆\f(x 2,5)+错误!=1的离心率为错误!,则m =________.[解析] 由题设知a 2=5,b2=m ,c 2=5-m,e2=错误!=错误!=(错误!)2=错误!,∴5-m=2,∴m=3.[答案] 33.椭圆的焦点坐标为(0,-6),(0,6),椭圆上一点P 到两焦点的距离之和为20,则椭圆的标准方程为_____.[解析] 椭圆的焦点在y轴上,且c =6,2a =20,∴a=10,b 2=a2-c 2=64,故椭圆方程为x 264+y 2100=1. [答案] 错误!+错误!=1 4.(2014·无锡质检)椭圆x24+\f(y 2,3)=1的左焦点为F ,直线x =m与椭圆相交于点A,B,当△F AB 的周长最大时,△F AB 的面积是________.[解析] 直线x=m 过右焦点(1,0)时,△F AB 的周长最大,由椭圆定义知,其周长为4a =8, 此时,|AB |=2×b 2a=错误!=3,∴S △F AB =错误!×2×3=3.[答案] 35.(2014·江西高考)过点M (1,1)作斜率为-错误!的直线与椭圆C :错误!+错误!=1(a >b>0)相交于A ,B 两点,若M是线段AB 的中点,则椭圆C的离心率等于________.[解析] 设A (x 1,y 1),B (x 2,y 2),则错误!∴错误!+错误!=0,∴y 1-y 2x1-x 2=-b2a2·\f(x 1+x 2,y1+y 2). ∵y 1-y 2x 1-x2=-\f (1,2),x 1+x 2=2,y1+y 2=2,∴-b 2a2=-错误!, ∴a 2=2b 2.又∵b 2=a 2-c2,∴a 2=2(a 2-c 2),∴a 2=2c 2,∴\f (c ,a )=错误!.[答案] 错误!考向1 椭圆的定义与标准方程【典例1】(1)(2014·全国大纲卷改编)已知椭圆C:错误!+错误!=1(a>b>0)的左、右焦点为F1、F2,离心率为\f(3,3),过F2的直线l交C于A、B两点.若△AF1B的周长为4\r(3),则C的方程为________.(2)(2014·苏州质检)椭圆的中心在原点,焦距为4,一条准线为x=-4,则该椭圆的方程为________.[解析](1)由条件知△AF1B的周长=4a=4错误!,∴a=错误!.∵e=错误!=错误!,c2+b2=a2,∴c=1,b=错误!.∴椭圆C的方程为错误!+错误!=1.(2)∵椭圆的一条准线为x=-4,∴焦点在x轴上且错误!=4,又2c=4,∴c=2,∴a2=8,b2=4,∴该椭圆方程为错误!+错误!=1.[答案] (1)错误!+错误!=1 (2)错误!+错误!=1,【规律方法】(1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决.(2)求椭圆的标准方程有两种方法①定义法:根据椭圆的定义,确定a2,b2的值,结合焦点位置可写出椭圆方程.②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a,b;若焦点位置不明确,则需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为Ax2+By2=1(A>0,B>0,A≠B).【变式训练1】(1)(2013·广东高考改编)已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于\f(1,2),则C的方程是________.(2)(2014·苏州质检)已知椭圆的方程是错误!+错误!=1(a>5),它的两个焦点分别为F1,F2,且|F1F2|=8,弦AB(椭圆上任意两点的线段)过点F1,则△ABF2的周长为________.[解析] (1)右焦点F(1,0),则椭圆的焦点在x轴上;c=1.又离心率为ca=\f(1,2),故a=2,b2=a2-c2=4-1=3,故椭圆的方程为x24+\f(y2,3)=1.(2)∵a>5,∴椭圆的焦点在x轴上,∵|F1F2|=8,∴c=4,∴a2=25+c2=41,则a=\r(41). 由椭圆定义,|AF1|+|AF2|=|BF2|+|BF1|=2a,∴△ABF2的周长为4a=441.[答案] (1)错误!+错误!=1(2)4错误!考向2椭圆的几何性质【典例2】(1)(2013·江苏高考)在平面直角坐标系xOy中,椭圆C的标准方程为x2a2+y2b2=1(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B.设原点到直线BF的距离为d1,F到l的距离为d2,若d2=6d1,则椭圆C的离心率为________.(2)(2014·扬州质检)已知F1、F2是椭圆C的左、右焦点,点P在椭圆上,且满足|PF1|=2|PF2|,∠PF1F2=30°,则椭圆的离心率为________.[解析](1)依题意,d2=错误!-c=错误!.又BF=错误!=a,所以d1=错误!.由已知可得错误!=\r(6)·\f(bc,a),所以\r(6)c2=ab,即6c4=a2(a2-c2),整理可得a2=3c2,所以离心率e=\f(c,a)=\f(3,3).(2)在三角形PF1F2中,由正弦定理得sin∠PF2F1=1,即∠PF2F1=错误!,设|PF2|=1,则|PF1|=2,|F2F1|=3,∴离心率e=错误!=错误!. [答案](1)错误!(2)错误!,【规律方法】1.椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF1|+|PF2|=2a,得到a,c的关系.2.椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法:(1)求出a,c,代入公式e=错误!;(2)只需要根据一个条件得到关于a,b,c的齐次式,结合b2=a2-c2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).【变式训练2】(1)(2013·课标全国卷Ⅱ改编)设椭圆C:错误!+错误!=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为________.(2)(2014·徐州一中抽测)已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.则椭圆离心率的范围为________.[解析](1)如图,在Rt△PF1F2中,∠PF1F2=30°,∴|PF1|=2|PF2|,且|PF2|=错误!|F1F2|,又|PF1|+|PF2|=2a,∴|PF2|=\f(2,3)a,于是|F1F2|=错误!a,因此离心率e=错误!=错误!=错误!.(2)法一:设椭圆方程为错误!+错误!=1(a>b>0),|PF1|=m,|PF2|=n,则m+n=2a.在△PF1F2中,由余弦定理可知,4c2=m2+n2-2mn cos 60°=(m+n)2-3mn=4a2-3mn≥4a2-3·错误!2=4a2-3a2=a2(当且仅当m=n时取等号).∴错误!≥错误!,即e≥错误!.又0<e<1,∴e的取值范围是错误!.法二:如图所示,设O是椭圆的中心,A 是椭圆短轴上的一个顶点,由于∠F 1PF2=60°,则只需满足60°≤∠F1AF 2即可,又△F 1AF 2是等腰三角形,且|AF1|=|AF 2|,所以0°<∠F 1F2A ≤60°,所以12≤cos ∠F 1F2A <1,又e=c os ∠F 1F2A ,所以e 的取值范围是错误!. [答案] (1)错误! (2)错误! 课堂达标练习 一、填空题1.在平面直角坐标系x Oy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为错误!.过F1的直线l 交C于A ,B 两点,且△AB F2的周长为16,那么椭圆C 的方程为________.[解析] 设椭圆方程为x 2a 2+\f (y2,b 2)=1(a >b >0),由e=错误!知错误!=错误!,故错误!=错误!.由于△AB F2的周长为|AB |+|BF 2|+|AF 2|=(|AF 1|+|AF 2|)+(|BF 1|+|BF 2|)=4a =16,故a =4.∴b 2=8. ∴椭圆C的方程为错误!+错误!=1.[答案] 错误!+错误!=12.(2013·四川高考改编)从椭圆错误!+错误!=1(a>b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A是椭圆与x 轴正半轴的交点,B是椭圆与y 轴正半轴的交点,且A B∥O P(O 是坐标原点),则该椭圆的离心率是________.[解析] 设P (-c,y0)代入椭圆方程求得y0,从而求得k OP ,由kOP =k A B及e=\f(c ,a)可得离心率e . 由题意设P(-c ,y 0),将P (-c ,y0)代入\f(x 2,a2)+错误!=1,得错误!+错误!=1,则y错误!=b 2错误!=b 2·错误!=错误!.∴y 0=错误!或y 0=-错误!(舍去),∴P 错误!,∴k OP =-错误!.∵A(a,0),B (0,b),∴k AB =b -00-a=-错误!. 又∵AB ∥OP ,∴kAB =k OP ,∴-错误!=-错误!,∴b=c.∴e =\f(c,a )=\f (c,b 2+c2)=错误!=错误!. [答案] 错误!3.(2014·辽宁高考)已知椭圆C :错误!+错误!=1,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则|AN |+|BN |=________.[解析] 椭圆错误!+错误!=1中,a =3. 如图,设MN 的中点为D ,则|DF 1|+|D F2|=2a =6.∵D ,F1,F 2分别为MN ,AM ,BM 的中点,∴|BN |=2|DF 2|,|AN |=2|D F1|, ∴|AN |+|BN |=2(|DF 1|+|D F2|)=12. [答案] 124.(2014·南京调研)如图,已知过椭圆错误!+错误!=1(a >b >0)的左顶点A (-a ,0)作直线l交y 轴于点P,交椭圆于点Q ,若△AO P是等腰三角形,且错误!=2错误!,则椭圆的离心率为________.[解析] ∵△AO P为等腰三角形,∴O A=O P,故A (-a,0),P(0,a ),又错误!=2错误!,∴Q 错误!,由Q在椭圆上得错误!+错误!=1,解得错误!=错误!. ∴e =错误!=错误!=错误!. [答案] 错误!5.(2014·南京质检)已知焦点在x轴上的椭圆的离心率为错误!,且它的长轴长等于圆C:x 2+y 2-2x -15=0的半径,则椭圆的标准方程是________.[解析] 由x 2+y 2-2x -15=0,知r =4=2a ⇒a =2. 又e =\f(c,a )=\f(1,2),c =1,则b2=a 2-c 2=3.因此椭圆的标准方程为\f (x 2,4)+错误!=1. [答案] 错误!+错误!=16.(2013·辽宁高考改编)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左焦点为F,椭圆C 与过原点的直线相交于A,B 两点,连接AF ,B F.若|AB |=10,|B F|=8,cos ∠AB F=\f(4,5),则椭圆C的离心率为__________.[解析] 在△ABF 中,由余弦定理得 ,|AF |2=|AB |2+|BF |2-2|A B|·|BF |c os ∠ABF ,∴|AF|2=100+64-128=36,∴|AF |=6,从而|AB |2=|AF |2+|BF |2,则AF ⊥BF . ∴c =|OF |=12|AB |=5,利用椭圆的对称性,设F ′为右焦点,则|BF ′|=|AF |=6, ∴2a=|B F|+|BF ′|=14,a =7. 因此椭圆的离心率e =错误!=错误!. [答案] 错误! 7.已知F 1,F 2是椭圆C :x2a 2+\f(y 2,b 2)=1(a >b >0)的两个焦点,P 为椭圆C上的一点,且\o(PF 1,→)⊥错误!.若△PF 1F 2的面积为9,则b =________.[解析] 由定义,|PF 1|+|PF 2|=2a,且错误!⊥错误!, ∴|P F1|2+|PF 2|2=|F 1F 2|2=4c 2,∴(|PF 1|+|P F2|)2-2|PF 1||PF 2|=4c 2,∴2|PF 1||PF 2|=4a 2-4c 2=4b 2,∴|PF 1||PF 2|=2b 2. ∴S△PF 1F 2=\f (1,2)|PF 1||PF 2|=12×2b 2=9,因此b =3. [答案] 38.(2013·大纲全国卷改编)已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x轴的直线交C于A ,B 两点,且|AB |=3,则C 的方程为________.[解析] 依题意,设椭圆C:错误!+错误!=1(a >b>0).过点F 2(1,0)且垂直于x 轴的直线被曲线C 截得弦长|AB |=3, ∴点A错误!必在椭圆上, ∴错误!+错误!=1.① 又由c =1,得1+b 2=a 2.② 由①②联立,得b 2=3,a 2=4.故所求椭圆C 的方程为x24+\f (y 2,3)=1. [答案] \f(x 2,4)+错误!=1二、解答题9.(2014·镇江质检)已知椭圆C 1:错误!+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率. (1)求椭圆C 2的方程;(2)设O为坐标原点,点A,B 分别在椭圆C1和C 2上,错误!=2错误!,求直线AB 的方程.[解] (1)设椭圆C 2的方程为错误!+错误!=1(a >2), 其离心率为错误!, 故错误!=错误!,解得a =4.故椭圆C2的方程为\f(y 2,16)+错误!=1.(2)法一:A ,B 两点的坐标分别记为(x A ,yA ),(x B,yB ),由错误!=2错误!及(1)知,O 、A、B 三点共线且点A 、B 不在y 轴上,因此可设直线A B的方程为y =kx . 将y=kx 代入错误!+y 2=1中,得(1+4k2)x2=4, 所以x错误!=错误!. 将y =kx 代入\f(y 2,16)+错误!=1中,得(4+k 2)x 2=16,所以x 错误!=错误!. 又由错误!=2错误!,得x 错误!=4x 错误!, 即错误!=错误!, 解得k =±1.故直线AB 的方程为y =x 或y =-x. 法二:A ,B两点的坐标分别记为(xA,y A ),(x B ,yB ),由错误!=2错误!及(1)知,O 、A、B三点共线且点A 、B 不在y 轴上,因此可设直线AB 的方程为y =kx . 将y =kx 代入\f(x2,4)+y 2=1中,得(1+4k 2)x 2=4,所以x2,A =41+4k2. 由错误!=2错误!,得x错误!=错误!,y 错误!=错误!.将x2B,y错误!代入错误!+错误!=1中,得错误!=1,即4+k2=1+4k2,解得k=±1.故直线AB的方程为y=x或y=-x.10.(2014·安徽高考)设F1,F2分别是椭圆E:\f(x2,a2)+错误!=1(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|F1B|.(1)若|AB|=4,△ABF2的周长为16,求|AF2|;(2)若cos∠AF2B=错误!,求椭圆E的离心率.[解](1)由|AF1|=3|F1B|,|AB|=4,得|AF1|=3,|F1B|=1.因为△ABF2的周长为16,所以由椭圆定义可得4a=16,|AF1|+|AF2|=2a=8.故|AF2|=2a-|AF1|=8-3=5.(2)设|F1B|=k,则k>0且|AF1|=3k,|AB|=4k.由椭圆定义可得|AF2|=2a-3k,|BF2|=2a-k.在△ABF2中,由余弦定理可得|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2|cos∠AF2B,即(4k)2=(2a-3k)2+(2a-k)2-\f(6,5)(2a-3k)·(2a-k),化简可得(a+k)(a-3k)=0.而a+k>0,故a=3k.于是有|AF2|=3k=|AF1|,|BF2|=5k.因此|BF2|2=|F2A|2+|AB|2,可得F1A⊥F2A,故△AF1F2为等腰直角三角形.从而c=\f(\r(2),2)a,所以椭圆E的离心率e=错误!=错误!.椭圆的定义与性质1.椭圆的定义(1)第一定义:平面内与两个定点F1,F2的距离之和等于(大于|F1F2|)的点的轨迹叫做椭圆,这两个叫做椭圆的焦点,两个的距离叫做焦距.(2)第二定义:平面内与一个定点F和一条定直线l的距离的比是常数( <e<)的动点的轨迹是椭圆,定点F叫做椭圆的焦点,定直线l叫做焦点F相应的准线,根据椭圆的对称性,椭圆有两个焦点和两条准线.2.椭圆的标准方程和几何性质标准方程错误!+错误!=1(a>b>0)错误!+错误!=1(a>b>0)图形性质范围≤x≤≤y≤≤x≤≤y≤顶点A1( ), A2( ) A1(), A2()B1( ),B2( ) B1(),B2()焦点F1() F2() F1()F2()准线l1:x=-a2c l2:x=\f(a2,c) l1:y=-错误!l2:y=错误!轴长轴A1A2的长为短轴B1B2的长为长轴A1A2的长为短轴B1B2的长为焦距F1F2=离心率e=\f(c,a),且e∈a,b,c的关系c2=对称性对称轴:对称中心:1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)动点P到两定点A(-2,0),B(2,0)的距离之和为4,则点P的轨迹是椭圆.()(2)椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c(其中a为椭圆的长半轴长,c为椭圆的半焦距).()(3)椭圆的离心率e越大,椭圆就越圆.()(4)已知点F为平面内的一个定点,直线l为平面内的一条定直线.设d为平面内一动点P到定直线l的距离,若d=错误!|PF|,则点P的轨迹为椭圆.()2.(教材习题改编)焦点在x轴上的椭圆错误!+错误!=1的离心率为错误!,则m=________.3.椭圆的焦点坐标为(0,-6),(0,6),椭圆上一点P到两焦点的距离之和为20,则椭圆的标准方程为_____. 4.(2014·无锡质检)椭圆错误!+错误!=1的左焦点为F,直线x=m与椭圆相交于点A,B,当△F AB的周长最大时,△F AB的面积是________.5.(2014·江西高考)过点M(1,1)作斜率为-12的直线与椭圆C:错误!+错误!=1(a>b>0)相交于A,B两点,若M是线段AB的中点,则椭圆C的离心率等于________.考向1 椭圆的定义与标准方程【典例1】(1)(2014·全国大纲卷改编)已知椭圆C:\f(x2,a2)+错误!=1(a>b>0)的左、右焦点为F1、F2,离心率为错误!,过F2的直线l交C于A、B两点.若△AF1B的周长为4错误!,则C的方程为________.(2)(2014·苏州质检)椭圆的中心在原点,焦距为4,一条准线为x=-4,则该椭圆的方程为________.【规律方法】(1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决.(2)求椭圆的标准方程有两种方法①定义法:根据椭圆的定义,确定a2,b2的值,结合焦点位置可写出椭圆方程.②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a,b;若焦点位置不明确,则需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为Ax2+By2=1(A>0,B>0,A≠B).【变式训练1】(1)(2013·广东高考改编)已知中心在原点的椭圆C的右焦点为F(1,0),离心率等于\f(1,2),则C的方程是________.(2)(2014·苏州质检)已知椭圆的方程是错误!+错误!=1(a>5),它的两个焦点分别为F1,F2,且|F1F2|=8,弦AB(椭圆上任意两点的线段)过点F1,则△ABF2的周长为________.考向2椭圆的几何性质【典例2】(1)(2013·江苏高考)在平面直角坐标系xOy中,椭圆C的标准方程为错误!+错误!=1(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B.设原点到直线BF的距离为d1,F到l的距离为d2,若d2=6d1,则椭圆C的离心率为________.(2)(2014·扬州质检)已知F1、F2是椭圆C的左、右焦点,点P在椭圆上,且满足|PF1|=2|PF2|,∠PF1F2=30°,则椭圆的离心率为________.【规律方法】1.椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF1|+|PF2|=2a,得到a,c的关系.2.椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法:(1)求出a,c,代入公式e=错误!;(2)只需要根据一个条件得到关于a,b,c的齐次式,结合b2=a2-c2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).【变式训练2】(1)(2013·课标全国卷Ⅱ改编)设椭圆C:x2a2+错误!=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为________.(2)(2014·徐州一中抽测)已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.则椭圆离心率的范围为________.课堂达标练习一、填空题1.在平面直角坐标系x Oy 中,椭圆C的中心为原点,焦点F1,F 2在x轴上,离心率为\f(\r(2),2).过F 1的直线l交C 于A ,B 两点,且△ABF 2的周长为16,那么椭圆C的方程为________.2.(2013·四川高考改编)从椭圆错误!+错误!=1(a>b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O是坐标原点),则该椭圆的离心率是________.3.(2014·辽宁高考)已知椭圆C :x 29+错误!=1,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C上,则|AN |+|B N|=________.4.(2014·南京调研)如图,已知过椭圆错误!+错误!=1(a >b>0)的左顶点A (-a,0)作直线l交y 轴于点P ,交椭圆于点Q ,若△AOP 是等腰三角形,且错误!=2错误!,则椭圆的离心率为________.5.(2014·南京质检)已知焦点在x 轴上的椭圆的离心率为\f(1,2),且它的长轴长等于圆C :x 2+y 2-2x -15=0的半径,则椭圆的标准方程是________.6.(2013·辽宁高考改编)已知椭圆C:错误!+错误!=1(a >b>0)的左焦点为F,椭圆C 与过原点的直线相交于A ,B 两点,连接AF ,BF .若|AB |=10,|BF |=8,cos ∠ABF =错误!,则椭圆C 的离心率为__________.7.已知F 1,F2是椭圆C :错误!+错误!=1(a >b >0)的两个焦点,P为椭圆C上的一点,且错误!⊥错误!.若△P F1F2的面积为9,则b =________.8.(2013·大纲全国卷改编)已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x轴的直线交C 于A,B 两点,且|A B|=3,则C 的方程为________.二、解答题9.(2014·镇江质检)已知椭圆C 1:x 24+y 2=1,椭圆C2以C 1的长轴为短轴,且与C 1有相同的离心率. (1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B分别在椭圆C 1和C 2上,错误!=2错误!,求直线AB 的方程.10.(2014·安徽高考)设F1,F2分别是椭圆E:错误!+错误!=1(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|F1B|.(1)若|AB|=4,△ABF2的周长为16,求|AF2|;(2)若cos∠AF2B=错误!,求椭圆E的离心率.。
椭圆知识点性质大全

椭圆知识点性质大全椭圆是数学中的一个重要概念,具有丰富的性质和应用。
下面是关于椭圆的知识点性质的详细介绍:1.定义:椭圆是平面上到两个给定点的距离之和等于常数的点的集合。
这两个给定点称为焦点,常数称为离心率。
2.基本元素:椭圆由两个焦点和连接两个焦点的线段组成。
以及连接焦点和椭圆上任意一点的线段,这条线段称为半径。
3.中心:椭圆的两个焦点的中点称为椭圆的中心,位于椭圆的对称轴上。
4.对称轴:椭圆上与两个焦点的连线垂直的直线称为椭圆的对称轴。
对称轴上的中心对称的两个点称为对称点。
5.长轴:椭圆的两个焦点所在的直线称为椭圆的长轴,长轴的长度称为椭圆的长轴长度。
6.短轴:椭圆的长轴的中垂线称为椭圆的短轴,短轴的长度称为椭圆的短轴长度。
7.半焦距:椭圆的长轴长度的一半称为椭圆的半焦距,半焦距与离心率之间存在关系。
8.离心率:椭圆的离心率是一个正实数,表示离心率与半焦距的比值。
离心率小于1时,椭圆为椭圆体;离心率等于1时,椭圆为抛物线;离心率大于1时,椭圆为双曲线。
9.焦点定理:椭圆上的任意一点到两个焦点的距离之和等于椭圆的长轴长度。
10.顶点定理:椭圆上的任意一点到离它最近的直线的距离等于椭圆的离心率与该点到两个焦点的距离之差的绝对值。
11.弦的性质:椭圆上任意两个焦点之间的直线称为弦。
椭圆上任意一点到两个焦点的连线与该点的切线所围成的角等于椭圆上该点与焦点所在的主半径所围成的角。
12.切线的性质:椭圆上任意一点的切线与焦点连线的夹角等于椭圆上该点与焦点所在的主半径的夹角。
13.弦愈的结论:椭圆上通过两个焦点且长度相等的弦所对的两条弦是相等的。
14.垂线的性质:椭圆上任意一点的垂线与两个焦点所在直线的夹角等于该点与两个焦点所在的主半径的夹角。
15.渐屈线性质:椭圆上任意一点到两个焦点所连的线段与该点的切线所围成的角是一个常数,称为渐屈线角。
渐屈线角的大小与离心率有关。
16.椭圆的参数方程:椭圆的参数方程是描述椭圆上的点坐标的方程,通常用参数t表示角度。
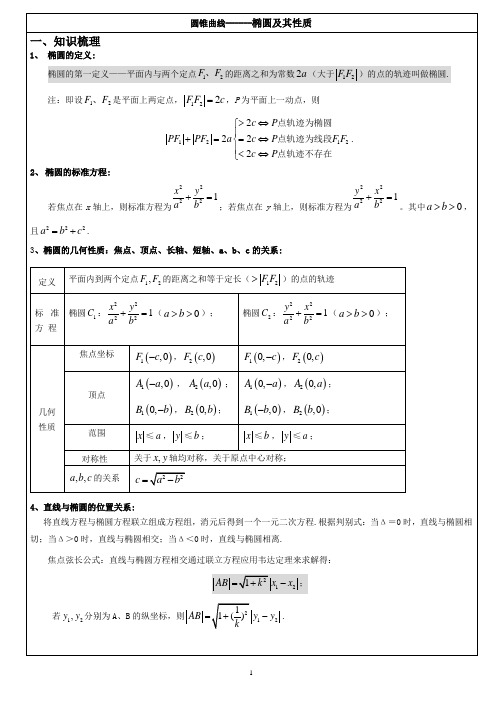
椭圆的概念与几何性质

椭圆的概念与几何性质一、知识梳理1.椭圆的定义在平面内与两定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.其数学表达式:集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数:(1)若a>c,则集合P为椭圆;(2)若a=c,则集合P为线段;(3)若a<c,则集合P为空集.2.椭圆的标准方程和几何性质a b a b3、点P(x0,y0)和椭圆的位置关系(1)点P(x0,y0)在椭圆内⇔x20a2+y20b2<1;(2)点P(x0,y0)在椭圆上⇔x20a2+y20b2=1;(3)点P(x0,y0)在椭圆外⇔x20a2+y20b2>1.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”)(1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆.()(2)椭圆的离心率e越大,椭圆就越圆.()(3)方程mx2+ny2=1(m>0,n>0,m≠n)表示的曲线是椭圆.()(4)x2a2+y2b2=1(a>b>0)与y2a2+x2b2=1(a>b>0)的焦距相同.()解析(1)由椭圆的定义知,当该常数大于|F1F2|时,其轨迹才是椭圆,而常数等于|F1F2|时,其轨迹为线段F1F2,常数小于|F1F2|时,不存在这样的图形.(2)因为e=ca=a2-b2a=1-⎝⎛⎭⎪⎫ba2,所以e越大,则ba越小,椭圆就越扁.答案(1)×(2)×(3)√(4)√2.若F1(3,0),F2(-3,0),点P到F1,F2的距离之和为10,则P点的轨迹方程是________.解析因为|PF1|+|PF2|=10>|F1F2|=6,所以点P的轨迹是以F1,F2为焦点的椭圆,其中a=5,c=3,b=a2-c2=4,故点P的轨迹方程为x225+y216=1.答案x225+y216=13.已知点P是椭圆x25+y24=1上y轴右侧的一点,且以点P及焦点F1,F2为顶点的三角形的面积等于1,则点P的坐标为________.解析设P(x,y),由题意知c2=a2-b2=5-4=1,所以c=1,则F1(-1,0),F2(1,0),由题意可得点P到x轴的距离为1,所以y=±1,把y=±1代入x25+y24=1,得x=±152,又x>0,所以x=152,∴P点坐标为(152,1)或(152,-1). 答案(152,1)或(152,-1)4.(2018·张家口调研)椭圆x 216+y 225=1的焦点坐标为( ) A.(±3,0)B.(0,±3)C.(±9,0)D.(0,±9)解析 根据椭圆方程可得焦点在y 轴上,且c 2=a 2-b 2=25-16=9,∴c =3,故焦点坐标为(0,±3). 答案 B5.(2018·全国Ⅰ卷)已知椭圆C :x 2a 2+y 24=1的一个焦点为(2,0),则C 的离心率为( ) A.13B.12C.22D.223解析 不妨设a >0.因为椭圆C 的一个焦点为(2,0),所以焦点在x 轴上,且c =2,所以a 2=4+4=8,所以a =22,所以椭圆C 的离心率e =c a =22. 答案 C6.(2018·武汉模拟)曲线x 225+y 29=1与曲线x 225-k +y 29-k =1(k <9)的( )A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等解析 曲线x 225+y 29=1表示焦点在x 轴上的椭圆,其长轴长为10,短轴长为6,焦距为8,离心率为45.曲线x 225-k +y 29-k =1(k <9)表示焦点在x 轴上的椭圆,其长轴长为225-k ,短轴长为29-k ,焦距为8,离心率为425-k.对照选项,知D 正确. 答案 D考点一 椭圆的定义及其应用【例1】 (1)如图,圆O 的半径为定长r ,A 是圆O 内一个定点,P 是圆上任意一点,线段AP 的垂直平分线l 和半径OP 相交于点Q ,当点P 在圆上运动时,点Q 的轨迹是( )A.椭圆B.双曲线C.抛物线D.圆(2)(2018·德阳模拟)设P 为椭圆C :x 249+y 224=1上一点,F 1,F 2分别是椭圆C 的左、右焦点,且△PF 1F 2的重心为点G ,若|PF 1|∶|PF 2|=3∶4,那么△GPF 1的面积为( ) A.24B.12C.8D.6解析 (1)连接QA .由已知得|QA |=|QP |. 所以|QO |+|QA |=|QO |+|QP |=|OP |=r .又因为点A 在圆内,所以|OA |<|OP |,根据椭圆的定义,点Q 的轨迹是以O ,A 为焦点,r 为长轴长的椭圆.(2)∵P 为椭圆C :x 249+y 224=1上一点,|PF 1|∶|PF 2|=3∶4,|PF 1|+|PF 2|=2a =14,∴|PF 1|=6,|PF 2|=8,又∵|F 1F 2|=2c =249-24=10,∴易知△PF 1F 2是直角三角形,S △PF 1F 2=12|PF 1|·|PF 2|=24,∵△PF 1F 2的重心为点G ,∴S △PF 1F 2=3S △GPF 1,∴△GPF 1的面积为8. 答案 (1)A (2)C 规律方法 (1)椭圆定义的应用主要有:判断平面内动点的轨迹是否为椭圆,求焦点三角形的周长、面积及弦长、最值和离心率等.(2)通常定义和余弦定理结合使用,求解关于焦点三角形的周长和面积问题.【训练1】 (1)(2018·福建四校联考)已知△ABC 的顶点B ,C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是( ) A.2 3B.6C.4 3D.2(2)(2018·衡水中学调研)设F 1,F 2分别是椭圆x 225+y 216=1的左、右焦点,P 为椭圆上任意一点,点M 的坐标为(6,4),则|PM |-|PF 1|的最小值为________. 解析 (1)由椭圆的方程得a = 3.设椭圆的另一个焦点为F ,则由椭圆的定义得|BA |+|BF |=|CA |+|CF |=2a ,所以△ABC 的周长为|BA |+|BC |+|CA |=|BA |+|BF |+|CF |+|CA |=(|BA |+|BF |)+(|CF |+|CA |)=2a +2a =4a =4 3.(2)由椭圆的方程可知F 2(3,0),由椭圆的定义可得|PF 1|=2a -|PF 2|,∴|PM |-|PF 1|=|PM |-(2a -|PF 2|)=|PM |+|PF 2|-2a ≥|MF 2|-2a ,当且仅当M ,P ,F 2三点共线时取得等号,又|MF 2|=(6-3)2+(4-0)2=5,2a =10,∴|PM |-|PF 1|≥5-10=-5,即|PM |-|PF 1|的最小值为-5. 答案 (1)C (2)-5考点二 椭圆的标准方程【例2】 (1)已知两圆C 1:(x -4)2+y 2=169,C 2:(x +4)2+y 2=9,动圆在圆C 1内部且和圆C 1相内切,和圆C 2相外切,则动圆圆心M 的轨迹方程为( ) A.x 264-y 248=1 B.x 248+y 264=1 C.x 248-y 264=1D.x 264+y 248=1(2)若椭圆经过两点(2,0)和(0,1),则椭圆的标准方程为________________. 解析 (1)设圆M 的半径为r ,则|MC 1|+|MC 2|=(13-r )+(3+r )=16>8=|C 1C 2|, 所以M 的轨迹是以C 1,C 2为焦点的椭圆,且2a =16,2c =8,所以a =8,c =4,b =a 2-b 2=82-42=48=43,故所求的轨迹方程为x 264+y 248=1.(2)法一 当椭圆的焦点在x 轴上时,设所求椭圆的方程为x 2a 2+y 2b 2=1 (a >b >0).∵椭圆经过两点(2,0),(0,1), ∴⎩⎪⎨⎪⎧4a 2+0b 2=1,0a 2+1b 2=1,解得⎩⎨⎧a =2,b =1.∴所求椭圆的标准方程为x 24+y 2=1;当椭圆的焦点在y 轴上时,设所求椭圆的方程为y 2a 2+x 2b 2=1 (a >b >0). ∵椭圆经过两点(2,0),(0,1), ∴⎩⎪⎨⎪⎧0a 2+4b 2=1,1a 2+0b 2=1,解得⎩⎨⎧a =1,b =2,与a >b 矛盾,故舍去.综上可知,所求椭圆的标准方程为x 24+y 2=1. 法二 设椭圆方程为mx 2+ny 2=1 (m >0,n >0,m ≠n ).∵椭圆过(2,0)和(0,1)两点,∴⎩⎨⎧4m =1,n =1, 解得⎩⎪⎨⎪⎧m =14,n =1.综上可知,所求椭圆的标准方程为x 24+y 2=1. 答案 (1)D (2)x 24+y 2=1规律方法 根据条件求椭圆方程的主要方法有:(1)定义法:根据题目所给条件确定动点的轨迹满足椭圆的定义.(2)待定系数法:根据题目所给的条件确定椭圆中的a ,b .当不知焦点在哪一个坐标轴上时,一般可设所求椭圆的方程为mx 2+ny 2=1(m >0,n >0,m ≠n ),不必考虑焦点位置,用待定系数法求出m ,n 的值即可.【训练2】 (1)(2018·济南模拟)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),若长轴长为6,且两焦点恰好将长轴三等分,则此椭圆的标准方程为( ) A.x 236+y 232=1 B.x 29+y 28=1 C.x 29+y 25=1D.x 216+y 212=1(2)(2018·榆林模拟)已知F 1(-1,0),F 2(1,0)是椭圆C 的焦点,过F 2且垂直于x 轴的直线交椭圆C 于A ,B 两点,且|AB |=3,则C 的方程为( ) A.x 22+y 2=1 B.x 23+y 22=1 C.x 24+y 23=1D.x 25+y 24=1解析 (1)椭圆长轴长为6,即2a =6,得a =3,∵两焦点恰好将长轴三等分, ∴2c =13×2a =2,得c =1, 因此,b 2=a 2-c 2=9-1=8,所以此椭圆的标准方程为x 29+y 28=1.(2)由题意,设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),将A (c ,y 1)代入椭圆方程得c 2a 2+y 21b 2=1,由此求得y 21=b 4a 2,所以|AB |=3=2b 2a ,又c =1,a 2-b 2=c 2,可解得a =2,b 2=3,所以椭圆C 的方程为x 24+y 23=1.答案 (1)B (2)C考点三 椭圆的几何性质 角度1 椭圆的长轴、短轴、焦距【例3-1】 (2018·泉州质检)已知椭圆x 2m -2+y 210-m =1的长轴在x 轴上,焦距为4,则m 等于( ) A.8B.7C.6D.5解析 因为椭圆x 2m -2+y210-m=1的长轴在x 轴上,所以⎩⎨⎧m -2>0,10-m >0,m -2>10-m ,解得6<m <10.因为焦距为4,所以c 2=m -2-10+m =4,解得m =8. 答案 A角度2 椭圆的离心率【例3-2】 (2018·全国Ⅱ卷)已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A.23B.12C.13D.14解析 由题意可知椭圆的焦点在x 轴上,如图所示,设|F 1F 2|=2c ,∵△PF 1F 2为等腰三角形,且∠F 1F 2P =120°, ∴|PF 2|=|F 1F 2|=2c .∵|OF 2|=c ,过P 作PE 垂直x 轴于点E ,则∠PF 2E =60°,所以|F 2E |=c ,|PE |=3c ,即点P (2c ,3c ).∵点P 在过点A ,且斜率为36的直线上, ∴3c 2c +a =36,解得c a =14,∴e =14. 答案 D 角度3 与椭圆性质有关的最值或范围问题【例3-3】 (2017·全国Ⅰ卷)设A ,B 是椭圆C :x 23+y 2m =1长轴的两个端点.若C 上存在点M 满足∠AMB =120°,则m 的取值范围是( ) A.(0,1]∪[9,+∞) B.(0,3]∪[9,+∞) C.(0,1]∪[4,+∞)D.(0,3]∪[4,+∞)解析 ①当焦点在x 轴上,依题意得 0<m <3,且3m≥tan ∠AMB 2= 3. ∴0<m <3且m ≤1,则0<m ≤1.②当焦点在y 轴上,依题意m >3,且m3≥tan ∠AMB 2=3,∴m ≥9,综上,m 的取值范围是(0,1]∪[9,+∞). 答案 A规律方法 1.求椭圆离心率的方法(1)直接求出a ,c 的值,利用离心率公式直接求解.(2)列出含有a ,b ,c 的齐次方程(或不等式),借助于b 2=a 2-c 2消去b ,转化为含有e 的方程(或不等式)求解.2.在求与椭圆有关的一些量的范围,或者最值时,经常用到椭圆标准方程中x ,y的范围、离心率的范围等不等关系.【训练3】 (1)以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1,则椭圆长轴长的最小值为( ) A.1B. 2C.2D.22(2)(2019·豫南九校联考)已知两定点A (-1,0)和B (1,0),动点P (x ,y )在直线l :y =x +3上移动,椭圆C 以A ,B 为焦点且经过点P ,则椭圆C 的离心率的最大值为( ) A.55B.105C.255D.2105解析 (1)设a ,b ,c 分别为椭圆的长半轴长、短半轴长、半焦距, 依题意知,当三角形的高为b 时面积最大, 所以12×2cb =1,bc =1,而2a =2b 2+c 2≥22bc =22(当且仅当b =c =1时取等号).即长轴长2a 的最小值为2 2.(2)不妨设椭圆方程为x 2a 2+y 2a 2-1=1(a >1),与直线l 的方程联立⎩⎪⎨⎪⎧x2a 2+y 2a 2-1=1,y =x +3,消去y 得(2a 2-1)x 2+6a 2x +10a 2-a 4=0, 由题意易知Δ=36a 4-4(2a 2-1)(10a 2-a 4)≥0,解得a ≥5, 所以e =c a =1a ≤55,所以e 的最大值为55. 答案 (1)D (2)A[思维升华]1.椭圆的定义揭示了椭圆的本质属性,正确理解、掌握定义是关键,应注意定义中的常数大于|F 1F 2|,避免了动点轨迹是线段或不存在的情况.2.求椭圆的标准方程,常采用“先定位,后定量”的方法(待定系数法).先“定位”,就是先确定椭圆和坐标系的相对位置,以椭圆的中心为原点的前提下,看焦点在哪条坐标轴上,确定标准方程的形式;再“定量”,就是根据已知条件,通过解方程(组)等手段,确定a 2,b 2的值,代入所设的方程,即可求出椭圆的标准方程.若不能确定焦点的位置,这时的标准方程常可设为mx 2+ny 2=1(m >0,n >0且m ≠n )三、课后练习1.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点为M ,上顶点为N ,右焦点为F ,若NM →·NF →=0,则椭圆的离心率为( ) A.32B.2-12C.3-12D.5-12解析 由题意知,M (-a ,0),N (0,b ),F (c ,0),∴NM→=(-a ,-b ),NF →=(c ,-b ).∵NM →·NF →=0,∴-ac +b 2=0,即b 2=ac .又b 2=a 2-c 2,∴a 2-c 2=ac .∴e 2+e -1=0,解得e =5-12或e =-5-12(舍).∴椭圆的离心率为5-12.答案 D2.(2019·湖南湘东五校联考)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 是椭圆上一点,△PF 1F 2是以F 2P 为底边的等腰三角形,且60°<∠PF 1F 2<120°,则该椭圆的离心率的取值范围是( ) A.(3-12,1)B.(3-12,12)C.⎝ ⎛⎭⎪⎫12,1D.⎝ ⎛⎭⎪⎫0,12 解析 由题意可得,|PF 2|2=|F 1F 2|2+|PF 1|2-2|F 1F 2|·|PF 1|cos ∠PF 1F 2 =4c 2+4c 2-2·2c ·2c ·cos ∠PF 1F 2,即|PF 2|=22c ·1-cos ∠PF 1F 2, 所以a =|PF 1|+|PF 2|2=c +2c ·1-cos ∠PF 1F 2,又60°<∠PF 1F 2<120°, ∴-12<cos ∠PF 1F 2<12,所以2c <a <(3+1)c ,则13+1<c a <12,即3-12<e <12. 答案 B3.(2018·浙江卷)已知点P (0,1),椭圆x 24+y 2=m (m >1)上两点A ,B 满足AP →=2PB →,则当m =________时,点B 横坐标的绝对值最大.解析 设A (x 1,y 1),B (x 2,y 2),由AP→=2PB →, 得⎩⎨⎧-x 1=2x 2,1-y 1=2(y 2-1),即x 1=-2x 2,y 1=3-2y 2.因为点A ,B 在椭圆上,所以⎩⎪⎨⎪⎧4x 224+(3-2y 2)2=m ,x 224+y 22=m ,得y 2=14m +34,所以x 22=m -(3-2y 2)2=-14m 2+52m -94=-14(m -5)2+4≤4,所以当m =5时,点B 横坐标的绝对值最大,最大值为2.答案 54.(2019·石家庄月考)已知点M (6,2)在椭圆C :x 2a 2+y 2b 2=1(a >b >0)上,且椭圆的离心率为63.(1)求椭圆C 的方程;(2)若斜率为1的直线l 与椭圆C 交于A ,B 两点,以AB 为底边作等腰三角形,顶点为P (-3,2),求△P AB 的面积.解 (1)由已知得⎩⎪⎨⎪⎧6a 2+2b 2=1,c a =63,a 2=b 2+c 2,解得⎩⎨⎧a 2=12,b 2=4. 故椭圆C 的方程为x 212+y 24=1.(2)设直线l 的方程为y =x +m ,A (x 1,y 1),B (x 2,y 2),AB 的中点为D (x 0,y 0). 由⎩⎪⎨⎪⎧y =x +m ,x 212+y 24=1,消去y ,整理得4x 2+6mx +3m 2-12=0, 由根与系数的关系得x 1+x 2=-32m ,x 1x 2=3m 2-124, 由Δ=36m 2-16(3m 2-12)>0得m 2<16,则x 0=x 1+x 22=-34m ,y 0=x 0+m =14m ,即D ⎝ ⎛⎭⎪⎫-34m ,14m . 因为AB 是等腰△P AB 的底边,所以PD ⊥AB ,即PD 的斜率k =2-m 4-3+3m 4=-1,解得m =2,满足m 2<16. 此时x 1+x 2=-3,x 1x 2=0,则|AB |=2|x 1-x 2|=2·(x 1+x 2)2-4x 1x 2=32,又点P 到直线l :x -y +2=0的距离为d =32, 所以△P AB 的面积为S =12|AB |·d =92.5.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F (1,0),其关于直线y =bx 的对称点Q 在椭圆上,则离心率e =________,S △FOQ =________.解析 设点Q (x ,y ),则由点Q 与椭圆的右焦点F (1,0)关于直线y =bx 对称得⎩⎪⎨⎪⎧y x -1=-1b ,y 2=b ·x +12,解得⎩⎪⎨⎪⎧x =1-b 21+b 2,y =2b 1+b 2,代入椭圆C 的方程得(1-b 2)2a 2(1+b 2)2+4b 2b 2(1+b 2)2=1,结合a 2=b 2+1解得⎩⎨⎧a =2,b =1,则椭圆的离心率e =c a =22,S △FOQ =12 |OF |·⎪⎪⎪⎪⎪⎪2b 1+b 2=12×1×21+12=12. 答案 22 12。
椭圆高中知识点总结

椭圆高中知识点总结【实用版】目录一、椭圆的概念与性质1.椭圆的定义2.椭圆的焦点与焦距3.椭圆的离心率4.椭圆的标准方程二、椭圆的计算方法1.待定系数法求标准方程2.椭圆的性质与应用三、椭圆的考点分析1.椭圆的定义与性质2.椭圆的标准方程及其应用3.椭圆与双曲线、抛物线的区别与联系正文一、椭圆的概念与性质1.椭圆的定义:在平面内到两定点 f1、f2 的距离的和等于常数(大于 f1f2)的点的轨迹叫做椭圆。
这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的焦点与焦距:椭圆的焦点有两个,分别记作 F1、F2,它们到椭圆上任意一点的距离之和等于常数 2a(a 为椭圆的长半轴长)。
焦距为 2c(c 为椭圆的焦距),有 a>c。
3.椭圆的离心率:椭圆的离心率是指焦点到椭圆中心的距离与长半轴长的比值,记作 e。
离心率的范围为 0<e<1,当 e=0 时,椭圆退化为圆,当 e=1 时,椭圆退化为抛物线。
4.椭圆的标准方程:椭圆的标准方程有两种形式,分别为(x^2)/(a^2)+(y^2)/(b^2)=1 和 (x^2)/(b^2)+(y^2)/(a^2)=1。
其中 a、b 分别为椭圆的长半轴和短半轴,且 a>b>0。
二、椭圆的计算方法1.待定系数法求标准方程:先设定椭圆的长半轴 a、短半轴 b 和焦距 c,然后根据椭圆的性质,建立关于 x 和 y 的方程,解方程可得椭圆的标准方程。
2.椭圆的性质与应用:椭圆具有许多重要的性质,如焦点、顶点、准线、离心率等,这些性质在解决实际问题中起着关键作用。
三、椭圆的考点分析1.椭圆的定义与性质:掌握椭圆的定义及性质,如焦点、焦距、离心率、标准方程等,能够帮助我们更好地理解和解决椭圆相关的问题。
2.椭圆的标准方程及其应用:熟练掌握椭圆的标准方程,能够帮助我们快速解决椭圆的计算问题。
同时,了解椭圆与其他曲线(如双曲线、抛物线)的区别与联系,有助于提高我们的解题能力。
椭圆及其性质

4.已知点 P 是椭圆x52+y42=1 上 y 轴右侧的一点,且以点 P 及焦点 F1,F2 为顶点
的三角形的面积等于 1,则点 P 的坐标为________. 解析:设 P(x,y),由题意知 c2=a2-b2=5-4=1, 所以 c=1,则 F1(-1,0),F2(1,0).由题意可得点 P 到 x 轴的距离为 1,所以 y=±1, 把 y=±1 代入x52+y42=1,得 x=± 215,又 x>0,所以 x= 215, 所以 P 点坐标为 215,1或 215,-1.
答案:D
(2)在△ABC 中,A(-4,0),B(4,0),△ABC 的周长是 18,则顶点 C 的轨迹方程是( )
A.2x52 +y92=1(y≠0) C.1x62 +y92=1(y≠0)
B.2y52 +x92=1(y≠0) D.1y62 +x92=1(y≠0)
解析:由|AC|+|BC|=18-8=10>8 知,顶点 C 的轨迹是以 A,B 为焦点的椭圆(A, B,C 不共线).设其方程为ax22+by22=1(a>b>0),则 a=5,c=4,从而 b=3.由 A,B, C 不共线知 y≠0.故顶点 C 的轨迹方程是2x52 +y92=1(y≠0).
2.焦点三角形:椭圆上的点 P(x0,y0)与两焦点构成的△PF1F2 叫做焦点三角形, ∠F1PF2=θ,△PF1F2 的面积为 S,则在椭圆ax22+by22=1(a>b>0)中 (1)当 P 为短轴端点时,θ 最大. (2)S=12|PF1||PF2|·sinθ=b2tan 2θ=c|y0|,当|y0|=b 时,即点 P 为短轴端点时,S 取最 大值,最大值为 bc. (3)焦点三角形的周长为 2(a+c).
椭圆及其性质
解:方法一:设所求直线方程为 .
代入椭圆方程,整理得
①
设直线与椭圆的交点为 , ,则 、 是①的两根,∴
∵ 为 中点,∴ , .
∴所求直线方程为 .
方法二:设直线与椭圆交点 , .∵ 为 中点,∴ , .又∵ , 在椭圆上,∴ , 两式相减得 ,
又 ,所以 , 适合.故 .
例3已知动圆P过定点 ,并且在定圆 的内部与其相内切,求动圆圆心P的轨迹方程.
解:如图所示,设动圆 和定圆 内切于点 .动点 到两定点,即定点 和定圆圆心 距离之和恰好等于定圆半径,即 .
∴点 的轨迹是以 , 为两焦点,半长轴为4,半短轴长为 的椭圆的方程: .
[补例练习]
定义
平面内到两个定点 的距离之和等于定长( )的点的轨迹
标准方程
椭圆 : ( );
椭圆 : ( );
几何性质
焦点坐标
,
,
顶点
, ; , ;
, ;
, ;
范围
≤ , ≤ ;
≤ , ≤ ;
对称性
关于 轴均对称,关于原点中心对称;
的关系
4、直线与椭圆的位置关系:
将直线方程与椭圆方程联立组成方程组,消元后得到一个一元二次方程.根据判别式:当Δ=0时,直线与椭圆相切;当Δ>0时,直线与椭圆相交;当Δ<0时,直线与椭圆相离.
焦点弦长公式:直线与椭圆方程相交通过联立方程应用韦达定理来求解得:
;
若 分别为A、B的纵坐标,则 .
5、点与椭圆的位置关系:设点 ,椭圆方程为 ,则:
(其中 为椭圆焦点).
二、典型例题
例1已知椭圆方程 ,长轴端点为A1,A2,焦点为F1,F2,P是椭圆上一点, .求: 的面积(用a、b、 表示).
椭圆高中知识点总结

椭圆高中知识点总结【原创版】目录一、椭圆的概念及几何性质二、椭圆的标准方程及其参数三、椭圆的性质定理四、椭圆的应用正文一、椭圆的概念及几何性质椭圆是数学中一种重要的曲线,它是在平面内到两个定点(称为焦点)的距离之和等于常数(大于焦点间距离)的点的轨迹。
椭圆有两个焦点 F1、F2 和两个顶点 A、B,其中 AF1 + AF2 = 2a,BF1 + BF2 = 2a,其中 a 为椭圆的长半轴。
椭圆的中心点 O 位于原点,且 OA = OB = a。
椭圆的几何性质包括:1.椭圆是对称的,即关于 x 轴、y 轴和原点对称。
2.椭圆的离心率 e 满足 0 < e < 1,其中 e = c / a,c 为焦距。
3.椭圆的周长为 2πa,面积为πab。
二、椭圆的标准方程及其参数椭圆的标准方程有两种形式,分别为:1.当焦点在 x 轴上时,椭圆的标准方程为:(x^2) / (a^2) + (y^2) / (b^2) = 1,其中 a > b > 0。
2.当焦点在 y 轴上时,椭圆的标准方程为:(x^2) / (b^2) + (y^2) / (a^2) = 1,其中 a > b > 0。
椭圆的参数有:长半轴 a、短半轴 b、焦距 c 和离心率 e。
三、椭圆的性质定理1.椭圆的离心率 e 满足 0 < e < 1,其中 e = c / a。
2.椭圆的周长为 2πa,面积为πab。
3.椭圆的焦点到椭圆上任意一点的距离之和等于常数 2a。
4.椭圆的两个顶点到椭圆上任意一点的距离之差相等。
四、椭圆的应用椭圆在实际生活和数学中有广泛的应用,例如:1.椭圆在物理学中,描述行星运动的轨迹。
2.椭圆在工程学中,用于设计望远镜的反射镜和卫星天线的轨道。
3.椭圆在数学中,与其他曲线(如双曲线、抛物线)共同构成了解析几何的基本研究对象。
总结:椭圆是一种重要的数学曲线,它具有丰富的几何性质和应用。
