椭圆定义及性质整合
椭圆的相关知识点

椭圆的相关知识点椭圆是数学中一个非常重要的几何形状。
它在各个领域中都有广泛的应用,如天文学、物理学、工程学等。
本文将详细介绍椭圆的相关知识点,包括椭圆的定义、性质、方程和应用。
一、定义与性质椭圆是平面上到两个固定点的距离之和等于常数的点的轨迹。
这两个固定点分别称为椭圆的焦点,连接两个焦点的线段称为主轴,主轴的中点称为椭圆的中心。
在椭圆上任取一点P,连接P到两个焦点的距离之和等于常数,记为PF1 + PF2 = 2a(a为常数)。
椭圆的性质如下:1. 所有点到两个焦点的距离之和等于常数。
2. 主轴是椭圆上最长的一段线。
3. 所有点到椭圆中心的距离之和等于椭圆的长轴长度。
4. 与椭圆的长轴垂直的线段称为短轴,长轴和短轴的长度之比称为椭圆的离心率。
离心率小于1的椭圆称为椭圆,等于1的椭圆称为抛物线,大于1的椭圆称为双曲线。
二、椭圆的方程椭圆的方程有两种形式:标准方程和一般方程。
1. 标准方程以椭圆的中心为原点,椭圆的长轴与x轴平行。
设椭圆的长轴长度为2a,短轴长度为2b,椭圆的标准方程为:x^2/a^2 + y^2/b^2 = 12. 一般方程一般方程是对标准方程进行平移和旋转得到的。
设椭圆的中心为(h, k),椭圆的标准方程为:((x-h)^2)/a^2 + ((y-k)^2)/b^2 = 1其中,a和b分别为椭圆的半长轴和半短轴的长度。
三、椭圆的应用椭圆在众多领域中有广泛的应用。
1. 天文学在天文学中,行星和卫星的轨道往往是椭圆。
开普勒定律描述了行星运动的规律,其中第一定律指出行星和太阳之间的轨道是一个椭圆。
2. 物理学在牛顿力学中,椭圆是一种机械能守恒的轨迹。
当质点在万有引力下运动时,其轨迹为椭圆。
3. 工程学在建筑工程中,椭圆的形状经常被利用于设计桥梁、隧道以及建筑物的拱形结构。
椭圆形的结构能够提供更好的均匀分布重量的能力,提高结构的稳定性和承载能力。
4. 地理学椭圆也常常用于地理学中,用来表示地球的形状。
椭圆相关知识点总结

椭圆相关知识点总结椭圆是数学几何中的一个重要概念,它在许多领域中都有广泛的应用,如天文学、航天工程、电子工程等。
本文将对椭圆的定义、性质、方程和应用进行总结和讨论。
一、椭圆的定义和性质1.定义:椭圆是平面上到两个给定点的距离之和等于常数的点的轨迹。
这两个给定点称为焦点,常数称为椭圆的离心率。
2.性质:–椭圆的离心率介于0和1之间,离心率越接近于0,椭圆越接近于圆形。
–椭圆的长轴是两个焦点之间的距离,短轴是椭圆的两个相互垂直的直径的长度之一。
–椭圆的焦点到任意一点的距离之和等于椭圆的长轴的长度。
二、椭圆的方程椭圆的标准方程可以表示为:(x - h)²/a² + (y - k)²/b² = 1其中,(h, k)是椭圆的中心坐标,a和b分别是椭圆长轴和短轴的长度。
通过标准方程,我们可以得到椭圆的一些重要参数: - 焦点的坐标为 (h ± c, k),其中 c² = a² - b²。
- 离心率为 e = c/a。
三、椭圆的应用1.天文学:行星和卫星的运动轨迹多为椭圆,椭圆方程可以用来描述它们的轨道。
2.航天工程:火箭发射轨迹也常用椭圆来描述,以便计算火箭的速度和位置。
3.电子工程:天线的辐射范围常用椭圆来描述,以便确定最佳的天线安装位置和方向。
4.地理测量学:椭圆体被用作地球的近似模型,以便进行地图绘制和测量。
5.光学:椭圆反射镜和椭圆透镜在光学系统中有着重要的应用,可以用来聚焦和成像。
综上所述,椭圆是数学几何中的重要概念,在许多领域中都有广泛的应用。
通过对椭圆的定义、性质、方程和应用的总结,我们对椭圆有了更深入的了解,也认识到椭圆在实际问题中的重要性。
椭圆基本知识点总结

椭圆基本知识点总结椭圆是平面上一条封闭的曲线,具有一对焦点和一条主轴。
下面将对椭圆的基本知识进行总结,包括椭圆的定义、方程、性质、参数方程、焦点、离心率等。
一、椭圆的定义和方程:椭圆是平面上到两个给定点的距离之和等于常数的点的集合。
这两个给定点称为椭圆的焦点,连结两个焦点的直线称为椭圆的主轴,主轴的中点称为椭圆的中心。
将两个焦点之间的距离称为焦距,将两焦点之间的距离称为椭圆的直径。
椭圆的标准方程为:x^2/a^2+y^2/b^2=1,其中a和b分别为椭圆在x轴和y轴上的半轴长,a>b,中心在原点。
二、椭圆的性质:1.对于椭圆上的任意一点P,焦点到P的距离之和等于常数。
设PF1和PF2分别是该点到焦点F1和F2的距离,那么PF1+PF2=2a(常数)。
2.椭圆的离心率e满足0<e<1、离心率e的定义是焦距与半轴长的比值:e=c/a,其中c为焦距。
3.离心率e越小,椭圆的形状越扁平;离心率接近于1,椭圆的形状越接近于长轴为直径的圆。
4. 椭圆的面积为πab,其中π为圆周率。
5.椭圆的边界上的点离中心的距离最远为a,该点称为椭圆的顶点;离中心的距离最近为b,该点称为椭圆的底点。
三、椭圆的参数方程:可以用参数方程来表示椭圆上的点的坐标(x,y)。
常用的参数方程为:x = a * cosθy = b * sinθ其中θ为参数,a和b为椭圆的半轴长。
四、椭圆的焦点和直线:1.椭圆的焦点是椭圆上特殊的两个点,它们与椭圆上的任意一点连线的长度之和是一个常数。
2.椭圆的两条主轴与椭圆相交于中心,相互垂直。
3.过椭圆的焦点F1和F2分别作直线L1和L2,与椭圆的边界交于两点P1和P2,那么直线L1和L2分别是椭圆的两条切线。
4.椭圆的两条主轴与椭圆的焦点、中心之间的连线围成的角称为离心角,它等于直角。
五、椭圆的离心率和焦距:1. 椭圆的离心率e定义为焦距与半轴长之比:e = c/a = sqrt(1 -b^2/a^2),其中c为焦距。
圆锥曲线(椭圆,双曲线,抛物线)的定义方程和性质知识总结

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2.3. 椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在x 轴上时,设12F F 、分别是椭圆的左、右焦点,()00P x y ,是椭圆上任一点,则10PF a ex =+,20PF a ex =-。
推导过程:由第二定义得11PF e d =(1d 为点P 到左准线的距离), 则211000a PF ed e x ex a a ex c ⎛⎫==+=+=+ ⎪⎝⎭;同理得20PF a ex =-。
简记为:左“+”右“-”。
由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。
22221x y a b +=;若焦点在y 轴上,则为22221y x a b+=。
有时为了运算方便,设),0(122n m m ny mx ≠>=+。
双曲线的定义、方程和性质1. 定义(1)第一定义:平面内到两定点F 1、F 2的距离之差的绝对值等于定长2a (小于|F 1F 2|)的点的轨迹叫双曲线。
说明:①||PF 1|-|PF 2||=2a (2a <|F 1F 2|)是双曲线;若2a=|F 1F 2|,轨迹是以F 1、F 2为端点的射线;2a >|F 1F 2|时无轨迹。
②设M 是双曲线上任意一点,若M 点在双曲线右边一支上,则|MF 1|>|MF 2|,|MF 1|-|MF 2|=2a ;若M 在双曲线的左支上,则|MF 1|<|MF 2|,|MF 1|-|MF 2|=-2a ,故|MF 1|-|MF 2|=±2a ,这是与椭圆不同的地方。
椭圆高中知识点总结

椭圆高中知识点总结椭圆是一个在数学中经常被研究的几何图形。
它有许多重要的性质和特点,是高中数学中的重要知识点之一、在以下的总结中,我将介绍椭圆的定义、方程、性质、焦点及其应用等方面的知识点。
一、椭圆的定义:椭圆可以通过两个焦点和一个定长的线段来定义。
具体地说,椭圆是平面上到两个给定点的距离之和等于定长的点的集合。
这两个给定点称为焦点,定长称为焦距。
二、椭圆的方程:椭圆的标准方程为:[(x-h)^2/a^2]+[(y-k)^2/b^2]=1,其中(h,k)是椭圆的中心坐标,a和b分别是椭圆的长半轴和短半轴的长度。
三、椭圆的性质:1.椭圆的长半轴和短半轴之间存在关系:c^2=a^2–b^2,其中c是焦点到椭圆中心的距离。
2.椭圆是对称图形,具有关于x轴和y轴的对称性。
3.椭圆的离心率e满足0<e<1,且离心率越大,椭圆越扁平;离心率为0时,椭圆退化成为一个点。
4.椭圆的周长可以用椭圆的长半轴和短半轴的长度来表示:L=4aE(e),其中E(e)是椭圆的第一类型椭圆积分。
5. 椭圆的面积可以用椭圆的长半轴和短半轴的长度来表示:S =πab。
四、椭圆的焦点:椭圆上有两个与焦点有关的重要的点,分别是两个焦点的位置。
焦点到椭圆上任一点的距离之和等于椭圆的焦距。
焦距与椭圆的半轴之间的关系为c^2=a^2–b^2五、椭圆的应用:1.椭圆在天文学中被广泛应用,用于描述行星和卫星的轨道形状。
2.椭圆在工程学中用于设计椭圆形的机械零件。
3.椭圆在地理学中用于描述地球的地理形状和地球上的纬度和经度线。
4.椭圆在艺术和建筑设计中被用于创作椭圆形的艺术品和建筑结构。
总结:椭圆是一个广泛应用于数学和其他科学领域的重要几何图形。
通过椭圆的定义、方程、性质和焦点等方面的知识点,我们可以更好地理解和应用椭圆。
椭圆的应用广泛,涉及到天文学、工程学、地理学、艺术和建筑设计等不同领域。
掌握椭圆的相关知识,对于我们理解和应用数学都有很大的帮助。
椭圆的知识点总结

椭圆的知识点总结一、椭圆的定义椭圆是平面上的一种特殊曲线,它的定义可以有多种方式。
在解析几何中,我们通常采用焦点-直线之和等于常数的定义来描述椭圆。
具体而言,椭圆定义为到两个固定点(焦点)的距离之和等于常数的点的集合。
这个常数被称为椭圆的长轴长度。
另外,椭圆还有一个短轴,它垂直于长轴且通过长轴的中点。
椭圆的长轴和短轴的长度决定了椭圆的形状。
二、椭圆的性质1. 焦点性质:椭圆有两个焦点,它们位于长轴上,且椭圆上任意一点到两个焦点的距离之和等于椭圆的长轴长度。
2. 直径性质:椭圆的直径是经过焦点的直线段,并且它恰好与椭圆相交于椭圆上的两点。
3. 周长性质:椭圆的周长可以用椭圆的半长轴和半短轴的长度来表示,即2πb+4aE(e),其中a和b分别为椭圆的长轴和短轴的长度,E(e)为第二类椭圆积分。
4. 质心性质:椭圆的质心位于椭圆的中心,且与椭圆的几何中心重合。
椭圆的质心满足椭圆上所有点到该质心的距离之和等于椭圆的长轴长度。
5. 对称性质:椭圆具有关于长轴和短轴的对称性,且同时具有关于两个焦点的对称性。
6. 离心率性质:椭圆的离心率e是一个重要的参数,它刻画了椭圆的形状。
椭圆的离心率满足0<e<1,且e=√(1-b²/a²)。
7. 焦点和直角坐标系的关系:椭圆在直角坐标系中的方程形式可以用来描述椭圆的形状,其一般方程为(x²/a²)+(y²/b²)=1。
三、椭圆的方程椭圆的方程通常以长轴和短轴的长度来表示,其一般方程为(x²/a²)+(y²/b²)=1。
在给定长轴和短轴的情况下,可以通过椭圆的方程来确定椭圆的形状和位置。
四、椭圆的焦点椭圆有两个焦点,它们分别位于长轴的两端。
椭圆上任意一点到两个焦点的距离之和等于椭圆的长轴长度。
焦点是椭圆的重要特性,它们的位置决定了椭圆的形状和方向。
五、椭圆的参数方程椭圆还可以用参数方程来描述。
有关椭圆的所有知识点

有关椭圆的所有知识点
1. 椭圆的定义:椭圆是一种特殊的抛物线,它是二维平面上的曲线,其中两条轴的长度不相等,椭圆的方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
2. 椭圆的性质:
(1)椭圆的对称轴是两个相交的线段,其中一个线段的长度大于另一个,称为长轴,另一个线段称为短轴;
(2)椭圆的中心点是两个对称轴的交点;
(3)椭圆的长轴和短轴的长度分别为a和b,椭圆的面积为S=πab;
(4)椭圆的边界是一个抛物线,称为椭圆弧,可以用参数方程表示:$$x=a\cos t,
y=b\sin t$$
3. 椭圆的标准方程:
(1)椭圆的标准方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
(2)椭圆的中心在原点时,标准方程为:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
(3)椭圆的中心在(h,k)处时,标准方程为:$$\frac{(x-h)^2}{a^2}+\frac{(y-
k)^2}{b^2}=1$$
4. 椭圆的对称性:
(1)椭圆是一种具有对称性的曲线,其对称轴是两个相交的线段,其中一个线段的长度大于另一个,称为长轴,另一个线段称为短轴;
(2)椭圆的对称性可以用参数方程表示:$$x=a\cos t,y=b\sin t$$
(3)椭圆的对称性可以用参数方程表示:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
5. 椭圆的离心率:椭圆的离心率是椭圆的一个重要参数,它可以表示椭圆的形状,它的定义是:椭圆的离心率等于椭圆的长轴与短轴之比,即:$$e=\frac{a-b}{a}$$。
椭圆定义及性质整合

椭圆定义及性质的应用一、椭圆的定义椭圆第一定义第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.★过点1F 作12PF F ∆的P ∠的外角平分线的垂线,垂足为Q ,则Q 的轨迹方程为222x y a +=. 推导过程:延长1FQ 交2F P 于M ,连接OQ , 由已知有PQ 为1MF 的中垂线,则1PF PM=,Q 为1F M 中点,212OQ F M ==()1212PF PF +=a ,所以Q 的轨迹方程为 222x y a +=.(椭圆的方程与离心率学案第5题)椭圆第二定义第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆.2PF e d=(d 为点P 到右准线的距离),右准线对应右焦点,其中2PF 称作焦半径,左、右准线公式2a x c=±..椭圆的焦半径公式为:1020,PF a ex PF a ex =+=-.推导过程:2200a PF ed e x a ex c ⎛⎫==-=- ⎪⎝⎭;同理得10PF a ex =+. 简记为:左加右减a 在前.由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数.(离心率、焦点弦问题)例1:(2010全国卷Ⅱ理数12题)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为32,过右焦点F 且斜率为(0)k k >的直线与C 相交于,A B 两点.若3AF FB =,则k =( )A.1B.2C.3D.2B 【解析】解法一:1122(,),(,)A x y B x y ,∵ 3AF FB =,∴ 123y y =-, ∵ 32e =,设2,3a t c t ==,b t =,∴ 222440x y b +-=,直线AB 方程为3x my b =+.代入消去x ,∴ 222(4)230m y mby b ++-=,∴212122223,44mb b y y y y m m +=-=-++,则222222232,344mb b y y m m -=--=-++,解得212m =,则2k =,0k >. 解法二:设直线l 为椭圆的右准线,e 为离心率,过,A B 别作11,AA BB 垂直于l ,11,A B 为垂足,过B 作BH 垂直于1AA 与H ,设BF m =,由第二定义得,11,AF BFAA BB e e==,由3AF FB =,得13m AA e =,2m AH e =,4AB m =,则213cos 423mAH e BAH AB m e ∠====,则6sin 3BAH ∠=,tan 2BAH ∠=,则2k =,0k >.故选B. (离心率、焦点弦问题)例2:倾斜角为6π的直线过椭圆)0(12222>>=+b a by a x 的左焦点F ,交椭圆于,A B 两点,且有3AF BF =,求椭圆的离心率.33【解析】解法一:,AF BF 为左焦点上的焦半径,所以过,A B 两点分别作垂直于准线的直线且和准线交于11,A B 两点,从B 点作1BH AA ⊥.因为3AF BF =,设BF m =,则3AF m =,4AB m =,又因为11AF BF e AA BB ==,则1BF m BB e e ==,13mAA e=,所以2m AH e =,在ABH ∆中,6BAH π∠=,所以32AH AB =,解得33e =. 解法二:如图,设,3BF m AF m==,则122,23BF a m AF a m =-=-,在12AF F ∆中,由余弦定理得222394(23)cos 62232m c a m m cπ+--==⨯⨯,化简得23326cm b am =-+①,222534(2)cos 6222m c a m m cπ+--=-=⨯⨯,化简得2322cm b am -=-+②,①+②×3化简得,223b m a =,代入①解得33e =. 椭圆第三定义第三定义:在椭圆)0(12222>>=+b a by a x 中,,A B 两点关于原点对称,P 是椭圆上异于,A B两点的任意一点,若PB PA k k ,存在,则1222-=-=⋅e ab k k PBPA .(反之亦成立).(★焦点在Y 轴上时,椭圆满足22ba k k PBPA -=⋅)推导过程:设(,)P x y ,11(,)A x y ,则11(,)B x y --.所以12222=+b y a x ①,1221221=+bya x ②;由①-②得22122212b y y a x x --=-,所以22212212a b x x y y -=--,所以222111222111PA PBy y y y y y b k k x x x x x x a-+-⋅=⋅==--+-为定值. 例1:已知椭圆)0(12222>>=+b a by a x 的长轴长为4,若点P 是椭圆上任意一点,过原点的直线l 与椭圆相交与N M ,两点,记直线PN PM ,的斜率分别为21,k k .若4121-=⋅k k ,则椭圆的方程为 .1422=+y x .【解析】解法一:(,)P x y ,11(,)M x y ,则11(,)N x y --,因为12222=+b y a x ,则)1(2222ax b y -=,)1(221221axb y -=,则222212222211112222221111(1)(1)14x x b b y y y y y y b a a k k x x x x x x x x a ----+-⋅=⋅===-=--+--.且42=a ,则椭圆方程为1422=+y x .解法二:由第三定义知4122-=-a b ,且42=a ,则则椭圆方程为1422=+y x .例2:已知椭圆)0(13422>>=+b a y x 的左右顶点分别为21,A A ,点P 在椭圆上,且直线2PA 的斜率的取值范围是]1,2[--,那么直线1PA 的斜率的取值范围是 .]43,83[.【解析】设1PA ,2PA 的斜率分别为21,k k ,则432221-=-=⋅a b k k ,又]1,2[2--∈k ,所以]43,83[1∈k .二、椭圆的性质焦点三角形椭圆焦点三角形的边角关系:122F F c =, 122PF PF a +=,周长为22a c +.设12F PF θ∠=. (1)当点P 处于短轴的顶点处时,顶角θ最大;(2)221221cos b PF PF a θ⋅=≤+,当且仅当12PF PF =时取等号;(3)122tan2PF F S b θ∆=;(4)12112122PF F B F F S S c b bc ∆∆≤=⨯⨯=,当且仅当12PF PF =时取等号. 推导过程:(1)()()()2222222212002222222120004444cos 12222PF PF c a ex a ex c a c PF PF a e x a e x θ+-++---===-⋅-+, 当00x =时,cos θ有最小值2222a c a -,即12F PF θ∠=最大; (2)22212124cos 2PF PF c PF PF θ+-=⋅,()221212122cos 24PF PF PF PF PF PF c θ⋅=+-⋅-则有,21221cos b PF PF θ⋅=+,2221220max 2221cos 1cos 12cos 12b b b PF PF θθθ⋅=≤=+++-,(当点P 为短轴顶点时θ取得最大值0θ,此时0cos 2b a θ=),代入化简得221221cos b PF PF a θ⋅=≤+. (3)由(2)得12222212sin 2sin cos tan21cos 2222cos 2PF F b b S b θθθθθθ∆=⨯⋅=⋅=+. (离心率问题)例1.已知12,F F 分别是椭圆)0(1:2222>>=+b a by a x C 的左右焦点,椭圆C 上存在一点P ,使得1290F PF ∠=︒,则椭圆C 的离心率的取值范围是__________.[2【解析】解法一:在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,由题意得145F BO ∠≥︒,所以1FO OB ≥,即c b ≥,解得[2e ∈. 解法二:设(,)P x y ,由题意得椭圆C 上存在一点P ,使得12F P F P ⊥,即(,)(,)0x c y x c y +-=,化简,得222x y c +=,与12222=+by a x 联立,消去y 得2222222a c ab x a b -=-,由椭圆范围知220x a ≤<,即22222220a c a b a a b -≤<-,化简得222b c a ≤<,解得2[,1)2e ∈. 变式1:已知12,F F 分别是椭圆)0(1:2222>>=+b a by a x C 的左右焦点,椭圆C 上存在一点P ,使得12F PF ∠为钝角,则椭圆C 的离心率的取值范围是__________.2(,1)2【解析】在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,12F PF ∠为钝角,所以145F BO ∠>︒,所以1FO OB >,即c b >,解得2(,1)2e ∈. 变式2:已知12,F F 分别是椭圆)0(1:2222>>=+b a by a x C 的左右焦点,椭圆C 上存在一点P ,使得1260F PF ∠=︒(变式3:12120F PF ∠=︒),则椭圆C 的离心率的取值范围是__________. 1[,1)2【解析】在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,由题意得130F BO ∠≥︒, 所以11sin sin 302c F BO a ∠=≥︒=,则1[,1)2e ∈.变式3:3[,1)2e ∈.(离心率问题)例2.已知12,F F 是椭圆)0(1:2222>>=+b a b y a x C 的左右焦点,若在直线2a x c=上存在点P ,使得线段1PF 的中垂线过点2F ,则椭圆的离心率的取值范围是________.3[3e ∈【解析】22PF c =,22PF F H ≥,即22a c c c ≥-解得:3[3e ∈.(焦点三角形面积问题)例 3.已知椭圆21221925F F y x 、,=+为焦点,点P 为椭圆上一点,123F PF π∠=,求21PF F S ∆.33【解析】解法一:设12,,PF m PF n ==则有10m n +=,在21F PF ∆中由余弦定理得mn n m c -+==222644,则mn mn n m 31003)(642-=-+=,则12=mn ,则333sin 2121==∆πmn S PF F . 解法二:122tan9tan3326PF F S b θπ∆==⨯=.(焦点三角形面积问题)例4.过椭圆)0(1:2222>>=+b a by a x C 中心的直线与椭圆交于,A B 两点,右焦点为2(c,0)F ,则 2ABF ∆的最大面积为_________.bc 【解析】由题意得,A B 关于原点对称,则有212ABF AF F S S ∆∆=,故当A 位于短轴的顶点处时,面积最大,为bc .(焦点三角形边角问题)例5.已知椭圆22194x y +=的两个焦点分别为12,F F ,点P 在椭圆上, (1)在椭圆上满足12PF PF ⊥的点P 的个数是?(2)12PF PF ⋅的最大值是?(3)12F PF ∠为钝角时,点P 的横坐标的取值范围是?【解析】(1)画图知,所求点的个数即为圆222x y c +=与椭圆的交点个数,由于52c b =>=,故有4个点.(2)解法一:设12,,PF m PF n ==则有6m n +=,212()92m n PFPF mn +⋅=≤=,当且仅当m n =时取等号.解法二:由性质得2221220min 2221cos 1(cos )12cos 12b b b PF PF θθθ⋅=≤=+++-,(当点P 为短轴顶点时取得最大值,此时0cos2b aθ=),代入化简得221221cos b PF PF a θ⋅=≤+.(3)如图所示,222x y c +=与椭圆有4个交点,假设在第一象限的交点为00(,)P x y ,此时122F PF π∠=,设12,,PF m PF n ==则有6m n +=,222420m n c +==,解得4,2m n ==(或2,4m n ==),由等面积法得0222y c mn⨯=,则045y =,则由勾股定理得22200()c x y n -+=,解得035x =,则由对称性可知,点P 的横坐标的取值范围是3535(,)55-. (焦点三角形中与距离最值有关的问题):注意在三角函数与解析几何中最值问题的一个很重要的用法:(1)三角形两边之和大于第三边,当三点在一条线上时取得最小值; (2)两边之差小于第三边.焦点三角形中的最值问题一般是距离之和的最值,且存在定点,故可以用三角形中的不等式来求;★若点A 为椭圆内一定点,点P 在椭圆上,则有:111AF PA PF AF -≤-≤.(三角形三边关系)★若点A 为椭圆内一定点,点P 在椭圆上,则有:12122a AF PA PF a AF -≤+≤+.推导过程:连接11,,AP AF PF ,()21122AP PF AP a PF a AP PF +=+-=+-由三角形三边关系得111AF PA PF AF -≤-≤,则有12122a AF PA PF a AF -≤+≤+(椭圆定义的应用,三角形三边关系).焦点弦经过椭圆焦点的弦是焦点弦.(1)焦点弦长可用弦长公式求22212121212211()41()4AB k x x x x y y y y k=++-=++-; *(2)设焦点弦所在的直线的倾斜角为θ,则有22222||=cos ab AB a c θ-.*(3)2211b a BF AF =+(F 为某一焦点).(4)2ABF ∆的周长为4a .(离心率、焦点弦问题)(同第二定义例1)例1:(2010全国卷Ⅱ理数12题)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为32,过右焦点F 且斜率为(0)k k >的直线与C 相交于,A B 两点.若3AF FB =,则k =( )A.1B.2C.3D.2B 【解析】解答题解法:1122(,),(,)A x y B x y ,∵ 3AF FB =,∴ 123y y =-, ∵ 32e =,设2,3a t c t ==,b t =,∴ 222440x y b +-=,直线AB 方程为3x my b =+.代入消去x ,∴ 222(4)230m y mby b ++-=,∴212122223,44mb b y y y y m m +=-=-++,则222222232,344mb b y y m m -=--=-++,解得212m =,则2k =,0k >. 中点弦AB 是椭圆2222:1(0)x y C a b a b +=>>的任意一弦,P 是AB 中点,则1222-=-=⋅e ab k k OPAB .证明:令()()1122,,,A x y B x y ,()00,P x y 则()1202x x x+=,()1202y y y+=,()()()()22112212121212222222221..01x y x x x x y y y y a b a b x y a b ⎫+=⎪+-+-⎪⇒+=⎬⎪+=⎪⎭, ()()()()2121221212y y b x x x x a y y -+⇒=--+,由于()()1212AB y y k x x -=-,00OPy k x =,则 22AB OP b k k a⋅=-. 例1:过点(2,1)M 作一条直线l 交椭圆221169x y+=于点AB ,若点M 恰好是弦AB 的中点,求直线l 的方程.【解析】解答题步骤:解法一(点差法):由题意得直线l 有斜率,设其斜率为k ,1122(,),(,)A x y B x y ,00(,)M x y ,代入椭圆方程,有222211221,1169169x y x y +=+=,两式作差得()()()()12121212..0169x x x x y y y y +-+-+=,()()120120916y y y x x x -⨯=--,即19216k ⨯=-,则98k =-.则直线l 的方程为91(2)8y x -=-⨯-,即98260x y +-=.解法二(代入法):由题意得直线l 有斜率,设其直线方程为1(2)y k x -=-,得12y kx k =+-,代入221169x y +=得222(916)32(12)16(12)1440k x k k x k ++-+--=,则120232(12)24916k k x x x k-+=-==+,解得98k =-,则直线l 的方程为98260x y +-=. 这两种方法都体现了设而不求的思想,这是圆锥曲线解题的常用思想.切线及切点弦切线方程:(1)设),(00y x P 为圆222r y x =+上一点,则过该点的切线方程为:200r y y x x =+;(2)设),(00y x P 为椭圆)0(12222>>=+b a by a x 上一点,则过该点的切线方程为:12020=+b y y a x x .切点弦方程:(1)设),(00y x P 是圆222r y x =+外的一点,过点P 作曲线的两条切线,切点N M 、,则切点弦MN 所在直线方程为200r y y x x =+;(2)设),(00y x P 是椭圆外的一点,过点P 作曲线的两条切线,切点N M 、,则切点弦MN 所在直线方程为12020=+byy a x x .例1:以422=+y x 上的点)3,1(P 为切点的切线方程为_________.【解析】解法一:由题意得切线有斜率,设切线方程为)1(3-=-x k y ,则03=-+-k y kx ,则有2132=+-k k,解得33-=k ,则切线方程为043=-+y x . 解法二:点)3,1(P 为切点,由公式得,切线方程为431=⨯+⨯y x ,即043=-+y x .例2:以13422=+y x 上的点)23,1(P 为切点的切线方程为_________. 【解析】解法一:由题意得切线有斜率,设切线方程为)1(23-=-x k y ,代入13422=+y x ,化简得3124)23(4)43(222=--+-++k k x k k x k ,则有0)3124)(43(4)23(162222=--+--=∆k k k k k ,解得21-=k ,则切线方程为042=-+y x . 解法二:点)23,1(P 为切点,由公式得,切线方程为132341=⨯+⨯y x ,即042=-+y x . ★过椭圆准线上任一点作椭圆和切线,切点弦AB 过该准线对应的焦点.推导过程:设20,a M y c ⎛⎫ ⎪⎝⎭,则AB 的方程为20221a x y y c a b +=, 即 021y y x c b +=必过点(),0c . ★过椭圆焦点弦的两端点作椭圆的切线,切线交点在准线上.光学性质★椭圆的光学性质:过一焦点的光线经椭圆反射后必过另一焦点.★椭圆上一个点P 的两条焦半径12,PF PF 的夹角12F PF ∠被椭圆在点P 处的法线平分.(入射光线、反射光线、镜面、法线)已知:如图,椭圆C 的方程为22221x y a b+=,12,F F 分别是其左、右焦点,l 是过椭圆上一点00(,)P x y 的切线,'l 为垂直于l 且过点P 的椭圆的法线,交x 轴于D ,设21,F PD F PD αβ∠=∠=,求证:αβ=. 证明:在2222:1x y C a b+=上,00(,)P x y C ∈, 则过点P 的切线方程为:00221x x y y a b+=,'l 是通过点 P 且与切线l 垂直的法线,则0000222211':()()()y x l x x y b a b a -=-, ∴法线'l 与x 轴交于20((),0)c D x a, ∴22102022||,||c c F D x c F D c x a a =+=-,∴201220||||a cx F D F D a cx +=-,又由焦半径公式得:1020||,||PF a ex PF a ex =+=-,∴1122||||||||F D PF F D PF =,∴PD 是12F PF ∠的平分线, ∴αβ=,∵90ααββ''+=︒=+,故可得αβαβ''=⇔=.例1. 已知椭圆方程为1162522=+y x ,若有光束自焦点(3,0)A 射出,经二次反射回到A 点,设二次反射点为,B C ,如图所示,则ABC 的周长为 .20【解析】:∵椭圆方程为1162522=+y x 中,225169c =-=, ∴(3,0)A 为该椭圆的一个焦点,∴自(3,0)A 射出的光线AB 反射后,反射光线BC 定过另一个焦点(3,0)A ,故ABC 的周长为:''44520AB BA A C CA a +++==⨯=.。
椭圆的性质及知识点总结

椭圆的性质及知识点总结一、椭圆的定义和基本性质1.1 椭圆的定义椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
设d1和d2分别表示P到F1和F2的距离,则椭圆的定义可以用数学表达式表示为|d1 + d2| = 2a 。
1.2 椭圆的基本性质(1)椭圆对称轴:椭圆有两个对称轴,分别称为长轴和短轴。
长轴的端点是两个焦点F1和F2,短轴与长轴垂直并通过椭圆的中心点。
(2)椭圆的焦点和离心率:椭圆的焦点是定义椭圆的两个定点F1和F2,离心率e是一个表示椭圆形状的参数,e的取值范围是0<e<1。
(3)椭圆的三大定律:椭圆有三个基本定律,分别是:(a)椭圆内到两个焦点的距离之和等于长轴的长度;(b)椭圆内到两个焦点的距离之差等于长轴的长度;(c)椭圆的面积等于πab,其中a和b分别是长轴和短轴的长度。
1.3 椭圆的方程椭圆的标准方程是x^2/a^2 + y^2/b^2 = 1,其中a和b分别是长轴和短轴的长度,椭圆的中心点位于原点(0,0)。
二、椭圆的相关知识点2.1 椭圆的离心率椭圆的离心率e的定义是e=c/a,其中c为焦距,a为长半轴的一半。
离心率越接近于0,椭圆形状越圆;离心率越接近于1,椭圆形状越扁。
2.2 椭圆的参数方程椭圆也可以用参数方程表示,参数方程为:x = a * cosθy = b * sinθ其中θ为参数,a和b分别是长轴和短轴的长度。
2.3 椭圆的焦半径椭圆的焦半径是指从椭圆的焦点到该椭圆上的任意一点P的距离,椭圆上各点的焦半径之和等于椭圆的周长。
2.4 椭圆的切线椭圆上的切线有一个特点:与椭圆相切的切线在切点处与切线的法线垂直。
根据这个特点可以求出椭圆上任意一点处的切线方程。
2.5 椭圆的焦点坐标椭圆的焦点坐标可以通过椭圆的离心率和焦距来求解。
焦点坐标为(±ae, 0),a为长轴的一半,e为椭圆的离心率。
2.6 椭圆的面积椭圆的面积可以通过参数法求解,面积为πab,其中a和b分别是长轴和短轴的长度。
椭圆知识点与性质大全

椭圆与方程【知识梳理】 1、椭圆的定义平面内,到两定点1F 、2F 的距离之和为定长()1222,0a F F a a <>的点的轨迹称为椭圆,其中两定点1F 、2F 称为椭圆的焦点,定长2a 称为椭圆的长轴长,线段12F F 的长称为椭圆的焦距。
此定义为椭圆的第一定义。
2、椭圆的简单性质3、焦半径椭圆上任意一点P 到椭圆焦点F 的距离称为焦半径,且[],PF a c a c ∈-+,特别地,若00(,)P x y 为椭圆()222210x y a b a b +=>>上的任意一点,1(,0)F c -,2(,0)F c 为椭圆的左右焦点,则10||PF a ex =+,20||PF a ex =-,其中c e a =.4、通径过椭圆()222210x y a b a b+=>>焦点F 作垂直于长轴的直线,交椭圆于A 、B 两点,称线段AB 为椭圆的通径,且22b AB a =。
P 为椭圆()222210x y a b a b+=>>上的任意一点,1(,0)F c -,2(,0)F c 为椭圆的左右焦点,称12PF F ∆为椭圆的焦点三角形,其周长为:1222F PF C a c ∆=+,若12F PF θ∠=,则焦点三角形的面积为:122tan 2F PF S b θ∆=.6、过焦点三角形直线l 过椭圆()222210x y a b a b +=>>的左焦点1F ,与椭圆交于11(,)A x y 、22(,)B x y 两点,称2ABF ∆为椭圆的过焦点三角形,其周长为:24ABF C a ∆=,面积为212y y c S ABF -=∆.7、点与椭圆的位置关系()00,P x y 为平面内的任意一点,椭圆方程为22221(0)x y a b a b+=>>:若2200221x y a b +=,则P 在椭圆上;若2200221x y a b +>,则P 在椭圆外;若2200221x y a b+<,则P 在椭圆内。
椭圆的几何性质知识点归纳及典型例题及练习(付答案)

(一)椭圆的定义:1、椭圆的定义:平面与两个定点F i 、F 2的距离之和等于定长(大于 IRF 2I )的点的轨迹叫做椭圆。
这两个定点 F i 、F 2叫做椭圆的 焦点,两焦点的距离 厅汀2|叫做椭圆的 焦距。
对椭圆定义的几点说明:(1) “在平面”是前提,否则得不到平面图形(去掉这个条件,我们将得到一个椭球面); (2) “两个定点”的设定不同于圆的定义中的“一个定点” ,学习时注意区分;(3) 作为到这两个定点的距离的和的 “常数”,必须满足大于| F i F 2|这个条件。
若不然, 当这个“常数”等于| F i F 2|时,我们得到的是线段 F 1F 2;当这个“常数”小于| F i F 2|时,无 轨迹。
这两种特殊情况,同学们必须注意。
(4) 下面我们对椭圆进行进一步观察,发现它本身具备对称性,有两条对称轴和一个 对称中心,我们把它的两条对称轴与椭圆的交点记为 A i , A 2, B i , B 2,于是我们易得| A i A 2|的值就是那个“常数”,且|B 2F 2|+|B 2F i |、|B i F 2|+|B i F i |也等于那个“常数”。
同学们想一想 其中的道理。
(5)中心在原点、焦点分别在 x 轴上,y 轴上的椭圆标准方程分别为:2 2 2 2i (a b 0),77i (a b 0),a ba b2 2 2相同点是:形状相同、大小相同;都有 a > b > 0, a c b 。
不同点是:两种椭圆相对于坐标系的位置不同, 它们的焦点坐标也不同(第一个椭圆的 焦点坐标为(一c , 0)和(c , 0),第二个椭圆的焦点坐标为(0,— c )和(0, c )。
椭圆的 焦点在x 轴上 标准方程中x 2项的分母较大;椭圆的焦点在 y 轴上标准方程中y 2项的分母较大。
(二)椭圆的几何性质:椭圆的几何性质可分为两类:一类是与坐标系有关的性质,如顶点、焦点、中心坐标; 一类是与坐标系无关的本身固有性质,如长、短轴长、焦距、离心率.对于第一类性质,只2 2要X 2 每 i (a b 0)的有关性质中横坐标x 和纵坐标y 互换,就可以得出 a b2 2^2 —2 i (a b 0)的有关性质。
椭圆知识点详细总结

椭圆知识点详细总结椭圆是平面上的一个特殊几何图形,其形状和性质具有独特的特点。
在学习椭圆的知识时,我们需要了解它的定义、性质、方程和应用等方面的内容。
一、椭圆的定义和性质:1.定义:在平面上给定一对焦点F1和F2以及一个距离2a(长轴),该点到两个焦点F1和F2的距离之和是常数2a(2a>0)。
以两个焦点F1、F2和连接它们的直线段为轴的点的轨迹,构成了一个椭圆。
2.性质:a)长轴和短轴:椭圆的长轴是两个焦点之间的距离2a,短轴是通过中点M的两条焦半径之间的距离2b。
b)焦点关系:椭圆上的任意一点到两个焦点的距离之和等于常数2a。
c)中点关系:椭圆上任意一点到两个焦点的距离之差等于长轴的长度。
d)准线:椭圆上的点到两条焦半径的距离之和等于准线的长度。
e) 离心率:椭圆的离心率ε的定义为eccentricity=e=c/a,其中c是焦点到中心的距离。
f)焦半径和法线:椭圆上的点到两个焦点的距离之和等于该点到准线的距离,即焦半径等于法线。
二、椭圆的方程和参数方程:1.方程:a)标准方程:椭圆的标准方程为x^2/a^2+y^2/b^2=1,其中a是长轴的长度,b是短轴的长度。
b) 参数方程:椭圆的参数方程为x = a*cosθ, y = b*sinθ,其中θ为参数。
2.其他形式的方程:椭圆还可以通过平移、旋转和缩放等变换得到其他形式的方程。
比如椭圆的中心在坐标原点的方程为x^2/a^2+y^2/b^2=1三、椭圆的性质:1.对称性:椭圆具有相对于两个轴的对称性,即关于x轴和y轴对称。
2.离心角和弧长:任意两个焦点之间的线段所对应的圆心角等于椭圆上的弧的长度。
3.焦点面积和弧长:椭圆上两个焦点和一点的连线所围成的三角形面积等于以该点为焦点的椭圆弧长的一半。
4.弦:椭圆上的弦的长度是准线的长度小于2a。
5.游程:椭圆上两个焦点之间的距离等于椭圆上两个点之间的最短路径长度。
6.光学性质:椭圆是一个反射光线的特殊曲面,具有反射原则和等角反射原理。
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是一种常见的几何图形,具有许多独特的性质和应用。
本文将介绍椭圆的基本概念和性质,包括定义、标准方程、焦点、直径、离心率、轨道和应用等方面。
1.椭圆的定义椭圆可以定义为平面上到两个固定点(焦点)的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
椭圆也可以视为一个平面上到定点的连线长度之和等于一定长度(主轴)的点的轨迹。
2.椭圆的标准方程以坐标原点为中心的椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b 分别表示椭圆的长短半轴。
可以看出,a表示椭圆离心率对应的焦距长度,b表示椭圆的短半轴长度。
3.焦点和直径椭圆的焦点是椭圆的一个重要属性,它是椭圆离心率定义的核心。
可以通过标准方程中的离心率公式e = c/a(c为焦点到原点的距离),求得焦点的坐标表达式为(c, 0)和(-c, 0)。
椭圆的直径是通过椭圆中心并且同时与椭圆上两个点相交的线段。
对于以坐标原点为中心的椭圆,直径的长度为2a。
4.椭圆的离心率椭圆的离心率是描述椭圆形状的重要指标。
离心率的取值范围为0到1,离心率为0时表示圆形,离心率为1时表示扁平的线段。
椭圆的离心率定义为离心焦距和长半径之比,即e = c/a。
5.椭圆的轨迹椭圆的轨迹是指通过一定规则的运动得到的点所形成的图形。
在天体力学中,行星绕太阳运动的轨迹就是椭圆。
椭圆的轨迹具有许多独特的性质,例如对称性、曲率等。
6.椭圆的应用椭圆在现实生活中有许多重要的应用。
例如,在通信中,为了提高信号传输的质量和距离,卫星轨道通常选择为椭圆轨道。
此外,椭圆也被广泛应用于地理测量、天体力学、光学设计等领域。
总结:椭圆作为几何图形中的重要一员,具有许多独特的概念和性质。
通过本文的介绍,我们了解到椭圆的定义、标准方程、焦点、直径、离心率、轨迹和应用。
对于几何学的学习和实际应用,理解和掌握椭圆的基本概念与性质至关重要。
椭圆的经典知识总结

椭圆的经典知识总结椭圆是一个非常重要的几何形状,广泛应用于数学、物理和工程等领域。
下面将对椭圆的经典知识进行总结,涵盖椭圆的定义、性质以及一些常见的应用。
一、定义和性质:1.椭圆定义:椭圆是平面上到两个给定点(焦点)距离之和等于一定常数(长轴)的点的集合。
2.主要要素:(1)焦点:椭圆的两个焦点是确定椭圆形状的关键要素。
(2)长轴和短轴:椭圆的长轴是连接两个焦点的线段,短轴则是垂直于长轴并通过中心点的线段。
长轴的长度称为椭圆的主轴,短轴的长度则称为次轴。
(3)中心:椭圆的中心是指长轴和短轴的交点。
(4)半焦距:则是焦点到中心的距离。
(5)离心率:椭圆的离心率是一个用来衡量椭圆形状的值,定义为离心距(焦点到中心的距离)与主轴长度之比。
3.离心率和几何性质:(1)离心率的取值范围为0到1之间,当离心率为0时,椭圆退化为一个点;当离心率为1时,椭圆退化为一个抛物线。
(2)在椭圆上的任意一点,到焦点的距离之和等于常数,称为焦散性质。
(3)椭圆的两个焦点到任意一点的距离之差等于长轴的长度。
4.椭圆的方程:椭圆的标准方程为(x-h)²/a²+(y-k)²/b²=1,其中(h,k)为椭圆中心点的坐标,a和b分别为长轴和短轴的长度,并且a>b。
二、椭圆的性质和应用:1.对称性:(1)椭圆具有对称性,关于中心对称,即中心点是对称中心。
(2)长轴和短轴也是椭圆的对称轴。
2.焦点与直线的关系:(1)焦点到椭圆上的任意一点的距离之和等于该点到椭圆的任意一条切线的长度。
(2)椭圆上的任意一条切线与焦点之间的两条线段的夹角相等。
3.切线和法线:(1)切线是与椭圆一点相切且垂直于切线的直线。
(2)法线是与切线垂直且通过椭圆上切点的直线。
4.面积公式:椭圆的面积为πab,其中a和b分别为长轴和短轴的长度。
5.椭圆的应用:(1)椭圆在天文学中被用来描述行星、彗星和其他天体的轨道。
(2)椭圆也广泛应用于工程学、建筑学和设计中,例如椭圆形的天花板和门窗等。
高三知识点总结椭圆

高三知识点总结椭圆一、椭圆的定义椭圆是平面上一个动点到两个不同的固定点的距离之和等于常数的轨迹。
这两个固定点分别称为焦点,这个常数称为椭圆的半长轴的长度。
椭圆的定义可以用数学表达式表示为:椭圆的标准方程为:$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1(a>b>0)$其中,a和b分别为椭圆的半长轴和半短轴的长度,且椭圆的长轴在x轴上,短轴在y轴上。
二、椭圆的性质1. 焦点性质:椭圆定义的两个焦点到椭圆曲线上的任意一点的距离之和等于常数2a。
2. 直径性质:椭圆的任意一条直径上任意一点到焦点的距离与到准位线的距离之和等于直径的长。
3. 对称性质:椭圆具有关于x轴、y轴和原点对称的性质。
4. 离心率:椭圆的离心率为$e = \sqrt{1-\frac{b^2}{a^2}}$,它描述了椭圆的扁平程度,离心率越接近于0,椭圆越圆。
三、椭圆的参数方程椭圆的参数方程可以表示为:$x=a \cos t$$y=b \sin t$其中,t为参数,a和b分别为椭圆的半长轴和半短轴的长度。
四、椭圆的焦点与准位线椭圆的焦点和准位线是椭圆的重要性质之一,它们在椭圆的图形、方程和计算中起着重要作用。
1. 焦点的坐标:椭圆的焦点坐标为$(\pm \sqrt{a^2 - b^2},0)$2. 准位线方程:椭圆的准位线方程为$x=\pm a \epsilon$,其中ε为椭圆的离心率。
五、椭圆的相关定理1. 椭圆的直径定理:椭圆的所有直径的长度之和为常数2a。
2. 椭圆的离心率定理:椭圆的离心率e的平方等于1减去b平方除以a平方。
六、椭圆的应用椭圆在生活和工程领域中有着广泛的应用,例如:1. 太阳系中行星的轨迹一般为椭圆,椭圆的性质可以帮助我们更好地理解天体运动规律。
2. 椭圆在工程中的应用:例如建筑、机械、航天等领域都会涉及到椭圆的应用,例如在建筑设计中椭圆形的圆顶结构、在机械制造中椭圆齿轮的设计等等。
高中椭圆的知识点总结

高中椭圆的知识点总结椭圆是数学中的一个重要概念,具有很多应用。
在高中数学中,椭圆也是一个必修的内容,考试中经常会涉及到相关的知识点。
在本文中,我们将对高中椭圆的知识点进行总结和归纳。
一、椭圆的定义椭圆是平面上到两个定点F1和F2距离之和等于定长2a的点P的轨迹。
这两个定点F1和F2被称作椭圆的焦点,定长2a被称为椭圆的长轴,长轴的中点O被称为椭圆的中心,距离中心最远的两点A和B被称为椭圆的顶点,椭圆的离心率为e=(F1F2)/2a。
二、椭圆的方程椭圆的标准方程为 (x^2/a^2)+(y^2/b^2)=1, 其中a>b>0,a为长轴长度,b为短轴长度。
当椭圆的中心不在坐标原点时,可通过平移变换将其移到原点,然后再求解方程。
三、椭圆的性质1. 椭圆的中心位于坐标原点或者与坐标轴的交点上。
2. 椭圆的长轴是平行于x或y轴的直线,短轴是垂直于长轴的直线。
3. 椭圆的离心率e=(F1F2)/2a, e<1。
4. 椭圆的焦点与顶点之间的距离F1A、F2B互相相等,且等于椭圆的长轴长度2a。
5. 椭圆上任意一点到两焦点的距离之和等于定长2a。
6. 椭圆的面积为πab。
7. 椭圆的周长无法用初等函数表示,通常用级数来表示。
四、椭圆的几何意义椭圆的几何意义可以简单地用两条绳子相互交错吊起一个重物来表现。
在两条绳子构成的平面上,可以画出一个椭圆形的轨迹,此时重物到两条绳子的距离之和为定值2a,而椭圆的顶点即为两条绳子的交点。
五、椭圆的应用椭圆具有很多应用,在物理、工程、天文学、生物学等领域中经常会涉及到。
1. 通讯卫星轨道:通讯卫星通常被放置在椭圆轨道上,使得其在地球上的可见度更广,信号传输距离更长。
2. 医学图像:医学图像中的组织轮廓通常是椭圆形的,因此椭圆形适用于医学图像处理。
3. 自动打标机:自动打标机通常采用椭圆形的摆线轮廓来控制字母和数字的运动轨迹。
4. 椭圆滤波器:椭圆滤波器是一种常用的数字信号处理技术,用于高通、低通、带通、带阻等滤波。
高中数学椭圆的定义与性质
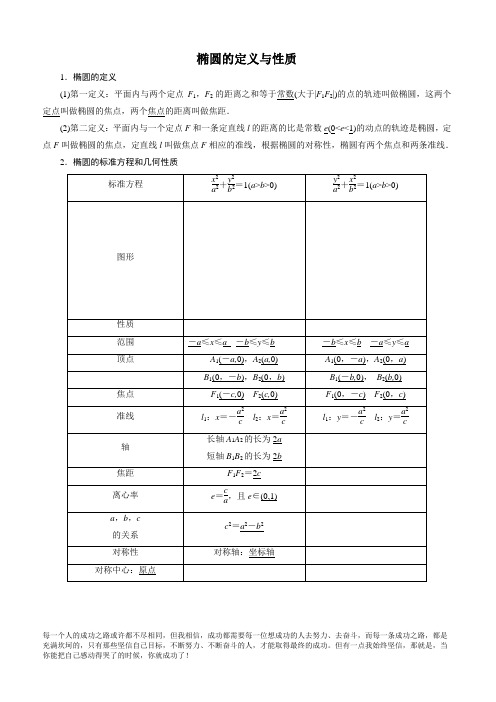
椭圆的定义与性质1.椭圆的定义(1)第一定义:平面内与两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两个焦点的距离叫做焦距.(2)第二定义:平面内与一个定点F和一条定直线l的距离的比是常数e(0<e<1)的动点的轨迹是椭圆,定点F叫做椭圆的焦点,定直线l叫做焦点F相应的准线,根据椭圆的对称性,椭圆有两个焦点和两条准线.2.椭圆的标准方程和几何性质1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)动点P 到两定点A (-2,0),B (2,0)的距离之和为4,则点P 的轨迹是椭圆.( )(2)椭圆上一点P 与两焦点F 1,F 2构成△PF 1F 2的周长为2a +2c (其中a 为椭圆的长半轴长,c 为椭圆的半焦距).( )(3)椭圆的离心率e 越大,椭圆就越圆.( )(4)已知点F 为平面内的一个定点,直线l 为平面内的一条定直线.设d 为平面内一动点P 到定直线l 的距离,若d =54|PF |,则点P 的轨迹为椭圆.( )[解析] (1)错误,|P A |+|PB |=|AB |=4,点P 的轨迹为线段AB ;(2)正确,根据椭圆的第一定义知PF 1+PF 2=2a ,F 1F 2=2c ,故△PF 1F 2的周长为2a +2c ;(3)错误,椭圆的离心率越大,椭圆越扁.(4)正确,根据椭圆的第二定义.[答案] (1)× (2)√ (3)× (4)√2.(教材习题改编)焦点在x 轴上的椭圆x 25+y 2m =1的离心率为105,则m =________.[解析] 由题设知a 2=5,b 2=m ,c 2=5-m ,e 2=c 2a 2=5-m 5=(105)2=25,∴5-m =2,∴m =3.[答案] 3 3.椭圆的焦点坐标为(0,-6),(0,6),椭圆上一点P 到两焦点的距离之和为20,则椭圆的标准方程为_____.[解析] 椭圆的焦点在y 轴上,且c =6,2a =20,∴a =10,b 2=a 2-c 2=64,故椭圆方程为x 264+y 2100=1. [答案] x 264+y 2100=14.(2014·无锡质检)椭圆x 24+y 23=1的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,当△F AB 的周长最大时,△F AB 的面积是________.[解析] 直线x =m 过右焦点(1,0)时,△F AB 的周长最大,由椭圆定义知,其周长为4a =8,此时,|AB |=2×b 2a =2×32=3,∴S △F AB =12×2×3=3.[答案] 35.(2014·江西高考)过点M (1,1)作斜率为-12的直线与椭圆C :x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率等于________.[解析] 设A (x 1,y 1),B (x 2,y 2),则⎩⎨⎧x 21a 2+y 21b 2=1,x 22a 2+y22b 2=1,∴(x 1-x 2)(x 1+x 2)a 2+(y 1-y 2)(y 1+y 2)b 2=0,∴y 1-y 2x 1-x 2=-b 2a 2·x 1+x 2y 1+y 2.∵y 1-y 2x 1-x 2=-12,x 1+x 2=2,y 1+y 2=2,∴-b 2a 2=-12,∴a 2=2b 2.又∵b 2=a 2-c 2,∴a 2=2(a 2-c 2),∴a 2=2c 2,∴c a =22.[答案] 22考向1 椭圆的定义与标准方程【典例1】 (1)(2014·全国大纲卷改编)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点为F 1、F 2,离心率为33,过F 2的直线l 交C 于A 、B 两点.若△AF 1B 的周长为43,则C 的方程为________. (2)(2014·苏州质检)椭圆的中心在原点,焦距为4,一条准线为x =-4,则该椭圆的方程为________. [解析] (1)由条件知△AF 1B 的周长=4a =43,∴a = 3.∵e =c a =33,c 2+b 2=a 2,∴c =1,b = 2.∴椭圆C 的方程为x 23+y 22=1.(2)∵椭圆的一条准线为x =-4,∴焦点在x 轴上且a 2c=4,又2c =4,∴c =2,∴a 2=8,b 2=4,∴该椭圆方程为x 28+y 24=1.[答案] (1)x 23+y 22=1 (2)x 28+y 24=1,【规律方法】(1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决. (2)求椭圆的标准方程有两种方法①定义法:根据椭圆的定义,确定a 2,b 2的值,结合焦点位置可写出椭圆方程.②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a ,b ;若焦点位置不明确,则需要分焦点在x 轴上和y 轴上两种情况讨论,也可设椭圆的方程为Ax 2+By 2=1(A >0,B >0,A ≠B ).【变式训练1】 (1)(2013·广东高考改编)已知中心在原点的椭圆C 的右焦点为F (1,0),离心率等于12,则C 的方程是________.(2)(2014·苏州质检)已知椭圆的方程是x 2a 2+y 225=1(a >5),它的两个焦点分别为F 1,F 2,且|F 1F 2|=8,弦AB (椭圆上任意两点的线段)过点F 1,则△ABF 2的周长为________.[解析] (1)右焦点F (1,0),则椭圆的焦点在x 轴上;c =1.又离心率为c a =12,故a =2,b 2=a 2-c 2=4-1=3,故椭圆的方程为x 24+y 23=1.(2)∵a >5,∴椭圆的焦点在x 轴上,∵|F 1F 2|=8,∴c =4,∴a 2=25+c 2=41,则a =41. 由椭圆定义,|AF 1|+|AF 2|=|BF 2|+|BF 1|=2a ,∴△ABF 2的周长为4a =441.[答案] (1)x 24+y 23=1 (2)441考向2 椭圆的几何性质【典例2】 (1)(2013·江苏高考)在平面直角坐标系xOy 中,椭圆C 的标准方程为x 2a 2+y 2b 2=1(a >b >0),右焦点为F ,右准线为l ,短轴的一个端点为B .设原点到直线BF 的距离为d 1,F 到l 的距离为d 2,若d 2=6d 1,则椭圆C 的离心率为________.(2)(2014·扬州质检)已知F 1、F 2是椭圆C 的左、右焦点,点P 在椭圆上,且满足|PF 1|=2|PF 2|,∠PF 1F 2=30°,则椭圆的离心率为________.[解析] (1)依题意,d 2=a 2c -c =b 2c .又BF =c 2+b 2=a ,所以d 1=bc a .由已知可得b 2c =6·bc a ,所以6c 2=ab ,即6c 4=a 2(a 2-c 2),整理可得a 2=3c 2,所以离心率e =c a =33.(2)在三角形PF 1F 2中,由正弦定理得sin ∠PF 2F 1=1,即∠PF 2F 1=π2,设|PF 2|=1,则|PF 1|=2,|F 2F 1|=3,∴离心率e =2c 2a =33. [答案] (1)33 (2)33,【规律方法】1.椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF 1|+|PF 2|=2a ,得到a ,c 的关系.2.椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法: (1)求出a ,c ,代入公式e =c a;(2)只需要根据一个条件得到关于a ,b ,c 的齐次式,结合b 2=a 2-c 2转化为a ,c 的齐次式,然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式),解方程(不等式)即可得e (e 的取值范围).【变式训练2】 (1)(2013·课标全国卷Ⅱ改编)设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 是C 上的点,PF 2⊥F 1F 2,∠PF 1F 2=30°,则C 的离心率为________.(2)(2014·徐州一中抽测)已知F 1、F 2是椭圆的两个焦点,P 为椭圆上一点,∠F 1PF 2=60°.则椭圆离心率的范围为________.[解析](1)如图,在Rt △PF 1F 2中,∠PF 1F 2=30°,∴|PF 1|=2|PF 2|,且|PF 2|=33|F 1F 2|, 又|PF 1|+|PF 2|=2a ,∴|PF 2|=23a ,于是|F 1F 2|=233a ,因此离心率e =c a =3a 3a =33.(2)法一:设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),|PF 1|=m ,|PF 2|=n ,则m +n =2a .在△PF 1F 2中,由余弦定理可知,4c 2=m 2+n 2-2mn cos 60°=(m +n )2-3mn =4a 2-3mn ≥4a 2-3·⎝⎛⎭⎫m +n 22=4a 2-3a 2=a 2(当且仅当m =n 时取等号).∴c 2a 2≥14,即e ≥12.又0<e <1,∴e 的取值范围是⎣⎡⎭⎫12,1.法二:如图所示,设O 是椭圆的中心,A 是椭圆短轴上的一个顶点,由于∠F 1PF 2=60°,则只需满足60°≤∠F 1AF 2即可,又△F 1AF 2是等腰三角形,且|AF 1|=|AF 2|,所以0°<∠F 1F 2A ≤60°,所以12≤cos ∠F 1F 2A <1,又e =cos ∠F 1F 2A ,所以e 的取值范围是⎣⎢⎡⎭⎪⎫12,1. [答案] (1)33 (2)⎣⎢⎡⎭⎪⎫12,1 课堂达标练习 一、填空题1.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22.过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为16,那么椭圆C 的方程为________.[解析] 设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),由e =22知c a =22,故b 2a 2=12.由于△ABF 2的周长为|AB |+|BF 2|+|AF 2|=(|AF 1|+|AF 2|)+(|BF 1|+|BF 2|)=4a =16,故a =4.∴b 2=8.∴椭圆C 的方程为x 216+y 28=1.[答案] x 216+y 28=12.(2013·四川高考改编)从椭圆x 2a 2+y 2b 2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是________.[解析] 设P (-c ,y 0)代入椭圆方程求得y 0,从而求得k OP ,由k OP =k AB 及e =ca可得离心率e .由题意设P (-c ,y 0),将P (-c ,y 0)代入x 2a 2+y 2b 2=1,得c 2a 2+y 20b 2=1,则y 20=b 2⎝⎛⎭⎫1-c 2a 2=b 2·a 2-c 2a 2=b 4a2.∴y 0=b 2a 或y 0=-b 2a (舍去),∴P ⎝⎛⎭⎫-c ,b 2a ,∴k OP =-b 2ac.∵A (a,0),B (0,b ),∴k AB =b -00-a =-b a . 又∵AB ∥OP ,∴k AB =k OP ,∴-b a =-b 2ac ,∴b =c .∴e =c a =c b 2+c2=c 2c 2=22. [答案] 223.(2014·辽宁高考)已知椭圆C :x 29+y 24=1,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则|AN |+|BN |=________.[解析] 椭圆x 29+y 24=1中,a =3. 如图,设MN 的中点为D ,则|DF 1|+|DF 2|=2a =6.∵D ,F 1,F 2分别为MN ,AM ,BM 的中点,∴|BN |=2|DF 2|,|AN |=2|DF 1|, ∴|AN |+|BN |=2(|DF 1|+|DF 2|)=12. [答案] 124.(2014·南京调研)如图,已知过椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点A (-a,0)作直线l 交y 轴于点P ,交椭圆于点Q ,若△AOP 是等腰三角形,且PQ →=2QA →,则椭圆的离心率为________.[解析] ∵△AOP 为等腰三角形,∴OA =OP ,故A (-a,0),P (0,a ),又PQ →=2QA →, ∴Q ⎝⎛⎭⎫-2a 3,a 3,由Q 在椭圆上得49+a 29b 2=1,解得b 2a 2=15. ∴e =1-b 2a 2=1-15=255. [答案] 2555.(2014·南京质检)已知焦点在x 轴上的椭圆的离心率为12,且它的长轴长等于圆C :x 2+y 2-2x -15=0的半径,则椭圆的标准方程是________.[解析] 由x 2+y 2-2x -15=0,知r =4=2a ⇒a =2. 又e =c a =12,c =1,则b 2=a 2-c 2=3.因此椭圆的标准方程为x 24+y 23=1. [答案] x 24+y 23=16.(2013·辽宁高考改编)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,椭圆C 与过原点的直线相交于A ,B 两点,连接AF ,BF .若|AB |=10,|BF |=8,cos ∠ABF =45,则椭圆C 的离心率为__________.[解析] 在△ABF 中,由余弦定理得 ,|AF |2=|AB |2+|BF |2-2|AB |·|BF |cos ∠ABF ,∴|AF |2=100+64-128=36,∴|AF |=6,从而|AB |2=|AF |2+|BF |2,则AF ⊥BF . ∴c =|OF |=12|AB |=5,利用椭圆的对称性,设F ′为右焦点,则|BF ′|=|AF |=6, ∴2a =|BF |+|BF ′|=14,a =7. 因此椭圆的离心率e =c a =57. [答案] 577.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________.[解析] 由定义,|PF 1|+|PF 2|=2a ,且PF 1→⊥PF 2→, ∴|PF 1|2+|PF 2|2=|F 1F 2|2=4c 2, ∴(|PF 1|+|PF 2|)2-2|PF 1||PF 2|=4c 2,∴2|PF 1||PF 2|=4a 2-4c 2=4b 2,∴|PF 1||PF 2|=2b 2. ∴S △PF 1F 2=12|PF 1||PF 2|=12×2b 2=9,因此b =3. [答案] 38.(2013·大纲全国卷改编)已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x 轴的直线交C 于A ,B 两点,且|AB |=3,则C 的方程为________.[解析] 依题意,设椭圆C :x 2a 2+y 2b2=1(a >b >0).过点F 2(1,0)且垂直于x 轴的直线被曲线C 截得弦长|AB |=3, ∴点A ⎝⎛⎭⎫1,32必在椭圆上, ∴1a 2+94b2=1.① 又由c =1,得1+b 2=a 2.② 由①②联立,得b 2=3,a 2=4. 故所求椭圆C 的方程为x 24+y 23=1. [答案] x 24+y 23=1二、解答题9.(2014·镇江质检)已知椭圆C 1:x 24+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率.(1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B 分别在椭圆C 1和C 2上,OB →=2OA →,求直线AB 的方程. [解] (1)设椭圆C 2的方程为y 2a 2+x 24=1(a >2), 其离心率为32, 故a 2-4a =32,解得a =4.故椭圆C 2的方程为y 216+x 24=1.(2)法一:A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ),由OB →=2OA →及(1)知,O 、A 、B 三点共线且点A 、B 不在y 轴上,因此可设直线AB 的方程为y =kx . 将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4, 所以x 2A =41+4k 2. 将y =kx 代入y 216+x 24=1中,得(4+k 2)x 2=16,所以x 2B =164+k 2. 又由OB →=2OA →,得x 2B =4x 2A , 即164+k 2=161+4k 2, 解得k =±1.故直线AB 的方程为y =x 或y =-x . 法二:A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ),由OB →=2OA →及(1)知,O 、A 、B 三点共线且点A 、B 不在y 轴上,因此可设直线AB 的方程为y =kx . 将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4,所以x 2A =41+4k 2. 由OB →=2OA →,得x 2B =161+4k 2,y 2B =16k 21+4k 2.将x 2B ,y 2B 代入y 216+x 24=1中,得4+k 21+4k 2=1,即4+k 2=1+4k 2,解得k =±1. 故直线AB 的方程为y =x 或y =-x .10.(2014·安徽高考)设F 1,F 2分别是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过点F 1的直线交椭圆E于A ,B 两点,|AF 1|=3|F 1B |.(1)若|AB |=4,△ABF 2的周长为16,求|AF 2|; (2)若cos ∠AF 2B =35,求椭圆E 的离心率.[解] (1)由|AF 1|=3|F 1B |,|AB |=4,得|AF 1|=3,|F 1B |=1.因为△ABF 2的周长为16,所以由椭圆定义可得4a =16,|AF 1|+|AF 2|=2a =8. 故|AF 2|=2a -|AF 1|=8-3=5.(2)设|F 1B |=k ,则k >0且|AF 1|=3k ,|AB |=4k . 由椭圆定义可得|AF 2|=2a -3k ,|BF 2|=2a -k .在△ABF2中,由余弦定理可得|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2|cos∠AF2B,即(4k)2=(2a-3k)2+(2a-k)2-65(2a-3k)·(2a-k),化简可得(a+k)(a-3k)=0.而a+k>0,故a=3k.于是有|AF2|=3k=|AF1|,|BF2|=5k.因此|BF2|2=|F2A|2+|AB|2,可得F1A⊥F2A,故△AF1F2为等腰直角三角形.从而c=22a,所以椭圆E的离心率e=ca=22.椭圆的定义与性质1.椭圆的定义(1)第一定义:平面内与两个定点F1,F2的距离之和等于(大于|F1F2|)的点的轨迹叫做椭圆,这两个叫做椭圆的焦点,两个的距离叫做焦距.(2)第二定义:平面内与一个定点F和一条定直线l的距离的比是常数( <e< )的动点的轨迹是椭圆,定点F叫做椭圆的焦点,定直线l叫做焦点F相应的准线,根据椭圆的对称性,椭圆有两个焦点和两条准线.2.椭圆的标准方程和几何性质1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)动点P 到两定点A (-2,0),B (2,0)的距离之和为4,则点P 的轨迹是椭圆.( )(2)椭圆上一点P 与两焦点F 1,F 2构成△PF 1F 2的周长为2a +2c (其中a 为椭圆的长半轴长,c 为椭圆的半焦距).( )(3)椭圆的离心率e 越大,椭圆就越圆.( )(4)已知点F 为平面内的一个定点,直线l 为平面内的一条定直线.设d 为平面内一动点P 到定直线l 的距离,若d =54|PF |,则点P 的轨迹为椭圆.( )2.(教材习题改编)焦点在x 轴上的椭圆x 25+y 2m =1的离心率为105,则m =________.3.椭圆的焦点坐标为(0,-6),(0,6),椭圆上一点P 到两焦点的距离之和为20,则椭圆的标准方程为_____. 4.(2014·无锡质检)椭圆x 24+y 23=1的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,当△F AB 的周长最大时,△F AB 的面积是________.5.(2014·江西高考)过点M (1,1)作斜率为-12的直线与椭圆C :x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率等于________.考向1 椭圆的定义与标准方程【典例1】 (1)(2014·全国大纲卷改编)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点为F 1、F 2,离心率为33,过F 2的直线l 交C 于A 、B 两点.若△AF 1B 的周长为43,则C 的方程为________. (2)(2014·苏州质检)椭圆的中心在原点,焦距为4,一条准线为x =-4,则该椭圆的方程为________.【规律方法】(1)一般地,解决与到焦点的距离有关问题时,首先应考虑用定义来解决. (2)求椭圆的标准方程有两种方法①定义法:根据椭圆的定义,确定a 2,b 2的值,结合焦点位置可写出椭圆方程.②待定系数法:若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a ,b ;若焦点位置不明确,则需要分焦点在x 轴上和y 轴上两种情况讨论,也可设椭圆的方程为Ax 2+By 2=1(A >0,B >0,A ≠B ).【变式训练1】 (1)(2013·广东高考改编)已知中心在原点的椭圆C 的右焦点为F (1,0),离心率等于12,则C 的方程是________.(2)(2014·苏州质检)已知椭圆的方程是x 2a 2+y 225=1(a >5),它的两个焦点分别为F 1,F 2,且|F 1F 2|=8,弦AB (椭圆上任意两点的线段)过点F 1,则△ABF 2的周长为________.考向2 椭圆的几何性质【典例2】(1)(2013·江苏高考)在平面直角坐标系xOy中,椭圆C的标准方程为x2a2+y2b2=1(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B.设原点到直线BF的距离为d1,F到l的距离为d2,若d2=6 d1,则椭圆C的离心率为________.(2)(2014·扬州质检)已知F1、F2是椭圆C的左、右焦点,点P在椭圆上,且满足|PF1|=2|PF2|,∠PF1F2=30°,则椭圆的离心率为________.【规律方法】1.椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF1|+|PF2|=2a,得到a,c的关系.2.椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法:(1)求出a,c,代入公式e=c a;(2)只需要根据一个条件得到关于a,b,c的齐次式,结合b2=a2-c2转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得e(e的取值范围).【变式训练2】(1)(2013·课标全国卷Ⅱ改编)设椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为________.(2)(2014·徐州一中抽测)已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.则椭圆离心率的范围为________.课堂达标练习一、填空题1.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为22.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么椭圆C的方程为________.2.(2013·四川高考改编)从椭圆x 2a 2+y 2b 2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是________.3.(2014·辽宁高考)已知椭圆C :x 29+y 24=1,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则|AN |+|BN |=________.4.(2014·南京调研)如图,已知过椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点A (-a,0)作直线l 交y 轴于点P ,交椭圆于点Q ,若△AOP 是等腰三角形,且PQ →=2QA →,则椭圆的离心率为________.5.(2014·南京质检)已知焦点在x 轴上的椭圆的离心率为12,且它的长轴长等于圆C :x 2+y 2-2x -15=0的半径,则椭圆的标准方程是________.6.(2013·辽宁高考改编)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,椭圆C 与过原点的直线相交于A ,B 两点,连接AF ,BF .若|AB |=10,|BF |=8,cos ∠ABF =45,则椭圆C 的离心率为__________.7.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________.8.(2013·大纲全国卷改编)已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x 轴的直线交C 于A ,B 两点,且|AB |=3,则C 的方程为________.二、解答题9.(2014·镇江质检)已知椭圆C 1:x 24+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率.(1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B 分别在椭圆C 1和C 2上,OB →=2OA →,求直线AB 的方程.10.(2014·安徽高考)设F 1,F 2分别是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过点F 1的直线交椭圆E于A ,B 两点,|AF 1|=3|F 1B |.(1)若|AB |=4,△ABF 2的周长为16,求|AF 2|; (2)若cos ∠AF 2B =35,求椭圆E 的离心率.仰望天空时,什么都比你高,你会自卑; 俯视大地时,什么都比你低,你会自负; 只有放宽视野,把天空和大地尽收眼底, 才能在苍穹泛土之间找准你真正的位置。
椭圆归纳总结

椭圆归纳总结在数学中,椭圆是一种常见的几何形状,具有许多独特的性质和特点。
通过归纳总结,我们可以更深入地理解椭圆,并在各个方面应用它们。
本文将对椭圆的定义、性质、公式以及实际应用进行详细讨论。
一、椭圆的定义与性质椭圆可由一个平面上到两个定点的距离之和等于常数的点的轨迹定义。
定点称为焦点,常数称为离心率。
椭圆有以下基本性质:1. 椭圆是平面上的一个封闭曲线,且具有对称性;2. 椭圆的长轴和短轴是互相垂直的,并通过椭圆的中心点;3. 椭圆的离心率小于1,且离心率越接近于0,椭圆越趋近于圆形;4. 椭圆的离心率决定了其扁平程度。
二、椭圆的参数方程与标准方程椭圆的参数方程由以下两个方程给出:x = a*cosθ,y = b*sinθ,其中a和b分别代表长轴与短轴的一半,θ为参数。
标准方程是描述椭圆的另一种形式,可由以下方程表示:((x-h)²/a²) + ((y-k)²/b²) = 1,其中(h,k)为椭圆的中心点坐标。
通过参数方程和标准方程,我们可以方便地描述和画出椭圆。
三、椭圆的周长与面积椭圆的周长和面积是我们在实际问题中常常需要计算的指标。
1. 椭圆的周长公式为:C = 4*a*E(e),其中E(e)为椭圆的第一类椭圆积分,e为离心率。
2. 椭圆的面积公式为:S = π*a*b,其中a和b分别代表长轴和短轴的一半。
四、椭圆的应用椭圆具有广泛的应用领域,下面我们将以几个具体的实例来说明椭圆在实际中的应用。
1. 天体运动:开普勒定律描述了行星围绕太阳运动的规律,其中椭圆轨道是行星运动的基础。
2. 抛物物体轨迹:若有一个物体在一个平面上沿抛物线轨迹运动,那么当物体的初始速度和投掷角度给定时,该轨迹是一个椭圆。
3. 天文测量:椭圆是描述天体轨道的最常见形状之一,对于行星、卫星、彗星等天体的轨道参数测量和计算,椭圆方程是非常重要的工具。
4. 圆椎曲线应用:椭圆是一种圆锥曲线,因此在光学领域应用广泛,如椭圆镜、椭圆透镜等。
(完整版)椭圆的性质及判定归纳

(完整版)椭圆的性质及判定归纳1. 背景介绍椭圆是几何学中的一种重要的二次曲线,具有独特的性质和形式。
在实际应用中,我们经常需要理解和判定一个曲线是否为椭圆,因此有必要深入了解椭圆的性质及其判定方法。
2. 椭圆的定义在平面解析几何中,椭圆是指到两个给定点的距离之和等于定值的所有点的集合。
这两个点称为椭圆的焦点,定值称为椭圆的长轴。
3. 椭圆的性质椭圆具有以下几个基本的性质:3.1 长轴和短轴椭圆的长轴是通过焦点且垂直于短轴的线段,是椭圆的最长直径。
而短轴是通过焦点且垂直于长轴的线段,是椭圆的最短直径。
3.2 焦点和准线椭圆的焦点是确定椭圆的两个点,修改这两个点的位置可以改变椭圆的形状和大小。
准线是垂直于长轴且通过焦点的直线。
3.3 离心率椭圆的离心率定义为焦点到准线的距离与长轴的比值。
离心率的值在0到1之间,离心率越接近于0,椭圆越接近于圆形。
3.4 对称性椭圆具有两种对称性:关于长轴的对称性和关于短轴的对称性。
通过这两种对称性,我们可以更好地理解和分析椭圆的性质。
4. 椭圆的判定方法在解决实际问题中,我们常常需要判断一个曲线是否为椭圆。
以下是几种常用的判定方法:4.1 椭圆方程椭圆方程是判定一个曲线是否为椭圆的主要方法之一。
一般而言,椭圆的方程形式为(x-h)²/a² + (y-k)²/b² = 1,其中h、k为椭圆的中心坐标,a、b分别为长轴和短轴的长度。
通过将曲线的方程与椭圆方程进行对比,我们可以确定该曲线是否为椭圆。
4.2 轴积性质椭圆具有轴积性质,即椭圆的长轴与短轴的乘积等于焦点到准线的距离与长轴的乘积。
通过计算曲线的焦点到准线的距离与长轴的乘积,我们可以判断该曲线是否满足轴积性质,从而确定是否为椭圆。
4.3 椭圆的图形特征椭圆的图形特征也可以用来判定是否为椭圆。
椭圆具有规则的椭圆形状,不会存在异常的伸缩或扭曲情况。
通过观察图形特征,我们可以直观地判断一个曲线是否为椭圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆定义及性质的应用一、椭圆的定义椭圆第一定义第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.★过点1F 作12PF F ∆的P ∠的外角平分线的垂线,垂足为Q ,则Q 的轨迹方程为222x y a +=.推导过程:延长1F Q 交2F P 于M ,连接OQ ,由已知有PQ 为1MF 的中垂线,则1PF PM =,Q 为1F M 中点,212OQ F M ==()1212PF PF +=a ,所以Q 的轨迹方程为 222x y a +=.(椭圆的方程与离心率学案第5题)椭圆第二定义第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆.2PF e d =(d 为点P 到右准线的距离),右准线对应右焦点,其中2PF 称作焦半径,左、右准线公式2a x c=±..椭圆的焦半径公式为:1020,PF a ex PF a ex =+=-.推导过程:2200aPF ed e x a exc⎛⎫==-=-⎪⎝⎭;同理得10PF a ex=+.简记为:左加右减a在前.由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数. (离心率、焦点弦问题)例1:(2010全国卷Ⅱ理数12题)已知椭圆2222:1(0)x yC a ba b+=>>的离心率为3,过右焦点F且斜率为(0)k k>的直线与C相交于,A B两点.若3AF FB=u u u r u u u r,则k=()A.1 D.2B【解析】解法一:1122(,),(,)A x yB x y,∵3AF FB=u u u r u u u r,∴123y y=-,∵2e=,设2,a t c==,b t=,∴222440x y b+-=,直线AB方程为x my=.代入消去x,∴222(4)0m y b++-=,∴2121222,44by y y ym m+=-=-++,则2222222,344by ym m-=--=-++,解得212m=,则k= 0k>.解法二:设直线l为椭圆的右准线,e为离心率,过,A B别作11,AA BB垂直于l,11,A B为垂足,过B作BH垂直于1AA与H,设BF m=,由第二定义得,11,AF BFAA BBe e==,由3AF FB=u u u r u u u r,得13mAAe=,2mAHe=,4AB m=,则21cos42mAH eBAHAB m e∠====,则sin BAH∠=tan BAH∠=,则k=0k>.故选B.(离心率、焦点弦问题)例2:倾斜角为6π的直线过椭圆)0(12222>>=+babyax的左焦点F,交椭圆于,A B 两点,且有3AF BF=,求椭圆的离心率.33【解析】解法一:,AF BF 为左焦点上的焦半径,所以过,A B 两点分别作垂直于准线的直线且和准线交于11,A B 两点,从B 点作1BH AA ⊥.因为3AF BF =,设BF m =,则3AF m =,4AB m =,又因为11AF BF e AA BB ==,则1BF m BB e e ==,13m AA e =,所以2m AH e=,在ABH ∆中,6BAH π∠=,所以32AH AB =,解得33e =. 解法二:如图,设,3BF m AF m ==,则122,23BF a m AF a m =-=-,在12AF F ∆中,由余弦定理得222394(23)cos 62232m c a m m cπ+--==⨯⨯,化简得23326cm b am =-+①,222534(2)cos 6222m c a m m cπ+--=-=⨯⨯,化简得2322cm b am -=-+②,①+②×3化简得,223b m a =,代入①解得3e =. 椭圆第三定义第三定义:在椭圆)0(12222>>=+b a by a x 中,,A B 两点关于原点对称,P 是椭圆上异于,A B 两点的任意一点,若PB PA k k ,存在,则1222-=-=⋅e a b k k PBPA .(反之亦成立).(★焦点在Y 轴上时,椭圆满足22ba k k PB PA -=⋅) 推导过程:设(,)P x y ,11(,)A x y ,则11(,)B x y --.所以12222=+b y a x ①,1221221=+by a x ②;由①-②得22122212b y y a x x --=-,所以22212212a b x x y y -=--,所以222111222111PA PB y y y y y y b k k x x x x x x a -+-⋅=⋅==--+-为定值. 例1:已知椭圆)0(12222>>=+b a by a x 的长轴长为4,若点P 是椭圆上任意一点,过原点的直线l 与椭圆相交与N M ,两点,记直线PN PM ,的斜率分别为21,k k .若4121-=⋅k k ,则椭圆的方程为 . 1422=+y x .【解析】解法一:(,)P x y ,11(,)M x y ,则11(,)N x y --,因为12222=+b y a x ,则)1(2222ax b y -=,)1(221221a x b y -=,则222212222211112222221111(1)(1)14x x b b y y y y y y b a a k k x x x x x x x x a ----+-⋅=⋅===-=--+--.且42=a ,则椭圆方程为1422=+y x .解法二:由第三定义知4122-=-a b ,且42=a ,则则椭圆方程为1422=+y x .例2:已知椭圆)0(13422>>=+b a y x 的左右顶点分别为21,A A ,点P 在椭圆上,且直线2PA 的斜率的取值范围是]1,2[--,那么直线1PA 的斜率的取值范围是 .]43,83[.【解析】设1PA ,2PA 的斜率分别为21,k k ,则432221-=-=⋅a b k k ,又]1,2[2--∈k ,所以]43,83[1∈k . 二、椭圆的性质焦点三角形椭圆焦点三角形的边角关系:122F F c =, 122PF PF a +=,周长为22a c +.设12F PF θ∠=. (1)当点P 处于短轴的顶点处时,顶角θ最大;(2)221221cos b PF PF a θ⋅=≤+,当且仅当12PF PF =时取等号;(3)122tan2PF F S b θ∆=;(4)12112122PF F B F F S S c b bc ∆∆≤=⨯⨯=,当且仅当12PF PF =时取等号. 推导过程:(1)()()()2222222212002222222120004444cos 12222PF PF c a ex a ex c a c PF PF a e x a e x θ+-++---===-⋅-+, 当00x =时,cos θ有最小值2222a c a-,即12F PF θ∠=最大; (2)22212124cos 2PF PF c PF PF θ+-=⋅,()221212122cos 24PF PF PF PF PF PF c θ⋅=+-⋅-则有,21221cos b PF PF θ⋅=+,2221220max 2221cos 1cos 12cos 12b b b PF PF θθθ⋅=≤=+++-,(当点P 为短轴顶点时θ取得最大值0θ,此时0cos 2b a θ=),代入化简得221221cos b PF PF a θ⋅=≤+. (3)由(2)得12222212sin 2sin cos tan21cos 2222cos 2PF F b b S b θθθθθθ∆=⨯⋅=⋅=+. (离心率问题)例1.已知12,F F 分别是椭圆)0(1:2222>>=+b a by a x C 的左右焦点,椭圆C 上存在一点P ,使得1290F PF ∠=︒,则椭圆C 的离心率的取值范围是__________.【解析】解法一:在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,由题意得145F BO ∠≥︒, 所以1FO OB ≥,即c b ≥,解得e ∈. 解法二:设(,)P x y ,由题意得椭圆C 上存在一点P ,使得12F P F P ⊥u u u r u u u u r,即(,)(,)0x c y x c y +-=,化简,得222x y c +=,与12222=+b y a x 联立,消去y 得2222222a c ab x a b -=-,由椭圆范围知220x a ≤<,即22222220a c a b a a b -≤<-,化简得222b c a ≤<,解得[2e ∈. 变式1:已知12,F F 分别是椭圆)0(1:2222>>=+b a by a x C 的左右焦点,椭圆C 上存在一点P ,使得12F PF ∠为钝角,则椭圆C 的离心率的取值范围是__________.【解析】在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,12F PF ∠为钝角,所以145F BO ∠>︒,所以1FO OB >,即c b >,解得,1)2e ∈. 变式2:已知12,F F 分别是椭圆)0(1:2222>>=+b a b y a x C 的左右焦点,椭圆C 上存在一点P ,使得1260F PF ∠=︒(变式3:12120F PF ∠=︒),则椭圆C 的离心率的取值范围是__________.1[,1)2【解析】在椭圆中,焦点三角形顶角最大时点B 位于短轴的交点处,由题意得130F BO ∠≥︒,所以11sin sin 302c F BO a ∠=≥︒=,则1[,1)2e ∈.变式3:e ∈.(离心率问题)例2.已知12,F F 是椭圆)0(1:2222>>=+b a b y a x C 的左右焦点,若在直线2a x c=上存在点P ,使得线段1PF 的中垂线过点2F ,则椭圆的离心率的取值范围是________.e ∈【解析】22PF c =,22PF F H ≥,即22a c c c ≥-解得:e ∈. (焦点三角形面积问题)例3.已知椭圆21221925F F y x 、,=+为焦点,点P 为椭圆上一点,123F PF π∠=,求21PF F S ∆.33【解析】解法一:设12,,PF m PF n ==则有10m n +=,在21F PF ∆中由余弦定理得mn n m c -+==222644,则mn mn n m 31003)(642-=-+=,则12=mn ,则333sin 2121==∆πmn S PF F .解法二:122tan9tan26PF F S b θπ∆==⨯=(焦点三角形面积问题)例4.过椭圆)0(1:2222>>=+b a b y a x C 中心的直线与椭圆交于,A B 两点,右焦点为2(c,0)F ,则 2ABF ∆的最大面积为_________.bc 【解析】由题意得,A B 关于原点对称,则有212ABF AF F S S ∆∆=,故当A 位于短轴的顶点处时,面积最大,为bc . (焦点三角形边角问题)例5.已知椭圆22194x y +=的两个焦点分别为12,F F ,点P 在椭圆上,(1)在椭圆上满足12PF PF ⊥的点P 的个数是?(2)12PF PF ⋅的最大值是?(3)12F PF ∠为钝角时,点P 的横坐标的取值范围是?【解析】(1)画图知,所求点的个数即为圆222x y c +=与椭圆的交点个数,由于52c b =>=,故有4个点.(2)解法一:设12,,PF m PF n ==则有6m n +=,212()92m n PF PF mn +⋅=≤=,当且仅当m n =时取等号.解法二:由性质得2221220min 2221cos 1(cos )12cos 12b b b PF PF θθθ⋅=≤=+++-,(当点P 为短轴顶点时取得最大值,此时0cos 2b a θ=),代入化简得221221cos b PF PF a θ⋅=≤+. (3)如图所示,222x y c +=与椭圆有4个交点,假设在第一象限的交点为00(,)P x y ,此时122F PF π∠=,设12,,PF m PF n ==则有6m n +=,222420m n c +==,解得4,2m n ==(或2,4m n ==),由等面积法得0222y c mn ⨯=,则05y =,则由勾股定理得22200()c x y n -+=,解得05x =,则由对称性可知,点P 的横坐标的取值范围是3535(,)-. (焦点三角形中与距离最值有关的问题):注意在三角函数与解析几何中最值问题的一个很重要的用法:(1)三角形两边之和大于第三边,当三点在一条线上时取得最小值; (2)两边之差小于第三边.焦点三角形中的最值问题一般是距离之和的最值,且存在定点,故可以用三角形中的不等式来求; ★若点A 为椭圆内一定点,点P 在椭圆上,则有:111AF PA PF AF -≤-≤.(三角形三边关系)★若点A 为椭圆内一定点,点P 在椭圆上,则有:12122a AF PA PF a AF -≤+≤+.推导过程:连接11,,AP AF PF ,()21122AP PF AP a PF a AP PF +=+-=+-由三角形三边关系得111AF PA PF AF -≤-≤,则有12122a AF PA PF a AF -≤+≤+(椭圆定义的应用,三角形三边关系).焦点弦经过椭圆焦点的弦是焦点弦.(1)焦点弦长可用弦长公式求22212121212211()41()4AB k x x x x y y y y k=++-=++-; *(2)设焦点弦所在的直线的倾斜角为θ,则有22222||=cos ab AB a c θ-. *(3)2211ba BF AF =+(F 为某一焦点). (4)2ABF ∆的周长为4a .(离心率、焦点弦问题)(同第二定义例1)例1:(2010全国卷Ⅱ理数12题)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为32,过右焦点F 且斜率为(0)k k >的直线与C 相交于,A B 两点.若3AF FB =u u u r u u u r ,则k =( )A.1B.2C.3D.2B 【解析】解答题解法:1122(,),(,)A x y B x y ,∵ 3AF FB =u u u r u u u r,∴ 123y y =-, ∵ 3e =,设2,3a t c t ==,b t =,∴ 222440x y b +-=,直线AB 方程为3x my b =+.代入消去x ,∴ 222(4)230m y mby b ++-=,∴ 21212223,4mb b y y y y m +=-=-+,则22222232,34mb b y y m -=--=-+,解得212m =,则2k =,0k >.中点弦AB 是椭圆2222:1(0)x y C a b a b +=>>的任意一弦,P 是AB 中点,则1222-=-=⋅e ab k k OPAB .证明:令()()1122,,,A x y B x y ,()00,P x y则()1202x x x+=,()1202y y y +=,()()()()22112212121212222222221..01x y x x x x y y y y a b a b x y a b ⎫+=⎪+-+-⎪⇒+=⎬⎪+=⎪⎭, ()()()()2121221212y y b x x x x a y y -+⇒=--+,由于()()1212AB y y k x x -=-,00OPy k x =,则 22AB OP b k k a⋅=-. 例1:过点(2,1)M 作一条直线l 交椭圆221169x y +=于点AB ,若点M 恰好是弦AB 的中点,求直线l 的方程.【解析】解答题步骤:解法一(点差法):由题意得直线l 有斜率,设其斜率为k ,1122(,),(,)A x y B x y ,00(,)M x y ,代入椭圆方程,有222211221,1169169x y x y +=+=,两式作差得()()()()12121212..0169x x x x y y y y +-+-+=,()()120120916y y y x x x -⨯=--,即19216k ⨯=-,则98k =-.则直线l 的方程为91(2)8y x -=-⨯-,即98260x y +-=. 解法二(代入法):由题意得直线l 有斜率,设其直线方程为1(2)y k x -=-,得12y kx k =+-,代入221169x y +=得222(916)32(12)16(12)1440k x k k x k ++-+--=,则120232(12)24916k k x x x k -+=-==+,解得98k =-,则直线l 的方程为98260x y +-=.这两种方法都体现了设而不求的思想,这是圆锥曲线解题的常用思想.切线及切点弦切线方程:(1)设),(00y x P 为圆222r y x =+上一点,则过该点的切线方程为:200r y y x x =+;(2)设),(00y x P 为椭圆)0(12222>>=+b a by a x 上一点,则过该点的切线方程为:12020=+b y y a x x .切点弦方程:(1)设),(00y x P 是圆222r y x =+外的一点,过点P 作曲线的两条切线,切点N M 、,则切点弦MN 所在直线方程为200r y y x x =+;(2)设),(00y x P 是椭圆外的一点,过点P 作曲线的两条切线,切点N M 、,则切点弦MN 所在直线方程为1220=+byyaxx.例1:以422=+yx上的点)3,1(P为切点的切线方程为_________.【解析】解法一:由题意得切线有斜率,设切线方程为)1(3-=-xky,则03=-+-kykx,则有2132=+-kk,解得33-=k,则切线方程为043=-+yx.解法二:点)3,1(P为切点,由公式得,切线方程为431=⨯+⨯yx,即043=-+yx.例2:以13422=+yx上的点)23,1(P为切点的切线方程为_________.【解析】解法一:由题意得切线有斜率,设切线方程为)1(23-=-xky,代入13422=+yx,化简得3124)23(4)43(222=--+-++kkxkkxk,则有0)3124)(43(4)23(162222=--+--=∆kkkkk,解得21-=k,则切线方程为042=-+yx.解法二:点)23,1(P为切点,由公式得,切线方程为132341=⨯+⨯yx,即042=-+yx.★过椭圆准线上任一点作椭圆和切线,切点弦AB过该准线对应的焦点.推导过程:设2,aM yc⎛⎫⎪⎝⎭,则AB的方程为2221ax y yca b+=,即021y yxc b+=必过点(),0c.★过椭圆焦点弦的两端点作椭圆的切线,切线交点在准线上.光学性质★椭圆的光学性质:过一焦点的光线经椭圆反射后必过另一焦点.★椭圆上一个点P 的两条焦半径12,PF PF 的夹角12F PF ∠被椭圆在点P 处的法线平分.(入射光线、反射光线、镜面、法线)已知:如图,椭圆C的方程为22221x y a b +=,12,F F 分别是其左、右焦点,l 是过椭圆上一点00(,)P x y 的切线,'l 为垂直于l 且过点P 的椭圆的法线,交x 轴于D ,设21,F PD F PD αβ∠=∠=, 求证:αβ=.证明:在2222:1x y C a b+=上,00(,)P x y C ∈, 则过点P 的切线方程为:00221x x y y a b+=,'l 是通过点 P 且与切线l 垂直的法线,则0000222211':()()()y x l x x y b a b a-=-, ∴法线'l 与x 轴交于20((),0)c D x a, ∴22102022||,||c c F D x c F D c x a a=+=-,∴201220||||a cx F D F D a cx +=-,又由焦半径公式得:1020||,||PF a ex PF a ex =+=-,∴1122||||||||F D PF F D PF =,∴PD 是12F PF ∠的平分线, ∴αβ=,∵90ααββ''+=︒=+,故可得αβαβ''=⇔=.例1. 已知椭圆方程为1162522=+y x ,若有光束自焦点(3,0)A 射出,经二次反射回到A 点,设二次反射点为,B C ,如图所示,则ABC D 的周长为 .20【解析】:∵椭圆方程为1162522=+y x 中,225169c =-=, ∴(3,0)A 为该椭圆的一个焦点,∴自(3,0)A 射出的光线AB 反射后,反射光线BC 定过另一个焦点(3,0)A ¢-,故ABC D 的周长为:''44520AB BA A C CA a +++==⨯=.。
