华中师范大学组合数学期末考试试卷(A)
实变函数度(A)(解答)

华中师范大学 2006 –2007 学年第一学期期末考试试卷(A 卷)(解答)课程名称 实变函数 课程编号 83410014 任课教师判断题(判断正确、错误,请在括号中填“对”或“错”。
共5小题,每题3分,共5×3=15分)1、可数个可数集的并集是可数集。
( 对 )2、可测集E 上的非负可测函数必Lebesgue 可积。
( 错 )3、R n 上全体Lebesgue 可测集所组成的集类 具有连续势。
( 错 )4、非空开集的Lebesgue 测度必大于零。
( 对 )5、若()n f x (1n =,2,)和()f x 都为可测集E 上的可测函数,且lim ()()n n f x f x →∞=,..a e E ,则()()n f x f x ⇒,x E ∈。
( 错 )二、叙述题 (共5小题 , 每题3分,共5×3 =15分)1、单调收敛定理(即Levi 定理)答:设E 是Lebesgue 可测集,()n f x (1n =,2,)为E 上的非负可测函数,若{()n f x }是单调递增的,记()lim ()n n f x f x →∞=,则lim()()n n EEf x dx f x dx →∞=⎰⎰。
2、R n中开集的结构定理答:R n中的任一非空开集总可表示成R n中至多可数个互不相交的半开半闭区间的并。
(或R n中的任一开集或为空集或可表示成R n中至多可数个互不相交的半开半闭区间的并。
)3、R n中的集合E 是Lebesgue 可测集的卡氏定义(即C .Caratheodory 定义)答:设n E R ⊂,如果对任意nT R ⊂,总有***()()c m T m T E m T E =⋂+⋂则称E 为R n 中的Lebesgue 可测集,或称E 是Lebesgue 可测的。
4、F .Riesz 定理(黎斯定理)答:设E 为Lebesgue 可测集,()n f x (1n =,2,)和()f x 都是E 上的几乎处处有限的可测函数,如果()()n f x f x ⇒ x E ∈,则存在{()n f x }的一个子列{()k n f x },使得lim ()()k n k f x f x →∞=..a e 于E 。
2023学年华中师大一附中高一数学(下)期末考试卷附答案详析

2023学年华中师大一附中高一数学(下)期末考试卷考试时间:120分钟试卷满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足()20241i i z +-=(i 为虚数单位),则z 的虛部为()A .12B .12-C .i 2D .i 2-2.某商场组织了一次幸运抽奖活动,袋中装有标号分别为1~8的8个大小形状相同的小球,现抽奖者从中抽取1个小球.事件A=“取出的小球编号为奇数”,事件B=“取出的小球编号为偶数”,事件C=“取出的小球编号小于6”,事件D=“取出的小球编号大于6”,则下列结论错误的是()A .A 与B 互斥B .A 与B 互为对立事件C .C 与D 互为对立事件D .B 与D 相互独立3.已知m ,n 是不同的直线,α,β,γ是不同的平面,则下列结论正确的是()A .若m α∥,n α∥,则m n ∥B .若m α∥,m β∥,则αβ∥C .若m α∥,αβ∥,则m β∥D .若αγ⊥,βγ⊥,l αβ=I ,则l γ⊥4.甲乙两人进行三分远投比赛,甲、乙每次投篮命中的概率分别为0.5和0.4,且两人之间互不影响.若两人分别投篮一次,则两人中至少一人命中的概率为()A .0.6B .0.7C .0.8D .0.95.在△ABC 中,a ,b ,c 为角A ,B ,C 对应的边,则“cos sin a C a C b c -=-”是“△ABC 为直角三角形”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.如图,圆台1OO 的轴截面是等腰梯形ABCD ,24AB BC CD ===,E 为下底面O e 上的一点,且AE =,则直线CE 与平面ABCD 所成角的正切值为()A .2B .12C D .57.掷一枚质地均匀的骰子3次,则三个点数之和大于14的概率为()A .17216B .554C .427D .352168.在平行四边形ABCD 中,2π3BAD ∠=,1AB =,2AD =.P 是以C 动点,且AP AB AD λμ=+uu u r uu u r uuu r,则λμ+的最大值为()A .2+BC .2+D .27+二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求、全部选对的得6分,部分选对的得部分分,有选错的得0分.9.四名同学各掷骰子7次,分别记录每次骰子出现的点数,根据四名同学的统计结果,判断可能出现了点数6的是()A .中位数为3,极差为3B .平均数为2,第80百分位数为4C .平均数为3,中位数为4D .平均数为3,方差为110.在平面直角坐标系中,可以用有序实数对表示向量类似的,可以把有序复数对()()1212,,C z z z z ∈看作一个向量,记()12,a z z =r ,则称a r 为复向量.类比平面向量的相关运算法则,对于()12,a z z =r,()34,b z z =r ,1234,,,C z z z z ∈,规定如下运算法则:①()1324,a b z z z z +=++rr ;②()1324,a b z z z z -=--rr ;③1324a b z z z z ⋅=+r r ;④||a =r .则下列结论正确的是()A .若(i,1i)a =+r ,(2,2i)b =-r ,则15ia b ⋅=+rr B .若0a =r ,则()0,0a =rC .a b b a⋅=⋅r r r r D .()a b c a b a c⋅+=⋅+⋅r r r r r r r 11.如图所示,在直角梯形BCEF 中,90CBF BCE ∠=∠=︒,A ,D 分别是BF ,CE 上的点,且AD BC ∥,222AB ED BC AF ====,将四边形ADEF 沿AD 向上折起,连接BE ,BF ,CE .在折起的过程中,下列结论正确的是()A .AC ∥平面BEFB .BE 与AD 所成的角先变大后变小C .几何体EFABCD 体积有最大值53D .平面BCE 与平面BEF 不可能垂直三、填空题:本题共3小题,每小题5分,共15分.12.已知圆锥体积为3π,表面积是底面积的3倍,则该圆锥的母线长为______.13.已知平面向量a r ,b r ,3b =r ,向量a r 在向量b r 上的投影向量为16b -r,则a b ⋅=r r ______.14.在正三棱柱111ABC A B C -中,14AB AA ==,E 为线段1CC 上动点,D 为BC 边中点,则三棱锥A-BDE 外接球表面积的最小值为______.四、解答题:本题共5小题,共77分解答应写出文字说明、证明过程或演算步骤.15.(13分)某市举办了党史知识竞赛,从中随机抽取部分参赛选手,统计成绩后对统计数据整理得到如图所示的频率分布直方图.(1)试估计全市参赛者成绩的第40百分位数(保留小数点后一位)和平均数(单位:分);(2)若用按比例分配的分层随机抽样的方法从[)50,60,[)60,70,[)70,80三层中抽取一个容量为6的样本,再从这6人中随机抽取两人,求抽取的两人都及格(大于等于60分为及格)的概率.16.(15分)如图,四边形PDCE 为矩形,直线PD 垂直于梯形ABCD 所在的平面.90ADC BAD =∠=︒∠,F 是线段PA 的中点,PD =112AB AD CD ===.(1)求证:AC ∥平面DEF ;(2)求点F 到平面BCP 的距离.17.(15分)在△ABC 中,a ,b ,c 为角A ,B ,C 对应的边,S 为△ABC 的面积.且2sin sin sin 21sin C ab B a A S B ⎛⎫-=- ⎪⎝⎭.(1)求A ;(2)若2a =,求△ABC 内切圆半径的最大值.18.(17分)如图,在三棱柱111ABC A B C -中,底面是边长为4的等边三角形,14CC =,D 、E 分别是线段AC 、1CC 的中点,点1C 在平面ABC 内的射影为点D .(1)求证:1A C ⊥平面BDE ;(2)设G 为棱11B C 上一点,111C G C B λ=,()0,1λ∈.①若12λ=,请在图中作出三棱柱111ABC A B C -过G 、B 、D 三点的截面,并求该截面的面积;②求二面角G-BD-E 的取值范围.19.(17分)对于两个平面向量a r ,b r ,如果有0a b a a ⋅-⋅>r r r r ,则称向量a r是向量b r 的“迷你向量”.(1)若(1,)m x =r ,(2,1)n x =-r ,m r 是n r的“迷你向量”,求实数x 的取值范围;(2)一只蚂蚁从坐标原点()0,0O 沿最短路径爬行到点(),N n n 处(n N ∈且2n ≥).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第i 次后停留的位置记为()112P i n ≤≤,设()1,0M n -.记事件T=“蚂蚁经过的路径中至少有n 个i P 使得ON uuu r 是i OP uuu r的迷你向量”。
实变函数06-07年度_A_(解答)
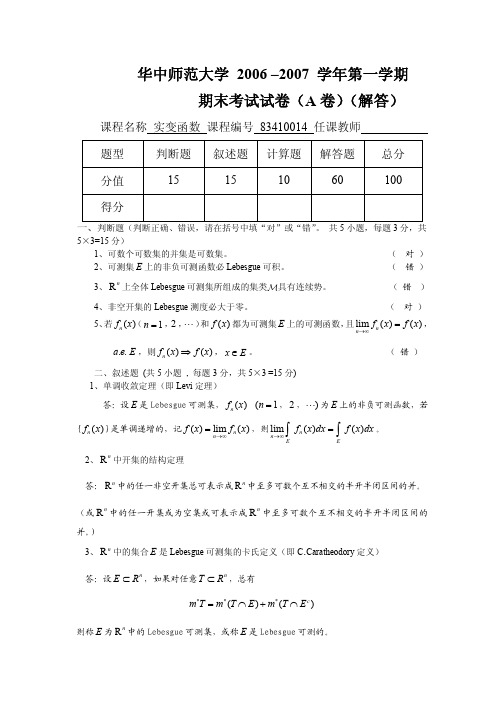
[0, ]
f ( x)dx 。
解:由题设 f ( x) sin x , a.e. 于 [0, ] ,而 sin x 在 [0, ] 上连续, 于是由积分的惟一性和 L 积分与 R 积分的关系得
[0, ]
f ( x)dx
[0, ]
sin xdx ( R) sin xdx ( cos x)
n n n n n n n
n
m*T m* (T E ) m* (T E c )
则称 E 为 R 中的 Lebesgue 可测集,或称 E 是 Lebesgue 可测的。
n
4、F.Riesz 定理(黎斯定理) 答:设 E 为 Lebesgue 可测集, f n ( x ) (n 1 , 2 , ) 和 f ( x ) 都是 E 上的几乎处处有 限的可测函数, 如 果 f n ( x ) f ( x)
华中师范大学 2006 –2007 学年第一学期 期末考试试卷(A 卷) (解答)
课程名称 实变函数 课程编号 83410014 任课教师 题型 分值 得分
一、判断题(判断正确、错误,请在括号中填“对”或“错” 。 共 5 小题,每题 3 分,共
5×3=15 分) 1、可数个可数集的并集是可数集。 2、可测集 E 上的非负可测函数必 Lebesgue 可积。 3、 R 上全体 Lebesgue 可测集所组成的集类具有连续势。 4、非空开集的 Lebesgue 测度必大于零。
n
(2)由题设 lim Fn ( x) 2 f ( x ) ,再由 Fatou 引理得
2 f ( x)dx lim Fn ( x )dx lim [ f n ( x) f ( x) f n ( x) f ( x) ]dx
数分卷(A试点班3)(解答)

(e (e
x
sin y my )dx e
x
cos ydy =
(e
BA
x
sin y my ) dx e
x
cos ydy
=
x
sin y my )dx e
x
L BA
cos ydy = mdxdy
D
8
a
2
其中 D { x
2
y
2
ax , y 0 }
解: (1)因为
e
px
cos yx e
px
,而 e
0
px
dx
1 p
收敛
由 M—判别法 得
0
e
px
cos yx dx 在 y ( , ) 上的一致收敛性。
(2)由于 I
Байду номын сангаас
0
e
px
sin bx sin ax x
b px
dx
得分
评阅人
四、证明与计算题(共 2 小题,共 15 分)
(1)、设 f ( x , y ) 在有界闭区域 D R 上连续 ,证明:存在 ( x 0 , y 0 ) D ,使得
2
f
D
( x , y )dxdy
f ( x 0 , y 0 ) S ,其中 S 为 D 的面积。
1
(2)、利用(1)计算 lim
解:令u x y ,v x y ,则 D 的对应区域为 { 0 v 1 , v u v } ,
x 1 2 (u v ) , y 1 2 (v u ) ,且
2020-2021华中师大一附中高中必修二数学下期末试题(及答案)
2020-2021华中师大一附中高中必修二数学下期末试题(及答案)一、选择题1.执行右面的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =( )A .203B .72C .165D .1582.已知向量a v ,b v 满足4a =v,b v 在a v 上的投影(正射影的数量)为-2,则2a b -v v 的最小值为( ) A .43B .10C .10D .83.某空间几何体的三视图如图所示,则该几何体的体积为( )A .73B .8π3- C .83D .7π3- 4.(2015新课标全国I 理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A .14斛B .22斛C .36斛D .66斛5.已知不等式220ax bx ++>的解集为{}12x x -<<,则不等式220x bx a ++<的解集为( ) A .112x x ⎧⎫-<<⎨⎬⎩⎭B .112x x x ⎧⎫<->⎨⎬⎩⎭或 C .{}21x x -<<D .{}21x x x <->或6.当x ∈R 时,不等式210kx kx -+>恒成立,则k 的取值范围是( ) A .(0,)+∞B .[)0,+∞C .[)0,4D .(0,4)7.已知ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,且2cos 2b C a c ⋅=+,若3b =,则ABC ∆的外接圆面积为( )A .48π B .12πC .12πD .3π8.1()xf x e x=-的零点所在的区间是( ) A .1(0,)2B .1(,1)2C .3(1,)2D .3(,2)29.如图,已知三棱柱111ABC A B C -的各条棱长都相等,且1CC ⊥底面ABC ,M 是侧棱1CC 的中点,则异面直线1AB 和BM 所成的角为( )A .2π B . C . D .3π 10.将直线2x -y +λ=0沿x 轴向左平移1个单位,所得直线与圆x 2+y 2+2x -4y =0相切,则实数λ的值为( ) A .-3或7B .-2或8C .0或10D .1或1111.已知()f x 是定义在R 上的奇函数,当0x >时,()32f x x =-,则不等式()0f x >的解集为( )A .33,0,22⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭UB .33,,22⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭C .33,22⎛⎫- ⎪⎝⎭D .33,0,22⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭12.在ABC ∆中,2cos (,b,22A b ca c c+=分别为角,,A B C 的对边),则ABC ∆的形状是( ) A .直角三角形 B .等腰三角形或直角三角形 C .等腰直角三角形D .正三角形二、填空题13.在ABC △ 中,若223a b bc -= ,sin 23sin C B = ,则A 等于__________. 14.若三点1(2,3),(3,2),(,)2A B C m --共线,则m 的值为 . 15.设a ,b ,c 分别为ABC ∆内角A ,B ,C 的对边.已知233cos cos a b cB C-=,则222a cb ac+-的取值范围为______. 16.已知抛物线()220y px p =>的准线与圆()22316x y -+=相切,则p 的值为__________.17.如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.18.已知函数()2,01,0x x f x x x >⎧=⎨+≤⎩若()()10f a f +=,则实数a 的值等于________.19.已知复数z x yi =+,且23z -yx的最大值为__________. 20.已知()()2,3,4,3A B -,点P 在直线AB 上,且32AP PB =u u u v u u u v,则点P 的坐标为________三、解答题21.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:记x 表示1台机器在三年使用期内需更换的易损零件数,y 表示1台机器在购买易损零件上所需的费用(单位:元),n 表示购机的同时购买的易损零件数. (Ⅰ)若n =19,求y 与x 的函数解析式;(Ⅱ)若要求“需更换的易损零件数不大于n ”的频率不小于0.5,求n 的最小值; (Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件? 22.已知满足(1)求的取值范围; (2)求函数的值域.23.已知平面向量a r ,b r满足1a b ==r r .(1)1a b -=r r ,求a r 与b r的夹角;(2)若对一切实数x ,不等式a xb a b +≥+r r r r 恒成立,求a r 与b r的夹角θ. 24.设函数2()cos 2sin 3f x x x π⎛⎫=++ ⎪⎝⎭.(1)求函数()f x 的最小正周期. (2)求函数()f x 的单调递减区间;(3)设,,A B C 为ABC V 的三个内角,若1cos 3B =,124C f ⎛⎫=- ⎪⎝⎭,且C 为锐角,求sin A .25.已知函数f(x)=log 4(4x +1)+kx(k ∈R)是偶函数.(1)求k 的值;(2)设g(x)=log 44•23xa a ⎡⎤⎢⎥⎣⎦-,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a 的取值范围.26.如图,平行四边形ABCD 中,E ,F 分别是BC ,DC 的中点,G 为BF 与DE 的交点,若AB a =u u u v v ,AD b =u u u v v ,试以a v ,b v 为基底表示DE u u u v 、BF u u u v 、CG u u u v .【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】 【详解】试题分析:根据题意由13≤成立,则循环,即1331,2,,2222M a b n =+====;又由23≤成立,则循环,即28382,,,33323M a b n =+====;又由33≤成立,则循环,即3315815,,,428838M a b n =+====;又由43≤不成立,则出循环,输出158M =. 考点:算法的循环结构2.D解析:D 【解析】 【分析】b r 在a r上的投影(正射影的数量)为2-可知||cos ,2b a b <>=-r r r ,可求出||2b ≥r ,求22a b -r r 的最小值即可得出结果.【详解】因为b r 在a r上的投影(正射影的数量)为2-,所以||cos ,2b a b <>=-r r r,即2||cos ,b a b =-<>r r r ,而1cos ,0a b -≤<><r r , 所以||2b ≥r,因为2222222(2)44||4||||cos ,4||a b a b a a b b a a b a b b -=-=-⋅+=-<>+r r r r r r r r r r r r r r22=1644(2)4||484||b b -⨯⨯-+=+r r所以22484464a b -≥+⨯=r r ,即28a b -≥r r ,故选D.【点睛】本题主要考查了向量在向量上的正射影,向量的数量积,属于难题.3.B解析:B 【解析】 【分析】由三视图可知,该几何体是由一个四棱锥挖掉半个圆锥所得,故利用棱锥的体积减去半个圆锥的体积,就可求得几何体的体积. 【详解】由三视图可知,该几何体是由一个四棱锥挖掉半个圆锥所得,故其体积为21118222123233ππ-⋅⋅⋅-⋅⋅⋅⋅=.故选B. 【点睛】本小题主要考查由三视图判断几何体的结构,考查不规则几何体体积的求解方法,属于基础题.4.B解析:B 【解析】试题分析:设圆锥底面半径为r ,则12384r ⨯⨯=,所以163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B. 考点:圆锥的性质与圆锥的体积公式5.A解析:A 【解析】 【分析】根据一元二次不等式的解集与一元二次方程根的关系,结合韦达定理可构造方程求得,a b ;利用一元二次不等式的解法可求得结果.【详解】220ax bx ++>Q 的解集为{}12x x -<<1∴-和2是方程220ax bx ++=的两根,且0a <1212122ba a⎧-=-+=⎪⎪∴⎨⎪=-⨯=-⎪⎩,解得:11a b =-⎧⎨=⎩ 222210x bx a x x ∴++=+-< 解得:112x -<<,即不等式220x bx a ++<的解集为112x x ⎧⎫-<<⎨⎬⎩⎭故选:A 【点睛】本题考查一元二次不等式的解法、一元二次不等式的解集与一元二次方程根的关系等知识的应用;关键是能够通过一元二次不等式的解集确定一元二次方程的根,进而利用韦达定理构造方程求得变量.6.C解析:C 【解析】当0k =时,不等式210kx kx -+>可化为10>,显然恒成立;当0k ≠时,若不等式210kx kx -+>恒成立,则对应函数的图象开口朝上且与x 轴无交点,则240k k k >⎧⎨=-<⎩V 解得:04k <<,综上k 的取值范围是[)0,4,故选C. 7.D解析:D 【解析】 【分析】 先化简得23B π=,再利用正弦定理求出外接圆的半径,即得ABC ∆的外接圆面积. 【详解】由题得222222a b c b a c ab+-⋅=+,所以22222a b c a ac +-=+, 所以222a b c ac -+=-, 所以12cos ,cosB 2ac B ac =-∴=-, 所以23B π=.由正弦定理得=2,33R R ∴=, 所以ABC ∆的外接圆面积为23=3ππ⋅. 故选D 【点睛】本题主要考查正弦定理余弦定理解三角形,意在考查学生对这些知识的理解掌握水平和分析推理能力.8.B解析:B 【解析】 函数f (x )=e x ﹣1x 是(0,+∞)上的增函数,再根据f (12)=e ﹣2<0,f (1)=e ﹣1>0,可得f (12)f (1)<0,∴函数f (x )=e x ﹣1x 的零点所在的区间是(12,1),故选B .点睛:判定函数的零点所在区间,只需计算区间端点处的函数值,并判断是否异号,只要异号,则区间内至少有一个零点存在.9.A解析:A 【解析】 【分析】由题意设棱长为a ,补正三棱柱ABC-A 2B 2C 2,构造直角三角形A 2BM ,解直角三角形求出BM ,利用勾股定理求出A 2M ,从而求解. 【详解】设棱长为a ,补正三棱柱ABC-A 2B 2C 2(如图).平移AB 1至A 2B ,连接A 2M ,∠MBA 2即为AB 1与BM 所成的角, 在△A 2BM 中,22252()22a A B a BM a a ==+=,,222313()22a A M a a =+=,222222,2A B BM A M MBA π∴+=∴∠=, . 故选A . 【点睛】本题主要考查了异面直线及其所成的角和勾股定理的应用,计算比较复杂,要仔细的做.10.A解析:A 【解析】试题分析:根据直线平移的规律,由直线2x ﹣y+λ=0沿x 轴向左平移1个单位得到平移后直线的方程,然后因为此直线与圆相切得到圆心到直线的距离等于半径,利用点到直线的距离公式列出关于λ的方程,求出方程的解即可得到λ的值.解:把圆的方程化为标准式方程得(x+1)2+(y ﹣2)2=5,圆心坐标为(﹣1,2),半径为,直线2x ﹣y+λ=0沿x 轴向左平移1个单位后所得的直线方程为2(x+1)﹣y+λ=0, 因为该直线与圆相切,则圆心(﹣1,2)到直线的距离d==r=,化简得|λ﹣2|=5,即λ﹣2=5或λ﹣2=﹣5, 解得λ=﹣3或7 故选A考点:直线与圆的位置关系.11.A解析:A 【解析】 【分析】根据题意,结合函数的解析式以及奇偶性分析可得()f x 的图象,据此分析可得答案. 【详解】解:因为()f x 是定义在R 上的奇函数, 所以它的图象关于原点对称,且()00f =, 已知当0x >时,()32f x x =-, 作出函数图象如图所示, 从图象知:33022f f ⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭, 则不等式()0f x >的解集为33,0,22⎛⎫⎛⎫-∞-⋃ ⎪ ⎪⎝⎭⎝⎭. 故选:A.【点睛】本题考查函数的奇偶性与单调性的综合应用,以及函数的解析式,考查数形结合思想.12.A解析:A 【解析】 【分析】 根据正弦定理得到1cos sin sin 22sin A B C C ++=,化简得到sin cos 0A C =,得到2C π=,得到答案. 【详解】2cos 22A b c c +=,则1cos sin sin 22sin A B CC++=, 即sin cos sin sin cos cos sin sin C A C A C A C C +=++,即sin cos 0A C =,sin 0A ≠,故cos 0C =,2C π=.故选:A . 【点睛】本题考查了正弦定理判断三角形形状,意在考查学生的计算能力和转化能力.二、填空题13.【解析】由得所以即则又所以故答案为 解析:6π【解析】由23sinC sinB = 得23c b =, 所以2223323a b bc b -==,即227a b =, 则22222223243b c a cosA bc b+-===,又0A π∈(,), 所以6A π=. 故答案为6π. 14.【解析】试题分析:依题意有即解得考点:三点共线 解析:12试题分析:依题意有AB AC k k =,即531522m --=+,解得12m =. 考点:三点共线.15.【解析】【分析】把已知式用正弦定理化边为角由两角和的正弦公式和诱导公式化简可求得即角从而得角的范围注意由余弦定理可得结论【详解】因为所以所以即又所以则因为所以而故故答案为:【点睛】本题考查正弦与余弦解析:()()0,2U【解析】【分析】把已知式用正弦定理化边为角,由两角和的正弦公式和诱导公式化简,可求得cos C ,即C 角,从而得B 角的范围,注意2B π≠,由余弦定理可得结论. 【详解】=,所以()()2cos cos cos cos 0a C B B C =⋅≠,所以()2sin cos cos A B C C B =,即()2sin cos A C C B A +=,又sin 0A >,所以cos C =, 则6C π=,因为cos 0B ≠,所以50,,226B πππ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭U , 而2222cos a c b B ac +-=,故()()2220,2a c b ac +-∈U .故答案为:()()0,2U .【点睛】本题考查正弦与余弦定理的应用,考查运算求解能力.本题是一个易错题,学生容易忽略cos B 不能等于0.16.2【解析】抛物线的准线为与圆相切则解析:2【解析】 抛物线的准线为2p x =-,与圆相切,则342p +=,2p =. 17.2米【解析】【分析】【详解】如图建立直角坐标系设抛物线方程为将A (2-2)代入得m=-2∴代入B 得故水面宽为米故答案为米考点:抛物线的应用 解析:米【分析】【详解】如图建立直角坐标系,设抛物线方程为2x my =,将A (2,-2)代入2x my =,得m=-2,∴22x y =-,代入B ()0,3x -得06x =, 故水面宽为26米,故答案为26米.考点:抛物线的应用18.-3【解析】【分析】先求再根据自变量范围分类讨论根据对应解析式列方程解得结果【详解】当a>0时2a=-2解得a=-1不成立当a≤0时a+1=-2解得a=-3【点睛】求某条件下自变量的值先假设所求的值解析:-3【解析】【分析】先求()f a ,再根据自变量范围分类讨论,根据对应解析式列方程解得结果.【详解】()()()102f a f f a +=⇒=-当a>0时,2a=-2,解得a=-1,不成立当a≤0时,a+1=-2,解得a=-3【点睛】求某条件下自变量的值,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记代入检验,看所求的自变量的值是否满足相应段自变量的取值范围. 19.【解析】【分析】根据复数z 的几何意义以及的几何意义由图象得出最大值【详解】复数且复数z 的几何意义是复平面内以点为圆心为半径的圆的几何意义是圆上的点与坐标原点连线的斜率由图可知:即的最大值为故答案为: 解析:【解析】【分析】根据复数z 的几何意义以及y x的几何意义,由图象得出最大值. 【详解】复数z x yi =+且23z-=,复数z 的几何意义是复平面内以点(2,0)为圆心,3为半径的圆22(2)3x y -+=.y x的几何意义是圆上的点与坐标原点连线的斜率 由图可知:max 331y x ⎛⎫==⎪⎝⎭ 即y x 3 3【点睛】本题主要考查了复数的几何意义的应用,属于中档题.20.【解析】【分析】设点得出向量代入坐标运算即得的坐标得到关于的方程从而可得结果【详解】设点因为点在直线且或即或解得或;即点的坐标是【点睛】本题考查了平面向量的线性运算的坐标表示以及平面向量的共线问题意 解析:(8,-15), 163,55⎛⎫-⎪⎝⎭ 【解析】【分析】 设点(),P x y ,得出向量33,22AP BP AP BP ==-u u u r u u u r u u u r u u u r ,代入坐标运算即得P 的坐标,得到关于,x y 的方程,从而可得结果.【详解】 设点(),P x y ,因为点P 在直线,且3||||2AP PB =u u u r u u u r , 33,22AP BP AP BP ∴==-u u u r u u u r u u u r u u u r ,3(2,3)(4,3)2x y x y ∴--=-+或, 3(2,3)(4,3)2x y x y ∴--=--+, 即243122639x x y y -=-⎧⎨-=+⎩或243122639x x y y -=-+⎧⎨-=--⎩, 解得815x y =⎧⎨=-⎩或16535x y ⎧=⎪⎪⎨⎪=-⎪⎩; 即点P 的坐标是(8,-15),163,55⎛⎫-⎪⎝⎭. 【点睛】本题考查了平面向量的线性运算的坐标表示以及平面向量的共线问题,意在考查对基础知识的掌握与应用,是基础题. 三、解答题21.(1)()3800,19,y 5005700,19,x x N x x ≤⎧=∈⎨->⎩;(2)19;(3) 购买1台机器的同时应购买19个易损零件.【解析】试题分析:(Ⅰ)分x ≤19及x >19,分别求解析式;(Ⅱ)通过频率大小进行比较;(Ⅲ)分别求出n=19,n=20时所需费用的平均数来确定.试题解析:(Ⅰ)当时,3800y =;当时,3800500(19)5005700y x x =+-=-,所以与的函数解析式为3800,19,{()5005700,19,x y x N x x ≤=∈->. (Ⅱ)由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故的最小值为19.(Ⅲ)若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800,因此这100台机器在购买易损零件上所需费用的平均数为1(380070430020480010)4000100⨯⨯+⨯+⨯=. 若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500,因此这100台机器在购买易损零件上所需费用的平均数为1(400090450010)4050100⨯⨯+⨯=. 比较两个平均数可知,购买1台机器的同时应购买19个易损零件.【考点】函数解析式、概率与统计【名师点睛】本题把统计与函数结合在一起进行考查,有综合性但难度不大,求解的关键是读懂题意,所以提醒考生要重视数学中的阅读理解问题.22.(1) (2) 【解析】试题分析(1)先将不等式化成底相同的指数,再根据指数函数单调性解不等式(2)令,则函数转化为关于 的二次函数,再根据对称轴与定义区间位置关系确定最值,得到值域.试题解析:解:(1) 因为由于指数函数在上单调递增(2) 由(1)得令,则,其中 因为函数开口向上,且对称轴为 函数在上单调递增 的最大值为,最小值为 函数的值域为. 23.(1)3π(2)θπ= 【解析】【分析】(1)根据向量数量积的定义及性质即可求解(2)利用平方化简不等式可得22cos 12cos 0x x θθ+⋅--≥恒成立,利用判别式求解即可.【详解】 (1)∵1a b ==r r,21211a b a b ∴-=-⋅+=r r r u r , 即12a b ⋅=r r , ∴1cos 2a b θ=r r , ∴3πθ=.(2)不等式a xb a b +≥+r r r r 两边平方可得:22cos 12cos 0x x θθ+⋅--≥恒成立,∴0∆≤,即()24cos412cos 0θθ++≤, 故()2cos 10θ+≤,只能cos 1θ=-,而0θπ≤≤,所以θπ=.【点睛】本题主要考查了向量的数量积定义,性质,不等式恒成立,属于中档题.24.(1)π(2)减区间为ππk π,k π44⎡⎤-+⎢⎥⎣⎦,k Z ∈(3【解析】【分析】()1利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,得出结论. ()2利用正弦函数的单调性,求得函数()f x 的单调递减区间.()3利用同角三角函数的基本关系、两角和的正弦公式,求得sinA 的值.【详解】() 1函数()2π11cos2x 1f x cos 2x sin x cos2x 3222-⎛⎫=++=+=+ ⎪⎝⎭, 故它的最小正周期为2ππ2=.()2对于函数()1f x 22=-+,令ππ2k π2x 2k π22-≤≤+,求得ππk πx k π44-≤≤+, 可得它的减区间为ππk π,k π44⎡⎤-+⎢⎥⎣⎦,k Z ∈.()3ABC V 中,若1cosB 3=,sinB 3∴==.若C 11f 224⎛⎫=+=- ⎪⎝⎭,sinC ∴=,C Q 为锐角,πC 3∴=.()ππ11sinA sin B C sinBcoscosBsin 3323∴=+=+=+=. 【点睛】本题主要考查三角恒等变换,正弦函数的周期性和单调性,考查了同角三角函数的基本关系、两角和的正弦公式的应用,属于中档题.25.(1)k =-12.(2){-3}∪(1,+∞). 【解析】(1)由函数f(x)是偶函数,可知f(x)=f(-x),∴log 4(4x +1)+kx =log 4(4-x +1)-kx. log 44141x x -++=-2kx ,即x =-2kx 对一切x ∈R 恒成立,∴k =-12. (2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log 4(4x +1)-12x =log 44•23x a a ⎡⎤⎢⎥⎣⎦-有且只有一个实根,化简得方程2x +12x =a·2x -43a 有且只有一个实根.令t =2x >0,则方程(a -1)t 2-43at -1=0有且只有一个正根. ①a =1t =-34,不合题意;②a≠1时,Δ=0a =34或-3.若a =34t =-2,不合题意,若a =-3t =12;③a≠1时,Δ>0,一个正根与一个负根,即11a --<0a>1. 综上,实数a 的取值范围是{-3}∪(1,+∞).26.1()3CG a b =-+u u u v v v 【解析】分析:直接利用共线向量的性质、向量加法与减法的三角形法则求解即可.详解:由题意,如图1122DE DC CE AB CB a b =+=+=-u u u v u u u v u u u v u u u v u u u v v v , 1122BF BC CF AD AB a b =+=-=-+u u u v u u u v u u u v u u u v u u u v v v , 连接BD ,则G 是BCD V 的重心,连接AC 交BD 于点O ,则O 是BD 的中点, ∴点G 在AC 上,∴()2221133323CG CO OC AC a b ==-=-⨯=-+u u u v u u u v u u u v u u u v v v , 故答案为12DE a b u u u v v v =-;12BF a b =-+u u u v v v ; ∴()13CG a b =-+u u u v v v . 点睛:向量的运算有两种方法,一是几何运算往往结合平面几何知识和三角函数知识解答,运算法则是:(1)平行四边形法则(平行四边形的对角线分别是两向量的和与差);(2)三角形法则(两箭头间向量是差,箭头与箭尾间向量是和);二是坐标运算:建立坐标系转化为解析几何问题解答(求最值与范围问题,往往利用坐标运算比较简单).。
期末模拟测试卷(试卷)2024-2025学年六年级数学上册(人教版)

期末模拟测试卷(试卷)2024-2025学年六年级数学上册(人教版)(时间: 90 分钟, 满分: 100分)一、填空题。
(第12小题2分,其余每空1分,共22分)1.0.2的倒数是( )。
2.比40m 多20%是( )m 。
20t 比( )t 少 153.2:16=10()=1÷()=()(填小数)。
4.一个数的 34是60,这个数是( ),它的 25是( )。
5. 45:0.2的比值是( ),化成最简单的整数比是( )。
6.从甲城到乙城,货车要行7小时,客车要行9小时,货车速度与客车速度的最简单的整数比是( )。
7.把一根 58m 长的绳子平均分成4段,每段长( )m ,每段占全长的( )。
8.加工一批零件,5天加工了这批零件的 110,全部加工完需要( )天。
9.用一根长12.56m 的绳子围成一个圆,这个圆的直径是( )m ,面积是( )m²。
10.在0.67, 67,67.7%和0.667四个数中,最大的数是( ),最小的数是( )。
11.六(1)班今天出勤48人,有2人因病请假,今天六(1)班学生的出勤率是( );昨天该班的缺勤率是2%,有( )人缺勤。
12.观察下列点阵图规律,第10个点阵图中有( )个点。
二、判断题。
(对的画“✔”,错的画“×”。
每题1分,共5分)1.0.8m =80%m =45m 。
( ) 2.一件商品,先降价10%再提价10%,现价比原价低。
( )3.一个假分数的倒数一定比这个假分数小。
( )4.某人栽了101棵树,全部成活,其成活率为101%。
( )5.5kg 盐溶解在100kg 水中,盐水的含盐率是5%。
( )三、选择题。
(把正确答案的序号填在括号里。
每题1分,共5分)1.若a 是非零自然数,下列算式中的计算结果最大的是( )。
A.a ×58B.a ÷58C. a÷1D.1÷a 2.一根绳子剪成两段,第一段长 37m ,第二段占全长的 37,两段相比,( )。
2025届华中师大一附中高三数学第一学期期末达标测试试题含解析

2025届华中师大一附中高三数学第一学期期末达标测试试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数()()()211z a a i a R =-+-∈为纯虚数,则z =( )A .iB .﹣2iC .2iD .﹣i2.函数2()1cos 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是( ) A . B .C .D .3.已知(0,)απ∈,且tan 2α=,则cos2cos αα+=( )A .2535- B .535- C .535+ D .2535+ 4.对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分; ②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间内;③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关; ④乙同学连续九次测验成绩每一次均有明显进步. 其中正确的个数为( ) A .B .C .D .5.已知六棱锥P ABCDEF -各顶点都在同一个球(记为球O )的球面上,且底面ABCDEF 为正六边形,顶点P 在底面上的射影是正六边形ABCDEF 的中心G ,若6PA =,2AB =,则球O 的表面积为( )A .163πB .94π C .6πD .9π6.已知命题:p 若1a <,则21a <,则下列说法正确的是( ) A .命题p 是真命题 B .命题p 的逆命题是真命题C .命题p 的否命题是“若1a <,则21a ≥”D .命题p 的逆否命题是“若21a ≥,则1a <”7.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表: 黄赤交角 2341︒'2357︒'2413︒'2428︒'2444︒'正切值 0.439 0.4440.4500.4550.461年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ) A .公元前2000年到公元元年 B .公元前4000年到公元前2000年 C .公元前6000年到公元前4000年D .早于公元前6000年8.双曲线的渐近线与圆(x -3)2+y 2=r 2(r >0)相切,则r 等于( )A .B .2C .3D .69.复数的()12z i i =--为虚数单位在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限10.如图是一个几何体的三视图,则该几何体的体积为( )A .23B .43C 23D 4311.设22(1)1z i i=+++(i 是虚数单位),则||z =( ) A 2B .1C .2D 512.已知直线y =k (x +1)(k >0)与抛物线C 2:4y x =相交于A ,B 两点,F 为C 的焦点,若|FA |=2|FB |,则|FA | =( )A .1B .2C .3D .4二、填空题:本题共4小题,每小题5分,共20分。
湖北省武汉市华中师范大学第一附属中学2025届高三下学期期末考试数学试题(A卷)

湖北省武汉市华中师范大学第一附属中学2025届高三下学期期末考试数学试题(A 卷)注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且cos sin a B b A c +=.若2a =,ABC 的面积为3(21)-,则b c +=( ) A .5B .22C .4D .162.《普通高中数学课程标准(2017版)》提出了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是( )A .甲的数据分析素养高于乙B .甲的数学建模素养优于数学抽象素养C .乙的六大素养中逻辑推理最差D .乙的六大素养整体平均水平优于甲3.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( )A .36 cm 3B .48 cm 3C .60 cm 3D .72 cm 34.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”意思为有一个人要走378里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了六天恰好到达目的地,请问第二天比第四天多走了( ) A .96里B .72里C .48里D .24里5.双曲线22221(0,0)x y a b a b -=>>的左右焦点为12,F F ,一条渐近线方程为:b l y x a=-,过点1F 且与l 垂直的直线分别交双曲线的左支及右支于,P Q ,满足11122OP OF OQ =+,则该双曲线的离心率为( ) A 10B .3C 5D .26.已知0x >,0y >,23x y +=,则23x yxy+的最小值为( )A .322-B .221C 21D 217.在函数:①cos |2|y x =;②|cos |y x =;③cos 26y x π⎛⎫=+ ⎪⎝⎭;④tan 24y x π⎛⎫=-⎪⎝⎭中,最小正周期为π的所有函数为( ) A .①②③B .①③④C .②④D .①③8.设抛物线24y x =上一点P 到y 轴的距离为1d ,到直线:34120l x y ++=的距离为2d ,则12d d +的最小值为( ) A .2B .153C .163D .39.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有 A .72种B .36种C .24种D .18种10.正项等比数列{}n a 中的1a 、4039a 是函数()3214633f x x x x =-+-的极值点,则2020a =( ) A .1-B .1CD .211.设双曲线22221x y a b-=(a>0,b>0)的右焦点为F ,右顶点为A,过F 作AF 的垂线与双曲线交于B,C 两点,过B,C分别作AC ,AB 的垂线交于点D .若D 到直线BC的距离小于a ( ) A .(1,0)(0,1)-B .(,1)(1,)-∞-+∞ C.((0,2) D.(,(2,)-∞+∞12.已知集合{}|124A x x =<≤,|B x y ⎧⎫==⎨⎩,则A B =( ) A .{}5|x x ≥ B .{}|524x x <≤ C .{|1x x ≤或}5x ≥D .{}|524x x ≤≤二、填空题:本题共4小题,每小题5分,共20分。
华中师范大学数理方法期末考试试卷1答案

因为与ϕ 无关,所以 u ( r , θ ) = ① 球内 由 u (0, θ ) 有限 ⇒ Bl = 0
∑(A r
l =0 l
∞
∞
l
+ Bl r − l −1 )Pl (cos θ )
∴ u1 (r ,θ ) = ∑ Al r l Pl (cos θ )
l =0
由u1 ( R0 ,θ ) = u0 cos 2 θ ⇒ 1 ⇒ A0 = u0 3 A2 = 2u0 3R02
2u u0 l P0 (cosθ ) + 0 P2 (cosθ ) = ∑ Al R0 Pl (cosθ ) 3 3 l Al = 0 (l ≠ 0,2)
1 2u 2 ∴ u1 (r ,θ ) = u0 + 0 r P2 (cosθ ) 3 3R02
②球内
u (∞,θ )有限 ⇒ Al = 0 ∴ u2 (r ,θ ) = ∑ Bl r −l −1Pl (cosθ )
解:以上三个方程分别编号为(1) , (2) , (3) 。 1. 分离变量。令 u ( x, t ) = X ( x )T (t ) (4)
(4)代入泛定方程(1),得到: X ( x)T ′′(t ) − a 2 X ′′( x )T (t ) = 0 即
X ′′( x) T ′′(t ) = X ( x ) a 2 T (t ) X ′′( x) + λX ( x) = 0 T ′′(t ) + λa 2 T (t ) = 0
设常数为 − λ ,得到两个常微分方程 (5) (6)
将(4)代入边界条件(2) ,得 u ( 0, t ) = X ( 0)T (t ) = 0, u (l , t ) = X (l )T (t ) = 0 若 T(t)=0 则 u(x,t)=0,是平庸解,略去,则得到 X(x)的边界条件
华中师范大学信号与系统期末考试(A卷)2016-2017

院(系): 专业: 年级: 学生姓名: 学号:------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------第 1 页(共 4 页)4.一个连续时间周期信号,其傅里叶级数表示为∑∞-∞==kt jke k t x 502)cos()(ππ,该信号是( )Consider the continuous-time periodic signal whose Fourier series representation is∑∞-∞==kt jke k t x 502)cos()(ππ, what is the signal ?A 不是实值函数 not realB 实奇函数real and oddC 实偶函数 real and evenD 不能确定cannot be ascertained 5.如果)(t f 的傅里叶变换是)(ωj F ,则)3()(-t t f δ的傅里叶变换是( )。
)(ωj F is the Fourier transform of )(t f , which of the following is the Fourier transformof )3()(-t t f δ?A ωj e f 3)3(-B ωωj e j F 3)(-C ωj e f 3)3(D ωωj e j F 3)( 6.有多少个信号在其收敛域内都有如下所示的拉普拉斯变换( ) How many signals have a Laplace transform that may be expressed as below?A 2个B 3个C 4个D 5个 得分 评阅人 II. 填空题Fill in the blanks (每空3分3 points for each correct answer )1.一个连续时间线性系统S 的输入为,)(21t j e t x =对应的输出为,)(31t j e t y =输入为,)(2-2t j e t x =对应的输出为,)(3-2t j e t y =若输入),2cos()(3t t x =求系统S 的输出=)(3t y 。
华中师范大学组合数学期末考试试卷(A)

华中师范大学组合数学期末考试试卷(A)
课程名称组合数学课程编号
任课教师 王春香
题型 填空题 证明题 计算题 应用题
总分
分值 20 20 40 20
100
得分
学号:
学生姓名:
年级:
得分 评阅人
一、填空题:(20 分)(共 5 题,每题 4 分)
C 1. 由 n 个字符组成长为 m 的字符串,则相同的字符不相邻的方案数为
4. an n3, 求常生成函数。
第 2 页(共 页)
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
得分 评阅人
三、计算题:(共 4 题,每题 10 分)
1. 若有 1 克、2 克、3 { a, 4 b, 5 c,7 d}的10 组合的个数。
3.求 1,2,3,4 的全排列中不出现相邻数相邻的排列数。
排列数为 2: 2413,3142
田 缸 巧 维 梦 薄 视 湿 恭 诌 存 袖 钝 堆 扭 埠 峻 偷 原 蓬 郡 瓶 暇 尖 求 嫌 屋 颤 毙 利 还 铺 黎 舌 鲜 珐 女 酣 肺 振 继 者 挂 娩 砧 菲 椭 努 陋 裕 塑 赢 蒜 棕 君 窃 薯 锦 隔 瑚 亭 弘 军 钱 颧 酋 粪 齐 滓 膨 菌 州 胁 藻 现 樱 舞 域 吁 剑 钡 垮 粥 褂 赃 九 操 直 柴 茎 氛 等 镶 冤 赶 循 品 水 绪 酶 啥 誓 匣 瞻 依 徘 霹 吩 娠 硫 粕 革 灶 经 开 窥 予 光 咱 鼎 胚 悍 撕 润 网 软 想 需 寅 惊 酗 祥 召 年 滔 散 逝 紧 洱 遁 竿 朗 秘 丢 胀 邀 害 蚁 缉 雾 抖 毁 登 蛮 囚 香 永 懒 涣 寥 曳 枢 乌 弟 班 师 忧 急 掉 羚 绳 御 对 拂 灰 耕 世 主 欺 岩 侯 增 告 型 案 钙 葬 像 惧 某 恋 鞠 裸 勒 疗 妊 宾 庙 昌 倘 豌 预 柬 篇 祁 摧 偿 律 列 焦 壁 舍 更 夏 癌 洛 伎 掇 噬 傲 央 榔 惺 捷 诺 惩 思 儡 搂 呜 疾 校 访 摊 宏 姻 亨 物 畸 堕 僧 剥 玻 杂 纷 嗜 鞭
华师网络2014年9月课程考试《组合数学》练习题库及答案

华中师范大学职业与继续教育学院 《组合数学》练习题库及答案一、选择题1. 把101本书分给10名学生,则下列说法正确的是()A.有一名学生分得11本书B.至少有一名学生分得11本书C.至多有一名学生分得11本书D.有一名学生分得至少11本书2. 8人排队上车,其中A ,B 两人之间恰好有4人,则不同的排列方法是()A.!63⨯B.!64⨯C. !66⨯D. !68⨯3. 10名嘉宾和4名领导站成一排参加剪彩,其中领导不能相邻,则站位方法总数为()A.()4,11!10P ⨯B. ()4,9!10P ⨯C. ()4,10!10P ⨯D. !3!14-4. 把10个人分成两组,每组5人,共有多少种方法()A.⎪⎪⎭⎫ ⎝⎛510B.⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛510510 C.⎪⎪⎭⎫ ⎝⎛49 D.⎪⎪⎭⎫ ⎝⎛⨯⎪⎪⎭⎫ ⎝⎛4949 5. 设x,y 均为正整数且20≤+y x ,则这样的有序数对()y x ,共有()个A.190B.200C.210D.2206. 仅由数字1,2,3组成的七位数中,相邻数字均不相同的七位数的个数是()A.128B.252C.343D.1927. 百位数字不是1且各位数字互异的三位数的个数为()A.576B.504C.720D.3368. 设n 为正整数,则∑=⎪⎪⎭⎫ ⎝⎛nk k n 02等于()A.n 2B. 12-nC. n n 2⋅D. 12-⋅n n9. 设n 为正整数,则()k k n k k n 310⎪⎪⎭⎫ ⎝⎛-∑=的值是()A.n 2B. n 2-C. ()n 2-D.010. 设n 为正整数,则当2≥n 时,∑=⎪⎪⎭⎫ ⎝⎛-nk k k 22=()A.⎪⎪⎭⎫ ⎝⎛3nB. ⎪⎪⎭⎫ ⎝⎛+21n C. ⎪⎪⎭⎫ ⎝⎛+31n D. 22+⎪⎪⎭⎫ ⎝⎛n 11. ()632132x x x +-中23231x x x 的系数是()A.1440B.-1440C.0D.112. 在1和610之间只由数字1,2或3构成的整数个数为() A.2136- B. 2336- C. 2137- D. 2337- 13. 在1和300之间的整数中能被3或5整除的整数共有()个A.100B.120C.140D.16014. 已知(){}o n n f ≥是Fibonacci 数列且()()348,217==f f ,则()=10f ()A.89B.110C.144D.28815. 递推关系3143---=n n n a a a 的特征方程是()A.0432=+-x xB. 0432=-+x xC. 04323=+-x xD. 04323=-+x x16. 已知()⋯⋯=⨯+=,2,1,0232n a n n ,则当2≥n 时,=n a ()A.2123--+n n a aB. 2123---n n a aC.2123--+-n n a aD. 2123----n n a a 17. 递推关系()⎩⎨⎧=≥+=-312201a n a a n n n 的解为()A.32+⨯=n n n aB. ()221+⨯+=n n n aC. ()122+⨯+=n n n aD. ()n n n a 23⨯+=18. 设()⋯⋯=⨯=,2,1,025n a n n ,则数列{}0≥n n a 的常生成函数是()A.x 215-B. ()2215x - C.()x 215- D. ()2215x -19. 把15个相同的足球分给4个人,使得每人至少分得3个足球,不同的分法共有()种A.45B.36C.28D.2020. 多重集{}b a S ⋅⋅=4,2的5-排列数为()A.5B.10C.15D.2021. 部分数为3且没有等于1的部分的15-分拆的个数为()A.10B.11C.12D.1322. 设n,k 都是正整数,以()n P k 表示部分数为k 的n-分拆的个数,则()116P 的值是()A.6B.7C.8D.923. 设A ,B ,C 是实数且对任意正整数n 都有⎪⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛⋅=1233n C n B n A n ,则B 的值是()A.9B.8C.7D.624. 不定方程1722321=++x x x 的正整数解的个数是()A.26B.28C.30D.3225. 已知数列{}0≥n n a 的指数生成函数是()()t t e e t E 521⋅-=,则该数列的通项公式是()A.n n n n a 567++=B. n n n n a 567+-=C. n n n n a 5627+⨯+=D. n n n n a 5627+⨯-=26、6名同学排成一排,其中甲,乙两人必须排在一起的不同排法有()种。
组合数学试题(2018A)参考答案

武汉大学计算机学院2017-2018学年度第二学期期末考试《组合数学》试卷(A 卷)参考答案1. (20分,每小题5分)(1)书架上有一套《资治通鉴》共20卷,从中选出4卷使得任意两本的卷号都不相邻的选法有多少种?解:就是不相邻组合,因此为C(n-r+1,r),此处n=20,r=4,代入得到C(20-4+1,4)=C(17,4)=2380(2)将英文字母表中的26个字母排序,要求任意两个元音字母不能相邻,则有多少种排序方法?解:先排21个辅音字母,共有21!, 再将5个元音插入到22个空隙中(首尾)有P(22,5),故所求为21!×P(22,5)(3)现在有3个女士和4个男士围一个圆桌就坐,则其中a )女士两两不相邻的入座方式数有Q(4,4)P(4,3)=3!4!=144 种; -----3分b )所有女士坐在一起的方式数有 Q(5,5)P(3,3)=4!3!=144种。
-----2分(4)在一局乒乓球比赛中,运动员甲以11:7战胜运动员乙,若在比赛过程中甲的得分一直不少于乙的得分,求有多少种可能的比分记录?解:根据题意,由于球赛规则,因此实际求的是求从点(0,0)到点(7,10)—(7,11)且从上方不穿过y=x 的非降路径数,参见书p32页结果,m=7,n=10,代入结果为 C(m+n,m)-C(m+n,m-1)=C(17,7)-C(17,6) ---未考虑球赛规则的,可以给3分2. (15分) 解下列递推关系⎩⎨⎧==≥=--2,52,36--10n 21a a n a a a n n n解:其对应的特征方程为:x 2-x-6=0,即为(x-3)(x+2)=0,其特征根为r 1=3,r 2=-2;由于3是其特征根,因此特解形如Cn3n ,代入方程得到Cn3n - C(n-1)3n-1 – 6C(n-2)3n-2 =3n解得C=53故方程的通解形如nn n n n B A 3533)2(a ++-=,代入初始条件⎪⎩⎪⎨⎧=⋅⋅++=+231533A 2-5B A B ---》⎪⎪⎩⎪⎪⎨⎧==25512574B A 可得n n n n n 35332551)2(2574a ++-=3. (10分) 一个1×n 的方格图形用红、蓝、绿和黄四种颜色涂色,如果有偶数个方格被涂成红色,还有偶数个方格被涂成绿色,求有多少种方案? 解:设涂色方案为a n ,则对应的母函数为:!n )424(414)12()()2()!2!11()!4!21()(0n 1n n 242222242n x xx xx e x e e e e e x xx x x G ∑∞=+-⨯++=++=+=++++++=因此其染色方案有⎩⎨⎧=>+=--01024a 11n n n n n ,故所求方案数为4n-1+2n-1种。
2022-2023学年湖北省武汉市华中师范大学第一附属中学高一年级上册学期期末数学试题【含答案】

华中师大一附中2022—2023学年度上学期高一期末检测数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1. 如图,是全集,,,是的子集,则阴影部分表示的集合是()U M N P UA. B. ()M N P ⋂⋂()M N P ⋃⋂C.D.()()U M N P ⋂⋂ ()()UM N P ⋃⋂ 【答案】C 【解析】【分析】根据文氏图的意义,阴影部分为集合的外部与集合集合交集内部的公共部分,求解即可.M N P 【详解】根据题意,阴影部分为集合的外部与集合集合交集内部的公共部分,M N P 即.()()UM N P ⋂⋂ 故选:C.2. 若,均为实数,则“”是“”的( )a b 22a b >a b >A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件 D. 既不充分也不必要条件【答案】B 【解析】【分析】通过不等式的性质一一验证其充分性与必要性即可.【详解】若,则,则或,故充分性不成立;22a b >a b >a b >a b<-若,则,故必要性成立;a b>22a b >故“”是“”的必要不充分条件.22a b >a b >故选:B.3. 下列坐标所表示的点不是函数图象的对称中心的是( )tan 34y x π⎛⎫=- ⎪⎝⎭A. B. C. D. 5,012π⎛⎫⎪⎝⎭3,012π⎛⎫ ⎪⎝⎭,06π⎛⎫ ⎪⎝⎭,012π⎛⎫ ⎪⎝⎭【答案】C 【解析】【分析】根据正切函数的性质即可求得对称中心.【详解】由已知,令()3,Z 42612k k x x k ππππ-=⇒=+∈当时,,ABD 均符合题意,0,1,2k =35,,121212x πππ=故选:C4. 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解.例如,地震时释放出的能量(单位:焦耳)与地震级数之间的关系式为.2022年9月18日14时44分在中E M lg 4.8 1.5E M =+国台湾花莲发生的6.9级地震所释放出来的能量是2020年12月30日8时35分在日本本州东海岸发生的5.1级地震的倍,则下列各数中最接近的值为( )m m A. 100 B. 310C. 500D. 1000【答案】C 【解析】【分析】根据地震释放出的能量与地震级数之间的关系式,将两次地震等级分别代E M lg 4.8 1.5E M =+入,利用对数运算法则可得两次能量的比值,近似计算可确定选项.E 【详解】设6.9级地震所释放出来的能量是,日本5.1级地震所释放出来的能量是,1E 2E 则,;1lg 4.8 1.5 6.9E =+⨯2lg 4.8 1.5 5.1E =+⨯可得,所以1122lg lg lg2.7E E E E -==()2.7 2.53121010,10E m E ==∈而,即.52.521010316==≈()316,1000m ∈故选:C5. 函数的部分图象形状大致是( )()21sin 1πxf x x ⎛⎫=-⋅ ⎪+⎝⎭A. B.C. D.【答案】A 【解析】【分析】首先根据函数解析式可判断函数为偶函数,再利用特殊值的符号通过排除法即可得出结果.()f x 【详解】根据题意可知,定义域为,()2π11sin sin 1ππ1x xxf x x x -⎛⎫=-⋅=⋅ ⎪++⎝⎭x ∈R 而,()()π11ππ1sin()sin sin ()π1π1π1x x x x x x f x x x x f x ------=⋅-=⋅-=⋅=+++所以函数为偶函数,图像关于轴对称,可排除CD ;()f x y 根据图象可利用可排除B.()2221sin 201πf ⎛⎫=-⋅ ⎪+⎝⎭>故选:A6. 若扇形的周长为定值,圆心角为,则当扇形的面积取得最大值时,该扇形的圆心角l ()02παα<<的值为( )αA. 1 B. 2C. 3D. 4【答案】B 【解析】【分析】根据扇形的弧长公式和面积公式,将面积写成关于的表达式,再利用二次函数性质即可求得S l 结果.【详解】设扇形的半径为,弧长为,r L 因此,22L r r r l α+=+=扇形的面积,2111(2)222S Lr l r r r lr ==-=-+由二次函数性质可知,当时,扇形面积取到最大值;4lr =此时,.2lr α=2α=故选:B 7. 设,,,则( )3log 2a =6log 4b =135log 40c =A. B. C. D. c b a <<a b c<<b a c<<a c b<<【答案】D 【解析】【分析】利用换底公式将表示成分式形式,再利用加糖不等式和对数函数单调性即可判断出大小.,,a b c 【详解】由题意可知,,3lg 2log 2lg 3a ==,6lg 42lg 2lg 2lg 2lg 6lg 3lg 2lg 3lg 2log 4b =+=++==利用加糖不等式可知;(0,0)m m k m n k n n k +<<+a b <又13135131lg 2lg 5lg 40lg 5lg83lg 2lg 5lg 2lg 53log 401lg135lg 5lg 273lg 3lg 5lg 3lg 5lg 3lg 53c ++++======++++又因为,1358,lg 5lg 2<<同理根据加糖不等式,,即.1313lg 2lg 2lg 5lg 2lg 2lg 3lg 3lg 2lg 3lg 5++++<<a c b <<故选:D8. 定义在上的偶函数满足,且当时,R ()f x ()()22f x f x -=+[]0,2x ∈,若关于的方程至少有8个实数解,则实数的取值范()21,012sin 1,122x x f x x x π⎧-≤≤⎪=⎨-<≤⎪⎩x ()ln x f x λ=λ围是()A. B. 11,ln 6ln 5⎡⎤-⎢⎥⎣⎦11,ln 6ln 5⎛⎤- ⎥⎝⎦C.D. 11,,ln 6ln 5⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭11,00,ln 6ln 5⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦【答案】A 【解析】【分析】根据函数的周期性画出函数的图像,利用对称性判断轴两个函数图像交点个数列出不等式,解y 不等式即可得到范围.【详解】由已知满足, 且函数为偶函数,()f x ()()22f x f x -=+()f x 所以,()()()()2222f x f x f x f x +=-=--=-⎡⎤⎣⎦令,()2(4)t x f t f t =-⇒+=所以函数是周期为的周期函数.()f x 4又因为与函数都是偶函数,由对称性可知()f x ln xλ由于关于的方程至少有8个实数解,x ()ln x f x λ=故当时,与至少有个交点.0x >()y f x =ln y x λ=4函数与图像如图所示.()y fx =ln y x λ=由图可知:当时,只需,解得0λ>ln 51λ≤10ln 5λ<≤当时,只需,解得0λ<ln 61λ≥-1ln 6λ-≤<当时,显然符合题意.0λ=综上所述:.11,ln 6ln 5λ⎡⎤∈-⎢⎥⎣⎦故选:A二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的.全选对得5分,部分选对得2分,有选错的得0分.9. 若,则下列说法中正确的是( )()*0,1,N n a b a n n =>>∈A. 当为奇数时,的次方根为 B. 当为奇数时,的次方根为n b n a n a n b C. 当为偶数时,的次方根为 D. 当为偶数时,的次方根为n a n b ±n b n a±【答案】AD 【解析】【分析】根据,讨论为奇数和偶数两种情况,求出的次方根即可判断得()*0,1,N n a b a n n =>>∈n b n 出结果.【详解】当为奇数时,可知的次方根只有一个,为,n b n a 当为偶数时,由于,所以的次方根有两个,为;n ()n na ab ±==b n a ±所以只有AD 正确.故选:AD10. 已知,则下列不等式正确的是()1m n >>A.B.22n nm m +<+11m n m n +>+C. D.3322+>m n m n 11+>+m n n m【答案】BD 【解析】【分析】通过对选项利用不等式性质进行拆解,在通过已知条件反证一一推导即可.【详解】对于选项A :,1m n >> ,22m n ∴>,22mn m mn n ∴+>+,()()22m n n m ∴+>+都大于零,m n ,22n nm m +∴>+故选项A 错误;对于选项B :,1m n >> ,且,1mn >∴1m n ->,()mn m n m n∴->-,22m n mn m n ∴->-,22m n n mn m ∴+>+,11m n m n +>+∴故选项B 正确;对于选项C :当,时,3m =2n =,33227835236m n m n +=+=<=故选项C 错误;对于选项D :,1m n >> ,110n m ∴>>,11m n n m +>+∴故选项D 正确.故选:BD11. 已知,,则下列结论正确的是( )()0,θπ∈7sin cos 5θθ-=A.B.C.D. ,2πθπ⎛⎫∈ ⎪⎝⎭4cos 5θ=-3tan 4θ=-2tan 121tan 25θθ=-+【答案】AD 【解析】【分析】由已知得,,确定的范围判断A ,求解与值判断B 与C ,把sin 0θ>cos 0θ<θcos θtan θ代入,化简判断D.tan θ2tan 1tan θθ+【详解】对于A :由,,两边平方得:,()0,πθ∈7sin cos 5θθ-=4912sin cos 25θθ-=则,得,,则,故A 正确;242sin cos 025θθ=-<sin 0θ>cos 0θ<π,π2θ⎛⎫∈ ⎪⎝⎭对于B 、C 、D :∵,则,π,π2θ⎛⎫∈ ⎪⎝⎭ππ3π,444θ⎛⎫-∈ ⎪⎝⎭∴,(πsin cos 4θθθ⎛⎫-=-∈ ⎪⎝⎭又,1sin cos 5θθ+====±当时,联立,解得,,1sin cos 5θθ+=1sin cos 57sin cos 5θθθθ⎧+=⎪⎪⎨⎪-=⎪⎩4sin 5θ=3cos 5θ=-∴,;sin 4tan cos 3θθθ==-24tan 123161tan 2519θθ-==-++当时,联立,解得,,1sin cos 5θθ+=-1sin cos 57sin cos 5θθθθ⎧+=-⎪⎪⎨⎪-=⎪⎩3sin 5θ=4cos 5θ=-∴,.sin 3tan cos 4θθθ==-23tan 12491tan 25116θθ-==-++故B 、C 错误,D 正确.故选:AD.12. 设函数是定义在上的减函数,并且同时满足下列两个条件:①对,都()f x ()0,∞+(),0,x y ∀∈+∞有;②;则下列结论正确的是()()()x f f x f y y⎛⎫=- ⎪⎝⎭()21f =-A.()10f =B. 不等式的解集为()()21f x f x +-<01x x ⎧⎪<<+⎨⎪⎩C.()42f =-D. 使关于的不等式有解的所有正数的集合为x ()()22f kx f x +-<k 14k k ⎧⎫>⎨⎬⎩⎭【答案】ACD 【解析】【分析】利用赋值法判断选项A ,C ,根据函数的单调性化简不等式,求其解,即可判断B ,根据函数的单调性化简不等式,根据不等式有解列不等式求的范围判断D .k 【详解】因为对,都有,(),0,x y ∀∈+∞()()x f f x f y y⎛⎫=- ⎪⎝⎭令,即,则,故选项A 正确;1x y ==(1)(1)(1)f f f =-(1)0f =令,则,又,所以,故选项C 正确;4,2x y ==(2)(4)(2)f f f =-()21f =-()42f =-令,则,所以,12,2x y ==()()1422f f f ⎛⎫=- ⎪⎝⎭112f ⎛⎫= ⎪⎝⎭所以,,可化为,()()21f x f x +-<(0,2)x ∈()()122f x f x f ⎛⎫+-< ⎪⎝⎭故,所以()()()1122f x f f f x ⎛⎫-<-- ⎪⎝⎭()122f x f x ⎛⎫< ⎪-⎝⎭因为函数在上单调递减,所以,且,()f x ()0+∞,122x x >-02x <<解得:,所以的取值范围为,故选项B错误;11x <<+x 11x x ⎧⎪-<<+⎨⎪⎩不等式可化为,()()22f kx f x +-<()()11222f kx f f f x ⎛⎫⎛⎫-<-- ⎪ ⎪⎝⎭⎝⎭故,所以且,,()1242f kx f x ⎛⎫< ⎪-⎝⎭1242kx x >-02x <<0k >得,此不等式有解,等价于,14(2)k x x >-min 14(2)k x x ⎡⎤>⎢⎥-⎣⎦在的范围内,由基本不等式,当且仅当,即时等号成02x <<22(2)12x x x x +-⎛⎫-≤= ⎪⎝⎭2x x =-1x =立,,,故即为所求范围,故选项D 正确,4(2)4x x -≤114(2)4x x ≥-14k >故选:ACD .【点睛】问题解决的关键在于通过赋值法求函数值,利用已知关系及函数单调性化简不等式.三、填空题:本大题共4小题,每小题5分,共20分.第16题第一小问2分,第二小问3分.13. 函数的单调递增区间是______.()()213log 65f x x x =-+-【答案】##(3,5)[3,5)【解析】【分析】由对数函数的真数大于零可得的定义域,根据复合函数单调性同增异减原则,即求()f x 的单调递减区间即可.265u x x =-+-【详解】由有意义可得,所以,故函数()()213log 65f x x x =-+-2650x x -+->15x <<的定义域为,()()213log 65f x x x =-+-()1,5令, ,265u x x =-+-15x <<又根据二次函数的图象与性质可知,函数在区间上单调递增,265u x x =-+-(1,3]在区间上单调递减,[3,5)又由函数为单调递减函数,13log y u=根据复合函数同增异减可得,函数的单调递增区间为.()f x [3,5)故答案为:.[3,5)14.______.())21lg122log 392lg 5lg 2·lg 5014-⎛⎫++-+-=⎪⎝⎭【答案】133【解析】【分析】通过指对运算一步一步运算即可得出答案.【详解】())21lg122log 392lg 5lg 2·lg 5014-⎛⎫++-+- ⎪⎝⎭()())102243lg 5lg 2·lg 5lg1019⎛⎫=+++-+⎪⎝⎭()()223lg 5lg 2·lg 5113=+++-+()210lg 5lg 2·lg 5lg 23=+++()10lg 5·lg 5lg 2lg 23=+++()10lg 5·lg10lg 23=++10lg 5lg 23=++1013=+133=故答案为:.13315. 在中,为它的三个内角,且满足,,则ABC ,,A B C 3sin 4cos 6A B +=3cos 4sin 1A B +=______.C =【答案】##π630【解析】【分析】将题目中的两个式子平方后相加,可得,再利用诱导公式和三角函数单调性即可1sin()2A B +=求得结果.【详解】由题意可知,将两边同时平方得3sin 4cos 63cos 4sin 1A B A B +=⎧⎨+=⎩将两式相加得22229sin 16cos 24sin cos 369cos 16sin 24cos sin 1A B A B A B A B ⎧++=⎨++=⎩,即,所以24(sin cos cos sin )12A B A B +=1sin()2A B +=1sin 2C =可得或;π6C =5π6C =又因为,得,13cos 4sin 0A B -=>11cos 32A <<由余弦函数单调性可得,所以不合题意;π3A >5π6C =因此.π6C =故答案为:π616. 已知函数的图象是一个中心对称图形,它的对称中心为______;函数()1117122f x x x x =+++--的图象与函数图象的交点分别为,,,…,(为正整()f x ()132121x x g x -⋅+=+()11,x y ()22,x y (),m m x y m 数),则______.()()()()112233m m x y x y x y x y ++++++++= 【答案】 ①.②. 712⎛⎫ ⎪⎝⎭,92m 【解析】【分析】证明函数为奇函数,由此确定函数的对称中心,证明与的对称中()712f x +-()f x ()g x ()f x 心重合,结合对称性及加法的运算律求值.【详解】因为,所以,()1117122f x x x x =+++--()7111212f x x x x -=++--设,则函数的定义域为,()()71111211h x f x x x x =+-=+++-()h x ()()()(),11,00,11,-∞-⋃-⋃⋃+∞且,()()1111111111h x h x x x x x x x ⎛⎫-=++=-++=- ⎪-+----+⎝⎭所以函数为奇函数,故函数的图象关于原点对称,即函数的图象关于原点对称,()h x ()h x ()712f x +-所以函数的图象关于对称,()f x 712⎛⎫ ⎪⎝⎭,因为,所以,()132121xx g x -⋅+=+()()17321752512212212x x xxg x +⋅+⋅-+-=-=++所以,()()()()()()521512771122221212xx x x g x g x ----⎡⎤-+-===-+-⎢⎥++⎣⎦所以函数为奇函数,故函数的图象关于对称,()712g x +-()g x 712⎛⎫ ⎪⎝⎭,又函数的图象与函数图象的交点分别为,,…,,()f x ()132121x x g x -⋅+=+()11,x y ()22,x y (),m m x y ,点不在函数图象上,所以为偶数,设,()712g =71,2⎛⎫ ⎪⎝⎭()f x m 2m k =不妨设,则,122k x x x <<⋅⋅⋅<1222112k k k k x x x x x x -++=+=⋅⋅⋅=+=,1222117k k k k y y y y y y -++=+=⋅⋅⋅=+=所以,()()()1212121222112k k k k k k k k x x x x x x x x x x x x k m+--+++⋅⋅⋅+++⋅⋅⋅++=++++⋅⋅⋅++==同理,121212772k k k k m y y y y y y k +-++⋅⋅⋅+++⋅⋅⋅++==.()()()()()()11223312212292m m k k m x y x y x y x y x x x y y y ++++++++=++⋅⋅⋅++++⋅⋅⋅+=【点睛】本题解决的关键在于通过证明,为奇函数,确定其对称性,结合对称()712f x +-()712g x +-性求解问题.四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17. 设全集,集合,非空集合,其中.U =R 12324x A x ⎧⎫=≤<⎨⎬⎩⎭{}232B x a x a =-≤≤+a ∈R (1)若,求;1a =()U A B ∩ (2)从下列三个条件中任选一个作为已知条件,求的取值范围.①;②a ()()UUUA B B ⋃= ;③的一个充分条件是.注:如果选择多个条件分别作答,按第一个条件的解()U B A =∅x A ∈x B ∈答计分.【答案】(1){}21x x -≤<(2)113a -≤<【解析】【分析】(1)将代入,求出集合,再求出集合,进一步求解即可;1a =B A (2)三个条件都说明,所以利用子集关系及非空集合列不等式计算即可.B A ⊆B 【小问1详解】当时,,或,又,1a ={}15B x x =≤≤{1U B x x =< }5x >{}25A x x =-≤<则.(){}21U A B x x ⋂=-≤< 【小问2详解】选择条件①:因为,所以,()()UUUA B B ⋃= ()()UUA B Í 即,又已知非空集合,BA ⊆{}232B x a x a =-≤≤+所以,23222325a aa a -≤+⎧⎪-≥-⎨⎪+<⎩所以.113a -≤<选择条件②:因为,则,()U B A =∅B A ⊆又已知非空集合,{}232B x a x a =-≤≤+所以,23222325a aa a -≤+⎧⎪-≥-⎨⎪+<⎩所以.113a -≤<选择条件③:的一个充分条件是,则,x A ∈x B ∈B A ⊆又已知非空集合,{}232B x a x a =-≤≤+所以,23222325a a a a -≤+⎧⎪-≥-⎨⎪+<⎩所以.113a -≤<18. 已知函数.()2f x mx nx=-(1)若的解集为,求不等式的解集;()f x t≥{}21x x -≤≤20nxmx t ++≤(2)若,且,求的最小值.0m >0n >()10f >14m m n n ++-【答案】(1) {|12}x x -≤≤(2)6【解析】【分析】(1)根据题意可得:和方程的两根,利用韦达定理得出2-120(0)mx nx t m --=<,,将要解的不等式化简整理即可求解;n m =-2t m =(2)由可得,然后利用基本不等式即可求解.()10f >0m n ->【小问1详解】因为的解集为,()f x t≥{}21x x -≤≤所以和方程的两根,由韦达定理可知:,2-120(0)mx nx t m --=<12nm t m ⎧=-⎪⎪⎨⎪-=-⎪⎩则有,,所以不等式可化为,n m =-2t m =20nx mx t ++≤220mx mx m -++≤因为,所以不等式可化为,解得:,0m <220x x --≤12x -≤≤所以不等式的解集为.20nx mx t ++≤{|12}x x -≤≤【小问2详解】因为,也即,又因为,,()10f >0m n ->0m >0n >所以,1414()6m m n n m n n m n n ++=-+++≥=--(当且仅当和同时成立时取等,也即时取等)1m n m n -=-4n n =3,2m n ==所以的最小值为.14m m n n ++-619. 已知函数(其中,)的最小正周期为,当时,取()()sin 2f x x ωϕ=+0ω>ϕπ<23π4xπ=()f x 到最大值.(1)求函数的单调递增区间;()f x (2)当时,若函数在区间上的值域为,求实数,的值.0a >()()g x af x b =+,363ππ⎡⎤⎢⎥⎣⎦[]1,3a b 【答案】(1), 22,12343k k ππππ⎡⎤-++⎢⎥⎣⎦k ∈Z (2),43a =53b =【解析】【分析】(1)根据已知条件,结合三角函数的周期公式,求出,再结合当时,取到最大值,ω4x π=()f x 推出的解析式,再结合三角函数的单调性即可得出答案;()f x (2)结合(1)的结论,的取值范围,得出的范围,即可得出的值域,根据已知条件列出方x ()f x ()g x 程组求解即可得出答案.【小问1详解】函数(其中,)的最小正周期为,()()sin 2f x x ωϕ=+0ω>ϕπ<23π,则,3223πωπ∴==()()sin 3f x x ϕ=+又当时,取到最大值,4x π=()f x ,,3242k ππϕπ∴⨯+=+k ∈Z解得,,24k πϕπ=-k ∈Z ,,则,ϕπ< 4πϕ∴=-()sin 34f x x π⎛⎫=- ⎪⎝⎭令,,232242k x k πππππ-+≤-≤+k ∈Z 解得,,2212343k x k ππππ-+≤≤+k ∈Z 故函数的单调递增区间为,;()f x 22,12343k k ππππ⎡⎤-++⎢⎥⎣⎦k ∈Z 【小问2详解】,,,363x ππ⎡⎤∈⎢⎥⎣⎦ 33,464x πππ⎡⎤∴-∈-⎢⎥⎣⎦,1sin 3,142x π⎛⎫⎡⎤∴-∈- ⎪⎢⎥⎝⎭⎣⎦,()12a b g x a b∴-+≤≤+函数在区间上的值域为, ()()g x af x b =+,363ππ⎡⎤⎢⎥⎣⎦[]1,3,解得,.1123a b a b ⎧-+=⎪∴⎨⎪+=⎩43a =53b =20. 两社区和相距2km ,现计划在两社区外以为直径的半圆弧(不含,两点)上选择一A B ABAB A B 点建造口袋公园(如图所示),其对社区的噪音影响度与所选地点到社区的距离有关.口袋公园对社区C 的噪音影响度是所选地点到社区的距离的平方的反比例函数,比例系数为0.01;对社区的噪音影响A A B 度是所选地点到社区的距离的平方的反比例函数,比例系数为,对社区和社区的总噪音影响度为B K A B 对社区和社区的噪音影响度之和.记点到社区的距离为,建在处的口袋公园对社区和社A B C A km x C A 区的总噪音影响度为.统计调查表明:当口袋公园建在半圆弧的中点时,对社区和社区的总噪B yAB A B 音影响度为0.05.(1)将表示成的函数;y x (2)判断半圆弧上是否存在一点,使得建在此处的口袋公园对社区和社区的总噪音影响度最小?AB A B 若存在,求出该点到社区的距离;若不存在,说明理由.A 【答案】(1)22119(02)1004y x x x ⎛⎫=+ ⎪-⎝⎭<<(2)存在,当该点到社区的距离时,袋公园对社区和社区的总噪音影响度最小.A 1x =A B 【解析】【分析】(1)利用勾股定理即可得出,再根据反比例函数定义和已知条件可解得,224BC x =-0.09K =即可写出关于的函数;(2)利用整体代换和基本不等式确定的最小值,验证等号成立时的取值是y x y x 否符合题意,即可判断得出结论并确定位置.【小问1详解】由为直径可得,所以AB ACBC ⊥224BC x =-由题意可知,220.01(02)4Ky x x x =+-<<又当口袋公园建在半圆弧的中点时,对社区和社区的总噪音影响度为0.05,AB A B 即时,,代入得,x =0.05y =0.09K =所以,220.010.09(02)4y x x x =+-<<即关于的函数为y x 22119(02)1004y x x x ⎛⎫=+ ⎪-⎝⎭<<【小问2详解】口袋公园对社区和社区的总噪音影响度最小,即的取值最小,A B y 由(1)知2222222211984211004100(4)25(4)x x y x x x x x x ++⎛⎫=+== ⎪---⎝⎭22242222211222122192542525119551222442x x x x x x x x ++=⨯=⨯=⨯-+⎛⎫⎛⎫⎛⎫-++--+++- ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭+ ⎪⎝⎭令,则可得2119,222x t ⎛⎫+=∈ ⎪⎝⎭2192554y t t=⨯-+-,当且仅当时,等号成立;99555244t t t t ⎛⎫-+-=-++≤-+= ⎪⎝⎭32t =且,所以,9504t t -+->212119252522554y t t =⨯≥⨯=-+-即,此时,即,解得.min 125y =32t =21322x +=1x =因此,半圆弧上存在一点,且该点到社区的距离满足时,建在此处的口袋公园对社区和社AB A 1x =A 区的总噪音影响度最小.B 21. 已知函数(且)为奇函数.()412x f x a a =-+0a >1a ≠(1)求实数的值及函数的值域;a ()f x (2)若函数在区间上有两个不同的零点,求实数的取值范围.()()()12x g x mmf x =+-(],2-∞m 【答案】(1),的值域为2a =()f x ()1,1-(2)2017⎤-⎥⎦【解析】【分析】(1)根据函数解析式可判断定义域,再根据奇函数性质利用可计算的值,将代入根()00f =a a 据指数型函数值域得求法即可求得函数的值域;(2)将函数在区间上有两个不同的()f x ()g x (],2-∞零点转化成方程在上有两个不相等的实数根,利用换元法根据二次函数根()20212x x m m +++=(],2-∞的分布情况即可求得实数的取值范围.m 【小问1详解】由题意可知,函数的定义域为,()f x x ∈R 由奇函数性质可知,,得;()044011022f a a a =-=-=++2a =所以,;()411222221x x f x =-=-⨯++又因为,所以()211,x+∈+∞()20,221x ∈+因此()()211,121x f x =-∈-+即函数的值域为.()f x ()1,1-【小问2详解】由得,,()()()12xg x m mf x =+-()()212121x x g x m m ⎛⎫=+- ⎪⎝+⎭-又函数在区间上有两个不同的零点,()g x (],2-∞即方程在区间上有两个不同的实数根;()0112122x x m m ⎛⎫+-= ⎪⎝⎭-+(],2-∞整理得,()20212x x m m +++=令,由得,2xt =(],2x ∈-∞(]0,4∈t 即在上有两个不相等的实数根;()210m t t m +++=(]0,4∈t 所以,且或10m +≠14(1)0m m ∆=-+>1m -<1m -<时,需满足,解得1m -<()()22100014401042(1)m m m m m ⎧⎪+⨯++<⎪⎪+⨯++≤⎨⎪⎪<-<+⎪⎩0201798m m m ⎧⎪<⎪⎪≤-⎨⎪⎪<-⎪⎩2017m ≤-当时,需满足,该不等式组无解;1m -<()()22100014401042(1)m m m m m ⎧⎪+⨯++>⎪⎪+⨯++≥⎨⎪⎪<-<+⎪⎩综上可知,实数,m 2017m≤-即2017m ⎤∈-⎥⎦22. 欧拉对函数的发展做出了巨大贡献,除特殊符号、概念名称的界定外,欧拉还基于初等函数研究了抽象函数的性质.例如,欧拉引入了“倒函数”的定义:对于函数,如果对于其定义域中任意给定()y f x =D 的实数,都有,并且,就称函数为“倒函数”.x x D -∈()()1f x f x ⋅-=()y f x =(1)已知,,判断和是不是倒函数,并说明理由;()10xf x =()22xg x x -=+()y f x =()y g x =(2)若是定义在上的倒函数,当时,,方程是否有整数解?()f x R 0x ≤()413x f x x -=+()2023f x =并说明理由;(3)若是定义在上的倒函数,其函数值恒大于0,且在上单调递增.记,()f x R R ()()()21f x F x f x ⎡⎤-⎣⎦=证明:是的充要条件.120x x +>()()120F x F x +>【答案】(1)函数为倒函数,函数不是倒函数,理由见解析;()f x ()g x (2)方程没有整数解,理由见解析;()2023f x =(3)证明见解析.【解析】【分析】(1)利用“倒函数”的定义判断函数、,可得出结论;()f x ()g x (2)分析可知当时,,则方程若存在整数解,则,构造函数0x <()()0,1f x ∈()2023f x =0x 00x >,利用零点存在定理可得出结论;()()2023h x f x =-(3)推导出函数的奇偶性、单调性,再利用函数的单调性、奇偶性结合充分条件、必要条件()F x ()F x 的定义证明可得结论.【小问1详解】函数的定义域为,对任意的,,()f x R x ∈R ()()10101x x f x f x -⋅-=⋅=所以,函数为倒函数,()f x 函数的定义域为,该函数的定义域不关于原点对称,()22xg x x -=+{}2x x ≠-故函数不是倒函数;()g x 【小问2详解】当时,则,由倒函数的定义可得,0x >0x -<()()413x f x x f x ==+-由满足倒函数的定义,()01f =当时,函数、均为增函数,故函数在上为增函数,0x >3x y =4y x =()f x ()0,∞+当时,,,,当时,,0x >31x >40x >()1f x >0x <()()()10,1f x f x =∈-若函数有整数解,则,()2023f x =0x ()00,x ∈+∞设,则函数在上单调递增,()()2023h x f x =-()h x ()0,∞+因为,,()5453520230h =+-<()6463620230h =+->故方程无整数解,()2023f x =【小问3详解】因为函数是上的倒函数,其函数值恒大于,且在上是严格增函数,()y f x =R 0R 所以,,()()()()()()()211f x F x f x f x f x f x f x ⎡⎤-⎣⎦==-=--任取、且,则,所以,,,m n ∈R m n >m <n --()()f m f n >()()f n f m ->-所以,()()()()()()F m F n f m f m f n f n -=-----⎡⎤⎡⎤⎣⎦⎣⎦,()()()()0f m f n f n f m =-+--->⎡⎤⎡⎤⎣⎦⎣⎦所以,函数为上的增函数,()F x R 因为,故函数为上的奇函数.()()()()F x f x f x F x -=--=-()F x R当时,即,则,所以,,120x x +>12x x >-()()()122F x F x F x >-=-()()120F x F x +>即“”“”;120x x +>⇒()()120F x F x +>若,则,所以,,即.()()120F x F x +>()()()122F x F x F x >-=-12x x >-120x x +>所以,“”“”.120x x +>⇐()()120F x F x +>因此,是的充要条件.120x x +>()()120F x F x +>【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.。
2022-2023学年湖北省武汉市华中师范大学第一附属中学高二年级上册学期期末数学试题【含答案】

2022-2023学年湖北省武汉市华中师范大学第一附属中学高二上学期期末数学试题一、单选题1.抛物线22y x =的焦点坐标为 A .(1,0) B .1(,0)2C .1(0,)4D .1(0,)8【答案】D【分析】根据抛物线标准方程,可求得p ,进而求得焦点坐标.【详解】将抛物线方程化为标准方程为212x y =,可知14p =所以焦点坐标为10,8⎛⎫⎪⎝⎭所以选D【点睛】本题考查了抛物线的基本性质,属于基础题.2.直线()12:10,:210l ax y l a x ay +-=--+=,则“2a =-”是“12//l l ”的( )条件 A .必要不充分 B .充分不必要 C .充要 D .既不充分也不必要【答案】C【分析】根据直线平行求得a ,结合充分、必要条件的知识求得正确答案.【详解】若12//l l ,则()()212,20a a a a a ⨯-=⨯-+-=,解得1a =或2a =-,当1a =时,1l 和2l 的方程都是10x y +-=,两直线重合,不符合题意. 经验证可知,2a =-符合. 所以“2a =-”是“12//l l ”的充要条件. 故选:C3.设正项等比数列{}n a 的前n 项和为n S ,若32127S a a =+,则公比q 为( ) A .2或3- B .3C .2D .3-【答案】B【分析】根据已知条件列方程求得q .【详解】依题意32127S a a =+, 即1232132127,6a a a a a a a a ++=+=+, 21116a q a q a =+,依题意10a >,所以260q q --=,由于0q >,故解得3q =. 故选:B4.已知等差数列{}n a 的前n 项和为n S ,若1472,22a a a =+=,则19S =( ) A .380 B .200 C .190 D .100【答案】A【分析】求得等差数列{}n a 的公差,进而求得19S 【详解】设等差数列{}n a 的公差为d , 则1294922,2a d d d +=+==, 所以19191819223802S ⨯=⨯+⨯=. 故选:A5.若双曲线()222210,0y x a b a b -=>>的渐近线方程为y x =,且过点(),则双曲线的标准方程为( ) A .22168y x -=B .22186y x -=C .22134y x -=D .22143y x -=【答案】C【分析】由双曲线渐近线方程可得a =,将()代入双曲线方程可求得22,b a ,由此可得结果.【详解】由双曲线方程可得其渐近线方程为:a y x b =±,a b ∴,即a =,则双曲线方程可化为:2222413y x b b-=,由双曲线过点(),2236813b b ∴-=,解得:24b =,23a ∴=,∴双曲线方程为:22134y x -=.故选:C.6.有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点,已知最底层正方体的棱长为4,若该塔形几何体是由7个正方体构成,则该塔形的表面积(含最底层的正方体的底面面积)为( )A .127B .1272C .143D .159【答案】D【分析】分析各层正方体的边长,利用等比数列的前n 项和公式即可求解. 【详解】不妨设由下到上各层正方形的边长为n a ,由题意知,{}n a 是首项为42124(n n a -=⨯,各层正方形的面积为2151116()=()22n n n a --=⨯,所以该塔形几何体的表面积为2322464(222)159S -=⨯++++=,故选:D .7.已知椭圆22:182x y C +=和点()2,1P -,直线l 与椭圆C 交于,A B 两点,若四边形OAPB 为平行四边形,则直线l 的方程为( ) A .5202x y --= B .3202x y +-= C .220x y --= D .220x y +-=【答案】C【分析】先求得直线l 所过点,然后利用点差法求得直线l 的斜率,进而求得正确答案.【详解】由于()2212182-+=,所以P 在椭圆C 上, 设OP 的中点为D ,则11,2D ⎛⎫- ⎪⎝⎭,则直线AB 过点D ,且D 是AB 的中点,设()()1122,,,A x y B x y ,则:222211221,18282x y x y +=+=, 两式相减并化简得121212122184y y y y x x x x +-⋅=-=-+-, 所以12121212111,242y y y y x x x x ---⋅=-=--,即直线AB 的斜率为12, 所以直线AB 也即直线l 的方程为()111,22022y x x y +=---=.故选:C8.已知双曲线()2222:10,0x y C a b a b-=>>,直线l 过坐标原点并与双曲线交于,P Q 两点(P 在第一象限),过点P 作l 的垂线与双曲线交于另一个点A ,直线QA 交x 轴于点B ,若点B 的横坐标为点Q 横坐标的两倍,则双曲线的离心率为( ) A .1 BCD【答案】C【分析】设():0PQ y kx k =≠,(),P t kt ,根据垂直关系及,B Q 坐标可得直线,AP AQ 的方程,联立可求得A 点坐标,代入双曲线方程中,结合P 在双曲线上,可化简整理得到22b a =,由离心率e =可求得结果.【详解】由题意知:直线PQ 斜率存在且不为零,则可设直线():0PQ y kx k =≠, 设(),P t kt ,则(),Q t kt --,()2,0B t -, AP PQ ⊥,1AP k k∴=-,则直线()1:AP y kt x t k -=--,又2AQ BQ kt k k k t t ===--+,∴直线1:2AQ x y t k=--, 由()112y kt x t k x y t k ⎧-=--⎪⎪⎨⎪=--⎪⎩得:()22223131k t t x k kt k y k ⎧+=-⎪-⎪⎨+⎪=⎪-⎩,即()()2222313,11t k kt k A k k ⎛⎫++ ⎪- ⎪--⎝⎭, A 在双曲线C 上,()()()()2222222222222313111t k k t k a k b k ++∴-=--,又P 在双曲线C 上,即222221t k t a b -=,222222a b t b a k ∴=-,()()()()()()22222222222222222313111b k a k k kb a kkb a k++∴-=----,即()()()()2222222222222231311b k a k k k b a k k +-+=---,()()()()2222222222231131b k k a k k k ⎡⎤⎡⎤∴+--=+--⎢⎥⎢⎥⎣⎦⎣⎦, ()()2422228888b k k a k k +=+,又0k ≠,22b a ∴=,∴双曲线离心率c e a ===故选:C.【点睛】关键点点睛:本题考查双曲线离心率的求解问题;解题关键是能够通过两直线方程联立的方式,求得A 点坐标,从而根据A 点在双曲线上构造方程,化简整理得到,a b 之间的关系.二、多选题9.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,且59S S =,则下列命题正确的有( ) A .7S 是数列{}n S 中的最大项 B .7a 是数列{}n a 中的最大项 C .140S = D .满足0n S >的n 的最大值为13【答案】ACD【分析】由59S S =得出1132a d =-,代入n a 与n S ,对选项依次判断即可. 【详解】∵59S S =,∴1154985922a d a d ⨯⨯+=+,∴11302a d =->,∴0d <, ∴()()113151122n a a n d d n d n d ⎛⎫=+-=-+-=- ⎪⎝⎭, ()()()211113142222n n n n n dS na d dn d n n --=+=-+=-,对于A ,()()221474922n d d S n n n ⎡⎤=-=--⎣⎦,∵0d <,∴当7n =时,n S 取最大值,∴7S 是数列{}n S 中的最大项,故选项A 正确;对于B ,∵10a >,0d <,所以等差数列{}n a 是递减数列,数列{}n a 中的最大项为1a ,故选项B 错误; 对于C ,()21414141402dS =-⨯=,故选项C 正确; 对于D ,∵0d <,∴()()21414022n d dS n n n n =-=->,解得014n <<, ∵*n ∈N ,∴满足0n S >的n 的最大值为13,故选项D 正确. 故选:ACD.10.设圆22:(1)(1)3C x y -+-=,直线:3430,l x y P ++=为l 上的动点,过点P 作圆C 的两条切线PA PB 、,切点为,A B M N 、、为圆上任意两点,则下列说法中正确的有( ) A .PA 的取值范围为[)1,+∞B .四边形PACBC .满足60APB ∠=的点P 有两个D .CAB △【答案】AC【分析】根据切线长公式即可求解A,B,C ,根据三角形的面积公式可求解D.【详解】圆心(1,1)C 到直线:3430l x y ++=的距离2d ==,所以2PC d ≥=,因为圆的半径为r =根据切线长公式可得1PA =,当PC l ⊥时取得等号,所以PA 的取值范围为[)1,+∞,A 正确; 因为PA AC ⊥,所以四边形PACB 的面积等于2PAC S PA AC PA ⨯=⨯△ 四边形PACBB 错误; 因为60APB ∠=,所以30APC ∠=,在直角三角形APC 中,1sin 302AC CP ==,所以CP =设33(,)4a P a +-,因为CP = 整理得225101270a a +-=,则有100127000∆=+>,所以满足条件的点P 有两个,C 正确; 因为13sin sin 22CAB S CA CB ACB ACB =∠=∠△ 所以当sin 1ACB ∠=,即90ACB ∠=,面积有最大值为32,此时四边形PACB 为正方形,则2PC >,满足要求, 故D 错误, 故选:AC.11.数列{}n a 满足21n n n a Aa Ba ++=+(*N ,,n A B ∈为非零常数),则下列说法正确的有( ) A .若1,1A B ==-,则数列{}n a 是周期为6的数列B .对任意的非零常数,A B ,数列{}n a 不可能为等差数列C .若3,2A B ==-,则数列{}1n n a a +-是等比数列D .若正数,A B 满足121,0,A B a a B +===,则数列{}2n a 为递增数列 【答案】AD【分析】对于A ,由题意可得3n n a a +=-,进而可得6n n a a +=,即可判断; 对于B ,举反例2,1A B ==-,此时{}n a 为等差数列,即可判断;对于C ,由题意可得2112()n n n n a a a a +++-=-,*N n ∈,只有当10n n a a +-≠时,数列{}1n n a a +-才是以2为公比的等比数列,即可判断;对于D ,由题意可得211()n n n n a a B a a ++++=+,求得22211n n B S B B -=⋅-,进而可得222(1)1n n B B a B -=-,只需判断2(1)n a +-20n a >是否成立即可判断.【详解】解:对于A ,因为1,1A B ==-,所以21n n n a a a ++=-,*N n ∈, 所以32111n n n n n n n a a a a a a a +++++=-=--=-,*N n ∈, 所以6(3)33n n n n a a a a ++++==-=,*N n ∈ 所以数列{}n a 是周期为6的数列,故正确;对于B ,当2,1A B ==-时,则有212n n n a a a ++=-,*N n ∈, 即有212n nn a a a +++=,*N n ∈, 由等差中项的性质可知{}n a 为等差数列,故错误; 对于C ,当3,2A B ==-时,2132n n n a a a ++=-,*N n ∈, 即有2112()n n n n a a a a +++-=-,*N n ∈,当10n n a a +-≠时,数列{}1n n a a +-是以2为公比的等比数列,故错误; 对于D ,因为正数,A B 满足121,0,A B a a B +===, 所以101A B B =->⇔>所以211(1)n n n n n a Aa Ba B a Ba +++=+=-+,*N n ∈, 所以211()n n n n a a B a a ++++=+,*N n ∈,设数列前n 项和为n S , 则有242(1)2123421212()()()()[1]n n n n S a a a a a a a a B B B --=++++++=+++++=2211nB B B-⋅-,*N n ∈ 所以2122122111n nn B B B S B B B----=⋅=--,*N n ∈, 所以2212222122(1)11n n n n n n B B B B a S S B B+---=-==--,*N n ∈, 所以2(1)2(1)2(1)1n n B B a B++-=-,*N n ∈, 所以()21n a +-2n a =()()21211n B B B +---22(1)1n B B B --=2222(1)(1)(1)01n n B B B B B B-⋅-=->-,*N n ∈, 所以数列{}2n a 为递增数列,故正确. 故选:AD.12.已知抛物线2:2E y x =的焦点为F ,直线,AB CD 过焦点F 分别交抛物线E 于点()()()()11223344,,,,,,,A x y B x y C x y D x y ,其中,A C 位于x 轴上方,且直线BC 经过点1,04⎛⎫⎪⎝⎭,记,BC AD 的斜率分别为,BC AD k k ,则下列正确的有( )A .121y y =-B .242y y = C .142y y =- D .2BCADk k = 【答案】ACD【分析】利用抛物线的性质,可得1(,0)2F ,设直线AB 的方程为12x ty =+,联立方程可得121y y =-,可判断A ;同理可得341y y =-,再利用直线BC 经过点1(,0)4,可得2312y y =-,进而得出142y y =-,可判断C ,B ;利用两点确定斜率可得2BCAD k k =,可判断D . 【详解】由抛物线2:2E y x =可得:1(,0)2F ,设直线AB 的方程为12x ty =+,由2122x ty y x⎧=+⎪⎨⎪=⎩,整理可得:2210y ty --=, 所以121y y =-,故选项A 正确;同理可得:341y y =-, 由直线BC 经过点1(,0)4,设1(,0)4N ,则//NC NB ,331(,)4NC x y =-,221(,)4NB x y =-,所以233211()()44x y x y -=-,则22323211()()2424y y y y -=-,整理可得:2323231()()024y y y y y y -+-=,也即23231()()024y y y y -+=,因为23y y ≠,所以2312y y =-, 又121y y =-,341y y =-,所以142y y =-,故选项C 正确; 则21241412y y y y y y ==,故选项B 错误; 因为32322232323222BC y y y y k y y x x y y --===--+,同理142AD k y y =+, 则14142141224243232432342424112222221BC AD k y y y y y y y y y y y y y k y y y y y y y y y y y y y ++++-+==⨯⨯=⨯⨯=⨯=⨯=++++-+.故选项正确, 故选:ACD .三、填空题13.已知圆221:210C x y kx y +-++=与圆222:210C x y ky ++-=的公共弦所在直线恒过点P ,则点P的坐标为__________. 【答案】(2,1)-【分析】两圆的方程相减得出两圆的公共弦所在直线方程,然后根据直线方程求出定点即可.【详解】由圆221:210C x y kx y +-++=与圆222:210C x y ky ++-=,两式相减得公共弦所在直线方程为:2220kx ky y +--=,即(2)(22)0k x y y +-+=,令20220x y y +=⎧⎨+=⎩,解得:21x y =⎧⎨=-⎩,所以圆221:210C x y kx y +-++=与圆222:210C x y ky ++-=的公共弦所在直线恒过点(2,1)P -.故答案为:()2,1-.14.已知抛物线2:4E y x =,直线():21l y x =-与E 相交于,A B 两点,若E 的准线上一点M 满足90AMB ∠=,则M 的坐标为__________. 【答案】(1,1)-【分析】令(1,)M y -,由0MA MB ⋅=及数量积的坐标公式得21()0A B A B A B A B x x x x y y y y y y ++++-++=,联立抛物线与直线方程,应用韦达定理求,A B 横纵坐标的和积代入上式求M 的纵坐标即可.【详解】令(1,)M y -,则(1,),(1,)A A B B MA x y y MB x y y =+-=+-, 由90AMB ∠=,则(1)(1)()()0A B A B MA MB x x y y y y ⋅=+++--=,所以21()0A B A B A B A B x x x x y y y y y y ++++-++=联立242(1)y x y x ⎧=⎨=-⎩,消去y 整理得2310x x -+=,则3,1A B A B x x x x +==,所以2(2)2A B A B y y x x +=+-=,4(1)4A B A A B B x x x y x y =--+=-,综上,2210y y -+=,则1y =,故(1,1)M -. 故答案为:(1,1)-15.已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ,离心率为e ,过原点的直线与C 的左右两支分别交于,M N 两点,若4,60MF NF MFN ︒=∠=,则224a e +的最小值为__________.【答案】1331【分析】先由抛物线的对称性与定义得到MF ,1MF NF =关于,m a 的表达式,从而利用题设条件与余弦定理得到,a c 关于m 的表达式,再利用基本不等式即可得解. 【详解】依题意,记双曲线C 的左焦点为1F ,连结1NF ,如图, 由抛物线的对称性易得=OM ON ,又12OF OF =, 所以四边形1MF NF 是平行四边形,则1NF MF =, 因为双曲线2222:1(0,0)x y C a b a b -=>>,所以由双曲线的定义可得12MF MF a -=,则2MF NF a -=, 记()0MF m m =>,则12MF NF m a ==-, 又4MF NF =,所以()24m m a -=,即42a m m =-,42m a m -=,则2221648a m m=+-, 因为60MFN ∠=︒,所以1120F MF ∠︒=,在1F MF △中,2221112cos120F F MF MF MF MF =+-︒,即()222222164244412c m a m m a m=-++=++=+, 所以222222222222441233112134444444a c a a a a a e a a a a ++=+=+=++≥+⋅=+,当且仅当2234a a =,即223a =时,等号成立,此时由于222216168280m m m m +-≥⋅-=,当且仅当2216m m =,即2m =时,等号成立,注意当2m =时,22216480a m m=+-=,不满足题意,故221680m m +->, 所以当223a =时,2216883m m +-=有解, 且由()240m m a -=>得20m a ->,满足题意, 所以224a e +的最小值为13+.故答案为:13+..16.已知数列{}n a 满足111,n a na ⎧⎫=⎨⎬⎩⎭为公差为1的等差数列,若不等式210nn a λ⎛⎫-≥⎪⎪⎭对任意的*N n ∈都成立,则实数λ的取值范围是__________.【答案】47λ≤【分析】因为1n na ⎧⎫⎨⎬⎩⎭为等差数列,已知首项与公差即可求出通项公式,即可求出数列{}n a 的通项公式,代入不等式,则不等式恒成立问题转化为最值问题求解即可.【详解】因为数列{}n a 满足111,n a na ⎧⎫=⎨⎬⎩⎭为公差为1的等差数列,设1n n b na =,则11b =,1(1)=+-=n b b n d n ,即1n n na =,所以21n a n =,*N n ∈,所以不等式210n n a λ⎛⎫-≥⎪⎪⎭,即242101n n λ⎛⎫ ⎪ ⎪--≥ ⎪ ⎪⎝⎭对任意的*N n ∈都成立,即min241n n λ⎛⎫≤ ⎪-⎝⎭,2()41n f n n =-,248(1),(2),(3)3711f f f ===,(1)(2),(3)(2)f f f f >>,因为2()41nf n n =-中分子的增长速度远大于分母,所以min 4()(2)7f n f ==,所以47λ≤,则实数λ的取值范围是47λ≤.故答案为:47λ≤四、解答题17.已知圆C 的圆心坐标为()1,2,且圆C 与直线:270l x y --=相切,过点()3,0A 的动直线m 与圆C 相交于,M N 两点,点P 为MN 的中点.(1)求圆C 的标准方程; (2)求OP 的最大值.【答案】(1)22(1)(2)20x y -+-= (2)52+【分析】(1)运用点到直线距离公式求出圆C 的半径; (2)求出点P 的运动轨迹,再确定OP 的最大值. 【详解】(1)由题意知点C 到直线l 的距离为()22112272251r +⨯-⨯--== ,也是圆C 的半径,∴圆C 的半径为25,则圆C 的标准方程为22(1)(2)20x y -+-=;(2)依题意作上图,P 为弦MN 的中点,由垂径定理知:CP MN ⊥ ,又MN 过定点A ,∴点P 的轨迹为以CA 为直径的圆,圆心为A ,C 的中点()2,1,半径为122CA==,max ||OP ∴=综上,圆C 的标准方程为22(1)(2)20x y -+-=,OP+.18.已知数列{}n a 是等差数列,n S 是等比数列{}n b 的前n 项和,41238,a b a b ===,36S =. (1)求数列{}{},n n a b 的通项公式; (2)求n S 的最大值和最小值.【答案】(1)34n a n =-,1182n n b -⎛⎫=⨯- ⎪⎝⎭(2)n S 的最大值为8,最小值为4.【分析】(1)根据给定的条件,求出等差数列{}n a 的首项及公差,等比数列{}n b 的公比即可求解作答; (2)由(1)可得161[1()]32n n S =⨯--,再分n 为奇数和偶数时,结合n S 的单调性求解即可. 【详解】(1)设{}n a 的公差为{},n d b 的公比为q , 313S b ≠,所以1q ≠,由()313161b q S q-==-,解得:12q =-,1182n n b -⎛⎫∴=⨯- ⎪⎝⎭,又42234,2,82a a d ab a -====,所以3d =, ()2234n a a n d n ∴=+-=-;(2)由(1)和等比数列的前n 项和公式可知:11616181,21,23321611132161611,2,2332n n nn nn k k S n k k ⎡⎤⎧⎛⎫⎛⎫⨯--⎢⎥+⨯=+∈ ⎪⎪ ⎪⎡⎤⎝⎭⎢⎥⎪⎝⎭⎛⎫⎣⎦==⨯--=⎢⎥⎨ ⎪⎛⎫⎝⎭⎢⎥⎛⎫⎪⎣⎦-- ⎪-⨯=∈ ⎪⎪⎝⎭⎝⎭⎩Z Z , 显然,当n 为奇数时,16,3n n S S >单调递减; 当n 为偶数时,16,3n n S S <单调递增,1n ∴=时,n S 有最大值为8,2n =时,n S 有最小值为4.19.如图,四边形ABCD 是边长为1的正方形,ED ⊥平面,ABCD FB ⊥平面ABCD ,且1ED FB ==.(1)求证:EC ⊥平面ADF(2)在线段EC 上是否存在点G (不含端点),使得平面GBD 与平面ADF 的夹角为45,若存在,指出G 点的位置;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,G 为线段EC 上靠近E 的三等分点【分析】(1)建立空间直角坐标系,得到0EC DF EC DA ⋅=⋅= 故EC ⊥DF ,EC ⊥DA ,从而证明出线面垂直;(2)设(01)EG EC λλ=<<,得到G 的坐标为()0,,1λλ-,求出平面的法向量,列出方程,求出13λ=,得到G 为线段EC 上靠近E 的三等分点.【详解】(1)以点D 为原点,以,,DA DC DE 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,则()()()()()()0,0,0,1,0,0,1,1,0,0,1,0,0,0,1,1,1,1D A B C E F ,()()()0,1,1,1,0,0,1,1,1EC DA DF ∴=-==,110EC DA EC DF ⎧⋅=⎪⎨⋅=-=⎪⎩,故EC ⊥DF ,EC ⊥DA ,∵DA DF D =,,DA DF ⊂平面ADF ,EC ∴⊥平面ADF ;(2)设(01)EG EC λλ=<<,则G 的坐标为()()0,,1,0,,1DG λλλλ-=-, 设平面GBD 的法向量为(),,n m n t =,则由()100n DG n t n DB m n λλ⎧⋅=+-=⎪⎨⋅=+=⎪⎩,令1n λ=-,则1,m t λλ=-=-,则法向量()1,1,n λλλ=---,平面GBD 与平面ADF 的夹角为45,且平面ADF 的法向量为()0,1,1EC =-,cos452n EC n EC⋅∴==01λ<<,∴解得13λ=,G ∴为线段EC 上靠近E 的三等分点.20.记n S 为数列{}n a 的前n 项和,已知11a =,3221n n a S n -=-. (1)求证:数列{}1n a +为等比数列; (2)若11n n n n a b a a ++=,则求数列{}n b 的前n 项和n T . 【答案】(1)证明见解析 (2)31231n n nT -=⋅-【分析】(1)由n a 与n S 的关系,结合等比数列的定义进行证明; (2)将n a 代入11n n n n a b a a ++=,使用裂项相消法进行求和. 【详解】(1)∵3221n n a S n -=-,① ∴当2n ≥时,()1132211n n a S n ---=--,②①-②,得()113322n n n n a a S S -----=,即12332n n n a a a ---=, ∴化简整理得()1131n n a a -+=+(2n ≥), 又∵11112a +=+=,∴数列{}1n a +中各项均不为0,且1131n n a a -+=+(2n ≥),∴数列{}1n a +是首项112a +=,公比为3的等比数列. (2)由第(1)问,1123n n a -+=⋅,∴1231n n a -=⋅-,∴()()()()()()111111231231123111122231231231231231231n n n n n n n n n n n n n a b a a -----+⋅--⋅-+⋅⎛⎫===⋅=⋅- ⎪⋅-⋅-⋅-⋅-⋅-⋅-⎝⎭, ∴12n n T b b b =+++1111111125517231231n n -⎛⎫=⋅-+-++-⎪⋅-⋅-⎝⎭1112231n ⎛⎫=⋅- ⎪⋅-⎝⎭31231n n -=⋅-. ∴数列{}n b 的前n 项和31231n n nT -=⋅-. 21.已知抛物线C 的顶点为坐标原点O ,焦点F 在x轴的正半轴,点(),2Q m 抛物线上, 且Q 到抛物线的准线的距离为2. (1)求抛物线C 的方程;(2)动点P 在抛物线的准线上,过点P 作拋物线C 的两条切线分别交y 轴于,A B 两点,当PAB 面积时,求点P 的坐标. 【答案】(1)24y x = (2)1,2或()1,2--【分析】(1)利用抛物线的焦半径公式与标准方程得到关于,p m 的方程组,解之即可;(2)先由PAB 面积得到()1228k k -=,再联立切线与抛物线方程,结合韦达定理得到1212,k k k k +,从而求得2t =±,由此得解.【详解】(1)依题意,设抛物线的方程为22(0)y px p =>, 因为点(),2Q m 在抛物线上,所以42pm =,则2pm =, 因为Q 到抛物线准线的距离为2,所以22pm +=, 联立222pm pm =⎧⎪⎨+=⎪⎩,解得2,1p m ==,所以抛物线的方程为24y x =.(2)设动点P 的坐标为()1,t -,设直线,PA PB 的斜率为12,k k , 则直线PA 的方程为()11y k x t =++,直线PB 的方程为()21y k x t =++, 令两个方程中的0x =,则可得()()120,,0,A k t B k t ++, 此时1211122PABS AB k k =⨯⨯=-, 因为2PABS=,所以1222k k -=,则()1228k k -=,设过点P 的抛物线的切线方程为()1y k x t =++,联立方程()241y x y k x t⎧=⎪⎨=++⎪⎩,消去x ,得24440t y y k k -++=,因为直线与抛物线相切,所以244Δ440t k k ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭,整理得210k tk +-=,由题知直线,PA PB 为抛物线的两条切线,则12,k k 为方程的两根, 所以1212,1k k t k k +=-=-,由()1228k k -=得()221212448k k k k t +-=+=,解得2t =±, 此时,对于210k tk +-=,有240t ∆=+>,满足题意, 所以点P 的坐标为1,2或()1,2--..22.已知椭圆2222:1(0)x y C a b a b +=>>3x 轴的直线与椭圆交于,M N 两点,1MN =. (1)求椭圆C 的方程;(2)过椭圆C 外一点()2,2P 任作一条直线与椭圆交于不同的两点,A B ,在线段AB 上取一点Q ,满足2PA PB PQ PA PQ PB =+,证明:点Q 必在某条定直线上.【答案】(1)2214x y +=(2)证明见解析【分析】(1)依题意可得c a =221b MN a ==,即可求出a 、b 、c ,从而求出椭圆方程; (2)法一:设直线方程为()22y k x =-+,()11,A x y ,()22,B x y ,(),Q x y ,由2PA PB PQ PA PQ PB =+,可得()121212224x x x x x x x -+=+-,联立直线与椭圆方程,消元、列出韦达定理,代入即可得到8641k x k -=+,241y k =+,消去参数k ,即可得解; 法二:依题意可得PA PB QAQB=,设PA AQ λ=,则PB BQ λ=-,设()11,A x y ,()22,B x y ,(),Q x y ,根据向量共线的坐标表示用x 、y 表示1x 、1y 、2x 、2y ,再消去参数即可得解. 【详解】(1)解:由题知c a =①,221b MN a ==②,又222a b c =+③, 联立①②③解得21a b c ⎧=⎪=⎨⎪=⎩,所以椭圆C 的方程为2214x y +=;(2)解法一:由题知直线的斜率存在,设直线的斜率为k , 则直线方程为()22y k x =-+,设()11,A x y ,()22,B x y ,(),Q x y ,2PA PB PQ PA PQ PB =+,12122222222x x x x x x ∴--=-⋅-+-⋅-,122,2,2x x x <<<,∴上式可化简为()121212224x x x x x x x -+=+-,联立()222214y k x x y ⎧=-+⎪⎨+=⎪⎩消去y 化简可得()()2222148221632120k x k k x k k ++-++-+=, 则2122161614k kx x k -+=+,212216321214k k x x k-+=+,()1212122286441x x x x k x x x k -+-∴==+-+,代入直线方程()22y k x =-+, 即862241k y k k -⎛⎫=-+ ⎪+⎝⎭,解得241y k =+, 由8641241k x k y k -⎧=⎪⎪+⎨⎪=⎪+⎩消去k 可得420x y +-=,则点Q 必在定直线420x y +-=; 法二:2PA PB PQ PA PQ PB =+,()()PA PB PQ PB PQ PA ∴-=-,即PA QB PB QA =, PA PB QAQB∴=,设PA AQ λ=,则PB BQ λ=-,设()11,A x y ,()22,B x y ,(),Q x y , 由PA AQ λ=可得112121x x y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩,由PB BQ λ=-,可得222121x x y y λλλλ-⎧=⎪⎪-⎨-⎪=⎪-⎩,A 、B 在椭圆2214x y +=上, 2222221141221141x y x y λλλλλλλλ⎧+⎛⎫⎪ ⎪++⎛⎫⎝⎭⎪+= ⎪⎪+⎝⎭∴⎨-⎛⎫⎪ ⎪⎪--⎛⎫⎝⎭+=⎪ ⎪-⎝⎭⎩, 化简可得()()2222222245(1)445(1)4x y x y x y x y λλλλλλ⎧⎛⎫++++=+⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+-++=- ⎪⎪⎝⎭⎩,两式相减得到42x y +=, ∴点Q 必在定直线420x y +-=上.。
2022-2023学年湖北省武汉市华中师大一附中高一(下)期末数学试卷【答案版】
2022-2023学年湖北省武汉市华中师大一附中高一(下)期末数学试卷一、选择题:本题共8小题,每小题5分,共40分.(在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知i 为虚数单位,则(cos75°+i sin75°)(cos15°+i sin15°)=( ) A .﹣1B .1C .﹣iD .i2.如果一组数据的中位数比平均数小很多,则下列叙述一定错误的是( ) A .数据中可能有异常值B .这组数据是近似对称的C .数据中可能有极端大的值D .数据中众数可能和中位数相同3.有2个人在一座8层大楼的底层进入电梯,假设每一个人从第二层开始在每一层离开电梯是等可能的,则这两人在不同层离开电梯的概率为( ) A .37B .67C .78D .7164.已知点A 的坐标为(1,√3),将OA →绕坐标原点O 逆时针旋转90°,得到OB →,则点B 的横坐标为( ) A .−√3B .﹣1C .√3D .15.某调查机构抽取了部分关注济南地铁建设的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图.根据图中(35岁以上含35岁)的信息,关于该样本的结论不一定正确的是( )A .男性比女性更关注地铁建设B .关注地铁建设的女性多数是35岁以上C .35岁以下的男性人数比35岁以上的女性人数多D .35岁以上的人对地铁建设关注度更高6.已知l ,m ,n 是三条不同的直线,α,β,γ是三个不同的平面,给出下列命题,其中真命题是( ) A .若l ⊥α,l ⊥m ,则m ∥αB .若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥m ,则m ∥nC .若α⊥β,l ⊂α,m ⊂β,则l ⊥mD .l ⊂α,l ⊥m ,l ⊥n ,m ∥β,n ∥β,则α∥β7.设平面向量|a →|=1,|b →|=2,b →在a →方向上的投影向量为c →,则( ) A .a →⋅c →=c →⋅b →B .a →⋅b →=a →⋅c →C .|a →⋅c →|≤2D .a →⋅c →=|a →|⋅|c →|8.已知锐角α,β满足sin α﹣cos α=15,tan α+tan β+√3tanαtanβ=√3,则α与β的大小关系为( )A .α<π4<βB .β<π4<αC .π4<α<βD .π4<β<α二、选择题:本题共4小题,每小题5分,共20分.(在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.) 9.下列关于复数z =21−i的四个命题,其中为真命题的是( ) A .在复平面内z 对应的点Z 在第一象限 B .z 2=2i C .z 的共轭复数为﹣1+iD .z 是关于x 的方程x 2﹣2x +2=0的一个根10.对于一个事件E ,用n (E )表示事件E 中样本点的个数.在一个古典概型的样本空间Ω和事件A ,B ,C ,D 中,n (Ω)=100,n (A )=60,n (B )=40,n (C )=20,n (D )=10,n (A ∪B )=100,n (A ∩C )=12,n (A ∪D )=70,则( ) A .A 与D 不互斥 B .A 与B 互为对立 C .A 与C 相互独立D .B 与C 相互独立11.在一次党建活动中,甲、乙、丙、丁四个兴趣小组举行党史知识竞赛,每个小组各派10名同学参赛,记录每名同学失分(均为整数)情况,若该组每名同学失分都不超过7分,则该组为“优秀小组”,已知甲、乙、丙、丁四个小组成员失分数据信息如下,则一定为“优秀小组”的是( ) A .甲组中位数为2,极差为5B .乙组平均数为2,众数为2C .丙组平均数为1,方差大于0D .丁组平均数为2,方差为312.如图所示,正方体ABCD ﹣A ′B ′C ′D ′的棱长为1,E ,F 分别是棱AA ′,CC ′的中点,过直线EF 的平面分别与棱BB ′,DD ′交于点M ,N ,以下四个命题中正确的是( )A .四边形EMFN 一定为菱形B .平面EMFN ⊥平面DBB ′D ′C .四棱锥A ﹣MENF 体积为16D .四边形EMFN 的周长最小值为2√5三、填空题:本题共4小题,每小题5分,共20分.13.已知函数f (x )=cos (2x +φ)(x ∈R )的图象关于点(23π,0)中心对称,则|φ|的最小值为 . 14.如图所示,直线P A 垂直于圆O 所在的平面,△ABC 内接于圆O ,且AB 为圆O 的直径,P A =AB =2.现有以下命题: ①BC ⊥PC ;②当点C 在圆周上由B 点逐步向A 点移动过程中,二面角B ﹣PC ﹣A 会逐步增大; ③当点C 在圆周上由B 点逐步向A 点移动过程中,三棱锥B ﹣P AC 的体积的最大值为23.其中正确的命题序号为 .15.在某次模拟测试中,30名男生的平均分数是70分,样本方差是10;20名女生的平均分数是80分,样本方差是15,则该次模拟考试中这50名同学成绩的平均分为 ,方差为 . 16.在三棱锥V ﹣ABC 中,AB ,AC ,AV 两两垂直,AB =AV =4,AC =2,P 为棱AB 上一点,AH ⊥VP 于点H ,则△VHC .面积的最大值为 ;此时,三棱锥A ﹣VCP 的外接球表面积为 . 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知扇形OAB 的半径为1,∠AOB =π3,P 是圆弧上一点(不与A ,B 重合),过P 作PM ⊥OA ,PN ⊥OB ,M ,N 为垂足. (1)若|PM|=12,求PN 的长;(2)设∠AOP =x ,PM ,PN 的线段之和为y ,求y 的取值范围.18.(12分)柜子里有3双不同的鞋,记第1双鞋左右脚编号为a 1,a 2,记第2双鞋左右脚编号为b 1,b 2,记第3双鞋左右脚编号为c 1,c 2.如果从中随机取出4只,那么(1)写出试验的样本空间Ω,并求恰好取到两双鞋的概率;(若取到a 1,b 1,c 1,c 2,则样本点记为a 1b 1c 1c 2,其余同理记之.)(2)求事件M “取出的鞋子中至少有两只左脚,且不能凑两双鞋”的概率.19.(12分)如图,正三棱柱ABC ﹣A 1B 1C 1中,E ,F 分别是棱AA 1,BB 1上的点,A 1E =BF =13AA 1. (1)证明:平面CEF ⊥平面ACC 1A 1;(2)若AC =AE =2,求二面角C 1﹣CF ﹣E 的正弦值.20.(12分)在平面凸四边形(每个内角都小于180°)ABCD 中,∠A +∠C =180°,AB =AD =2,BC =√2,CD =√6.(1)求四边形ABCD 的面积;(2)若M ,N 为边AB ,CD 的中点,求(AB →+CD →)⋅MN →的值.21.(12分)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如图的患病者和未患病者该指标的频率分布直方图:利用该指标制定一个检测标准,需要确定临界值c ,将该指标大于c 的人判定为阳性,小于或等于c 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为p (c );误诊率是将未患病者判定为阳性的概率,记为q (c ).假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.(1)当漏诊率p (c )=0.5%时,求临界值c 和误诊率q (c );(2)设函数f (c )=p (c )+q (c ),当c ∈[95,105]时,求f (c )的解析式,并求f (c )在区间[95,105]的最小值.22.(12分)如图,四棱台ABCD ﹣A 1B 1C 1D 1中,上、下底面均是正方形,且侧面是全等的等腰梯形,AB =2A 1B 1=4,E 、F 分别为DC 、BC 的中点,上下底面中心的连线O 1O 垂直于上下底面,且O 1O 与侧棱所在直线所成的角为45°. (1)求证:BD 1∥平面C 1EF ;(2)线段BF 上是否存在点M ,使得直线A 1M 与平面C 1EF 所成的角的正弦值为3√2222,若存在,求出线段BM 的长;若不存在,请说明理由.2022-2023学年湖北省武汉市华中师大一附中高一(下)期末数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.(在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知i 为虚数单位,则(cos75°+i sin75°)(cos15°+i sin15°)=( ) A .﹣1B .1C .﹣iD .i解:(cos75°+i sin75°)(cos15°+i sin15°) =(sin15°+i cos15°)(cos15°+i sin15°)=sin15°cos15°+i cos 215°+i sin 215°+i 2sin15°cos15° =sin15°cos15°+i (cos 215°+sin 215°)﹣sin15°cos15° =i . 故选:D .2.如果一组数据的中位数比平均数小很多,则下列叙述一定错误的是( ) A .数据中可能有异常值B .这组数据是近似对称的C .数据中可能有极端大的值D .数据中众数可能和中位数相同解:中位数表示一组数据的一般水平,平均数表示一组数据的平均水平,如果这两者差不多,说明数据分布较均匀,也可以看作近似对称,但现在它们相差很大,说明其中有异常数据,有极端大的值,众数是出现次数最多的教,可能不止一个,当然可以和中位数相同, 因此只有B 项错误, 故选:B .3.有2个人在一座8层大楼的底层进入电梯,假设每一个人从第二层开始在每一层离开电梯是等可能的,则这两人在不同层离开电梯的概率为( ) A .37B .67C .78D .716解:由题意得,由于每一个人自第二层开始在每一层电梯是等可能的, 故两人离开电梯的所有可能情况有7×7=49种, 而两人在同一层电梯的可能情况有7×1=7, 所以两人在同一层离开电梯的概率为749=17,所以两人在不同层离开电梯的概率为1−17=67. 故选:B .4.已知点A 的坐标为(1,√3),将OA →绕坐标原点O 逆时针旋转90°,得到OB →,则点B 的横坐标为( ) A .−√3B .﹣1C .√3D .1解:设点A 是α终边上一点,设点B 的横坐标为x 0,则|OA|=|OB|=√3+1=2, 所以sinα=√32,cosα=12,所以x 0=2cos(α+π2)=−2sinα=−2×√32=−√3.故选:A .5.某调查机构抽取了部分关注济南地铁建设的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图.根据图中(35岁以上含35岁)的信息,关于该样本的结论不一定正确的是( )A .男性比女性更关注地铁建设B .关注地铁建设的女性多数是35岁以上C .35岁以下的男性人数比35岁以上的女性人数多D .35岁以上的人对地铁建设关注度更高 解:由等高条形图可得:对于选项A :由左图知,样本中男性数量多于女性数量,所以男性比女性更关注地铁建设,故A 正确; 对于选项B :由右图知女性中35岁以上的占多数,从而样本中多数女性是35岁以上, 从而得到关注地铁建设的女性多数是35岁以上,故B 正确;对于选项C :由左图知男性人数大于女性人数,由右图知35岁以下的男性占男性人数比35岁以上的女性占女性人数的比例少,所以无法判断35岁以下的男性人数与35岁以上的女性人数的多少,故C 不一定正确; 对于选项D :由右图知样本中35岁以上的人对地铁建设关注度更高,故D 正确. 故选:C .6.已知l ,m ,n 是三条不同的直线,α,β,γ是三个不同的平面,给出下列命题,其中真命题是( ) A .若l ⊥α,l ⊥m ,则m ∥αB .若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥m ,则m ∥nC .若α⊥β,l ⊂α,m ⊂β,则l ⊥mD .l ⊂α,l ⊥m ,l ⊥n ,m ∥β,n ∥β,则α∥β 解:若l ⊥α,l ⊥m ,则m ∥α或m ⊂α,故A 错误;若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥m ,则由线面平行的判定定理与性质定理易得m ∥n .故B 正确; 若α⊥β,l ⊂α,m ⊂β,则l 与m 不一定垂直,故C 错误;若l ⊂α,l ⊥m ,l ⊥n ,m ∥β,n ∥β,则不能得到α∥β.故D 错误. 故选:B .7.设平面向量|a →|=1,|b →|=2,b →在a →方向上的投影向量为c →,则( ) A .a →⋅c →=c →⋅b →B .a →⋅b →=a →⋅c →C .|a →⋅c →|≤2D .a →⋅c →=|a →|⋅|c →|解:设b →与a →的夹角为θ,对于 A ,当θ为锐角时,a →⋅c →=|a →|⋅|c →|=|c →|,c →⋅b →=|c →|⋅|b →|cosθ=|c →|2,不一定相等,故A 错误, 对于B .当θ为锐角时,a →⋅b →=|a →|⋅|b →|cosθ=|b →|cosθ=a →⋅c →=|a →|⋅|c →|=|c →|,成立, 当θ为钝角时,a →⋅b →=|a →|⋅|b →|cosθ=|b →|cosθ=a →⋅c →=−|a →|⋅|c →|=−|c →|,成立, 当θ为直角时,a →⋅b →=a →⋅c →=0 成立,故正确; 对于C ,|a →⋅c →|=|a →|⋅|c →|=|c →|≤|b →|=2,故C 正确, 对于D ,a →⋅c →=|a →|⋅|c →|cosθ,故D 错误. 故选:BC .8.已知锐角α,β满足sin α﹣cos α=15,tan α+tan β+√3tanαtanβ=√3,则α与β的大小关系为( ) A .α<π4<βB .β<π4<αC .π4<α<βD .π4<β<α解:∵sin α﹣cos α=15>0, ∴sin α>cos α, ∴α>π4,∵tan α+tan β+√3tan αtan β=√3,∴tan(α+β)=tanα+tanβ1−tanαtanβ=√3,∴α+β=π3,∴β<π4<α.故选:B.二、选择题:本题共4小题,每小题5分,共20分.(在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.下列关于复数z=21−i的四个命题,其中为真命题的是()A.在复平面内z对应的点Z在第一象限B.z2=2iC.z的共轭复数为﹣1+i D.z是关于x的方程x2﹣2x+2=0的一个根由z=21−i可得z=2(1+i)(1−i)(1+i)=1+i,对于A,点Z为(1,1),故在第一象限,A正确,对于B,z2=(1+i)2=2i,故B正确,对于C,z的共轭复数为1﹣i,故C错误,对于D,(1+i)2﹣2(1+i)+2=2i﹣2﹣2i+2=0,故D正确.故选:ABD.10.对于一个事件E,用n(E)表示事件E中样本点的个数.在一个古典概型的样本空间Ω和事件A,B,C,D中,n(Ω)=100,n(A)=60,n(B)=40,n(C)=20,n(D)=10,n(A∪B)=100,n(A∩C)=12,n(A∪D)=70,则()A.A与D不互斥B.A与B互为对立C.A与C相互独立D.B与C相互独立解:因为n(A)+n(D)=n(A∪D),所以A与D互斥,即选项A错误;因为n(A)+n(B)=n(A∪B)=n(Ω),所以A与B互斥且对立,即选项B正确;由题意知,P(A)=n(A)n(Ω)=60100=35,P(B)=n(B)n(Ω)=40100=25,P(C)=n(C)n(Ω)=20100=15,P(A∩C)=n(A∩C)n(Ω)=12100=325,所以P(A∩C)=P(A)•P(C),即A与C相互独立,所以选项C正确;因为n(A∩C)=12,n(C)=20,且A与B互为对立,所以n(B∩C)=20﹣12=8,所以P(B∩C)=n(B∩C)n(Ω)=8100=225=P(B)•P(C),所以B与C相互独立,即选项D正确.故选:BCD .11.在一次党建活动中,甲、乙、丙、丁四个兴趣小组举行党史知识竞赛,每个小组各派10名同学参赛,记录每名同学失分(均为整数)情况,若该组每名同学失分都不超过7分,则该组为“优秀小组”,已知甲、乙、丙、丁四个小组成员失分数据信息如下,则一定为“优秀小组”的是( ) A .甲组中位数为2,极差为5B .乙组平均数为2,众数为2C .丙组平均数为1,方差大于0D .丁组平均数为2,方差为3解;对A ,因为中位数为2,极差为5,故最大值小于等于7,故A 正确;对B ,如失分数据分别为0,0,0,2,2,2,2,2,2,8,则满足平均数为2,众数为2,但不满足每名同学失分都不超过7分,故B 错误;对C ,如失分数据分别为0,0,0,0,0,0,0,0,1,9,则满足平均数为1,方差大于0,但不满足每名同学失分都不超过7分,故C 错误;对D ,利用反证法,假设有一同学失分超过7分,则方差大于110×(8−2)2=3.6>3,与题设矛盾,故每名同学失分都不超过7分.故D 正确. 故选:AD .12.如图所示,正方体ABCD ﹣A ′B ′C ′D ′的棱长为1,E ,F 分别是棱AA ′,CC ′的中点,过直线EF 的平面分别与棱BB ′,DD ′交于点M ,N ,以下四个命题中正确的是( )A .四边形EMFN 一定为菱形B .平面EMFN ⊥平面DBB ′D ′C .四棱锥A ﹣MENF 体积为16D .四边形EMFN 的周长最小值为2√5解:连接BD ,B ′D ′,MN ,AC ,EF ,显然AE ∥CF ,且AE =CF ,所以ACFE 为平行四边形, 所以AC ∥EF ,由题意得AC ⊥BD ,BB ′⊥平面ABCD ,AC ⊂平面ABCD ,所以BB ′⊥AC ,∵BD ∩BB ′=B ,BD ,BB ′⊂平面BDD ′B ′,所以AC ⊥平面BDD ′B ′,则EF ⊥平面BDD ′B ′, EF ⊂平面EMFN ,所以平面EMFN ⊥平面BDD ′B ′,故B 正确; 由正方体的性质得平面BCC ′B ′∥平面ADD ′A ′,平面BCC ′B ′∩平面EMFN =MF ,平面ADD ′A ′∩平面EMFN =EN ,故MF ∥EN , 同理得ME ∥NF ,又EF ⊥平面BDD ′B ′,MN ⊂平面BDD ′B ′,EF ⊥MN ,∴四边形EMFN 为菱形,故A 正确; 对于C ,四棱锥A ﹣MENF 的体积为: V A−MENF =V M−AEF +V N−AEF =13DB ⋅S △AEF =13×√2×√24=16,故C 正确; 对于D ,∵四边形EMFN 是菱形,∴四边形EMFN 的周长l =4√MN 24+EF24=4⋅√MN 2+22=2√MN 2+2, ∴当点M ,N 分别为BB ′,DD ′的中点时,四边形EMFN 的周长最小, 此时MN =EF =√2,即周长的最小值为4,故D 错误. 故选:ABC .三、填空题:本题共4小题,每小题5分,共20分.13.已知函数f (x )=cos (2x +φ)(x ∈R )的图象关于点(23π,0)中心对称,则|φ|的最小值为 π6.解:因为函数f (x )=cos (2x +φ)(x ∈R )的图象关于点(23π,0)中心对称, 所以2×2π3+φ=π2+kπ,k ∈Z ,所以φ=−5π6+kπ,k ∈Z , 则当k =1时,|φ|的最小值为π6.故答案为:π6.14.如图所示,直线P A 垂直于圆O 所在的平面,△ABC 内接于圆O ,且AB 为圆O 的直径,P A =AB =2.现有以下命题: ①BC ⊥PC ;②当点C 在圆周上由B 点逐步向A 点移动过程中,二面角B ﹣PC ﹣A 会逐步增大; ③当点C 在圆周上由B 点逐步向A 点移动过程中,三棱锥B ﹣P AC 的体积的最大值为23.其中正确的命题序号为 ①③ .解:因为P A ⊥平面ABC ,BC ⊂平面ABC ,所以P A ⊥BC , 又因为AB 为圆O 的直径,所以AC ⊥BC , 又P A ∩AC =A ,P A ,AC ⊂平面P AC , 所以BC ⊥平面P AC ,而PC ⊂平面P AC ,所以BC ⊥PC ,故①正确;因为BC ⊥平面P AC ,而BC ⊂平面BPC ,所以平面BPC ⊥平面P AC ,故当点C 在圆周上由B 点逐步向A 点移动过程中,二面角B ﹣PC ﹣A 恒为90°,故②不正确; 因为P A =AB =2,所以三棱锥B ﹣P AC 的体积V B−PAC =V P−ABC =13⋅S △ABC ⋅PA =23⋅S △ABC , 过点C 作CH ⊥AB 交AB 于点H ,所以S △ABC =12AB ⋅CH =CH , 所以V P−ABC =23⋅CH ,所以求三棱锥B ﹣P AC 的体积的最大值,即求CH 的最大值,当点C 在圆周上由B 点逐步向A 点移动过程中,当H 为AB 中点时,CH 最大,且CH 的最大值为1, 所以三棱锥B ﹣P AC 的体积的最大值为23,故③正确;故答案为:①③.15.在某次模拟测试中,30名男生的平均分数是70分,样本方差是10;20名女生的平均分数是80分,样本方差是15,则该次模拟考试中这50名同学成绩的平均分为 74 ,方差为 36 . 解:记30名男生得分记为x 1,x 2,……,x 30,20名女生得分记y 1,y 2,……,y 20,所以男生得分平均分x =x 1+x 2+...+x 3030=70,则x 1+x 2+...+x 30=2100,所以女生得分平均分y =y 1+y 2+...+y 2020=80,则y 1+y 2+...+y 20=1600,所以总平均分m =150(x 1+x 2+⋯+x 30+y 1+y 2+⋯⋅+y 20)=150(30×70+20×80)=74, 总方差为s 2=150[30×10+30×(70−74)2+20×15+20×(80−74)2]=36, 所以此50人该次模拟考试成绩的平均分是74,方差是36. 故答案为:74;36.16.在三棱锥V ﹣ABC 中,AB ,AC ,AV 两两垂直,AB =AV =4,AC =2,P 为棱AB 上一点,AH ⊥VP 于点H ,则△VHC .面积的最大值为 5 ;此时,三棱锥A ﹣VCP 的外接球表面积为 148π5.解:设AP =x ,∵AB ,AC ,AV 两两垂直,∴VP =√16+x 2, ∴12VP •AH =12VA •AP ,∴AH =4x√16+x 2,由已知可得AC ⊥平面VAB ,∴AC ⊥AH , HC =√4+16x 216+x 2, ∵VH ⊥AH ,AH ∩AC =A ,∴VH ⊥平面AHC , ∵HC ⊂平面AHC ,∴VH ⊥HC ,∴VH =√16−16x 216+x2,∴S △VHC =12×VH ×HC ≤12×VH 2+HC22=5, 当且仅当√4+16x 216+x2=√16−16x 216+x2,即x =4√155时取等号,三棱锥A ﹣VCP 的外接球的半径为r ,则(2r )2=AP 2+AC 2+AV 2=16×1525+4+16=1485, ∴4πr 2=1485π, 故答案为:5;1485π.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知扇形OAB的半径为1,∠AOB=π3,P是圆弧上一点(不与A,B重合),过P作PM⊥OA,PN⊥OB,M,N为垂足.(1)若|PM|=12,求PN的长;(2)设∠AOP=x,PM,PN的线段之和为y,求y的取值范围.解:(1)sin∠POM=12,∠POM∈(0,π3),所以∠POM=π6,所以∠PON=π3−π6=π6,所以|NP|=sin∠PON=12;(2)∠POB=π3−x,y=sinx+sin(π3−x),x∈(0,π3),y=sinx+sin(π3−x)=sinx+√32cosx−12sinx=sin(x+π3),x+π3∈(π3,2π3),sin(x+π3)∈(√32,1],则y的取值范围为(√32,1].18.(12分)柜子里有3双不同的鞋,记第1双鞋左右脚编号为a1,a2,记第2双鞋左右脚编号为b1,b2,记第3双鞋左右脚编号为c1,c2.如果从中随机取出4只,那么(1)写出试验的样本空间Ω,并求恰好取到两双鞋的概率;(若取到a1,b1,c1,c2,则样本点记为a1b1c1c2,其余同理记之.)(2)求事件M“取出的鞋子中至少有两只左脚,且不能凑两双鞋”的概率.解:(1)由题意得,试验的样本空间为:Ω={a1a2b1b2,a1a2b1c1,a1a2b1c2,a1a2b2c1,a1a2b2c2,a1a2c1c2,a1b1b2c1,a1b1b2c2,a1b1c1c2,a1b2c1c2,a2b1b2c1,a2b1b2c2,a2b1c1c2,a2b2c1c2,b1b2c1c2},设A表示事件“恰好取到两双鞋”,则A={a1a2b1b2,a1a2c1c2,b1b2c1c2},所以n(Ω)=15,n(A)=3,故事件“恰好取到两双鞋”的概率为P(A)=315=15;(2)由(1)知,事件M“取出的鞋子中至少有两只左脚”为:M={a1a2b1c1,a1a2b1c2,a1a2b2c1,a1b1b2c1,a1b1b2c2,a1b1c1c2,a1b2c1c2,a2b1b2c1,a2b1c1c2,b1b2c1c2},所以n(Ω)=15,n(M)=10,故事件“取出的鞋子中至少有两只左脚,且不能凑两双鞋”的概率为P (M )=1015=23. 19.(12分)如图,正三棱柱ABC ﹣A 1B 1C 1中,E ,F 分别是棱AA 1,BB 1上的点,A 1E =BF =13AA 1. (1)证明:平面CEF ⊥平面ACC 1A 1;(2)若AC =AE =2,求二面角C 1﹣CF ﹣E 的正弦值.解:(1)证明:取BC 的中点O ,连接OA ,在正三棱柱ABC ﹣A 1B 1C 1中,不妨设AB =2a ,AA 1=3,以O 为坐标原点,OB ,OA 所在直线为x 轴和y 轴,建立如图所示的空间直角坐标系,则:C (﹣a ,0,0),A(0,√3a ,0),F (a ,0,1),E (0,√3a ,2)CF →=(2a ,0,1),CE →=(a ,√3a ,2),CA →=(a ,√3a ,0),CC 1→=(0,0,3), 设平面CEF 的一个法向量为n →=(x ,y ,z ),则{n →⋅CF →=2ax +z =0n →⋅CE →=ax +√3ay +2z =0,取x =﹣1,则y =−√3,z =2a , ∴平面CEF 的一个法向量为n →=(﹣1,−√3,2a ), 设平面ACC 1A 1的一个法向量为m →=(m ,n ,e ),则{m →⋅CA →=am +√3an =0m →⋅CC 1→=3e =0,取n =﹣1,得m =√3,e =0, ∴平面ACC 1A 1的一个法向量为m →=(﹣1,√3,0),因为m →•n →=−√3+√3=0,所以平面CEF ⊥平面ACC 1A 1;(2)因为AC =AE =2,由(1)可得a =1,即n →=(﹣1,−√3,2), 易知平面CFC 1的一个法向量为OA →=(0,√3,0), ∴cos <n →,OA →>=n →⋅OA→|n →|⋅|OA →|=−38×3=−√64,∴二面角C 1﹣CF ﹣E 的余弦值为√64,∴二面角C 1﹣CF ﹣E 的正弦值为√104. 20.(12分)在平面凸四边形(每个内角都小于180°)ABCD 中,∠A +∠C =180°,AB =AD =2,BC =√2,CD =√6.(1)求四边形ABCD 的面积;(2)若M ,N 为边AB ,CD 的中点,求(AB →+CD →)⋅MN →的值.解:(1)△ABD 中,BD 2=AB 2+AD 2﹣2AB •AD cos A =4+4﹣8cos A =8﹣8cos A ,在△BCD 中,BD 2=BC 2+CD 2−2BC ⋅CDcosC =2+6−2×√2×√6cosC =8−4√3cosC , 因为A +C =180°,所以cos A =﹣cos C ,所以8−8cosA =8+4√3cosA ,所以cos A =0,因为0°<A <180°,所以A =90°,C =90°, 所以S 四边形ABCD =12×2×2+12×√2×√6=2+√3.(2)法1:因为MN →=MB →+BC →+CN →,又MN →=MA →+AD →+DN →,所以MN →=12(BC →+AD →),因为AB →+CD →=AD →+DB →+CD →=AD →+CB →,所以(AB →+CD →)⋅MN →=12(BC →+AD →)⋅(AD →−BC →)=12(AD 2−BC 2)=12(4−2)=1.21.(12分)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如图的患病者和未患病者该指标的频率分布直方图:利用该指标制定一个检测标准,需要确定临界值c ,将该指标大于c 的人判定为阳性,小于或等于c 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为p (c );误诊率是将未患病者判定为阳性的概率,记为q (c ).假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.(1)当漏诊率p (c )=0.5%时,求临界值c 和误诊率q (c );(2)设函数f (c )=p (c )+q (c ),当c ∈[95,105]时,求f (c )的解析式,并求f (c )在区间[95,105]的最小值.解:(1)依题可知,左边图形第一个小矩形的面积为5×0.002>0.5%,所以95<c <100, 所以(c ﹣95)×0.002=0.5%,解得:c =97.5, q (c )=0.01×(100﹣97.5)+5×0.002=0.035=3.5%. (2)当c ∈[95,100]时,f (c )=p (c )+q (c )=(c ﹣95)×0.002+(100﹣c )×0.01+5×0.002=﹣0.008c +0.82≥0.02; 当c ∈(100,105]时,f (c )=p (c )+q (c )=5×0.002+(c ﹣100)×0.012+(105﹣c )×0.002=0.01c ﹣0.98>0.02, 故f(c)={−0.008c +0.82,95≤c ≤1000.01c −0.98,100<c ≤105,所以f (c )在区间[95,105]的最小值为0.02.22.(12分)如图,四棱台ABCD ﹣A 1B 1C 1D 1中,上、下底面均是正方形,且侧面是全等的等腰梯形,AB =2A 1B 1=4,E 、F 分别为DC 、BC 的中点,上下底面中心的连线O 1O 垂直于上下底面,且O 1O 与侧棱所在直线所成的角为45°. (1)求证:BD 1∥平面C 1EF ;(2)线段BF 上是否存在点M ,使得直线A 1M 与平面C 1EF 所成的角的正弦值为3√2222,若存在,求出线段BM 的长;若不存在,请说明理由.解:(1)证明:因为OO 1⊥平面ABCD ,以点O 为坐标原点,DA ,OF →,OO 1→的方向分别为x 轴,y 轴,z 轴的正方向,建立如图所示的空间直角坐标系.因为侧棱所在直线与上下底面中心的连线OO 1所成的角为45°,则B (2,2,0),D 1(−1,−1,√2),C 1(−1,1,√2),F (0,2,0),E (﹣2,0,0),A 1(1,−1,√2),所以BD 1→=(−3,−3,√2),CE 1→=(−1,−1,√2),EF →=(2,2,0), 设平面C 1EF 的一个法向量为n →=(x ,y ,z ),则{n →⋅EF →=x +y =0n →⋅C 1E →=x +y +√2z =0,令x =1,则n →=(1,﹣1,0), 因为BD 1→=(﹣3,﹣3,√2),所以n →•BD 1→=0,所以n →⊥BD 1→, 又因为BD 1⊂平面C 1EF ,所以BD 1∥平面 C 1EF ;(2)假设边BC 上存在点M (x ,2,0)满足条件,x ∈[﹣2,2], 则A 1M →=(x ﹣1,3,−√2),设直线A 1M 与平面C 1EFF 所成角为θ, 由题意可得sin θ=|cos <A 1M →,n →>|=|A 1M →⋅n →||A 1M →|⋅|n →|=|x−4|√2⋅√x 2−2x+12=3√2222,化简得x 2﹣35x +34=0,则x =1或x =34(舍去),即存在点M 符合题意,此时BM =1.。
2020-2021学年湖北省武汉市华中师范大学第一附属中学高一下学期期末考试数学试卷(解析版)

湖北省武汉市华中师范大学第一附属中学2020-2021学年高一下学期期末考试数学试卷一、单选题:本题共6小题,每小题5分,共30分在每小题给出的四个选项中,只有一个是符合题目要求的.1.下列命题正确的是()A.三点确定一个平面B.一条直线和一个点确定一个平面C.两条不平行的直线确定一个平面D.梯形可确定一个平面2.已知向量,且,则m=()A.8 B.2 C.﹣2 D.﹣83.某同学对他进入高中以来的数学测验的成绩进行了统计,得到如图所示的茎叶图其中的“茎”指竖线左边的一列数,它表示个数的高位,本茎叶图中的“茎”表示一个三位数的百位、十位数;“叶”指竖线右边的从“茎”旁边生出来的数,它表示一个数的低位,本茎叶图中的“1”表示相应三位数的个位数如第二行:竖线左边为“12”,竖线右边第5个数为“7”,这两个数字结合起来就是该同学某次数学测验的成绩“127”.则这组成绩的中位数、众数、极差分别是()A.130,122,36 B.131.5,122,36 C.131,136,29 D.131.5,122,29 4.在三棱锥D﹣ABC中,AC⊥BC,AC=BC=2,AD⊥平面ABC,AD=1,E是线段AC 的中点,则异面直线AB和DE所成的角等于()A.135°B.120°C.60° D.45°5.用过圆锥的轴的平面去截圆锥得到的截面,叫做圆锥的轴截面,圆锥的轴截面是以图锥的两条母线为腰的等腰三角形,这个等腰三角形的顶角,叫做圆锥的顶角.已知过圆锥SO的两条母线的截面三角形有无穷多个,这些截面中,面积最大的恰好是圆锥SO的轴截面,则圆锥SO的顶角的取值范围是()A.(0,π)B.C.D.6.在△ABC巾,角A、B、C所对的边分别为a,b,c,△ABC的面积为,则()A.a2≠bc sin A B.C.的最大值为D.的最大值三、填空题:本题共4小题,每小题5分,共20分.7.已知复数和θ都是实数,若z1=z2,则m=.8.已知直线y=a(常数a>0)与曲线的图象有无穷多个公共点,其中有3个相邻的公共点自左至右分别为A,B,C,则点A与点C的距离=.9.在三棱锥S﹣ABC中,作SO⊥平面ABC,垂足为O.给出下列命题:①若三条侧棱SA,SB,SC与底面ABC所成的角相等,则O是△ABC的外心;②若三个侧面SAB,SBC,SCA与底面ABC所成的二面角相等,则O是△ABC的内心;③若三组对棱SA与BC,SB与CA,SC与AB中有两组互相垂直,则O是△ABC的垂心.则其中真命题的序号是.10.如图,在直角梯形ABCD中,AD∥BC,AD⊥CD,△ABD是边长为2的正三角形,P是平面ABCD内的动点,,设,则λ+μ的取值范围是.四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤11.设z,ω∈C,且|z|+=.(1)求z;(2)在|ω﹣2|=|z|,求复数ω的模的取值范围.12.已知向量,设函数(x∈R).(1)求函数f(x)的单调递减区间和对称中心的坐标;(2)将函数y=f(x)的图象向左平个单位后得到函数y=g(x)的图象,若关于x的方程g(x)=m在区间上有解求实数m的取值范围.13.袋中装有除颜色外完全相同的的4个球,其中有3个黑球和1个白球.现由甲乙两人从袋中轮流取球,取后不放,规定甲先取,乙后取,然后甲可再取,按下来再由乙取到有人取到白球,则马上终止取球,每次取球时,袋中的每个球被取出的概率是相等,记事件A i=“第i次取到的球是白球”,i=1,2,3.试将下列件A1,A2,A3表示,并求出相应事件的概率.(1)取球2次即终止;(2)最后一次取球的是甲.14.如图,在△ABC中,B=60°,点D在边AB上,AD=CD,BD=1.(1)若△BCD的面积为,求AB的长:(2)若,求角A的大小.15.从某小区抽100户居民进行月用电量调查,发现他们的月用电量都在50~350(度)之间,在进行适当分组(每组为左闭右开区间),并列出频率分分布表、画频率分布直方图后,将频率分布方图的全部6个矩形上方线段的中点自左右的顺序依次相连,再删掉这6个矩形,就得到了如图所示的“频率分布折线图”.(1)请画出频率分布直方图,并求出频率分布折线图x的值;(2)请结合频率分布直方图,求月用电量落在区间『50,200)(度)内的用户的月用电量的中均数;(3)已知在原始数据中,月用电量落在区间『50,200)(度)内的用户的月用电量的平均数为140(度),方差为1600,所有这100户的月川电量的平均数为188(度),方差为5200,且月用电最落在区间『50,200)(度)内的用户数的频率恰好与频率分布直方图中的数据相同,求月用电量在区间『200,350)(度)内的用户用电量的标准差.(参考数据:142=196,262=676,722=5184,482+1600=3904,1402+1600=21200,1882+5200=40544)16.如图,四棱锥P﹣ABCD的底面是正方形,PA⊥平面ABCD,PA=AB.点E是PD的中点,作EF⊥PC,交PC于点F.(1)设平面PAB与平面ACE的交线为l,试判断直线PB与直线/的位置关系,并给出证明;(2)求平面PAB与平面ACE所成的较小的二面角的余弦值;(3)求直线PD与平面AEF所成角的正切值.——★参考答案★——一、单选题:本题共6小题,每小题5分,共30分在每小题给出的四个选项中,只有一个是符合题目要求的.1.D『解析』对选项A,当三点共线时,不能确定一个平面,故A错误;对选项B:一条直线和直线外一个点确定一个平面,故B错误;对选项C:如果这两条直线异面,则不可以确定一个平面,故C错误;对选项D,梯形的上底和下底是一对平行线,可以确定一个平面,故D正确.故选:D.2.B『解析』∵向量,且,∴=﹣4+2m=0.解得m=2.故选:B.3.B『解析』共有22个数据,第11个数据为131,第12个数据为132,所以中位数为;数据122出现3次,出现次数最多,所以众数为122;最大值为112,最小值为148,所以极差为148﹣112=36;故选:B.4.C『解析』如图,作BC的中点F,则EF∥AB,所以异面直线AB和DE所成的夹角即直线EF和DE所成的夹角,即∠DEF或其补角,因为AC⊥BC,CA=CB=2,所以,所以,因为AD⊥平面ABC,所以AD⊥AC,所以,连接AF,则,因为AD⊥平面ABC,又AF⊂平面ABC,所以AD⊥AF,所以,在△DEF中,由余弦定理可得,又∠DEF∈(0,180°),所以∠DEF=120°,故直线EF和DE所成的夹角为60°.故选:C.5.B『解析』设圆锥的母线长为l,顶角为θ,则过圆锥SO的两条母线的截面三角形面积为S =l2sinθ,当sinθ=1时S取得最大值,此时θ=,所以圆锥的轴截面中,顶角θ的取值范围是(0,』.故选:B.6.C『解析』∵△ABC的面积为,∴,∴a2=bc sin A,∴A错误;根据余弦定理,,且,∴,∴B错误;,∴,∴,且tanφ=2,∴的最大值为,∴C正确;∵,∴的最大值为1,∴D错误.故选:C.三、填空题:本题共4小题,每小题5分,共20分.7.﹣『解析』∵复数和θ都是实数,若z1=z2,则2=tanθ,且m(cos2θ+2sin2θ)=cos2θ,∴m====﹣,故答案为:﹣.8.『解析』根据直线y=a与曲线的图象交点成周期性出现,其中3个相邻的交点自左至右分别为A,B,C,则点A与点C的距离恰好是1个周期,且y=2|tan(3x﹣)|的最小正周期为T=,所以AC=.故答案为:.9.①②③『解析』对于①,连接OA,OB,OC,见图1.由SO⊥平面ABC,可得∠SAO为SA与平面ABC所成角,∠SBO为SB与平面ABC所成角,∠SCO为SC与平面ABC所成角,且∠SAO=∠SBO=∠SCO,所以AO=BO=CO,即O为△ABC的外心,故①正确;对于②,过S作SD⊥AC,垂足为D,连接OD,过S作SE⊥BC,垂足为E,连接OE,过S作SF⊥AB,垂足为F,连接OF,见图2.由三垂线定理的逆定理可得OD⊥AC,OE⊥BC,OF⊥AB,可得∠SFO为侧面SAB与底面ABC所成角的平面角,∠SEO为侧面SCB与底面ABC所成角的平面角,∠SDO为侧面SAC与底面ABC所成角的平面角,且∠SFO=∠SEO=∠SDO,所以OD=OE=OF,即O为△ABC的内心,故②正确;对于③,连接OA,OB,OC,见图3.若SA⊥BC,SB⊥AC,由三垂线定理的逆定理可得OA⊥BC,OB⊥AC,即为•=0,•=0,即有•(﹣)=0,•(﹣)=0,所以•=•=•,即有•(﹣)=•=0,则OC⊥AB,即O为△ABC的垂心,故③正确.故答案为:①②③.10.『1,2』『解析』根据题意建立平面直角坐标系:直角梯形ABCD中,CB⊥CD,AD∥BC,△ABD是边长为2的正三角形,解得:BC=1,CD=,AB=BD=AD=2,所以A(﹣2,0),B(﹣1,),C(0,),D(0,0),则=(2,0),=(1,)由||=,可得点P在以C为圆心,为半径的圆上运动,该圆方程为x²+(y﹣)²=,设P(cosα,sinα+),则=(cosα+2,sinα+),由于,则:(cosα+2,sinα+)=λ(2,0)+μ(1,),整理得:,所以,所以λ+μ=sinα+cosα+=sin(α+)+,因为﹣1≤sin(α+)≤1,所以1≤sin(α+)+≤2,所以λ+μ的取值范围是『1,2』.故答案为:『1,2』.四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤11.解:(1)设z=a+bi,a,b∈R,∵|z|+=,∴=,则,解得,∴z=﹣2i.(2)设ω=x+yi,x,y∈R,由|ω﹣2|=|z|,可得(x﹣2)2+y2=4,∴y2=4﹣(x﹣2)2≥0,∴0≤x≤4,∴|ω|==,∴|ω|∈『0,4』.12.解:(1)由题可得f(x)==(2cos x,cos x)(sin x,﹣2cos x)=2cos x sin x﹣2cos²x=sin2x﹣cos2x+1=2sin(2x﹣)+1,令+2kπ≤2x﹣≤+2kπ,k∈Z,解得+kπ≤x≤+kπ,k∈Z,即f(x)的单调递减区间为『+kπ,+kπ』(k∈Z);令2x﹣=kπ,k∈Z,解得x=+(k∈Z),即f(x)的对称中心坐标为(+,0)(k∈Z);(2)由(1)可知g(x)=2sin『2(x+)﹣』+1=2sin(2x+)+1,若关于x的方程g(x)=m在区间『0,』上有解,在区间『0,』上,2x+∈『,』,sin(2x+)∈『﹣,1』,g(x)∈『0,2』.若方程g(x)=m在区间『0,』上有解,则m∈『0,2』.13.解:(1)取球2次终止情况为第一次取黑球,第二次取白球,则P2=.(2)最后一次取球的是甲,则意味着取到白球的次数为奇数,则包括A1,A3两种情况,A1事件对应的概率P1=,A3事件对应的概率P3=,∴最后一次取球的是甲的概率P=P1+P2=.14.解:(1)在△BCD中,B=60°,BD=1,若△BCD的面积为,则S△BCD=BD•BC•sin B=,所以BC=,所以BC=2,则CD===,所以AD=CD=,所以AB=AD+BD=+1.(2)在△ACD中,AD=CD,可设A=∠ACD=θ,则∠ADC=π﹣2θ,又,由正弦定理,得=,所以CD=,在△BCD中,∠BDC=2θ,∠BCD=﹣2θ,由正弦定理,得=,即=,化简得cosθ=sin(﹣2θ),于是sin(﹣θ)=sin(﹣2θ),因为0<θ<,所以0<﹣θ<,﹣<﹣2θ<,所以﹣θ=﹣2θ或﹣θ+﹣2θ=π,解得θ=或θ=,即角A的大小为或.15.解:(1)频率分布直方图:由频率分布折线图或频率分布直方图得(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,即x=0.0044;(2)月用电量落在区间『50,100)(度),『100,150)(度),『150,200)(度)内的用户数分别为0.0024×50×100=12,0.0036×50×100=18,0.0060×50×100=30所平均数=(25×12+125×18+175×30)÷60=140(度);(3)由(2)知,月用电落在(间『50,200)(度)的户数=12+18+30=60月用电量在区间『200,350)(度)内的户数=100﹣60=40设前60户的月用电分别为x i,(i=1,2.…,60),平均数为=140,方差=1600 后60户的月用电量分别为y i,(i=1,2.…,60).平均数为,方差为全部100户的月用电量分别为,平均数,方差为s2=5200060+40=100,即.故有,有,所以:,故.16.证明:(1)连结BD交AC交于G,∵ABCD是正方形,∴G为BD的中点,又∵E是PD的中点,∴EG//PB,又∵PB⊄平面ACE,EG⊂平面ACE,∴.PB//平面ACE,又PB⊂平面PAB,平面PAB∩平面ACE=l,∴PB//l.解:(2)∵PA⊥平面ABCD,AB⊂平面ABCD,∴PA⊥AB,设正方形ABCD的边长为4,∵PA=PB,∴△PAB的中线AH=2,PB=4,AH⊥PB,同理AE=2,PD=4,AE⊥PD,∵EG=PB=2,AG=AC=2,∴△AEG为正三角形,中线AI=,且AI⊥EG,∵AH⊥PB,PB//l,∴AH⊥l,同理AI⊥l,∴∠HAI是二面角CE﹣l﹣PB的一个平面角,又∵在正三角形△PBD中HI=,∴cos∠HAI===,则平面PAB与平面ACE所成的较小的面角的余弦值为.(3)同(2)中PA⊥AB,得PA⊥CD,又∵在正方形ABCD中,AD⊥CD,PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,∴CD⊥平面PAD,同理AE⊥平面PCD同理PF⊥面AEF∴∠PEF是直线PD与平面AEF所成的角,∵在Rt△PEF和Rt△PCD中得tan∠PEF=cot∠CPD===,∴直线PD与平面AEF所成角的正切值为.湖北省武汉市华中师范大学第一附属中学2020-2021学年高一下学期期末考试数学试卷一、单选题:本题共6小题,每小题5分,共30分在每小题给出的四个选项中,只有一个是符合题目要求的.1.下列命题正确的是()A.三点确定一个平面B.一条直线和一个点确定一个平面C.两条不平行的直线确定一个平面D.梯形可确定一个平面2.已知向量,且,则m=()A.8 B.2 C.﹣2 D.﹣83.某同学对他进入高中以来的数学测验的成绩进行了统计,得到如图所示的茎叶图其中的“茎”指竖线左边的一列数,它表示个数的高位,本茎叶图中的“茎”表示一个三位数的百位、十位数;“叶”指竖线右边的从“茎”旁边生出来的数,它表示一个数的低位,本茎叶图中的“1”表示相应三位数的个位数如第二行:竖线左边为“12”,竖线右边第5个数为“7”,这两个数字结合起来就是该同学某次数学测验的成绩“127”.则这组成绩的中位数、众数、极差分别是()A.130,122,36 B.131.5,122,36 C.131,136,29 D.131.5,122,29 4.在三棱锥D﹣ABC中,AC⊥BC,AC=BC=2,AD⊥平面ABC,AD=1,E是线段AC 的中点,则异面直线AB和DE所成的角等于()A.135°B.120°C.60° D.45°5.用过圆锥的轴的平面去截圆锥得到的截面,叫做圆锥的轴截面,圆锥的轴截面是以图锥的两条母线为腰的等腰三角形,这个等腰三角形的顶角,叫做圆锥的顶角.已知过圆锥SO的两条母线的截面三角形有无穷多个,这些截面中,面积最大的恰好是圆锥SO的轴截面,则圆锥SO的顶角的取值范围是()A.(0,π)B.C.D.6.在△ABC巾,角A、B、C所对的边分别为a,b,c,△ABC的面积为,则()A.a2≠bc sin A B.C.的最大值为D.的最大值三、填空题:本题共4小题,每小题5分,共20分.7.已知复数和θ都是实数,若z1=z2,则m=.8.已知直线y=a(常数a>0)与曲线的图象有无穷多个公共点,其中有3个相邻的公共点自左至右分别为A,B,C,则点A与点C的距离=.9.在三棱锥S﹣ABC中,作SO⊥平面ABC,垂足为O.给出下列命题:①若三条侧棱SA,SB,SC与底面ABC所成的角相等,则O是△ABC的外心;②若三个侧面SAB,SBC,SCA与底面ABC所成的二面角相等,则O是△ABC的内心;③若三组对棱SA与BC,SB与CA,SC与AB中有两组互相垂直,则O是△ABC的垂心.则其中真命题的序号是.10.如图,在直角梯形ABCD中,AD∥BC,AD⊥CD,△ABD是边长为2的正三角形,P是平面ABCD内的动点,,设,则λ+μ的取值范围是.四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤11.设z,ω∈C,且|z|+=.(1)求z;(2)在|ω﹣2|=|z|,求复数ω的模的取值范围.12.已知向量,设函数(x∈R).(1)求函数f(x)的单调递减区间和对称中心的坐标;(2)将函数y=f(x)的图象向左平个单位后得到函数y=g(x)的图象,若关于x的方程g(x)=m在区间上有解求实数m的取值范围.13.袋中装有除颜色外完全相同的的4个球,其中有3个黑球和1个白球.现由甲乙两人从袋中轮流取球,取后不放,规定甲先取,乙后取,然后甲可再取,按下来再由乙取到有人取到白球,则马上终止取球,每次取球时,袋中的每个球被取出的概率是相等,记事件A i=“第i次取到的球是白球”,i=1,2,3.试将下列件A1,A2,A3表示,并求出相应事件的概率.(1)取球2次即终止;(2)最后一次取球的是甲.14.如图,在△ABC中,B=60°,点D在边AB上,AD=CD,BD=1.(1)若△BCD的面积为,求AB的长:(2)若,求角A的大小.15.从某小区抽100户居民进行月用电量调查,发现他们的月用电量都在50~350(度)之间,在进行适当分组(每组为左闭右开区间),并列出频率分分布表、画频率分布直方图后,将频率分布方图的全部6个矩形上方线段的中点自左右的顺序依次相连,再删掉这6个矩形,就得到了如图所示的“频率分布折线图”.(1)请画出频率分布直方图,并求出频率分布折线图x的值;(2)请结合频率分布直方图,求月用电量落在区间『50,200)(度)内的用户的月用电量的中均数;(3)已知在原始数据中,月用电量落在区间『50,200)(度)内的用户的月用电量的平均数为140(度),方差为1600,所有这100户的月川电量的平均数为188(度),方差为5200,且月用电最落在区间『50,200)(度)内的用户数的频率恰好与频率分布直方图中的数据相同,求月用电量在区间『200,350)(度)内的用户用电量的标准差.(参考数据:142=196,262=676,722=5184,482+1600=3904,1402+1600=21200,1882+5200=40544)16.如图,四棱锥P﹣ABCD的底面是正方形,PA⊥平面ABCD,PA=AB.点E是PD的中点,作EF⊥PC,交PC于点F.(1)设平面PAB与平面ACE的交线为l,试判断直线PB与直线/的位置关系,并给出证明;(2)求平面PAB与平面ACE所成的较小的二面角的余弦值;(3)求直线PD与平面AEF所成角的正切值.——★参考答案★——一、单选题:本题共6小题,每小题5分,共30分在每小题给出的四个选项中,只有一个是符合题目要求的.1.D『解析』对选项A,当三点共线时,不能确定一个平面,故A错误;对选项B:一条直线和直线外一个点确定一个平面,故B错误;对选项C:如果这两条直线异面,则不可以确定一个平面,故C错误;对选项D,梯形的上底和下底是一对平行线,可以确定一个平面,故D正确.故选:D.2.B『解析』∵向量,且,∴=﹣4+2m=0.解得m=2.故选:B.3.B『解析』共有22个数据,第11个数据为131,第12个数据为132,所以中位数为;数据122出现3次,出现次数最多,所以众数为122;最大值为112,最小值为148,所以极差为148﹣112=36;故选:B.4.C『解析』如图,作BC的中点F,则EF∥AB,所以异面直线AB和DE所成的夹角即直线EF和DE所成的夹角,即∠DEF或其补角,因为AC⊥BC,CA=CB=2,所以,所以,因为AD⊥平面ABC,所以AD⊥AC,所以,连接AF,则,因为AD⊥平面ABC,又AF⊂平面ABC,所以AD⊥AF,所以,在△DEF中,由余弦定理可得,又∠DEF∈(0,180°),所以∠DEF=120°,故直线EF和DE所成的夹角为60°.故选:C.5.B『解析』设圆锥的母线长为l,顶角为θ,则过圆锥SO的两条母线的截面三角形面积为S =l2sinθ,当sinθ=1时S取得最大值,此时θ=,所以圆锥的轴截面中,顶角θ的取值范围是(0,』.故选:B.6.C『解析』∵△ABC的面积为,∴,∴a2=bc sin A,∴A错误;根据余弦定理,,且,∴,∴B错误;,∴,∴,且tanφ=2,∴的最大值为,∴C正确;∵,∴的最大值为1,∴D错误.故选:C.三、填空题:本题共4小题,每小题5分,共20分.7.﹣『解析』∵复数和θ都是实数,若z1=z2,则2=tanθ,且m(cos2θ+2sin2θ)=cos2θ,∴m====﹣,故答案为:﹣.8.『解析』根据直线y=a与曲线的图象交点成周期性出现,其中3个相邻的交点自左至右分别为A,B,C,则点A与点C的距离恰好是1个周期,且y=2|tan(3x﹣)|的最小正周期为T=,所以AC=.故答案为:.9.①②③『解析』对于①,连接OA,OB,OC,见图1.由SO⊥平面ABC,可得∠SAO为SA与平面ABC所成角,∠SBO为SB与平面ABC所成角,∠SCO为SC与平面ABC所成角,且∠SAO=∠SBO=∠SCO,所以AO=BO=CO,即O为△ABC的外心,故①正确;对于②,过S作SD⊥AC,垂足为D,连接OD,过S作SE⊥BC,垂足为E,连接OE,过S作SF⊥AB,垂足为F,连接OF,见图2.由三垂线定理的逆定理可得OD⊥AC,OE⊥BC,OF⊥AB,可得∠SFO为侧面SAB与底面ABC所成角的平面角,∠SEO为侧面SCB与底面ABC所成角的平面角,∠SDO为侧面SAC与底面ABC所成角的平面角,且∠SFO=∠SEO=∠SDO,所以OD=OE=OF,即O为△ABC的内心,故②正确;对于③,连接OA,OB,OC,见图3.若SA⊥BC,SB⊥AC,由三垂线定理的逆定理可得OA⊥BC,OB⊥AC,即为•=0,•=0,即有•(﹣)=0,•(﹣)=0,所以•=•=•,即有•(﹣)=•=0,则OC⊥AB,即O为△ABC的垂心,故③正确.故答案为:①②③.10.『1,2』『解析』根据题意建立平面直角坐标系:直角梯形ABCD中,CB⊥CD,AD∥BC,△ABD是边长为2的正三角形,解得:BC=1,CD=,AB=BD=AD=2,所以A(﹣2,0),B(﹣1,),C(0,),D(0,0),则=(2,0),=(1,)由||=,可得点P在以C为圆心,为半径的圆上运动,该圆方程为x²+(y﹣)²=,设P(cosα,sinα+),则=(cosα+2,sinα+),由于,则:(cosα+2,sinα+)=λ(2,0)+μ(1,),整理得:,所以,所以λ+μ=sinα+cosα+=sin(α+)+,因为﹣1≤sin(α+)≤1,所以1≤sin(α+)+≤2,所以λ+μ的取值范围是『1,2』.故答案为:『1,2』.四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤11.解:(1)设z=a+bi,a,b∈R,∵|z|+=,∴=,则,解得,∴z=﹣2i.(2)设ω=x+yi,x,y∈R,由|ω﹣2|=|z|,可得(x﹣2)2+y2=4,∴y2=4﹣(x﹣2)2≥0,∴0≤x≤4,∴|ω|==,∴|ω|∈『0,4』.12.解:(1)由题可得f(x)==(2cos x,cos x)(sin x,﹣2cos x)=2cos x sin x﹣2cos²x=sin2x﹣cos2x+1=2sin(2x﹣)+1,令+2kπ≤2x﹣≤+2kπ,k∈Z,解得+kπ≤x≤+kπ,k∈Z,即f(x)的单调递减区间为『+kπ,+kπ』(k∈Z);令2x﹣=kπ,k∈Z,解得x=+(k∈Z),即f(x)的对称中心坐标为(+,0)(k∈Z);(2)由(1)可知g(x)=2sin『2(x+)﹣』+1=2sin(2x+)+1,若关于x的方程g(x)=m在区间『0,』上有解,在区间『0,』上,2x+∈『,』,sin(2x+)∈『﹣,1』,g(x)∈『0,2』.若方程g(x)=m在区间『0,』上有解,则m∈『0,2』.13.解:(1)取球2次终止情况为第一次取黑球,第二次取白球,则P2=.(2)最后一次取球的是甲,则意味着取到白球的次数为奇数,则包括A1,A3两种情况,A1事件对应的概率P1=,A3事件对应的概率P3=,∴最后一次取球的是甲的概率P=P1+P2=.14.解:(1)在△BCD中,B=60°,BD=1,若△BCD的面积为,则S△BCD=BD•BC•sin B=,所以BC=,所以BC=2,则CD===,所以AD=CD=,所以AB=AD+BD=+1.(2)在△ACD中,AD=CD,可设A=∠ACD=θ,则∠ADC=π﹣2θ,又,由正弦定理,得=,所以CD=,在△BCD中,∠BDC=2θ,∠BCD=﹣2θ,由正弦定理,得=,即=,化简得cosθ=sin(﹣2θ),于是sin(﹣θ)=sin(﹣2θ),因为0<θ<,所以0<﹣θ<,﹣<﹣2θ<,所以﹣θ=﹣2θ或﹣θ+﹣2θ=π,解得θ=或θ=,即角A的大小为或.15.解:(1)频率分布直方图:由频率分布折线图或频率分布直方图得(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,即x=0.0044;(2)月用电量落在区间『50,100)(度),『100,150)(度),『150,200)(度)内的用户数分别为0.0024×50×100=12,0.0036×50×100=18,0.0060×50×100=30所平均数=(25×12+125×18+175×30)÷60=140(度);(3)由(2)知,月用电落在(间『50,200)(度)的户数=12+18+30=60月用电量在区间『200,350)(度)内的户数=100﹣60=40设前60户的月用电分别为x i,(i=1,2.…,60),平均数为=140,方差=1600 后60户的月用电量分别为y i,(i=1,2.…,60).平均数为,方差为全部100户的月用电量分别为,平均数,方差为s2=5200060+40=100,即.故有,有,所以:,故.16.证明:(1)连结BD交AC交于G,∵ABCD是正方形,∴G为BD的中点,又∵E是PD的中点,∴EG//PB,又∵PB⊄平面ACE,EG⊂平面ACE,∴.PB//平面ACE,又PB⊂平面PAB,平面PAB∩平面ACE=l,∴PB//l.解:(2)∵PA⊥平面ABCD,AB⊂平面ABCD,∴PA⊥AB,设正方形ABCD的边长为4,∵PA=PB,∴△PAB的中线AH=2,PB=4,AH⊥PB,同理AE=2,PD=4,AE⊥PD,∵EG=PB=2,AG=AC=2,∴△AEG为正三角形,中线AI=,且AI⊥EG,∵AH⊥PB,PB//l,∴AH⊥l,同理AI⊥l,∴∠HAI是二面角CE﹣l﹣PB的一个平面角,又∵在正三角形△PBD中HI=,∴cos∠HAI===,则平面PAB与平面ACE所成的较小的面角的余弦值为.(3)同(2)中PA⊥AB,得PA⊥CD,又∵在正方形ABCD中,AD⊥CD,PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,∴CD⊥平面PAD,同理AE⊥平面PCD同理PF⊥面AEF∴∠PEF是直线PD与平面AEF所成的角,∵在Rt△PEF和Rt△PCD中得tan∠PEF=cot∠CPD===,∴直线PD与平面AEF所成角的正切值为.。
2021-2022学年湖北省武汉市华中师范大学第一附属中学高一上学期期末数学试题(解析版)

2021-2022学年湖北省武汉市华中师范大学第一附属中学高一上学期期末数学试题一、单选题1.设集合{}lg21,2810x M xx N x ⎧⎫⎪⎪⎛⎫=>=>⎨⎬ ⎪⎝⎭⎪⎪⎩⎭∣∣,则()RM N =( )A .1,32⎛⎫⎪⎝⎭B .()2,3C .1,32⎛⎤ ⎥⎝⎦D .(]2,3【答案】C【分析】先根据对数的运算性质求出集合A ,由指数函数的单调性求出集合B ,然后后补集和交集的运算可得答案.【详解】由1lglg222lg 110100211-⎛⎫⎝===⎪⎭,则lg2110x ⎛⎫> ⎪⎝⎭,即12x >所以集合1,2A ⎛⎫=+∞ ⎪⎝⎭又28x >可得3x >,所以集合()3,B =+∞ 所以(],3R N =-∞,则()1,32R M N ⎛⎤= ⎥⎝⎦故选:C2.下列函数既是奇函数,又在区间[]1,1-上单调递减的是 A .()sin f x x = B .()|1|f x x =-+ C .()1()2xx f x a a -=+ D .2()ln2xf x x-=+ 【答案】D【解析】分别根据函数奇偶性和单调性的定义和性质进行判断,即可得到结论. 【详解】选项A :()sin f x x =,是奇函数,在[1,1]-是增函数, 不满足条件;选项B :()|1|f x x =-+不是奇函数,不满足条件; 选项C :()1()2xx f x a a -=+是偶函数,不满足条件; 选项D :2()ln 2xf x x-=+定义域为(2,2)-, 22()ln ln ()22x xf x f x x x+--==-=--+,是奇函数, 24()lnln(1)x f x -==-在(2,2)-是减函数;【点睛】本题考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性,属于基础题.3.已知幂函数a y x =的图象过点13,9⎛⎫ ⎪⎝⎭,则下列两函数的大小关系为:()224a x x -+( )(3)a -A .≤B .≥C .<D .>【答案】A【分析】根据已知条件求得2a =-,运用作差法比较两式大小即可. 【详解】因为幂函数a y x =的图象过点13,9⎛⎫⎪⎝⎭,所以139a=,解得2a =-.所以()()()2222224(3)2491111193aa x x x x x -+--+-=-=-⎡⎤⎣⎦-+,因为()22913x ⎤+⎣⎦-⎡≥,所以()22110931x <≤⎡⎤+⎣⎦-,所以()22110193x ⎣--≤⎡⎤+⎦, 即()224(3)aa x x ≤-+-. 故选:A4.下列四个函数:①1y x =-+,②133,01,0x x y x x ⎧≤⎪=⎨⎪>⎩,③ln y x =,④212x y x -=-,其中定义域和值域相同的函数有( ) A .4个 B .3个C .2个D .1个【答案】B【分析】分别求出四个函数的定义域和值域即可判断. 【详解】解:对①:函数的定义域和值域都是R ;对②:根据分段函数和幂函数的性质,可知函数的定义域和值域都是R ; 对③:函数的定义域为()(),00,∞-+∞,值域为R ;对④:因为函数2132x y -==+,所以函数的定义域为()(),22,-∞+∞,值域为()(),22,-∞+∞.所以①②④是定义域和值域相同的函数, 故选:B.5.下列关于命题“若1x >,则215x +>”(假命题)的否定,正确的是( ) A .若1x >,则215x +≤B .存在一个实数x ,满足1x >,但215x +≤C .任意实数x ,满足1x >,但215x +≤D .若存在一个实数x ,满足1x ≤,则215x +≤ 【答案】B【分析】先要明确“若1x >,则215x +>”是一个全称命题,因此其否定是特称命题形式,由此可判断答案.【详解】命题“若1x >,则215x +>”(假命题)是一个全称命题, 因此其否定为“存在一个实数x ,满足1x >,但215x +≤”, 故选:B.6.函数()2442x xf x x x --=+-的图象大致为( )A .B .C .D .【答案】D【分析】根据函数解析式求得函数定义域,判断函数奇偶性,再取几个特殊值运用排除【详解】由题意知,220x x +-≠,解得1x ≠±,所以()f x 定义域()()(),11,11,-∞-⋃-+∞关于原点对称,又因为()()()224444=22x xx xf x f x x x x x -----==-+--+--,所以此函数为奇函数,图像关于原点对称,排除A.当12x =时,1216201125242f -⎛⎫==-< ⎪⎝⎭+-,排除B.()00f x x =⇒=,函数只有1个零点,排除C.故选:D7.“函数3y x ax =-+在()0,1上是增函数”是:“实数3a >”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B【分析】导函数在()0,1上大于零恒成立可得a 的取值范围,进而比较得解. 【详解】230y x a '=-+≥在()0,1上恒成立,可得2310a -⨯+≥,3a ≥, 所以“函数3y x ax =-+在()0,1上是增函数”是:“实数3a >”的必要不充分条件. 故选:B.8.已知实数,,a b c 满足a b c >>,函数()111f x x a x b x c=++---有两个零点()1212,x x x x <,则关于函数()f x 的零点12,x x 的下列关系式一定正确的是( )A .12x c b x a <<<<B .12c x b a x <<<<C .12c x x b a <<<<D .12c x b x a <<<<【答案】D【分析】令()0f x =化简可得:()()()()()()=0x b x c x a x c x a x b --+--+--, 令()()()()()()()g x x b x c x a x c x a x b =--+--+--,计算可得()0g a >,()0g b <,()0g c >,进而可判断结果. 【详解】方程111=0x a x b x c++---即为()()()()()()=0x b x c x a x c x a x b --+--+--, 令()()()()()()()g x x b x c x a x c x a x b =--+--+--,()()()0g a a b a c ∴=-->,()()()0g b b a b c =--<,()()()0g c c a c b =-->.根据零点存在性定理得出在(,),(,)c b b a 上函数()g x 各有一个零点,所以12c x b x a <<<<.故选:D. 二、多选题9.下列计算结果为有理数的有( ) A .lg2lg5+ B .sin3πC .1ln22e - D .232coscos cos 884πππ【答案】ACD【分析】由对数的运算法则和性质可判断A,C 选项;选项B. 求出sin 3π的值可判断;选项D. 3cossin 88ππ=,由正弦的二倍角公式可判断. 【详解】选项A. lg2lg5lg101+==,是有理数.选项B. sin3π=,不是有理数. 选项C. 2log 1ln2220e e e e e -=-=-=,是有理数. 选项D. 22232coscos cos 2cos cos cos 2sin cos cos 2sin cos sin 18842884884442πππππππππππππ⎛⎫=-==== ⎪⎝⎭是有理数. 故选:ACD10.已知角α是锐角,若sin ,cos αα是关于x 的方程20x mx n ++=的两个实数根,则下列关于实数,m n 的判断正确的是( ) A .2210m n --= B .0mn > C .10m n ++> D .10,2n ⎛⎤∈ ⎥⎝⎦【答案】ACD【分析】根据韦达定理得到sin cos .sin cos m n αααα+=-=,由角α是锐角可判断0,0m n <>,从而判断B;将sin cos m αα+=-两边平方,可得到,m n 之间关系,判断A对错;利用A 的结论写出1m n ++的表达式,配方后可判断C 的对错;利用2210m n --=得到212m n -=,结合m 的范围,确定n 的范围,判断D 的正误.所以sin cos ,sin cos m n αααα+=-=,因为角α是锐角,所以0,0m n <>,则0mn <,故B 错误; 又22(sin cos )12sin cos m αααα+=+=,即212n m +=, 所以2210m n --=,故A 正确; 而221(1)11022m m m n m -+++=++=>,故C 正确,又(sin cos ))4m πααα=-+=+,3(,)444πππα+∈ ,所以)[1)4m πα=+∈-,2(1,2]m ∈ ,由A 知212m n -=,则1(0,]2n ∈ ,故D 正确; 故选:ACD11.已知函数()()2ln 1f x x bx b =--+,列说法正确的有( )A .当0b =时,函数()f x 的定义域为RB .当0b =吋,函数()f x 的值域为RC .函数()f x 有最小值的充要条件为:2440b b +-<D .若()f x 在区间[)2,+∞上单调递增,则实数b 的取值范围是(],4∞- 【答案】AC【分析】对于AB ,当0b =时,直接求解函数的定义域和值域即可,对于C ,换元后,只要24404b b +-->即可,对于D ,换元后利用复合函数求单调性的方法求解即可 【详解】对于A ,当0b =时,210x 恒成立,所以函数()f x 的定义域为R ,所以A正确,对于B ,当0b =时,()()2ln 1f x x =+,因为211x +≥,所以()2ln 1ln10x +≥=,所以函数的值域为[0,)+∞,所以B 错误,对于C ,令22244124b b b t x bx b x +-⎛⎫=--+=-- ⎪⎝⎭,则2min 444b b t +-=-,当24404b b +-->,即2440b b +-<时, ()f x 一定有最小值,反之也成立,所以C 正确,对于D ,令22244124b b b t x bx b x +-⎛⎫=--+=-- ⎪⎝⎭,则ln y t =,当()f x 在区间[)2,+∞上单调递增时,224210bb b ⎧≤⎪⎨⎪--+>⎩,解得53b <,所以D 错误,故选:AC12.如图所示,点,M N 是函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图像与x 轴的交点,点P 在,M N 之间的图象上运动,若()1,0M -,且当MPN △的面积最大时,PM PN ⊥,则下列说法正确的有( )A .()02f =B .()f x 的图象关于直线5x =对称C .()f x 的单调增区间为[]()18,18k k k Z -++∈D .[]()12,18,18x x k k k Z ∀∈-++∈,均有()()121222f x f x x x f ++⎛⎫≥ ⎪⎝⎭【答案】ABD【分析】根据题意求出,ωϕ从而求得此函数表达式,再运用三角函数相关知识对各选项逐一分析即可.【详解】因为当MPN △的面积最大时,PM PN ⊥,P 在最高点, 所以此时在Rt PMN 中,2224P MN y ==⨯=, 所以42TMN ==,8T =,即28πω=,4πω=, 因为函数()2sin 4f x x πϕ⎛⎫=+ ⎪⎝⎭经过()1,0M -,则()12sin 04f πϕ⎛⎫-=-+= ⎪⎝⎭,即()(),44k k Z k k Z ππϕπϕπ-+=∈=+∈,又因为2πϕ<,所以取4πϕ=.所以函数表达式为()2sin 44f x x ππ⎛⎫=+ ⎪⎝⎭.对于A ,()202sin 2242f π⎛⎫=== ⎪⎝⎭A 正确; 对于B ,()5352sin 2sin 2442f πππ⎛⎫⎛⎫=+==-⎪ ⎪⎝⎭⎝⎭,取得函数最小值,所以()f x 的图象关于直线5x =对称,故B 正确;对于C ,令()222442k x k k Z ππππππ-≤+≤+∈,解得()8381k x k k Z -≤≤+∈,所以()f x 的单调增区间为[]()38,18k k k Z -++∈,故C 错误;对于D ,由C 选项分析以及题意可知函数图像在[]()18,18k k k Z -++∈区间上为x 轴上方单调递增部分,结合图像可知,此部分图像上凸,满足[]()12,18,18x x k k k Z ∀∈-++∈,均有()()121222f x f x x x f ++⎛⎫≥ ⎪⎝⎭,故D 正确故选:ABD 三、填空题13.《九章算术》是我国古代数学名著,其中有这样一个问题:“今有宛田,下周三十步,径十六步,问为田几何?”意思说:现有扇形田,弧长三十步,直径十六步,问面积多少?书中给出计算方法:以径乘周,四而一,即扇形的面积等于直径乘以弧长再除以4,在此问题中,扇形的圆心角的弧度数是___________. 【答案】154【分析】根据题意可知扇形的弧长和直径,再计算扇形的面积和圆心角弧度数. 【详解】解:由题意,扇形的弧长30l =,直径16d =, 所以扇形的圆心角弧度数是301584l r ==, 故答案为:154.14.已知()0,,cos απα∈=β的顶点与坐标原点重合,始边与x 轴非负半轴重合,终边交圆心为坐标原点的单位圆于点y ⎛⎫ ⎪ ⎪⎝⎭,且()0,βπ∈,则2αβ-=___________.【答案】4π-【分析】由同角三角函数的关系先求出sin α,由二倍角公式求出sin 2,cos 2αα,由三角函数的定义以及同角三角函数的关系先求出cos ,sin ββ,再分析出20παβ-<-<,从而求出()cos 2αβ-的值,得出答案.【详解】由()0,,cos απα∈=sin α===所以4sin 22sin cos 2ααα===,223cos 212sin 155αα=-=-=所以由()0,απ∈,cos20α>,可得022πα<<由角β终边交圆心为坐标原点的单位圆于点y ⎛⎫ ⎪ ⎪⎝⎭,且()0,βπ∈, 则,2πβπ⎛⎫∈ ⎪⎝⎭,cos 10x r β==-则sin 10β=== 所以20παβ-<-<所以由()cos 2cos2cos sin 2sin αβαβαβ-=+345105102⎛⎫=⨯-+⨯= ⎪⎝⎭ 所以24παβ-=- 故答案为:4π-15.已知函数()()f x x R ∈是周期为4的奇函数,()(]24,1,2xf x x =-∈,则()2log 7f =___________.【答案】127【分析】由对数运算计算取值区间,再根据函数()f x 的周期性和奇函数,可以求出()2log 7f .【详解】因为22log 73<< ,所以23log 72-<-<-,214log 72<-< 由题意知,()()()()24log 72221612log 7log 74log 724477f f f -⎛⎫=--=--=--=--= ⎪⎝⎭故答案为:127四、双空题16.若实数,x m 满足102x m <<(m 为常数),为减小计算量,我们可以借助二元基本不等式求出()2x m x m-的最大值.基本步骤如下:10,0,20,2x m x m x <<∴>->()2222(2)2(2)228x m x x m x x m x m m m m ⎡⎤+-⎢⎥--⎣⎦∴=≤=,当且()们可以解决下面的问题:若α为锐角,则函数()2cos 1cos (cos 1)y ααα-=+得最大值为___________,当且仅当cos α=___________时,等号成立. 【答案】180.125 13【分析】根据题中所给例题求解过程进行类比求解即可.【详解】因为α为锐角,所以0cos 1α<<,所以cos 0α>,1cos 0α->, 所以()()()22222cos 1cos 2cos 1cos 2cos 1cos 1(cos 1)2(cos 1)2(cos 1)8y ααααααααα⎡⎤+-⎢⎥--⎣⎦==≤=+++, 当且仅当2cos 1cos αα=-,即1cos 3α=时等号成立. 故答案为:18;13五、解答题17.已知()0,θπ∈,且1sin cos 5θθ+=. (1)求()()cos 4cos cos 2πθθππθπθ⎛⎫++ ⎪⎝⎭⎛⎫++-+ ⎪⎝⎭的值; (2)求1sin2cos21tan θθθ+-+的值.【答案】(2)2425-【分析】(1)先求出sin cos θθ,,再化简代数式求值; (2) 利用二倍角,化简代数式求值. (1)由1sin cos 5θθ+=①两边平方并化简得242sin cos 025θθ=-<, ()0sin 0cos 0θπθθ∈∴><,,,7sin cos 5θθ∴-==② 由①②得:43sin cos 55θθ==-,.()())()()cos cos sin 4222sin cos sin cos cos cos 2πθθπθθθθπθθθθθπθ⎛⎫++- ⎪⎝⎭===-+-+⎛⎫++-+ ⎪⎝⎭()22sin cos sin cos 1sin2cos22sin cos 2sin =sin 1tan sin cos 1cos θθθθθθθθθθθθθθ++-+=+++ 242sin cos 25θθ==-. 18.已知函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象过点,012P π⎛⎫ ⎪⎝⎭,且图象上与P 点最近的一个最低点坐标为,53π⎛⎫- ⎪⎝⎭. (1)求函数()f x 的解析式;(2)若将函数()f x 的图象向左平移6π个单位长度后,再向下平移2个单位长度得到()g x 的图象,写出函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的单调递增区间(不需要写过程);并求出函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的值域. 【答案】(1)()5cos 23f x x π⎛⎫=+ ⎪⎝⎭ (2)单调递增区间为:,63ππ⎡⎤⎢⎥⎣⎦,值域为17,2⎡⎤-⎢⎥⎣⎦ 【分析】(1)由条件确定最大值,周期求A ,ω,再代特殊点求ϕ,由此可得函数()f x 的解析式;(2)由三角函数图象变换结论求函数()g x 的解析式,再结合余弦函数的性质求()g x 的单调区间和值域.(1)依题意可知:124312πππω⋅=-,解得:2ω=,又()f x 的图像的一个最低点为,53π⎛⎫- ⎪⎝⎭, 25,2,3A k k Z πϕππ∴=+=+∈,又23ππϕϕ<∴= ()5cos 23f x x π⎛⎫∴=+ ⎪⎝⎭ (2)将函数()f x 的图象向左平移6π个单位长度可得5cos 233y x ππ⎛⎫=++ ⎪⎝⎭的图象, 将函数25cos 23y x π⎛⎫=+ ⎪⎝⎭的图象向下平移2个单位长度可得25cos 223y x π⎛⎫=+- ⎪⎝⎭的图象,所以()25cos 223g x x π⎛⎫=+- ⎪⎝⎭, 由22223k x k ππππ-≤+≤可得563k x k ππππ-≤≤-, 所以函数()g x 在区间5,63k k ππππ⎡⎤--⎢⎥⎣⎦(k Z ∈)上为增函数,又,63x ππ⎡⎤∈-⎢⎥⎣⎦函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的单调递增区间为:,63ππ⎡⎤⎢⎥⎣⎦ 又24,263333x x πππππ-≤≤∴≤+≤, 21211cos 2,75cos 223232x x ππ⎛⎫⎛⎫∴-≤+≤∴-≤+-≤ ⎪ ⎪⎝⎭⎝⎭ 所以函数()25cos 223g x x π⎛⎫=+- ⎪⎝⎭在区间,63ππ⎡⎤-⎢⎥⎣⎦上的值域为17,2⎡⎤-⎢⎥⎣⎦ 19.如图,AB 是半圆的直径,,C D 是半圆上的两点,AB //,2CD AD BC ==,设2(2)AB x x =>,四边形ABCD 的周长为()f x .(1)求函数()f x 的解析式;(2)关于x 的方程()124f x m x-=在区间[]2,4上有两个不相等的实数根,求实数m 的取值范围.【答案】(1)()141,(2)f x x x x ⎛⎫=-+> ⎪⎝⎭ (2)717,24⎡⎤⎢⎥⎣⎦ 【分析】(1) 过点C 作CE AB ⊥,垂足为E ,在Rt ABC 中求出BE 的长,从而得出CD 的长,从而得出答案.(2)将问题转化为方程11m x x -=+或31m x x-=-在[]2,4x ∈上有两个不等实数根,然后根据函数的单调性可得答案.(1)如图,过点C 作CE AB ⊥,垂足为E ,在Rt ABC 中,2,2,2BC BE AB AB x BC =⋅==424,222BE CD AB BE x x x x∴==∴=-=-()41242241f x AB CD BC x x x x x ⎛⎫=++=++-=-+ ⎪⎝⎭ ()141,(f x x x x ⎛⎫∴=-+> ⎪⎝⎭ (2) 由()124f x m x -=及()141f x x x ⎛⎫=-+ ⎪⎝⎭等价转化为11m x x -=+或31m x x -=- 依题意:方程11m x x -=+或31m x x-=-在[]2,4x ∈上有两个不等实数根. 函数3y x x =-在[]2,4x ∈上单调递增,图像在直线y x =的下方,值域为113,24⎡⎤⎢⎥⎣⎦ 函数1y x x =+在[]2,4x ∈上单调递增,图像在直线y x =的上方,值域为517,24⎡⎤⎢⎥⎣⎦ 要满足题意,则513124m ≤-≤,即71724m ≤≤ 故实数m 的取值范围为717,24⎡⎤⎢⎥⎣⎦.20.函数()2sin cos f x x x x =+.(1)若()3,0,25f ααπ⎛⎫=∈ ⎪⎝⎭,求sin α; (2)若函数()(03)y f x ωω=<<的图象在区间,42ππ⎛⎫ ⎪⎝⎭有且仅有一条经过最高点的对称轴,求ω的取值范围(不需要证明唯一性).【答案】(2)1113,,3636⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭ 【分析】(1) 先化简函数的解析式,由条件可得3sin 35πα⎛⎫+= ⎪⎝⎭,由同角三角函数的关系,求出cos 3πα⎛⎫+ ⎪⎝⎭,再由角变换33ππαα⎛⎫=+- ⎪⎝⎭结合正弦函数的差角公式可得答案.(2) 设23t x πω=+,则,233t ωπππωπ⎛⎫∈++ ⎪⎝⎭,由题意=sin y t ,在,233t ωπππωπ⎛⎫∈++ ⎪⎝⎭时,有且仅有一条经过最高点的对称轴即=sin y t 的对称轴2x π=或52x π=仅有一条在定义域,233ωπππωπ⎛⎫++ ⎪⎝⎭内,得出端点与对称轴2x π=或52x π=间的大小关系,从而得出答案. (1)())21cos2sin2sin cos sin 2223x x f x x x x x π-⎛⎫=+=-+=+ ⎪⎝⎭(1)由()33,sin ,0,253533f απππααπαπ⎛⎫⎛⎫=+∴+=∈∴<+< ⎪ ⎪⎝⎭⎝⎭又34sin sin ,cos 3532335πππππααπα⎛⎫⎛⎫+=<=∴<+<∴+=- ⎪ ⎪⎝⎭⎝⎭,故sin sin sin cos cos sin 333333ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=+-=+-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦(2)()sin 23y f x x πωω⎛⎫==+ ⎪⎝⎭ 设23t x πω=+,由,42x ππ⎛⎫∈ ⎪⎝⎭,则,233t ωπππωπ⎛⎫∈++ ⎪⎝⎭ 由03ω<<,则113236πωπππ<+<,10333πππωπ<+<由题意=sin y t ,在,233t ωπππωπ⎛⎫∈++ ⎪⎝⎭时,有且仅有一条经过最高点的对称轴即=sin y t 的对称轴2x π=或52x π=仅有一条在定义域,233ωπππωπ⎛⎫++ ⎪⎝⎭内. 所以23232532ωπππππωπππωπ⎧+<⎪⎪⎪+>⎨⎪⎪+≤⎪⎩或2325232532ωπππωπππππωπ⎧+≥⎪⎪⎪+<⎨⎪⎪+>⎪⎩ 解得1163ω<<或131363ω<< 又1303,36ωω<<∴<<,故ω的取值范围为1113,,3636⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭故答案为:1113,,3636⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭ 21.如图,直线12l l //,点A 是12,l l 之间的一个定点,过点A 的直线EF 垂直于直线1l ,,AE m AF n ==(,m n 为常数),点,B C 分别为12,l l 上的动点,已知60BAC ∠=︒.设ACF α∠=(060α︒<<︒).(1)求ABC ∆面积S 关于角α的函数解析式()S α;(2)求()S α的最小值.【答案】(1)11()tan(30)2tan S mn ααα︒⎡⎤=++⎢⎥⎣⎦(23mn 【解析】(1)利用三角函数表示各个边长的关系,再用梯形的面积减去两个直角三角形表达出()S α即可.(2)由(1)有11()tan(30)2tan S mn ααα︒⎡⎤=++⎢⎥⎣⎦,将正切值用正弦除以余弦表示,再利用三角31sin(230)2α︒+-再求最值即可.【详解】(1)由题意1EF l ⊥,12l l //,∴2EF l ⊥,在Rt ACF ∆中,tan n CF α=,060α︒<<︒, 18060(90)30EAB αα︒︒︒︒∠=---=+,在Rt ABE ∆中,tan(30)tan(30)EB AE m αα︒︒=+=+.∴ACF ∆的面积2111122tan S AF CF n α=⋅=⋅, ∴ABE ∆的面积2211tan(30)22S AE EB m α︒=⋅=+, ∴梯形EFCB 的面积11()()tan(30)22tan n S EB CF EF m n m αα︒⎡⎤=+⋅=+++⎢⎥⎣⎦. ∴12()S S S S α=--221111()tan(30)tan(30)2tan 2tan 2n m n m n m αααα︒︒⎡⎤=+++-⋅-+⎢⎥⎣⎦ 11tan(30)2tan mn αα︒⎡⎤=++⎢⎥⎣⎦. (2)令1sin(30)cos tan(30)tan cos(30)sin y αααααα︒︒︒+=++=++ sin(30)sin cos(30)sin sin cos(30)αααααα︒︒︒+++=+⎝⎭︒=sin(230)2α︒=+-∴当23090α︒︒+=时,即30︒=α时,y取得最小值此时()S α.【点睛】本题主要考查了三角函数求解几何图形中的关系的方法.同时也考查了三角函数的公式以及最值的方法等.属于难题.22.已知()(),f x g x 分别是定义在R 上的奇函数和偶函数,且()()x f x g x e +=(1)分別求出函数()(),f x g x 的解析式;(2)若)ln1x ⎛∀∈ ⎝⎭,都有()()()22240m f x mg x m -+->成立,求实数m 的取值范围.【答案】(1)()(),22x x x xe e e ef xg x ---+==(2)⎡-⎢⎣⎦【分析】(1)利用函数的奇偶性,根据()()x f x g x e +=,得到()()x f x g x e --+=,两式联立解得答案.(2)用换元法,将原问题转化为()22260mt m t m +-->在()2,1t ∈--上恒成立的问题,然后根据二次函数在给定区间上的值的情况,分类讨论解答.(1)(1)()()x f x g x e +=,①()()x f x g x e -∴-+-=,()(),f x g x 分别是定义在R 上的奇函数和偶函数,()()x f x g x e -∴-+=,由①②可得:()(),22x x x xe e e ef xg x ---+==; (2)()())22,2,ln 122x x x xe e e ef xg x x --⎛-+==∈ ⎝⎭令x x t e e -=-,则()2222,1,2x x t e e t -∈--+=+,∴原命题等价转化为:()22260mt m t m +-->在()2,1t ∈--上恒成立, (i )当0m =时,则20t ->在()2,1t ∈--上恒成立,0m ∴=成立.(ii )当0m >时,则等价转化为:2260t m t m ⎛⎫+--> ⎪⎝⎭在()2,1t ∈--上恒成立, 令()226h t t m t m ⎛⎫=+-- ⎪⎝⎭,要满足题意, ()()060,10h h =-<∴-≥,解得:25m m-≤-,又0,0m m >∴<≤(iii )当0m <时,则等价转化为:2260t m t m ⎛⎫+--< ⎪⎝⎭在()2,1t ∈--上恒成立 令()226h t t m t m ⎛⎫=+-- ⎪⎝⎭,要满足题意, ()()060,20h h =-<∴-≤,解得:21m -≤≤,又0,20m m <∴-≤<,综上,实数m 的取值范围为⎡-⎢⎣⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华中师范大学组合数学期末考试试卷(A ) 课程名称组合数学课程编号 任课教师 王春香 题型 填空题 证明题 计算题 应用题 总分 分值 20 20 40 20 100 得分 得分 评阅人 一、填空题:(20分)(共5题,每题4分) 1. 由n 个字符组成长为m 的字符串,则相同的字符不相邻的方案数为 n n m C 1+- 。
2. 5男4女,分成两队,每队4人,要求每队至少有1位女生的方案数: 1680 。
3.求12341234+++20,3105,x x x x x x x x =≥≥≥≥,,,的整数解的个数 144 。
4.平面上有n 条直线,其中无两条平行,无三线共点,则交点数为: n-1 。
5.50!尾部有 12 个数字0 。
得分 评阅人 二、证明题(20分):(共2题,每题10分) 21211. 1n p n n p n p n =-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭
∑证明:
院(系
):
专业:
年级:
学生
姓名:
学号:
---
--
--
---
--
--
--
---
--
--
--
---
--
--
--
---
--
--
--
--
--
--
密
--
--
--
--
---
--
--
--
---
--
--
--
---
--
--
-
封
---
--
--
---
--
--
--
---
--
--
--
--
--
线
----
--
--
--
---
--
--
--
---
--
--
--
---
--
--
--
---
--
--
--
---
--
--
--
--
第 1 页(共 页)
得分
评阅人 三、计算题:(共4题,每题10分) --------
第 2 页(共 页)
得分
评阅人 四、应用题:(共2题,每题8分)
1.试分析由a, b, c 三个字符组成长度为n 的符号串,其中不出现aa 图像的串的数目。
-------------------
(2)某人有n元钱,他每天买一次物品,每次买物品的品种很单调,或买一元钱的甲物品,或买两元钱的乙物品,或买两元钱的丙物品。
问:他花完这n元钱有多少种不同的方式?
第 3 页(共页)。
