第二章正弦交流电路
合集下载
电工电子技术-第2章 正弦交流电路
区别与一般复数，相量的头顶上一般加符号“·”。 例：正弦量i=14.1sin(ωt+36.9°)A的最大值相量表示为：
•
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
•
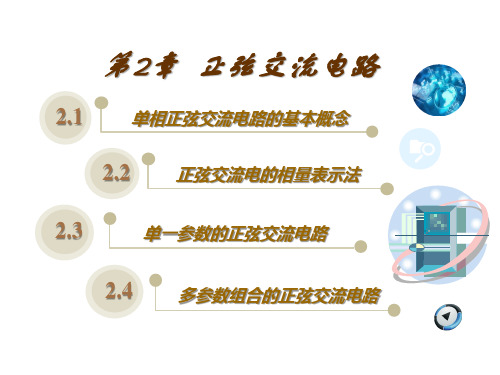
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
电工学 正弦交流电
相量
复数表示法 复数运算
相量的复数表示—相量式
将复数 A 放到复平面上，可如下表示：
j
•
A
A a2 b2
bU
tan 1 b
+1
a
a
A a jb A c o s jA sin
•
A
b A
a
欧 拉
cos
e j e j 2
公 式
sin
e j
e j
2j
A a jb A(cos jsin )
t
i i 领先于
1
2
相 位
i1
落 后
2 1
i2
120 t i i1 落后于 2
三相交流电路：三种电压初相位各差120。
uA uB uC
t
可以证明同频率正弦波运算后，频率不变。
如： u1 2U 1sin t1 u2 2U 2sin t2
uu1u2
2U1sin t1 2U2sin t2 2Usin t 幅度、相位变化
复数
瞬时值
正误判断
已知： i1s0i n t4 ()5
？ I 10 45 2
j45
有效值
？ Im10e45
正误判断
已知： u2 1s0i(n t 1)5
则：
U10？15
？ U 1 0ej15
正误判断
已知： I10 5 00
则： i 1
Im 2I102 0
代数式
A e j
指数式
A
极坐标形式
相量的复数运算
1. 加 、减运算 • 设： A 1 a 1 j b1 • A 2 a 2 jb2
则：
•• •
电工第2章 正弦交流电路
函数(cos)。 1.正弦量数学表达式
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值，是正弦量的最大值，用带右下标m的大写 字母表示，如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度，用ω表示，其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间，称为周期T， 其单位为秒（s），正弦量在单位时间内变化的次数，称为频率f， 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R，两端同除 以 ，可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下，电阻元件的 瞬时功率(用小写字母p表示)：
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V， 试求正弦量的三要素、有效值及变化周期。 解：对照式(2-1)，可知三要素：
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V，，i2=28.2sin(ωt +45°)A，试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解：以电压u为参考量， 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系（注意：正弦量和相量不是相等
关系！）。在复平面中，例如相量可用长度为 ，与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值，是正弦量的最大值，用带右下标m的大写 字母表示，如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度，用ω表示，其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间，称为周期T， 其单位为秒（s），正弦量在单位时间内变化的次数，称为频率f， 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R，两端同除 以 ，可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下，电阻元件的 瞬时功率(用小写字母p表示)：
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V， 试求正弦量的三要素、有效值及变化周期。 解：对照式(2-1)，可知三要素：
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V，，i2=28.2sin(ωt +45°)A，试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解：以电压u为参考量， 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系（注意：正弦量和相量不是相等
关系！）。在复平面中，例如相量可用长度为 ，与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
第二章：正弦稳态交流电路
相量的图形，称为相量图。
第2章 正弦稳态交流电路
[例] 若 i1= I1 msin( t+ i1) i2= I2 msin( t+ i2)，
电
画相量图
j •
相
路 分析：根据i1、i2的振幅、初相， I2m
•量
与 可直接画出其相量图。
i2
I1m 图
电 小结：
i1
1
0
子 只有正弦周期量才能用相量表示； 技
第一篇 电路分析
电
第2章 正弦稳态交流电路
路
与 主要内容：
电
子 ➢正弦量的相量表示及相量图
技 ➢简单正弦交流电路分析
术
第2章 正弦稳态交流电路
第一节 正弦稳态交流电路的基本概念
电
正弦交流电路是指含有正弦电源(激励)，且电路各部分
路 所产生的电压电流(响应)均按正弦规律变化的电路。
与 一、正弦量
电
在电路中常见到随时间变化的电压和电流。 如下图所示：
与
例如: i Im sin t
i Im sin( t )
电
t =0时，i0 0
i0 Im sin 不等于零
i 子
i
技
0
t
0
t
术 （2）初相位
t=0 时的相位角称为初相角或初相，规定：
若计时时刻不同，则正弦量初相位不同。
（3）相位差
同频率正弦量的相位角之差
电 或是初相角之差，用 表示。
u
Z R j( X L XC ) 30 j(79.8 - 39.8)
(30 j40) 5053.1o
–
+ u–R
u+–L uC+
2.正弦交流电路
解： I = 100∠30o A = 100e j30° A
•
= 100(cos 30° + j sin 30°)A = 86.6 + j 50 A
U = 220∠ − 60 o V = 220e - j60°V = 220(cos 60° − j sin 60°)V = 110 − j190.5V
= i = I m sin (ω t + ϕ ) = I m e
？
jϕ
= Im ϕ
②只有正弦量才能用相量表示， 只有正弦量才能用相量表示， 非正弦量不能用相量表示。 非正弦量不能用相量表示。 ③只有同频率的正弦量才能画在同一相量图上。 只有同频率的正弦量才能画在同一相量图上。 同频率的正弦量才能画在同一相量图上
& ⋅ A = A e jθ1 ⋅ A e jθ2 = A A e j (θ1 +θ2 )= A A ∠θ +θ A1 &2 1 2 1 2 1 2 1 2
乘法：模相乘， 乘法：模相乘，角相加
| A1 | ∠ θ1 | A1 | e jθ1 | A1 | j( θ1−θ 2 ) | A1 | = = = e = • jθ 2 | A2 | | A2 | A 2 | A2 | ∠ θ 2 | A2 | e A1
ϕ = ϕu − ϕi
ϕ
3 ϕ =− π 4
应有ϕ ≤180 °
ϕu
ϕi
ϕ > 0, u 超前 i ϕ 角度 ϕ = 0 ，u 与 i 同相位 ϕ < 0, 则 u 滞后 i 一个ϕ角 π ϕ =± ， 则说 u 与 i 正交
ϕ =π ， 则说 u 与 i 反相
2
特殊相位关系： 特殊相位关系：
第二章 正弦交流电路
第2章 正弦交流电路判断题2.1 正弦交流电的基本概念1．若电路的电压为)30sin(︒+=t U u m ω，电流为)45sin(︒-=t I i m ω， 则u 超前i 的相位角为75°。
[ ]答案:V2．如有电流t i 100sin 261=Ａ，)90100sin(282︒+=t i Ａ，则电流相量分别是︒=0/61I Ａ，︒=90/82I Ａ。
所以二者的电流相量和为：21I I I += [ ] 答案:V3．若电路的电压为u ＝I m sin(ωt+30°)，电流为i =I m sin(ωt-45°)，则u 超前i 的相位角为15°。
[ ]答案:X4．正弦量的三要素是指其最大值、角频率和相位。
[ ] 答案:X5．正弦量可以用相量表示，因此可以说，相量等于正弦量。
[ ] 答案:X6．任何交流电流的最大值都是有效值的2倍。
[ ] 答案:X7．正弦电路中，相量不仅表示正弦量，而且等于正弦量。
[ ] 答案:X2.2 正弦量的相量表示法1．如有电流t i 100sin 261=Ａ，)90200sin(282︒+=t i Ａ，则电流相量分别是︒=0/61I Ａ，︒=90/82I Ａ。
所以二者的电流相量和为：21I I I += 。
[ ] 答案:X2.3 单一参数的正弦交流电路1．电容元件的容抗是电容电压与电流的瞬时值之比。
[ ] 答案:X2．在电感元件的电路中，电压相位超前于电流90º，所以电路中总是先有电压后有电流。
[ ]答案:X3．电感元件的感抗是电感电压与电流的瞬时值之比。
[ ]答案:X4．电感元件的感抗是电感电压与电流的有效值之比。
[ ]答案:V5．直流电路中，电容元件的容抗为零，相当于短路。
[ ]答案:X6．直流电路中，电感元件的感抗为无限大，相当于开路。
[ ]答案:X7．直流电路中，电容元件的容抗为无限大，相当于开路。
[ ]答案:V8．直流电路中，电感元件的感抗为零，相当于短路。
第2章 正弦交流电路
同相反相的概念
同相:相位相同，相位差为零。 反相:相位相反，相位差为180°。 下面图中是三个正弦电流波形。 i1与 i2 同相， i1与 i3反相。
i
i1 i2
O
i3
ωt
总 结
描述正弦量的三个特征量：
幅值、频率、初相位
9
电气与自动化工程学院
2.2 正弦量的相量表示法
正弦量的表示方法：
★ 三角函数式： i
相位 表示正弦量的变化进程，也称相位角。 初相位 t =0时的相位。
i I m sint 相位： t 初相位： 0
i I m sin t
相位：
i
O
t
i
t
说 明
初相位：
ψ
t
初相位给出了观察正弦波的起点或参考点。
7
电气与自动化工程学院
相位差
两个同频率的正弦量的相位之差或初相位之差称为相位差。 正弦交流电路中电压和电流的频率是相同的，但初相不 一定相同，设电路中电压和电流为：
26
电气与自动化工程学院
2.3.3 电容元件的交流电路 电压电流关系
对于电容电路：
dq du i C dt dt
i
＋
如果电容两端加正弦电压：
u
_
C
u Um sin t
则：
注意u 和i的参考方向！
dU m sint i C CUm cost CUm sin t 90 I m sin t 90 dt
2.1.1 频率和周期
正弦量变化一次所需要的时间（秒）称为周期（T）。 每秒内变化的次数称为频率（ f ），单位是赫兹（Hz）。
u i
频率是周期的倒数:
电路 第二章 正弦交流电路(1)
11
所以交流电的有效值就是与它热效应相等的直流电的数值， 它们之间的关系由焦耳－楞次定律确定。为了区别，交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i＝Imsin(ωt+ψ)，通过计算可知，正弦电流的有 效值是其最大值的1/√2倍，如图2—9(c)所示，即 I＝Im/√2 ＝0.707Im (2—9) 同理，正弦电压和电动势的有效值分别为 U＝Um/√2 ; E＝Um/√2 在工程上，主要使用有效值，今后不加特别声明，交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值， 即它不随时间变化，因此，和最大值比较，有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形，叫相量图，相量图与力学和物理学中 的向量图相似。但是，相量表示的是随时间作正弦变动的函 数，而向量指的是力、电 场强度等空间向量。 2 因为实际工程中，常采用正弦量的有效值，而且最大值与 有效值之间有着固定的 2关系，所以有效值相量应用较多。 它等于最大值相量除以 2 ，即 U=Um/ 2 同理 I＝Im/ 2
上式表明，为了保证电动势的频率稳定，必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz，称为工频。一般我 们讲交流电时，如果不加说明，指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状，使电枢表面的磁感应强度B 沿圆周按正弦规律分布，如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率，故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O～O',B＝ 0，称为磁中性面。在磁极的轴线上，磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面，与磁中性面的 夹角为α，则AA'边所处位置的磁感应强度为(见图 2—2) B＝Bmsinα 当电枢被原动机拖动，在磁场中以逆时 针方向作 等速旋转时，电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e＝Emsinωt (2—1)
所以交流电的有效值就是与它热效应相等的直流电的数值， 它们之间的关系由焦耳－楞次定律确定。为了区别，交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i＝Imsin(ωt+ψ)，通过计算可知，正弦电流的有 效值是其最大值的1/√2倍，如图2—9(c)所示，即 I＝Im/√2 ＝0.707Im (2—9) 同理，正弦电压和电动势的有效值分别为 U＝Um/√2 ; E＝Um/√2 在工程上，主要使用有效值，今后不加特别声明，交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值， 即它不随时间变化，因此，和最大值比较，有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形，叫相量图，相量图与力学和物理学中 的向量图相似。但是，相量表示的是随时间作正弦变动的函 数，而向量指的是力、电 场强度等空间向量。 2 因为实际工程中，常采用正弦量的有效值，而且最大值与 有效值之间有着固定的 2关系，所以有效值相量应用较多。 它等于最大值相量除以 2 ，即 U=Um/ 2 同理 I＝Im/ 2
上式表明，为了保证电动势的频率稳定，必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz，称为工频。一般我 们讲交流电时，如果不加说明，指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状，使电枢表面的磁感应强度B 沿圆周按正弦规律分布，如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率，故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O～O',B＝ 0，称为磁中性面。在磁极的轴线上，磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面，与磁中性面的 夹角为α，则AA'边所处位置的磁感应强度为(见图 2—2) B＝Bmsinα 当电枢被原动机拖动，在磁场中以逆时 针方向作 等速旋转时，电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e＝Emsinωt (2—1)
正弦交流电路_单一参数的正弦交流电路
电压超前于电流90°
iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（2）大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值： U m L I m 有效值： U ω L I
定义： X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（3）相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 （1）瞬时功率
p ui
U m I m s in t s in t 90
（能量的吞吐）。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（3）无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较，设电流 i I m s in t
u
i
为参考量，则： u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率（有功功率） P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能， 也称有功功率。
iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（2）大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值： U m L I m 有效值： U ω L I
定义： X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（3）相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 （1）瞬时功率
p ui
U m I m s in t s in t 90
（能量的吞吐）。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
（3）无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较，设电流 i I m s in t
u
i
为参考量，则： u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率（有功功率） P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能， 也称有功功率。
正弦交流电路_正弦交流电路的频率特性;串联谐振
工程上根据输出端口对信号频率范围的要求，设计专 门的网络，置于输入-输出端口之间，使输出端口所需频 率信号能顺利通过，而抑制不需要的频率信号，这种带有 选频功能的中间网络，工程上称为滤波器。
希望保留的频率范围称为通带 希望抑制的频率范围称为阻带
U
i
+
( j
−
)
选频 网络
U
+ o−(
j
)
第二章 正弦交流电路
( ) arctan( ) 0
T ( j )
1
0.707 通
阻
带
带
T ( j ) 0 ( )
2
0
0
( )
0
T ( j ) 0.707 ( )
4
0 4
0 ——截止（转折）频率
2
第二章 正弦交流电路
2.5 交流电路的频率特性
2.高通滤波电路
C
传递函数
T ( j )
第二章 正弦交流电路
2.5 交流电路的频率特性
2.5.1 频率特性的概念和传递函数 1.频率特性（频率响应）：
幅频特性: 电压或电流的大小与频率的关系。 相频特性: 电压或电流的相位与频率的关系。
+
U i ( j )
−
RLC
电路
+
U o ( j )
−
第二章 正弦交流电路
2.5 交流电路的频率特性
−
jC
T ( j )
1
1 j
0
幅
1
arctan
1 ( )2
0
0
相
0
1 RC
频 T ( j )
1
频 ( ) arctan( )
希望保留的频率范围称为通带 希望抑制的频率范围称为阻带
U
i
+
( j
−
)
选频 网络
U
+ o−(
j
)
第二章 正弦交流电路
( ) arctan( ) 0
T ( j )
1
0.707 通
阻
带
带
T ( j ) 0 ( )
2
0
0
( )
0
T ( j ) 0.707 ( )
4
0 4
0 ——截止（转折）频率
2
第二章 正弦交流电路
2.5 交流电路的频率特性
2.高通滤波电路
C
传递函数
T ( j )
第二章 正弦交流电路
2.5 交流电路的频率特性
2.5.1 频率特性的概念和传递函数 1.频率特性（频率响应）：
幅频特性: 电压或电流的大小与频率的关系。 相频特性: 电压或电流的相位与频率的关系。
+
U i ( j )
−
RLC
电路
+
U o ( j )
−
第二章 正弦交流电路
2.5 交流电路的频率特性
−
jC
T ( j )
1
1 j
0
幅
1
arctan
1 ( )2
0
0
相
0
1 RC
频 T ( j )
1
频 ( ) arctan( )
电工学 第二章正弦交流电路
e = Em sin (wt + j e )
(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im：电流幅值（最大值）
三要素
w： 角频率（弧度/秒）
.
U Z = I
j = j u - ji
结论：Ｚ的模为电路总电压和总电流有效值之比， 而Ｚ的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL－ XC )
阻抗角
j = ju－ ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中：
瞬时值
有效值
U I= R
？
U i= R
？
u ？ i = R
(1-40)
正 误 判 断
在电感电路中：
u i= XL
？
U I= ωL
u i= ωL
？
？
& U = XL & I
U = jω L I
？
？
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为：
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写，瞬时值功率
所以：
i
u
wt
(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im：电流幅值（最大值）
三要素
w： 角频率（弧度/秒）
.
U Z = I
j = j u - ji
结论：Ｚ的模为电路总电压和总电流有效值之比， 而Ｚ的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL－ XC )
阻抗角
j = ju－ ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中：
瞬时值
有效值
U I= R
？
U i= R
？
u ？ i = R
(1-40)
正 误 判 断
在电感电路中：
u i= XL
？
U I= ωL
u i= ωL
？
？
& U = XL & I
U = jω L I
？
？
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为：
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写，瞬时值功率
所以：
i
u
wt
电工电子技术及应用第2章
需要强调的是，相量只表示正弦量，并不等于正
弦量；只有同频率的正弦量其相量才能相互运算，
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等！！
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V，
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值（最大值） 正弦量在任一时刻的值称为瞬 时值，用小写字母表示， 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值，用大写字母加下
o
Um2
Um1
t
图2-2
标m表示，如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ，求AB和A/B。
起点不同，正弦量的初相不同，因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度，即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下，已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
弦量；只有同频率的正弦量其相量才能相互运算，
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等！！
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V，
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值（最大值） 正弦量在任一时刻的值称为瞬 时值，用小写字母表示， 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值，用大写字母加下
o
Um2
Um1
t
图2-2
标m表示，如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ，求AB和A/B。
起点不同，正弦量的初相不同，因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度，即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下，已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
第2章 正弦交流电路
eU Em sin t eV Em sin(t 120 ) eW Em sin(t 120 )
（2-31）
相应的波形图、相量图如图2-16（a）、 （b）所示。
图2-16 三相对称电动势
2．三相电源的星形联结
（1）星形联结
把上述三相绕组的末端U2、V2和W2连在一 起，就构成星形联结，如图2-17所示。
UR U 311 2 V 220V
【例2-4】
根据式（2-10），电流有效值为
P 100W IR 0.455A U R 220V
2.2.2 纯电感电路
1．电压和电流的关系
纯电感电路如图2-10（a）所示，电感电
流与电压参考方向一致，设电感电流为
iL 2 I L sin t
2.3.1 电压和电流关系 2.3.2 电路的功率和能量转换
2.3.1 电压和电流关系
RLC串联电路如图2-12所示，取电压和电 流的参考方向一致。 为便于分析，电路中各量均采用相量表 示，各元件也采用相量化模型。
图2-12 RLC串联电路
用相量法分析电路如下。
（1）作相量图
图2-13 相量图
（2）求相量和
IL IP
【例2-8】三相电源作星形联结，线电压是 380V，负载是额定电压为220V的电灯组，问： （1）三相负载采用什么联结方式； （2）若三相负载的等效电阻 R1=R2=R3=510 ， 求相电流、线电流和中线电流； （3）若三相负载的等效电阻分别为 R1=510 ， R2=510，R3=2k，求中线电流。
QC UC IC 50 0.157 var 7.85var
当 f 5 000Hz 时，
XC IC 1 1 3.19 2π fC 2 3.14 5 000 10 106
第二章 正弦交流电路
如：
u1 u2
2U1 sin t 1
2U 2 sin t 2
u u1 u2
2U1 sin t 1 2U 2 sin t 2 2U sin t
幅度、相位变化 频率不变
结论:因角频率（）不变，所以以下讨论同 频率正弦波时， 可不考虑，主要研究幅度 与初相位的变化。
电容的相量欧姆定律
总结：R、L、C相量形式的欧姆定律
、I 表示， 在正弦交流电路中，若正弦量用相量 U
电路参数用复数阻抗（ R R、L jX L、C jX C ) 表示，则复数形式的欧姆定律和直流电路中的形式相 似。
RI U R jLI jX I U L L 1 j jX I U I C C C
R、L、C正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
I R U
UI
0
i 2I sin t
设
u、 i 同相
du iC dt
2U sin t
du iC 2UC cos t dt 2U C sin(t 90 )
特点:
1. 频率相同
2. 相位相差 90°（u 落后 i 90° ）
u
i
I
UC
90
t
U
U
u 2U sin t
i 2U C sin(t 90 )
U I XL
u1 u2
2U1 sin t 1
2U 2 sin t 2
u u1 u2
2U1 sin t 1 2U 2 sin t 2 2U sin t
幅度、相位变化 频率不变
结论:因角频率（）不变，所以以下讨论同 频率正弦波时， 可不考虑，主要研究幅度 与初相位的变化。
电容的相量欧姆定律
总结：R、L、C相量形式的欧姆定律
、I 表示， 在正弦交流电路中，若正弦量用相量 U
电路参数用复数阻抗（ R R、L jX L、C jX C ) 表示，则复数形式的欧姆定律和直流电路中的形式相 似。
RI U R jLI jX I U L L 1 j jX I U I C C C
R、L、C正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
I R U
UI
0
i 2I sin t
设
u、 i 同相
du iC dt
2U sin t
du iC 2UC cos t dt 2U C sin(t 90 )
特点:
1. 频率相同
2. 相位相差 90°（u 落后 i 90° ）
u
i
I
UC
90
t
U
U
u 2U sin t
i 2U C sin(t 90 )
U I XL
电工学第2章正弦交流电路PPT课件
p=ui=Um sin(ωt+90°) Imsinωt
=UmIm cosωtsinωt =UIsin2ωt
电感元件的功率波形
上式表明， 电感元件的瞬时功率是一个幅值为UI 并以2ω的角频率随时间而变化的正弦量。瞬时功率 的变化曲线如右图所示。
26
当p>0时，表明电感元件吸收能量并作负载 使用，即将电能转换成磁场能量储存起来；
1. 相位角（或相位）——（ωt +ψi） 2. 初相位——t=0时的相位角，即ωt +ψi|t=0＝ψi
初相位不同，正弦波的起始点不同，如下图所 示。
(a)ψi＝0
(b)ψi＞0
(c)ψi<0
由于正弦量是周期性变化量，其值经2π后又重复，所
以一般取主值，| ψi |≤π。
8
2.1.3 初相位
在一个正弦交流电路中， 电压u和电流i的频率是相同的， 但初相位却可以不同。设：
19
在电阻元件的交流电路中，电压u与电流i 相 位相同、频率相同。其波形图、相量图如下所示：
根据 i=Imsinωt ；u=iR=ImRsinωt
可知电压幅值: Um=Im R；
U=I R
如果用相量来表 示电压与电流的
•
•
U
•
Um
•
R
或
••
U IR
关系，则有： I I m
20
瞬时功率：p=ui= Umsinωt Imsinωt=UmImsin²ωt
③指数形式可改写为极坐标形式：
A=r
三种复数式可以互相转换。复数的加减运 算可用直角坐标式；复数的乘除运算用指数形 式或极坐标形式则比较方便。
13
e e 例如: 设A1= a1+jb1 ＝r1 j 1 ；A2= a2+jb2 ＝r2 j 2
电工学第二章 正弦交流电
电流超前电压 90 u i u i ωt O 90°
O
ωt
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数， 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知：
幅度：
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率：
1000 rad/s
f
2
1000 2
159 Hz
初相位：
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
（耗能元件）,且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
O
ωt
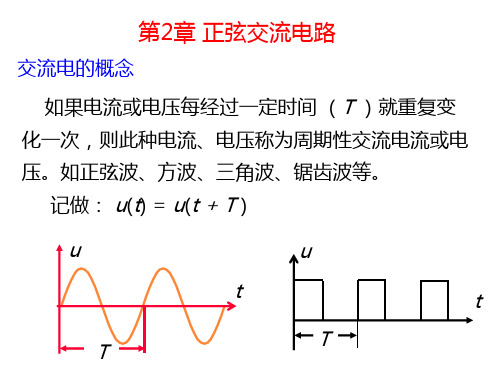
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数， 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知：
幅度：
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率：
1000 rad/s
f
2
1000 2
159 Hz
初相位：
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
（耗能元件）,且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
第2章正弦交流电-2.5三相交流电路
三相交流电路之所以获得广泛应用，是因为它比单相交流电路具有下列优点： （1）在发电设备上，三相交流发电机比同容量的单相交流发电机节省材料，而且体积小， 有利于制造大容量机组。 （2）在电能输送上，三相供电比单相供电节省有色金属约25％，从而降低了成本。 （3）在用户使用上，可以广泛地使用三相异步电动机，而它比单相电动机结构简单、价 格低廉、运行可靠、维护方便。
2.5三相交流电路
三相电源的连接
三相负载的连接
三相电路的功率
如果三相电路为对称电路，则表明各相负载的有功功率相等，则有 P＝3UPIPcosφP
同单相交流电路一样，三相对称负载的无功功率和视在功率分别为
2.5三相交流电路
三相电源的连接
三相负载的连接
三相电路的功率
例题：一台三相电炉，其每相电阻R=10Ω。试问：①当电源线电压为380V时，接成三角形和 星形时各从电网取用多少功率？②在220V线电压下，接成三角形消耗的功率是多少？
单相负载：负载只需由三相电源中一相电源供电即可工作， 通常功率较小的负载均为单相负载，如照明灯、电风扇、洗衣 机、电冰箱、电视机、小功率电炉、电焊机等。为了使三相电 源供电均衡，这种负载要大致平均分配到三相电源的三相上。 这类负载的每相阻抗一般不相等，属于不对称三相负载。
典型的三相负载联结如图所示。
2.5三相交流电路
三相电源的连接
三相负载的连接
1 星形（Y形）联结
（1） 电压和电流之间的关系
三相电源的负端（末端）连接成一点N，N称为中性点，简称 中点，俗称零点。三相电源的正端（首端）引出与负载相接，从电 源正端引出的三根供电线称为相线或端线，俗称火线，用L1、L2、 L3分别表示。从中点N引出的供电线称中性线，俗称零线，用N表 示。在应用最多的低压供电系统中，中点通常是接地的，因而中线 又俗称地线。
2.5三相交流电路
三相电源的连接
三相负载的连接
三相电路的功率
如果三相电路为对称电路，则表明各相负载的有功功率相等，则有 P＝3UPIPcosφP
同单相交流电路一样，三相对称负载的无功功率和视在功率分别为
2.5三相交流电路
三相电源的连接
三相负载的连接
三相电路的功率
例题：一台三相电炉，其每相电阻R=10Ω。试问：①当电源线电压为380V时，接成三角形和 星形时各从电网取用多少功率？②在220V线电压下，接成三角形消耗的功率是多少？
单相负载：负载只需由三相电源中一相电源供电即可工作， 通常功率较小的负载均为单相负载，如照明灯、电风扇、洗衣 机、电冰箱、电视机、小功率电炉、电焊机等。为了使三相电 源供电均衡，这种负载要大致平均分配到三相电源的三相上。 这类负载的每相阻抗一般不相等，属于不对称三相负载。
典型的三相负载联结如图所示。
2.5三相交流电路
三相电源的连接
三相负载的连接
1 星形（Y形）联结
（1） 电压和电流之间的关系
三相电源的负端（末端）连接成一点N，N称为中性点，简称 中点，俗称零点。三相电源的正端（首端）引出与负载相接，从电 源正端引出的三根供电线称为相线或端线，俗称火线，用L1、L2、 L3分别表示。从中点N引出的供电线称中性线，俗称零线，用N表 示。在应用最多的低压供电系统中，中点通常是接地的，因而中线 又俗称地线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.3.2 电容电路
（1）直流充电过程称作暂态 K闭合后电容电压通过充电（或放电）从最初值达到最终 值的过程称作暂态。下图中当uC=US时充电结束电路进入 稳态，直流稳态电路中的电容相当于开路。
(a)电路
(b) 波形图 图2-7直流电路中电容的充电过程
2.3.2 电容电路
du C iC = C dt
2.5 复阻抗的串联和并联
例： 电路如图2-23，试求电源发出的有功 功率和无功功率以及功率因数。
图2-23
2.5 复阻抗的串联和并联
解：
Z = 1+ ( j )(1 + j ) = 2 j ( ) ( j ) + (1 + j ) & US 10 2 &= I = = 4 + j 2 = 20∠arctg ( Α) Z 2 j 4
串联
& & & & & U = U 1 + U 2 = I ( Z 1 + Z 2 ) = IZ
等效阻抗 Z = Z1 + Z2
2.5 复阻抗的串联和并联
并联
& 1 1 & U & & & I = I1 + I 2 = ( + )U = Z1 Z 2 Z
Z1 Z 2 等效阻抗 Z = Z1 // Z 2 = Z1 + Z 2
2.4.1 RLC 串联电路
(a)复阻抗电路
(b)相量图为感性负载
(c)相量图为容性负载
图2-13 RLC串联电路
2.4.1 RLC 串联电路
应用KVL列回路电压方程
& & & & U = U R +U L +UC & & & = R I + jX L I jX C I & & = [ R + j ( X X )] I = Z I
2.2 正弦交流电的相量表示法
解: 用相量运算
& I1 m = 8∠60° = 8(cos 60° + j sin 60°) = 4 + j 6.928( Α) & I 2 m = 6∠ 30° = 6(cos 30° j sin 30°) = 5.196 j 3( Α) & & I + I = (4 + j 6.928) + (5.196 j 3) = 10∠23.1°( Α)
2.3.3 电感电路
(a)电感电路
(b)复阻抗电路与相量图
(c)波形图
图2-11 电感上的电压和电流以及功率波形
2.3.3 电感电路
交流稳态电路中
di L π π uL = L = ωLI m sin(ωt + ) = U Lm sin(ωt + ) dt 2 2
& & & U Lm = jL I Lm = jX L I Lm 欧姆定律的相量形式
L C
复阻抗 Z = R + j ( X L X C ) = R + jX =| Z | ∠ ， 其中电抗 X = X L X C
2.4.1 RLC 串联电路
复阻抗的模 阻抗角
| Z |= R 2 + X 2
X = arctg = u i R
＞0，电路呈感性； ＜0，电路呈容性；
2 2
I 1m 8 + 30 = arctg = arctg = 53.1ο I 2m 6
ο
= 53.1ο 30ο = 23.1ο
2.3 单一参数的正弦交流电路
2.3.1 电阻电路 u = R i = RI m sin ωt = U m sin t & 或 U = R I&
(a)时域电阻电路
= 0 ，电路呈纯阻性，电路发生串联谐振
2.4.1 RLC 串联电路
串联谐振特点： & & ① U L U C = 0 ，& 与 I& 同相位，Z = R , U 阻抗最小电流最大 ②串联谐振又称作电压谐振，谐振频率
=
1 LC
③电感中的磁场能量与电容中的电场能量相 互转换，两元件与外电路无能量交换。
P = I 2 × R = ( 20 ) 2 × 2 = 40( W ) 有功功率
无功功率 Q = I × Χ = ( 20 ) × 1 = 20( VAR )
2 2
功率因数
P cos = = UI
40 40 + 20
2 2
=
2 5
≈ 0.89
单位：VA（伏安）
视在功率 S = UI =
2.4.1 RLC 串联电路
RLC串联电路中，阻抗三角形、电压三角 形、功率三角形是相似三角形，如图2-15
图2-15阻抗、电压、功率三角形
2.4.2 RLC 并联电路
(a) RLC并联电路 图2-18
(b)相量图
2.4.2 RLC 并联电路
& & & U U U & & & & & I = I R + I L + IC = + = YU R jX L jX L
jX L = jL 称作复数感抗
2.3.3 电感电路
瞬时功率
p L = u L i L = U Lm sin(ωt +
平均功率
1 PL = T
π
2
) I Lm sin ωt = U L I L sin 2ωt
∫
ห้องสมุดไป่ตู้
T
0
p L dt = 0
说明电感只贮能、不耗能
2
无功功率
UL 2 QL = U L I L = I L X L = XL
1 2 1 1 2 2 1 2 1 2
& Α1 Α1∠1 Α1 = = ∠1 2 & Α 2 Α 2 ∠ 2 Α 2
2.2 正弦交流电的相量表示法
用相量代数式进行除法运算，应在分子和 分母中先同乘以分母的共轭复数，如
2 + j 3 (2 + j 3)(3 + j1) 3 + j11 = = = 0.3 + j1.1 3 j1 (3 j1)(3 + j1) 10
2.1 正弦交流电的基本概念
计时起点改变初相位也改变，但相位差不 变。规定初相位和相位差均用小于180°的 角度表示。 周期电流的有效值是在热效应方面与它相 等的直流电流的数值。与极大值关系为：
Im = 2 I
U m = 2 U
Em = 2 E
工程上或产品铭牌上的交流电压、电流以 及交流测量仪表指示的都是有效值。
& i = I m sin(t 20°) ←→ I&m = I m ∠ 20° 或 I = I∠ 20°
2.2 正弦交流电的相量表示法
相量的4种形式 & Α = a + jb = Α(cos + j sin ) = Α∠ = Αe j 代数式 三角函数式 极坐标式 指数式
2.2 正弦交流电的相量表示法
1 或 u C = ∫ iC dt C
电容上只有施加变化的电压，才会有电流 出现；电容电压是对电流的积分得到。
2.3.2 电容电路
（2）交流稳态电路中
(a) 电容电路 (b)复阻抗电路与相量图 (c)波形图 图2-8 电容上的电压和电流以及功率波形
2.3.2 电容电路
Im 1 1 π u c = ∫ idt = ∫ I m sin ωt dt = cos ωt = U m sin(ωt ) ωC 2 c C
1m 2m
故
i = i1 + i2 = 10 sin(314t + 23.1 )(A)
ο
2.2 正弦交流电的相量表示法
I 做相量图：&1 m 和 I&2 m 两相量垂直，虚线是两 个相量的平行线与两相量构成平行四边形。 从原点出发到达对角的连线就是两相量之 和 。 I&m
I m = I 1m + I 2 m = 8 2 + 6 2 = 10 Α
2.2 正弦交流电的相量表示法
由于电路中各部分的电压、电流都是同频 率的，只需要确定它们的幅值（或有效值） 和初相位。正弦量的相量表示法用相量表 示正弦量的幅值（或有效值）和初相位， 用相量的代数运算代替瞬时值的三角函数 运算。
2.2 正弦交流电的相量表示法
例如：
& & u = U m sin(t + 45°) ←→ U m = U m ∠45° 或 U = U∠45°
电感储存的磁场能量
1 2 1 2 WL = Li (t ) Li (0) 2 2
2.3.3 电感电路
下图是电感和电容组成的Π型低通滤波电路， 电感串联在电路中使直流成分容易通过，电 容并联在电路中使交流成分被短路而不被传 送到输出端。
图2-12 Π型低通滤波电路
2.4 非单一参数的正弦交流电路
2.1 正弦交流电的基本概念
频率f：正弦量每秒钟的循环次数称为频率f，频率 是周期的倒数，即
1 f = T
单位: HZ (赫兹) 角频率：正弦量变化一个循环经历了360° 或2π弧度，每秒钟变化的弧度是角频率， 即 = 2πf = 2π 单位：rad/s(弧度/秒)
T
我国采用50HZ的电力频率，其周期是 T =0.02秒，角频率是=314弧度/秒
2.4.1 RLC 串联电路
瞬时功率
p = ui = 2UI sin(ωt + ) sin ωt = UI cos UI sin(2ωt + )