第三章正弦交流电路
电工学课件--第三章 正弦交流电路

U • o I= U =U 0 ∠ R
• •
u =Um sinω t u Um i = = sinω = Im sinω t t R R
U =I R
U =I R
•
•
可见: 可见:电压与电流同相位 ui
i
u
•
IU
•
I
•
U
+−
2.功率关系
ui
i
⑴ 瞬时功率
•
u
IU
p=ui=UmImsin2ωt =UI(1-cos2ωt)
角频率ω: 单位时间里正弦量变化的角度 称为角频率。单位是弧度/秒 (rad/s). ω=2π/T=2πf 周期,频率,角频率从不同角度描 述了正弦量变化的快慢。三者只要知 道其中之一便可以求出另外两时值, 瞬时值中最大的称为最大值。Im、 U m 、E m 分别表示电流、电压和电动 势的最大值. 表示交流电的大小常用有效值的概 念。
单位是乏尔(Var) 单位是乏尔(Var)
第四节 RLC串联交流电路 串联交流电路 一.电压与电流关系
i R u L C
uR uL
u =uR +uL +uC
U =UR+UL+UC
• • • •
uC
以电流为参考相量, 以电流为参考相量, 相量图为: 相量图为:
•
UL UL+UC
φ
• • • •
•
U I
•
U
φ UR
UL-UC
UR
UC
2 可见: 可见: U = UR +(UL −UC)2
U L −UC X L − XC = arctg = arctg UR R
电工电子学第三章

负半周
3
设正弦交流电流: 设正弦交流电流:
Im
Ψ
i
O π T 2π π
ωt
i = I m sin (ω t + ψ )
初相角:决定正弦量起始位置 初相角: 角频率:决定正弦量变化快慢 角频率: 幅值:决定正弦量的大小 幅值:
幅值、角频率、初相角成为正弦量的三要素。 幅值、角频率、初相角成为正弦量的三要素。
5
3.1.2 幅值与有效值 幅值: 幅值:Im、Um、Em
幅值必须大写, 幅值必须大写, 下标加 m。
有效值: 有效值:与交流热效应相等的直流定义为交流电的 有效值。 有效值。
∫0
T
2 i 2R dt = I RT
交流
直流
则有
I =
1 T
∫
T
0
i 2dt
Im 1 T 2 2 有效值必 = ∫0 Imsin ωt dt = 2 须大写 T U Em 同理: 同理: U = m E= 2 2
12
3. 正弦量的相量表示
实质:用复数表示正弦量 实质: 复数表示形式 为复数: 设A为复数 为复数 (1) 代数式 A =a + jb 式中: a = r cos ψ 式中
+j
b
A
r ψ
0
2 2
a
+1
b = r sin ψ
(2) 三角式 由欧拉公式: 由欧拉公式
r = a + b 复数的模 b ψ = arctan 复数的辐角 a
16
⑥“j”的数学意义和物理意义 因子: 旋转 90o因子:e± j90o
± j90o
e
= cos 90° ± jsin90° = ±j
第3章 正弦交流电路

Um 正弦交流电压的有效值为 U = = 0.707U m 2 正弦交流电压的有效值为 E = Em = 0.707 Em 2
i = I m sin (ω t + ψ i )时,可得 也可以写为 i = 2 I sin (ω t + ψ i )
当电流
e = E m sin ( ω t + ψ e ) 时,可得 E = 2 也可以写为 e = 2 E sin ( ω t + ψ e )
1 1 T= = = 0.02s f 50
我国工业和民用交流电源的有效值为220V,频率为50Hz, ,频率为 我国工业和民用交流电源的有效值为 因而通常将这一交流电压简称为工频电压 频率称为工频 工频电压, 工频。 因而通常将这一交流电压简称为工频电压,频率称为工频。
例:已知正弦交流电流为i=2sin(ωt-30˚) A。电路中的电阻 已知正弦交流电流为 。电路中的电阻R=10Ω, , 试求电流的有效值和电阻消耗的功率。 试求电流的有效值和电阻消耗的功率。 解:电流有效值 电阻消耗的功率 I=0.707×Im=0.707×2=1.414A × × P=I2R=20W
已知一正弦电流的有效值为5A,频率为50Hz,初 例:已知一正弦电流的有效值为 ,频率为 , 相为50˚,试写出其解析式。 相为 ,试写出其解析式。 由题目可知, 解:由题目可知,m = 5 2V,ψ=50˚ I 又频率f=50Hz,则角频率 又频率 , ω=2πf=2×3.14×50=314rad/s × × 则该电流解析式为
(三)相位与相位差 相位:表示正弦量的变化进程,也称相位角。 相位:表示正弦量的变化进程,也称相位角。 相位角 初相位: 时的相位 时的相位, 初相位:t=0时的相位,用ψ表示。
第三章 正弦交流电路

m
式中,Im正弦交流电流的幅值。说明正弦交流电压和 电流的幅值之间满足欧姆定律。
(二)电压、电流的有效值关系
据电压、电流幅值之间的关系,把等式两边同 时除以 2 即得到有效值关系,即 或 U IR 这说明,正弦交流电压和电流的有效值之间 也满足欧姆定律。
I U R
(三)相位关系
(黄色)
电动势、电压和电流的大小和方向随时间按正弦规 律性变化。叫做正弦交流电流、电压、电动势。在任一 时刻可用三角函数表示。
e Em sin(t e ) u U m sin(t u ) i I m sin(t i )
第四章
交流电路
第一节 交流电的基本概念
三、描述正弦交流电特征的物理量
(三)相位、初相位与相位差
1、相位(或相角):
t i I m sin(t )
i
O
反映正弦量变化的进程。 2、初相位: 表示正弦量在t =0时的初相位。
——
如:
给出了观察正弦波 的起点或参考点。
ωt
e1 Em sin(t 1 ) e2 Em sin(t 2 )
X L 2fL 2 3.14 50 0.1 31.4Ω
U 10 I 318m A XL 31.4
(2)当 f = 5000Hz 时
X L 2fL 2 3.14 5000 0.1 3140 Ω
U 10 I 3.18m A XL 3140
4
可知
(1)最大值
(2)有效值 (3)角频率 (4)频率 (5)周期
m 30 2 42.6
m 30 2
100s 1 314rad / s
第3章 正弦交流电路

3.3.1 单一参数的正弦交流电路
1.纯电阻电路 (1) 电压与电流的关系
+
u iR
u
i I m sin t
_
u iR I m R sin t U m sin t
i R
对于正弦交流电路中的电阻电路(又称纯电阻 电路),一般结论为:
1)电压、电流均为同频率的正弦量。
2)电压与电流初相位相同,即两者同相。
y
i
ω
Im
i1
ωt1 φ
Im
i0
90
o
x
o
ωt1
ωt
φ
t t1 i1 I m sin(t 1)
对于一个正弦量可以找到一个与其对应的旋转矢量,反之, 一个旋转矢量也都有一个对应的正弦量。
3.2.2 复数及复数的运算 1、复数
A a jb
A r cos r sin
e j cos j sin
作相量图时要注意: 只有同频率的正弦量才 能画在一个相量图上,不 同频率的正弦量不能画在 一个相量图上。
+j
U
Φu
o
Φi
+1
I
3.3正弦交流电路的简单分析与运算
电阻元件、电感元件与电容元件都是组成 电路模型的理想元件。
所谓理想元件,就是突出元件的主要电磁 性质,而忽略其次要因素。如电阻元件具 有消耗电能的性质(电阻性),其它的电 磁性质如电感性、电容性等忽略不计。。
f = 1/T T = 1/f
i
角频率是指交流电在1s内变化的电 Im
角度。正弦量每经过一个周期T,
o
对应的角度变化了2π弧度,所以
φ
ωt
T
2f 2
电工学第三章

3-1正弦交流电的基本概念 3-1-1 正弦交流电的三要素 正弦交流电: 大小和方向都随时间按正弦规律作周期性变化 的电量(电压、电流、电动势)。
i
设正弦交流电流:
Im
O
t
T
i I m sin t
初相角:决定正弦量起始位置 角频率:决定正弦量变化快慢 in( t 2 )
I I1 I 2
i i1 i 2
上节复习:
1、写出下列正弦量对应的相量,并作出相量图
i1 4 2 s in ( t 3 0 )
i2 1 0 2 c o s ( t 1 2 0 )
i3 1 4 .1 4 s in ( t 1 5 0 )
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
U
U
u U m sin ( t )
电压的有效值相量
U
U
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
例1:
u 10 sin( 314 t 60 )
写出其相量形式
U 5 2 60
U m 10 60
3-1-3 正弦交流电的参考方向
i
O
i I m sin t
ωt
i 0,实际方向与参考方向相 同
i 0,实际方向与参考方向 相反
3-2正弦交流电的相量表示法
1.正弦量的表示方法 波形图
O
u/i
ωt
瞬时值表达式
u U m sin ( t )
i I m s in
第三章单相正弦交流电路【PPT课件】PPT课件

HOME
R-L-C串联交流电路中的复数形式欧姆定律
I
U IZ
Z R j(L 1 ) C
Z:复数阻抗
实部为阻 虚部为抗
R U R
U jL U L
1
jC
U C
感抗 容抗
HOME
3.4.1 阻抗三角形
I
Z R jபைடு நூலகம் 1
C
Z 是一个复数,但并不是正弦交流
U
量,上面不能加点。
R U R
j
L
1
C
IZ
Z
R
j(L
1
C
)
Z
Z
R2
(L
1
C
)
2
tg 1
L
1
C
U
I
R
Z
>0 ,u领先i =0 ,u与i同相 <0 ,u落后i
HOME
tg 1
L
1
C
R
时L ,1C 表示u 0领先 i --电路呈感性
时L,
1 C
表示u0落后 i
--电路呈容性
当L 1C时, 0表示 u 、i同相 --电路呈电阻性
第三章单相正弦交 流电路【PPT课件】
3.4 电阻、电感、电容串联的电路
相量模型
I
jLR U R
U
1
jC
U L
U C
相量方程式:
U U R U L UC
设 I I0 (参考相量)
U R IR
则 U L I jL
U C
I
1
jC
HOME
U IR I jL I 1 jC
I
R
第三章正弦交流电路

1 = U 2
cm m
I sin2 ωi = U Isin2 t
第四节电容和纯电容交流电路
纯电容电路瞬时功率波形图
第三章 正弦交流电路
上一页
下一页
返 回
结 束
第四节电容和纯电容交流电路
二、纯电容正弦交流电路
• 2.电路的功率 (2)平均功率(有功功率) 瞬时功率在一个周期内的平均功率等于零,即:
2
2 C
第三章 正弦交流电路
上一页
下一页
返 回
结 束
第四节电容和纯电容交流电路
二、纯电容正弦交流电路
例题
0
把一个C 80μ F的电容器接在 u 220 2sin(314t 30 ) 的电源上。试求:(1 ) 电流相量并写出其解析 式; (2) 无功功率 (3)画出电压和电流 的相量图.
• 若万用表的指针向小电阻方向摆动,不 能回摆至“∞”,而停在某一位置上,说 明电容器有漏电现象。
第三章 正弦交流电路
上一页
下一页
返 回
结 束
第四节电容和纯电容交流电路
u C
5.技能训练:用万用表检测电容器
• 若万用表的指针立即指到“0”位置上不 回摆,说明电容器内部已短路 。
第三章 正弦交流电路
上一页
下一页
返 回
结 束
最大值
上一页
下一页
返 回
结 束
(3)有效值
正弦量的有效值是根据电流的热效应来规 定的。如图3-5所示,在相同的时间里, 直流电和交流电在相同的负载上产生相 同的热量,就把该直流电的值叫做该交 流电的有效值
上一页
下一页
返 回
结 束
I
Im 2
电路分析基础第3章 正弦交流电路
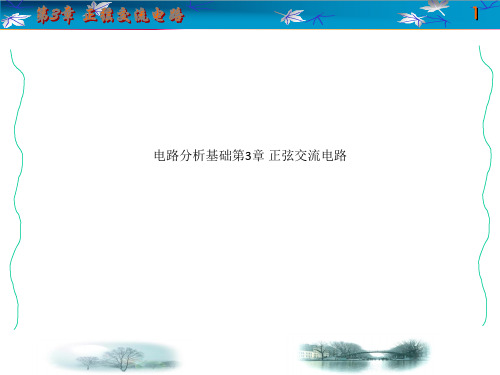
20 图3.2.4 不同初相时的正弦电流波形
21
在正弦交流电路的分析中,有时需要比较同频率的正弦 量之间的相位差。例如在一个电路中,某元件的端电压u和 流过的电流i
u=Umsin(ωt+ψu) i=Imsin(ωt+ψi) 它们的初相分别为ψu和ψi,则它们之间的相位差(用φ表 示)为 φ=(ωt+ψu)-(ωt+ψi)=ψu-ψi (3.2.7) 即两个同频率的正弦量之间的相位差就是其初相之差,相位 差φ
以复数运算为基础的,复数的表示如图3.3.1所示。
32 图3.3.1 复数的表示
33
一个复数A可以用下述几种形式来表示。
1.代数形式
A=a+jb
(3.3.1)
式中, j 1 2.三角形式
A=rcosψ+jrsinψ=r(cosψ+jsinψ)
(3.3.2)
式中,r a2b2, t gb,arctban
28
I B I Bm 7 .07 5 A 22
A
100
π
1 300
π 60 3
B
100
π
1 600
π 30 6
A
B
π 3
π 6
π 2
90
(2)
iA=14.1sin(314t+60°)A
iB=7.07sin(314t-30°)A
29 图3.2.6 例3.2.5的波形图
a
a
ψ称为A的辐角。
34
3.指数形式
根据欧拉公式
ejψ=cosψ+jsinψ
第3章正弦交流电路
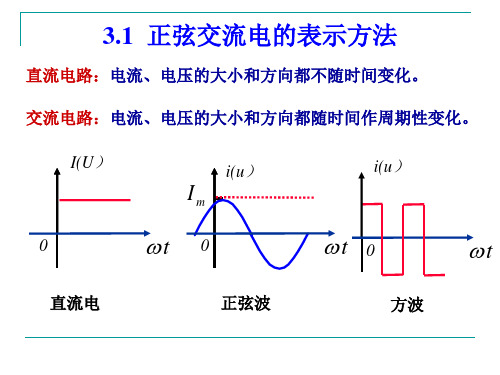
3)指数形式
A =r (cos jsin) = re j
4)极坐标形式
A=r∠
从图中可以看出,复数A的实部a、虚部b与模r构成一个直角三角形。
三者之间的关系为
r a2 b2
arctan b
个正弦量同相,如图4.2 (b)所示;
(4) 当 12 = 时,一个正弦量到达正最大值时,另一个正弦量到达
负最大值,此时称第1个正弦量与第2个正弦量反相,如图4.2 (c)所示;
(5) 当 12 = /2时,一个正弦量到达零时,另一个正弦量到达正最
大值(或负最大值),此时称第1个正弦量与第2个正弦量正交。如图4.2 (d) 所示。
U1 U1 1
U U1 U 2
U 2 U 2 2
u(t ) 2 U cos( t )
故同频正弦量相加减运算变成对 应相量的相加减运算。
i1 i2 = i3
I1 I2 I3
3.2 单一参数正弦交流电路的分析
一、纯电阻元件电路
1. 电阻元件 在正弦电路中,电流、电压虽然都是随时间变化
= 311sin(30°)= 115.5V
i= 5sin(314t 90°) = 5sin(314×0.00333 90°) = 5sin(150°)
= 2.5A
可见,当两个同频率正弦量的计时起点变化时,各自的相位将发生
变化,但其相位差不变。说明相位的大小与计时起点的选择有关,
而相位差与计时起点的选择无关。
(2)、 乘除运算——极坐标为例
若 A1= r1 1 ,若A2= r2 2
则
A 1
电工学第三章

本章内容
●正弦交流电的基本概念 ●正弦交流电的相量表示法 ●单一参数交流电路
●串联交流电路
●并联交流电路 ●交流电路的功率 ●电路的功率因数
●电路中的谐振
第3章 交流电路
3.1 正弦交流电的基本概念
3.1 正弦交流电的基本概念
正弦交流电—其大小和方向随时间按正弦函数变化的电
动势、电压和电流总称为正弦交流电。其函数表达式(又 为瞬时表达式)和波形图如下所示
阻抗串联电路及其等效电路
= Ri + X i
(2)分压原理
U1 = U
Z1 Z1 + Z 2
U1 = U
Z1 Z1 + Z 2
第3章 交流电路
3.5 并联交流电路
3.5 并联交流电路
(1)等效阻抗的计算 U U I = I1 + I 2 = + Z1 Z 2 ( 1 + 1 ) = U =U Z1 Z 2 Z
第3章 交流电路
3.4 UL
串联交流电路
① u与i的大小关系
2 U = U R + (U L U C ) 2 = ( IR) 2 + ( IX L IXC ) 2
U
UL+ UC UR I
= I R + (X L XC )
2
2
U = R 2 + ( X L X C )2 = R 2 + X 2 = Z I
.
I L
.
u i
i u ωt 2π
U = jIX L d ( I m sin wt ) di u=L =L dt dt U = wLI m coswt
第三章 正弦交流电路的稳态分析
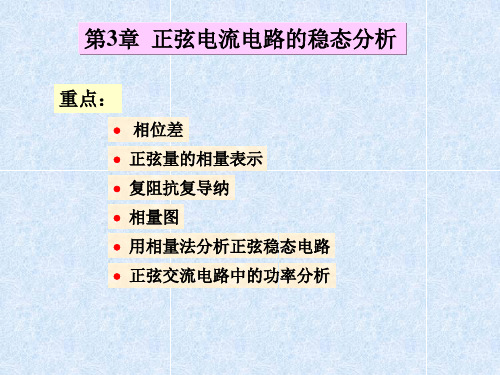
w
Im3
y1
一、复数及运算
y2
y3
Im b
1. 复数A表示形式: Im b
A
A |A|
y
0 a
Re 0 a Re
A a jb
A A e jy | A | y
2. 复数运算 (1)加减运算——直角坐标 (2) 乘除运算——极坐标 3. 旋转因子 A1±A2=(a1±a2)+j(b1±b2)
Im( 2 U 1 e
jw t
) Im( 2 U 2 e jw t )
jwt
2U2 e
jw t
) Im( 2 (U 1 U 2 )e jw t )
得:
U U1 U 2
U
这实际上是一种变换思想,由时域变换到频域
i1 i2 = i 3 时域 频域
第四节 复阻抗和复导纳及等效变换 U R I U jw L I 一. 复阻抗
正弦激励下 +
U
I
无源 线性 纯电阻
I
+
U
U
Z
1 I jw C
-
-
U 复阻抗 Z I
ZR R
纯电感
Z L jwL jX L 纯电容 ZC 1 jwC jXC
定义
XC
1 wC
错误的写法 1 u wC i
1 U wC I
(1) 表示限制电流的能力; (2) 容抗的绝对值和频率成反比。
XC
w 0(直流), X C , 隔直作用; w , X C 0, 旁路作用;
w
交流电路

t
如果相位差为+180 或-180 ,称为两波形反相
三、 正弦量的表示方法
i
波形图
t
i sin 1000 30 t
必须 小写
瞬时值表达式
相量
重点
前两种不便于运算,重点介绍相量表示法
正弦波的相量表示法
概念 :一个正弦量的瞬时值可以用一个旋转矢量 在纵轴上的投影值来表示。
努力 努力 目标一定能达到
第三章 正弦交流电路
主要内容 §3~1.正弦交流电 §3~2.电阻、电感和电容元件 §3~3.功率因数的提高 §3~3 三相交流电动势的产生、
电源的连接
§3~3 三相负载的连接
条形磁铁的磁感线
第一节 正弦交流电
直流电——电流大小与方向不随时间而变化 交流电——电流大小与方向随时间而变化 如果在电路中电动势的大小与方向均随时间按正 弦规律变化,由此产生的电流、电压大小和方向
则有
1 T 2 I i dt 0 T
当 i I m sin
t 时,
可得
Im I 2
问题与讨论
若购得一台耐压为 300V 的电器,是否可用于
220V 的线路上?
~ 220V
电器
最高耐压 =300V
有效值 U = 220V 电源电压 最大值 Um =
2 220V = 311V
用正弦定理求角: U2 U = sin sin
u=
2U sin t
= 1+
注意 :
1. 只有正弦量才能用相量表示,非正弦量不可以。 2. 只有同频率的正弦量才能画在一张相量图上,
不同频率不行。
新问题提出: 平行四边形法则可以用于相量运算,但不方便。 故引入相量的复数运算法。 相量 复数表示法 复数运算
正弦交流电路

2. 平均功率(有功功率)P:一个周期内的平均值
i
P=UI
=I2R=i U2/2RI
sint
Uu =IRR
u 2U sint
P1 Tpd t1Tuidt
T0
T0
大写 1 T 2UIsin2t dt
T0
1
T
UI(1cos2t)dtUI
T0
§ 3.4 理想电感元件上的正弦稳态响应
一、电压电流关系
即:瞬时值和相量满足基尔霍夫定律,有效值不满足
I1I2I30
I1
I3
I1-I2+I3= 0
I2
U 3
U 4
U 2 U 1 U 2 U 3 U 4 U 5 U 6 0 U 1
U 5
U 6
例: i162si nt (3)0
i282si nt (6)0
求i=i1+i2
i
解: I 1 6 3 0 5 .1 9 j3 6
Im[Ime ji e jt ]
复指数函数中的一个复常数
复常数定义为正弦量的相量,记
为
Im
相量 的表示
Im 为“最大值”相量
Im Im eji Im i
I 为“有效值”相量 IIeji Ii
相量是一个复数
注意
1)相量可以代表一个正弦量,但不等于该
正弦量。
U 50ej15° 50
2
sin(
实部是余弦量 虚部是正弦量
则 I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
电路课件第3章 交流电路

退出
3.2 正弦量的 相量表示法
例3 求正弦量i (t) =–5cos(100 t-π/3)A和
长
i1 (t) = 5cos(314t + 2π/3)V 对应的振幅相量
沙 理
解:
工
大
学 计
i (t) = 5cos(π+100 t–π/3) = 5cos(100 t + 2π/3)
信
工 程
是已知的,可不必考虑。
学
院 制
故一个正弦量可用幅值和初相角两个特征量
作
来确定。
比照复数和正弦量,正弦量可用复数来表示。
第 1-17 页 前一页 下一页
退出
3.2 正弦量的 相量表示法
相量—专门用于表示正弦量的复数
设正弦电压 : u(t) = Umcos(ωt +ψ)
长 沙 理
u的振幅相量: UmUmej= Um e jψ= Um∠ψ
院
制 作
(3) 初相位
i
T
正弦量的计时起点的相位。
Im
/w O
2 twt
3.1 正弦交流 电的基本概念
例
i
100
已知正弦电流波形如图,w=103rad/s,(1) 写出i(t)表达式;
长 沙
50
(2)求最大值发生的时间t1
理 工
t 解 i(t)10 c0 o1s30 t()
大 学
0 t1
i , Im , I
第 1-10 页 前一页 下一页
退出
3.2 正弦量的 相量表示法
1、 复数A的表示形式
Im
b
A
|A|
长 沙
直角坐标:A = a + jb
单相正弦交流电路

二、正弦交流电的基本物理量
3、频率 交流电在1秒内完成周期性变化的次数叫做 交流电的频率,用字母f表示,单位名称是赫 兹,简称赫,单位符号为Hz。频率较大的单 位有千赫(kHz)和兆赫(MHz),它们之间 的关系为 1千赫=1000赫 1兆赫=1000千赫
二、正弦交流电的基本物理量
根据以上定义,周期和频率的关系为
二、正弦交流电的基本物理量
注意,初相的大小与时间起点的选择密切相 关,而相位差与时间起点的选择无关。根据两 个同频率交流电的相位差,可以确立两个交流 电的相位关系。
二、正弦交流电的基本物理量
如果Δφ=φ1-φ2>0,那么i1超前i2,或者说i2 滞后i1; 如果Δφ=φ1-φ2=0,那么就称这两个交流 电同相; 如果Δφ=φ1-φ2=180°,那么就称这两个 交流电反相。 如果Δφ=φ1-φ2=90°,那么就称这两个 交流电正交。
O
ωt
• 当线圈按逆时针方向以速度υ作等速旋转时,线 圈边分别切割磁力线,产生感应电动势,其大小 为: e=Emsinα= Emsinωt 。
• 上式是从线圈平面与中性面重合的时刻开始计时 的,如果线圈平面与中性面成一夹角φ时开始计时 的,那么,经过时间t,线圈平面与中性面的夹角 是ωt+ φ ,感应电动势的公式变为: e=Emsin(ωt+ φ)
二、正弦交流电的基本物理量
例如,正弦交流电压u1=10sin(314t+60°), u2=5sin(314t-45°)则u1与u2的相位差为 (314t+60°)-(314t-45°)=105° 即u1超前u2 105°电角度。 若正弦交流电流i1=20sin(314t+30°), i2=8sin(314t+70°) 则i1与i2的相位差为 (314t+30°)-(314t+70°)=-40° 即i1滞后i2 40°电角度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 正弦交流电路
一、选择题
1.在负载为纯电容元件的正弦交流电路中,电压u 与电流i 的相位关系是( A ) A.u 滞后i 90º B.u 超前i 90º C.反相
D.同相
2.已知正弦电流的有效值相量为 则此电流的瞬时值表达式是下列式中的( C )
A .10sin(ωt-45º)A
B .10sin(ωt+45º)A
C .102sin(ωt-45º)A
D .102 sin(ωt+45º)A
3.通过电感L 的电流为i L =62sin(200t+30º)A ,此电感的端电压U L =2.4V ,则电感L 为( B )
A.2mH
B.2mH
C.8mH
D.400Mh
4.某电路元件中,按关联方向电流)90314sin(210︒-=t i A ,两端电压
t u 314sin 2220=V ,则此元件的无功功率Q 为( c )
A.-4400W
B.-2200var
C.2200var
D.4400W
5.纯电感元件的正弦交流电路如图示,已知电源的角频率为ω,其U 与I 的正确关系是
( b )
A.L I j U ω-=
B.L I j U ω=
C.L
1I j U ω-= D. L
1I
j U ω=
6.图示电路中,u 为正弦交流电压,其角频率为ω,则此电路中的阻抗模|Z|为( a ) A.2
221)C
1L ()R R (ω-
ω++ B.2221)C 1L ()R R (ω+ω++ C. C
1L )R R (21ω-ω++ D.C
1L R R 21ω+ω++
交流电路中,若u R =52sin(ω
7.R 、L 串联的正弦
I
U •
•
R 1
L
R 2C
u
t+10°)V ,u L =52sin(ωt+100°)V ,则总电压u 为( b )
A . 5sin(ωt+45°)V
B . 10sin(ωt+55°)V
C . 52sin(ωt+110°)V
D . 102sin(ωt+70°)V
8.在正弦交流电路中,某负载的有功功率P=1000W ,无功功率Q=577var ,则该负载的功率因数为( d ) A. 0.5
B. 0.577
C. 0.707
D. 0.866
9.图示正弦交流电路中U=220V ,R=ωL=
1
ωC
=100Ω,此电路消耗的有功功率是( b )
A . 2.2×100W
B . 2.22
×100W
C . 2.2×300W
D . 2.22
×300W
C
•
U
10.电路如图所示,已知I 1=3A ,I 2=8A ,I 3=4A 则电流I 等于( b ) A .1A B .5A C .7A D .15A
I 3
•
•
11.为了提高感性负载电路的功率因数,通常采用的方法有( d ) A .串联电感 B .串联电容 C .并联电感
D .并联电容
12.图示正弦交流电路中,若C I 超前U
角︒45,则R 应等于( c ) A.
3
2
Ω B. 1Ω C.1.5Ω D. 2Ω
13.在图示的正弦电路中,5,C AB BC R X U U ==Ω=,且电路处于谐振状态,则复阻抗Z 为( a )
Z R
-jX C
B
+-I U •
•
A.(2.5 2.5)j +Ω
B.(2.5 2.5)j -Ω
C.545∠Ω
D.0∠Ω
14.有一RLC 串联电路,已知5L C R X X ===Ω,端电压U=10V ,则I =( c )A A.
23 B. 1
2
C. 2
D. 1 15.已知某感性负载的阻抗模7.07,5Z R =Ω=Ω,则其功率因数是( c ) A. 0.5 B. 0.6 C. 0.707 D.0.8
二、填空题
1.在正弦交流电路中,电源的频率越高,电感元件的感抗越 大 。
2.已知正弦电压的有效值为200V ,频率为100Hz ,初相角为︒-45,则其瞬时 值表达式u =______2002sin(62845)t V -__ 。
3.已知某负载Z=|Z| 的端电压为U U
= ,则此负载中的电流I
=____u U Z
ϕϕ∠-___ _。
4.图示正弦交流电路中,电压u 、u 1、u 2、u 3的关系式可写为u =_______u u u 123-+_ 。
u
u u 2
3
5.R 、C 串联的正弦交流电路中,电阻元件的端电压为12V ,电容元件的端电压为16V ,则电路的总电压为__20______V.
6.图示正弦交流电路中,已知电流表A 1的读数为0.1A ,表A 2的读数为0.4A ,表A 的读数为0.5A ,则表A 3的读数为__0.3______A ,表A 4的读数为___0.4_____A 。
S
u
7.已知工频正弦电压U ab 的最大值为311V ,初相位为60-,其有效值为________,其瞬时值表达式为________。
8.正弦量314u tV =的相量表达式为________,正弦量5sin(31460)i t A =--的相量表达式为________。
9.一个RL 串联交流电路,其复阻抗为(44)Z j =+Ω,该电路的功率因数是________,电压与电流的相位差是________。
10. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 ,该电路为 性电路。
电路中吸收的有功功率为 ,无功功率又为 。
三、计算题
1.有一电感线圈接于100V 、50Hz 的正弦交流电源上,测得此电感线圈的电流
I=2A ,有功功率P=120W ,求此线圈的电阻R 和电感L 。
2.电路如图所示,已知R=10k Ω,C=5100pF ,外接电源电压u=tV ωsin 2,频率为
1000Hz ,试求:
•
U
•
U C
•
(1)电路的复数阻抗Z
; (2)•I 、•
R U 、•
C U 。
3. 一个电感为20mH 的纯电感线圈,接在电压u =311sin (314t+300)V 的电源上,求:(1)通过线圈的电流为多少?写出电流的解析式;(2)电路的无功功率是多少?
4.如图所示,已知三个表 A 1、 A 2、 V 的读数分别为,5A ,5V ,1000/rad s ω=,12U U •
•
滞后角90,求R 、L 、C 。
U 2
•
•
•
•
L
5.单相交流电路如图所示,已知 0502∠=U V ,Ω=5C
X ,Ω==4L X R 。
求:(1)电流I 及电压1
U 、U ;(2)电路的P 、Q 、S 。
6.阻抗Z 1 = 3 + j4 Ω,Z 2 = 6 + j8 Ω 串联于V 1.53225 ∠=U 的电源上工作。
求:(1) Z 1 ,
Z 2上的电压 u 1 ,u 2 ;(2)有功功率P ,无功功率Q
及功率因数cos ϕ,该电路呈何性质?
Z Z 12
7.在图中,电流表A 1和A 2的读数分别为I 1=3A ,I 2=4A 。
(1)设Z l =R ,Z 2=-jX c ,则电流表A 0的读数应为多少?(2)设Z l =R ,问Z 2为何种参数才能使电流表A 0的读数最大?此读数应为多少?(3)设Z 1=jX L ,问Z 2为何种参数才能使电流表A 0的读数最小?此读数应为多少?
8. 日光灯管-镇流器串联接到交流电压上,可看作RL 串联电路,如已知灯管的等效电阻R 1=280Ω,镇流器的电阻和电感分别为R 2=20Ω,L=1.65H ,电源电压U=220V ,试求:
2
+
-
2
I
电路中的电流和灯管两端与镇流器上的电压,这两个电压加起来是否等于220V ?电源频率为50HZ 。
9.无源二端网络输入端的电压和电流为
V
)33314sin(24.4V )20314sin(2220︒-=︒+=t i t u
试求此二端网络由两个元件串联的等效电路和元件的参数值,并求二端网络的功率因数及输
入的有功功率和无功功率。
10.在电阻、电感、电容串联谐振电路中,电阻R =50Ω,电感L =5 mH ,电容C =50pF ,外加电压有效值U =10 mV 。
求:(1)电路的谐振频率;(2)谐振时的电流;(3)电路的品质因数;(4)电容器两端的电压。
11.把一个线圈接到电压为20 V 的直流电源上,测得流过线圈的电流为0.4 A 。
当把它改接到频率为50 Hz ,电压有效值为65 V 的交流电源上,测得流过线圈的电流为0.5 A 。
求线圈的参数R 和L 。
-。
