大连市数学中考25几何压轴题-阅读材料专项精选25题
中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题(共30小题)1.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点,使∠AB′B=∠AC′C=∠BAC(1)如图1中∠BAC为直角,∠BAC=∠AB′B=∠AC′C=90°(点B′与点C′重合),则△ABC∽△B'BA∽△C'AC,,,进而可得AB2+AC2=;(2)如图2中当∠BAC为锐角,图3中∠BAC为钝角时(1)中的结论还成立吗?若不成立,则AB2+AC2等于什么(用含用BC和B′C′的式子表示)?并说明理由(3)若在△ABC中,AB=5,AC=6,BC=9,请你先判断出△ABC的类型,再求出B′C′的长3.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE 的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE 和AF数量关系.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.如图,在平行四边形ABCD中,AC与BD交于点O,以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F,且∠EOF与∠BAD互补.(1)若四边形ABCD是正方形,则线段OE与OF有何数量关系?请直接写出结论;(2)若四边形ABCD是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由;(3)若AB:AD=m:n,探索线段OE与OF的数量关系,并证明你的结论.6.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC=.7.如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.8.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.(3)解决问题是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.9.等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD 的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN 和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.10.四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD中,AB=AD,CB=CD,则AC与BD的位置关系是,请说明理由.(2)试探究图1中四边形ABCD的两组对边AB,CD与BC,AD之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.11.问题发现:如图(1)在Rt△ABC和Rt△BDE中,∠A=∠DEB=30°,BC=BE=6,Rt△BDE绕点B逆时针旋转,H为CD的中点,当点C与点E重合时,BH与AE的位置关系为,BH与AE的数量关系为;问题证明:在Rt△BDE绕点B旋转的过程中,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明若不成立,请说明理由;拓展应用:在Rt△BDE绕点B旋转的过程中,当DE∥BC时,请直接写出BH2的长.12.如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,(1)问题发现的值为;(2)探究与证明将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH=,则AH的长为.13.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.14.如图,已知点E是射线BC上的一点,以BC、CE为边作正方形ABCD和正方形CEFG,连接AF,取AF的中点M,连接DM、MG(1)如图1,判断线段DM和GM的数量关系是,位置关系是;(2)如图2,在图中的正方形CEFG绕点C逆时针旋转的过程中,其他条件不变,(1)中的结论是否成立?说明理由;(3)已知BC=10,CE=2,正方形CEFG绕点C旋转的过程中,当A、F、E共线时,直接写出△DMG的面积.15.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.16.如图(1),在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.(1)观察猜想,图(1)中△PMN是(填特殊三角形的名称)(2)探究证明,如图(2),△ADE绕点A按逆时针方向旋转,则△PMN的形状是否发生改变?并就图(2)说明理由.(3)拓展延伸,若△ADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出△PMN 的周长的最大值.17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.18.问题提出:(1)如图1,在四边形ABCD中,连接AC、BD,AB=AD,∠BAD=∠BCD=90°,将△ABC绕点A逆时针旋转90°,得到△ADE,点B的对应点落在点D,点C的对应点为点E,可知点C、D、E在一条直线上,则△ACE为三角形,BC、CD、AC的数量关系为;探究发现:(2)如图2,在⊙O中,AB为直径,点C为的中点,点D为圆上一个点,连接AD、CD、AC、BC、BD,且AD<BD,请求出CD、AD、BD间的数量关系.拓展延伸:(3)如图3,在等腰直角三角形ABC中,点P为AB的中点,若AC=13,平面内存在一点E,且AE=10,CE=13,当点Q为AE中点时,PQ=.19.已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.(1)【观察猜想】如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是;②∠BDE的度数是;(2)【探究证明】如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;(3)【拓展延伸】如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC 边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.20.如图①,在正方形ABCD和正方形AB'C'D'中,AB=2,AB'=,连接CC’(1)问题发现:.(2)拓展探究:将正方形AB'C'D'绕点A逆时针旋转,记旋转角为θ,连接BB',试判断:当0°≤θ<360°时,的值有无变化?请仅就图②中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C,C′,D'三点共线时BB′的长.21.如图1,在正方形ABCD中,点O是对角线BD的中点.(1)观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是,直线AC与DE的位置关系是.(2)类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.(3)拓展延伸将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.22.如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为°,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为;(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.23.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF与线段EG的数量关系是;(2)探究证明:如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求的值.24.如图1,在Rt△ABC中,∠B=90°,AB=2,BC=1,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、B、E三点共线时,直接写出线段BD的长.25.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究如图(1),当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸如图(2),当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移如图(3),当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.26.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE ⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O 于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;②若AB=8,CD=5,求△DEF的面积.28.【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.30.如图1和图2,在△ABC中,AB=AC,BC=8,tan C=.点K在AC边上,点M,N 分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.参考答案与试题解析一.解答题(共30小题)1.【解答】解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.2.【解答】解:(1)如图1中,∵△ABC∽△B'BA∽△C'AC,∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC×BC=BC2,故答案为BC2.(2)不成立.理由:如图2中当∠BAC为锐角时,BB′+CC′﹣B′C′=BC,且△ABC∽△B'BA∽△C'AC,∴∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC2+BC•B′C′.图3中∠BAC为钝角时,BB′+CC′+B′C′=BC.AB2+AC2=BC(BB′+CC′)=BC2﹣BC•B′C′.(3)当AB=5,AC=6,BC=9时,则AB2+AC2<BC2,可知△ABC为钝角三角形,由图3可知:AB2+AC2=BC2﹣BC•B′C′,∴52+62=92﹣9B′C′,∴B′C′=.3.【解答】解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,∴∠ABC=∠CAB=45°=∠CDE=∠CED,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠CAB=∠CBE=45°,∴∠DBE=∠ABC+∠CBE=90°,=1,故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,∵△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣4.【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,∴AD=BD=DC,∠BDA=90°,∵四边形DFGE是正方形,∴DE=DF,∠EDF=90°,∴∠BDE=∠ADF=90°,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF故答案为:BE=AF;(2)成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立;(3)在△ADE中,∵AE<AD+DE,∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.如图④所示:则AD=BC=1,DE=DF=2,∴AE=AD+DE=3,即AE的最大值为3.5.【解答】解:(1)如图1,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是正方形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(2)(1)的结论成立;理由:如图2,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是菱形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(3)如图3,过点O作OG⊥AB于G,OH⊥AD于H,∴∠OGE=∠OHF=90°,∴∠BAD+∠GOH=180°,∵∠BAD+∠EOF=180°,∴∠GOH=∠EOF,∴△EOG∽△FOH,∴,∵O是▱ABCD的对角线的交点,∴S△AOB=S△AOD,∵S△AOB=AB•OG,S△AOD=AD•OH,∴AB•OG=AD•OH,∴=,∴.6.【解答】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.7.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.8.【解答】解:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;③当6<m<10时,由∠DBE=120°>90°,∴此时不存在;④当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14,综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.9.【解答】解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠ABD+∠ADB=90°,∠ADB=∠CDH,∴∠ADH+∠DCH=90°,∴∠CHD=90°,∴EC⊥BH,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.故答案为:45°(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠AOC+∠ACO=90°,∠AOC=∠BOH,∴∠OBH+∠BOH=90°,∴∠BHO=90°,∴EC⊥BD,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.(3):如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,∵AD=AE,AB=AC,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠ABD,BD=EC,∵∠ABD+∠AOB=90°,∠AOB=∠CPO,∴∠CPB=90°,∵PB是⊙A的切线,∴∠ADP=90°,∵∠DPE=∠ADP=∠DAE=90°,∴四边形ADPE是矩形,∵AE=AD,∴四边形ADPE是正方形,∴AD=AE=PD=PE=2,BD=EC==2,∴PC=2﹣2,PB=2+2,∴S△BCP的最小值=×PC×PB=(2﹣2)(2+2)=4.10.【解答】(1)解:AC⊥BD,理由如下:连接AC、BD,如图2所示:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,故答案为:AC⊥BD;(2)解:AD2+BC2=AB2+CD2;理由如下:如图1,已知四边形ABCD中,AC⊥BD,设BD、AC相交于E,∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)解:如图3,连接CG、BE,∵四边形ACFG和四边形ABDE是正方形,∴AC=AG,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,由(2)得,CG2+BE2=CB2+GE2,在Rt△ABC中,AC=4,AB=5,根据勾股定理得,BC2=52﹣42=9,∵CG和BE分别是正方形ACFG和正方形ABDG的对角线,∴CG2=42+42=32,BE2=52+52=50,∴GE2=CG2+BE2﹣CB2=32+50﹣9=73,∴GE=.11.【解答】解:问题发现:如图1中,结论:AE=2BH,AE⊥BH.理由:在Rt△ABC中,∵BC=6,∠A=30°,∴AE=2BC=12,在Rt△CDB中,∵∠DCB=30°,∴CD==4,∵CH=DH,∴BH=CD=2,∴==2,∴AE=2BH.故答案为AE⊥BH,AE=2BH.问题证明:如图2中,(1)中结论成立.理由:延长BH到F使得HF=BH,连接CF.设AE交BF于O.∵CH=DH,BH=HF,∠CHF=∠BHD,∴△CHF≌△DHB(SAS),∴BD=CF,∠F=∠DBH,∴CF∥BD,∵AB=BC,BE=BD,∴BE=CF,∴==,∵CF∥BD,∴∠BCF+∠CBD=180°,∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°,∴∠BCF=∠ABE,∴△ABE∽△BCF,∴∠CBF=∠BAE,==,∴AE=BF=2BH,∵∠CBF+∠ABF=90°,∴∠ABF+∠BAE=90°,∴∠AOB=90°,∴BH⊥AE.拓展应用:如图3﹣1中,当DE在BC的下方时,延长AB交DE于F.∵DE∥BC∴∠ABC=∠BFD=90°,由题意BC=BE=6,AB=6,BD=2,DE=4,∵•BD•BE=•DE•BF,∴BF==3,∴EF=BF=3,∴AF=6+3,∴AE2=AF2+EF2=(6+3)2+(3)2=144+36.∵AE=2BH,∴AE2=12BH2,∴BH2=12+3如图3﹣2中,当DE在BC的上方时,同法可得AF=6﹣3,EF=3,∴BH2==(=12﹣3.12.【解答】解:(1)如图1中,作EH⊥CG于H.∵四边形ECFG是菱形,∠ECF=60°,∴∠ECH=∠ECF=30°,EC=EG,∵EH⊥CG,∴GH=CG,∴=cos30°=,∴=2•=,∵EG∥CD,AB∥CD,∴GE∥AB,∴==.故答案为.(2)结论:AG=BE.理由:如图2中,连接CG.∵四边形ABCD,四边形ECFG都是菱形,∠ECF=∠DCB=60°,∴∠ECG=∠EGC=∠BCA=∠BAC=30°,∴△ECG∽△BCE,∴=,∵∠ECB=∠GCA,∴△ECB∽△GCA,∴==,∴AG=BE.(3)如图3中,∵∠AGH=∠CGF=30°.∠AGH=∠GAC+∠GCA,又∵∠DAC=∠HAG+∠GAC=30°,∴∠HAG=∠ACH,∵∠AHG=∠AHC,∴△HAG∽△HCA,∴HA:HC=GH:HA,∴AH2=HG•HC,∴FC=2,CG=CF,∴GC=2,∵HG=,∴AH2=HG•HC=•3=9,∵AH>0,∴AH=3.故答案为3.13.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.14.【解答】解:(1)如图1,延长GM交AD于H,∵AD∥GF,∴∠GFM=∠HAM,在△FMG和△AMH中,,∴△FMG≌△AMH(ASA),∴HM=GM,AH=FG,∵AD=CD,AH=FG=CG,∴DH=DG,∵∠HDG=90°,HM=GM,∴DM=MG,DM⊥MG,故答案为DM=MG,DM⊥MG.(2)结论成立:DM=MG,DM⊥MG,理由:如图2中,延长GM使得MH=GM,连接AH、DH、DG,延长AD交GF的延长线于N,交CD于O.∵AM=MF,∠AMH=∠FMG,MH=MG,∴△AMH≌△FMG(SAS),∴AH=GF=CG,∠AHM=∠FGM,∴AH∥GN,∴∠HAD=∠N,∵∠ODN=∠OGC=90°,∠DON=∠GOC,∴∠N=∠OCG,∴∠HAD=∠DCG,∵AH=CG,AD=CD,∴△HAD≌△GCD(SAS),∴DH=DG,∠HDA=∠CDG,∴∠HDG=∠ADC=90°,∴△HDG是等腰直角三角形,∵MH=MG,∴DM⊥GH,DM=MH=MG,(3)①如图3﹣1中,连接AC.在Rt△ABC中,AC==10,在Rt△ACE中,AE==14,∴AF=AE=EF=14﹣2=12,∴FM=AM=AF=6,在Rt△MGF中,MG==2,∴S△DMG=×2×2=20,②如图3﹣2中,连接AC.同法可得AE=14,AF=16,FM=8,MG==2,∴S△DMG=×2×2=34,综上所述,满足条件的△DMG的面积为20或34.15.【解答】解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.16.【解答】解:(1)结论:△PMN是等边三角形.理由:如图1中,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∵AD=AE,∴BD=EC,∵PB=PC,CN=ND,BM=EM,∴PN∥BD,PM∥EC,PN=BD,PM=EC,∴PM=PN,∠NPC=∠ABC=60°,∠MPB=∠ACB=60°,∴∠MPN=60°,∴△PMN是等边三角形,故答案为等边三角形.(2)△PMN的形状不发生改变,仍为等边三角形,理由如下:如图2中,连接BD,CE.由旋转可得∠BAD=∠CAE,∵△ABC是等边三角形,∴AB=AC,∠ACB=∠ABC=60°又∵AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵M是BE的中点,P是BC的中点,∴PM是△BCE的中位线,∴PM=,且PM∥CE.同理可证PN=BD且PN∥BD,∴PM=PN,∠MPB=∠ECB,∠NPC=∠DBC,∴∠MPB+∠NPC=∠ECB+∠DBC=(∠ACB+∠ACE)+(∠ABC﹣∠ABD)=∠ACB+∠ABC=120°,∴∠MPN=60°,∴△PMN是等边三角形.(3)∵PM=EC,∴当EC最大时,等边△PMN的周长最大,∵EC≤AE+AC,∴EC≤8,∴PM≤4,∴PM的最大值为4,∴△PMN的周长的最大值为12.17.【解答】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(3)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠ACE=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.18.【解答】解:(1)由旋转变换的性质可知,∠CAE=90°,AC=AE,∴△ACE为等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC,故答案为:等腰直角;BC+CD=AC;(2)延长CO交⊙O于E,连接AE、BE、DE,则∠CDE=90°,∵点C为的中点,∴点E为的中点,∴EA=EB,∵AB为⊙O的直径,∴∠ADB=90°,由(1)得,DE=(AD+BD),由勾股定理得,CD2=CE2﹣DE2=AD2+BD2﹣(AD+BD)2=(AD﹣BD)2,∴CD=(BD﹣AD);(3)如图3,当点E在直线AC的左侧时,连接CQ、PC,∵CA=CB,点P为AB的中点,∴CP⊥AB,∵CA=CE,点Q为AE中点,∴CQ⊥AE,AQ=QE=AE=5,∴由勾股定理得,CQ==12,由(1)得,AQ+CQ=PQ,。
数学中考25题压轴题总结

Ⅲ、间接法求面积
求 SΔEFP 的 面 积 , 三 角 形 的 三 条 边 都 难 以 表 示 出 来 例 : 如图所示,在直角三角形 ABC 中,点 E 为边 AB 的中点,点 P 为 BC 边上一动
25.已知梯形 ABCD 中, AD // BC , ∠D = 90o, BC = 5 , CD = 3 , cot B = 1. P 是边 BC 上的一个动点(不与点 B 、点 C 重合),过点 P 作射线 PE ,使射线 PE 交射 线 BA 于点 E , ∠BPE = ∠CPD .
(1)当点 E 落在线段 AB 上时,设 BP = x , BE = y,试求 y 与 x 之间的函数解析
例 :如图,梯形 ABCD 中,AB ∥ CD ,∠ABC = 90! , AB = 6 , BC = 8 , tan D = 2 ,
点 E 是射线 CD 上一动点(不与点 C 重合),将 ΔBCE 沿着 BE 进行翻折,点 C 的对应点 记为点 F . (1)如图 2,当点 E 在线段 CD 上时,设 CE = x , EH = y ,求 y 与 x 之间的函数关系式,
25、如图,在 Rt ΔABC 中, ∠ACB = 90° , AC = 2 ,点 D 、 E 分别在边 BC 、 AB 上, ED ⊥ BC ,以 AE 为半径的⊙ A 交 DE 的延长线于点 F ; (1)当 D 为边 BC 中点时(如图 1),求弦 EF 的长;
(2)设 DC = x , EF = y ,求 y 关于 x 的函数解析式(不用写出定义域); BC
②面 积 ( 直 接 求 面 积 和间 接 求 面 积 ) 基本模型: Ⅰ、
大连市大连市第九中学中考数学期末几何综合压轴题模拟汇编

大连市大连市第九中学中考数学期末几何综合压轴题模拟汇编一、中考几何压轴题 1.问题发现:(1)正方形ABCD 和正方形AEFG 如图①放置,AB =4,AE =2.5,则DGCF=___________. 问题探究:(2)如图②,在矩形ABCD 中,AB =3,BC =4,点P 在矩形的内部,∠BPC =135°,求AP 长的最小值. 问题拓展:(3)如图③,在四边形ABCD 中,连接对角线AC 、BD ,已知AB =6,AC =CD ,∠ACD =90°,∠ACB =45°,则对角线BD 是否存在最大值?若存在,求出最大值;若不存在,请说明理由.2.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.原题:如图1,在平行四边形ABCD 中,点E 是BC 的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G .若3AFEF ,求CD CG的值.(1)尝试探究在图1中,过点E 作//EH AB 交BG 于点H ,则AB 和EH 的数量关系是_________,CG 和EH 的数量关系是_________,CDCG的值是_________. (2)类比延伸如图2,在原题的条件下,若()0AF m m EF =>,则CDCG的值是_________(用含有m 的代数式表示),试写出解答过程. (3)拓展迁移如图3,梯形ABCD 中,//DC AB ,点E 是BC 的延长线上的一点,AE 和BD 相交于点F .若ABa CD =,BCb BE=,()0,0a b >>,则AF EF 的值是________(用含a 、b 的代数式表示).3.《函数的图象与性质》拓展学习展示:(问题)如图①,在平面直角坐标系中,抛物线1G :232yax bx与x 轴相交于()1,0A -,()3,0B 两点,与y 轴交于点C ,则a =______,b =______.(操作)将图①中抛物线1G 沿BC 方向平移BC 长度的距离得到拋物线2G ,2G 在y 轴左侧的部分与1G 在y 轴右侧的部分组成的新图象记为G ,如图②.请直接写出图象G 对应的函数解析式.(探究)在图②中,过点C 作直线l 平行于x 轴,与图象G 交于D ,E 两点,如图③.求出图象G 在直线l 上方的部分对应的函数y 随x 的增大而增大时x 的取值范围. (应用)P 是抛物线2G 对称轴上一个动点,当PDE △是直角三角形时,直接写出P 点的坐标.4.(1)问题发现如图1,△ABC 与△ADE 都是等腰直角三角形,且∠BAC =∠DAE =90°,直线BD ,CE 交于点F ,直线BD ,AC 交于点G .则线段BD 和CE 的数量关系是 ,位置关系是 ;(2)类比探究如图2,在△ABC和△ADE中,∠ABC=∠ADE=α,∠ACB=∠AED=β,直线BD,CE交于点F,AC与BD相交于点G.若AB=kAC,试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数,并说明理由;(3)拓展延伸如图3,在平面直角坐标系中,点M的坐标为(3.0),点N为y轴上一动点,连接MN.将线段MN绕点M逆时针旋转90得到线段MP,连接NP,OP.请直接写出线段OP 长度的最小值及此时点N的坐标.5.(教材呈现)下面是华师版八年级下册教材第89页的部分内容.如图,G,H是平行四边形ABCD对角线AC上的两点,且AG=CH,E,F分别是边AB和CD 的中点求证:四边形EHFG是平行四边形证明:连接EF交AC于点O∵四边形ABCD是平行四边形∴AB=CD,AB∥CD又∵E,F分别是AB,CD的中点∴AE=CF又∵AB∥CD∴∠EAO=∠FCO又∵∠AOE=∠COF∴△AOE≌△COF请补全上述问题的证明过程.(探究)如图①,在△ABC中,E,O分别是边AB、AC的中点,D、F分别是线段AO、CO 的中点,连结DE、EF,将△DEF绕点O旋转180°得到△DGF,若四边形DEFG的面积为8,则△ABC的面积为.(拓展)如图②,GH是正方形ABCD对角线AC上的两点,且AG=CH,GH=AB,E、F分别是AB和CD的中点.若正方形ABCD的面积为16,则四边形EHFG的面积为.6.综合与实践背景阅读:“旋转”即物体绕一个点或一个轴做圆周运动.在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载:“船盘回旋转,不能前进.”而图形旋转即:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,这个定点叫做旋转中心,转动的角叫做旋转角.综合实践课上,“睿智”小组专门探究了正方形的旋转,情况如下:在正方形ABCD 中,点O 是线段BC 上的一个动点,将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''(点A ',B ',C ',D 分别是点A ,B ,C ,D 的对应点).设旋转角为α(0180α<<︒).操作猜想:(1)如图1,若点O 是BC 中点,在正方形ABCD 绕点旋转过程中,连接AA ',BB ',DD ',则线段AA '与DD '的数量关系是_______;线段AA '与BB '的数量关系是________.探究验证:(2)如图2,在(1)的条件下,在正方形ABCD 绕点O 旋转过程中,顺次连接点B ,B ',C ,C ',B .判断四边形''BB CC 的形状,并说明理由.拓展延伸:(3)如图3,若2BO CO =,在正方形ABCD 绕点O 顺时针旋转的过程中,设直线BB '交线段AA '于点P .连接OP ,并过点O 作OQ BB '⊥于点Q .请你补全图形,并直接写出OPOQ的值. 7.将抛物线y =ax 2的图像(如图1)绕原点顺时针旋转90度后可得新的抛物线图像(如图2),记为C :y 2=1ax .(概念与理解)将抛物线y 1=4x 2和y 2=x 2按上述方法操作后可得新的抛物线图像,记为:C 1:_____________;C 2:____________.(猜想与证明)在平面直角坐标系中,点M(x,0)在x轴正半轴上,过点M作平行于y轴的直线,分别交抛物线C1于点A、B,交抛物线C2于点C、D,如图3所示.(1)填空:当x=1时,ABCD=______;当x=2时,ABCD=_______;(2)猜想:对任意x(x>0)上述结论是否仍然成立?若成立,请证明你的猜想;若不成立,请说明理由.(探究与应用)①利用上面的结论,可得△AOB与△COD面积比为;②若△AOB和△COD中有一个是直角三角形时,求△COD与△AOB面积之差;(联想与拓展)若抛物线C3:y2=mx、C4:y2=nx(0<m<n),M(k,0)在x轴正半轴上,如图所示,过点M作平行于y轴的直线,分别交抛物线C3于点A、B,交抛物线C4于点C、D.过点A 作x轴的平行线交抛物线C4于点E,过点D作x轴的平行线交抛物线C3于点F.对于x轴上任取一点P,均有△PAE与△PDF面积的比值1:3,请直接写出m和n之间满足的等量关系是______.8.综合与实践数学活动课上,老师让同学们结合下述情境,提出一个数学问题:如图1,四边形ABCD是正方形,四边形BEDF是矩形.探究展示:“兴趣小组”提出的问题是:“如图2,连接CE.求证:AE⊥CE.”并展示了如下的证明方法:证明:如图3,分别连接AC,BD,EF,AF.设AC与BD相交于点O.∵四边形ABCD是正方形,∴OA=OC=12AC,OB=OD=12BD,且AC=BD.又∵四边形BEDF是矩形,∴EF经过点O,∴OE=OF=12EF,且EF=BD.∴OE=OF,OA=OC.∴四边形AECF是平行四边形.(依据1)∵AC =BD ,EF =BD , ∴AC =EF .∴四边形AECF 是矩形.(依据2) ∴∠CEA =90°, 即AE ⊥CE . 反思交流:(1)上述证明过程中“依据1”“依据2”分别是什么? 拓展再探:(2)“创新小组”受到“兴趣小组”的启发,提出的问题是:“如图4,分别延长AE ,FB 交于点P ,求证:EB =PB .”请你帮助他们写出该问题的证明过程.(3)“智慧小组”提出的问题是:若∠BAP =30°,AE =31-,求正方形ABCD 的面积.请你解决“智慧小组”提出的问题. 9.(发现问题)(1)如图1, 已知CAB ∆和CDE ∆均为等边三角形,D 在AC 上,E 在CB 上, 易得线段AD 和BE 的数量关系是 .(2)将图1中的CDE ∆绕点C 旋转到图2的位置, 直线AD 和直线BE 交于点F ①判断线段AD 和BE 的数量关系,并证明你的结论. ②图2中AFB ∠的度数是 .(3)(探究拓展)如图3,若CAB ∆和CDE ∆均为等腰直角三角形,90ABC DEC ∠=∠=,AB BC =,DE EC =, 直线AD 和直线BE 交于点F , 分别写出AFB ∠的度数, 线段AD 、BE 之间的数量关系 .10.如图,在ABC 中,AB AC =,90BAC ∠=︒,5AB =,D 为底边BC 上一动点,连接AD ,以AD 为斜边向左上方作等腰直角ADE ,连接BE .观察猜想:(1)当点E 落在线段AB 上时,直接写出EB ,ED 的数量关系:EB _______ED . 类比探究:(2)如图2,当点D 在线段BC 上运动时,请问(1)中结论是否仍然成立?若成立,请证明;若不成立,请说明理由;拓展延伸:(3)在点D 运动过程中,当7BE =时,请直接写出线段CD 的长.11.定义:如图1,点M 、N 把线段AB 分割成AM 、MN 和BN ,若以AM 、MN 、BN 为边的三角形是一个直角三角形,则称点M 、N 是线段AB 的勾股点.已知点M 、N 是线段AB 的勾股点,若AM =1,MN =2,则BN = .(1)(类比探究)如图2,DE 是△ABC 的中位线,M 、N 是AB 边的勾股点(AM <MN <NB ),连接 CM 、CN 分别交DE 于点G 、H .求证:G 、H 是线段DE 的勾股点.(2)(知识迁移)如图3,C,D是线段AB的勾股点,以CD为直径画⊙O,P在⊙O上,AC=CP,连结PA,PB,若∠A=2∠B,求∠B的度数.(3)(拓展应用)如图4,点P(a,b)是反比例函数y=2x(x>0)上的动点,直线2y x=-+与坐标轴分别交于A、B两点,过点P分别向x、y轴作垂线,垂足为C、D,且交线段AB于E、F.证明:E、F是线段AB的勾股点.12.(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①∠AEB的度数为;②线段AD,BE之间的数量关系为.(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.(3)解决问题如图3,在正方形ABCD中,CD=2,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.13.(探究证明)(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形ABCD中,EF⊥GH,EF分别交AD、BC于点E、F,GH分别交AB、DC于点G、H,求证:EF AB GH AD=;(结论应用)(2)如图②,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3.求折痕EF的长;(拓展运用)(3)如图③,将矩形ABCD沿EF折叠.使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF 210,请求BP的长.14.我们定义:连结凸四边形一组对边中点的线段叫做四边形的“准中位线”.(1)概念理解:如图1,四边形ABCD 中,F 为CD 的中点,90ADB ∠=︒,E 是AB 边上一点,满足DE AE =,试判断EF 是否为四边形ABCD 的准中位线,并说明理由.(2)问题探究:如图2,ABC ∆中,90ACB ∠=︒,6AC =,8BC =,动点E 以每秒1个单位的速度,从点A 出发向点C 运动,动点F 以每秒6个单位的速度,从点C 出发沿射线CB 运动,当点E 运动至点C 时,两点同时停止运动.D 为线段AB 上任意一点,连接并延长CD ,射线CD与点,,,A B E F 构成的四边形的两边分别相交于点,M N ,设运动时间为t .问t 为何值时,MN 为点,,,A B E F 构成的四边形的准中位线.(3)应用拓展:如图3,EF 为四边形ABCD 的准中位线,AB CD =,延长FE 分别与BA ,CD 的延长线交于点,M N ,请找出图中与M ∠相等的角并证明. 15.综合与实践:问题情境:在数学课上,以“等腰直角三角形为主体,以点的对称为基础,探究线段间的变化关系”.如图1,在ABC 中,90ACB ∠=︒,AC BC =,点E 为ACB ∠的角平分线CD 上一动点但不与点C 重合,作点E 关于直线BC 的对称点为F ,连接AE 并延长交CB 延长线于点H ,连接FB 并延长交直线AH 于点G . 探究实践:(1)勤奋小组的同学发现AE BF =,请写出证明; 探究发现:(2)智慧小组在勤奋小组的基础上继续探究,发现线段FG ,EG 与CE 存在数量关系,请写出他们的发现并证明; 探究拓展:(3)如图2,奇异小组的同学在前两个小组探究的基础上,连接GC ,得到三条线段GE ,GC 与GF 存在一定的数量关系,请直接写出.16.(1)观察发现:如图1,在ABC ∆中,AC BC =,90ACB ∠=︒,点D 是ACB ∠的平分线CM 上一点,将线段CD 绕点C 逆时针旋转90°到CE ,连结BE 、BD ,DE 交BC 于F .填空:①线段BD 与BE 的数量关系是_________; ②线段BC 与DE 的位置关系是_________.(2)拓展探究:如图2,在ABC ∆中,AC BC =,ACB α∠=,点D 是边AB 的中点,将CD 绕点C 逆时针旋转α到CE ,连结BE 、DE ,DE 交BC 于F .(1)中的结论是否仍然成立?请说明理由.(3)拓展应用:如图3,在ABC ∆中,AB AC =,60BAC ∠=︒,2BC =,ACB ∠的平分线交AB 于D ,点E 是射线CD 上的一点,将CE 绕点C 顺时针旋转60°到CF ,连结AE 、AF 、EF ,EF 与AC 相交于G ,若以A 、F 、G 为顶点的三角形与ADE ∆全等,直接写出EF 的长.17.如图1,在等腰三角形ABC 中,120,,A AB AC ∠==点D E 、分别在边AB AC 、上,,AD AE =连接,BE 点M N P 、、分别为DE BE BC 、、的中点.(1)观察猜想图1中,线段NM NP 、的数量关系是____,MNP ∠的大小为_____;(2)探究证明把ADE 绕点A 顺时针方向旋转到如图2所示的位置,连接,MP BD CE 、、判断MNP △的形状,并说明理由;(3)拓展延伸把ADE 绕点A 在平面内自由旋转,若1,3AD AB ==,请求出MNP △面积的最大值. 18.如图1所示,边长为4的正方形ABCD 与边长为()14a a <<的正方形CFEG 的顶点C 重合,点E 在对角线AC 上.(问题发现)如图1所示,AE 与BF 的数量关系为________;(类比探究)如图2所示,将正方形CFEG 绕点C 旋转,旋转角为()030αα<<︒,请问此时上述结论是否还成立?如成立写出推理过程,如不成立,说明理由;(拓展延伸)若点F 为BC 的中点,且在正方形CFEG 的旋转过程中,有点A 、F 、G 在一条直线上,直接写出此时线段AG 的长度为________19.如图,在△ABC 中,∠ACB=90°,AC=BC ,点D 是AB 边上的动点,DE ⊥BC 于点E ,连接AE ,CD ,点F ,G ,H 分别是AE ,CD ,AC 的中点.(1)观察猜想:△FGH 的形状是(2)探究论证:把△BDE 绕点B 按逆时针方向旋转到如图所示的位置,(1)中的结论是否仍然成立?请说明理由.(3)拓展延伸:把△BDE 绕点B 在平面内自由旋转,若BC=6,BE=2,请直接写出△FGH 周长的取值范围.20.如图1,已知ABC 和ADE 均为等腰直角三角形,点D 、E 分别在线段AB 、AC 上,90C AED ∠=∠=︒.(1)观察猜想:如图2,将ADE 绕点A 逆时针旋转,连接BD 、CE ,BD 的延长线交CE 于点F .当BD 的延长线恰好经过点E 时,点E 与点F 重合,此时,①BD CE的值为______; ②∠BEC 的度数为______度;(2)类比探究:如图3,继续旋转ADE ,点F 与点E 不重合时,上述结论是否仍然成立,请说明理由;(3)拓展延伸:若2AE DE ==.10AC BC ==,当CE 所在的直线垂直于AD 时,请你直接写出线段BD 的长.【参考答案】***试卷处理标记,请不要删除一、中考几何压轴题1.(1);(2)AP 的最小值为;(3)存在,BD 的最大值为6+6【分析】(1)连接AC 、AF 、DG 、CF ,证△ADG ∽△ACF ,根据线段比例关系可求;(2)以BC 为斜边作等腰直角三角形BOC ,以解析:(1)22;(2)AP 的最小值为2922-;(3)存在,BD 的最大值为62+6 【分析】(1)连接AC 、AF 、DG 、CF ,证△ADG ∽△ACF ,根据线段比例关系可求;(2)以BC 为斜边作等腰直角三角形BOC ,以O 为圆心BO 为半径画圆,则P 的运动轨迹在矩形ABCD 内的劣弧BC 上,连接AO 交弧BC 于点P ,此时AP 最小,根据给出数据求值即可;(3)以AB 为斜边向下做等腰直角三角形AEB ,连接CE ,根据△DAB ∽△CAE ,得出BD =2CE ,以AB 为斜边向上做等腰直角三角形AOB ,以O 为圆心OA 为半径画圆,根据C 点的轨迹求出CE 最大值,即求出BD 最大值.【详解】解:(1)如图①,连接AC 、AF 、DG 、CF ,在正方形ABCD 和正方形AEFG 中,AB =4,AE =2.5,∴AC =2AB ,AF =2AE ,AG =AE =2.5,AD =AB =4,∴AD AC AG AF=, 又∵∠DAG =∠DAC -∠GAC =45°-∠GAC ,∠CAF =∠GAF -∠GAC =45°-∠GAC ,∴∠DAG =∠CAF ,∴△DGA ∽△CFA ,∴42242DG AD CF AC ===, 故答案为22; (2)如图②,以BC 为斜边作等腰直角三角形BOC ,以O 为圆心BO 为半径画圆,则∠BPC 作为圆周角刚好是135°,∴P 的运动轨迹在矩形ABCD 内的劣弧BC 上,连接AO 交弧BC 于点P ,此时AP 最小,作OE 垂直AB 延长线于点E ,∵△BOC 为等腰直角三角形,BC =4,∴OB =OC 222∠OBC =45°, ∴∠OBE =90°-∠OBC =90°-45°=45°,又∵OE ⊥AE ,∴△BEO 为等腰直角三角形,∴BE =OE =22OB =222=2, 又∵AB =3,∴AE =AB +BE =3+2=5,∴22225229AO AE OE =++∵OP =OB 2∴AP =AO -OP =29-22, 即AP 的最小值为29-22;(3)存在,如图3,以AB 为斜边向下做等腰直角三角形AEB ,连接CE ,则∠EAB =45°,2AB AE∵AC =AD ,∠ACD =90°,∴DAC =45°,2AD AC = ∴AB AD AE AC=,∠DAB =∠CAE =45°, ∴△DAB ∽△CAE , ∴2BD AD CE AC = ∴BD 2,∴当CE 最大时,BD 取最大值,以AB 为斜边向上做等腰直角三角形AOB ,以O 为圆心OA 为半径画圆,∵∠AOB =90°,∠ACB =45°,∴点C 在优弧AB 上,由图知当C 在OE 延长线C '位置时C 'E 有最大值,此时C 'E =OE +OC ',∵AB =6,△AOB 和△AEB 都是以AB 为斜边的等腰直角三角形, ∴四边形AOBE 为正方形,∴OE =AB =6,OC '=OA 22, ∴CE 的最大值为2,∵BD 2,∴BD 2(2)2.【点睛】本题主要考查了图形的变换,三角形相似,等腰直角三角形,正方形,圆周角,圆心角等知识点,熟练掌握并灵活运用这些知识点是解题的关键.2.(1);;;(2);(3).【分析】(1)本问体现“特殊”的情形,是一个确定的数值.如答图1,过E 点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH 来表示,最解析:(1)3AB EH =;2CG EH =;32;(2)2m ;(3)ab . 【分析】(1)本问体现“特殊”的情形,3AF EF =是一个确定的数值.如答图1,过E 点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH 来表示,最后求得比值;(2)本问体现“一般”的情形,AF m EF =不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示.(3)本问体现“类比”与“转化”的情形,将(1)(2)问中的解题方法推广转化到梯形中,如答图3所示.【详解】解:(1)依题意,过点E 作//EH AB 交BG 于点H ,如图1所示.则有ABF EHF , ∴3AB AF EH EF==, ∴3AB EH =. ∵ABCD ,//EH AB , ∴//EH CD ,又∵E 为BC 中点,∴EH 为BCG 的中位线,∴2CG EH =.3322CD AB EH CG CG EH ===. 故答案为:3AB EH =;2CG EH =;32. (2)如图2所示,作//EH AB 交BG 于点H ,则EFH AFB △△. ∴AB AF m EH EF==, ∴AB mEH =.∵AB CD =,∴CD mEH =.∵////EH AB CD ,∴BEH BCG △△.∴2CG BC EH BE ==, ∴2CG EH =. ∴22CD mEH m CG EH ==. 故答案为:2m . (3)如图3所示,过点E 作//EH AB 交BD 的延长线于点H ,则有////EH AB CD . ∵//EH CD ,∴BCD BEH △△,∴=CD BC b EH BE=, ∴CD bEH =. 又AB a CD =, ∴AB aCD abEH ==.∵//EH AB ,∴ABF EHF , ∴==AF AB abEH ab EF EH EH=. 故答案为:ab .【点睛】本题的设计独特:由平行四边形中的一个特殊的例子出发(第1问),推广到平行四边形中的一般情形(第2问),最后再通过类比、转化到梯形中去(第3问).各种图形虽然形式不一,但运用的解题思想与解题方法却是一以贯之:即通过构造相似三角形,得到线段之间的比例关系,这个比例关系均统一用同一条线段来表达,这样就可以方便地求出线段的比值.本题体现了初中数学的类比、转化、从特殊到一般等思想方法,有利于学生触类旁通、举一反三.3.【问题】,1;【操作】当时,,当时,;【探究】或;【应用】点的坐标为:或【分析】问题:即可求解;操作:抛物线G1沿BC 方向平移BC 长度的距离得到抛物线G2,相当于抛物线向左平移3个单位,向上平解析:【问题】12-,1;【操作】当0x <时,213222y x x =--+,当0x ≥时,21322y x x =--+;【探究】42x -<<-或01x <<;【应用】点P 的坐标为:32,222⎛-+ ⎝或32,222⎛-- ⎝ 【分析】问题:23(1)(3)2y ax bx a x x =++=+-即可求解; 操作:抛物线G 1沿BC 方向平移BC 长度的距离得到抛物线G 2,相当于抛物线向左平移3个单位,向上平移32个单位,即可求解; 探究:将点C 的坐标代入两个函数表达式,求出G 1、G 2的顶点坐标,即可求解; 应用:证明∠EPN =∠MDP ,利用tan ∠EPN =tan ∠MDP ,即可求解.【详解】 解:问题:()()23132y ax bx a x x =++=+-,解得:12a =-,1b =,故答案为:12-,1; 操作:抛物线1G 沿BC 方向平移BC 长度的距离得到抛物线2G ,相当于抛物线向左平移3个单位,向上平移32个单位, 1G :()2223131122222y ax bx x x x =++=-++=--+, 2G :()22131313222222y x x x =--+++=--+, 当0x <时,213222y x x =--+, 当0x ≥时,21322y x x =--+; 探究:C 点的坐标为30,2⎛⎫ ⎪⎝⎭. 当32y =时,2133222x x -++=, 解得:10x =,22x =,∴32,2E ⎛⎫ ⎪⎝⎭, 当32y =时,21332222x x --+=, 解得:10x =,24x =-,∴34,2D ⎛⎫- ⎪⎝⎭, ∵()2213112222y x x x =-++=--+,()221317222222y x x x =--+=-++, ∴抛物线1G 的顶点为()1,2,抛物线2G 的顶点为72,2⎛⎫- ⎪⎝⎭, ∴42x -<<-或01x <<时,函数y 随x 的增大而增大;应用:如图,过点P 作x 轴的平行线交过点D 与x 轴的垂线于点M ,交过E 点与x 轴的垂直的直线于点N ,设点()2,P m -,则32EN m =-,4PN =,32DM m =-,2PM =,∵90EPN MPD ∠+∠=︒,90MDP DPM ∠+∠=︒,∴EPN MDP ∠=∠,∴tan tan EPN MDP ∠=∠,即EN MP PN DM =,即322342m m -=-,解得:32m =± 故点P的坐标为:32,2⎛-+ ⎝或32,2⎛-- ⎝. 【点睛】本题考查的是二次函数综合运用,涉及解直角三角形、图形的平移等,具有一定的综合性,关键在于根据题意作出图形进行解答.4.(1)BD =CE ,BD ⊥CE ,理由见详解;(2)AB=kAC , 180°-α-β;(3)N(0,3),OP 的最小值为3【分析】(1)先证明△ABD ≌△ACE ,从而得BD =CE ,∠ABD =∠ACE解析:(1)BD =CE ,BD ⊥CE ,理由见详解;(2)AB =kAC , 180°-α-β;(3)N (0,3),OP 的最小值为3【分析】(1)先证明△ABD ≌△ACE ,从而得BD =CE ,∠ABD =∠ACE ,结合∠AGB =∠FGC ,即可得到结论;(2)先证明ABC ∽ADE ,从而得AB AD AC AE =,结合∠BAD =∠CAE ,可得BAD∽CAE ,进而即可得到结论;(3)把OPM 绕点M 顺时针旋转90°得到O P M '' (P '与N 重合),则OM O M '⊥,OM O M '=,O '(3,3),OP O P ''=,进而即可求解.【详解】解:(1)BD =CE ,BD ⊥CE ,∵△ABC 和△ADE 都是等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =90°,∵∠BAD =∠BAC −∠DAC ,∠CAE =∠DAE −∠DAC∴∠BAD =∠CAE ,在△ABD 和△ACE 中,∵AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩===, ∴△ABD ≌△ACE ,∴BD =CE ,∠ABD =∠ACE ,∵∠AGB =∠FGC ,∴∠CFG =∠BAG =90°,即BD ⊥CE ,故答案是:BD =CE ,BD ⊥CE ;(2)∵∠ABC =∠ADE =α,∠ACB =∠AED =β, ∴ABC ∽ADE , ∴AB AD AC AE=, ∵∠ABC =∠ADE =α,∠ACB =∠AED =β,∴∠BAC =∠DAE ,∴∠BAD =∠CAE ,∴BAD ∽CAE ,∴∠ABD =∠ACE ,BD AB k CE AC == 又∵∠AGB =∠FGC ,∴∠BFC =∠BAC =180°-∠ABC -∠ACB =180°-α-β,∴AB =kAC ,直线BD 和CE 相交所成的较小角的度数为:180°-α-β;(3)由题意得:MN =MP ,∠NMP =90°,把OPM 绕点M 顺时针旋转90°得到O P M '' (P '与N 重合),则OM O M '⊥,OM O M '=,∵点M 的坐标为(3,0),∴O '(3,3)∵OPM ≌O P M '',∴OP O P ''=,即线段OP 长度最小时,O P ''的长度最小,∴当O P ''⊥y 轴时,O P ''的长度最小,此时P '(0,3),∴N (0,3),OP 的最小值为3 .【点睛】本题主要考查全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,通过旋转变换,构造相似三角形或全等三角形,是解题的关键.5.教材呈现:见解析;探究:16;拓展:4【分析】教材呈现:先根据三角形全等的性质可得,再根据线段的和差可得,然后根据平行四边形的判定即可得证;探究:先由旋转的性质可得,再根据等底同高可得,从而可解析:教材呈现:见解析;探究:16;拓展:42 【分析】 教材呈现:先根据三角形全等的性质可得,OE OF OA OC ==,再根据线段的和差可得OG OH =,然后根据平行四边形的判定即可得证;探究:先由旋转的性质可得4DGF S=,再根据等底同高可得2ADE DOE EOF S S S ===,从而可得4AOE S =,然后根据三角形中位线定理即可得;拓展:先根据正方形的性质和面积可得4,90AB BC B ==∠=︒,从而可得42,4,2AC GH AE ===,再根据等腰直角三角形和勾股定理可得2OE =,然后利用三角形的面积公式可得22EGH S=,最后利用平行四边形的性质即可得.【详解】 解:教材呈现:补充完整证明过程如下:∴OE =OF ,OA =OC ,又∵AG =CH ,∴OA -AG =OC -CH ,即OG =OH ,∴四边形EHFG 是平行四边形;探究:如图,连接OE ,BO ,由旋转的性质得:118422DGF DEF DEFG S S S ===⨯=四边形, 点O 是AC 的中点,点D 是AO 的中点,点F 是CO 的中点,AD OD OF CF ∴===,由等底同高得:114222ADE DOE EOF DEF SS S S ====⨯=, 224AOE ADE DOE S S S ∴=+=+=,又点E 是AB 的中点,点O 是AC 的中点,∴S △BEO =S △AEO =4,∴S △ABO = S △BEO +S △AEO =8,22816ABC AOB S S ∴==⨯=,故答案为:16;拓展:如图,过点E 作EO GH ⊥于点O ,四边形ABCD 是面积为16的正方形,4,90AB BC B ∴==∠=︒,在Rt △ABC 中,由勾股定理得22224424A C B B A C ++=∵AC 为正方形的对角线,∴∠EAO =45°,点E 是AB 的中点, 122AE AB ∴==, ∵EO GH ⊥,∴45AEO EAO ∠=∠=︒,∴AO =EO ,在Rt △AEO 中由勾股定理的AO 2+EO 2=AE 2,即2OE 2=4解得2OE =,GH AB =,4GH ∴=,11422222EGH S GH OE ∴=⋅=⨯⨯=, 由教材呈现可知,四边形EHFG 是平行四边形,则四边形EHFG 的面积为222242EGH S=⨯=,故答案为:42.【点睛】本题考查了旋转的性质、三角形中线性质、平行四边形的判定与性质、正方形的性质,等腰直角三角形性质,勾股定理等知识点,较难的是拓展,通过作辅助线,构造等腰直角三角形是解题关键.6.(1);;(2)矩形,见解析;(3)见解析,.【分析】(1)如图,连接OA 、OA′、OD 、OD′,根据旋转的性质可得OA=OA′、OD=OD′,∠AOA′=∠DOD′=,根据勾股定理可得OA=O解析:(1)AA DD ''=;5AA BB ''=;(2)矩形,见解析;(3)见解析,13OP OQ 【分析】(1)如图,连接OA 、OA ′、OD 、OD ′,根据旋转的性质可得OA =OA ′、OD =OD ′,∠AOA ′=∠DOD ′=α,根据勾股定理可得OA =OD ,利用SAS 可证明△AOA ′≌△DO D′,根据全等三角形的性质可得AA ′=DD ′,根据旋转的性质可得∠BOB ′=α,根据5OB OB OA OA'='△OAA ′∽△OBB ′,根据相似三角形的性质即可得答案;(2)根据旋转的性质可得BC B C ''=,OB OB '=,OC OC '=,根据点O 是BC 中点即可得出OB OC OB OC ''===,根据对角线相等且互相平分的四边形是矩形即可证明四边形''BB CC 是矩形;(3)根据题意,补全图形,连接OA 、OA ′,作AM ⊥BP 于M ,A ′N ⊥BP 于N ,根据勾股定理可得132OA OA OB ''==,根据平角的定义及直角三角形两锐角互余的性质可得''ABM A B N ∠=∠,利用AAS 可证明△ABM ≌△A ′B ′N ,可得AM =A ′N ,利用AAS 可证明△APM ≌△A ′PN ,可得AP A P '=,根据等腰三角形“三线合一”的性质可得∠A ′OP =12∠AOA ′=12α,∠QOB ′=1122BOB α'∠=,根据角的和差关系可得∠POQ =∠A ′OB ′,即可证明△OQP ∽△OB ′A ′,根据相似三角形的性质即可得答案.【详解】(1)如图,连接OA 、OA ′、OD 、OD ′,∵将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D '''',旋转角为α,∴OA =OA ′、OD =OD ′,∠AOA ′=∠DOD ′=α,∴△AOA ′≌△DO D′,∴AA ′=DD ′,∵点O 是BC 中点,∴OB =1122BC AB =, ∴OA =225OB AB OB +=,∵将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D '''',旋转角为α,∴∠BOB ′=∠AOA ′=α,∵5OB OB OA OA'==', ∴△OAA ′∽△OBB ′,∴''AA OA BB OB==5, ∴5AA BB ''=,故答案为:AA DD ''=;5AA BB ''=(2)四边形''BB CC 是矩形;理由如下:∵正方形ABCD 绕点O 顺时针旋转得到正方形A B C D '''',∴BC B C ''=,OB OB '=,OC OC '=,∵点O 是BC 中点,∴OB OC OB OC ''===四边形''BB CC 是平行四边形,∵BC B C ''=,∴四边形''BB CC 是矩形.(3)如图,补全图形如下:连接OA 、OA ′,作AM ⊥BP 于M ,A ′N ⊥BP 于N , ∵2BO CO =,∴AB =BC =32OB , ∴OA ′=OA 2213AB OB +'13, ∵∠OB ′A ′=90°, ∴'''90A B N OB B ∠+∠=︒,∵'OB OB =,∴''OB B OBB ∠=∠,∵'90ABM OBB ∠+∠=︒,∴ABM A B N ''∠=∠,∵''AB A B =,''AMB A NB ∠=∠,∴△ABM ≌△A ′B ′N ,∴AM =A ′N (AAS ),∵''AMB A NB ∠=∠,'APM A PN ∠=∠,∴△APM ≌△A ′PN ,∴AP=A′P ,∵OA =OA ′,∴∠A ′OP =12∠AOA ′=12α, ∵OB =OB ′,OQ ⊥BB ′,∴∠QOB ′='1122BOB α∠=, ∴∠QOB ′+∠B ′OP =∠A ′OP +∠B ′OP ,即∠POQ =∠A ′OB ′,∵∠OQP =∠OB ′A ′=90°,∴△OQP ∽△OB ′A ′, ∴''132OP OA OQ OB ==.【点睛】本题考查旋转的性质、矩形的判定、全等三角形的判定与性质及相似三角形的判定与性质,熟练掌握全等三角形及相似三角形的判定定理并正确作出辅助线构造全等三角形及相似三角形是解题关键.7.【概念与理解】,;【猜想与证明】(1),;(2)成立,证明见解析;【探究与应用】①;②△COD 与△AOB 面积之差为或;【联想与拓展】n3=9m3.【分析】【概念与理解】:根据题意信息即可得出答案解析:【概念与理解】214y x =,2y x =;【猜想与证明】(1)12,12;(2)成立,证明见解析;【探究与应用】①12;②△COD 与△AOB 面积之差为116或12;【联想与拓展】n 3=9m 3.【分析】【概念与理解】:根据题意信息即可得出答案; 【猜想与证明】:(1)当x =1时,求出A ,B ,C ,D 的坐标进而得出AB ,CD 即可得出答案;当x =2时,求出A ,B ,C ,D 的坐标进而得出AB ,CD 即可得出答案;(2)任意x (x >0),求出A ,B ,C ,D 的坐标进而得出AB ,CD 即可得出答案;【探究与应用】:①根据已知条件表示出△AOB 与△COD 面积即可得出答案; ②设M (x ,0)(x >0),根据已知条件可得出2COD AOB x x S S -=△AOB 是直角三角形时解得14x =,当△COD 是直角三角形时,解得1x =,把x 代入即可; 【联想与拓展】:根据题意求出AEDF 的坐标然后表示出面积再利用△PAE 与△PDF 面积的比值1:3,即可得出关系式;【详解】【概念与理解】∴由题意可得C 1:214y x = ∵y 2=x 2∴由题意可得C 2:2y x =故答案为:C 1:214y x =,C 2:2y x =; 【猜想与证明】(1)当x =1时,∵点A 、B 在抛物线C 1上∴令x =1,则112y =± ∴A 1(1,)2,B 1(1,)2- ∴AB =1∵点C 、D 在抛物线C 2上∴令x =1,则21y ==±∴C (1,1),D (1,1)-∴CD =2 ∴AB CD =12当x =2时,∵点A 、B 在抛物线C 1上∴令x =2,则1y ==∴A (2,)2,B (2,2 ∴AB∵点C 、D 在抛物线C 2上∴令x =2,则2y =∴C ,D (2,∴CD =∴AB CD 12= (2)对任意x (x >0)上述结论仍然成立理由如下:对任意x (x >0),1y =∴A (x ,B (,x对任意x (x >0),2y x =±∴C (,)x x ,D (,)x x - ∴CD =2x∴AB CD =122x x = 【探究与应用】①连接OA ,OB ,OC ,OD12AOB SAB OM = 12COD S CD OM = ∴12AOB COD S AB S CD == 故答案为:12②设M (x ,0)(x >0),∵M (x ,0)∴1y = ∴AB∵M (x ,0), ∴2y =∴CD =∵122AOB x SAB OM == 1222COD x S CD OM ==∴2COD AOB x S S -=当△AOB 是直角三角形时,由题意可知OA =OB∴△△AOB 为等腰直角三角形∴OM =AM∴x =解得:14x =∴1216COD AOB x S S -== 当△COD 是直角三角形时,由题意可知OD =OC∴△△COD 为等腰直角三角形∴OM=CM∴x =解得:1x =∴122COD AOB x S S -== 综上所述:△COD 与△AOB 面积之差为116或12 【联想与拓展】∵M (k ,0)且点A 、B 在抛物线C 3上∴令x =k ,则1y ==∴A (k∵AE ∥x 轴,且交C 4于点E∴E (km n()km AE k n -∴=。
【备考期末】大连市中考数学几何综合压轴题易错专题

【备考期末】大连市中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1.(探究函数y=x+的图象与性质)(1)函数y=x+的自变量x的取值范围是;(2)下列四个函数图象中函数y=x+的图象大致是;(3)对于函数y=x+,求当x>0时,y的取值范围.请将下列的求解过程补充完整.解:∵x>0∴y=x+=()2+()2=(﹣)2+∵(﹣)2≥0∴y≥.[拓展运用](4)若函数y=,则y的取值范围.解析:(1)x≠0;(2)C(3)4;4;(4)y≥13【解析】试题分析:根据反比例函数的性质,一次函数的性质;二次函数的性质解答即可.试题解析:(1)函数y=x+的自变量x的取值范围是x≠0;(2)函数y=x+的图象大致是C;(3)解:∵x>0∴y=x+=()2+()2=(﹣)2+4∵(﹣)2≥0∴y≥4. (4)y==x+﹣5═()2+()2﹣5=(+)2+13∵(﹣)2≥0,∴y≥13.考点:1.反比例函数的性质;一次函数的性质;二次函数的性质. 2.(了解概念)定义:在平面直角坐标系xOy 中,组成图形的各点中,与点Р所连线段最短的点叫做点Р关于这个图形的短距点,这条最短线段的长度叫做点Р到这个图形的短距.(理解运用)(1)已知点()3,0P -,以原点为圆心,l 为半径作O ,则点Р关于O 的短距点的坐标是 ;(2)如图,点(3P ,等边三角形OAB 的顶点A 的坐标为()6,0,顶点B 在第一象限,判断点Р关于OAB 的短距点的个数,并说明理由; (拓展提升)(3)已知(),6P p p -+,()6,0A ,()0,6B ,点C 在第一象限内,且75CBO ∠=︒,90ACB ∠=︒,若点Р到四边形OACB 的短距大于2,请直接写出p 的取值范围.解析:(1)(-1,0);(2)点Р关于OAB 的短距点的个数有3个;(3)当p <22p <4或p >2Р到四边形OACB 的短距大于2. 【分析】(1)连接PO ,交O 于点M ,点M 即是点Р关于O 的短距点,进而即可求解; (2)根据题意得点P 是三角形OAB 的中心,进而即可求解;(3)由题意得点P ,A ,B 在直线y =-x +6上,以点P 为圆心,半径长为2画圆,分3种情况:①当点P 在AB 的延长线上,圆P 过点B 时,②当点P 在线段AB 上,圆P 与BC 相切于点N ,过点P 作PM ⊥y 轴,③当点P 在BA 的延长线上,圆P 过点A 时,过点P 作PM ⊥y 轴,分别求解,即可得到答案. 【详解】解:(1)连接PO ,交O 于点M ,点M 即是点Р关于O 的短距点, ∵()3,0P -,、O 的半径为1, ∴M (-1,0), 故答案是:(-1,0);(2)∵点(3P ,等边三角形OAB 的顶点A 的坐标为()6,0, ∴点P 是三角形OAB 的中心,∴点P 到OA ,OB ,OC 3 ∴点Р关于OAB 的短距点的个数有3个; (3)∵(),6P p p -+,()6,0A ,()0,6B , ∴点P ,A ,B 在直线y =-x +6上, ∴∠ABO =∠BAO =45°,∵点C 在第一象限内,且75CBO ∠=︒,90ACB ∠=︒, ∴∠ABC =75°-45°=30°,以点P 为圆心,半径长为2画圆,如图所示:当点P 在AB 的延长线上,圆P 过点B 时,过点P 作PM ⊥y 轴,∵PB=2,∠PBM=45°,∴PM=2×22=2,∴p<-2时,点Р到四边形OACB的短距大于2;①当点P在线段AB上,圆P与BC相切于点N,过点P作PM⊥y轴,则BP=2PN=2×2=4,PM=BP×22=22,②当点P在线段AB上,圆P与OA相切于点N,过点P作PM⊥y轴,则AP=2PN=22,BP=AB-AP=62-22=42,PM= BP×22=42×22=4,∴22<p<4时,点Р到四边形OACB的短距大于2;③当点P在BA的延长线上,圆P过点A时,过点P作PM⊥y轴,则PM=(2)22∴p >6+2时,点Р到四边形OACB 的短距大于2;综上所述:当p <-2或22<p <4或p >6+2时,点Р到四边形OACB 的短距大于2.【点睛】本题主要考查图形与坐标以及圆的综合题,根据题意画出图形,掌握圆与直线相切的性质是解题的关键.3.定义:有一组对角互补的四边形叫做“对补四边形”,例如,四边形ABCD 中,若180A C ∠+∠=︒或180B D ∠+∠=︒,则四边形ABCD 是“对补四边形”.(概念理解)(1)如图1,四边形ABCD 是“对补四边形”. ①若::3:2:1A B C ∠∠∠=,则D ∠=________;②若90B ∠=︒.且3,2AB AD ==时.则22CD CB -=_______; (拓展提升)(2)如图,四边形ABCD 是“对补四边形”,当AB CB =,且12EBF ABC ∠=∠时,图中,,AB CF EF 之间的数量关系是 ,并证明这种关系;(类比应用)(3)如图3,在四边形ABCD 中,,AB CB BD =平分ADC ∠; ①求证:四边形ABCD 是“对补四边形”; ②如图4,连接AC ,当90ABC ∠=︒,且12ACD ABCSS=时,求tan ACD ∠的值. 解析:(1)①90︒,②5;(2)AE CF EF +=,理由见解析;(3)①见解析,②23±. 【分析】(1)①根据“对补四边形”的定义,结合::3:2:1A B C ∠∠∠=,即可求得答案; ②根据“对补四边形”的定义,由90B ∠=︒,得D ∠90=︒,再利用勾股定理即可求得答案;(2)延长EA 至点K ,使得AK CF =,连接BK ,根据“对补四边形”的定义,可证明ABK CBF △≌△,继而证明BEK BEF △≌△,从而可得结论;(3)①过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒,可证Rt ABM Rt CBN △≌△,进而可证四边形ABCD 是“对补四边形”;②设,AD a DC b ==,则tan a ACD b∠=根据222AC a b =+,再运用12ACD ABCS S=建立方程,解方程即可求得tan ACD ∠. 【详解】 (1)::3:2:1A B C ∠∠∠=,设3,2,A x B x C x ∠=∠=∠=, 根据“对补四边形”的定义, 180A C ∠+∠=︒,即3180x x +=︒, 解得45x =︒,290B x ∴∠==︒,180B D ∠+∠=︒,90D ∴∠=︒.故答案为:90︒. ②如图1,连接AC ,90B ∠=︒,180B D ∠+∠=︒,90D ∴∠=︒,在Rt ABC 中22BC AC AB =-, 在Rt ADC 中222CD AC AD =-,22222222()CD CB AC AD AC AB AB AD ∴-=---=-,3,2AB AD ==,2222325CD CB ∴-=-=,故答案为:5.(2)AE CF EF +=,理由如下:如图2,延长EA 至点K ,使得AK CF =,连接BK ,四边形ABCD 是“对补四边形”,∴180BAD C ∠+∠=︒,180BAK BAD ∠+∠=︒,∴BAK C ∠=∠,,AK CF AB CB ==,∴()ABK CBF SAS △≌△,∴,ABK CBF BK BF ∠=∠=, ∴ABK ABF CBF ABF ∠+∠=∠+∠,即KBF ABC ∠=∠,12EBF ABC ∠=∠,∴12EBF KBF ∠=∠, ∴EBK EBF ∠=∠,,BK BF BE BE ==,∴()BEK BEF SAS △≌△,∴EK EF =,∴AE CF AE AK EK EF +=+==,即AE CF EF +=, 故答案为:AE CF EF +=.(3)①证明:如图3,过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒,BD 平分ADC ∠,BM BN ∴=,AB CB =,()Rt ABM Rt CBN HL ∴△≌△,BAM C ∴∠=∠,180BAM BAD ∠+∠=︒,180C BAD ∴∠+∠=︒,BAD ∴∠与C ∠互补,∴四边形ABCD 是“对补四边形”;②由①可知四边形ABCD 是“对补四边形”, 180ABC ADC ∴∠+∠=︒,90ABC ∠=︒,90ADC ∴∠=︒,设AD a DC b ==,,则22222AC AD CD a b =+=+,AB BC =,2222211()22AB BC AC a b ∴===+, 1122ACD S AD CD ab ∴=⋅=△, 222111()224ABC S AB BC AB a b =⋅==+△,12ACD ABCS S=, 22112=12()4ab a b ∴+,整理得:2()410a ab b-⨯+=,解得:23ab=在Rt ABC中,tana ACDb∠=,∴tan ACD∠=23±.【点睛】本题考查了勾股定理,四边形内角和定理,全等三角形的性质与判定,解一元二次方程,三角函数的定义等知识,熟练掌握勾股定理和全等三角形的判定和性质,准确理解新定义是解题的关键.4.情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是▲,∠CAC′= ▲ °.问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.解析:情境观察:AD(或A′D),90问题探究:EP =FQ . 证明见解析 结论: HE =HF . 证明见解析 【详解】 情境观察 AD (或A′D ),90 问题探究 结论:EP=FQ.证明:∵△ABE 是等腰三角形,∴AB=AE ,∠BAE=90°.∴∠BAG+∠EAP=90°.∵AG ⊥BC ,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP . ∵EP ⊥AG ,∴∠AGB=∠EPA=90°,∴Rt △ABG ≌Rt △EAP . ∴AG=EP . 同理AG=FQ. ∴EP=FQ 拓展延伸结论: HE=HF.理由:过点E 作EP ⊥GA ,FQ ⊥GA ,垂足分别为P 、Q. ∵四边形ABME 是矩形,∴∠BAE=90°,∴∠BAG+∠EAP=90°.AG ⊥BC ,∴∠BAG+∠ABG=90°, ∴∠ABG=∠EAP .∵∠AGB=∠EPA=90°,∴△ABG ∽△EAP , 同理△ACG ∽△FAQ , ∵AB= k AE ,AC= kAF ,∴EP=FQ.∵∠EHP=∠FHQ ,∴Rt △EPH ≌Rt △FQH. ∴HE=HF5.(感知)如图1,在平面直角坐标系中,点C 的坐标为(0,0.5),点A 的坐标为(1,0),将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,过点B 作BM y ⊥轴,垂足为点M ,易知AOC CMB ∆∆≌,得到点B 的坐标为(0.5,1.5).(探究)如图2,在平面直角坐标系中,点A 的坐标为(1,0),点C 的坐标为(0,)(0)m m >,将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB .(1)求点B 的坐标.(用含m 的代数式表示)(2)求出BC 所在直线的函数表达式.(拓展)如图3,在平面直角坐标系中,点A 的坐标为(1,0),点C 在y 轴上,将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,连结BO 、BA ,则BO BA +的最小值为_______.解析:【探究】(1)点B 坐标为(,1)m m +;(2)1y x m m=+;【拓展】5. 【分析】探究:(1)证明△AOC ≌△CMB (AAS ),即可求解;(2)根据点B 的坐标为(m ,m+1),点C 坐标()0,m ,即可求解;拓展:BO+BA=2222(1)(1)(1)m m m m +++-++,BO+BA 的值,相当于求点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,即可求解.【详解】解:探究:(1)过点B 作BM y ⊥轴,垂足为点M .BMC 90∠∴=︒,MCB B 90∠∠∴+=︒.线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,BCA 90CB CA ∠∴=︒=,.MCB ACO 90∠∠∴+=︒.B ACO ∠∠∴=.ACO 90∠=︒,ΔAOC ΔCMB ∴≌,MC OA,MB OC ∴==.点C 坐标()0,m ,点A 坐标()1,0,∴点B 坐标为()m,m 1+(2)∵点B 的坐标为(m ,m+1),点C 为(0,m ),设直线BC 为:y=kx+b ,1b m km b m =⎧⎨+=+⎩,解得:1k m b m ⎧=⎪⎨⎪=⎩, ∴1y x m m=+; 则BC 所在的直线为:1y x m m=+; 拓展:如图作BH ⊥OH 于H .设点C 的坐标为(0,m ),由(1)知:OC=HB=m ,OA=HC=1,则点B (m ,1+m ),则:BO+BA=2222(1)(1)(1)m m m m +++-++,BO+BA 的值,相当于求点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,相当于在直线y=x 上寻找一点P (m ,m ),使得点P 到M (0,-1),到N (1,-1)的距离和最小,作M 关于直线y=x 的对称点M′(-1,0),易知PM+PN=PM′+PN≥NM′, M′N=22(11)(01)5--++=,故:BO+BA 的最小值为5,故答案为:5.【点睛】本题为一次函数综合题,主要考查的是三角形全等的思维拓展,其中拓展,将BO+BA 的值转化点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,是本题的新颖点 6.探究:如图1和2,四边形ABCD 中,已知AB AD =,90BAD ∠=︒,点E ,F 分别在BC 、CD 上,45EAF ∠=︒.(1)①如图 1,若B 、ADC ∠都是直角,把ABE △绕点A 逆时针旋转90︒至ADG ,使AB 与AD 重合,则能证得EF BE DF =+,请写出推理过程;②如图 2,若B 、D ∠都不是直角,则当B 与D ∠满足数量关系_______时,仍有EF BE DF =+;(2)拓展:如图3,在ABC 中,90BAC ∠=︒,22AB AC ==,点D 、E 均在边BC 上,且45DAE ∠=︒.若1BD =,求DE 的长.解析:(1)①见解析;②180B D ∠+∠=︒,理由见解析;(2)5=3DE 【分析】(1)①根据旋转的性质得出AE =AG ,∠BAE =∠DAG ,BE =DG ,求出∠EAF =∠GAF =45°,根据SAS 推出△EAF ≌△GAF ,根据全等三角形的性质得出EF =GF ,即可求出答案; ②根据旋转的性质得出AE =AG ,∠B =∠ADG ,∠BAE =∠DAG ,求出C 、D 、G 在一条直线上,根据SAS 推出△EAF ≌△GAF ,根据全等三角形的性质得出EF =GF ,即可求出答案; (2)根据等腰直角三角形性质好勾股定理求出∠ABC =∠C =45°,BC =4,根据旋转的性质得出AF =AE ,∠FBA =∠C =45°,∠BAF =∠CAE ,求出∠FAD =∠DAE =45°,证△FAD ≌△EAD ,根据全等得出DF =DE ,设DE =x ,则DF =x ,BF =CE =3−x ,根据勾股定理得出方程,求出x 即可.【详解】(1)①如图1,∵把ABE △绕点A 逆时针旋转90︒至ADG ,使AB 与AD 重合,∴AE AG =,BAE DAG ∠=∠,BE DG =∵90BAD ∠=︒,45EAF ∠=︒,∴45BAE DAF ∠+∠=︒,∴45DAG DAF ∠+∠=︒,即45EAF GAF ∠=∠=︒,在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS ≌,∴EF GF =,∵BE DG =,∴EF GF BE DF ==+;②180B D ∠+∠=︒,理由是:把ABE △绕A 点旋转到ADG ,使AB 和AD 重合,则AE AG =,B ADG ∠=∠,BAE DAG ∠=∠,∵180B ADC ︒∠+∠=,∴180ADC ADG ∠+∠=︒,∴C ,D ,G 在一条直线上,和①知求法类似,45EAF GAF ∠=∠=︒,在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS △≌△,∴EF GF =,∵BE DG =,∴EF GF BE DF ==+;故答案为:180B D ∠+∠=︒(2)∵ABC 中,22AB AC ==90BAC ∠=∴45ABC C ∠=∠=︒,由勾股定理得:2222(22)(22)4BC AB AC =++= ,把AEC 绕A 点旋转到AFB △,使AB 和AC 重合,连接DF .则AF AE =,45FBA C ∠=∠=︒,BAF CAE ∠=∠,∵45DAE ∠=︒,∴904545FAD FAB BAD CAE BAD BAC DAE ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒, ∴45FAD DAE ∠=∠=︒,在FAD △和EAD 中AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩∴FAD EAD △≌△,∴DF DE =,设DE x =,则DF x =,∵1BC =,∴413BF CE x x ==--=-,∵45FBA ∠=︒,45ABC ∠=︒,∴90FBD ∠=︒,由勾股定理得:222DF BF BD =+,222(3)1x x =-+, 解得:5=3x , 即5=3DE . 【点睛】本题考查了旋转的性质,全等三角形的性质和判定,勾股定理的应用,此题是开放性试题,首先在特殊图形中找到规律,然后再推广到一般图形中,对学生的分析问题,解决问题的能力要求比较高.7.()1问题发现如图①,正方形,ABCD DEFG 、将正方形DEFG 绕点D 旋转,直线AE CG 、交于点,P 请直接写出线段AE 与CG 的数量关系是 ,位置关系是 _;()2拓展探究如图②,矩形,2,2,ABCD DEFG AD DE AB DG ==、将矩形DEFG 绕点D 旋转,直线,AE CG 交于点,P ()1中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段AE CG 、的数量关系和位置关系,并说明理由;()3解决问题在()2的条件下,24,28,AD DE AB DG ====矩形DEFG 绕D 点旋转过程中,请直接写出当点P 与点G 重合时,线段AE 的长,解析:()1,AE CG AE CG =⊥;()()21中数量关系不成立,位置关系成立.1,2AE AE CG CG =⊥,理由见解析;()3【分析】(1)证明△ADE ≌△CDG (SAS ),可得AE =CG ,∠DAG =∠DCG ,再由直角三角形两个锐角互余即可证得AE ⊥CG ;(2)先证明△ADE ∽△CDG ,利用相似三角形的性质证明即可.(3)先通过作图找到符合题意的两种情况,第一种情况利用勾股定理求解即可;第二种情况借助相似三角形及勾股定理计算即可.【详解】(1),AE CG AE CG =⊥;理由如下:由题意知在正方形ABCD DEFG 、中,90EDG ADC ∠=∠=︒,,AD DC DE DG ==,EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠在△ADE 与△CDG 中,AD DC ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CDG (SAS )∴AE CG =,DEA DGC ∠=∠∵对顶角相等,∴,DEA EDG DGC GPE ∠+∠=∠+∠90.GPE ∴∠=AE CG ∴⊥.(2)(1)中数量关系不成立,位置关系成立.即:1,2AE AE CG CG =⊥ 理由如下:由题意知在矩形ABCD DEFG 、中,90EDG ADC ∠=∠=︒, EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠2,2AD DE AB DG ==,12ED DG AD DC ∴== .EDAGDC ∴ 12AE CG ∴=,DEA DGC ∠=∠ ∵对顶角相等∴,DEA EDG DGC GPE ∠+∠=∠+∠90.GPE ∴∠=AE CG ∴⊥. 综上所述:1,2AE AE CG CG =⊥ (3)如图1,当点G 、P 在点A 处重合时,连接AE ,则此时∠ADE =∠GDE =90°∴在Rt △ADE 中,AE =22224225AD DE +=+= ,如图1,当点G 、P 重合时, 则点A 、E 、G 在同一直线上, ∵AD =DG =4,∴∠DAG =∠DGA ,∵∠ADC =∠AGP =90°,∠AOD =∠COG ,∴∠DAG =∠COG ,∴∠DGA =∠COG ,又∵∠GDO =∠CDG ,∴△GDO ∽△CDG ,∴DO DG OG DG DC CG == ∴448DO OG CG== ∴DO =2,CG =2OG ,∴OC =DC -DO =8-2=6,∵在Rt △COG 中,OG 2+GC 2=OC 2,∴OG 2+(2OG )2=62,∴OG 655∴CG=1255,由(2)得:12 AE CG=∴AE=655,综上所述,AE的长为25或655.【点睛】本题综合考查了全等三角形及相似三角形的判定及性质,以及勾股定理的应用,根据题意画出符合题意的图形是解决本题的关键.8.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究:如图1,当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸:如图2,当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移:如图3,当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.解析:(1)23BFAB=;(2)仍然成立,见解析;(3)221BF nAB n=+【分析】(1)尝试探究:过点D作DM CF,交AB于M,可证BDM BCF∽,,AFE AMD∽,可得11,22BD BM AE AFBC BF AD AM====,可证BM MF AF==,可得BF,BA之间的数量关系;(2)类比延伸:过点D作DM CF,交AB于M,可证BDM BCF∽,AFE AMD∽,可得11,22BD BM AE AFBC BF AD AM====,可证BM MF AF==,可得BF BA,之间的数量关系;(3)拓展迁移:过点D作DM CF,交AB于M,由平行线分线段成比例可得BM MF FM nAF=,=,可得22AB nAF AF BF nAF+=,=,即可求BF BA,之间的数量关系.【详解】解:(1)尝试探究 如图,过点D 作DM CF ,交AB 于M∵AD 是中线,AE DE = ∴1122BD CD BC AE AD ==,= ∵DM CF ,∴BDM BCF ∽,AFE AMD ∽ ∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF =,= ∴BM MF AF FM =,= ∴BM MF AF == ∴23BF AB = (2)类比延伸: 结论仍然成立,理由如下:如图,过点D 作DM CF ,交AB 于M∵AD 是中线,AE DE =∴1122BD CD BC AE AD ==,= ∵DM CF ,∴BDM BCF ∽,AFE AMD ∽ ∴11,22BD BM AE AF BC BF AD AM ==== ∴22BF BM AM AF =,= ∴BM MF AF FM =,= ∴BM MF AF ==∴23BF AB = (3)拓展迁移 如图,过点D 作DMCF ,交AB 于M∵DM FC ,且BD CD = ∴1BD BMDC FM== ∴BM MF =∵DM CF DE nEA ,= ∴1AE AF DE FM n== ∴FM nAF = ∴BM MF nAF ==∴2AB nAF AF += 2BF nAF = ∴221BF nAB n =+ 【点睛】本题主要考查了相似三角形的判定和性质综合,根据题干条件作出辅助线并得到对应的相似三角形是解决本题的关键.9.问题背景 如图1,点E 在BC 上,AB ⊥BC ,AE ⊥ED ,DC ⊥DC ,求证:=AE BEDE DC.尝试应用 如图2,在▱ABCD 中,点F 在DC 边上,将△ADF 沿AF 折叠得到△AEF ,且点E 恰好为BC 边的中点,求FCFD的值. 拓展创新 如图3,在菱形ABCD 中,点E ,F 分别在BC ,DC 边上,∠AFE =∠D ,AE ⊥FE ,FC =2.EC =6.请直接写出cos ∠AFE 的值.解析:(1)见解析;(2)12FC FD =;(3)cos ∠AFE =25.【分析】(1) 根据相似三角形的判定定理证△ABE ∽△ECD 即可;(2) 在AB 边取点G ,使GE =BE ,则∠B =∠BGE ,证△AGE ∽△ECF ,列比例式即可; (3) 作FM =FD ,FN ⊥AD ,同(2)构造△AMF ∽△FCE ,证△AEF ∽△FHD ,求出AM 长即可. 【详解】解:(1)∵ AB ⊥BC ,AE ⊥ED ,DC ⊥DC∴∠B =∠C =90° ,∠BAE +∠AEB =90°,∠CED +∠AEB =90°, ∴∠BAE =∠CED , ∴△ABE ∽△ECD ∴AE BEDE DC=. (2)在AB 边取点G ,使GE =BE ,则∠B =∠BGE又∵∠B +∠C =180° ,∠BGE +∠AGE =180° ∴∠AGE =∠C ∵∠B =∠D =∠AEF又∵∠B +∠BAE =∠AEF +∠FEC ∴∠BAE =∠FEC , ∴△AGE ∽△ECF ∴FC EF EG AE =,即FC EGEF AE=∵EF =FD , ∴FC EGFD AE= ∵GE =BE ,AE =BC =2BE , ∴12FC BE FD BC == (3)cos ∠AFE =25如图:作FM =FD ,FN ⊥AD ,由(2)同理可证△AMF ∽△FCE , ∴3FM ECAM FC== 设AM =x ,FM =FD =3x ,则AD =CD =32x +,MD =22x +,ND =1x + ∵∠AEF =∠FND =90°,∠AFE =∠D , ∴△AEF ∽△FND , ∴EF AF ND FD =,即EF NDAF FD =, ∵FC EF AM AF=,FC NDAM FD∴= ∴213x x x+=, 解得,5x =,经检验,是原方程的解; ∴ cos ∠AFE =25EF FC AF AM ==. 【点睛】本题考查了相似三角形的判定与性质和解直角三角形,解题关键是依据已知条件构造相似三角形,列比例式解决问题.10.如图1,在Rt ABC △中,90B ∠=︒,30C ∠=︒,4BC =,点D ,E 分别是边BC ,AC 的中点,连接DE .将EDC △绕点C 按逆时针方向旋转,记旋转角为α.(1)问题发现 ①当0α=︒时,BD AE =;②当180α=︒时,BDAE=; (2)拓展探究试判断:当0360α︒≤<︒时,BDAE的大小有无变化?请仅就图2的情形给出证明; (3)问题解决当EDC △旋转至//DE AC 时,请直接写出BD 的长.解析:(1)①32;②32;(2)不变,证明见解析;(3)23或27 【分析】(1)①当α=0°时,在Rt △ABC 中,由勾股定理,求出AC 的值是多少;然后根据点D 、E 分别是边BC 、AC 的中点,分别求出AE 、BD 的大小,即可求出BD 、AE 的比值; ②中,图形如下,与①有所变化,但求解方法完全相同; (2)证明△ECA ∽△DCB ,从而根据边长成比例得出比值;(3)存在2种情况,一种是当0180α︒<<︒时,//DE AC ;另一种是当180360α︒<<︒时,//DE AC ,分别利用勾股定理可求得.【详解】(1)①∵在Rt ABC △中,90B ∠=︒,30C ∠=︒,4BC =,点D ,E 分别是边BC ,AC 的中点∴CD=BD=2,在Rt △ABC 中,AB=433,AC=833∴AE=433∴232433BD AE ==;②图形如下:同理可知:BC=4,83,DC=2,2343∴BD=DC+CB=2+4=6,4383123∴3123BD AE ==(2)不变,理由如下 ∵∠ECD=∠ACB ,∴∠ECA=∠DCB , 又∵32DC CB EC CA ==, ∴△ECA ∽△DCB , ∴32BD DC AE EC ==; (3)情况一:当0180α︒<<︒时,//DE AC ,图形如下,过点D 作BC 的垂线,交BC 延长线于点F∵ED ∥AC ,∴∠ACD=∠EDC=90° ∵∠ACB=∠ECD=30° ∴∠ECF=30°,∴∠FCD=60° ∵CD=2∴在Rt △DCF 中,CF=1,FD=3 ∴FB=FC=CB=1+4=5∴在Rt △FDB 中,DB=22DF FB +=27;情况二:当180360α︒<<︒时,//DE AC ,图形如下,过点D 作BC 的垂线,交BC 于点F∵DE ∥AC ,∴∠ACD=90° ∵∠ACB=30°,∴∠DCF=60°∵CD=2,∴在Rt △CDF 中,CF=1,3∴FB=CB -CF=4-1=3∴在Rt △FDB 中,22DF FB +=3综上得:DB 的长为37 【点睛】此题属于旋转的综合题.考查了旋转的性质、相似三角形的判定与性质以及勾股定理等知识.注意掌握分类讨论思想的应用是解此题的关键.11.某数学兴趣小组在数学课外活动中,对多边形内两要互相垂直的线段做了如下探究: (观察与猜想)(1)如图1,在正方形ABCD 中,点E ,F 分别是AB ,AD 上的两点,连接DE ,CF ,DE CF ⊥,则DECF的值为__________;(2)如图2,在矩形ABCD 中,7AD =,4CD =,点E 是AD 上的一点,连接CE ,BD ,且CE BD ⊥,则CEBD的值为__________;(类比探究)(3)如图3,在四边形ABCD 中,90A B ∠=∠=︒,点E 为AB 上一点,连接DE ,过点C 作DE 的垂线交ED 的延长线于点G ,交AD 的延长线于点F ,求证:DE AB CF AD ⋅=⋅;(拓展延伸)(4)如图4,在Rt ABD ∆中,90BAD ∠=︒,9AD =,1tan 3ADB ∠=,将ABD ∆沿BD 翻折,点A 落在点C 处得CBD ∆,点E ,F 分别在边AB ,AD 上,连接DE ,CF ,且DE CF ⊥.①求DECF的值; ②连接BF ,若1AE =,直接写出BF 的长度.解析:(1)1;(2)47;(3)证明见解析;(4)①53;②3295BF =【分析】(1)先根据正方形的性质可得,90AD DC A CDF =∠=∠=︒,再根据直角三角形的性质可得ADE DCF ∠=∠,然后根据三角形全等的判定定理与性质可得DE CF =,由此即可得出答案;(2)先根据矩形的性质可得90A CDE ∠=∠=︒,再根据直角三角形的性质可得ADB DCE ∠=∠,然后根据相似三角形的判定与性质即可得;(3)如图(见解析),先根据矩形的判定与性质可得,90A B CH G H A ∠=∠===∠︒,再根据直角三角形的性质、对顶角相等可得FCH EDA ∠=∠,然后根据相似三角形的判定可得DEA CFH ~,由此即可得证;(4)①如图(见解析),先证出DEA CFG ~,从而可得9DE AD CF CG CG==,再分别在Rt ABD △和Rt ADH 中,解直角三角形可得91010AH =271010DH 的性质可得9,2105DH AC AC AH ⊥=ADC 的面积公式求出CG 的长,由此即可得出答案;②先根据(4)①中,相似三角形的性质可得53DE A FG CF E ==,可求出35FG =,再根据翻折的性质可得9CD AD ==,然后在Rt CDG 中,利用勾股定理可得365DG =,从而可得65AF =,最后在Rt ABF 中,利用勾股定理即可得. 【详解】解:(1)四边形ABCD 是正方形, ,90AD DC A CDF ∴=∠=∠=︒,90ADE CDE ∴∠+∠=︒, DE CF ⊥,90DCF CDE ∴∠+∠=︒, ADE DCF ∴∠=∠,在ADE 和DCF 中,90A CDF AD DC ADE DCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,()ADE DCF ASA ∴≅,DE CF ∴=,1DECF∴=; (2)四边形ABCD 是矩形,90A CDE ∴∠=∠=︒, 90ADB CDB ∴∠+∠=︒,CE BD ⊥,90DCE CDB ∴∠+∠=︒, ADB DCE ∴∠=∠,在ADB △和DCE 中,90A CDE ADB DCE∠=∠=︒⎧⎨∠=∠⎩,ADB DCE ∴~,47CE CD BD AD =∴=; (3)如图,过点C 作CH AF ⊥交AF 的延长线于点H ,∵CG EG ⊥,90A B ∠=∠=︒, ∴90G H A B ∠=∠=∠=∠=︒, ∴四边形ABCH 为矩形,∴AB CH =,90FCH CFH DFG FDG ∠+∠=∠+∠=︒,CFH DFG ∠=∠, FCH FDG ∴∠=∠, EDA FDG ∠=∠, FCH EDA ∴∠=∠,在DEA △和CFH △中,90EDA FCHA H ∠=∠⎧⎨∠=∠=︒⎩,∴DEA CFH ~, ∴DE ADCF CH =, ∴DE ADCF AB=, ∴DE AB CF AD ⋅=⋅;(4)①过C 作CG AD ⊥于点G ,连接AC 交BD 于点H ,∵CF DE ⊥,90BAD ∠=︒,∴90FCG CFG CFG EDA ∠+∠=∠+∠=︒, ∴FCG EDA ∠=∠,在DEA △和CFG △中,90EDA FCGEAD FGC ∠=∠⎧⎨∠=∠=︒⎩,∴DEA CFG ~, ∴DE ADCF CG=, 在Rt ABD △中,1tan 3AB ADB AD ∠==,9AD =, ∴3AB =,在Rt ADH 中,1tan 3AH ADH DH ∠==, 设AH a =,则3DH a =,∴222AH DH AD +=,即()22239a a +=, ∴91010a 91010a = ∴91010AH =271010DH = 由翻折的性质得:9,2105DH AC AC AH ⊥== 1122ADCSAC DH AD CG =⋅=⋅,∴11922CG =⨯, 解得275CG =, ∴952735DE AD CF CG ===;②由(4)①已证:DEA CFG ~,53DE CF =, 53DE C AE FG F ∴==, 1AE =,513FG ∴=,解得35FG =, 由翻折的性质得:9CD AD ==,在Rt CDG中,365DG =, 33669555AF AD FG DG ∴=--==--,在Rt ABF中,BF ===【点睛】本题考查了正方形的性质、相似三角形的判定与性质、翻折的性质、解直角三角形等知识点,较难的是题(4)①,通过作辅助线,构造直角三角形和相似三角形是解题关键. 12.(1)问题发现如图1,在△OAB 和△OCD 中,OA=OB ,OC=OD ,∠AOB=∠COD=40°,连接AC ,BD 交于点M .填空: ①ACBD的值为 ; ②∠AMB 的度数为 . (2)类比探究如图2,在△OAB 和△OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M .请判断ACBD的值及∠AMB 的度数,并说明理由; (3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD=1,C 与点M 重合时AC 的长.解析:(1)①1;②40°;(2)3,90°;(3)AC 的长为33或23.【分析】(1)①证明△COA ≌△DOB (SAS ),得AC=BD ,比值为1;②由△COA ≌△DOB ,得∠CAO=∠DBO ,根据三角形的内角和定理得:∠AMB=180°-(∠DBO+∠OAB+∠ABD )=180°-140°=40°;(2)根据两边的比相等且夹角相等可得△AOC ∽△BOD ,则3AC OC BD OD==,由全等三角形的性质得∠AMB 的度数;(3)正确画图形,当点C 与点M 重合时,有两种情况:如图3和4,同理可得:△AOC ∽△BOD ,则∠AMB=90°,3AC BD =,可得AC 的长. 【详解】(1)问题发现:①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB ,∵OC=OD ,OA=OB ,∴△COA ≌△DOB (SAS ),∴AC=BD ,∴1AC BD,= ②∵△COA ≌△DOB ,∴∠CAO=∠DBO ,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°-(∠CAO+∠OAB+∠ABD )=180°-(∠DBO+∠OAB+∠ABD )=180°-140°=40°,(2)类比探究:如图2,3AC BD =,∠AMB=90°,理由是: Rt △COD 中,∠DCO=30°,∠DOC=90°, ∴3033OD tan OC ︒==, 同理得:3033OB tan OA ︒==, ∴OD OB OC OA=, ∵∠AOB=∠COD=90°,∴∠AOC=∠BOD ,∴△AOC ∽△BOD ,∴3AC OC BD OD== ,∠CAO=∠DBO , 在△AMB 中,∠AMB=180°-(∠MAB+∠ABM )=180°-(∠OAB+∠ABM+∠DBO )=90°; (3)拓展延伸:①点C 与点M 重合时,如图3,同理得:△AOC ∽△BOD ,∴∠AMB=90°,3AC BD= 设BD=x ,则3,Rt △COD 中,∠OCD=30°,OD=1,∴CD=2,BC=x-2,Rt △AOB 中,∠OAB=30°,7,∴7在Rt △AMB 中,由勾股定理得:AC 2+BC 2=AB 2,3)2+(x −2)2=7)2,x 2-x-6=0,(x-3)(x+2)=0,x 1=3,x 2=-2,∴AC=33; ②点C 与点M 重合时,如图4,同理得:∠AMB=90°,3AC BD=, 设BD=x ,则AC=3x ,在Rt △AMB 中,由勾股定理得:AC 2+BC 2=AB 2,(3x )2+(x+2)2=(27)2.x 2+x-6=0,(x+3)(x-2)=0,x 1=-3,x 2=2,∴AC=23;.综上所述,AC 的长为33或23.【点睛】本题是三角形的综合题,主要考查了三角形全等和相似的性质和判定,几何变换问题,解题的关键是能得出:△AOC ∽△BOD ,根据相似三角形的性质,并运用类比的思想解决问题,本题是一道比较好的题目.13.问题背景(1)如图1,△ABC 中,DE ∥BC 分别交AB ,AC 于D ,E 两点,过点E 作EF ∥AB 交BC 于点F .请按图示数据填空:四边形DBFE 的面积S = ,△EFC 的面积1S = ,△ADE 的面积1S = .探究发现(2)在(1)中,若BF a =,BF a =,DE 与BC 间的距离为h .请证明2124S S S =.拓展迁移(3)如图2,□DEFG 的四个顶点在△ABC 的三边上,若△ADG 、△DBE 、△GFC 的面积分别为2、5、3,试利用(2)中的结论求△ABC 的面积.解析:(1)6S =,19S =,21S =;(2)见解析;(3)18【分析】(1)根据平行四边形面积公式、三角形面积公式,相似三角形的性质即可解决问题. (2)根据平行四边形面积公式、三角形面积公式,相似三角形的性质,分别求出S 1、S 2即可解决问题.(3)过点G 作GH ∥AB 交BC 于H ,则四边形DBHG 为平行四边形,利用(2)的结论求出□DBHG 的面积,△GHC 的面积即可.【详解】(1)∵DE ∥BC ,EF ∥AB ,∴四边形DBFE 是平行四边形,∴S=2×3=6,116392S =⨯⨯= ∴∠AED=∠C ,∠A=∠CEF∴△ADE ∽△EFC2211(),9s DE s CF ∴== ∴S 2=1,故答案为6,9,1.(2)证明:∵DE ∥BC ,EF ∥AB ,∴四边形DBFE 为平行四边形,AED C ∠=∠,A CEF ∠=∠.∴△ADE ∽△EFC . ∴22212()DE FC S a S b==. ∵112S bh =, ∴222122a a h S S b b=⨯=.∴2212144()22a h S S bh ah b=⨯⨯=. 而S ah =,∴2124S S S =(3)解:过点G 作GH ∥AB 交BC 于H ,则四边形DBHG 为平行四边形.∴∠GHC=∠B ,BD=HG ,DG=BH ,∵四边形DEFG 为平行四边形,∴DG=EF .∴BH=EF .∴BE=HF ,∴△DBE ≌△GHF .∴△GHC 的面积为5+3=8.由(2)得,□DBHG 的面积为2288⨯=.∴△ABC 的面积为28818++=.【点睛】本题考查四边形综合题、相似三角形的性质等知识,解题的关键是学会转化的思想,把问题转化为我们熟悉的题型,属于中考压轴题,14.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现如图2,固定△ABC ,使△DEC 绕点C 旋转.当点D 恰好落在BC 边上时,填空:线段DE 与AC 的位置关系是 ;②设△BDC 的面积为S 1,△AEC 的面积为S 2.则S 1与S 2的数量关系是 .(2)猜想论证当△DEC 绕点C 旋转到图3所示的位置时,小明猜想(1)中S 1与S 2的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中BC ,CE 边上的高,请你证明小明的猜想. (3)拓展探究已知∠ABC=60°,点D 是其角平分线上一点,BD=CD=4,OE ∥AB 交BC 于点E (如图4),若在射线BA 上存在点F ,使S △DCF =S △BDC ,请直接写出相应的BF 的长解析:解:(1)①DE ∥AC .②12S S =.(2)12S S =仍然成立,证明见解析;(3)433或833. 【详解】(1)①由旋转可知:AC=DC ,∵∠C=90°,∠B=∠DCE=30°,∴∠DAC=∠CDE=60°.∴△ADC 是等边三角形.∴∠DCA=60°.∴∠DCA=∠CDE=60°.∴DE ∥AC .②过D 作DN ⊥AC 交AC 于点N ,过E 作EM ⊥AC 交AC 延长线于M ,过C 作CF ⊥AB 交AB 于点F .由①可知:△ADC 是等边三角形, DE ∥AC ,∴DN=CF,DN=EM .∴CF=EM .∵∠C=90°,∠B =30°∴AB=2AC .又∵AD=AC∴BD=AC .∵1211S CF BD S AC EM 22=⋅=⋅, ∴12S S =.(2)如图,过点D 作DM ⊥BC 于M ,过点A 作AN ⊥CE 交EC 的延长线于N ,∵△DEC 是由△ABC 绕点C 旋转得到,∴BC=CE ,AC=CD ,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,∴∠ACN=∠DCM ,∵在△ACN 和△DCM 中,ACN DCM CMD N AC CD ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△ACN ≌△DCM (AAS ),∴AN=DM ,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2;(3)如图,过点D 作DF 1∥BE ,易求四边形BEDF 1是菱形,所以BE=DF 1,且BE 、DF 1上的高相等,此时S △DCF1=S △BDE ;过点D 作DF 2⊥BD ,∵∠ABC=60°,F 1D ∥BE ,∴∠F 2F 1D=∠ABC=60°,∵BF 1=DF 1,∠F 1BD=12∠ABC=30°,∠F 2DB=90°,∴∠F 1DF 2=∠ABC=60°,∴△DF 1F 2是等边三角形,∴DF 1=DF 2,过点D 作DG ⊥BC 于G ,∵BD=CD ,∠ABC=60°,点D 是角平分线上一点,∴∠DBC=∠DCB=12×60°=30°,∴∠CDF 1=180°-∠BCD=180°-30°=150°,∠CDF 2=360°-150°-60°=150°,∴∠CDF 1=∠CDF 2,∵在△CDF 1和△CDF 2中, 1212DF DF CDF CDF CD CD ⎧⎪∠⎨⎪⎩===, ∴△CDF 1≌△CDF 2(SAS ),∴点F 2也是所求的点,∵∠ABC=60°,点D 是角平分线上一点,DE ∥AB ,∴∠DBC=∠BDE=∠ABD=12×60°=30°,又∵BD=4,∴BE=12×4÷cos30°, ∴BF 1BF 2=BF 1+F 1F 2,故BF的长为433或833.15.(1)方法选择如图①,四边形ABCD是O的内接四边形,连接AC,BD,AB BC AC==.求证:BD AD CD=+.小颖认为可用截长法证明:在DB上截取DM AD=,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN AD=…请你选择一种方法证明.(2)类比探究(探究1)如图②,四边形ABCD是O的内接四边形,连接AC,BD,BC是O的直径,AB AC=.试用等式表示线段AD,BD,CD之间的数量关系,并证明你的结论.(探究2)如图③,四边形ABCD是O的内接四边形,连接AC,BD.若BC是O的直径,30ABC∠=︒,则线段AD,BD,CD之间的等量关系式是______.(3)拓展猜想如图④,四边形ABCD是O的内接四边形,连接AC,BD.若BC是O的直径,::::BC AC AB a b c=,则线段AD,BD,CD之间的等量关系式是______.解析:(1)方法选择:证明见解析;(2)【探究1】:2BD CD=;【探究2】32BD CD AD=+;(3)拓展猜想:c aBD CD ADb b=+.【分析】(1)方法选择:根据等边三角形的性质得到∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,由圆周角定理得到∠ADB=∠ACB=60°,得到AM=AD,根据全等三角形的性质得到BM=CD,于是得到结论;(2)类比探究:如图②,由BC是⊙O的直径,得到∠BAC=90°,根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,过A作AM⊥AD交BD于M,推出△ADM是等腰直角三角形,求得2根据全等三角形的性质得到结论;【探究2】如图③,根据圆周角定理和三角形的内角和得到∠BAC=90°,∠ACB=60°,过A 作AM ⊥AD 交BD 于M ,求得∠AMD=30°,根据直角三角形的性质得到MD=2AD ,根据相似三角形的性质得到,于是得到结论;(3)如图④,由BC 是⊙O 的直径,得到∠BAC=90°,过A 作AM ⊥AD 交BD 于M ,求得∠MAD=90°,根据相似三角形的性质得到BM=c b CD ,DM=a bAD ,于是得到结论. 【详解】(1)方法选择:∵AB BC AC ==,∴60ACB ABC ∠=∠=︒,如图①,在BD 上截取=DM AD ,连接AM ,∵60ADB ACB ∠=∠=︒,∴ADM ∆是等边三角形,∴AM AD =,∵ABM ACD ∠=∠,∵120AMB ADC ∠=∠=︒,∴()ABM ACD AAS ∆≅∆,∴BM CD =,∴BD BM DM CD AD =+=+;(2)类比探究:如图②,∵BC 是O 的直径,∴90BAC ∠=︒,∵AB AC =,∴45ABC ACB ∠=∠=︒,过A 作AM AD ⊥交BD 于M ,∵45ADB ACB ∠=∠=︒,∴ADM ∆是等腰直角三角形,∴AM AD =,45AMD ∠=︒, ∴DM =,∴135AMB ADC ∠=∠=︒,∵ABM ACD ∠=∠,∴()ABM ACD AAS ∆≅∆,∴BM CD =, ∴BD BM DM CD =+=;[探究2]如图③,∵若BC 是O 的直径,30ABC ∠=︒,∴90BAC ∠=︒,60ACB ∠=︒,过A 作AM AD ⊥交BD 于M ,∵60ADB ACB ∠=∠=︒,∴30AMD ∠=︒,∴2MD AD =,∵ABD ACD ∠=∠,150AMB ADC ∠=∠=︒,∴ABMACD ∆∆, ∴3BM AB CD AC ==, ∴3BM CD =, ∴32BD BM DM CD AD =+=+;故答案为32BD CD AD =+;(3)拓展猜想:c a BD BM DM CD AD b b=+=+; 理由:如图④,∵若BC 是O 的直径,∴90BAC ∠=︒,过A 作AM AD ⊥交BD 于M ,∴90MAD ∠=︒,∴BAM DAC ∠=∠,∴ABMACD ∆∆, ∴BM AB c CD AC b==, ∴c BM CD b=, ∵ADB ACB ∠=∠,90BAC NAD ∠=∠=︒,∴ADMACB ∆∆, ∴AD AC b DM BC a==, ∴a DM AD b =, ∴c a BD BM DM CD AD b b=+=+. 故答案为c a BD CD AD b b=+. 【点睛】本题考查了圆周角定理,圆内接四边形的性质,相似三角形的判定和性质,等腰直角三角形的性质,等边三角形的性质,正确的作出辅助线是解题的关键.16.(问题)如图1,在Rt ABC 中,90,ACB AC BC ∠=︒=,过点C 作直线l 平行于。
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
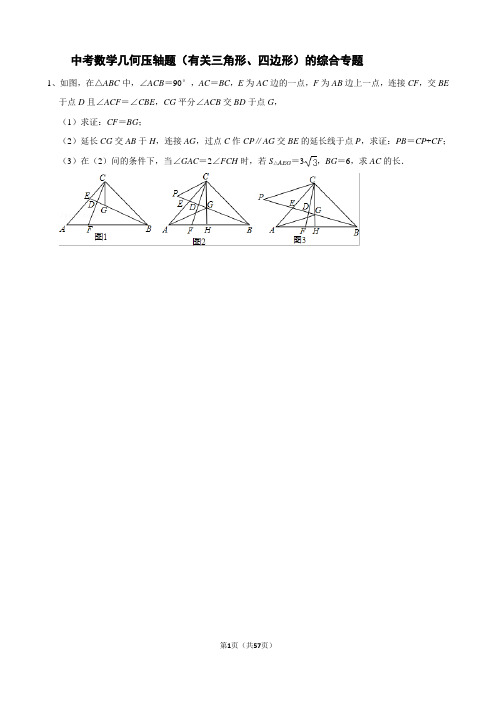
中考数学几何压轴题(有关三角形、四边形)的综合专题1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.中考数学几何压轴题(有关三角形、四边形)的综合专题参考答案1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线。
中考数学专题-----几何类阅读并解决问题(压轴题)

中考数学专题-----阅读并解决问题1、在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为.[运用](1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为(2,1.5).(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D 与点A、B、C构成平行四边形的顶点,求点D的坐标.考点:平行四边形的性质;坐标与图形性质;矩形的性质。
专题:几何综合题。
分析:(1)根据矩形的对角线互相平分及点E的坐标即可得出答案.(2)根据题意画出图形,然后可找到点D的坐标.解答:解:(1)M=(,)=(2,1.5).(2)根据平行四边形的对角线互相平分可得:D'(1,﹣1),D''(﹣3,5),D''(5,3).点评:本题考查了平行四边形的性质及矩形的性质,比较简单,关键是掌握已知两点求其中点坐标的方法.2.如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.(1)三角形有 3 条面积等分线,平行四边形有无数条面积等分线;(2)如图①所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线;(3)如图②,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并写出理由.:解:(1)根据“面积等分线”的定义知,对于三角形,一定是三角形的面积等分线的是三角形的中线所在的直线;对于平行四边形应该有无数条,只要过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分;故答案是:3;无数;(2)如图①所示:连接2个矩形的对角线的交点的直线即把这个图形分成2个相等的部分.即OO′为这个图形的一条面积等分线;(3)如图②所示.能,过点B作BE∥AC交DC的延长线于点E,连接AE.∵BE∥AC,∴△ABC和△AEC的公共边AC上的高也相等,3.在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).(1)当△ABC三边分别为6、8、9时,△ABC为锐角三角形;当△ABC三边分别为6、8、11时,△ABC为钝角三角形.(2)猜想,当a2+b2>c2时,△ABC为锐角三角形;当a2+b2<c2时,△ABC为钝角三角形.(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.后得到c的取值范围,然后分情况讨论即可得解.解:(1)两直角边分别为6、8时,斜边==10,∴△ABC三边分别为6、8、9时,△ABC为锐角三角形;当△ABC三边分别为6、8、11时,△ABC为钝角三角形;故答案为:锐角;钝角;(2)当a2+b2>c2时,△ABC为锐角三角形;当a2+b2<c2时,△ABC为钝角三角形;故答案为:>;<;(3)∵c为最长边,2+4=6,∴4≤c<6,a2+b2=22+42=20,①a2+b2>c2,即c2<20,0<c<2,∴当4≤c<2时,这个三角形是锐角三角形;②a2+b2=c2,即c2=20,c=2,∴当c=2时,这个三角形是直角三角形; ③a 2+b 2<c 2,即c 2>20,c >2,∴当2<c <6时,这个三角形是钝角三角形.本题考查了勾股定理,勾股定理逆定理,读懂题目信息,理解理解三角形4.如图,在平面直角坐标系中,有一条直线l :与x 轴、y 轴分别交于点M 、N ,一个高为3的等边三角形ABC ,边BC 在x 轴上,将此三角形沿着x 轴的正方向平移.(1)在平移过程中,得到△A 1B 1C 1,此时顶点A 1恰落在直线l 上,写出A 1点的坐标 (,3) ;(2)继续向右平移,得到△A 2B 2C 2,此时它的外心P 恰好落在直线l 上,求P 点的坐标;(3)在直线l 上是否存在这样的点,与(2)中的A 2、B 2、C 2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.一次函数综合题(1)根据等边三角形ABC 的高为3,得出A 1点的纵坐标为3,再代入即可;(2)设P (x ,y ),连接A 2P 并延长交x 轴于点H ,连接B 2P ,先求出A 2B 2=2,HB 2=,根据点P 是等边三角形A 2B 2C 2的外心,得出PH=1,将y=1代入,即可得出点P 的坐标;(3)根据点P 是等边三角形A 2B 2C 2的外心,得出△PA 2B 2,△PB 2C 2,△PA 2C 2是等腰三角形,得P (3,1),由(2)得,C 2(4,0),点C 2满足直线的关系式,得出点C 2与点M 重合,∠PMB 2=30°,设点Q 满足的条件,△QA 2B 2,△B 2QC 2,△A 2QC 2能构成等腰三角形,则QA 2=QB 2,B 2Q=B 2C 2,A 2Q=A 2C 2,作QD ⊥x 轴与点D ,连接QB 2,根据QB 2=2,∠QB 2D=2∠PMB 2=60°,求出Q (,3),设点S 满足的条件,△SA 2B 2,△C 2B 2S ,△C 2PA 2是等腰三角形,则SA 2=SB 2,C 2B 2=C 2S ,C 2A 2=C 2S ,作SF ⊥x 轴于点F ,根据SC 2=2,∠SB 2C 2=∠PMB 2=30°,求出S (4﹣3,), 设点R 满足的条件,△RA 2B 2,△C 2B 2R ,△C 2A 2R 能构成等腰三角形,则RA 2=RB 2,C 2B2=C2R,C2A2=C2R,作RE⊥x轴于点E,根据RC2=2,∠RC2E=∠PMB2=30°,R(4+3,﹣).解:(1)∵等边三角形ABC的高为3,∴A1点的纵坐标为3,∵顶点A1恰落在直线l上,∴3=,解得;x=,∴A1点的坐标是(,3),故答案为:(,3);(2)设P(x,y),连接A2P并延长交x轴于点H,连接B2P,在等边三角△A2B2C2中,高A2H=3,∴A2B2=2,HB2=,∵点P是等边三角形A2B2C2的外心,∴∠PB2H=30°,∴PH=1,即y=1,将y=1代入,解得:x=3,∴P(3,1);(3)∵点P是等边三角形A2B2C2的外心,∴△PA2B2,△PB2C2,△PA2C2是等腰三角形,∴点P满足的条件,由(2)得P(3,1),由(2)得,C2(4,0),点C2满足直线的关系式,∴点C2与点M重合,∴∠PMB2=30°,设点Q满足的条件,△QA2B2,△B2QC2,△A2QC2能构成等腰三角形,此时QA2=QB2,B2Q=B2C2,A2Q=A2C2,作QD⊥x轴与点D,连接QB2,∵QB2=2,∠QB2D=2∠PMB2=60°,∴QD=3,∴Q(,3),设点S满足的条件,△SA2B2,△C2B2S,△C2PA2是等腰三角形,此时SA2=SB2,C2B2=C2S,C2A2=C2S,作SF⊥x轴于点F,∵SC2=2,∠SB2C2=∠PMB2=30°,∴SF=,∴S(4﹣3,),设点R满足的条件,△RA2B2,△C2B2R,△C2A2R能构成等腰三角形,此时RA2=RB2,C2B2=C2R,C2A2=C2R,作RE⊥x轴于点E,∵RC2=2,∠RC2E=∠PMB2=30°,∴ER=,∴R(4+3,﹣),答:存在四个点,分别是P(3,1),Q(,3),S(4﹣3,),R.(4 +3,﹣).此题考查了一次函数综合,用到的知识点是一次函数的图象与性质、解直所有符合条件的点的坐标.ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6cm.(1)AE的长为4cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.考点几何变换综合题.分析(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案;(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC于点P,此时DP+EP值为最小,进而得出答案;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.解答解:(1)∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm,∵∠ACD=30°,∠DAC=90°,AC=12cm,∴CD=AC÷cos30°=12÷=12×=8(cm),∵点E为CD边上的中点,∴AE=DC=4cm.故答案为:4;(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE,∴△ADE为等边三角形,∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°,∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′,∴点E,D′关于直线AC对称,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′,∵△ADE是等边三角形,AD=AE=4,∴DD′=2×AD×=2×6=12,即DP+EP最小值为12cm;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=4,在△ABD′和△CBD′中,,∴△ABD′≌△CBD′(SSS),∴∠D′BG=45°,∴D′G=GB,设D′G长为xcm,则CG长为(6﹣x)cm,在Rt△GD′C中x2+(6﹣x)2=(4)2,解得:x1=3﹣,x2=3+(不合题意舍去),∴点D′到BC边的距离为(3﹣)cm.点评此题主要考查了全等三角形的判定与性质和锐角三角函数关系以及等边三角形的判定与性质等知识,利用垂直平分线的性质得出点E,D′关于直线AC对称是解题关键.6.如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD 边上的点M处,折痕为PE,此时PD=3.(1)求MP的值;(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF 的周长最小?(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)考点:几何变换综合题..专题:综合题.分析:(1)根据折叠的性质和矩形性质以得PD=PH=3,CD=MH=4,∠H=∠D=90°,然后利用勾股定理可计算出MP=5;(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,利用两点之间线段最短可得点F即为所求,过点E作EN⊥AD,垂足为N,则AM=AD﹣MP﹣PD=4,所以AM=AM′=4,再证明ME=MP=5,接着利用勾股定理计算出MN=3,所以NM′=11,然后证明△AFM′∽△NEM′,则可利用相似比计算出AF;(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,易得QE=GR,而GM=GM′,于是MG+QE=M′R,利用两点之间线段最短可得此时MG+EQ最小,于是四边形MEQG 的周长最小,在Rt△M′RN中,利用勾股定理计算出M′R=5,易得四边形MEQG 的最小周长值是7+5.解答:解:(1)∵四边形ABCD为矩形,∴CD=AB=4,∠D=90°,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴PD=PH=3,CD=MH=4,∠H=∠D=90°,∴MP==5;(2)如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,∴AM=AM′=4,∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,∴∠CEP=∠MEP,而∠CEP=∠MPE,∴∠MEP=∠MPE,∴ME=MP=5,在Rt△ENM中,MN===3,∴NM′=11,∵AF∥ME,∴△AFM′∽△NEM′,∴=,即=,解得AF=,即AF=时,△MEF的周长最小;(3)如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,∵ER=GQ,ER∥GQ,∴四边形ERGQ是平行四边形,∴QE=GR,∵GM=GM′,∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,在Rt△M′RN中,NR=4﹣2=2,M′R==5,∵ME=5,GQ=2,∴四边形MEQG的最小周长值是7+5.点评:本题考查了几何变换综合题:熟练掌握折叠的性质和矩形的性质;会利用轴对称解决最短路径问题;会运用相似比和勾股定理计算线段的长.7.(1)阅读理解:如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD 绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是2<AD<8 ;(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF 交AC于点F,连接EF,求证:BE+CF>EF;(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.【考点】三角形综合题.【分析】(1)延长AD至E,使DE=AD,由SAS证明△ACD≌△EBD,得出BE=AC=6,在△ABE中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;(2)延长FD至点M,使DM=DF,连接BM、EM,同(1)得△BMD≌△CFD,得出BM=CF,由线段垂直平分线的性质得出EM=EF,在△BME中,由三角形的三边关系得出BE+BM>EM即可得出结论;(3)延长AB至点N,使BN=DF,连接CN,证出∠NBC=∠D,由SAS证明△NBC≌△FDC,得出CN=CF,∠NCB=∠FCD,证出∠ECN=70°=∠ECF,再由SAS证明△NCE ≌△FCE,得出EN=EF,即可得出结论.【解答】(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:∵AD是BC边上的中线,∴BD=CD,在△BDE和△CDA中,,∴△BDE≌△CDA(SAS),∴BE=AC=6,在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,∴10﹣6<AE<10+6,即4<AE<16,∴2<AD<8;故答案为:2<AD<8;(2)证明:延长FD至点M,使DM=DF,连接BM、EM,如图②所示:同(1)得:△BMD≌△CFD(SAS),∴BM=CF,∵DE⊥DF,DM=DF,∴EM=EF,在△BME中,由三角形的三边关系得:BE+BM>EM,∴BE+CF>EF;(3)解:BE+DF=EF;理由如下:延长AB至点N,使BN=DF,连接CN,如图3所示:∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,∴∠NBC=∠D,在△NBC和△FDC中,,∴△NBC≌△FDC(SAS),∴CN=CF,∠NCB=∠FCD,∵∠BCD=140°,∠ECF=70°,∴∠BCE+∠FCD=70°,∴∠ECN=70°=∠ECF,在△NCE和△FCE中,,∴△NCE≌△FCE(SAS),∴EN=EF,∵BE+BN=EN,∴BE+DF=EF.8.在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.(Ⅰ)探究新知如图①,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.(1)求证:内切圆的半径r1=1;(2)求tan∠OAG的值;(Ⅱ)结论应用(1)如图②,若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;(2)如图③,若半径为rn 的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On 与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.:压轴题.:(Ⅰ)(1)根据切线的性质以及正方形的判定得出四边形CEOF是正方形,进而得出CE=CF=r1,再利用切线长定理求出即可;(2)在Rt△AOG中,根据r1=1,AG=3﹣r1=2,求出tan∠OAG的值即可;(Ⅱ)(1)由tan∠OAG=,知tan∠O1AD=,同理可得:tan∠O2BE==,进而得出AD=2r2,DE=2r2,BE=3r2,即可求出r2=;(2)根据(1)中所求可以得出AD=2rn ,DE=2rn,…,MB=3rn,得到2rn+2rn+ (3)n=5,求出即可.:(Ⅰ)(1)证明:在图①中,连接OE,OF,OA.tan∠OAG==;(Ⅱ)(1)解:连接O1A、O2B,作O1D⊥AB交于点D、O2E⊥AB交于点E,AO1、BO2分别平分∠CAB、∠ABC.由tan∠OAG=,知tan∠O1AD=,同理可得:tan∠O2BE==,∴AD=2r2,DE=2r2,BE=3r2.∵AD+DE+BE=5,r 2=;(2)解:如图③,连接O1A、OnB,作O1D⊥AB交于点D、O2E⊥AB交于点E、…、OnM⊥AB交于点M.则AO1、BOn分别平分∠CAB、∠ABC.tan∠O1AD=,tan∠OnBM=,AD=2rn ,DE=2rn,…,MB=3rn,又∵AD+DE+…+MB=5,2rn +2rn+ (3)n=5,(2n+3)rn=5,rn=.点评:此题主要考查了切线长定理以及锐角三角函数关系以及相切两圆的性质,根据已知得出tan∠O1AD=,tan∠O2BE==是解题关键.EDF的直角边DE上,点C、D、B、F在同一直线上,点D、B是CF的三等分点,CF=6.(1)三角板ACB固定不动,将三角板EDF绕点D逆时针旋转,使DE与AC交于点M,DF与AB交于点N,当EF∥CB时(如图2),DF旋转的度数为30°;(2)求图2中的四边形AMDN的周长;(3)将图2中的三角板EDF绕点D继续逆时针旋转15°得图3,猜想图3中的四边形AMDN是什么四边形,并证明你的猜想.考点:几何变换综合题.分析:(1)DF转过的角度是∠FDB,根据EF∥CB,就可以得到∠FDB=∠F,判断A是否在EF上,只要求出直角△DEF的斜边EF上的高就可以;(2)根据三角形全等得出CM=DN,AM=BN,四边形的周长就是AB和AC的和.(3)首先求出旋转的角度,然后可以进行判断.解答:解:(1)∵EF∥CB,∴∠FDB=∠F=30°.即DF旋转的度数是30°,(2)如图2,∵∠CDM+∠ADE=90°,∠ADN+∠ADE=90°,∴∠CDM=∠ADN,在△CDM与△ADN中,,∴△CDM≌△ADN(ASA),∴CM=DN,同理可证:AM=BN,∴AM+MD+DN+AN=AM+MC+AN+NB=AC+AB=2+2=4,∴四边形AMDN的周长为4.(3)在图2的位置,将三角板EDF绕点D继续逆时针旋转15°,如图3,∴∠FDB=45°,∴∠FDB=∠C,∴AC∥DF,∵∠EDF=∠BAC=90°,∴∠AMD=∠EDF=90°,∠AND=∠CAB=90°,∵∠DAB=45°,∴AN=DN,∴四边形AMDN是正方形.点评:本题是一道需要把旋转角的概念和直角三角形的性质结合求解的综合题,考查学生综合运用数学知识的能力.正确确定旋转角是解答本题的关键.10.如图(1),矩形纸片ABCD,把它沿对角线BD向上折叠,(1)在图(2)中用实线画出折叠后得到的图形(要求尺规作图,保留作图痕迹,不写作法)(2)折叠后重合部分是什么图形?说明理由.考点:翻折变换(折叠问题).证得∠FDB=∠FBD,即可证得△FBD是等腰三角形.:解:(1)做法参考:方法1:作∠BDG=∠BDC,在射线DG上截取DE=DC,连接BE;方法2:作∠DBH=∠DBC,在射线BH上截取BE=BC,连接DE;方法3:作∠BDG=∠BDC,过B点作BH⊥DG,垂足为E方法4:作∠DBH=∠DBC,过,D点作DG⊥BH,垂足为E;方法5:分别以D、B为圆心,DC、BC的长为半径画弧,两弧交于点E,连接DE、BE (2)分(做法合理均可得分)∴△DEB为所求做的图形…3分.(2)等腰三角形.…4分证明:∵△BDE是△BDC沿BD折叠而成,∴∠FDB=∠CDB,…5分∵四边形ABCD是矩形,∴AB∥CD,∴∠ABD=∠BDC,…6分∴∠FDB=∠ABD,…7分∴△BDF是等腰三角形.…8分:此题考查了矩形的性质、等腰三角形的判定,折叠的性质以及尺规作图.此题难度不大,11.如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE 沿DE折叠,点C的对应点为C′.(1)若点C′刚好落在对角线BD上时,BC′= 4 ;(2)若点C′刚好落在线段AB的垂直平分线上时,求CE的长;(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.【解答】解:(1)如图1,∵点B,C′,D在同一直线上,∴BC′=BD﹣DC′=BD﹣DC=10﹣6=4;故答案为:4;(2)如图2,连接CC′,∵点C′在AB的垂直平分线上,∴点C′在DC的垂直平分线上,∴CC′=DC′=DC,则△DC′C是等边三角形,设CE=x,易得DE=2x,由勾股定理得:(2x)2﹣x2=62,解得:x=2,即CE的长为2;(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:①当点C′在矩形内部时,如图3,∵点C′在AD的垂直平分线上,∴DM=4,∵DC′=6,由勾股定理得:MC′=2,∴NC′=6﹣2,设EC=y,则C′E=y,NE=4﹣y,故NC′2+NE2=C′E2,即(6﹣2)2+(4﹣y)2=y2,解得:y=9﹣3,即CE=9﹣3;②当点C′在矩形外部时,如图4,∵点C′在AD的垂直平分线上,∴DM=4,∵DC′=6,由勾股定理得:MC′=2,∴NC′=6+2,设EC=z,则C′E=a,NE=z﹣4故NC′2+NE2=C′E2,即(6+2)2+(z﹣4)2=z2,解得:z=9+3,即CE=9+3,综上所述:CE的长为9±3.12.如图,四边形ABCD是正方形,E是直线CD上的点,将△ADE沿AE对折得△AFE,直线EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)当DE是线段CD的一半时,请你在备用图中利用尺规作图画出符合题意的图形(保留作图痕迹,不写作法)(3)在(2)的条件下,求∠EAG的度数.【考点】四边形综合题.【分析】(1)利用正方形的性质和折叠的性质可得AF=AB,∠AFE=∠D,由HL定理可证得Rt△ABG≌Rt△AFG;(2)首先作出CD的垂直平分线,与CD相交于点E,再以E点为圆心,DE为半径作弧,A点为圆心,AF为半径作弧,两弧相交于点F,连接AF,AE,EF,延长EF与BC相交于点G,如下图所示;(3)由△AFE≌△ADE,△ABG≌△AFG,利用全等三角形的性质可得∠EAF=∠EAD,∠GAF=∠GAB,易得∠EAG=∠EAF+∠GAF=∠BAD,可得结论.【解答】(1)证明:∵四边形ABCD为正方形,∴AB=AD,∠B=∠D=90°,∵将△ADE沿AE对折得△AFE,∴AF=AD=AB,∠AFE=∠D=90°,在Rt△ABG与Rt△AFG中,,∴△ABG≌△AFG(HL);(2)如图所示:(3)解:∵△AFE≌△ADE,△ABG≌△AFG,∴∠EAF=∠EAD,∠GAF=∠GAB,∵在正方形ABCD中,∠BAD=90°.∴∠EAG=∠EAF+∠GAF=90°=45°.13.(1)数学课上,老师出了一道题,如图①,Rt△ABC中,∠C=90°,,求证:∠B=30°,请你完成证明过程.(2)如图②,四边形ABCD是一张边长为2的正方形纸片,E、F分别为AB、CD 的中点,沿过点D的折痕将纸片翻折,使点A落在EF上的点A′处,折痕交AE 于点G,请运用(1)中的结论求∠ADG的度数和AG的长.(3)若矩形纸片ABCD按如图③所示的方式折叠,B、D两点恰好重合于一点O (如图④),当AB=6,求EF的长.【考点】翻折变换(折叠问题).【专题】压轴题.【分析】(1)Rt△ABC中,根据sinB═=,即可证明∠B=30°;(2)求出∠FA′D的度数,利用翻折变换的性质可求出∠ADG的度数,在Rt△A'FD中求出A'F,得出A'E,在Rt△A'EG中可求出A'G,利用翻折变换的性质可得出AG的长度.(3)先判断出AD=AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.【解答】(1)证明:Rt△ABC中,∠C=90°,,∵sinB==,∴∠B=30°;(2)解:∵正方形边长为2,E、F为AB、CD的中点,∴EA=FD=×边长=1,∵沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,∴A′D=AD=2,∴=,∴∠FA′D=30°,可得∠FDA′=90°﹣30°=60°,∵A沿GD折叠落在A′处,∴∠ADG=∠A′DG,AG=A′G,∴∠ADG===15°,∵A′D=2,FD=1,∴A′F==,∴EA′=EF﹣A′F=2﹣,∵∠EA′G+∠DA′F=180°﹣∠GA′D=90°,∴∠EA′G=90°﹣∠DA′F=90°﹣30°=60°,∴∠EGA′=90°﹣∠EA′G=90°﹣60°=30°,则A′G=AG=2EA′=2(2﹣);(3)解:∵折叠后B、D两点恰好重合于一点O,∴AO=AD=CB=CO,∴DA=,∵∠D=90°,∴∠DCA=30°,∵AB=CD=6,在Rt△ACD中, =tan30°,则AD=DC•tan30°=6×=2,∵∠DAF=∠FAO=∠DAO==30°,∴=tan30°=,∴DF=AD=2,∴DF=FO=2,同理EO=2,∴EF=EO+FO=4.【点评】本题考查了翻折变换的知识,涉及了含30°角的直角三角形的性质、平行四边形的性质,综合考察的知识点较多,注意将所学知识融会贯通.。
中考数学几何压轴题及答案及答案

中考数学几何压轴题及答案一、解答题(共30小题)1.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论2.在△ABC的边BC上取B′、C′两点,使∠AB′B=∠AC′C=∠BAC(1)如图1中∠BAC为直角,∠BAC=∠AB′B=∠AC′C=90°(点B′与点C′重合),则△ABC∽△B'BA∽△C'AC,,,进而可得AB2+AC2=;(2)如图2中当∠BAC为锐角,图3中∠BAC为钝角时(1)中的结论还成立吗?若不成立,则AB2+AC2等于什么(用含用BC和B′C′的式子表示)?并说明理由(3)若在△ABC中,AB=5,AC=6,BC=9,请你先判断出△ABC的类型,再求出B′C′的长3.(1)问题发现如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE填空:①的值为;②∠DBE的度数为.(2)类比探究如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断的值及∠DBE的度数,并说明理由;(3)拓展延伸如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE 的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.4.(1)问题发现:如图①,在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,以点D为顶点作正方形DFGE,使点A、C分别在DE和DF上,连接BE、AF.则线段BE 和AF数量关系.(2)类比探究:如图②,保持△ABC固定不动,将正方形DFGE绕点D旋转α(0°<α≤360°),则(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)解决问题:若BC=DF=2,在(2)的旋转过程中,连接AE,请直接写出AE的最大值.5.如图,在平行四边形ABCD中,AC与BD交于点O,以点O为顶点的∠EOF的两边分别与边AB、AD交于点E、F,且∠EOF与∠BAD互补.(1)若四边形ABCD是正方形,则线段OE与OF有何数量关系?请直接写出结论;(2)若四边形ABCD是菱形,那么(1)中的结论是否成立?若成立,请画出图形并给出证明;若不成立,请说明理由;(3)若AB:AD=m:n,探索线段OE与OF的数量关系,并证明你的结论.6.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC=.7.如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.8.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.(1)问题发现如图1,△CDE的形状是三角形.(2)探究证明如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.(3)解决问题是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.9.等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB=4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD 的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN 和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.10.四边形是我们在学习和生活中常见的图形,而对角线互相垂直的四边形也比较常见,比如筝形、菱形、图1中的四边形ABCD等.它们给我们的学习和生活带来了很多的乐趣和美感.(1)如图2,在四边形ABCD中,AB=AD,CB=CD,则AC与BD的位置关系是,请说明理由.(2)试探究图1中四边形ABCD的两组对边AB,CD与BC,AD之间的数量关系,请写出证明过程.(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE的长.11.问题发现:如图(1)在Rt△ABC和Rt△BDE中,∠A=∠DEB=30°,BC=BE=6,Rt△BDE绕点B逆时针旋转,H为CD的中点,当点C与点E重合时,BH与AE的位置关系为,BH与AE的数量关系为;问题证明:在Rt△BDE绕点B旋转的过程中,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明若不成立,请说明理由;拓展应用:在Rt△BDE绕点B旋转的过程中,当DE∥BC时,请直接写出BH2的长.12.如图1,菱形ABCD与菱形GECF的顶点C重合,点G在对角线AC上,且∠BCD=∠ECF=60°,(1)问题发现的值为;(2)探究与证明将菱形GECF绕点C按顺时针方向旋转α角(0°<α<60°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:菱形GECF在旋转过程中,当点A,G,F三点在一条直线上时,如图3所示连接CG并延长,交AD于点H,若CE=2,GH=,则AH的长为.13.如图,在Rt△ABC中,∠ACB=90°,=,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则=;(2)数学思考:①如图2,若点E在线段AC上,则=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.14.如图,已知点E是射线BC上的一点,以BC、CE为边作正方形ABCD和正方形CEFG,连接AF,取AF的中点M,连接DM、MG(1)如图1,判断线段DM和GM的数量关系是,位置关系是;(2)如图2,在图中的正方形CEFG绕点C逆时针旋转的过程中,其他条件不变,(1)中的结论是否成立?说明理由;(3)已知BC=10,CE=2,正方形CEFG绕点C旋转的过程中,当A、F、E共线时,直接写出△DMG的面积.15.在Rt△ABC中,∠ACB=90°,AB=,AC=2,过点B作直线m∥AC,将△ABC绕点C顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分别交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在CA′,CB′的延长线上时,试探究四边形P A'B′Q的面积是否存在最小值.若存在,求出四边形P A′B′Q的最小面积;若不存在,请说明理由.16.如图(1),在等边三角形ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M,N,P分别是BE,CD,BC的中点,连接DE,PM,PN,MN.(1)观察猜想,图(1)中△PMN是(填特殊三角形的名称)(2)探究证明,如图(2),△ADE绕点A按逆时针方向旋转,则△PMN的形状是否发生改变?并就图(2)说明理由.(3)拓展延伸,若△ADE绕点A在平面内自由旋转,AD=2,AB=6,请直接写出△PMN 的周长的最大值.17.已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.18.问题提出:(1)如图1,在四边形ABCD中,连接AC、BD,AB=AD,∠BAD=∠BCD=90°,将△ABC绕点A逆时针旋转90°,得到△ADE,点B的对应点落在点D,点C的对应点为点E,可知点C、D、E在一条直线上,则△ACE为三角形,BC、CD、AC的数量关系为;探究发现:(2)如图2,在⊙O中,AB为直径,点C为的中点,点D为圆上一个点,连接AD、CD、AC、BC、BD,且AD<BD,请求出CD、AD、BD间的数量关系.拓展延伸:(3)如图3,在等腰直角三角形ABC中,点P为AB的中点,若AC=13,平面内存在一点E,且AE=10,CE=13,当点Q为AE中点时,PQ=.19.已知△ABC中,CA=CB,0°<∠ACB≤90°,点M、N分别在边CA,CB上(不与端点重合),BN=AM,射线AG∥BC交BM延长线于点D,点E在直线AN上,EA=ED.(1)【观察猜想】如图1,点E在射线NA上,当∠ACB=45°时,①线段BM与AN的数量关系是;②∠BDE的度数是;(2)【探究证明】如图2点E在射线AN上,当∠ACB=30°时,判断并证明线段BM与AN的数量关系,求∠BDE的度数;(3)【拓展延伸】如图3,点E在直线AN上,当∠ACB=60°时,AB=3,点N是BC 边上的三等分点,直线ED与直线BC交于点F,请直接写出线段CF的长.20.如图①,在正方形ABCD和正方形AB'C'D'中,AB=2,AB'=,连接CC’(1)问题发现:.(2)拓展探究:将正方形AB'C'D'绕点A逆时针旋转,记旋转角为θ,连接BB',试判断:当0°≤θ<360°时,的值有无变化?请仅就图②中的情形给出你的证明;(3)问题解决:请直接写出在旋转过程中,当C,C′,D'三点共线时BB′的长.21.如图1,在正方形ABCD中,点O是对角线BD的中点.(1)观察猜想将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是,直线AC与DE的位置关系是.(2)类比探究将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.(3)拓展延伸将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.22.如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为°,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为;(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.23.如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.(1)观察猜想:线段EF与线段EG的数量关系是;(2)探究证明:如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)拓展延伸:如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求的值.24.如图1,在Rt△ABC中,∠B=90°,AB=2,BC=1,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、B、E三点共线时,直接写出线段BD的长.25.在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.(1)尝试探究如图(1),当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是;(2)类比延伸如图(2),当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)拓展迁移如图(3),当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.26.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE ⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.(1)求证:CD是⊙O的切线;(2)小明在研究的过程中发现是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.27.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)如图2,四边形ABCD内接于⊙O,=,四边形ABCD的外角平分线DF交⊙O 于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;②若AB=8,CD=5,求△DEF的面积.28.【性质探究】如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.(1)判断△AFG的形状并说明理由.(2)求证:BF=2OG.【迁移应用】(3)记△DGO的面积为S1,△DBF的面积为S2,当=时,求的值.【拓展延伸】(4)若DF交射线AB于点F,【性质探究】中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的时,请直接写出tan∠BAE的值.29.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.30.如图1和图2,在△ABC中,AB=AC,BC=8,tan C=.点K在AC边上,点M,N 分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.参考答案与试题解析一.解答题(共30小题)1.【解答】解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.2.【解答】解:(1)如图1中,∵△ABC∽△B'BA∽△C'AC,∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC×BC=BC2,故答案为BC2.(2)不成立.理由:如图2中当∠BAC为锐角时,BB′+CC′﹣B′C′=BC,且△ABC∽△B'BA∽△C'AC,∴∴=,=,∴AB2=BB′×BC,AC2=CC′×BC,∴AB2+AC2=BC(BB′+CC′)=BC2+BC•B′C′.图3中∠BAC为钝角时,BB′+CC′+B′C′=BC.AB2+AC2=BC(BB′+CC′)=BC2﹣BC•B′C′.(3)当AB=5,AC=6,BC=9时,则AB2+AC2<BC2,可知△ABC为钝角三角形,由图3可知:AB2+AC2=BC2﹣BC•B′C′,∴52+62=92﹣9B′C′,∴B′C′=.3.【解答】解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,∴∠ABC=∠CAB=45°=∠CDE=∠CED,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD,∠CAB=∠CBE=45°,∴∠DBE=∠ABC+∠CBE=90°,=1,故答案为:1,90°(2),∠DBE=90°理由如下:∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴∠ACD=∠BCE,∠CED=∠ABC=30°∴tan∠ABC=tan30°==∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,∴Rt△ACB∽Rt△DCE∴∴,且∠ACD=∠BCE∴△ACD∽△BCE∴=,∠CBE=∠CAD=60°∴∠DBE=∠ABC+∠CBE=90°(3)若点D在线段AB上,如图,由(2)知:=,∠ABE=90°∴BE=AD∵AC=2,∠ACB=90°,∠CAB=90°∴AB=4,BC=2∵∠ECD=∠ABE=90°,且点M是DE中点,∴CM=BM=DE,∵△CBM是直角三角形∴CM2+BM2=BC2=(2)2,∴BM=CM=∴DE=2∵DB2+BE2=DE2,∴(4﹣AD)2+(AD)2=24∴AD=+1∴BE=AD=3+若点D在线段BA延长线上,如图同理可得:DE=2,BE=AD∵BD2+BE2=DE2,∴(4+AD)2+(AD)2=24,∴AD=﹣1∴BE=AD=3﹣综上所述:BE的长为3+或3﹣4.【解答】解:(1)∵△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,∴AD=BD=DC,∠BDA=90°,∵四边形DFGE是正方形,∴DE=DF,∠EDF=90°,∴∠BDE=∠ADF=90°,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF故答案为:BE=AF;(2)成立;理由如下:当正方形DFGE在BC的上方时,如图②所示,连接AD,∵在Rt△ABC中,AB=AC,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADE+∠EDB=90°,∵四边形DFGE为正方形,∴DE=DF,且∠EDF=90°,∴∠ADE+∠ADF=90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;当正方形DFGE在BC的下方时,连接AD,如图③所示:∵∠BDE=∠BDF+90°,∠ADF=∠BDF+90°,∴∠BDE=∠ADF,在△BDE和△ADF中,,∴△BDE≌△ADF(SAS),∴BE=AF;综上所述,(1)中的结论BE=AF成立;(3)在△ADE中,∵AE<AD+DE,∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.如图④所示:则AD=BC=1,DE=DF=2,∴AE=AD+DE=3,即AE的最大值为3.5.【解答】解:(1)如图1,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是正方形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(2)(1)的结论成立;理由:如图2,过点O作OM⊥AB于M,ON⊥AD于N,∴∠OME=∠ONF=90°,∴∠BAD+∠MON=180°,∵∠BAD+∠EOF=180°,∴∠MON=∠EOF,∴∠EOM=∠FON,∵O是菱形ABCD的对角线的交点,∴∠BAO=∠DAO,∵OM⊥AB,ON⊥AD,∴OM=ON,∴△OME≌△ONF(AAS)∴OE=OF;(3)如图3,过点O作OG⊥AB于G,OH⊥AD于H,∴∠OGE=∠OHF=90°,∴∠BAD+∠GOH=180°,∵∠BAD+∠EOF=180°,∴∠GOH=∠EOF,∴△EOG∽△FOH,∴,∵O是▱ABCD的对角线的交点,∴S△AOB=S△AOD,∵S△AOB=AB•OG,S△AOD=AD•OH,∴AB•OG=AD•OH,∴=,∴.6.【解答】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.7.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.8.【解答】解:(1)证明:∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;故答案为:等边;(2)存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=2,∴△BDE的最小周长=CD+4=2+4;(3)存在,①∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意,②当0≤m<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴m=2;③当6<m<10时,由∠DBE=120°>90°,∴此时不存在;④当m>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴m=14,综上所述:当m=2或14时,以D、E、B为顶点的三角形是直角三角形.9.【解答】解:(1)如图1中,连接DB,MF,CE,延长BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠ABD+∠ADB=90°,∠ADB=∠CDH,∴∠ADH+∠DCH=90°,∴∠CHD=90°,∴EC⊥BH,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.故答案为:45°(2):如图2中,连接MF,EC,BD.设EC交AB于O,BD交EC于H.∵AC=AB,AE=AD,∠BAD=∠CAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ACE=∠ABD,∵∠AOC+∠ACO=90°,∠AOC=∠BOH,∴∠OBH+∠BOH=90°,∴∠BHO=90°,∴EC⊥BD,∵BM=MC,BF=FE,∴MF∥EC,MF=EC,∵CM=MB,CN=ND,∴MN∥BD,MN=BD,∴MN=MF,MN⊥MF,∴∠NMF=90°,∴∠MNF=45°,NF=MN.(3):如图3中,如图以A为圆心AD为半径作⊙A.当直线PB与⊙A相切时,此时∠CBP的值最小,点P到BC的距离最小,即△BCP的面积最小,∵AD=AE,AB=AC,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴∠ACE=∠ABD,BD=EC,∵∠ABD+∠AOB=90°,∠AOB=∠CPO,∴∠CPB=90°,∵PB是⊙A的切线,∴∠ADP=90°,∵∠DPE=∠ADP=∠DAE=90°,∴四边形ADPE是矩形,∵AE=AD,∴四边形ADPE是正方形,∴AD=AE=PD=PE=2,BD=EC==2,∴PC=2﹣2,PB=2+2,∴S△BCP的最小值=×PC×PB=(2﹣2)(2+2)=4.10.【解答】(1)解:AC⊥BD,理由如下:连接AC、BD,如图2所示:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,故答案为:AC⊥BD;(2)解:AD2+BC2=AB2+CD2;理由如下:如图1,已知四边形ABCD中,AC⊥BD,设BD、AC相交于E,∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)解:如图3,连接CG、BE,∵四边形ACFG和四边形ABDE是正方形,∴AC=AG,AB=AE,∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,由(2)得,CG2+BE2=CB2+GE2,在Rt△ABC中,AC=4,AB=5,根据勾股定理得,BC2=52﹣42=9,∵CG和BE分别是正方形ACFG和正方形ABDG的对角线,∴CG2=42+42=32,BE2=52+52=50,∴GE2=CG2+BE2﹣CB2=32+50﹣9=73,∴GE=.11.【解答】解:问题发现:如图1中,结论:AE=2BH,AE⊥BH.理由:在Rt△ABC中,∵BC=6,∠A=30°,∴AE=2BC=12,在Rt△CDB中,∵∠DCB=30°,∴CD==4,∵CH=DH,∴BH=CD=2,∴==2,∴AE=2BH.故答案为AE⊥BH,AE=2BH.问题证明:如图2中,(1)中结论成立.理由:延长BH到F使得HF=BH,连接CF.设AE交BF于O.∵CH=DH,BH=HF,∠CHF=∠BHD,∴△CHF≌△DHB(SAS),∴BD=CF,∠F=∠DBH,∴CF∥BD,∵AB=BC,BE=BD,∴BE=CF,∴==,∵CF∥BD,∴∠BCF+∠CBD=180°,∵∠ABC+∠DBE=∠ABD+∠CBD+∠CBD+∠CBE=∠CBD+∠ABE=180°,∴∠BCF=∠ABE,∴△ABE∽△BCF,∴∠CBF=∠BAE,==,∴AE=BF=2BH,∵∠CBF+∠ABF=90°,∴∠ABF+∠BAE=90°,∴∠AOB=90°,∴BH⊥AE.拓展应用:如图3﹣1中,当DE在BC的下方时,延长AB交DE于F.∵DE∥BC∴∠ABC=∠BFD=90°,由题意BC=BE=6,AB=6,BD=2,DE=4,∵•BD•BE=•DE•BF,∴BF==3,∴EF=BF=3,∴AF=6+3,∴AE2=AF2+EF2=(6+3)2+(3)2=144+36.∵AE=2BH,∴AE2=12BH2,∴BH2=12+3如图3﹣2中,当DE在BC的上方时,同法可得AF=6﹣3,EF=3,∴BH2==(=12﹣3.12.【解答】解:(1)如图1中,作EH⊥CG于H.∵四边形ECFG是菱形,∠ECF=60°,∴∠ECH=∠ECF=30°,EC=EG,∵EH⊥CG,∴GH=CG,∴=cos30°=,∴=2•=,∵EG∥CD,AB∥CD,∴GE∥AB,∴==.故答案为.(2)结论:AG=BE.理由:如图2中,连接CG.∵四边形ABCD,四边形ECFG都是菱形,∠ECF=∠DCB=60°,∴∠ECG=∠EGC=∠BCA=∠BAC=30°,∴△ECG∽△BCE,∴=,∵∠ECB=∠GCA,∴△ECB∽△GCA,∴==,∴AG=BE.(3)如图3中,∵∠AGH=∠CGF=30°.∠AGH=∠GAC+∠GCA,又∵∠DAC=∠HAG+∠GAC=30°,∴∠HAG=∠ACH,∵∠AHG=∠AHC,∴△HAG∽△HCA,∴HA:HC=GH:HA,∴AH2=HG•HC,∴FC=2,CG=CF,∴GC=2,∵HG=,∴AH2=HG•HC=•3=9,∵AH>0,∴AH=3.故答案为3.13.【解答】解:(1)当m=n时,即:BC=AC,∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴=1,∴=1(2)①∵∠ACB=90°,∴∠A+∠ABC=90°,∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE﹣∠CDE=∠ADC﹣∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴②成立.如图,∵∠ACB=90°,∴∠A+∠ABC=90°,又∵CD⊥AB,∴∠DCB+∠ABC=90°,∴∠A=∠DCB,∵∠FDE=∠ADC=90°,∴∠FDE+∠CDE=∠ADC+∠CDE,即∠ADE=∠CDF,∴△ADE∽△CDF,∴,∵∠A=∠DCB,∠ADC=∠BDC=90°,∴△ADC∽△CDB,∴,∴.(3)由(2)有,△ADE∽△CDF,∵=,∴=,∴CF=2AE,在Rt△DEF中,DE=2,DF=4,∴EF=2,①当E在线段AC上时,在Rt△CEF中,CF=2AE=2(AC﹣CE)=2(﹣CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(﹣CE)]2=40∴CE=2,或CE=﹣(舍)而AC=<CE,∴此种情况不存在,②当E在AC延长线上时,在Rt△CEF中,CF=2AE=2(AC+CE)=2(+CE),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(+CE)]2=40,∴CE=,或CE=﹣2(舍),③如图1,当点E在CA延长线上时,CF=2AE=2(CE﹣AC)=2(CE﹣),EF=2,根据勾股定理得,CE2+CF2=EF2,∴CE2+[2(CE﹣)]2=40,∴CE=2,或CE=﹣(舍)即:CE=2或CE=.14.【解答】解:(1)如图1,延长GM交AD于H,∵AD∥GF,∴∠GFM=∠HAM,在△FMG和△AMH中,,∴△FMG≌△AMH(ASA),∴HM=GM,AH=FG,∵AD=CD,AH=FG=CG,∴DH=DG,∵∠HDG=90°,HM=GM,∴DM=MG,DM⊥MG,故答案为DM=MG,DM⊥MG.(2)结论成立:DM=MG,DM⊥MG,理由:如图2中,延长GM使得MH=GM,连接AH、DH、DG,延长AD交GF的延长线于N,交CD于O.∵AM=MF,∠AMH=∠FMG,MH=MG,∴△AMH≌△FMG(SAS),∴AH=GF=CG,∠AHM=∠FGM,∴AH∥GN,∴∠HAD=∠N,∵∠ODN=∠OGC=90°,∠DON=∠GOC,∴∠N=∠OCG,∴∠HAD=∠DCG,∵AH=CG,AD=CD,∴△HAD≌△GCD(SAS),∴DH=DG,∠HDA=∠CDG,∴∠HDG=∠ADC=90°,∴△HDG是等腰直角三角形,∵MH=MG,∴DM⊥GH,DM=MH=MG,(3)①如图3﹣1中,连接AC.在Rt△ABC中,AC==10,在Rt△ACE中,AE==14,∴AF=AE=EF=14﹣2=12,∴FM=AM=AF=6,在Rt△MGF中,MG==2,∴S△DMG=×2×2=20,②如图3﹣2中,连接AC.同法可得AE=14,AF=16,FM=8,MG==2,∴S△DMG=×2×2=34,综上所述,满足条件的△DMG的面积为20或34.15.【解答】解:(1)由旋转可得:AC=A'C=2,∵∠ACB=90°,AB=,AC=2,∴BC=,∵∠ACB=90°,m∥AC,∴∠A'BC=90°,∴cos∠A'CB==,∴∠A'CB=30°,∴∠ACA'=60°;(2)∵M为A'B'的中点,∴∠A'CM=∠MA'C,由旋转可得,∠MA'C=∠A,∴∠A=∠A'CM,∴tan∠PCB=tan∠A=,∴PB=BC=,∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°,∴∠BQC=∠BCP=∠A,∴tan∠BQC=tan∠A=,∴BQ=BC×=2,∴PQ=PB+BQ=;(3)∵S四边形P A'B′Q=S△PCQ﹣S△A'CB'=S△PCQ﹣,∴S四边形P A'B′Q最小,即S△PCQ最小,∴S△PCQ=PQ×BC=PQ,法一:(几何法)取PQ的中点G,∵∠PCQ=90°,∴CG=PQ,即PQ=2CG,当CG最小时,PQ最小,∴CG⊥PQ,即CG与CB重合时,CG最小,∴CG min=,PQ min=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣;法二(代数法)设PB=x,BQ=y,由射影定理得:xy=3,∴当PQ最小时,x+y最小,∴(x+y)2=x2+2xy+y2=x2+6+y2≥2xy+6=12,当x=y=时,“=”成立,∴PQ=+=2,∴S△PCQ的最小值=3,S四边形P A'B′Q=3﹣.16.【解答】解:(1)结论:△PMN是等边三角形.理由:如图1中,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∵AD=AE,∴BD=EC,∵PB=PC,CN=ND,BM=EM,∴PN∥BD,PM∥EC,PN=BD,PM=EC,∴PM=PN,∠NPC=∠ABC=60°,∠MPB=∠ACB=60°,∴∠MPN=60°,∴△PMN是等边三角形,故答案为等边三角形.(2)△PMN的形状不发生改变,仍为等边三角形,理由如下:如图2中,连接BD,CE.由旋转可得∠BAD=∠CAE,∵△ABC是等边三角形,∴AB=AC,∠ACB=∠ABC=60°又∵AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵M是BE的中点,P是BC的中点,∴PM是△BCE的中位线,∴PM=,且PM∥CE.同理可证PN=BD且PN∥BD,∴PM=PN,∠MPB=∠ECB,∠NPC=∠DBC,∴∠MPB+∠NPC=∠ECB+∠DBC=(∠ACB+∠ACE)+(∠ABC﹣∠ABD)=∠ACB+∠ABC=120°,∴∠MPN=60°,∴△PMN是等边三角形.(3)∵PM=EC,∴当EC最大时,等边△PMN的周长最大,∵EC≤AE+AC,∴EC≤8,∴PM≤4,∴PM的最大值为4,∴△PMN的周长的最大值为12.17.【解答】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(3)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠ACE=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.18.【解答】解:(1)由旋转变换的性质可知,∠CAE=90°,AC=AE,∴△ACE为等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC,故答案为:等腰直角;BC+CD=AC;(2)延长CO交⊙O于E,连接AE、BE、DE,则∠CDE=90°,∵点C为的中点,∴点E为的中点,∴EA=EB,∵AB为⊙O的直径,∴∠ADB=90°,由(1)得,DE=(AD+BD),由勾股定理得,CD2=CE2﹣DE2=AD2+BD2﹣(AD+BD)2=(AD﹣BD)2,∴CD=(BD﹣AD);(3)如图3,当点E在直线AC的左侧时,连接CQ、PC,∵CA=CB,点P为AB的中点,∴CP⊥AB,∵CA=CE,点Q为AE中点,∴CQ⊥AE,AQ=QE=AE=5,∴由勾股定理得,CQ==12,由(1)得,AQ+CQ=PQ,。
大连市数学中考25几何压轴题-阅读材料专项精选25题

大连市数学中考25几何压轴题-阅读材料专项精选25题1.阅读下面材料:小明遇到这样一个问题:如图1,在锐角△ABC中,AD、BE、CF分别为△ABC的高,求证:∠AFE=∠ACB.小明是这样思考问题的:如图2,以BC为直径作半⊙O,则点F、E在⊙O上,∠BFE+∠BCE=180°,所以∠AFE=∠ACB.请回答:若∠ABC=40°,则∠AEF的度数是.参考小明思考问题的方法,解决问题:如图3,在锐角△ABC中,AD、BE、CF分别为△ABC的高,求证:∠BDF=∠CDE.2.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE 的值.小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).请回答:BC+DE的值为.参考小明思考问题的方法,解决问题:如图3,已知▱ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数.3.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.小明发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).(1)请回答:∠ACE的度数为,AC的长为.(2)参考小明思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求AC的长.4.阅读下面材料:小明遇到这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB度数.小明发现,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决(如图2).请回答:图1中∠APB的度数等于,图2中∠PP′C的度数等于.参考小明思考问题的方法,解决问题:如图3,在平面直角坐标系xOy中,点A坐标为(-3,1),连接AO.如果点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x之间的函数表达式.5.(1)【问题发现】小明遇到这样一个问题:如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D作DF∥AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:;(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件不变),试猜想AD与DE之间的数量关系,并证明你的结论.(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.6.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC 中,D 为BC 中点,E 、F 分别为AB 、AC 上一点,且ED ⊥DF ,求证:BE+CF >EF . 小明发现,延长FD 到点H ,使DH=FD ,连结BH 、EH ,构造△BDH 和△EFH ,通过证明△BDH 与△CDF 全等、△EFH 为等腰三角形,利用△BEH 使问题得以解决(如图2). 参考小明思考问题的方法,解决问题:如图3,在矩形ABCD 中,O 为对角线AC 中点,将矩形ABCD 翻折,使点B 恰好与点O 重合,EF 为折痕,猜想EF 、AE 、FC 之间的数量关系?并证明你的猜想.7.阅读下面材料:小明遇到这样一个问题:如图1,在Rt △ABC 中,∠ACB=90°,∠A=60°,CD 平分∠ACB ,试判断BC 和AC 、AD 之间的数量关系.小明发现,利用轴对称做一个变化,在BC 上截取CA ′=CA ,连接DA ′,得到一对全等的三角形,从而将问题解决(如图2). 请回答:(1)在图2中,小明得到的全等三角形是△ ≌△ ; (2)BC 和AC 、AD 之间的数量关系是 . 参考小明思考问题的方法,解决问题:如图3,在四边形ABCD 中,AC 平分∠BAD ,BC=CD=10,AC=17,AD=9.求AB 的长.8.阅读下面材料:小明遇到这样一个问题:如图1,在边长为a (a>2)的正方形ABCD 各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ 的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED 的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE 是四个全等的等腰直角三角形(如图2)请回答: (1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;(2)求正方形MNPQ 的面积.参考小明思考问题的方法,解决问题:如图3,在等边△ABC 各边上分别截取AD=BE=CF,再分别过点D,E,F 作BC,AC,AB 的垂线,得到等边△RPQ,若33RPQ S △,则AD 的长为__________.9.阅读下面材料:小明遇到这样一个问题:如图1,△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°.若△BOC的面积为1,试求以AD、BC、OC+OD的长度为三边长的三角形的面积.小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO到E,使得OE=CO,连接BE,可证△OBE≌△OAD,从而得到的△BCE即是以AD、BC、OC+OD的长度为三边长的三角形(如图2).请你回答:图2中△BCE的面积等于______.请你尝试用平移、旋转、翻折的方法,解决下列问题:如图3,已知△ABC,分别以AB、AC、BC为边向外作正方形ABDE、AGFC、BCHI,连接EG、FH、ID.(1)在图3中利用图形变换画出并指明以EG、FH、ID的长度为三边长的一个三角形(保留画图痕迹);(2)若△ABC的面积为1,则以EG、FH、ID的长度为三边长的三角形的面积等于______.10.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6求BC的长.小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).请回答:(1)△BDE是_________三角形.(2)BC的长为__________.参考小聪思考问题的方法,解决问题:如图3,已知△ABC中,AB=AC, ∠A=20°, BD平分∠ABC,BD=2.3 ,BC=2,求AD的长.1.阅读下面材料:小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足关系时,仍有EF=BE+DF;(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.2.阅读下面文字,解决下列问题(1)问题背景宇昕同学遇到这样一个问题:如图1,在正方形ABCD中,点E,F分别为BC,CD上的点,且∠EAF=45°,求证:BE+DF=EF.宇昕是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADF绕点A顺时针旋转90°得到△ABG(如图2),此时GE即是DF+BE.请回答:在图2中,∠GAF的度数是、△AGE≌△.(2)拓展研究如图3,若E,F分别在四边形ABCD的边BC,CD上,∠B+∠D=180°,AB=AD,要使(1)中线段BE,EF,FD的等量关系仍然成立,则∠EAF与∠BAD应满足的关系是;(3)构造运用运用(1)(2)解答中所积累的经验和知识,完成下面问题:如图4,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,3,试求线段AD,BE的长.点E在AB上,且∠DCE=67.5°,DE⊥AB于点E,若AE=2。
大连中考25题解法[精华]
![大连中考25题解法[精华]](https://img.taocdn.com/s3/m/99b21bd109a1284ac850ad02de80d4d8d15a012d.png)
一.相似中常引辅助线方法1.过分点做垂线2.过分点做平行线条件:线段和差线段比(相等)十六.割补法1.截取相等线段2.过分点做垂线3.过分点做平行线条件:1.八字形2.有相等,互补的角3.出现一大一小两个△十七.倍长法1.中线倍长(有△中线)2中点所在线段倍长(见到一个中点)可连RT△直角顶点3。
过分点做平行线(相似)十八.面积法1连两分点把要求的线段分为两个△条件:求线段和差线段比十九.旋转中常引辅助线方法1.见到三个中点其中一个到另两个中点距离相等解法1:连接公共中点与其它中点所在的线段的两个端点构造出△的中位线,利用△全等,平行四边形,中位线可解答。
解法2.:取与公共中点相邻的一对非对应的边的中点。
和两个已知中点相连。
利用△全等,平行四边形,中位线可解答。
2.见到一个中点到两个直角△的直角顶点的距离相等,解法1:倍长中线法,证明等腰直角△,解法2:取直角△斜边中点和直角顶点相连,公共中点相连,构造出直角△斜边中线和△中位线。
利用△全等,平行四边形,相似,△中位线,直角△斜边中点性质可解答。
3.见到两边相等另两边中点解法取中点所在线段取中点所在线段两个端点连线的中点和已知两中点相连利用△中位线4.见到平行线段研究线段和差问题解法1:截长补短(四边形连接对角线交点做另一组平行线段利用梯形中位线=½(上底+下底))二十.旋转法条件1:有公共端点的两条相等线段条件:2:要研究的三条边三个角不在同一个三角形中解法:将有公共端点的相等的一个边所在的△绕着公共端点顺时针或逆时针旋转到另一条相等的边上得到两个全等或相似三角形二十一.截长补短法条件a±b=c截长或补短特殊角常做垂直二十二.备分问题1倍长法2加倍法3折半法4RT△30°60°45°作⊥构造RT△56三角形梯形中位线7平行或垂直8旋转9面积10割补11截长补短二十三.几何证明定式1角分线2中垂线3三角形中点(1个——倍长2个以上——中位线)4证明中点5取RT△斜边中点6与梯形中点有关腰中点底中点对角线中点7菱形梯形矩形正方形。
中考数学大连2018年第25题

中考数学大连2018年第25题
大连2018年中考数学第25题,是一个纯几何综合题,是由全等和相似两部分知识点,在一个完整的问题里,加以综合的。
我们先来看看他的试题,由于题目较长,内容也比较复杂,我把题目分解成三部分,加以分别说明。
先看已知条件部分:
分析已知条件的过程,就是完全理解小明的意思,他到底传达了
什么解题方法。
第一个意思:条件∠BAC=2∠BCD很重要,是两种方法的共同起点。
第一个方法做大角的平分线.
第二个方法是做小角的2倍角.
其结果都是转化成两个等角。
第一个方法,会最终得到两个全等三角形,从而证明结论。
第二个方法,对证明两个底角相等,带来了方便,从而用等角对等边得到结论。
我们来看一下第一个问题:
这个问题,只是我们如上分析的文字再现,它的设置,只是为了帮助我们加深、详细领会小明的意图。
接下来,我们再看看压轴问题:
我们看出,压轴条件的叙述,只是位置改变了,2倍角的条件还有,我们就按如上的方法。
第一个问题太简单了,我们姑且放下不理。
先用解法2,作出如下辅助线,再用解法1,说明两个三角形全等,两个三角形相似就可以了。
具体点说,就是延长AC至点 K,使得:
∠KBC=∠ABC,显然,
△KBC≌△DBC,以及
△ABK∽△DEF,我们将得到,
BD= BK,DE:BK= DF:AB,结论得出就自然而然了。
2011年大连市中考压轴25题
1、已知,E 点在△ABC 内,∠ABC=∠EBD α=,∠ACB=∠EDB=600,∠AEB=1500,∠BEC=900。
(1)当α=60O时,(如图1)①判断△ABC 的形状,并说明理由;②求证:BD=√3AE. (2)当α=90O 时,(如图2)求BD :AE 的值。
图2 AEABCEDBDC2、已知,△ABC 是等边三角形,CD ⊥AC ,AE ∥CD ,且EA=ED ,BE 与AD 交于点F , (1)若∠CAD=1/2∠DAE ,如图1,试判断BF 与FE 的数量关系,并说明理由; (2)若∠CAD=2∠DAE ,如图2,求BF :FE 的值。
图1 图2AB CDEFABCDEF3.如图11,在△OAB 和△OCD 中,∠A < 90°,OB = kOD (k > 1),∠AOB =∠COD ,∠OAB 与∠OCD 互补.试探索线段AB 与CD 的数量关系,并证明你的结论.说明:如果你反复探索没有解决问题,可以选取⑴⑵中的一个条件,其中⑴满分为7分;⑵满分为3分. ⑴k = 1(如图12);⑵点C 在OA 上,点D 与点B 重合(如图13).图 13图 12图 11B (D )C AODB CAO O ACBD4、如图,在△ABC中,AB=kAC,∠BAC+∠DAE=1800,AD=kAE,探索△AEB与△ACD面积之间的数量关系,并说明理由。
EADB C5、如图,在四边形ABCD 中,AD ∥BC ,∠BAC=∠D,AB=kBC ,点E 、F 分别在BC 、CD 上,且∠AEF=∠ACD ,探索线段AE 与EF 的数量关系,并证明你的结论。
FEDCB A6、在△ABC 中,点D 、M 、N 分别在边AB 、CA 、CB 上, (1)若D 为AB 中点,且∠MDN=∠CAB+∠CBA.①如图1,当BC=AC 时,探索MD 、ND 的数量关系,并证明②如图2,当BC=kAC 时,探索MD 、ND 的数量关系(用含k 的式子表示)图1 图2 图3⑵如图3,点D ,M ,N 分别在AB ,CA ,CB 的延长线上,BC=kAC ,AB=mBD ,且∠MDN=∠ACB ,猜想MD ,ND 的数量关系:(直接写出答案,用含k,m 的式子表示)NNNMMMDDDCCCBBBAA A。
【试题解析】——2021年大连市中考25题解析

【试题解析】——2021年大连市中考25题解析TODAY'S NEWS试题解析2021年大连市中考25题
作者简介
杨微,毕业于东北师范大学,数学与统计学院,大连市第76中学数学教师。
连续五年初三备考教师,数学学科名优教师、骨干教师,优秀共产党员。
《等式的性质》获得全国绿色课堂杯“一等奖”;《正多边形和圆》荣获辽宁省优质课一等奖;《分式方程》《提公因式法》两次荣获大连市优质课一等奖。
多次受邀前去沈阳、长春、吉林市送教和培训。
在省级和国家级刊物上发表多篇文章。
微说试题——2021年大连市中考25题
因为篇幅有限,这里面只讲几个思路简单的解法,强烈建议初三的孩子把最近三年的中考、市模压轴题反复刷,精华就在其中
仙女都读到这里,点个赞再走~
下期——阿氏圆模型。
大连中考数学压轴题训练

25.如图1,是线段上的一点,在的同侧作和,使,,,连接,点分别是的中点,顺次连接.(1)猜想四边形的形状,直接回答....,不必说明理由;,不必说明理由;(2)当点在线段的上方时,如图2,在的外部作和,其它条件不变,(1)中结论还成立吗?说明理由;)中结论还成立吗?说明理由; (3)如果(2)中,,其它条件不变,先补全图3,再判断四边形的形状,并说明理由.的形状,并说明理由.26.(2010辽宁锦州,26,14分)如图14,抛物线与x 轴交于A (x 1,0),B (x 2,0)两点,且x 1>x 2,与y 轴交于点C (0,4),其中x 1,x 2是方程x 2-2x -8=0的两个根. (1)求这条抛物线的解析式;求这条抛物线的解析式; (2)点P 是线段AB 上的动点,过点P 作PE ∥AC ,交BC 于点E ,连接CP ,当△CPE 的面积最大时,求点P 的坐标;的坐标;(3)探究:若点Q 是抛物线对称轴上的点,是否存在这样的点Q ,使△QBC 成为等腰三角形,若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由.26、(2011•鞍山)如图,在平面直角坐标系中,O 是坐标原点,平行四边形的顶点C 的坐标为(8,8),顶点A 的坐标为(﹣6,0),边AB 在x 轴上,点E 为线段AD 的中点,点F 在线段DC 上,且横坐标为3,直线EF 与y 轴交于点G ,有一动点P 以每秒1个单位长度的速度,从点A 沿折线A ﹣B ﹣C ﹣F 运动,当点P 到达点F 时停止运动,设点P 运动时间为t 秒.秒.(1)求直线EF 的表达式及点G 的坐标;的坐标;(2)点P 在运动的过程中,设△EFP 的面积为S (P 不与F 重合),试求S 与t 的函数关系式;式;(3)在运动的过程中,是否存在点P ,使得△PGF 为直角三角形,若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.P AB AB APC △BPD △PC PA =PD PB =APC BPD Ð=ÐCD E F G H ,,,AC AB BD CD ,,,E F G H ,,,EFGH P AB APB △APC △BPD △90APC BPD Ð=Ð=°EFGH xy EC B A o P HD G BP F AE C 图1CHD G BP F E A图2 P BA 图3第25题图题图2424.已知,△.已知,△.已知,△ABC ABC 为等边三角形,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作菱形ADEF ADEF,使∠,使∠,使∠DAF=60DAF=60DAF=60°,连接°,连接CF CF。
2023年辽宁省大连市中考数学真题(解析版)

大连市2023年初中毕业升学考试数学注意事项:1.请在答题卡上作答,在试卷上作答无效.2.本试卷共五大题,26小题,满分150分.考试时间为120分钟.参考公式:抛物线20y ax bx c a的顶点为24,24b ac ba a.一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有1个选项正确)1.-6的绝对值是()A.-6B.6C.-16 D.16【答案】B【解析】【分析】在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.【详解】负数的绝对值等于它的相反数,所以-6的绝对值是6.故选:B.2.如图所示的几何体中,主视图是()A.B.C.D.【分析】根据主视图是从正面看得到的图形解答即可.【详解】解:从正面看看到的是,故选:B .【点睛】本题考查了三视图的知识,属于简单题,熟知主视图是从物体的正面看得到的视图是解题的关键.3.如图,直线,45,20AB CD ABE D ∥,则E 的度数为()A.20B.25C.30D.35【答案】B【解析】【分析】先根据平行线的性质可得45ABE BCD ,再根据三角形的外角性质即可得.【详解】解:,45AB CD ABE ∵∥,45ABE BCD ,20D ∵,25BCD D E ,故选:B .【点睛】本题考查了平行线的性质、三角形的外角性质,熟练掌握平行线的性质是解题关键.4.某种离心机的最大离心力为17000g .数据17000g 用科学计数法表示为()A.40.1710 B.51.710 C.41.710 D.31710【分析】用科学记数法表示较大的数时,一般形式为10n a ,其中1||10a ,n 为整数.【详解】解:417000 1.710 .故选:C .【点睛】本题考查了科学记数法,科学记数法的表示形式为10n a 的形式,其中1||10a ,n 为整数.确定n 的值时,要看把原来的数,变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值10 时,n 是正数;当原数的绝对值1 时,n 是负数,确定a 与n 的值是解题的关键.5.下列计算正确的是()A.0B.C.D. 26【答案】D【解析】【分析】根据零指数幂,二次根式的加法以及二次根式的性质,二次根式的混合运算进行计算即可求解.【详解】解:A. 1 ,故该选项不正确,不符合题意;B. ,故该选项不正确,不符合题意;C.D.26 ,故该选项正确,符合题意;故选:D .【点睛】本题考查了零指数幂,二次根式的加法以及二次根式的性质,二次根式的混合运算,熟练掌握二次根式的运算法则是解题的关键.6.将方程13311x x x去分母,两边同乘 1x 后的式子为()A.1331x x B. 1313x x C.133x xD. 1313x x 【答案】B【解析】【分析】根据解分式方程的去分母的方法即可得.【详解】解:13311x x x,两边同乘 1x 去分母,得 1313x x ,故选:B .【点睛】本题考查了解分式方程,熟练掌握去分母的方法是解题关键.7.已知蓄电池两端电压U 为定值,电流I 与R 成反比例函数关系.当4A I 时,10ΩR ,则当5A I 时,R 的值为()A.6ΩB.8ΩC.10ΩD.12Ω【答案】B【解析】【分析】利用待定系数法求出U 的值,由此即可得.【详解】解:由题意得:UR I ,∵当4A I 时,10ΩR ,104U,解得40U ,40R I ,则当5A I 时, Ω4085R ,故选:B .【点睛】本题考查了反比例函数,熟练掌握待定系数法是解题关键.8.圆心角为90 ,半径为3的扇形弧长为()A.2B.3C.32 D.12π【答案】C【解析】【分析】根据弧长公式180n rl (弧长为l ,圆心角度数为n ,圆的半径为r ),由此计算即可.【详解】解:该扇形的弧长90331801802n r l,故选:C .【点睛】本题考查了扇形的弧长计算公式180n r l(弧长为l ,圆心角度数为n ,圆的半径为r ),正确记忆弧长公式是解答此题的关键.9.已知抛物线221y x x ,则当03x 时,函数的最大值为()A.2B.1C.0D.2【答案】D【解析】【分析】把抛物线221y x x 化为顶点式,得到对称轴为1x ,当1x 时,函数的最小值为2 ,再分别求出0x 和3x 时的函数值,即可得到答案.【详解】解:∵ 222112y x x x ,∴对称轴为1x ,当1x 时,函数的最小值为2 ,当0x 时,2211y x x ,当3x 时,232312y ,∴当03x 时,函数的最大值为2,故选:D【点睛】此题考查了二次函数的最值,熟练掌握二次函数的性质是解题的关键.10.某小学开展课后服务,其中在体育类活动中开设了四种运动项目:乒乓球、排球、篮球、足球.为了解学生最喜欢哪一种运动项目,随机选取100名学生进行问卷调查(每位学生仅选一种),并将调查结果绘制成如下的扇形统计图.下列说法错误的是()A.本次调查的样本容量为100B.最喜欢篮球的人数占被调查人数的30%C.最喜欢足球的学生为40人D.“排球”对应扇形的圆心角为10【答案】D【解析】【分析】A.随机选取100名学生进行问卷调查,数量100就是样本容量,据此解答;B.由扇形统计图中喜欢篮球的占比解答;C.用总人数乘以40%即可解答;D.先用1减去足球、篮球、乒乓球的占比得到排球的占比,再利用360 乘以排球的占比即可解答.【详解】解:A.随机选取100名学生进行问卷调查,数量100就是样本容量,故A正确;B.由统计图可知,最喜欢篮球的人数占被调查人数的30%,故B正确;(人),故C正确;C.最喜欢足球的学生为10040%40,故D错误D.“排球”对应扇形的圆心角为360(140%30%20%)36010%36故选:D.【点睛】本题考查扇形统计图及其相关计算、总体、个体、样本容量、样本、用样本估计总体等知识,是基础考点,掌握相关知识是解题关键.二、填空题(本题共6小题,每小题3分,共18分)的解集为_______________.11.93x【答案】3x【解析】【分析】根据不等式的性质解不等式即可求解.,【详解】解:93x解得:3x ,故答案为:3x .【点睛】本题考查了求不等式的解集,熟练掌握不等式的性质是解题的关键.12.一个袋子中装有两个标号为“1”“2”的球.从中任意摸出一个球,记下标号后放回并再次摸出一个球,记下标号后放回.则两次标号之和为3的概率为_______________.【答案】12【解析】【分析】先画出树状图,从而可得两次摸球的所有等可能的结果,再找出两次标号之和为3的结果,然后利用概率公式求解即可得.【详解】解:由题意,画出树状图如下:由图可知,两次摸球的所有等可能的结果共有4种,其中,两次标号之和为3的结果有2种,则两次标号之和为3的概率为2142P,故答案为:12.【点睛】本题考查了利用列举法求概率,熟练掌握列举法是解题关键.13.如图,在菱形ABCD 中,AC BD 、为菱形的对角线,60,10DBC BD ,点F 为BC 中点,则EF 的长为_______________.【答案】5【解析】【分析】根据题意得出BDC 是等边三角形,进而得出10DC BD ,根据中位线的性质即可求解.【详解】解:∵在菱形ABCD 中,AC BD 、为菱形的对角线,∴AB AD DC BC ,AC BD ,∵60DBC ,∴BDC 是等边三角形,∵10BD ,∴10DC BD ,∵E 是BD 的中点,点F 为BC 中点,∴152EF DC ,故答案为:5.【点睛】本题考查了菱形的性质,等边三角形的性质与判定,中位线的性质,熟练掌握以上知识是解题的关键.14.如图,在数轴上,1OB ,过O 作直线l OB 于点O ,在直线l 上截取2OA ,且A 在OC 上方.连接AB ,以点B 为圆心,AB 为半径作弧交直线OB 于点C ,则C 点的横坐标为_______________.【答案】1 1【解析】【分析】根据勾股定理求得AB ,根据题意可得BC AB,进而即可求解.【详解】解:∵l OB ,1OB ,2OA ,在Rt AOB △中,AB,∴BC AB ,∴1OC OB BC ,O 为原点,OC 为正方向,则C 点的横坐标为1 ;故答案为:1 .【点睛】本题考查了勾股定理与无理数,实数与数轴,熟练掌握勾股定理是解题的关键.15.我国的《九章算术》中记载道:“今有共买物,人出八,盈三;人出七,不足四.问有几人.”大意是:今有人合伙购物,每人出8元钱,会多3钱;每人出7元钱,又差4钱,问人数有多少.设有x 人,则可列方程为:_______________.【答案】8374x x 【解析】【分析】设有x 人,每人出8元钱,会多3钱,则物品的钱数为: 83x 元,每人出7元钱,又差4钱,则物品的钱数为: 74 x 元,根据题意列出一元一次方程即可求解.【详解】设有x 人,每人出8元钱,会多3钱,则物品的钱数为: 83x 元,每人出7元钱,又差4钱,则物品的钱数为: 74 x 元,则可列方程为:8374x x 故答案为:8374x x .【点睛】本题考查了一元一次方程的应用,根据题意列出一元一次方程是解题的关键.16.如图,在正方形ABCD 中,3AB ,延长BC 至E ,使2CE ,连接AE ,CF 平分DCE 交AE 于F ,连接DF ,则DF 的长为_______________.【答案】4【解析】【分析】如图,过F 作FM BE 于M ,FN CD 于N ,由CF 平分DCE ,可知45FCM FCN ,可得四边形CMFN 是正方形,FM AB ∥,设FM CM NF CN a ,则2ME a ,证明EFM EAB ∽,则FM ME AB BE ,即2332a a ,解得34a ,94DN CD CN ,由勾股定理得DF 【详解】解:如图,过F 作FM BE 于M ,FN CD 于N ,则四边形CMFN 是矩形,FM AB ∥,∵CF 平分DCE ,∴45FCM FCN ,∴ CM FM ,∴四边形CMFN 是正方形,设FM CM NF CN a ,则2ME a ,∵FM AB ∥,∴EFM EAB ∽,∴FM ME AB BE ,即2332a a ,解得34a ,∴94DN CD CN ,由勾股定理得4DF ,故答案为:4.【点睛】本题考查了正方形的判定与性质,勾股定理,相似三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.三、解答题(本题共4小题,其中17题9分,18、19、20题各10分,共39分)17.计算:21123926a a a a.【答案】23a 【解析】【分析】先计算括号内的加法,再计算除法即可.【详解】解:21123926a a a a312333323a a a a a a a223323a a a a a 232332a a a a a 23a【点睛】此题考查了分式的混合运算,熟练掌握分式的运算法则和顺序是解题的关键.18.某服装店的某件衣服最近销售火爆.现有A B 、两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:Ⅰ.A供应商供应材料的纯度(单位:%)如下:A72737475767879频数1153311Ⅱ.B供应商供应材料的纯度(单位:%)如下:727572757877737576777178797275Ⅲ.A B、两供应商供应材料纯度的平均数、中位数、众数和方差如下:平均数中位数众数方差A757574 3.07B a75b c根据以上信息,回答下列问题:(1)表格中的a_______________,b _______________,c _______________;(2)你认为服装店应选择哪个供应商供应服装?为什么?【答案】(1)75,75,6(2)服装店应选择A供应商供应服装.理由见解析.【解析】【分析】(1)根据平均数、众数、方差的计算公式分别进行解答即可;(2)根据方差的定义,方差越小数据越稳定即可得出答案.【小问1详解】解:B供应商供应材料纯度的平均数为1(72375478277273767179)75 15,故75a ,75出现的次数最多,故众数75b ,方差22222222 1[3(7275)4(7575)2(7875)2(7775)(7375)(7675)(7175)(7975)]6 15c 故答案为:75,75,6【小问2详解】解:服装店应选择A供应商供应服装.理由如下:由于A、B平均值一样,B的方差比A的大,故A更稳定,所以选A供应商供应服装.【点睛】本题考查了方差、平均数、中位数、众数,熟悉相关的统计量的计算公式和意义是解答此题的关键.19.如图,在ABC 和ADE V 中,延长BC 交DE 于F ,,BC DE AC AE ,180ACF AED .求证:AB AD .【答案】证明见解析【解析】【分析】由180ACF AED ,180ACF ACB ,可得ACB AED ,证明SAS ABC ADE △≌△,进而结论得证.【详解】证明:∵180ACF AED ,180ACF ACB ,∴ACB AED ,∵BC DE ,ACB AED ,AC AE ,∴ SAS ABC ADE △≌△,∴AB AD .【点睛】本题考查了全等三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.20.为了让学生养成热爱图书的习惯,某学校抽出一部分资金用于购买书籍.已知2020年该学校用于购买图书的费用为5000元,2022年用于购买图书的费用是7200元,求20202022 年买书资金的平均增长率.【答案】20%【解析】【分析】设20202022 年买书资金的平均增长率为x ,根据2022年买书资金 2020年买书资金 21x 建立方程,解方程即可得.【详解】解:设20202022 年买书资金的平均增长率为x ,由题意得: 2500017200x ,解得0.220%x 或 2.20x (不符合题意,舍去),答:20202022 年买书资金的平均增长率为20%.【点睛】本题考查了一元二次方程的应用,找准等量关系,正确建立方程是解题关键.四、解答题(本题共3小题,其中21题9分,22、23题各10分,共29分)21.如图所示是消防员攀爬云梯到小明家的场景.已知,,AE BE BC BE CD BE ∥,10.4m, 1.26m AC BC ,点A 关于点C 的仰角为70 ,则楼AE 的高度为多少m ?(结果保留整数.参考数据:sin700.94,cos700.34,tan70 2.75 )【答案】楼AE 的高度为11m【解析】【分析】延长CD 交AE 于点F ,依题意可得 1.26m EF BC ,在Rt ACF ,根据sin AF AC ACF ,求得AF ,进而根据AE AF EF ,即可求解.【详解】解:如图所示,延长CD 交AE 于点F ,∵,,AE BE BC BE CD BE ∥,∴ 1.26mEF BC 在Rt ACF 中,70ACF ,10.4m AC ,∵sin AF ACF AC,∴sin 10.4sin 7010.40.949.776mAF AC ACF ∴9.776 1.2611m AE AF EF ,答:楼AE 的高度为11m .【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.22.为了增强学生身体素质,学校要求男女同学练习跑步.开始时男生跑了50m ,女生跑了80m ,然后男生女生都开始匀速跑步.已知男生的跑步速度为4.5m /s ,当到达终点时男、女均停止跑步,男生从开始匀速跑步到停止跑步共用时120s .已知x 轴表示从开始匀速跑步到停止跑步的时间,y 轴代表跑过的路程,则:(1)男女跑步的总路程为_______________.(2)当男、女相遇时,求此时男、女同学距离终点的距离.【答案】(1)1000m(2)315m【解析】【分析】(1)根据男女同学跑步的路程相等,求得男生跑步的路程,乘以2,即可求解(2)根据题意男生从开始匀速跑步到停止跑步的直线解析式为:50 4.5y x ,求得女生的速度,进而得出解析式为 3.580y x ,联立求得30s x ,进而即可求解.【小问1详解】解:∵开始时男生跑了50m ,男生的跑步速度为4.5m /s ,从开始匀速跑步到停止跑步共用时100s .∴男生跑步的路程为50 4.5100500 m ,∴男女跑步的总路程为50021000m ,故答案为:1000m .【小问2详解】解:男生从开始匀速跑步到停止跑步的直线解析式为:50 4.5y x ,设女生从开始匀速跑步到停止跑步的直线解析式为:80y kx ,依题意,女生匀速跑了50080420 m ,用了120s ,则速度为420120 3.5 m/s ,∴ 3.580y x ,联立50 4.53.580y xy x解得:30x 将30x 代入50 4.5y x解得:185y ,∴此时男、女同学距离终点的距离为500185315 m .【点睛】本题考查了一次函数的应用,根据题意求得函数解析式是解题的关键.23.如图1,在O 中,AB 为O 的直径,点C 为O 上一点,AD 为CAB 的平分线交O 于点D ,连接OD 交BC 于点E .(1)求BED 的度数;(2)如图2,过点A 作O 的切线交BC 延长线于点F ,过点D 作DG AF 交AB 于点G .若4AD DE ,求DG 的长.【答案】(1)90 ;(2).【解析】【分析】(1)根据圆周角定理证明两直线平行,再利用平行线的性质证明角度相等即可;(2)由勾股定理找到边的关系,求出线段长,再利用等面积法求解即可.【小问1详解】∵AB 是O 的直径,∴90ACB ,∵AD 平分CAB ,∴12BAD BAC ,即2BAC BAD ,∵OA OD ,∴BAD ODA ,∴2BOD BAD ODA BAD ,∴BOD BAC ,∴OD AC ,∴90OEB ACB ,∴90BED ,【小问2详解】如图,连接BD ,设OA OB OD r ,则4OE r ,228AC OE r ,2AB r ,∵AB 是O 的直径,∴90ADB ,在Rt ADB 中,有勾股定理得:222BD AB AD 由(1)得:90BED ,∴90BED BEO ,由勾股定理得:222BE OB OE ,222BE BD DE ,∴22222222BD AB AD BE DE OB OE DE ,∴ 22222244r r r ,整理得:22350r r ,解得:7r 或5r (舍去),∴214AB r ,∴BD ,∵AF 是O 的切线,∴AF AB ,∵DG AF ,∴DG AB ,∴11··22ABD S AD BD AB DG,∴·23521414AD BD DG AB 【点睛】此题考查了圆周角定理和勾股定理,三角形中位线定理,切线的性质,解一元二次方程,熟练掌握圆周角定理和勾股定理是解题的关键.五、解答题(本题共3小题,其中24、25题各11分,26题12分,共34分)24.如图1,在平面直角坐标系xOy 中,直线y x 与直线BC 相交于点A , ,0P t 为线段OB 上一动点(不与点B 重合),过点P 作PD x 轴交直线BC 于点D .OAB 与DPB 的重叠面积为S .S 关于t 的函数图象如图2所示.(1)OB 的长为_______________;OAB 的面积为_______________.(2)求S 关于t 的函数解析式,并直接写出自变量t 的取值范围.【答案】(1)4,83(2)2218402331424443t t S t t t 【解析】【分析】(1)根据函数图象即可求解.(2)根据(1)的结论,分403t ,443t ,根据OAB 与DPB 的重叠面积为S ,分别求解即可.【小问1详解】解:当0 t 时,P 点与O 重合,此时83ABO S S ,当4t 时,0S ,即P 点与B 点重合,∴4OB ,则 4,0B,故答案为:4,83.【小问2详解】∵A 在y x 上,则45OAB 设 ,A a a ,∴1184223AOB S OB a a ∴43a ,则44,33A 当403t 时,如图所示,设DP 交OA 于点E ,∵45OAB ,DP OB ,则EP OP t∴28132S t 当443t 时,如图所示,∵ 4,0B ,44,33A 设直线AB 的解析式为y kx b ,∴404433k b k b 解得:212b k,∴直线AB 的解析式为122y x ,当0x 时,2y ,则 0,2C ,∴2OC ,∵21tan 42DP OC CBO PD OB ,∵4BP t ,则122DP t,∴12DPB S S DP BP 222111144242244t t t t ,综上所述:2218402331424443t t S t t t.【点睛】本题考查了正切的定义,动点问题的函数图象,一次函数与坐标轴交点问题,从函数图象获取信息是解题的关键.25.综合与实践问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.已知,90AB AC A ,点E 为AC 上一动点,将ABE 以BE 为对称轴翻折.同学们经过思考后进行如下探究:独立思考:小明:“当点D 落在BC 上时,2EDC ACB .”小红:“若点E 为AC 中点,给出AC 与DC 的长,就可求出BE 的长.”实践探究:奋进小组的同学们经过探究后提出问题1,请你回答:问题1:在等腰ABC 中,,90,AB AC A BDE △由ABE 翻折得到.(1)如图1,当点D 落在BC 上时,求证:2EDC ACB ;(2)如图2,若点E 为AC 中点,43AC CD ,,求BE 的长.问题解决:小明经过探究发现:若将问题1中的等腰三角形换成90A 的等腰三角形,可以将问题进一步拓展.问题2:如图3,在等腰ABC 中,90,4,2A AB AC BD D ABD .若1CD ,则求BC 的长.【答案】(1)见解析;(2)32 ;问题2:BC 【解析】【分析】(1)根据等边对等角可得ABC C ,根据折叠以及三角形内角和定理,可得BDE A 1802C ,根据邻补角互补可得180EDC BDE ,即可得证;(2)连接AD ,交BE 于点F ,则EF 是ADC △的中位线,勾股定理求得,AF BF ,根据BE BF EF 即可求解;问题2:连接AD ,过点B 作BM AD 于点M ,过点C 作CG BM 于点G ,根据已知条件可得BM CD ∥,则四边形CGMD 是矩形,勾股定理求得AD ,根据三线合一得出,MD CG ,根据勾股定理求得BC 的长,即可求解.【详解】(1)∵等腰ABC 中,,90,AB AC A BDE △由ABE 翻折得到∴ABC C ,BDE A 1802C ,∵180EDC BDE ,∴2EDC ACB ;(2)如图所示,连接AD ,交BE 于点F ,∵折叠,∴EA ED ,AF FD ,122AE AC ,AD BE ,∵E 是AC 的中点,∴EA EC ,∴1322EF CD ,在Rt AEF 中,2AF ,在Rt ABF 中,2BF ,∴3572BE BF EF ;问题2:如图所示,连接AD ,过点B 作BM AD 于点M ,过点C 作CG BM 于点G ,∵AB BD ,∴AM MD ,12ABM DBM ABD ,∵2BDC ABD ,∴BDC DBM ,∴BM CD ∥,∴CD AD ,又CG BM ,∴四边形CGMD 是矩形,则CD GM ,在Rt ACD △中,1CD ,4 AD ,AD,∴2AM MD ,2CG MD在Rt BDM 中,72BM ,∴75122BG BM GM BM CD ,在Rt BCG 中,BC .【点睛】本题考查了等腰三角形的性质,折叠的性质,勾股定理,矩形的性质与判定,熟练掌握以上知识是解题的关键.26.如图,在平面直角坐标系中,抛物线21:C y x 上有两点A B 、,其中点A 的横坐标为2 ,点B 的横坐标为1,抛物线22:C y x bx c 过点A B 、.过A 作AC x ∥轴交抛物线1C 另一点为点C .以12AC AC 、长为边向上构造矩形ACDE .(1)求抛物线2C 的解析式;(2)将矩形ACDE 向左平移m 个单位,向下平移n 个单位得到矩形A C D E ,点C 的对应点C 落在抛物线1C 上.①求n 关于m 的函数关系式,并直接写出自变量m 的取值范围;②直线A E 交抛物线1C 于点P ,交抛物线2C 于点Q .当点E 为线段PQ 的中点时,求m 的值;③抛物线2C 与边E D A C 、分别相交于点M N 、,点M N 、在抛物线2C 的对称轴同侧,当2103MN 时,求点C 的坐标.【答案】(1)224y x x (2)① 2404n m m m ;②5172m ;③5959,636C 或5959,636C 【解析】【分析】(1)根据题意得出点 2,4A , 1,1B ,待定系数法求解析式即可求解;(2)①根据平移的性质得出 2,4C m n ,根据点C 的对应点C 落在抛物线1C 上,可得 224m n ,进而即可求解;②根据题意得出 222,442,24,P m m m Q m m m ,求得中点坐标,根据题意即可求解;③连接MN ,过点N 作NG E D 于点G ,勾股定理求得23MG ,设N 点的坐标为 2,24a a a ,则22,263M a a a,将22,263M a a a代入224y x x ,求得56a ,求得559,636N,进而根据C 落在抛物线1C 上,将5936y 代入21:C y x ,即可求解.【小问1详解】解:依题意,点A 的横坐标为2 ,点B 的横坐标为1,代入抛物线21:C y x∴当2x 时, 224y ,则 2,4A ,当1x 时,1y ,则 1,1B ,将点 2,4A , 1,1B ,代入抛物线22:C y x bx c ,∴ 222411b c b c 解得:24b c ∴抛物线2C 的解析式为224y x x ;【小问2详解】①解:∵AC x ∥轴交抛物线21:C y x 另一点为点C ,当4y 时,2x ,∴ 2,4C ,∵矩形ACDE 向左平移m 个单位,向下平移n 个单位得到矩形A C D E ,点C 的对应点C 落在抛物线1C 上∴ 2,4C m n , 224m n整理得24n m m∵0,0m n ∴04m ∴ 2404n m m m ;②如图所示,∵ 2,4A ,2,4C ∴4AC ,∵122AE AC ∴ 2,6E ,由①可得 22,44A m m m ,22,46E m m m ∴P ,Q 的横坐标为2m ,分别代入21:C y x ,224y x x ∴ 222,442,24,P m m m Q m m m ,∴22442442m m m m m ∴PQ 的中点坐标为2,4m m ∵点E 为线段PQ 的中点,∴2464m m m 解得:5172m 或5172m (大于4,舍去)③如图所示,连接MN ,过点N 作NG E D 于点G ,则2NG ,∵2103MN ∴22222102233MG MN MG,设N 点的坐标为 2,24a a a ,则22,263M a a a,将22,263M a a a代入224y x x ,2222242633a a a a,解得:56a ,当56a ,22555924246636a a ∴559,636N,将5936y 代入21:C y x 解得:125959,66x x,∴5959,636C 或5959,636C.【点睛】本题考查了二次函数综合运用,矩形的性质,平移的性质,熟练掌握二次函数的性质是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大连市数学中考25几何压轴题-阅读材料专项精选25题1.阅读下面材料:
小明遇到这样一个问题:
如图1,在锐角△ABC中,AD、BE、CF分别为△ABC的高,求证:∠AFE=∠ACB.
小明是这样思考问题的:如图2,以BC为直径作半⊙O,则点F、E在⊙O上,
∠BFE+∠BCE=180°,所以∠AFE=∠ACB.
请回答:若∠ABC=40°,则∠AEF的度数
是.
参考小明思考问题的方法,解决问题:
如图3,在锐角△ABC中,AD、BE、CF分别为△ABC
的高,求证:∠BDF=∠CDE.
2.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE 的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
请回答:BC+DE的值为.
参考小明思考问题的方法,解决问题:
如图3,已知▱ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,
求∠AGF的度数.
3.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.小明发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).
(1)请回答:∠ACE的度数为,
AC的长为.
(2)参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,∠BAC=90°,
∠CAD=30°,∠ADC=75°,AC与BD交
于点E,AE=2,BE=2ED,求AC的长.4.阅读下面材料:
小明遇到这样一个问题:如图1,在等边三角形ABC内有一点P,且PA=3,PB=4,PC=5,求∠APB度数.
小明发现,利用旋转和全等的知识构造△AP′C,连接PP′,得到两个特殊的三角形,从而将问题解决(如图2).
请回答:图1中∠APB的度数等于,图2中∠
PP′C的度数等于.
参考小明思考问题的方法,解决问题:
如图3,在平面直角坐标系xOy中,点A坐标为
(-3,1),连接AO.如果点B是x轴上的一动
点,以AB为边作等边三角形ABC.当C(x,y)
在第一象限内时,求y与x之间的函数表达式.5.(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.小明发现,过点D作DF∥AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系:;
(2)【类比探究】如图2,当点D是线段BC上(除B,
C外)任意一点时(其它条件不变),试猜想AD与DE之
间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足
CD=BC(其它条件不变)时,请直接写出△ABC与△ADE的面积之比.
6.阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,求证:BE+CF>EF.小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、AE、FC之间的数量关系?并证明你的猜想.
7.阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).请回答:
(1)在图2中,小明得到的全等三角形是△≌△;
(2)BC和AC、AD之间的数量关系是.
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
8.阅读下面材料:
小明遇到这样一个问题:如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方
形(无缝隙,不重叠),则这个新的正方形的边长为
__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,
再分别过点D,E,F 作BC,AC,AB 的垂线,得到等边△RPQ,若3
3
RPQ
S △,则AD 的长为__________.
9.阅读下面材料:
小明遇到这样一个问题:如图1,△ABO 和△CDO 均为等腰直角三角形,∠AOB=∠COD=90°.若△BOC 的面积为1,试求以AD 、BC 、OC+OD 的长度为三边长的三角形的面积.
小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他利用图形变换解决了这个问题,其解题思路是延长CO 到E ,使得OE=CO ,连接BE ,可证△OBE ≌△OAD ,从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形(如图2). 请你回答:图2中△BCE 的面积等于______.
请你尝试用平移、旋转、翻折的方法,解决下列问题:
如图3,已知△ABC ,分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI ,连接EG 、FH 、ID . (1)在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形(保留画图痕迹); (2)若△ABC 的面积为1,则以EG 、FH 、ID 的长度为三边长的三角形的面积等于______. 10.阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC 中, ∠A=2∠B ,CD 平分∠ACB ,AD=2.2,AC=3.6 求BC 的长.
小聪思考:因为CD 平分∠ACB ,所以可在BC 边上取点E ,使EC=AC ,连接DE. 这样很容易得到△DEC ≌△DAC ,经过推理能使问题得到解决(如图2).
请回答:(1)△BDE 是_________三角形. (2)BC 的长为__________.
参考小聪思考问题的方法,解决问题: 如图3,已知△ABC 中,AB=AC, ∠A=20°, BD 平分 ∠ABC,BD=2.3
,BC=2,求AD 的长.
1.阅读下面材料:
小炎遇到这样一个问题:如图1,点E 、F 分别在正方形ABCD 的边BC ,CD 上,∠EAF=45°,连结EF ,则EF=BE+DF ,试说明理由.
小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB ,AD 是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着点A 逆时针旋转90°得到△ADG ,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题: (1)如图3,四边形ABCD 中,AB=AD ,∠BAD=90°点E ,F 分别在边BC ,CD 上,∠EAF=45°.若∠B ,∠D 都不是直角,则当∠B 与∠D 满足 关系时,仍有EF=BE+DF ; (2)如图4,在△ABC 中,∠BAC=90°,AB=AC ,点D 、E 均在边BC 上,且∠DAE=45°,若BD=1, EC=2,求DE 的长.
2.阅读下面文字,解决下列问题
(1)问题背景 宇昕同学遇到这样一个问题:如图1,在正方形ABCD 中,点E ,F 分别为BC ,CD 上的点,且∠EAF=45°,求证:BE+DF=EF . 宇昕是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.
他的方法是将△ADF 绕点A 顺时针旋转90°得到△ABG (如图2),此时GE 即是DF+BE .
请回答:在图2中,∠GAF 的度数是 、△AGE ≌△ .
(2)拓展研究如图3,若E,F分别在四边形ABCD的边BC,CD上,∠B+∠D=180°,AB=AD,要使(1)中线段BE,EF,FD的等量关系仍然成立,则∠EAF与∠BAD应满足的关系是;
(3)构造运用运用(1)(2)解答中所积累的经验和知识,完成下面问题:如图4,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,
3,试求线段AD,BE的长.
点E在AB上,且∠DCE=67.5°,DE⊥AB于点E,若AE=2
[此文档可自行编辑修改,如有侵权请告知删除,感谢您的支持,我们会努力把内容做得更好]。
