3.4.1相似三角形的判定同步练习含答案解析
【湘教版】九年级数学上册:3.4.1 相似三角形的判定定理1(含答案)

第2课时 相似三角形的判定定理101 基础题知识点 两角分别相等的两个三角形相似1.如图,D 是BC 上的点,∠ADB =∠BAC,则下列结论正确的是(B) A.△ABC ∽△DAC B.△ABC ∽△DBA C.△ABD ∽△ACD D.以上都不对2.如图,在矩形ABCD 中,E 在AD 上,EF ⊥BE,交CD 于F,连接BF,则图中与△ABE 一定相似的三角形是(B)A.△EFBB.△DEFC.△CFBD.△EFB 和△DEF3.∠1=∠2是下列四个图形的共同条件,则四个图中不一定有相似三角形的是(D)4.(长春中考)如图,∠ABD =∠BDC =90°,∠A =∠CBD,AB =3,BD =2,则CD 的长为(B)A.34B.43C.2D.35.如图,锐角△ABC的边AB和AC上的高线CE和BF相交于点D.请写出图中的一对相似三角形:答案不唯一,如△ABF∽△DBE或△ACE∽△DCF或△EDB∽△FDC等.6.如图,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=3.7.(怀化中考)如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.证明:在△ABC中,∠B=180°-∠A-∠C=79°,∴∠B=∠E.又∵∠C=∠F,∴△ABC∽△DEF.8.如图,点B.D.C.F在一条直线上,且AB∥EF,AC∥DE,求证:△ABC∽△EFD.证明:∵AB∥EF,AC∥DE,∴∠B=∠F,∠ACB=∠EDF.∴△ABC∽△EFD.02 中档题9.(江阴模拟)下列条件中,能判定两个等腰三角形相似的是(C)A.都含有一个30°的内角B.都含有一个45°的内角C.都含有一个60°的内角D.都含有一个80°的内角10.(安徽中考)如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为(B)A.4B.4 2C.6D.4 311.如图,∠1=∠2,请补充一个条件:∠C=∠E或∠B=∠ADE(答案不唯一),使△ABC∽△ADE.12.如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,则CD的长为23 .13.如图,AD.BE 是钝角△ABC 的边BC.AC 上的高,求证:AD BE =ACBC.证明:∵AD.BE 是钝角△ABC 的高,∴∠BEC =∠ADC =90°. 又∵∠DCA =∠ECB, ∴△DAC ∽△EBC. ∴AD BE =AC BC. 14.如图,在矩形ABCD 中,E 为BC 上一点,DF ⊥AE 于点F. (1)△ABE 与△DFA 相似吗?请说明理由;(2)若AB =6,AD =12,AE =10,求DF 的长. 解:(1)△ABE ∽△DFA. 理由:∵四边形ABCD 是矩形, DF ⊥AE,∴∠B =∠DFA =90°.∴∠FAD +∠FDA =90°,∠BAE +∠FAD =90°. ∴∠BAE =∠FDA. ∴△ABE ∽△DFA. (2)∵△ABE ∽△DFA,∴AB DF =AE AD. ∴DF =AB·AD AE =6×1210=7.2.03 综合题15.在△ABC 中,P 为边AB 上一点.(1)如图1,若∠ACP =∠B,求证:AC 2=AP·AB; (2)若M 为CP 的中点,AC =2.①如图2,若∠PBM =∠ACP,AB =3,求BP 的长;②如图3,若∠ABC =45°,∠A =∠BMP =60°,直接写出BP 的长. 解:(1)证明:∵∠ACP =∠B,∠BAC =∠CAP, ∴△ACP ∽△ABC. ∴AC AB =APAC . ∴AC 2=AP·AB .(2)①作CQ∥BM 交AB 的延长线于点Q. ∴∠PBM=∠AQC . ∵∠PBM=∠ACP , ∴∠AQC=∠ACP . 又∵∠PAC=∠CAQ , ∴△APC∽△ACQ .∴AC AP =AQAC .∴AC 2=AP·AQ .∵M为PC的中点,BM∥CQ,∴PBPQ=PMPC=12.设BP=x,则PQ=2x,BQ=x,∴22=(3-x)(3+x),解得x1=5,x2=-5(不合题意,舍去). ∴BP= 5.②BP=7-1.。
泰州市第五中学九年级数学上册第3章图形的相似3.4相似三角形的判定与性质3.4.1相似三角形的判定第

【素养提升】 18.(12 分)如图所示,已知 AB∥CD,AD 与 BC 相交于点 E, EF∥AB,交 BD 于点 F,求证:A1B +C1D =E1F .
证明:∵AB∥CD,EF∥AB,∴AB∥EF∥CD. ∴EAFB =BDDF ,CEDF =BBDF ,EAFB +CEDF =BDDF +BBDF =1, 故A1B +C1D =E1F .
〕.
〔重点〕
3.能根据具体问题的数量关系,建立一元二次方程的模型.〔难点〕
导入新课
复习引入
1.下列式子哪些是方程?
2+6=8
没有未知数
2x+3
代数式
5x+6=22 x+3y=8
一元一次方程 二元一次方程
x-5<18
不等式
2.什么叫方程 ?我们学过哪些方程 ?
含有未知数的等式叫做方程.
我们学过的方程有一元一次方程 , 二元一次方程〔组〕及 分式方程 , 其中前两种方程是整式方程.
特点:
1.只含有一个未知数; 2.未知数的最高次数是2;
知识要点
u一元二次方程的概念 只含有一个未知数x的整式方程 , 并且都可以化为ax2+bx+c=0
(a,b,c为常数, a≠0)的形式 , 这样的方程叫做一元二次方程.
u一元二次方程的一般形式是
ax2+bx +c = 0(a , b , c为常数, a≠0)
3x2-8x-10=0.
其中二次项是3x2,系数是3 ; 一次项是-8x,
当堂练习
1.以下方程哪些是一元二次方程? 为什么?
(1)7x2 - 6x = 0
√
(2)2x2 - 5xy + 6y = 0
3.4.1相似三角形的判定定理3

B AC 1 ∠C =∠C ′= 90°,且 A AB AC 2 求证:△ ABC∽△ABC.
还可以根据相似三角形 的判定定理2,来证明这两 个直角三角形相似.
练习 1.如图,O为△ABC内一点,D、E、F
分别是OA、OB、OC中点. 求证:△ABC∽△DEF.
= 4 BC 2 =(2 BC )2. 由此得出,BC = 2BC .
BC 1 AB AC . 从而 BC 2 AB AC
因此△ AB C ∽△ABC.
(三边对应成比例的两个三角形相似)
说一说
在例2的证明中,还可以根据哪个判定定理说明 △ ABC ∽ △ABC ?
AD AE DE AB AC BC AD AB A B AE DE AB AC BC A ' B ' A ' C ' BC AB AC BC ∴ AE= A'C', DE= B'C',
A
A'
D B' C' B E
C
∴△A'B'C' ≌ △ADE ∴ △A'B'C' ∽ △ABC
证明: E O
A D F
B
C
D, E , F 分别为OA,OB,OC的中点, 1 1 1 DE = AB , EF BC , DF AC . 2 2 2 DE EF DF 1 . AB BC AC 2 △ABC∽△DEF.
练习
AB AC BC 2.如图, = = , AD AE DE
AB AC 1 ∠C =∠C ′= 90°,且 AB AC 2
相似三角形 同步练习(含答案)

4.5相似三角形一、目标导航1.相似三角形的定义:三角对应相等,三边对应成比例的两个三角形叫做相似三角形; 2.相似三角形的对应角相等,对应边成比例. 二、基础过关1.如果两个三角形的相似比为1,那么这两个三角形________.2.若△ABC ∽△A /B /C /相似,一组对应边的长为AB =3 cm ,A /B /= 4 cm ,那么△A /B /C /与△ABC 的相似比是________.3.若△ABC 的三条边长的比为3∶5∶6,与其相似的另一个△A 'B 'C '的最小边长为12 cm ,那么△A 'B 'C '的最大边长是________.4.两个三角形相似,其中一个三角形两个内角分别是006040、,那么另一个三角形的最大角为 度,最小角为 度.三、能力提升5.已知△ABC 的三条边长分别为3 cm ,4 cm , 5 cm ,△ABC ∽△A /B /C /,那么△A /B /C /的形状是______,又知△A /B /C /的最大边长为20 cm ,那么△A /B /C /的面积为________. 6.如图,△ABC ∽△ADE ,AE =3,EC =5,DE =1.2,则BC 的长度为 . 7.下列说法正确的是( )A .相似三角形一定全等B .不相似的三角形不一定全等C .全等三角形不一定是相似三角形D .全等三角形一定是相似三角形 8.下列命题错误的是( )A .两个全等的三角形一定相似B .两个直角三角形一定相似C .两个相似三角形的对应角相等,对应边成比D .相似的两个三角形不一定全等 9.若△ABC ∽△DEF ,它们的周长分别为6 cm 和8 cm ,那么下式中一定成立的 是( )A .3AB =4DE B .4AC =3DEC .3∠A =4∠D D .4(AB +BC +AC )=3(DE +EF +DF ) 10.若△ABC ∽△A /B /C /,∠A =55°,∠B =100°,那么∠C /的度数是( ) A .55°B .100°C .25°D .不能确定6题EDCBA11.把△ABC 的各边分别扩大为原来的3倍得到△A ′B ′C ′,下列结论不成立的是( ) A .△ABC ∽△A ′B ′C ′ B .△ABC 与△A ′B ′C ′的各对应角相等 C .△ABC 与△A ′B ′C ′的相似比为41D .△ABC 与△A ′B ′C ′的相似比为3112.已知△ABC 的三边长分别为2,6,2,△A ′B ′C ′的两边长分别是1和3,如果△ABC 与△A 'B 'C '相似,那么△A 'B 'C '的第三边长应该是 ( ) A .2 B .22 C .26 D .33 13.一个钢筋三角架三 长分别为20cm ,50cm ,60cm ,现要再做一个与其相似的钢筋三角架,而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有 ( )A .一种B .两种C .三种D .四种14.△ABC 中,AB =12 cm ,BC =18 cm ,AC =24 cm ,若△A /B /C /∽△ABC ,且△A /B /C /的周长为81 cm .求△A /B /C /各边的长.四、聚沙成塔如图,分别取等边三角形ABC 各边的中点D 、E 、F ,得△DEF .若△ABC 的边长为a . ⑴△DEF 与△ABC 相似吗?如果相似,相似比是多少? ⑵分别求出这两个三角形的面积.⑶这两个三角形的面积比与边长之比有什么关系吗?FEDCBA参考答案1.全等;2.4:3;3.24cm ;4.80,40;5.直角三角形,96cm 2;6.3.2;7.D ;8.B ;9.D ;10.C ;11.C ;12.A ;13.B ;14.A /B /=18cm ,B /C /=27cm ,A /C /=36cm ;15.⑴相似,1:2.⑵分别为43a 2和163a 2. ⑶面积之比等于边长之比的平方.。
湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案

湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.已知△ABC∽△A′B′C′且ABA′B′=12,则S△ABC∶S△A′B′C′为( )A.1∶2B.2∶1C.1∶4D.4∶12.如图,△ABC与△DE F相似,相似比为1∶2,BC的对应边是EF,若BC=1,则EF的长是( )A.1B.2C.3D.43.已知△ABC∽△DEF,且AB∶DE=1∶2,则△ABC的面积与△DEF的面积之比为( )A.1∶2B.1∶4C.2∶1D.4∶14.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF :S△ABF=4:25,则DE:EC=()A.2:3 B.2:5 C.3:5 D.3:25.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )A.1对B.2对C.3对D.4对6.如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )A.1条B.2条C.3条D.4条7.如图,点P是△ABC的边AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )A.2条B.3条C.4条D.5条8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )A.P1 B.P2C.P3D.P49.要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架乙共有( )A.1种B.2种C.3种D.4种10.如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是( )A.①②④B.②③④C.①②③④D.①③二、填空题11.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比值为.12.若两个相似三角形的周长比为2:3,则它们的面积比是.13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.14.下图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是.(写出满足条件的所有的点)15.如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有对.16.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是.三、解答题17.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°. 求证:△ADC∽△DEB.18.如图,A、B、C、P四点均在边长为1的小正方形网格格点上.(1)判断△PBA与△ABC是否相似,并说明理由;(2)求∠BAC的度数.19.如图所示,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1) ∠EAF=∠B;(2) AF2=FE·FB.20.如图,在△ABC中,AD和BG是△ABC的高,连接GD.(1)求证△ADC∽△BGC;(2)求证CG·AB=CB·DG.21.如图,已知P是正方形ABCD边BC上一点,BP=3PC,Q是CD的中点(1)求证:△ADQ∽△QCP;(2)若AB=10,连接BD交AP于点M,交AQ于点N,求BM,QN的长.22.在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.(1)如图①,若BD=CE,求证:DF=EF.(2)如图②,若BD=1nCE,试写出DF和EF之间的数量关系,并证明.(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.答案1.C2.B3.B4.A5.C.6.C7.C.8.B9.C.10.C.11.答案为:1:4.12.答案为:4:9.13.答案为:16cm.14.答案为:Q.15.答案为:4.16.答案为(﹣3×4n﹣1,4n).17.证明:∵△ABC是等边三角形∴∠B=∠C=60°∴∠ADB=∠CAD+∠C=∠CAD+60°∵∠ADE=60°∴∠ADB=∠BDE+60°∴∠CAD=∠BDE∴△ADC∽△DEB.18.解:(1)△PBA与△ABC相似,理由如下:∵AB=5,BC=5,BP=1∴∵∠PBA=∠ABC∴△PBA∽△ABC;(2)∵△PBA∽△ABC∴∠BAC=∠BPA∵∠BPA=90°+45°=135°∴∠BAC=135°.19.证明:(1)∵AB∥CD∴∠B=∠C又∠C=∠EAF∴∠EAF=∠B(2)∵∠EAF=∠B,∠AFE=∠BFA ∴△AFE∽△BFA则AFBF=FEFA∴AF2=FE·FB20.解:(1) ∵在△ABC中,AD和BG是△ABC的高∴∠BGC=∠ADC=90°.又∠C=∠C∴△ADC∽△BGC.(2)∵△ADC∽△BGC∴CGDC=BCAC.∴CGBC=DCAC.又∠C=∠C∴△GDC∽△BAC.∴CGBC=DGAB.∴CG·AB=CB·DG.21.证明:(1)∵正方形ABCD中,BP=3PC,Q是CD的中点∴PC=14﹣BC,CQ=DQ=12CD,且BC=CD=AD∴PC :DQ =CQ :AD =1:2 ∵∠PCQ =∠ADQ =90° ∴△PCQ ∽△ADQ (2)∵△BMP ∽△AMD ∴BM :DM =BP :AD =3:4 ∵AB =10 ∴BD =10 2 ∴BM =同理QN =53 5.22.证明:(1)在题图①中作EG ∥AB 交BC 于点G 则∠ABC =∠EGC ,∠D =∠FEG. ∵AB =AC ,∴∠ABC =∠C. ∴∠EGC =∠C.∴EG =EC. ∵BD =CE ,∴BD =EG. ∵∠D =∠FEG ,∠BFD =∠GFE ∴△BFD ≌△GFE. ∴DF =EF. (2)解:DF =1nEF.证明:在题图②中作EG ∥AB 交BC 于点G ,则∠D =∠FEG.由(1)得EG =EC. ∵∠D =∠FEG ,∠BFD =∠EFG ∴△BFD ∽△GFE.∴BD EG =DF EF. ∵BD =1n CE =1n EG∴DF =1n EF.(3)解:成立.证明:在题图③中作EG ∥AB 交CB 的延长线于点G则仍有EG=EC,△BFD∽△GFE.∴BDEG=DFEF.∵BD=1nCE=1nEG,∴DF=1nEF.。
相似三角形的判定 (沪教版) 同步练习及解析

相似三角形的判定--巩固练习(基础)【巩固练习】一、选择题1. 下列判断中正确的是( ).A.全等三角形不一定是相似三角形B.不全等的三角形一定不是相似三角形C.不相似的三角形一定不全等D.相似三角形一定不是全等三角形2.已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ).A. B. C. D.3.(2015•大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC 相似的是()A.B.C.D.4.在△ABC和△DEF中,①∠A=35°,∠B=100°,∠D=35°,∠F=45°;②AB=3cm,BC=5cm,∠B=50°,DE=6cm,DF=10cm,∠D=50°;其中能使△ABC与以D、E、F为顶点的三角形相似的条件( ).A.只有①B.只有②C.①和②分别都是D.①和②都不是5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有().A.ΔADE∽ΔAEF B.ΔECF∽ΔAEF C.ΔADE∽ΔECF D.ΔAEF∽ΔABF 6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ).A. B.8 C.10 D.16二、填空题7.(2015•伊春模拟)如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为.8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C 的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.三.解答题13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.15.(2014秋•射阳县校级月考)如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,(1)求证:AC2=CE•CF;(2)若∠B=38°,求∠CFD的度数.【答案与解析】一.选择题1.【答案】C.2.【答案】A.2第三边,所以第三边是3.【答案】B.【解析】已知给出的三角形的各边AB 、CB 、AC 分别为、2、、 只有选项B 的各边为1、、与它的各边对应成比例.故选B .4.【答案】C.5.【答案】C.【解析】∵∠AEF =90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°, 即∠1=∠3,∴△ADE ∽△ECF.6.【答案】C.【解析】∵ EF ∥AB ,∴, ∵ ,∴ ,, ∴ CD=10,故选C.二. 填空题7.【答案】 ∠ADE=∠C 或∠AED=∠B 或AD AE AC AB= . 【解析】据判定三角形相似的方法来找条件.8.【答案】 3 .【解析】∵ ∠C=∠E ,∠CAB=∠EAD ,∴ △ACB ∽△AED ,∴,BC=4, 在Rt △ABC 中,.9.【答案】; . 10.【答案】4.【解析】∵AB ⊥BD ,ED ⊥BD ,∴∠B=∠D=90°,又∵AC ⊥CE ,∴∠BCA+∠DCE=90°,∴∠BCA=∠E,∴△ABC ∽△CDE.∵C 是线段BD 的中点,ED=1,BD=4∴BC=CD=2 ∴AB CD CD DE=,即AB=4. 11.【答案】△OAB,△OCD.12.【答案】3.【解析】∵平行四边形ABCD ,∴AD ∥BE.AB ∥CD∴△EFC ∽△EAB; △EFC ∽△AFD; △AFD ∽△EAB.三综合题13.【解析】∵DE∥BC,∴△ADE∽△ABC,∵,,∴,∴AC=,∴EC=AC-AE=.14.【解析】∵AD∥BC,∴∠ADB=∠DBC,又∵,∴△ABD∽△DCB,∴∠A=∠BDC,∵∠A=90°,∴∠BDC=90°,∴BD⊥CD .15.【解析】解:(1)∵AD⊥BC,∴∠CFA=90°,∵∠BAC=90°,∴∠CFA=∠BAC,∵∠ACF=∠FCA,∴△CAF∽△CEA,∴=,∴CA2=CE•CF;(2)∵∠CAB=∠CDA,∠ACD=∠BCA,∴△CAD∽△CBA,∴=,∴CA2=CB×CD,同理可得:CA2=CF×CE,∴CD•BC=CF•CE,∴=,∵∠DCF=∠ECB,∴△CDF∽△CEB,∴∠CFD=∠B,∵∠B=38°,∴∠CFD=38°.。
九年级数学上册3.4相似三角形的判定与性质3.4.1相似三角形的判定第4课时相似三角形的判定定理3测试题新版湘

第4课时 相似三角形的判定定理301 基础题知识点 三边成比例的两个三角形相似1.将一个三角形的各边都缩小12后,得到的三角形与原三角形(A) A .一定相似 B .一定不相似C .不一定相似D .不能判断是否相似2.甲三角形的三边分别为1,2,5,乙三角形的三边分别为5,10,5,则甲乙两个三角形(A)A .一定相似B .一定不相似C .不一定相似D .无法判断是否相似3.已知△ABC 的三边长分别为6 cm 、7.5 cm 、9 cm ,△DEF 的一边长为4 cm ,要使这两个三角形相似,则△DEF 的另两边长可以是(C)A .2 cm ,3 cmB .4 cm ,5 cmC .5 cm ,6 cmD .6 cm ,7 cm4.如图,两个三角形的关系是相似(填“相似”或“不相似”),理由是三边成比例的两个三角形相似.5.若△ABC 各边分别为AB =10 cm ,BC =8 cm ,AC =6 cm ,△DEF 的两边为DE =5 cm ,EF =4 cm ,则当DF =3cm 时,△ABC∽△DEF.6.△ABC 和△A′B′C′符合下列条件,判断△ABC 与△A′B′C′是否相似.BC =2,AC =3,AB =4;B′C′=2,A′C′=3,A′B′=2.解:在△ABC 中,AB>AC>BC ,在△A′B′C′中,A′B′>A′C′>B′C′,BC B′C′=22=2,AC A′C′=33=3,AB A′B′=42=2. ∴BC B′C′≠AB A′B′≠AC A′C′. ∴△ABC 与△A′B′C′不相似.7.如图所示,根据所给条件,判断△ABC 和△DBE 是否相似,并说明理由.解:△ABC∽△DBE.理由如下:∵AC DE =36=12,BC BE =48=12,AB DB =510=12, ∴AC DE =BC BE =AB DB. ∴△ABC∽△DBE.02 中档题8.下列能使△ABC 和△DEF 相似的条件是(C)A .AB =c ,AC =b ,BC =a ,DE =a ,EF =b ,DF = cB .AB =1,AC =1.5,BC =2,DE =12,EF =8,DF =1C .AB =3,AC =4,BC =6,DE =12,EF =8,DF =6D .AB =2,AC =3,BC =5,DE =6,EF =3,DF =39.如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R 应是甲、乙、丙、丁四点中的(C)A .甲B .乙C .丙D .丁10.(东营中考)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的三条边长分别是3、4及x ,那么x 的值(B)A .只有1个B .可以有2个C .可以有3个D .有无数个11.如图,△ABC 中,点D 、E 、F 分别是AB 、BC 、AC 的中点,求证:△ABC∽△EFD.。
相似三角形的判定及习题精讲(含答案)

14.75或27, 提示:当小多边形的周长为45时,大多边形的周长为 ×45=75;当大多边形的周长为45时,小多边形的周长为 ×45=27。 15.100cm和40cm
(二)选择题: 1. D 2.A 。 提示:过E作EG//AD交BD于G,则 = = ,设BG=2k, GD=3k, 则BD=5k, CD=15k,
A、 B、 C、 D、
6.正方形ABCD中,E是AD中点,BM⊥CE于M,AB=6cm, 则BM的长为 ( )。
A、12 cm B、
cm C、3 cm D、 cm 7.要把一个三角形的面积扩大到原来面积的8倍,而它的形状不变, 那么它的边长要增大到原来的( )倍。
A、2 B、4 C、2 D、64 8.梯形ABCD中,AD//BC,AC、BD交于E点,SΔADE∶SΔADC=1∶3, 则SΔADE∶SΔDBC=( )。 A、1∶3 B、1∶4 C、1∶5 D、1∶6 (三)已知:如图,在ΔABC中,AD为中线,E在AB上,AE=AC,CE交 AD于F,EF∶FC=3∶5,
(五)略 (六)提示:过点D作DM//AC交BC于M,证ΔBDM∽ΔBAC及 ΔQDM∽ΔQBD,通过等比代换可得。
(七)本题由正方形在三角形中的位置不同引起分类讨论。提示如 下: 解:直角三角形内接正方形有两种不同的位置。 如下图:
(1)如图(1),作CP⊥AB于P,交GF于H,则CH⊥GF, ∵ GF//AB, ∴ ΔCGF∽ΔCAB, ∴ = , ∵ ∠ACB=90°,AC=8,BC=6由勾股定理得AB=10, ∵ AC·BC=AB·CP, ∴ CP= = = , 设GF=x, 则CH=
∵ EG//PD,∴ = = =
3.C 4. A 5.D
6.B。 提示:如图,易证ΔBMC∽ΔCDE, ∵ ED=
相似三角形的判定(含答案)

学生做题前请先回答以下问题问题1:相似三角形的判定:①________________________________________;②________________________________________;③________________________________________;④_________________________________________________________.在证明两个三角形相似时,首先考虑角度信息,其次考虑对应边成比例.问题2:想一想相似三角形的判定与性质的区别是什么?问题3:如果两个图形___________,而且____________________________,那么这样的两个图形叫做位似图形,这个点叫做________;位似图形上__________________________________________________.相似三角形的判定一、单选题(共9道,每道11分)1.如图,下列条件不能判定△ADB∽△ABC的是( )A.∠ABD=∠ACBB.∠ADB=∠ABCC. D.答案:D解题思路:试题难度:三颗星知识点:相似三角形的判定2.如图,在△ABC中,DE∥BC,,则下列结论中正确的是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:相似三角形的判定与性质3.如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F,若,CD=3,则AF的长为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:相似三角形的判定与性质4.如图,已知AD为△ABC的角平分线,DE∥AB,交AC于点E,若,则的值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:相似三角形的判定5.如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB的延长线于点E,则下列结论正确的是( )A.△AED∽△ACBB.△AEB∽△ACDC.△BAE∽△ACED.△AEC∽△DAC答案:C解题思路:试题难度:三颗星知识点:相似三角形的判定6.如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )A.2DE=3MNB.3DE=2MNC.3∠A=2∠FD.2∠A=3∠F答案:B解题思路:试题难度:三颗星知识点:位似变换7.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大为原来的2倍,得到△.若点A的坐标是(1,2),则点的坐标是( )A.(2,4)B.(-1,-2)C.(-2,-4)D.(-2,-1)答案:C解题思路:试题难度:三颗星知识点:相似三角形的性质和判定8.如图,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形相似,则AQ的长为( )A.3B.3或C.3或D.答案:B解题思路:试题难度:三颗星知识点:相似三角形的性质和判定9.如图,在Rt△ABO中,∠AOB=90°,∠ABO=60°,,D为BO的中点,若E是线段AB上的一动点,连接DE,当△BDE与△AOB相似时,点E的坐标为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:相似三角形的性质和判定。
初中数学经典相似三角形练习题附参考答案
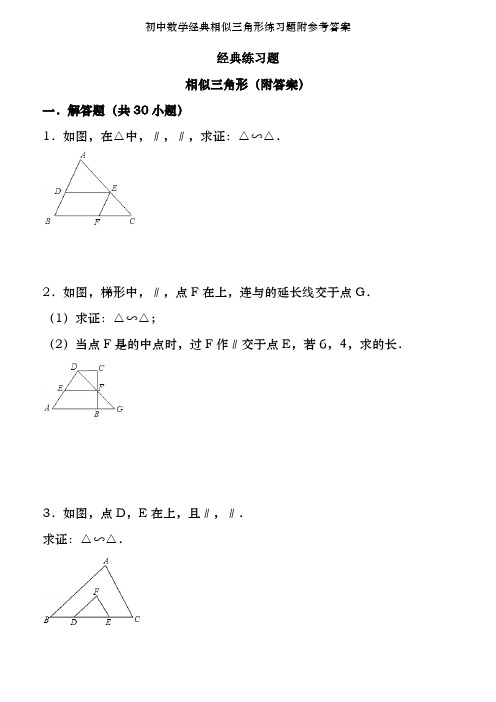
经典练习题相似三角形(附答案)一.解答题(共30小题)1.如图,在△中,∥,∥,求证:△∽△.2.如图,梯形中,∥,点F在上,连与的延长线交于点G.(1)求证:△∽△;(2)当点F是的中点时,过F作∥交于点E,若6,4,求的长.3.如图,点D,E在上,且∥,∥.求证:△∽△.4.如图,已知E是矩形的边上一点,⊥于F,试说明:△∽△.5.已知:如图①所示,在△和△中,,,∠∠,且点B,A,D在一条直线上,连接,,M,N分别为,的中点.(1)求证:①;②△是等腰三角形;(2)在图①的基础上,将△绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长交线段于点P.求证:△∽△.6.如图,E是▱的边延长线上一点,连接,交于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△和△的顶点都在边长为1的小正方形的顶点上.(1)填空:∠°,;(2)判断△与△是否相似,并证明你的结论.8.如图,已知矩形的边长3,6.某一时刻,动点M从A点出发沿方向以1的速度向B点匀速运动;同时,动点N从D点出发沿方向以2的速度向A点匀速运动,问:(1)经过多少时间,△的面积等于矩形面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形中,若∥,,对角线、把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△中,D为上一点,2,∠45°,∠60°,⊥于E,连接.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△与△的面积之比.11.如图,在△中,,M为底边上的任意一点,过点M分别作、的平行线交于P,交于Q.(1)求四边形的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于的什么位置时,四边形为菱形并证明你的结论.12.已知:P是正方形的边上的点,且3,M是的中点,试说明:△∽△.13.如图,已知梯形中,∥,2,8,10.(1)求梯形的面积S;(2)动点P从点B出发,以1的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1的速度,沿C⇒D⇒A方向,向点A运动,过点Q作⊥于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线将梯形的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形,长12,宽8,P、Q分别是、上运动的两点.若P自点A 出发,以1的速度沿方向运动,同时,Q自点B出发以2的速度沿方向运动,问经过几秒,以P、B、Q为顶点的三角形与△相似?15.如图,在△中,10,20,点P从点A开始沿边向B点以2的速度移动,点Q从点B开始沿边向点C以4的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△与△相似.16.如图,∠∠90°,,2.问当的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形中,M是的中点,能否在边上找一点N(不含A、B),使得△与△相似?若能,请给出证明,若不能,请说明理由.18.如图在△中,∠90°,8,6,点Q从B出发,沿方向以2的速度移动,点P从C出发,沿方向以1的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△相似?19.如图所示,梯形中,∥,∠90°,7,2,3,试在腰上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△和△是两个等腰直角三角形,∠∠90°,△的顶点E位于边的中点上.(1)如图1,设与交于点M,与交于点N,求证:△∽△;(2)如图2,将△绕点E旋转,使得与的延长线交于点M,与交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形中,15,10,点P沿边从点A开始向B以2的速度移动;点Q沿边从点D开始向点A以1的速度移动.如果P、Q同时出发,用t (秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O 点)20米的A点,沿所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:;(2)请在下图中画出测量示意图;(3)设树高的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80的竹竿的影长为60.乙组:如图2,测得学校旗杆的影长为900.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200,影长为156.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离8.7m,窗口高1.8m,求窗口底边离地面的高.26.如图,李华晚上在路灯下散步.已知李华的身高,灯柱的高′P′,两灯柱之间的距离′.(1)若李华距灯柱的水平距离,求他影子的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和()是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S123.(1)如图②,分别以直角三角形三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△∽△,15,9,5.求.29.已知:如图△∽△,若3,4.(1)求、的长;(2)过B作⊥于E,求的长.30.(1)已知,且34z﹣240,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△中,∥,∥,求证:△∽△.考点:相似三角形的判定;平行线的性质。
湘教版数学九年级上册第三章3.4《相似三角形的判定》解答题专项练习+解析

湘教版九年级数学上册第三章3.4《相似三角形的判定》解答题专项练习+解析一.解答题(共12小题)1.如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;(2)选择(1)中一对加以证明.2.如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.(1)求证:△ABE∽△DEF;(2)若正方形的边长为4,求BG的长.3.如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.4.如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.5.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C 点重合),∠ADE=45°.求证:△ABD∽△DCE.6.如图,在8×8的正方形网格中,△CAB和△DEF的顶点都在边长为1的小正方形的顶点上,AC与网格上的直线相交于点M.(1)填空:AC= ,AB= .(2)求∠ACB的值和tan∠1的值;(3)判断△CAB和△DEF是否相似?并说明理由.7.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.(1)若BC=8,求FD的长;(2)若AB=AC,求证:△ADE∽△DFE.8.如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.①判断△ABC和△DEF是否相似,并说明理由;②点P1,P2,P3,D,F都是△DEF边上的5个格点,请在这5个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似.(写出一个即可,并在图中连接相应线段,不必说明理由)9.如图,已知△ABC中CE⊥AB于E,BF⊥AC于F,求证:△AEF∽△ACB.10.如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.(1)证明:△ABD∽△DCF;(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.11.如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.(1)求证:△ABD≌△BCE;(2)图中共有对相似三角形(全等除外).并请你任选其中一对加以证明.你选择的是.12.如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)写出图中两对相似三角形(不得添加字母和线).(2)请选择其中的一对三角形,说明其相似的理由.湖南省澧县张公庙镇中学2015-2016学年湘教版九年级数学上册第三章3.4《相似三角形的判定》解答题专项练习+解析参考答案与解析一.解答题(共12小题)1.解:(1)△ADE≌△BDE,△ABC∽△BCD;(2)证明:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD为角平分线,∴∠ABD=∠ABC=36°=∠A,在△ADE和△BDE中∵,∴△ADE≌△BDE(AAS);证明:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD为角平分线,∴∠DBC=∠ABC=36°=∠A,∵∠C=∠C,∴△ABC∽△BCD.2.(1)证明:∵ABCD为正方形,∴AD=AB=DC=BC,∠A=∠D=90°,∵AE=ED,∴,∵DF=DC,∴,∴,∴△ABE∽△DEF;(2)解:∵ABCD为正方形,∴ED∥BG,∴,又∵DF=DC,正方形的边长为4,∴ED=2,CG=6,∴BG=BC+CG=10.3.解:①图1,作MN∥BC交AC于点N,则△AMN∽△ABC,有,∵M为AB中点,AB=,∴AM=,∵BC=6,∴MN=3;②图2,作∠ANM=∠B,则△ANM∽△ABC,有,∵M为AB中点,AB=,∴AM=,∵BC=6,AC=,∴MN=,∴MN的长为3或.4.证明:∵AB=AC,D是BC中点,∴AD⊥BC,∴∠ADC=90°,∴∠FAE+∠AFE=90°,∵BE⊥AC,∴∠BEC=90°,∴∠CBE+∠BFD=90°,∵∠AFE=∠BFD,∴∠FAD=∠CBE,∴△AFE∽△BCE.5.证明:∵∠BAC=90°,AB=AC=1,∴△ABC为等腰直角三角形,∴∠B=∠C=45°,∴∠1+∠2=180°﹣∠B=135°,∵∠ADE=45°,∴∠2+∠3=135°,∴∠1=∠3,∵∠B=∠C,∴△ABD∽△DCE.6.解:(1)如图,由勾股定理,得AC==2.AB==2故答案是:2,2;(2)如图所示,BC==2.又由(1)知,AC=2,AB=2,∴AC2+BC2=AB2=40,∴∠ACB=90°.tan∠1==.综上所述,∠ACB的值是90°和tan∠1的值是;(3)△CAB和△DEF相似.理由如下:如图,DE=DF==,EF==.则===2,所以△CAB∽△DEF.7.解:(1)∵D、E分别是边AB、AC的中点,∴,DE∥BC.∴∠AED=∠C.∵∠F=∠C,∴∠AED=∠F,∴FD==4;(2)∵AB=AC,DE∥BC.∴∠B=∠C=∠AED=∠ADE,∵∠AED=∠F,∴∠ADE=∠F,又∵∠AED=∠AED,∴△ADE∽△DFE.8.解:①△ABC和△DEF相似.理由如下:∵根据图示知:AB=2,AC=,BC=5,ED=4,DF=2,EF=2,∴===,∴△ABC∽△DEF;②△ACB∽△DP3P2.理由如下:∵由①知,△ABC∽△DEF,∴∠D=∠A.连接DP2P3,DP3=,DP2=,P2P3=.∵==,∴△ACB∽△DP3P2.9.证明:∵CE⊥AB,BF⊥AC,∴∠AEC=∠AFB=90°.∵∠A是公共角,∴△ABF∽△ACE.∴,∴,又∠A是公共角,∴△AEF∽△ACB.10.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.11.(1)证明:∵△ABC是等边三角形,∴AC=BA,∠ABD=∠C=60°,在△ABD和△BCE中,∴△ABD≌△BCE(SAS);(2)4对,分别是△BDF∽△BEC,△DBF∽△DAB,△AFE∽△ACD,△AFE∽△BAE,选择证明△AEF∽△BEA,∵△ABC是等边三角形,∴AC=BA,∠C=∠BAE=60°,AC=BC,∵BD=CE,∴AE=CD,∴△ACD≌△BAE(SAS),∴∠DAC=∠ABE,又∵∠AEF=∠BEA,∴△AEF∽△BEA.12.(1)解:△ABC∽△ADE,△ABD∽△ACE;(2)△ABD∽△ACE.证明:由(1)知△ABC∽△ADE,∴=,∴AB×AE=AC×AD,∴=,∵∠BAD=∠CAE,∴△ABD∽△ACE.初中数学试卷。
新洲区三中九年级数学上册第3章图形的相似3.4相似三角形的判定与性质3.4.1相似三角形的判定第4课

O , ∠BAD=60° , BD =6 , 求菱形的边长AB和対角线AC的
长.
解 : ∵四边形ABCD是菱形 ,
∴AC⊥BD(菱形的対角线互相垂直)
OB=OD= 1
2
平分)
BD1 =
2
×6=3(菱形的対角线互相 B
在等腰三角形ABC中 ,
O
针对训练
1. 已知 : 如右图,在□ABCD中,対角线AC与BD相交于点O,
解 : ∵四边形ABCD是矩形.
A
D
∴AC = BD(矩形的対角线相等).
O
OA= OC= 1 AC,OB = OD = 1 BD , B
C
2
2
∵∠AOD=120°,
∴∠ODA=∠OAD= 1
A (180°- 120°)=30°.
D
2
又∵∠DAB=90° ,
O
B
C
〔矩形的四个角都是直角〕
∴BD = 2AB = 2 ×2.5 = 5.
看看远处,要保护好眼睛哦~站起来动一动 对身体不好哦~
证明: ∵ BF∥CE,CF∥BE ,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
A
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
针对训练
4.如下图,在□ABCD中,対角线AC与BD相交于点O , △ABO是
等边三角形, AB=4,求□ABCD的面积.
解 : ∵四边形ABCD是平行四边形,
∴OA= OC,OB = OD.
A
D
3.4.1 相似三角形的判定 (课件)2024-2025湘教版 数学九年级上册

2-1. [ 模拟·株洲荷塘区 ] 如图,在 ▱ABCD中, 点 E
在 AD 上,且 BE 平分∠ ABC,交AC 于点 O,若
AB=3,BC=4,则
AOOC=
3 ___4___.
课堂新授
知识点 2 角的关系判定三角形相似定理
1. 相似三角形的判定定理1:两角分别相等的两个三角形 相似.
2. 数学表达式: 如图3.4-4 所示, 在△ABC和△DEF中, ∵∠A=∠D,∠B=∠E,∴△ABC ∽△DEF.
课堂新授
知识点 3 边角关系判定三角形相似定理
1. 相似三角形的判定定理2:两边成比例且夹角相等的 两个三角形相似. 特别提醒 运用该定理证明相似时,一定要注意边角的关 系,相等的角一定是成比例的两组对应边的夹角. 类似于判定三角形全等的SAS的方法.
课堂新授
2. 数学表达式:如图3.4-7 所示, 在△ABC和△DEF 中, ∵DABE=BEFC,且∠B=∠E, ∴△ABC∽△DEF.
3-1. 【二模·广州越秀区】 如图,在平行四边形ABCD 中,点 E 为 BC边上的点(不与点 B,点C 重合), 连接 DE 并延长,交 AB 的延长线于点 F.
求证: △ CDE ∽△ AFD. 证明:∵四边形ABCD是平行四边形, ∴DC∥AF,∠C=∠A. ∴∠CDE=∠F. ∴△CDE∽△AFD.
∴ AB=CD, AB∥CD,AD∥BC,∴△BEF ∽△CDF,
△BEF ∽ △AED. ∴△CDF ∽△AED.
∵ AB=CD,AB=3BE,∴ CD=3BE,AE=4BE. ∴△BEF ∽△CDF,相似比k1=CBDE=13; △BEF ∽△AED,相似比k2=BAEE=14; △CDF ∽△AED,相似比k3=CADE=34.
3.4.1相似三角形的判定课件++2024-2025学年湘教版数学九年级上册

B.10
C.16
16
D.
3
课堂练习
【知识技能类作业】必做题:
3.如图, ∥
,、相交于点E,
=
2
,则
3
=
2
3
.
课堂练习
【知识技能类作业】必做题:
4.如图,在中,//, = 9, = 3, = 2,则的长
为( C )
A.6
B.7
C.8
3.4.1相似三角形的判定(1)
按定义判定:
利用平行线:
习题讲解书写部分
作业布置
【知识技能类作业】必做题:
1.如图, ∥ , ∥
2
A.
3
B.5
C.6
D.15
,
=
2
,
3
= 9,则 的长为( C )
作业布置
【知识技能类作业】必做题:
2.如图,点O是矩形 的对角线AC的中点, ∥ 交 于点M,
结论还成立吗?
解:∵ ∠A = ∠A,∠ADE=∠B,∠AED=∠C,
AD AE DE
= =
AB AC BC
. A
∴△ADE∽△ABC.
D
E
只要 DE∥ BC, 那么△ADE与△ABC是相似
的.
B
F
C
新知讲解
平行于三角形一边的直线与其他两边相交, 截得的三角形
与原三角形相似.
A
几何语言:
D
∵DE∥ BC
形.
按定义判定:
A
∵∠A=∠A′,∠B=∠B′,∠C=∠C′,
A'
AB BC CA
3.4.1相似三角形的判定-2024-2025学年数学湘教九年级上册课件

小结与复习
判定两个三角形相似的条件有哪些?
1.根据定义判定 2.平行于三角形一边的判定方法 3.有两个角对应相等的判定方法 4.有两边对应成比例且夹角相等的判定方法
5.有三边对应成比例的判定方法
当我们在应用这些判定方法解题的时候一定要做正确的选择!
中考试题
1.如
图
在
正
方
形
网
格
上
有
A1
B1C1和
A2
B
C B'
C'
一个是三角形相似的定义(显然条件不具备);
二是利用平行线来判定三角形相似的定理.
已知:在△ABC 和△ A'B'C' 中,
求证:ΔABC∽ △ A'B'C'
证明:在ΔABC的边AB、AC上,分别 A
截取AD=A'B',AE=A'C' ,连结DE.
A'
∵ AD=A'B ,∠A=∠A',AE=A'C'
两个等边三角形呢?为什么?
1.所有的等腰三角形不都相似; 2.所有的等边三角形都相似.
练习 判断4×4方格中的两个三角形是否相似.
D 想一想:找角的关系容易,
还是找边的关系容易?
解:根据勾股定理,得:
CA 2 AB 2 2 BC 10 E B
A C
DE 5 EF 2 5 FD 5
CA AB BC 2
即:两边对应成比例且夹角相等的两个三 角形相似.
A B
如果
AB A'B'
AC A'C'
A
∠A=∠A',
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4.1相似三角形的判定同步练习含答案解析《3.4.1 相似三角形的判定》一、填空题1.三角形一边的和其他两边,所构成的三角形与原三角形相似.2.如果两个三角形的对应边的,那么这两个三角形相似.3.如果两个三角形的对应边的比相等,并且相等,那么这两个三角形相似.4.如果一个三角形的角与另一个三角形的,那么这两个三角形相似.5.在△ABC和△A′B′C′中,如果∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,那么这两个三角形能否相似的结论是,理由是.6.在△ABC和△A′B′C′中,如果∠A=48°,∠C=102°,∠A′=48°,∠B′=30°,那么这两个三角形能否相似的结论是,理由是.7.在△ABC和△A′B′C′中,如果∠A=34°,AC=5cm,AB=4cm,∠A′=34°,A′C′=2cm,A′B′=1.6cm,那么这两个三角形能否相似的结论是,理由是.8.在△ABC和△DEF中,如果AB=4,BC=3,AC=6,DE=2.4,EF=1.2,FD=1.6.那么这两个三角形能否相似的结论是,理由是.9.如图,△ABC的两条高AD、BE交于点H,则图中的相似三角形共有对.10.如图所示,▱ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有对.二、选择题11.如图,不能判定△ABC∽△DAC的条件是()A.∠B=∠DAC B.∠BAC=∠ADC C.AC2=DC•BC D.AD2=BD•BC12.如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是()A.5 B.8.2 C.6.4 D.1.813.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是()A. B. C.D.三、解答题14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)图中有哪两个三角形相似?(2)求证:AC2=AD•AB;BC2=BD•BA;CD2=AD•BD;(3)若AD=2,DB=8,求AC,BC,CD的长;(4)若AC=6,DB=9,求AD,CD,BC的长;(5)求证:AC•BC=AB•CD.15.如图所示,如果D、E、F分别在OA、OB、OC上,且DF∥AC,EF∥BC.求证:(1)OD:OA=OE:OB;(2)△ODE∽△OAB;(3)△ABC∽△DEF.16.如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE•FB.17.已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.18.如图,AB是⊙O的直径,BC是⊙O的切线,切点为点B,点D是⊙O上的一点,且AD∥OC.求证:AD•BC=OB•BD.19.已知:如图,在⊙O中,CD过圆心O,且CD⊥AB,垂足为D,过点C任作一弦CF交⊙O于F,交AB于E.求证:CB2=CF•CE.20.已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.21.已知:如图,在△ABC中,∠BAC=90°,AH⊥BC于H,以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,试判断△BDH与△AEH是否相似,并说明理由.22.如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC 边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.《3.4.1 相似三角形的判定》参考答案与试题解析一、填空题1.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.【考点】相似三角形的判定.【分析】平行于三角形一边的直线和其他两边(或两边的延长线)相交,所得的三角形与原三角形的三边对应成比例.所以所构成的三角形与原三角形相似.【解答】解:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.故答案是:平行于;直线;相交.【点评】本题考查了相似三角形的判定.(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.2.如果两个三角形的三组对应边的比相等,那么这两个三角形相似.【考点】相似三角形的判定.【分析】由三边法:三组对应边的比相等的两个三角形相似;即可求得答案.【解答】解:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.故答案为:三组,比相等.【点评】此题考查了相似三角形的判定.注意熟记相似三角形的判定定理是关键.3.如果两个三角形的两组对应边的比相等,并且夹角对应相等,那么这两个三角形相似.【考点】相似三角形的判定.【分析】由两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;即可求得答案.【解答】解:如果两个三角形的两组对应边的比相等,并且夹角对应相等,那么这两个三角形相似.故答案为:两组,夹角对应.【点评】此题考查了相似三角形的判定.注意熟记相似三角形的判定定理是关键.4.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.【考点】相似三角形的判定.【分析】根据“两角法”来判定两个三角形相似.【解答】解:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.故答案为:两个,两个角对应相等.【点评】本题考查了相似三角形的判定.两角法:有两组角对应相等的两个三角形相似.5.在△ABC和△A′B′C′中,如果∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,那么这两个三角形能否相似的结论是△ABC∽△A′C′B′,理由是有两组角对应相等的两个三角形相似.【考点】相似三角形的判定.【分析】由已知条件易得∠A=∠A′,∠B=∠C′,则根据有两组角对应相等的两个三角形相似可判断两三角形相似.【解答】解:∵∠A=56°,∠B=28°,∠A′=56°,∠C′=28°,∴∠A=∠A′,∠B=∠C′,∴△ABC∽△A′C′B′.故答案为△ABC∽△A′C′B′;有两组角对应相等的两个三角形相似.【点评】本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.6.在△ABC和△A′B′C′中,如果∠A=48°,∠C=102°,∠A′=48°,∠B′=30°,那么这两个三角形能否相似的结论是△ABC∽△A′B′C′,理由是有两组角对应相等的两个三角形相似.【考点】相似三角形的判定.【专题】常规题型.【分析】先根据三角形内角和定理计算出∠B=30°,于是得到∠A=∠A′,∠B=∠B′,所以根据有两组角对应相等的两个三角形相似可证明∴△ABC∽△A′B′C′.【解答】解:∵∠A=48°,∠C=102°,∴∠B=180°﹣∠A﹣∠C=30°,而∠A′=48°,∠B′=30°,∴∠A=∠A′,∠B=∠B′,∴△ABC∽△A′B′C′.故答案为△ABC∽△A′B′C′;有两组角对应相等的两个三角形相似.【点评】本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.7.在△ABC和△A′B′C′中,如果∠A=34°,AC=5cm,AB=4cm,∠A′=34°,A′C′=2cm,A′B′=1.6cm,那么这两个三角形能否相似的结论是△ABC∽△A′B′C′,理由是两组对应边的比相等且夹角对应相等的两个三角形相似.【考点】相似三角形的判定.【专题】常规题型.【分析】先计算出=, =,得到=,加上∠A=∠A′=34°,于是根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断两三角形相似.【解答】解:∵AC=5cm,AB=4cm,A′C′=2cm,A′B′=1.6cm,∴==, =,∴=,而∠A=∠A′=34°,∴△ABC∽△A′B′C′.故答案为△ABC∽△A′B′C′;两组对应边的比相等且夹角对应相等的两个三角形相似.【点评】本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.8.在△ABC和△DEF中,如果AB=4,BC=3,AC=6,DE=2.4,EF=1.2,FD=1.6.那么这两个三角形能否相似的结论是△ABC∽△DEF ,理由是三组对应边的比相等的两个三角形相似.【考点】相似三角形的判定.【分析】先求出两三角形对应边的比,进而可得出结论.【解答】解:∵ ==, ==, ==,∴==,∴△ABC∽△DEF.故答案为:△ABC∽△DEF,三组对应边的比相等的两个三角形相似.【点评】本题考查的是相似三角形的判定定理,熟知三组对应边的比相等的两个三角形相似是解答此题的关键.9.如图,△ABC的两条高AD、BE交于点H,则图中的相似三角形共有 6 对.【考点】相似三角形的判定.【分析】根据相似三角形的判定定理进行解答即可.【解答】解:∵AD⊥BC,BE⊥AC,∴∠ADC=∠ADB=∠AEB=∠BED=90°,∴△AEH∽△ADC∽△BDH∽△BEC,∴共有6对相似三角形.故答案为:6.【点评】本题考查的是相似三角形的判定定理,熟知有两组角对应相等的两个三角形相似是解答此题的关键.10.如图所示,▱ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有 6 对.【考点】相似三角形的判定;平行四边形的性质.【分析】根据平行四边形的对边平行,再根据平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似找出相似三角形即可得解.【解答】解:在▱ABCD中,∵AB∥CD,∴△ABE∽△FDE,△ABG∽△FCG;∵AD∥BC,∴△ADE∽△GBE,△FDA∽△FCG,∴△ABG∽△FDA,△ABD∽△BCD∴图中相似三角形有6对.故答案为:6.【点评】本题考查了相似三角形的判定,主要利用了平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似,要注意△ABG与△FDA都与△FCG相似,所以也相似,这也是本题容易出错的地方.二、选择题11.如图,不能判定△ABC∽△DAC的条件是()A.∠B=∠DAC B.∠BAC=∠ADC C.AC2=DC•BC D.AD2=BD•BC【考点】相似三角形的判定.【专题】常规题型.【分析】已知有公共角∠C,则A、B选项可根据有两组角对应相等的两个三角形相似来判定;C选项可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;D选项虽然也是对应边成比例但无法得到其夹角相等,所以不能推出两三角形相似.【解答】解:已知△ABC和△DCA中,∠ACD=∠BAC;如果△ABC∽△DAC,需满足的条件有:①∠DAC=∠B或∠ADC=∠BAC;②AC2=DC•BC;故选D.【点评】此题主要考查学生对相似三角形判定方法的运用.12.如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是()A.5 B.8.2 C.6.4 D.1.8【考点】相似三角形的性质;平行四边形的性质.【专题】压轴题.【分析】由△CBF∽△CDE,根据相似三角形的对应边对应成比例,可知BF:DE=BC:DC,即BF=BC:DC×DE.又四边形ABCD是平行四边形,根据平行四边形的对边相等,可知BC=AD=6,DC=AD=10,易知DE=3,从而求出BF的长.【解答】解:∵在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,∴CD=10,BC=6,DE=3.∵△CBF∽△CDE,∴BF:DE=BC:DC,∴BF=6÷10×3=1.8.故选D.【点评】本题主要考查了平行四边形的性质及相似三角形的性质:平行四边形的对边相等.相似三角形的对应边成比例.13.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是()A. B. C.D.【考点】相似三角形的判定.【分析】根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.【解答】解:根据题意得:AB==,AC=2,BC==,∴BC:AC:AB=1::,A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;B、三边之比:2:3,图中的三角形(阴影部分)与△ABC不相似;C、三边之比为1::2,图中的三角形(阴影部分)与△ABC相似;D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.故选A.【点评】此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.三、解答题14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.(1)图中有哪两个三角形相似?(2)求证:AC2=AD•AB;BC2=BD•BA;CD2=AD•BD;(3)若AD=2,DB=8,求AC,BC,CD的长;(4)若AC=6,DB=9,求AD,CD,BC的长;(5)求证:AC•BC=AB•CD.【考点】相似三角形的判定与性质.【分析】(1)由条件可知∠A=∠DCB,∠ACD=∠B,可证得△ACD∽△ABC∽△CDB;(2)利用(1)可得到=, =, =,可证得结论;(3)代入(2)中结论可求得;(4)同(3)代入(2)可求得;(5)利用面积相等即可得出结论.【解答】(1)解:∵∠ACB=90°,CD⊥AB,∴∠ADC=∠ACB,∴∠ACD+∠A=∠A+∠B=90°,∴∠ACD=∠B,∴△ACD∽△ABC,△ACD∽△CDB,同理可证得△CDB∽△ABC,∴相似的三角形有:△ACD和△ABC,△ACD和△CDB,△CDB和△ABC;(2)证明:∵△ACD ∽△ABC ,∴=,∴AC 2=AD •AB ,同理可得=, =,∴BC 2=BD •AB ,CD 2=AD •BD ;(3)解:∵AD=2,DB=8,∴CD 2=AD •BD=2×8=16,∴CD=4,又∵AB=AD+BD=10,∴AC 2=AD •AB=2×10=20,BC 2=BD •AB=8×10=80,∴AC=2,BC=4;(4)解:∵AC=6,DB=9,且AB=AD+BD ,∴AC 2=AD (AD+BD ),即62=AD 2+9AD ,解得AD=3或(﹣12舍去),∴CD 2=AD •BD=3×9=27,∴CD=3,∴AB=AD+BD=12,∴BC 2=BD •AB=9×12=108,∴BC=6;(5)证明:∵S △ABC =AC •BC ,且S △ABC =CD •AB ,∴AC •BC=CD •AB .【点评】本题主要考查相似三角形的判定和性质,掌握直角三角形中角之间的关系是解题的关键,注意方程思想的应用.15.如图所示,如果D 、E 、F 分别在OA 、OB 、OC 上,且DF ∥AC ,EF ∥BC .求证:(1)OD :OA=OE :OB ;(2)△ODE ∽△OAB ;(3)△ABC ∽△DEF .【考点】相似三角形的判定与性质.【专题】证明题.【分析】(1)根据平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似就可以得出结论;(2)根据OD:OA=OE:OB由∠AOB=∠AOB就可以得出△ODE∽△OAB;(3)由△ODE∽△OAB就可以得出就可以得出结论.【解答】证明:(1)∵DF∥AC,EF∥BC,∴△ODF∽△OAC,△OEF∽△OBC,∴,,∴OD:OA=OE:OB;(2)∵OD:OA=OE:OB,∠DOE=∠AOB,∴△ODE∽△OAB.(3)∵△ODE∽△OAB,∴,∴.∴△ABC∽△DEF.【点评】本题考查了平行于三角形一边的直线截其他两边所得的新三角形与原三角形相似的判定方法的运用,相似三角形的性质的运用,相似三角形的判定的运用,解答时证明三角形相似是关键.16.如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE•FB.【考点】相似三角形的判定与性质;平行线的性质.【专题】证明题.【分析】(1)欲证∠EAF=∠B,通过AB∥CD及已知发现它们都与∠C相等,等量转换即可;(2)欲证AF2=FE•FB,可证△AFB∽△EFA得出.【解答】证明:(1)∵AB∥CD,∴∠B=∠C,又∵∠EAF=∠C,∴∠EAF=∠B;(2)在△AFB与△EFA中,∵∠EAF=∠B,∠AFB=∠EFA,∴△AFB∽△EFA,∴,即AF2=FE•FB.【点评】乘积的形式通常可以转化为比例的形式,由相似三角形的性质得出,同时考查了平行线的性质.17.已知:如图,在梯形ABCD中,AB∥CD,∠B=90°,以AD为直径的半圆与BC相切于E点.求证:AB•CD=BE•EC.【考点】相似三角形的判定与性质;梯形;切线的性质.【专题】证明题.【分析】连结AE、ED,由平行线的性质推出∠B=∠C,由AD为直径,得出∠AED=90°,从而证得∠AEB=∠CDE=90°﹣∠DEC,根据相似三角形的判定证得△ABE∽△ECD,由相似三角形的性质即可证得结论.【解答】解:连结AE、ED,∵AB∥CD,∠B=90°,∴∠C=90°,∴∠B=∠C,∵AD为直径,∴∠AED=90°,∠AEB=∠CDE=90°﹣∠DEC,∴△ABE∽△ECD,∴,∴AB•CD=BE•EC.【点评】本题主要考查了直径所对的圆周角的性质,相似三角形的判定和性质,能证得∠AEB=∠CDE 是解题的关键.18.如图,AB是⊙O的直径,BC是⊙O的切线,切点为点B,点D是⊙O上的一点,且AD∥OC.求证:AD•BC=OB•BD.【考点】切线的性质;圆周角定理;相似三角形的判定与性质.【专题】证明题.【分析】要证AD•BC=OB•BD,即要证AD:OB=BD:BC,于是求证△ABD∽△OCB即可.【解答】证明:∵BC是⊙O的切线,AB是圆的直径,∴∠CBO=∠D=90°.∵AD∥OC,∴∠COB=∠A.∴△ABD∽△OCB.∴AD:OB=BD:BC.∴AD•BC=OB•BD.【点评】本题利用了相似三角形的判定和性质求解.19.已知:如图,在⊙O中,CD过圆心O,且CD⊥AB,垂足为D,过点C任作一弦CF交⊙O于F,交AB于E.求证:CB2=CF•CE.【考点】垂径定理;相似三角形的判定与性质.【专题】证明题.【分析】连接BF,证所求的对应边成比例线段所在的三角形相似即可,即证△CBE∽△CFB.【解答】证明:连接FB,(1分)∵CD过圆心O,且CD⊥AB,∴=.(2分)∴∠CBE=∠F.∵∠BCE为公共角,∴△CBE∽△CFB.(4分)∴=.(5分)∴CB2=CE•CF.(6分)【点评】此题考查了垂径定理及相似三角形的判定和性质.20.已知D是BC边延长线上的一点,BC=3CD,DF交AC边于E点,且AE=2EC,试求AF与FB的比.【考点】平行线分线段成比例.【分析】过C作CG∥AB交DF于G,于是得到△CDG∽△BDF,△CEG∽△AFE,根据相似三角形的性质得到,,求得BF=4CG,AF=2CG,即可得到结论.【解答】解:过C作CG∥AB交DF于G,∴△CDG∽△BDF,△CEG∽△AFE,∴,,∵BC=3CD,∴=,∴=,∴BF=4CG,∵AE=2EC,∴=,∴AF=2CG,∴=.【点评】本题考查了相似三角形的判定和性质熟练掌握相似三角形的判定和性质是解题的关键.21.已知:如图,在△ABC中,∠BAC=90°,AH⊥BC于H,以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,试判断△BDH与△AEH是否相似,并说明理由.【考点】相似三角形的判定;等边三角形的性质.【分析】首先由在△ABC中,∠BAC=90°,AH⊥BC于H,证得△BHA∽△AHC,即可得=,又由以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,可得=,∠HBD=∠HAE,则可证得△BDH ∽△AEH.【解答】解:相似.理由:∵在△ABC中,∠BAC=90°,∴∠BAH+∠CAH=90°,∵AH⊥BC,∴∠AHB=∠CHA=90°,∴∠ABH+∠BAH=90°,∴∠BAH=∠CAH,∴△BAH∽△ACH,∴=,∵△ABD和△ACE是等边三角形,∴BA=BD,AC=AE,∠ABD=∠CAE=60°,∴=,∠HBD=∠HAE,∴△BDH∽△AEH.【点评】此题考查了相似三角形的判定与性质以及直角三角形的性质.注意证得△BAH∽△ACH是关键.22.如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC 边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.【考点】相似三角形的判定与性质;根据实际问题列一次函数关系式;勾股定理.【专题】代数几何综合题;数形结合.【分析】四边形PECB的周长为PE+EC+CB+BP,其中BC在直角△ABC中运用勾股定理可以求出,BP=AB ﹣AP=10﹣x,另外两条边均可根据△AEP∽△ABC,借助于比例线段,用含有x的式子表示出来.关键还需求出自变量x的取值范围,这可以令E点运行到C时,求特殊值.【解答】解:∵在△ABC中,∠C=90°AB=10,AC=8,∴BC=6.∵EP⊥AB且∠A为公共角,∴△AEP∽△ABC,∴.∵AP=x,∴,即AE=,PE=,∴.∴.当E与C重合时,CP⊥AB,∴△APC∽△ACB,∴CA2=AP•AB,∴82=10AP,AP=.因为P与A不重合,E与C不重合,所以.即.【点评】本题实际还是考查相似三角形的判定以及一次函数在几何图形中的应用.第21页(共21页)。
