最新古诺寡头竞争
古诺模型学习

古诺模型学习寡头竞争/垄断时的均衡情况这是最近经常听到和被问到的问题,在寡头垄断(Oligopoly),或者是寡头竞争的情况下,最后的均衡情况是怎么样的。
然后在现实世界里,什么情况下寡头垄断应该受到管制机构的调控。
在经济学中,对寡头垄断均衡的研究有很多,结果也有很大差异。
和其他经济理论一样,为了研究的需要,每一个寡头竞争模型的建立或者是结论的得出,都是在一定的假设条件下做出来的。
所以,在现实经济世界里的以这些理论作为指导,首先应该看到的是所研究的情形是否符合理论模型的条件。
一般情况,现实经济世界里的情况都远比理论要复杂得多。
正如张伯伦(E.H.Chamberlin)所阐述的一样,实际的市场没有完全的竞争和完全的垄断,而只有这两种要素的混合。
实际寡头竞争市场的复杂性在于,可能出现多种多样的“均衡”,并且是不稳定的。
这既取决于市场的本身构造,也取决于各公司的决策行为。
现在我们就用一个比较具体的例子通过不同的模型来描述这种不确定的均衡情况。
我们假定一个寡头垄断市场,有两家公司E1和E2,产量分别是q1和q2,成本函数为C1=20*q1, C2=20*q2*q2 (不方便打平方) (假设固定成本为零);市场价格由总产量Q=q1+q2决定,P=f(q1+q2) =400-2*(q1+q2)企业利润分别记作T1和T2, 总收入记作R1和R2, 总成本记作C1和C2。
首先,我们研究古诺(Cournot)模型下的均衡情况。
在这种情况下,T1=R1-C1=P*q1-20*q1=380*q1 – 2*q1*q1 – 2*q1*q2T2=R2-C2=P*q2-20*q2*q2=400*q2 – 2*q1*q2 – 4*q2*q2分别对以上两式求q1和q2的导数,求T1和T2最大值的条件:T1’(q1) = 380-4*q1-2*q2=0T2’(q2)= 400-2*q1 -8*q2=0–> q1=80, q2=30 ; P=180, T1=12600, T2=3600 ;q1=g(q2)=95-0.5*q2 ; q2=g(q1) =50-0.25*q1 (在以下的分析中会用到)以上便是古诺模型的解。
寡头竞争模型

q
c 2
R1 R2
((qq21cc))
可以看出,在古诺—纳会均衡中,每个企业都正确估计了对
手的产量(即
q1c
=
q1e
,
q
c 2
=
q
e 2
),从而获得自己的最大利
润
。
例1:
假设市场的需求函数为P=130-Q,P为 产品的市场价格,Q=q1+q2为市场供应 量,两家企业的边际生产成本为 MC1=MC2=10。求两企业在古诺均衡 状态下的产出、价格和利润?
三、存在N个企业时的古诺——纳什均衡
以上我们的分析是在两个企业的框架中进行的。下面我们考
虑存在 N 个企业时的古诺—纳什均衡。
假设产业中存在 N 个企业,这些企业符合古诺竞争一开始的
模型设定条件。将企业 i 的竞争对手的产出向量记为
q-i={q1, q2,……,qi-1,qi+1,…… ,qN}。
根据上面的分析,企业 1 面临的剩余需求曲线为
P=(130-q2)-q1
利润函数为π1=[(130- q2)- q1]q1-10 q1
利润最大化法则要求企业 1 的边际收益和边际成本满足
MR=MC,所以 130- q2-2q1=10
从而企业
1
的反应函数为
q1=60-
1 2
q2
同理,企业
2
的反应函数为
寡头竞争模型分类
博弈类型 决策变量
静态
产量 古诺模型
价格 伯川德模型
动态
斯塔克尔伯模型 价格领导模型
第一节 古诺竞争
古诺模型是19世纪著名的法国经济学家 Augustin Cournot于1838年发表的《对 财富理论的数学原理的研究》中提出。 古诺考虑两家相互竞争的矿泉水厂商如 何决定产量的问题。为简单起见,古诺 假设两家厂商进行的是静态博弈,即他 们同时决定产量大小。
寡头竞争.ppt

企业2的最优策略
pi
k1+k2
P(k1+k2)
k1 k2
r2 d2
D
q1,q2
生产能力的约束
D(p)是需求曲线,两条垂直的直线表示每家的生产能力。企业2 的生产能力大于企业1的生产能力k2 > k1 。第三条直线k1+k2代表 总的产业生产能力。假设两家企业的边际成本均为0。
R 2 ( y1 )
45
4
y1
.
古诺-纳什均衡
8
y*1,y*2 13,8.
13
48 y1
古诺竞争
练习:假设反需求函数为p(Q)=a-bQ, 两个企业的成本均为C (q)=cq。求解古诺竞争的均衡解。
提示:企业1的反应函数
q1* (q2
)
ac 2b
q2 2
古诺模型; 一个例子
y2
60
y1
2y2
15
2y2
0.
数量竞争; 一个例子
同样地, 给定y1, 厂商2的利润函数为 (y2;y1) (60 y1 y2 )y2 15y2
y22 .
因此, 给定 y1, 厂商2的利润最大化产出数量为解
y2
60
y1
2y2
15
2y2
企业1的最佳战略
企业1的最优定价取决于其对企业2定价的猜测。 假设企业1预计企业2的定价将高于垄断价格,那么企业1的最优战略
古诺模型推出的寡头产量之间的关系函数

古诺模型推出的寡头产量之间的关系函数古诺模型是经济学中的一种主要的理论模型,用来描述垄断市场的运作,即一个有限的几个参与者进入市场,受自身的成本限制,临近市场收支分析,探讨出了古诺说的寡头竞争模型,把寡头产量之间的关系函数推出来了。
一、什么是古诺模型
古诺模型是经济学中的一个主要的理论模型,由意大利经济学家廖博士于1893年提出。
古诺模型主要用来研究垄断市场竞争。
古诺模型被定义为有一个有限数量的竞争对手,他们之间在市场上经营,最终进行竞争,其竞争会影响产量、价格及其他支出。
二、古诺模型推出的寡头产量之间的关系函数
古诺模型里推出的寡头产量之间的关系函数也叫做“古诺公式”。
它是指寡头之间竞争产品的总量,公式为:
Q = N1 × q1 + N2 × q2 + ……. + Nn × qn
其中:
Q = 总量
Nn = 参与者数量
Qn = 每参与者产出量
古诺模型的关系函数中,参与者之间的竞争总是相互取舍,任何一方
都无法完全控制,结果往往是产量减少,价格上涨,且最终形成垄断
或者寡头市场。
三、总结
从古诺模型推出的寡头产量之间的关系函数来看,参与者之间的竞争
总无法决定最终的市场分配结果,总体来说,参与者的产量都会减少,价格上涨,最终形成一种垄断或者寡头市场环境,这种市场可能成为
资源的浪费。
因此,要建立一个有效的经济环境,必须健全竞争法律,加强反垄断审查,维护竞争性自由市场。
微观经济学(古诺模型)

微观经济学
第十二章 垄断竞争与寡头垄断
模型的求解
如果市场是完全竞争的,则所有企业的 利润最大化产量之和恰好等于 。 原因:在完全竞争条件下,利润最大化 的条件是价格等于边际成本。由于假设 边际成本为0,则价格也为0,;当价格 为零时,相应产量为 。
微观经济学
第十二章 垄断竞争与寡头垄断
模型的求解
1 2
- Q2
3 2
Q2
微观经济学
如果市场是垄断的,则垄断企业的利润 最大化产量为 2 。 原因:在垄断时,利润最大化的条件是 边际收益等于边际成本。由于假设边际 成本为0,而边际收益曲线与横轴的交 点正好是需求曲线与横轴交点的一半。
微观经济学
第十二章 垄断竞争与寡头垄断
模型的求解
双寡头时,企业1的总收益函数为
R1 PQ1= - Q1 Q2 Q1
5、每家企业对对方的情况了如指掌, 并总是在把对方的产量看成固定 不变的情况下来决定自己的利润 最大化产量。
微观经济学
第十二章 垄断竞争与寡头垄断
模型假设
假设在该寡头市场,市场需求曲线 P - Q1 Q2 在该式中, 和 均为大于零的常数; Q1 和 Q2 分别是企业1和企业2的产量, 两者之和恰好等于整个市场的全部产 量Q。
第十二章 垄断竞争与寡头垄断
九、古诺模型
微观经济学
第十二章 垄断竞争与寡头垄断
模型假设
1、其他企业的产量或价格不随寡头 企业的改变而改变。
2、双寡头,即市场上只有两家企业。 3、两家企业生产的产品完全相同。
微观经济学
第十二章 垄断竞争与寡头垄断
模型假设
4、两家企业的生产成本均为0,且பைடு நூலகம் 临的都是线性需求曲线。
note8补充:古诺均衡、伯川德均衡与不完全竞争解析

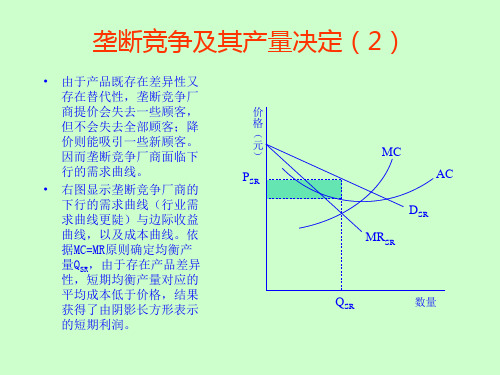
第六节 垄断竞争
短期垄断竞争市场的特征
j ( p) q j ( p) p j c j (q j ( p))
D需求曲线表示在垄断竞争生产集 团的某个厂商改变产品价格,而且 集团内的其他所有厂商也使产品价 格发生相同变化时,该厂商的产品 价格和销售量之间的关系。
的,并有x(c)>0
这时,p1*=p2*不再是一个均衡。因为厂商2在 p2*=c不能满足所有需求,则厂商1预期如果他 使p1稍高于c也可以有一个正的销售量,所有 他有积极性偏p1*=c
关于生产能力约束
由厂商2满足的需求
p(q )
p1 p2 c
q
x( p1)
x, q
厂商1的销售量
当存在生产 能力约束时, 竞争通常不会 使得价格下降 到成本水平。
垄断竞争厂商的长期均衡条件为:
p(q) p(q1 q2e )
max{ (q1 )
p(q1
q2e
)q1
C (q1 )}
反应函数: q1
f1(q2e )
q2 f2 (q1e )
古诺均衡
古诺均衡是指存在着这样一对产量,使得两个企
业的产出满足:
q1 q2
ff12((qq2*1*))
古诺均衡包含:
1、给定对于另一个企业的产量信念,每个企业都做出了 自己最优的产量选择,使自己的利润极大化。
p* c t
第三节 Stackelberg模型 ---先行一步优势
假定:领导者具有先行一步的优势;一旦 自己宣布一个产量,追随型企业会做出反 应,这就要求
求解思路:反向归纳法,即先求追随者的 反应函数。
垄断竞争与寡头垄断

过去的10年里,苹果公司借力这几款明星产品销售额迅速增长 ,公司利润率持续处于行业内高水平。2004年以来,苹果公司一直保 持着两位数的增长率,平均利润率近32%。同时期,索尼公司的增长 率最高为13%,最低为负增长,其平均利润率近23%。
今年来,苹果产品销量继续增加:
第二节 寡头垄断市场
寡头垄断市场是介于垄断竞争与完全垄断之间 的一种市场类型。在这样一种市场条件下,厂商如 何决定自己的行为,决定自己的均衡价格与均衡产 量呢?
iPHONE
iphone相关数据
先来看iPhone。瑞士信贷的报告称,苹果iPhone自五年前发布后至 今,虽然不乏有实力的对手出现,但从系统、软件、芯片、品 牌等诸多因素构成的生态系统看,对手很难缩小与苹果iPhone 的优势差距。 在过去的2010年,苹果iPhone占据着智能手机市场16%的份额,位 居全球智能手机三甲之列,而在营收上,苹果凭借着这16%的份额获 得了29%的营收,排在第一位。 在以App Store为代表的软件应用上,HIS的统计显示,其收入达到 17.8亿美元,占据了四大程序商店总收入的82.7%,遥遥领先于同行 的对手。而ABI研究公司发布的有关应用下载的研究数据称,近79亿 个应用程序已被从移动应用商店中下载,这之中的56亿个来自于苹果 的App Store,占了70.9%。 总之,苹果iPhone不但在智能手机的整个生态系统,就是在生态系 统的各主要组成部分上都有着压倒性的优势。
2001年10月, 苹果公司推出第一款Mp3播放器( iPod G1)。
IPOD推出后, 大大改变了公司长期低迷的盈利状况。 该产品问世后,创造了惊人的销售奇迹,五年全球累计销量超过了6000万台。 纳斯达克的股票价格也随着iPod产品的不断升级和其销量的不断上升而一路走 高,从2001年9月每股不到10美元升至2007年1月16日最高的每股97美元;2012年5 月4日股价高达565.25美元。苹果电脑的销量也被iPod热销带动, 该公司财务报告 ,苹果电脑的销量增长了28%,销售额增长了40%。 在iPod成功的基础上,苹果公司的产品范围还得到了横向拓展,从apple tv(传 输转换装置)扩展到iPhone。
寡头合作竞争基本概念

1.寡头竞争及形式 ------ ——1页2.纳什均衡及博弈均衡-■--------- 2页3. 资源配置效率 ------- ——2页4. 卡特尔模型 --------- ---3页5.双寡头模型 --------- ---3页寡头(Oligopoly)市场又称为寡头垄断市场,它是指少数几家厂商控制整个市场的极大部分产品的生产和销售,因此行业的竞争只是在几家大企业之间展开。
寡头市场被认为是一种较为普遍的市场组织,西方国家中不少行业都表现出寡头垄断的特点,例如,美国的汽车业、电气设备业、罐头行业等,都被几家企业所控制。
1、寡头竞争是竞争和垄断的混合物,也是一种不完全竞争。
在垄断竞争的条件下,市场上有许多卖主,他们生产和供应的产品不同。
在寡头竞争的条件下,在一个行业中只有少数几家大公司(大卖主),它们所生产和销售的某种产品占这种产品的总产量和市场销售总量的绝大部分比重,它们之间的竞争就是寡头竞争。
显然,在这种情况下,它们有能力影响和控制市场价格。
在寡头竞争的条件下,各个寡头企业是相互依存、相互影响的。
各个寡头企业调整价格都会马上影响其他竞争对手的定价政策,因而,任何一个寡头企业做出决策时都必须密切注意其他寡头企业的反应和决策。
寡头竞争态势下,由于部分企业基本控制了市场,在一段时间内,别的企业要进入是相当困难的,但并不等于永远没有市场机会。
寡头之间仍然存在竞争,他们互相依存,任何一个企业的独立活动都会导致其他几家企业迅速而有力的反应而难独自奏效,它们一般都具有很强的成本意识。
寡头竞争的形式:①完全寡头竞争。
在这里,各个寡头企业的产品都是同质的(如钢铁、石油、轮胎等)。
用户对这些企业的产品并无偏好,不一定非得买哪一家企业或哪一总品牌的产品不可。
例如,用户购买钢材时可按钢种、型号、规格等技术指标定货,而不一定非得买哪一家公司的钢材。
因为用户认为这些寡头企业是无区别的,所以完全寡头竞争又叫作无区别的寡头竞争。
最新寡头竞争情况下价格刚性古诺模型卡特尔教学讲义PPT课件

寡头垄断的例
• 美国 – 石油行业中八大公司拥有60%的炼油能力。如美孚石油公司提价必须 考虑其它公司的反应 – 汽车行业:通用汽车、福特和克莱斯勒 – 电气行业许多部门被通用电气和西屋电子所垄断
• 英国
– 糖果行业三大寡头:雀巢、玛氏、加德布里.希威皮斯 – 银行业三大寡头:National Westminster, Barclays, Midland and Lloyds
寡头竞争情况下价格刚性古诺 模型卡特尔
▪垄断竞争情况下的市场需求
垄断竞争的定义
垄断竞争monopolistic:是指有许多厂商在市场上 销售近似但不完全相同的产品。
➢ 垄断竞争市场模式的提出
本世纪20年代末30年代初以前,经济学上主要只有完全竞争和完 全垄断两种市场模型。西方经济学家认为将这两种市场结合在一起 便可以分析任何一种案例。
• 如果边际成本是相同的,则产量分配均匀 • 如果边际成本不同,则产量分配不同
– 边际成本小的,产量分配得多 – 边际成本大的,产量分配得少
– 横向兼并、纵向兼并、混合兼并 – 减少竞争对手
如何衡量寡头垄断?
• 行业集中度
– 集中度指数concentration index
• 赫芬达尔指数(H指数),指数越大,市场集中度 越高
寡头垄断模型
• 价格刚性和弯折的需求曲线(kinked demand curve)
• 古诺模型Augustin Cournot model
新企业进入 其它企业模仿使产品差异性受影响或增加广告费
任何短期内的亏损也会在长期消失。
亏损的企业会离开
垄断竞争是否存在 社会资源的浪费?
P
MC
古诺模型双寡头计算题

古诺模型双寡头计算题古诺模型作为现代经济理论的重要组成部分,被广泛应用于市场竞争模拟中。
其中,双寡头市场竞争是一种非常经典和常见的情形。
在双寡头模型中,有两个企业A和B,他们生产同一种商品,市场中的消费者则将商品的需求分成两部分,分别对这两家企业进行购买。
在这种情况下,企业A 和企业B会通过制定价格互相竞争,从而争夺市场份额。
在这一过程中,企业A的销售额和市场份额分别为qa和fa,同理,企业B的销售额和市场份额分别为qb和fb。
假设市场总需求为D,市场价格为p,则有以下的条件:p=a-b(qa+qb)fa=qa/Dfb=qb/D其中,a、b均为常数,有时将a称作基准价格,b则为价格弹性系数。
在这种情况下,企业A和企业B的目标很简单,就是尽可能地获得更多的市场份额和利润。
因此,企业A和企业B需要定价,以便在市场竞争中取得优势。
假设企业A设定的价格为pa,企业B设定的价格为pb。
则有:qa=(pa+fb)/2bqb=(pb+fa)/2b当然,如果企业A的价格高于企业B,则企业A的市场份额将下降,而企业B 的市场份额将上升。
因此,企业A面对的一个很重要的问题就是要确定自己的价格,以便获得最大的市场份额。
与此同时,企业B也需要在价格和市场份额之间取得平衡。
假设企业B采取的策略是与企业A的价格相同,则有:fa=fqqb=D-qap=a-b(qa+D-qa)以上就是双寡头市场竞争中企业A和企业B的策略。
如此一来,我们就可以应用相关的计算公式,在企业A和企业B之间计算,以确定他们能够获得的市场份额和利润。
当然,在实际中,双寡头市场的竞争远比上述过程中复杂。
不同企业的战略调整,市场需求的波动,消费者购买习惯的变化,都会影响企业之间的竞争格局。
但是,古诺模型为我们提供了一个理论模型,让我们更好地理解企业间的市场竞争,并更好地制定应对策略。
总的来说,双寡头市场竞争计算题是一个很好的训练案例。
它不仅能够帮助我们更好地理解经济学理论,同时也可以让我们学到许多模拟和计算方法,增强我们在实践中解决问题的能力。
古诺竞争寡头垄断
上 厂商A 下
左 1,2
厂商B
右 0,1
2,1
1,0
博弈论与策略行为(4):囚徒困境
什么是寡头垄断市场?(2)
• 与寡头垄断市场结构相联系,寡头厂商之间关系兼有竞争和串谋 的两面性。寡头厂商市场控制力大小和利润水平高低,取决于它 们之间行为的相互作用方式。如果它们更多采取合作和串谋而不 是竞争方式,寡头们有可能在在显著高于边际成本水平上制定价 格,从而获得丰厚利润。另一方面,寡头之间也可能发生激烈的 竞争,并降低它们获得的利润。
博弈论与策略行为(1):学科概念
• 博弈论(Game Theory)又名对策论,游戏论。顾名思义,是 一门研究互动关系的游戏中参与者各自选择策略的科学,换言 之,是研究机智而理性的决策者之间冲突及合作的学科。博奕 论把这些复杂关系理论化,以便分析其中的逻辑和规律,并对 实际决策提供指导或借鉴。
• 一个所谓游戏至少需要三个要素:(1)博弈或游戏参加者。博 奕论分析假定参与者都是机智而理性的。(2)行动或策略空间。 博奕参与者必须知道他自己及其对手伙伴的策略选择范围,并 了解各种策略之间的因果关系。(3)有可评价优劣高下的决策 行为结果。博弈论用数字表示这类结果,并称之为支付 (Payoff).上述3部分描述了一个博弈的规则或结构。
博弈论与策略行为(9):序列博弈
• 至此讨论的博弈是参与者同时选择。在序列博弈(Sequential Game)中,各 博弈方先后依次行动。下面支付矩阵描述了一个博弈,如果同时行动,它有两 个纳什均衡点(“甜,咸”与“咸,甜”)。假定厂商A可以先推出甜饼干 (如较快投入生产),我们就有了序列博弈:A先作决策,B随后选择。A决策 时必须考虑竞争者的理性反应:它知道不论自己推出那种饼干,B出于自身利 益会推出另一种。因而A推出甜饼干,B在给定A决策时选择咸饼干;给定B的 选择A的选择仍然最佳。结果两个纳什均衡点收敛为一个(下,左)。其中A 由于具有先行者优势(First Mover’s Advantage)而得到较大利益,
寡头市场古诺模型的结论

寡头市场古诺模型的结论
“古诺小组结论”是一种描述多数控制垄断市场的经济模型,由国际知名的经济学家一范·古诺(Johan van Genuchen)最先提出。
古诺模型的结论认为,在少数控制的市场中,即使在有十几位独立企业的情况下,如果几家企业都可以给出相同的价格,那么也会存在竞争的危险性。
古诺小组指出,市场上存在少数控制者或者称作“寡头”,会占据市场绝对大多数的市场份额,而他们一直保持守恒竞争阻止新企业进入市场,从而获取超额利润,同时造成企业家无法真正发挥出最优价格,也就是垄断价格。
高校与高等教育具有很强的多数控制垄断能力,特别是对于前沿的科学研究和最新技术的发现,大多数顶级高等学府有着独特的竞争优势,资源和技术在高校内部是垄断的,学生只能选择拥有强大的教学资源和研究基地的高校。
结论:因此,根据古诺小组的结论,高校和高等教育的存在,伴随着多数控制者的存在,很可能会存在竞争危机,导致企业家不能发挥价格出最佳效果,从而降低教育资源和机会的分配效率,造成学者可能无法拥有更多的机会和适合的学习环境。
第三章 古诺竞争

本书由vince上传于世界工厂--学堂中心精品下载栏目
(3)新技术和利润
• 实例:生产化学品的两家企业,企业1使用旧 技术,边际成本为15元;企业2使用新技术, 边际成本为10元。目前市场的均衡价格16元, 需求量为8.33。企业1面临着企业2的竞争压 力。请问:企业1愿意支付新技术多少费用?
本书由vince上传于世界工厂--学堂中心精品下载栏目
本书由vince上传于世界工厂--学堂中心精品下载栏目
q1 QN q1
N
q2 *( q1 ) N’’ N’
45
。
不对称成本 变化会引起 均衡向一侧倾斜
q1*( q2 )
q2N 汇率下降后的古诺均衡
本书由vince上传于世界工厂--学堂中心精品下载栏目
q2
校准与贬值评估
先推算有关参数,这一过程称为校准。 能够掌握的市场参数:售价、边际成本和汇率 贬值前售价P=13.33,边际成本MC=10,由 P=(a+2c)/3,解出a=20,c1=c2=10; 贬值后,c2=10,c1=10/1.5=6.66,根据份额公式 s1=71%,即市场份额会从各50%上升到71%。 这就是贬值的好处。
本书由vince上传于世界工厂--学堂中心精品下载栏目
q1 qC q1+q2 = qC qM N q1+q2 = qM
qM
本书由vince上传于世界工厂--学堂中心精品下载栏目
qC
q2
*古诺均衡、垄断和完全竞争的比较
3、模型的应用:比较静态分析
• 比较静态分析方法:把连续的市场变化 分成若干种典型的状态,如两个均衡状 态,与其所发生的外生条件进行对比, 预测均衡结果的变化。 • 问题: 1、投入成本变化会引起均衡如何变化? 2、汇率变化会引起市场份额如何改变? 3、技术变化会引起利润如何变化?
古诺寡头竞争

古诺(Cournot)产量竞争模型——双寡头古诺竞争模型法国经济学家奥古斯丁·古诺于1838年首次提出了双寡头进行产量竞争的静态博弈模型,这实际上是以后纳什均衡思想的最早阐述。
这一模型是用博弈论研究产业组织理论的重要基础,其后这一模型被扩展到对多个寡占厂商行为的研究。
一、在古诺模型中两个寡头的行为及其有关条件的假定①两个寡头厂商生产的产品是同质或无差别的;②每个厂商都根据对手的策略采取行动,并假定对手会继续这样做,据此来做出自己的决策;③为方便起见,假定每个厂商的边际成本为常数,并假设每个厂商的需求函数是线形的;④两个厂商都通过调整产量来实现各自利润的最大化;⑤两个厂商不存在任何正式的或非正式的串谋行为。
二、对古诺模型进行博弈分析设q1、q2分别表示企业1和企业2生产的同质产品的产量,市场中该产品的总供给Q=q1+q2,令P(Q)=a-Q表示市场出清时的价格(更精确地表述为:Q<a时,P(Q)=a-Q,Q>a时,P(Q)=0)。
设企业i生产qi 的总成本Ci(q i)=cq i,即企业不存在固定成u i (s i , s j ) ≥ u i (s i , s j )max π i (q i , q j ) = max q i [a - (q i + q j ) - c ]2 (a - q j- c )本,且生产每单位产品的边际成本为常数 c (这里假定 c < a )。
根据古诺的假定,两个企业同时进行产量决策。
假定产品是连续可分割的,由于产出不可能为负,因此,每一企业的战略空间可表示为 S i = [0, ∞],其中一个代表性战略 s i 就是企业选择的产量 q i ( q i ≥ 0 )。
假定企业的收益是其利润额π用 u i (s i , s j ) 表示,则π i (q i , q j ) = q i [ p (q i + q j ) - c ] = q i [a - (q i + q j ) - c ](1)若一对战略( s i * , s j * )是纳什均衡,则对每个参与者 i ,,s i * 应满足* * *(2)(2)式对 s i 中每一个可选战略 s i 都成立。
竞争策略-实例分析古诺双寡头竞争各模型(PDF7页)

∂π = 0 对 Q 求偏导 ∂Q ,即
100 − 2Q = 0
解得市场总利润最大时的总产量是: Qm = 50
-2-
垄断利润: 两个企业的合谋产量: 合谋利润:
π m = (130 − Qm )Qm − 30Qm = 2500 qm = Qm 2 = 25 π m 2 = 1250
⎧⎨⎩ qq12∗∗
= (a + c2 − 2c1) = (a + c1 − 2c2 )
3 3
假设两个企业具有相同的边际成本 c1 = c2 = c ,这时古诺模型的
均衡产量为
qc = q1 = q2 = (a − c) 3
均衡价格为
pc = p1 = p2 = (a + 2c) 3
均衡利润为
π c = π1 = π2 = (a − c)2 9
2. 用古诺各模型解决同一产出问题的原理及算法
2.1 古诺模型的原型
2.1.1 应用古诺模型原型的原理
古诺寡头垄断模型是产业组织理论中十分基本的模型,它是研究企业竞争策略等经济管
理问题的基础。设有两个企业生产完全可以替代的同质产品,它们在市场上进行产量竞争,
即相互提出自己的产量,以使利润达到最大。分别以 q1, q2 表示它们的产量,并记 Q = q1 + q2
− ci
− 2qi
=0
Ri (q j ) = qi = (a − q j − ci ) 2
-1-
(2)类似可得企业 j 关于企业 i 的产量的反应函数
Rj (qi ) = q j = (a − qi − c j ) 2
(3)两条反应曲线的交点即为纳什均衡,解得
2.3.2 利用不完全信息下的古诺模型解决实际问题
库诺特寡头竞争模型(1)

总结
通过分析, 可以总结出具有指导意义的一些主要结 论: ( 1) 根据库诺特模型的假设条件推导出了该动态库 诺特模型长期是趋于稳定的, 其稳定性不依赖于信 息的获取程度. ( 2) 寡占市场中, 信息透明的一方( 如 A 厂商) 获取 隐藏信息的一方( 如 B 厂商) 的信息愈多时, 其均衡 产量愈大; 相应地, 信息被获取的一方的均衡产量却 随之降低; 当获取信息的一方掌握的信息量达到一 定程度时, 其均衡产量则会超出对方.
两寡头博弈过程 第二轮
P
根据第一轮的博弈经验, A厂商预期B进入后留 P* 下的市场容量为Q*-Q2 =3Q*/4,并第二次决定 自己的最优产量, 最优 产量为3Q*/8,与上一轮 相比,A厂商的产量减 少了Q*/8.
F H G Q
O
Q2
Q3
Q*
第二轮
B也第二次进入市
场,面临的剩余市 场容量是Q4=5Q*/8, 即Q*-3Q*/8,决定 的最优产量是 5Q*/16,与上次Q2 相比,增加了 Q*/16.
大家思考一下
为什么在奇瑞、吉利、长城以及比亚迪等中
国自主车出现后,国外品牌的汽车价格下降 很多。如以前一辆捷达就要20多万,现在性 能车型差不多的长城腾翼C30,奇瑞A3等就 7~9万,而一旦中国的SUV,如长城的哈弗 被市场认可后,外国品牌的的SUV就不断降 价?经常看到的本田CR-V,要20万,自主品 牌在安全性还要好的情况下,也就14万左右。 说明了有了竞争之后,价格下降,产量上升。
Байду номын сангаас
扩展
*企业技术创新给我们带来的利益
1. 2.
3.
4.
寡头企业通过技术创新投资可以提高企业的商品市场占有 份额、降低产品价格,并使企业赚取更多利润; 两家寡头企业同时进行技术创新比只有一家企业进行技术 创新给社会及消费者带来更大利益; 合谋垄断条件下,进行技术创新后社会总供给增加、产品出 清价格降低,技术创新给消费者带来更大利益; 两家寡头企业联合进行技术创新,相对于一家企业独立创新 中,只有技术创新的固定投入使得创新产品的单位成本降低 的幅度满足一定条件时,联合创新的产品价格才会降低,产品 的总产量增加,产品总利润提高。基于上述结论得出技术创 新投资的可行域。
古诺竞争模型

Figure 14.6 Incumbent Loss if it Deters Entry Incumbent goes to highest point on thick
在位厂商吓阻对手的其他策略
• • • • 增大投资 提高自己的固定成本减低边际成本 提高自己成本同时提高对手的成本 …
Figure 14.7 Investment Game Tree: investment is profitable only because it deters entry
q2
2 3
best response function for firm 1
o
1 3
q1
简例1
• 类似地,可以算出厂商2 的反应函数: q2= (1- q1-1/3)/2 • 两个反应函数的曲线的焦 点就是Nash均衡。 • 这时 q1 = q2 = 2/9
q2
2 3
RF(1)
NE
RF价的博弈树
Figure 14.4 Cournot and Stackelberg Equilibria -profit curve if incumbent can move first
Figure 14.5 Incumbent Commits to a Large Quantity to Deter Entry incumbent moves along thick line
• 由此得到: q1* =1/3 • 代如厂商2的反应函数: q2*=1/3-q1*/2=1/6 • 厂商1的产量是厂商2 的两倍.
限制性定价
• 在斯塔克尔伯格竞争中,如果跟随厂商的 固定成本f比较高,领导厂商有可能生产高 于斯塔克尔伯格均衡的产量,让市场价格 足够低(如果跟随厂商也进入的话),使 得跟随者得不到正常利润因而决定不进入 市场。领导厂商这种行为叫做限制性定价。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
古诺(Cournot)产量竞争模型——双寡头古诺竞争模型
法国经济学家奥古斯丁·古诺于1838年首次提出了双寡头进行产量竞争的静态博弈模型,这实际上是以后纳什均衡思想的最早阐述。
这一模型是用博弈论研究产业组织理论的重要基础,其后这一模型被扩展到对多个寡占厂商行为的研究。
一、在古诺模型中两个寡头的行为及其有关条件的假定
①两个寡头厂商生产的产品是同质或无差别的;
②每个厂商都根据对手的策略采取行动,并假定对手会
继续这样做,据此来做出自己的决策;
③为方便起见,假定每个厂商的边际成本为常数,并假
设每个厂商的需求函数是线形的;
④两个厂商都通过调整产量来实现各自利润的最大化;
⑤两个厂商不存在任何正式的或非正式的串谋行为。
二、对古诺模型进行博弈分析
设q
1、q
2
分别表示企业1和企业2生产的同质产品的产量,
市场中该产品的总供给Q q q
=+
12,令Q
a
Q
P-
=
)
(表示市场出清
时的价格(更精确地表述为:Q a<时,P Q a Q
()=-,Q a>时,P Q
()=0)。
设企业i生产q
i 的总成本C q cq
i i i
()=,即企业不存在固定成
本,且生产每单位产品的边际成本为常数c(这里假定c a<)。
根据古诺的假定,两个企业同时进行产量决策。
假定产品是连续可分割的,由于产出不可能为负,因此,每一企业的战略空间可表示为[]S i =∞0,,其中一个代表性战略i s 就是企业选择的产量i q (q i
≥0)。
假定企业的收益是其利润额π,
用),(j i i s s u 表示,则
πi i j i i j i i j q q q p q q c q a q q c (,)[()][()]
=+-=-+-
(1)
若一对战略(**j i s s ,)是纳什均衡,则对每个参与者i ,*i s 应满足
)
,(),(*
*
*
≥j i i j i i s s u s s u
(2)
(2)式对i s 中每一个可选战略s i 都成立。
在古诺的双头垄断模型中,上面的条件可具体表述为:若一对产出组合(,)q q 12**为纳什均衡,则对每一个企业i ,q i *应为下面最大化问题的解:
max (,)max [()]00≤≤∞
*
≤≤∞
*
=-+-q i i j q i i j i i q q q a q q c π
设q a c j *<-,企业i 最优化问题的一阶条件为:
q a q c i j =
--*
12
() 也即是,若产量组合(,)q q 12**为纳什均衡,则企业的产量选择必须满足:
)
(2
1
2
1
c q a q --=*
(3)
)
(2
1
1
2
c q a q --=*
(4)
联立以上两式,解得q q a c 123
**==-
三、用反应函数或反应曲线来说明纳什均衡时的产量 等式)(2
1c q a q j i
--=
*给出的是针对企业j 的均衡战略s j *
时企业i 的最优反应,同样的方法可以推导出针对企业 1 的一个任意战略企业2的最优反应,以及针对企业2的任意一个战略企业1的最优反应。
假定企业1的战略q 1满足c a q -<1,企业2的最优反应为
R q a q c 2111
2
()()=
--
(5)
类似地,如果c a q -<2,则企业1的最优反应为:
R q a q c 1221
2
()()=
-- (6)
以上两式分别是企业2对企业1产量q 1的反应函数和企业1对企业2产量q 2的反应函数。
在这里,反应函数表示的是每个企业的最优战略(产量)是另一个企业产量的函数。
由于这两个函数都是连续的线形函数,因此可用坐标平面上的两条直线表示(见图1)。
这两个最优反应函数表示的曲线为反应曲线。
两条反应曲线只有一个交点,其交点就是纳什均衡时两个企业的产量组合。
以上假定两个企业不存在任何形式的串谋。
现在假定市场上的两个寡头垄断企业通过串谋如同一个垄断者一样行
事,使两企业总的利润最大化。
这时,两企业的产量之和q 1+q 2应等于垄断产量q m (如2/21m q q q ==)。
通过计算可得:
垄断企业的最优产量为:q a c m =-12
()
市场垄断利润为: πm
a c =
-()2
4
两个企业平分垄断利润: ππ1
2
28
m
m
a c ==
-()
古诺均衡时的企业利润水平为:
9
)(),(),(2
212211c a q q q q -=
=*
*
*
*
ππ
下面通过图1比较古诺均衡、竞争均衡和企业串谋情况下的产量、价格和利润水平。
由此可见,寡头垄断条件下企业的古诺竞争产量大于垄
断产量,而企业所得利润大于古诺竞争均衡时的利润水平。
但现实是,每一家企业都有动机偏离垄断条件下的产量水平,因为垄断产量较低,相应的市场价格就比较高。
在这种条件下,任何一方都企图扩大产量,获取更多的利润。
由此,将导致市场供给的增加,价格的降低。
只有纳什均衡产量才是双方稳定的产量组合。
四、多家企业的古诺竞争模型
设古诺模型中有n 家厂商,q i 为厂商i 的产量,Q q i i n
==∑1为
市场总产量,p 市场出清价格,且已知P Q a Q ()=-。
假设厂商
i 生产q i 产量的总成本为C q cq i i i ()=,也就是说没有固定成本,
且各厂商的边际成本都相同(c a <)。
设各厂商同时选择产量,则
πi i i i j j i n
i i pq cq a q q q cq =-=---≠∑()
(8.7)
其中,i =1,2,…n
将利润函数对q i 求导,并令导数为0,得
∑≠=---=∂∂n
i
j j i i c q q a q 02π
解得各厂商对其他厂商产量的反应函数为:
q a q c i j j i n
=--≠∑()/2
(8.8)
根据n 个企业之间的对称性,可知q q q n 12***=== 成立 代入(8.8)式,得
q q q n
12***
=== =a c n -+1
行业总产量为: q n a c n j j n
*==-+∑()1
1
市场价格为: 1
1)(++=
+--
=n nc
a n c a n a p 每
个企业的
利
润
:
2
2
)1()(1]1)([)(+-=
+-⋅-+--=-=*
n c a n c a c n c a n a q c p j
j π
需注意的是,在古诺均衡时,价格高出边际成本的幅度为:
p c a n a c n c a c n -=-
-+-=-+>()11
显然,lim()n p c →∞
-=0 这说明,当企业个数无穷多时,产出和价格均趋于完全竞争条件下的均衡水平,市场结构会趋于完全竞争市场;
当n=1时,该市场即为完全垄断市场,厂商所提供的产量只是完全竞争市场的1/2,而价格则比完全竞争价格高出()a c -/2,这意味着完全垄断厂商将比竞争厂商获取更高的利润;
当n=2时,即为古诺揭示的双边寡头垄断模型,两个寡头厂商所提供的市场产量只是完全竞争市场的2/3,价格比完全竞争价格高出()a c -/3,但比完全垄断要低()a c -/6。
通过以上分析可知,在一个产业中,如果新企业不断进入,市场产量将会不断增加,而价格将会下降,从而有助于增加消费者的福利。
当新进入企业数量增加到一定程度,市
场结构将趋近完全竞争状态。
这说明,通过降低产业进入壁垒或放松进入管制,使潜在进入企业能够顺利进入行业,并对产业中原有企业的市场地位形成一种威胁,就能够降低产业市场价格,增加产量,提高资源配置效率。
