求正弦余弦函数的单调区间
1.4.2第2课时 正、余弦函数的单调性与最值 课件

第一章 三角函数
(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时, 要注意使用复杂函数的判断方法来判断. 2.解析正弦函数、余弦函数的最值 (1)明确正弦、余弦函数的有界性,即|sin x|≤1,|cos x|≤1. (2)对有些函数,其最值不一定就是1或-1,要依赖函数的定 义域来决定. (3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数求最值时,通常利 用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的 形式求最值.
第一章 三角函数
栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π+2kπ,74π+ 2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
【名师点评】 正弦、余弦函数单调区间的求解技巧: (1)结合正弦、余弦函数的图象,熟记它们的单调区间. (2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采 用“换元”法整体代换,将ωx+φ看作一个整体,可令“z= ωx+φ”,即通过求y=Asin z的单调区间而求出函数的单调 区间.若ω<0,则可利用诱导公式将x的系数转变为正数.
栏目 导引
第一章 三角函数
跟踪训练
1.求函数 y=sin(π3-12x),x∈[-2π,2π]的单调递增区间. 解:y=sin(π3-12x)=-sin(12x-π3). 由 y=sin x 与 y=-sin x 的图象关于 x 轴对称可知,y=sin x 的递增 区间就是 y=-sin x 的递减区间.因此,要求 y=-sin(12x-π3)的递 增区间,只要求出 y=sin(12x-π3)的递减区间即可.
正弦余弦函数的性质

y=sinu y=|sinu|
2 3 x [k , k ], k Z y为增函数 4 4 x [k , k ], k Z y为减函数 4 4
正弦、余弦函数的奇偶性、单调性
小 结:
奇偶性 [ 正弦函数 奇函数 单调性(单调区间)
+2k, +2k],kZ 单调递增 2 2 3 [ +2k, +2k],kZ 单调递减 2 2
正弦、余弦函数的奇偶性、单调性
例1 不通过求值,指出下列各式大于0还是小于0: (1) sin(
) – sin( 18
10
)
解: 2 10 18 sin(
5
2
又 y=sinx 在[
)
10
) < sin(
18
即:sin( 18 ) – sin( 10 )>0
17 cos( 17 )=cos 4 4
, ] 上是增函数 2 2
(2) cos( 23 ) - cos( 解: cos( 23 )=cos 23 5 5
0
) - cos( 从而 cos( 23 5
17 ) 4
=cos
cos
3 5
4
<cos 4
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
y=sinx
;/ 小程序制作 微信小程序制作;
给送到了姑素家大长老大夫人那里,由她带晴文婷给带大了."
三角函数奇偶性、单调性

)-
cos( 17 )
4
解: cos( 23 )=cos 23
5
5
=cos 3 5
cos( 17 )=cos 17
4
4
=cos
4
0 3
45
cos 3 <cos
5
4
又 y=cosx 在 [0, ]上是减函数
3
即: cos 5
– cos
4
x∈ R
[-1,1]
x= 2kπ时 ymax=1 x= 2kπ+ π时 ymin=-1 周期为T=2π
偶函数
在x∈[2kπ, 2kπ+ π ]
上都是增函数 ,
在x∈[2kπ- π , 2kπ ]
上都是减函数 。
(kπ+
π
2
,0)
x = kπ
正弦、余弦函数的奇偶性、单调性
例1 不通过求值,指出下列各式大于0还是小于0:
2
2
O
3
2 u
2
2
-1
y=y-=|ssiinnuu|
即: 增区间为 kuk,kZ
减区间为 k2 uk,kZ
k3xk,kZy为2增函数
k4xk4,kZy为减函数
4
4
2
4
所以:单调增区间为
[k2 ,k8 3](kZ)8
单调减区间为 [k38,k8 7](kZ)
(2) y=2sin(-x )
8
8
解:y=2sin(-x ) = -2sinx
函数在 [
2
Байду номын сангаас
+2k,
【高中数学必修四】第1章 正弦函数、余弦函数的性质(二)

1.4.2 正弦函数、余弦函数的性质(二)学习目标 1.掌握y =sin x ,y =cos x 的最大值与最小值,并会求简单三角函数的值域和最值.2.掌握y =sin x ,y =cos x 的单调性,并能利用单调性比较大小.3.会求函数y =A sin(ωx +φ)及y =A cos(ωx +φ)的单调区间.知识点一 正弦、余弦函数的定义域、值域 观察下图中的正弦曲线和余弦曲线. 正弦曲线:余弦曲线:可得如下性质:由正弦、余弦曲线很容易看出正弦函数、余弦函数的定义域都是实数集R ,值域都是[-1,1]. 对于正弦函数y =sin x ,x ∈R ,有:当且仅当x =π2+2k π,k ∈Z 时,取得最大值1;当且仅当x =-π2+2k π,k ∈Z 时,取得最小值-1.对于余弦函数y =cos x ,x ∈R ,有: 当且仅当x =2k π,k ∈Z 时,取得最大值1; 当且仅当x =(2k +1)π,k ∈Z 时,取得最小值-1. 知识点二 正弦、余弦函数的单调性思考1 观察正弦函数y =sin x ,x ∈⎣⎡⎦⎤-π2,3π2的图象.正弦函数在⎣⎡⎦⎤-π2,3π2上函数值的变化有什么特点?推广到整个定义域呢?答案 观察图象可知:当x ∈⎣⎡⎦⎤-π2,π2时,曲线逐渐上升,是增函数,sin x 的值由-1增大到1; 当x ∈⎣⎡⎦⎤π2,3π2时,曲线逐渐下降,是减函数,sin x 的值由1减小到-1. 推广到整个定义域可得当x ∈⎣⎡⎦⎤-π2+2k π,π2+2k π(k ∈Z )时,正弦函数y =sin x 是增函数,函数值由-1增大到1; 当x ∈⎣⎡⎦⎤π2+2k π,3π2+2k π(k ∈Z )时,正弦函数y =sin x 是减函数,函数值由1减小到-1. 思考2 观察余弦函数y =cos x ,x ∈[-π,π]的图象.余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢? 答案 观察图象可知:当x ∈[-π,0]时,曲线逐渐上升,函数是增函数,cos x 的值由-1增大到1; 当x ∈[0,π]时,曲线逐渐下降,函数是减函数,cos x 的值由1减小到-1. 推广到整个定义域可得当x ∈[2k π-π,2k π],k ∈Z 时,余弦函数y =cos x 是增函数,函数值由-1增大到1; 当x ∈[2k π,(2k +1)π],k ∈Z 时,余弦函数y =cos x 是减函数,函数值由1减小到-1. 思考3 正弦函数、余弦函数的单调区间是什么?答案 y =sin x 的增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z ,减区间为⎣⎡⎦⎤π2+2k π,3π2+2k π,k ∈Z . y =cos x 的增区间为[-π+2k π,2k π],k ∈Z ,减区间为[2k π,π+2k π],k ∈Z . 梳理 解析式y =sin xy =cos x图象值域[-1,1] [-1,1]单调性在⎣⎡ -π2+2k π,π2 ]+2k π,k ∈Z 上递增,在⎣⎡ π2+2k π,3π2+ ]2k π,k ∈Z 上递减 在[-π+2k π,2k π],k ∈Z 上递增, 在[2k π,π+2k π],k ∈Z 上递减 最值当x =π2+2k π,k ∈Z 时,y max =1;当x=-π2+2k π,k ∈Z 时,y min =-1当x =2k π,k ∈Z 时,y max =1;当x =π+2k π,k ∈Z 时,y min =-11.正弦函数在定义域上是单调函数.( × ) 提示 正弦函数不是定义域上的单调函数. 2.正弦函数在第一象限是增函数.( × )提示 正弦函数在第一象限不是增函数,因为在第一象限,如-5π3<π6,但sin ⎝⎛⎭⎫-5π3=sin π3=32,sin π6=12,sin ⎝⎛⎭⎫-5π3>sin π6. 3.存在实数x ,使得cos x = 2.( × ) 提示 余弦函数最大值为1.4.余弦函数y =cos x 在[0,π]上是减函数.( √ ) 提示 由余弦函数的单调性可知正确.类型一 求正弦、余弦函数的单调区间 例1 求函数y =2sin ⎝⎛⎭⎫π4-x 的单调递增区间. 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的判断 解 y =2sin ⎝⎛⎭⎫π4-x =-2sin ⎝⎛⎭⎫x -π4, 令z =x -π4,则y =-2sin z .因为z 是x 的一次函数,所以要求y =-2sin z 的单调递增区间,即求sin z 的单调递减区间, 即2k π+π2≤z ≤2k π+3π2(k ∈Z ).∴2k π+π2≤x -π4≤2k π+3π2(k ∈Z ),即2k π+3π4≤x ≤2k π+7π4(k ∈Z ),∴函数y =2sin ⎝⎛⎭⎫π4-x 的单调递增区间为⎣⎡⎦⎤2k π+3π4,2k π+7π4(k ∈Z ). 反思与感悟 用整体替换法求函数y =A sin(ωx +φ)或y =A cos(ωx +φ)的单调区间时,如果式子中x 的系数为负数,先利用诱导公式将x 的系数变为正数再求其单调区间.求单调区间时,需将最终结果写成区间形式.跟踪训练1 求函数f (x )=2cos ⎝⎛⎭⎫2x -π6的单调递增区间. 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的判断 解 令-π+2k π≤2x -π6≤2k π,k ∈Z ,解得-5π12+k π≤x ≤π12+k π,k ∈Z ,所以函数f (x )的单调递增区间是⎣⎡⎦⎤-5π12+k π,π12+k π,k ∈Z .类型二 正弦、余弦函数单调性的应用命题角度1 利用正、余弦函数的单调性比较大小 例2 利用三角函数的单调性,比较下列各组数的大小. (1)sin 196°与cos 156°; (2)cos ⎝⎛⎭⎫-235π与cos ⎝⎛⎭⎫-174π. 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 解 (1)sin 196°=sin(180°+16°)=-sin 16°, cos 156°=cos(180°-24°)=-cos 24°=-sin 66°. ∵0°<16°<66°<90°,且y =sin x 在[0°,90°]上是增函数, ∴sin 16°<sin 66°,从而-sin 16°>-sin 66°,即sin 196°>cos 156°. (2)cos ⎝⎛⎭⎫-235π=cos 235π=cos ⎝⎛⎭⎫4π+35π=cos 35π, cos ⎝⎛⎭⎫-174π=cos 174π=cos ⎝⎛⎭⎫4π+π4=cos π4. ∵0<π4<35π<π,且y =cos x 在[0,π]上是减函数,∴cos 35π<cos π4,即cos ⎝⎛⎭⎫-235π<cos ⎝⎛⎭⎫-174π. 反思与感悟 用正弦函数或余弦函数的单调性比较大小时,应先将异名化同名,把不在同一单调区间内的角用诱导公式转化到同一单调区间,再利用单调性来比较大小. 跟踪训练2 cos 1,cos 2,cos 3的大小关系是________.(用“>”连接) 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 答案 cos 1>cos 2>cos 3解析 由于0<1<2<3<π,而y =cos x 在[0,π)上单调递减,所以cos 1>cos 2>cos 3. 命题角度2 已知三角函数的单调性求参数范围例3 已知ω是正数,函数f (x )=2sin ωx 在区间⎣⎡⎦⎤-π3,π4上是增函数,求ω的取值范围. 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 解 由-π2+2k π≤ωx ≤π2+2k π(k ∈Z ),ω>0,得-π2ω+2k πω≤x ≤π2ω+2k πω,k ∈Z , ∴f (x )的单调递增区间是⎣⎡⎦⎤-π2ω+2k πω,π2ω+2k πω,k ∈Z . 根据题意,得⎣⎡⎦⎤-π3,π4⊆⎣⎡⎦⎤-π2ω+2k πω,π2ω+2k πω(k ∈Z ), 从而有⎩⎨⎧-π2ω≤-π3,π2ω≥π4,ω>0,解得0<ω≤32.故ω的取值范围是⎝⎛⎦⎤0,32.反思与感悟 此类问题可先解出f (x )的单调区间,将问题转化为集合间的包含关系,然后列不等式组求出参数范围.跟踪训练3 已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是( ) A.⎣⎡⎦⎤12,54 B.⎣⎡⎦⎤12,34 C.⎝⎛⎦⎤0,12 D .(0,2]考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 答案 A解析 取ω=54,f (x )=sin ⎝⎛⎭⎫54x +π4, 其减区间为⎣⎡⎦⎤85k π+π5,85k π+π,k ∈Z , 显然⎝⎛⎭⎫π2,π⊆⎣⎡⎦⎤85k π+π5,85k π+π,k ∈Z ,排除B ,C. 取ω=2,f (x )=sin ⎝⎛⎭⎫2x +π4, 其减区间为⎣⎡⎦⎤k π+π8,k π+58π,k ∈Z , 显然⎝⎛⎭⎫π2,π⊈⎣⎡⎦⎤k π+π8,k π+58π,k ∈Z ,排除D.类型三 正弦、余弦函数的值域或最值例4 求函数f (x )=2sin 2x +2sin x -12,x ∈⎣⎡⎦⎤π6,5π6的值域. 考点 正弦函数、余弦函数的最大值与最小值 题点 正弦函数的最大值与最小值 解 令t =sin x ,因为x ∈⎣⎡⎦⎤π6,5π6, 所以t ∈⎣⎡⎦⎤12,1,则f (x )可化为y =2t 2+2t -12=2⎝⎛⎭⎫t +122-1,t ∈⎣⎡⎦⎤12,1, 所以当t =12时,y min =1,当t =1时,y max =72,故f (x )的值域是⎣⎡⎦⎤1,72. 反思与感悟 一般函数的值域求法有:观察法、配方法、判别式法、反比例函数法等.三角函数是函数的特殊形式,一般方法也适用,但要结合三角函数本身的性质. 常见的三角函数求值域或最值的类型有以下几种:(1)形如y =sin(ωx +φ)的三角函数,令t =ωx +φ,根据题中x 的取值范围,求出t 的取值范围,再利用三角函数的单调性、有界性求出y =sin t 的最值(值域).(2)形如y =a sin 2x +b sin x +c (a ≠0)的三角函数,可先设t =sin x ,将函数y =a sin 2x +b sin x +c (a ≠0)化为关于t 的二次函数y =at 2+bt +c (a ≠0),根据二次函数的单调性求值域(最值). (3)对于形如y =a sin x (或y =a cos x )的函数的最值还要注意对a 的讨论.跟踪训练4 已知函数f (x )=2a sin x +b 的定义域为⎣⎡⎦⎤-π3,2π3,函数的最大值为1,最小值为-5,求a 和b 的值.考点 正弦函数、余弦函数的最大值与最小值 题点 正弦函数的最大值与最小值 解 ∵-π3≤x ≤2π3,∴-32≤sin x ≤1.若a =0,不满足题意.若a >0,则⎩⎪⎨⎪⎧2a +b =1,-3a +b =-5,解得⎩⎪⎨⎪⎧a =12-63,b =-23+12 3.若a <0,则⎩⎪⎨⎪⎧2a +b =-5,-3a +b =1,解得⎩⎪⎨⎪⎧a =-12+63,b =19-12 3.故a =12-63,b =-23+123或a =-12+63,b =19-12 3.1.函数y =cos x -1的最小值是( ) A .0 B .1 C .-2 D .-1考点 正弦函数、余弦函数的最大值与最小值 题点 余弦函数的最大值与最小值 答案 C解析 cos x ∈[-1,1],所以y =cos x -1的最小值为-2. 2.函数y =sin 2x 的单调递减区间是( ) A.⎣⎡⎦⎤π2+2k π,3π2+2k π(k ∈Z ) B.⎣⎡⎦⎤k π+π4,k π+3π4(k ∈Z ) C.[]π+2k π,3π+2k π(k ∈Z ) D.⎣⎡⎦⎤k π-π4,k π+π4(k ∈Z ) 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的判断 答案 B解析 由2k π+π2≤2x ≤2k π+3π2,k ∈Z ,得k π+π4≤x ≤k π+3π4,k ∈Z ,∴y =sin 2x 的单调递减区间是⎣⎡⎦⎤k π+π4,k π+3π4(k ∈Z ). 3.下列不等式中成立的是( ) A .sin ⎝⎛⎭⎫-π8>sin ⎝⎛⎭⎫-π10 B .sin 3>sin 2 C .sin 75π>sin ⎝⎛⎭⎫-25π D .sin 2>cos 1考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 答案 D解析 ∵sin 2=cos ⎝⎛⎭⎫π2-2=cos ⎝⎛⎭⎫2-π2, 且0<2-π2<1<π,∴cos ⎝⎛⎭⎫2-π2>cos 1, 即sin 2>cos 1.故选D.4.函数y =cos x 在区间[-π,a ]上为增函数,则a 的取值范围是________. 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的应用 答案 (-π,0]解析 因为y =cos x 在[-π,0]上是增函数,在[0,π]上是减函数,所以只有-π<a ≤0时满足条件,故a ∈(-π,0].5.求函数y =3-2sin 12x 的最值及取到最值时的自变量x 的集合.考点 正弦函数、余弦函数的最大值与最小值 题点 正弦函数的最大值与最小值 解 ∵-1≤sin 12x ≤1,∴当sin 12x =-1,12x =2k π-π2,k ∈Z ,即x =4k π-π,k ∈Z 时,y max =5,此时自变量x 的集合为{x |x =4k π-π,k ∈Z }; 当sin 12x =1,12x =2k π+π2,k ∈Z ,即x =4k π+π,k ∈Z 时,y min =1,此时自变量x 的集合为{x |x =4k π+π,k ∈Z }.1.求函数y =A sin(ωx +φ)(A >0,ω>0)的单调区间的方法把ωx +φ看成一个整体,由2k π-π2≤ωx +φ≤2k π+π2(k ∈Z )解出x 的范围,所得区间即为增区间,由2k π+π2≤ωx +φ≤2k π+3π2(k ∈Z )解出x 的范围,所得区间即为减区间.若ω<0,先利用诱导公式把ω转化为正数后,再利用上述整体思想求出相应的单调区间.2.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断. 3.求三角函数值域或最值的常用方法将y 表示成以sin x (或cos x )为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y 的范围.一、选择题1.当-π2≤x ≤π2时,函数f (x )=2sin ⎝⎛⎭⎫x +π3有( ) A .最大值1,最小值-1 B .最大值1,最小值-12C .最大值2,最小值-2D .最大值2,最小值-1考点 正弦函数、余弦函数的最大值与最小值 题点 正弦函数的最大值与最小值 答案 D解析 因为-π2≤x ≤π2,所以-π6≤x +π3≤5π6,所以-12≤sin ⎝⎛⎭⎫x +π3≤1,所以-1≤f (x )≤2. 2.下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( )A .y =sin ⎝⎛⎭⎫2x +π2B .y =cos ⎝⎛⎭⎫2x +π2C .y =sin ⎝⎛⎭⎫x +π2D .y =cos ⎝⎛⎭⎫x +π2考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的判断答案 A3.下列关系式中正确的是( )A .sin 11°<cos 10°<sin 168°B .sin 168°<sin 11°<cos 10°C .sin 11°<sin 168°<cos 10°D .sin 168°<cos 10°<sin 11°考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 C解析 ∵sin 168°=sin(180°-12°)=sin 12°,cos 10°=sin(90°-10°)=sin 80°.∴由正弦函数的单调性,得sin 11°<sin 12°<sin 80°,即sin 11°<sin 168°<cos 10°.4.(2017·九江高一检测)y =2sin xsin x +2的最小值是( )A .2B .-2C .1D .-1考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值答案 B解析 由y =2sin x sin x +2=2-4sin x +2,当sin x =-1时,y =2sin xsin x +2取得最小值-2.5.(2017·全国Ⅲ)函数f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6的最大值为() A.65 B .1 C.35 D.15考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值答案 A 解析 ∵⎝⎛⎭⎫x +π3+⎝⎛⎭⎫π6-x =π2, ∴f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6 =15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫π6-x =15sin ⎝⎛⎭⎫x +π3+sin ⎝⎛⎭⎫x +π3 =65sin ⎝⎛⎭⎫x +π3≤65. ∴f (x )max =65. 故选A.6.函数y =sin x 的定义域为[a ,b ],值域为⎣⎡⎦⎤-1,12,则b -a 的最大值与最小值之和等于( ) A.4π3 B.8π3C .2πD .4π 考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值答案 C解析 作出y =sin x 的一个简图,如图所示,∵函数的值域为⎣⎡⎦⎤-1,12, 且sin π6=sin 5π6=12,sin 3π2=-1, ∴定义域[a ,b ]中,b -a 的最小值为3π2-5π6=2π3, 定义域[a ,b ]中,b -a 的最大值为2π+π6-5π6=4π3, 故可得,最大值与最小值之和为2π.7.若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω的值可为( )A.32B.23 C .2 D .3考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 A解析 由题意知,T 4=π3,即T =4π3,4π3=2πω, ∴ω=32. 二、填空题8.sin 1,sin 2,sin 3按从小到大排列的顺序为__________.考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 sin 3<sin 1<sin 2解析 ∵1<π2<2<3<π, sin(π-2)=sin 2,sin(π-3)=sin 3.y =sin x 在⎝⎛⎭⎫0,π2上递增,且0<π-3<1<π-2<π2, ∴sin(π-3)<sin 1<sin(π-2),即sin 3<sin 1<sin 2.9.函数y =2sin ⎝⎛⎭⎫2x +π3⎝⎛⎭⎫-π6≤x ≤π6的值域是________. 考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值答案 [0,2]解析 ∵-π6≤x ≤π6,∴0≤2x +π3≤2π3, ∴0≤sin ⎝⎛⎭⎫2x +π3≤1,∴y ∈[0,2]. 10.函数y =13sin ⎝⎛⎭⎫π6-x (x ∈[0,π])的单调递增区间为________. 考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的判断答案 ⎣⎡⎦⎤2π3,π解析 原式可化为y =-13sin ⎝⎛⎭⎫x -π6, ∵x ∈[0,π],∴-π6≤x -π6≤5π6. 要求函数的单调递增区间,只需求f (x )=13sin ⎝⎛⎭⎫x -π6的单调递减区间. 则π2≤x -π6≤5π6, 即2π3≤x ≤π. ∴y =13sin ⎝⎛⎭⎫π6-x (x ∈[0,π])的单调递增区间为⎣⎡⎦⎤2π3,π. 11.若f (x )=2sin ωx (0<ω<1)在区间⎣⎡⎦⎤0,π3上的最大值是2,则ω=________. 考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值答案 34解析 ∵x ∈⎣⎡⎦⎤0,π3,即0≤x ≤π3,且0<ω<1, ∴0≤ωx ≤ωπ3<π3, ∵f (x )max =2sinωπ3=2, ∴sin ωπ3=22,ωπ3=π4, 即ω=34. 三、解答题12.求下列函数的单调递增区间.(1)y =1-sin x 2;(2)y =12log sin ⎝⎛⎭⎫x 2-π3. 考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的判断解 (1)由2k π+π2≤x 2≤2k π+32π,k ∈Z , 得4k π+π≤x ≤4k π+3π,k ∈Z .∴y =1-sin x 2的单调递增区间为[4k π+π,4k π+3π](k ∈Z ).(2)要求函数y =12log sin ⎝⎛⎭⎫x 2-π3的单调递增区间,即求使y =sin ⎝⎛⎭⎫x 2-π3>0且单调递减的区间.∴2k π+π2≤x 2-π3<2k π+π,k ∈Z ,整理得4k π+5π3≤x <4k π+8π3,k ∈Z .∴函数y =12log sin ⎝⎛⎭⎫x 2-π3的单调递增区间为⎣⎡⎭⎫4k π+5π3,4k π+8π3,k ∈Z .13.求下列函数的最大值和最小值.(1)f (x )=sin ⎝⎛⎭⎫2x -π6,x ∈⎣⎡⎦⎤0,π2;(2)f (x )=-2cos 2x +2sin x +3,x ∈⎣⎡⎦⎤π6,5π6.考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数、余弦函数最值的综合问题解 (1)当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6,由函数图象知,f (x )=sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤sin ⎝⎛⎭⎫-π6,sin π2=⎣⎡⎦⎤-12,1.所以,f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值分别为1,-12.(2)f (x )=-2(1-sin 2x )+2sin x +3=2sin 2x +2sin x +1=2⎝⎛⎭⎫sin x +122+12.因为x ∈⎣⎡⎦⎤π6,5π6,所以12≤sin x ≤1.当sin x =1时,y max =5;当sin x =12时,y min =52.所以,f (x )在⎣⎡⎦⎤π6,5π6上的最大值和最小值分别为5,52.四、探究与拓展14.已知奇函数f (x )在[-1,0]上单调递减,α,β为锐角三角形两内角,则() A .f (cos α)>f (cos β) B .f (sin α)>f (sin β)C .f (sin α)>f (cos β)D .f (sin α)<f (cos β)考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用 答案 D解析 由题意,得α+β>π2,∴π2>α>π2-β>0, ∴sin α>sin ⎝⎛⎭⎫π2-β,即1>sin α>cos β>0,∴-1<-sin α<-cos β<0.∵奇函数f (x )在[-1,0]上单调递减,∴f (-sin α)>f (-cos β),∴-f (sin α)>-f (cos β),∴f (sin α)<f (cos β).15.已知函数f (x )=a sin ⎝⎛⎭⎫2x -π3+b (a >0).当x ∈⎣⎡⎦⎤0,π2时,f (x )的最大值为3,最小值是-2,求a 和b 的值.考点 正弦函数、余弦函数的最大值与最小值 题点 正弦函数的最大值与最小值解 ∵0≤x ≤π2,∴-π3≤2x -π3≤2π3, ∴-32≤sin ⎝⎛⎭⎫2x -π3≤1, 又a >0,∴f (x )max =a +b =3,f (x )min =-32a +b =-2. 由⎩⎪⎨⎪⎧ a +b =3,-32a +b =-2,得⎩⎪⎨⎪⎧a =2,b =-2+ 3.。
1.4.2 正弦 余弦函数的性质(单调性、最值)

3 5 对称中心: ( ,0),( ,0),( ,0),( ,0) 2 2 2 2
2
k ,0) k Z
1 例5:求函数 y sin( x ) 的单调递增区间: 2 3
解:
2
1 y sin x 3 2
y sin z
2k z
余弦函数的单调性
y
1 -3
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
-
-1
…
2
…
0
1
…
2
…
-1
0
0
y=cosx (xR) 增区间为 [ +2k, 2k],kZ + ], kZ 减区间为 [2k, 2k, 其值从-1增至1 其值从 1减至-1
y cos x
3 5 2
2
y
1
任意两相邻对称轴 ( 或对称中心 ) 的间距为 3 2 O 5 x 3 半个周期;
2
2
1
2
2
3
2
对称轴与其相邻的对称中心的间距为
对称轴:x
,0, , 2
四分之一个周期.
(
x k , k Z
o
-1
2
3
4
5
6
x
sin(-x)= - sinx (xR) cos(-x)= cosx (xR)
最全三角函数的图像与性质知识点总结

三角函数的图像与性质一、正弦函数、余弦函数的图像与性质
(
二、正切函数的图象与性质
三、三角函数图像的平移变换和伸缩变换
1. 由x y sin =的图象得到)sin(ϕω+=x A y (0,0A ω>>)的图象
注意:图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
2. )sin(ϕω+=x A y (0,0A ω>>)的性质
(1)定义域、值域、单调性、最值、对称性:
将ϕω+x 看作一个整体,与相应的简单三角函数比较得出; (2)奇偶性:只有当ϕ取特殊值时,这些复合函数才具备奇偶性:
)sin(ϕω+=x A y ,当πϕk =时为奇函数,当2
ππϕ±=k 时为偶函数;
(3)最小正周期:ω
π2=T
3. y =A sin(ωx +φ), x ∈[0,+∞) (0,0A ω>>)中各量的物理意义
(1) A 称为振幅; (2)2T πω
=称为周期;
(3)1f
T
=
称为频率;
(4)x ωϕ+称为相位;
(5)ϕ称为初相 (6)ω称为圆频率.。
正弦、余弦函数的奇偶性、单调性

y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
sin(-x)= - sinx (xR)
y=sinx (xR) 是奇函数 定义域关于原点对称
cos(-x)= cosx (xR)
y
1 -4 -3 -2 -
y=cosx (xR) 是偶函数
o
-1
2
4
4
y 1
y=|sinu|
2
2
3 2
2
O -1
2
3 2
2
u
y=sinu y=|sinu|
, k ], k Z
即: 增区间为 减区间为
x [k x [k 3
u [k
u [k , k
2
], k Z
4
, k , k
10
10
)
2
18
又 y=sinx
)
在[
18
2
,
2
] 上是增函数
10
sin(
5
10
) < sin(
18
即:sin(
) – sin(
)>0
(2) cos( 解: cos(
23
) - cos(
17 4
)
3 5
23 5
)=cos
3 5
3 3
2
正弦函数和余弦函数的图像和性质单调性(主要内容)

(其中A、B、、为常数,且A 0, 0)
(1)周期函数:对任意x D,都有f (x T ) f (x),T 0 (2)奇函数: 对任意x D,都有f (x) f (x) (3)偶函数: 对任意x D,都有f (x) f (x)
2
单调递增区间.
在指定范围内确定
解: y 2 sin( x )
24
单调区间,要考虑 单调区间和指定范围
由2k x 2k 两个集合的交集.
2 24
2
4k 3 x 4k (k Z )
又 2
x
2
3
2 x
2
2
2
所求递增区间为[ 3 , ]
2 2 青苗辅导1
19
例4、 利用函数的单调性,比较下列各组数的大小.
(2) f (x) sin | x |;
(2) f (x)定义域为R,关于原点对称 对任意x R,有f (x) sin x sin x f (x)
f (x) sin x 是偶青函苗辅数导1
6
(3) f (x) sin x cos x;
(3) f (x)定义域为R,关于原点对称
12
例2、 求下列函数的单调区间.
(1) f (x) sin( x); (2) f (x) cos( x );
(3) f (x) 2 3 sin x cos x 2 sin 2 x. 2 12
解:(1) f (x) sin x
所求递增区间为[2k ,2k 3 ],k Z
2
2
(4) 1 sin x cos x 0
2 sin( x ) 1 sin( x ) 2
正弦、余弦函数的奇偶性、单调性

3
4
5
6
x
正弦、余弦函数的奇偶性
正弦、余弦函数的奇偶性
例1:判定下列函数的奇偶性
(1) y sin 3 x, (2) y sin x cos x (3) y 1 sin x
例2:已知函数f ( x) 2ax x sin x 3, 若f(2)=3,
3
1)求证:函数g(x)=f ( x) 3是奇函数; 2)求f(-2)的值
1 2k x 2k 2 3 4 2
正弦、余弦函数的单调性
(5) y = -| sin(x+ )| 4 解: 令x+ =u , 则 y= -|sinu| 大致图象如下: 4
y 1
y=|sinu|
2
2
3 2
2
O -1
3 2
2
u
即: 增区间为 u [k , k ], k Z 2 减区间为 u [k , k ], k Z
6
x
正弦、余弦函数的奇偶性
正弦、余弦函数的奇偶性
y
1 -4 -3 -2 -
o
-1
234ຫໍສະໝຸດ 56xsin(-x)= - sinx (xR)
y=sinx (xR) 是奇函数
一般的,对于函数f(x)的定义域内的任 意一个x,都有f(-x) = -f(x),则称f(x)为这 一定义域内的奇函数。
正弦、余弦函数的奇偶性
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
sin(-x)= - sinx (xR)
y=sinx (xR) 是奇函数 定义域关于原点对称
正弦、余弦、正切函数图象及其性质
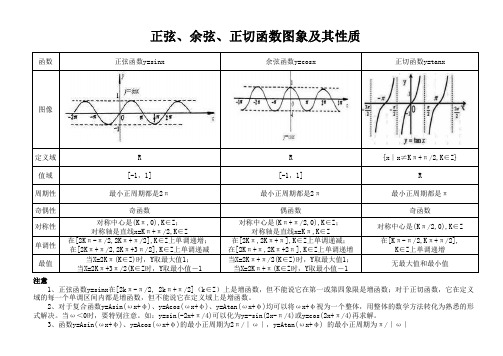
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1,1][-1,1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z;对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时,Y取最大值1;当X=2Kπ+3π/2(K∈Z时,Y取最小值-1当X=2Kπ+π/2(K∈Z)时,Y取最大值1;当X=2Kπ+π(K∈Z时,Y取最小值-1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2](k∈Z)上是增函数,但不能说它在第一或第四象限是增函数;对于正切函数,它在定义域的每一个单调区间内都是增函数,但不能说它在定义域上是增函数。
2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体,用整体的数学方法转化为熟悉的形式解决。
当ω<0时,要特别注意。
如:y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。
3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣,y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。
正弦、余弦函数的性质(奇偶性、单调

(奇偶性、单调性) 奇偶性、单调性)
武汉睿升学校: 武汉睿升学校:关俊
正弦、余弦函数的周期性: 正弦、余弦函数的周期性: 正、余弦函数的一般形式: 余弦函数的一般形式:
f ( x) = A sin(ω x + ϕ ) f ( x) = A cos(ω x + ϕ )
T= 2π
ω
f ( x + T ) = f ( x)
y = − sin(πx +
π
6
)
下列函数是周期函数吗?如果是,周期是多少? 下列函数是周期函数吗?如果是,周期是多少?
1,y = sin x
2,y = sin x 3,y = sin x + sin x
1 4,y = sin x + 2
1 5、函数 对于任意实数x满足条件 、函数f(x)对于任意实数 满足条件 f ( x + 2) = 对于任意实数 f ( x)
y
1 -4π -3π -3π
−
5π 2
y
1 π
π
2
-2π -2π
− 3π 2
-π -π
−Leabharlann oπy=sinx
2π π
3π 2
3π 2π
5π 2
4π 3π
5π
7π 2
6π 4π
-1
2
o
-1
x x
关于与x轴的交点对称 关于与 轴的交点对称 (kπ ,0) k ∈ Z
2k + 1 y=cosx关于 ( 关于 π ,0) k ∈ Z 点对称 2
f ( − x ) = cos( − x ) = cos x = f ( x )
正、余弦函数的单调性与最值

比较三角函数值的大小 比较下列各组数的大小. (1)cos-253π与 cos-147π; (2)sin2 012°和 cos157°.
【思路探索】 利用诱导公式将异名三角函数转化为 同名三角函数,非同一单调区间的角,转化到同一单调区 间上,再利用函数的单调性比较.
【解】 (1)解法一: ∵cos-253π=cos-6π+75π=cos75π, cos-147π=cos-6π+74π=cos74π, ∵π<75π<74π<2π, 又 y=cosx 在[π,2π]上单调递增, ∴cos75π<cos74π,
求函数y=Asin(ωx+φ)(A>0,ω≠0)或y=Acos(ωx+ φ)(A>0,ω≠0)的单调区间,一般将ωx+φ视作整体,代入y =sinx或y=cosx相关的单调区间所对应的不等式,解之即 得.这里实际上采用的是整体的思想,这是研究三角函数 性质的重要数学思想,一般地,ω<0时,y=Asin(ωx+ φ)(Aω≠0)变形为y=-Asin(-ωx-φ),y=Acos(ωx+ φ)(Aω≠0)变形为y=Acos(-ωx-φ),再求函数的单调区 间.所有的这些变形都是为了使x前面的系数为正值.同 时要注意A<0时单调区间的变化.
单调减区间为2kπ+π6,2kπ+76π. (2)函数 y=2sinπ3-2x=-2sin2x-3π,令 2kπ-2π≤2x -π3≤2kπ+2π(k∈Z),得 kπ-1π2≤x≤kπ+152π(k∈Z),∴函数 y=2sin3π-2x的单调减区间为kπ-1π2,kπ+152(k∈Z).令π2 +2kπ≤2x-3π≤32π+2kπ,k∈Z,解得152π+kπ≤x≤1112π+kπ, k∈Z,即原函数的单调递增区间为152π+kπ,1112π+kπ(k∈Z).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 63 6
3 63 2
变式:
求函数
y=3sin(2x-
4
) 的单调区间:
解:2k 2 x 2k
2
4
2
(k z)
k x k 3
8
8
(k z)
2k 2 x 2k 3
2
4
2
k 3 x k 7
3
(3) y cos(2x )
3
正弦函数图像
y
1
3 5
2
2 3
2
O
2
2
1
3 2
2
5 3
2
x
余弦函数图像
y
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
[
2
+2k,
2
+2k],kZ
单调递增
[
2
+2k,
3 2
+2k],kZ
单调递减
[ +2k, 2k],kZ 单调递增 [2k, 2k + ], kZ 单调递减
课后作业:
求下列函数的单调区间(三选一)
(1) y sin 2x
(2) y sin(2x )
求正弦、余弦函数的单调区间
三维目标 教学重点 教学难点 教学过程 课堂小结 课后作业
y
3
2
2o
2
3 2
2
2 x
三维目标
❖ 1、知识与技能
❖ 理解正弦函数、余弦函数的性质,并能在解题中 应用。
❖ 2、过程与方法
❖ 根据正弦曲线和余弦曲线,总结出这两种函数的 单调性,进一步体验“形”对“数”的体现作用。
(D)在[ , ] 及 [ , ]上是增函数,在 [ , ] 上是减函数
2
2
22
例题:确定下列函数的单调区间。
(1) y cosx
分析:利用y sin x, y cos x的单调性来解。
解:1、函数 y cosx 的单调递增区间为 [2k , 2k ] (k z)
正确的是( B ) 变式 y 4sin(x) x [ , ] ( D )
(A)在 [ , 0]上是增函数,在 [0 , ]上是减函数
(B)在
[
2
,
] 上是增函数,在 [
2
,]及
2
[
2
, ]上是减函数
(C)在 [0 , ]上是增函数,在 [ , 0]上是减函数
8
8
(k z) (k z)
所以:单调增区间为 单调减区间为
[k , k 3 ]
8
8
[k 3 , k 7 ]
8
8
(k z) (k z)
小 结:
y
2
2o
3 2
3
2
2
2
x
函数 奇偶性 正弦函数 奇函数 余弦函数 偶函数
单调性(单调区间)
❖ 3、情感、态度与价值观
❖ 感受数形结合思想的重要作用,养成多动手、多 观察、勤思考、善总结的习惯。
教学重点
求正弦、余弦函数的单调区间
教学难点
求复合型正弦、余弦函数的单调区间
引入:请作出下列函数的图象
(1) y sin x x [ , 3 ]
22
(2) y cosx x [ , ]
正弦函数图像
y
1
3 5
2
2 3
2
O
2
2
1
3 2
2
5 3
2
x
正弦函数在每个闭区间[2k ,2k ]
2
2
(k Z )上都是增函数,在每一个闭区间[2k
,2k 3 ](k Z )上都是减函数;
2
2
余弦函数图像
单调递减区间为 [ 2k , 2k ] (k z)
例题:确定下列函数的单调区间。
(2) y sin 3x
(2)令z 3x,则y sin z,在[ 2k , 2k ](k Z )上单增。
在[ 2k ,3 2k ]
2
2
(k z)上单减
由
2
2k
2
3x
2k
2
2
(k
z) 得
6
2k
3
x
6
2k
3
(k z)
由 2k 3x 3 2k
2
(k z) 得 2k x 2k
63
23
(k z)
所以y sin 3x 在
[2k , 2k ]上单增,在[2k , 2k ]上单减。
y
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
余弦函数在每个闭区间[2k ,2k ](k Z )上都是增函数,在每一个闭区间[2k ,2k ](k Z )上都是减函数;
正弦曲线的应用
下列关于函数 y 4sin x x [ , ] 的单调性的叙述,
