正弦函数、余弦函数的单调性与最值.pdf
合集下载
1.4.2第2课时 正、余弦函数的单调性与最值 课件

栏目 导引
第一章 三角函数
(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时, 要注意使用复杂函数的判断方法来判断. 2.解析正弦函数、余弦函数的最值 (1)明确正弦、余弦函数的有界性,即|sin x|≤1,|cos x|≤1. (2)对有些函数,其最值不一定就是1或-1,要依赖函数的定 义域来决定. (3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数求最值时,通常利 用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的 形式求最值.
第一章 三角函数
栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π+2kπ,74π+ 2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
【名师点评】 正弦、余弦函数单调区间的求解技巧: (1)结合正弦、余弦函数的图象,熟记它们的单调区间. (2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采 用“换元”法整体代换,将ωx+φ看作一个整体,可令“z= ωx+φ”,即通过求y=Asin z的单调区间而求出函数的单调 区间.若ω<0,则可利用诱导公式将x的系数转变为正数.
栏目 导引
第一章 三角函数
跟踪训练
1.求函数 y=sin(π3-12x),x∈[-2π,2π]的单调递增区间. 解:y=sin(π3-12x)=-sin(12x-π3). 由 y=sin x 与 y=-sin x 的图象关于 x 轴对称可知,y=sin x 的递增 区间就是 y=-sin x 的递减区间.因此,要求 y=-sin(12x-π3)的递 增区间,只要求出 y=sin(12x-π3)的递减区间即可.
第一章 三角函数
(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时, 要注意使用复杂函数的判断方法来判断. 2.解析正弦函数、余弦函数的最值 (1)明确正弦、余弦函数的有界性,即|sin x|≤1,|cos x|≤1. (2)对有些函数,其最值不一定就是1或-1,要依赖函数的定 义域来决定. (3)形如y=Asin(ωx+φ)(A>0,ω>0)的函数求最值时,通常利 用“整体代换”,即令ωx+φ=z,将函数转化为y=Asin z的 形式求最值.
第一章 三角函数
栏目 导引
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π+2kπ,74π+ 2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
栏目 导引
第一章 三角函数
【名师点评】 正弦、余弦函数单调区间的求解技巧: (1)结合正弦、余弦函数的图象,熟记它们的单调区间. (2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采 用“换元”法整体代换,将ωx+φ看作一个整体,可令“z= ωx+φ”,即通过求y=Asin z的单调区间而求出函数的单调 区间.若ω<0,则可利用诱导公式将x的系数转变为正数.
栏目 导引
第一章 三角函数
跟踪训练
1.求函数 y=sin(π3-12x),x∈[-2π,2π]的单调递增区间. 解:y=sin(π3-12x)=-sin(12x-π3). 由 y=sin x 与 y=-sin x 的图象关于 x 轴对称可知,y=sin x 的递增 区间就是 y=-sin x 的递减区间.因此,要求 y=-sin(12x-π3)的递 增区间,只要求出 y=sin(12x-π3)的递减区间即可.
正弦函数、余弦函数的单调性与最值

∵函数y=sin
π π x在-2+2kπ,2+2kπ(k∈Z)上是增函数,
π π π ∴- +2kπ≤2x- ≤ +2kπ, 2 3 2 π 5π 即- +kπ≤x≤ +kπ(k∈Z). 12 12
π π 5π ∴函数y=3sin 3 -2x 的单调递减区间为 -12+kπ,12+kπ
π π π 13π ∴cos >cos ,即cos-8 >cos . 8 7 7
(2)sin 194°=sin (180°+14°)=-sin 14°, cos 160°=cos(180°-20°)=-cos 20°=-sin 70°. ∵0°<14°<70°<90°且y=sin
比较三角函数值大小的方法 (1)比较两个同名三角函数值的大小,先利用诱导公 式把两个角化为同一单调区间内的角,再利用函数的单调 性比较. (2)比较两个不同名的三角函数值的大小,一般应先 化为同名的三角函数,后面步骤同上.
[活学活用] 比较下列各组数的大小.
π 13π (1)cos -8 与cos ; 7
(3)在区间[0,2π]上,函数y=cos x仅当x=0时取得最大值1. ( × )
2.在下列区间中,使函数y=sin x为增函数的是 ( A.[0,π]
π π C.-2,2 π 3π B.2 , 2
)
D.[π,2π]
答案:C
3.函数y=2-sin x的最大值及取最大值时x的值为 π A.ymax=3,x= 2 π B.ymax=1,x= +2kπ(k∈Z) 2 π C.ymax=3,x=- +2kπ(k∈Z) 2 π D.ymax=3,Biblioteka = +2kπ(k∈Z) 2值域
[点睛]
正弦、余弦函数的奇偶性、单调性

正弦、余弦函数的单调性
例1 不通过求值,指出下列各式大于0还是小于0: (1) sin(
) – sin( 18
10
)
解: 2 10 18 sin(
5
2
又 y=sinx 在[
)
10
) < sin(
18
即:sin( 18 ) – sin( 10 )>0
正弦、余弦函数的奇偶性
一般的,对于函数f(x)的定义域内的任 意一个x,都有f(-x) = f(x),则称f(x)为这一 定义域内的偶函数。
关于y轴对称
cos(-x)= cosx (xR)
y
1 -4 -3 -2 -
y=cosx (xR) 是偶函数
o
-1
2
3
4
5
6
x
正弦、余弦函数的奇偶性
+2k, +2k],kZ 上单调递减 2 2 3 [ +2k , +2k],kZ上单调递增 函数在 2 2
3 8 8 3 3 7 2k 2 x 2k k x k 2 4 2 8 8 3 所以:单调增区间为 [k , k ] 8 8 3 7 , k ] 单调减区间为 [k 8 8 k x k
1 2k x 2k 2 3 4 2
正弦、余弦函数的单调性
(5) y = -| sin(x+ )| 4 解: 令x+ =u , 则 y= -|sinu| 大致图象如下: 4
y 1
y=|sinu|
2
2
3 2
正弦函数、余弦函数的单调性与最值

________ T=2π
函数名称 图象与性质 性质分类 图象 奇偶性 _________ 奇函数 _________ 偶函数 y=sinx y=cosx
不同处
函数名 称 图象与性质 性质分类 在 不同 处 y=sinx y=cosx
单调性
π π [2kπ-π,2kπ](k∈Z) 上 2kπ- ,2kπ+ (k∈Z) 在 ____________________ 2 2 ________________________ 递增; 上递增; 在 在 π 3 [2kπ,2kπ+π](k∈Z) 2kπ+ ,2kπ+ π(k∈Z) ________________________ 2 2 ________________________ 上递减 上递减
π π π 【解】 (1)由 2kπ-2≤x+3≤2kπ+2(k∈Z), 5 π 得 2kπ-6π≤x≤2kπ+6(k∈Z). π π 3 由 2kπ+2≤x+3≤2kπ+2π(k∈Z), π 7 得 2kπ+6≤x≤2kπ+6π(k∈Z). ∴函数
π y=2sinx+3的单调增区间为
(2)可化为 y=Asin2x+Bsinx+C 或 y=Acos2x+Bcosx+C(A≠0) 的最大、最小值可利用二次函数在区间[-1,1]上的最大、最小值 的求法来求(换元法). Asinx+B Acosx+B 2 (3)形如 y= 或 y= (A +C2≠0)的最大值最 Csinx+D Ccosx+D 小值可解出 sinx 或 cosx 后利用其有界性来求.
2.比较三角函数值大小的方法 先利用诱导公式把要比较的三角函数值转化为同一单调区间 上的同名三角函数值,再利用三角函数的单调性比较大小. 3.求三角函数值域或最值的常用方法 (1)可化为单一函数 y=Asin(ωx+φ)+k 或 y=Acos(ωx+φ)+k 的最大值为|A|+k, 最小值为-|A|+k(其中 A、 ω、 k 为常数, A≠0, ω≠0).
函数名称 图象与性质 性质分类 图象 奇偶性 _________ 奇函数 _________ 偶函数 y=sinx y=cosx
不同处
函数名 称 图象与性质 性质分类 在 不同 处 y=sinx y=cosx
单调性
π π [2kπ-π,2kπ](k∈Z) 上 2kπ- ,2kπ+ (k∈Z) 在 ____________________ 2 2 ________________________ 递增; 上递增; 在 在 π 3 [2kπ,2kπ+π](k∈Z) 2kπ+ ,2kπ+ π(k∈Z) ________________________ 2 2 ________________________ 上递减 上递减
π π π 【解】 (1)由 2kπ-2≤x+3≤2kπ+2(k∈Z), 5 π 得 2kπ-6π≤x≤2kπ+6(k∈Z). π π 3 由 2kπ+2≤x+3≤2kπ+2π(k∈Z), π 7 得 2kπ+6≤x≤2kπ+6π(k∈Z). ∴函数
π y=2sinx+3的单调增区间为
(2)可化为 y=Asin2x+Bsinx+C 或 y=Acos2x+Bcosx+C(A≠0) 的最大、最小值可利用二次函数在区间[-1,1]上的最大、最小值 的求法来求(换元法). Asinx+B Acosx+B 2 (3)形如 y= 或 y= (A +C2≠0)的最大值最 Csinx+D Ccosx+D 小值可解出 sinx 或 cosx 后利用其有界性来求.
2.比较三角函数值大小的方法 先利用诱导公式把要比较的三角函数值转化为同一单调区间 上的同名三角函数值,再利用三角函数的单调性比较大小. 3.求三角函数值域或最值的常用方法 (1)可化为单一函数 y=Asin(ωx+φ)+k 或 y=Acos(ωx+φ)+k 的最大值为|A|+k, 最小值为-|A|+k(其中 A、 ω、 k 为常数, A≠0, ω≠0).
【课件】正弦函数、余弦函数的性质+(2)+课件-高一上学期数学人教A版(2019)必修第一册

23
33
4.变式:求函数y sin( 1 x ), x [ , ]的单调递增区间.
23
解 : y sin( 1 x ) sin(1 x ),
23
23
令z 1 x , x [2 ,2 ], 则z [ 4 , 2 ].
23
33
因为y
sin
z,
z
[
4
,
2
]的单调递减区间是[
4
时取得最小值
1;
7.最大值与最小值
由余弦函数的图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
余弦函数当且仅当 x _2_k__,_k____Z__ 时取得最大值1,
当且仅当x _____2_k__,_k___Z_时取得最小值 1.
8. 正弦函数、余弦函数的图象和性质
函 数 y sin x, x R
在每个闭区间 [2k , 2k ](k Z ) 上都单调递减,
其值从1减小到-1.
7.最大值与最小值
正弦函数图象知
y1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
正弦函数当且仅当
x
2k , k Z
_2__________
时取得最大值 1,
当且仅当
x
2k , k Z
___2__________
5
)在区间[0,
]上的单调递增区间为(
)
3
A.[5 ,11 ]
12 12
5
、B.[0, 12 ]
正弦,余弦函数的单调性和奇偶性[优质ppt]
![正弦,余弦函数的单调性和奇偶性[优质ppt]](https://img.taocdn.com/s3/m/4dd658754b73f242326c5f0d.png)
x 内的任意一个 ,都有 f(x)f(x)则称 f (x) 为
这一定义域内的偶函数。偶函数的图像关于 y
轴对称。
定义:一般地,如果对于函数 f ( x)的定义
域内的任意一个 x都 f(x)f(x),则称 f (x)
为这一定义域内的奇函数。奇函数图像关于原 点对称。
x 注意:1、 是任意的
2.奇函数,偶函数的定义域必须关于原点对称
正弦、余弦函数的性质
(奇偶性、单调性)
X
知识回顾 y
1
3 5 2
2 3
2
2
O 3 2 5 3 x
2
2
2
1
y=sinx (xR) 定义域 xR
值 域 y[ - 1, 1 ]
y=cosx (xR) 周期性 T = 2
y
1
3 5 2
x( , )
x( , )
且f(x)(x)si nx)(
且f(x)1si nx)(
xsinx
1sin x
f (x)
f(x)f(x)且 f(x)f(x)
函数 yxsinx是偶函数 y 1sinx是非奇非偶函数
判断下列函数的 ( 1)yxsinx
再观察正弦函数图像
y
1
3 5 2
2 3
2
2
O 3 2 5 3 x
2
2
2
1
正弦函数 ysinx在
在每个闭区间 [2k,2k]k (Z)上是增函数,
22
其函数值从-1增大到1
在每个闭区间 [2k,32k](kZ)是减函数,
其关于原点的对称点 P'(x,sinx) , 由诱导公式 sinx()sixn, 即 P'(x,sinx()) 故P '也在正弦函数的图像上。
这一定义域内的偶函数。偶函数的图像关于 y
轴对称。
定义:一般地,如果对于函数 f ( x)的定义
域内的任意一个 x都 f(x)f(x),则称 f (x)
为这一定义域内的奇函数。奇函数图像关于原 点对称。
x 注意:1、 是任意的
2.奇函数,偶函数的定义域必须关于原点对称
正弦、余弦函数的性质
(奇偶性、单调性)
X
知识回顾 y
1
3 5 2
2 3
2
2
O 3 2 5 3 x
2
2
2
1
y=sinx (xR) 定义域 xR
值 域 y[ - 1, 1 ]
y=cosx (xR) 周期性 T = 2
y
1
3 5 2
x( , )
x( , )
且f(x)(x)si nx)(
且f(x)1si nx)(
xsinx
1sin x
f (x)
f(x)f(x)且 f(x)f(x)
函数 yxsinx是偶函数 y 1sinx是非奇非偶函数
判断下列函数的 ( 1)yxsinx
再观察正弦函数图像
y
1
3 5 2
2 3
2
2
O 3 2 5 3 x
2
2
2
1
正弦函数 ysinx在
在每个闭区间 [2k,2k]k (Z)上是增函数,
22
其函数值从-1增大到1
在每个闭区间 [2k,32k](kZ)是减函数,
其关于原点的对称点 P'(x,sinx) , 由诱导公式 sinx()sixn, 即 P'(x,sinx()) 故P '也在正弦函数的图像上。
1.4.2 正弦 余弦函数的性质(单调性、最值)

3 5 对称中心: ( ,0),( ,0),( ,0),( ,0) 2 2 2 2
2
k ,0) k Z
1 例5:求函数 y sin( x ) 的单调递增区间: 2 3
解:
2
1 y sin x 3 2
y sin z
2k z
余弦函数的单调性
y
1 -3
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
-
-1
…
2
…
0
1
…
2
…
-1
0
0
y=cosx (xR) 增区间为 [ +2k, 2k],kZ + ], kZ 减区间为 [2k, 2k, 其值从-1增至1 其值从 1减至-1
y cos x
3 5 2
2
y
1
任意两相邻对称轴 ( 或对称中心 ) 的间距为 3 2 O 5 x 3 半个周期;
2
2
1
2
2
3
2
对称轴与其相邻的对称中心的间距为
对称轴:x
,0, , 2
四分之一个周期.
(
x k , k Z
o
-1
2
3
4
5
6
x
sin(-x)= - sinx (xR) cos(-x)= cosx (xR)
1.4.2正弦函数、余弦函数的最值

(2)y 3sin 2x, x R.
解(:2)令t=2x,因为使函数y 3sin t,t R取最大值的t的集合是
{t | t 2k , k Z}
由
2x
t
2
2k
得
x k
2
4
所以使函数 y 3sin 2x, x R取最大值的x的集合是 {x | x k , k Z} 4
2
O
2
1
2
3 2
2
5 3
2
x
分析:令 z 2x
2 则 y 3cosz
化未知为已知
• P46 A2最值问题 使原函数取得最大值的集合是
(4)
y
1 2
sin
1 2
x
3
解:令z 1 x
23
x
|
x
3
4k
,k
Z
要使y 1 sin z有最小值, 2
要使y 1 sin z有最大值, 2
2
零点: x k (k Z )
探究:余弦函数的最大值和最小值 y
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值:当 x 0 2k 时,有最大值 y 1 最小值:当 x 2k 时,有最小值 y 1
零点:x k (k Z )
2
例1.下列函数有最大、最小值吗?如果有,请写出取最大、最 小值时的自变量x的集合,并说出最大、最小值分别是什么.
同理,使函数y 3sin 2x, x R 取最小值的x的集合是 {x | x k , k Z} 4
函数 y 3sin 2x, x R取最大值是3,最小值是-3。
解(:2)令t=2x,因为使函数y 3sin t,t R取最大值的t的集合是
{t | t 2k , k Z}
由
2x
t
2
2k
得
x k
2
4
所以使函数 y 3sin 2x, x R取最大值的x的集合是 {x | x k , k Z} 4
2
O
2
1
2
3 2
2
5 3
2
x
分析:令 z 2x
2 则 y 3cosz
化未知为已知
• P46 A2最值问题 使原函数取得最大值的集合是
(4)
y
1 2
sin
1 2
x
3
解:令z 1 x
23
x
|
x
3
4k
,k
Z
要使y 1 sin z有最小值, 2
要使y 1 sin z有最大值, 2
2
零点: x k (k Z )
探究:余弦函数的最大值和最小值 y
1
3 5
2
2 3
2
O
2
1
2
3 2
2
5 3
2
x
最大值:当 x 0 2k 时,有最大值 y 1 最小值:当 x 2k 时,有最小值 y 1
零点:x k (k Z )
2
例1.下列函数有最大、最小值吗?如果有,请写出取最大、最 小值时的自变量x的集合,并说出最大、最小值分别是什么.
同理,使函数y 3sin 2x, x R 取最小值的x的集合是 {x | x k , k Z} 4
函数 y 3sin 2x, x R取最大值是3,最小值是-3。
三角函数的图象、定义域、最值(值域)、单调性

三角函数的图象、定义域、最值(值域)、单调性
[学习要求] 1.能画出 y = sin x , y = cos x , y =tan x 的图象. 2.理解
正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小
值、图象与 x 轴的交点等). 3.理解正切函数在区间
π
π
− ,
2
2
上的性质.
π
π
− <<
2
2
由题意得 y = cos x ·|tan x |=ቐ
的大致图象是(
sin,0 ≤
π
< ,
2
π
−sin, − <
2
所以其图象的大致形状如选项C所示.
< 0,
C )
2. 已知函数 f ( x )= sin x +2| sin x |, x ∈[0,2π],若直线 y = k
与其仅有两个不同的交点,则 k 的取值范围为
, k ∈Z,
2
2
π
π
π
+ ≥ + 2π,
4
2
所以ቐ 2
k ∈Z,
π
3π
π+ ≤ + 2π,
4
2
1
5
解得4 k + ≤ω≤2 k + , k ∈Z.
2
4
1
5
5
又由4 k + - 2+ ≤0, k ∈Z,且2 k + >0, k ∈Z,解得 k =0,
2
4
4
1
5
所以ω∈ , .
2
4
方法总结
A. [-1,1]
令 sin x = t , t ∈[-1,1],
则 y = t 2+ t -1=
1 2
[学习要求] 1.能画出 y = sin x , y = cos x , y =tan x 的图象. 2.理解
正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小
值、图象与 x 轴的交点等). 3.理解正切函数在区间
π
π
− ,
2
2
上的性质.
π
π
− <<
2
2
由题意得 y = cos x ·|tan x |=ቐ
的大致图象是(
sin,0 ≤
π
< ,
2
π
−sin, − <
2
所以其图象的大致形状如选项C所示.
< 0,
C )
2. 已知函数 f ( x )= sin x +2| sin x |, x ∈[0,2π],若直线 y = k
与其仅有两个不同的交点,则 k 的取值范围为
, k ∈Z,
2
2
π
π
π
+ ≥ + 2π,
4
2
所以ቐ 2
k ∈Z,
π
3π
π+ ≤ + 2π,
4
2
1
5
解得4 k + ≤ω≤2 k + , k ∈Z.
2
4
1
5
5
又由4 k + - 2+ ≤0, k ∈Z,且2 k + >0, k ∈Z,解得 k =0,
2
4
4
1
5
所以ω∈ , .
2
4
方法总结
A. [-1,1]
令 sin x = t , t ∈[-1,1],
则 y = t 2+ t -1=
1 2
正弦函数余弦函数的性质

1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
y
1
y=sinx (xR)
2 3 4 5 6
-4
-3
-2
-
o
-1
y=cosx (xR) 单调性(单调区间)
x
函数
奇偶性 [
2
+2k, +2k],kZ 单调递增 +2k,
3 2 2
y=sinx
奇函数
余弦函数的单调性
y
1
-3
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
- -1
…
2
…
0
1
…
2
…
-1
0
0
y=cosx (xR) 增区间为 [ +2k, 2k],kZ 减区间为 [2k, 2k + ], kZ , 其值从-1增至1 其值从 1减至-1
k
k
4
x k
4
,k Z
y为减函数
函数
奇偶性 [
2
单调性(单调区间) +2k, +2k],kZ 单调递增
正弦函数 奇函数
[
2
+2k,
3 2
2
+2k],kZ 单调递减
单调递增
o
-1
2
3
4
5
6
x
y
1
y=sinx (xR)
2 3 4 5 6
-4
-3
-2
-
o
-1
y=cosx (xR) 单调性(单调区间)
x
函数
奇偶性 [
2
+2k, +2k],kZ 单调递增 +2k,
3 2 2
y=sinx
奇函数
余弦函数的单调性
y
1
-3
5 2
-2
3 2
-
2
o
-1
2
3 2
2
5 2
x
3
7 2
4
x
cosx
- -1
…
2
…
0
1
…
2
…
-1
0
0
y=cosx (xR) 增区间为 [ +2k, 2k],kZ 减区间为 [2k, 2k + ], kZ , 其值从-1增至1 其值从 1减至-1
k
k
4
x k
4
,k Z
y为减函数
函数
奇偶性 [
2
单调性(单调区间) +2k, +2k],kZ 单调递增
正弦函数 奇函数
[
2
+2k,
3 2
2
+2k],kZ 单调递减
单调递增
5.4.2正弦函数、余弦函数的性质(第2课时)-高一数学上学期同步精讲课件(人教A版必修第一册2)

令−
2
则−
3
即−
6
)的单调区间和函数
6
+ 2 ≤ 2 − ≤ + 2, ∈ .
6
2
2
+ 2 ≤ 2 ≤ + 2, ∈ .
3
+ ≤ ≤ + , ∈ .
3
所以函数的单调递减区间是[− + , + ], ∈ .
6
3
3
令 + 2 ≤ 2 − ≤ + 2��, ∈ .
调递增,其值从 − 增大到 ;在每一个闭区间 [, + ] ( ∈ )上都单调递减,
其值从减小到−.
新知探索
思考3:在前面函数的性质中,我们除了奇偶性、单调性外,还学习了函数的最
值.请结合着前面对正余弦函数单调性的研究,找出正余弦函数的最值及其取得
最值时对应的自变量的值.
= , ∈ 取得最小值的的集合{| =
−
2
+ 2,得 =
−
4
−
2
+ 2, ∈ }.由2 = =
+ .所以,使函数 = −3 2, ∈ 取得最大值的的
4
集合是{| = − + , ∈ }.同理,使函数 = −3 2, ∈ 取得最小值的
[− , ]的单调增区间是[− , ],且由−
3 3
2 2
2
≤
1
2
+
3
3
≤≤ .
所以,函数 =
正余弦函数的性质(最值与单调性)

k = −1, k = 0, k = 1,
17π 11π − 3 , − 3 5π π − 3 , 3 7π 11π 3 , 3
√
变式二
• 求函数的单调增区间
π 1 y = sin − x + 3 2
增
y = sin z 减
上时,曲线逐渐下降, 上时,曲线逐渐下降, sinα的值由1减小到 −1 。 α
探究: 探究:正弦函数的单调性
y
1
−3 5 π π − 2
−2π −3π
2
−π
−
π
2
O
π
2
π
−1
3π 2
2π
5π 2
3π
x
正弦函数在每个闭区间[− + 2kπ , + 2kπ ](k ∈ Z) 2 2 都是增函数,其值从- 增大到 增大到1; 都是增函数,其值从-1增大到 ; π 3π 而在每个闭区间[ + 2kπ , + 2kπ ](k ∈ Z)上都是 2 2 减函数,其值从1减小到 减小到- 。 减函数,其值从 减小到-1。
应
用
举
例
例2:利用三角函数的单调性பைடு நூலகம்比较下列各组数的大小: :利用三角函数的单调性,比较下列各组数的大小:
π π 23π 17π (1)sin − 与sin − ; (2)cos − 与cos − ; 18 10 5 4 23π 23π 3π 解:
y = cos z y = cos z
y = A sin(ω x + ϕ ) → y = A sin z
增 (1)化未知为已知 增
高中数学第五章三角函数4.2第二课时正余弦函数的单调性与最值课件新人教A版必修第一册

1.判断正误.(正确的画“√”,错误的画“×”) (1)正弦函数y=sin x在R 上是增函数. (2)余弦函数y=cos x的一个减区间是[0,π]. (3)∃x∈[0,2π]满足sin x=2. (4)当余弦函数y=cos x取最大值时,x=π+2kπ,k∈Z . 答案:(1)× (2)√ (3)× (4)×
函数单调递减,故函数的单调递减区间是
4kπ-23π,4kπ+43π
(k∈Z ).
(2)∵y=2sinπ4 -x=-2sinx-π4 ,
∴函数y=-2sinx-π4 的单调增区间、单调减区间分别由下面的不等式确定.
2kπ+π2 ≤x-π4 ≤2kπ+3π2 (k∈Z ),
①
ππ
π
2kπ- 2 ≤x- 4 ≤2kπ+ 2 (k∈Z ).
知识点 正、余弦函数的单调性与最值 正弦函数
图象
值域
_[-__1_,__1_]
ห้องสมุดไป่ตู้
余弦函数 _[-__1_,__1_]
正弦函数
余弦函数
单
增区间 __-_π_2_+__2_k_π__,___π2__+_2_k_π___, [_π__+__2k_π__,__2_π__+__2_kπ__]_,_
调
__k_∈_Z____
所以sinπ5 <sin2π 5 ,
所以sin215π<425π.
答案:<
4.求函数f(x)=sin2x-π4 在0,π2 上的单调递增区间.
π
π
π
解:令2kπ- 2 ≤2x- 4 ≤2kπ+ 2 ,k∈Z ,
解得kπ-π8 ≤x≤kπ+3π8 ,k∈Z ,又0≤x≤π2 ,
所以f(x)在0,π2 上的单调递增区间是0,3π 8 .
高一数学必修第一册正弦函数、余弦函数的性质课件
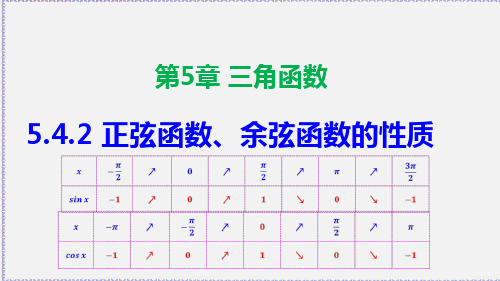
上都单调递减,其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到:
+ ( ∈ ) 时取得最大值1,
当且仅当 = − + ( ∈ ) 时取得最小值-1;
①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1,
【1】周期性:观察正弦函数的图像,可以发现,在图像上,横坐标每隔2π个单位
长度,就会出现纵坐标相同的点,这就是正弦函数值具有的“周而复始”的
变化规律.实际上,这一点既可以从定义中看出,也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值,与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢?
事实上,令 = + ,那么由 ∈ 得 ∈ ,且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +
+ ,所以自变量增加 ,函数值
+ ,
+ ( ∈ ) 上都单调递减,其值从1减小到-1.
单调性
−
−
−
同样的道理结合余弦函数的周期性我们可以知道:
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增,其值从-1增大到1;
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数,余弦函数是偶函数.
正、余弦函数的单调性与最值

函数 名称
图象与 性质
性质分类
定义域 相
同
值域
处 周期性
y=sinx
(-∞,+∞) [-1,1] T=2π
y=cosx
(-∞,+∞) [-1,1] T=2π
正、余弦函数的所有性质都是针对自变量x本身而言 的.正弦函数y=sinx(x∈R)的图象关于原点成中心对称, 其图象在对称中心和对称轴处对应的分别为函数的零点和 最值点.正弦函数有单调区间,但并不是定义域上的单调 函数,即:它在整个定义域内并不单调.
求函数y=Asin(ωx+φ)(A>0,ω≠0)或y=Acos(ωx+ φ)(A>0,ω≠0)的单调区间,一般将ωx+φ视作整体,代入y =sinx或y=cosx相关的单调区间所对应的不等式,解之即 得.这里实际上采用的是整体的思想,这是研究三角函数 性质的重要数学思想,一般地,ω<0时,y=Asin(ωx+ φ)(Aω≠0)变形为y=-Asin(-ωx-φ),y=Acos(ωx+ φ)(Aω≠0)变形为y=Acos(-ωx-φ),再求函数的单调区 间.所有的这些变形都是为了使x前面的系数为正值.同 时要注意A<0时单调区间的变化.
【名师点拨】
(1)对于形如y=a+bsinx或y=a+bcosx类型的函数求 值域时,主要是利用三角函数的图象求解,在解题时一定 要注意函数的定义域.
(2)对于形如y=Asin2x+Bsinx+C或y=Acos2x+Bcosx +C类型的函数求值域时,可采用换元法求解.
已知函数 y=2acos2x-3π+b 的定义域是 0,π2,值域是[-5,1],求 a,b 的值.
【名师点拨】
求三角函数y=Asin(ωx+φ)(A、ω≠0)或y=Acos(ωx+ φ)(Aω≠0)的单调区间,一定要注意到函数中A与ω的符 号.如果ω<0,一般利用诱导公式将x的系数化为正数, 再求解.
第2课时正弦函数、余弦函数的单调性与最值

易错提醒:求函数 y=Asin(ωx+φ)的单调区间时,把 ωx+φ 看作一个整体,借助 y=sin x 的单调区间来解决.当 A<0 或 ω<0 时,要注意原函数的单调性与函数 y=sin x 的单调性的关系.
【跟踪训练】 1.变式练将本例(2)变为:求函数 y=2cos( -x)的单调递 增区间. 解:y=2cos( -x)=2cos(x- ), 由 2kπ+π≤x- ≤2kπ+2π,k∈Z, 得 2kπ+ ≤x≤2kπ+ ,k∈Z. 所以原函数的单调递增区间是[2kπ+ ,2kπ+ ](k∈Z).
解析:当 sin x=-1,即 x=- +2kπ,k∈Z 时, 函数 y=2-sin x 取得最大值 3.
4.函数 y=3-2cos( x+ )的最大值为 5 , 此时自变量 x 的 取值是 3kπ+π,k∈Z .
解析:当 cos( x+ )=-1 时,ymax=3-2×(-1)=5.此时自变量 x=3kπ+π,k∈Z.
所以 ≤ω≤ ,故选 C. 答案:C
探索点二 比较三角函数值大小问题 【例 2】 比较下列各组数的大小:
(1)cos(- )与 cos(- );(2)sin 194°与 cos 160°.
【解题模型示范】
【跟踪训练】 4.cos 1,cos 2,cos 3 的大小关系是cos 1>cos 2>cos 3.(用 “>”连接)
课堂建构
解:(1)因为-1≤sin 2x≤1, 所以-2≤-2sin 2x≤2,所以 1≤3-2sin 2x≤5, 所以函数 y=3-2sin 2x 的值域是[1,5].
(2)由 y=cos(x+ ),x∈[0, ],得 x+ ∈[ , ].
【跟踪训练】 1.变式练将本例(2)变为:求函数 y=2cos( -x)的单调递 增区间. 解:y=2cos( -x)=2cos(x- ), 由 2kπ+π≤x- ≤2kπ+2π,k∈Z, 得 2kπ+ ≤x≤2kπ+ ,k∈Z. 所以原函数的单调递增区间是[2kπ+ ,2kπ+ ](k∈Z).
解析:当 sin x=-1,即 x=- +2kπ,k∈Z 时, 函数 y=2-sin x 取得最大值 3.
4.函数 y=3-2cos( x+ )的最大值为 5 , 此时自变量 x 的 取值是 3kπ+π,k∈Z .
解析:当 cos( x+ )=-1 时,ymax=3-2×(-1)=5.此时自变量 x=3kπ+π,k∈Z.
所以 ≤ω≤ ,故选 C. 答案:C
探索点二 比较三角函数值大小问题 【例 2】 比较下列各组数的大小:
(1)cos(- )与 cos(- );(2)sin 194°与 cos 160°.
【解题模型示范】
【跟踪训练】 4.cos 1,cos 2,cos 3 的大小关系是cos 1>cos 2>cos 3.(用 “>”连接)
课堂建构
解:(1)因为-1≤sin 2x≤1, 所以-2≤-2sin 2x≤2,所以 1≤3-2sin 2x≤5, 所以函数 y=3-2sin 2x 的值域是[1,5].
(2)由 y=cos(x+ ),x∈[0, ],得 x+ ∈[ , ].
