厦门市翔安区2014年九年级质量检查考试及答案
福建厦门市翔安区2014年九年级质量检查物理试题及答案

厦门市翔安区2014年九年级质量检查考试物 理 试 题 有 答 案(试卷满分:100分; 考试时间:90分钟) 考生注意:1.全卷六大题,33小题,试卷共6页,另有答题卡;2.答案一律写在答题卡上,否则不能得分,交卷时只交答题卡;3.作图题可以直接用2B 笔画;4.2×103J/(kg•℃)。
一、选择题(本大题12小题,每小题2分,共24分。
每小题只有1个选项符合题意)1.总结了伽利略等人的研究成果,经概括和推理得出牛顿第一定律的科学家是A .牛群B .牛顿C .欧姆D .安培2.今年频发的雾霾天气给人们的生活产生了严重的影响,下列措施不.能.降低雾霾天气的是 A .发展新清洁能源汽车 B .垃圾处理采取焚烧法C .坐公交车或骑自行车出行D .建筑工地和公路注意洒水防尘3.同窗三年,同学们互相非常熟悉了,甚至可以“闻其声,知其人”。
通过声音识别同学的主要依据是 A .音调 B .响度 C .音色 D .声速4.神舟十号载人飞船在远离地球的神奇太空中航行,若宇航员在飞船内玩推铅球游戏,下列说法中正确的是A .铅球推出后静止B .铅球推出后作匀速直线运动C .宇航员拿着铅球仍觉得很费力D .铅球碰到宇航员后,宇航员不觉得痛5.马航MH370客机疑似坠海后,搜救人员利用声纳设备探测坠入大海中的飞机残骸,以下说法正确的是A.声纳设备是利用超声波工作的B.声纳设备是利用次声波工作的C.声波不能在海水中传播D.声纳设备不能探测出残骸所处位置的海水深度 6.图1所示的四幅图中能说明发电机工作原理的是AB C D电源 a b a a b A B图17.通过超导体的学习,让同学们做了关于它的“中国梦”,超导体投入大量使用,下列物体可以用超导体来制作的是A .家用保险丝B .白炽灯泡的灯丝C .电炉的电热丝D .输电导线8.图2是禁烟标志,吸烟有损自己和他人的健康,据世卫组织统计,每年因吸烟导致近600万人失去生命,造成他人吸二手烟是由于A .烟分子间存在着引力B .烟分子间有空隙C .烟分子在不停地做无规则运动D .烟分子间存在着斥力9. 随着智能手机的普及,人们的聊天方式也不断推陈出新,微信就是时下流行的一款手机语音聊天软件,语音信息进行传播是利用手机发射A .电磁波B .激光C .红外线D .紫外线10.2014年2月11日,一张“同安下雪了”的微博图片(如图3所示),引起网友的热议。
2014年厦门市初三毕业班质量检测 思想品德参考答案

2014年厦门市初三毕业班质量检测思想品德参考答案一、选择题(下列各题的四个选项中,只有一个最符合题意,请选出来。
每小题2分,共50分)1D、2B 、3A 、4B 、5C 、6C、7D、8C 、9B 、10C 、11C 、12B、13B 、14A 、15B、16C 、17D 、18B、19C、20D 、21C 22B、23 、24B、25D二、根据要求回答下列问题(共50分)26题(8分)(1)《弟子规》文字揭示了哪一项基本道德要求?(1分)答:揭示了孝敬父母的基本道德要求。
(1分)(2)古人要求“弟子”恪守这些规矩的理由是什么(4分)答:天下父母无不疼爱自己的儿女,父母对子女的爱是无私的,对子女的爱是无保留的;孝敬父母是中华民族的传统美德。
子女回报父母的养育之恩被视为做人的本分,是社会的基本道德要求。
为人子女孝敬父母也是感恩的一种表现。
(4分、每小点都1分)(3)作为当代中学生,应如何传承这一道德要求?(3分)答:当前,孝敬父母表现在对父母的体谅、关心,尽可能为父母分担生活的压力和苦恼,让父母为自己的良好行为高兴、骄傲,不使父母为自己的错误行为忧虑、烦恼。
(3分)27、题(10分)(1)实现美丽厦门的“两个百年愿景”需要弘扬什么精神?(2分)答:需要弘扬以爱国主义为核心的民族精神和以改革创新为核心的时代精神。
(2分)(2)“规划”中提到的建党百年“愿景”中,哪些指标属于生态文明范畴?(2分)为了实现这些指标,请你为政府提两条合理化建议。
(4分)答:为了实现这些指标,政府应该坚持科学发展观,走科学发展道路,增强可持续发展能力,坚持节约资源、保护环境的基本国策,把生态文明放在更突出的位置等。
(以上内容酌情写2点即可)。
更具体的,符合政府的角度、有利于生态文明的也可以。
(3)作为厦门的一名中学生,你能为“美丽厦门”做些什么?(2分)答:从中学生的角度、生态文明的角度,言之有理即可。
正确的一点1分,最多2分。
2014—2015学年(上)厦门市九年级质量检测语文试题参考答案与评分标准

2014—2015学年(上)厦门市九年级质量检测语文试题参考答案与评分标准第一部分积累与运用(满分:37分)一、语言积累(13分)1.请根据提示填写相应的古诗文。
(13分)(13分)要点与评分:填空每处1分,有错、漏、添、乱序者,该处不得分。
(1)人迹板桥霜(2)念此私自愧(3)西北望射天狼(4)四面边声连角起千嶂里长烟落日孤城闭(5)叶底黄鹂一两声(6)生子当如孙仲谋(7)了却君王天下事赢得生前身后名(8)受任于败军之际奉命于危难之间二、语言运用(24分)2.根据情境,将下列对话补充完整。
(4分)(1)(2分)要点与评分:有称呼,使用礼貌用语1分,符合情境1分。
示例1:老大爷,请问有什么需要帮助的吗?示例2:老大爷,需要帮忙吗?(2)(2分)要点与评分:指示方向正确1分,叙述有条理1分。
示例1:您沿着海后路往升平路方向走,到了升平路口后再向右拐,然后沿着升平路走一段,在您的右手边就可以看到龙头旅社了。
示例2:您沿着海后路往西北方向走,到了升平路口后再向右拐,然后沿着升平路走一段,在升平路的右边就可以看到龙头旅社了。
3.根据提示,完成以下(1)-(3)小题。
(9分)(1)(3分)要点与评分:能用正楷清楚工整地把词语写在田字格里,不出现错别字即可得2分,字迹整洁清晰1分。
(2)(2分)D(3)①(2分)要点与评分:上下文语句通顺连贯,能扣住建筑的“壮”(建筑的力量)来谈,即可得分。
示例:规模宏大、气势宏伟、保存完整,给人们心理上的震撼感受。
②(2分)要点与评分:上下文语句通顺连贯,能扣住艺术珍品的“美”来谈,即可得分示例1:所传达的中国传统美学内涵。
示例2:精美绝伦、美不胜收。
4.综合性学习。
(11分)(1)(3分)要点与评分:每空1分,出现错别字不得分。
答案:(吉祥)图案款式工艺(2)(4分)要点与评分:找出1个元素1分,结合元素谈创意2分。
(创意方面:能够结合具体服饰将中国元素的内涵与作用进行一定的解读即可,示例仅供参考,按照元素和创意两方面进行评价)示例1:A图,2011年戛纳电影节范冰冰大红仙鹤礼服,采用了中国红的大红底色和洁白的仙鹤图案这两种中国元素,结合西方露肩拖地长礼服造型,渲染了电影节吉祥喜庆的氛围,展现出人物热情飘逸的东方美的气质。
厦门市翔安区2014年九年级质量检查考试物理试题(含答案)

物理试题(第 1 页,共 9 页) 厦门市翔安区2014年九年级质量检查考试物 理 试 题 (试卷满分:100分; 考试时间:90分钟)考生注意:1.全卷六大题,33小题,试卷共6页,另有答题卡;2.答案一律写在答题卡上,否则不能得分,交卷时只交答题卡;3.作图题可以直接用2B 笔画;4.2×103J/(kg•℃)。
一、选择题(本大题12小题,每小题2分,共24分。
每小题只有1个选项符合题意)1.总结了伽利略等人的研究成果,经概括和推理得出牛顿第一定律的科学家是A .牛群B .牛顿C .欧姆D .安培2.今年频发的雾霾天气给人们的生活产生了严重的影响,下列措施不.能.降低雾霾天气的是 A .发展新清洁能源汽车 B .垃圾处理采取焚烧法C .坐公交车或骑自行车出行D .建筑工地和公路注意洒水防尘3.同窗三年,同学们互相非常熟悉了,甚至可以“闻其声,知其人”。
通过声音识别同学的主要依据是 A .音调 B .响度 C .音色 D .声速4.神舟十号载人飞船在远离地球的神奇太空中航行,若宇航员在飞船内玩推铅球游戏,下列说法中正确的是A .铅球推出后静止B .铅球推出后作匀速直线运动C .宇航员拿着铅球仍觉得很费力D .铅球碰到宇航员后,宇航员不觉得痛5.马航MH370客机疑似坠海后,搜救人员利用声纳设备探测坠入大海中的飞机残骸,以下说法正确的是A.声纳设备是利用超声波工作的B.声纳设备是利用次声波工作的C.声波不能在海水中传播D.声纳设备不能探测出残骸所处位置的海水深度 6.图1所示的四幅图中能说明发电机工作原理的是AB C D电源 a b a a b A B图1。
翔安2014答案

厦门市翔安区2014年九年级质量检查考试物理试题参考答案及评分标准一、选择题(本大题共12小题,每小题2分,共24分)二、填空题(本大题10小题,每空1分,共20分)13.运动状态惯性14.浮力 115.断开闭合16.机械做功17.短路并联18.4.2X10570%19.小于连通器20.前方凹透镜21.实像照相机22. A 200三、简答题(本大题1小题,共4分)23.答:不同。
因为冰棒熔化时需要从人体吸热,所以小明感觉到凉快,而小华的皮肤擦上酒精后,酒精蒸发时需要从人体和周围环境中吸热,带走人体上一部分热量,所以小华也感觉凉快。
四、作图题(本大题2小题,每小题2分,共4分)(略)五、实验与探究(本大题5小题,共28分)26.(4分)(1)49 (2)30 偏小(3)0.827.(4分)(1)(1分)反射光线、法线、入射光线在同一平面内(2)(1分)靠近(3)(2分)光将沿OE反射28.(6分)(1)甲乙相同(2)质量相同的物体,运动的速度越大,动能越大(3)动能 C (2分)29.(8分)(1)温度计(2)质量相等初温相同(3)电流与通电时间相同(2分),电阻(4)略(2分)30.(6分)①压强(1)h1ρ水/ h2,(2)(4分)大②六、计算题(本大题3小题,31题6分,32题6分,33题8分,共20分)考生用其它方法计算正确的,参照评分标准分步给分。
31.(6分)解:(1)R=P U 2=WV 3)6(2=12 Ω ……………………………………………………(2分)(2)I L =R U =Ω123V =0.25 A ……………………………………………………(2分) (3)∵R 与L 并联,U R =U L =U =3 V I R =I-I L =0.55A-0.25A=0.3 A ……………(1分)∴R R =R R I U =AV3.03=10 Ω……………………………………………………(1分) 32.(6分)解:(1)G=mg =140kg ×10N/kg=1400 N ……………………………………………(2分)p=S F =S G 61=21.0140061m N =2333.3 Pa ……… ………… ……………………(2分) (2) ∴t=v s =sm m/03.090=3000 s ………………………………………………(2分)33.(8分)解:(1)空载时 F=0,R=300 ΩI=R U =00Ω38.4V=0.016 A ……………………………………………………(2分) (2)∵G=300N , AO :BO=3:1∴F=100 N ,R=240 ΩP=R U 2=Ω240)8.4(2V =0.096 W ……………………………………………(2分)(3)当I=0.024 A R=I U =AV24.08.4=200 Ω … ………………………………(1分) ∵F 与R 成线性关系 ∴200300-F =240300100-N… ……………………………………………(1分)F=3500 N ………………………………………………………………(1分)AO :BO=3:1故G 人=500 N … ………………………………………………………………(1分)。
2014-2015学年(上)厦门市九年级数学质量检测(含答案)

2014-2015学年(上)厦门市九年级质量检测数 学(考试满分:150分 考试时间:120分钟)一、选择题(本大题有10小题,每小题4分,共40分。
每小题都有四个选项,其中有且只有一个选项正确)1、下列事件中,属于必然事件的是 A 、任意画一个三角形,其内角和是180° B 、某射击运动员射击一次,命中靶心 C 、在只装了红球的袋子中摸到白球D 、掷一枚质地均匀的正方体骰子,向上的一面点数是3 2、在下列图形中,属于中心对称图形的是A 、锐角三角形B 、直角三角形C 、钝角三角形D 、平行四边形3、二次函数522+-=)(x y 的最小值是A 、2B 、2-C 、5D 、5- 4、如图1,点A 在⊙O 上,点C 在⊙O 内,点B 在⊙O 外,则图中的 圆周角是A 、∠OAB B 、∠OAC C 、∠COAD 、∠B5、已知一个元二次方程的二次项系数是3,常数项是1,则这个一元二次方程可能是 A 、013=+x B 、032=+x C 、0132=-x D 、01632=++x x6、已知)12(+m m P ,是平面直角坐标系中的点,则点P 的纵坐标随横坐标变化的函数解析 式可以是A 、x y =B 、x y 2=C 、12+=x yD 、2121-=x y 7、已知点)21(,A ,O 是坐标原点,将线段OA 绕点O 逆时针旋转90°,点A 旋转后的对应点是1A ,则点1A 的坐标是A 、)(1,2-B 、)(1,2-C 、)(2,1-D 、)(2,1--8、抛物线3)21(2+-=x y 的对称轴是A 、1=xB 、1-=xC 、21-=x D 、21=x 9、青山村种的水稻2010年平均每公顷产7200kg ,设水稻每公顷产量的年平均增长率为x , 则2012年平均每公顷比2011年增加的产量是ABCO 图1A 、()217200+x kg B 、()172002+x kg C 、()x x +27200 kg D 、()17200+x kg10、如图2,OA ,OB ,OC 都是⊙O 的半径,若∠AOB 是锐角,且∠AOB=2∠BOC ,则下 列结论正确的是A 、AB=2BCB 、AB<2BC C 、∠AOB=2∠CABD 、∠ACB=4∠CAB二、填空题(本大题有6小题,每小题4分,共24分)11、一个圆盘被平均分成红、黄、蓝、白四个扇形区域,向其投掷一枚飞镖,且落在圆盘内, 则飞镖落在白色区域的概率是___________。
2014-2015年厦门九年级质量检测语文试卷及答案

2014—2015学年(上)厦门市九年级质量检测语文(试卷满分:150分考试时间:120分钟)考生注意:1.全卷分三个部分,计17小题;2.答案一律写在答题卡上,否则不能得分。
第一部分语言积累与运用(满分:37分)一、语言积累(13分)1.请根据提示填写相应的古诗文。
(13分)(1)鸡声茅店月,。
(温庭筠《商山早行》)(1分)(2),尽日不能忘。
(白居易《观刈麦》)(1分)(3)会挽雕弓如满月,,。
(苏轼《江城子.密州出猎》)(2分)(4)塞下秋来风景异,衡阳雁去无留意。
,,。
(范仲淹《渔家傲.秋思》)(3分)(5)池上碧苔三四点,。
(晏殊《破阵子》)(1分)(6)天下英雄谁敌手?曹刘。
(辛弃疾《南乡子.登京口北固亭有怀》)(1分)(7)读辛弃疾《破阵子.为陈同普赋壮词以寄之》,我们可以领略到“,。
”那建功立业的豪情和现实中壮志难酬、白发早生的伤感与无奈!(2分)(8)任命一个人来挽救危局时,人们常引用诸葛亮《出师表》中:“,。
”来形容。
(2分)二、语言运用(24分)2.根据情境,将下列对话补充完整。
(4分)你在东海大厦前看见一位老大爷正焦急地张望着,你走过去询问:“(1)?”老大爷说:“我要去龙头旅社找一个朋友,不知道该怎么走。
”你急忙拿出手机,查了导航,告诉老大爷“(2)。
”(提示:请参照右边的路线图作答)3.根据提示,完成(1)-(3)小题。
(9分)中新社厦门11月23日电(记者陈悦)北京故宫龙凤吉祥物“壮壮”、“美美”23日在厦亮相。
故宫发言人表示,A历史优.....fēi弘.的故宫博物院首度有了自己的吉祥物,希望它们能成为C家喻...yōu久.、B气势恢yì户晓....yìng”的文化产品。
..,具有“D明星效应今次亮相的吉祥物形象,源自中国传统的吉祥龙凤,分别为龙“壮壮”和凤“美美”......故宫发言人介绍,“壮”是体现龙的力量,用来形容明清紫禁城的建筑①。
凤则是中国传统文化“美”的象征,用来比喻故宫所珍藏的艺术珍品②。
厦门市翔安区2014年九年级质量检查考试(含答案)

厦门市翔安区2014年九年级质量检查考试数 学 试 题(试卷满分:150分 考试时间:120分钟)考生注意:1.试卷共4页,另有答题卡.解答内容一律写在答题卡上,否则不能得分.2.作图或辅助线请使用2B 铅笔.一、选择题(本大题有7题,每小题3分,共21分,每小题都有四个选项,其中有且只有一个选项是正确的) 1.计算23-+的值是 A . 1B .1-C .5D .5-2. 下列四个几何体中,三视图都是相同图形的是3. 在函数21-=x y 在,自变量x 的取值范围是 A .2≠xB .2>xC .2≥xD.0≠x4.气象台预报“本市明天下雨的概率为80%”这句话指的是A .明天一定下雨B .明天80%的地区下雨,20%的地区不下雨C .明天下雨的可能性是80% D. 明天80%的时间下雨,20%的时间不下雨5. 正方形网格中,AOB ∠如图1放置,则sin AOB ∠的值是 A .55B .255C . 12 D. 26.不等式组⎩⎨⎧<->+04201x x 的解集是A .21<<-xB .1->xC .2<xD.21>-<x x 或7.如图2,A 、B 的坐标分别为)02(,,)(1,0,若将线段AB 平移至11B A ,则b a +的值为 A .2B .3C .4 D.5DCBAABO图1图2y OA(2,0) B(0,1)B 1(a,2)xA 1(3,b)ABCDE 图3二、填空题(本大题有10小题,每小题4分,共40分) 8.21-的相反数是 . 9.“节约光荣,浪费可耻”。
据统计,我国每年浪费粮食8000000吨,这个数据用科学计数法表示为 吨 .10. 抛物线2)1(2+-=x y 的顶点坐标是 ( , ) .11.如图3,点D E 、分别是ABC △中AB AC 、边的中点,已知3=DE , 则=BC . 12.已知反比例函数k y x=(0x >),请你写出一个k 值 ,使y 的值随着x 值的增大而减小.13.某市6月2日至8日的每日最高温度如图4所示,则这组数据 的中位数是 .14.已知 622=-n m ,3=+n m ,则n m -的值是 .15.某市按以下规定收取每月的水费:用水量不超过6吨,按每吨1.2元收费;如果超过6吨,未超过部分仍按每吨1.2元收取,而超过部分则按每吨2元收费。
2013—2014学年(上)厦门市九年级质量检测语文参考答案

2013—2014学年(上)厦门市九年级质量检测语文试题参考答案与评分标准第一部分语言积累与运用(满分:42分)一、语言积累(13分)1.请根据提示填写相应的古诗文。
(13分)(13分)要点与评分:填空每处1分,有错、漏、添、乱序者,该处不得分。
(1)凫雁满回塘(2)不求闻达于诸侯(3)一任群芳妒零落成泥碾作尘(4)五月人倍忙小麦覆陇黄(5)村南村北响缲车牛衣古柳卖黄瓜(6)浊酒一杯家万里醉里挑灯看剑酒酣胸胆尚开张含有“酒”字的古诗词皆可二、语言运用(29分)2.根据下列情境,把对话补充完整。
(4分)(4分)要点与评分:注意说话对象,有称呼,语言文明得体,符合话语情境即可。
每处2分。
示例1:小明:“大妈(奶奶),请别闯红灯,车辆很多,非常危险”。
小红:“大妈(奶奶),闯红灯会有生命危险,再大的事情也比不上生命重要,请您再耐心等待几秒钟好吗?”示例2:小明:“大妈(奶奶),红灯停绿灯行,闯红灯非常危险,您再等等,绿灯亮了再过马路”。
小红:“大妈(奶奶),等红灯只需几秒钟,闯红灯万一出危险岂不更耽误您办事?”3.根据提示,完成以下(1)-(2)小题。
(5分)(1)(2分)C(2)(3分)要点与评分:运用描写的表达方式,描写的必须是夏日的情景2分,表达1分。
4.名著阅读(7分)(1)(2分)要点与评分:施耐庵(有专家认为是罗贯中和施耐庵共同创作,故写施耐庵、罗贯中亦可)1分;《水浒》(或《水浒传》)1分。
(2)(2分)要点与评分:只要能把主要原因讲清楚即可。
示例1:郑屠镇关西虚钱实契,强骗了金翠莲,始乱终弃,被赶出门,却又要求其卖唱还钱。
金翠莲因这两日酒客稀少,怕郑屠来讨时受他羞辱。
示例2:地痞恶棍郑屠镇关西,强抢民女金翠莲做妾,先奸后弃,并讹诈虚钱实契的三千贯钱两,金氏父女无力和他争辩,只得含泪卖唱还债,因这两日酒客稀少,金翠莲怕郑屠来讨时受他羞辱,故此哭泣。
(3)(3分)要点与评分:能扣住《鲁提辖拳打镇关西》这则故事中鲁达的相关言行,分析其嫉恶如仇、见义勇为、勇而有谋、粗中有细、性格急躁、蛮横无礼等方面的特点,并谈谈自己的看法即可。
2013-2014学年(上)厦门九年级质量检测化学试题和参考答案

2013-2014学年(上)厦门九年级质量检测化学试题参考答案及评分标准化学方程式评分说明:每个化学方程式3分,所有化学式都正确1分,配平1分,其他都正确再给1分。
一、选择题(共10题,1~5题各2分,6~10题各3分,共25分。
多选、错选不给分)二、填空与简答(共5题,44分,除化学方程式及特别注明外每空各1分) 11.(7分)(1)①化合物 ②碳、氢、氧 ③6 ④CO 2和H 2O (2)① 2Mg ② 3NO 3—(3)Ⅰ12.(8分)(1) C (2)石油 CH 4 (3)+2 (4)4Na+ 3CO 22Na 2CO 3 + C(5)可燃性(或还原性、吸附性、稳定性等合理答案也可以) 13.(8分)(1)过滤 肥皂水 (2)A D(3)NH 3 (2分)O通电15.(11分)(1)C(2)①2H 2+O 2 点燃 2H 2O 化合反应 ②H 2CO 3=H 2O+CO 2↑ (3)CaCO 3+2HCl = CaCl 2+CO 2↑+H 2O 三、实验与探究(共2题,21分) 16.(13分)(1)长颈漏斗(2)2KMnO 4 △ K 2MnO 4 + MnO 2+ O 2↑ 酒精灯(3)Zn+H 2SO 4 = ZnSO 4+H 2↑ 方便添加液体反应物,控制生成物的速率排水法(或向下排空气法) ACDE (或BCDF 等合理答案也可以) (4)b 防止装置内的液体排出4400C 高压17.(8分)(1)固体药品熔化后会流到试管口冷凝水会倒流到试管底,造成试管破裂(2)①除去草酸蒸气,防止对二氧化碳的检验产生干扰收集未反应的一氧化碳,防止空气污染 ②澄清石灰水变浑浊 D 中黑色固体变红(3)一氧化碳没有全部与氧化铜反应(其他合理答案也可以) (2分) 四、计算与应用(共l 题,10分) 18.(10分)解:(1)生成氧气的质量=29.4 g +5.6 g - 25.4 g = 9.6 g (2分) (2)设剩余固体中氯化钾的质量为m2KClO 3MnO 2=====△2KCl + 3O 2↑2×74.5 3×32 (1分) m 9.6 g (1分)2×74.5 2×32m 9.6 g (1分) m =14.9 g (1分) (3)∵ 14.9 g+5.6 g=20.5 g 25.4 g >20.5 g∴ 剩余固体中还含氯酸钾(也可直接计算消耗的氯酸钾的质量,进行判断)(2分)答:制得氧气的质量为9.6 g ,剩余固体中氯化钾的质量为14.9 g ,剩余固体中还含氯酸钾。
【精品·打印版】2013-2014厦门市九年级物理质检试题及答案

2013-2014学年(上)厦门市九年级质量检测物理试题答案及评分标准一、选择题(本大题12小题,每小题2分,共24分) 1-5CACDC 6-10 DCBDB 11-12AB 二、填空题(本大题10小题,每小题2分,共20分) 13.无规则升高 14.B 汽化15.总开关并16.电源不适合 17.13.5 热 18.同种电荷相互排斥从B 到A 19.增加液化过程要放热 20.增大突然增大 21.天然气 7.2×108 22. 小于小于 三、简答题(4分)23.①污水杯中的水汽化成水蒸气,汽化吸热;②水蒸气上升,在塑料罩上遇冷液化成小水珠,液化放热。
四、作图题(本大题共2题。
每小题2分,共4分) 24.25.28分)26.(每小题2分,共4分)(1) 38.5 (2)2014.1 27.(每空1分,共4分)(1) 0 冰(2)小(3)受热均匀 28.(每小题2分,共4分)(1)滑动变阻器的滑片没有放在阻值最大处; (2)移动滑片电阻R 两端的电压(3)电压一定时,通过导体的电流与导体的电阻成反比。
29.(每小题2分,共8分)(1)A 电阻(2)温度计的示数变化比热容 (3)c 水(t 水-t 0)/(t 煤油-t 0)30.(每小题2分,共6分)(1)连接电源负极与滑动变阻器的左下接线柱 (2)滑动变阻器的电阻太大,电流太小(3)D (4)电压表接在滑动变阻器的两端。
六、计算题(本大题3小题,共20分)*其它方法计算正确的,参照评分标准分步给分。
31.解:(1)由Rt I Q 2=, 得A1s6040J4002=⨯Ω==Rt QI ………2分(2)电热丝剪去一半时,R 1=20 Ω,………1分U 总=I R =1 A×40 Ω=40 V ………1分11=R U I A 220V 40=Ω=………1分Q 1=I 12R 1t 1=(2A )2×20 Ω×60 s=4 800J ………1分乙 甲32.解:(1)V =1.5 L=1.5×10-3 m 3kg 5.1m 105.1kg/m 103333=⨯⨯===-V m V mρρ ……1分Q =c mΔt=4.2×103 J/(kg·℃) ×1.5kg×(100 ℃-20 ℃)=5.04×105 J ………………2分(2) J106.590%J 105.0455⨯=⨯==ηQW …………1分 s700W 800J 106.55=⨯===P W t t W P ………2分33.解:(1)当只闭合S 3时,L 与R 2串联,R 2=20 Ω,I 1=0.4 AΩ====30A 4.0V121I U R R U I ……1分R L =R 总-R 2=30 Ω-20 Ω=10 Ω…1分当只闭合S 2时,L 与R 1串联,R L =10 Ω,I 2=0.4 AR ′总=Ω==30A 4.0V 122I UR 1= R ′总- R L =30 Ω-10 Ω=20 Ω……1分(2)只闭合S 3时,L 与R 2串联,灯泡L 正常发光,U L =5 VI L=A 5.010V 5L L =Ω=R U ……1分∵U 2= U -U L=12 V-5 V=7 V ∴R ′2=Ω==14A 5.0V7'22I U ……1分(3)当闭合S 1、S 2、S 3时,L 被短路,R 1与R 2并联,U 1=U 2=U =12 V 1分I 1=A 6.020V1211=Ω=R U∵电流表示数不超过3 A ,∴R 2支路的最大电流 I 2=I -I 1=3 A-0.6 A=2.4 A …………1分R 2的最小阻值为R 2=Ω==5A 4.2V1222I U即R 2的阻值变化范围为5~40 Ω……1分。
厦门市2013—2014学年(上)九年级质量检测化学试题含答案

2013—2014 学年(上)厦门市九年级质量检测化学试题(满分:100 分;时间:60分钟)友情提示:1.本考试有两张试卷,一是答题卡,二是本试题卷(共 5 页,18题);将全部答案填在答题卡的相应答题栏内,否则不能得分。
2.可能用到的相对原子质量:H-1;C-12;N-14;O-16;Cl-35.5;K-39;Ca-40;Mn-55;Cu-63.5 一、选择题(共10题,25分。
1~5题各2分,6~10题各3分。
每题仅一个选项正确)1.下列关于化学发展的看法错误的是()A.导致生态环境恶化B.提升人类健康水平C.有助于人类开发新能源D.帮助人类研制新材料2.属于“空气污染指数”监测的污染物是()A.氮气B.二氧化碳 C.稀有气体D.可吸入颗粒物3.利用化学反应获得能量的是()A.微波炉B.风力发电机 C.酒精灯D.太阳灶4.下列处理方法错误的是()A.进入久未开启的菜窖前,用燃着的蜡烛做“灯火试验”B.电线短路起火,用水泼灭C.炒菜时油锅着火,用锅盖盖灭D.桌面上酒精燃烧,用湿抹布盖灭5.根据右图信息,说法正确的是()A.硫属于金属元素B.硫原子的核电荷数为16C.硫的相对原子质量32.06g D.在化学反应中,硫原子容易失去6 个电子6.下列实验操作正确的是()7.我国长征二F 运载火箭使用的燃料含有液态偏二甲肼(C2H8N2)。
下列关于偏二甲肼说法正确的是()A.含有氮分子B.相对分子质量为27C . C 、H 元素质量比为12 : 1D . 10g偏二甲联含碳元素4gCaO+CO2↑。
下列坐标图能正确反映一定质量碳酸钙充分灼烧过程变化关系的是()8.已知:CaCO3高温====9.在一个密闭容器中放人X 、Y 、Z 、W 四种物质,一定条件下发生化学反应,一段时间后,测得有关数据如下表。
关于此反应的说法正确的是()物质X Y Z W反应前质量(g) 2 1 16 16反应后质量(g)11 m 8 14A . m 的值为0 B.该反应类型为分解反应C.Z 与W 的质量变化比为4 : 1 D.物质Y 是该反应的催化剂选项方案结论A 人呼出的气体全部是CO2B 燃烧条件之一是可燃物的温度达到着火点C 温度升高,分子运动加快D 细铁丝与氧气反应比粗铁丝更激烈二、填空与简答(共5 题,44 分)11. ( 7 分)在宏观、微观和符号之间建立联系是化学学科的特点。
2014年质检真题.

2013—2014学年(上)厦门市九年级质量检测语文试题(试卷满分:150分考试时间:120分钟)考生注意:1.全卷分四个部分,计18小题;2.答案一律写在答题卡上,否则不能得分。
第一部分语言积累与运用(满分:42分)一、语言积累(13分)1.请根据提示填写相应的古诗文。
(13分)(1)____________________________________________ 因思杜陵梦,。
(温庭筠《商山早行》)(1分)(2)苟全性命于乱世,___________________ 。
(诸葛亮《出师表》)(1分)(3)无意苦争春,__________________ 。
________________ ,只有香如故。
(陆游《卜算子.咏梅》)(2分)(4)田家少闲月,__________________ 。
夜来南风起, ____________________ 。
(白居易《观刈麦》)(2分)(5)比起城市的喧嚣,乡村的生活何等的温馨、祥和:“簌簌衣巾落枣花, ____________________ 。
_________________ 。
”(苏轼《浣溪沙》)(2分)(6)“酒”在古诗词中很常见。
范仲淹举起的是一杯思乡的酒,“_______________________ 燕然未勒归无计。
”(《渔家傲.秋思》);辛弃疾痛饮的是一壶豪迈的酒,“_______________________ 梦回吹角连营。
”(《破阵子.为陈同普赋壮词以寄之》);苏轼畅饮的是一盏壮行的酒,“_______________________ 鬓微霜,又何妨?” (《江城子.密州出猎》)。
除此之外,请写出两句含有“酒”字的相对完整的古诗词:“___________________ ,________________ 。
”(5 分)二、语言运用(29分)2.根据下列情境,把对话补充完整。
(4分)星期天,小明和同学到学校附近的十字路口当小交通执勤员。
2013-2014学年(上)厦门九年级质量检测数学试题及参考答案和评分标..

20132013——2014学年(上)厦门市九年级质检数学(试卷满分:150分考试时间:120分钟)准考证号姓名座位号考生注意:本学科考试有两张试卷,分别是本试题(共4页26题)和答题卡.试题答案要填在答题卡相应的答题栏内,否则不能得分.一、选择题(本大题有7小题,每小题3分,共21分.每小题有四个选项,其中有且只有一个选项正确)1.下列计算正确的是()A .333=´B .933=´C .333=+D .633=+2.方程022=+x x 的根是()A .0 B .-2 C .0或-2 D .0或2 3.下列事件中,属于随机事件的是()A .掷一枚质地均匀的正方体骰子,向上的一面点数小于7 B .某射击运动员射击一次,命中靶心C .在只装了红球的袋子中摸到白球D .在三张分别标又数字2,4,6的卡片中摸两张,数字和是偶数4.已知⊙O 的半径是3,OP =3,那么点P 和⊙O 的位置关系是()A .点P 在⊙O 内B .点P 在⊙O 上C .点P 在⊙O 外D .无法确定5.下列图行中,属于中心对称图形的是()A .等边三角形B .直角三角形C .矩形D .等腰梯形6.反比例函数xm y 2-=的图像在第二、四象限内,则m 的取值范围()A .0>mB .2>mC .0<mD .2<m 7.如图1,在⊙O 中,弦AC 和BD 相交于点E,⌒AB =⌒BC =⌒CD ,若∠BEC =110°,则∠BDC ()A .35°B .45°C .55°D .70°D C A B E 二、填空题(本大题有10小题,每小题4分,共40分)分) 8.化简:3-= .9. 一个圆形转盘平均分成红、黄、蓝、白4个扇形区域,向其投掷一枚飞镖,个扇形区域,向其投掷一枚飞镖, 飞镖落在红色区域的概率是飞镖落在红色区域的概率是 .10.已知点)2,1(--A 与点)2,(m B 关于原点对称,则m 的值是的值是 .11.已知△ABC 的三边长分别是6,8,10,则△ABC 外接圆的直径是__________. 12.九年级有一个诗歌朗诵小组,其中男生5人,女生12人,先从中随机抽取人,先从中随机抽取一名同学参加表演,抽到男生的概率是一名同学参加表演,抽到男生的概率是 .13.若直线12)2(-+-=k x k y 与y 轴交于点(0,1),则k 的值等于的值等于 .14.如图,A 、B 、C 、D 是⊙O 上的三个点,若∠AOC =110°,则∠ABC = .15.电流通过导线时会产生热量,设电流是I(安培),导线电阻为R(欧姆),t 秒产生的热量为Q(焦), 根据物理公式Q=I²Q=I²Rt Rt ,如果导线的电阻为5欧姆,2秒时间导线产生60焦热量,焦热量, 则电流I 的值是的值是 安培.安培.16.如图,以正方形ABCD 的顶点D 为圆心画圆,分别交AD 、CD 两边于两边于点E 、F ,若∠ABD =15°,BE =2,则扇形DEF 的面积是________.17.求代数式12411)2411(2++-+--+c aac a ac a 的值是的值是. 三、解答题(本大题有9小题,共89分)分) 18.(本题满分21分)分) (1)计算32762-+´; (2)在平面直角坐标系中,已知点A (2,1),B (2,0), C (1,-1),请在图上画出△ABC ,并画出与,并画出与 △ABC 关于原点O 对称的图形;对称的图形;C F A B D E (3)如图,AB 是⊙O 的直径,直线AC ,BD 是⊙O 的 切线,A ,B 是切点.求证:AC ∥BD .19.(本题满分21分)分)(1)第一盒乒乓球中有2个白球1个黄球,第二盒子乒乓球中有1个白球1个黄球,分别从每个盒中随机地取出1个球,求这两个球中欧一个是白球一个是黄球的概率;个球,求这两个球中欧一个是白球一个是黄球的概率;(2)解方程:0232=-+x x ; (3)如图,在⊙O 中,⌒AB =⌒AC ,∠A=30°,求∠B 的度数20.(本题满分6分)分)判断关于x 的方程0)2(2=-++p px x 的根的情况.A C O B D 21.(本题满分6分)分)已知O 是平面直角坐标系的原点,点A (1,n ),B (-1,-n )(n >0),AB 的长是52, 若点C 在x 轴上,且OC =AC ,求点C 的坐标.22.(本题满分6分)分)如图,利用一面长度为7米的墙,用20米长的篱笆能否围出一个面积为48平方米的矩形菜园?若能,求出该菜园与墙平行一边的长度;若不能,说明理由.求出该菜园与墙平行一边的长度;若不能,说明理由.23.(本题满分6分)分)如图,平行四边ABCD 中,O 为AB 上的一点,连接OD 、OC ,以O 为圆心,OB 为半径画圆,分别交OD ,OC 于点P 、Q .若OB =4,OD =6,∠ADO =∠A ,=2π,判断直线D C 与⊙O 的位置关系,并说明理由.D A O B C 24.(本题满分6分)分)已知点))(,(),,(212211m m n m B n m A <在直线b kx y +=上,若b m m 321=+,,2421>+=+b kb n n , 试比较1n 和2n的大小,并说明理由.25.(本题满分6分)分)如图,⊙O 是△ABC 的外接圆,D 是弧ACB 的中点,DE ∥BC 交AC 的延长线于点E ,若AE =10,∠ACB =60°,求BC 的长.C A B E D 26.(本题满分11分)分)已知关于的方程)0(02¹=++b b ax x 与02=++d cx x 都有实数根,都有实数根,若这两个方程有且只有一个公共根,且cd ab =,则称它们互为“同根轮换方程”. 如062=--x x 与0322=--x x 互为“同根轮换方程”.(1)若关于x 的方程042=++m x x 与062=+-n x x 互为“同根轮换方程”,求m 的值;的值; (2)若p 是关于x 的方程)0(02¹=++b b ax x 的实数根,q 是关于x的方程02122=++b ax x 的实数根,当p 、q 分别取何值时,方程)0(02¹=++b b ax x 与02122=++b ax x互为“同根轮换方程”,请说明理由.,请说明理由.2013—2014学年(上) 厦门市九年级质量检测数学参考答案及评分标准一、选择题(本大题共7小题,每小题3分,共21分)分)题号题号 1 2 3 4 5 6 7 选项选项A C BB C D A 二、填空题(本大题共10小题,每题4分,共40分)分)8. 3; 9. 14; 101; 11. 10; 12. 517; 13. 1;14. 125; 15. 6; 16. π2; 17. 1.18(本题满分21分)分) (1)(本题满分7分)分)计算:2×6+27-3 解:原式=23+33-3 ……………………………4分=43. ……………………………7分(2)(本题满分7分)分)解:解: 正确画出△ABC . . …………………………………………………………3分 正确画出△A ,B ,C .,……………………………7分(3) (本题满分7分)分)证明:∵直线AC ,BD 是⊙O 的切线,的切线, 又∵AB 是⊙O 的直径,的直径, ……………………………3分 ∴OA ⊥AC .OB ⊥BD . …………………………………………………………5分 ∴AC ∥BD . . …………………………………………………………7分19.(本题满分21分)分) (1)(本题满分7分)分)P (一个白球一个黄球)(一个白球一个黄球)……………………………1分 =12. . …………………………………………………………7分(2)(本题满分7分)分)解:∵a =1,b =3,c =-2,∴∴ △=b 2-4ac=17. . …………………………………………………………2分∴∴ x =-b ±b 2-4ac 2a=-3±172. . …………………………………………………………5分∴∴x 1=-3+172,x 2=-3-172. …………………………………………………………7分(3)(本题满分7分)分) 解:在⊙O 中,∵︵AB =︵AC ,∴∠B =∠C .……………………………3分 ∵∠A =30°,∠A +∠B +∠C =180°,°, ∴∠∴∠B =75°.°. …………………………………………………………7分20.(本题满分6分)分)解:解: ∵ △=b 2-4ac=p 2-4×1×(p -2) =p 2-4p +8 ……………………………2分 =(p -2)2+4. …………………………………………………………4分 ∵∵(p -2)2≥0,∴(p -2)2+4﹥0. …………………………………………………………5分 即△﹥即△﹥0.∴方程∴方程x 2+px +(p -2)=0有两个不相等的实数根.…………………6分21.(本题满分6分)分)解:解: 过点A 作AD ⊥x 轴于点D , ∵A (1,n ),B (-1,-n ),∴点A 与点B 关于原点O 对称.对称.∴点A 、B 、O 三点共线.三点共线. …………………………1分 ∴AO =BO =5. ……………………………………2分 在Rt △AOD 中,中,n 2+1=5, ∴ n =±2. ∵∵ n >0,∴ n =2. …………………………………………………………3分若点C 在x 轴正半轴,设点C (a ,0),则CD =a -1.在Rt △ACD 中,中,AC 2=AD 2+CD2 OCBA=4+(a -1)2. …………………………………………………………4分又∵OC =AC∴ a 2=4+(a -1)2.∴ a =52. …………………………………………………………5分若点C 在x 轴负半轴,轴负半轴,∵AC >CD >CO ,不合题意.,不合题意.∴点C (52,0). …………………………………………………………6分22.(本题满分6分)分)答:不能.答:不能. …………………………………………………………1分设该菜园与墙平行的一边的长为x 米,米, 则该菜园与墙垂直的一边的长为则该菜园与墙垂直的一边的长为12(20-x )米,若米,若12(20-x ) x =48.即即 x 2-20x +96=0. …………………………………………………………4分解得解得x 1=12,x 2=8. …………………………………………………………5分∵墙长为∵墙长为7米,12﹥7且8﹥7, …………………………………………………………6分 ∴∴ 用20米长的篱笆不能围出一个面积为48平方米的矩形菜园.平方米的矩形菜园. 23.(本题满分6分)分) 解:如图解:如图,, 在⊙O 中,半径OB =4,设∠POQ 为n °,则有°,则有 2π=8πn 360.n =90°.……………………………1分 ∴∠POQ =90°.°. ∵∠ADO =∠A , ∴∴AO =DO =6. ……………………………2分∴AB =10.∵四边形ABCD 是平行四边形,是平行四边形,∴DC =AB =10. ……………………………3分 ∴ CO =8. ……………………………4分过点过点O 作OE ⊥CD 于点E , 则OD ×OC =OE ×CD . ∴∴OE =4.8. ……………………………5分 ∵4.8>4, ∴直线∴直线DC 与⊙O 相离.相离. ……………………………6分PQOED CBA24.(本题满分6分)分)解:∵A (m 1,n 1),B (m 2,n 2)在直线y =kx +b 上,上, ∴∴ n 1=k m1+b ,n 2=km 2+b . ……………………………1分∴∴ n 1+n 2=k (m 1+m 2) +2b .∴∴ kb +4=3kb +2b .∴k +1=2b . ……………………………3分∵ b >2,∴∴ 0<2b <1. ……………………………4分∴ 0<k +1<1. ∴ --1<k <0. ……………………………5分 ∵ m 1<m 2, ∴∴ n 2<n 1. ……………………………6分25.(本题满分6分)分)解:连结DA 、DB .∵D 是︵ACB 的中点,的中点,∴ DA =DB .∵∠ACB=60°,∴∠ADB=60°……………1分∴△ADB 是等边三角形.是等边三角形.∴∠DAB=∠DBA=60°.°. 连结DC .则∠DCB=∠DAB=60°.°. ∵ DE ∥BC ,∴∠E=∠ACB=60°.°.∴∠DCB=∠E . ……………………………2分∵ ∠ECD=∠DBA=60°,°, ∴ △ECD 是等边三角形.是等边三角形.∴ ED=CD . ……………………………3分∵ ︵CD=︵CD ,∴∠EAD=∠DBC . ……………………………4分 ∴△EAD ≌△CBD . ……………………………5分 ∴ BC=EA=10. ……………………………6分26.(本题满分11分)分)(1)(本小题满分4分)分) 解:∵方程x 2+4x +m =0与x 2-6x +n =0互为“同根轮换方程”, ∴∴ 4m =-6n . ……………………………1分设t 是公共根,则有t 2+4t +m =0,t 2-6t +n =0. 解得,t =n -m10. ……………………………2分OEDCBA∵ 4m =-6n . ∴ t =-m6. ……………………………3分∴(-m 6)2+4(-m6)+m =0.∴ m =-12. ……………………………4分(2)(本小题满分7分)分) 解1:∵:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”, 它们的公共根是它们的公共根是3. ……………………………1分而而 3=(-3)×(-1)=-3×(-1). 又∵又∵又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程”互为“同根轮换方程” .它们的公共根是-3. 而-3=-3×1.∴当p =q =-3a 时,时, ……………………………3分有9a 2-3a 2+b =0.解得,b =-6a 2.∴ x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,p =-3a ,x 1=2a ;q =-3a ,x 2=a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0. ∴ 2a ≠a .即x 1≠x 2. ……………………………5分 又∵又∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” . ……………………………7分 解2:∵:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”; 它们的非公共根是-它们的非公共根是-2,-1. ……………………………1分而-而-2=2×(-1), -1=1×(-1). 又∵又∵又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程”互为“同根轮换方程” . 它们的非公共根是2,1. 而2=2×1,1=1×1.∴当p =2a ,q =a 时,时, ……………………………3分有有4a 2+2a 2+b =0.解得,b =-6a 2.∴有∴有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,p =2a ;x 3=-3a ,q =a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即p ≠q . ……………………………5分且x 1=x 3=-3a . ∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” . ……………………………7分解3:若方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0有公共根.有公共根. 则由x 2+ax +b =0,x 2+2ax +12b =0解得解得x =b2a . ……………………………1分∴ b 24a 2+b2+b =0.∴b =-6a 2. ……………………………3分当b =-6a 2时,时,有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,x 2=2a ;x 3=-3a ,x 4=a .…………………………4分若 p =q =-3a ,∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即x 2≠x 4. …………………………5分 ∵ 2a ×12b =ab , …………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” .…………………………7分2013—2014学年(上) 厦门市九年级质量检测数学参考答案及评分标准三、选择题(本大题共7小题,每小题3分,共21分)分)题号题号 1 2 3 4 5 6 7 选项选项A C BB C D A 四、填空题(本大题共10小题,每题4分,共40分)分)8. 3; 9. 14; 101; 11. 10; 12. 517; 13. 1;14. 125; 15. 6; 16. π2; 17. 1.18(本题满分21分)分) (1)(本题满分7分)分)计算:2×6+27-3 解:原式=23+33-3 ……………………………4分=43. ……………………………7分(2)(本题满分7分)分)解:解: 正确画出△ABC . . …………………………………………………………3分 正确画出△A ,B ,C .,……………………………7分(3) (本题满分7分)分)证明:∵直线AC ,BD 是⊙O 的切线,的切线, 又∵AB 是⊙O 的直径,的直径, ……………………………3分∴OA ⊥AC .OB ⊥BD . …………………………………………………………5分 ∴AC ∥BD . . …………………………………………………………7分19.(本题满分21分)分) (1)(本题满分7分)分)P (一个白球一个黄球)(一个白球一个黄球)……………………………1分 =12. . …………………………………………………………7分(2)(本题满分7分)分)解:∵a =1,b =3,c =-2,∴∴ △=b 2-4ac=17. . …………………………………………………………2分∴∴ x =-b ±b 2-4ac2a=-3±172. . …………………………………………………………5分∴∴x 1=-3+172,x 2=-3-172. …………………………………………………………7分(3)(本题满分7分)分) 解:在⊙O 中,∵︵AB =︵AC ,∴∠B =∠C .……………………………3分 ∵∠A =30°,∠A +∠B +∠C =180°,°, ∴∠∴∠B =75°.°. …………………………………………………………7分20.(本题满分6分)分)解:解: ∵ △=b 2-4ac=p 2-4×1×(p -2) =p 2-4p +8 ……………………………2分=(p -2)2+4. …………………………………………………………4分∵∵(p -2)2≥0,∴(p -2)2+4﹥0. …………………………………………………………5分 即△﹥即△﹥0.∴方程∴方程x 2+px +(p -2)=0有两个不相等的实数根.…………………6分21.(本题满分6分)分)解:解: 过点A 作AD ⊥x 轴于点D , ∵A (1,n ),B (-1,-n ),∴点A 与点B 关于原点O 对称.对称. ∴点A 、B 、O 三点共线.三点共线. …………………………1分∴AO =BO =5. ……………………………………2分 在Rt △AOD 中,中,n 2+1=5, ∴ n =±2. ∵∵ n >0,∴ n =2. …………………………………………………………3分若点C 在x 轴正半轴,设点C (a ,0),则CD =a -1.在Rt △ACD 中,中,AC 2=AD 2+CD2 =4+(a -1)2. …………………………………………………………4分OCBA又∵OC =AC∴ a 2=4+(a -1)2.∴ a =52. …………………………………………………………5分若点C 在x 轴负半轴,轴负半轴,∵AC >CD >CO ,不合题意.,不合题意.∴点C (52,0). …………………………………………………………6分22(本题满分6分)分)答:不能.答:不能. …………………………………………………………1分设该菜园与墙平行的一边的长为x 米,米,则该菜园与墙垂直的一边的长为则该菜园与墙垂直的一边的长为12(20-x )米,若米,若12(20-x ) x =48.即即 x 2-20x +96=0. …………………………………………………………4分解得解得x 1=12,x 2=8. …………………………………………………………5分∵墙长为∵墙长为7米,12﹥7且8﹥7, …………………………………………………………6分∴∴ 用20米长的篱笆不能围出一个面积为48平方米的矩形菜园.平方米的矩形菜园. 23.(本题满分6分)分)解:如图解:如图,, 在⊙O 中,半径OB =4,设∠POQ 为n °,则有°,则有 2π=8πn360.n =90°.……………………………1分 ∴∠POQ =90°.°. ∵∠ADO =∠A , ∴∴AO =DO =6. ……………………………2分∴AB =10.∵四边形ABCD 是平行四边形,是平行四边形,∴DC =AB =10. ……………………………3分 ∴ CO =8. ……………………………4分过点过点O 作OE ⊥CD 于点E , 则OD ×OC =OE ×CD . ∴∴OE =4.8. ……………………………5分 ∵4.8>4, ∴直线∴直线DC 与⊙O 相离.相离. ……………………………6分24.(本题满分6分)分)解:∵A (m 1,n 1),B (m 2,n 2)在直线y =kx +b 上,上, ∴∴ n 1=k m1+b ,n 2=km 2+b . ……………………………1分PQOE DCBA∴∴ n 1+n 2=k (m 1+m 2) +2b . ∴∴ kb +4=3kb +2b .∴k +1=2b . ……………………………3分∵ b >2,∴∴ 0<2b <1. ……………………………4分∴ 0<k +1<1. ∴ --1<k <0. ……………………………5分 ∵ m 1<m 2,∴∴ n 2<n 1. ……………………………6分25.(本题满分6分)分)解:连结DA 、DB . ∵D 是︵ACB 的中点,的中点,∴ DA =DB .∵∠ACB=60°,∴∠ADB=60°……………1分∴△ADB 是等边三角形.是等边三角形. ∴∠DAB=∠DBA=60°.°. 连结DC .则∠DCB=∠DAB=60°.°.∵ DE ∥BC ,∴∠E=∠ACB=60°.°.∴∠DCB=∠E . ……………………………2分∵ ∠ECD=∠DBA=60°,°, ∴ △ECD 是等边三角形.是等边三角形.∴ ED=CD . ……………………………3分∵ ︵CD=︵CD ,∴∠EAD=∠DBC . ……………………………4分 ∴△EAD ≌△CBD . ……………………………5分 ∴ BC=EA=10. ……………………………6分26(本题满分11分)分)(1)(本小题满分4分)分) 解:∵方程x 2+4x +m =0与x 2-6x +n =0互为“同根轮换方程”, ∴∴ 4m =-6n . ……………………………1分设t 是公共根,则有t 2+4t +m =0,t 2-6t +n =0. 解得,t =n -m10. ……………………………2分∵ 4m =-6n .∴ t =-m6. ……………………………3分OEDC BA∴(-m 6)2+4(-m6)+m =0.∴ m =-12. ……………………………4分(2)(本小题满分7分)分) 解1:∵:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”, 它们的公共根是它们的公共根是3. ……………………………1分而而 3=(-3)×(-1)=-3×(-1). 又∵又∵又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程”互为“同根轮换方程” . 它们的公共根是-3. 而-3=-3×1.∴当p =q =-3a 时,时, ……………………………3分有9a 2-3a 2+b =0.解得,b =-6a 2.∴ x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,p =-3a ,x 1=2a ;q =-3a ,x 2=a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0. ∴ 2a ≠a .即x 1≠x 2. ……………………………5分 又∵又∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” . ……………………………7分 解2:∵:∵ x 2-x -6=0与x 2-2x -3=0互为“同根轮换方程”; 它们的非公共根是-它们的非公共根是-2,-1. ……………………………1分而-而-2=2×(-1), -1=1×(-1). 又∵又∵又∵ x 2+x -6=0与x 2+2x -3=0互为“同根轮换方程”互为“同根轮换方程” . 它们的非公共根是2,1. 而2=2×1,1=1×1.∴当p =2a ,q =a 时,时, ……………………………3分有有4a 2+2a 2+b =0.解得,b =-6a 2. ∴有∴有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,p =2a ;x 3=-3a ,q =a .……………………………4分 ∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即p ≠q . ……………………………5分且x 1=x 3=-3a . ∵ 2a ×12b =ab , ……………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” . ……………………………7分解3:若方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0有公共根.有公共根. 则由x 2+ax +b =0,x 2+2ax +12b =0解得解得 x =b 2a . ……………………………1分∴ b 24a 2+b2+b =0.∴b =-6a 2. ……………………………3分当b =-6a 2时,时,有 x 2+ax -6a 2=0,x 2+2ax -3a 2=0.解得,x 1=-3a ,x 2=2a ;x 3=-3a ,x 4=a .…………………………4分若 p =q =-3a ,∵b ≠0,∴-6a 2≠0,∴a ≠0.∴2a ≠a .即x 2≠x 4. …………………………5分 ∵ 2a ×12b =ab , …………………………6分∴方程x 2+ax +b =0(b ≠0)与x 2+2ax +12b =0互为“同根轮换方程”互为“同根轮换方程” .。
2014年厦门市翔安区初中学业质量检查数学试卷含答案解析

2014年福建省厦门市翔安区初中学业质量检查数学试卷参考答案与试题解析一、选择题(本大题有7题,每小题3分,共21分,每小题都有四个选项,其中有且只有一个选项是正确的)1.(3分)计算:﹣2+3=()A. 1 B.﹣1 C. 5 D.﹣5分析:根据异号两数相加,取绝对值较大的加数的符号,再用较大的绝对值减去较小的绝对值,可得答案.解答:解:﹣2+3=+(3﹣2)=1.故选:A.点评:本题考查了有理数的加法,先确定和的符号,再进行绝对值得运算.2.(3分)四个几何体中,三视图都是相同图形的是()A.长方体B.圆柱C.球D.三棱柱考点:简单几何体的三视图.分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.解答:解:A、长方体的三视图分别为长方形,长方形,正方形,不符合题意;B、圆柱的三视图分别为长方形,长方形,圆,不符合题意;C、球的三视图均为圆,正确;D、正三棱柱的主视图为两个长方形的组合体,左视图为长方形,俯视图为三角形,错误,故选:C.点评:本题考查了几何体的三视图,从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.3.(3分)在函数y=中,自变量x的取值范围是()A.x≠2B. x>2 C.x≥2D.x≠0考点:函数自变量的取值范围.分析:根据分母不等于0列式计算即可得解.解答:解:由题意得,x﹣2≠0,解得x≠2.故选A.点评:本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.4.(3分)“明天下雨的概率为80%”这句话指的是()A.明天一定下雨B.明天80%的地区下雨,20%的地区不下雨C.明天下雨的可能性是80%D.明天80%的时间下雨,20%的时间不下雨考点:概率的意义.分析:根据概率的意义找到正确选项即可.解答:解:“明天下雨的概率为80%”说明明天下雨的可能性是80%,即P(A)=80%.故选C.点评:关键是理解概率表示随机事件发生的可能性大小:可能发生,也可能不发生.5.(3分)正方形网格中,∠AOB如图放置,则sin∠AOB=()A.B.C.D. 2考点:锐角三角函数的定义.专题:网格型.分析:找出以∠AOB为内角的直角三角形,根据正弦函数的定义,即直角三角形中∠AOB的对边与斜边的比,就可以求出.解答:解:如图,作EF⊥OB,则EF=2,OF=1,由勾股定理得,OE=,∴sin∠AOB===.故选B.点评:通过构造直角三角形来求解,利用了锐角三角函数的定义.6.(3分)不等式组的解集是()A. x>﹣1 B.﹣1<x<2 C. x<2 D. x<﹣1或x>2考点:解一元一次不等式组.分析:分别求出各不等式的解集,再求出其公共解集即可.解答:解:由①得,x>﹣1,由②得,x<2,∴原不等式组的解集是﹣1<x<2.故选B.点评:主要考查了一元一次不等式解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).7.(3分)如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b 的值为()A. 2 B. 3 C. 4 D. 5考点:坐标与图形变化-平移.专题:压轴题.分析:直接利用平移中点的变化规律求解即可.解答:解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.点评:本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.二、填空题(本大题有10小题,每小题4分,共40分)8.(4分)﹣的相反数是.考点:相反数.分析:求一个数的相反数就是在这个数前面添上“﹣”号.解答:解:根据相反数的定义,﹣的相反数是.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.9.(4分)“节约光荣,浪费可耻”,据统计我国每年浪费粮食约8000000吨,这个数据用科学记数法可表示为8×106吨.考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:将8000000用科学记数法表示为:8×106.故答案为:8×106.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.10.(4分)抛物线y=(x﹣1)2+2的顶点坐标是(1,2).考点:二次函数的性质.分析:直接利用顶点式的特点可求顶点坐标.解答:解:因为y=(x﹣1)2+2是抛物线的顶点式,根据顶点式的坐标特点可知,顶点坐标为(1,2).点评:主要考查了求抛物线的对称轴和顶点坐标的方法.11.(4分)如图,点D、E分别是△ABC中AB、AC边的中点,已知DE=3,则BC= 6.考点:三角形中位线定理.分析:根据三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半可知,ED=BC,进而由DE的值求得BC.解答:解:∵D,E分别是△ABC的边AC和AC的中点,∴DE是△ABC的中位线,∵DE=2,∴BC=2DE=6.故答案是:6.点评:本题主要考查三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.12.(4分)已知反比例函数y=(x>0),请你补充一个条件k=1(答案不唯一),使y的值随着x值的增大而减小.考点:反比例函数的性质.专题:开放型.分析:本题考查反比例函数的图象和性质.解答:解:由于x>0,根据反比例函数的性质,y的值随着x值的增大而减小时,k>0,可取k=1,k=2,k=3等.点评:定义:一般地,如果两个变量x、y之间的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的反比例函数.因为y=是一个分式,所以自变量x的取值范围是x≠0.而y=有时也被写成xy=k或y=kx﹣1.性质:①当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y 随x的增大而增大.k>0时,函数在x<0上为减函数、在x>0上同为减函数;k<0时,函数在x<0上为增函数、在x>0上同为增函数.定义域为x≠0;值域为y≠0.③因为在y=(k≠0)中,x不能为0,y也不能为0,所以反比例函数的图象不可能与x轴相交,也不可能与y轴相交.④在一个反比例函数图象上任取两点P,Q,过点P,Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2,则S1=S2=|k|.⑤反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴y=x,y=﹣x(即第一、三象限,第二、四象限角平分线),对称中心是坐标原点.13.(4分))某市6月2日至8日的每日最高温度如图,则这组数据的中位数是29℃.考点:中位数;折线统计图.分析:先根据图表写出2日到8日的气温,然后根据中位数的概念求解.解答:解:2日到8日的气温为:27,30,28,29,30,29,30,这组数据按照从小到大的顺序排列为:27,28,29,29,30,30,30,则中位数为:29℃.故答案为:29℃.点评:本题考查了中位数的知识:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.14.(4分)已知m2﹣n2=6,m+n=3,则m﹣n的值是2.考点:平方差公式.分析:直接利用平方差公式求出即可.解答:解:∵m2﹣n2=6,m+n=3,∴(m﹣n)(m+n)=6,则m﹣n的值是2.故答案为:2.点评:此题主要考查了平方差公式的应用,熟练利用公式法求出是解题关键.15.(4分)某市按以下规定收取每月的水费:用水量不超过6吨,按每吨1.2元收费;如果超过6吨,未超过部分仍按每吨1.2元收取,而超过部分则按每吨2元收费.如果某用户5月份水费平均为每吨1.4元,那么该用户5月份实际用水8吨.考点:一元一次方程的应用.分析:水费平均为每吨1.4元大于1.2元,说明本月用水超过了6吨,那么标准内的水费加上超出部分就是实际水费.根据这个等量关系列出方程求解.解答:解:设该用户5月份实际用水x吨,则1.2×6+(x﹣6)×2=1.4x,7.2+2x﹣12=1.4x,0.6x=4.8,x=8.答:该用户5月份实际用水8吨.故答案为8.点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.16.(4分)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是2.4.考点:矩形的判定与性质;垂线段最短;勾股定理.分析:连接CP,利用勾股定理列式求出AB,判断出四边形CFPE是矩形,根据矩形的对角线相等可得EF=CP,再根据垂线段最短可得CP⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.解答:解:如图,连接CP.∵∠C=90°,AC=3,BC=4,∴AB===5,∵PE⊥AC,PF⊥BC,∠C=90°,∴四边形CFPE是矩形,∴EF=CP,由垂线段最短可得CP⊥AB时,线段EF的值最小,此时,S△ABC=BC•AC=AB•CP,即×4×3=×5•CP,解得CP=2.4.故答案为:2.4.点评:本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CP⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.17.(4分)如图,直线y=x+4与x轴、y轴分别交于A、B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则点C的坐标是(0,1.5).考点:一次函数综合题.专题:压轴题.分析:利用三角形全等性质.解答:解:由题意得:A(﹣3,0),B(0,4);∴OA=3,OB=4.那么可得AB=5.易得△ABC≌△ADC,∴AD=AB=5,∴OD=AD﹣OA=2.设OC为x.那么BC=CD=4﹣x.那么x2+22=(4﹣x)2,解得x=1.5,∴C(0,1.5).点评:本题用到的知识点为:翻折前后的三角形全等.三、解答题(本题有9题,共89分)18.(7分)|﹣1|﹣2÷+(﹣2)2.考点:有理数的混合运算.专题:计算题.分析:原式第一项利用绝对值的代数意义化简,第二项利用除法法则计算,最后一项利用乘方的意义计算即可得到结果.解答:解:原式=1﹣2×3+4=1﹣6﹢4=﹣1.点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.19.(7分)画出如图中的△ABC关于y轴对称的图形.考点:作图-轴对称变换.专题:作图题.分析:根据网格结构找出点B、C关于y轴的对称点的位置,然后与点A顺次连接即可.解答:解:△ABC关于y轴对称的图形△AB′C′如图所示.点评:本题考查了利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.20.(7分)如图,已知AB∥CD,若∠A=20°,∠E=35°,求∠C.考点:三角形的外角性质;平行线的性质.分析:根据三角形的外角等于和它不相邻的两个内角的和以及平行线的性质进行求解.解答:解:∵∠A=20°,∠E=35°,∴∠EFB=∠A+∠E=55°,∵AB∥CD,∴∠C=∠EFB=55°.点评:此题考查了三角形的外角的性质以及平行线的性质.三角形的外角等于和它不相邻的两个内角的和;两条直线平行,则同位角相等.21.(6分)为了解“节约用水”活动开展一个月来的成效,某单位随机调查了20名职工家庭一个月来的节约用水情况,如下表所示:节约水量(吨)0.5 1 1.5 2职工数(人)10 5 4 1请你根据上表提供的信息估计该单位100位职工的家庭一个月大约能节约用水多少吨?考点:用样本估计总体;加权平均数.分析:根据加权平均数的计算公式求出样本的平均数,再乘以100,即可得出答案.解答:解:根据题意得:(0.5×10+1×5+1.5×4+2×1)÷20×100=0.9×100=90(吨).答:该单位100位职工家庭一个月大约节约用水90吨.点评:此题考查了加权平均数和用样本估计总体,根据加权平均数的计算公式求出样本的平均数是本题的关键;用样本估计整体让整体×样本的百分比即可.22.(6分)先化简,再求值:(a+b)2+a(a﹣2b),其中a=1,b=.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:(a+b)2+a(a﹣2b)=a2+2ab+b2+a2﹣2ab=2a2+b2,当a=1,b=时,原式=2×12+()2=4.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,题目比较典型,难度适中.23.(6分)如图,已知DE是AC的垂直平分线,AB=10cm,BC=11cm,求△ABD的周长.考点:线段垂直平分线的性质.分析:先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可得出结论.解答:解:∵DE垂直平分,∴AD=CD,∴BD+AD=BD+CD=BC=11cm,又∵AB=10cm,∴△ABD的周长=AB+BC=10+11=21(cm).点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.24.(6分)在学习概率知识时,王老师布置了这样一道题目:在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个.要求同学按两种规则摸球:①摸出一个球后放回,再摸出一个球;②一次性摸两个球.那么,请你通过计算说明哪种方法摸到两个红球的概率较大?考点:列表法与树状图法.分析:列举出所有情况,看两次都摸到红球的情况占总情况的多少即可知道哪种方法摸到两个红球的概率较大.解答:解:①:摸出一个球后放回,再摸出一个球时,,共有16种等可能的结果数,其中两个都是红球的占4种,所以两次都摸到红球的概率=;②一次性摸两个球时,∴一共有12种情况,有2种情况两次都摸到红球,∴两次都摸到红球的概率是=.∵>,∴两次摸球的概率较大.点评:本题考查了列表法与树状图法,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比25.(6分)如图,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm.(1)求∠CBD的度数;(2)求下底AB的长.考点:梯形;等腰三角形的性质.分析:(1)求∠CBD的度数,根据BC=CD,得到∠CDB=∠ABD,根据AB∥CD,只要求出∠ABD的度数就可以.(2)Rt△ABD中,∠ABD=30°,则AB=2AD.解答:解:(1)∵∠A=60°,BD⊥AD∴∠ABD=30°(2分)又∵AB∥CD∴∠CDB=∠ABD=30°(4分)∵BC=CD∴∠CBD=∠CDB=30°(5分)(2)∵∠ABD=∠CBD=30°∴∠ABC=60°=∠A(7分)∴AD=BC=CD=2cm∴AB=2AD=4cm.(9分)点评:本题主要考查了等腰三角形的性质,等边对等角.26.(6分)为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?考点:反比例函数的应用.分析:由于当每立方米空气中含药量低于16mg时,对人体方能无毒害作用,把y=16代入反比例函数解析式中即可求出从燃烧开始,经多长时间学生才可以回教室.解答:解:设燃烧后的函数解析式为y=,∵图象经过点(10,16),∴k=160,∴y=.由,得x=40∴从消毒开始要经过40分钟后学生才能进教室.点评:此题主要考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法即可求出它们的关系式.27.(6分)如图,已知菱形AOBD的A、B、D三点在⊙O上,延长BO至点P,交⊙O于点C,且BP=3OB.求证:AP是⊙O的切线.考点:切线的判定.专题:证明题.分析:连接OD、AO,根据菱形的性质得AO=OB=BD=DA,则可判断△OAD和△OBD都为等边三角形,所以∠AOD=∠BOD=60°,则∠AOP=60°,于是又可判断△AOC为等边三角形,所以AC=OC,∠ACO=∠OAC=60°,由PB=3BO得到CP=OC=AC,根据等腰三角形的性质得∠P=∠CAP,然后利用三角形外角性质有∠P+∠CAP=∠ACO=60°,得到∠CAP=30°,所以∠OAP=90°,最后利用切线的判定定理得到AP为⊙O的切线.解答:证明:连接OD、AO,如图,∵四边形AOBD为菱形,∴AO=OB=BD=DA,∴△OAD和△OBD都为等边三角形,∴∠AOD=∠BOD=60°,∴∠AOP=60°,又∵OA=OC,∴△AOC为等边三角形,∴AC=OC,∠ACO=∠OAC=60°,∵PB=3BO,OC=OB,∴CP=OC=AC,∴∠P=∠CAP,∵∠P+∠CAP=∠ACO=60°,∴∠CAP=30°,∴∠OAP=90°,∴OA⊥AP,∴AP为⊙O的切线.点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了菱形的性质和等边三角形的判定与性质.28.(6分)如图,已知A(a,m)、B(2a,n)是反比例函数y=(k>0)与一次函数y=﹣x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.考点:反比例函数系数k的几何意义.分析:先根据函数图象上点的坐标特征得出m=,n=,=﹣a+b,=﹣a+b,于是k=a2,再由反比例函数系数k的几何意义可知S△OAC=S△OBD,那么S△OAB=S△OAC﹣S+S梯形ABDC=S梯形ABDC=2a2,根据二次函数的性质即可求解.△OBD解答:解:∵A(a,m)、B(2a,n)在反比例函数y=(k>0)的图象上,∴m=,n=,∵A(a,m)、B(2a,n)在一次函数y=﹣x+b图象上,∴=﹣a+b,=﹣a+b,解得:k=a2,∴S△OAB=S△OAC﹣S△OBD+S梯形ABDC=S梯形ABDC=(+)(2a﹣a)=××a=k=×a2=2a2.当1≤a≤2时,S△OAB=2a2,随自变量的增大而增大,此时2≤S△OAB≤8.点评:本题考查了函数图象上点的坐标特征,反比例函数系数k的几何意义,梯形的面积,二次函数的性质,综合性较强,难度适中.29.(10分)如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.(1)求证:△ABF≌△ECF;(2)连接AC、BE,则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由.考点:矩形的判定;全等三角形的判定与性质;平行四边形的性质.分析:(1)由四边形ABCD是平行四边形,CE=DC,易证得∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,则可证得△ABF≌△ECF;(2)首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.解答:解:(1)证明:在平行四边形ABCD中,AB∥CD,AB=CD,∴∠BAE=∠AEC,又∵CE=CD,∴AB=CE,在△ABF和△ECF中,,∴△ABF≌△ECF(AAS);(2)当∠AFC=2∠D时,四边形ABEC是矩形.∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,∴FC=FE,∴四边形ABEC是矩形.点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.30.(10分)如果一元二次方程ax2+bx+c=0的两根x1、x2均为正数,且满足(其中x1>x2),那么称这个方程有“邻近根”.(1)判断方程是否有“邻近根”,并说明理由;(2)已知关于x的一元二次方程mx2﹣(m﹣1)x﹣1=0有“邻近根”,求m的取值范围.考点:根的判别式;解一元二次方程-公式法;解一元二次方程-因式分解法;正比例函数的性质;反比例函数的性质.分析:(1)先解方程得到x1=,x2=1,则满足,所以可判断方程有“邻近根”;(2)根据判别式的意义得到m≠0且△=(m﹣1)2﹣4m×(﹣1)=(m+1)2≥0,利用求根公式解得x1=1,或,x2=1,则m<0,然后讨论:若x1=1,,则,是关于m的正比例函数,根据正比例函数性质得到﹣2<m<﹣1;若,x2=1,则,是关于m的反比例函数,根据反比例函数性质得,最后综合得到m的取值范围.解答:解:(1)方程有“邻近根”.理由如下:∵,∴(x﹣1)(x﹣)=0,∵x1>x2,∴x1=,x2=1,这时x1>0,x2>0,且,∵,∴满足,∴方程有“邻近根”;(2)由已知m≠0且△=(m﹣1)2﹣4m×(﹣1)=(m+1)2≥0,∴∴x1=1,或,x2=1,∵一元二次方程ax2+bx+c=0有“邻近根”,∴x1、x2均为正数,∴m<0若x1=1,,则,是关于m的正比例函数,∵﹣1<0,∴随m的增大而减小.当1<﹣m<2时,∴﹣2<m<﹣1;若,x2=1,则,是关于m的反比例函数,∵﹣1<0,∴在第二象限,随m的增大而增大.当时,∴.…(9分)综上,m的取值范围是﹣2<m<﹣1或.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程和正比例与反比例函数性质.。
2014—2015学年(上)厦门市九年级质量检测答案
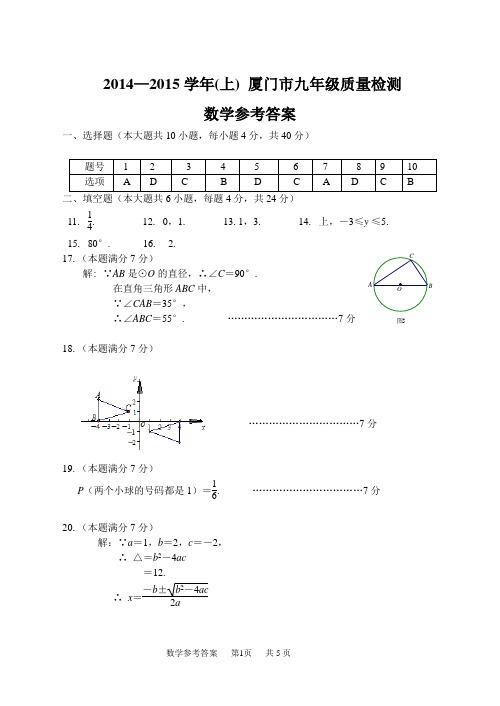
2014—2015学年(上) 厦门市九年级质量检测 数学参考答案一、选择题(本大题共10小题,每小题4分,共40分)11. 14. 12. 0,1. 13.1,3. 14. 上,-3≤y ≤5.15. 80°. 16. 2. 17.(本题满分7分)解: ∵AB 是⊙O 的直径,∴∠C =90°.在直角三角形ABC 中,∵∠CAB =35°,∴∠ABC =55°. ……………………………7分18.(本题满分7分)……………………………7分19.(本题满分7分)P (两个小球的号码都是1)=16. ……………………………7分20.(本题满分7分)解:∵a =1,b =2,c =-2,∴ △=b 2-4ac=12. ∴ x =-b ±b 2-4ac2a图5=-2±122. ……………………………5分∴x 1=-1+3,x 2=-1-3. ……………………………7分 21.(本题满分7分) 解:……………………………7分22.(本题满分7分)解:画示意图……………………………2分 ∵线段BA 1是线段BA 绕点B 逆时针旋转90°所得, ∴ BA 1=BA ,且∠ABA 1=90°.连接AA 1,则△ABA 1是等腰直角三角形.在Rt △ABC 中,AB 2=BC 2+AC 2, =9+16 =25.∴AB =5.∴ AA 12=AB 2+ A 1B 2=25+25=50 . ∴AA 1=52. ……………………………7分 23.(本题满分7分) 证明:连接OD ,∵AD ∥OC ,∴∠BOC =∠OAD , …………………2分 ∠COD =∠ADO .∵OA =OD ,∴∠OAD =∠ADO . …………………3分∴∠BOC =∠COD . ……………………………4分 ∵OB =OD ,OC =OC ,∴ △BOC ≌△DOC . ……………………………5分∴ ∠OCB =∠OCD .即OC 是∠DCB 的平分线. ……………………………6分 ∴ 点O 到直线CB ,CD 的距离相等,记为d . ∵直线BC 与⊙O 相交,∴d <OB =OD .∴直线DC 与⊙O 相交. ……………………………7分A 1ACB24.(本题满分7分)解:设直线y =x +b (b >0)与x 轴交于点C ,则点C (-b ,0).由题意得点A (13,0),B (0,b ).∵ 点P 是直线y =x +b (b >0)与直线y =3x -1的交点,记P (m ,n ). ∴n =m +b ,且n =3m -1.∴n =32b +12. ……………………………2分∴ △PCA 的面积是 12³AC ³n =12(13+b )(32b +12).△ABC 的面积是 12³AC ³b =12(13+b )b . ……………………………5分△P AB 的面积是12(13+b )(32b +12)-12(13+b )b .即12(13+b )(32b +12)-12(13+b )b =23. ……………………………6分解得b =1. ……………………………7分25.(本题满分7分)解:当x=-2时, ……………………………4分 由方程x 2+bx +b +2=0得到 4-2b +b +2=0,∴b =4+2. ……………………………5分 ∴有x 2+(4+2) x +4+22=0.解得,x 1=-2,x 2=-2-2. ……………………………6分而x 1+2x 2=2+4+22=6+22,c +2=4+22+2=6+22.即当b =4+2时,方程x 2+bx +b +2=0是“T 系二次方程” .……7分 26.(本题满分11分) (1)(本小题满分5分)解:设直线l 的解析式为y=kx +b , ∵点B (0,4)在直线l 上, ∴ b=4.又∵A (2,0)在直线l 上, ∴0=2k +4.∴k=-2. ……………………………3分直线l 的解析式为y=-2x +4 ∵点P (m ,n )在直线l 上,∴n=-2m +4. ……………………………4分 ∵OP =2,∴4=m 2+n 2,即4=m 2+(-2m +4)2.解得,m =2,m =65.当m =2时,n =0,不合题意,∴点P (65,85). ……………………………5分(2)(本小题满分6分)解:由(1)题得直线l 的解析式为y=-2x +4.当m <0时, ………………………6分t =PM +PN =n -m =-2m +4-m =-3m +4.∴t >4. ………………………7分 ∴m =-13t +43.s =PM ²PN =-mn=-(-13t +43)(-2m +4)=-(-13t +43)(23t +43)=29t 2-49t -169(t >4) . ……………………8分当0<m <2时, ………………………9分 t =PM +PN =n +m =-2m +4+m =-m +4.∴2<t <4. ………………………10分∴m =-t +4.∴s =PM ²PN =mn=-2m 2+4m=-2t 2+12t -16(2<t <4) . ………………………11分27.(本题满分12分) (1)(本小题满分5分)证明:设∠AOB 的值是n 1,∠DOC 的值是n 2,则∵︵AB l +︵CD l =πr ,∴n 1πr 180+n 2πr 180=πr . ………………………2分∴ n 1+n 2=180°. ………………………3分 ∴ 2∠ADB +2∠DAC =180°. ………………………4分 ∴ ∠ADB +∠DAC =90°. ∴∠APD =90°.∴AC ⊥BD . ………………………5分 (2)(本小题满分7分)证明: ∵ DH ⊥BC ,AE ⊥BC , ∴DF ∥AE .∴ ∠AEF +∠DFE =180°.∵ 四边形ABCD 内接于⊙O , ∴ ∠DAE +∠DFE =180°. ∴ ∠AEF =∠DAE . ∴︵DE =︵AF . ∴ ︵AD =︵EF .∴ AD =EF . ………………………8分 ∵ AC ⊥BD ,∴∠P AM +∠AMP =90°. ∵ AG ⊥BC ,∴ ∠P AM +∠ACB =90°. ∴ ∠AMP =∠ACB , ∵ ∠ADB =∠ACB , ∴ ∠ADB =∠AMP .∴ AD =AM . ………………………10分 ∴ PD =PM .∵ DF ∥AE ,∴∠AMP =∠NDP .∴ △NDP ≌AMP . ………………………11分 ∴ ND =AM .∴ 四边形AMND 是平行四边形. ∴ MN =AD .∴ MN =EF . ………………………12分。
福建省厦门市2014年九年级毕业班质量检测思想品德试题(word版,有答案)

福建省厦门市2014年九年级毕业班质量检测思想品德试题(word版,有答案)2014年厦门市初三毕业班质量检测思想品德(试卷满分:100分考试时间:90分钟)准考证号姓名座位号注意事项:1.全卷两大题,共30小题,试卷共6页,另有答题卡;2.答案一律写在答题卡上,否则不能得分。
一、选择题(下列各题的四个选项中,只有一个最符合题意,请选出来。
每小题2分,共50分)1.2013年9月26日,我国第一条连接海峡西岸和中部内陆腹地的快速铁路铁路正式开通。
A.福厦B.龙厦C.厦深D.向莆2.2013年9月29日,中国自由贸易试验区正式挂牌成立,成为我国进一步融入经济全球化的重要载体。
A.厦门B.上海C.深圳D.广州3.2013年10月21日,由厦门爱国华侨先生创办的迎来百年校庆,来自海内外的2000多名校友齐聚一堂,共祝母校百年华诞。
A.陈嘉庚集美学校B.陈嘉庚厦门大学C.鲁迅厦门大学D.鲁迅集美学校4.2013年12月2日凌晨,我国在西昌卫星发射中心用“长征三号乙”运载火箭,将我国探月工程二期的月球探测器成功送入太空。
A.玉兔号B.嫦娥三号C.神舟十号D.天宫一号5.2013年12月1日,中美英三国发表《》70周年。
这份得到国际社会普遍认可的国际法文件,明确了台湾及包括钓鱼岛在内的附属岛屿是中国的神圣领土。
A.雅尔塔协定B.波茨坦公告C.开罗宣言D.联合国家共同宣言6.鹭鹭很在乎他人的评价,不愿与人交往,没有知心朋友,与同学关系紧张。
他要处理好与同学的关系,应该①客观、全面地认识自己②克服闭锁心理,主动与人交往③不要理会他人评价④培养热情开朗的性格A.①②③B.②③④ C.①②④D.①③④7.教师是人类灵魂的工程师,自古以来受人赞颂。
下列名言中赞美教师工作的是A.和为贵,与人为善B.天下兴亡,匹夫有责C.天行健,君子以自强不息D.春蚕到死丝方尽,蜡炬成灰泪始干8.鹭鹭上中学后,越来越不愿意与父母交流,什么事情都想自己做主。
厦门市翔安区2014年九年级质量检查考试

厦门市翔安区2014年九年级质量检查考试V. 选择填空:从A、B、C中,选出一个最佳答案完成句子。
17. –What’s your favorite _________, Anna?–The Strongest Brain. It can help me learn a lot about the potential(潜能)of our brain.A. researchB. subjectC. program18. – ______ do you come to see your grandparents?– Once a week. And sometimes three times a month.A. How muchB. How oftenC. How long19. – How was your vacation in Canada?–It couldn’t be ______! I don’t even want to talk about it.A. worseB. betterC. more20. – Could you tell me what he said just now?– Sorry, I _________ what was happening outside.A. had thoughtB. was thinkingC. thought21. – What do you think of Gulang Island?– Oh, you will find it a beautiful place _______ you may spend your holiday.A. whenB. whereC. which22. – Why is your bedroom so dirty?– Sorry, Mum. It ___________. I felt very tired after playing soccer.A. wasn’t cleanedB. didn’t cleanC. wasn’t cleaning23. –I broke Jack’s cup. He was angry with me.– I think you _______ buy a new one for him.A. can’tB. mustn’tC. should24. A lot of flights were _______ because of the smog(雾霾)yesterday.A. put offB. put upC. put down25. – Does your grandpa like to exercise?– Yes, he runs every morning _______ he is already eighty years old.A. butB. becauseC. although26. – Bill, can you give me the dictionary on that desk, please?–I’m afraid I can’t ________ it, Daddy. It’s too high.A. buyB. findC. reach27. – Can you guess _______ the new Nike sports shoes?– Yes, maybe he asked his Daddy for the money, I think.A. how he paid forB. where he boughtC. who did he buy28. – Would you like to have a cup of coffee, Susan?– __________. Nothing is worse than coffee.A. No problemB. Of course I canC. I can’t stand i tVI. 完形填空:从A、B、C中,选择一个最佳答案,使短文意思完整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
厦门市翔安区2014年九年级质量检查考试数 学 试 题(试卷满分:150分 考试时间:120分钟)考生注意:1.试卷共4页,另有答题卡.解答内容一律写在答题卡上,否则不能得分.2.作图或辅助线请使用2B 铅笔.一、选择题(本大题有7题,每小题3分,共21分,每小题都有四个选项,其中有且只有一个选项是正确的) 1.计算23-+的值是 A . 1B .1-C .5D .5-2. 下列四个几何体中,三视图都是相同图形的是3. 在函数21-=x y 在,自变量x 的取值范围是 A .2≠xB .2>xC .2≥xD.0≠x4.气象台预报“本市明天下雨的概率为80%”这句话指的是A .明天一定下雨B .明天80%的地区下雨,20%的地区不下雨C .明天下雨的可能性是80% D. 明天80%的时间下雨,20%的时间不下雨5. 正方形网格中,AOB ∠如图1放置,则sin AOB ∠的值是 A .55B .255C . 12 D. 26.不等式组⎩⎨⎧<->+04201x x 的解集是A .21<<-xB .1->xC .2<xD.21>-<x x 或7.如图2,A 、B 的坐标分别为)02(,,)(1,0,若将线段AB 平移至11B A ,则b a +的值为 A .2B .3C .4 D.5DCBAABO图1图2y OA(2,0) B(0,1)B 1(a,2)xA 1(3,b)ABCDE 图3二、填空题(本大题有10小题,每小题4分,共40分) 8.21-的相反数是 . 9.“节约光荣,浪费可耻”。
据统计,我国每年浪费粮食8000000吨,这个数据用科学计数法表示为 吨 .10. 抛物线2)1(2+-=x y 的顶点坐标是 ( , ) .11.如图3,点D E 、分别是ABC △中AB AC 、边的中点,已知3=DE , 则=BC . 12.已知反比例函数k y x=(0x >),请你写出一个k 值 ,使y 的值随着x 值的增大而减小.13.某市6月2日至8日的每日最高温度如图4所示,则这组数据 的中位数是 .14.已知 622=-n m ,3=+n m ,则n m -的值是 .15.某市按以下规定收取每月的水费:用水量不超过6吨,按每吨1.2元收费;如果超过6吨,未超过部分仍按每吨1.2元收取,而超过部分则按每吨2元收费。
如果某用户5月份水费平均为每吨1.4元,那么该用户5月份实际用水 吨. 16..如图5,在ABC Rt ∆中,4390==︒=∠BC AC C ,,, P 为AB 边上(不与重合)、B A 的一动点,过点P 分别作AC PE ⊥于点E , BC PF ⊥于点F ,则线段EF 的最小值是 . .17.如图6,直线434+=x y 与x 轴,y 轴分别交于A ,B 两点,点C 在OB 上, 若将△ABC 沿AC 折叠,使点B 恰好落在x 轴上的点D 处,则点C 的坐标 为 ( , ) .三、解答题(本题有9题,共89分)18.(本题满分21分,每小题7分) (1)2)2(3121-+÷--(2)画出图7中的△ABC 关于y 轴对称的图形.(3)如图8,已知AB CD ∥,若20A ∠=°,35E ∠=°, 求∠C 的度数.O 日期最高温度(℃) 31 30 29 28 27 262 3 4 5 6 7 8 9图4图6BPCEA F 图5 图7 AB E F19.(本题满分18分,每小题6分)(1)为了解“节约用水”活动开展一个月来的成效,某单位随机调查了20名职工家庭一个月来的节约用水情况,如下表所示:节约水量(吨) 0.5 1 1.5 2 职工数(人)10541请你根据上表提供的信息估计该单位100位职工的家庭一个月大约能节约用水多少吨?(2)先化简,再求值:)2()2b a a b a -++(,其中2,1==b a .(3)如图9,已知DE 是AC 的垂直平分线,10cm AB =,11cm BC =, 求ABD △的周长.20.(本题满分6分)在学习概率知识时,王老师布置了这样一道题目:在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个。
要求同学按两种规则摸球:①摸出一个球后放回,再摸出一个球;②一次性摸两个球。
那么,请你通过计算说明哪种方法摸到两个红球的概率较大?21.(本题满分6分)如图10,在梯形ABCD 中,AB ∥CD ,BD ⊥AD ,BC=CD , ∠A=60°,CD=2cm ,求AB 的长.22.(本题满分6分)为了预防流感,学校对教室进行“药熏消毒”。
已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y 与x 成反比(如图11),现测得药物10min 燃烧完,此时,教室内每立方米空气含药量为16mg 。
已知每立方米空气中含药量低于4mg 时对人体无害,那么从消毒开始经多长时间后学生才能进教室?23.(本题满分6分)如图12,已知菱形AOBD 的A 、B 、D 三点在⊙O 上,延长BO 至点P ,交⊙O 于点C ,且BP=3OB. 求证:AP 是⊙O 的切线.图9 A B CD图10 A O 16 X/min 10 Y/mg 图11图1224.(本题满分6分)如图13,已知A(a ,m)、B(2a ,n)是反比例函数ky=(k>0)x与一次函数b x y +-=34图象上的两个不同的交点,分别过A 、B 两点作x 轴的垂线,垂足分别为C 、D ,连结OA 、OB ,若已知21≤≤a ,则求OAB S ∆的取值范围.25.(本题满分10分)如图14,将平行四边形ABCD 的边DC 延长至点E ,使DC CE =,连接AE ,交BC 于点F .(1)求证:ABF ∆≌ECF ∆;(2)连接AC 、BE ,则当AFC ∠与D ∠满足什么条件时,四边形ABEC 是矩形?请说明理由.26.(本题满分10分)如果一元二次方程)0(02≠=++a c bx ax 的两根21x x 、均为正数,且满足2121<<x x (其中21x x >),那么称这个方程为“邻近根方程”. (1)判断方程03)13(2=++-x x 是否为“邻近根方程”?并说明理由;(2)已知关于x 的一元二次方程01)1(2=---x m mx 是“邻近根方程”,求m 的取值范围.A BC DEF 图14厦门市翔安区2014年九年级质量检查考试数学参考答案一、选择题(本大题有7小题,每小题3分,共21分)二、填空题(本大题有10小题,每小题4分,共40分) 8:12;9: 6810⨯;10:(12),;11:6BC =;12:1k =; 13:29;14:2m n -=;15 :8;16:2.4;17:C (30,2); 三、解答题(本大题有9小题,共89分)18.(本题有3小题,每小题7分,共21分)(1)解:原式=1-2×3+4 ...............3 =1-6﹢4 (4)=-1 (7)(2)画对一点得2分,下结论1分.(3)解:如图,∵∠A=20°,∠E=35°,∴∠BFE=20°+35° (4)=55° (5)又∵AB ∥CD ,∴∠C=∠BFE=55º (7)19. (本题满分18分,每小题6分) (1)解:100.5514 1.51220X ⨯+⨯+⨯+⨯= (4)=0.9 (5)∴W=100×0.9=90 (6)答该单位100位职工家庭一个月大约节约用水90吨. (2)解:原式=22222a ab b a ab +++- =222a b +……………3 当1,2a b ==时,原式=2221(2)224⨯+=+= (6)(3)解:如图,∵DE 垂直平分,∴AD CD = (3)∴11BD AD BD CD BC cm +=+== (5)1 2 3 4 5 6 7 ACACBAA又10AB cm = ∴101121()ABD C cm ∆=+= (6)20. (本题满分6分)解:(P 两次摸球)=14 (3)P(一次性摸球)=16……………5 ∵14>16∴两次摸球的概率较大. (6)21. (本题满分6分)解:如图,在梯形ABCD 中,∵AB ∥CD, ∴∠CDB=∠ABD∵CD=CB, ∴∠CDB=∠CBD (2)在Rt △ABD 中, ∠A=60°, ∴∠ABD=30º, ∴∠CBD=30°, ∴∠CBA=60°, ∴∠CBA=∠A, ∴AD=BC=CD=2cm. (5)在Rt △ABD 中,∠ABD=30°, ∴AB=2AD=4 (6)22. (本题满分6分)解:设燃烧后的函数解析式为ky x=,……………1 ∵图象经过点(10,16),∴k=160, ∴160y x= (3)由1604x=得x=40…………… 从消毒开始要经过40分钟后学生才能进教室. ……………6 23. (本题满分6分)证明:连接OD ,∵菱形AOBD ,∴AO=OB=BD=DA, ∴∠AOD=∠BOD=∠AOC=60°……………2 又∵OA=OC, ∴ △AOC 为等边三角形, ∴AC=OC, ∠ACO=60°, ∵PB=3BO,OC=OB, ∴CP=AC=OC ∴∠P=∠CAP∵∠P+∠CAP=∠ACO=60°, (5)∴∠CAP=30°, ∴∠OAP=90°,∴AP 为⊙O 的切线. ……………6 24.(本题满分6分)解:点A 、B 在k y x =图象上,则有,2k km n a a==,……………1 48,323k k a b a b a a =-+=-+ 解得:283k a =, (3)21814814()223233232OABAOC BOD ABDCS S S S a a a a a a a a ∆∆=-+=⨯++-⨯⨯=……………5 当12a ≤≤时,22OABSa =随自变量的增大而增大,28a ≤≤ (6)25.(本题满分10分)(1)证明:在平行四边形ABCD 中,AB ∥CD,AB =CD,∴∠BAE=∠AEC (2)又∵CE=CD, ∴AB=CE (3)∵∠BAE=∠EFC, ∠AFB=∠EFC, ∴△ABF ≌△ECF. ...............5 (2)当∠AFC=2∠D 时,四边形ABEC 是矩形. (6)∵四边形ABCD 是平行四边形,∴BC ∥AD ,∠BCE=∠D, (7)由题意易得AB ∥EC ,AB ∥EC ,∴四边形ABEC 是平行四边形。
