加法交换律和乘法交换律.
加法交换律和乘法交换律

加法交换律和乘法交换律1、加法交换律:用字母表示为:a+b=b+a两个数相加,交换加数的位置,和不变。
2、加法结合律:用字母表示为:(a+b)+c=a+(b+c)三个数相加,先把前两个数相加,再和第三个数相加,或者先把后两个数相加,再和第一个数相加,和不变。
3、乘法结合律:用字母表示是:(a×b)×c=a×(b×c)。
三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。
使用时机:当几个数相乘时,如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
如25和4、50和2、125和8、50和4、500和2等。
4、乘法分配律:用字母表示数:(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c两个数的和(或差)与一个数相乘,可以把两个加数(或被减数、减数)分别与这个数相乘,在把两个积相加(或相减),结果不变。
5、乘法交换律用字母表示为:axb=bxa。
两个数相乘,交换乘数的位置,积不变。
扩展资料1、在连加计算中,当某些加数相加可以凑成整十、整百、整千的数时,运用加法运算律可使计算简便。
口诀:连加计算仔细看,考虑加数是关键。
整十、整百与整千,结合起来更简单。
交换定律记心间,交换位置和不变。
结合定律应用广,加数凑整更简便。
2、在连乘计算中,当某两个乘数的积正好是整十、整百、整千的数时,运用乘法运算律可使计算简便。
运用分解的方法,将某个乘数拆分成几个数相乘的形式,使其中的乘数与其他乘数的乘积“凑整”。
乘法分配律特别要注意“两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加”中的分别两个字。
注意:1、一定要括号外的数分别乘括号里的两个数,再把积相加。
乘法对于减法的分配律是括号外的数分别乘括号里的两个数,再把积相减。
小学四年级上加法交换律_结合律_乘法交换结合分配律及商不变规律汇总
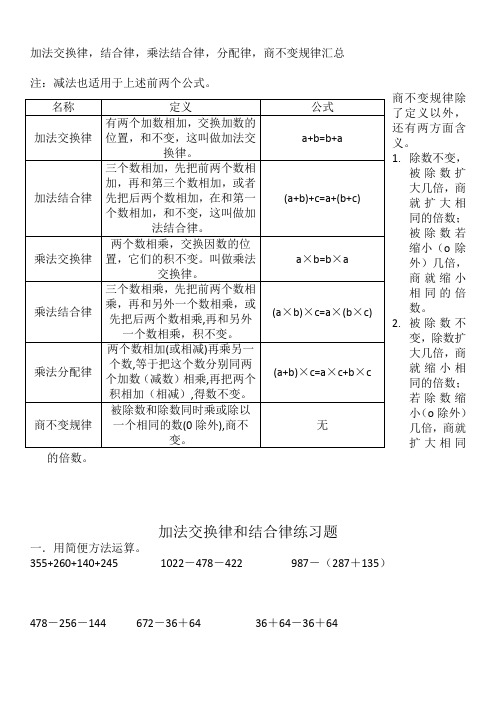
加法交换律,结合律,乘法结合律,分配律,商不变规律汇总注:减法也适用于上述前两个公式。
商不变规律除Array了定义以外,还有两方面含义。
1.除数不变,被除数扩大几倍,商就扩大相同的倍数;被除数若缩小(o除外)几倍,商就缩小相同的倍数。
2.被除数不变,除数扩大几倍,商就缩小相同的倍数;若除数缩小(o除外)几倍,商就扩大相同的倍数。
加法交换律和结合律练习题一.用简便方法运算。
355+260+140+245 1022-478-422 987-(287+135)478-256-144 672-36+64 36+64-36+641814-378-422 568-(68+178)561-19+58382+165+35-82 155+256+45-98 512+(373—212)228+(72+189)169+199 109+(291—176)二. 判断。
1、56+72+28=56+(72+28)运用了加法交换律。
()2、83+63+27=83+27+63运用了加法交换律。
()三.应用题。
1.小明买了88斤苹果,10斤雪梨,12斤李子,总共买了多少斤水果!2.小明有3条数学题要做,5条英语题要做,2条语文题要做,今天一共需要做多少题3.小明,小红,小芳分别有68支铅笔,小明先给小芳26支,小红给小芳32支,问芳芳现在有多少支铅笔乘法交换律和结合律练习题一、用简便方法计算下面各题23×15×2 125×7×8 250×56×4 75×9×2二、在□里填上适当的数35×8=35×(□×□) 45×12=45×(□×□)16×15=16×(□×□) 18×25=18×(□×□)125×32=125×(□×□) 25×24=25×(□×□)三、用简便方法计算:45×8 28×15 25×12 125×32 75×24四、判断18×12×5=18×(12×5),这应用了乘法结合律。
加法交换律和乘法交换律教案

加法交换律和乘法交换律教案教案:加法交换律和乘法交换律年级:小学四年级学科:数学一、教学目标:理解和掌握加法交换律和乘法交换律的概念;能够应用加法交换律和乘法交换律解决实际问题;培养学生善于观察和发现规律的能力。
二、教学内容:加法交换律的概念和运用;乘法交换律的概念和运用;实际问题中的应用。
三、教学过程:导入:回顾加法和乘法的基本概念,简单复习加法和乘法的计算方法。
加法交换律的引入:出示示意图:3 + 5 = 5 + 3引导学生观察,并问:这两个算式的结果相同吗?学生思考后回答:相同。
解释加法交换律:交换加法算式中的加数位置,结果不变。
练习加法交换律:出示算式:2 + 8 = ?6 + 4 = ?学生完成计算,比较两个算式的结果。
乘法交换律的引入:出示示意图:4 ×3 = 3 ×4引导学生观察,并问:这两个算式的结果相同吗?学生思考后回答:相同。
解释乘法交换律:交换乘法算式中的因数位置,结果不变。
练习乘法交换律:出示算式:2 ×5 = ?3 ×4 = ?学生完成计算,比较两个算式的结果。
实际问题的应用:出示实际问题:小明有3个苹果,小红有5个苹果,他们一起有几个苹果?引导学生用加法交换律解决问题:3 + 5 = 5 + 3 = 8。
出示实际问题:小明有4个苹果,他买了3份相同的水果,一共有几个苹果?引导学生用乘法交换律解决问题:4 ×3 = 3 ×4 = 12。
总结:复习加法交换律和乘法交换律的概念,强调在实际问题中的应用。
四、课堂作业:计算:(1)2 + 7 = (2)4 ×6 =解决问题:小明有5个橙子,小红有6个橙子,他们一共有几个橙子?五、教学反思:通过本节课的教学,学生对加法交换律和乘法交换律的概念和应用有了初步了解,能够灵活运用在实际问题中。
同时,通过实际问题的引导,培养了学生观察和发现规律的能力。
但还需要进一步加强学生的练习和巩固,确保学生能够熟练掌握这两个交换律的运用。
四年级加法交换和结合律、乘法交换律、结合律、分配律练习

加法交换律、结合律加法交换律:多个加数相加,可以任意交换加数的位置。
a+b=b+a加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176)43+189+57 591+482+118986+1999 216+89+11 473+79—63 645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-132 1814-378-422 155+264+36+45 698-291-9568-(68+178) 382+165+35-82 169+199184+507 236+189+64 759—126—259 569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457) 68+24+32+76 425+64+75+36 235+102 902-98 634-273+466-127 (337+464)+536 727-194-106 374-(35+174)765-(96+65)247-185+53-15 384-297乘法交换律、结合律乘法交换律:多个因数相乘,可以任意交换因数的位置。
a×b=b×a乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
四年级加法交换和结合律、乘法交换律、结合律、分配律练习

加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176)43+189+57 591+482+118986+1999 216+89+11 473+79—63645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-1321814-378-422 155+264+36+45 698-291-9568-(68+178) 382+165+35-82 169+199184+507 236+189+64 759—126—259569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457) 68+24+32+76 425+64+75+36235+102 902-98 634-273+466-127(337+464)+536 727-194-106 374-(35+174)765-(96+65)247-185+53-15 384-297乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
a÷b÷c= a÷(b×c)可以任意交换除数的位置。
四年级加法交换和结合律、乘法交换律、结合律、分配律练习

加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176)43+189+57 591+482+118986+1999 216+89+11 473+79—63645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-1321814-378-422 155+264+36+45 698-291-9568-(68+178) 382+165+35-82 169+199184+507 236+189+64 759—126—259569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457) 68+24+32+76 425+64+75+36235+102 902-98 634-273+466-127(337+464)+536 727-194-106 374-(35+174)765-(96+65)247-185+53-15 384-297乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
a÷b÷c= a÷(b×c)可以任意交换除数的位置。
四年级加法交换和结合律、乘法交换律、结合律、分配律练习

加法交换律、结合律加法交换律:多个加数相加,可以任意交换加数的位置。
a+b=b+a加法结合律:多个加数相加,可以任意两个加数先加。
a+b+c= a+(b+c)连减律:连减两个数,可以减去这两个数的和(减去两个数的和,可以连减这两个数)。
a—b—c= a—(b+c)可以任意交换减数的位置。
a—b—c= a—c—b598+99 396—28—22 355+260+140+245109+(291—176) 43+189+57 591+482+118986+1999 216+89+11 473+79—63 645—180—245 1022-478-422 987-(287+135)478-256-144 672-36-64 36+64-36+64487-287-139-61 500-257-143 2000-368-1321814-378-422 155+264+36+45 698-291-9568-(68+178)382+165+35-82 169+199184+507 236+189+64 759—126—259 569—256—44 514+189—214 228+(72+189)28+45+72 123+38+62 1+13+85+7+99100-57-23 37+56+63+44 574-3981457-(185+457)68+24+32+76 425+64+75+36235+102 902-98 634-273+466-127 (337+464)+536 727-194-106 374-(35+174)765-(96+65) 247-185+53-15 384-297乘法交换律、结合律乘法交换律:多个因数相乘,可以任意交换因数的位置。
a×b=b×a乘法结合律:多个因数相乘,可以任意两个因数先乘。
a×b×c= a×(b×c)(25×4=100、125×8=1000)连除律:连除以两个数,可以除以这两个数的积(除以两个数的积,可以连除以这两个数)。
加法交换律和乘法交换律

我们来总结一下:
两个数相加,交换加数的位置,和不变,
这叫加法交换律。母表示为
说一说
举生活中的例子,证明加法交换律和乘法交换律成立。
学校
少年宫
电影院
.
.
.
35米
42米
35+42 42+35 35+42=42+35 加法交换律成立
358 + 2 1716
634
验算:
276 + 31 51 8
634
5×107 =535
107 ×5
535
乘法交换律
判断下列算式是否使用加法交换律和乘法交换律。
(1)3+6=2+7 ×
(2)34+43=34+43 ×
(3) 7×9=9×7
√
(4)25+61=21+65 ×
(5)62×53=53×26
(6)54+46=46+54
×
(7)36+52+24=36+24+√52
√
(8)25×345×4=25×4×345
√
1.结合下面的例子说明等式为什么成立。
2.运用加法交换律和乘法交换律填一填。
45+76= 76 +45
28+13= 13 + 28
+=
+
45×102=102× 45
296×200= 200 × 296
6×5 5×6 6×5=5×6
乘法交换律成立
加法交换律
乘法交换律
加法交换律
乘法交换律
我们来总结一下:
两个数相加,交换加数的位置,和不变,
这叫加法交换律。用字母表示为
小学四年级上加法交换律-结合律-乘法交换结合分配律及商不变规律汇总

小学四年级上加法交换律-结合律-乘法交换结合分配律及商不变规律汇总加法交换律,结合律,乘法结合律,分配律,商不变规律汇总注:减法也适用于上述前两个公式。
商不变规律除了定义以外,还有两方面含义。
1. 除数不变,被除数扩大几倍,商就扩大相同的倍数;被除数若缩小(o 除外)几倍,商就缩小相同的倍数。
2. 被除数不变,除数扩大几倍,商就缩小相同的倍数;若除数缩小(o 除外)几倍,商就扩大相同的倍数。
加法交换律和结合律练习题一.用简便方法运算。
355+260+140+245 1022-478-422 987-(287+135)名称 定义公式加法交换律有两个加数相加,交换加数的位置,和不变,这叫做加法交换律。
a+b=b+a加法结合律三个数相加,先把前两个数相加,再和第三个数相加,或者先把后两个数相加,在和第一个数相加,和不变,这叫做加法结合律。
(a+b)+c=a+(b+c)乘法交换律两个数相乘,交换因数的位置,它们的积不变。
叫做乘法交换律。
a ×b=b ×a乘法结合律三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
(a ×b)×c=a ×(b ×c)乘法分配律两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),得数不变。
(a+b)×c=a ×c+b ×c 商不变规律被除数和除数同时乘或除以一个相同的数(0除外),商不变。
无1814-378-422 568-(68+178) 561-19+58382+165+35-82 155+256+45-98 512+(373—212)228+(72+189) 169+199 109+(291—176)二. 判断。
1、56+72+28=56+(72+28)运用了加法交换律。
()2、83+63+27=83+27+63运用了加法交换律。
加法交换律---公式

数学公式加法交换律:a+b=b+a加法结合律:a+b+c=a+(b+c)乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),a ×(b+c) =a×b +a×c或a ×(b-c) = a×b-a×c长方形周长=(长+宽)×2面积=长×宽正方形周长= 边长×4面积= 边长×边长路程=速度×时间;路程÷时间=速度路程÷速度=时间1千米=1000米1米=10分米1分米=10厘米1米=100厘米1 厘米=10毫米1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米1吨=1000千克1千克=1000克每份数×份数=总数总数÷每份数=份数总数÷份数=每份数小学的数学所有公式1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1、正方形:C周长S面积a边长周长=边长×4C=4a面积=边长×边长S=a×a2、正方体:V:体积a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形:C周长S面积a边长周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab4、长方体:V:体积s:面积a:长b: 宽h:高(1)表面积(长×宽+长×高+宽高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5、三角形s面积a底h高面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形:s面积a底h高面积=底×高s=ah7、梯形:s面积a上底b下底h高面积=(上底+下底)×高÷2 s=(a+b)×h÷28 、圆形:S面C周长∏ d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9、圆柱体:v:体积h:高s:底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体:v体积h高s底面积r底面半径体积=底面积×高÷3总数÷总份数=平均数和差问题的公式(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1、非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2、封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有: 1\3\5\7\8\10\12月小月(30天)的有: 4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1小时=60分1分=60秒1小时=3600秒小学数学几何形体周长面积体积计算公式1、长方形的周长=(长+宽×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷28、直径=半径×2 d=2r半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2c=πd =2πr10、圆的面积=圆周率×半径×半径变化的量图上距离/实际距离=比例尺图上距离=比例尺×实际距离实际距离=图上距离÷比例尺正比例的关系式x/y=k(一定)反比例的关系式x.y=k(一定)。
加法交换律和乘法交换律

√ √ × × √
加法交换律
乘法交换律
4.脑筋急转弯
(1) 846 + 365 = 365 +( 846 ) (2) 70 × 3 =( 70 )×(3 ) (3) 316 +( 92 ) = 92 + 316 85 (4) ( 85 )× 320 =320 ×( )
90
3 70 85 85 90 92 846
5.计算
642+879+358=
两个数相加,交换加数的位置, 它们的和不变。这叫做加法交换律。
两个数相乘,交换因数的位置, 它们的积不变。这叫做乘法交换律。
思考:
减法和除法也满足交 换律吗?举例试一 Nhomakorabea。谢谢! 再见!
45×102=102× 45 296×200= 296 × 200 × = ×
2.一共有多少个圆?(1)用加法交换 律表示出来;(2)用乘法交换律表示出来。
3.判断,下面的式子符合交换律 吗?符合画“√”,不符合画“×”。
(1)43+0=0+43 (2)4×6=6×4 (3)2×2=2+2 (4)▲+■=■+● (5)b×c=c×b
北师大版
小学数学四年级上册
第四单元
交换律
加法交换律和乘法交换律
执教:刘明达
两个数相加,交换加数的位置, 它们的和不变。这叫做加法交换律。
两个数相乘,交换因数的位置, 它们的积不变。这叫做乘法交换律。
1.运用加法交换律和乘法交换律填一填。 45+76= 76 +45 28+13= 13 + 28 + = +
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)125 + 36 + 75 = 125 + 75 + 36 = 200 + 36 = 236
知识应用:
为了丰富同学们的课余生活,学校准备购置足 球和篮球各20个,根据提供的信息,你能提出
哪些数学问题?
4 0 元 各 买 2 0 个
6 5 元
说一说:
通过本节课的学习, 你有什么收获?
用字母表示是:
讨论归纳
加法交换律:a + b = b + a
乘法交换律:a × b = b × a
学校
少年宫 35米
电影院 42米
从学校到电影院的距离和从电 影院到学校的距离有什么关系?
一共有多少块? 你是怎么算的?
练习一
学校购买校服。
每件 27元, 每条18元。
买这样1套校服,一共要多少元 ?
= 6 × 25 + 5 〖
√
〗
25 × 4 = 4 + 25 〖
3
×〗 35 + 65 = 35 + 56〖×〗练习四Biblioteka 用竖式计算并运用运算律验算。
1
358+276=
2
16×25
看谁算得快?
(1)3 6 + 4 4 = 80
(2) 4 5 + 1 8 + 55 = 45 + 55 + 18 = 100 + 18 = 118 (4) 7 8 + 4 5 + 2 2 = 78 + 22 + 45 = 100 + 45 = 145
单击页面即可演示
算一算:
62+53=115 53+62=115 62+53=53+62
7×9=63 9×7=63 7×9=9×7
从刚才的计算中,
你发现了什么
?
7 × 9 = 9 × 7
62 + 53 =
53 + 62
讨论归纳 两个数相加,交换加数的位置,和 不变,这叫做加法交换律。 两个数相乘,交换乘数的位置,积 不变,这叫做乘法交换律。
27 18
共?元 27+18=( )(元) 18+27=( )(元)
练习二
填一填:
45+76=( )+45 45×102=102×( ) 28+13=( )+( ) 296×200=( )×( ) ( )+( )=( )+( ) ( )×( )=( )×( )
数
练习三
1 2
医
院
学
判断正误
25 × 6 + 5
