公开课《加法交换律和乘法交换律》教学课件上课讲义
北师大版四年数学上册四运算律《加法交换律和乘法交换律》课件

加法交换律和 乘法交换律
情境导入
他们一共得到多少个苹果? 4+6=10(个)
4个
6个
情境导入
他们一共得到多少个苹果? 6+4=10(个)
6个
4个
情境导入
他们一共得到多少个苹果?
4+6=10(个) 6+4=10(个)
分苹果的顺序变了,一 共得到的苹果数没变。
探索新知
10÷2=5,可2÷10肯 定不等于5。所以除法 不满足交换律。
5.根据加法交换律把方框补充完整。 160+340= 340 + 160 45 +68= 68 +45 a+ 45 =45+ a +□= □ +
6.想一想,在( )内填上合适的数。 12×45=( 45 )×12 32×( 66 )=66×( 32 ) ( 22 )×88=( 88 )×22
请你再多写几组 4+6=6+4 这样的式子,来
6+4=10
验证你的想法。
62+53=115 53+62=115
62+53=53+62
13+17=30
验证 17+13=30
13+17=17+13
25+12=37 12+25=37 102+213=315 213+102=315
25+12=12+25 102+213=213+102
两个数相加,交换加数的位置,和不变。
你能利用生活中的事例解释你的发现吗?
学校
少年宫
电影院
加法交换律和乘法交换律ppt课件

两个数相加,交换加数的位置,和不变。 两个数相乘,交换乘数的位置,积不变。
游戏
我说前面,你说后面。
讨论
1、4人小组,讨论生活中有没有这样的例子。
2、时间3分钟。
35+42=42+35
6×5=5×6
任务1:结合点子图圈一圈,解释6×5=5×6
长×宽 宽×长
回头看
用一个算式概括刚才的发现。
a+b=b+a
加法交换律
a×b=b×a
乘法交换律
学以致用
结合今天所学的知识解释下面计算的道理。
学以致用
结合下面的例子说明等式为什么成立。
16+12=12+16
20×6=6×20
花牛16头。
黄牛12头。
20颗珠子1串, 穿6串。
6颗珠子1串,穿 20串。
学以致用
18+66+82 25+16×4
25×3×4
通过本节课的学习,你有什么收获?
感谢聆听!
加法交换律和乘法交换律课件

猜想: 乘法具有交换律吗?举例试一试。
总结: 两个数相乘,交换两个乘数的位置,
积不变。叫乘法交换律。
如果用a,b表示两个乘数,你能写出发 现的规律吗?
a×b=b×a
拓展延伸:
减法和除法也满足交换律吗? 举例试一试。
一、运用加法交换律和乘法交换律填一填。
45+76= 76 +45
28+13= 13 + 28
四年级上册第4单= 10 6+4= 10 23+35= 58
35+23= 58 420+30= 450
30+420= 450
总结:
两个数相加,交换两加数的位置, 和不变。这叫做加法交换律。
如果用字母a,b表示两个加数,你能用这 两个字母表示我们发现的规律吗?
a+b = b+a
+=
+
45×102=102× 45
296×200= 200 × 296
×=
×
练一练:
• 二、判断下列等式是否符合加法交换律和乘法交
换律,符合的打√
• 60×7 =7×60 ( √ ) • 50+80=80+50(√ ) • 30+20=40+10(× ) • 50×4=2×100(× ) • 75+8+25=25+75+8(√ ) • 5×6×2=2×5×6(√ )
三、计算下列各题,并运用加法交换律或乘 法交换律进行验算。
918+395
35×27
小结: 这节课你学到了什么?
谢谢大家!
北师大版四年级数学上册《加法交换律和乘法交换律》运算律PPT教学课件
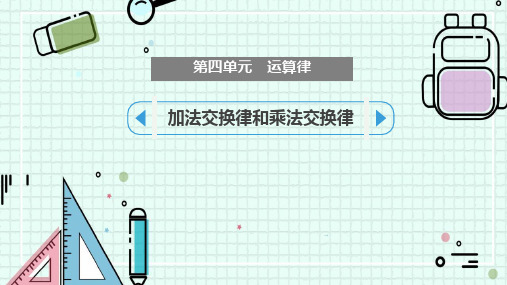
5×3=15
4+6=6+4
3×5=5×3
交换两个加数的位置,结果不变;交换两个乘数的位置,结果也不变。 小结:在加法里,交换加数的位置,和不变,这就是加法交换律。在乘法里,交换乘数的位置,积不变,这就是乘法交换律。
4
2.阅读教材,你能利用生活中的事例解释你的发现吗?
第四单元
第2课
(1)观察图一:从学校到电影院的距离和从电影院到学校的距离
137+98+263
=137+263+98 =400+98 =498
=25×8×23 =200×23 =4600
25×23×8
=121+279+254 =400+254 =654
第四单元
第2课
121+254+279
10
学习目标
第四单元
第2课
二、解决问题。
1.雨季快要到了,市政府决定对市区内的道路进行修缮,甲队每 天修168米,乙队每天修232米,28天后,两队一共修了多少米?
85×865+15×988=88345(元) 答:慈善总会购买这些防疫设备共花了88345元。
12
END
第四单元
第2课
感谢观看 下节课再会
13
2
学习目标
在○里填上“>”、“<”或“=”。 12+8○=8+12 399+698○=698+399 16×17○ 1=7×16 103×15○1=5×103
第四单元
第2课
3
学习目标
第四单元
第2课
★任务驱动 1.分别观察下面的式子,照样子再写一组,说说发现了什么。
北师大版小学4年级数学上册第四单元(加法交换律和乘法交换律)PPT教学课件

错解分析:
易错提醒
加法交换律和乘法交换律必须是在只有加法或者是只有乘法中应用,此题中既要加法又有乘法,不能用乘法交换律,因此错误。
课件PPT
计算: 25×19+4
错误解答
易错提醒
25×19+4=25×4+19=119
25×19+4=475+4=479
正确解答
1.结合下面的例子说明等式为什么成立。
76
13
28
45
296
200
课件PPT
a
b
b
a
a
b
b
a
3.计算下列各题,并运用加法交换律或乘法交换律进行验算。
918+395
35×27
课件PPT
918+395=1313 验算:395+918=1313
35×27=945 验算:27×35=945
4.减法和除法也满足交换律吗?举例试一试。
175-96-75=175-75-96
课件PPT
解题思路:
运用乘法交换律,是49和4交换位置,先算25乘4,使运算变得更加简单。
1. 计算: 25×49×4
课件PPT
解答:
25×49×4=25×4×49=100×49=4900
课件PPT
计算: 25×19+4
错误解答
易错提醒
25×19+4=25×4+19=119
课件PPT
125÷25÷5=125÷5÷25
课件PPT
5.明光小学新建了一栋5层的教学楼,每层有4间教室,每间教室能放25张课桌,这栋楼一共能放多少张课桌?
提示:运用乘法交换律可以使计算更加简单。
北师大版数学四年级上册《加法交换律和乘法交换律》教学课件

分别观察下面的式子,请你照样子再写 一组,说说你发现了什么。
4 + 6 = 10 4+6=6+4
6 + 4 = 10
加数相同,只是交换了加数的位置,和都是10。
分别观察下面的式子,请你照样子再写 一组,说说你发现了什么。
3 × 5 = 15 5×3=3×5
5 × 3 = 15.Fra bibliotek..
35米
42米
35+42 42+35 35+42=42+35 加法交换律成立
6×5 5×6 6×5=5×6
乘法交换律成立
加法交换律:a + b = b + a 乘法交换律: a × b = b × a
358+276=634
358 + 2 17 16
634
验算:
276 + 31518
634
5×107 =535
107 ×5
535
判断:加法和乘法满足交换律,减法 和除法也同样满足交换律。( × )
在减法和除法中不存在交换律。
乘数相同,只是交换了乘数的位置,积都是15。
62+53= 115 62+53=53+62
53+62= 115
发现:任意两个数相加,交换加数的位置,和不 变,这就是加法交换律。
7×9= 63 9×7= 63
7×9=9×7
发现:任意两个数相乘,交换乘数的位置,积不 变,这就是乘法交换律。
学校
少年宫
电影院
加法交换律和乘法交换律课件

加法交换律和乘法交换律课件Title: Commutative Laws of Addition and MultiplicationSlide 1:Introduction- Welcome to our lesson on the Commutative Laws of Addition and Multiplication.- In this lesson, we will explore the commutative property, its application to addition and multiplication, and how it simplifies mathematical operations.Slide 2:Commutative Property Overview- The commutative property states that changing the order of the numbers or terms being added or multiplied does not change the result.- This property is applicable to addition and multiplication but not subtraction or division.Slide 3:Commutative Property of Addition- The commutative property of addition states that changing the order of the addends does not affect the sum.- Example: 3 + 5 = 5 + 3Slide 4:Commutative Property of Multiplication- The commutative property of multiplication states that changing the order of the factors does not affect the product.- Example: 2 x 4 = 4 x 2Slide 5:Applying Commutative Property to Addition- The commutative property of addition allows us to rearrange the order of the addends.- Example: 7 + 2 + 6 = 6 + 7 + 2Slide 6:Applying Commutative Property to Multiplication- The commutative property of multiplication allows us to rearrange the order of the factors.- Example: 3 x 2 x 5 = 5 x 2 x 3Slide 7:Simplifying Mathematical Operations- The commutative property can be used to simplify mathematical operations by rearranging the numbers or terms.- Example: 2 + 7 + 4 = 4 + 7 + 2- Example: 3 x 5 x 6 = 6 x 5 x 3Slide 8:Real-World Examples- The commutative property is applicable in various real-world scenarios, such as arranging objects in a certain order.- Example: Packing books in a box does not change the total number of books regardless of their order.- Example: Counting money does not change the total amount regardless of the order in which different denominations are added. Slide 9:Summary- The commutative property states that changing the order of the numbers or terms being added or multiplied does not change the result.- The commutative property applies to addition and multiplication but not subtraction or division.- Applying the commutative property can simplify mathematical operations.- The commutative property is applicable in real-world scenarios, such as arranging objects or counting money.Slide 10:References- Include any references or sources used in creating the presentation.Note: This is just a sample outline for a lesson on the commutative laws. Please feel free to modify and expand the content to suit your specific needs.。
《乘法交换律和结合律》(公开课)ppt课件

2.判断。 (1)任何数与0相乘都得0。所以任何数与0相加也都得0。 ( ) (2)1+1=1×1 ( ) (3)134+196=134+200+4 ( ) (4)求剩余部分的运算叫做减法。 ( )
492×5×2
1
25×166×4
2
8×5×125×40
3
挑 战 场
今天我们学习了乘法的交换律和结合律,同学们掌握的怎么样呢?同学们自己在练习本上写一下本节课我们学习的两个运算定律的公式,并举例说明。
学得怎么样?
25×10=250(桶)
列成综合算式是:
01
你能不能用自己喜欢的方法来表示 乘法结合律呢?
02
(甲数×乙数)×丙数=甲数×(乙数×丙数)
03
(▲ × ★) × ●=__ ×(__ × __)
04
05
06
07
(a × b) × c = __ ×(__ × __)
08
a
09
b
10
c
通过字母公式比较加法交换律和乘法交换律,加法结合律和乘法结合律的, 你有什么发现?
(a+b)+c=a+(b+c)
复习:
加法交换律: 加法结合律:
a+b=b+a
猜一猜: 乘法可能有哪些运算定律?
人教新课标四年级数学下册
乘法交换律和结合律
每组要种5棵树,每棵树要浇2桶水。
一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。
4×25=100(人) 一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。
53×72 = 72× 53 观察这几个乘法算式之后,你发现了什么规律吗?
7 × 8 = 8 ×7
01
25×4=100(人) 25×4 = 4×25 你能再写出几个这样的等式吗? 观察比较:这两个算式什么是相同的?什么是不相同的? 例1:负责挖坑、种树的一共有多少人?
加法交换律和乘法交换律精选课件PPT

1
小故事:朝三暮四
从前,宋国有一个老人,他在家中养了许多猴子。老
人每天都会给每只猴子8颗栗子,早晚各4颗。后来
,猴子越来越多,老人也越来越穷,所以他想每天只
给猴子7颗栗子,于是他就和猴子们商量:“从今天
开始,我每天早上给你们4颗粟子,晚上给你们3颗
栗子,行不行?” 猴子们想了一想,晚上怎么少了一 颗呢?于是大叫起来,非常不愿意。老人一看,连忙
说:“那么我早上给你们3颗,晚上再给你们4颗, 可以了吧?” 猴子们听了,以为晚上的栗子已经由3
个变成4个,跟以前一样,就高兴地同意了。老人也
偷着乐了。
加法交换律: a+b=a+b 乘法交换律: a×b=b×a
加法交换律
乘法交换律
1.结合下面的例子说明等式为什么成立。
2.运用加法交换律和乘法交换律填一填。
感谢您的观看!本教学内容具有更强的时代性和丰富性,更适合学习需要和特点。为了 方便学习和使用,本文档的下载后可以随意修改,调整和打印。欢迎下载!
45+76= 76 +45
28+13= 13 + 28
+=
+
45×102=102× 45
296×200= 296 × 200
×=
×
3.计算下列各题,并运用加法交换律或乘法交换律进行验
算。
918+3举例试一试。
Thank you
感谢聆听 批评指导
汇报人:XXX 汇报日期:20XX年XX月XX日
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如7×693= 9×7= 63
7×9=9×7
发现:任意两个数相乘,交换乘数的位置,积不 变,这叫乘法交换律。
我来问 你来接
32+7=
5×107=
判断下列算式是否使用加法交换律和乘法交换律。(每组 4号准备回答。)
(1)3+6=2+7 × (2)34+43=34+43 ×
(3) 7×9=9×7 √ (4)25+61=21+65 ×
▲+★ =★ +▲
乘法b交×换律高=高× b
a + b =b + a
a×b=b×a
5+4=4+5 a+b=b+a 6×5=5×6 a×b = b×a
用字母表示规律比用文字描 述规律更容易、更准确、更简明、 更有效。
用一用 说一说下面的算式用了什么运算律?
358+276=634
加法交3 5换8律 + 217 16
6×5﹦3 5×60﹦30 6×5=5×6
乘法交换律成立
1加26乘×620法+×2+交16012换26=1=6律2=×+028成2(801(头 颗立6头))
编一编请同学们用喜欢的方式表示加法交换律和乘法交换 律。(建议可以用图形、字母等,比比谁最有创意,最容 易记忆。)
甲数+乙数=乙数+甲数 加法交a 换+律5=5+ a
本节课小结
任意两个数相加,交换加数的位置,和不变, 这叫加法交换律。
a+b=b+a 记住
任意两个数相乘,交换乘数的位置,积不变, 这叫乘法交换律。
a×b = b×a 记住
作业:把加法和乘法交换律的文字叙述抄
在数学书50页的最上面。再完成数学书 50—51页的内容。
(5)62×53=53×26 × (6)54+46=46+54 √ (7)36+52+24=36+24+52 √ (8)25×345×4=25×4×345 √
说一说
举生活中的例子,证明加法交换律和乘法交换律成立。
学校
少年宫
电影院
.
.
.
35米
42米
34加52法+的43交25 换 =律73成75﹢(立米42)
• 13+19﹦32(人) • 19 +13 ﹦32(人)
• 13+19﹦ 19 +13 为什么?
由 我们四年级班的同学
组成4组仪仗队。有多少人? 怎么计算?
1234
5
6
7
8
• 8×4﹦32(人) • 4×8﹦32(人)
• 8×4﹦ 4×8 为什么?
看一看
观察下面的两块黑板上的式子,完成以下任务。
634
验算:
276 + 31518
634
乘法交5×换1律07 =535
107 ×5
535
翻开数学书51 和除法也同样满足交换律。( × )
10-6﹦6﹣10吗? 10-6≠6﹣10
20÷5﹦ 5÷20吗? 20÷5≠ 5÷20
注意:在减法和除法中不存在交换律。
请你先说说发现了什么,再照样子每人各编一 个式子写下来。
发现:4+6﹦6﹢4 3×5 ﹦5×3 照样子每人各编一个式子写下来。
写出同学们编写的加法和乘法式子,观察— 你发现了什么规律?说给大家听听。
我们大家一起来总结吧!
例如:621+15 5533+= 62= 115 62+53=53+62
发现:任意两个数相加,交换加数的位置,和不 变,这叫加法交换律。
