chapter1-1+离散时间信号
合集下载
离散时间信号(序列)
y(n) x(n) x(n R) | | 1
为了生成间隔为R个周期的多重回声，可将上式改为： y(n) x(n) x(n R) 2 x(n 2R) N1x(n (N 1)R) | | 1
原声：
混响1：
混响2：
=0.3, R=5000 =0.3, R=10000
4、序列的反褶 ： y(n) = x(-n)
设有序列x(n)， 则x(-n)是以n=0为纵轴将x(n)反褶后的序列。
x(n)
3 2 11
-4 -3 -2 -1 0 1 2 3 4 5 6 n
3 x(-n)
2 1
-4 -3 -2 -1 0 1 2 3 4 5 6 n
x(n)
3
3
3
2
2
2
…1
1
1
0 1234
x(0)=1
x(1)=2
n
x(2)=3
xx(n(n) -1)
xx((nn)+1)
33 22 11
0 123456
n
33 22 11
-3 -2 -1）的应用
延时单元可以将以前的某采样时刻的数据暂存起来，参 与这个时刻的运算。
回声可以用延迟单元来生成。直接声音和它的延迟了R 个周期的单个回声可以用下面的式子来表示（ 为回声的 衰减系数）：
3、矩形序列RN(n) - Rectangular sequence
1 0 n N 1
RN
(
n)
0
其它n
RN(n)
1
…… ……
0 1 2 3 …… …… N-1
n
用单位阶跃序列u(n)表示矩形序列RN(n)：
为了生成间隔为R个周期的多重回声，可将上式改为： y(n) x(n) x(n R) 2 x(n 2R) N1x(n (N 1)R) | | 1
原声：
混响1：
混响2：
=0.3, R=5000 =0.3, R=10000
4、序列的反褶 ： y(n) = x(-n)
设有序列x(n)， 则x(-n)是以n=0为纵轴将x(n)反褶后的序列。
x(n)
3 2 11
-4 -3 -2 -1 0 1 2 3 4 5 6 n
3 x(-n)
2 1
-4 -3 -2 -1 0 1 2 3 4 5 6 n
x(n)
3
3
3
2
2
2
…1
1
1
0 1234
x(0)=1
x(1)=2
n
x(2)=3
xx(n(n) -1)
xx((nn)+1)
33 22 11
0 123456
n
33 22 11
-3 -2 -1）的应用
延时单元可以将以前的某采样时刻的数据暂存起来，参 与这个时刻的运算。
回声可以用延迟单元来生成。直接声音和它的延迟了R 个周期的单个回声可以用下面的式子来表示（ 为回声的 衰减系数）：
3、矩形序列RN(n) - Rectangular sequence
1 0 n N 1
RN
(
n)
0
其它n
RN(n)
1
…… ……
0 1 2 3 …… …… N-1
n
用单位阶跃序列u(n)表示矩形序列RN(n)：
数字信号处理第1章_离散时间信号与系统__01
19序列的运算都是有实际物理意义的运算可能在多个信号之间进行也可能是单一信号自身的变通过各种有效的运算将基本信号变换组合起来使系统处理信号的能力更强
第1章 离散时间信号与系统
1
第1章 离散时间信号与系统
• 离散时间信号 • 采样 • 离散时间信号的傅氏变换与Z变换 • 离散时间系统 • 系统的频率响应及其系统函数
任何序列均可以分解成: 偶对称序列和奇对称序列的和的形式。
x(n) xe (n) xo(n)
xe
(
n)
1 [x(n) 2
x(n)]
xo
(n)
1 [x(n) 2
x(n)]
25
6、任意序列的单位脉冲序列表示
---典型序列与一般序列之间的关系
任意一个序列x(n)均可以表示成单位脉冲序列
2 0
k
N k N为最小正整数，
k
2 N
0 k
（3）2π/ω0为无理数时，正弦序列为非周期序列。
17
【例】试判断以下正弦序列的周期性，若为周期序列，
求出该周期序列。
①
sin(
n
)
② sin(4 n)
4
5
③ sin(n)
4
解：
①
由于 0
4,N
2 0
k
8k
因此该序列为周期序列，且周期N=8。
x(n/2)
2 1 1/2
-1 0 1
2
1
1/2
n
n
-1。 0 1。
-2 -1 0 1 2
n
31
10、序列的翻褶
第1章 离散时间信号与系统
1
第1章 离散时间信号与系统
• 离散时间信号 • 采样 • 离散时间信号的傅氏变换与Z变换 • 离散时间系统 • 系统的频率响应及其系统函数
任何序列均可以分解成: 偶对称序列和奇对称序列的和的形式。
x(n) xe (n) xo(n)
xe
(
n)
1 [x(n) 2
x(n)]
xo
(n)
1 [x(n) 2
x(n)]
25
6、任意序列的单位脉冲序列表示
---典型序列与一般序列之间的关系
任意一个序列x(n)均可以表示成单位脉冲序列
2 0
k
N k N为最小正整数，
k
2 N
0 k
（3）2π/ω0为无理数时，正弦序列为非周期序列。
17
【例】试判断以下正弦序列的周期性，若为周期序列，
求出该周期序列。
①
sin(
n
)
② sin(4 n)
4
5
③ sin(n)
4
解：
①
由于 0
4,N
2 0
k
8k
因此该序列为周期序列，且周期N=8。
x(n/2)
2 1 1/2
-1 0 1
2
1
1/2
n
n
-1。 0 1。
-2 -1 0 1 2
n
31
10、序列的翻褶
第1章 离散时间信号和系统
第1章 思考题参考解答1．变化规律已知的信号称之为确定信号，反之，变化规律不确定的信号称之为随机信号。
以固定常数周期变化的信号称之为周期信号，否则称之为非周期信号。
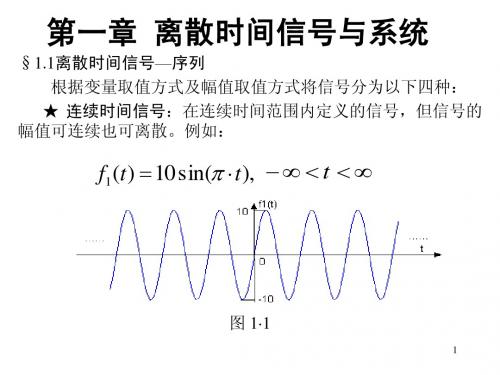
函数随时间连续变化的信号称之为连续时间信号，也称之为模拟信号。
自变量取离散值变化的信号称之为离散时间信号。
离散信号幅值按照一定精度要求量化后所得信号称之为数字信号。
2．对于最高频率为f c 的非周期信号，选取f s ＝2f c 可以从采样点恢复原来的连续信号。
而对于最高频率为f c 的非周期信号，选取f s ＝2f c 一般不能从采样点恢复原来的连续信号的周期信号，通常采用远高于2f c 的采样频率才能从采样点恢复原来的周期连续信号。
3．被采样信号如果含有折叠频率以上的高频成分，或者含有干扰噪声，这些频率成分将不满足采样恢复定理的条件，必然产生频率混叠，导致无法恢复被采样信号。
4．线性时不变系统的单位脉冲响应h (n )满足n <0，h (n )=0，则系统是因果的。
若∞<=∑∞-∞=P n h n |)(|，则系统是稳定的。
5．ω表示数字角频率，Ω表示模拟角频率。
ω=ΩT (T 表示采样周期)。
6．不一定。
只有当周期信号的采样序列满足x (n )= x (n +N )时，才构成一个周期序列。
7．常系数差分方程描述的系统若满足叠加原理，则一定是线性时不变系统。
否则，常系数差分方程描述的系统不是线性时不变系统。
8．该说法错误。
需要增加采样和量化两道工序。
9．受采样频率、有限字长效应的约束，与模拟信号处理系统完全等效的数字系统不一定找得到。
因此，数字信号处理系统的分析方法是先对采样信号及系统进行分析，再考虑幅度量化及实现过程中有限字长效应所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
10、只有当系统是线性时不变时，有y (n )= h (n )*x (n )。
11、时域采样在频域产生周期延拓效应。
12．输入信号x a (t )先通过一个前置低通模拟滤波器限制其最高频率在一定数值之内，使其满足采样频率定理的条件。
1第一章-离散时间信号与系统
2
2
1 Px N
2 | x ( n ) |
n
x ( n)
n
x ( n)
x(n) Bx
离散时间信号重点掌握内容： 1 连续、离散、模拟、数字的异同
2 离散序列的表示方法: x(n)
3 最常见的三种典型序列:单位脉冲、单位阶跃、矩形
x[m]h[n m]
m
m
x[n] * h[n]
y[n] x[n] h[n]
牢记该式，并 深刻领会！
通常把上式称为离散卷积或线性卷积。 这一关系常用符号“*”表示：
y ( n)
m
x(m)h(n m) x(n) h(n)
LTI系统
h(n)是系统特性的表征，滤波器设计本质上就是 找合适的h(n)。
3. LTI系统的运算性质（卷积运算性质)
LTI系统对任意输入的响应是一种卷积运算，满 足以下运算规律： 3.1 交换律
y ( n)
m
x ( m) h ( n m) x ( n ) h ( n ) h ( m) x ( n m ) h ( n ) x ( n )
课后思考！ 解：输入信号x[k]产生的输出信号y[k]为 y[k]=T{ x[k]}= x[Mk] 输入信号x[kn]产生的输出信号T{x[kn]}为 T{x[kn]}= x[Mkn] 由于 x[Mkn] y[kn] 故系统是时变的。
x1[k ]
1 2
3
4
5
6
5 3
k
2 3 4 5
1 -1 0 1 2
而 ay1(n)+by2(n) = a[5x1(n)+3]+b[5x2(n)+3] = 5 ax1(n) + 5bx2(n)+3(a+b)
2
1 Px N
2 | x ( n ) |
n
x ( n)
n
x ( n)
x(n) Bx
离散时间信号重点掌握内容： 1 连续、离散、模拟、数字的异同
2 离散序列的表示方法: x(n)
3 最常见的三种典型序列:单位脉冲、单位阶跃、矩形
x[m]h[n m]
m
m
x[n] * h[n]
y[n] x[n] h[n]
牢记该式，并 深刻领会！
通常把上式称为离散卷积或线性卷积。 这一关系常用符号“*”表示：
y ( n)
m
x(m)h(n m) x(n) h(n)
LTI系统
h(n)是系统特性的表征，滤波器设计本质上就是 找合适的h(n)。
3. LTI系统的运算性质（卷积运算性质)
LTI系统对任意输入的响应是一种卷积运算，满 足以下运算规律： 3.1 交换律
y ( n)
m
x ( m) h ( n m) x ( n ) h ( n ) h ( m) x ( n m ) h ( n ) x ( n )
课后思考！ 解：输入信号x[k]产生的输出信号y[k]为 y[k]=T{ x[k]}= x[Mk] 输入信号x[kn]产生的输出信号T{x[kn]}为 T{x[kn]}= x[Mkn] 由于 x[Mkn] y[kn] 故系统是时变的。
x1[k ]
1 2
3
4
5
6
5 3
k
2 3 4 5
1 -1 0 1 2
而 ay1(n)+by2(n) = a[5x1(n)+3]+b[5x2(n)+3] = 5 ax1(n) + 5bx2(n)+3(a+b)
chap1离散时间信号与系统
… n
指数序列 (a) |a|<1; (b) |a|>1; (c) a=-|a|
5． 正弦型序列 ． x(n)=A sin(nω0+φ) 式中: A为幅度; φ为起始相位; ω0为数字域的频率，它反映了序列 变化的速率。 ω0=0.1π时, x(n)序列如图所示，该序列值每20个重复一次循 环。
例1-2 证
2πn π y(n) = x(n) sin + 是否是时不变系统。 7 9
2πn π + T[x(n − m)] = x(n − m) sin 7 9 2π (n − m) π y(n − m) = x(n − m) sin + 9 7
x ( n) = x ( n ) * δ ( n) =
∞
m =−∞
∑ x(m)δ (n − m)
m =−∞
∞
y (n) = T [ ∑ x(m)δ (n − m)] =
m =−∞
∑ x(m)T [δ (n − m)]
∞
=
m =−∞
∑ x ( m) h ( n − m) = x ( n ) * h ( n )
所以此系统不满足叠加性， 故不是线性系统。
二、时不变系统
系统的变换关系T［·］在整个运算过程中不随时间（也即不 随序列的延迟）而变化，这种系统称为时不变系统（或称移不变 系统）。即若 T［x(n)］=y(n) ［ ］ 则 T［x(n-m)］=y(n-m) ［ ］ （m为任意整数）
满足以上关系的系统就称为时不变系统。
δ (n)
1 … …
－5 －4 －3 －2 －1 0
1
2
3
4
5
n
第一章 离散时间信号与系统1
根据定义
n y ( n ) 1 ( 1 ) k , n 1 2 2 k 1 y ( n) 0, n 1
14
我们计算几个值，画出图形。显然，
n 2 n 1 n0 n 1 n2
y(2) 0
1 3 2 2 3 1 7 y(1) y(0) x(1) 2 4 4 7 1 15 y(2) y(1) x(2) 4 8 8
j 0 n
0 ：复正弦的数字域频率 用欧拉公式将复指数序列展开： n n n x(n) e (cos0 n j sin 0 n) e cos0 n j e sin 0 n
用极坐标表示 其中 x(n)
x(n) x (n)
n
e
j arg[ x ( n )]
f2 (t )
0 1 1 0
, t 1 , 1 t 1 , 1 t 3 , t 3
定义域是连续的（-∞，∞），但是函数值只取-1，0，1三个离 散的值。（在间断点-1，1，3处一般不定义其函数值） f 以上两例中，1 (t ) 我们也称为模拟信号。
8
2 n , n 1 1 1 1 1 z (n) x(n) y(n) 2 ( 2 ) 2 3 , n 1 2 1 1 n 2 ( 2 ) n 1, n 0
图 1· 9 在求序列的和的时候要注意：相同序列 (n) 的序列值相加。
9
4．积（相乘） 两序列的积指相同序号 (n) 的序列值逐项对应相乘： z (n) x(n) y(n) 0.5, n 1 1.5, n 0 例1.1.4已知序列 x(n) = 1, n 1 求 y(n) x(n) 2 x(n) x(n 2) 0.5, n 2 0, n为其它值
第一章 离散时间信号 01
2
-1 。 0 -2 -1 0
1 。 1 2
n n
19
小 结
20
小 结
21
1.2 采
样
xa(t)
预滤
A/DC
数字信号处理
D/AC
平滑滤波
ya(t)
22
1.2 采
研究内容：
样
采样是对连续时间信号进行数字化处理的第一个环节。
•信号经采样后发生的变化（如频谱的变化）
•信号内容是否丢失（采样序列能否代表原始信号）
37
模拟到数字
1 xa ( nT ) sin(2 fnT ), T 8 fs 50 sin(2 n ) 200 8 1 sin( n ) 2 8
当n=…0，1，2，3，…时，得到序列x(n)如下： x(n)={…0.382683,0.923879,-0.382683,-0.923879…}
a n a
27
3. 采样信号的频谱
采样前xa(t)的
X a ( j) F[ xa (t )] xa (t )e jt dt
傅里叶正变换
傅里叶逆变换
1 xa ( t ) F [ X a ( j)] 2
1
X a ( j)e jt d
38
39
5
1.1.1 几种常见的典型的序列 3. 矩形序列
1, 0 n N 1 RN (n) 0, n 0, n N
RN(n)
1
RN(n)和u(n)、δ(n)的关系为
RN ( n) u( n) u( n N )
N 1 k 0
0123
-1 。 0 -2 -1 0
1 。 1 2
n n
19
小 结
20
小 结
21
1.2 采
样
xa(t)
预滤
A/DC
数字信号处理
D/AC
平滑滤波
ya(t)
22
1.2 采
研究内容：
样
采样是对连续时间信号进行数字化处理的第一个环节。
•信号经采样后发生的变化（如频谱的变化）
•信号内容是否丢失（采样序列能否代表原始信号）
37
模拟到数字
1 xa ( nT ) sin(2 fnT ), T 8 fs 50 sin(2 n ) 200 8 1 sin( n ) 2 8
当n=…0，1，2，3，…时，得到序列x(n)如下： x(n)={…0.382683,0.923879,-0.382683,-0.923879…}
a n a
27
3. 采样信号的频谱
采样前xa(t)的
X a ( j) F[ xa (t )] xa (t )e jt dt
傅里叶正变换
傅里叶逆变换
1 xa ( t ) F [ X a ( j)] 2
1
X a ( j)e jt d
38
39
5
1.1.1 几种常见的典型的序列 3. 矩形序列
1, 0 n N 1 RN (n) 0, n 0, n N
RN(n)
1
RN(n)和u(n)、δ(n)的关系为
RN ( n) u( n) u( n N )
N 1 k 0
0123
清华大学数字信号处理课件--第一章1离散时间信号与系统
1 1 2 如sin( n )， 0 ， 8 4 4 0 该序列不是周期序列
课件
33
例：判断
x ( n) e
n j ( ) 6
是否是周期序列
解：x(n N ) e
j( n N ) 6
e
n N j ( ) 6 6
若x ( n )为周期序列，则必须满足x ( n ) x ( n N )， N 即满足 2 k，且N，k为整数 6
课件 5
1、序列的运算
移位 翻褶 和 积 累加 差分 时间尺度变换 卷积和
课件
6
1）移位
序列x(n)，当m>0时 x(n-m)： 延时/右移m位 x(n+m)：超前/左移m位
课件
7
2）翻褶
x(-n)是以n=0的纵轴为 对称轴将序列x(n) 加以翻褶
课件
8
3）和
x(n) x1 (n) x2 (n)
m 0 n
k
(k )
课件 21
3）矩形序列
1 0 n N 1 RN (n) 其它n 0
与其他序列的关系
RN (n) u (n) u (n N )
RN (n) (n m) (n) (n 1) ... [n ( N 1)]
同序列号n的序列值 逐项对应相加
课件
9
4）积
x(n) x1 (n) x2 (n)
同序号n的序列值 逐项对应相乘 序列与常数相乘 各项分别乘以该常数
课件
10
5）累加
y ( n)
k
x(k )
数字信号处理第一章离散时间信号与系统 课件
1, RN (n) 0, 0 n N 1 n 0, n N
R5 ( n)
1 n
0 1 2 3 4
4. 实指数序列
x(n) a nu(n)
5. 正弦序列
x(n) A sin(0 n )
6. 复指数序列
x(n) Ae( j0n) Ae (cos0n j sin 0n)
x(n) h(n)
结论：任何离散时间线性时不变系统， 都可以通过单位取样响应h(n)来表征。
x ( n)
y(n) x(n) h(n)
h( n)
二、稳定系统
1. 定义
对于每一个有界输入产生一个有界输出的系统为稳定系统。
2. 线性时不变系统稳定的充要条件为系统的单位取样响
应绝对可和。即：
m
x(m)h(n m)
包含运算：翻褶、移位、相乘、相加 ************************************************* 例：
3 n 0 n 2 x(n) 其他n 0
*************
*************
1 0 n 3 h(n) 0 其他n
x ( n)
T[ . ]
y ( n)
y(n) T [ x(n)]
对T[· ]加以种种约束,可定义出各类离散时间系统。离散 时间系统中最重要、最常用的是“线性、时不变系 统”。
2. 线性系统 齐次性： 若 y(n) T [ x(n)] ， 则
T [ax(n)] aT[ x(n)] ay(n), a为常数
2 （1） T[ax1 (n) bx2 (n)] [ax1 (n) bx2 (n)]sin( n ) 5 3
R5 ( n)
1 n
0 1 2 3 4
4. 实指数序列
x(n) a nu(n)
5. 正弦序列
x(n) A sin(0 n )
6. 复指数序列
x(n) Ae( j0n) Ae (cos0n j sin 0n)
x(n) h(n)
结论：任何离散时间线性时不变系统， 都可以通过单位取样响应h(n)来表征。
x ( n)
y(n) x(n) h(n)
h( n)
二、稳定系统
1. 定义
对于每一个有界输入产生一个有界输出的系统为稳定系统。
2. 线性时不变系统稳定的充要条件为系统的单位取样响
应绝对可和。即：
m
x(m)h(n m)
包含运算：翻褶、移位、相乘、相加 ************************************************* 例：
3 n 0 n 2 x(n) 其他n 0
*************
*************
1 0 n 3 h(n) 0 其他n
x ( n)
T[ . ]
y ( n)
y(n) T [ x(n)]
对T[· ]加以种种约束,可定义出各类离散时间系统。离散 时间系统中最重要、最常用的是“线性、时不变系 统”。
2. 线性系统 齐次性： 若 y(n) T [ x(n)] ， 则
T [ax(n)] aT[ x(n)] ay(n), a为常数
2 （1） T[ax1 (n) bx2 (n)] [ax1 (n) bx2 (n)]sin( n ) 5 3
数字信号处理第一章离散时间信号与系统课件
x(n)
y(n) x(n n0 )
n
0
当 n0>0 时，序列右移 ——延迟
x(n-2)
当 n0<0 时，序列左移
0
n
——超前
1.1 离散时间信号——序列
4. 序列的翻转
❖ x(-n)是x(n)的翻转序列。x(-n)是以纵 轴（n=0）为对称轴将序列x(n)加以翻转。
x(n)
n 0
x(-n) n
同序号的序列值逐项对应相加
x1(n)
n 0
x2(n)
n 0
x1(n) +x2(n)
n 0
1.1 离散时间信号——序列
2. 序列的乘法
x1(n)
n
x(n) x1(n) x2 (n) 0
x2(n)
同序号的序列值逐项对应相乘
n 0
x1(n) ·x2(n)
n 0
1.1 离散时间信号——序列
3. 序列的移位
1 a1n 1 a
x(m)
(3)在4<n≤6区间上
m
4
y(n) x(m)h(n m) m0
04 h(n-m)
4
4
1 anm an am
m0
m0
m
n-6 0
46 n
an 1 a(14) an4 a1n
y(n) T[x(n)]
1.2.1 线性系统
若系统满足可加性与比例性,则称此系统为离散 时间线性系统。
设 y1(n) T[x1(n)], y2(n) T[x2(n)]
T[ax1(n) bx2 (n)] aT[x1(n)] bT[x2 (n)] ay1(n) by2 (n)
其中a、b为任意常数。
第一章离散时间信号与系统
(1-3)
这就是u(nn) (n m) (n) (n 1) (n 2) m0
令n-m=k，代入此式可得
n
u(n) (k)
k
这里就用到了累加的概念。
(1-4) (1-5)
3．矩形序列RN(n)
RN
(n)
1 0
(n)
1
…
…
－ 5 － 4 － 3－ 2 － 1 0 1 2 3 4 5 n
图 1-4 δ(n)序列
这是最常用、最重要的一种序列，它在离散时间系统中的 作用，很类似于连续时间系统中的单位冲激函数δ(t)。但是， 在连续时间系统中，δ(t)是 t=0 点脉宽趋于零，幅值趋于无限大， 面积为1的信号，是极限概念的信号， 并非任何现实的信号。 而离散时间系统中的δ(n)，却完全是一个现实的序列， 它的脉 冲幅度是1， 是一个有限值。
xp (t) xa (t) p(t)
一般开关闭合时间都是很短的，而且τ越小，采样输出脉冲的
幅度就越准确地反映输入信号在离散时间点上的瞬时值。当τ<<T时，
采样脉冲就接近于δ函数性质。
xa(t)
(a)
xa(t)
xˆa (t)
(b)
o
t
T
p(t)
s(t)
1
(c)
o
T
t
(e)
o
T
t
xp(t)
(1-8)
4．实指数序列
x(n) anu(n)
式中，a为实数。当|a|<1 时，序列是收敛的; 而当|a|>1时，序列 是发散的。a为负数时，序列是摆动的，如图1-7所示。
anu(n)
1-1离散时间信号-序列
▲ ■ 25
[例1-1-3]两个序列如下，试求二序列的卷积和 例 两个序列如下， 两个序列如下 y (n) = x(n) * h(n)
1 n, x ( n) = 2 0 ,
1≤ n ≤ 3 其他n
1, 0 ≤ n ≤ 2 h( n) = 0 , 其他n
2011-3-11 26
第一章 离散时间信号与系统
1.1 离散时间信号——序列 离散时间信号—— ——序列 1.2 线性移不变系统 1.3 常系数线性差分方程 1.4 连续时间信号的抽样
• • • •
■
1
§1.1 离散时间信号-----序列 离散时间信号 序列
离散时间信号的定义、表示和产生 离散时间信号的定义、 基本序列 序列的基本运算 重点: 重点 卷积运算 用δ(n)表示任意序列 表示任意序列
▲
■
17
三、序列的基本运算
2. 翻褶 x ( n ) → x (－ n) 以n=0的纵轴为对称轴翻褶 的纵轴为对称轴翻褶
x ( n)
x ( − n)
▲
■
18
三、序列的基本运算
3. 和
z ( n) = x ( n) + y ( n)
点对点运算
4. 积
z ( n) = x ( n) • y ( n)
u ( n)
1, n ≥ 0 u ( n) = 0, n ≤ 0
δ(n)与u(n)之间的关系: ① δ(n)是u(n)的一次差分 是 的 是延时单位序列的叠加 ② u(n)是延时单位序列的叠加 是延时单位序列的
L
δ(n) =u(n) −u(n−1 )
u(n) = ∑ (n−m δ )
m=0 ∞
▲ ■ 3
一、离散信号的定义、表示和产生 离散信号的定义、
[例1-1-3]两个序列如下，试求二序列的卷积和 例 两个序列如下， 两个序列如下 y (n) = x(n) * h(n)
1 n, x ( n) = 2 0 ,
1≤ n ≤ 3 其他n
1, 0 ≤ n ≤ 2 h( n) = 0 , 其他n
2011-3-11 26
第一章 离散时间信号与系统
1.1 离散时间信号——序列 离散时间信号—— ——序列 1.2 线性移不变系统 1.3 常系数线性差分方程 1.4 连续时间信号的抽样
• • • •
■
1
§1.1 离散时间信号-----序列 离散时间信号 序列
离散时间信号的定义、表示和产生 离散时间信号的定义、 基本序列 序列的基本运算 重点: 重点 卷积运算 用δ(n)表示任意序列 表示任意序列
▲
■
17
三、序列的基本运算
2. 翻褶 x ( n ) → x (－ n) 以n=0的纵轴为对称轴翻褶 的纵轴为对称轴翻褶
x ( n)
x ( − n)
▲
■
18
三、序列的基本运算
3. 和
z ( n) = x ( n) + y ( n)
点对点运算
4. 积
z ( n) = x ( n) • y ( n)
u ( n)
1, n ≥ 0 u ( n) = 0, n ≤ 0
δ(n)与u(n)之间的关系: ① δ(n)是u(n)的一次差分 是 的 是延时单位序列的叠加 ② u(n)是延时单位序列的叠加 是延时单位序列的
L
δ(n) =u(n) −u(n−1 )
u(n) = ∑ (n−m δ )
m=0 ∞
▲ ■ 3
一、离散信号的定义、表示和产生 离散信号的定义、
第一章 离散时间信号和系统
N 1 运动平均系统 : y ( n) x(n k ) M N 1 k M
30
一、线性时不变系统
1.线性系统
y1 ( n) T [ x1 ( n)]
y2 ( n) T [ x2 ( n)]
（1）可加性 （2）奇次性
y1 (n) y2 (n) T [ x1 (n) x2 (n)]
u( n) ( n m )
m 0
(n)
1
0 u(n)
1
0 1
n
…
n
22
(3). 矩形序列
1, 0 n N 1 R N ( n) 0 , 其他n
RN (n) 和 (n) 、 (n) 的关系为： u
RN (n)
RN (n) u(n) u(n N )
取和
11
例1 - 1 - 2 已知x(n) h(n) 1 ， 3，求x(n) h(n)。 2， n 0
x(m)
解：
（1）翻褶 (2) 移位、相乘、累加
n<0, y(n)=0 n＝0, y(n)=1 n=1, y(n)=1•2+2•1=4 n=2, y(n)=1•3+2•2+ 1•3 =10
(n 1) 2 (n) (n 2) 0.5 (n 3) 1.5 (n 4) 28
1.2 离散时间系统
29
离散时间系统定义: 离散时间系统是将输入序列变换成输出序列的一种运算。
x(n)
T[.]
y(n)
y(n)=T[x(n)]
例如 理想时延系统 : y ( n) x( n n0 )
2
30
一、线性时不变系统
1.线性系统
y1 ( n) T [ x1 ( n)]
y2 ( n) T [ x2 ( n)]
（1）可加性 （2）奇次性
y1 (n) y2 (n) T [ x1 (n) x2 (n)]
u( n) ( n m )
m 0
(n)
1
0 u(n)
1
0 1
n
…
n
22
(3). 矩形序列
1, 0 n N 1 R N ( n) 0 , 其他n
RN (n) 和 (n) 、 (n) 的关系为： u
RN (n)
RN (n) u(n) u(n N )
取和
11
例1 - 1 - 2 已知x(n) h(n) 1 ， 3，求x(n) h(n)。 2， n 0
x(m)
解：
（1）翻褶 (2) 移位、相乘、累加
n<0, y(n)=0 n＝0, y(n)=1 n=1, y(n)=1•2+2•1=4 n=2, y(n)=1•3+2•2+ 1•3 =10
(n 1) 2 (n) (n 2) 0.5 (n 3) 1.5 (n 4) 28
1.2 离散时间系统
29
离散时间系统定义: 离散时间系统是将输入序列变换成输出序列的一种运算。
x(n)
T[.]
y(n)
y(n)=T[x(n)]
例如 理想时延系统 : y ( n) x( n n0 )
2
第一章离散时间信号与系统
n5 n5
n0 n0
1.1.5 用单位脉冲序列表示任意序列
任意序列x(n)都可用单位脉冲序列 (n) 表示成加权和的形式，即
x ( n)
如:
m
x(m) (n m)
n
可表示为
a x ( n) 0
x ( n)
10 n 10 其他
m 10
m
上式为x(n)与h(n)的线性卷积，它说明线性 时不变系统的响应等于输入序列与单位脉冲响 应序列的卷积。 一般用h(n)代表系统，示意图如下
y(n) x(n) * h(n)
1. 卷积的性质 *可交换性
*结合性
y ( n ) x ( n) h( n) h ( n) x ( n)
RN (n) 与 u(n) 的关系
RN (n)
1
0 1
2 3
n
RN (n) u(n) u(n N )
4.复指数序列
x(n) e
x ( n) e
n
( j0 ) n
式中ω0为数字频率
n
将复指数表示成实部与虚部
cos 0 n je sin 0 n
其示意图如下：
5.正弦序列
示例见下
例：求z(n)=x(n)+y(n)
解： z(0)=x(0)+y(0) z(1)=x(1)+y(1) z(2)=x(2)+y(2) …
2. 序列的乘积 序列的乘积是指同序号的序列值对 应相乘。即
z ( n ) x ( n ) y ( n)
示例见下
例：求z(n)=x(n)· y(n)
可见系统为时不变系统。
n0 n0
1.1.5 用单位脉冲序列表示任意序列
任意序列x(n)都可用单位脉冲序列 (n) 表示成加权和的形式，即
x ( n)
如:
m
x(m) (n m)
n
可表示为
a x ( n) 0
x ( n)
10 n 10 其他
m 10
m
上式为x(n)与h(n)的线性卷积，它说明线性 时不变系统的响应等于输入序列与单位脉冲响 应序列的卷积。 一般用h(n)代表系统，示意图如下
y(n) x(n) * h(n)
1. 卷积的性质 *可交换性
*结合性
y ( n ) x ( n) h( n) h ( n) x ( n)
RN (n) 与 u(n) 的关系
RN (n)
1
0 1
2 3
n
RN (n) u(n) u(n N )
4.复指数序列
x(n) e
x ( n) e
n
( j0 ) n
式中ω0为数字频率
n
将复指数表示成实部与虚部
cos 0 n je sin 0 n
其示意图如下：
5.正弦序列
示例见下
例：求z(n)=x(n)+y(n)
解： z(0)=x(0)+y(0) z(1)=x(1)+y(1) z(2)=x(2)+y(2) …
2. 序列的乘积 序列的乘积是指同序号的序列值对 应相乘。即
z ( n ) x ( n ) y ( n)
示例见下
例：求z(n)=x(n)· y(n)
可见系统为时不变系统。
第01章 离散时间信号和离散时间
h n e
n
称为系统的频率响应，或系统的特征值
h是离散的， H是连续的 h表征了系统的时域特征，H表征了系统的频域特征 二者之间是离散傅里叶变换的关系。
“域”的概念和种类
时域、频域、Z域、 时频域、空域、空时域
1.7 频率响应（Frequency Response）
H e
j
h n e
n
j n
DTFT
H e j H R e j jH I e j
H e j H e j e
幅频响应
j
相频响应
1.8 相关函数(Correlation Function)
相关系数
1 x(n) sin(0.01 n) sin 2 n 200
N 200
N 20
N 20
7. Chirp 信号：
8．脉冲串
p 号的分解
“抽取”性质
离散信号x(n)在某一时刻k的取值x(k)可以表示为
a n , n 0 h n 0, n 0
h n a nu n
1.5 离散时间系统
1.5.6 FIR系统
h n y n bk n k
k 0 2
h 0 b0 h 1 b1 h 2 b2
4
20
40 (a)
60
80
100
5
histogram of u(n)
4 3 2 1 0 -1.5 -1 -0.5 0 (b) 0.5 1 1.5 2
直方图
白噪声：
White Noise
功率谱为一直线； 自相关函数为
第一章 离散时间信号与离散时间系统
1-2 离散时间系统的基本概念 4)卷积的性质 交换率：
此外：
结合率：
分配律：
卷积应用举例——连续卷积
卷积应用举例——离散卷积
核矩阵
积阵列
卷积应用举例——离散卷积
设当前的待处理像素为f(i,j) ,给出 一个处理模板如下所示。
(i-1, j-1)
(i , j-1)
(i-1, j) (i, j)
2a 1 u k 2 u k 1 u (k ) 0 a
1-3 离散时间系统模型
讨论： （1）差分方程： 由激励序列、响应序列以及其移序序列组成的方程。 含y(k)，y(k-1)，…的差分方程: 含y(k)，y(k+1)，…的差分方程: 后向差分方程 前向差分方程
（2）差分方程 阶数：响应最高序号与最低序号的差值。 （3）离散自变量k不一定限于时间。
1-1 离散时间信号的基本概念
正弦序列周期性的讨论
0 0.2 , N
2
0
10
0 0.1 , N
2
0
20
4 2 0 , N k 11(k 2) 11 0
0 0.4, 无周期
习题 例1：判断是否为周期序列，如果是，周期是多少？
推广： 1)
2)
k 0 k 0
0, k j U (k j ) 1, k j
AU (k ), AU (k j )
性质： f (k )U (k ) f (k ) k 0
Байду номын сангаас0
k 0
可见，U(k)作用类似于U(t)， 但二者有较大差别：
U(t) ：奇异信号，数学抽象函数； U(k)：非奇异信号，可实现信号。
(研) 第1讲 离散时间信号与系统
w(n)=x(n)* h1(n)=∑x(k) h1(n-k)= ∑u(k) h1(n-k) = ∑u(k) [δ(n-k)- δ(n-k-4)]=u(n)-u(n-4) = δ(n)+δ(n-1)+δ(n-2)+ δ(n-3) y(n)= w(n)* h2(n)=[δ(n)+δ(n-1)+δ(n-2)+ δ(n-3)] * h2(n) = h2(n)+ h2(n-1) +h2(n-2)+ h2(n-3) = an u(n)+ an-1u(n-1)+ an-2u(n-2)+ an-3u(n-3)
n
N 1 2 lim x ( n) 5、功率信号 P N 2 N 1 n N
6、一维、二维及多维信号 （信号的变量可以是时间、频率、空间或 其他的物理量。） 一维：语音 二维：静止图象 多维信号：心电图、遥感
§1.3 噪声
1、噪声来源（50Hz工频干扰*、电子器 件的热噪声、量化噪声等） 2、噪声模型（噪声都是随机信号） 白噪声（理想化的噪声模型） 信号的功率 信噪比： Ps SNR 10lg Pu
x(k) 3/2 1 1/2 k 1
h(k)
0
1
2 3
0
1
2
k
翻转 h(-k)=h(0-k)
移位 h(1-k)
-2 -1 0
k
-1 0 1 得y(1)
k
对应相乘，逐个相加得y(0)
y (0) 0 1 1 y (1) 1 2 2 1 3 y ( 2) 1 1 1 2 2 1 3 y (3) 1 1 1 1 3 2 2 1 3 5 y ( 4) 0 1 1 1 0 1 2 2 2 3 3 y (5) 1 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Chapter 1 Discrete Signal and System – Time Domain
1、单位抽样序列（单位序列、单位脉冲序列、
单位函数、单位冲激序列）
• 定义
1 n 0 ( n) 0 n 0
1
( n)
1 0 1 2 3
n
• 延迟的 (n)
1 n m (n m) 0 n m
Digital Signal Processing
零点位置
Chapter 1 Discrete Signal and System – Time Domain
例
试写出
序列形式并画出图形。
解：序列形式
x ( n) L , 0, 0, 1 , 2, 4, 8, L n 0
1 n m u( n m ) 0 n m
任意序列与 1 单位阶跃序 列相乘 -1 0 1 2 3 4 单边右序列 5 6…
u( n 3)
n
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
数字信号处理
第一章
离散时间信号与 系统
Chapter 1 Discrete Signal and System – Time Domain
本章主要内容（6学时）
1-0、概述
1-1、离散时间信号 1-2、连续时间信号的采样 1-3、离散时间系统及时域分析
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
任意离散信号的单位抽样序列表示
x ( n) ... x( n) ( n 1) x ( n) ( n) x ( n) ( n 1) ...
m
x( n) (n m)
4、斜变序列
r ( n) nu( n)
斜变序列是在单位阶 跃序列u(n)上乘以系
nu(n)
n 数n
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
5、单边实指数序列 x( n) a u( n)
(k )
1
( n) ( )d
n
( n) u( n) u( n 1)
n 与u n 是差和关系，
不再是微分关系。
d (t ) (t ) 1 t 0 1 2 3 d u( n 1)
1
n
-1 0 1 2 3 4 5 6 …
n
Digital Signal Processing
一、离散信号的定义
• 定义
• 仅在规定的离散时刻 n(n=0,±1, ±2,…)上才有定义
(确定的函数值)的信号。一般用符号x(nT)或x(n)或
x[n]表示，n=0, ±1, ±2, … ，表示信号值在序列中
出现的序号。
• 获取方法：
• 从实际系统直接获取
• 连续信号取样，取样间隔一般取均匀间隔(取样周期T)
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
一、离散信号的定义
x ( n)
x ( nT )
n
n
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
2、单位阶跃序列
• 定义
1 n 0 u( n) 0 n 0
1
u( n)
-1 0 1 2 3 4 5 6 …
n
• 延迟的阶跃序列
单位序列与单位阶跃序列
u( n)
u(n)可看作是无数个出现在不同 序号上的单位序列信号之和。 1
u( n) ( n) ( n 1) ( n 2) (n m)
m 0 n
-1 0 1 2 3 4 5 6 …
(t )
t
k
n
• a为实数。
• 当|a|<1 时，序列收敛
• 当|a|>1时，序列发散 • a为负数时，序列摆动
在单位阶跃序列u(n)
上乘以系数an
n
0 1
1
0
n
1 0
1 2
3
4
n
1 0 1 2 3 4
n
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
(t)：奇异信号，数学抽象函数，用面
积（强度）表示，(幅度为，但强度 为面积)
1
(n)作用类似于(t)，但有较大差别：
(t )
t 0 (t ) 0 t 0
( t )dt 1
0
t
(n)：非奇异信号，可实现信号，在
n=0时取有限值1（不是面积）
一、离散信号的表示
1、图形表示：线段的长短表示实际的函数值。
x ( n)
图中横坐标n表示离散的 时间坐标，且仅在n为整 数时才有意义；纵坐标 n 代表信号样点的值。
2、数据表格
n x(n)
1 1.2
2 1.4
3 1.3
4 1.7
5 1.1
6 1.9
7 1.8
3、序列表示
L 0.9, 0.8, 0.3, 0.1L n 0
x( ) ( t )d x( t ) ( t l Signal Processing
-1 0 1 2 3
…
n
i
Chapter 1 Discrete Signal and System – Time Domain
单位序列与冲激函数
思考: 分解的好处？
x ( n) ( n m )
x ( 1) ( n 1) x(0) ( n) x(1) ( n 1)
x( m) ( n m) x( t ) 任意序列都可以用(n)
m
x ( n)
x ( m ) ( n m )
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
二、典型离散时间信号
单位(抽样)序列 单位阶跃序列 矩形/门序列 斜变序列 正弦序列 复指数序列 z序列
Digital Signal Processing
波形：
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
序列的几种形式
单边序列： 右序列（有始序列） n<N1，f(n)=0
左序列（有终序列） nN2，f(n)=0
双边序列：-<n<, f(n)0
Chapter 1 Discrete Signal and System – Time Domain
1-1 离散时间信号
1 定义及表示
2 典型信号 3 信号运算
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
有限序列：N1<n<N2, f(n)0
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
课堂问答题
1、x(n)中的n表示什么？
答：n表示抽样离散时间点，并且只能为整数．
2、n=0,n=1和n=-1分别表示什么？ 答： n=0：当前采样时刻（正在发生，其值可看成已知）； n=1：下一个采样时刻（还未发生，是将来的情况，其 值看成是未知的，即使是确定信号，其值只可说可预 测）； n=-1：上一个采样时刻（已经发生，变成了历史，其 值看成是已知的，且不可改变）。 在通项中，n表示当前输入时刻，n-1表示上一个采样 时刻，n+1表示下一个采样时刻。 注意：序列的时间长度是无限的，即-∞<n<∞ ，但仿 真或图形显示只能显示有限的部分。
任意序列与 窗序列相乘
RN ( n m )
加窗
n
Digital Signal Processing
Chapter 1 Discrete Signal and System – Time Domain
问：
RN ( n) u( n) u( n N )
RN ( n)
N 1 k 0
x ( n) ( n) x (0) ( n) x 0 x ( n) ( n m ) x ( m ) ( n m ) x ( m )
( n)
1 1 0 1 2 3 1
m为常数
( n 3)
n
1 0 1 2 3
n
Digital Signal Processing
注意：矩形序列是有限长 矩形/门序列是否还有其它表示方式 序列，而单位阶跃序列是 RN ( n) 无限长序列