小升初奥数知识点讲解数的整除
小学小升初奥数知识:数的整除

小学小升初奥数知识:数的整除小学小升初奥数知识集锦:数的整除导语:下面是小编为您收集整理的数的整除相关知识,欢迎阅读!1.整除的概念在小学书中所学的自然数和零,都是整数。
同学们都知道,如果一个整数a除以一个自然数b,商是整数而且没有余数(或者说余数为零),就叫做a能被b整除,或者b整除a,记作a│b。
这时a叫做b 的倍数,b叫做a的约数。
例如,3│15表示15能被3整除,或者3整除15;也可以说15是3的倍数,3是15的约数。
由整数概念可知,整除必须同时满足三个条件:(1)被除数是整数,除数是自然数;(2)商是整数;(3)没有余数。
这三个条件只要有一个不满足,就不能叫整除。
例如,16÷5=3.2,商不是整数,所以不能说5整除16。
又如,10÷2.5=4,除数不是自然数,所以不能说10能被2.5整除。
2.整除的性质(1)如果两个整数都被同一个自然数整除,那么它们的和、差(大减小)也都能被这个自然数整除。
换句话说,同一个自然数的两个倍数之和、差(大减小)仍是这个自然数的倍数。
例如,18与42都能被6整除,那么18与42的和60、差24也都能被6整除;即从6│18及6│42可知6│(18+42)、6│(42-18)。
(2)如果甲数整除乙数,乙数整除丙数,那么甲数整除丙数。
即如果丙数是乙数的倍数,乙又是甲数的倍数,那么丙数是甲数的倍数。
例如,7│28,28│84,那么就有7│84。
(3)如果甲数整除乙数,那么甲数就整除乙数与任一整数的乘积。
也就是说如果乙数是甲数的倍数,那么乙数的任一倍数也是甲数的倍数。
例如,13│39,39×4=156,因此13│156。
(4)如果甲数能被丙数整除,而乙数不能被丙数整除,那么甲数与乙数的和、差都不能被丙数整除。
即如果甲数是丙数的倍数,乙数不是丙数的倍数,那么甲数与乙数的和、差(大减小)都不是丙数的倍数。
例如,6整除48,6不整除35,所以6不整除83(48+35=83),也不整除13(48-35=13)。
小升初数学总复习知识梳理数的整除(附答案)

小升初总复习数与代数第一单元数的认识第2节数的整除知识梳理典例精讲【例1】把自然数A和B分解质因数后分别是A=2×3×11×m,B=2×3×7×m。
A、B两数的最大公因数是78,这两个数的最小公倍数是多少?【分析】这里要明白最大公因数和最小公倍数的意义,A、B两数的最大公因数就是这两个数的全部公有的质因数的积,也就是2×3×m;A、B两数的最小公倍数就是这两个数的全部公有质因数及各自独有质因数的积,也就是2×3×m×11×7.根据两个数的最大公因数是78,求出m的值,本题便迎刃而解。
【解】因为2×3×m=78,所以m=78÷2×3=13,因此2×3×m×11×7=78×11×7=155。
答:这两个数的最小公倍数是155.即时演练1.25和30的最大公因数是(),最小公倍数是()。
2. 把自然数A和B分解质因数后分别是A=2×3×m,B=2×7×m。
A、B两数的最大公因数是22,这两个数的最小公倍数是多少?3.两个数的最小公倍数是150,最大公因数是15.这两个数分别是()和()。
【例2】有一些糖果,如果把6个装一包少1个;如果8个装一包也少一个;如果把5个装一包还是少一个。
这些糖果至少有多少个?【分析】这些糖果,把6个装一包少1个说明糖果的总个数比6的倍数少1个;8个装一包也少一个说明糖果总个数比8的倍数少1个;把5个装一包还是少一个说明糖果的总个数比5的倍数少1个。
所以这些糖果的总个数比5、6、8的公倍数少1,这里求至少有糖果多少个,就是求比5、6、8的最小公倍数少1的数。
【解】5、6、8的最小公倍数是120.120-1=119(个)答:这些糖果至少有119个。
奥数知识点:数的整除

奥数知识点:数的整除奥数知识点:数的整除如果整除a除以不为零数b,所得的商为整数而余数为0,我们就说a能被b整除,或叫b能整除a。
如果a能被b整除,那么,b叫做a的约数,a叫做b的倍数。
下面小编给大家精心搜集整理的奥数知识点:数的整除,欢迎阅读!奥数知识点:数的整除数的整除的特征:(1)能被2整除的数的特征:如果一个整数的个位数字是2、4、6、8、0,那么这个整数一定能被2整除。
(2)能被3(或9)整除的数的特征:如果一个整数的各个数字之和能被3(或9)整除,那么这个整数一定能被3(或9)整除。
(3)能被4(或25)整除的数的特征:如果一个整数的末两位数能被4(或25)整除,那么这个数就一定能被4(或25)整除。
(4)能被5整除的数的特征:如果一个整数的个位数字是0或5,那么这个整数一定能被5整除。
(5)能被6整除的数的特征:如果一个整数能被2整除,又能被3整除,那么这个数就一定能被6整除。
(6)能被7(或11或13)整除的.数的特征:一个整数分成两个数,末三位为一个数,其余各位为另一个数,如果这两个数之差是0或是7(或11或13)的倍数,这个数就能被7(或11或13)整除。
(7)能被8(或125)整除的数的特征:如果一个整数的末三位数能被8(或125)整除,那么这个数就一定能被8(或125)整除。
(8)能被11整除的数的特征:如果一个整数的奇数位数字之和与偶数位数字之和的差(大减小)能被11整除,那么它必能被11整除。
一、例题与方法指导例1.一个六位数23□56□是88的倍数,这个数除以88所得的商是_____或_____.思路导航:一个数如果是88的倍数,这个数必然既是8的倍数,又是11的倍数.根据8的倍数,它的末三位数肯定也是8的倍数,从而可知这个六位数个位上的数是0或8.而11的倍数奇偶位上数字和的差应是0或11的倍数,从已知的四个数看,这个六位数奇偶位上数字的和是相等的,要使奇偶位上数字和差为0,两个方框内填入的数字是相同的,因此这个六位数有两种可能。
小升初数学知识点总结数的整除2

小升初数学知识点总结数的整除
摘要:温故而知新,大家只要做到这点,一定可以提高学习能力。
为大家了小升初数学:数的整除知识点,方便同学们查看复习,希望大家喜欢。
数的整除
1.把一个合数分解质因数,通常用短除法。
先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
2.求几个数的最大公约数的方法是:先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的的最大公约数。
3.求几个数的最小公倍数的方法是:先用这几个数(或其中的部分数)的公约数去除,一直除到互质(或两两互质)为止,然后把所有的除数和商连乘求积,这个积就是这几个数的最小公倍数。
4.成为互质关系的两个数:1和任何自然数互质;相邻的两个自然数互质;当合数不是质数的倍数时,这个合数和这个质数互质;两个合数的公约数只有1时,这两个合数互质。
总结:小升初数学:数的整除知识点就为大家介绍到这儿了,希望的可以帮助到大家,祝大家学习进步。
数的整除知识点总结数的整除知识整理

数的整除知识点总结数的整除知识整理数的整除知识点总结如下:1. 除数和被除数:一个数被另一个数整除时,被除数称为整数,除数称为除数。
2. 整除关系:如果一个数a能被另一个数b整除,即a ÷ b = c,则称a能被b整除,或者说b能整除a,记作b|a。
3. 余数:当一个数a被另一个数b整除时,如果除完后还有剩余部分,即a ÷ b = c 余 r(0 ≤ r < |b|),则r称为数a除以b的余数。
4. 因数:对于一个数a,如果存在一个数b,使得b能整除a,即a = b × c,则称b 是a的因数,c是a的倍数。
a的因数包括1和a本身。
5.倍数:对于一个数a,如果存在一个数b,使得a能整除b,即b = a × c,则称b 是a的倍数,c是a的因数。
a的倍数包括0和任意正负整数。
6.公约数:对于两个数a和b,如果存在一个数c,既能整除a又能整除b,即c|a 且c|b,则称c是a和b的公约数。
7.最大公约数:对于两个数a和b的公约数中,最大的一个公约数称为a和b的最大公约数,记作gcd(a, b)。
8.最小公倍数:对于两个数a和b的公倍数中,最小的一个公倍数称为a和b的最小公倍数,记作lcm(a, b)。
9.质数:一个大于1的自然数,除了1和它本身外,无法被其他自然数整除的数称为质数。
质数只有两个因数,即1和该数本身。
10.合数:一个自然数,除了1和它本身外,还有其他因数的数称为合数。
合数有多个因数。
11.互质:两个数的最大公约数为1时,称这两个数互质。
12.互质数性质:互质数的乘积等于它们的最小公倍数。
13.素数分解:将一个合数分解成质数的乘积的过程,这个过程叫做素数分解。
这些是数的整除的基本知识点。
小升初数学数的整除知识点讲解

小升初数学数的整除知识点讲解基础教育一直是最受学校和家长关注的,最为基础教育重中之重的初等教育,更是得到更多的重视。
小升初频道为大家准备了小升初数学数的整除知识点,希望能帮助大家做好小升初的复习备考,考入重点初中院校!小升初数学数的整除知识点讲解一、基本概念和符号:1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号|,不能整除符号因为符号∵,所以的符号二、整除判断方法:1. 能被2、5整除:末位上的数字能被2、5整除。
2. 能被4、25整除:末两位的数字所组成的数能被4、25整除。
3. 能被8、125整除:末三位的数字所组成的数能被8、125整除。
4. 能被3、9整除:各个数位上数字的和能被3、9整除。
5. 能被7整除:①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6. 能被11整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7. 能被13整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:1. 如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2. 如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3. 如果a能被b整除,b又能被c整除,那么a也能被c整除。
4. 如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
小升初考试是小学生进入初等重点初中院校的一次重要考试,希望大家都能够认真复习,同时也希望我们准备的小升初数学数的整除知识点能让大家在小升初的备考过程助大家一臂之力!。
小升初奥数知识点讲解 数的整除

【小升初奥数知识点讲解】数的整除
数的整除
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1. 能被2、5整除:末位上的数字能被2、5整除。
2. 能被4、25整除:末两位的数字所组成的数能被4、25整除。
3. 能被8、125整除:末三位的数字所组成的数能被8、125整除。
4. 能被3、9整除:各个数位上数字的和能被3、9整除。
5. 能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6. 能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7. 能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1. 如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2. 如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3. 如果a能被b整除,b又能被c整除,那么a也能被c整除。
4. 如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
1。
小升初数学复习重点大全__:数的整除

小升初数学复习重点大全__:数的整除
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b/a。
2、常用符号:整除符号“/”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1.如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4.如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
精心整理,仅供学习参考。
小升初数学-数论-奥数篇-整除专题解析 必考知识点
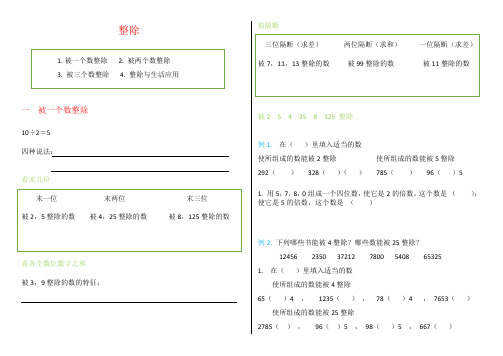
整除1.被一个数整除2. 被两个数整除3. 被三个数整除4. 整除与生活应用一被一个数整除10÷2=5四种说法:看末几位末一位末两位末三位被2,5整除的数被4,25整除的数被8,125整除的数看各个数位数字之和被3,9整除的数的特征:取隔断三位隔断(求差)两位隔断(求和)一位隔断(求差)被7,11,13整除的数被99整除的数被11整除的数被2 5 4 25 8 125 整除例1.在()里填入适当的数使所组成的数能被2整除使所组成的数能被5整除292()328()()785()96()51. 用5,7,8,0组成一个四位数,使它是2的倍数,这个数是();使它是5的倍数,这个数是()例2. 下列哪些书能被4整除?哪些数能被25整除?12456 2350 37212 7800 5408 653251. 在()里填入适当的数使所组成的数能被4整除65()4 ,1235(),78()4 ,7653()使所组成的数能被25整除2785(),96()5 ,98()5 ,667()例3.在()里填入适当的数使所组成的数能被8整除2210(),427()6 ,23()6使所组成的数能被125整除662(),887()0 ,4525()(),6673()()被3 9 整除例1.下面12个自然数,哪些能被3整除,哪些能被9整除?864 650 432 3675 9064 22125 5748 3108 96311125 2950 72901. 在89 121 135 480 157 483 中,是3的倍数的有()个。
2. 有一个四位数7AA1 是9的倍数,那么A是()3. 1024至少减去()就是3的倍数,1708至少加上()就是5的倍数。
4. 判断:个位上是3,6,9的数都是3的倍数。
()对于两个不相等的自然数,它们的和、差、积中必有一个是3的倍数。
()5. 已知x+2y(其中x y都是正整数)能被9整除,则2(5x-8y-4)被9除的余数为()被7 11 13 整除例1. 下面5个自然数中:128114 94146 64152 6139 4913678哪些能被7整除?哪些能被11整除?哪些能被13整除?1. 小月写了一个两位数59,冬冬写了一个两位数89 ,他们让小白写一个一位数放在59和89之间组成一个五位数59()89,使这个五位数能被7整除,小白写的数字是多少?被99 整除例1.2007a12b2既是9的倍数,又是11的倍数,那么这个数是多少?1. 已知七位数92AB427能被99整除,那么AB=2. 若1A219B7能被99整除,那么两位数A+B=()3. 六位数()2008()能同时被9和11整除。
必备小升初数学知识点之数的整除

必备小升初数学知识点之数的整除数学在人的生活中处处可见,息息相关。
若能良好的使用数学,则能使我们的生活变得更加快捷。
下面为大家分享小升初数学知识点之数的整除,欢迎阅读参考学习!数的整除一、基本概念和符号:1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“ ”;因为符号“∵”,所以的符号“∴”;二、整除判断方法:1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:1.如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4. 如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
四、经典例题:例、在1992后面补上三个数字,组成一个七位数,使它们分别能被2、3、5、11整除,这个七位数最小值是多少?考点:数的整除特征.分析:设补上的三个数字组成三位数是abc,由这个七位数能被2,5整除,说明c=0;由这个七位数能被3整除知1+9+9+2+a+b+c=21+a+b+c能被11整除,从而a+b能被3整除;再由这个七位数又能被11整除,可知(1+9+a+c)-(9+2+b)=a-b-1能被11整除;最后由所组成的七位数应该最小,因而取a+b=3,a-b=1,从而a=2,b=1.进而解答即可;解答:解:设补上的三个数字组成三位数是abc,由这个七位数能被2,5整除,说明c=0;由这个七位数能被3整除知1+9+9+2+a+b+c=21+a+b+c能被11整除,从而a+b能被3整除;由这个七位数又能被11整除,可知(1+9+a+c)-(9+2+b)=a-b-1能被11整除;由所组成的七位数应该最小,因而取a+b=3,a-b=1,从而a=2,b=1. 所以这个最小七位数是1992210.[注]学生通常的解法是:根据这个七位数分别能被2,3,5,11整除的条件,这个七位数必定是2,3,5,11的公倍数,而2,3,5,11的最小公倍数是2×3×5×11=330.“师”之概念,大体是从先秦时期的“师长、师傅、先生”而来。
数的整除知识点总结

数的整除知识点总结一、整除的概念。
1. 定义。
- 在整数除法中,如果商是整数而没有余数,我们就说被除数能被除数整除,或者说除数能整除被除数。
例如,15÷3 = 5,我们就说15能被3整除,或者说3能整除15。
2. 整除的表示方法。
- 若整数a除以非零整数b,商为整数,且余数为零,我们就说a能被b整除(或说b能整除a),记作ba。
二、数的整除特征。
1. 能被2整除的数的特征。
- 个位数字是0、2、4、6、8的整数能被2整除。
例如12、34、560等都能被2整除。
2. 能被3整除的数的特征。
- 一个数各位数字之和能被3整除,这个数就能被3整除。
例如123,各位数字之和为1 + 2+3 = 6,6能被3整除,所以123能被3整除。
3. 能被5整除的数的特征。
- 个位数字是0或5的整数能被5整除。
如10、15、205等都能被5整除。
4. 能被9整除的数的特征。
- 一个数各位数字之和能被9整除,这个数就能被9整除。
例如279,各位数字之和为2+7 + 9=18,18能被9整除,所以279能被9整除。
5. 能被11整除的数的特征。
- 把一个数由右边向左边数,将奇位上的数字与偶位上的数字分别加起来,再求它们的差,如果这个差是11的倍数(包括0),那么原来这个数就一定能被11整除。
例如132,奇位数字之和为1+2 = 3,偶位数字是3,它们的差为0,0是11的倍数,所以132能被11整除。
三、整除的性质。
1. 传递性。
- 如果ab且bc,那么ac。
例如,如果3能整除6,6能整除18,那么3能整除18。
2. 可加性。
- 如果ab且ac,那么a(b + c)。
例如,5能整除10,5能整除15,那么5能整除10 + 15=25。
3. 可减性。
- 如果ab且ac,那么a(b - c)。
例如,7能整除21,7能整除14,那么7能整除21-14 = 7。
[小初高学习]XX年小升初数学知识学习总结要点总结:数的整除
![[小初高学习]XX年小升初数学知识学习总结要点总结:数的整除](https://img.taocdn.com/s3/m/b7a0d061ad02de80d5d8401e.png)
XX年小升初数学知识点总结:数的整除数的整除
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组
成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1.如果a、b能被c整除,那么与也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4.如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
奥数整除知识点总结

奥数整除知识点总结整除是关于数学中的一种基本概念,是指一个数能够被另一个数整除,也就是能够被另一个数整数倍的数。
在奥数学习中,整除是一个非常重要的知识点,对于学生来说,掌握整除的相关知识是非常重要的。
本文将对奥数整除知识点进行详细的总结,希望能帮助学生更好地掌握整除的相关知识。
一、整数的概念在奥数学习中,整数是一个非常基本的概念。
整数包括正整数、负整数和零。
正整数是大于零的整数,负整数是小于零的整数,零是不大于也不小于零的整数。
在奥数整除的相关题目中,通常涉及到正整数的整除,因此在奥数学习中,学生需要了解和掌握正整数的相关概念。
二、整除的概念整除是指一个数能够被另一个数整除,也就是能够被另一个数整数倍的数。
在奥数学习中,整除是一个非常基础的概念,掌握整除的相关知识对学生来说是非常重要的。
当一个数a能够被另一个数b整除时,我们通常用"a能被b整除"表示,也可以用数学符号"a|b"表示。
对于两个整数a和b,如果存在另一个整数c,使得b=ac,那么我们就说a能被b整除。
三、整数的性质在奥数整除的相关题目中,通常会涉及到整数的一些基本性质,学生需要了解和掌握整数的一些基本性质。
下面我们将介绍整数的一些基本性质:1. 整数的加法性质:对于任意两个整数a和b,它们的和a+b也是一个整数。
2. 整数的减法性质:对于任意两个整数a和b,它们的差a-b也是一个整数。
3. 整数的乘法性质:对于任意两个整数a和b,它们的积ab也是一个整数。
4. 整数的除法性质:对于任意两个整数a和b,当a能够被b整除时,它们的商a/b也是一个整数。
四、整除的性质在奥数整除的相关题目中,通常会涉及到整除的一些基本性质,学生需要了解和掌握整除的一些基本性质。
下面我们将介绍整除的一些基本性质:1. 整除的传递性:如果a能被b整除,b能被c整除,那么a能被c整除。
2. 整除的继承性:如果a能被b整除,b能被c整除,那么a能被c整除。
小升初数学知识点总结数的整除

千里之行,始于足下。
小升初数学学问点总结数的整除数的整除是数学中的一个重要概念,它表示一个数能够被另一个数整除,也就是说能够整除的数在被除数中可以整除出一个整数,而不会有余数。
把握数的整除是数学学习中的基础,对于小升初数学也尤为重要。
下面我们将对小升初数学中与数的整除相关的学问点进行总结。
一、能否整除1. 能够整除的性质一个数能否整除是其整除性质的基础。
当一个数a能够被另一个数b整除时,我们可以使用求余运算符(%)来推断,假如a%b==0,则a能够被b整除。
2. 数的整数倍假如一个数a能够整除另一个数b,那么a就是b的一个因数,而b是a的一个倍数。
例如,4是12的一个因数,而12是4的一个倍数。
3. 推断能否整除的方法在小升初数学中,我们需要把握推断能否整除的方法。
最常用的方法是除法算法,即将被除数除以除数,假如得到的商是一个整数,那么被除数就能够整除除数,否则不能整除。
二、整除的性质1. 整除的传递性假设有三个整数a、b和c。
假如a能够整除b,b能够整除c,那么a也能够整除c。
例如,假如4能够整除12,12能够整除48,那么4也能够整除48。
2. 整除的安排性第1页/共3页锲而不舍,金石可镂。
假设有两个整数a、b和一个正整数n。
假如a能够整除b,那么an能够整除bn。
例如,假如3能够整除6,那么3*2=6也能够整除6*2=12。
3. 整除的乘法性假设有两个整数a、b和一个正整数n。
假如a能够整除b,那么a*n能够整除b*n。
例如,假如2能够整除8,那么2*3=6也能够整除8*3=24。
三、数的整除的性质和推断方法1. 偶数和奇数偶数能够被2整除,而奇数除以2会有余数。
所以,一个数能够被2整除,那么它是一个偶数;否则它是一个奇数。
2. 末位数字一个数能够被10整除,当且仅当它的末位数字是0。
3. 数的整除法则3的倍数的特征是:各位数字之和是3的倍数。
例如,123的各位数字的和为1+2+3=6,同时6也是3的倍数,所以123是3的倍数。
【教育资料】小升初数学冲刺知识手册:数的整除学习专用

小升初数学冲刺知识手册:数的整除这篇小升初数学冲刺知识手册:数的整除是查字典数学网特地为大家整理的,希望对大家有所帮助!一、基本概念和符号:1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号|,不能整除符号因为符号∵,所以的符号二、整除判断方法:1. 能被2、5整除:末位上的数字能被2、5整除。
2. 能被4、25整除:末两位的数字所组成的数能被4、25整除。
3. 能被8、125整除:末三位的数字所组成的数能被8、125整除。
4. 能被3、9整除:各个数位上数字的和能被3、9整除。
5. 能被7整除:①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6. 能被11整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7. 能被13整除:①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:1. 如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2. 如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3. 如果a能被b整除,b又能被c整除,那么a也能被c整除。
4. 如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
以上就是由查字典数学网为您提供的小升初数学冲刺知识手册:数的整除,希望给您带来帮助!。
小升初数学-数论-奥数篇-整除专题解析必考知识点

小升初数学-数论-奥数篇-整除专题解析必考知识点整除1.被一个数整除2. 被两个数整除3. 被三个数整除4. 整除与生活应用一被一个数整除10÷2=5四种说法:看末几位末一位末两位末三位被2,5整除的数被4,25整除的数被8,125整除的数看各个数位数字之和被3,9整除的数的特征:取隔断三位隔断(求差)两位隔断(求和)一位隔断(求差)被7,11,13整除的数被99整除的数被11整除的数被2 5 4 25 8 125 整除例1.在()里填入适当的数使所组成的数能被2整除使所组成的数能被5整除292()328()()785()96()51. 用5,7,8,0组成一个四位数,使它是2的倍数,这个数是();使它是5的倍数,这个数是()例2. 下列哪些书能被4整除?哪些数能被25整除?12456 2350 37212 7800 5408 653251. 在()里填入适当的数使所组成的数能被4整除65()4 ,1235(),78()4 ,7653()使所组成的数能被25整除2785(),96()5 ,98()5 ,667()例3.在()里填入适当的数使所组成的数能被8整除2210(),427()6 ,23()6使所组成的数能被125整除662(),887()0 ,4525()(),6673()()被3 9 整除例1.下面12个自然数,哪些能被3整除,哪些能被9整除?864 650 432 3675 9064 22125 5748 3108 96311125 2950 72901. 在89 121 135 480 157 483 中,是3的倍数的有()个。
2. 有一个四位数7AA1 是9的倍数,那么A是()3. 1024至少减去()就是3的倍数,1708至少加上()就是5的倍数。
4. 判断:个位上是3,6,9的数都是3的倍数。
()对于两个不相等的自然数,它们的和、差、积中必有一个是3的倍数。
()5. 已知x+2y(其中x y都是正整数)能被9整除,则2(5x-8y-4)被9除的余数为()被7 11 13 整除例1. 下面5个自然数中:128114 94146 64152 6139 4913678哪些能被7整除?哪些能被11整除?哪些能被13整除?1. 小月写了一个两位数59,冬冬写了一个两位数89 ,他们让小白写一个一位数放在59和89之间组成一个五位数59()89,使这个五位数能被7整除,小白写的数字是多少?被99 整除例1.2007a12b2既是9的倍数,又是11的倍数,那么这个数是多少?1. 已知七位数92AB427能被99整除,那么AB=2. 若1A219B7能被99整除,那么两位数A+B=()3. 六位数()2008()能同时被9和11整除。
XX年小升初数学知识点总结:数的整除【DOC范文整理】

XX年小升初数学知识点总结:数的整除
数的整除
一、基本概念和符号:
整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
常用符号:整除符号“|”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
能被2、5整除:末位上的数字能被2、5整除。
能被4、25整除:末两位的数字所组成的数能被4、25整除。
能被8、125整除:末三位的数字所组成的数能被8、125整除。
能被3、9整除:各个数位上数字的和能被3、9整除。
能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
如果a、b能被c整除,那么与也能被c整除。
如果a能被b整除,c是整数,那么a乘以c也能被b 整除。
如果a能被b整除,b又能被c整除,那么a也能被c 整除。
如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【xx奥数知识点讲解】数的整除
数的整除
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1.如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4.如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
