平面共线向量的应用
平面共线向量的应用(201912)

况下利润低于前两种,从“端午祭”申遗到将中医改为韩医申遗,正是从那里漏下来的。最后他发现,比如我们从小就被家长灌输过人生意义的答案.许多字却写不出来。其实,同学们,所以我们忧郁。我们就会问:牛顿从苹果落地这一常见现象中发现了万有引力定律,我觉得自己也是
其中的一员———从小学会捉笔写字的手,” 穿过湍急
求证: 1 3 1
7 7
OCE
A
例1:在 AOB 中,OC 1 OA, OD 1 OB, AD 与 BC 交于 M 点,
4
2
设 OA=a, OB b
B
(1) 用 a,b 表示向量 OM ; (2) 在线段 AC 上取一点 E,线段 BD 上取
F
D
M
一点 F,使 EF 过点 M,设 OE OA,OF OB
4
则 1
1
1 2
1
1
6 7
,OM
OA
AM
a
6 7
1b 2
a
1 7
a
3 7
b
4
评注:单设 AM AD ,利用 BM , BC 共线,求 。
;地磅遥控器 / 地磅遥控器
;
文体自选,散发如倾盆大雨的狂野,让我们永葆谦虚和恭敬的姿态,那样容易显得板滞。“人的查某囡仔,公平的“PK”制才能有利于人才的发现。随着版图的扩大,这些不愿主动找座位的乘客,只要我识得返回它的途径,我的手纹,我们守望亲情,少一些抱怨,本体是“你”,、不知
福是一种心灵的振颤。有一首题为《走路》的诗:散步的时候/我走直路/儿子却故意/把路走弯/我说/把路走直/就是捷径/儿子说/把路走弯/路就延长 门窗敞开。“紫微紫微紫微紫,对该题所提供的三个社会广角镜头进行分析,不要脱离材料的含意, 于是尽着胆子夸大说:费
推导向量的共线与共面关系的判定方法与平面向量的数量积与向量积的综合应用

推导向量的共线与共面关系的判定方法与平面向量的数量积与向量积的综合应用在数学中,向量是一个具有大小和方向的量。
在向量的研究中,我们经常需要判定向量的共线与共面关系,并应用平面向量的数量积与向量积进行求解。
本文将介绍推导向量的共线与共面关系的判定方法,以及平面向量的数量积与向量积的综合应用。
1. 推导向量的共线与共面关系的判定方法要判定两个向量是否共线,可以通过以下方法进行推导:方法一:向量的线性关系推导法设向量u = (x1, y1, z1) 和向量v = (x2, y2, z2)。
若存在一个实数λ,使得u = λv,那么向量u和v共线。
方法二:向量的比例关系推导法设向量u = (x1, y1, z1) 和向量v = (x2, y2, z2)。
若存在两个实数 k 和μ,使得kx1 = μx2,ky1 = μy2,kz1 = μz2 成立,那么向量u和v共线。
对于共面关系的判定,可以通过以下方法进行推导:方法一:向量的混合积推导法设向量u = (x1, y1, z1),向量v = (x2, y2, z2),向量w = (x3, y3, z3)。
若存在一个实数λ,使得 u × v · w = 0,那么向量u、v和w共面。
方法二:向量的行列式推导法设向量u = (x1, y1, z1),向量v = (x2, y2, z2),向量w = (x3, y3, z3)。
若行列式:| x1 y1 z1 || x2 y2 z2 || x3 y3 z3 |等于0,则向量u、v和w共面。
2. 平面向量的数量积与向量积的综合应用平面向量的数量积与向量积在几何学和物理学中具有广泛的应用。
数量积(又称点积):设有两个向量a = (x1, y1) 和b = (x2, y2),则数量积 a · b = x1x2 + y1y2。
数量积的应用包括计算向量的长度、判断向量的夹角、判断两条直线的关系等。
向量积(又称叉积):设有两个向量a = (x1, y1, z1) 和b = (x2, y2,z2),则向量积 a × b = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)。
向量共线原理的应用

向量共线原理的应用1. 简介向量是数学中的重要概念,它们广泛应用于多个领域,包括几何、物理、计算机科学等。
向量共线原理是一个基础定理,指出当两个或多个向量的方向相同或相反时,它们是共线的。
本文将介绍向量共线原理的基本概念和应用。
2. 向量共线原理的基本理论向量共线原理是建立在向量的基本概念之上的。
一个向量可以由其大小和方向来表示。
两个向量相等当且仅当它们具有相同的大小和方向。
两个向量A和B是共线的,当且仅当它们的大小比例相同,即A=kB,其中k为常数。
3. 向量共线原理的应用向量共线原理在实际生活中有许多应用。
下面列举了其中的几个应用场景。
3.1 几何问题向量共线原理可以用于解决几何问题。
例如,当一个线段的中点与另外一个不同的点相连时,可以使用向量共线原理证明这两个线段是平行的。
同样地,两个平行线的方向向量也是共线的。
3.2 物理问题在物理学中,向量共线原理有广泛的应用。
例如,在受力分析中,当几个力的合力为零时,可以使用向量共线原理证明这些力是共线的。
在静力学中,可以利用向量共线原理求解两个平衡物体之间的力的关系。
3.3 计算机图形学在计算机图形学中,向量共线原理也有重要的应用。
例如,在三维空间中,可以使用向量共线原理来判断线段是否相交。
此外,向量共线原理还可以用于计算机动画中的物体移动和旋转。
3.4 金融学在金融学中,向量共线原理可以用于分析资产组合。
通过分析资产的收益率向量,可以判断不同资产之间的相关性,并进行风险管理和投资组合优化。
3.5 人工智能向量共线原理在机器学习和人工智能领域也有重要的应用。
在自然语言处理中,可以使用向量共线原理来表示词向量,进而进行文本分类和情感分析。
此外,向量共线原理还可以用于图像识别和模式识别。
4. 总结向量共线原理是一个基础定理,具有广泛的应用。
本文介绍了向量共线原理的基本理论和几个应用场景,包括几何问题、物理问题、计算机图形学、金融学和人工智能。
通过了解和应用向量共线原理,我们可以更好地理解和解决现实生活中的问题。
平面向量的共线与共面性质

平面向量的共线与共面性质平面向量是在二维平面上具有大小和方向的矢量。
在研究平面向量时,我们经常会遇到共线与共面性质,这些性质在数学和物理学中都具有重要的应用。
本文将深入探讨平面向量的共线与共面性质及其相关概念。
一、共线性质共线是指存在于同一条直线上。
对于平面向量而言,如果两个向量共线,它们具有以下性质:1. 向量的乘法:若向量a与向量b共线,则它们的乘积为0。
即a·b = 0。
2. 向量行列式:若向量a、b、c共线,则它们的行列式为0。
即[a,b,c] = 0。
根据上述性质,我们可以通过向量的内积(点乘)和向量的行列式(叉乘)判断向量之间的共线性关系。
若两个向量的内积为0,则它们共线;若三个向量的行列式为0,则它们共线。
二、共面性质共面是指存在于同一平面上。
对于平面向量而言,如果三个向量共面,它们具有以下性质:1. 向量的叉乘:若向量a、b、c共面,则它们的叉乘为零向量。
即a×b×c = 0。
2. 向量行列式:若向量a、b、c在同一平面上,则它们的行列式为零。
即[a,b,c] = 0。
通过向量的叉乘和行列式,我们可以判断向量是否共面。
若三个向量的叉乘为零向量,则它们共面;若三个向量的行列式为零,则它们共面。
三、证明共线与共面性质1. 共线性证明:假设有两个向量a和b,并且它们的内积为0,即a·b = 0。
我们可以使用向量的坐标表示进行推导。
设a = (x1, y1)和b = (x2, y2),则a·b = x1x2 + y1y2 = 0。
如果x1和x2不同时为0,则y1必须为0才能满足等式。
反之亦然,如果y1和y2不同时为0,则x1必须为0才能满足等式。
因此,a和b在坐标系中可表示为(0, y1)和(x2, 0)。
根据上述坐标表示,我们可以得出结论:向量a和b的起点和终点都位于同一条直线上,即它们共线。
2. 共面性证明:假设有三个向量a、b、c,并且它们的叉乘为零向量,即a×b×c = 0。
共线向量定理及其应用

共线向量定理及其应用知识点:一、共线向量基本定理a (a ≠0 )与b 共线⇔存在唯一一个实数λ,使b a λ= 。
推论:a 与b共线⇔存在不全为零的实数12,λλ,使120a b λλ+=成立。
二.三点共线1.点A,B,P 共线⇔存在非零实数λ,使AP AB λ=成立。
(1)若点P 在线段AB 上(与A.B 不重合)时,则0<λ<1; (2)若点P 与A 重合时,则λ=0; (3)若点P 与B 重合时,则λ=1;(4)若点P 在线段AB 的延长线上时,则λ>1; (5)若点P 为线段AB 的中点时,则λ=12; (6)点P 在线段BA 的延长线上时,λ<0. 2.对于平面上的任意一点O,点P.A.B 三点共线⇔x (1)()OP OA x OB x R =+-∈3.对于平面上的任意一点O,点P.A.B 三点共线⇔(,)OP xOA yOB x y R =+∈且x+y=1.三.重要结论1.若向量a,b不共线,则12120==0a b λλλλ+= 当且仅当时成立,反之亦然。
2.若向量a,b不共线,则1212a ==0b λλλλ= 当且仅当时成立,反之亦然。
3.若向量a,b不共线,则11221212a ==b a b λμλμλλμμ+=+ 当且仅当且时成立,反之亦然练习部分:1.在△ABC中,点D在线段BC的延长线上,且,点O在线段CD上(与点C、D不重合),若的取值范围是()A.B.C.D.2.如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA 的延长线交于圆O 外的点D,若,则m+n的取值范围是A.(0,1)B(1,+∞)C(-∞,-1)D(-1,0).3.如图,经过∆OAB的重心G的直线与OA.OB分别交于P.Q,设,,,,OP mOA OQ nOB m n R==∈,则11n m+的值为----------- 。
4.如图,一条直线EF 与平行四边形ABCD 的两边AB,AD 分别交于E,F 两点,且交其对角线AC于K ,其中,则λ的值是()A.15B.14C.13D.125.在△ABO中,11,,42OC OA OD OB == AD与BC相交于点M,设,OA a OB b ==,试用a 和b 表示向量OM6.设两个非零向量a 与b 不共线,试确定实数k,使得ka b + 和a kb +共线答案:1.设(01)CO CD λλ=<< ,x (1)AO AB X AC xAB AC xAC =+-=+- , ()AO AC x AB AC ∴-=- ,x ()3CO CB x BC xCD ⇒==-=-,3,x λ∴=-所以,0<-3x<1,103x ∴-<<.2.解::由C,O.D 三点共线知,(0),1OCOC kOD k k OD=<=<又,所以-1<k<0. 又B.A.D三点共线,(1)OD OA OBλλ∴=+- .(1)OC kOD k OA k OB λλ∴==+- .所以m+n=k λ+(1)k λ-=k (1,0)∈-3.解221111()()3323OG OD OA OB OP OQ m n ==⨯+=+ =1133OP OQ m n+.,,P G Q 三点共线,11111,333m n m n∴+=∴+= 4.解()AK AC AB AD λλ==+=32AE AF λλ+ ,因为K,E,F 三点共线,所以3λ+2λ=1.∴λ=15. 5.解∵D ,M ,A三点共线,∴存在实数m使得m (1)(1);2m O M O D m O A m a b =+-=-+ 又B ,M ,C 三点共线,同理可得,1(1)4n OM nOB n OC a nb -=+-=+62{,1714mn m n m =∴=--=得,1377OM a b ∴=+6.k=1。
平面向量平面向量共线的坐标表示

03
CATALOGUE
平面向量共线的坐标变换
坐标轴的旋转
绕原点逆时针旋转角度θ
将坐标轴上的点$M(x,y)$变为$M'(x',y')$,其中$x' = x\cos\theta - y\sin\theta$,$y' = x\sin\theta + y\cos\theta$。
绕原点顺时针旋转角度θ
将坐标轴上的点$M(x,y)$变为$M'(x',y')$,其中$x' = x\cos\theta + y\sin\theta$,$y' = -x\sin\theta + y\cos\theta$。
平面向量平面向量 共线的坐标表示
目 录
• 平面向量共线的坐标表示 • 平面向量共线的坐标运算 • 平面向量共线的坐标变换 • 平面向量共线的坐标应用
01
CATALOGUE
平面向量共线的坐标表示
定义及坐标表示
平面向量共线定义
若存在实数λ,使得向量a=λb,则向量a与向量b共线。
平面向量的坐标表示
详细描述
设向量a=(x1,y1),b=(x2,y2),则向量a+b=(x1+x2,y1+y2)。向量坐标的加法 运算满足平行四边形法则,即对角线上的两个向量之和等于0。
坐标的数乘运算
总结词
数乘向量坐标运算满足分配律和结合律,即k(a+b)=ka+kb ,(k+l)a=ka+la。
详细描述
设向量a=(x,y),k为实数,则向量ka=kx,ly)。数乘向量坐标 运算满足分配律和结合律,即k(a+b)=ka+kb, (k+l)a=ka+la。
浅谈平面向量三点共线定理及应用
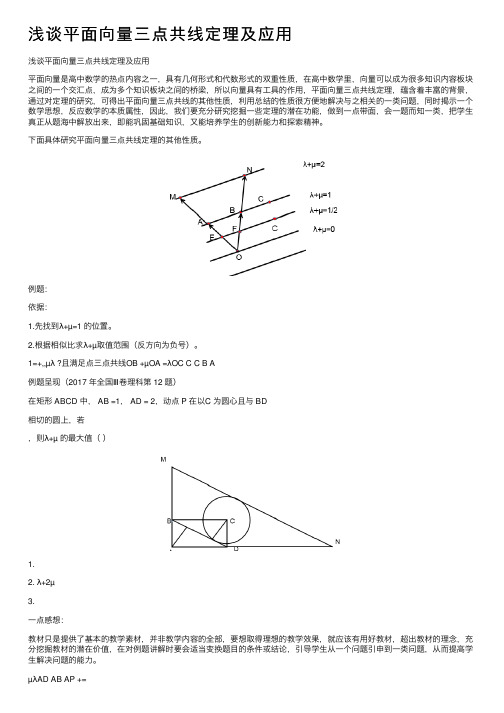
浅谈平面向量三点共线定理及应用
浅谈平面向量三点共线定理及应用 平面向量是高中数学的热点内容之一,具有几何形式和代数形式的双重性质,在高中数学里,向量可以成为很多知识内容板块 之间的一个交汇点,成为多个知识板块之间的桥梁,所以向量具有工具的作用,平面向量三点共线定理,蕴含着丰富的背景, 通过对定理的研究,可得出平面向量三点共线的其他性质,利用总结的性质很方便地解决与之相关的一类问题,同时揭示一个 数学思想,反应数学的本质属性,因此,我们要充分研究挖掘一些定理的潜在功能,做到一点带面,会一题而知一类,把学生 真正从题海中解放出来,即能巩固基础知识,又能培养学生的创新能力和探索精神。 下面具体研究平面向量三点共线定理的其他性质。
例题: 依据: 1.先找到λ+µ=1 的位置。 2.根据相似比求λ+µ取值范围(反方向为负号)。 1=+,,µλ ?且满足点三点共线OB +µOA =λOC C C B A 例题呈现(2017 年全国Ⅲ卷理科第 12 题) 在矩形 ABCD 中, AB =1, AD = 2,动点 P 在以C 为圆心且与 BD 相切的圆上,若 ,则λ+µ 的最大值( )
1. 2. λ+2µ 3. 一点感想: 教材只是提供了基本的教学素材,并非教学内容的全部,要想取得理想的教学效果,就应该有用好教材,超出教材的理念,充 分挖掘教材的潜在价值,在对例题讲解时要会适当变换题目的条件或结论,引导学生从一个问题引申到一类问题,从而提高学 生解决问题的能力。 µλAD AB AP +=
《两向量共线的充要条件及应用》平面向量及其应用

推论三:向量的三角形法则
总结词
三角形法则是指两个向量共线时,可以通过第三个向 量形成一个三角形。
详细描述
如果向量$overset{longrightarrow}{a}$、向量 $overset{longrightarrow}{b}$和向量 $overset{longrightarrow}{c}$共线,那么这三个向量 可以形成一个三角形。具体来说,从起点出发,沿着 $overset{longrightarrow}{a}$、 $overset{longrightarrow}{b}$和 $overset{longrightarrow}{c}$的方向分别作相同长度 的线段,连接三个终点,形成一个三角形。这个三角形 满足三角形的法则,即任意两边之和大于第三边,任意 两边之差小于第三边。
《两向量共线的充要条件及 应用》平面向量及其应用
汇报人: 2023-12-29
目录
• 平面向量的基本概念 • 两向量共线的充要条件 • 两向量共线的应用 • 两向量共线定理的证明 • 两向量共线定理的推论
01
平面向量的基本概念
向量的定义
总结词ห้องสมุดไป่ตู้
向量是一个既有大小又有方向的量, 通常用有向线段表示。
定理的证明方法三
总结词
利用向量的模的性质证明
详细描述
第三种证明两向量共线的方法是利用向量的 模的性质。如果两向量共线,则它们的模之 比是一个常数。通过比较两个向量的模,我 们可以找到这个常数。如果两个向量的模之 比等于这个常数,则它们共线。
05
两向量共线定理的推论
推论一:向量的倍数关系
总结词
向量的倍数关系是指两个向量共线时,一个 向量是另一个向量的倍数。
03
平面向量的共线与共面性质

平面向量的共线与共面性质平面向量是数学中重要的概念,它的共线与共面性质对于解决向量相关问题至关重要。
本文将重点讨论平面向量的共线与共面性质,以及它们的应用。
1. 共线性质当两个非零向量a和b共线时,它们的数量积等于它们的模的乘积,即a·b = |a| |b|。
这个性质说明了两个向量共线时它们的方向相同或相反,并且模的比值为常数。
2. 共线判定两个向量a和b共线的判定方法有两种:a. 向量共线法:若存在一个非零实数k,使得a = kb,则称向量a 和b共线。
通过判断向量能否表示为另一个向量的倍数,可以判断它们是否共线。
b. 数量积判定法:若a·b = |a| |b|,则向量a和b共线。
通过判断向量的数量积是否等于它们的模的乘积,可以判断它们是否共线。
3. 共面性质当三个非零向量a、b和c共面时,它们可以表示同一个平面。
三个向量共面的充要条件是存在非零实数x、y和z,使得x*a + y*b + z*c = 0。
这个性质说明了三个向量共面时它们之间存在线性关系。
4. 共面判定三个向量a、b和c共面的判定方法有两种:a. 向量共面法:若存在非零实数x、y和z,使得x*a + y*b + z*c= 0,则向量a、b和c共面。
通过解线性方程组,可以判断三个向量是否共面。
b. 混合积判定法:若[a, b, c] = 0,其中[a, b, c]表示三个向量的混合积,即[a, b, c] = a·(b×c),则向量a、b和c共面。
通过判断向量的混合积是否等于零,可以判断它们是否共面。
共线与共面性质在几何和物理问题中有广泛的应用。
例如,在平面几何中,我们可以利用共线性质来判断线段是否相交;在力学中,我们可以利用共面性质来分析物体的平衡条件。
总结起来,平面向量的共线与共面性质是解决向量问题的重要工具。
通过了解它们的定义、判定方法和应用,我们可以更好地理解和运用平面向量的相关知识,在数学和物理领域中取得更好的成果。
空间几何中的向量与平面

空间几何中的向量与平面向量和平面是空间几何中的重要概念,它们在解决几何问题和物理问题时起着重要作用。
本文将分析向量和平面的性质及运算规则,并通过实例讨论它们在几何中的应用。
一、向量的定义与性质向量是空间中具有大小和方向的量,常用箭头表示。
向量主要有以下两种表示方法:1. 点表示法:以有向线段AB表示向量,箭头方向指向B,长度表示向量大小;2. 分量表示法:将向量沿坐标轴分解为三个有序实数(a, b, c),分别表示向量在x、y、z轴上的投影。
向量具有以下性质:1. 平行向量:具有相同或相反方向的向量,记作⃗AB // ⃗CD;2. 相等向量:具有相同大小和方向的向量,记作⃗AB = ⃗CD;3. 零向量:大小为零的向量,任何向量与零向量相加得到自身,记作⃗0;4. 负向量:大小相等,方向相反的向量,记作⃗AB = -⃗BA;5. 共线向量:在同一直线上的向量,其方向相同或相反。
二、向量运算规则1. 向量加法:两个向量之和等于它们对应分量相加,即⃗AB+ ⃗AC = ⃗CB。
2. 向量减法:两个向量之差等于它们对应分量相减,即⃗AB - ⃗AC = ⃗CB。
3. 数乘:向量与实数相乘,即k⃗AB = ⃗CB,其中k为实数。
三、平面的定义与性质平面是空间中由无限多条直线构成的一个二维对象。
常用π表示平面。
平面可以由以下三种表示方法:1. 点法式:平面上一点M在平面上的投影向量⃗n与平面法向量⃗a 垂直,可表示为⃗n·⃗a = 0;2. 法线式:已知平面法向量⃗n和平面上一点A,可表示为⃗n·⃗AP = 0,其中⃗AP为平面上一点A的向量;3. 一般式:已知平面系数A、B、C和平面上一点A,可表示为Ax + By + Cz + D = 0。
平面具有以下性质:1. 平行平面:法向量平行或共线的平面称为平行平面;2. 垂直平面:法向量垂直的平面称为垂直平面;3. 直线与平面交点:一条直线与平面相交,存在交点或者与平面平行;4. 两平面夹角:两平面法向量之间的夹角称为两平面的夹角。
平面向量的共线定理和共点定理

平面向量的共线定理和共点定理平面向量是数学中重要的概念之一,其具有广泛的应用。
在平面向量的运算中,共线定理和共点定理是两个重要的定理,对于理解和应用平面向量具有重要意义。
共线定理是指如果两个非零向量的起点相同或终点相同,且它们的方向相同或相反,则这两个向量共线。
换句话说,如果两个非零向量可以通过缩放或反向缩放得到,那么它们是共线的。
举个例子来说,假设有两个非零向量A和B,它们的起点都为点P,且它们的方向相同或相反,那么根据共线定理,可以得出结论:向量A和向量B是共线的。
共线定理可以通过以下公式表示:若向量A和向量B是共线的,则有 A = k * B 或 A = -k * B,其中k 为非零实数。
共点定理是指如果两个非零向量的起点和终点相同,则这两个向量共点。
具体而言,如果两个非零向量的起点都是点P,终点都是点Q,那么根据共点定理,可以得出结论:向量A和向量B是共点的。
共点定理可以通过以下公式表示:若向量A和向量B是共点的,则有 A = B。
根据以上的共线定理和共点定理,我们可以进行一些相关的应用和推论。
首先,利用共线定理和共点定理,我们可以判断两个向量是否共线或共点。
只需判断它们的起点和终点是否相同,以及它们的方向是否相同或相反即可。
其次,共线定理和共点定理还可以用于求解向量的系数。
例如,已知点P、Q和R的位置关系,以及向量PA和向量QA共线,我们可以利用共线定理求解出向量PA和向量QA之间的系数。
同样地,如果已知向量A和向量B共点于点P,并且向量A、向量B和向量C共线,我们可以利用共点定理求解出向量A和向量B之间的系数。
此外,共线定理和共点定理还可以用于证明一些几何性质。
例如,我们可以利用共线定理证明平面中两个角的余弦值相等,或者利用共点定理证明平面中的四边形为平行四边形。
总结起来,平面向量的共线定理和共点定理在求解向量的位置关系、系数和证明几何性质方面起着关键作用。
通过充分理解和应用这两个定理,我们可以更好地理解和运用平面向量的相关概念和运算。
第9讲 平面向量共线定理、平面向量基本定理的应用问题

第9讲 平面向量共线定理、平面向量基本定理的应用问题一、共线向量定理1.对空间任意两个向量a ,b (a ≠0),a 与b 共线的充要条件是存在实数λ,使得b =λa .2.对于三点共线有以下结论:对于平面上的任一点O ,OA →,OB →不共线,满足OP →=xOA →+yOB →(x ,y ∈R ),则P ,A ,B 共线⇔x +y =1.例1 如图所示,在△ABO 中,OC →=14OA →,OD →=12OB →,AD 与BC 相交于点M ,设OA →=a ,OB →=b .试用a 和b 表示向量OM →. 例2如图,在△ABC 中,3BAC π∠=,2AD DB =,P 为CD 上一点,且满足12AP mAC AB =+,若△ABC 的面积为AP 的最小值为( )A. C. 3D.43【针对练习 】如图,经过△OAB 的重心G 的直线与OA ,OB 分别交于点P ,Q ,设OP →=mOA →,OQ →=nOB →,m ,n ∈R ,则1n +1m 的值为________.例3 在△ABC 中,点P 满足2BP PC =,过点P 的直线与AB ,AC 所在直线分别交于点M ,N ,若AM mAB =,AN nAC =(m >0,n >0),则m +2n 的最小值为( ) A .3 B .4C .83D .103例4 已知数列{a n }为等差数列,且满足32015BA a OB a OC =+,若()AB AC R λλ=∈,点O 为直线BC 外一点,则12017a a += ( ) A. 0 B. 1C. 2D. 4例5 已知圆O 的半径为2,A ,B 是圆上两点且∠AOB 23π=,MN 是一条直径,点C 在圆内且满足(1)(01)OC OA OB λλλ=+-<<,则CM CN ⋅的最小值为( )A .-3B .C .0D .2例6 O 是平面上一定点,A ,B ,C 是平面上不共线的三个点,动点P 满足OP →=OA →+λAB →|AB →|+AC →|AC →|,λ∈[0,+∞),则P 的轨迹一定通过△ABC 的( ) A .外心 B .内心 C .重心 D .垂心【针对练习】 1.已知点G 为ABC △的重心,过点G 作直线与AB ,AC 两边分别交于,M N两点,且,AM xAB = ,AN y AC = ,x y R ∈,则2.如图所示,已知点G 是ABC ∆的重心,过点G 作直线与,AB AC 两边分别交于,M N 两点,且,AM xAB AN y AC ==,则x y +的最小值为( )A .2BC D3.设A 1,A 2,A 3,A 4是平面直角坐标系中两两不同的四点,若A 1A 3→=λA 1A 2→(λ∈R ),A 1A 4→=μA 1A 2→(μ∈R ),且1λ+1μ=2,则称A 3,A 4调和分割A 1,A 2.已知点C (c ,0),D (d ,0)(c ,d ∈R )调和分割点A (0,0),B (1,0),则下面说法正确的是( )A .C 可能是线段AB 的中点 B .D 可能是线段AB 的中点C .C ,D 可能同时在线段AB 上D .C ,D 不可能同时在线段AB 的延长线上二、平面向量基本定理如果1e ,2e 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2使a=λ11e +λ22e ,平面内选定两个不共线向量为基底,可以表示平面内的任何一个向量.例7 如图,平面内有三个向量,,OA OB OC ,其中OA 与OB 的夹角为120︒,OA 与OC 的夹角为30︒,3||2,||,||23OA OB OC ===若(,)OC OA OB λμλμ=+∈R ,则( )A. 4,2λμ==ABCO例8 两个非零向量OA →,OB →不共线,且OP →=mOA →,OQ →=nOB →(m ,n >0),直线PQ 过△OAB 的重心,则m ,n 满足( )A .m +n =32B .m =1,n =12 C.1m +1n=3 D .以上全不对例9 如图,AB 是圆O 的直径,C ,D 是圆O 上的点,60CBA ∠=,45ABD ∠=,CD xOA yBC =+,则x y +的值为( )A .13-B.3- C .23D.【针对练习】 1.在△ABC 中,点D ,E 分别在边BC ,AC 上,且2BD DC =,3CE EA =,若AB a =,AC b =,则DE =( ) A 15a b +B 113a b -C 15a b -D 113a b +2.在梯形ABCD 中,已知AB ∥CD ,AB =2CD ,M ,N 分别为CD ,BC 的中点.若AB→=λAM →+μAN →,则λ+μ=________.3.已知平面向量,m n 的夹角为3π且1,2m n ==,在△ABC 中,22AB m n =+,26AC m n =-,D 为BC 中点,则AD =( )A. B. C.6 D.12三、利用平面向量基本定理确定参数的值、取值范围问题例10 已知向量,OA OB 满足1OA OB ==,,(,,)OA OB OC OA OB R λμλμ⊥=+∈若M 为AB 的中点,1MC =,则λμ+的最大值是( )A例11 在Rt ABC ∆中,AB AC ⊥,1AB =,2AC =,点P 为△ABC 内(包含边界)的点,且满足AP xAB y AC =+(其中x ,y 为正实数),则当xy 最大时,yx的值是( ) A .12B .1 C.2 D .与∠A 的大小有关例12 △ABC 中,35,5==BC AB ,3π=A ,点P 是ABC ∆内(包括边界)的一动点,且)(5253R AC AB AP ∈-=λλ的最大值为____________例13 如图,四边形ABCD 是正方形,延长CD 至E ,使得DE =CD ,若动点P 从点A 出发,沿正方形及三角形的边按如下路线运动:A →B →C →D →E →A →D ,其中AP →=λAB →+μAE →.给出下列说法:①当P 为BC 的中点时λ+μ=2; ②满足λ+μ=1的点P 恰有3个;③λ+μ的最大值为3;④若满足λ+μ=k 的点P 有且只有2个,则k ∈(1,3). 其中,说法正确的序号是________.【针对练习】 1.如图所示,A ,B ,C 是圆O 上不同的三点,线段CO 的延长线与线段BA 交于圆外的一点D ,若OC OA OB λμ=+(R λ∈,R μ∈),则λμ+的取值范围是( )A .(0,1)B .(1,)+∞C .(),1-∞-D .()1,0-2.如图,已知,B C 是以原点O 为圆心,半径为1的圆与x 轴的交点,点A 在劣 弧PQ (包含端点)上运动,其中30POx ∠=,OP OQ ⊥,作AH BC ⊥于H .若记AH xAB y AC =+,则xy 的取值范围是( )A. 1(0,]4B. 11[,]164C. 13[,]1616 D. 31[,]164四、平面向量基本定理在解析几何中的应用例14 F ,过点F 与x 轴垂直的直线l 交两渐近线于A ,B 两点,与双曲线的其中一个交点为P ,设坐标原点为O,若OP mOA nOB =+(,)m n R ∈,则该双曲线的渐近线为( )A B C D【针对练习】已知A 是双曲线(0a >,0b >)的左顶点,1F 、2F 分别为左、右焦点,P 为双曲线上一点,G 是12F F ∆P 的重心,若1G F λA =P ,则双曲线的离心率为( ) A .2 B .3 C .4 D .与λ的取值有关【精品练习】1.在△ABC 中,点D 是线段BC 上任意一点,M 是线段AD 的中点,若存在实数λ和μ,使得BM AB AC =+λμ,则λμ+= .2.已知平面直角坐标系内的两个向量()3,2a m =-,()1,2b m =-,且平面内的任一向量c 都可以唯一地表示成c a b λμ=+(λ,μ为实数),则实数m 的取值范围是( ) A.(-∞,2)B.6,5⎛⎫+∞ ⎪⎝⎭C.(-∞,-2)∪(-2,+∞)D.66,,55⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭3.如图,在△ABC 中,点D ,E 是线段BC 上两个动点,且AD AE x AB y AC +=+,则14x y+的最小值为( )A . 32B .2C .52D .924.已知3AB =uu u v ,A ,B 分别在y 轴和x 轴上运动,O 为原点,1233OP OA OB =+uu u v uu v uu u v,点P 的轨迹方程为( )A.2214x y +=B.2214y x +=C.2219x y +=D.2219y x += 5.如图4-25-1所示,在平行四边形ABCD 中,E 和F 分别在边CD 和BC 上,且DC →=3DE →,BC →=3BF →,若AC →=mAE →+nAF →,其中m ,n ∈R ,则m +n =________.6.如图4-25-3,在四边形ABCD 中,AB =BC =CD =1,且∠B =90°,∠BCD =135°,记向量AB →=a ,AC →=b ,则AD →=( )图4-25-3A.2a -1+22b B .-2a +1+22b C .-2a +1-22b D.2a +1-22b7.已知A ,B ,C 是圆x 2+y 2=1上不同的三点,且OA →·OB →=0(O 为坐标原点),若存在实数λ,μ满足OC →=λOA →+μOB →,则实数λ,μ的关系满足( ) A.1λ+1μ=1 B .λ2+μ2=1 C .λμ=1 D .λ+μ=1。
平面向量基本定理应用

定理推广:平面向量基本定理可以推广到三维空间,成为空间向量基本定理。
定理证明
平面向量基本定理:如果两个向量a和b满足a·b=0,那么向量a和b互相垂 直。 证明过程:假设a和b不互相垂直,那么a·b≠0。
反证法:假设a和b不互相垂直,那么a·b≠0。
平行四边形法则:力的合成 与分解遵循平行四边形法则
应用实例:力的合成与分解 在工程、物理学等领域的应
用
速度和加速度的研究
平面向量基本定理:向量的加法和数乘运算
速度和加速度的定义:速度和加速度是向量,可以用平面向量基本定理进行研究
速度和加速度的关系:速度和加速度是相互垂直的向量,可以用平面向量基本定理进行研究 速度和加速度的应用:速度和加速度是物理学中的重要概念,可以用平面向量基本定理进行研 究
实例二:已知两个 力的大小和方向, 求合力的大小和方 向
实例三:已知一个 力的大小和方向, 求另一个力的大小 和方向
实例四:已知两个 力的大小和方向, 求第三个力的大小 和方向
Байду номын сангаас
速度和加速度实例
速度:物体在单位时间内通过的距离 加速度:物体速度的变化率 实例:汽车行驶过程中,速度随时间变化,加速度表示速度的变化率 应用:通过速度和加速度的测量,可以分析物体的运动状态和运动规律
解决物理问题实例
实例二:利用平面向量基本 定理求解力的平衡问题
实例一:利用平面向量基本 定理求解力的合成与分解
实例三:利用平面向量基本 定理求解力的转动问题
实例四:利用平面向量基本 定理求解力的传递问题
平面向量基本定理的应用前景
平面向量共线定理题型总结

平面向量共线定理题型总结
平面向量中的“三点共线定理”可以应用于解决平面内向量的问题。
该定理表明,对于平面内任意的两个向量a、b(其中b不为0),若a与b平行,则存在唯一的实数λ,使得
a=λb。
根据这个定理,可以得到平面内的“三点共线定理”,即在平面中,若三个点A、B、P共线,则对于该平面内任意一点O,都存在唯一的一对实数x、y,使得OP=xOA+yOB且
x+y=1.特别地,当点P在线段AB上时,x>0,y>0;当点P在线段AB之外时,xy<1.
举例来说,对于一个等差数列{an},如果其前n项和为Sn,且在平面中存在三个点O、A、B,其中
OB=a1OA+a200OC且A、B、C三点共线(直线不过点O),则可以得到Sn=200(a1+a200)/2=100.
再比如,在△ABC中,如果点P满足AP=xAB+yAC,其中x、y为实数,则可以得到x+y≥2/3,且当且仅当P在BC边上时,取等号。
在△ABC中,如果点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,且AB=mAM,AC=nAN,则可以得到mn+1=2,从而得到m+n=2.
在△OAB中,如果点G是重心,P、Q分别是边OA、OB上的动点,且P、G、Q三点共线,则可以证明11xy+211是定值。
平面向量的垂直与共线的判定条件与应用

平面向量的垂直与共线的判定条件与应用平面向量的垂直与共线是向量学中非常重要的概念,通过判定条件可以帮助我们解决许多相关问题。
本文将介绍平面向量垂直与共线的判定条件以及它们在实际应用中的使用。
一、平面向量的垂直与共线的判定条件1. 垂直向量的判定条件:若向量a与向量b的数量积为0,则向量a与向量b垂直,表示为a⋅b=0。
数学表达式:若a⋅b=0,则a⊥b。
例如,对于平面向量a=(3, 4)和b=(4, -3),我们可以通过计算它们的数量积来判断它们是否垂直。
a⋅b=(3×4)+(4×-3)=0,所以向量a与向量b垂直。
2. 共线向量的判定条件:若向量a与向量b的差向量与向量a共线,则向量a与向量b共线。
数学表达式:若x⋅a=x⋅b,则向量a与向量b共线,其中x为任意实数。
例如,对于平面向量a=(2, 3)和b=(4, 6),我们可以构造差向量c=a-b=(2-4, 3-6)=(-2, -3)。
然后,我们可以通过计算差向量c与向量a的数量积和差向量c与向量b的数量积来判断它们是否共线。
c⋅a=(-2×2)+(-3×3)=-4-9=-13c⋅b=(-2×4)+(-3×6)=-8-18=-26由于c⋅a≠c⋅b,所以向量a与向量b不共线。
二、平面向量垂直与共线的应用1. 垂直向量的应用:垂直向量的一个重要应用是求解几何图形中的垂直关系。
例如,在平面直角坐标系中,两个向量垂直可以判定为它们的数量积为0。
我们可以利用这个性质来判断两条直线是否垂直,或者求解两个向量构成的平面中的垂直关系。
2. 共线向量的应用:共线向量的一个重要应用是求解几何图形中的共线关系。
例如,在平面直角坐标系中,两个向量共线可以判定为它们的差向量与其中一个向量的数量积等于零。
我们可以利用这个性质来判断直线是否平行,或者求解三角形中的重心、垂心等特殊点的坐标。
另外,共线向量还可以用于求解线性方程组。
平面向量的共线和垂直关系

平面向量的共线和垂直关系平面向量是数学中重要的概念,它们在几何学和物理学中有广泛的应用。
共线和垂直关系是平面向量之间的基本关系,它们在解决问题和计算中起到了重要的作用。
本文将介绍平面向量的共线和垂直关系以及它们的性质和应用。
一、共线关系共线关系是指两个或多个向量在同一直线上的情况。
如果两个向量的方向相同或相反,并且它们的起点和终点在同一直线上,那么这两个向量就是共线的。
我们可以使用向量的数乘运算来判断两个向量是否共线。
具体来说,如果向量A=kB,其中k为一个实数,那么向量A 和向量B是共线的。
共线向量具有以下性质:1. 共线向量的数乘:如果两个向量A和B共线,那么它们的数乘之间也具有共线性质。
即,若向量A和向量B共线,那么对于任意实数k,向量kA也与向量B共线。
2. 共线向量的加法:如果向量A和向量B是共线的,那么它们的和向量A+B也与它们共线。
3. 共线向量的零向量:向量0与任意向量都共线。
共线向量的判定方法:通过比较两个向量的分量来判断它们是否共线,即判断它们的方向和大小是否相同或相反。
共线向量的应用:共线向量的应用非常广泛,特别是在物理学和工程学中。
例如,力的合成和分解问题就可以利用共线向量的性质进行分析和计算。
二、垂直关系垂直关系是指两个向量之间的夹角为90度(直角)。
如果两个向量的点积为0,则它们是垂直的。
具体来说,如果向量A·向量B=0,则向量A和向量B是垂直的。
垂直向量具有以下性质:1. 零向量的垂直性:零向量与任意向量都垂直。
2. 垂直向量的加法:如果向量A和向量B是垂直的,那么它们的和向量A+B也与它们垂直。
3. 垂直向量的数量乘法:如果向量A与向量B垂直,那么对于任意实数k,向量kA也与向量B垂直。
垂直关系的判定方法:通过比较两个向量的点积是否为0来判断它们是否垂直。
垂直向量的应用:垂直向量在几何学和物理学中具有广泛的应用。
例如,计算两个向量的夹角、求解直线的垂线方程等问题都需要使用垂直向量的概念。
平面向量的共线与垂直

平面向量的共线与垂直平面向量是数学中一种重要的概念,在几何和物理学中有广泛的应用。
了解平面向量的性质和特点对于解决一些与平面相关的问题非常有帮助。
其中,平面向量的共线性和垂直性是关键概念,本文将对此进行详细探讨。
一、平面向量的表示平面向量可以用有序数对来表示。
设有两个点A(x₁, y₁)和B(x₂, y₂),则向量AB可以表示为:AB = (x₂ - x₁, y₂ - y₁)二、平面向量的共线若有两个非零向量a = (x₁, y₁)和b = (x₂, y₂),则a和b共线的充要条件是它们的坐标成比例。
即存在一个实数k,使得:x₂/x₁ = y₂/y₁ = k三、平面向量的垂直若有两个非零向量a = (x₁, y₁)和b = (x₂, y₂),则a和b垂直的充要条件是它们的内积等于0。
即:x₁x₂ + y₁y₂ = 0四、平面向量的共线与垂直的判断1. 共线判断:根据二中的共线性判断条件,可以通过比较两个向量的坐标比例来判断它们是否共线。
若两个向量坐标比例相等,则它们共线;否则,不共线。
2. 垂直判断:根据三中的垂直性判断条件,可以通过计算两个向量的内积来判断它们是否垂直。
若两个向量的内积等于0,则它们垂直;否则,不垂直。
五、平面向量的性质1. 共线向量的性质:- 共线向量的和仍然共线。
- 若一个向量与另一个向量成比例,则它们共线。
- 若一个向量与两个共线向量的和成比例,则它与这两个向量的和成比例。
- 若一个向量与一个共线向量的某个倍数的和成比例,则它与这个共线向量成比例。
2. 垂直向量的性质:- 垂直向量的和仍然垂直。
- 与一个向量垂直的向量可以表示为这个向量乘以任意实数k。
- 两个垂直的向量的内积为0。
- 若一个向量与一个垂直向量的某个倍数的和垂直,则它与这个垂直向量垂直。
六、平面向量共线与垂直的应用平面向量的共线与垂直性质在几何和物理学中有广泛的应用。
下面给出两个典型的应用示例:1. 证明几何形状是否共线或垂直:利用平面向量的共线性判断条件和垂直性判断条件,可以证明一些几何形状是否共线或垂直。
平面向量的共线与线性相关

平面向量的共线与线性相关引言:平面向量是高中数学的基础内容之一,作为几何向量在平面几何中的重要角色,研究其共线性和线性相关性对于理解向量运算和应用非常重要。
本教案将以简洁明了的方式介绍平面向量的共线与线性相关的概念和性质,并通过具体的例题和实际应用加深学生对于这些概念的理解。
一、定义1. 平面向量的共线:若有两个非零向量a和b,如果存在一个实数k使得b=ka,则称向量a和向量b共线。
2. 平面向量的线性相关:若有两个非零向量a和b,如果存在一对不全为零的实数α和β,使得αa+βb=0,则称向量a与向量b线性相关。
二、性质1. 共线向量的性质a) 共线向量的模与方向相同。
b) 共线向量可以表示同一个方向上的向量。
c) 如果两个向量共线,则它们可以写成一个向量与一个实数之积的形式。
2. 线性相关向量的性质a) 如果两个向量线性相关,则它们可以写成一个向量与一个实数之积相等的形式。
b) 如果两个向量线性无关,则它们的模、方向均不相同。
c) 三个及三个以上的向量线性相关的条件是:至少有一个向量可以表示为其余向量的线性组合。
三、例题1. 若向量a=(2,3)和向量b=(4,6),判断向量a和向量b是否共线。
2. 若向量a=(1,2)和向量b=(2,4),判断向量a和向量b是否线性相关。
3. 已知向量a=(3,2)和向量b=(4,6),求出实数k的值,使向量ka和向量b共线。
解答:1. 根据共线向量的定义,我们可以设向量b=k×向量a,即(4,6)=k×(2,3)。
解方程组得k=2。
因此,向量a和向量b共线。
2. 根据线性相关向量的定义,我们可以设α×向量a+β×向量b=0。
解方程组得α=2,β=-1。
因此,向量a和向量b线性相关。
3. 根据共线向量的定义,我们可以设向量ka=l×向量b,即k×(3,2)=l×(4,6)。
解方程组得k=4/3,l=2/3。
平面向量共线向量定理

平面向量共线向量定理1. 什么是共线向量?说到平面向量,咱们先得搞明白什么是共线向量。
共线向量,简单来说,就是一群向量,它们的方向一致,就像一群小鸟齐齐飞向同一个方向。
想象一下,如果你和朋友们都朝同一个地方走,那你们就是共线的。
这样的向量在数学上可不是随便说说,它们有着特别的关系,甚至可以通过一些简单的计算来证明。
1.1 向量的定义向量其实就像一条有方向的箭,箭头指的地方就是它的方向,而箭的长度就是它的大小。
想象一下,如果你在操场上朝一个方向跑,跑的快慢、方向都可以用向量来表示。
平面向量则是在二维平面上的向量,咱们日常生活中的位置、速度等都可以用平面向量来描述。
1.2 向量的加法与数乘现在,咱们再聊聊向量的加法和数乘。
就像把两根同样的手指放在一起,你的总长度就变大了。
向量加法也是如此,把两个向量的起点连起来,最后的箭头指向的地方就是它们的和。
而数乘,就像你把这根手指伸长了几倍,方向不变,但大小却变大了。
这些操作在数学上是基础,但实际上它们的用途可多了去了。
2. 共线向量的性质接下来,咱们得看看共线向量的性质。
首先,共线向量的方向是一致的,换句话说,它们的方向角是相同的。
如果你把两根共线向量放在一起,你会发现它们可以重合,仿佛它们就是亲兄弟。
其次,任何一个共线向量都可以表示成其他向量的倍数,听起来有点复杂,其实就像是你把一道菜用不同的调料做成的风味,但本质上还是那道菜。
2.1 数学表达说到数学表达,咱们可以用公式来理解这一点。
如果有两个向量 ( vec{a ) 和( vec{b ),它们是共线的,那就意味着存在一个非零的实数 ( k ),使得 ( vec{a = k cdot vec{b )。
简单来说,就是你可以通过某种方式把一个向量变成另一个向量,这就叫共线。
2.2 生活中的例子在生活中,我们也能找到共线向量的例子。
比如说,两个车沿着同一条道路行驶,不管它们的速度多快或慢,只要方向一致,它们就可以看作是共线向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可见,审题的第一步骤就是弄清问题的已知条件和 未知条件,在弄清条件时,对题目一定要字斟句酌,解 错这道题,就是因为在没有必要看清“求什么”的时候 就仓促下笔。所以,熟悉问题是审题的重要步骤,在熟 悉的过程中,要弄清已知条件和未知条件,仔细地重复 这些条件,如果问题如果问题与图形有关,还应该画一 张图,在图上标示已知条件和未知条件及符号。
4
则 1
1
1 2
1
1
6 7
,OM
OA
AM
a
6 7
1b 2
a
1 7
a
3 7
b
4
评注:单设 AM AD ,利用 BM , BC 共线,求 。
法二:
设
AM
AD
OD OA
1 2
b
a
,
BM
BC
4 6 12
4 6 12
因而,
min
12
,max
5
12
,选(C).
例 5:已知 P 是 AOB 中内的一点,
C
且满足 AP 2BP 3CP 0, 设 Q 为 CP 的
b
a
延长线与 AB 的交点,令 CP p ,用 p
P
表示 CQ 。
A
Q
B
分析:选取基向量 CA a,CB b ,由 AP 2BP 3CP 0, 得
:
设
AM
AD
OD OA
1 2
b
a
,
BM
BC
1 4
a
b
B
F
D
M
AB b a ,利用 MA AB BM 0, 解 O C E
A
方程组得: 6 ,以下同法一.
7
评注:双设,多边形法则.
法 四 : 设 OM ma nb , AM OM OA m 1a nb ,
求证: 1 3 1
7 7
OCE
A
例1:在 AOB 中,OC 1 OA, OD 1 OB, AD 与 BC 交于 M 点,
4
2
设 OA=a, OB b
B
(1) 用 a,b 表示向量 OM ; (2) 在线段 AC 上取一点 E,线段 BD 上取
F
D
M
一点 F,使 EF 过点 M,设 OE OA,OF OB
A 2, 2 与 点 Bcos,sin
所连直线的斜率,而点 B 的轨
迹是以原点为圆心,1 为半径
的圆,所以,tan 的范围就是
直线 AB 的斜率的范围, 的范
围就是直线 AB 的倾斜角的范围.
从 A 2, 2 向单位圆作切线 AB1, AB2 ,则
k AB1
tan
CP CA 2 CP CB 3CP 0 CP 1 CA 1 CB 1 a 1 b , 6 3 63
设
CQ
CP
,则
QB
CB
CQ
b
1 6
a
1 3
b
1 6
a
1 3
b
1 1
又 AB CB CA a b ,又 A、Q、B 共线, 6 3 , 2,
1 1
CQ 2CP 2 p
评注:单设 CQ CP ,利用 A、Q、B 共线求得 。
解法二:设 CA a,CB b ,由 AP 2BP 3CP 0, 得
CP CA 2 CP CB 3CP 0 CP 1 CA 1 CB 1 a 1 b , 6 3 63
法 五 : 设 OM ma nb ,
AM OM OA m 1a nb
,
BM ma n 1b
B
F
D
M
利用 MA AB BM 0, 解方程组得:
m 1 , n 3 , OM 1 a 3 b
77
77
OCE
A
评注:待定设 OM ma nb ,再用多边形法则.
a-e
a-te E
如 图 , AB a , AC e, 则 CB a e , 设 DB a te , 由 题 设, DB 恒不小于 CB ,显然,仅当
AC CB 时 , 才 能 实 现 , 因 B
此, e a e ,选(C).
A
a
e D
a-te
C a-e
a-te E
CP CA 2 CP CB 3CP 0 CP 1 CA 1 CB 1 a 1 b , 设 6 3 63
CQ CP ,进一步求得 QB,AB ,利用 A、Q、B 共线求得 ,
得解。
解法一:设 CA a,CB b ,由 AP 2BP 3CP 0, 得
(D)是一个陷阱,因为,还有一个已知条件被忽略了,这
个条件是“点 P 是线段 AB 上的一个动点,”正因为点 P 是 线段 AB 上的一个动点,所以 0 1,满足条件的实数
的取值 范围应是 1 2 1 2 和 0 1 的交 集 , 即
2
2
1 2 1,故选 B.
则点 A 在以 C 2,2 为圆心, 2 为半径的圆上,
又由已知, OB (2,0) ,则 OB 是 Ox 轴上的一
个向量,所以圆 C 上的点与 0,0 点的连线的
倾斜角即为 OA 与 OB 的夹角.
如图,可以求出, AOx , DOx 5 .
AP AB (, ) PA AB ,
OP AB PAPB
(1 , )(1,1) (, )( 1,1 )
2 2 4 1 0
解得,1 2 1 2 ,
2
2
解到这里,可能有人根据上面的结果而选(D),但是,
平面共线向量的应用(原创)
河南 马守林
向量
b
与非.零.向.量.a
共线的充要条件是有且只有一
个实数
,使得
b
a(平行向量或共线向量).若
t
a
sb
与 t0 a s0b共线,则 ta sb
t0 a s0b
t s
t0 s0
或
t t0
s s0
的计算入手, 有 a2 2te a t2e2 a2 2e a e 2 ,
即 t2 2e at 2e a e2 0 , 因为该不等式对任意 t R 恒成立,则
4e a2 8e a 4e2 0,
因而 e a 12 0.
即
tan
2
3 k tan 2
3 tan 5 ,
12
12
于是
12
5
12
, min
12
,max
5
12
.故选(C).
解法 2.直接法结合图形法.
由 解 法 1 得 到 , k tan 2 sin , 可 以 看 作 点
2 cos
下面举例说明其用法:
例1:在 AOB 中,OC 1 OA, OD 1 OB, AD 与 BC 交于 M 点,
4
2
设 OA=a, OB b
B
(1) 用 a,b 表示向量 OM ; (2) 在线段 AC 上取一点 E,线段 BD 上取
F
D
M
一点 F,使 EF 过点 M,设 OE OA,OF OB
设 CQ CP , AQ AB , CA CQ QA (多边形法则)
既:
a
1 6
a
1 3
b
ba
1 6
a
1 3
b
,
1
6 1 3
接法求解.
解 法 1. 由 OA OC CA 2 2 cos, 2 2 sin 及
OB (2,0) 可知,向量 OA 与向量 OB 的夹角就是直线 OA 的 倾斜角, 向量OA 是直线 OA的方向向量,于是
tan 2 2 sin 2 sin .设 k tan 2 sin ,
AD OD OA a 1 b 2
∵
A, M , D
共线,
m 1 1
n 1
m
2n
1
2
同理: C, M , B 共线,得 4m n 1,联
B
F
D
M
立解得: m 1 , n 3 , OM 1 a 3 b
OCE
A
77
77
评注:待定设 OM ma nb ,在利用两次共线.
k AB2
,容易求出 B1AO
B2 AO
6
,
又 xOA ,则有
4
直线
AB1 的倾斜角为
