6469和差倍角半角公式的综合应用二
高一数学倍角公式和半角公式知识精讲

高一数学倍角公式和半角公式【本讲主要内容】倍角公式和半角公式(正弦、余弦、正切)【知识掌握】 【知识点精析】1. 倍角公式:二倍角公式sin sin cos ()cos cos sin ()cos sin tan tan tan ()222211222122222222αααααααααααααα==-=-=-=-⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪S C T注意:①公式T 2α只有当αππαππ≠+≠+∈k k k Z 242和()才成立; ②二倍角公式不仅限于2α是α的二倍的形式,其它只要两个角有二倍的关系,如4α是2α的二倍,α2是α4的二倍,3α是32α的二倍等等都可以用二倍角公式。
例如:cos cos sin sin cos sin αααααα3663312622=-=, 12242151153022-=-=sin cos tan tan tan αα,°°°③熟悉“倍角”与“二次”的关系(升角——降次,降角——升次)④注意公式的变形应用与逆用。
特别是公式:cos cos sin 2211222ααα=-=-可变形为cos cos sin cos 22122122αααα=+=-,,两式相除得tan cos cos 21212ααα=-+,这样就得到了降幂公式。
降幂公式sin cos cos cos tan cos cos 2221221221212ααααααα=-=+=-+⎧⎨⎪⎪⎪⎩⎪⎪⎪升幂公式cos cos sin cos sin 221122222ααααα=-=-=-⎧⎨⎪⎩⎪2. 半角公式:()()半角公式,,sin cos cos cos tan cos cos sin cos cos sin ααααααααααππαααπααα212212*********=±-⎛⎝ ⎫⎭⎪=±+⎛⎝ ⎫⎭⎪=±-+⎛⎝ ⎫⎭⎪=+≠+∈=-≠∈⎧⎨⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪S C T k k Z k k Z 注意:①应用半角公式时,要特别注意根号前的符号,它是由α2所在象限的三角函数符号确定。
倍角公式和半角公式

半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-cosα)/si nα=+或-[1-cosα)/(1+c osα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαco sαt an2α=2t anα/(1-tan^2(α))c os2α=c os^2(α)-si n^2(α)=2c os^2(α)-1=1-2si n^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nαtan(2α)=2tanα/[1-tan^2(α)]·倍角公式:si n(2α)=2sinα·c osαc os(2α)=c os^2(α)-sin^2(α)=2c os^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:si n3α=3sinα-4si n^3(α)c os3α=4c os^3(α)-3c osαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:si n^2(α/2)=(1-cosα)/2c os^2(α/2)=(1+c osα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=si nα/(1+c osα)=(1-c osα)/si nα·万能公式:si nα=2tan(α/2)/[1+tan^2(α/2)]c osα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:si nα·cosβ=(1/2)[si n(α+β)+sin(α-β)]c osα·si nβ=(1/2)[si n(α+β)-sin(α-β)]c osα·c osβ=(1/2)[c os(α+β)+c os(α-β)]si nα·si nβ=-(1/2)[c os(α+β)-cos(α-β)]·和差化积公式:si nα+si nβ=2si n[(α+β)/2]cos[(α-β)/2]si nα-si nβ=2cos[(α+β)/2]si n[(α-β)/2]c osα+c osβ=2c os[(α+β)/2]c os[(α-β)/2]c osα-c osβ=-2si n[(α+β)/2]si n[(α-β)/2]·其他:si nα+si n(α+2π/n)+sin(α+2π*2/n)+si n(α+2π*3/n)+……+si n[α+2π*(n-1)/n]=0c osα+c os(α+2π/n)+c os(α+2π*2/n)+cos(α+2π*3/n)+……+c os[α+2π*(n-1)/n]=0 以及si n^2(α)+si n^2(α-2π/3)+si n^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:si n4A=-4*(cosA*si nA*(2*si nA^2-1))c os4A=1+(-8*c os A^2+8*c os A^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:si n5A=16si nA^5-20si nA^3+5si nAc os5A=16c os A^5-20c os A^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:si n6A=2*(cosA*si nA*(2*si nA+1)*(2*sinA-1)*(-3+4*si nA^2))c os6A=((-1+2*c os A^2)*(16*c os A^4-16*c os A^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:si n7A=-(sinA*(56*si nA^2-112*si nA^4-7+64*si nA^6))c os7A=(c osA*(56*c osA^2-112*c osA^4+64*c os A^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:si n8A=-8*(cosA*si nA*(2*si nA^2-1)*(-8*si nA^2+8*sinA^4+1))c os8A=1+(160*c os A^4-256*c os A^6+128*c os A^8-32*c os A^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:si n9A=(sinA*(-3+4*si nA^2)*(64*sinA^6-96*si nA^4+36*si nA^2-3))c os9A=(c osA*(-3+4*cosA^2)*(64*c os A^6-96*cosA^4+36*c os A^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:si n10A=2*(c os A*sinA*(4*sinA^2+2*si nA-1)*(4*sinA^2-2*si nA-1)*(-20*si nA^2+5+16*si nA^4))c os10A=((-1+2*c os A^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*c os A^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
第3讲 和差倍半角公式
第2课时 课时
(
)
化简: 化简 : )3 15 sin x + 3 5 cos x. 1
2 π 6 π 2) sin( − x) + cos( − x) 4 4 4 4
小结】 关健在于1+3·tan10°, 通过 “ 切化弦 ” 及 “ 【 小结 】 关健在于 ° 通过“ 切化弦” 辅助角公式”使其得到化简. 辅助角公式”使其得到化简. a ⋅ cosα + b⋅ sinα a 一般地, 一般地, + btanα = cosα 而 a ⋅ cosα + b⋅ sinα 又可以化为一个角的一个三角函 形如1± 的式子的化简应熟练掌握. 数. 形如 ±cosα、1±sinα的式子的化简应熟练掌握 、 ± 的式子的化简应熟练掌握
作业: 导与练》P49第 作业:一.《导与练》P49第5、6、7、8、9题
二、1.在△ABC中,若sinA=3/5,cosB=5/13,求cosC 在 中 , ,
3 2.已知 cos ( + x) + 3 cos ( − x) = ,求cotx的值 的值. 已知 的值 4 4 2
2 2
π
π
自测题: 导与练》 自测题:《导与练》P48第1、2、3、4题 第 、 、 、 题
已知α∈ 例2.已知 ∈(0,π/2), β∈(π/2,π), 已知 ∈
1 5 3 cos α = , sin β = 7 14
的值. 求β-α的值 的值
小结】求角,先求其某一个三角函数值, 【小结】求角,先求其某一个三角函数值,再 根据三角函数的值 角的范围得出角 得出角。 根据三角函数的值及角的范围得出角。
高考一轮复习课件:和角,差角,倍半角公式

例4、活页例2、
(二)知值求角
例5、活页例3、
小结:本节课涉及给值求值、给角求值、给值求角的问题. 小结:本节课涉及给值求值、给角求值、给值求角的问题.着眼于
和差、倍角公式的正用、逆用、变形用,通过切割化弦、 和差、倍角公式的正用、逆用、变形用,通过切割化弦、 升降幂、转换为特殊角等技巧. 、升降幂、转换为特殊角等技巧.
2、辅助角公式 、
( a > 0, b > 0 )
2 2
a sin α ± b cos α = a + b sin (α ± ϕ )
b 其中tanϕ = a
3.倍角公式 倍角公式
cos 2α = cos α − sin α = 2 cos α − 1 2 = 1 − 2sin α
π
思维点拨:注意观察角与角之间的关系,
三.公式应用: 公式应用 求值: 和角.差角公式的应用 (一)求值: 1. 和角 差角公式的应用 例1 已知 cos π − α = 3 , sin 3π + β = 5 . 其中 π < α < 3π , 0 < β < π ,
求 sin (α + β )的值.
4 5
4
13
4
4
4
小结:本题是给值求值问题, 小结:本题是给值求值问题,解这类题时应认真
分析已知式子中的角与未知式子中的角的关系 .函数名称和式子结构的 函数名称和式子结构的 再决定如何利用以知条件,采用哪些公式 考虑角的整体运用 再决定如何利用以知条件 采用哪些公式,考虑角的整体运用.常用角的 采用哪些公式 考虑角的整体运用. 变换, 变换,如:
sin 2 α − cos2 α = − cos 2α + sin α cos α
两角和与差、倍角、半角公式

题目 第四章三角函数两角和与差的正弦、余弦、正切高考要求1.掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式2.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明知识点归纳1.和、差角公式βαβαβαsin cos cos sin )sin(±=±; βαβαβαsin sin cos cos )cos( =±;tan tan tan()1tan tan αβαβαβ±±=.2.二倍角公式αααcos sin 22sin =;ααααα2222sin 211cos 2sin cos 2cos -=-=-=; 22tan tan 21tan ααα=-.3.降幂公式ααα2sin 21cos sin =;22cos 1sin 2αα-=;22cos 1cos 2αα+=.4.半角公式 2cos 12sinαα-±=;2cos 12cosαα+±=;sin 1cos tan21cos sin ααααα-===+.5.万能公式22tan2sin 1tan2ααα=+;221tan2cos 1tan2ααα-=+;22tan 2tan 1tan2ααα=-.6.积化和差公式)]sin()[sin(21cos sin βαβαβα-++=;)]sin()[sin(21sin cos βαβαβα--+=; )]cos()[cos(21cos cos βαβαβα-++=;)]cos()[cos(21sin sin βαβαβα--+-=.7.和差化积公式2cos 2sin 2sin sin βαβαβα-+=+;2sin2cos 2sin sin βαβαβα-+=-;2cos 2cos 2cos cos βαβαβα-+=+;2sin2sin2cos cos βαβαβα-+-=-.8.三倍角公式:sin3α=αα3sin 4sin 3- cos3α=ααcos 3cos 43-9.辅助角公式:()sin cos sin a x b x x ϕ+=+sin cos ϕϕ==其中两角和与差的三角函数,二倍角公式是高考的重点内容之一,同时也是三角部分中后继学习的基础,最重要的是多数考生得分的主要阵地之一。
高考数学总复习 4.3和角公式、倍角公式与半角公式配套文档 理 新人教b版

§4.3 和角公式、倍角公式与半角公式1. 两角和与差的余弦、正弦、正切公式cos(α-β)=cos αcos β+sin αsin β (C α-β) cos(α+β)=cos_αcos_β-sin_αsin_β (C α+β) sin(α-β)=sin_αcos_β-cos_αsin_β (S α-β) sin(α+β)=sin_αcos_β+cos_αsin_β (S α+β) tan(α-β)=tan α-tan β1+tan αtan β (T α-β)tan(α+β)=tan α+tan β1-tan αtan β (T α+β)2. 二倍角公式sin 2α=2sin_αcos_α;cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; tan 2α=2tan α1-tan 2α.3. 半角公式sin α2=±1-cos α2;cos α2=± 1+cos α2; tan α2=±1-cos α1+cos α=sin α1+cos α=1-cos αsin α.根号前的正负号,由角α2所在象限确定.4. 函数f (x )=a sin α+b cos α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)(其中tan φ=ba)或f (α)=a 2+b 2cos(α-φ)(其中tan φ=ab).1. 判断下面结论是否正确(请在括号中打“√”或“×”)(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( √ )(2)存在实数α,β,使等式sin(α+β)=sin α+sin β成立. ( √ ) (3)在锐角△ABC 中,sin A sin B 和cos A cos B 大小不确定.( × )(4)公式tan(α+β)=tan α+tan β1-tan αtan β可以变形为tan α+tan β=tan(α+β)(1-tan αtan β),且对任意角α,β都成立.( × ) (5)存在实数α,使tan 2α=2tan α.( √ ) (6)当α+β=π4时,(1+tan α)(1+tan β)=2.( √ ) 2. (2013·浙江)已知α∈R ,sin α+2cos α=102,则tan 2α等于( )A.43B.34 C .-34 D .-43 答案 C解析 ∵sin α+2cos α=102, ∴sin 2α+4sin α·cos α+4cos 2α=52.化简得:4sin 2α=-3cos 2α, ∴tan 2α=sin 2αcos 2α=-34.故选C.3. (2012·江西)若sin α+cos αsin α-cos α=12,则tan 2α等于( )A .-34 B.34 C .-43 D.43答案 B解析 由sin α+cos αsin α-cos α=12,等式左边分子、分母同除cos α得,tan α+1tan α-1=12,解得tan α=-3,则tan 2α=2tan α1-tan 2α=34.4. (2012·江苏)设α为锐角,若cos ⎝⎛⎭⎫α+π6=45,则sin ⎝⎛⎭⎫2α+π12的值为________. 答案17250解析 ∵α为锐角且cos ⎝⎛⎭⎫α+π6=45,∴sin ⎝⎛⎭⎫α+π6=35. ∴sin ⎝⎛⎭⎫2α+π12=sin ⎣⎡⎦⎤2⎝⎛⎭⎫α+π6-π4 =sin 2⎝⎛⎭⎫α+π6cos π4-cos 2⎝⎛⎭⎫α+π6sin π4=2sin ⎝⎛⎭⎫α+π6cos ⎝⎛⎭⎫α+π6-22⎣⎡⎦⎤2cos 2⎝⎛⎭⎫α+π6-1 =2×35×45-22⎣⎡⎦⎤2×⎝⎛⎭⎫452-1 =12225-7250=17250. 5. (2013·课标全国Ⅱ)设θ为第二象限角,若tan ⎝⎛⎭⎫θ+π4=12,则sin θ+cos θ=________. 答案 -105解析 ∵tan ⎝⎛⎭⎫θ+π4=12,∴tan θ=-13, 即⎩⎪⎨⎪⎧3sin θ=-cos θ,sin 2θ+cos 2θ=1, 解得sin θ=1010,cos θ=-31010. ∴sin θ+cos θ=-105.题型一 三角函数式的化简与给角求值例1 (1)化简:(1+sin θ+cos θ)(sin θ2-cos θ2)2+2cos θ(0<θ<π);(2)求值:1+cos 20°2sin 20°-sin 10°(1tan 5°-tan 5°).思维启迪 (1)分母为根式,可以利用二倍角公式去根号,然后寻求分子分母的共同点进行约分;(2)切化弦、通分.解 (1)由θ∈(0,π),得0<θ2<π2,∴cos θ2>0.因此2+2cos θ=4cos 2θ2=2cos θ2.又(1+sin θ+cos θ)(sin θ2-cos θ2)=(2sin θ2cos θ2+2cos 2θ2)(sin θ2-cos θ2)=2cos θ2(sin 2θ2-cos 2θ2)=-2cos θ2cos θ.故原式=-2cos θ2cos θ2cosθ2=-cos θ.(2)原式=2cos 210°2×2sin 10°cos 10°-sin 10°(cos 5°sin 5°-sin 5°cos 5°)=cos 10°2sin 10°-sin 10°·cos 25°-sin 25°sin 5°cos 5° =cos 10°2sin 10°-sin 10°·cos 10°12sin 10°=cos 10°2sin 10°-2cos 10°=cos 10°-2sin 20°2sin 10°=cos 10°-2sin (30°-10°)2sin 10°=cos 10°-2(12cos 10°-32sin 10°)2sin 10°=3sin 10°2sin 10°=32.思维升华 (1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)对于给角求值问题,往往所给角都是非特殊角,解决这类问题的基本思路有: ①化为特殊角的三角函数值; ②化为正、负相消的项,消去求值; ③化分子、分母出现公约数进行约分求值.(1)在△ABC 中,已知三个内角A ,B ,C 成等差数列,则tan A 2+tan C2+3tan A 2tan C2的值为________.(2)2cos 10°-sin 20°sin 70°的值是( )A.12B.32 C.3 D. 2 答案 (1)3 (2)C解析 (1)因为三个内角A ,B ,C 成等差数列,且A +B +C =π,所以A +C =2π3,A +C 2=π3,tan A +C 2=3,所以tan A 2+tan C 2+3tan A 2tan C2=tan ⎝⎛⎭⎫A 2+C 2⎝⎛⎭⎫1-tan A 2tan C 2+3tan A 2tan C 2 =3⎝⎛⎭⎫1-tan A 2tan C 2+3tan A 2tan C2= 3. (2)原式=2cos (30°-20°)-sin 20°sin 70°=2(cos 30°·cos 20°+sin 30°·sin 20°)-sin 20°sin 70°=3cos 20°cos 20°= 3.题型二 三角函数的给值求值、给值求角例2 (1)已知0<β<π2<α<π,且cos ⎝⎛⎭⎫α-β2=-19,sin ⎝⎛⎭⎫α2-β=23,求cos(α+β)的值; (2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,求2α-β的值.思维启迪 (1)拆分角:α+β2=⎝⎛⎭⎫α-β2-⎝⎛⎭⎫α2-β,利用平方关系分别求各角的正弦、余弦. (2)2α-β=α+(α-β);α=(α-β)+β. 解 (1)∵0<β<π2<α<π,∴-π4<α2-β<π2,π4<α-β2<π,∴cos ⎝⎛⎭⎫α2-β= 1-sin 2⎝⎛⎭⎫α2-β=53, sin ⎝⎛⎭⎫α-β2= 1-cos 2⎝⎛⎭⎫α-β2=459,∴cosα+β2=cos ⎣⎡⎦⎤⎝⎛⎭⎫α-β2-⎝⎛⎭⎫α2-β =cos ⎝⎛⎭⎫α-β2cos ⎝⎛⎭⎫α2-β+sin ⎝⎛⎭⎫α-β2sin ⎝⎛⎭⎫α2-β =⎝⎛⎭⎫-19×53+459×23=7527, ∴cos(α+β)=2cos 2α+β2-1=2×49×5729-1=-239729. (2)∵tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=12-171+12×17=13>0,∴0<α<π2,又∵tan 2α=2tan α1-tan 2α=2×131-⎝⎛⎭⎫132=34>0, ∴0<2α<π2,∴tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171-34×17=1.∵tan β=-17<0,∴π2<β<π,-π<2α-β<0,∴2α-β=-3π4. 思维升华 (1)解题中注意变角,如本题中α+β2=(α-β2)-(α2-β);(2)通过求角的某种三角函数值来求角,在选取函数时,遵照以下原则:①已知正切函数值,选正切函数;②已知正、余弦函数值,选正弦或余弦函数;若角的范围是⎝⎛⎭⎫0,π2,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为⎝⎛⎭⎫-π2,π2,选正弦较好.(1)若0<α<π2,-π2<β<0,cos(π4+α)=13,cos(π4-β2)=33,则cos(α+β2)等于( )A.33 B .-33 C.539 D .-69(2)已知sin α=55,sin(α-β)=-1010,α,β均为锐角,则角β等于 ( )A.5π12B.π3C.π4D.π6 答案 (1)C (2)C解析 (1)cos(α+β2)=cos[(π4+α)-(π4-β2)]=cos(π4+α)cos(π4-β2)+sin(π4+α)sin(π4-β2),∵0<α<π2,则π4<π4+α<3π4,∴sin(π4+α)=223. 又-π2<β<0,则π4<π4-β2<π2,则sin(π4-β2)=63.故cos(α+β2)=cos[π4+α-(π4-β2)]=cos(π4+α)cos(π4-β2)+sin(π4+α)sin(π4-β2)=13×33+223×63=539,故选C. (2)∵α、β均为锐角,∴-π2<α-β<π2.又sin(α-β)=-1010,∴cos(α-β)=31010. 又sin α=55,∴cos α=255, ∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β) =55×31010-255×(-1010)=22. ∴β=π4.题型三 三角变换的简单应用例3 已知函数f (x )=sin ⎝⎛⎭⎫x +7π4+cos ⎝⎛⎭⎫x -3π4,x ∈R . (1)求f (x )的最小正周期和最小值;(2)已知cos(β-α)=45,cos(β+α)=-45,0<α<β≤π2,求证:[f (β)]2-2=0.思维启迪 (1)可将f (x )化成y =A sin(ωx +φ)的形式; (2)据已知条件确定β,再代入f (x )求值. (1)解 ∵f (x )=sin ⎝⎛⎭⎫x +7π4-2π+cos ⎝⎛⎭⎫x -π4-π2 =sin ⎝⎛⎭⎫x -π4+sin ⎝⎛⎭⎫x -π4=2sin ⎝⎛⎭⎫x -π4, ∴T =2π,f (x )的最小值为-2.(2)证明 由已知得cos βcos α+sin βsin α=45,cos βcos α-sin βsin α=-45,两式相加得2cos βcos α=0,∵0<α<β≤π2,∴β=π2,∴[f (β)]2-2=4sin 2π4-2=0.思维升华 三角变换和三角函数性质相结合是高考的一个热点,解题时要注意观察角、式子间的联系,利用整体思想解题.(1)函数f (x )=3sin x +cos(π3+x )的最大值为( )A .2 B. 3 C .1 D.12(2)函数f (x )=sin(2x -π4)-22sin 2x 的最小正周期是________.答案 (1)C (2)π解析 (1)f (x )=3sin x +cos π3·cos x -sin π3·sin x=12cos x +32sin x =sin(x +π6).∴f (x )max =1. (2)f (x )=22sin 2x -22cos 2x -2(1-cos 2x ) =22sin 2x +22cos 2x -2=sin(2x +π4)-2, ∴T =2π2=π.高考中的三角变换问题典例:(20分)(1)若tan 2θ=-22,π<2θ<2π,则2cos 2θ2-sin θ-12sin (θ+π4)=________.(2)已知锐角α,β满足sin α=55,cos β=31010,则α+β等于( )A.3π4B.π4或3π4C.π4D .2k π+π4(k ∈Z )(3)(2012·大纲全国)已知α为第二象限角,sin α+cos α=33,则cos 2α等于( ) A .-53 B .-59 C.59 D.53(4)(2012·重庆)sin 47°-sin 17°cos 30°cos 17°等于( )A .-32 B .-12 C.12 D.32思维启迪 (1)注意和差公式的逆用及变形;(2)可求α+β的某一三角函数值,结合α+β的范围求角.(3)可以利用sin 2α+cos 2α=1寻求sin α±cos α与sin αcos α的联系;(4)利用和角公式将已知式子中的角向特殊角转化.解析 (1)原式=cos θ-sin θsin θ+cos θ=1-tan θ1+tan θ,又tan 2θ=2tan θ1-tan 2θ=-22,即2tan 2θ-tan θ-2=0, 解得tan θ=-12或tan θ= 2.∵π<2θ<2π,∴π2<θ<π.∴tan θ=-12,故所求=1+121-12=3+2 2.(2)由sin α=55,cos β=31010且α,β为锐角,可知cos α=255,sin β=1010,故cos(α+β)=cos αcos β-sin αsin β=255×31010-55×1010=22,又0<α+β<π,故α+β=π4.解析 (3)由sin α+cos α=33两边平方得1+2sin αcos α=13,∴2sin αcos α=-23.∵α为第二象限角,∴sin α>0,cos α<0,∴sin α-cos α=(sin α-cos α)2=1-2sin αcos α=153. 由⎩⎨⎧sin α+cos α=33,sin α-cos α=153,得⎩⎪⎨⎪⎧sin α=3+156,cos α=3-156.∴cos 2α=2cos 2α-1=-53. (4)利用两角和的正弦公式化简. 原式=sin (30°+17°)-sin 17°cos 30°cos 17°=sin 30°cos 17°+cos 30°sin 17°-sin 17°cos 30°cos 17°=sin 30°cos 17°cos 17°=sin 30°=12.答案 (1)3+22 (2)C (3)A (4)C温馨提醒 三角变换中的求值问题要注意利用式子的特征,灵活应用公式;对于求角问题,一定要结合角的范围求解.方法与技巧1. 巧用公式变形:和差角公式变形:tan x ±tan y =tan(x ±y )·(1∓tan x ·tan y );倍角公式变形:降幂公式cos 2α=1+cos 2α2,sin 2α=1-cos 2α2, 配方变形:1±sin α=⎝⎛⎭⎫sin α2±cos α22,1+cos α=2cos 2α2,1-cos α=2sin 2α2. 2. 利用辅助角公式求最值、单调区间、周期.由y =a sin α+b cos α=a 2+b 2sin(α+φ)(其中tan φ=ba)有a 2+b 2≥|y |.3. 重视三角函数的“三变”:“三变”是指“变角、变名、变式”;变角:对角的分拆要尽可能化成同名、同角、特殊角;变名:尽可能减少函数名称;变式:对式子变形一般要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的三角公式恒等变形. 失误与防范1. 运用公式时要注意审查公式成立的条件,要注意和、差、倍角的相对性,要注意升次、降次的灵活运用,要注意“1”的各种变通. 2. 在(0,π)范围内,sin(α+β)=22所对应的角α+β不是唯一的. 3. 在三角求值时,往往要估计角的范围后再求值.A 组 专项基础训练 (时间:40分钟)一、选择题1. 若θ∈[π4,π2],sin 2θ=378,则sin θ等于( )A.35B.45C.74D.34 答案 D解析 由sin 2θ=387和sin 2θ+cos 2θ=1得(sin θ+cos θ)2=378+1=(3+74)2,又θ∈[π4,π2],∴sin θ+cos θ=3+74.同理,sin θ-cos θ=3-74,∴sin θ=34. 2. 已知tan(α+β)=25,tan ⎝⎛⎭⎫β-π4=14,那么tan ⎝⎛⎭⎫α+π4等于( ) A.1318 B.1322 C.322 D.16答案 C 解析 因为α+π4+β-π4=α+β,所以α+π4=(α+β)-⎝⎛⎭⎫β-π4,所以tan ⎝⎛⎭⎫α+π4=tan ⎣⎡⎦⎤(α+β)-⎝⎛⎭⎫β-π4=tan (α+β)-tan ⎝⎛⎭⎫β-π41+tan (α+β)tan ⎝⎛⎭⎫β-π4=322.3. (2013·重庆)4cos 50°-tan 40°等于 ( ) A. 2 B.2+32 C.3 D .22-1答案 C解析 4cos 50°-tan 40°=4sin 40°cos 40°-sin 40°cos 40°=2sin 80°-sin 40°cos 40°=2sin (50°+30°)-sin 40°cos 40° =3sin 50°+cos 50°-sin 40°cos 40°=3sin 50°cos 40°= 3.4. 若tan α+1tan α=103,α∈(π4,π2),则sin(2α+π4)的值为( )A .-210 B.210 C.3210 D.7210答案 A解析 由tan α+1tan α=103得sinαcos α+cos αsin α=103,∴1sin αcos α=103,∴sin 2α=35.∵α∈(π4,π2),∴2α∈(π2,π),∴cos 2α=-45.∴sin(2α+π4)=sin 2αcos π4+cos 2αsin π4=22×(35-45)=-210.5. 在△ABC 中,tan A +tan B +3=3tan A ·tan B ,则C 等于( )A.π3B.2π3C.π6D.π4答案 A解析 由已知可得tan A +tan B =3(tan A ·tan B -1),∴tan(A +B )=tan A +tan B 1-tan A tan B =-3, 又0<A +B <π,∴A +B =23π,∴C =π3. 二、填空题6. 若sin(π2+θ)=35,则cos 2θ=________. 答案 -725解析 ∵sin(π2+θ)=cos θ=35, ∴cos 2θ=2cos 2θ-1=2×(35)2-1=-725. 7. 若α=20°,β=25°,则(1+tan α)(1+tan β)的值为________.答案 2解析 由tan(α+β)=tan α+tan β1-tan αtan β=tan 45°=1可得 tan α+tan β+tan αtan β=1,所以(1+tan α)(1+tan β)=1+tan α+tan β+tan αtan β=2.8. 3tan 12°-3(4cos 212°-2)sin 12°=________. 答案 -4 3解析 原式=3sin 12°cos 12°-32(2cos 212°-1)sin 12° =23⎝⎛⎭⎫12sin 12°-32cos 12°cos 12°2cos 24°sin 12°=23sin (-48°)2cos 24°sin 12°cos 12°=-23sin 48°sin 24°cos 24° =-23sin 48°12sin 48°=-4 3. 三、解答题9. 已知tan α=-13,cos β=55,α∈(π2,π),β∈(0,π2),求tan(α+β)的值,并求出α+β的值. 解 由cos β=55,β∈(0,π2),得sin β=255,tan β=2.∴tan(α+β)=tan α+tan β1-tan αtan β=-13+21+23=1. ∵α∈(π2,π),β∈(0,π2),∴π2<α+β<3π2,∴α+β=5π4.10.已知α∈⎝⎛⎭⎫π2,π,且sin α2+cos α2=62.(1)求cos α的值;(2)若sin(α-β)=-35,β∈⎝⎛⎭⎫π2,π,求cos β的值.解 (1)因为sin α2+cos α2=62, 两边同时平方,得sin α=12.又π2<α<π,所以cos α=-32.(2)因为π2<α<π,π2<β<π,所以-π<-β<-π2,故-π2<α-β<π2.又sin(α-β)=-35,得cos(α-β)=45.cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=-32×45+12×⎝⎛⎭⎫-35=-43+310.B 组 专项能力提升(时间:30分钟)1. 已知tan(α+π4)=12,且-π2<α<0,则2sin 2α+sin 2αcos (α-π4)等于( ) A .-255 B .-3510 C .-31010 D.255答案 A解析 由tan(α+π4)=tan α+11-tan α=12,得tan α=-13. 又-π2<α<0,所以sin α=-1010. 故2sin 2α+sin 2αcos (α-π4)=2sin α(sin α+cos α)22(sin α+cos α)=22sin α=-255. 2. 定义运算⎪⎪⎪⎪⎪⎪ab c d =ad -bc ,若cos α=17,⎪⎪⎪⎪⎪⎪sin α sin βcos α cos β=3314,0<β<α<π2,则β等于 ( ) A.π12 B.π6 C.π4 D.π3答案 D解析 依题意有sin αcos β-cos αsin β=sin(α-β)=3314, 又0<β<α<π2,∴0<α-β<π2, 故cos(α-β)=1-sin 2(α-β)=1314, 而cos α=17,∴sin α=437, 于是sin β=sin[α-(α-β)] =sin αcos(α-β)-cos αsin(α-β)=437×1314-17×3314=32, 故β=π3,选D. 3. 设x ∈⎝⎛⎭⎫0,π2,则函数y =2sin 2x +1sin 2x的最小值为________. 答案 3 解析 方法一 因为y =2sin 2x +1sin 2x =2-cos 2x sin 2x, 所以令k =2-cos 2x sin 2x.又x ∈⎝⎛⎭⎫0,π2, 所以k 就是单位圆x 2+y 2=1的左半圆上的动点P (-sin 2x ,cos 2x )与定点Q (0,2)所成直线的斜率.又k min =tan 60°=3,所以函数y =2sin 2x +1sin 2x的最小值为 3. 方法二 y =2sin 2x +1sin 2x =3sin 2x +cos 2x 2sin x cos x=3tan 2x +12tan x =32tan x +12tan x. ∵x ∈(0,π2),∴tan x >0. ∴32tan x +12tan x≥232tan x ·12tan x = 3. (当tan x =33,即x =π6时取等号) 即函数的最小值为 3.4. 已知tan(π+α)=-13,tan(α+β)=sin 2(π2-α)+4cos 2α10cos 2α-sin 2α. (1)求tan(α+β)的值;(2)求tan β的值.解 (1)∵tan(π+α)=-13,∴tan α=-13. ∵tan(α+β)=sin 2(π2-α)+4cos 2α10cos 2α-sin 2α=sin 2α+4cos 2α10cos 2α-sin 2α=2sin αcos α+4cos 2α10cos 2α-2sin αcos α=2cos α(sin α+2cos α)2cos α(5cos α-sin α)=sin α+2cos α5cos α-sin α=tan α+25-tan α=-13+25-(-13)=516. (2)tan β=tan[(α+β)-α]=tan (α+β)-tan α1+tan (α+β)tan α=516+131-516×13=3143. 5. 已知函数f (x )=2cos ⎝⎛⎭⎫ωx +π6(其中ω>0,x ∈R )的最小正周期为10π. (1)求ω的值;(2)设α,β∈⎣⎡⎦⎤0,π2,f ⎝⎛⎭⎫5α+53π=-65,f ⎝⎛⎭⎫5β-56π =1617,求cos(α+β)的值. 解 (1)由T =2πω=10π得ω=15.(2)由⎩⎨⎧f ⎝⎛⎭⎫5α+53π=-65,f ⎝⎛⎭⎫5β-56π=1617得⎩⎨⎧ 2cos ⎣⎡⎦⎤15⎝⎛⎭⎫5α+53π+π6=-65,2cos ⎣⎡⎦⎤15⎝⎛⎭⎫5β-56π+π6=1617,整理得⎩⎨⎧ sin α=35,cos β=817. ∵α,β∈⎣⎡⎦⎤0,π2, ∴cos α=1-sin 2α=45,sin β=1-cos 2β=1517. ∴cos(α+β)=cos αcos β -sin αsin β =45×817-35×1517=-1385.。
《两角和与差的三角函数》《倍角、半角的三角函数》复习[1]
![《两角和与差的三角函数》《倍角、半角的三角函数》复习[1]](https://img.taocdn.com/s3/m/b8b4fd12f18583d049645983.png)
两角和与差的三角函数三角函数基本公式总结1.和、差角公式βαβαβαsin cos cos sin )sin(±=±;βαβαβαsin sin cos cos )cos( =±;βαβαβαtg tg tg tg tg 1)(±=±.2.二倍角公式αααcos sin 22sin =;ααααα2222sin 211cos 2sin cos 2cos -=-=-=;ααα2122tg tg tg -=.3.降幂公式ααα2sin 21cos sin =;22cos 1sin 2αα-=;22cos 1cos 2αα+=.4.半角公式 2cos 12sinαα-±=;2cos 12cosαα+±=;αααααααsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg.5.万能公式2122sin 2αααtgtg+=;2121cos 22αααtgtg+-=;21222αααtgtg tg -=.6.积化和差公式)]sin()[sin(21cos sin βαβαβα-++=;)]sin()[sin(21sin cos βαβαβα--+=; )]cos()[cos(21cos cos βαβαβα-++=;)]cos()[cos(21sin sin βαβαβα--+-=.7.和差化积公式2cos2sin2sin sin βαβαβα-+=+;2sin2cos2sin sin βαβαβα-+=-; 2cos2cos2cos cos βαβαβα-+=+;2sin2sin2cos cos βαβαβα-+-=-.例. 求下列各式的值①sin15°②sin24°cos36°+cos24°cos54°③④tan20°+tan40°+tan20°tan40°分析与解答:①可将15°改写成60°-45°,再利用两角差的正弦公式sin15°=sin(60°-45°)=sin60°cos45°-cos60°sin45°=.②若将式中的cos54°改写为sin36°则恰为两角和的正弦:原式=sin24°cos36°+cos24°sin36°=sin(24°+36°).③将1+tan15°视为tan45°+tan15°,将1-tan15°视为1-tan45°tan15°,即利用tan45°=1,则式子恰为两角和的正切:原式.④由于20°+40°=60°,又,将其变形tan20°+tan40°(1-tan20°tan40°)tan20°tan40°将移到左边得.[例题选讲]例1.求下列各式的值①tan15°+tan30°+tan15°tan30°②(1+tan1°)(1+tan2°)(1+tan3°)……(1+tan44°)③分析与解答:①解法一:∵,∴tan15°+tan30°=1-tan15°tan30°∴原式=1-tan15°tan30°+tan15°tan30°=1解法二:原式=tan15°(1+tan30°)+tan30°②∵(1+tan1°)(1+tan44°)=1+tan1°+tan44°+tan1°tan44°=1+tan(1°+44°)(1-tan1°tan44°)+tan1°tan44°=2.∴同理(1+tan2°)(1+tan43°)=(1+tan3°)(1+tan42°)=……=(1+tan22°)(1+tan23°)=2故原式.③原式例2.解下列各题(1)已知:,求cos(α-β)的值.(2)已知:,,0°<α<90°, 0°<β<90°,求cosβ的值. (3)已知:tanα和tanβ是方程2x2+x-6=0的两个根,求tan(α+β)的值.分析与解答:(1)由已知可求得.当α在第一象限而β在第二象限时,cos(α-β)=cosαcosβ+sinαsinβ.当α在第一象限而β在第三象限时,cos(α-β).当α在第二象限而β在第二象限时,cos(α-β).当α在第二象限而β在第三象限时,cos(α-β).(2)∵0°<α<90°, ∴,又∵0°<α<90°,0°<β<90°,∴0°<α+β<180°, ∴,∴cosβ=cos[(α+β)-α] =cos(α+β)cosα+sin(α+β)sinα=.说明:解题中应用了β=(α+β)-α式子的变换,体现了灵活解决问题的能力,应着重体会,常见的变换技巧还有2α=(α+β)+(α-β), 2β=(α+β)-(α-β), 2α+β=(α+β)+α等.(3)由韦达定理,得,,∴.例3.求证下列恒等式①cos(150°-β)=-②③分析与解答:①左边=cos150°·cosβ+sin150°·sinβ∴原式成立.②左边=∴原式成立.③证法一:左式=∴原式成立.证法二:∵(tanα+sinα)(tanα-sinα)=tan2α-tanαsinα+sinαtanα-sin2α =tan2α-sin2α=tan2α(1-cos2α)=tan2αsin2α=tanα·sinα·tanα·sinα由比例的性质有.证法三:左式右式∴左式=右式.课外练习:1.不查表求下列各式的值.①cos(33°-x)cos(27°+x)-sin(33°-x)sin(27°+x)②cos(80°+2α)cos(35°+2α)+sin(80°+2α)cos(55°-2α)③sin68°·sin22°+cos112°·sin428°④cos275°-sin275°⑤csc60°·2.设,则cosαcosβ=().A、B、C、D、3.已知sin(α-β)cosα-cos(α-β)sinα=, 且β为第三象限角,则cosβ等于().A、B、C、D、[参考答案]1.①原式=cos[(33°-x)+(27°+x)]=cos60°=.②原式=sin[(80°+2α)+(55°-2α)]=sin135°=.③原式=sin68°·sin22°-cos68°·cos22°=-cos(68°+22°)=-cos90°=0.④原式=cos(75°+75°)=cos150°=⑤原式=2. ∴,∴.选B.3.由已知,∴,∵β为第三象限角,∴cosβ<0,,选B.倍角、半角的三角函数二倍角公式是两角和公式的特殊情况,即:由此可继续导出三倍角公式.观察角之间的联系应该是解决三角变换的一个关键.二倍角公式中余弦公式有三种形式,采用哪种形式应根据题目具体而定.倍角和半角相对而言,两倍角余弦公式的变形可引出半角公式.推导过程中可得到一组降次公式,即,进一步得到半角公式:降次公式在三角变换中应用得十分广泛,“降次”可以作为三角变换中的一个原则.半角公式在运用时一定要注意正、负号的选取,而是正是负取决于所在的象限.而半角的正切可用α的正弦、余弦表示,即:.这个公式可由二倍角公式得出,这个公式不存在符号问题,因此经常采用.反之用tan也可表示sinα, cosα, tanα,即:,,这组公式叫做“万能”公式.教材中只要求记忆两倍角公式,其它公式并没有给出,需要时可根据二倍角公式及同角三角函数公式推出.例1.推导三倍角的正弦、余弦公式解:sin3α=sin(2α+α)cos3α=cos(2α+α)例2.利用三倍角公式推导sin18°的值.解:∵sin36°=cos54°,∴2sin18°cos18°=4cos318°-3cos18°∵cos18°≠0∴2sin18°=4cos218°-3∴2sin18°=4-4sin218°-3∴4sin218°+2sin18°-1=0∴. 本题还可根据二倍角公式推出cos36°.即.例3.化简求值:(1) csc10°-sec10°(2) tan20°+cot20°-2sec50°解:(1) csc10°-sec10°(2) tan20°+cot20°-2sec50°例4.求:sin220°+cos250°+sin30°sin70°解:sin220°+cos250°+sin30°sin70°例5.已知:.求: cos4θ+sin4θ的值.解:∵,∴, 即,即,∴cos4θ+sin4θ例6.求cos36°·cos72°的值.解:cos36°·cos72°例7.求:的值.解:例8.已知:2cosθ=1+sinθ,求.方法一: ∵2cosθ=1+sinθ,∴∴或,∴,∴,∴或=2.方法二:∵2cosθ=1+sinθ,∴,∴,∴或,∴或=2.例9.已知:,求:tanα的值.解:∵,∴,∵0≤α≤π,∴,∴(1)当时,,则有,∴,∴,∴,∴.(2)当,则有,∴,∴,∴.注意:1与sinα在一起时,1往往被看作,而1与cosα在一起时,往往应用二倍角余弦公式把1去掉.例10.已知:sinθ, sinα, cosθ为等差数列;sinθ,sinβ, cosθ为等比数列.求证:2cos2α=cos2β.证明:∵,∴∴4sin2α=1+2sin2β∴2-4sin2α=2-1-2sin2β∴2cos2α=cos2β.课后练习:1.若,则().A、P QB、P QC、P=QD、P∩Q=2.若A为ΔABC的内角,,则cos2A=().A、B、C、D、3.若,则sin2θ=().A、B、C、D、4.若,则sinθ=().A、B、C、D、-5.若,则=().A、B、C、1D、-16.若,则cosα=________.7. 若θ为第二象限角,且,则=_____. 8.已知sinA+cosA=2sinB. 求证:cos2B=cos2.参考答案:1.C2.B3.C4.C5.B6.7. 6。
倍角公式和半角公式] · [提高] · [知识点+典型例题]
![倍角公式和半角公式] · [提高] · [知识点+典型例题]](https://img.taocdn.com/s3/m/d61e81b6b9d528ea81c77982.png)
倍角公式和半角公式知识讲解一、倍角公式sin 22sin cos ααα=;2222cos 2cos sin 12sin 2cos 1ααααα=-=-=-22tan tan 21tan ααα=- 3sin 33sin 4sin ααα=-;3cos34cos 3cos ααα=-;323tan tan tan 313tan αααα-=- 二、半角公式sin2α=cos 2α=1cos sin tan2sin 1cos ααααα-===+ 三、万能公式22tan2sin 1tan 2ααα=+;221tan 2cos 1tan 2ααα-=+;22tan2tan 1tan 2ααα=-四、公式的推导sin 2sin()sin cos cos sin 2sin cos ααααααααα=+=+=22cos2cos()cos cos sin sin cos sin ααααααααα=+=⋅-⋅=- 再利用22sin cos 1αα+=,可得:2222cos2cos sin 2cos 112sin ααααα=-=-=- ()2tan tan 2tan tan 2tan 1tan tan 1tan ααααααααα+=+==-⋅-sin 2tan2cos2ααα===sin 2sinsin1cos 222tan2sin cos 2sin cos 222ααααααααα-=== sin 2cossinsin 222tan21cos cos2cos cos222ααααααααα===+ 【说明】这里没有考虑cossin22αα==,实际处理题目的时候需要把等于0的情况分出来单独讨论一下.五、综合运用1.倍角、半角、和差化积、积化和差等公式的运用1)并项功能: 2)升次功能 : 3)降次功能: 2.三角变换中常用的数学思想方法技巧有:1)角的变换:和、差、倍、半、互余、互补的相对性,有效沟通条件与结论中角的差异, 比如:3015453060452︒︒=︒-︒=︒-︒=, ()()22αααββαββ=-+=+-=⋅()()()()ππ2()()44ααβαβαββααα=++-=+--=+--()()222βαβαβαααβα⎛⎫-=-+=-=-- ⎪⎝⎭ππππππ244362αααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-=++-=++-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭π3ππ2ππ5ππ443366αααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++-=++-=++-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭2221sin 2sin cos 2sin cos (sin cos )ααααααα±=+±=±2222cos 2cos sin 2cos 112sin ααααα=-=-=-221cos 21cos 2cos ,sin 22αααα+-==2)函数名称的变换:三角变形中,常常需要变函数名称为同名函数,在三角函数中正余弦是基础,通常化切为弦,变异名为同名;有时可以使用万能公式将所有函数名化为正切; 3)常数代换:在三角函数运算、求值、证明中,有时需要将常数转化为三角函数值,例如:2222ππππ1sin cos sec tan sintan 2sin 2464αααα=+=-===; 4)幂的变换:降幂是三角变换时常用的方法 常用的降幂公式有:21cos2cos 2αα+=,21cos2sin 2αα-=但降幂并非绝对,有时也需要对某些式子进行升幂处理,比如221cos22cos ,1cos22sin αααα+=-=;21sin 2(sin cos )ααα±=±;5)公式变形:三角公式是变换的依据,应熟练掌握三角公式的顺用,逆用及变形应用, 例如:tan tan tan()(1tan tan )αβαβαβ±=±⋅⋅; 6)辅助角公式的运用:在求值问题中,要注意辅助角公式() sin cos y a b αααϕ=++的应用,其中tan b aϕ=,ϕ所在的象限由,a b 的符号确定.典型例题一.选择题(共8小题)1.(2017•南充模拟)函数y=sin(2x+)﹣sinxcosx的单调减区间是()A.[kπ﹣,kπ+](k∈Z)B.[kπ﹣,kπ﹣](k∈Z)C.[kπ﹣,kπ+](k∈Z)D.[kπ+,kπ+](k∈Z)【解答】解:y=sin2x+cos2x﹣sin2x=﹣sin(2x﹣),由﹣+2kπ≤2x﹣≤+2kπ,则x∈[kπ﹣,kπ+](k∈Z),即函数y=sin(2x+)﹣sinxcosx的单调减区间是[kπ﹣,kπ+](k∈Z),故选:A.2.(2017春•韶关期末)设α是第二象限角,且,则tan2α=()A.B.C.D.【解答】解:∵,∴sin2α=1﹣cos2α=.又∵α是第二象限角,得sinα>0,∴sinα=,由此可得tanα=﹣,因此tan2α==.故选:D.3.(2016春•天台县月考)若f(cosx)=cos2x,则f(1)=()A.1 B.﹣1 C.2 D.﹣2【解答】解:f(cosx)=cos2x=2cos2x﹣1,令cosx=1,得到f(1)=2﹣1=1;故选:A.4.(2016•诸暨市模拟)已知θ为钝角,且sinθ+cosθ=,则tan2θ=()A.﹣B.C.﹣D.【解答】解:法一:∵sinθ+cosθ=①,θ为钝角,∴两边平方可得:1+2sinθcosθ=,可得:2sinθcosθ=﹣,∵由θ∈(,π),得到sinθ﹣cosθ>0,可得:sinθ﹣cosθ===,②∴由①+②可得:sinθ=,由①﹣②可得:cosθ=﹣,∴tanθ==﹣,∴tan2θ==.法二:∵θ为钝角,可得:sinθ>0,cosθ<0,又sinθ+cosθ=>0,可得:θ∈(,),可得:2θ∈(π,),可得:tan2θ>0,再由sinθ+cosθ=,∴两边平方可得:1+2sinθcosθ=,可得:sin2θ=﹣,∴tan2θ=.故选:B.5.(2015秋•潮州期末)已知,则=()A.B.C.﹣D.﹣【解答】解:∵,∴=.故选:C.6.(2016•湖北模拟)若α∈(0,π),且sinα+2cosα=2,则tan等于()A.3 B.2 C.D.【解答】解:∵α∈(0,π),∴∈(0,),设tan=x,x>0,∵sinα==,cosα==,∴sinα+2cosα=+2•==2,即x+1﹣x2=1+x2,即x(2x﹣1)=0,解得x=故选:C.7.(2013秋•吉安期末)已知θ为第二象限角,25sin2θ+sinθ﹣24=0,则sin的值为()A.B.C.D.【解答】解:∵θ为第二象限角,∴sinθ>0,则2kπ<θ<2kπ+π,k∈Z,则kπ<<kπ+,k∈Z,当k是偶数,设k=2n,则2nπ<<2nπ+,n∈Z,此时为第一象限,当k是奇数,设k=2n+1,则2nπ+π<<2nπ+,n∈Z,此时为第三象限,则为第一或第三象限,∵25sin2θ+sinθ﹣24=0,∴sinθ=﹣1(舍去)或,∴cos,∴sin==±=,故选:D.8.(2012春•锦州期末)已知sinα=,<α<π,则tan的值为()A.B.﹣2 C.2 D.【解答】解:∵已知sinα=,<α<π,∴<<,且cosα=﹣.再由二倍角公式可得2﹣1=﹣,求得cos=,∴sin=,则tan==2,故选:C.二.填空题(共8小题)9.(2018春•杨浦区校级月考)已知cos(α+)=,≤α≤,则cos(2α+)=﹣.【解答】解:∵≤α≤,cos(α+)=>0,∴<α+≤,∴sin(α+)=﹣=﹣,∴sinα=sin[(α+)﹣]=sin(α+)﹣cos(α+)=﹣,cosα=﹣=﹣,∴cos2α=2cos2α﹣1=﹣,sin2α=2sinαcosα=,则cos(2α+)=cos2α﹣sin2α=﹣.故答案为:﹣10.(2018春•小店区校级期中)已知函数f(x)=cos2x+sinxcosx,,,则f (x)的单调递增区间为,(或,).【解答】解:f(x)=cos2x+sinxcosx=+sin2x=sin(2x+)+,∵,,可得:2x+∈(,),∴当2x+∈(,]或∈(,)时,即x∈,或,时,f(x)单调递增.∴f(x)的单调递增区间为,(或,).故答案为:,(或,).11.(2018春•福田区校级期中)已知α为第二象限角,sinα+cosα=,则cos2α=﹣.【解答】解:∵sinα+cosα=,两边平方得:1+sin2α=,∴sin2α=﹣,①∴(sinα﹣cosα)2=1﹣sin2α=,∵α为第二象限角,∴sinα>0,cosα<0,∴sinα﹣cosα=,②∴cos2α=﹣(sinα﹣cosα)(sinα+cosα)=﹣×=﹣.故答案为:﹣.12.(2018春•海州区校级月考)求cos cos cos cos cos=.【解答】解:cos cos cos cos cos=﹣cos cos cos cos cos=====,故答案为:.13.(2016春•云南校级月考)已知sinα=,且α为锐角,则cos=.【解答】解:∵sinα=,且α为锐角,∴<<,∴1>>,∴=,=1,解得cos=.故答案为:.14.(2016春•陕县校级月考)已知cosα=﹣,α∈(π,),则sin=.【解答】解:∵α∈(π,),∴∈(,),∴sin>0.∵cosα=1﹣2sin2=﹣,∴sin=.故答案是:.15.(2016春•浦东新区校级期中)已知,α在第二象限,则=3.【解答】解:∵已知,α在第二象限,∴cosα=﹣=﹣,∴===3,故答案为:3.16.(2014•新余二模)若tanα+=,α∈(,),则sin(2α+)的值为.【解答】解:∵tanα+=,∴=,∴,∴sin2α=,∵α∈(,),∴cos2α=﹣,∴sin(2α+)=sin2αcos+cos2αsin=.故答案为:.三.解答题(共8小题)17.(2018春•沙市区校级期中)已知tanα,tanβ是方程x2+p(x+1)+1=0的两根,α+β∈(0,π)(1)求α+β;(2)若,,,求sinθ.【解答】解:(1)由题可得,tanα+tanβ=﹣p,tanα•tanβ=p+1,∴.因为α+β∈(0,π),所以.(2)由题意可得,,,,,,得,∴sinθ=sin[()+]=sin()cos+cos(θ﹣)sin=•+•=.18.(2018•临川区校级模拟)已知函数f(x)=cos2(x+),g(x)=1+sin2x.(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(2x0)的值;(2)求函数h(x)=f(x)+g(x),x∈[0,]的值域.【解答】解:(1)f(x)=cos2(x+)=,∵x=x0是函数y=f(x)图象的一条对称轴,∴2x0+=kπ(k∈Z),∴2x0=kπ﹣(k∈Z),∴g(2x0)=1+sin4x0=1+sin(﹣)=.(2)∵h(x)=f(x)+g(x)=+1+sin2x=+(cos2x+sin2x)=+sin(2x+),∴x∈[0,]⇒2x+∈[,],∴sin(2x+)∈[,],∴h(x)=+sin(2x+)∈[,2].19.(2017秋•湛江月考)已知函数f(x)=2sinxcosx+cos2x.(Ⅰ)求的值;(Ⅱ)设,,,求cos2α的值.【解答】解:(Ⅰ)∵f(x)=sin2x+cos2x,∴f()=sin+cos=1+0=1.(Ⅱ)∵f()=sinα+cosα=,∴1+sin2α=,sin2α=﹣,∴cos2α=±.∵α∈(0,π),sin2α=﹣,∴2α∈(π,π),∴cos2α<0,故cos2α=﹣.20.(2017春•如东县校级期中)由倍角公式cos2x=2cos2x﹣1,可知cos2x可以表示为仅含cosx的二次多项式.(1)类比cos2x公式的推导方法,试用仅含有cosx的多项式表示cos3x;(2)已知3×18°=90°﹣2×18°,试结合第(1)问的结论,求出sin18°的值.【解答】解:(1)cos2x═cos(2x+x)=cos2xcosx﹣sin2xsinx=(2cos2x﹣1)cosx﹣2sin2xcosx=2cos3x﹣cosx﹣2(1﹣cos2x)cosx=4cos3x﹣3cosx,(2)因为cos(3×18°)=cos(90°﹣2×18°),所以4cos318°﹣3cos18°=2sin18°cos18°,所以4cos218°﹣3=2sin18°,所以4sin218°+2sin18°﹣1=0,解得sin18°=(舍去).21.(2015•安徽模拟)已知向量=(sinx,sinx),=(cosx,﹣sinx),且f(x)=2•+2.(Ⅰ)求函数f(x)的最大值,并求出此时的x的取值;(Ⅱ)函数f(x)图象与y轴的交点、y轴右侧第一个最低点、与x轴的第二个交点分别记为P,Q,R,求•的值.【解答】解:(Ⅰ)f(x)=2•+2=2sinxcosx,﹣2sinx•sinx+2=sin2x+2•=2sin(2x+)+1,故当2x+=2kπ+,k∈z时,即x=kπ+(k∈z)时,f(x)取得最大值为3.(Ⅱ)由f(0)=2,知P(0,2).由2x+=2kπ+,得x=kπ+(k∈z),此时f(x)=﹣1,则Q(,﹣1).而由2x+=2kπ﹣,得x=kπ﹣(k∈z),故R(,0),从而=(﹣,3),=(,1),因此=﹣+3×1=3﹣.22.(2014•湖北校级二模)已知函数f(x)=2sinx•cos2+cosx•sinθ﹣sinx(0<θ<π)在x=π处取最小值.(1)求θ的值;(2)在△ABC中,a,b,c分别为内角A,B,C的对边,已知a=1,b=,f(A)=,求角C.【解答】解:(1)∵当x=π时,f(x)取得最小值∴sin(π+θ)=﹣1即sinθ=1又∵0<θ<π,∴(2)由(1)知f(x)=cosx∵,且A为△ABC的内角∴由正弦定理得知或当时,,当时,综上所述,或23.(2010春•闸北区期末)已知,,,请用m分别表示tanθ、tan2θ、..【解答】解:由题意,…(3分)…(3分)…(3分)用万能公式求对同样给分.24.(2006•江西)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知,(1)求的值;(2)若a=2,,求b的值.【解答】解:(1)因为锐角△ABC中,A+B+C=π,,所以cosA=,则=(2)因为,又,则bc=3.将a=2,cosA=,c=代入余弦定理:a2=b2+c2﹣2bccosA中得b4﹣6b2+9=0解得b=。
高中数学3.2倍角公式和半角公式同步训练新人教B版必修4(2021学年)

高中数学3.2倍角公式和半角公式同步训练新人教B版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学 3.2倍角公式和半角公式同步训练新人教B版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学 3.2 倍角公式和半角公式同步训练新人教B版必修4的全部内容。
3。
2 倍角公式和半角公式知识点一:倍角公式1.错误!·错误!等于A.tanα B.tan2α C.1 D.错误!2.log2(sin15°cos15°)的值为A.-1 B .错误!C.2 D.-23.(2010全国高考Ⅱ,文3)已知sinα=\f(2,3),则cos(π-2α)等于A.-错误! B.-错误!C。
错误!D。
错误!4.若错误!=-错误!,则cosα+sinα=__________.5.错误!=__________。
6.(2010全国高考Ⅰ,文14)已知α为第二象限的角,sinα=错误!,则tan2α=__________。
7.已知函数f(x)=2sin(π-x)cosx。
(1)求f(x)的最小正周期;(2)求f(x)在区间[-π6,错误!]上的最大值和最小值.知识点二:半角公式8.已知cosθ=-15,错误!<θ<3π,那么sin错误!等于A.错误!B.-错误!C。
错误!D.-错误!9.已知θ为第二象限角,sin(π-θ)=错误!,则cos错误!的值为A。
\f(3,35) B。
45C.±错误! D.±错误!10.已知sinθ=错误!,错误!〈θ〈3π,那么tan错误!+cos错误!的值为__________.11.(2010全国高考Ⅱ,理13)已知α是第二象限的角,tan(π+2α)=-43,则tanα=________.12.已知sinα=\f(12,13),sin(α+β)=错误!,α,β均为锐角,求cos错误!的值.能力点一:利用倍角、半角公式求值、化简13.若3sinα+cosα=0,则\f(1,cos2α+sin2α)的值为A。
考研数学备考:两角和差公式

考研数学备考:两角和差公式考研复习的路上总会遇上许多复习问题,今天小编就帮助各位考研党整理一下比较常见的复习问题,下面由小编为你精心准备了“考研数学备考:两角和差公式”,持续关注本站将可以持续获取更多的考试资讯!考研数学备考:两角和差公式1、两角和与差的三角函数公式:sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)2、二倍角公式:二倍角的正弦、余弦和正切公式(升幂缩角公式)sin2α=2sinαcosαcos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan2α=2tanα/[1-tan^2(α)]3、半角公式:半角的正弦、余弦和正切公式(降幂扩角公式)sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)另也有tan(α/2)=(1-cosα)/sinα=sinα/(1+cosα)4、万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]万能公式推导:附推导:sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......* (因为cos^2(α)+sin^2(α)=1)再把*分式上下同除cos^2(α),可得sin2α=2tanα/(1+tan^2(α))然后用α/2代替α即可。
同理可推导余弦的万能公式。
上海市高三数学专题教案:半角公式与万能公式(2)新人教版

上海市2010届高三数学专题教案:半角公式与万能公式(2)[知识梳理] (一) 主要知识: 1.半角公式:cos 2α=sin2α=tan 2α=2.万能置换公式:22tan2tan 1tan 2ααα=- 22tan2sin 1tan 2ααα=+221tan 2cos 1tan 2ααα-=+ [例题举隅]例1.1.已知)0,2(πα-∈,54cos =α,求2αtg 。
2.已知)0,2(πα-∈,532cos =α,求αtg 。
3..已知πθπ23<<,54cos -=θ,则=2cos θ_________________。
4.在△ABC 中,已知53cos -=A ,则=2sin A______________。
例2:1.已知)0,2(πα-∈,54cos =α,则=α2tg _________________。
2.若121=+-θθtg tg ,则θθ2sin 12cos +的值为3. 已知54cos =α,若α是第四象限角, (1)问α2是第几象限角? (2)求αtg 的值。
例3:1.已知α为锐角,且21=αtg ,求ααααα2cos 2sin sin cos 2sin -的值2.已知21)4(=+απtg .(1)求αtg 的值;(2)求ααα2cos 1cos 2sin 2+-的值.3.已知21)4(-=-απtg ,则α2cos 的值是( )(A) 54- (B) 257 (C) 257- (D) 54 [巩固练习]1. 已知α为锐角,且21tan =α,求ααααα2cos 2sin sin cos 2sin -的值2.已知34παπ<<,10tan cot 3αα+=- (Ⅰ)求tan α的值;(Ⅱ)求225sin 8sincos11cos 822222ααααπα++-⎛⎫- ⎪⎝⎭的值3.已知α为第二象限的角,3sin 5α=,β为第一象限的角,5cos 13β=. 求tan(2)αβ-的值.4.已知1cos 7α=,13cos()14αβ-=,02πβα<<<,(Ⅰ)求α2tan 的值.(Ⅱ)求β. 5.已知1sin cos 5θθ+=,且324θππ≤≤,则cos2θ的值是 6.已知2sin 23A =,()0,A π∈,则sin cos A A += 7.已知tan 32α=,则cos α=.A 54 .B 45-.C 154.D 35- 8.已知4cos 5θ=,(),2θππ∈,则sin2θ=.A 10.B 10-.C 10±.D 5±9. 1sin 63πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭。
第1部分 第三章 § 3 第二课时 半角公式及其应用
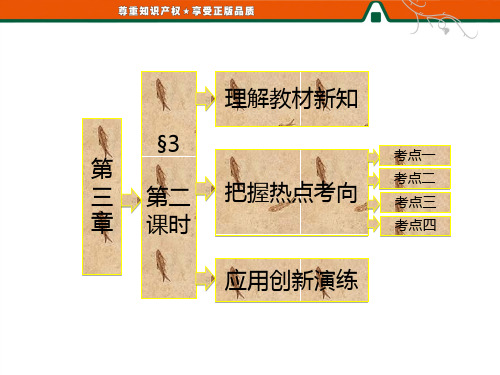
3.化简: 12-12 12+12cos 2α(α∈(32π,2π)).
解:∵α∈(
3π 2
,2π),∴cos
α>0,则由半角公式得
12+12cos 2α=cos α,∴原式= 12-12cos α.又α2∈
(34π,π),∴sin α2>0,从而 即原式=sinα2.
12-12cos α=sin α2,
返回
解:设∠ABD=α,则∠CAE=α,AB=sihn2α, AC=coshα1 , ∴S△ABC=12AB·AC=shin1h22α.∵0<α<π2, ∴当2α=π2,即α=π4时,S△ABC的最小值为h1h2.
返回
三角恒等变换常用的方法: (1)常值代换: 用某些三角函数值或三角函数式来代替某些常 数,使得代换后能运用相关公式进行变形.这种代换 称之为常值代换.如1=sin2α+cos2α,1=tanπ4等.
11- +ccoossππ66=
1- 1+
3 23=2- 2
3.
返回
π
1
法二:tan1π2=1+sinco6sπ6=1+2
3=2- 2
3.
法三:∵1π2=π3-π4,
∴tan1π2=tan(π3-π4).
=1t+antπ3a-nπ3ttaannπ4π4=1+3-3×1 1=2- 3.
答案:2- 3
返回
= -
21+cossα2in+αsinα2+
1-sin α 2sinα2-cosα2
=-c2oscα2o+sα2s+inα2sin2α2+
sinα2-cosα22 2sinα2-cosα2
=-
α 2cos2.
返回
[一点通] 利用半角公式进行化简时,应正确选用 升、降幂公式:当待化简式中含有根式时,应选用升幂 公式去根号;当待化简式中含有高次式时,应选用降幂 公式减少运算量,开方运算时要注意角的范围.
半角公式 积化和差 和差化积

半角公式 积化和差 和差化积【本讲的主要内容】半角公式,积化和差,和差化积二、学习目标1、了解半角公式及积化和差、和差化积公式的推导过程,能应用公式进行三角函数求值、化简、证明,能初步运用公式进行和、积互化.2、通过公式的推导,了解半角公式和倍角公式之间的内在联系,从而培养逻辑推理能力和辩证唯物主义观点。
3、培养用联系的观点看问题。
三、知识要点1、半角的正弦,余弦和正切cos 2α=sin 2α= tan 2α=说明:(1)公式用cos α表示出cos 2αsin 2αtan 2α的三角函数,公式前的符号取决于2α所在的象限(2)用根式求值时一般处理办法如下①如果没有给出决定符号的条件,则在根号前保留正负两个符号②如果给出α的具体范围时,则先求出2α所在范围,然后再根据2α所在范围选用符号(3)公式可以用来化简,证明,求值 2、积化和差公式:cos cos αβ=12[cos()αβ++cos()αβ-];sin sin αβ=12-[cos()αβ+-cos()αβ-];sin cos αβ=12[sin()αβ++sin αβ(-)];cos sin αβ=12[sin()αβ+-sin αβ(-)].3、和差化积公式:sin sin x y +=2sincos ;22x y x y+-sin sin x y -=2cos sin22x y x y +-;cos cos x y +=2cos cos22x y x y +-;cos cos x y -=2sin sin22x y x y +--说明: (1)运用这些公式进行三角函数和差与积的互化,并能够运用这些公式解决一些求值、化简和证明问题;(2)把一个式子化为积的形式是一类重要题型,尤其要注意其最后结果的形式是否符合要求;(3)在公式的推导过程中我们用到了换元法,要注意该方法在解题中的应用.4、技巧与方法:①要寻求角与角关系的特殊性,化非特殊角为特殊角,熟练准确地应用公式②注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用③对于条件求值问题,要认真寻找条件和结论的关系,寻找解题的突破口,很难入手的问题,可利用分析法④求最值问题,常用配方法、换元法来解决【典型例题】例1、不查表求sin 220°+cos 280°+3sin20°cos80°的值命题意图:本题主要考查两角和、二倍角公式及降幂求值的方法,对计算能力的要求较高知识依托:熟知三角公式并能灵活应用 错解分析:公式不熟,计算易出错技巧与方法:解法一利用三角公式进行等价变形;解法二转化为函数问题,使解法更简单更精妙,需认真体会解法一:sin 220°+cos 280°+3sin20°cos80°=21(1-cos40°)+21(1+cos160°)+ 3sin20°cos80°=1-21cos40°+21cos160°+3sin20°cos (60°+20°)=1-21cos40°+21(cos120°cos40°-sin120°sin40°)+3sin20°(cos60°cos20°-sin60°sin20°)=1-21cos40°-41cos40°-43sin40°+43sin40°-23sin 220°=1-43cos40°-43(1-cos40°)= 41解法二:设x =sin 220°+cos 280°+3sin20°cos80° y =cos 220°+sin 280°-3cos20°sin80°,则x +y =1+1-3sin60°=21,x -y =-cos40°+cos160°+3sin100° =-2sin100°sin60°+3sin100°=0∴x =y =41,即x =sin 220°+cos 280°+3sin20°cos80°=41例2、已知函数2πππ()12sin 2sin cos 888f x x x x ⎛⎫⎛⎫⎛⎫=-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.求: (I )函数()f x 的最小正周期;(II )函数()f x 的单调递增区间.解:ππ()cos(2)sin(2)44f x x x =+++ πππ))2442x x x=++=+=.(I )函数()f x 的最小正周期是2ππ2T ==;(II )当2ππ22πk x k -≤≤,即πππ2k x k -≤≤(k ∈Z )时,函数()2f x x =是增函数,故函数()f x 的单调递增区间是π[ππ]2k k -,(k ∈Z ).例3、已知△ABC 的三个内角A 、B 、C 满足A +C =2BB C A cos 2cos 1cos 1-=+,求cos 2C A -的值 解法一:由题设条件知B =60°,A +C =120°设α=2CA -,则A -C =2α,可得A =60°+α,C =60°-α,1111cos cos cos(60)cos(60)A C αα+=+︒+︒-所以=222cos cos ,133cos sin cos 444ααααα==--依题设条件有,cos 243cos cos 2B-=-αα.2243cos cos ,21cos 2-=-αα∴=B整理得42cos 2α+2cos α-32=0(2cos α-2)(22cos α+3)=0, ∵22cos α+3≠0, ∴2cos α-2=0从而得cos 222=-C A 解法二:由题设条件知B =60°,A +C =120°22cos 1cos 1,2260cos 2-=+∴-=︒-C A①, 把①式化为cos A +cos C =-22cos A cos C②,利用和差化积及积化和差公式,②式可化为)]cos()[cos(22cos 2cos 2C A C A CA C A -++-=-+ ③,将cos 2CA +=cos60°=21,cos (A +C )=-21代入③式得 )cos(2222cosC A C A --=-④将cos (A -C )=2cos 2(2CA -)-1代入 ④42cos 2(2C A -)+2cos 2CA --32=0,(*),(2cos3)0,22A C A C---+= 22cos 30,2cos 0,22A C A C--+=∴= :cos 2A C -=从而得例4、已知函数π124()πsin 2x f x x ⎛⎫- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭.(Ⅰ)求()f x 的定义域;(Ⅱ)若角α在第一象限且3cos 5α=,求()f α.解:(Ⅰ) 由πsin 02x ⎛⎫+≠ ⎪⎝⎭得ππ2x k ≠-+,即ππ2x k ≠-()k ∈Z . 故()f x 的定义域为π|π2x x k k ⎧⎫∈≠-∈⎨⎬⎩⎭R Z ,.(Ⅱ)由已知条件得4sin 5α===.从而π124()πsin 2f ααα⎛⎫+- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭ππ1cos 2cos sin 2sin 44cos ααα⎫+⎪⎝⎭=21cos 2sin 22cos 2sin cos cos cos ααααααα+++==142(cos sin )5αα=+=.本讲涉及的主要数学思想方法1、重视新旧知识的联系,新知识在旧知识基础上形成并得到引申和发展,形成新知识的同时提升了能力。
11、微专题:半角公式及其应用-讲义-2021-2022学年高中数学沪教版(2020)必修第二册

【学生版】微专题:半角公式及其应用半角公式半角公式 正弦1cos sin22αα-=±余弦1cos cos 22αα+=±正切1cos tan21cos a αα-=±+;sin tan 21cos a αα=+;1cos tan 2sin a αα-=; 【注意】(1)重视得到结果的过程,从思考α与2α之间的关系入手,理解角的倍、半的相对性,思考cos α与2sin 2α之间的关系;(2)使用公式时要深刻体会α与2α的含义,如2α与α,αβ+与2αβ+等都可看成倍半关系. (3)半角公式根号前符号的确定①当给出的角是某一象限的角时,可根据下表确定半角的函数值的符号α 2α sin2αcos2αtan2α第一象限 第一、三象限 ,+- ,+- + 第二象限 第一、三象限 ,+- ,+- +第三象限 第二、四象限 ,+- ,-+ -第四象限第二、四象限,+-,-+-②当给出角α的范围(即某一区间)时,可先求2α的范围,再根据2α的范围来确定各函数值的符号; ③若没有给出确定符号的条件,则在根号前保留正、负两个符号; 【典例】题型1、利用半角公式求值 例1、已知cos α=33,α为第四象限的角,求:tan α2的值; 【提示】; 【答案】;【解析】解法1、解法2、解法3、 【说明】题型2:利用半角公式化简 例2、设α∈(3π2,2π),化简:12+1212+12cos 2α. 【提示】; 【答案】 【解析】 【说明】题型3、利用半角公式证明 例3、求证:cos 2α1tan α2-tan α2=14sin 2α;题型4、利用半角求值,注意角的范围 例4、已知角α为钝角,β为锐角,且4sin 5α=,12sin 13β=,求cos 2αβ-与tan 2αβ-的值 【归纳】 1、半角公式:1cos sin22αα-=;1cos cos 22αα+=1cos tan 21cos a αα-=+; 2、半角公式的推导3、对半角公式的理解 ①;②;③;④;⑤; 【即时练习】 1、设α∈(π,2π),则1-cos (π+α)2等于( )A .sin α2B .cos α2C .-sin α2D .-cos α22、化简4cos 2α÷(1tan α2-tan α2)的结果为( )A .-12cos αsin α B .sin 2α C .-sin 2α D .2sin 2α3、已知sin 2θ=1213,θ∈(0,π4),则tan θ等于4、已知tan α2=3,则cos α为5、化简:sin 2x 2cos x (1+tan x tan x2)= .6、在△ABC 中,sin ⎝⎛⎭⎫A +π2=32,则tan A2=7、在△ABC 中,若cos A =13,则sin 2B +C 2+cos 2A 的值为________.8、已知sin α2-cos α2=-55,若450°<α<540°,则tan α2=________.9、已知sin α=-45,180°<α<270°,求sin α2,cos α2,tan α2的值.10、求证:sin 2α4-1=-cos α2+12.【教师版】微专题:半角公式及其应用半角公式半角公式 正弦1cos sin22αα-=±余弦1cos cos 22αα+=±正切1cos tan21cos a αα-=±+;sin tan 21cos a αα=+;1cos tan 2sin a αα-=; 【注意】(1)重视得到结果的过程,从思考α与2α之间的关系入手,理解角的倍、半的相对性,思考cos α与2sin 2α之间的关系;(2)使用公式时要深刻体会α与2α的含义,如2α与α,αβ+与2αβ+等都可看成倍半关系. (3)半角公式根号前符号的确定①当给出的角是某一象限的角时,可根据下表确定半角的函数值的符号α 2α sin2αcos2αtan2α第一象限 第一、三象限 ,+- ,+- + 第二象限 第一、三象限 ,+- ,+- +第三象限 第二、四象限 ,+- ,-+ -第四象限第二、四象限,+-,-+-②当给出角α的范围(即某一区间)时,可先求2α的范围,再根据2α的范围来确定各函数值的符号; ③若没有给出确定符号的条件,则在根号前保留正、负两个符号; 【典例】题型1、利用半角公式求值 例1、已知cos α=33,α为第四象限的角,求:tan α2的值; 【提示】注意:角“α2”、“α”呈二倍关系;注意:二倍角、半角公式的特征;【答案】2-62; 【解析】解法1、(用tan α2=±1-cos α1+cos α来处理).因为,α为第四象限的角,所以,α2是第二或第四象限的角,所以,tan α2<0.则,根据公式tan α2=-1-cos α1+cos α=-1-331+33=- 2-3=-128-43=-12(6-2)2=2-62. 解法2、(用tan α2=1-cos αsin α来处理)因为,α为第四象限的角,所以,sin α<0,所以,sin α=- 1-cos 2α=-1-13=-63; 则,tan α2=1-cos αsin α=1-33-63=2-62.解法3、(用tan α2=sin α1+cos α来处理)因为,α为第四象限的角,所以,sin α<0,所以,sin α=- 1-cos 2α=-1-13=-63; 则tan α2=sin α1+cos α=-631+33=-63+3=2-62;【说明】本题根据“α2”与“α”成二倍关系;结合公式特点,用了3种解法;在求半角的正切tan α2时,用tan α2=±1-cos α1+cos α来处理,要由α所在的象限确定α2所在的象限,再用三角函数值的符号取舍根号前的双重符号;而用tan α2=1-cos αsin α或tan α2=sin α1+cos α来处理,可以避免这些问题.尤其是tan α2=1-cos αsin α,分母是单项式,容易计算.因此常用tan α2=1-cos αsin α求半角的正切值;请同学们在比较中寻找适合自己的解法; 题型2:利用半角公式化简 例2、设α∈(3π2,2π),化简:12+1212+12cos 2α. 【提示】注意:根据题设,在保证有意义前提下,出现“平方再开方”形式;【答案】 cos α2;【解析】因为,α∈⎝⎛⎭⎫3π2,2π,所以,cos α>0,cos α2<0. 故原式=12+12cos 2α=12+12cos α=cos 2α2=|cos α2|=-cos α2;【说明】利用半角公式进行化简时,应正确选用升、降幂公式:当待化简式中含有根式时,应选用升幂公式(cos 2α=1-2sin 2α=2cos 2α-1)去根号; 当待化简式中含有高次式时,应选用降幂公式(sin 2α=1-cos 2α2,cos 2α=1+cos 2α2)降低次数以减少运算量, 注意隐含条件中角的范围; 题型3、利用半角公式证明 例3、求证:cos 2α1tan α2-tan α2=14sin 2α;【提示】注意:二倍角公式、半角公式在“升幂、降幂”中的作用;【证明】左边=cos 2αcos α2sin α2-sin α2cos α2=cos 2αsin α2cos α2cos 2α2-sin 2α2=12cos 2αsin αcos α=12sin αcos α=14sin 2α= 右边;所以,等式成立;【说明】证明三角恒等式的实质是消除等式两边的差异,有目的地化繁为简、左右归一或变更论证;常用定义法、化弦法、化切法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法;证明条件三角恒等式,首先应观察条件与结论之间的差异(三角函数名及结构),从解决某一差异入手,采用条件转化法或条件代入法;题型4、利用半角求值,注意角的范围 例4、已知角α为钝角,β为锐角,且4sin 5α=,12sin 13β=,求cos 2αβ-与tan 2αβ-的值 【提示】注意:已知角与所求角之间的关系;【解析】因为角α为钝角,β为锐角,且4sin 5α=,12sin 13β=,所以3cos 5α=-,5cos 13β=. 所以()cos cos cos sin sin αβαβαβ-=+35412513513⎛⎫=-⨯+⨯ ⎪⎝⎭3365=.又因为2παπ<<,且02πβ<<,所以0αβπ<-<,即022αβπ-<<.所以()1cos cos22αβαβ+--=33176565265+==; 方法1、由022αβπ-<<,得2sin1cos 22αβαβ--=-46565=,所以tan 2αβ-sin2cos2αβαβ-=-47=;方法2、由330,cos()65αβπαβ<-<-=,得256sin()1cos ()65αβαβ-=--=. 所以56sin()465tan .3321cos()7165αβαβαβ--===+-+【说明】对于含有半角的求值问题,一定要判断角的取值范围,以免产生增根; 【归纳】 1、半角公式:1cos sin22αα-=±;1cos cos 22αα+=±;1cos tan 21cos a αα-=±+; 2、半角公式的推导(1)2cos212sin αα=-2αααα−−−−→代替2代替21cos cos 12sin sin222αααα-=-→=±; (2)222cos 22cos 1αααααα=-−−−−→代替代替21cos cos 2cos 1cos222αααα+=-→=±; (3)sin1cos 2tan21cos cos 2ααααα-==±+.3、对半角公式的理解①半角公式中的正弦、余弦公式实际上是由二倍角的余弦公式变形得到的;②半角公式给出了求α2的正弦、余弦、正切的另一种方式,即只需知道cos α的值及相应的α的条件,sin α2,cos α2,tan α2便可求出; ③对“半角”的理解应是广义的,不能仅限于α2是α的一半,其他如α是2α的一半,α4是α2的一半,3α2是3α的一半等,这里面蕴含着换元思想,半角是相对而言的,描述的是两个角之间的数量关系;④由tan α2=sin α1+cos α=1-cos αsin α的推导过程可知,tan α2的符号与sin α的符号相同,且由于该式中不含被开方数,故不涉及符号问题,所以求解题目时,使用相对方便,但要注意该公式成立的条件,由1+cos α≠0⇒α≠(2k +1)π,k ∈Z ,由sin α≠0⇒α≠k π,k ∈Z.⑤解答涉及函数的升降幂及角的二倍关系的题目时,常用sin 2α2=1-cos α2,cos 2α2=1+cos α2;【即时练习】 1、设α∈(π,2π),则1-cos (π+α)2等于( )A .sin α2B .cos α2C .-sin α2D .-cos α2【答案】D ;【解析】因为,α∈(π,2π),所以,π2<α2<π,所以,cos α2<0,所以,原式=1+cos α2=|cos α2|=-cos α2. 2、化简4cos 2α÷(1tan α2-tan α2)的结果为( )A .-12cos αsin α B .sin 2α C .-sin 2α D .2sin 2α【答案】B ;【解析】原式=4cos 2αtanα21-tan 2α2=2cos 2αtan α=2cos 2αsin αcos α=2sin αcos α=sin 2α.3、已知sin 2θ=1213,θ∈(0,π4),则tan θ等于【答案】23;【解析】因为,0<θ<π4,0<2θ<π2,所以,cos 2θ=1-sin 22θ=1-(1213)2=513.则tan θ=1-cos 2θsin 2θ=1-5131213=23.4、已知tan α2=3,则cos α为【答案】-45;【解析】方法1、cos α=cos 2α2-sin 2α2=cos 2α2-sin 2α2cos 2α2+sin 2α2=1-tan 2α21+tan 2α2=1-91+9=-45.方法2、因为,tan α2=3,所以,1-cos α1+cos α=9,即1-cos α=9+9cos α,解得cos α=-45.5、化简:sin 2x 2cos x (1+tan x tan x2)= .【答案】tan x ;【解析】原式=2sin x cos x 2cos x (1+sin x cos x ·1-cos x sin x )=sin x (1+1-cos x cos x )=sin x 1cos x =tan x ;6、在△ABC 中,sin ⎝⎛⎭⎫A +π2=32,则tan A2= 【答案】2-3;【解析】因为在△ABC 中,sin ⎝⎛⎭⎫A +π2=32,所以cos A =32,且A 为锐角,所以tan A 2=1-cos A1+cos A=2-3;7、在△ABC 中,若cos A =13,则sin 2B +C 2+cos 2A 的值为________.【答案】-19【解析】因为,cos A =13,所以,原式=cos 2A 2+cos 2A =1+cos A 2+2cos 2A -1=1+132+2×(13)2-1=-19.8、已知sin α2-cos α2=-55,若450°<α<540°,则tan α2=________.【答案】2;【解析】由条件知1-2sin α2cos α2=15,所以,2sin α2cos α2=45,即sin α=45又450°<α<540°,c os α<0,所以,cos α=-35;则tan α2=1-cos αsin α=1+3545=2.9、已知sin α=-45,180°<α<270°,求sin α2,cos α2,tan α2的值.【解析】因为,180°<α<270°,所以,90°<α2<135°;又因为,sin α=-45,所以,cos α=-35;所以,sin α2=1-cos α2= 1-(-35)2=255. cos α2=- 1+cos α2= 1+(-35)2=-55. tan α2=sinα2cosα2=-2;10、求证:sin 2α4-1=-cos α2+12.【证明】由sin α2=±1-cos α2,知sin α4=± 1-cos α22,所以,sin 2α4=1-cosα22,则sin 2α4-1=1-cos α22-1=-cos α2+12,原等式得证;。
